Distributed secondary control of microgrids with unknown disturbances and non-linear dynamics

In this paper, the voltage and frequency regulation of microgrid with unknown disturbances and non-linear dynamics was studied. The disturbance observer was designed and the sliding mode control (SMC) method was used to realize the secondary regulation of voltage and frequency. First, a distributed secondary control protocol was designed to reduce the communication burden between generators and to solve voltage and frequency deviations. Second, a consensus protocol for secondary control of voltage and frequency was designed, based on the idea of multi-agent consensus, to indirectly ensure that the voltage and frequency to be adjusted reach the reference values when the consensus is realized. In addition, considering unknown disturbances in the microgrid, a sliding mode control strategy, based on a disturbance observer, was designed to overcome the influence of disturbances and to reduce chatter. This SMC scheme ensured finite time accessibility of the sliding mode surface. This design provides sufficient conditions for voltage and frequency regulation. The effectiveness of this design scheme was verified through simulation.

1 Introduction

In the context of the current industrial development, the scale of equipment has become more complex and information transmission between equipment is more frequent. The traditional centralized control mode lacks flexibility and cannot handle situations in which the controlled equipment or information source are too far from the host, which leads to a distributed control problem (Ding et al., 2019; Liu et al., 2022). In the context of the power grid, the control of distributed generators (DGs) has also received increasing attention, especially in microgrid systems comprising distributed energy, load, and energy storage systems, with many interesting results achieved (Espina et al., 2020; Fan et al., 2021; Lu and Lai, 2021; Fan et al., 2022; Mohiuddin and Qi, 2022). In recent years, with the rapid development of microgrid integration technology, DGs are increasingly used in grid-connected or off-grid microgrid systems (Sarangi et al., 2020; Akbari et al., 2022; Wong et al., 2022). In this scenario, it is particularly important to control microgrid frequency and voltage by adjusting DG output to ensure microgrid stability.

Raeispour et al. (2021) described that, at the primary level of the microgrid, a primary controller is designed for current, voltage, and droop control loops and proposed a robust control structure. However, this method produced voltage and frequency deviations, which affect microgrid stability. To solve this problem, the idea of secondary control was introduced. Because of the superiority of distributed secondary control in saving communication resources between agents, this control has been studied in microgrids (Shan et al., 2021; Sun et al., 2022a; Deng et al., 2022). Bidram et al. (2013) designed a sparse communication network based on the concept of directed graphs to provide secondary control of the microgrid. Compared with centralized control, this strategy effectively improved the robustness of communication link failures. Zhang et al. (2021) described a finite time controller based on the secondary control strategy, which effectively improved the transient response of the control loop by adding an integrand to the consensus strategy. Choi et al., (2022) reported that, combined with an event-triggered strategy, communication resources are further saved by distributed secondary control and that information on neighbor generators is only obtained at the triggering instant. Fonseca et al (2022) proposed a distributed model predictive secondary control scheme to solve difficulties caused by unbalanced voltage sharing between generators.

In microgrids, due to the influence of the internal components of the grid and the internal and external environments of the system, it is often necessary to consider disturbances to the system (Lai et al., 2022). Such disturbances make secondary control of the microgrid more challenging. Sliding mode control (SMC), an effective method to address these disturbances, is widely used to improve system robustness and stability (Hu et al., 2022; Veysi et al., 2022; Alipour et al., 2023). Sun et al. (2022b) designed an SMC strategy for secondary control based on the reactive power dynamics model, which showed robust control against external disturbances such as communication failure. Alfaro et al. (2022) demonstrated that the combination of SMC and state observer ensured the elastic consensus of an AC microgrid in the presence of network attacks. Abianeh et al. (2022) designed a sliding mode cooperative controller using consensus logic, which demonstrated recovery of voltage and frequency without relying on DG parameters and correspondingly overcame the influence of system disturbances. Zehra et al. (2022) presented a novel model and non-linear barrier function-based first-order SMC of a hybrid hydrogen-electric energy storage system in a DC microgrid. By designing an obstacle Lyapunov equation, asymptotic stability of the expected tracking error is achieved.

In actual microgrids, the disturbances are usually unknown, whereas most of the disturbances considered in the aforementioned research are known. It is not ideal to address disturbances by designing to the upper bound of the disturbance, as the system often exhibits chatter under this control strategy. Researchers have designed disturbance observers to estimate the upper bound of unknown disturbances (Wang et al., 2021; Xu et al., 2021; Badar et al., 2022; Ding et al., 2022). Xu et al. (2020) designed a sliding mode surface based on the system error and applied a new estimation method to estimate unknown disturbances. Error convergence was indirectly guaranteed through the convergence of the compensation signal, resulting in voltage regulation of the DC microgrid. Ge et al. (2021) set factors such as parameter disturbance and external influence as the disturbance set and applied the Kalman filter to design disturbance observers of extended states, thus simplifying parameter selection. Jiang et al. (2021) applied an observer to estimate the state and spurious signals, considering the impact of spurious signal injection on the DC microgrid, which resulted in an elastic scheme of bus voltage output current and power sharing.

Although many results have been reported for the control of microgrid systems, few studies have simultaneously considered distributed secondary control and system chatter problems. In this context, the present article assessed the distributed secondary control of microgrid systems using the idea of multi-agent consensus. The main contributions are:

1) Based on the idea of multi-agent systems, this study designed consensus protocols for the voltage and frequency of DGs, respectively. By reaching a consensus, the voltage and frequency to be adjusted can reach the reference values. At the same time, the distributed control method does not require continuous communication between generators, instead requiring only information from their neighbors, which effectively reduces the communication burden.

2) Combined with SMC, a disturbance observer was designed to estimate unknown disturbances in the microgrid. Compared with previous results (Ge et al., 2021; Sun et al., 2022b), SMC law only depends on the bound of disturbance estimation error and not the bound of the disturbance. Therefore, this observer-based SMC scheme can effectively address the chatter phenomenon while solving the influence of disturbance on the system.

3) Unlike traditional SMC (Abianeh et al., 2022), the control strategy proposed in this study can ensure that the controlled trajectory has a finite time to reach the sliding mode surface, which improves the rapidity of the first stage of SMC. In addition, two sufficient conditions are obtained to ensure that the controlled voltage and frequency will converge to the reference values along the designed trajectory after reaching the sliding mode surface.

2 Model description and observer

2.1 Microgrid model

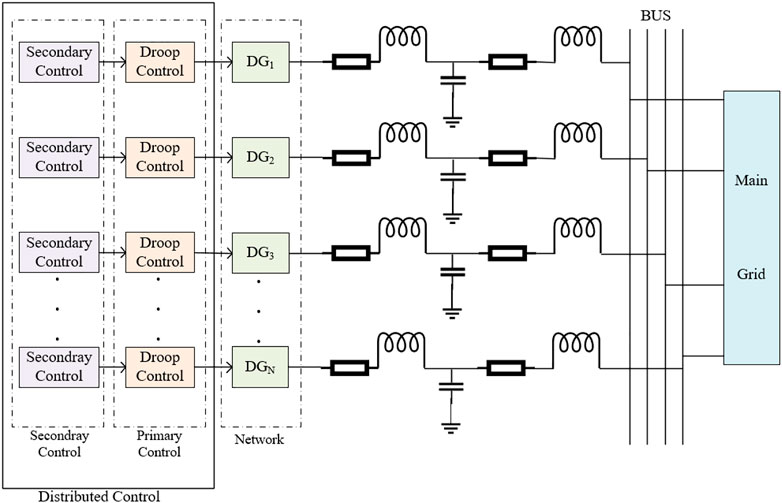
In microgrids, the voltage and frequency regulation of the system can usually be realized by improved droop control strategies. In the traditional primary control, the voltage and frequency of each distributed generator are transferred to the secondary control layer under the droop control strategy to achieve consensus control. The basic principle is to design a controller that solves errors and fluctuations caused by droop control. The general structure of DGs is shown in Figure 1.

Due to the influence of internal equipment or the external environment of microgrids, disturbances are widespread and often unknown. Hence, the microgrid model must consider unknown disturbance factors. Therefore, we provide the following frequency model of DGs:

$\left\{\begin{array}{c}{\dot{\omega }}_i\left(t\right)=u_{\omega i}\left(t\right)+f\left(w_i\left(t\right)\right)+d_i\left(t\right),\hfill \\ y_{\omega i}\left(t\right)={\omega }_i\left(t\right),\hfill \end{array}\right.(1)$

where ${\dot{\omega }}_i(t)$ represents the frequency of DGs, u_ωi(t) represents the frequency input signal of each generator, f (w_i(t)) denotes the non-linearity of power, d_i(t) is an unknown disturbance and satisfies $\left|{\dot{d}}_i(t)\right|\le \epsilon$, and y_ωi(t) indicates the output of each generator.

Similar to the frequency model (1), the voltage model of the generator can be described as

$\left\{\begin{array}{c}{\dot{v}}_i\left(t\right)=u_{vi}\left(t\right)+f\left(v_i\left(t\right)\right)+d_i\left(t\right),\hfill \\ y_{vi}\left(t\right)=v_i\left(t\right),\hfill \end{array}\right.(2)$

where v_i(t) represents the voltage of each distributed generator, f (v_i(t)) indicates the non-linearity caused by the power, and y_ωi(t) represents the voltage input signal of each generator.

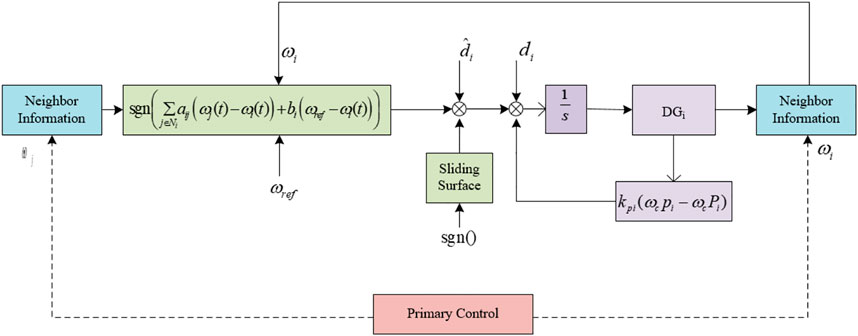
To clearly describe the control strategy used in this study, the frequency and voltage block diagrams of the secondary control are shown in Figure 2 and Figure 3, respectively.

Secondary control of the microgrid is essentially a tracking problem in the control system, even if the voltage and frequency reach the desired reference values. In this study, each generator in the microgrid is considered to be an agent. Using the idea of a multi-agent system (Fan et al., 2019; Wang et al., 2020; Ferreira et al., 2022), this tracking problem can be transformed into a leader-following problem, with a fixed value for the leader agent. Then, by applying graph theory, the communication relationships between generators can be represented as a communication topology network. Assuming that the microgrid is composed of N DGs, generator j can communicate with generator i as a neighbor agent, and these can communicate in both directions; that is, the information transmission is undirected.

Then, the undirected graph G is expressed as G=(υ, ɛ, A), where the vertex set υ=(υ₁, υ₂, υ₃, … , υ_N) is a non-empty finite set of DGs, N is the total number of nodes, and the edge set ɛ ⊆ υ*υ represents the communication links between DGs. $A=\left[a_{ij}\right]\in R^{N*N}$ is the weighted adjacent matrix. If a path exists between DG i and DG j, the communication topology graph Γ is called a connection graph, which means that if (υ_i, υ_j) ∈ ɛ, then a_ij = 1; otherwise, a_ij = 0. Assuming that there is no self-loop, then a_ii = 0.

Through the aforementioned conversion, the control objectives under the consensus protocol are as follows:

$\underset{t\to \infty }{\lim }\left|{\omega }_i\left(t\right)-{\omega }_{\mathrm{r}\mathrm{e}\mathrm{f}}\right|=0,\forall i=\mathrm{1,2,3},\dots ,N.(3)$

$\underset{t\to \infty }{\lim }\left|v_i\left(t\right)-v_{\mathrm{r}\mathrm{e}\mathrm{f}}\right|=0,\forall i=\mathrm{1,2,3},\dots ,N.(4)$

Here, ω_ref and v_ref represent the reference values of frequency and voltage, respectively.

2.2 Design of the disturbance observer

To overcome the influence of unknown disturbances on the system, we design a disturbance observer to estimate the upper bound of the disturbance. The design satisfies the following form:

${\widehat{d}}_i\left(t\right)=g_i\left(t\right)-m{v}_i\left(t\right),(5)$

${\dot{g}}_i\left(t\right)=m\left(g_i\left(t\right)-m{v}_i\left(t\right)\right)+m\left(f\left(v_i\left(t\right)\right)+u_{v_i}\right),(6)$

where ${\widehat{d}}_i(t)\in R$ is the disturbance estimation, g_i(t) is the observer state, and m < 0. ${\tilde{d}}_i(t)=d_i(t)-{\widehat{d}}_i(t)$ is the estimation error.

Combining (5) and (6),

$\begin{array}{ll}\hfill {\dot{\widehat{d}}}_i\left(t\right)& ={\dot{g}}_i\left(t\right)-m{\dot{v}}_i\left(t\right)\hfill \\ \hfill & =m\left(g_i\left(t\right)-m{v}_{\text{i}}\left(t\right)\right)+m\left(u_{v_i}\left(t\right)+f\left(v_i\left(t\right)\right)\right)\hfill \\ \hfill & -m\left(u_{v_i}+d_i\left(t\right)+f\left(v_i\left(t\right)\right)\right)\hfill \\ \hfill & =m\left(g_i\left(t\right)-m{v}_i\left(t\right)\right)-m{d}_i\left(t\right)\hfill \\ \hfill & =-m{\tilde{d}}_i\left(t\right).\hfill \end{array}(7)$

Then, the derivative of the estimation error is

$\begin{array}{ll}\hfill {\dot{\stackrel{̃}{d}}}_i\left(t\right)& ={\dot{d}}_i\left(t\right)-{\dot{\widehat{d}}}_i\left(t\right)\hfill \\ \hfill & ={\dot{d}}_i\left(t\right)+m{\tilde{d}}_i\left(t\right).\hfill \end{array}(8)$

To analyze the stability of the microgrid, the following assumptions must be met.

3 Main results

We design a distributed secondary controller based on the idea of consensus so that the voltage and frequency of each generator can reach the reference values ω_ref and v_ref. We also design an SMC strategy based on a disturbance observer to overcome the influence of unknown disturbances. Sufficient conditions for voltage and frequency regulation are obtained.

First, the voltage error control protocol for each generator is

$e_{v_i}\left(t\right)=\sum _{j\in N_i}{a}_{ij}\left(v_j\left(t\right)-v_i\left(t\right)\right)+b_i\left(v_{\mathit{ref}}-v_i\left(t\right)\right).(10)$

4 Simulation results

We validate the effectiveness of the control method we proposed by building the simulation models of three DGs in MATLAB. We choose the reference voltage value to be V_ref = 400V and the reference frequency value f_ref = 50Hz. As the communication topology is an undirected graph structure, and this study did not consider the influence of other factors on topology selection, we select the adjacency matrices A and B as follows:

$A=\left[\begin{array}{ccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill \end{array}\right],B=\left[\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right].(29)$

FIGURE 1

FIGURE 1. DG structure.

FIGURE 2

FIGURE 2. Frequency control block diagram.

FIGURE 3

FIGURE 3. Voltage control block diagram.

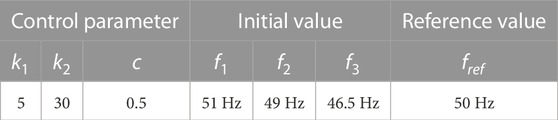
The initial frequency values of DG1, DG2, and DG3 are selected as f₁ = 51 Hz, f₂ = 49 Hz, and f₃ = 46.5 Hz, respectively. The unknown disturbance is d = cos 2t, and the non-linear function is $f\left({\omega }_i(t)\right)={\omega }_i*\sin (t)$. The other selected parameters are shown in Table 1.

TABLE 1

TABLE 1. Parameters for the selection of frequency.

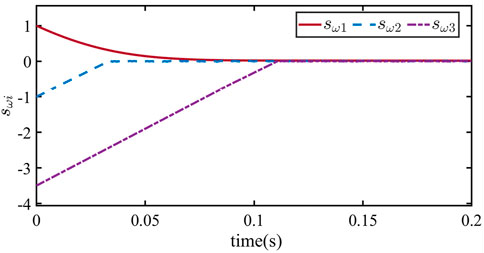
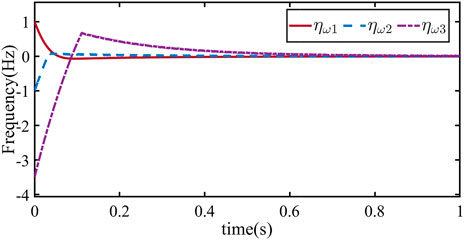
Figures 4 and 5 can be obtained through simulations. Figure 4 shows the trajectory curves of s_ωi, while Figure 5 depicts the trajectory curves of η_ωi. As shown in Figure 4, the state trajectory of the frequency errors system is driven to the sliding surface within 0.15 s. Moreover, as shown in Figure 5, the frequencies of DG1, DG2, and DG3 converge to f_ref = 50Hz within 0.8 s. Based on this, we conclude that under the proposed control method, the frequency of the microgrid system can be quickly adjusted to the reference frequency in a finite time, achieving secondary control of the microgrid (3).

FIGURE 4

FIGURE 4. Trajectory curves of s_ωi.

FIGURE 5

FIGURE 5. Trajectory curves of η_ωi.

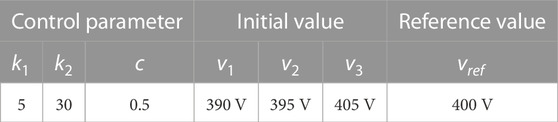
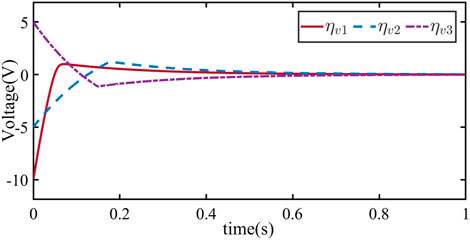
To verify that the proposed control method can achieve the control objective (4), we choose the reference voltage as v_ref = 400 V. The other selected parameters are shown in Table 2. The initial voltage values of DG1, DG2, and DG3 are v₁ = 390 V, v₂ = 395 V, and v₃ = 405 V, respectively, as shown in Figures 6 and 7. Figure 6 shows the trajectory curves of s_vi, while Figure 7 depicts the trajectory curves of η_vi. As shown in Figure 6, the state trajectory of the voltage errors system is driven to the sliding surface within 0.2 s. As shown in Figure 7, the voltages of DG1, DG2, and DG3 converge to v_ref = 400 V within 0.8 s. Based on this, the proposed control method can quickly adjust the frequency and voltage of DGs to the reference values, thus realizing secondary control of the microgrid.

TABLE 2

TABLE 2. Parameters for the selection of voltage.

FIGURE 6

FIGURE 6. Trajectory curves of s_vi.

FIGURE 7

FIGURE 7. Trajectory curves of η_vi.

5 Conclusion

This study focused on the secondary control problem of microgrids with unknown disturbances. The distributed secondary control strategy proposed in this study only requires communication with neighboring generators, thus effectively reducing the communication burden. The designed SMC scheme, based on disturbance observers, can effectively address the influence of unknown disturbances and reduce chatter. Sufficient conditions for voltage and frequency regulation of microgrids were obtained, which create conditions for relevant work. To further reduce resource demand, subsequent work will study an event-triggered control strategy to achieve distributed secondary control relying on discontinuous communication. In addition, based on the idea of terminal SMC, another possible research direction is to realize preset time control in the two stages of SMC.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding authors.

Author contributions

SH, LH, HZ, and HL participated in article writing. XL and JQ participated in the study design.

Funding

This work was supported in part by the National Natural Science Foundation of China (grant nos. 62173175, 61877033, and 61833005), the Natural Science Foundation of Shandong Province (grant nos. ZR2019BF045, ZR2019MF021, and ZR2019QF004), and the Talent Introduction and Cultivation Plan for Youth Innovation of Universities in Shandong Province.

Conflict of interest

XL is employed by the Linyi Power Supply Company, State Grid Shandong Electric Power Company.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, are not guaranteed or endorsed by the publisher.

References

Abianeh, A. J., Mardani, M. M., Ferdowsi, F., Gottumukkala, R., and Dragičević, T. (2022). Cyber-Resilient sliding-mode consensus secondary control scheme for islanded AC microgrids. IEEE Trans. Power Electron. 37 (5), 6074–6089. doi:10.1109/tpel.2021.3125985

CrossRef Full Text | Google Scholar

Akbari, E., Shafaghatian, N., Zishan, F., Montoya, O. D., and Giral-Ramírez, D. A. (2022). Optimized two-level control of islanded microgrids to reduce fluctuations. IEEE Access 10, 95824–95838. doi:10.1109/access.2022.3203730

CrossRef Full Text | Google Scholar

Alfaro, C., Guzman, R., de Vicuña, L. G., Komurcugil, H., and Martín, H. (2022). Distributed direct power sliding-mode control for islanded AC microgrids. IEEE Trans. Industrial Electron. 69 (10), 9700–9710. doi:10.1109/tie.2021.3135612

CrossRef Full Text | Google Scholar

Alipour, M., Zarei, J., Razavi-Far, R., Saif, M., Mijatovic, N., and Dragičević, T. (2023). Observer-based backstepping sliding mode control design for microgrids feeding a constant power load. IEEE Trans. Industrial Electron. 70 (1), 465–473. doi:10.1109/tie.2022.3152028

CrossRef Full Text | Google Scholar

Badar, M., Ahmad, I., Rehman, S., Nazir, S., and Waqas, A. (2022). Hierarchical control of hybrid direct current microgrid with variable structure based sliding mode control and fuzzy energy management system. J. Frankl. Inst. 359 (13), 6856–6892. doi:10.1016/j.jfranklin.2022.06.044

CrossRef Full Text | Google Scholar

Bidram, A., Davoudi, A., Lewis, F. L., and Qu, Z. (2013). Secondary control of microgrids based on distributed cooperative control of multi-agent systems. IET Generation, Transm. Distribution 7 (8), 822–831. doi:10.1049/iet-gtd.2012.0576

CrossRef Full Text | Google Scholar

Choi, J., Habibi, S. I., and Bidram, A. (2022). Distributed finite-time event-triggered frequency and voltage control of AC microgrids. IEEE Trans. Power Syst. 37 (3), 1979–1994. doi:10.1109/tpwrs.2021.3110263

CrossRef Full Text | Google Scholar

Deng, C., Guo, F., Wen, C., Yue, D., and Wang, Y. (2022). Distributed resilient secondary control for DC microgrids against heterogeneous communication delays and DoS attacks. IEEE Trans. Industrial Electron. 69 (11), 11560–11568. doi:10.1109/tie.2021.3120492

CrossRef Full Text | Google Scholar

Ding, D., Han, Q., Wang, Z., and Ge, X. (2019). A survey on model-based distributed control and filtering for industrial cyber-physical systems. IEEE Trans. Industrial Inf. 15 (5), 2483–2499. doi:10.1109/tii.2019.2905295

CrossRef Full Text | Google Scholar

Ding, S., Hou, Q., and Wang, H. (2022). Disturbance-observer-based second-order sliding mode controller for speed control of PMSM drives. IEEE Trans. Energy Convers., 1–10. doi:10.1109/TEC.2022.3188630

CrossRef Full Text | Google Scholar

Espina, E., Llanos, J., Mellado, C. B., Dobson, R. C., Gómez, M. M., and Sáez, D. (2020). Distributed control strategies for microgrids: An overview. IEEE Access 8, 193412–193448. doi:10.1109/access.2020.3032378

CrossRef Full Text | Google Scholar

Fan, B., Guo, S., Peng, J., Yang, Q., Liu, W., and Liu, L. (2019). A consensus-based algorithm for power sharing and voltage regulation in DC microgrids. IEEE Trans. Industrial Inf. 16 (6), 3987–3996. doi:10.1109/tii.2019.2941268

CrossRef Full Text | Google Scholar

Fan, B., Peng, J., Yang, Q., and Liu, W. (2022). Distributed control of DC microgrids with improved ZIP load adaptability. IEEE Trans. Syst. Man, Cybern. Syst. 52 (7), 4623–4633. doi:10.1109/tsmc.2021.3101813

CrossRef Full Text | Google Scholar

Fan, Z., Fan, B., and Liu, W. (2021). Distributed control of DC microgrids for optimal coordination of conventional and renewable generators. IEEE Trans. Smart Grid 12 (6), 4607–4615. doi:10.1109/tsg.2021.3094878

CrossRef Full Text | Google Scholar

Ferreira, D., Silva, S., Silva, W., Brandao, D., Bergna, G., and Tedeschi, E. (2022). Overview of consensus protocol and its application to microgrid control. Energies 15 (22), 8536. doi:10.3390/en15228536

CrossRef Full Text | Google Scholar

Fonseca, A. N., Mellado, C. B., Gómez, J. S., Donoso, F., Tarisciotti, L., Sáez, D., et al. (2022). Distributed predictive secondary control for imbalance sharing in AC microgrids. IEEE Trans. Smart Grid 13 (1), 20–37. doi:10.1109/tsg.2021.3108677

CrossRef Full Text | Google Scholar

Ge, P., Zhu, Y., Green, T. C., and Teng, F. (2021). Resilient secondary voltage control of islanded microgrids: An ESKBF-based distributed fast terminal sliding mode control approach. IEEE Trans. Power Syst. 36 (2), 1059–1070. doi:10.1109/tpwrs.2020.3012026

CrossRef Full Text | Google Scholar

Hu, J., Sun, Q., Wang, R., Wang, B., Zhai, M., and Zhang, H. (2022). Privacy-preserving sliding mode control for voltage restoration of AC microgrids based on output mask approach. IEEE Trans. Industrial Inf. 18 (10), 6818–6827. doi:10.1109/tii.2022.3141428

CrossRef Full Text | Google Scholar

Jiang, Y., Yang, Y., Tan, S., and Hui, S. (2021). Distributed sliding mode observer-based secondary control for DC microgrids under cyber-attacks. IEEE J. Emerg. Sel. Top. Circuits Syst. 11 (1), 144–154. doi:10.1109/jetcas.2020.3046781

CrossRef Full Text | Google Scholar

Lai, J., Lu, X., Dong, Z., and Cheng, S. (2022). Resilient distributed multiagent control for AC microgrid networks subject to disturbances. IEEE Trans. Syst. Man, Cybern. Syst. 52 (1), 43–53. doi:10.1109/tsmc.2021.3056559

CrossRef Full Text | Google Scholar

Liu, Y., Yao, D., Li, H., and Lu, R. (2022). Distributed cooperative compound tracking control for a platoon of vehicles with adaptive NN. IEEE Trans. Cybern. 52 (7), 7039–7048. doi:10.1109/tcyb.2020.3044883

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, X., and Lai, J. (2021). Communication constraints for distributed secondary control of heterogeneous microgrids: A survey. IEEE Trans. Industry Appl. 57 (6), 5636–5648. doi:10.1109/tia.2021.3104792

CrossRef Full Text | Google Scholar

Mohiuddin, S. M., and Qi, J. (2022). Optimal distributed control of AC microgrids with coordinated voltage regulation and reactive power sharing. Hoboken: IEEE Transactions on Smart Grid. doi:10.1109/TSG.2022.3147446

CrossRef Full Text | Google Scholar

Raeispour, M., Atrianfar, H., Baghaee, H. R., and Gharehpetian, G. B. (2021). Robust sliding mode and mixed H2/H∞ output feedback primary control of AC microgrids. IEEE Syst. J. 15 (2), 2420–2431. doi:10.1109/jsyst.2020.2999553

CrossRef Full Text | Google Scholar

Sarangi, S., Sahu, B. K., and Rout, P. K. (2020). A comprehensive review of distribution generation integrated DC microgrid protection: Issues, strategies, and future direction. Int. J. Energy Res. 45 (4), 5006–5031. doi:10.1002/er.6245

CrossRef Full Text | Google Scholar

Shan, Y., Hu, J., Chan, K. W., and Islam, S. (2021). A unified model predictive voltage and current control for microgrids with distributed fuzzy cooperative secondary control. IEEE Trans. Industrial Inf. 17 (12), 8024–8034. doi:10.1109/tii.2021.3063282

CrossRef Full Text | Google Scholar

Sun, J., Tan, S., Zheng, H., Qi, G., Tan, S., Peng, D., et al. (2022). A DoS attack-resilient grid frequency regulation scheme via adaptive V2G capacity based integral sliding mode control. IEEE Trans. Smart Grid, 1. doi:10.1109/TSG.2022.3220763

CrossRef Full Text | Google Scholar

Sun, Q., Wang, B., Feng, X., and Hu, S. (2022). Small-signal stability and robustness analysis for microgrids under time-constrained DoS attacks and A mitigation adaptive secondary control method. Sci. China Inf. Sci. 65, 162202. Art. no. 162202. doi:10.1007/s11432-021-3290-3

CrossRef Full Text | Google Scholar

Veysi, M., Aghaei, J., Soltanpour, M. R., Shasadeghi, M., Bahrani, B., and Ryan, D. J. (2022). Robust, accurate, and fast decentralized power sharing mechanism for isolated DC microgrid using droop-based sliding-mode control. IEEE Trans. Smart Grid 13 (6), 4160–4173. doi:10.1109/tsg.2022.3181494

CrossRef Full Text | Google Scholar

Wang, R., Sun, Q., Sun, C., Zhang, H., Gui, Y., and Wang, P. (2021). Vehicle-vehicle energy interaction converter of electric vehicles: A disturbance observer based sliding mode control algorithm. IEEE Trans. Veh. Technol. 70 (10), 9910–9921. doi:10.1109/tvt.2021.3105433

CrossRef Full Text | Google Scholar

Wang, Y., Nguyen, T. L., Xu, Y., Tran, Q. T., and Caire, R. (2020). Peer-to-Peer control for networked microgrids: Multi-layer and multi-agent architecture design. IEEE Trans. Smart Grid 11 (6), 4688–4699. doi:10.1109/tsg.2020.3006883

CrossRef Full Text | Google Scholar

Wong, J. Y. R., Tan, C., Bakar, A. H. A., and Che, H. S. (2022). Selectivity problem in adaptive overcurrent protection for microgrid with inverter-based distributed generators (IBDG): Theoretical investigation and HIL verification. IEEE Trans. Power Deliv. 37 (4), 3313–3324. doi:10.1109/tpwrd.2021.3126897

CrossRef Full Text | Google Scholar

Xu, B., Zhang, L., and Ji, W. (2021). Improved non-singular fast terminal sliding mode control with disturbance observer for PMSM drives. IEEE Trans. Transp. Electrification 7 (4), 2753–2762. doi:10.1109/tte.2021.3083925

CrossRef Full Text | Google Scholar

Xu, D., Zhang, W., Jiang, B., Shi, P., and Wang, S. (2020). Directed-graph-observer-based model-free cooperative sliding mode control for distributed energy storage systems in DC microgrid. IEEE Trans. Industrial Inf. 16 (2), 1224–1235. doi:10.1109/tii.2019.2933227

CrossRef Full Text | Google Scholar

Zehra, S. S., Rahman, A. U., and Ahmad, I. (2022). Fuzzy-barrier sliding mode control of electric-hydrogen hybrid energy storage system in DC microgrid: Modelling, management and experimental investigation. Energy 239, 122260. Art. no. 122260. doi:10.1016/j.energy.2021.122260

CrossRef Full Text | Google Scholar

Zhang, Y., Shotorbani, A. M., Wang, L., and Mohammadi-Ivatloo, B. (2021). Distributed secondary control of a microgrid with A generalized PI finite-time controller. IEEE Open Access J. Power Energy 8, 57–67. doi:10.1109/oajpe.2021.3056507

CrossRef Full Text | Google Scholar