
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res. , 15 February 2023
Sec. Process and Energy Systems Engineering
Volume 10 - 2022 | https://doi.org/10.3389/fenrg.2022.1109063
This article is part of the Research Topic Advances in Modeling and Simulation of Wind and Solar Energy Systems for the Built Environment View all 8 articles
Automatic generation control (AGC) in modern power systems (PS) is difficult because the output power of many power resources is intermittent, and the load and system parameters vary widely. In this paper, a novel control scheme known as the wavelet based multiresolution proportional integral derivative (MRPID) controller for multiple interconnected hybrid power sources is presented. The discrete wavelet transform (DWT) is used in the proposed wavelet based MRPID controller to split the error between the actual and target responses into different frequency components at several stages. To ensure optimum system performance, the gains of the MRPID controller are fine-tuned using the Fox Optimizer Algorithm (FOA), a new powerful metaheuristic technique. The proposed MRPID controller is evaluated in a three-area hybrid system where each area contains a combination of conventional generation (gas, thermal reheat and hydro) and renewable generation sources (solar, and wind). The proposed controller also accounts for system non-linearities, including boiler dynamics, time delay, dead band, generation rate limitation, system uncertainties, and load changes. In the hybrid system studied, the proposed MRPID is compared with FOA-tuned PID and PI controllers. The proposed MRPID controller tuned with FOA algorithm effectively reducing the peak overshoot of 89.03%, 76.89 and 56.96% and undershoot of 69.52%,66.90 and 94.29% for ∆Ptie12, ∆Ptie23 and ∆Ptie13 respectively as compared to FOA based PI controller.
The power system (PS) is a link of vital elements that ensures the successful transmission of electricity across a large region. To ensure the effective operation and stability of the interlinked PS, the generation, transmission, and distribution components of the system must work together effectively. The dynamics of the power grid influence the resulting transient response. Consequently, the abrupt change in active power requirement leads to vigorous changes in the system. The nominal value of the system frequency must be observed, which is derived from the active power. Load-frequency control (LFC) is employed to sustain the power and frequency between grid areas in an interconnected grid based on the planned value. If the load-generation balance is not sustained, the frequency of the system suffers. Frequency excursions occur when there is a difference between the load demand and the generated power. When the system’s load demand exceeds the generator’s power, the system’s frequency drops. To avoid system instability, control measures must be commenced as soon as possible in response to huge frequency trips. When the maximum frequency overshoot goes a particular threshold, load shedding is automatically commenced to sustain the minimal frequency. The peak overshoot and time settling of the system should be kept as low as possible to ensure reliable system operation. (Liu et al., 2021; Ali et al., 2022; Liu et al., 2022).
Initially, AGC regulators, governor model, control performance, excitation control model, distinct load profile and parameter variation were discussed (Alghamdi and Canizares, 2021; Baros et al., 2021). A linearized structure of the LFC is built, but non-linearity is present throughout the power system and can be further elaborated in the manuscript. The reference (Bevrani et al., 2021) proposes using the permanence equation approach to evaluate and build two areas of IPS with non-linear speed governor backlash. The design of the interlinked scheduled PS consists of Governor Dead Zone (GDZ), delay time and Generation Rate Constraints (GRC). An interconnected three network PS with non-linearity is proposed as a query system for various loading situations (Pradhan et al., 2016). According to in Naidu et al. (2014), the PID controller based on the artificial bee colony (ABC) technique was employed in a multi-objective task for the management of LFC an IPS. In this study, the weighted sum method was utilized to reduce both the time settling and overshoot. Regardless of its importance in comparison to single objective optimization, the biased sum method is extremely sensitive to the coefficients that are specified.
In this research paper, it is found that most researchers have dealt with LFC issues that are limited to conventional interconnected grids (Shah et al., 2018; Zhang et al., 2019). However, due to changes in people’s lifestyles, increased demand for energy, increasing industrialization, environmental concerns, and modernization of power supply, the architecture of the interconnected grid is changing (Gupta et al., 2019; Latif et al., 2020). Therefore, we are moving from a conventional power supply to a hybrid PS (Ganguly et al., 2017; Khezri et al., 2019). The variation of frequency deviation is caused by the diversity of renewable energy generation and the obstruction of load need, and a disturbance in one area of the control system causes a disturbance in other regions of the dynamics control system. The main reason of system oscillations is the extreme saturation of non-traditional energy reserves combined with the inertia of the system, which starts to fluctuations in the grid frequency and exchangeable interconnection power (Guha et al., 2021; Latif et al., 2021). Exceeding the set frequency limit, on the other hand, leads to a power interruption and a so-called blackout. With the presence of renewable energy sources (RES), it is obvious that the emerging energy grid will have problems with frequency regulation (Prostejovsky et al., 2018; Irudayaraj et al., 2020). Therefore, a contemporary control method is essential to provide inevitable power with enhanced cohesive frequency control that takes into account today’s renewable resources.
Several control strategies are being developed to guarantee the frequency stability of RES. Reference (Gulzar et al., 2022) provides a broad overview of the control methodologies used for the AGC problem in PS. The PID controller and its modifications remain the most used controllers for low-frequency control of PS due to their low price and ease of operation associated to other controllers (Hasanien, 2018), (Hasanien and El-Fergany, 2019), (Khadanga et al., 2019), and (Magdy et al., 2019). Moreover, PI controllers have been implemented in various energy storage systems (ESS) to improve the frequency strength of PS with a high percentage of RES (Guha et al., 2018; Magdy et al., 2020). However, traditional controllers are more susceptible to non-linearities and uncertainties in the system. Therefore, their performance may decrease. According to the literature review, traditional PID and PI controllers, as well as the neural network (NN) controller, are widely employed for frequency control of various PS. However, the implementation of these controllers is influenced by constraint modifications, non-linearity, and unknown system dynamics. Wavelet transforms (WT), on the other hand, which are top fitted for non-periodic and non-stationary control signals, do not use the control system model. Wavelet transforms non-periodic and non-stationary signals simultaneously into frequency and time localized elements. To focus on a signal with prolonged time intervals for low frequency elements and sharp time intervals for high frequency elements, WT are suitable. Therefore, this paper presents a novel multi-resolution PID controller based on WT for modeling and frequency control of an interconnected network with multiple domains. The proposed control method was evaluated based on experimental and simulation results and compared with traditional PI and PID controllers.
Previous studies have shown that the choice of controller parameters is as vital as the choice of controller type. In terms of frequency stability, the evolutionary optimization methods used to adjust the controller boundary conditions are crucial. Therefore, the selection of an effective optimization approach is a vital and crucial difficulty in controller design. In the past, the optimal gains of frequency controllers have been selected using some conventional optimization methods (Young-Hyun et al., 2000; Topno and Chanana, 2017). The nomenclature applied in this study is shown in Table 1.
Furthermore, a fuzzy gain scheduling (FGS) controller is suggested in reference (Revathi and Mohan Kumar, 2020) for the choice of controller gains. Yet, these techniques face several obstacles, such as the collapse of local minima, death traps at local minima, the necessary for numerous iterations, and the dependence on initial requirements when determining the optimal parameters. For this reason, researchers have developed metaheuristic optimization techniques, such as the PSO (Jagatheesan et al., 2015), moth swarm algorithm (MSO) (Magdy et al., 2018), electric optimization algorithm (EOA) (Dahab et al., 2020), improved lightning attachment algorithm (ILAO) (Khamies et al., 2021), moth flame optimization (MFO) (Nandi et al., 2019), lightning attachment optimizer (LAO) (Mohamed et al., 2020), Fitness Dependent Optimizer (FDO) (Daraz et al., 2020a), path finder algorithm (PFA) (Priyadarshani et al. 2020), genetic algorithm (GA) (Soleimani and Mazloum, 2018), hybrid teaching learning-based algorithm with pattern search (hTLBO-PS) (Dillip Khamari et al., 2020), hybridized sine cosine algorithm with FDO (hSCA-FDO) (Daraz et al., 2022), water cycle algorithm (WCA) (Kumari and Shankar, 2018) and hybridized DE with PS (Pradhan et al., 2021). Elkasem et al. in (Elkasem et al., 2022) used the cascaded configuration of tilt derivative with tilt integral term controller to adjust their gains using improved form of chaos game algorithm. The authors in (Hasanien and El-fergany, 2017) have been utilized PID controller adjusted with algorithm based on symbiotic organism exploration by probing high wind form (WF) for IPS. The authors in reference (Elkasem et al., 2021) proposed a control tactic to enhance the frequency IPS composing of diverse power sources and the high diffusion concentration of wind energy. The anticipated control approach is based on FLC-PID controller optimized with arithmetic optimization algorithm (AOA). In addition, special attention has been paid to the application of various optimization methods to solve industrial problems, especially the LFC crisis. This is the motivation for the author to use the Fox Optimizer Algorithm (FOA) to ascertain the optimal parameters of the suggested MRPID controller in this study.
The integration of a well-designed control unit into the power system is therefore of great importance. In addition, the power system frequency and the interconnection line must be kept within adequate constraints and the balance of the system must be restored as soon as possible. In this study, a novel multi-resolution PID controller is presented as a reliable alternative method to improve the sustainability, reliability and stability of a hybrid PS containing conventional and RES such as photovoltaic and wind energy. A FOA, a novel metaheuristic optimization method, is used to tune the gains of the proposed MRPID controller. The inspiration, significance and contributions of the current study are highlighted as follows:
1) To control the system behavior in terms of frequency and power fluctuations, a new attempt was made to develop a PID controller based on wavelet resolutions.
2) Using a new strong FDO optimization approach to determine the ideal controller parameters to ensure optimal controller behavior.
3) The realistic model, which includes various non-linearities such as GDZ, GRC, BD, and TD, was considered for a hybrid energy system with conventional and RES such as photovoltaics and wind energy.
4) Comparing the performance of the MRPID controller with other controllers, such as the traditional PID and PI controllers, to demonstrate its superiority.
5) The robustness of the suggested controller algorithm was evaluated in a series of test cases where the load step perturbation (SLP) and system parameters were randomly adjusted.
As indicated in Figure 1, the PS under study is a three-unit IPS with a thermal reheat, hydro, solar, wind, and a gas power plant in each control area. Appendix A (Liu et al., 2022) contains the description of the given system and its parameters. Furthermore, the physical limitations of the PS such as GDZ and GRC, are considered for the non-linearity and a more practical analysis of the thermal units, taking the GRC rate (0.0017 pu/s and 0.003 pu/s). Moreover, the generation rate limitation of the hydropower system is (0.06 p. u.) and (0.045 pu/s) for decreasing and increasing rates, respectively (Arya, 2019; Daraz et al., 2020b). The Fourier series is used to obtain the transfer function (TF) for GDZ with 0.50% backlash, as indicated in Eq. 1:
Where N1 = 0.8 and
The time delays can affect the execution of the controller and amplify oscillations in the system. For this reason, this work includes a simulation analysis that accounts for the time delays in ACE as well as other non-linearities in the system. The TF model for the BD is shown in Figure 2. This model can be used to analyze both well-regulated coal-fired power plants and poorly regulated gas- or oil-fired power plants. As soon as the boiler control unit identifies a change in steam flow rate or pressure variations, the appropriate controls are instantly initiated (Daraz et al., 2020c; Zhang et al., 2020). This is how generation adjustment works in conventional steam power plants. The following equation shows the TF model of the boiler dynamics:
The overall, TF model for the gas power unit (GG(s)) consists of the TF of the fuel combustion (G1(s)), TF of the compressor discharge (G2(s)), TF of the speed governor (G3(s)) and TF of the valve position (G4(s)) and is denoted by Eqs 4, 5, 7, 8 respectively.
The overall, TF model for the thermal reheat unit (GG(s)) consists of TF of the turbine (GTR1(s)), TF of the reheat (GTR2(s)), and TF of the governor (GTR3(s)) and is denoted Eqs 9, 10, 11, 12 respectively.
The combined, TF model for hydral us with penstock (GH2(s)), and TF of the hydro governor (GH3(s)) and is denoted by Eqs 13, 14, 15, 16 respectively.
Solar thermal power plants absorb solar radiation and convert it into usable heat and electricity. Concentration of solar energy is critical to generating sufficient heat to efficiently operate a power plant. A thermodynamic heat-to-electricity cycle (Zhang et al., 2020) using concentrated solar thermal power. The essential elements of an STPG system are the solar accumulators and the working liquid. Solar energy is collected using parabolic troughs that direct sunlight onto a circulating tube of working fluid (air, water, or oil). During the energy cycle, the working liquid is boiled to generate high pressure steam in a boiler, which is then expanded in a turbogenerator to produce electricity. With some approximations, the STPG system can be linearized, and the TF model is described for small signal analysis as follows:
where KT and KS stand for the gain constants, TT for the time constants of the steam turbine and Ts for the time constants of the solar collector. As a mature form of RES, wind energy has grown steadily in recent years, and its share of the power grid continues to increase. Although wind energy has utility and environmental benefits, its erratic nature overloads interconnectors and causes frequency deviations in the power grid. When wind speed fluctuates, a rotor-tilt control mechanism is activated to ensure constant wind turbine output. Three WTPGs are considered and characterized by a first order delay-based TF, as shown in Figure 3A (Jampeethong and Khomfoi, 2020; Li et al., 2021).
Where KWTG is the gain of wind energy generation and TWTG is the time constant of the wind energy plant.
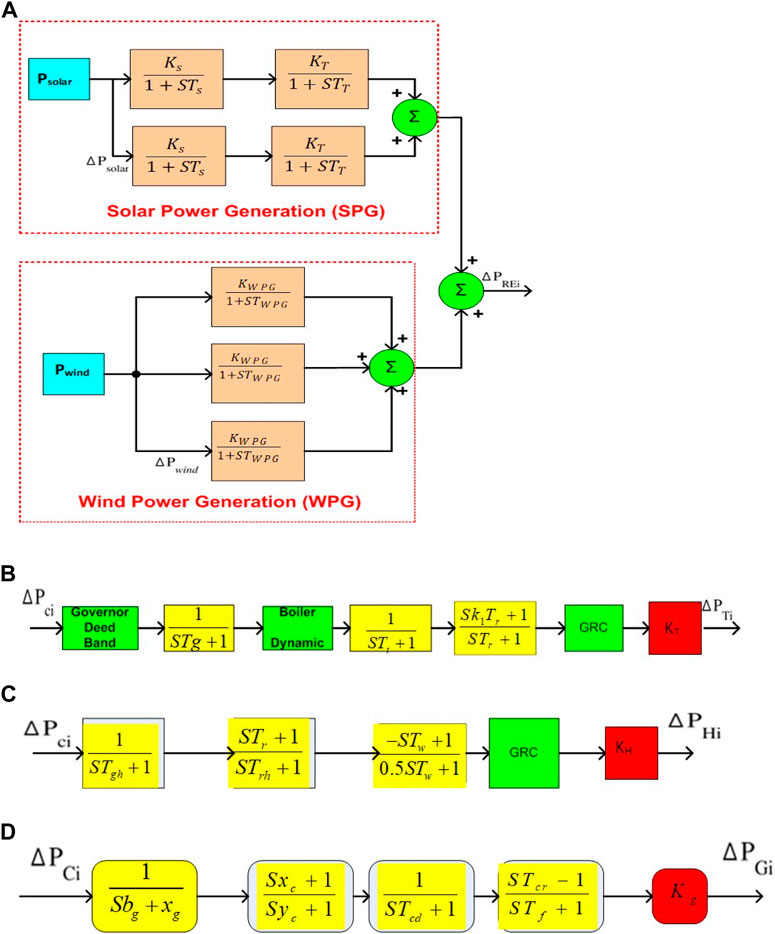
FIGURE 3. TF model of (A) Renewable Energy Sources (RES) (B) Thermal Reheat system (C) Hydro generation system (D) Gas generation system.
The instinctive hunting strategies of foxes served as inspiration for this metaheuristic algorithm. Fox adjusts the population, also called X-matrix, at the beginning. The position of a fox is denoted by X. The cost functions are then used to determine the fitness of each search agent in each iteration. The fitness values of each search agent are compared with the fitness values of the other agents to determine the best fitness and the best position. A condition that compares the fitness of the recent row with the fitness of the prior row across all repetitions is used to execute best fitness and best X. Furthermore, the algorithm consists of two main sections: exploration and exploitation (Mohammed and Rashid, 2022).
In this stage, there is a condition regarding the probability of killing the prey. The value of the arbitrary variable (p) is between 0 and 1, so if the arbitrary value is greater than 0.18, the recent location of the fox must be determined. We must determine the separation between the sound waves (Dis_S_Tit)) and the red fox’s prey (Dis_Fox_Preyit). Therefore, a random value between 0 and 1 is generated for the sound runtime (Time_S_Tit). Multiplying the pace of sound (Sp_S) by the time sound takes to travel (Time_S_Tit) yields the sound distance from the fox.
where Sp_S is the speed of sound in the medium and Time_S_Tit is a random number between 0 and 1. The range for the number of iterations is between 1 and 500. Eq. 10 demonstrates how to calculate Sp_S based on the optimal position.
Therefore, the distance between prey and fox (Dis_Fox_Preyit) can be determined by halving the distance (Time_S_Tit).
After the fox has determined the distance between him and his prey, he must position himself to jump in order to catch his prey. Therefore, the fox must determine its jump height Jumpit.
where t is the average travel time of the sound and is squared based on the up and down steps of the jump. The following equation represents the calculation of the red fox’s new position.
Here, c1 and c2 represent the values of the variables in the range of [0, 0.18] and [0.19, 1], respectively.
In this phase, to control the random walk, the fox performs a random search based on the fit location it has found so far. In this phase, the fox lacks a jumping technique because it must randomly walk to investigate potential prey in the search area. The variable (a) and minimum time variable (Min_T) are employed to monitor the search and guarantee that the fox runs randomly to the suited location. In Eqs 25, 26, Min_T and the variables are calculated. Min_T is determined by searching for the minimum value of tt.
To find the minimum time average tt, divide the problem dimension by the sum of Time_S_Tit (i,:)
where Maxit, is the number of iterations allowed. The calculation of both Min_T and a variable (a) has a significant impact on the quest period to get closer to the optimal result. Eq. 27 illustrates the assessment strategy of the fox when seeking for a new location in the quest space X(it+1).
The equations in both phases do not require any change except a problem-specific adjustment. The flowchart for the Fox optimization algorithm (FOA) is indicated in Figure 4.
Classic PID controllers are broadly used in industry because they have historically proven to be easy to implement and extremely effective. By continuously calculating an error signal as the difference between the setpoint and a measured process variable, the PID controller, a feedback-based closed-loop device, generates the control signal for the system. The following equation illustrates the basic operation of a PID controller that uses the error signal (e) as an input to adjust the control output (u) (Parvez and Gao, 2005).
Here KI, Kd and Kp are the integral, derivative and proportional gains of the PID controller respectively. In this research study, a multi-resolution wavelet controller is developed to improve the LFC problem in hybrid PS with multiple domains. Wavelet transform is extensively employed in signal processing, but in this research work, it is employed for the first time to design a controller to solve the LFC problem. A multi-resolution wavelet controller is designed by splitting the error signal into frequency packets called wavelets. The splitting of the error signal includes
ki represents the control parameter. In common, a PID controller accepts the control error e as the input signal and then uses the control error to produce the control output signal u, as indicated in Eq. 28. The proportional and integral parameters tend to take the low-frequency data of the error signal, while the derivative constant take the high-frequency data of the error signal (Parvez and Gao, 2005). As shown in Figure 5; Eq. 30, an MRPID split the error signal into its high, mid, and low-scale factors.
The application of wavelet disintegration to the error signal, as well as the accumulative impact of several fundamental phenomena, such as external disturbances and effects of measurement noise, manifested at different levels. Then, each of these components is multiplied by its gain before being combined to form the control signal (u).
The schematic flow of parameter optimization for the proposed control methodology is shown in Figure 6. Proper tuning of the metrics of the MRPID controller is required to improve the operation of the PS in different modes. Model uncertainty and dynamic variations should be managed by optimizing the MRPID controller parameters. The PS must be extremely responsive to fluctuate in load disturbance and follow the predicted situation for all variables. Among the various performance indices used to assess the efficacy of PS, the Integral Time Square Error (ITSE) (Naidu et al., 2014; Hasanien and El-fergany, 2017; Morsali et al., 2018; Daraz et al., 2021; Elkasem et al., 2021; Liu et al., 2022) has been found to be well suited for parametric optimization based on the overshoot and time settling. Therefore, in this research study, the ITSE is deemed as the cost function to be minimized, and its representation in terms of a three-field network is as follows:
Subject to
Where
In this section, the proposed controller and the selected optimization technique were tested for validity, effectiveness and robustness using simulation results from different scenarios. For this purpose, a MATLAB/SIMULINK model was created to simulate the proposed MRPID controller integrated with a three-grid interconnected hybrid grid with conventional and RES solar and wind power systems. The comparison of the performance of the suggested MRPID controller with other types of controllers, such as the conventional PI and PID controllers with the same parameters obtained by the Fox optimization algorithm, was used to test the simulated model (FOA). The number of iterations is put to 100, the simulation time is 30S, and the process is repeated 15 times for each algorithm to allow a fair comparison. Table 2 shows the best PID gains of the 15 runs and the convergence diagram for FOA is depicted in Figure 7. The system parameters shown for each controller type are the frequency deviation in each region and the power deviation between neighboring regions. The reliability, robustness, and superiority of the presented controller were evaluated based on the results, as shown later.
The considered three-area system is investigated by independently feeding PI, PID and MRPID controllers, where the controller gains are each optimized by FOA for 1% SLP in control zone 1. Figure 8 shows the dynamic responses of the controllers. From the responses indicated in Figures 8A–C, the settling time, peak undershoot, and maximum overshoot can be calculated (see Table 3). Table 3 shows that the responses generated by the proposed MRPID controller have shorter settling times and lower peak overshoot and undershoot values compared to the responses generated by the PI and PID controllers. In this way, the suggested MRPID controller achieves superior dynamic performance over PID and PI controllers in respect of time settling, undershoot and peak overshoot. It can be seen from Table 1 that the recommended FOA-MRPID control technique gave very satisfactory results in terms of settling time in each area. In areas 1, 2, and 3, FOA-MRPID provided settling times of 11.4 S, 10.13 S, and 8.60 S, respectively, which is faster than the FOA-PID and FOA-PI control methods. Compared to the FOA algorithms based on PI, the MRPID controller tuned to FOA significantly reduced overshoot for F1, F2 and F3 by 87.21%, 49.71%, and 10.56%, respectively. It also improved the settling time by 51.56%, 11.83%, and 14.39%. Table 3 displays that compared with the path finder algorithm (PFA) based FOTID controller, the FOA based tuned MRPID controller provides significant enhancement of 79.38% and 73.99% in terms of Ts, effectively reducing the maximum Osh of 76.33% and 89.00% and undershoot of 57.52% and 76.29% for F1 and F2 respectively. The MRPID -based FOA controller improves the settling time by 63.81%, 71.88%, and 19.81% for F1 andF2 respectively, compared to I-TD controller optimized with WCA techniques. The percentage comparison of different techniques is shown in Figure 9.
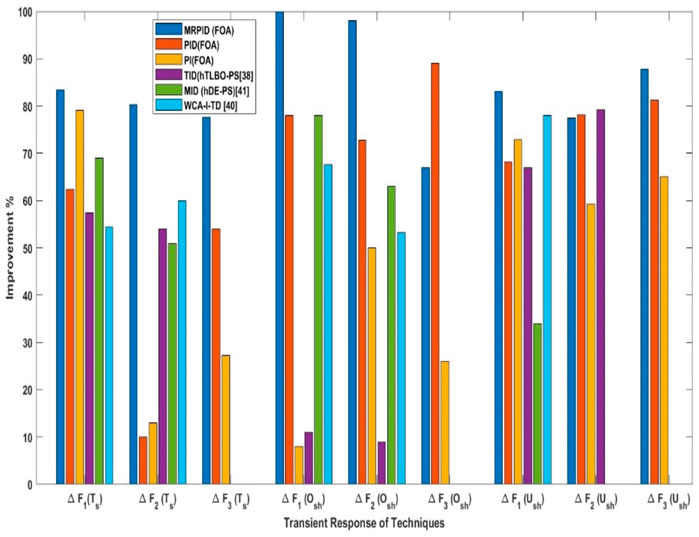
FIGURE 9. Comparison of different techniques for each area in terms of percentage improvement for Ts, Osh and Ush.
The FOA -based MRPID controller provided a time settling of 10.13S for the area-1, which is faster than other control strategies and 53% faster than the FPA-FOTID controller in comparison (Priyadarshani et al. 2020). FOA based MRPID controller produced zero overshoot as compared to FOA based PI controllers for tie line power interconnected between area-2 and area-3. Similarly, the FOA based MRPID controllers provided a time settling of 11.60S for the area 2, which is 78.93% more effective than the FPA-FOTID controller. Moreover, FOA based MRPID control schemes eliminates overshoot for area1, area 2 and area 3.
Table 4; Figures 10A–C show that the proposed FOA-MRPID control technique gives very satisfactory outcomes in respect of Ts, Ush, and Osh for the link line between areas 1 and 2 (Ptie12), the interconnected area between areas 2 and 3 (Ptie23), and the link line between areas 1 and 3 (Ptie13). In areas 1, 2, and 3, FOA-MRPID provided settling times of 6.23 S, 10.08 S, and 8.10 S, respectively, which is faster than the FOA-PID and FOA-PI control methods. Similarly, the FOA based tuned MRPID controller provides significant enhancement of 89.11%, 83.67% and 56.78% in terms of Ts for ∆Ptie12, ∆Ptie23 and ∆Ptie13 respectively as compared to FOA based PI controller. The proposed MRPID controller tuned with FOA algorithm effectively reducing the peak overshoot of 89.03%, 76.89 and 56.96% and undershoot of 69.52%,66.90 and 94.29% for ∆Ptie12, ∆Ptie23 and ∆Ptie13 respectively as compared to FOA based PI controller. The percentage comparison of different techniques is shown in Figure 11.
To test the loading capacity and robustness of the proposed MRPID controller, the parameters of the studied system were changed in a range of ±30% without changing the ideal values of the controller parameters. These variables include the time constants of the turbine, thermal reheat, droops, governor, and frequency distortions for each area. The synchronization coefficient and power system operating load conditions are also changed. The dynamic responses shown in Figures 12A–C; Table 5 indicate that the FOA-based MRPID controller was successful even when system settings were changed. Since the values of all performance metrics, such as Ts, % Osh, % Ush, and steady state, hardly changed when the system parameters were adjusted, the recommended technique may work well in dynamic situations. The attained findings show that the suggested FOA-based MRPID controller is quite reliable and robust and does not require any readjustment within ±30% variation of the system parameters.
In this work, a novel multi-resolution based PID controller has been recommended for frequency control of a hybrid PS with three domains, where each domain contains a combination of conventional generation (gas, thermal, and hydro) and renewable generation units (solar and wind). The proposed controller also accounts for system non-linearities, including time delay, boiler dynamics, dead band, generation rate limiting, system uncertainties, and load changes. To ensure optimal system performance, the MRPID controller gains are well-tuned using the Fox optimization algorithm (FOA), a powerful new metaheuristic technique. In the hybrid system under study, the proposed MRPID is compared with FOA-tuned PID and PI controllers, WCA-based I-TD controllers, FPA-based FOTID controllers, hDE-PS based MID controllers, and hTLBO- PS based TID controllers. The MRPID -based FOA controller improves the settling time by 63.81%, 71.88%, and 19.81% for each respectively compared to I-TD controller optimized with WCA techniques. The proposed MRPID controller tuned with FOA algorithm effectively reducing the peak overshoot of 89.03%, 76.89 and 56.96% and undershoot of 69.52%,66.90 and 94.29% for ∆Ptie12, ∆Ptie23 and ∆Ptie13 respectively as compared to FOA based PI controller. From the attained outcomes, it can be analyzed that the proposed FOA-based MRPID controller is quite reliable and robust and does not require any readjustment within a range of  ± 30% alterations in the system parameters. In future, the proposed hybrid power system will be evaluated on the IEEE 30-bus, 39-bus, and 118-bus test system by utilizing the graph theory.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Conceptualization, SM and GZ; Methodology, AD; Software, AD and AB; Validation, PZ, SM, and CS; Formal analysis, SM and AB; Investigation, GZ; Resources, PZ; Data curation, SM; Writing—Original draft preparation, AD and AB; Writing—Review and editing, PZ and GZ; Visualization, GZ and CS; Supervision, GZ; Project administration, SM and GZ; Funding acquisition. All authors have read and agreed to the published version of the manuscript.
This work was supported by Tianjin Natural Science Foundation under grant number: 19JCQNJC06100.
CS was employed by the company Department of Cloud Core Platform, China Telecom Corporation Limited Tianjin Branch
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Alghamdi, B., and Canizares, C. A. (2021). Frequency regulation in isolated microgrids through optimal droop gain and voltage control. IEEE Trans. Smart Grid. 12, 988–998. doi:10.1109/TSG.2020.3028472
Ali, T., Suheel, A. M., Daraz, A., Aslam, S., and Alkhalifah, T. (2022). Dandelion optimizer-based combined automatic voltage regulation and load frequency control in a multi-area, multi-source interconnected power system with nonlinearities. Energies 15 (22), 8499. doi:10.3390/en15228499
Arya, Y. (2019). A new optimized fuzzy FOPI-FOPD controller for automatic generation control of electric power systems. J. Frankl. Inst. 356 (11), 5611–5629. doi:10.1016/j.jfranklin.2019.02.034
Baros, S., Chen, Y. C., and hople, S. V. D. (2021). Examining the economic optimality of automatic generation control. IEEE Trans. Power Syst. 36, 4611–4620. doi:10.1109/TPWRS.2021.3067445
Bevrani, H., Golpîra, H., Messina, A. R., Hatziargyriou, N., Milano, F., and Ise, T. (2021). Power system frequency control: An updated review of current solutions and new challenges. Electr. Power Syst. Res. 194 (2021)–107114. doi:10.1016/j.epsr.2021.107114
Dahab, Y. A., Hussein, A., and Mohamed, T. H.(2020). Adaptive load frequency control of power systems using electro-search optimization supported by the balloon effect. IEEE Access 8, 7408–7422. doi:10.1109/access.2020.2964104
Daraz, A., Malik, S. A., Azar, A. T., Aslam, S., Alkhalifah, T., and Alturise, F. (2022). Optimized fractional order integral-tilt derivative controller for frequency regulation of interconnected diverse renewable energy resources. IEEE Access 10, 43514–43527. doi:10.1109/ACCESS.2022.3167811
Daraz, A., Malik, S. A., Haq, I. U., Khan, K. B., Laghari, G. F., and Zafar, F. (2020). Modified pid controller for automatic generation control of multi-source interconnected power system using fitness dependent optimizer algorithm. PloS one 15 (11), e0242428. doi:10.1371/journal.pone.0242428
Daraz, A., Malik, S. A., Mokhlis, H., Haq, I. U., Laghari, G. F., and Mansor, N. N. (2020). Fitness dependent optimizer-based automatic generation control of multi-source interconnected power system with non-linearities. IEEE Access 8, 100989–101003. doi:10.1109/access.2020.2998127
Daraz, A., Malik, S. A., Mokhlis, H., Haq, I. U., Zafar, F., and Mansor, N. N. (2020). Improved-fitness dependent optimizer based foi-pd controller for automatic generation control of multi-source interconnected power system in deregulated environment. IEEE Access 8, 197757–197775. doi:10.1109/access.2020.3033983
Daraz, A., Malik, S. A., Waseem, A., Azar, A. T., Haq, I. U., Ullah, Z., et al. (2021). Automatic generation control of multi-source interconnected power system using foi-td controller. Energies 14 (18), 5867. doi:10.3390/en14185867
Dillip Khamari, T. S. G. S. P., Kumar Sahu, R., Gorripotu, T. S., and Panda, S. (2020). Automatic generation control of power system in deregulated environment using hybrid tlbo and pattern search technique. Ain Shams Eng. J. 11 (3), 553–573. doi:10.1016/j.asej.2019.10.012
Elkasem, A. H. A., Khamies, M., Hassan, M. H., Agwa, A. M., and Kamel, S. (2022). Optimal design of TD-TI controller for LFC considering renewables penetration by an improved chaos game optimizer. Fractal Fract. 6, 220. doi:10.3390/fractalfract6040220
Elkasem, A. H. A., Khamies, M., Magdy, G., Taha, I. B. M., and Kamel, S. (2021). Frequency stability of AC/DC interconnected power systems with wind energy using arithmetic optimization algorithm-based fuzzy-PID controller. Sustainability 13, 12095. doi:10.3390/su132112095
Ganguly, S., Mahto, T., and Mukherjee, V. (2017). Integrated frequency and power control of an isolated hybrid power system considering scaling factor based fuzzy classical controller. Swarm Evol. Comput. 32, 184–201. doi:10.1016/j.swevo.2016.08.001
Guha, D., Roy, P. K., and Banerjee, S. (2018). Optimal tuning of 3 degree-of-freedom proportional-integral-derivative controller for hybrid distributed power system using dragonfly algorithm. Comput. Electr. Eng. 72 (Nov), 137–153. doi:10.1016/j.compeleceng.2018.09.003
Guha, D., Roy, P. K., and Banerjee, S. (2021). Performance evolution of different controllers for frequency regulation of a hybrid energy power system employing chaotic crow search algorithm. ISA Trans. 113, 128–146. 10.1016/j. isatra.2021.03.017.
Gulzar, M. M., Iqbal, M., Shahzad, S., Muqeet, H. A., Shahzad, M., and Hussain, M. M. (2022). Load frequency control (LFC) strategies in renewable energy-based hybrid power systems: A review. Energies 15, 3488. doi:10.3390/en15103488
Gupta, A. K., Verma, K., and Niazi, K. R. (2019). Robust coordinated control for damping low frequency oscillations in high wind penetration power system. Int. Trans. Electr. Energ Syst. 29, e12006. doi:10.1002/2050-7038.12006
Hasanien, H. M., and El-Fergany, A. A. (2019). Salp swarm algorithm-based optimal load frequency control of hybrid renewable power systems with communication delay and excitation cross-coupling effect. Electr. Power Syst. Res. 176 (Nov), 105938. doi:10.1016/j.epsr.2019.105938
Hasanien, H. M., and El-fergany, A. A. (2017). Symbiotic organisms search algorithm for automatic generation control of interconnected power systems including wind farms. IET Gener. Transm. Distrib. 11 (7), 1692–1700. doi:10.1049/iet-gtd.2016.1245
Hasanien, H. M. (2018). Whale optimisation algorithm for automatic generation control of interconnected modern power systems including renewable energy sources. IET Gener. Transm. Distrib. 12 (3), 607–614. doi:10.1049/iet-gtd.2017.1005
Irudayaraj, A. X. R., Wahab, N. I. A., Umamaheswari, M. G., Radzi, M. A. M., Bin Sulaiman, N., eerasamy, V., et al. (2020). A Matignon’s theorem based stability analysis of hybrid power system for automatic load frequency control using atom search optimized FOPID controller. IEEE Access 8, 168751–168772. doi:10.1109/ACCESS.2020.3021212
Jagatheesan, K., Anand, B., Dey, N., Gaber, T., Hassanien, A. E., and Kim, T-H. (2015) A design of PI controller using stochastic particle swarm optimization in load frequency control of thermal power systems. Presented at the Proceedings of the 2015 Fourth International Conference on Information Science and Industrial Applications (ISI), Beijing China , September 2015. doi:10.1109/isi.2015.8
Jampeethong, P., and Khomfoi, S. (2020). Coordinated control of electric vehicles and renewable energy sources for frequency regulation in microgrids. IEEE Access 8, 141967–141976. doi:10.1109/ACCESS.2020.3010276
Khadanga, R. K., Kumar, A., and Panda, S. (2019). A novel modified whale optimization algorithm for load frequency controller design of a two-area power system composing of PV grid and thermal generator. Applic 32 (12), 8205–8216. doi:10.1007/s00521-019-04321-7
Khamies, M., Magdy, G., Ebeed, M., and Kamel, S. (2021). A robust PID controller based on linear quadratic Gaussian approach for improving frequency stability of power systems considering renewables. ISA Trans. 117, 118–138. doi:10.1016/j.isatra.2021.01.052
Khezri, R., Oshnoei, A., Oshnoei, S., Bevrani, H., and Muyeen, S. M. (2019). An intelligent coordinator design for GCSC and AGC in a two-area hybrid power system. Appl. Soft Comput. J. 76, 491–504. doi:10.1016/j.asoc.2018.12.026
Kumari, S., and Shankar, G. (2018). Novel application of integral-tilt-derivative controller for performance evaluation of load frequency control of interconnected power system. Transm. Distribution 12 (14), 3550–3560. doi:10.1049/iet-gtd.2018.0345
Latif, A., Hussain, S. M. S., Das, D. C., and Ustun, T. S. (2021). Double stage controller optimization for load frequency stabilization in hybrid wind-ocean wave energy based maritime microgrid system. Appl. Energy. 282 (2021)–116171. doi:10.1016/j.apenergy.2020.116171
Latif, A., Hussain, S. M. S., Das, D. C., and Ustun, T. S. (2020). State-of-the-art of controllers and soft computing techniques for regulated load frequency management of single/multi-area traditional and renewable energy based power systems. Appl. Energy. 266–114858. doi:10.1016/j.apenergy.2020.114858
Li, C., Zhang, Z., Li, J., Ma, Y., and Zou, J. (2021). Design of control strategy and effect evaluation for primary frequency regulation of wind storage system. Front. Energy Res. 9–739439. doi:10.3389/fenrg.2021.739439
Liu, C., Li, Q., Tian, X., Wei, L., Chi, Y., and Li, C. (2022). Multi-objective mayfly optimization-based frequency regulation for power grid with wind energy penetration. Front. Energy Res. 10–848966. doi:10.3389/fenrg.2022.848966
Liu, Y., Zhang, L., Xi, L., Sun, Q., and Zhu, J. (2021). Automatic generation control for distributed multi-region interconnected power system with function approximation. Front. Energy Res. 9–700069. doi:10.3389/fenrg.2021.700069
Magdy, G., Mohamed, E. A., Shabib, G., Elbaset, A. A., and Mitani, Y. (2018). SMES based a new PID controller for frequency stability of a real hybrid power system considering high wind power penetration. IET Renew. Power Gener. 12 (11), 1304–1313. doi:10.1049/rpg2.v12.1110.1049/iet-rpg.2018.5096
Magdy, G., Shabib, G., Elbaset, A. A., Kerdphol, T., Qudaih, Y., Bevrani, H., et al. (2019). Tustin's technique based digital decentralized load frequency control in a realistic multi power system considering wind farms and communications delays. Shams Eng. J. 10 (2), 327–341. doi:10.1016/j.asej.2019.01.004
Magdy, G., Bakeer, A., Nour, M., and Petlenkov, E. .(2020). A new virtual synchronous generator design based on the SMES system for frequency stability of low-inertia power grids. Energies 13 (21), 5641. doi:10.3390/en13215641
Mohamed, K., Gaber, M., Mohamed, E. H., Banakhr Fahd, A., and Kamel, S. (2020). An efficient control strategy for enhancing frequency stability of multi-area power system considering high wind energy penetration. IEEE Access 8, 140062–140078. doi:10.1109/access.2020.3012119
Mohammed, H., and Rashid, T. F. O. X. (2022). Fox: A FOX-inspired optimization algorithm. Appl. Intell. 53, 1030–1050. doi:10.1007/s10489-022-03533-0
Morsali, J., Zare, K., and Tarafdar Hagh, M. (2018). Comparative performance evaluation of fractional order controllers in lfc of two-area diverse-unit power system with considering gdb and grc effects. J. Electr. Syst. Inf. Technol. 5 (3), 708–722. doi:10.1016/j.jesit.2017.05.002
Nandi, M., Shiva, C. K., and Mukherjee, V. (2019). Moth-flame algorithm for TCSC- and SMES-based controller design in automatic generation control of a two-area multi-unit hydro-power system. Iran. J. Sci. Technol. Trans. Electr. Eng. Dec 44 (3), 1173–1196. doi:10.1007/s40998-019-00297-1
Naidu, K., Mokhlis, H., and Abu Bakar, A. H. (2014). Multiobjective optimization using weighted sum artificial bee colony algorithm for load frequency control. Int. J. Electr. Power & Energy Syst. 55, 657–667. doi:10.1016/j.ijepes.2013.10.022
Parvez, S., and Gao, Z. (2005). A wavelet-based multiresolution PID controller. IEEE Trans. Industry Appl. 41 (2), 537–543. doi:10.1109/tia.2005.844378
Pradhan, P. C., Sahu, R. K., and Panda, S. (2021). Comparative performance analysis of hybrid differential evolution and pattern search technique for frequency control of the electric power system. J. Electr. Syst. Inf Technol 8, 11. doi:10.1186/s43067-021-00033-y
Pradhan, P. C., Sahu, R. K., and Panda, S. (2016). Firefly algorithm optimized fuzzy pid controller for agc of multi-area multi-source power systems with upfc and smes. Eng. Sci. Technol. Int. J. 19 (1), 338–354. doi:10.1016/j.jestch.2015.08.007
Prostejovsky, A. M., Marinelli, M., Rezkalla, M., Syed, M. H., and Guillo-Sansano, E. (2018). Tuningless load frequency control through active engagement of distributed resources. IEEE Trans. Power Syst. 33, 2929–2939. doi:10.1109/TPWRS.2017.2752962
Priyadarshani, S., Subhashini, K. R., and Satapathy, J. K. (2020). Pathfinder algorithm optimized fractional order tilt-integral-derivative (fotid) controller for automatic generation control of multi-source power system. Microsyst. Technol. 10, 23–35. doi:10.1007/s00542-020-04897-4
Revathi, D., and Mohan Kumar, G. (2020). Analysis of LFC in PV-thermal-thermal interconnected power system using fuzzy gain scheduling. Int. Trans. Electr. Energ Syst. 30 (5). doi:10.1002/2050-7038.12336
Shah, R., Preece, R., and Barnes, M. (2018). The impact of voltage regulation of multi-infeed VSC-HVDC on power system stability. IEEE Trans. Energy Conv. 33, 1614–1627. doi:10.1109/TEC.2018.2831692
Soleimani, K., and Mazloum, J. (2018). Designing a GA-based robust controller for load frequency control (LFC). Eng. Technol. Appl. Sci. Res. Apr 8 (2), 2633–2639. doi:10.48084/etasr.1592
Topno, P. N., and Chanana, S. (2017). Differential evolution algorithm-based tilt integral derivative control for LFC problem of an interconnected hydro-thermal power system. J. Vib. Control Jul 24 (17), 3952–3973. doi:10.1177/1077546317717866
Young-Hyun, M., Heon-Su, Ryu, Kim, B., and Song, K. B. (2000) Optimal tracking approach to load frequency control in power systems. Presented at the Proceedings of the 2000 IEEE Power Engineering Society Winter Meeting. Conference Proceedings. January 2000 Singapore. doi:10.1109/pesw.2000.850163
Zhang, G., Mccalley, J., and Wang, Q. (2019). An AGC dynamics-constrained economic dispatch model. IEEE Trans. Power Syst. 34, 3931–3940. doi:10.1109/TPWRS.2019.2908988
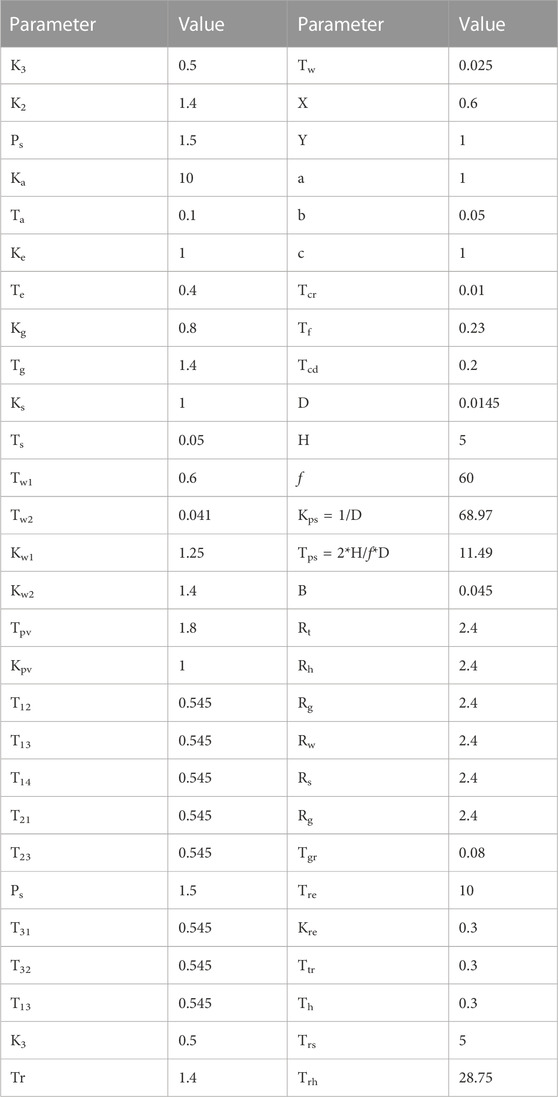
TABLE A1. Parameters of multi source hybrid power system (Liu et al., 2022).
Keywords: power system, renewable energies, automatic generation control, load frequency control, metaheuristic techniques, smart grids
Citation: Zhang P, Daraz A, Malik SA, Sun C, Basit A and Zhang G (2023) Multi-resolution based PID controller for frequency regulation of a hybrid power system with multiple interconnected systems. Front. Energy Res. 10:1109063. doi: 10.3389/fenrg.2022.1109063
Received: 27 November 2022; Accepted: 31 December 2022;
Published: 15 February 2023.
Edited by:
Petru Simionescu, Texas A&M University Corpus Christi, United StatesReviewed by:
Sahaj Saxena, Thapar Institute of Engineering & Technology, IndiaCopyright © 2023 Zhang, Daraz, Malik, Sun, Basit and Zhang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Guoqiang Zhang, Z3VvcWlhbmdfemhhbmdAbmJ0LmVkdS5jbg==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.