An improved LSTM-Seq2Seq-based forecasting method for electricity load

Power load forecasting has gained considerable research interest in recent years. The power load is vulnerable to randomness and uncertainty during power grid operations. Therefore, it is crucial to effectively predict the electric load and improve the accuracy of the prediction. This study proposes a novel power load forecasting method based on an improved long short-term memory (LSTM) neural network. Thus, an long short-term memory neural network model is established for power load forecasting, which supports variable-length inputs and outputs. The conventional convolutional neural network (CNN) and recurrent neural network (RNN) cannot reflect the sequence dependence between the output labels. Therefore, the LSTM-Seq2Seq prediction model was established by combining the sequence-to-sequence (Seq2Seq) structure with that of the long short-term memory model to improve the prediction accuracy. Four prediction models, i.e., long short-term memory, deep belief network (DBN), support vector machine (SVM), and LSTM-Seq2Seq, were simulated and tested on two different datasets. The results demonstrated the effectiveness of the proposed LSTM-Seq2Seq method. In the future, this model can be extended to more prediction application scenarios.

1 Introduction

Smart grids are the future direction of development for power grids. For the safe, stable, and efficient operation of power systems, it is necessary to develop advanced information processing and application technologies (Majeed Butt et al., 2021; Javed et al., 2022). Current power industry research is gradually progressing toward the refinement and dispatching optimization stage, which has the potential to improve the optimal allocation of social resources. Consequently, all entities in the power industry, including power generation companies, power planning enterprises, and scheduling departments, must be able to perceive the shifting patterns and growth trends of grid loads with greater precision. Therefore, accurate grid load forecasting is a crucial prerequisite for scientific power generation, dispatch, and distribution (Aslam et al., 2021). Forecasting grid loads entails analyzing historical loads in addition to meteorological, economic, and other factors to determine the changing characteristics and operating modes of future power grid loads. It is the basis for power generation planning, market trading, and power dispatching. In addition, it is an indispensable resource for the construction and maintenance of power grids (Velasquez et al., 2022). There are four forecasting scales based on the forecast time: Long-term, medium-term, short-term, and ultra-short-term. The accuracy of the prediction of the power load directly affects the safety and stability of the development of the power industry. A more accurate load forecast leads to a more efficient utilization of power generation equipment and an increase in the dispatching precision (Jahan et al., 2020). Therefore, improving power load forecasting technology is essential for the effective operation of the power sector.

Among the four scales of prediction, the short-term and ultra-short-term predictions are the most significant. It is crucial for power planning and dispatching systems to improve the accuracy of short-term load forecasts. In addition, the improvement of the algorithm for short-term load forecasting provides the foundation for refined power dispatching and management. However, the short-term load forecasting system for the power grid necessitates flawless load forecasting, analysis, and management functions. In this study, a method of deep learning was used to improve the accuracy of power load forecasting. To predict the power load, a long-short-term memory (LSTM) neural network model was established. Further, we developed a novel sequence-to-sequence (Seq2Seq) prediction model by adapting an LSTM neural network to irregular inputs.

It is essential for the operation and design of a power system to determine the load change law during the day, night, and year. Typically, the power loads are continuous and do not fluctuate abruptly. The majority of factors influencing system load exhibit regularity, which facilitates accurate prediction. Nevertheless, the short-term or ultra-short-term load is a non-stationary stochastic process in the time series due to the influence of a variety of factors, such as weather changes and social activities. Therefore, randomness and uncertainty must be taken into account to improve the accuracy of the forecasting model’s predictions. This study presents a method for load forecasting based on a network with LSTM neural network. The following are the main contributions of this study:

(i) Utilizing an LSTM neural network, a model for predicting electricity load was developed. The process of modeling is described in detail. In the electricity load forecasting problem involving a time series, the simulation results demonstrated that the prediction performance of the LSTM-based model was better than that of the feedforward neural network.

(ii) On the basis of the aforementioned LSTM model, a Seq2Seq optimization model was proposed. This model solves the issue encountered by conventional recurrent neural networks (RNN), which cannot account for the sequence dependency between output tags. Furthermore, it supports inputs and outputs of variable length, which enhances the adaptability of the entire framework for prediction.

(iii) The established hybrid LSTM-Seq2Seq-based model’s efficacy was evaluated utilizing two distinct electricity load datasets from the United States and Switzerland. The experimental results demonstrated that the structure of the LSTM-Seq2Seq-based prediction model is superior to that of other prediction models, regardless of whether the influencing factors are included in the prediction process.

The remainder of the paper is organized as follows: The Section 2 presents an introduction to related works on power load forecasting. In Section 3, an LSTM-based forecasting method is proposed. On this basis, an improved LSTM-Seq2Seq forecasting framework is put forward in Section 4. The paper provides experiments in the next section. Lastly, the concluding remarks are provided in Section 6.

2 Related works

In the past several decades, extensive research has been conducted on power-load forecasting. There are lots of methods including artificial neural networks, support vector regression, decision tree, linear regression, and fuzzy sets (Jahan et al., 2020). Velasquez et al. (2022) examined three time series approximations and their respective combinations. The results demonstrated that the seasonal regression method presented the best approximation effect, while a combination of the time series methods assisted in reducing the approximation error. Löschenbrand et al. (2021) developed a fitted non-linear Bayesian regression model utilizing Bayesian neural networks for short-term load forecasting. It permitted the generation of samples from non-linear probabilistic forecasts that do not require the tuning properties of deep-learning methods. The uncertainty in the data and the probability distribution of the electric load data can be statistically formulated. Liu et al. (2022) proposed a model forecasting method by combining multivariate phase space reconstruction and support vector regression, and obtained improved short-term load forecasting results for multiple energy sources.

Machine-learning methods have been widely implemented in load forecasting due to the development of non-linear research. They present better learning abilities in the complex non-linear correlation of power data when compared to the conventional prediction techniques (Lee and Cho, 2021). Currently, various machine learning methods are being implemented, including the back-propagation neural network (BP) (Bian et al., 2020), convolutional neural network (CNN) (Imani, 2021; Zhang et al., 2021), artificial neural network (ANN) (Xiao et al., 2022; Sa’ad et al., 2022; Aly, 2020), LSTM networks (Bouktif et al., 2018; Kong et al., 2019; Yu et al., 2019; Memarzadeh and Keynia, 2021; Peng et al., 2022; Zhaorui Meng and Xie, 2022), support vector machine (SVM) (Xia et al., 2018; Mayur Barman, 2020), extreme learning machine (ELM) (Chen et al., 2020; Jeddi and Sharifian, 2020; Sahu et al., 2021; Krishna Rayi et al., 2022), and deep belief network (DBN) (Gao et al., 2022; Hong et al., 2022). Using only a neural network for load forecasting faces several limitations since it cannot fully utilize historical data for learning and generalization. Therefore, extensive research has been conducted to overcome these limitations by combining optimization algorithms and neural networks to improve the accuracy of the prediction results.

Peng et al. (2021) proposed and evaluated a forecasting method that combined a backtracking search optimization algorithm with a double-reservoir echo state network. Hu et al. (2019) proposed a short-term power load forecasting model based on a hybrid GA-PSO-BPNN algorithm that was used to optimize the parameters of the BPNN; however, it could not prevent the prediction results from easily falling into the local optimum. Krishna Rayi et al. (2022)developed an efficient hybrid time series forecasting model by combining variational mode decomposition and a deep learning mixed kernel ELM autoencoder which presented a precise prediction of wind power. Dong et al. (2021) proposed a distributed belief network (DDBN) with a Markov switching topology to avoid manually adjusting the weights of hidden layer nodes. It presents good model generalization performance and generates an accurate solution of output weights through the generalized least squares method, thus conserving storage space and improving the prediction accuracy. Bashir et al. (2022) proposed a hybrid method using prophet and LSTM models to circumvent the low-speed convergence limitation in an effort to accurately predict load. Zheng et al. (2017) developed an improved hybrid short-term load prediction model by combining similar day selection, empirical mode decomposition, and an LSTM neural network. It presented a higher prediction accuracy than the LSTM model.

3 LSTM-based forecasting framework

The process of power load forecasting can generally be divided into data acquisition, dataset production, forecasting model establishment, load forecasting, and result evaluation. The acquisition of actual and reliable power load data is crucial in the first stage of load forecasting. Two different sets of power load data were used in this study. These are the Swiss power load data obtained from the European Internet Network website (ENTSO-e) and the power load data obtained from Atlanta city in the United States from the data platform. In the second stage, the collected data were preprocessed and the training, verification, and test datasets were established. A prediction model was established in the third stage. Subsequently, the established load forecasting model is tested using the data in the validation dataset, and the model is continuously corrected and improved until it is adjusted to the optimal state. Lastly, the prepared dataset was verified, and the effectiveness of the model was evaluated using evaluation indicators. Figure 1 depicts the power load forecasting process.

FIGURE 1

FIGURE 1. Flowchart of power load forecasting.

Time series is an important factor in power load data. RNNs typically present more advantages in predictions involving time series when compared to feedforward neural networks. However, they face two major problems during the training process. Firstly, the longer the distance from the current time step during the training process, the less significant the gradient signal. They also face capture capability failure, which is a problem of gradient disappearance. Secondly, each training step must take a derivative of the activation function. If the result of this part is greater than one, the gradient update will increase exponentially with the increase in the number of layers, and a gradient explosion will eventually occur.

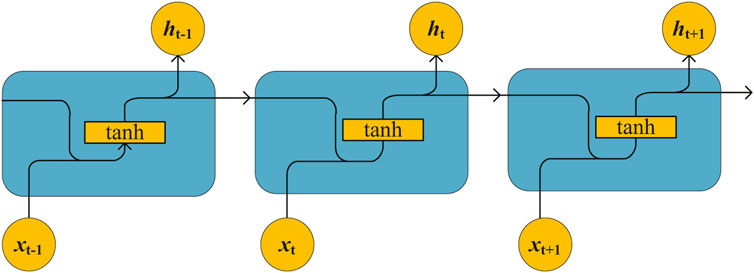
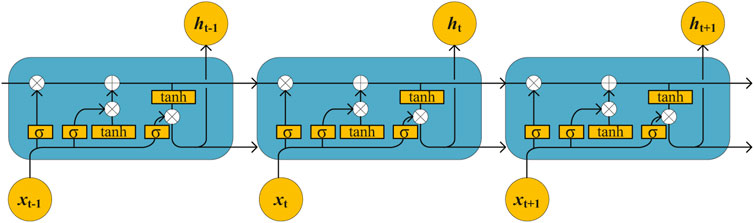
This paper proposes a load forecasting model based on an LSTM neural network to overcome the drawbacks of the RNN; the LSTM neural network is an improved RNN. The RNN network has the chained form of an RNN module; this loop module has a very simple structure, as shown in Figure 2. Each module of the RNN network contains a tanh layer. The network structure of the LSTM is similar to that of an RNN, except in the recurrent module, as shown in Figure 3. Unlike the single neural network layer of RNN, the LSTM neural network has four layers, which interact differently.

FIGURE 2

FIGURE 2. The chain of RNN.

FIGURE 3

FIGURE 3. The chain of LSTM neural network.

There are four parts in an LSTM neural network cell model: the input and output, and the forgetting and updating parts, as shown in Figure 4. In Figure 4, x_t denotes the input at moment t, h_t denotes the hidden state at moment t, and c_t denotes the cell state at moment t. σ represents the logistic sigmoid function which outputs a probability value between zero and one, indicating the possibility of signal passing. Zero indicates that the signal cannot pass, and 1 indicates that all the signals are allowed to pass.

FIGURE 4

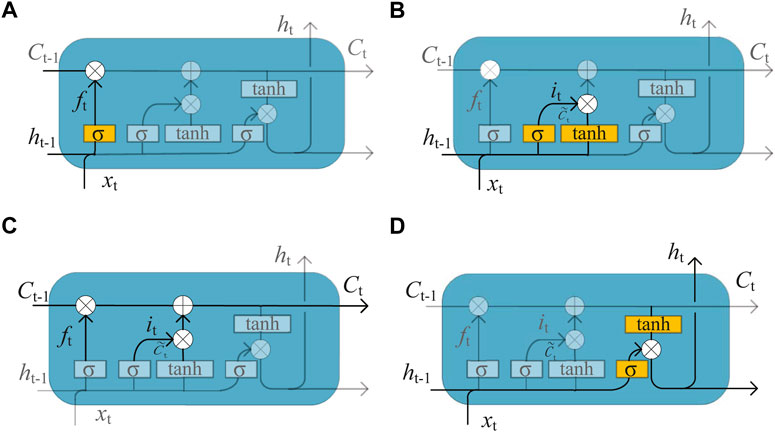
FIGURE 4. Structure of a cell in the LSTM neural network. (A) Forgetting gate. (B) Input gate. (C) State updating part. (D) Output gate.

Each cell has a complex structure, which is controlled by three gates: the forgetting gate, input gate, and output gate. The cell controls the information in the network using the three gates to remove or add information to the cellular state c_t, i.e., “memory.” The forgetting gate determines the forgetting intensity, as shown in Figure 4A f_t denotes the gate control switch of the forgetting door, which controls the number of previous forgotten cell states. Similar to human memory, the forgetting gate can obtain the function of forgetting unimportant information, while retaining important information.

$f_t=\sigma \left(W_f\left[h_{t-1},x_t\right]+b_f\right)(1)$

Figure 4B depicts the input gate, which receives new information from the extracellular input and selectively remembers the input at the current state and the data in the previously hidden state. This creates a new vector that holds the data; this vector can be updated. In the input gate, the tanh layer determines the candidate value of the updated content and the sigmoid layer determines the content to be updated. The probability value lies between 0 and 1.

$i_t=\sigma \left(W_i\left[h_{t-1},x_t\right]+b_i\right)(2)$

${\stackrel{\sim }{c}}_t=\text{tanh}\left(W_c\left[h_{t-1},x_t\right]+b_c\right)(3)$

The next step involves updating the cell state, as shown in Figure 4C. The specific process is as follows. Firstly, c_t−1 of the previous moment is updated to c_t, where c_t−1 is multiplied by f_t. Subsequently, the unimportant information is forgotten and the important information is retained. Lastly, the information left in the current input is retained to obtain the latest cell status. This step changes based on the extent to which each state is updated.

$c_t=f_t\cdot c_{t-1}+i_t\cdot {\stackrel{\sim }{c}}_t(4)$

The sigmoid layer in the output gate determines the output from the current cell state, as shown in Figure 4D. This process is performed using the tanh function. The output of the sigmoid layer is then multiplied by the processed value between -1 and 1 to obtain the output. Lastly, the output gate transfers the obtained cell state c_t and the output h_t to the next cell.

$o_t=\sigma \left(W_o\left[h_{t-1},x_t\right]+b_o\right)(5)$

$h_t=o_t\cdot \text{tanh}\left(c_{t-1}\right)(6)$

where W_f, W_i, W_c, and W_o are the weight matrices of the forgetting gate, input gate, cell state, and output gate, respectively; b_f, b_i, b_c, and b_o are the corresponding bias vectors.

The conventional LSTM neural network model solves the n-step prediction problem by adding a dense layer when outputting h_t. This maps the hidden state to an n-dimensional vector, thus satisfying the data format of the problem. The n steps to be predicted are completely independent at this point. Consequently, the sequence dependence between the output tags cannot be considered when using the LSTM neural network for prediction. Furthermore, the LSTM neural networks cannot support variable-length input. Essentially, if a sensor suddenly fails during monitoring, resulting in a partial loss of the prediction data, an LSTM neural network may not be able to complete the training. These limitations can be overcome using the proposed LSTM-based power load forecasting model, which employs the sequence-to-sequence method.

4 LSTM-Seq2Seq forecasting framework

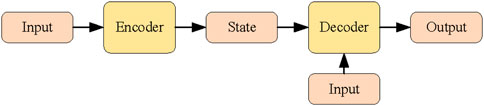
Cho et al. (2014) proposed the first sequence-to-sequence (Seq2Seq) model and used it to solve the problem of phrase representation learning. Their model was developed by combining an encoder-decoder architecture with an RNN. Sutskever et al. (2014) employed an encoder-decoder with an LSTM neural network to perform sequence-to-sequence learning tasks in the field of machine translation and achieved good results. In this study, an LSTM-Seq2Seq forecasting framework was designed and an LSTM neural network was deployed for the encoder and decoder. It contains two main components: an encoder and a decoder. The encoder accepts a variable-length sequence and converts it into a coded state in a fixed format by using an LSTM neural network. The decoder also comprises an LSTM neural network which maps the fixed-form encoded state to a variable-length sequence. This is called the encoder-decoder architecture, as shown in Figure 5. This structure can overcome the problem faced during the training process, where training cannot be performed due to the lack of input data.

FIGURE 5

FIGURE 5. Encoder-Decoder architecture.

In the encoding process, the encoder first encodes the variable-length sequence data into a fixed-length intermediate vector. The intermediate state vector can be considered as a fixed-length representation of the input sequence, which is generally known as the background vector. In the decoding process, the decoder decodes a fixed-length intermediate vector as the prediction output. This enables an input sequence of any length to be mapped to an output sequence of any length.

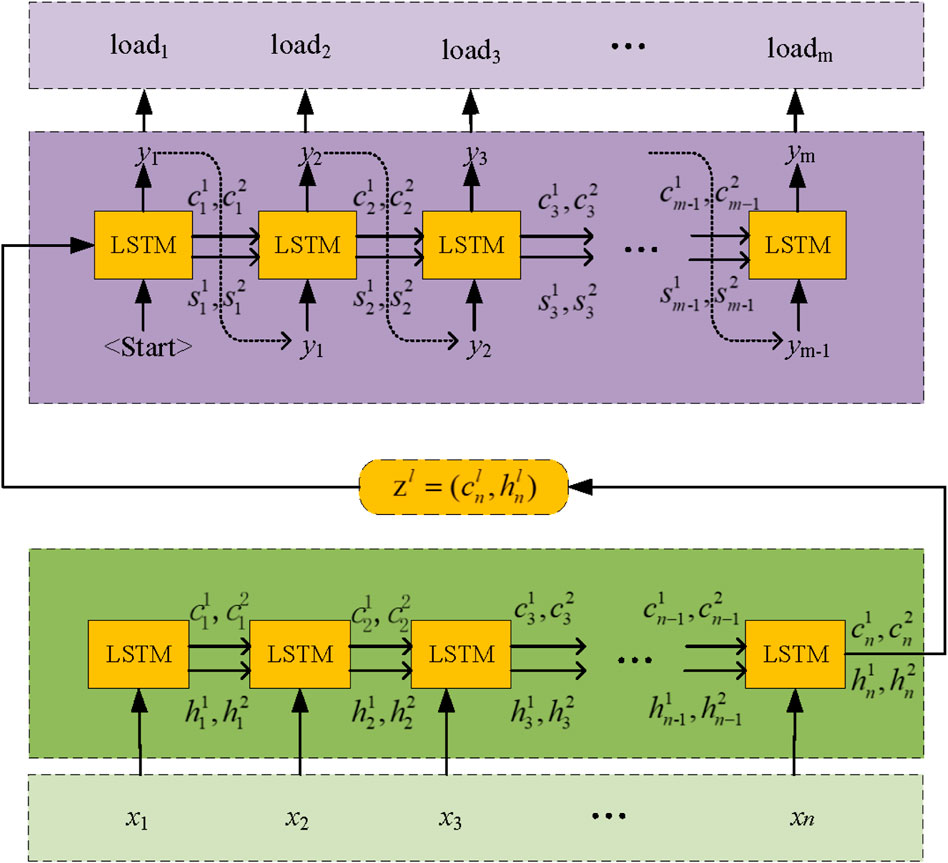
Figure 6 depicts the LSTM-Seq2Seq framework proposed for predicting power load. Define an input sequence x = (x₁, x₂, … , x_n) and encode it using a multi-layer LSTM. After being embedded, the input array x is fed into the first layer of a multi-layer LSTM, and the hidden states h = {h₁, h₂, …, h_n} output by this layer serve as inputs to the LSTM in the layer above. Thus, representing each layer with a superscript l (l = 1, 2, …, k) yields the following expression for the hidden states in the corresponding layer.

$h_n^l={\text{EncoderLSTM}}^l\left(x_n,h_{n-1}^l\right)(7)$

FIGURE 6

FIGURE 6. The framework of the LSTM-Seq2Seq model.

Using a multi-layer LSTM also necessitates the input of an initial hidden state per layer $h_0^l$ and the output of a state vector per layer z^l. This paper simply views c_n as another type of hidden state. Similar to $h_0^l$, $c_0^l$ will be initialized to a tensor of all zeros. In addition, the intermediate state vector is now the final hidden state and the final cell state, i.e. $z^l=(h_n^l,c_n^l)$.

We obtain the following by extending our multilayer equations to LSTMs:

$\left(h_n^l,c_n^l\right)={\text{EncoderLSTM}}^l\left(x_n,\left(h_{n-1}^l,c_{n-1}^l\right)\right)(8)$

Next, we construct a decoder, that is also a multi-layer LSTM. The “Decoder” class performs a single decoding step per time-step, i.e., it outputs a single token. $(s_{m-1}^l,c_{m-1}^l)$, s_m and c_m represent the hidden layer state and final cell state of the decoder, respectively. And feeds it to the LSTM along with the current embedded token y_m to generate a new hidden and cell state $(s_m^l,c_m^l)$. The subsequent layers will utilize the hidden state of the layer beneath them $s_m^{l-1}$ as well as the previous hidden and cell states from their layer $(s_{m-1}^l,c_{m-1}^l)$. This provides equations that closely resemble those in the encoder.

$s_m=\text{DecoderLSTM}\left(y_m,s_{m-1}\right)(9)$

$\left(s_m^l,c_m^l\right)={\text{DecoderLSTM}}^l\left(y_m,\left(s_{m-1}^l,c_{m-1}^l\right)\right)(10)$

Initial hidden and cell states for the decoder are intermediate state vectors, which are the encoder’s final hidden and cell states from the same layer, i.e. $(s_0^l,c_0^l)=z^l=(h_m^l,c_m^l)$. Then, we pass the hidden state of the LSTM’s top layer $s_m^l$ through a linear layer f to make a prediction of what the next token in the target (output) sequence should be ${\widehat{y}}_{m+1}$. The data in the decoder are always produced sequentially, one per time step. Use the actual next data from the dataset y_m sometimes and the word predicted by our decoder ${\widehat{y}}_{m-1}$ other times. This is referred to as “teacher forcing.”

${\widehat{y}}_{m+1}=f\left(s_m^l\right)(11)$

5 Experiment

5.1 Dataset selection

The effectiveness of the proposed LSTM-Seq2Seq model is verified using two datasets from different regions. Dataset 1 is Switzerland’s power-load data, which was provided by the European Internet Network (ENTSO-e). Contrary to other EU countries, Swiss electricity is primarily generated by hydropower, nuclear power, and conventional thermal power plants, accounting for 59.9%, 33.5%, and 2.3%, respectively. The dataset includes the hourly power load data from 2015 to 2017, as well as weather features, such as the temperature and wind speed. Dataset 2 contains the power load data of Atlanta in the United States from 2015 to 2017, which was provided by the data platform. It also recorded the hourly electric load data during this period. Unlike Dataset 1, Dataset 2 contains only the time-series and power load data. The prediction performance of the proposed LSTM-Seq2Seq model was evaluated by comparing it with three prediction methods: the DBN, SVM, and conventional LSTM. Each prediction model selects the 100-day data from the dataset for testing. Figures 7A, B present the real power load data of Switzerland and Atlanta, the United States, respectively.

FIGURE 7

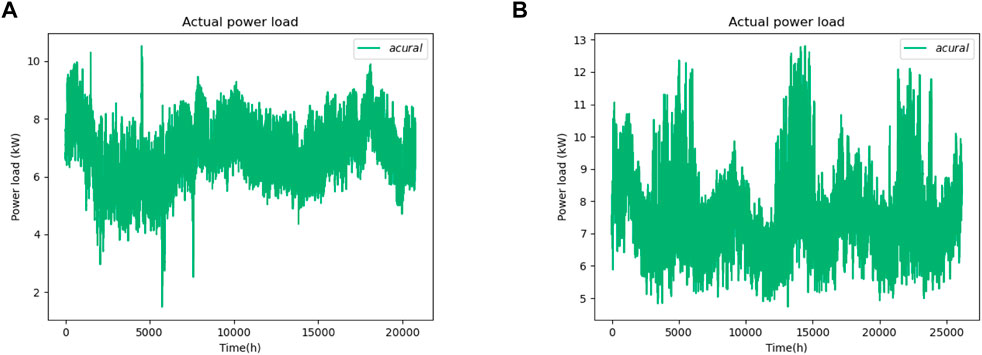
FIGURE 7. Diagrams on electricity loads of Switzerland and the city Atlanta, United States. (A) Electricity data of Switzerland. (B) Electricity data of the city Atlanta.

5.2 Experimental environment

The simulation experiments were conducted on a computer equipped with Intel Core i7-9800X @ 3.8 G Hz and 32.0 GB RAM. The development software Pycharm, was used as the software environment for this testing. It was combined with the Anaconda platform to install the dependency environment for the algorithms and required packages. The electrical load forecasting models were implemented using Keras 2.3.1 and Tensorflow 1.14.0.

5.3 Evaluation indicators

There are evaluation indicators for prediction models, such as the mean square error (MSE), root mean square error (RMSE), and mean absolute percentage error (MAPE). RMSE and MAPE are described as follows:

$RMSE=\sqrt{\frac{\sum _{i=1}^n{\left({\widehat{y}}_i-y_i\right)}^2}{n}}(12)$

$MAPE=\frac{\sum _{i=1}^n\left|{\widehat{y}}_i-y_i\right|}{y_i}\cdot \frac{100\%}{n}(13)$

5.4 Comparison of the LSTM model and a FFNN model

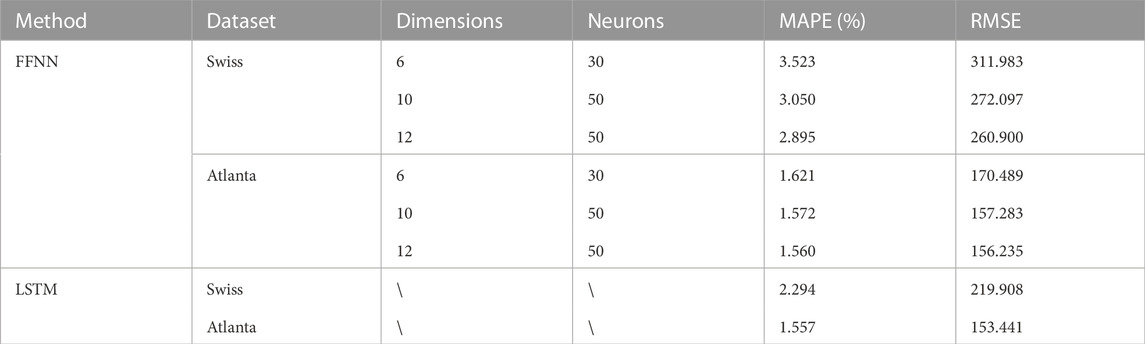
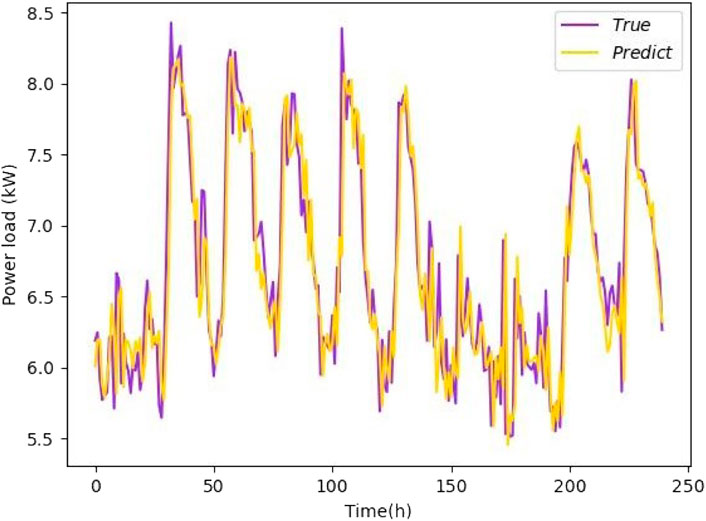
We trained and tested the proposed LSTM neural network power load forecasting model. We evaluated its performance by comparing it with the feedforward neural network (FFNN) model. Several groups of FFNN parameters were set for specific parameter settings, as shown in Table 1. Datasets 1 and 2 were used for load forecasting. Dataset 1 contains the electricity load data for Switzerland. Dataset 2 contains the electricity load data for Atlanta in the United States. To facilitate visual observation, we intercepted a segment of 240 data points from 2,400 forecast data points and drew forecast curves, as shown in Figure 8. Figures 8A, B present the experimental results of the FFNN model with datasets 1 and 2, respectively, and Figures 8C, D present the experimental results of the LSTM model with datasets 1 and 2, respectively. Table 1 presents the performances of the two load prediction models. It can be observed that the LSTM model performed slightly better than the FFNN model for both datasets. However, the performance of the LSTM model was not outstanding in terms of the prediction accuracy.

TABLE 1

TABLE 1. Experimental results of LSTM and FFNN.

FIGURE 8

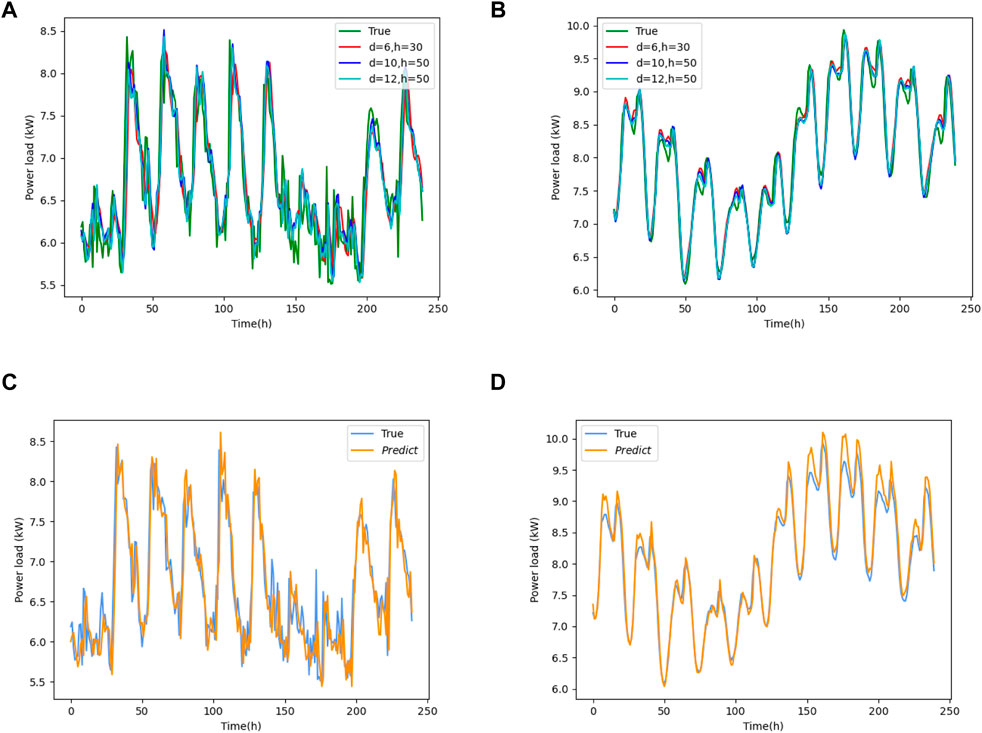
FIGURE 8. Prediction results of the FFNN model and the LSTM Model with the two Datasets. (A) Results of the FFNN model with Dataset 1. (B) Results of the FFNN model with Dataset 2. (C) Results of the LSTM model with Dataset 1. (D) Results of the LSTM model with Dataset 1.

5.5 Testing of the LSTM-Seq2Seq model

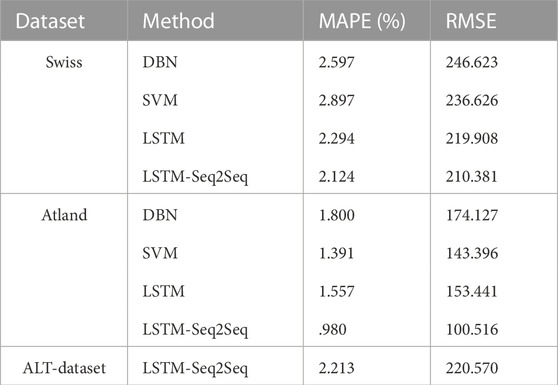
The LSTM-Seq2Seq model primarily handles the time-series and variable-length input and output problems. The two datasets from the above section were used to test the model. The LSTM-Seq2Seq model proposed in this paper can be optimized by changing the model parameters of the encoder and decoder, and the parameter adjustment method is the same as that of the LSTM model. Both the encoder and decoder in this paper use a two-layer LSTM model, in which the number of hidden layer nodes of the encoder and decoder is 512, the batch size is 50, and the epoch is 50. The validation sample rate validation_split of the dataset is .05, which means that 5% of the data in the dataset is used to validate the prediction results. Figure 9 presents the experimental results of the three forecasting models on the two datasets, including the DBN, SVM, and LSTM-Seq2Seq models. The DBN and SVM models were compared with the LSTM-Seq2Seq model. Figures 9A, B present the prediction results of the DBN model, Figures 9C, D present the prediction results of the SVM model, and Figures 9E, F present the experimental results of the LSTM-Seq2Seq model. Table 2 lists the evaluation indices for the four prediction models. The MAPE of the LSTM model was 2.294% and 1.557% for Datasets 1 and 2, respectively. When compared to the experimental results of the LSTM-Seq2Seq model, the MAPE of the LSTM-Seq2Seq model on Dataset 1 decreased by .17%. However, the MAPE for Dataset 2 decreased by .577%. Therefore, the LSTM-Seq2Seq structure can significantly improve the prediction accuracy of the power-load forecasting system.

FIGURE 9

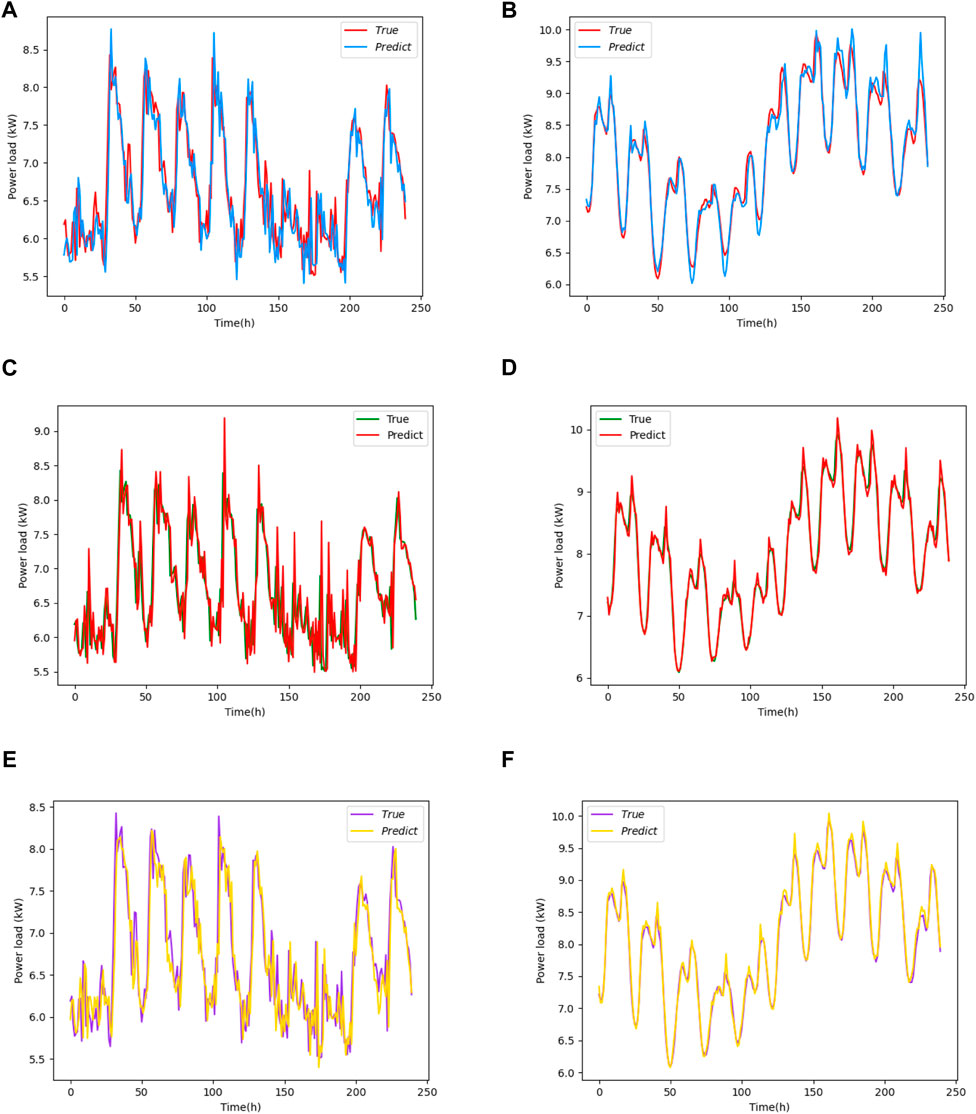
FIGURE 9. True and predicted load with different models with dataset 1 and dataset 2. (A) Results of the DBN model with dataset 1. (B) Results of the DBN model with dataset 1. (C) Results of the SVM model with dataset 1. (D) Result of the SVM model with dataset 2. (E) Results of the LSTM-Seq2Seq model with dataset 1. (F) Results of the LSTM-Seq2Seq with dataset 2.

TABLE 2

TABLE 2. Experimental results of DBN, SVM, LSTM and LSTM-Seq2Seq.

The LSTM-Seq2Seq model also supports variable-length input data. For example, when the temperature factor in the prediction dataset is partially missing due to sensor faults, the conventional LSTM network cannot perform arithmetic prediction. This problem can be solved by the improved LSTM-Seq2Seq model. We changed the data in Dataset 1 to obtain a new dataset called the ALT-dataset, in which the data of weather characteristics such as the temperature, wind speed, and humidity were randomly removed. The new ALT-dataset was used to test the LSTM-SeqSeq model and the MAPE is obtained as 2.213%. The accuracy of this prediction was only slightly lower than that of the original dataset. Figure 10 depicts the experimental curves. Figures 11A, B depict the error curves of Datasets 1 and 2, respectively. Since the ALT dataset was generated by randomly removing the input data, only the LSTM-Seq2Seq method proposed in this paper was applicable. Table 2 demonstrated that the LSTM-Seq2Seq method cannot significantly improve MAPE performance, but it had its own unique advantages when dealing with time series problems with variable length inputs.

FIGURE 10

FIGURE 10. Results of the LSTM-Seq2Seq model with ALT-dataset.

FIGURE 11

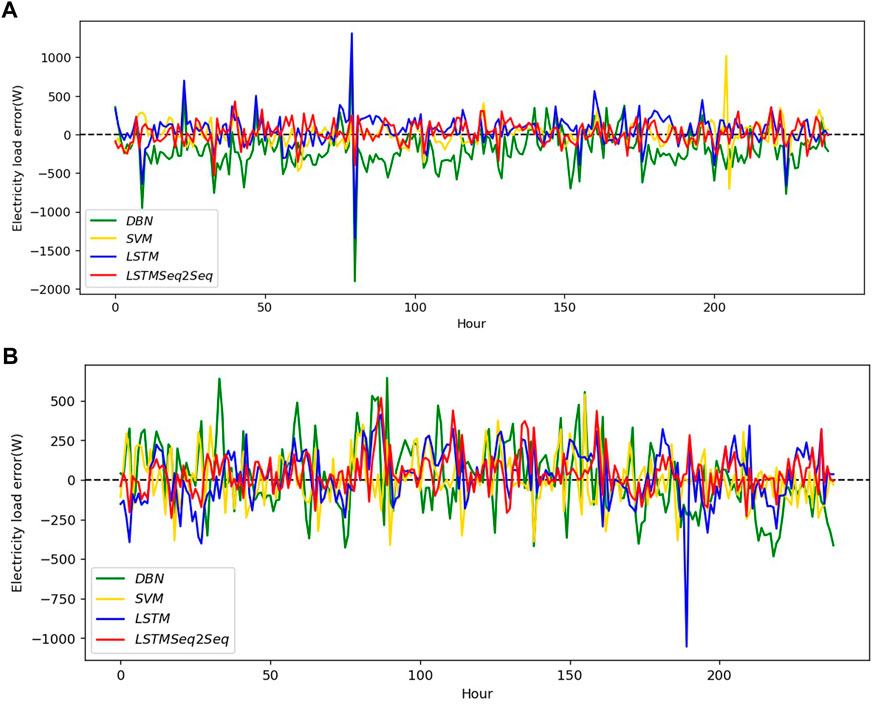
FIGURE 11. Error curves with different models with the two datasets. (A) Error curves with different models with dataset 1. (B) Error curves with different models with dataset 2.

6 Conclusion

Ensuring the precision of the power industry load forecasting is crucial for improving the utilization rate of the power generation equipment and the effectiveness of economic dispatch. In this paper, we proposed a new forecasting framework by combining the Seq2Seq structure and LSTM network, and by considering the time series and variable length input-output factors. This model supports variable-length inputs and outputs and also improves the flexibility of the prediction model. Furthermore, it overcomes the limitations faced by the conventional RNN and CNN, which cannot consider the sequence dependence between the output labels. The actual data from different countries and regions were used for testing and evaluating the proposed prediction model. Additionally, four prediction models, i.e., DBN, SVM, LSTM, and LSTM-Seq2Seq, were compared to determine the effectiveness of the proposed model. The experimental results demonstrate that the LSTM-Seq2Seq prediction model presents a better prediction performance. This model can be extended to more prediction application scenarios in the future due to the consideration of the variable-length input-output characteristics.

When CNN is used to learn time series, additional processing is required, and the results are typically subpar. Typically, RNN is better suited for time series-sensitive problems, but it has long-term dependence and gradient explosion or vanishing issues. It is difficult for RNN to store data for an extended period of time. The LSTM with a special implicit unit is intended to maintain the input for an extended period of time, making it suitable for time series problems. Concurrently, LSTM solves the Vanishing Gradient problem caused by the gradual decrease of RNN during gradient backpropagation. It is evident that LSTM is advantageous for the power load forecasting problem. However, when the input variable changes, LSTM becomes ineffective. Currently, the proposed LSTM-Seq2Seq model can effectively address the issue of variable input or output scale. However, the LSTM-Seq2Seq model does not have an advantage in parallel processing. When the network is large, it is computationally intensive and time-consuming. Additionally, parameter adjustment becomes challenging. In order for it to be calculated faster, we are currently working to simplify the LSTM-Seq2Seq model by reducing the number of parameters and making it easy to tune, while maintaining its prediction accuracy.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: https://github.com/dafrie/lstm-load-forecasting/blob/master/data/fulldataset.csv https://dataminer2.pjm.com/feed/hrl_load_prelim/definition.

Author contributions

YM: Writing—original draft preparation, methodology, software. MW: Conceptualization, validation, supervision. XZ: Data curation, visualization, investigation. HG: Writing—reviewing and editing.

Funding

This work is supported by the National Natural Science Foundation of China under Grant Nos. 62073196 and U1806204.

Conflict of interest

Author HG was employed by Shandong Zhengchen Technology Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aly, H. H. (2020). A proposed intelligent short-term load forecasting hybrid models of ann, wnn and kf based on clustering techniques for smart grid. Electr. Power Syst. Res. 182, 106191. doi:10.1016/j.epsr.2019.106191

CrossRef Full Text | Google Scholar

Aslam, S., Herodotou, H., Mohsin, S. M., Javaid, N., Ashraf, N., and Aslam, S. (2021). A survey on deep learning methods for power load and renewable energy forecasting in smart microgrids. Renew. Sustain. Energy Rev. 144, 110992. doi:10.1016/j.rser.2021.110992

CrossRef Full Text | Google Scholar

Bashir, T., Haoyong, C., Tahir, M. F., and Liqiang, Z. (2022). Short term electricity load forecasting using hybrid prophet-lstm model optimized by bpnn. Energy Rep. 8, 1678–1686. doi:10.1016/j.egyr.2021.12.067

CrossRef Full Text | Google Scholar

Bian, H., Zhong, Y., Sun, J., and Shi, F. (2020). Study on power consumption load forecast based on k-means clustering and fcm–bp model. Energy Rep. 6, 693–700. doi:10.1016/j.egyr.2020.11.148

CrossRef Full Text | Google Scholar

Bouktif, S., Fiaz, A., Ouni, A., and Serhani, M. A. (2018). Optimal deep learning lstm model for electric load forecasting using feature selection and genetic algorithm: Comparison with machine learning approaches †. Energies 11, 1636. doi:10.3390/en11071636

CrossRef Full Text | Google Scholar

Chen, X., Wang, Y., and Tuo, J. (2020). Short-term power load forecasting of gwo-kelm based on kalman filter. IFAC-PapersOnLine 53, 12086–12090. doi:10.1016/j.ifacol.2020.12.760

CrossRef Full Text | Google Scholar

Cho, K., van Merrienboer, B., Gülçehre, Ç., Bougares, F., Schwenk, H., and Bengio, Y. (2014). Learning phrase representations using RNN encoder-decoder for statistical machine translation. Available at: http://org.CoRR/abs/1406.1078

CrossRef Full Text | Google Scholar

Dong, Y., Dong, Z., Zhao, T., Li, Z., and Ding, Z. (2021). Short term load forecasting with markovian switching distributed deep belief networks. Int. J. Electr. Power & Energy Syst. 130, 106942. doi:10.1016/j.ijepes.2021.106942

CrossRef Full Text | Google Scholar

Gao, J., Wang, X., and Yang, W. (2022). Spso-dbn based compensation algorithm for lackness of electric energy metering in micro-grid. Alexandria Eng. J. 61, 4585–4594. doi:10.1016/j.aej.2021.10.018

CrossRef Full Text | Google Scholar

Hong, F., Wang, R., Song, J., Gao, M., Liu, J., and Long, D. (2022). A performance evaluation framework for deep peak shaving of the cfb boiler unit based on the dbn-lssvm algorithm. Energy 238, 121659. doi:10.1016/j.energy.2021.121659

CrossRef Full Text | Google Scholar

Hu, Y., Li, J., Hong, M., Ren, J., Lin, R., Liu, Y., et al. (2019). Short term electric load forecasting model and its verification for process industrial enterprises based on hybrid ga-pso-bpnn algorithm—A case study of papermaking process. Energy 170, 1215–1227. doi:10.1016/j.energy.2018.12.208

CrossRef Full Text | Google Scholar

Imani, M. (2021). Electrical load-temperature cnn for residential load forecasting. Energy 227, 120480. doi:10.1016/j.energy.2021.120480

CrossRef Full Text | Google Scholar

Jahan, I. S., Snasel, V., and Misak, S. (2020). Intelligent systems for power load forecasting: A study review. Energies 13, 6105. doi:10.3390/en13226105

CrossRef Full Text | Google Scholar

Javed, A. R., Shahzad, F., ur Rehman, S., Zikria, Y. B., Razzak, I., Jalil, Z., et al. (2022). Future smart cities: Requirements, emerging technologies, applications, challenges, and future aspects. Cities 129, 103794. doi:10.1016/j.cities.2022.103794

CrossRef Full Text | Google Scholar

Jeddi, S., and Sharifian, S. (2020). A hybrid wavelet decomposer and gmdh-elm ensemble model for network function virtualization workload forecasting in cloud computing. Appl. Soft Comput. 88, 105940. doi:10.1016/j.asoc.2019.105940

CrossRef Full Text | Google Scholar

Kong, W., Dong, Z. Y., Jia, Y., Hill, D. J., Xu, Y., and Zhang, Y. (2019). Short-term residential load forecasting based on lstm recurrent neural network. IEEE Trans. Smart Grid 10, 841–851. doi:10.1109/TSG.2017.2753802

CrossRef Full Text | Google Scholar

Krishna Rayi, V., Mishra, S., Naik, J., and Dash, P. (2022). Adaptive vmd based optimized deep learning mixed kernel elm autoencoder for single and multistep wind power forecasting. Energy 244, 122585. doi:10.1016/j.energy.2021.122585

CrossRef Full Text | Google Scholar

Lee, J., and Cho, Y. (2021). National-scale electricity peak load forecasting: Traditional, machine learning, or hybrid model? Energy 239, 122366. doi:10.1016/j.energy.2021.122366

CrossRef Full Text | Google Scholar

Liu, H., Tang, Y., Pu, Y., Mei, F., and Sidorov, D. (2022). Short-term load forecasting of multi-energy in integrated energy system based on multivariate phase space reconstruction and support vector regression mode. Electr. POWER Syst. Res. 210, 108066. doi:10.1016/j.epsr.2022.108066

CrossRef Full Text | Google Scholar

Löschenbrand, M., Gros, S., and Lakshmanan, V. (2021). “Generating scenarios from probabilistic short-term load forecasts via non-linear bayesian regression,” in 2021 INTERNATIONAL CONFERENCE ON SMART ENERGY SYSTEMS AND TECHNOLOGIES (SEST), Vaasa, Finland, 06-08 September 2021 (IEEE).

Google Scholar

Majeed Butt, O., Zulqarnain, M., and Majeed Butt, T. (2021). Recent advancement in smart grid technology: Future prospects in the electrical power network. Ain Shams Eng. J. 12, 687–695. doi:10.1016/j.asej.2020.05.004

CrossRef Full Text | Google Scholar

Mayur Barman, N. B. D. C., and Dev Choudhury, N. B. (2020). A similarity based hybrid gwo-svm method of power system load forecasting for regional special event days in anomalous load situations in Assam, India. Sustain. Cities Soc. 61, 102311. doi:10.1016/j.scs.2020.102311

CrossRef Full Text | Google Scholar

Memarzadeh, G., and Keynia, F. (2021). Short-term electricity load and price forecasting by a new optimal lstm-nn based prediction algorithm. Electr. Power Syst. Res. 192, 106995. doi:10.1016/j.epsr.2020.106995

CrossRef Full Text | Google Scholar

Peng, L., Lv, S.-X., Wang, L., and Wang, Z.-Y. (2021). Effective electricity load forecasting using enhanced double-reservoir echo state network. Eng. Appl. Artif. Intell. 99, 104132. doi:10.1016/j.engappai.2020.104132

CrossRef Full Text | Google Scholar

Peng, L., Wang, L., Xia, D., and Gao, Q. (2022). Effective energy consumption forecasting using empirical wavelet transform and long short-term memory. Energy 238, 121756. doi:10.1016/j.energy.2021.121756

CrossRef Full Text | Google Scholar

Sa’ad, A., Nyoungue, A. C., and Hajej, Z. (2022). An integrated maintenance and power generation forecast by ann approach based on availability maximization of a wind farm. Energy Rep. 8, 282–301. doi:10.1016/j.egyr.2022.06.120

CrossRef Full Text | Google Scholar

Sahu, R. K., Shaw, B., Nayak, J. R., and Shashikant, (2021). Short/medium term solar power forecasting of Chhattisgarh state of India using modified tlbo optimized elm. Eng. Sci. Technol. Int. J. 24, 1180–1200. doi:10.1016/j.jestch.2021.02.016

CrossRef Full Text | Google Scholar

Sutskever, I., Vinyals, O., and Le, Q. V. (2014). Sequence to sequence learning with neural networks. Available at: http://arxiv.org/abs/1409.3215

Google Scholar

Velasquez, C. E., Zocatelli, M., Estanislau, F. B., and Castro, V. F. (2022). Analysis of time series models for brazilian electricity demand forecasting. Energy 247, 123483. doi:10.1016/j.energy.2022.123483

CrossRef Full Text | Google Scholar

Xia, C., Zhang, M., and Cao, J. (2018). A hybrid application of soft computing methods with wavelet svm and neural network to electric power load forecasting. J. Electr. Syst. Inf. Technol. 5, 681–696. doi:10.1016/j.jesit.2017.05.008

CrossRef Full Text | Google Scholar

Xiao, X., Mo, H., Zhang, Y., Shan, G., Lund, H., and Kaiser, M. J. (2022). Meta-ann a dynamic artificial neural network refined by meta-learning for short-term load forecasting. Energy 246, 123418. doi:10.1016/j.energy.2022.123418

CrossRef Full Text | Google Scholar

Yu, R., Gao, J., Yu, M., Lu, W., Xu, T., Zhao, M., et al. (2019). Lstm-efg for wind power forecasting based on sequential correlation features. Future Gener. Comput. Syst. 93, 33–42. doi:10.1016/j.future.2018.09.054

CrossRef Full Text | Google Scholar

Zhang, G., Bai, X., and Wang, Y. (2021). Short-time multi-energy load forecasting method based on cnn-seq2seq model with attention mechanism. Mach. Learn. Appl. 5, 100064. doi:10.1016/j.mlwa.2021.100064

CrossRef Full Text | Google Scholar

Zhaorui Meng, J. S., Xie, Y., and Sun, J. (2022). Short-term load forecasting using neural attentionmodel based on emd. Electr. Eng. 104, 1857–1866. doi:10.1007/s00202-021-01420-4

CrossRef Full Text | Google Scholar

Zheng, H., Yuan, J., and Chen, L. (2017). Short-term load forecasting using emd-lstm neural networks with a xgboost algorithm for feature importance evaluation. Energies 10, 1168. doi:10.3390/en10081168

CrossRef Full Text | Google Scholar