Deep learning-aided joint DG-substation siting and sizing in distribution network stochastic expansion planning

The rapid growth of distributed generation (DG) and load has highlighted the necessity of optimizing their ways of integration, as their siting and sizing significantly impact distribution networks. However, little attention has been paid to the siting and sizing of new substations which are to be installed. This paper proposes deep learning-aided joint DG-substation siting and sizing in distribution network stochastic expansion planning. First, as the model depends on an accurate forecast, Long Short-Term Memory (LSTM) deep neural network is used to forecast DG output and load, where electricity growth rate, bidding capacity of the electric expansion, and industrial difference are all considered. Then, a two-stage stochastic mixed integer bilinear programming model was established for joint DG-substation siting and sizing under uncertainties, where multiple objective functions are comprehensively addressed. By using the Fortuny-Amat McCarl Linearization, the resultant bilinear model is equivalently transformed into a mixed integer linear program, which can be efficiently solved. Finally, stochastic power flow calculation in the IEEE 69-node system is conducted to analyze the influence of electric expansion and DG integration on the node voltage and power flow distribution of the power system. The effectiveness of the proposed method is also verified by simulation tests.

1 Introduction

With the forthcoming shortage of fossil fuels, the accommodation of renewable energy is a critical topic in power systems. Although large-scale integration of DGs is favorable to promoting the development of the economy, environment, and society (Singh and Sharma, 2017), curtailment of renewable energy is still significant and remains a critical issue to date (Zheng et al., 2021; Zheng et al., 2022). On the other hand, the expansion capacity of different industries will also impact the demand side of the system. It is left open how to reasonably plan the location and capacity of the renewables and the expanded industrial load to be integrated into the system, as the planning scheme has a huge impact on the operation of the power system.

Load forecasting and DG forecasting are important basis for power system decision-making and planning. In terms of load forecasting, due to the volatility of DG and load, how to accurately forecast the load in the presence of electric expansion is the focus of this research. The existing load forecasting research is mainly divided into statistics-based and learning-based methods, and the latter is the current mainstream method. Statistical methods mainly include multiple linear regression, autoregression, autoregressive moving average, and so on (Kim et al., 2018; Ahmad and Chen, 2019), but they can hardly deal with load data with random and dynamic development. (Yang et al., 2019). establishes a hybrid power load forecasting model by combining the autocorrelation function and least squares support vector machine in short-term power load forecasting. Compared with the benchmark model, experimental results show that this method can significantly improve forecasting accuracy. (Gul et al., 2021). adopts CNN-Bi-LSTM to process time series data sets for medium-term electricity prediction. However, the industrial difference in electricity consumption needs to be studied, while the quantitative relationship between industrial expansion capacity and the growth of load needs to be revealed. In this paper, the influence of industrial expansion will be considered in load forecasting, while the influence of direct irradiance and diffuse irradiance will be considered in DG sizing forecasting.

Although pioneering studies have investigated the siting and sizing of DG in the distribution network, little attention has been paid to installing new substations for industrial expansion. (Ho et al., 2016). proposes an optimal energy storage scheduling of DG distributed power generation system, which was formulated as a mixed integer linear program (MILP). (Vale et al., 2010). adopts the artificial neural network method to carry out distributed energy scheduling in isolated grids, and the construction of virtual power participants (VPP) can aggregate large-scale integration of DG and other distributed energy resources. (Daud et al., 2016). studies how to deploy the optimal location capacity of distributed photovoltaics. This paper considers multiple objectives such as power loss, voltage deviation, average voltage total harmonic distortion, and system average voltage decline to construct a multi-objective optimization problem, and the multi-objective optimization problem is converted into a single-objective optimization problem in a weighted way. In the research on industrial expansion, (Chen and Hsu, 1989). establishes an expert system for load allocation in the industrial expansion planning of the distribution network. The artificial language PROLOG is used to integrate the heuristic rules followed by the load allocation planner into the knowledge base, generating several appropriate load distribution schemes. (Aghaei et al., 2014). proposes a multi-stage distribution network expansion planning algorithm based on improved particle swarm optimization to ensure energy reliability and security, and realize the integration of distributed generation units into the distribution network. (Fan et al., 2020). considers the uncertainties of DG and electric vehicles and develops a comprehensive extended programming framework based on multi-objective mixed integer non-linear programming, where the Chebyshev decomposition is employed to solve the problem. However, heuristic algorithms can barely consider the uncertainty of DG and load, and their computational efficiency is generally low, which cannot satisfy the need for real-time dispatch.

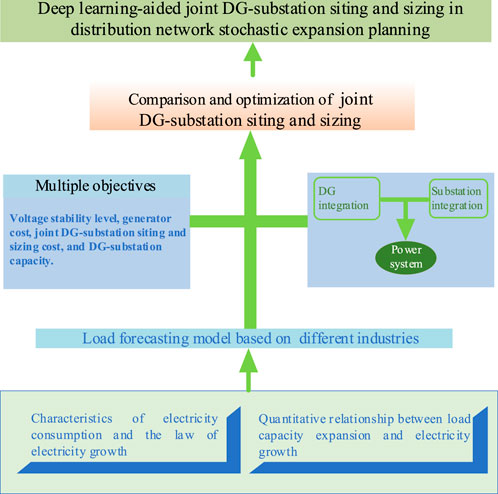
Compared with the existing research on the siting and sizing of DGs, this paper tackles the scenario with industrial expansion by using the research framework in Figure 1. Utility companies process customers’ applications for new substation installation and additional electricity capacity, referred to as industrial expansion and installation. Meanwhile, the main ways to achieve capacity growth include the installation of DG and substation. Therefore, this paper further explores the problem of joint DG-substation siting and sizing. The contributions are three-fold:

1) Industrial expansion data are fully employed in the LSTM network to forecast the increment load brought by the expansion.

2) A two-stage stochastic optimization model for joint DG-substation siting and sizing is established, which is reformulated into a mixed-integer linear program for an efficient solution.

3) Simulation tests are conducted on an IEEE system to prove the effectiveness of the research. Stochastic power flow is carried out to evaluate the impact of DG/substation integration on the system states, highlighting the merits of joint DG-substation siting and sizing.

FIGURE 1

FIGURE 1. The research framework of this paper.

Deep learning-based load forecasting and DG capacity forecasting

Load forecasting considering industrial expansion

As the industrial load is affected by industrial expansion and seasonal fluctuations, this paper improves the traditional LSTM load forecasting network, and applies the data of industrial expansion and electricity growth of different industries to the neural network, to more accurately forecast the load level under the influence of industrial expansion (Zheng et al., 2020).

In this section, the monthly load data of the pharmaceutical manufacturing industry, rubber and plastic products industry, and transportation, electrical and electronic equipment manufacturing industry in a province under the influence of industrial expansion are used to build an LSTM network, providing a basis for the load growth generated by industry expansion business.

The constructed model consists of the following steps:

1) Data selection

A large number of industrial expansion data are screened to eliminate the data caused by fault maintenance and line change and to ensure that the analyzed industrial expansion capacity generates actual load.

2) Data pre-processing

Assuming that the current time period is t, we select the industry monthly load data, annual load growth rate, and industrial expansion capacity of the past d time period for normalization and use them as the input of LSTM.

3) LSTM network structure

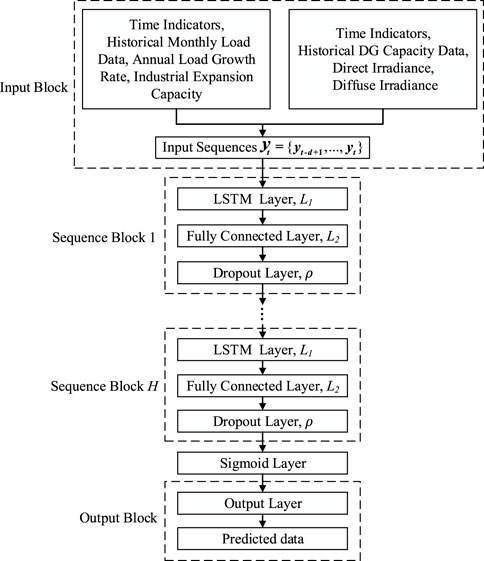
As shown in Figure 2, the network consists of an input layer, H sequence blocks, and an output layer. Firstly, the input layer is used to preprocess the load data, then the sequence blocks constructed by H custom LSTMs are used to extract the features of the input sequence, and finally, the output layer generates the load forecast for the industry.

FIGURE 2

FIGURE 2. LSTM network structure diagram.

Each sequence block has the same structure, including an LSTM layer, a fully connected layer, and a dropout layer. LSTM network is a recurrent neural network that can establish the temporal correlation between previous information and the current environment, so LSTM is used as a basic component of sequence blocks. Each LSTM layer L₁ has multiple units, each of which has a memory unit ${\mathit{s}}_{\mathit{\tau }}\in R^{L_1}$ and an input node ${\mathit{g}}_{\mathit{\tau }}\in R^{L_1}$, an input gate ${\mathit{i}}_{\mathit{\tau }}\in R^{L_1}$, a forgetting gate ${\mathit{f}}_{\mathit{\tau }}\in R^{L_1}$, and an output gate ${\mathit{o}}_{\mathit{\tau }}\in R^{L_1}$, where L₁ is a hyperparameter, and the output of each unit $\circ$ is in a hidden state. Taking the input sequence ${\chi }_t=\left\{x_{\mathit{t}-\mathit{d}+\mathbf{1}},...,x_{\mathit{t}}\right\}$ as an example, the structure of LSTM is represented by (1)-(6) (Hochreiter and Schmidhuber, 1997), for the time period $\tau =t-∆+1,t-∆+2,...,t$:

${\mathit{g}}_{\mathit{\tau }}=\tanh \left({\mathit{W}}_{\mathit{g}\mathit{y}}{\mathit{x}}_{\mathit{\tau }}+{\mathit{W}}_{gh}{\mathit{h}}_{\mathit{\tau }-\mathbf{1}}+{\mathit{b}}_{\mathit{g}}\right)(1)$

${\mathit{i}}_{\mathit{\tau }}=\sigma \left({\mathit{W}}_{\mathit{i}\mathit{y}}{\mathit{x}}_{\mathit{\tau }}+{\mathit{W}}_{\mathit{i}\mathit{h}}{\mathit{h}}_{\mathit{\tau }-\mathbf{1}}+{\mathit{b}}_{\mathit{i}}\right)(2)$

${\mathit{f}}_{\mathit{\tau }}=\sigma \left({\mathit{W}}_{\mathit{f}\mathit{y}}{\mathit{x}}_{\mathit{\tau }}+{\mathit{W}}_{fh}{\mathit{h}}_{\mathit{\tau }-\mathbf{1}}+{\mathit{b}}_{\mathit{f}}\right)(3)$

${\mathit{o}}_{\mathit{\tau }}=\sigma \left({\mathit{W}}_{\mathit{o}y}{\mathit{x}}_{\mathit{\tau }}+{\mathit{W}}_{oh}{\mathit{h}}_{\mathit{\tau }-\mathbf{1}}+{\mathit{b}}_{\mathit{o}}\right)(4)$

${\mathit{s}}_{\mathit{\tau }}={\mathit{g}}_{\mathit{\tau }}\circ {\mathit{i}}_{\mathit{\tau }}+{\mathit{s}}_{\mathit{\tau }-\mathbf{1}}\circ {\mathit{f}}_{\mathit{\tau }}(5)$

${\mathit{h}}_{\mathit{\tau }}=\tanh \left({\mathit{s}}_{\mathit{\tau }}\right)\circ {\mathit{o}}_{\mathit{\tau }}(6)$

Where ${\mathit{h}}_{\mathit{\tau }-\mathbf{1}}\in R^{L_1}$ is the LSTM layer output of the historical time period $\tau -1$, matrix ${\mathit{W}}_{\mathit{g}\mathit{y}}\in R^{L_1\times n}$, ${\mathit{W}}_{\mathit{g}\mathit{h}}\in R^{L_1\times n}$, ${\mathit{W}}_{\mathit{i}\mathit{y}}\in R^{L_1\times n}$, ${\mathit{W}}_{\mathit{i}\mathit{h}}\in R^{L_1\times n}$, ${\mathit{W}}_{\mathit{f}\mathit{y}}\in R^{L_1\times n}$, ${\mathit{W}}_{\mathit{f}\mathit{h}}\in R^{L_1\times n}$, ${\mathit{W}}_{\mathit{o}\mathit{y}}\in R^{L_1\times n}$ and ${\mathit{W}}_{\mathit{o}\mathit{h}}\in R^{L_1\times n}$ is the weight of the network activation function input, ${\mathit{b}}_{\mathit{g}}\in R^{L_1}$, ${\mathit{b}}_{\mathit{i}}\in R^{L_1}$, ${\mathit{b}}_{\mathit{f}}\in R^{L_1}$ and ${\mathit{b}}_{\mathit{o}}\in R^{L_1}$ is the bias vector, $\sigma$ is the sigmoid activation function, and $\circ$ represents Hadamard product. In deep learning, the sigmoid function is often used as the activation function of neural networks due to its monotonically increasing nature and the monotonically increasing inverse function, which maps variables between [0,1] and normalizes the output of each neuron. Since the probabilities range from 0 to 1, the sigmoid function is a good fit for models that take predicted probabilities as output. Hadamard product is a kind of matrix operation. If $A=\left(a_{ij}\right)$ and $B=\left(b_{ij}\right)$ are two matrices of the same order, and if $c_{ij}=a_{ij}\times b_{ij}$, then the matrix $C=\left(c_{ij}\right)$ is the Hadamard product of $A$ and $B$, i.e. $C=A\circ B$.

The input node, input gate, forgetting gate, and output gate are shown in Eq. 1–4. Different activation functions are used to calculate the activation of the weighted sum of input ${\mathit{x}}_{\mathit{\tau }}$ and LSTM hidden output ${\mathit{h}}_{\mathit{\tau }-\mathbf{1}}$. These three doors regulate the flow of information to and from the storage unit ${\mathit{s}}_{\mathit{\tau }}$. As shown in Eq. 5, the storage unit ${\mathit{s}}_{\mathit{\tau }}$ is the Hadamard product of ${\mathit{g}}_{\mathit{\tau }}$ and ${\mathit{i}}_{\mathit{\tau }}$ plus the Hadamard product of ${\mathit{s}}_{\mathit{\tau }-\mathbf{1}}$ and ${\mathit{f}}_{\mathit{\tau }}$. It remembers values in any time period, which are controlled by input nodes ${\mathit{g}}_{\mathit{\tau }}$, input gates ${\mathit{s}}_{\mathit{\tau }}$, and forget gates ${\mathit{f}}_{\mathit{\tau }}$, to determine which elements in the LSTM cell should be updated, maintained, or deleted. The hidden LSTM output ${\mathit{h}}_{\mathit{\tau }}$ is shown in Eq. 6, which is obtained by the memory unit ${\mathit{s}}_{\mathit{\tau }}$ and the output gate ${\mathit{o}}_{\mathit{\tau }}$. Finally, in order to improve the generalization ability of LSTM, the fully connected layer and dropout layer are added after the LSTM layer. The main purpose of the dropout layer is to prevent the overfitting of the neural network. In the forward propagation process of training, the neural network is sampled and the activation value of neurons is randomly set to 0, while the dropout layer is not used in the test process.

4) The setting of training parameters

In the above network structure, each Bernoulli random variable has probability $\rho =1$. The fully connected layer in Eq. 6 is used to capture useful features in the target domain (Zhang et al., 2018). Meanwhile, in order to prevent overfitting, the output of the fully connected layer is randomly set to zero in the dropout layer with probability $\rho$.

Finally, in the training of the network, the time algorithm is used for back-propagation (Gers et al., 1999) to minimize the loss between the predicted output of the neural network ${\stackrel{\sim }{\mathit{y}}}_{\mathit{\tau }}$ and the corresponding output label ${\mathit{y}}_{\mathit{\tau }}$. During network initialization, set ${\mathit{s}}_{\mathbf{0}}=\mathbf{0}$ and ${\mathit{h}}_{\mathbf{0}}=\mathbf{0}$ (Shi et al., 2015), the weight matrix is initialized by Glorot initializer (Glorot and Bengio, 2010), the deviation of the forgetting gate is initialized to 1, and other deviations are initialized to 0.

The historical data of training is input into the above network, and the predicted load value of the current time period $t$ is obtained through forward propagation. Then the loss of the predicted load and the true value of the label is backpropagated through the network, and then the Adam optimizer is used to update the weight and deviation of the network. The detailed training process can be found in (Gers et al., 1999).

DG capacity forecasting

Given that the output of DG is affected by some factors, such as environment, time, and so on, this section similarly uses the LSTM network to learn the historical data output by DG to predict the output capacity of DG more accurately. Therefore, as shown in Figure 2, the DG capacity data, direct irradiance, and diffuse irradiance of the same period in the province are selected for normalization and used as the input of LSTM. The network structure and training process are the same as in the previous section, and finally, the DG output data at this moment is obtained.

A multi-objective two-stage stochastic optimization model for joint DG-substation siting and sizing

The previous section forecasts the load yielded by industrial expansion and DG output, which provides the data basis for the modeling in this section. This section will use multi-objective two-stage stochastic programming to deal with the uncertainties of DGs and loads, which will be reformulated into an MILP for an efficient solution.

Objective function

A multi-objective two-stage stochastic optimization model is established. The system voltage stability and generator cost are considered in the objective function. The location and capacity of new DGs and substations are formulated as the first-stage variables, and the other variables are the second-stage variables:

$\min f_1={\displaystyle \sum }_{s=1}^{N_s}{\varpi }_s{\displaystyle \sum }_{i=1}^{N_{\mathit{bus}}}\left|U_{i,s}-1\right|(7)$

$\min f_2={\displaystyle \sum }_{s=1}^{N_s}{\varpi }_s{\displaystyle \sum }_{i=1}^{N_g}{C}_{Gi}{P}_{Gi,s}(8)$

$\min f_3={\displaystyle \sum }_{i=1}^{N_{bus}}{\displaystyle \sum }_{k=1}^{N_{ext}}{\displaystyle \sum }_{s=1}^{N_s}{C}_{ki}^{ext}{\alpha }_{ki}{P}_{extk,s}+{\displaystyle \sum }_{i=1}^{N_{bus}}{\displaystyle \sum }_{k=1}^{N_{DG}}{\displaystyle \sum }_{s=1}^{N_s}{C}_{ki}^{DG}{\beta }_{ki}\left(P_{DGk,s}+Q_{DGk,s}\right)(9)$

$\min f_4=-\left({\displaystyle \sum }_{s=1}^{N_s}{\displaystyle \sum }_{k=1}^{N_{ext}}{\alpha }_{ki}{P}_{extk,s}+{\displaystyle \sum }_{s=1}^{N_s}{\displaystyle \sum }_{k=1}^{N_{DG}}{\beta }_{ki}\left(P_{DGk,s}+Q_{DGk,s}\right)\right)(10)$

where s is the number of scenarios, ω_s is the probability of scenario s, and N_bus is the number of nodes in the system, N_s is the number of scenarios. U_i,s is the square of the voltage amplitude of node i in scenario s. N_g is the number of generators in the system, P_Gi,s is the output of the ith generator in scenario s, C_Gi is the cost coefficient of the ith generator. N_ext is the number of substation installation, $C_{ki}^{ext}$ is the cost of the kth substation installation task at node i, α_ki is a binary variable, α_ki is 1 if the kth substation installation task is installed at node i, otherwise, α_ki is 0. N_DG is the number of DGs to be integrated, $C_{ki}^{DG}$ is the cost of the kth DG siting task at node i, β_ki is a binary variable, if the kth DG siting task is at node i, β_ki is 1, otherwise it is 0. $P_{extk,s}$ is the expected load supplied by the kth new substation under scenario s, and $P_{DGk,s},Q_{DGk,s}$ is the active/reactive power flowing from kth DG in node i to other adjacent nodes under scenario s. In the above objective function, f₁ reflects the voltage stability level of the system, f₂ is the generator cost, f₃ is the joint DG-substation siting and sizing cost, and f₄ is the DG-substation capacity.

The original problem can be transformed into a single-objective optimization problem by weighting the multi-objective, which can be directly solved by the mainstream solver. Therefore, this paper converts the above multi-objective optimization problem into the following single-objective optimization problem:

$\min F={\displaystyle \sum }_{i=1}^4{\gamma }_i{f}_i(11)$

In Eq. 11, ${\gamma }_i$ is the corresponding weight of the ith objective function, ${\displaystyle \sum }_{i=1}^4{\gamma }_i=1$ and the weight coefficient of each objective function can be set according to the actual demand of the project.

Network constraint

Since the joint DG-substation siting and sizing are usually in the distribution network, considering the distribution network is a radial network, LinDistFlow model is used to describe the power flow (Šulc et al., 2014):

$P_{ji,s}+P_{DG,i,s}-P_{di}-P_{di,s}^{ext}+P_{Gi,s}-{\displaystyle \sum }_w{P}_{iw,s}=0(12)$

$Q_{ji,s}+Q_{DG,i,s}-Q_{di}+Q_{Gi,s}-{\displaystyle \sum }_w{Q}_{iw,s}=0(13)$

$U_{i,s}=U_{j,s}-2R_{ij}{P}_{ji,s}-2X_{ij}{Q}_{ji,s}(14)$

${\underset{\_}{P}}_{ji}\le P_{ji,s}\le {\overline{P}}_{ji}(15)$

${\underset{\_}{Q}}_{ji}\le Q_{ji,s}\le {\overline{Q}}_{ji}(16)$

${\underset{\_}{U}}_i\le U_{i,s}\le {\overline{U}}_i(17)$

$0\le P_{DG,i,s}\le {\overline{P}}_{DG,i}(18)$

$0\le Q_{DG,i,s}\le {\overline{Q}}_{DG,i}(19)$

$0\le P_{di,s}^{ext}\le {\overline{P}}_{di}^{ext}(20)$

Among them, Equations 12, 13 are the active and reactive power balance constraints of node i, P_ji,s/Q_ji,s is the active and reactive power flow between nodes j and i in scenario s, P_DG,i,s/Q_DG,i,s is the active and reactive power capacity of DG integration at node i in scenario s. P_di/Q_di is the active/reactive power load of node i, $P_{di,s}^{ext}$ is the expected load supplied by the new substation at node i, and $P_{iw,s}$/$Q_{iw,s}$ is the active/reactive power flowing from node i to other adjacent nodes under scenario s, where $w$ is the set of downstream nodes with respect to node i. Equation 14 is the voltage relationship between nodes j and i. Equations 15, 16 line power flow upper and lower bound constraints, ${\overline{P}}_{ji}$/${\underset{\_}{P}}_{ji}$ is the upper/lower bound of active power between nodes j and i, and ${\overline{Q}}_{ji}$/${\underset{\_}{Q}}_{ji}$ is the upper/lower bound of reactive power between nodes j and i. Eq. 17 is the voltage constraint of node, and ${\overline{U}}_i$/${\underset{\_}{U}}_i$ is the upper/lower bound of the square voltage amplitude of node i. Equations 18, 19 are the constraints on the active and reactive power capacity of the DG of node i integrated in the system, and ${\overline{P}}_{DG,i}/{\overline{Q}}_{DG,i}$ are the upper bound of the capacity of DG at node i. Eq. 20 is the constraint on the capacity of the substation at node i, and ${\overline{P}}_{di}^{ext}$ is the corresponding upper bound.

In scenario s, the additional load at node i is shown in Eqs 21, 22.

$\begin{array}{l}{P}_{di,s}^{ext}={\displaystyle \sum }_{k=1}^{N_{ext}}{\alpha }_{ki}{P}_{extk,s}\\ {\alpha }_{ki}=\left\{\begin{array}{l}0,substationinstallationtaskkisnotatnodei\\ 1,substationinstallationtaskkisnotatnodei\end{array}\right.\end{array}(21)$

${\displaystyle \sum }_{i=1}^{N_{bus}}{\alpha }_{ki}=1(22)$

In scenario s, the capacity of DG integrated at node i is shown in Eqs 23, 24.

$\begin{array}{l}{S}_{DG,i,s}={\displaystyle \sum }_{k=1}^{N_{DG}}{\beta }_{ki}\left(P_{DGk,s}+Q_{DGk,s}\right)\\ {\beta }_{ki}=\left\{\begin{array}{l}0,DGintegrationtaskkisnotatnodei\\ 1,DGintegrationtaskkisatnodei\end{array}\right.\end{array}(23)$

${\displaystyle \sum }_{i=1}^{N_{bus}}{\beta }_{ki}=1(24)$

Among all variables, α_ki, β_ki are the first-stage variables, U_i,s, P_Gi,s, P_ji,s/Q_ji,s, P_di/Q_di, P_DG,i,s/Q_DG,i,s, $P_{extk,s}$ are the second-stage variables. Since ${\alpha }_{ki}/{\beta }_{ki}$ are binary variables, while $P_{extk,s},P_{DGk,s},Q_{DGk,s}$ are continuous variables, and the multiplication of the two is non-linear, this paper introduces auxiliary variables $W_{ks}^{ext},W_{ks}^{DG}$ and uses Fortuny-Amat McCarl Linearization (Fortuny-Amat and McCarl, 1981) to deal with the problem. $W_{ks}^{ext}={\alpha }_{ki}{P}_{dl.s}^{ext}$ is an auxiliary variable, which represents the substation capacity of scenario s integrating the system, and $W_{ks}^{DG}={\beta }_{ki}\left(P_{DG,i,s}+Q_{DGi,s}\right)$ is an auxiliary variable, which represents the active and reactive power capacity of DG integrating the system at scenario s.

$0\le W_{ks}^{ext}\le M(25)$

$0\le W_{ks}^{DG}\le M(26)$

$W_{ks}^{ext}\le M{\alpha }_{ki}(27)$

$W_{ks}^{DG}\le M{\beta }_{ki}(28)$

$W_{ks}^{ext}\le P_{extk,s}(29)$

$W_{ks}^{DG}\le S_{DG,i,s}(30)$

$W_{ks}^{ext}\ge P_{extk,s}-M\left(1-{\alpha }_{ki}\right)(31)$

$W_{ks}^{DG}\ge S_{DG,i,s}-M\left(1-{\beta }_{ki}\right)(32)$

Among them, constraints (25), (27), (29) and (31) are to deal with the non-linearity arising from the multiplication of binary variables and continuous variables in Eq. 21, and constraints (26), (28), (30) and (32) are to deal with the non-linear problem in Eq. 23, and the parameter M is set to a large number.

Finally, our final model using Fortuny-Amat McCarl Linearization is as follows:

$\min F={\displaystyle \sum }_{i=1}^4{\gamma }_i{f}_i(33)$

$\left\{\begin{array}{l}{f}_1={\displaystyle \sum }_{s=1}^{N_s}{\varpi }_s{\displaystyle \sum }_{i=1}^{N_{bus}}\left|U_{i,s}-1\right|\\ f_2={\displaystyle \sum }_{s=1}^{N_s}{\varpi }_s{\displaystyle \sum }_{i=1}^{N_g}{C}_{Gi}{P}_{Gi,s}\\ f_3={\displaystyle \sum }_{i=1}^{N_{bus}}{\displaystyle \sum }_{k=1}^{N_{ext}}{\displaystyle \sum }_{s=1}^{N_s}{C}_{ki}^{ext}{W}_{ks}^{ext}+{\displaystyle \sum }_{i=1}^{N_{bus}}{\displaystyle \sum }_{k=1}^{N_{DG}}{\displaystyle \sum }_{s=1}^{N_s}{C}_{ki}^{DG}{W}_{ks}^{DG}\\ f_4=-\left({\displaystyle \sum }_{s=1}^{N_s}{\displaystyle \sum }_{k=1}^{N_{ext}}{W}_{ks}^{ext}+{\displaystyle \sum }_{s=1}^{N_s}{\displaystyle \sum }_{k=1}^{N_{DG}}{W}_{ks}^{DG}\right)\end{array}\right.(34)$

Constraints include Eqs. 12-32. The reformulated problem is an MILP.

Case study

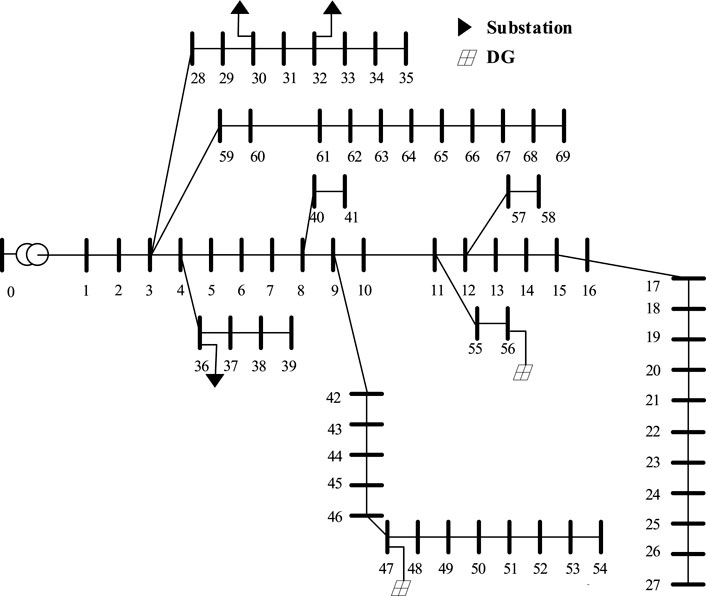
Case studies are conducted on the IEEE 69-node system. The deep learning part is implemented by using tensorflow 1.14.0. The MILP model is established by Yalmip, and solved by the commercial solver Gurobi. In this section, firstly, stochastic power flow is used to measure the impact of DG-substation siting and sizing on the distribution network, highlighting the merits of this research. Then, the accuracy of the load forecast under industrial expansion is tested. Finally, based on two-stage stochastic programming, the optimization results of joint DG-substation siting and sizing are analyzed.

Impact of DG-substation siting on the distribution network under uncertainties

In this paper, the Monte Carlo method is used to measure the impact of DG integration on the distribution system. Firstly, it generated several groups of data through the probability distribution of DG integration to reflect the uncertainty of DG, then used these data to carry out Monte Carlo stochastic power flow simulation respectively. Finally, it statistically analyzed the voltage probability distribution of four typical nodes, node 2, node 26, node 53, and node 68, and analyzed the results. The sample size of the Monte Carlo simulation is set to 1000, the fluctuation of DG integration is set to the Gaussian distribution of mathematical expectation is $\mu =0$, and the standard deviation is $\sigma =0.3$. Figures 3A–D respectively set the DG integration locations at node 3, node 25, node 52, and node 67, and the branch impedance of node 67 is significantly smaller than that of other branches.

FIGURE 3

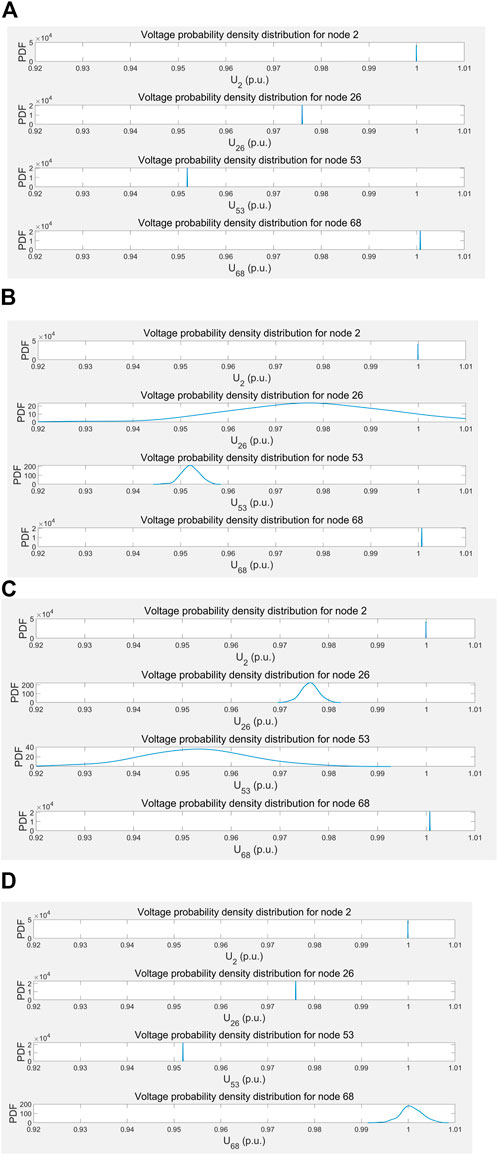
FIGURE 3. Voltage probability distribution of four typical nodes: (A) the DG is connected to node 3, (B) the DG is connected to node 25, (C) the DG is connected to node 52, (D) the DG is connected to node 67.

The simulation results are shown in Figures 3A–D, whose scenarios are explained as follows. Figure 3A: When DG is connected to node 3, there is no voltage fluctuation everywhere. Figure 3B: When DG is connected to node 25, the voltage fluctuation of node 26 is relatively obvious, the voltage of node 53 fluctuates slightly, and the voltage of the other two places has no fluctuation. Figure 3C: When DG is connected to node 52, the voltage fluctuation of node 53 is relatively significant, the voltage of node 26 fluctuates slightly, and the voltage of the other two places has no fluctuation. Figure 3D: When DG is connected to node 67, the voltage at node 68 fluctuates slightly, while the voltage at other places does not fluctuate.

The sensitivity of each node to DG integration is different. Because the location of node 2 is very close to the root node, the voltage of node 2 is almost not affected by the location of DG. The locations of nodes 26, 53, and 68 are all at the end of their branches, and their voltages are greatly affected by the location of DG.

Different locations of DG integration have different effects on the voltage of each node in the system. It can be seen from Figures 3B–D that when the DG integration causes the voltage fluctuation of a node, the voltage of the node closer to the node will be more affected by it. Therefore, the DG is connected to a location far away from the important load, which can reduce the adverse impact on the voltage of the important load.

The amplitude of node voltage fluctuation is significantly affected by the branch impedance sum of the branch where the node is located. Due to the small sum of branch impedances of node 68, the voltage in Figures 3A–C is not affected by the integration to DG basically, and it is also less affected by the integration to DG in Figure 3D. The voltage of node 26 and node 53 have obvious fluctuations when the DG is connected to node 25 (Figure 3B) and node 52 (Figure 3C), respectively. Therefore, DG is connected to the branch impedance and the small branch, which can maximize the absorption of DG.

Load forecasting and DG capacity forecasting results

In load forecasting, this paper chooses a province pharmaceutical manufacturing industry, rubber and plastic products industry, and transportation, electrical and electronic equipment manufacturing industry for 3 months in load data, load growth, industry reporting for expanding capacity, and load time series as input of LSTM, as shown in Figure 4. The detailed data are available in (Han et al., 2022).

FIGURE 4

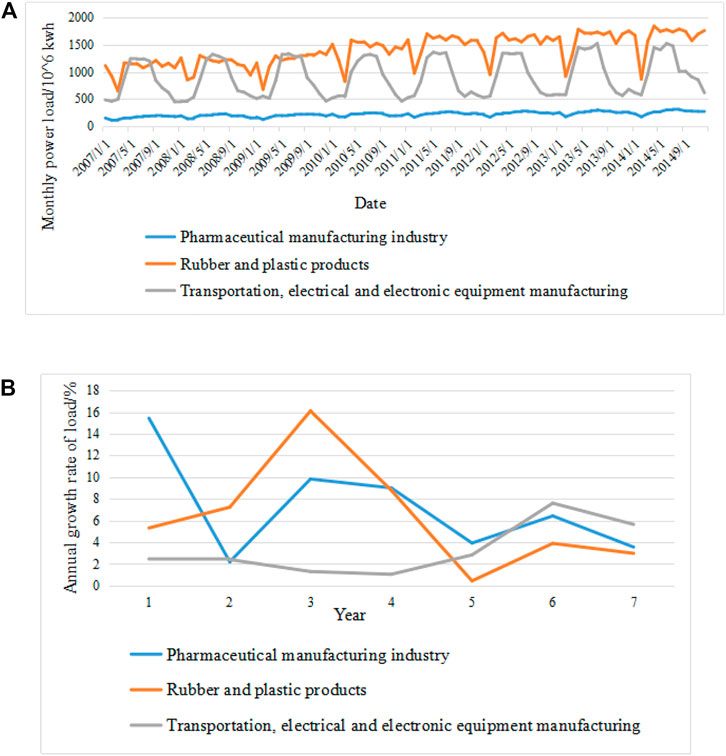
FIGURE 4. The input of LSTM: (A) monthly load curves for three industries, (B) Annual load growth curves for three industries.

Taking the pharmaceutical manufacturing industry as an example, the training loss function curve is shown in Figure 5A. It can be seen that the loss value of the training set is reduced from 0.20 to 0.00045, the loss value of the validation set is reduced from 0.175 to 0.00032, and the iteration can converge.

FIGURE 5

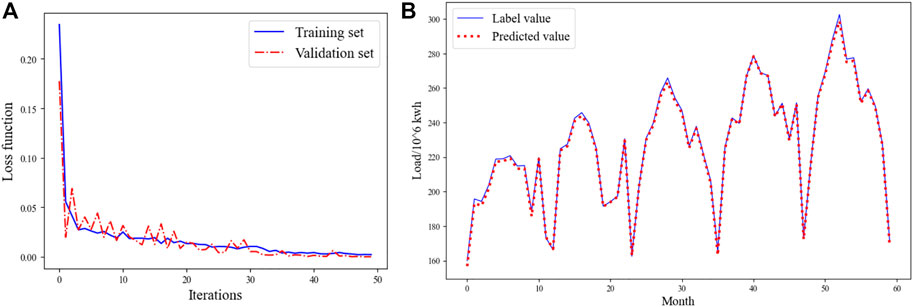
FIGURE 5. The result of pharmaceutical manufacturing industry load forecasting: (A) loss function curve, (B) comparison curve between the predicted value and the label value.

Further, the model is used to generate the predicted value of the test set and compare it with the actual label value, as shown in Figure 5B. The average absolute error of the statistical data is 782.2870.

Finally, the average relative percentage error of the predicted value of the three industry loads is no more than 2.9820%, and the error value is no more than 10%, which means the accuracy meets the system’s requirements.

In the prediction of DG capacity, the historical DG capacity data, direct irradiance, and diffuse irradiance of the same period are selected for normalization and used as the input of LSTM as shown in Figure 6. Since the historical data of the DG capacity, direct irradiance and diffuse irradiance in the IEEE 69-node system are not available, we use the real data from the platform Open Power System Data (Open Power System). The data in France in a period of 96 months from Jan. 2007 to Dec. 2014 are used, for their data integrity is relatively better. The loss function curve of DG capacity data forecasting is shown in Figure 7A, while the comparison curve between the predicted value and the label value is shown in Figure 7B. Their average relative error does not exceed 0.5451%, which is acceptable.

FIGURE 6

FIGURE 6. Monthly DG capacity data curve.

FIGURE 7

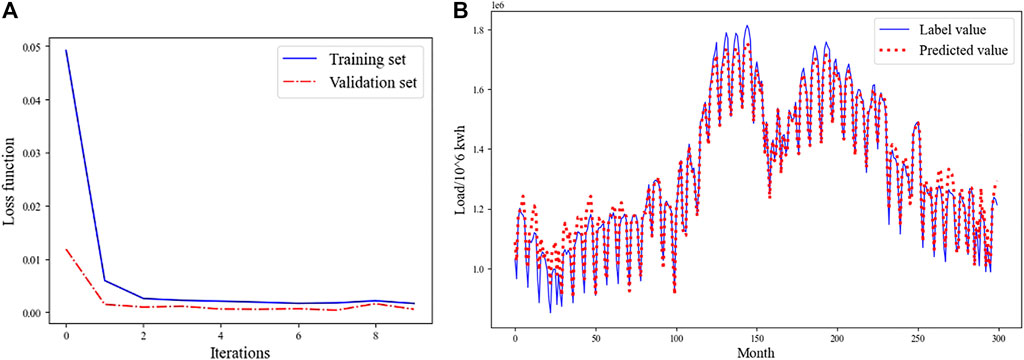
FIGURE 7. The result of DG capacity data forecasting: (A) loss function curve, (B) comparison curve between the predicted value and the label value.

Analysis of joint DG-substation siting and sizing

The load forecasting and DG capacity forecasting results obtained in the previous section under different scenarios are normalized. In order to consider the error of the forecasting results, Gaussian distribution error is added to the forecasting results, and k-means algorithm is used to generate the load and DG capacity of three groups of typical scenarios and the probability of the scenario. The load and DG capacity of the three sets of scenarios are taken as the input of the substation and DG integration model and are denoted as the maximum value of the system. It can be known that there are three joint DG-substation siting and sizing tasks, and at the same time, two DG integration tasks are set with the same probability to optimize the joint DG-substation siting and sizing.

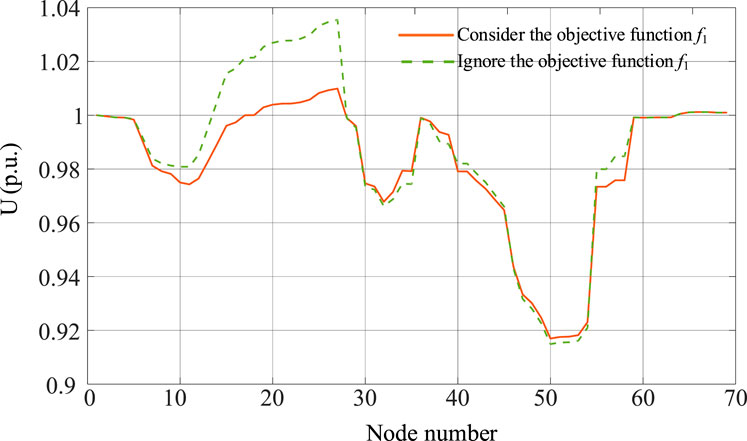
In order to test the effect of comprehensive consideration of the multi-objective of the proposed method, ${\gamma }_1\sim {\gamma }_4$ in the objective functions are set to 0.25, 0.25, 0.4, and 0.1, respectively. Table 1 shows the integration points of substation and DG obtained by solving (33). The corresponding objective function values f₁, f₂, f₃ and f₄ are 0.1190, 0.1452, 2.2020 and −5.8166, respectively. Due to the comprehensive consideration of various factors, its joint DG-substation siting and sizing, DG integration locations are shown in Table 1 and Figure 8, and the solution time is 0.4533 s. It can be seen that the running time of this method is short, which can meet the real-time application in engineering.

TABLE 1

TABLE 1. Multi-objective optimization of joint DG-substation siting and sizing.

FIGURE 8

FIGURE 8. Optimal sites of DG and substation based on multiple objective optimization.

Figure 9 shows the influence of whether the objective function f₁ is considered on the voltage of each node in the system in scenario 1. It can be seen that when f₁ is not considered, many nodes deviate from the rated voltage significantly. However, after considering the objective function f₁, the node voltage level of the system is significantly improved.

FIGURE 9

FIGURE 9. Squared node voltage in scenario one based on multiple objective optimization.

To verify the effectiveness of joint DG-substation siting and sizing, we set the control group which only considers DG siting and sizing, a total of three groups are compared, and the obtained optimization results are shown in Table 2.

1) Joint DG-substation: joint DG-substation siting and sizing are optimized.

2) Method 1: The location of the substation is fixed and the capacity is optimized, and DG siting and sizing are optimized.

3) Method 2: The location of the substation is fixed and the capacity is fixed, and DG siting and sizing are optimized.

TABLE 2

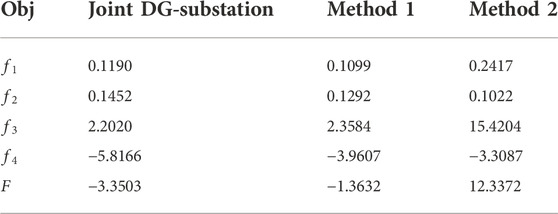
TABLE 2. Comparison of objective function values between the proposed joint DG-substation optimization and other methods.

It can be found that the voltage stability level of the system f₁ and the generator cost f₂ are not far apart in method 1 and joint DG-substation, but in method 2, the voltage stability level of the system f₁ is relatively worse. However, the integration cost f₃ is less in the case of joint DG-substation, and the expansion capacity f₄ is larger, so the total objective function value is smaller in the end.

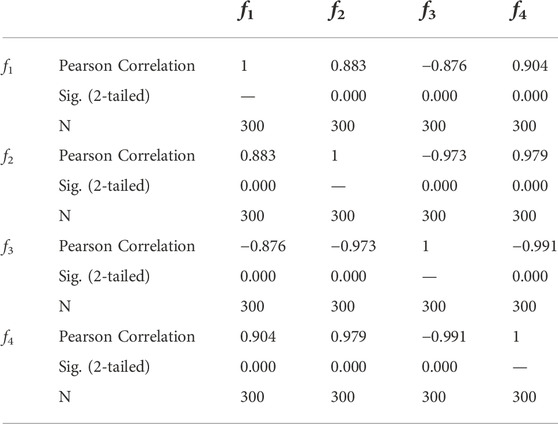
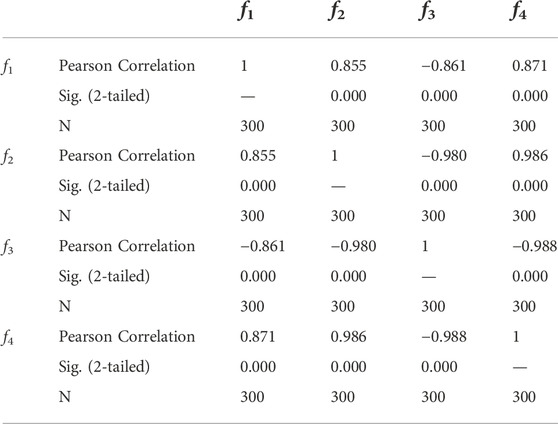
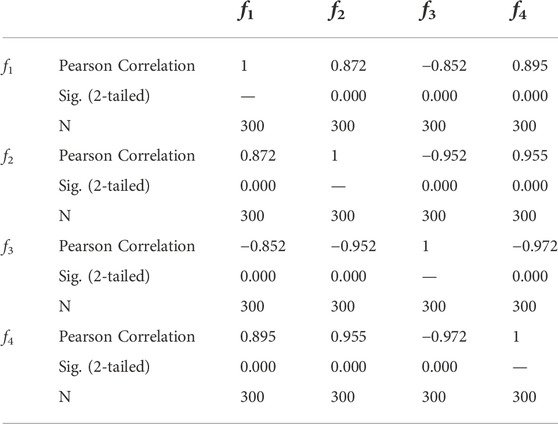
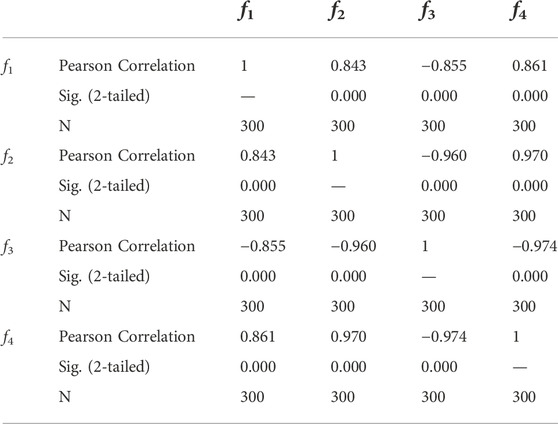
Further, 300 scenarios under four different weights $\gamma =\left(\mathrm{0.25,0.25,0.4,0.1}\right)$, $\gamma =\left(\mathrm{0.3,0.3,0.3,0.1}\right)$, $\gamma =\left(\mathrm{0.2,0.2,0.3,0.3}\right)$, and $\gamma =\left(\mathrm{0.25,0.25,0.25,0.25}\right)$ are selected; that is, the load fluctuated randomly at 90%–110%, and the objective function value is obtained. The correlation of each objective function value $f_1-f_4$ under four different weights is shown in Tables 3–6. It can be found from the table that $f_1$, $f_2$ and $f_4$ are significantly positively correlated with each other, while $f_3$ is significantly negatively correlated with $f_1$, $f_2$ and $f_4$.

TABLE 3

TABLE 3. Correlation analysis of the objective function in weight $\gamma =\left(\mathrm{0.25,0.25,0.4,0.1}\right)$.

TABLE 4

TABLE 4. Correlation analysis of the objective function in weight $\gamma =\left(\mathrm{0.3,0.3,0.3,0.1}\right)$.

TABLE 5

TABLE 5. Correlation analysis of the objective function in weight $\gamma =\left(\mathrm{0.2,0.2,0.3,0.3}\right)$.

TABLE 6

TABLE 6. Correlation analysis of the objective function in weight $\gamma =\left(\mathrm{0.25,0.25,0.25,0.25}\right)$.

Therefore, the scheme of joint DG-substation siting and sizing determined by this method can make the power flow distribution of the distribution network reasonable and the voltage level close to the rated voltage by optimizing the integration location, and also reduce the system operation cost and the joint DG-substation siting and sizing cost to some extent.

Conclusion

To answer the call of industrial expansion, this paper proposes deep learning-aided joint DG-substation siting and sizing in distribution network stochastic expansion planning. Industrial expansion data are fully employed in the LSTM network to forecast the increment load brought by the expansion. A two-stage stochastic optimization model for joint DG-substation siting and sizing is established, which is reformulated into a mixed-integer linear program for an efficient solution. Simulation tests are conducted on an IEEE system to prove the effectiveness of the research. Stochastic power flow is carried out to evaluate the impact of DG/substation integration on the system states, highlighting the merits of joint DG-substation siting and sizing. Case studies show that the forecasting results meet the accuracy requirements, and the proposed siting and sizing method is computationally efficient. It can reduce the total cost of system operation as well as alleviate the system voltage fluctuation. In future work, we will investigate an objective manner to determine the weights for multiple objective functions.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/supplementary material.

Author contributions

ZH: Conceptualization, Methodology, Resources, Writing–Original Draft; JL: Conceptualization, Methodology, Writing–Review and Editing; QW: Methodology, Data Curation, Writing–Review and Editing; HL: Software, Writing–Original Draft; SX: Validation, Writing–Original Draft; WZ: Funding acquisition, Project administration, Writing–Review and Editing; ZZ: Writing–Review and Editing.

Funding

This work is supported by the Management Scientific and Technological Project of State Grid Liaoning Electric Power Supply Co. LTD. under Grant No. 2022YF-57.

Conflict of interest

Author JL was employed by the company State Grid Liaoning Electric Power Supply Co., LTD.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The authors declare that this study received funding from State Grid Liaoning Electric Power Supply Co. LTD. The funder had the following involvement in the study: study design.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aghaei, J., Muttaqi, K. M., Azizivahed, A., and Gitizadeh, M. (2014). Distribution expansion planning considering reliability and security of energy using modified PSO (Particle Swarm Optimization) algorithm. Energy 65, 398–411. doi:10.1016/j.energy.2013.10.082

CrossRef Full Text | Google Scholar

Ahmad, T., and Chen, H. (2019). Nonlinear autoregressive and random forest approaches to forecasting electricity load for utility energy management systems. Sustain. Cities Soc. 45, 460–473. doi:10.1016/j.scs.2018.12.013

CrossRef Full Text | Google Scholar

Chen, J. L., and Hsu, Y. Y. (1989). An expert system for load allocation in distribution expansion planning. IEEE Power Eng. Rev. 9 (7), 77–78. doi:10.1109/mper.1989.4310835

CrossRef Full Text | Google Scholar

Daud, S. b., Kadir, A. F. A., Gan, C. K., Mohamed, A., and Khatib, T. J. (2016). A comparison of heuristic optimization techniques for optimal placement and sizing of photovoltaic based distributed generation in a distribution system. Sol. Energy 140, 219–226. doi:10.1016/j.solener.2016.11.013

CrossRef Full Text | Google Scholar

Fan, V. H., Dong, Z., and Meng, K. (2020). Integrated distribution expansion planning considering stochastic renewable energy resources and electric vehicles. Appl. Energy 278, 115720. doi:10.1016/j.apenergy.2020.115720

CrossRef Full Text | Google Scholar

Fortuny-Amat, J., and McCarl, B. (1981). A representation and economic interpretation of a two-level programming problem. J. Operational Res. Soc. 32 (9), 783–792. doi:10.2307/2581394

CrossRef Full Text | Google Scholar

Gers, F. A., Schmidhuber, J., and Cummins, F. (1999). “Learning to forget: Continual prediction with LSTM,” in 1999 Ninth International Conference on Artificial Neural Networks ICANN 99, Edinburgh, UK, 07-10 September 1999, 850–855. (Conf. Publ. No. 470). doi:10.1049/cp:19991218

CrossRef Full Text | Google Scholar

Glorot, X., and Bengio, Y. (2010). “Understanding the difficulty of training deep feedforward neural networks,” in Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, PMLR, Sardinia, Italy, May 13–May 15, 2010, 249–256.

Google Scholar

Gul, M. J. J., Urfa, G. M., Paul, A., Moon, J., Rho, S., and Hwang, E. (2021). Mid-term electricity load prediction using CNN and Bi-LSTM. J. Supercomput. 77, 10942–10958. doi:10.1007/s11227-021-03686-8

CrossRef Full Text | Google Scholar

Han, Z., Li, J., Wang, Q., Lu, H., Xu, S., Zheng, W., et al. (2022). Detailed data of the test system. Available at: https://pan.baidu.com/s/1174VbXVrqHA0ICoj5EnwOQ?pwd=uo3b.

Google Scholar

Ho, W. S., Macchietto, S., Lim, J. S., Hashim, H., Muis, Z. A., and Liu, W. H. (2016). Optimal scheduling of energy storage for renewable energy distributed energy generation system. Renew. Sustain. Energy Rev. 58, 1100–1107. doi:10.1016/j.rser.2015.12.097

CrossRef Full Text | Google Scholar

Hochreiter, S., and Schmidhuber, J. (1997). Long short-term memory. Neural Comput. 9 (8), 1735–1780. doi:10.1162/neco.1997.9.8.1735

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, J., Cho, S., Ko, K., and Rao, R. R. (2018). “Short-term electric load prediction using multiple linear regression method,” in 2018 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids (SmartGridComm), Aalborg, Denmark, 9-31 October 2018, 1–6. doi:10.1109/SmartGridComm.2018.8587489

CrossRef Full Text | Google Scholar

Open Power System (n.d.). Open power system data. Available at: https://open-power-system-data.org (Accessed October 6, 2022).

Google Scholar

Shi, X., Chen, Z., Wang, H., Yeung, D.-Y., Wong, W.-K., and Woo, W.-c. (2015). Convolutional LSTM network: A machine learning approach for precipitation nowcasting. NIPS. Available at: https://arxiv.org/abs/1506.04214.

Google Scholar

Singh, B., and Sharma, J. (2017). A review on distributed generation planning. Renew. Sustain. Energy Rev. 76, 529–544. doi:10.1016/j.rser.2017.03.034

CrossRef Full Text | Google Scholar

Šulc, P., Backhaus, S., and Chertkov, M. (2014). Optimal distributed control of reactive power via the alternating direction method of multipliers. IEEE Trans. Energy Convers. 29 (4), 968–977. doi:10.1109/tec.2014.2363196

CrossRef Full Text | Google Scholar

Vale, Z. A., Faria, P., Morais, H., Khodr, H. M., Silva, M., and Kadar, P. (2010). “Scheduling distributed energy resources in an isolated grid — an artificial neural network approach,” in IEEE PES General Meeting, Minneapolis, MN, USA, 25-29 July 2010, 1–7. doi:10.1109/PES.2010.5589701

CrossRef Full Text | Google Scholar

Yang, A., Li, W., and Yang, X. (2019). Short-term electricity load forecasting based on feature selection and Least Squares Support Vector Machines. Knowledge-Based Syst. 163, 159–173. doi:10.1016/j.knosys.2018.08.027

CrossRef Full Text | Google Scholar

Zhang, C.-L., Luo, J.-H., Wei, X.-S., and Wu, J. (2018). “Defense of fully connected layers in visual representation transfer,” in Advances in multimedia information processing – pcm 2017 (Cham: Springer International Publishing), 807–817.

CrossRef Full Text | Google Scholar

Zheng, W., Hou, Y., and Li, Z. (2021). A dynamic equivalent model for district heating networks: Formulation, existence and application in distributed electricity-heat operation. IEEE Trans. Smart Grid 12 (3), 2685–2695. doi:10.1109/tsg.2020.3048957

CrossRef Full Text | Google Scholar

Zheng, W., Huang, W., and Hill, D. J. (2020). A deep learning-based general robust method for network reconfiguration in three-phase unbalanced active distribution networks. Int. J. Electr. Power & Energy Syst. 120, 105982. doi:10.1016/j.ijepes.2020.105982

CrossRef Full Text | Google Scholar

Zheng, W., Zhu, J., and Luo, Q. (2022). Distributed dispatch of integrated electricity-heat systems with variable mass flow. IEEE Trans. Smart Grid, in press. doi:10.1109/tsg.2022.3210014

CrossRef Full Text | Google Scholar