- College of Electrical and Information Engineering, Lanzhou University of Technology, Lanzhou, China
Aiming at the strong non-linear and non-stationary characteristics of power load, a short-term power load forecasting method based on bald eagle search (BES) optimization variational mode decomposition (VMD), convolutional bi-directional long short-term memory (CNN-Bi-LSTM) network and considering error correction is studied to improve the accuracy of load forecasting. Firstly, a decomposition loss evaluation criterion is established, and the VMD optimal decomposition parameters under the evaluation criterion are determined based on BES to improve the decomposition quality of the signal. Then, the original load sequence is decomposed into different modal components, and the corresponding CNN-Bi-LSTM network prediction models are established for each modal component. In addition, considering the influence of various modal components, holiday and meteorological factors on the error, an error correction model considering short-term factors is established to mine the hidden information contained in the error to reduce the inherent error of the model. Finally, the proposed method is applied to a public dataset provided by a public utility in the United States. The results show that this method can better track the changes of load and effectively improve the accuracy of short-term power load forecasting.
1 Introduction
With the implementation of renewable energy policy, renewable energy has gradually replaced fossil fuels and been rapidly applied to the power system. However, the large-scale renewable energies are connected to the power grid, which could affect customers’ electricity consumption behavior and load forecasting (Yang D. et al., 2023). Accurate power demand forecasting is the basis for realizing safe and economic operation of power system and scientific management of power grid, it helps to estimate future loads from recent loads using various techniques in efforts to save energy, reduce costs, perform power management, and implement economic dispatch plans (Talaat et al., 2020). The research shows that if the prediction error is reduced by 1%, a 10 GW power station may save $1.6 million per year (Hobbs et al., 1999). Therefore, establishing an accurate short-term power load forecasting model for a power system is both required and beneficial.
The factors that affect the short-term power load mainly include meteorological, holidays, user habits, etc. These factors are working together to make the power load sequence show obvious volatility and nonlinearity characteristics, which undoubtedly increases the difficulty of accurate prediction (Zhao et al., 2022). Therefore, it is necessary to study more accurate short-term power load forecasting methods. For the short-term power load forecasting model, the research mainly includes statistical methods and machine learning methods. Among them, the statistical methods mainly include autoregressive integrated moving average model (Lee and Ko, 2011), Kalman filter (Zhao et al., 2016), etc. The principle and modeling of such methods are simple, and the statistical method can fully reflect the temporal relationship between power load data, but its nonlinear characteristics are not fully considered. Machine learning algorithms can effectively deal with nonlinear problems. The traditional machine learning methods mainly include: artificial neural network (ANN) (Garcia-Ascanio and Mate, 2009), support vector machine (SVM) (Jiang et al., 2018), random forest (RF) (Wu et al., 2015), etc. ANN has self-learning ability and can effectively solve the nonlinear problems in load data, but it is difficult to determine the network structure scientifically, and has some defects such as local minimum, large generalization error, the prediction accuracy is usually difficult to meet the requirements. The SVM method solves the local minimum question and has stronger generalization ability, but the disadvantage of SVM is that it is sensitive to parameter adjustment and kernel function selection. The RF algorithm is applied to short-term power load forecasting, which has the advantages of higher prediction accuracy and controllable generalization error, but when the load fluctuation is large, the prediction accuracy is not high. Although the above machine learning methods can better reflect the nonlinear relationship between data, the common problem of these methods lies in the lack of consideration of the temporal correlation of time series data (Rodrigues and Pereira, 2020).
With the development of deep learning, different types of neural networks have been proposed one after another, which provides different solutions to the problem that the timing and nonlinearity of data cannot be considered at the same time in power load forecasting. Such as long short-term memory network (LSTM), convolutional neural network (CNN) and deep belief network (DBN) (Chen et al., 2021). Among them, LSTM network has the characteristics of preserving the timing and nonlinearity of data at the same time, so its application in power load forecasting, renewable energy output power forecasting and other fields is increasing. As an optimization of LSTM network, gated recurrent unit (GRU) not only achieves its approximate accuracy, but also has the advantages of less training parameters and fast speed. In addition, bi-directional long short-term memory (Bi-LSTM) network is used for load forecasting, which has better expression ability for continuous time series, and the reuse of weight parameters makes it have lower requirements for data (Kwon et al., 2020; Zang et al., 2021).
However, although GRU and other models can fully respond to the long-term historical process in the input time series data, the effective information between discontinuous data cannot be extracted, and thus the potential relationship between data cannot be deeply mined. With the diversification of training data types and the increase of power grid demand for load forecasting accuracy, the combined forecasting model came into being to further improve the accuracy of load forecasting (Muhammed et al., 2021). Lu et al. (2019) proposed a short-term load forecasting model combining CNN with LSTM network. CNN is used to extract the potential relationship between continuous data and discontinuous data in the feature map and form the feature vector. Then, the feature vector is used as the input of LSTM for load forecasting. Lee and Cho, (2022) determined the most accurate peak load-forecasting model by comparing the performance of time series (Seasonal autoregressive integrated moving average with exogenous variables, SARIMAX), machine learning (Support vector regression, SVR, etc.) and hybrid models (SARIMAX-ANN, etc.). The results indicate that the hybrid models exhibit significant prediction performance.
With the continuous development of data decomposition algorithm, in order to reduce the impact of volatility and nonlinearity in power load series and further improve the accuracy of short-term load forecasting, the hybrid forecasting method combining data decomposition algorithm with existing forecasting models has been widely used in power load forecasting (Zhang et al., 2022). Empirical mode decomposition (EMD) is an adaptive signal decomposition method based on local characteristics of signals. This method overcomes the difficulty of selecting wavelet basis and determining decomposition scale in wavelet transform (WT), so it is more suitable for nonlinear and non-stationary signal analysis (Zhang et al., 2021). Meng et al. (2021) proposed a short-term load forecasting approach integrating EMD, bi-directional long short-term memory and attention mechanism. EMD decomposes the load series into a finite number of components or modes [called intrinsic mode functions (IMFs)] with different characteristic scales, and decomposes the fluctuations or trends of different scales that actually exist in the signal step by step, then a Bi-LSTM neural network based on attention mechanism is applied on each of the extracted IMFs to predict the tendencies of these IMFs, finally, the prediction results of each component are superposed to obtain the load prediction value. Compared with the original load data series, the decomposed series has stronger regularity and can improve the prediction accuracy. Kassa et al. (2019) proposed a short-term load forecasting model of microgrid by combining empirical mode decomposition, particle swarm optimization (PSO) and adaptive neural fuzzy inference system (ANFIS). The complex load sequence is decomposed into a set of modal functions and a residual by EMD, and then the ANFIS model of each modal function component and residual are optimized by PSO algorithm, each modal function component and residual are predicted separately to improve the prediction accuracy. However, EMD needs to solve the problems of modal mixing, end effect and over envelope. Liang et al. (2018) decomposed the original sequence of power load into multiple modal functions with different characteristics by VMD, and the prediction model is established through DBN optimized by PSO algorithm, to improve the prediction accuracy; Ye et al. (2022) proposed a load forecasting method based on VMD and multi-model fusion to solve the problem of strong volatility and randomness of multi load in user level integrated energy system and the difficulty of accurate forecasting; Yang Y. et al. (2023) used VMD to decompose the original data into several sub-sequences, which enables it to extract the implied features to separately predict each sub-sequence to improve the prediction accuracy of the short-term load forecasting. Compared with WT and EMD, VMD is widely used in the fields of power load forecasting and renewable energy power signal decomposition due to its strong self-adaptability and ability to overcome modal mixing (Zhou et al., 2021). However, the following problems still exist:
(1) In VMD process, there is no evaluation standard to guide parameter setting, and parameters are often given by experience, which leads to unsatisfactory decomposition effect. Yuan and Che, (2022), Dou et al. (2018).
(2) VMD uses a quadratic penalty factor in the construction of the variational problem, which over punishes the internal jump of the signal, which is easy to generate prediction errors, and the previous research did not make full use of the implicit information in the error. Yan and Tian, (2019).
According to the literatures above, to solve the above problems, meet the challenges of short-term power load forecasting brought by the obvious volatility and nonlinear characteristics of power load due to its vulnerability to various factors, and further improve the accuracy of short-term power load forecasting, a combined short-term power load forecasting method based on BES-VMD-CNN-Bi-LSTM-EC model is proposed in this paper. The forecasting process is divided into two stages: In the first stage, the VMD method optimized by BES algorithm is used to decompose the complex power load data into different subsequence components and then the CNN-Bi-LSTM forecasting model of each load component is established, subsequently, the independent prediction results of each component are reconstructed to obtain the predicted load sequence. In the second stage, an error correction model based on CNN-Bi-LSTM network is established to obtain the predicted error sequence to correct the predicted load sequence before. At last, the final load forecasting results are obtained and further improve the short-term load forecasting effect.
The main contributions of this paper are as follows: 1) The VMD method optimized by bald eagle search (BES) decomposes the non-stationary and nonlinear power load series into components with different frequencies, which effectively reduces the complexity of the load series. 2) The CNN-Bi-LSTM prediction model of each load subsequence is established to improve the feature extraction and dimension reduction ability of the model to the original data. 3) An error correction model considering short-term factors, such as holiday and meteorological factors on the error is established, which reduces the inherent error of the prediction model by mining the effective information hidden in the error. 4) The method proposed in this paper is applied to the actual load verification of the data set published in the 2012 global energy forecasting competition, and the experimental results show its effectiveness in short-term power load forecasting.
The rest of this paper is organized as follows: Section 2 provides the methodology of VMD. Section 3 analyzes the superiority of BES optimization algorithm by simulation experiments. Section 4 introduces the proposed hybrid prediction method in detail. A case study is given to verify the effectiveness of the proposed model in Section 5. Finally, the conclusion is presented in Section 6.
2 Methodology of VMD
VMD is an adaptive signal decomposition method, which can effectively deal with non-stationary and nonlinear signals. By iteratively searching the variational mode, the original time series f(t) is decomposed into different components uk(t) with limited bandwidth, and its corresponding center frequency is ωk. Taking the decomposition of power load signal as an example, the steps of constructing the variational problem are as follows:
(1) For each load component uk(t), Hilbert transform is used to calculate and analyze the signal, and its one-sided spectrum is obtained as follows:
(2) For each uk(t), the spectrum of each component is modulated to the corresponding fundamental frequency band by mixing an exponential term of its corresponding center frequency, as follows:
(3) The Gaussian smoothing method of demodulated signal is used to estimate the signal bandwidth of each subsequence, and the variational problem with constraints is solved. The objective function is:
where, {uk} = {u1,u2···uK} is the k modal components obtained after decomposition. {ωk} = {ω1,ω2···ωK} is the center frequency corresponding to each modal component. ∂t means partial derivative. δ(t) represents the impulse function. * represents a convolution operation.
By introducing Lagrange multiplication operator λ and the quadratic penalty factor α, the above constrained extreme value problem is transformed into an unconstrained problem for solution, as shown in the following formula:
The alternating direction multiplier method is used for ωk and uk is optimized as follows:
Where,
Carry out cyclic iterative solution according to (5), update uk and ωk, and bring in (6) for update λ:
where τ is the renewal coefficient of λ. For discrimination accuracy ξ > 0, iteration stop condition exists:
If ξ meets the iteration stop condition, the iteration cycle ends and the adaptive decomposition of the input signal is realized. if not, brings uk and ωk in (5) again and starts a new round of iteration until the condition is met.
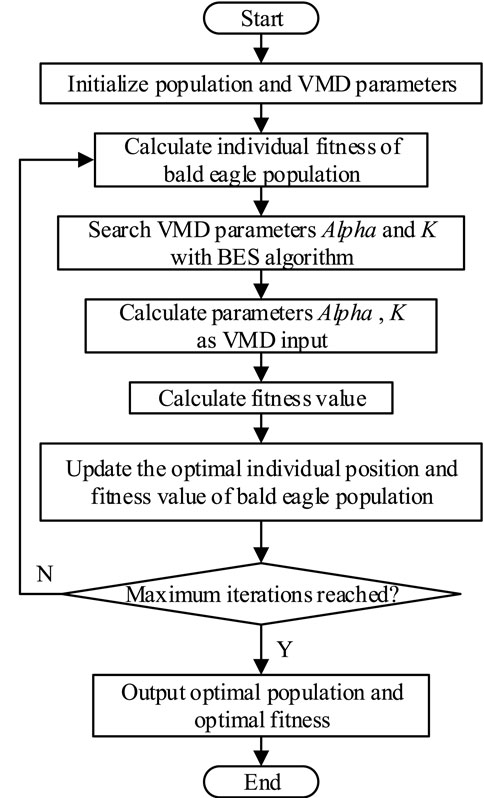
The flow chart of VMD is shown in Figure 1.
3 BES optimization algorithm
3.1 Bald eagle search
BES is a novel metaheuristic algorithm, which has strong global search ability and can effectively solve various complex numerical optimization problems (Ahmed et al., 2022). The selection of VMD parameters can be regarded as an optimization problem. Therefore, this paper decides to use BES algorithm to optimize VMD parameters. BES algorithm simulates the predator-prey mechanism of bald eagle. The core optimization part of each iteration mainly includes three stages: selection space, search space and swooping phase.
(1) Selection space: bald eagles recognize and choose the best space, this selected space should be rich in prey, this can be implemented by the following equation:
where, Pbest is the search area selected using the best position identified in the previous search. α is a controlling parameter that adapts the positions’ changes. γ is a random number in range of [0,1]. Pmean is the mean position. Pi is the current position of ith bald eagle.
(2) Search space: the bald eagle accelerates the search in a spiral shape to determine the best capture position. The position is updated as follows:
where, x(i) and y(i) are the position coordinates of ith bald eagle. r(i) is the polar radius of the equation. θ(i) is the polar angle of the direction. a determines the angle between the search point and the central point, it is assigned in range of [5,10]. R is a parameter that determines the search cycles’ number, it is assigned in range of [0.5, 2]. rand is a random number.
(3) Swooping phase: the bald eagle quickly pounced on the prey according to the best position obtained in the previous stage and told other bald eagles to start swooping. Its position was updated as follows:
where, x1(i) and y1(i) denote the position coordinates of the target prey. c1 and c2 are the parameters used to control the exercise intensity, and the values are [1,2].
3.2 Simulation experiment and analysis
In order to discuss the significance of the BES algorithm, the optimization comparison experiment of the two-dimensional simulation function in (13) is carried out.
Whale optimization algorithm (WOA) (Mirjalili and Lewis, 2016), particle swarm optimization (PSO) algorithm (Massaoudi et al., 2021), grey wolf optimizer (GWO) algorithm (Mirjalili et al., 2014), moth-flame optimization (MFO) algorithm (Mirjalili, 2015) and BES algorithm are used respectively to find the minimum value of this function. In order to maintain the rationality of the experimental results and the consistency of the parameters of various algorithms, the population size is set to 30 and the maximum iterations is set to 100. The function space is shown in Figure 2.
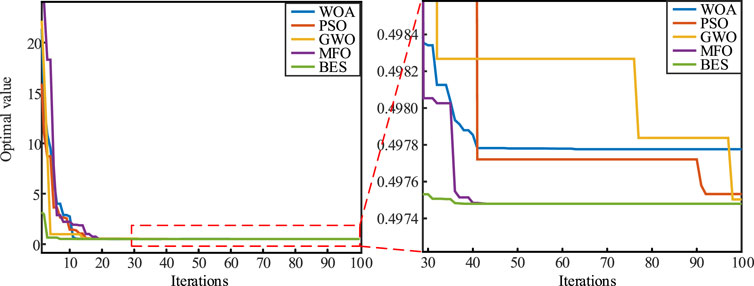
The optimization process of each optimization algorithm is shown in Figure 3.
As can be seen from Figure 3, in terms of optimization speed, WOA finds the minimum value after the 41st iteration, which is 0.49778. PSO finds the minimum value after the 92nd iteration, which is 0.49753. GWO finds the minimum value after the 98th iteration, which is 0.4975. MFO finds the minimum value after the 43rd iteration, which is 0.49748. BES finds the minimum value after the 36th iteration, which is 0.4974797. In terms of optimization accuracy, the accuracy of BES reaches 7 digits after the decimal point, which is closer to the global minimum value. WOA, PSO, GWO, MFO meta heuristic optimization algorithms have certain advantages in optimization, BES optimization is a new meta heuristic optimization algorithm, which has strong global search ability and can effectively solve various complex numerical optimization problems. Based on the above analysis, for VMD parameter selection, it can be regarded as an optimization problem. Compared with WOA, PSO, GWO and MFO, BES optimization algorithm shows certain advantages among them, so this paper uses BES algorithm to optimize VMD parameters.
4 Hybrid models and prediction methods
4.1 CNN-Bi-LSTM hybrid model
CNN model can obtain effective representation directly from the original signal through the alternate use of convolutional layer and pooling layer through local connection and weight sharing, and automatically extract the local features of the data, so as to establish a dense and complete feature vector. So, this paper selects CNN model to extract load data features.
For Bi-LSTM, the input of the model is output after passing through the LSTM network in sequential and reverse directions respectively (Tang et al., 2019; Tian et al., 2021). The output of the model contains the information of the input sequence in forward direction and backward direction at the same time, and the weight reuse further improves the expression ability of the network, while the total amount of data demand remains unchanged, so the risk of under fitting is reduced. Therefore, considering the fluctuation and uncertainty of input data in power load forecasting, CNN is fused on deep Bi-LSTM network to improve the ability of feature extraction and dimension reduction of the model on the original data.
According to the existing experience, there are various factors that affect power load, mainly include: historical load, meteorological factors, date type, etc. Yang J. et al. (2021). Among them, due to the time series characteristics of load, the prediction model can learn the recent change rule of load according to the load daily data that is close to the date to be predicted, which can enrich the prior information of the prediction model. Based on this, this paper selects the historical load data 1 day before the forecast date as one of the characteristics that affect short-term load forecasting; Meteorological factors have a crucial impact on short-term load forecasting. Among them, the common influencing factors are temperature, followed by humidity, wind speed, precipitation, air pressure, etc. Due to the limitations of the experimental data in this paper, only considers temperature as one of the characteristics that affect short-term load forecasting; Date type is another important factor affecting short-term forecast. At present, urban power load is still dominated by industrial power, and the power load on non-working days (Saturday, Sunday, holidays) is significantly less than that on working days (Monday to Friday). Therefore, this paper lists the date type (weather it is Saturday or Sunday, whether it is a legal holiday) as characteristics that affect the load forecasting results.
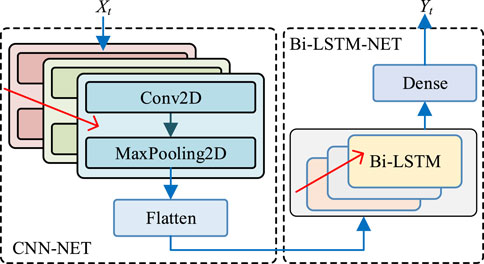
Based on the above analysis, in this paper, the input X includes the following 8 characteristics: historical load, temperature, data (x year, x month, x day), time (x hour), whether it is Saturday or Sunday, whether it is a legal holiday, expressed as X = [x1, x2, x3, x4, x5, x6, x7, x8]. And the other prediction models maintain the same input characteristics. The structure of CNN-Bi-LSTM hybrid model proposed in this paper is shown in Figure 4.
As show in Figure 4, CNN is used to extract the effective feature vector, and the feature vector is constructed in the form of time series and used as the input data of Bi-LSTM network. The depth of the prediction model can be increased by adding Bi-LSTM network units to improve the prediction effect of the network. In order to facilitate the subsequent comparison, the sliding window width is 24 records; Step size is 1. The hyperparameters of each CNN-Bi-LSTM model are obtained by grid search method. Dropout technology is used between Bi-LSTM layers to prevent model over fitting. Finally, vectors in the specified format are output through dense.
4.2 BES-VMD-CNN-Bi-LSTM-EC hybrid model
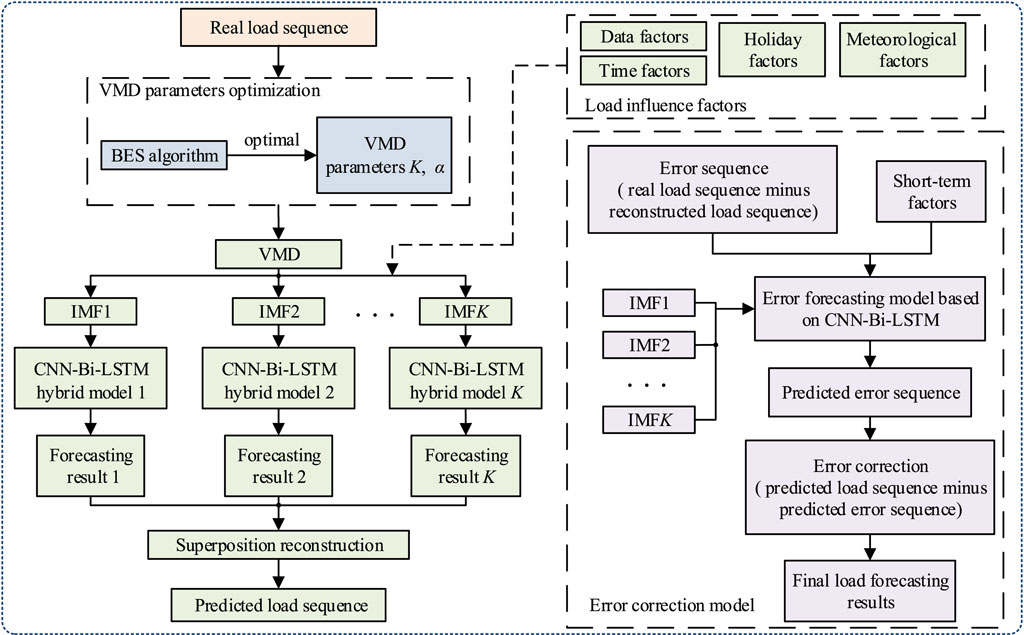
For the data-driven prediction model, it is necessary to determine its input sequence and output sequence. Since the load at the time of the day to be predicted has a strong correlation with the load of the previous day, the 24-h characteristic data of the previous day is selected as the input, and the output is the load value of each hour of the day to be predicted. The short-term power load forecasting model based on BES-VMD-CNN-Bi-LSTM-EC in this paper is shown in Figure 5.
The whole forecasting process is divided into two stages:
(1) In the first stage, several component prediction models based on BES-VMD-CNN-Bi-LSTM hybrid network are constructed. Firstly, a decomposition loss function (Loss) is defined as the evaluation criteria, and the optimal number of components K and the penalty factor α are found through the BES algorithm under this evaluation criteria. Then, the real load sequence is decomposed into K modal components by VMD, which are recorded as IMF1, IMF2, …, IMFK and the corresponding CNN-Bi-LSTM hybrid network models are established. Finally, the independent prediction results of each sub series are reconstructed to obtain the predicted load sequence.
(2) In the second stage, an error correction model considering short-term factors is proposed. Considering that the influence of nonlinear and short-term fluctuation factors of the sequence itself, various modal components, holiday (whether it is Saturday or Sunday and whether it is a legal holiday) and meteorological factors (ambient temperature) are selected as the input of the error correction model. The error sequence obtained by subtracting the reconstructed load sequence from the real load sequence is used as the output. Subsequently, an error correction model based on CNN-Bi-LSTM network is established to obtain the predicted error sequence to correct the predicted load sequence before. At last, the final load forecasting results are obtained and further improve the short-term load forecasting effect.
4.3 Evaluation indices
To verify the effectiveness of the proposed model, mean absolute percentage error (MAPE) and root mean square error (RMSE) are used to evaluate the forecasting results, and their specific expressions are as follows:
where, n represents the total number of samples. yact(i) and ypred(i) are the real and predicted load values at time i, respectively.
5 Case study
The experimental computer is configured as: Windows 10 64-bit operating system; Intel(R) Core (TM)i7-8700 CPU; 32GB memory; NVIDIA GeForce RTX 2070 graphics card, which is based on Python 3.6 and tensorflow1.12 operating environment.
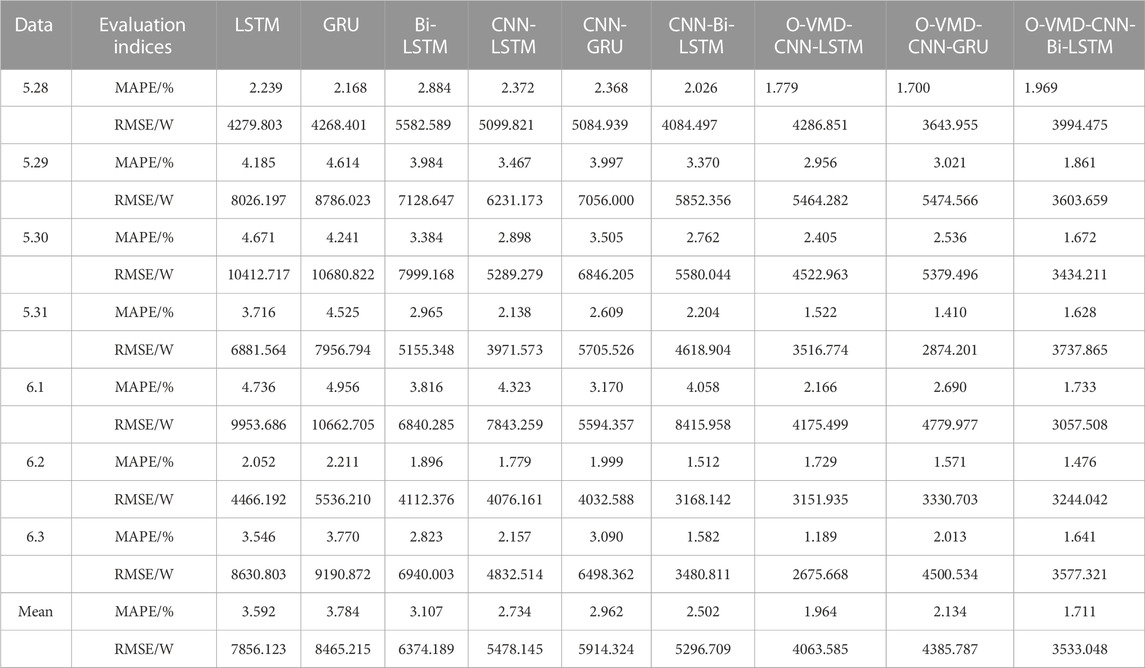
5.1 Dataset collection
The experimental data comes from the 2012 global energy forecasting competition published data set, including the hourly load data, the corresponding temperature dataset and holiday information of 20 areas (Hong et al., 2014). The case takes the load data of area 6 from 29 November 2006 to 29 June 2008 as the original data, and divides it into training set, verification set and test set according to the ratio of 8:1:1. The sampling interval is 1 h and 24 points are collected in 1 day. The input includes 8 characteristics: historical load, temperature, year, month, day, hour, whether it is Saturday or Sunday and whether it is a legal holiday. RF, SVM, LSTM, GRU, Bi-LSTM, CNN-LSTM, CNN-GRU, CNN-Bi-LSTM, O-VMD-CNN-LSTM, O-VMD-CNN-GRU, O-VMD-CNN-Bi-LSTM and BES-VMD-CNN-Bi-LSTM are selected as comparison models to verify the feasibility and effectiveness of the proposed model BES-VMD-CNN-Bi-LSTM-EC.
After determining the input characteristics, it is necessary to normalize them to improve the convergence speed of the model. In this paper, the max-min normalization method is used to normalize the characteristic series such as historical load, temperature, year, month, day and hour to the range of [0,1]. The dummy variable is used to represent the weekend and legal holiday characteristics, where logic not represented by 0 and logic yes is represented by 1.
5.2 VMD parameter optimization
5.2.1 Central frequency method
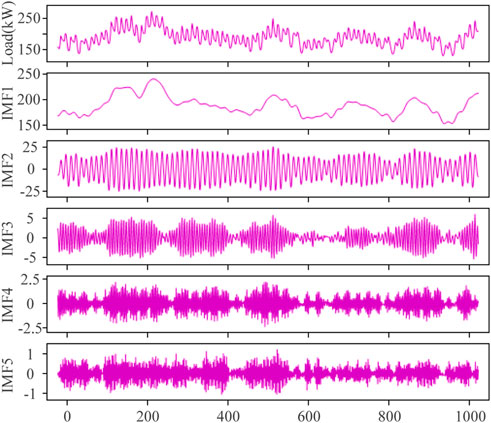
The selection of the number of modal components K directly affects the results of VMD. If K is too large, it will lead to modal repetition or additional noise; if K is too small, the modal under decomposition will occur, resulting in the decline of the accuracy of the subsequent prediction model. Generally, the range of K is set to [3, 8], and the center frequencies corresponding to different components are different (Yang L. et al., 2021). Therefore, set K = 3, 4, …, 8 to conduct experiments respectively, and obtain the center frequencies of each component corresponding to different K values. When the K with similar center frequency appears for the first time, it is marked, and determine K-1 as the number of modal components to decompose the original load sequence. In this paper, the method of determining VMD parameter by central frequency method is expressed as O-VMD. 1000 time series load samples with non-linear and non-stationary are randomly selected and decomposed by VMD to obtain different components. Table 1 shows the center frequencies of various component corresponding to different K values.
It can be seen from Table 1 that when K is 6, the center frequencies of modal components u4 and u5 are 1.8296 and 2.0914 respectively. The center frequencies of the two components are approximate and it is over decomposed at this time. When K = 8, the center frequencies of u5 and u6 are approximate, so the number of components K is determined to be 5. Based on this, the above 1000 time series load samples and their O-VMD decomposition results are shown in Figure 6. It can be seen from Figure 6 that the average amplitude of IMF3, IMF4 and IMF5 is small, with large fluctuations and poor regularity; For mode function IMF2, the regularity is relatively good and the periodicity is relatively obvious; the average amplitude of the modal function IMF1 is large, the change is gentle, and the regularity is easiest to grasp. Later, these five modal functions will be modeled separately for short-term load forecasting of O-VMD combined method.
5.2.2 VMD parameters optimized by BES
In addition to the selection of the value of K, the penalty factor α affects the reconstruction accuracy of VMD signal. Considering the influence of decomposition loss on forecasting accuracy, an evaluation criterion suitable for load forecasting is selected to determine VMD parameters. The evaluation criterion is defined as follows:
where, f(t) is the original load sequence, f*(t) is the reconstructed sequence, T is the length of time.
Loss is the average absolute error between the original load sequence and the reconstructed sequence. The smaller Loss is, the smaller the signal decomposition loss is and the more accurate the prediction model is. Therefore, the parameter selection problem of VMD is expressed as a constrained optimization problem, as follows:
where, K∈[3,10], α∈[100,10000].
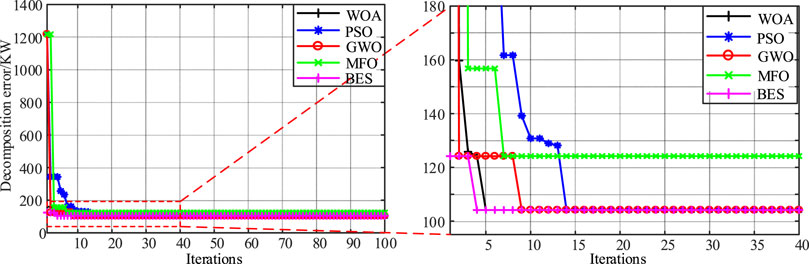
The flow chart of VMD parameters optimized by BES algorithm is shown in Figure 7. WOA, PSO, GWO, MFO and BES algorithms are used to optimize the parameters of the VMD respectively. In order to maintain the consistency of the parameters of various algorithms, the population size is set to 20 and the maximum iterations is set to 100. Figure 8 shows the optimization process of the decomposition loss of different algorithms.
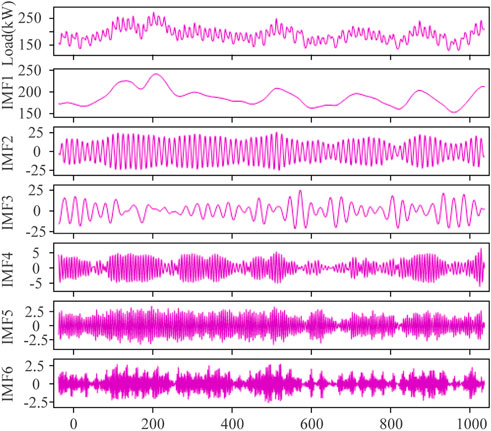
It can be seen from Figure 8 that when the MFO algorithm is used to determine the decomposition parameters, the decomposition loss is high and after the 7th iteration, the minimum decomposition loss is 124.1831. PSO, GWO and WOA algorithms achieve the minimum decomposition loss after the 14th, 9th and 5th iterations respectively. For BES algorithm, the minimum decomposition loss is 104.1395 after the 4th iteration, the optimization speed is the fastest, at this time, the K is 6 and α is 100. Thus, BES-VMD algorithm can adaptively determine the optimal decomposition parameters to improve the decomposition effect of VMD. The original load sequence and their BES-VMD decomposition results are shown in Figure 9. It can be seen from Figure 9 that the average amplitude of IMF4, IMF5 and IMF6 is small, with large fluctuations and poor regularity; For mode function IMF2, IMF3, the regularity is relatively good and the periodicity is relatively obvious; the average amplitude of the modal function IMF1 is large, the change is gentle, and the regularity is easiest to grasp. Later, these six modal functions will be modeled separately for the short-term load forecasting of BES-VMD combined method.
5.3 Analysis of prediction results
5.3.1 Results analysis of CNN feature extraction and O-VMD
To verify the effectiveness of CNN feature extraction and the effectiveness of VMD decomposition in the load forecasting model, 9 different models are used to conduct short-term load forecasting on the load data of a continuous week (from 28 May to 3 June 2008). Figure 10A shows the load forecasting results for a continuous week; Figure 10B shows the load forecast results of 1 day (June 2). The statistical description of specific prediction results is shown in Table 2.
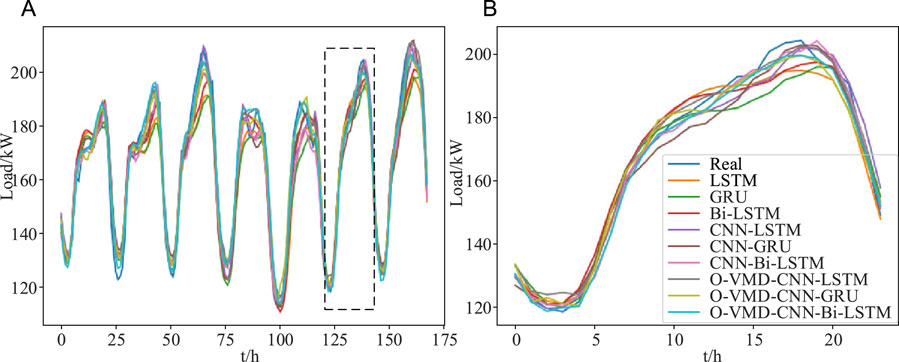
FIGURE 10. (A) Load forecasting results for a continuous week. (B) Load forecasting results of 1 day.
About the effectiveness of CNN feature extraction prediction model, it can be seen from Figure 10 and Table 2 that, compared with single prediction models like LSTM, GRU and Bi-LSTM, the prediction accuracy of the corresponding CNN-LSTM, CNN-GRU and CNN-Bi-LSTM hybrid models established by CNN feature extraction has been improved to varying degrees. Among them, MAPE decreased by 0.858%, 0.822% and 0.605% respectively. RMSE decreased by 2377.978W, 2550.891W and 1077.48W respectively. Compared with CNN-LSTM and CNN-GRU, the load forecasting accuracy based on CNN-Bi-LSTM model is higher.
About the effectiveness of the VMD (take O-VMD as an example) signal decomposition load forecasting model, According to Figure 10 and Table 2, the outputs of each load forecasting model are compared and analyzed from the perspective of the average value of its evaluation indices. Compared with CNN-LSTM, CNN-GRU and CNN-Bi-LSTM models before VMD, the prediction performance of the corresponding hybrid prediction models O-VMD-CNN-LSTM, O-VMD-CNN-GRU and O-VMD-CNN-Bi-LSTM established after VMD of the original load series has been improved. Among them, MAPE decreased by 0.770%, 0.828% and 0.791% respectively. RMSE decreased by 1414.560W, 1528.537W and 1763.661W respectively. Compared with O-VMD-CNN-LSTM and O-VMD-CNN-GRU models, the MAPE of O-VMD-CNN-Bi-LSTM model decreased by 0.253% and 0.423% respectively. RMSE decreased by 530.537W and 852.739W respectively.
In conclusion, the effectiveness of VMD and CNN feature extraction are verified. Among them, the MAPE and RMSE of O-VMD-CNN-Bi-LSTM model is the smallest. Besides, although the hybrid prediction model based on Bi-LSTM takes a relatively long time, it obtains the highest prediction accuracy and meets the requirements of engineering applications.
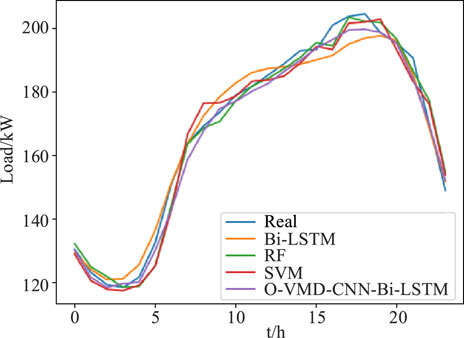
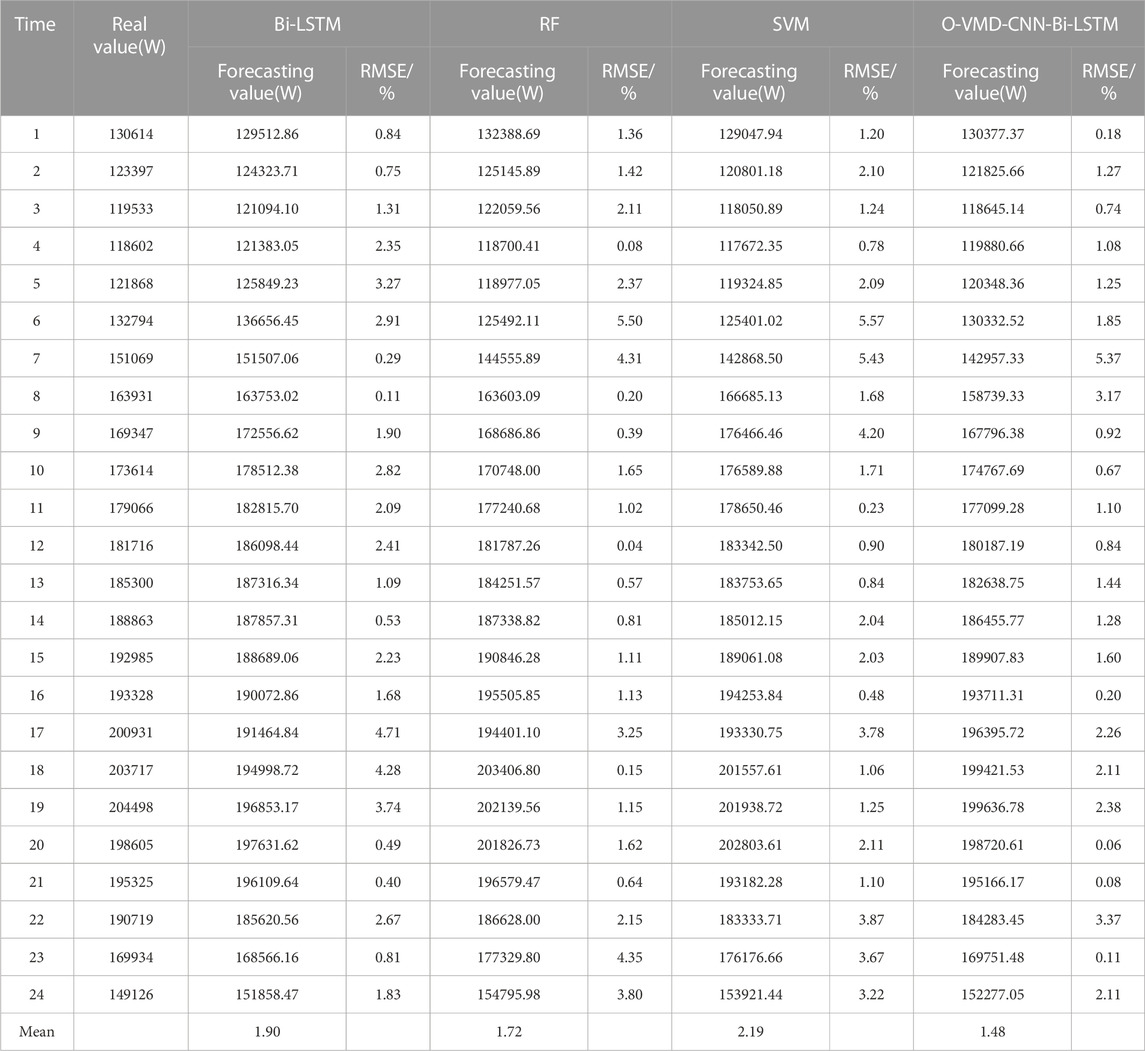
In order to further verify the effectiveness of the proposed O-VMD-CNN-Bi-LSTM model, Bi-LSTM, RF and SVM are used as comparison models to predict the load at 24 h (2 June). The load forecasting results of different models are shown in Figure 11, and the statistical description results are shown in Table 3.
As shown in Figure 11, each model can better predict the change trend of load. Combined with Table 3, compared with Bi-LSTM, RF and SVM prediction methods, the mean RMSE of O-VMD-CNN-Bi-LSTM model at 24 h decreased by 0.42%, 0.24% and 0.71% respectively. Thus, the effectiveness of the prediction method based on O-VMD-CNN-Bi-LSTM is further verified.
5.3.2 Results analysis of BES-VMD and error correction
First, according to the above analysis, the prediction error of O-VMD-CNN-Bi-LSTM model is the smallest, so the comparison experiment is carried out based on this model to analyse the effectiveness of the power load prediction model of BES-VMD-CNN-Bi-LSTM.
Secondly, the prediction error correction experiment is carried out based on BES-VMD-CNN-Bi-LSTM (the prediction model before error correction). Taking various modal components, holidays (whether Saturday or Sunday, and whether it is a legal holiday) and meteorological factors (ambient temperature) as the input of the error correction model, the load prediction model after error correction is established (the proposed method, BES-VMD-CNN-Bi-LSTM-EC).
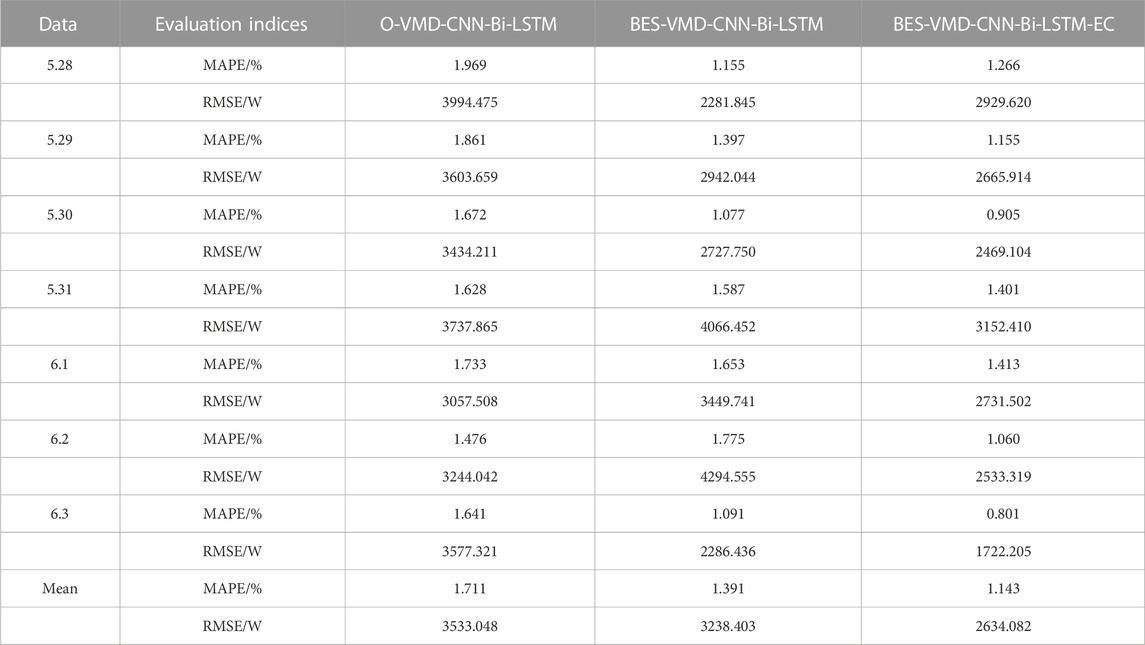
Table 4 shows the statistical results of load forecasting errors for a week (from 5.28 to 6.3) based on O-VMD-CNN-Bi-LSTM, BES-VMD-CNN-Bi-LSTM and BES-VMD-CNN-Bi-LSTM models.
According to Table 4, compared with O-VMD-CNN-Bi-LSTM method, the weekly mean MAPE and RMSE of BES-VMD-CNN-Bi-LSTM method are reduced by 0.320% and 294.645W respectively, indicating that the overall prediction accuracy and model performance of this method are greatly improved. Thus, the effectiveness of BES optimization algorithm in power load forecasting is further verified.
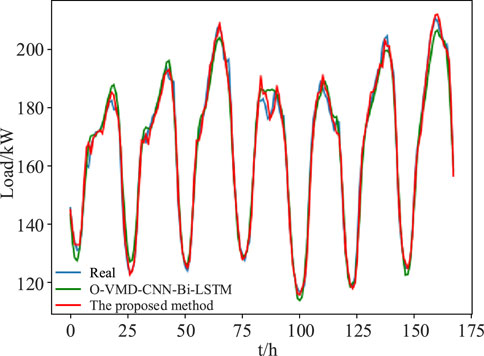
It can be seen from Table 4 that compared with BES-VMD-CNN-Bi-LSTM method, the weekly mean MAPE and RMSE of BES-VMD-CNN-Bi-LSTM-EC method are reduced by 0.248% and 604.321W respectively, which verifies the effectiveness of the error correction method. Figure 12 shows the prediction results of the proposed method with O-VMD-CNN-Bi-LSTM method.
More intuitively, it can be seen from Figure 12 that the proposed method can better fit the actual load change trend, especially near the peak point, and the prediction accuracy is higher, which further verifies that the BES-VMD-CNN-Bi-LSTM-EC method can effectively reduce the prediction error of short-term power load with excellent prediction performance.
6 Conclusion
Aiming at the characteristics that short-term power load forecasting is easily affected by many factors, in order to improve the accuracy of short-term load forecasting, a short-term load combination forecasting method based on BES-VMD-CNN-Bi-LSTM-EC is proposed in this paper. The conclusions are as follows:
(1) As the current forecasting methods based on traditional statistical analysis and machine learning are difficult to consider both the temporal and nonlinear characteristics of load data, Bi-LSTM model can better fit the temporal and complex nonlinear relationship of load data, it can learn the information of the load sequence in the forward direction and the backward direction at the same time to improve the expression ability of the network, so it is applied to the forecasting model in this paper.
(2) This paper gives full play to the potential feature extraction advantages of CNN model and provides a large amount of effective input data for Bi-LSTM model. It overcomes the defect that a single Bi-LSTM model cannot effectively mine the hidden information between discontinuous data. The simulation results show that compared with the model without CNN feature extraction, which effectively improves the prediction accuracy.
(3) In order to reduce the complexity of load series and further improve the accuracy of short-term load forecasting, this paper uses the advantages of VMD in processing non-stationary and nonlinear signals, and uses BES algorithm to optimize VMD parameters. The load series is decomposed into components with different frequencies, and a CNN-Bi-LSTM forecasting model is established for each component. The simulation results show that compared with the model without signal decomposition, which effectively improves the forecasting accuracy.
(4) An error correction model considering short-term factors is established, which reduces the inherent error of the prediction model by mining the effective information hidden in the error. The simulation results show that compared with the forecasting method without error correction, the VMD-CNN-Bi-LSTM-EC combined forecasting model can further improve the accuracy of short-term load forecasting. The proposed method has better forecasting ability and stability and several application values as follows: 1) It can provide theoretical guidance for power production departments and management departments to formulate production plans and development plans, and determine the power supply quantity and production plans of each power supply area. 2) It can improve the accuracy of power system short-term load forecasting, and further improve the security and economy of power system operation.
The load forecasting feature set established in the proposed method does not considering the diversified load types, and does not include electricity price factors, other meteorological factors, etc. Therefore, in the future work, this paper will further study the impact of load characteristic classification on load forecasting, build a richer feature set including electricity price factors and other meteorological factors such as humidity, wind speed, precipitation, air pressure, etc., explore the internal relationship of input characteristics, and further improve the accuracy of short-term load forecasting. At the same time, the forecasting model needs to be optimized to shorten the prediction time and improve the real-time performance.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
NW and ZL contributed to conception and design of the study. NW organized the database. NW and ZL performed the statistical analysis. NW wrote the first draft of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.
Funding
This work was supported in part by the National Natural Science Foundation of China under Grant 51967011 and the Natural Science Foundation of Gansu Province under Grant 21JR7RA207.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Ahmed, F., Hegazy, R., Dalia, Y., Kandil, T., and Abo-Khalil, A. G. (2022). Real-time bald eagle search approach for tracking the maximum generated power of wind energy conversion system. Energy 249 (C), 123661. doi:10.1016/j.energy.2022.123661
Chen, Z., Zhang, D., Jiang, H., Wang, L., Chen, Y., Xiao, Y., et al. (2021). Load forecasting based on LSTM neural network and applicable to loads of “replacement of coal with electricity”. J. Electr. Eng. Technol. 16 (5), 1–10. doi:10.1007/s42835-021-00768-8
Dou, C., Zheng, Y., Yue, D., Zhang, Z., and Ma, K. (2018). Hybrid model for renewable energy and loads prediction based on data mining and variational mode decomposition. IET Generation Transm. Distribution 12 (11), 2642–2649. doi:10.1049/iet-gtd.2017.1476
García-Ascanio, C., and Maté, C. (2009). Electric power demand forecasting using interval time series: A comparison between var and iMLP. Energy Policy 38 (2), 715–725. doi:10.1016/j.enpol.2009.10.007
Hobbs, B. F., Jitprapaikulsarn, S., Konda, S., Chankong, V., Loparo, K., and Maratukulam, D. (1999). Analysis of the value for unit commitment of improved load forecasts. IEEE Trans. Power Syst. 14 (4), 1342–1348. doi:10.1109/59.801894
Hong, T., Pinson, P., and Fan, S. (2014). Global energy forecasting competition 2012. Int. J. Forecast. 30 (2), 357–363. doi:10.1016/j.ijforecast.2013.07.001
Jiang, H., Zhang, Y., Eduard, M., Zhang, J. J., and Gao, D. W. (2018). A short-term and high-resolution distribution system load forecasting approach using support vector regression with hybrid parameters optimization. IEEE Trans. Smart Grid 9 (4), 3341–3350. doi:10.1109/tsg.2016.2628061
Kassa, Y., Zhang, J., and Zheng, D. (2019). EMD-PSO-ANFIS based hybrid approach for short-term load forecasting in microgrids. IET Generation Transm. Distribution 14 (3), 470–475. doi:10.1049/iet-gtd.2019.0869
Kwon, B. S., Park, R. J., Song, K. B., and Song, K. B. (2020). Short-term load forecasting based on deep neural networks using LSTM layer. J. Electr. Eng. Technol. 15 (4), 1501–1509. doi:10.1007/s42835-020-00424-7
Lee, C. M., and Ko, C. N. (2011). Short-term load forecasting using lifting scheme and ARIMA models. Expert Syst. Appl. 38 (5), 5902–5911. doi:10.1016/j.eswa.2010.11.033
Lee, J., and Cho, Y. (2022). National-scale electricity peak load forecasting: Traditional, machine learning, or hybrid model? Energy 239 (D), 122366–122416. doi:10.1016/j.energy.2021.122366
Liang, Z., Sun, G., and Li, H. (2018). Short-Term load forecasting based on VMD and PSO optimized deep belief network. Power Syst. Technol. 42 (2), 598–606. doi:10.13335/j.1000-3673.pst.2017.0937
Lu, J., Zhang, Q., and Yang, Z. (2019). Short-term load forecasting method based on CNN-LSTM hybrid neural network model. Automation Electr. Power Syst. 43 (08), 131–137. doi:10.7500/AEPS20181012004
Massaoudi, M., Refaat, S., Chihi, I., Trabelsi, M., Oueslati, F. S., and Abu-Rub, H. (2021). A novel stacked generalization ensemble-based hybrid LGBM-XGB-MLP model for Short-Term Load Forecasting. Energy 214, 118874. doi:10.1016/j.energy.2020.118874
Meng, Z., Xie, Y., and Sun, J. (2021). Short-term load forecasting using neural attention model based on EMD. Electr. Eng. 104 (3), 1857–1866. doi:10.1007/s00202-021-01420-4
Mirjalili, S., and Lewis, A. (2016). The whale optimization algorithm. Adv. Eng. Softw. 95, 51–67. doi:10.1016/j.advengsoft.2016.01.008
Mirjalili, S., Mirjalili, S. M., and Lewis, A. (2014). Grey wolf optimizer. Adv. Eng. Softw. 69, 46–61. doi:10.1016/j.advengsoft.2013.12.007
Mirjalili, S. (2015). Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowledge-Based Syst. 89, 228–249. doi:10.1016/j.knosys.2015.07.006
Muhammad, B., Mohsin, S., Muhammad, A., Ullah, B., Hisham, S. B., and Ali, S. S. A. (2021). Annual cost and loss minimization in a radial distribution network by capacitor allocation using PSO. Appl. Sci. 11 (24), 11840. doi:10.3390/app112411840
Rodrigues, F., and Pereira, F. C. (2020). Beyond expectation: Deep joint mean and quantile regression for spatiotemporal problems. IEEE Trans. Neural Netw. Learn. Syst. 31 (12), 5377–5389. doi:10.1109/tnnls.2020.2966745
Talaat, M., Farahat, M. A., and Mansour, N. (2020). Load forecasting based on grasshopper optimization and a multilayer feed-forward neural network using regressive approach. Energy 196, 1–12. doi:10.1016/j.energy.2020.117087
Tang, X., Dai, Y., Wang, T., and Chen, Y. (2019). Short-term power load forecasting based on multi-layer bidirectional recurrent neural network. IET Generation, Transm. Distribution 13 (17), 3847–3854. doi:10.1049/iet-gtd.2018.6687
Tian, P., Zhang, C., Zhou, J., and Nazir, M. S. (2021). An integrated framework of Bi-directional Long-Short Term Memory (BiLSTM) based on sine cosine algorithm for hourly solar radiation forecasting. Energy 221 (C), 119887. doi:10.1016/j.energy.2021.119887
Wu, X., He, J., and Zhang, P. (2015). Power system short-term load forecasting based on improved random forest with grey relation projection. Automation Electr. Power Syst. 39 (12), 50–55. doi:10.7500/AEPS20140916005
Yan, H., and Tian, C. (2019). A novel two-stage forecasting model based on error factor and ensemble method for multi-step wind power forecasting. Appl. Energy 238 (15), 368–383. doi:10.1016/j.apenergy.2019.01.063
Yang, D., Guo, J., and Li, Y. (2023). Short-term load forecasting with an improved dynamic decomposition-reconstruction-ensemble approach. Energy 263, 1–16. doi:10.1016/j.energy.2022.125609
Yang, J., Zhang, S., and Liu, J. (2021). Short-term photovoltaic power prediction based on variational mode decomposition and long short-term memory with dual-stage attention mechanism. Automation Electr. Power Syst. 45 (3), 174–182. doi:10.7500/AEPS20200226011
Yang, L., Wu, H., and Ding, M. (2021). Short-term load forecasting in renewable energy grid based on Bi-directional long short-term memory network considering feature selection. Automation Electr. Power Syst. 45 (03), 166–173. doi:10.7500/AEPS20200202002
Yang, Y., Wang, Z., and Zhao, S. (2023). An integrated federated learning algorithm for short-term load forecasting. Electr. Power Syst. Res. 214, 1–10. doi:10.1016/J.EPSR.2022.108830
Ye, J., Cao, J., and Yang, L. (2022). Ultra short-term load forecasting of user level integrated energy system based on variational mode decomposition and multi-model fusion. Power Syst. Technol. 46 (07), 2610–2622. doi:10.13335/j.1000-3673.pst.2021.2566
Yuan, F., and Che, J. (2022). An ensemble multi-step M-RMLSSVR model based on VMD and two-group strategy for day-ahead short-term load forecasting. Knowledge-Based Syst. 252, 109440–109516. doi:10.1016/j.knosys.2022.109440
Zang, H., Xu, R., Cheng, L., Ding, T., Liu, L., Wei, Z., et al. (2021). Residential load forecasting based on LSTM fusing self-attention mechanism with pooling. Energy 229, 120682. doi:10.1016/j.energy.2021.120682
Zhang, L., Mahmoud, A., and Jin, W. (2021). Comparison of time-frequency-analysis techniques applied in building energy data noise cancellation for building load forecasting: A real-building case study. Energy Build. 231, 110592–110611. doi:10.1016/j.enbuild.2020.110592
Zhang, S., Li, J., and Jiang, A. (2022). A novel two-stage model based on FPA-VMD and BiLSTM neural network for short-term power load forecasting. Power Syst. Technol. 46 (08), 3269–3279. doi:10.13335/j.1000-3673.pst.2021.0969
Zhao, F., Sun, B., and Zhang, C. (2016). Cooling, heating and electrical load forecasting method for CCHP system based on multivariate phase space reconstruction and kalman filter. Proc. CSEE 36 (02), 399–406. doi:10.13334/j.0258-8013.pcsee.2016.02.010
Zhao, Y., Wang, H., and Kang, L. (2022). Temporal convolution network-based short-term electrical load forecasting. Trans. China Electrotech. Soc. 37 (05), 1242–1251. doi:10.1109/DDCLS49620.2020.9275148
Keywords: short term load forecasting, BES, variational modal decomposition, CNN-Bi-LSTM, error correction
Citation: Wang N and Li Z (2023) Short term power load forecasting based on BES-VMD and CNN-Bi-LSTM method with error correction. Front. Energy Res. 10:1076529. doi: 10.3389/fenrg.2022.1076529
Received: 21 October 2022; Accepted: 19 December 2022;
Published: 06 January 2023.
Edited by:
Sarat Kumar Sahoo, Parala Maharaja Engineering College (P.M.E.C), IndiaReviewed by:
Ashwin Sahoo, C. V. Raman College of Engineering, IndiaPrabhakar Karthikeyan Shanmugam, VIT University, India
Sachidananda Prasad, National Institute of Science and Technology, India
Razia Sultana Wahab, VIT University, India
Copyright © 2023 Wang and Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhanming Li, bGl6bUBsdXQuZWR1LmNu
 Nier Wang
Nier Wang Zhanming Li*
Zhanming Li*