Optimal operation of urban tidal drainage pumping station based on genetic algorithm coupled with head-water level successive approximation

Aiming at the method of solving the optimization scheme for urban tidal drainage pumping stations during heavy rainfall below the urban drainage design standard, and the problems such as the mismatch between the head and water level of pumping stations at each divided time period during the solution process, a nonlinear mathematical model for optimal operation of urban tidal drainage pumping station was constructed which took the minimal operation cost of drainage pumping station during given operating period as the study target, and the blade angle of each pump unit in each divided time period as decision variables with the constraints of total water quantity of target drainage, matched motor power of each pump unit, water level of in the drainage area, number of switches and the shortest operation time of pump unit. For the problem of head-water level mismatch at each divided time period of pumping station, the genetic algorithm of coupled head-water level successive approximation is proposed, which can make the optimization scheme realize the matching of river network water level and pumping station operating head. Taking Guazhou Pumping Station in Yangzhou City of Jiangsu Province encountering 10% frequency designed rainfall as an example, optimization schemes under typical working conditions which included different starting drainage water levels and peak-valley electricity prices was obtained, as well as the influence of electricity price of divided time period, average head of each divided time period and inflow on the optimization scheme was carried out. The unit optimal operation drainage costs of Guazhou Pumping Station is 45.46 yuan/10⁴ m³ and 51.32 yuan/10⁴ m³ respectively when the starting drainage water level is set as 4.8 m and 4.6 m, which has the corresponding operation benefit of 15.34% and 4.40% less than that of conventional operation, and the water level variation of river network has dropped 6.61% and 7.85% than that of conventional operation. The constructed optimal operation model of urban tidal drainage pumping station and the proposed solution method can effectively improve the matching degree of pumping head and water level variation, and effectively make a compromise of economic operation of drainage pumping station and the safety requirements of water level control of river network in drainage area. The obtained optimization schemes can offer decision-making reference for relevant dispatching and management departments of drainage pumping stations.

1 Introduction

In recent years, the frequency of regional extreme short-calendar heavy rainfall in China has increased significantly, and urban drainage pumping stations, as an important infrastructure for urban construction, play an important role in safeguarding people’s lives and property and protecting urban infrastructure. Such projects are characterized by large single machine flow, long seasonal operation time, etc., and consume a lot of energy especially during flood operation. Therefore, many scholars recently carried out various optimization studies on the operation of pumping stations (Chen et al., 2022; Gong and Zhu, 2022; Zhu et al., 2022). Scholars have proposed objective functions in the form of pumping station energy consumption, pumping station cost, discharge (Tao et al., 2022), ecological benefits (Wu et al., 2010), etc. The solution methods are not lack of linear programming (Jowitt Paul and George, 1992), dynamic programming (Sterling and Coulbeck, 2015), genetic algorithm (Fang et al., 2016), multi-objective genetic algorithm (Yang et al., 2019), hybrid nonlinear programming genetic algorithm (NLP-GA) (Rasoulzadeh Gharibdousti et al., 2011), particle swarm algorithm (Liu and Chen, 2020), hybrid wolf swarm algorithm (Feng et al., 2020), acoustic search algorithm (Yazdi and Kim, 2015), etc. Fecarotta et al. (2018) constructed a mixed integer optimization model to solve the problem of minimizing energy consumption in drainage pumping stations; Wang et al. (2019) constructed a rainfall model to solve the problem of optimal start-up water depth in drainage pumping stations based on a particle swarm optimization algorithm; Fatemeh et al. (Jafari et al., 2018) derived real-time control strategies for urban drainage system operations, using an EPA stormwater management model associated with a particle swarm optimization algorithm as a way to evaluate the operational performance of each strategy set; Yazdi et al. (2016) designed long-term operation rules for drainage pumping stations by coupling a mathematical model and a new hybrid search algorithm considering the stochastic nature of rainfall events; Eui et al. (2016) proposed a new scheme for the collaborative operation of urban drainage systems through shared monitoring of nodal water levels and innovatively developed a resilience index to assess urban mitigation and recovery capacity; Graber (Graber, 2010) considered storage conditions for storm duration effects and upstream inundation area geometry to determine small and medium stormwater pumping station operation design options with actual pumping station flow and head relationships; Saliba et al. (2020) proposed a Deep Deterministic Policy Gradient (DDPG) algorithm to cope with the impact of data uncertainty for realistic situations such as rainfall forecasts, and validated it with three scenarios: complete data, incomplete rainfall forecasts, and incomplete water level and forecast data; Zhe et al. (Xu et al., 2011) aimed to improve the traditional drainage network water level control, combined with the sewage convergence node prediction model, and proposed a fuzzy optimal control method, which solved the problems of control lag caused by pump station isolation control, frequent switching of pumps caused by conservative control, sewage overflow and energy saving in pump station operation; Hwang et al. (2020) considered local vulnerability points in the overall area as well as reservoir water level limitations to respond to sudden urban flooding through non-engineering measures consisting of pump optimization schemes, gate opening and closing schemes, etc., derived by harmonious search algorithms; Wei et al. (Dong and Yang, 2020) introduced many complex hydro-meteorological constraints for river pollution prevention and flood control requirements of urban river network systems, proposed a data-driven model, and solved the cycle operation cost minimization problem including water quality and pumping stations by particle swarm optimization (PSO) algorithm; Liu et al. (2017) developed a multi-period multivariate joint optimal flood control scheduling model with the number of discharge holes, the number of pump openers, and gate opening and closing as decision variables, which was solved using an improved genetic algorithm and validated with the Huai’an water conservancy project, resulting in improvements in power generation as well as total energy consumption; Wang et al. (2022) compared three intelligent optimization algorithms: PSO-LWSM, MOPSO-TOPSIS, and NSGA-II-TOPSIS, based on four optimization objectives of pump station switching times, operating time, energy consumption, and drainage capacity, and the results showed that PSO-LWSM has a better optimization effect; Cheng Jilin, Gong Yi, Zhang Lihua et al. (Gong et al., 2010; Jilin et al., 2010; Gong et al., 2011a; Gong et al., 2011b) constructed an optimized operation model for single units, pump stations and pump station groups with the objective of minimizing power consumption costs for the inter-basin pump station project of the South-North Water Transfer East Line, using original methods such as dynamic planning, experimental selection-dynamic planning successive approximation, large system decomposition-dynamic planning aggregation, large system secondary decomposition-dynamic planning aggregation, and large system decomposition-dynamic planning aggregation based on successive approximation, which significantly improved the economic efficiency of unit operation; Liu Jingsen et al. (Liu et al., 2013; Liu et al., 2015) combined the optimal selection of the total energy consumption test for drainage and the de-inferiority of the water level control condition on the basis of considering the water level of the river in the polder area, and came up with an optimal scheduling scheme for urban drainage pumping stations for reference; Gao Yuqin et al. (Gao et al., 2020) first solved the optimization scheme of orthogonal test by genetic algorithm to maximize the drainage capacity, and then used hydrodynamic model to screen the solution that does not meet the safe water level requirement, which makes the optimization results more suitable to the reality.

In the past, most of the drainage pumping station studies were based on the pre-assumed average head of each divided time period as the basis for calculating flow and other important parameters, in practice, the operation of drainage pumping stations led to a decline in the water level of the river network in the drainage area, which inevitably also affects the upstream water level of pumping stations, which in turn directly affects the pumping station lift head during the drainage period, resulting in a deviation from the established head, affecting the determination of performance characteristics and the actual operation of the pumping station benefits. In particular, for the tide-influenced urban tidal drainage pumping stations, upstream and downstream water level of pumping stations are changing synchronously during the operation process by the pumping station drainage and tidal influence respectively, resulting in complex changes in the head at each divided time period. In view of the above, this article intends to construct a tide-influenced pumping station operation with the minimum power consumption cost as the goal under the peak-valley tariff standard, the highest and lowest control water level requirements in the drainage area, and the number of pumping station switch-on and switch-offs as the constraints, by taking the real-time head under the pumping station pumping flow after the initial head and the hydrodynamic calculation water level are approximated one by one as the basis for pumping station flow calculation. The complex nonlinear model for optimal operation of urban tide-sensitive drainage pumping stations, using systems engineering combined with non-constant flow numerical simulation methods, and the obtained optimization scheme, has important theoretical and practical significance for optimal operation decision scheduling of urban drainage pumping station projects.

2 Model construction

For a typical rainstorm below the urban drainage design standard, the following nonlinear mathematical model for optimal operation of drainage pumping stations is constructed with the objective of minimizing the total power consumption during the given drainage period of the tide sensitive pumping station, taking into account the supporting power of the unit motor, the water level limitation requirements of the river network in the drainage area, the number of times the unit is turned on and off, and the length of time the unit is turned on as constraints.

2.1 Objective function

In this paper, the objective is to minimize the power consumption cost of drainage pumping station during the drainage period, and the blade placement angle of each unit of the pumping station is the decision variable. The specific objective function is as follows:

$f=\min {\displaystyle \sum }_{j=1}^{JZ}{\displaystyle \sum }_{i=1}^{SN}\frac{\rho \cdot g\cdot Q_{i,j}\left({\theta }_{i,j}\right)\cdot \left(C_i-Z_i\right)}{{\eta }_{zi,j}\left({\theta }_{i,j}\right)\cdot {\eta }_{mot,j}\cdot {\eta }_{\mathrm{int},j}}\cdot \Delta T_i\cdot P_i(1)$

where: f is the minimum cost of electricity consumption in the drainage period of the pumping station, yuan; JZ is the number of pumping units, units; j is the unit number, j = 1, 2, 3, ..., JZ; SN is the number of time periods divided into drainage periods of the pumping station; i is the time period number, i = 1, 2, 3, ..., SN; ρ is the density of water, kg/m³; Q_{i, j} (θ_i,j), η_zi,j (θ_i,j) are the flow rate (m³/s) and pump unit efficiency of the j-th unit at the blade placement angle (θ_i,j) in the i-th time period, respectively; C_i is the downstream tide level of the pumping station in the i-th time period, m; Z_i is the river level on the pump station in the i-th time period, m; ΔT_i is the length of the time period in the i-th time period, h; P_i is the peak and valley tariff in the i-th time period, yuan/(kWh); η_{mot, j}, η_{int, j} are the motor efficiency and transmission efficiency of the jth unit, respectively, η_{mot, j} remains 94% when the motor load is over 60%, η_{int, j} can be viewed as 100% when the unit adopts a direct connection.

2.2 Constraint conditions

(1) Target total drainage constraint: under a storm below the design standard, the target total drainage determined after considering the calculation of drainage area production and sink flow shall satisfy.

${\displaystyle \sum }_{j=1}^{JZ}{\displaystyle \sum }_{i=1}^{SN}{Q}_{i,j}\left({\theta }_{i,j}\right)\cdot ∆T_i\ge W_e(2)$

(2) Motor power constraint: the actual power of each unit of the pump station operating at each divided time period shall not exceed the motor supporting power requirement, i.e.

$N_{i,j}\left({\theta }_{i,j}\right)\le N_{0,j}(3)$

(3) Water level constraint of river network in drainage area: in meeting certain drainage standards, the pumping station drainage process, the drainage area river network water level should meet the highest control level and the lowest ecological water level requirements, that is

$Z_{\min }\le Z_i\le Z_{\max }(4)$

(4) Unit start and stop times constraint: considering that large units should not be frequently start and stop requirements, the number of start and stop times during the drainage period of the unit should meet.

$D_j\le D_{0,j}(5)$

(5) Minimum duration constraint of unit operation: Once each unit is started and running, it cannot be lower than the specified minimum duration of start-up, i.e.

$t_{i,j}\ge t_{\min }(6)$

where: W_e is the total target discharge volume in the drainage period of the pumping station meeting certain drainage standards, m³; N_i,j (θ_i,j) is the actual power of the jth unit at the blade placement angle (θ_i,j) in the ith time period, kW, which should be less than the motor matching power N_0,j; Z_min and Z_max are the lowest ecological control water level (m) and the highest control water level (m) of the river in the drainage area, respectively; D_j is the opening and closing times of the jth unit during the drainage period, considering that frequent opening and closing will shorten the service life of the unit and increase energy consumption, the maximum closing times D_0,j should not be exceeded; t_i,j and tmin are the actual opening time (h) and the shortest prescribed opening time (h) of the jth unit in the i time period, respectively.

3 Model solving

3.1 Model characteristics and solving methods

The constructed model (1) to (6) are complex nonlinear mathematical models containing multiple decision variables and multiple constraints, which are solved by genetic algorithm in this article.

Genetic algorithm (Moradi-Jalal and Karney, 2008; Wu et al., 2015) is a search heuristic that simulates the superiority and inferiority of natural organisms. The algorithm is independent of the solution domain in solving the optimization problem and has strong robustness. In recent years, some chinese scholars have applied genetic algorithms to optimal water resource allocation (Zheng et al., 2013; Niu et al., 2017), and achieved good application results. The algorithm initially draws on some phenomena in evolutionary biology, including selection, crossover, and variation, which have good adaptability for the model proposed in this article. In the process of solving the genetic algorithm, it is necessary to calculate the size of the individual adaptation degree, and the adaptation degree calculation formula is the objective function Eq. 1, in which there are many factors that vary with the unit blade placement angle, including the time average head of the pump station H_i and the corresponding flow rate Q_i,j (θ_i,j), the pump unit efficiency η_zi,j (θ_i,j) at each time. If the time average head H_i is known for each divided time period, the corresponding flow rate Q_i,j (θ_i,j) and pump unit efficiency η_zi,j (θ_i,j) can be determined according to the dynamic characteristics of the unit device, under the condition that the pump blade placement angle θ_i,j is known for each divided time period of each unit, and the target discharge cost of the pump station under the combination of the blade placement angle can be obtained by combining with Eq. 1. As the time average head H_i is determined by C_i-Z_i at each time, and the upstream level Z_i at time i changes due to the actual optimized outflow process of the pump station, resulting in the upstream level Z_i of the station and the pump blade placement angle θ_i,j being mutually constrained, the actual decision variables of the model are the pump blade placement angle θ_i,j and the river level Z_i at the station, and it is difficult to solve the model effectively by the traditional system optimization method.

In view of above considerations, in the process of optimizing the operation of pumping stations, the flow process of optimizing the operation of pumping stations for the purpose of reducing the water level of the river network is closely related to the water level of the river network in the drainage area, especially the upstream level Z_i, and it is necessary to take into account the coupled solution of the pumping station optimization model and the non-constant flow model of the river network. In this article, based on genetic algorithm and coupled with head–water level successive approximation to achieve the effective matching between the time average head H_i and the real-time change of upstream level Z_i of the station during the optimized operation of the tidal drainage pumping station, and then obtain the optimization scheme that takes into account the economic operation of the pumping station and the requirement of reducing the water level of the river network, the solution flow chart is shown in Figure 1.

FIGURE 1

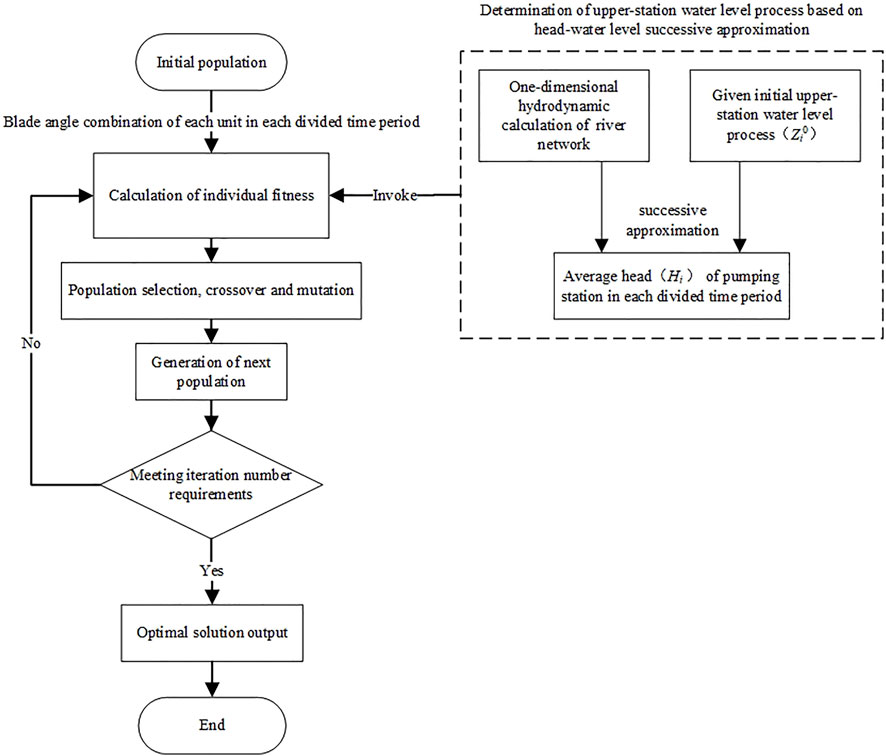
FIGURE 1. Algorithm flow chart of genetic algorithm coupled with head-water level successive approximation.

3.2 Construction of one-dimensional hydrodynamic model of the river network based on the system of St. Venant equations

(1) Construct a set of St. Venant equation for the river network in the control area of the drainage pumping station (Zhao, 2004; Zhou et al., 2010), and the typical form of the set of St. Venant equation for the one-dimensional single-width flow case is

$\frac{\partial Q}{\partial s}+B\frac{\partial Z}{\partial t}=q(7)$

$\frac{\partial Q}{\partial t}+\frac{2Q}{A}\frac{\partial Q}{\partial s}+\left[gA-B{\left(\frac{Q}{A}\right)}^2\right]\frac{\partial Z}{\partial s}={\left(\frac{Q}{A}\right)}^2{\frac{\partial A}{\partial s}|}_Z-g\frac{Q\left|Q\right|}{A{C}^{2}R}(8)$

Where: Z is the water level, m; Q is the flow rate, m³/s; B is the water surface width, m; R is the hydraulic radius, m; A is the cross-sectional area, m²; q is the side inlet flow rate, m³/s; t and s are the time and space coordinates.

(2) The Preissmann four-point implicit difference method is used to construct the difference equations for the above system of St. Venant equations in a simplified four-point linear implicit form as

${f|}_M=\frac{f_{j+1}^n+f_j^n}{2}(9)$

${\frac{\partial f}{\partial X}|}_M=\theta \left(\frac{f_{j+1}^{n+1}-f_j^{n+1}}{\Delta X}\right)+\left(1-\theta \right)\left(\frac{f_{j+1}^n-f_j^n}{\Delta X}\right)(10)$

${\frac{\partial f}{\partial t}|}_M=\frac{f_{j+1}^{n+1}+f_j^{n+1}-f_{j+1}^n-f_j^n}{2\Delta t}(11)$

where: θ is the weighting factor, 0 ≤ θ ≤ 1.

(3) Collect the information required for the hydrodynamic model solution and complete the generalized river network settings, including the initial water depth of the river network, the initial flow of the river network, the channel number of the river network, the division of the river section, the information of each river section (side slope coefficient, roughness, bottom elevation, bottom width), the type and number of branching points of the river section, the information of the upper and lower boundary conditions of the river (water level or flow) and the side inlet flow, etc.

(4) According to the catch-up method to solve the water level and flow data of each section of a single river, for ordinary micro-segments directly solve the coefficients in the difference equation corresponding to the Saint Venant equation; For micro-segments containing branching points, the coefficients in the equation corresponding to the form of the difference equation for the river segment are found according to the specific type of branching points. Substituting the known upstream and downstream boundary conditions of the river containing the branching points, a system of algebraic equations is formed with a diagonal matrix of coefficients, and for such solutions the system of equations with diagonally dominant coefficient matrices can generally be solved by the catch-up method with the following steps.

(i) Let the system of equations with one solution coefficient matrix diagonally dominant be of the form AX = f.

$A=\left[\begin{array}{cccc}{b}_1& c_1& & \\ a_2& b_2& c_2& \\ & & & \\ & & a_n& b_n\end{array}\right]\begin{array}{ccc}& & X=\left[\begin{array}{c}{x}_1\\ \\ x_n\end{array}\right]\end{array}\begin{array}{ccc}& & f=\left[\begin{array}{c}{f}_1\\ \\ f_n\end{array}\right]\end{array}(12)$

Where: A is the coefficient matrix of the system of equations, X is the solution of the system of equations to be solved, and a_i, b_i, c_i are the elements in the coefficient matrix A.

(ii) Decompose the diagonal square A into PQ.

$A=\left[\begin{array}{cccc}{p}_1& & & \\ a_2& p_2& & \\ & & & \\ & & a_n& p_n\end{array}\right]\left[\begin{array}{cccc}1& q_1& & \\ & 1& q_2& \\ & & 1& q_{n-1}\\ & & & 1\end{array}\right](13)$

where: P and Q are the lower and upper triangular matrices obtained after the Kraut decomposition of A, respectively, and p_i and q_i are the elements within matrices P and Q, respectively.

(iii) Solve PY = f and QX = Y separately to obtain the solution of the original system of equations.where: Y is the solution vector of the system of equations PY = f.

(5) Perform the rest of the river hydrodynamic calculations in the same way, complete one iteration of the river network flow calculation. Judging whether the iteration converges after one iteration is completed, if it converges, the solution of the hydraulic elements such as water level and flow on the unknown time layer of the river network is completed; If it does not converge, return and continue with the iteration. After the calculation of one time layer is finished, the calculation continues to the next time layer, until the completion of the whole calculation calendar is completed.

3.3 Determination of upstream water level process of the station based on head-water level successive approximation

For the complex correlation between the head and the upstream water level changes of the station at each time during the optimal operation of the pump station, The coupled head—water level successive approximation method is proposed. After the construction of the hydrodynamic model described in Section 2.2 is completed, the real-time head variation process under the pumping station start-up scenario is obtained by successive approximation of the initial given head to the real-time water level obtained after solving the hydrodynamic model. The specific steps are as follows.

(1) Randomly generate the operation scheme θ_ij (i = 1, 2, 3, ..., SN; j = 1, 2, 3, ..., JZ) for each unit of each group of pump stations for each divided time period.

(2) Given a set of water level processes Z_i⁰ (i = 1, 2, 3, ..., SN), The time-averaged head process H_i⁰ (i = 1, 2, 3, ..., SN) can be obtained for each divided time period at the pump station by the difference with the downstream tidal process of the pumping station. In turn, based on the head-flow characteristic relationship of the pump, the flow process Q_i⁰ (i = 1, 2, 3, ..., SN) is deduced for each divided time period of the pump station discharge.

(3) The flow process Q_i⁰ (i = 1, 2, 3, ..., SN) obtained from step (2) for each divided time period of pump station discharge is substituted into the one-dimensional hydrodynamic model based on the system of Saint Venant equations described in Section 2.2. Simulation to determine the water level process Z_i¹ (i = 1, 2, 3, ..., SN), to derive H_i¹ (i = 1, 2, 3, ..., SN), and Q_i¹ (i = 1, 2, 3, ..., SN) corresponding to this power-on scheme θ_ij.

(4) Comparing the mean value of the difference σ_i¹ between Z_i¹ and Z_i⁰ for each divided time period, If it satisfies less than a predetermined threshold σ, the corresponding upstream water level process Z_i¹ is output, If not satisfied, continue steps (3) to (4) until the threshold σ is satisfied, and output the corresponding upstream water level process Z_i^m (where m is the successive approximation sequence number).

(5) Through the above head - water level successive approximation process, the output water level process can be approximated as the upstream water level process Z_i under the pump station operation scheme determined in Eq. 1.

3.4 Model optimization solution based on genetic algorithm

In this article, we construct a coupled river network one-dimensional hydrodynamic model with genetic algorithm of head-level successive approximation to solve the optimization scheme of drainage pumping stations, and its specific steps are as follows.

(1) Initialize the population: set the evolutionary generation counter t = 0 according to the genetic algorithm, set the maximum evolutionary generation T, and randomly generate M individuals as the initial population P (0). In this article, the maximum evolutionary generation T is 300, the genetic algorithm population individual M is 100, the individual contains genes for the array consisting of each pump blade placement angle at each time of the pump station, this article takes the individual gene length as 54, any one body from M individuals, the individual consists of the blade placement angle θ_ij (i = 1, 2, 3, ..., SN; j = 1, 2, 3, ..., JZ) at each time of each unit of the pump station.

(2) Individual evaluation of the population: the fitness of each individual in the population P (t) is calculated, and the size of the fitness is the size of the objective function according to Eq. 1. The objective function involves the real-time head variation process under the pump station start-up scenario as well as the real-time flow rate and efficiency can be solved as described in Section 3.3 before calculating the objective function value.

(3) Selection operator: Acts the selection operator on the population. The purpose of selection is to pass on optimized individuals directly to the next generation or to generate new individuals by pairwise crossover and pass them on to the next generation. The selection operation is based on the assessment of the fitness of individuals in the population, and the tournament method is used as the type of selection operation in this article.

(4) Crossover operation: the crossover operator is applied to the population, and the crossover probability is formulated as 0.9 in this article. The crossover operation is judged one by one in the population whether the individuals trigger the crossover operation, and if the probability requirement is met, the crossover of gene values is performed for the specified motifs within the selected individuals θ_ijm, θ_ijn (i = 1, 2, 3, ..., SN; j = 1, 2, 3, ..., JZ; m, n are the selected individual numbers).

${\theta }_{ab}^m={\theta }_{ab}^{n^{\prime }}(14)$

${\theta }_{ab}^n={\theta }_{ab}^{m^{\prime }}(15)$

where: θ_ab^m (a = 1, 2, 3, ..., SN; b = 1, 2, 3, ..., JZ) is the value left on locus ab for individual m after crossover; θ_abⁿ (a = 1, 2, 3, ..., SN; b = 1, 2, 3, ... JZ) is the value left on locus ab for individual n after crossover; θ_ab^m′ (a = 1, 2, 3, ..., SN; b = 1, 2, 3, ..., JZ) is the value left on locus ab for individual m before crossover; θ_ab^n′ (a = 1, 2, 3, ..., SN; b = 1, 2, 3, ..., JZ) are the values left on locus ab for individual n before the crossover.

(5) Variation operation: The variation operator is applied to the population, and the variation probability is formulated as 0.1 in this article. In the population, we judge whether the variation operation is triggered by individuals one by one, and if the probability requirement is met, then the selected individuals θ_ij^m (i = 1, 2, 3, ..., SN; j = 1, 2, 3, ..., JZ; m is the selected individual number) within specified locus for gene value change. The next generation population P(t) is obtained after selection, crossover and mutation operations, and steps (2) to (5) are repeated.

(6) Termination condition judgment: Repeat the above operation. If t = T, the individual with the maximum adaptation obtained in the evolutionary process is used as the output of the optimal solution. Terminating calculation, obtaining the optimization scheme (i.e., combination of blade placement angles) for the period of the drainage pumping station.

4 Example solution and analysis

4.1 Overview of the main city of Yangzhou

Guazhou Pumping Station is located in Yangzhou City, Jiangsu Province, the ancient canal into the mouth of the Yangtze River, serving the main city of Yangzhou City, flood removal. The area is surrounded externally by watersheds and regional rivers such as the Beijing-Hangzhou Grand Canal, Yangtze River, Runyang River, Wutagou and Yanshan River, and internally by the Ancient Canal (Guazhou Canal) and Yiyang River as the main veins forming the backbone river network water system. The ground elevation in the main city of Yangzhou is 5.0 m–7.5 m, and the normal water level of the river network is 4.5 m–5.0 m. The drainage design standard is a 20-year maximum 24 h design storm, and the water level at each time does not exceed the river control level. The highest control level of the ancient canal is 5.5 m (at the mouth of the new river into the ancient canal), the lowest control level is 4.2 m (upstream water level of the pumping station), according to the drainage requirements of Yangzhou city. 2 large external pumping stations are planned to be built in the region, namely Guazhou Pumping Station and Yangzhou Pumping Station, among them, the Yangzhou pumping station has not yet been completed. Considering the optimization workload, this article generalizes the control area of Guazhou Pumping Station into a river network consisting of five rivers, and the generalized map of the river network in the study area is shown in Figure 2.

FIGURE 2

FIGURE 2. River network generalization of study area.

This article intends to consider the overall drainage layout of pumping and draining into the Yangtze River by scheduling and operating the Guazhou Pumping Station to meet the drainage requirements of the main urban area. The main rivers in the region are Qiligou, Zhaojiagou, Xincheng River, Yiyang River, and Ancient Canal. When the drainage pumping station is in operation, the outer side of the river network in the study area is directly connected to Yangzhou gate and Yiyang River gate for flow control, Zhaojiagou and Xincheng River flow into Yanshan River through culverts, and Qiligou converges into Yanshan River through the outer river network, all of which are finally controlled by Yanshan River West gate. Therefore, considering the calculation workload when generalizing the river network, it is proposed to set the upper boundaries of the flow of Qili Ditch, Zhaojiagou, Xincheng River, Yiyang River and Ancient Canal as 0 m³/s for each divided time period for one-dimensional hydrodynamic simulation. The completed Guazhou pumping station is equipped with 6 sets of 3000ZLQ-28.4 vertical fully adjustable axial flow pumps, with a rotating speed of 125 r/min, impeller diameter of 3 m and impeller center elevation of 1.1 m. The design blade angle of the pump is 0°, the design flow of a single machine is 28.4 m³/s, and the adjustment range of blade angle is [−6°C,+6°C]. The total installed speed and capacity of the pumping station is 170 m³/s and 9600kw. The matching motor model of the pumping station is TL1600-48/3250, the motor speed is 125 r/min, and the motor capacity is 1,600 kW. The unit flow head relationship and flow efficiency relationship can be obtained from the pump unit characteristic curve (College of Water and Energy Power Engineering and Yangzhou University, 2017). The roughness of the Grand Canal, Xincheng River, Yiyang River, Qiligou and Zhaojiagou is set to 0.021, 0.025, 0.024, 0.029, and 0.028 respectively (College of Water and Energy Power Engineering and Yangzhou University, 2017). The average daily tide difference of the Yangtze River in the discharge area of this pumping station is 1.1 m–1.3 m (Gong, 2011), and the tidal pattern is of informal semi-daily mixed tide type with fast rise and slow fall. Heavy rainfall mostly occurs in the flood season period from June to September. Therefore, this article selects the 20–year average daily high tide level of 6.77 m as the high downstream tide level of the Guazhou Pumping Station, and the tidal difference is 1.1 m. It also coincides with the time when the maximum flow rate of the 10-year design storm process occurs (as shown in Figure 2), in order to highlight the optimal scheduling process of Guazhou Pumping Station under the unfavorable situation of the dual influence of the 10-year design storm process and the high tide level of Yangtze River.

Guazhou Pumping Station existing conventional operation scheme is: when there is rainfall or rainfall forecast in the region, first open 2 units to design blade placement angle for pre-submergence. As the rainfall increases and the upstream water level rises, the flow rate of the pumping station is gradually adjusted by controlling the number of units on to make the water level of the river network stable. When the upstream water level of the pumping station is greater than the specified start-discharge level, the unit is fully open and the water level at the node of the ancient canal at the mouth of the New Town does not exceed 5.5 m. When the upstream water level of the pumping station is lower than 4.2 m, the Guazhou Pumping Station is closed.

4.2 Main urban area produced catchment calculation

The catchment area of the main urban area of Yangzhou City is 105.5 km². According to the rainfall information of Yangzhou station given in the “Atlas of Storm Floods in Jiangsu Province”, the P-Ⅲ curve is used to take C_v = 0.50, C_s = 3.5C_v, ‾x = 96.76 mm for frequency calculation, and the maximum one-day 24-h rainfall of 176.7 mm is obtained for a 10-year event. The time allocation of heavy rainfall adopts the allocation method of design rain type in the 1984 “Atlas of Heavy Rainfall Floods in Jiangsu Province”, and the calculation period is 1 h. The proposed runoff coefficient is 0.85 (Sheng et al., 2006; Liu, 2009) based on the subsurface of the main urban area of Yangzhou City. The calculated 10-year confluence production and confluence process line within the confluence of the main urban area of Yangzhou City is shown in Figure 3.

FIGURE 3

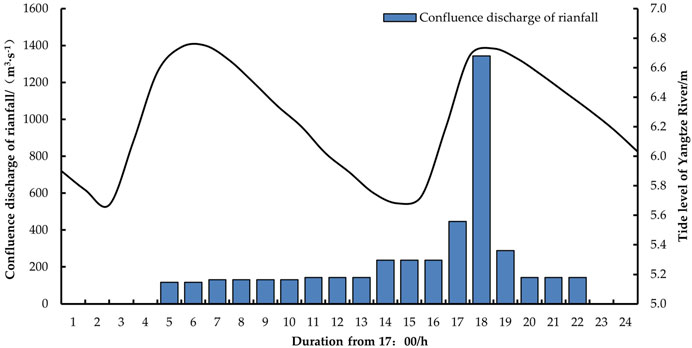
FIGURE 3. 5% frequency tidal level process at the downstream side of Guazhou pumping station and 10% frequency process curve of designed rainfall in drainage area.

4.3 Model solving parameters setting

According to the “Notice of Provincial Development and Reform Commission on Matters Relating to Transmission and Distribution Tariffs and Sales Tariffs of Jiangsu Power Grid in 2020–2022” (Development and Reform Commission of Jiangsu Province, 2020), the time period peak and valley tariff division is proposed, 1 day is divided into 9 time periods, and 17:00 is used as the starting time of the optimized operation, as shown in Table 1, considering the pump station should not frequently adjust the blade placement angle, the Yangtze River tide level process, the influence of model accuracy, and the optimization workload.

TABLE 1

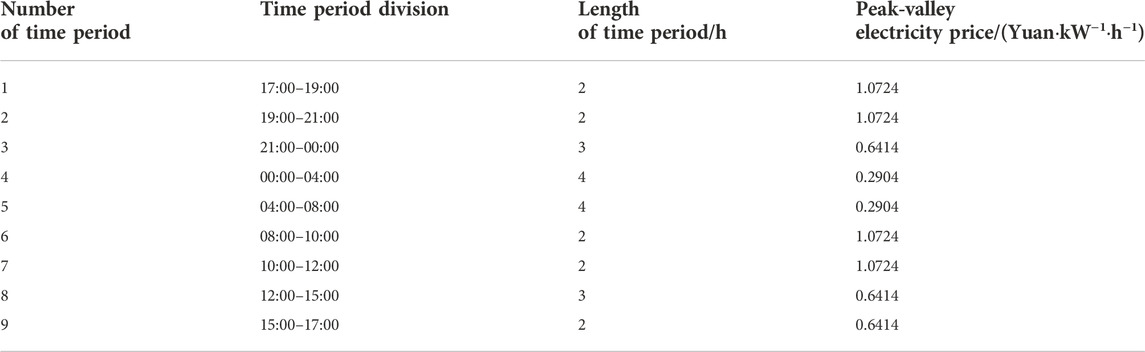
TABLE 1. Time period division and corresponding peak-valley electricity price during water-logging drainage process.

The remaining parameters of the model solution are set as follows.

Designed blade placement angle: 0°C; blade placement angle adjustment range: [−6°C, +6°C]; from “Preliminary design report of Guazhou Pumping Station project in Yangzhou” (Jiangsu Water Conservancy Survey and Design Research Institute Co, 2016) to determine the pumping station start-up and discharge level for 4.8 m, in order to facilitate comparative analysis, the proposed pumping station start-up and discharge level for 4.6 m, 4.8 m; taking into account the optimization solution workload, the time average head and time average flow rate of each divided time period is calculated for 1 h, water level and flow rate The iterative relaxation factor is set to 0.3, the water level iterative control accuracy is set to 10^–3, the flow rate iterative control accuracy is set to 10^–2, and the discrete step of blade placement angle is proposed to be 2°C in the optimization process.

4.4 Optimized operation analysis of Guazhou pumping station

It is known from the literature (Jiangsu Water Conservancy Survey and Design Research Institute Co, 2016) that the Guazhou Pumping Station operates without considering the standby units when draining floods, so it is proposed to optimize the six units of Guazhou Pumping Station. The optimization scheme of Guazhou Pumping Station is shown in Table 2 when the starting and discharging levels are 4.8 m and 4.6 m respectively under the peak and valley tariff standards.

TABLE 2

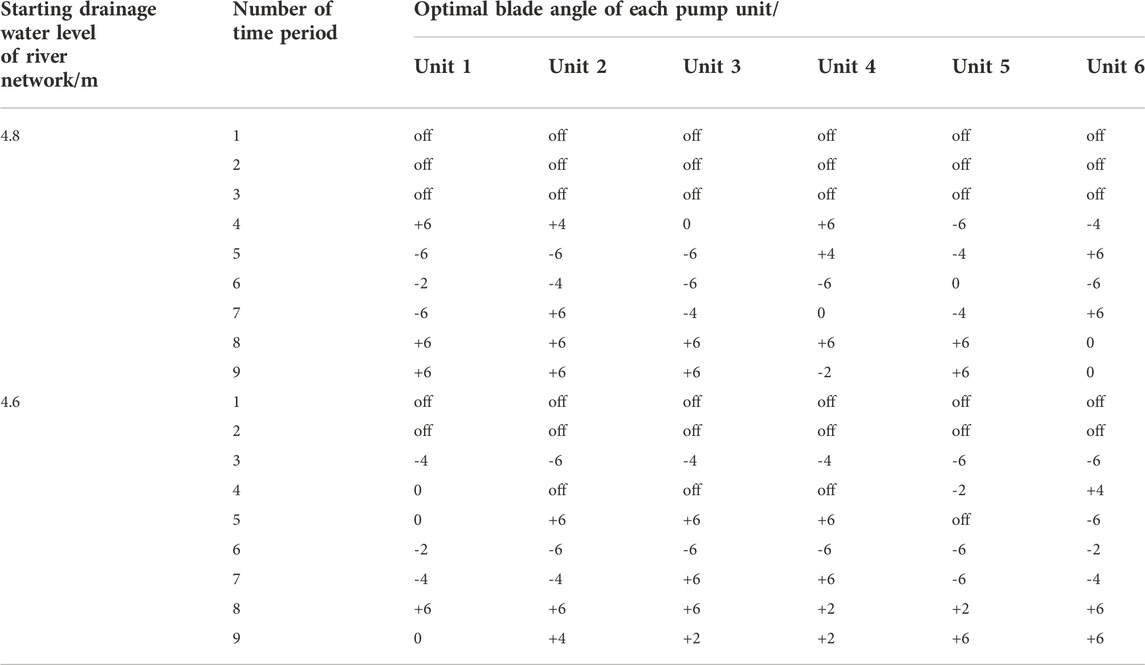
TABLE 2. Optimization schemes of Guazhou pumping station under different starting drainage water levels considering peak-valley electricity prices: Off means stop.

4.4.1 Optimized matching relationship between upstream water level and head of the Guazhou pumping station

According to Section 2.1, in order to realize the accurate matching of the upstream water level change and head of the pumping station during the optimized operation of the sensing tide pumping station, before using the genetic algorithm to calculate the objective function of the individual population, it is necessary to invoke the head-water level successive approximation optimization module once. That is, through the hydrodynamic model simulation cycle pump station drainage derived from the upstream water level process of the pumping station, and then from the given downstream water level of the pumping station to determine the pump station head at each time. The calculated head and flow rate of the pump station for each divided time period are repeatedly substituted into the hydrodynamic model to simulate the upstream water level of the pumping station, so as to approximate each other and optimize the matching. This article intends to set the successive approximation control accuracy of 1.010⁻¹ m, set the initial value of the successive approximation of the water level for each time 4.7 m normal water level, adjacent head—water level successive approximation results between each time the water level, head are to meet the control accuracy after termination.

The optimization of the pumping station at a start-up level of 4.8 m under the peak and valley tariff is verified by a successive approximation process. The upstream water level and head of Guazhou Pumping Station optimization program are approximated as shown in Figure 4. The maximum difference between the initial upstream water level and head data of each divided time period and the calculated real-time upstream water level and head of the pump station is 0.481 m, and the calculated real-time upstream water level and head of the pump station is 0.673, which is a poor fit, and it is necessary to reduce the error between the real-time upstream water level and head through successive approximation, so as to truly reflect the flooding process at the pump station. After one approximation, the maximum difference between the upstream water level and head of the pump station and the real-time upstream water level and head in each divided time is 0.077 m, and the fitting degree of upstream water level and head of the pump station is 0.997, and the fitting degree has increased by 48.15%, so the approximation effect is significant. After 1 approximation of the water level, head has converged to the real-time value, but due to the constant blade placement angle of each time under the water level, head change brought about by the flow perturbation has not been smooth, 1 approximation of the pump station each time head, water level than the real-time data still has a certain error, the maximum error is 0.08 m. For this purpose, 2 approximation and 3 approximation are necessary, and the calculated water level and head curve of 2 and 3 approximations overlap 100%, and the approximation is stopped. After 2 approximations of head—water level, the final calculation results are consistent with the real-time upstream water level and head data under the start-up plan of the pumping station.

FIGURE 4

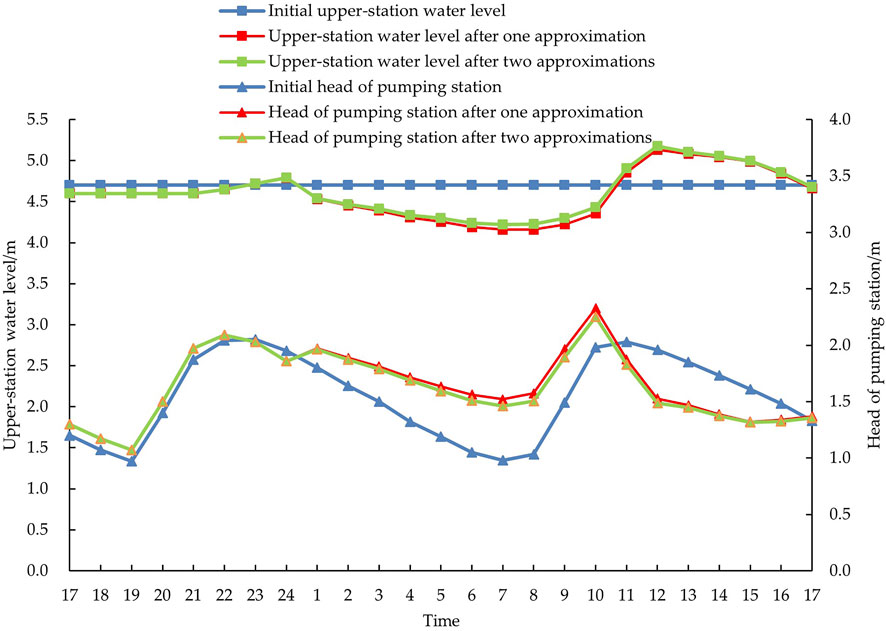
FIGURE 4. Head-water level successive approximation at the upstream side of Guazhou Pumping Station at starting drainage water levels of 4.8 m considering peak-valley electricity prices.

4.4.2 Analysis of discharge volume at each time of Guazhou pumping station

The relationship between flow rate and tariff and head at each starting and discharging level of Guazhou Pumping Station under the peak and valley tariff standard for each divided time period is shown in Figures 5, 6. The pumping station shown in the figure after the start of the discharge of a certain amount of flow in each period, mainly due to the optimized pumping station start program needs to meet the urban river network water level control requirements for each period. When the short calendar period of heavy rainfall when the catchment flow of each period is large, resulting in the pumping station discharge flow of each period and this period of incoming water flow has a greater correlation. At the same time, compared with the conventional operation scheme, which usually takes the upstream water level of the station as the basis for controlling the flow rate of the unit, the discharge flow rate at each time under the optimized scheme can be further optimized under the multiple factors of electricity price, head and incoming water flow at each time when the control water level requirement is met.

FIGURE 5

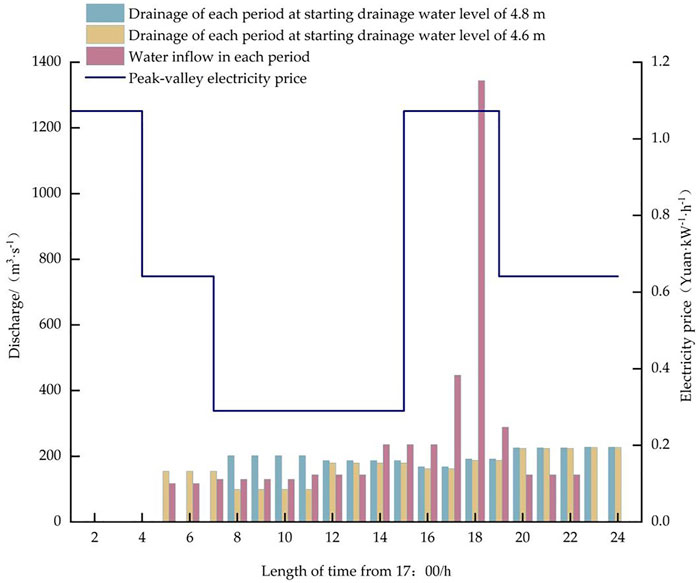
FIGURE 5. Time-average flow and electricity prices relationship of Guazhou Pumping Station at different starting drainage water levels considering peak-valley electricity prices for each optimization scheme.

FIGURE 6

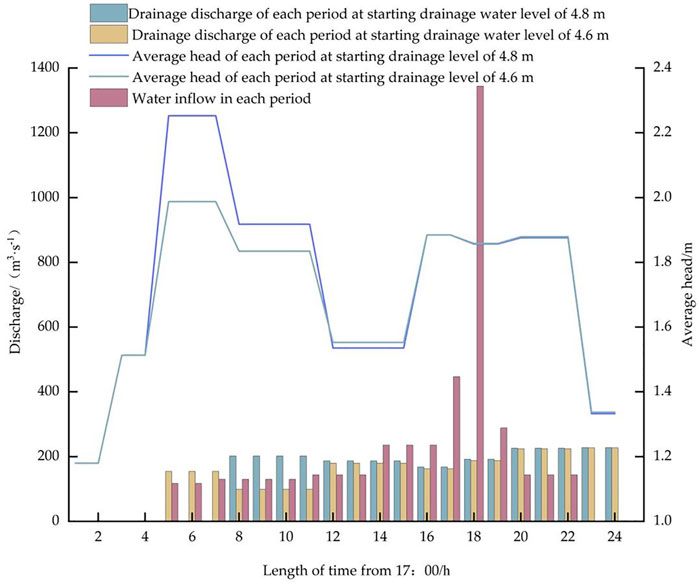
FIGURE 6. Time-average flow and pumping head relationship of Guazhou Pumping Station at different starting drainage water levels considering peak-valley electricity prices for each optimization scheme.

It can be seen from the relationship between discharge volume and tariff for each divided time period in Figure 5 that the pumping station discharges higher returns during low tariff periods. Taking the optimized scheme with a start-up water level of 4.8 m as an example, during the low tariff period, when ignoring the effect of lagging incoming water from the production sink, the amount of water discharged during the same period accounts for 78.88% of the total amount of water discharged when facing a sink that accounts for 39.15% of the total incoming water; The discharge yield is even lower during the high tariff hours, so when faced with a sink that accounts for 60.85% of the total incoming water during the hours, the discharge only accounts for 21.12% of the total discharge. Unlike the traditional pumping station optimization, due to the constraints of changing incoming water conditions and upper and lower water level limits, the pumping station cannot continuously discharge water at maximum capacity during low tariff hours, and completely stop storing incoming water during high tariff hours, so the optimal solution for drainage pumping stations must take into account the economics of pumping station operation and meet the safety requirements of regional flood removal.

As can be seen from Figure 6, the hourly average head of the pumping station under the optimization scheme of each start-up and discharge level generally varies around the design head of 1.8 m up and down. Due to the constraint of the maximum and minimum control water level, the pumping station head variation is small, and the effect of head variation on the discharge flow in each divided time period under the influence of electricity price is not clear. For this reason, this article further elaborates the effect of time head by the relationship between head and discharge flow during the same time of electricity price when the start-up and discharge level is 4.6 m. The electricity price is 0.2904 Yuan·kW⁻¹·h⁻¹ for all time periods from time period 8 to time period 15. The average hourly head of the pumping station is 1.918 m and 1.535 m. When the average hourly head of the pumping station is 1.918 m, ignoring the influence of the lagging incoming water from the sink, the water discharged in the same period only accounts for 11.69% of the total water volume in the corresponding time when the sink accounts for 12.14% of the total incoming water; When the average hourly head of the pumping station is 1.535 m, the corresponding time in the face of 17.23% of the total incoming water catchment, the discharge of water amounted to 21.07% of the total water, the difference is more obvious, it can be seen that in the case of the time period tariff remains unchanged, with the reduction of the hourly average head, the pumping station time flow is rising trend, but the flow rate variation is limited by the control of water level requirements.

4.4.3 Analysis of operation benefits of optimal operation of Guazhou pumping station

The upstream water level of the pumping station control node under each scheme and the upstream water level change curve are shown in Figure 7.

(1) When the starting drainage level is 4.8 m, the power consumption cost per unit drainage of the optimized scheme is 45.46 yuan/10⁴ m³, which is 15.34% less than the conventional operation scheme. Drainage power consumption costs decreased significantly, mainly by the time peak and valley electricity prices, the average hourly head impact, the pumping station operation preference for low electricity prices, low head time, so that the target cost tends to be minimal. At the same time, the genetic algorithm of coupled head-water level approximation can obtain real-time head and water level matching data under the joint influence of pumping station discharge flow, rainfall confluence flow and Yangtze tide level at each time of the pumping station, reflecting the real difference of head and water level after the flow feedback at each time of the cycle. Compared with operating directly under the set head determined according to the initial water level, the optimization scheme obtained is closer to the actual head matching under the change of water level, which is more conducive to the economic operation advantages brought by the electricity price and head at each time. From the safety point of view, the highest water level of the river network control node (the mouth of the Ancient Canal New Town) under the optimized scheme is 5.305 m, which has a larger safety margin than the control maximum water level of 5.5 m and is conducive to the control of the water level of the river network in the pumping station drainage area. The lowest upstream water level of the pumping station during optimized operation is 4.218 m, which meets the regional minimum water level requirement of 4.2 m. In addition, the drainage pumping station also needs to pay attention to the smallest possible variation of water level when removing waterlogging in the region, in order to guarantee the safety requirements such as slope stability and vessel navigation when removing waterlogging from the river network. In this article, the sum of squares of upstream water level variation in adjacent time periods of the station is used to characterize the magnitude of water level variation in the river network, and the sum of squares of upstream water level variation in adjacent time periods of the station is 0.479 m² under the optimized scheme with the starting water level of 4.8 m, which is 6.61% lower than the conventional scheme, and the economic and safety benefits are improved.

(2) When the starting drainage level is 4.6 m, the unit drainage cost of the optimized scheme is 51.32 yuan/10⁴ m³, which is 4.40% less than the conventional operation scheme. The highest water level in the control node of the river network under the optimized plan (the mouth of the ancient canal New Town) is 5.304 m, and the lowest upstream water level of the station is 4.211 m, which meets the requirements of the control water level. For the water level variation, there is a significant decrease, and the sum of squared upstream water level variation of the station in the optimized scheme is 0.472 m², which is 7.85% lower than the conventional operation scheme. Due to the peak and valley tariff, start-up time and tide level setting, the pump station units are forced to start up during the high head and high tariff hours when the start-up level is 4.6 m. Therefore, the improvement in the unit discharge cost is smaller, but the water level variation is better than the optimized solution with the start-up level of 4.8 m, mainly because more start-up hours are beneficial to the water level control during the discharge cycle.

FIGURE 7

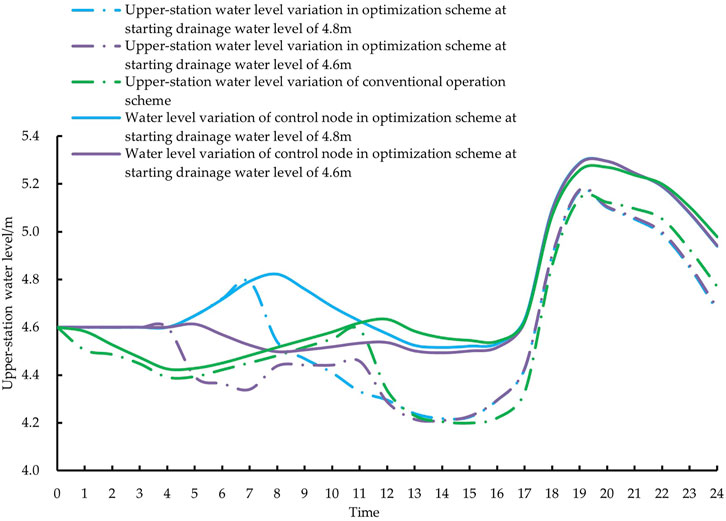
FIGURE 7. Water level variation curves at the upstream side of Guazhou Pumping Station at different starting drainage water levels under optimal and conventional operation modes.

5 Conclusion

This article addresses the economic and safe operation of urban tide sensitive drainage pumping stations in drainage areas experiencing design storms below the design drainage standard. With the objective of minimizing the drainage cost within the drainage cycle, a complex nonlinear mathematical model is constructed with the decision variables of the start-up placement angle of each unit at each time of the pump station, and a genetic algorithm for coupled head-water level successive approximation is proposed, taking into account the constraints of the total amount of target drainage, power, water level changes in the river network in the drainage area, the number of unit starts and stops, and the shortest duration of unit starts. Taking Guazhou Pumping Station in Yangzhou City as a research example, the optimization scheme of Guazhou Pumping Station with different start-up and discharge levels under peak and valley tariff standards was obtained.

The results show that: the innovative coupled head-level successive approximation genetic algorithm is proposed in this paper, the water level and pumping station head at each time of the drainage pumping station match each other and meet the control accuracy of 0.01 m, the flow, head and efficiency of the pumping station at each time reflect the real-time operation parameters of the pumping station, the calculated objective function is more accurate and the optimization benefit is more practical. The article sets two start-up and discharge levels to solve the optimized scheme, and the optimized scheme of different start-up and discharge levels saves 15.34% and 4.40% on average compared with the conventional operation scheme under the peak and valley tariff. The average reduction of water level variation in the control area is 6.61% and 7.85% compared with the conventional operation, and the benefit of optimized operation of Guazhou pumping station is significant. At the same time, the optimal plan for each time discharge flow in the time head, time tariff and incoming water flow under the combined influence of optimal allocation, in the case of the same incoming water conditions pumping station priority in the low price of electricity, low head time discharge. Different water conditions at different times, compared to a single cost optimization, in order to meet the drainage cycle of the pumping station power consumption costs minimum premise to take into account the drainage cycle to control the water level requirements and pumping station operational safety needs, more conducive to drainage pumping station control under the regional stability. It can be used for decision making and reference by the relevant drainage pumping station scheduling and operation management departments.

6 Discussion

In this article, we take into account the safety requirements of drainage pumping stations and urban river network water level control, optimize the operation of drainage pumping stations under typical rainfall below the design standard, innovate the coupled head-water level approximation to achieve accurate acquisition of the blade placement angle of each pumping station unit at each time, and obtain a more reliable minimum drainage power consumption cost. In the future, a multi-objective optimization model with minimum cost of drainage cycle and minimum variation of water level of river network in drainage area can be constructed for drainage areas with multiple drainage pumping stations, and multi-objective optimization operation study of urban drainage pumping station group can be carried out to further improve the practicality and solution accuracy of the model.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

Conceptualization, YG; methodology, YG and WZ; software, WZ; validation, YG; formal analysis, YG; investigation, YG; resources, YG; data curation, YG; writing—original draft preparation, WZ; writing—review and editing, YG and WZ; funding acquisition, YG All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by the 12th Five-Year National Science and Technology Support Project (2015BAB07B01); the 57th Batch of China Postdoctoral Science Foundation Project (2015M571826); Science and Technology Innovation Cultivating Fund of Yangzhou University (2019CXJ071).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chen, B., Li, X., and Zhu, Z. (2022). Time-resolved particle image velocimetry measurements and proper orthogonal decomposition analysis of unsteady flow in a centrifugal impeller passage. Front. Energy Res. 9. doi:10.3389/fenrg.2021.818232

CrossRef Full Text | Google Scholar

College of Water and Energy Power Engineering, Yangzhou University (2017). Test report of model pump device for Guazhou pumping station project in Yangzhou city. Yangzhou: College of Water and Energy Power Engineering, Yangzhou University.

Google Scholar

Development and Reform Commission of Jiangsu Province (2020). Notice of provincial development and Reform commission on Matters relating to transmission and distribution tariffs and Sales tariffs of Jiangsu power Grid in 2020-2022. Jiangsu Province: Development and Reform Commission of Jiangsu Province.

Google Scholar

Dong, W., and Yang, Q. (2020). Data-driven solution for optimal pumping units scheduling of smart water conservancy. IEEE Internet Things J. 7 (3), 1919–1926. doi:10.1109/jiot.2019.2963250

CrossRef Full Text | Google Scholar

Eui, L., Yong, L., Jin, J., Jung, D., and Kim, J. (2016). Flood reduction in urban drainage systems: Cooperative operation of centralized and decentralized reservoirs. Water 8 (10), 469. doi:10.3390/w8100469

CrossRef Full Text | Google Scholar

Fang, G. H., Cao, R., Liu, Q., and Chen, C. (2016). Improved genetic algorithm and its application in the optimal operation for pumping station. South-to-North Water Transf. Water Sci. Technol. 14 (2), 142–147. (in Chinese with English abstract).

Google Scholar

Fecarotta, O., Carravetta, A., Morani, M. C., and Padulano, R. (2018). Optimal pump scheduling for urban drainage under variable flow conditions. Resources 7 (4), 73. doi:10.3390/resources7040073

CrossRef Full Text | Google Scholar

Feng, X., Wang, Y., and Qiu, B. (2020). Optimization of pumping station group operation based on optimized parameters using hybrid wolf pack algorithm. Trans. Chin. Soc. Agric. Eng. 36 (3), 30–36. (in Chinese with English abstract). doi:10.11975/j.issn.1002-6819.2020.03.004

CrossRef Full Text | Google Scholar

Gao, Y. Q., Du, C. L., Zhang, Z. Y., and Liu, Y. (2020). Optimal operation of drainage pumping station in plain polder area based on orthogonal test method. Adv. Sci. Technol. Water Resour. 40 (6), 48–53. (in Chinese with English abstract). doi:10.3880/j.issn.1006-7647.2020.06.009

CrossRef Full Text | Google Scholar

Gong, Y., Cheng, J. L., Zhang, R. T., and Zhang, L. H. (2010). Study of optimal operation method on multiple pump units with adjustable-blade for single pumping station based on decomposition-dynamic programming aggregation method. Trans. Chin. Soc. Agric. Mach. 41 (9), 27–31. (in Chinese with English abstract). doi:10.3969/j.issn.1000-1298.2010.09.006

CrossRef Full Text | Google Scholar

Gong, Y., and Zhu, B. (2022). The optimal operation of parallel pumping stations for inter-basin water transfer based on the multi-objective optimization of a single pumping station. Process. (Basel). 10 (10), 1935. doi:10.3390/pr10101935

CrossRef Full Text | Google Scholar

Gong, Y., Cheng, J., Zhang, R., and Zhang, L. (2011). Algorithm of daily operation scheme for parallel pumping stations. J. Drainage Irrigation Mach. Eng. 29 (3), 230–235. (in Chinese with English abstract). doi:10.3969/j.issn.1674-8530.2011.03.010

CrossRef Full Text | Google Scholar

Gong, Y., Cheng, J., Zhang, R., and Zhang, L. (2011). Optimization on variable speed operation with VFD for No.3 Huaiyin pumping station based on decomposition-dynamic programming aggregation method. Trans. Chin. Soc. Agric. Eng. 27 (3), 79–83. (in Chinese with English abstract). doi:10.3969/j.issn.1002-6819.2011.03.014

CrossRef Full Text | Google Scholar

Gong, Y. (2011). Study on some related optimal methods for operation of pumping stations in Eastern Route of South-to-North Water Diversion Project. Phd (Yangzhou: Yangzhou University). (in Chinese with English abstract).

Graber, S. D. (2010). Generalized method for storm-water pumping station design. J. Hydrol. Eng. 15 (11), 901–908. doi:10.1061/(asce)he.1943-5584.0000268

CrossRef Full Text | Google Scholar

Hwang, Y. K., Kwon, S. H., Lee, E. H., and Kim, J. H. (2020). Development of optimal pump operation method for urban drainage systems. Adv. Intelligent Syst. Comput. 1063, 63–69. doi:10.1007/978-3-030-31967-0_7

CrossRef Full Text | Google Scholar

Jafari, F., Jamshid Mousavi, S., Yazdi, J., and Kim, J. H. (2018). Real-time operation of pumping systems for urban flood mitigation: Single-period vs. Multi-period optimization. Water Resour. manage. 32 (14), 4643–4660. doi:10.1007/s11269-018-2076-4

CrossRef Full Text | Google Scholar

Jiangsu Water Conservancy Survey and Design Research Institute Co (2016). Preliminary design report of Guazhou pumping station project in Yangzhou. Yangzhou: Jiangsu Water Conservancy Survey and Design Research Institute Co.

Google Scholar

Jilin, C., Lihua, Z., and Rentian, Z. (2010). Study on optimal day-operation of single adjustable-blade pump unit. J. Hydraulic Eng. 41 (4), 499–504. (in Chinese with English abstract).

Google Scholar

Jowitt Paul, W., and George, Germanopoulos (1992). Optimal pump scheduling in water-supply networks. J. Water Resour. Plan. Manag. 118 (4), 406–422. doi:10.1061/(asce)0733-9496(1992)118:4(406)

CrossRef Full Text | Google Scholar

Liu, J. S., Cheng, J. L., and Gong, Y. (2013). Study on optimal scheduling methods of urban drainage pumping stations based on orthogonal test. Appl. Mech. Mater. 373-375, 2169–2174. doi:10.4028/www.scientific.net/amm.373-375.2169

CrossRef Full Text | Google Scholar

Liu, J. S., Cheng, J. L., Huang, Y., and Gong, Y. (2015). Optimization on conventional operation schemes of drainage pumping stations in urbanized polders unaffected by tides. J. Irrigation Drainage 34 (3), 17–23. (in Chinese with English abstract). doi:10.13522/j.cnki.ggps.2015.03.004

CrossRef Full Text | Google Scholar

Liu, Q., and Chen, W. (2020). Energy saving optimization of pumping station based on knapsack model and particle swarm optimization algorithm. Comput. Digital Eng. 48 (5), 1029–1035. (in Chinese with English abstract). doi:10.3969/j.issn.1672-9722.2020.05.008

CrossRef Full Text | Google Scholar

Liu, Q., Fang, G. H., Sun, H. B., and Wu, X. w. (2017). Joint optimization scheduling for water conservancy projects in complex river networks. Water Sci. Eng. 10 (1), 43–52. doi:10.1016/j.wse.2017.03.008

CrossRef Full Text | Google Scholar

Liu, X. P. (2009). Parameter calibration method for urban rainfall-runoff model based on runoff coefficient. Water & Wastewater Eng. 35 (11), 213–217. (in Chinese with English abstract). doi:10.3969/j.issn.1002-8471.2009.11.056

CrossRef Full Text | Google Scholar

Moradi-Jalal, M., and Karney, B. W. (2008). Optimal design and operation of irrigation pumping stations using mathematical programming and Genetic Algorithm (GA). J. Hydraulic Res. 46, 237–246. doi:10.1080/00221686.2008.9521858

CrossRef Full Text | Google Scholar

Niu, W., Feng, Z., Cheng, C., Wu, X., and Shen, J. (2017). Parallel multi-objective optimal operation of cascaded hydropower system. J. Hydraulic Eng. 48 (1), 104–112. (in Chinese with English abstract). doi:10.13243/j.cnki.slxb.20160096

CrossRef Full Text | Google Scholar

Rasoulzadeh Gharibdousti, S., Haddad, O. B., and Mario, M. A. (2011). Optimal design and operation of pumping stations using NLP-GA. Proc. Institution Civ. Eng. - Water Manag. 164 (4), 163–171. doi:10.1680/wama.1000044

CrossRef Full Text | Google Scholar

Saliba, S. M., Bowes, B. D., Adams, S., Beling, P. A., and Goodall, J. L. (2020). Deep reinforcement learning with uncertain data for real-time stormwater system control and flood mitigation. Water 12, 3222. doi:10.3390/w12113222

CrossRef Full Text | Google Scholar

Sheng, W., Zhirong, W., Jianfeng, Z., Jiancang, X., and Yamei, W. (2006). Experimental study on relationship among runoff coefficients of different underlying surfaces, rainfall intensity and duration. J. China Agric. Univ. 11 (5), 55–59. (in Chinese with English abstract). doi:10.3321/j.issn:1007-4333.2006.05.012

CrossRef Full Text | Google Scholar

Sterling, M., and Coulbeck, B. (2015). A dynamic programming solution to optimization of pumping costs. Proc. Institution Civ. Eng. 59 (4), 813–818. doi:10.1680/iicep.1975.3642

CrossRef Full Text | Google Scholar

Tao, X., Qiu, J., and Kan, Y. (2022). Study on optimal operation of single adjustable-blade pump unit in pumping station according to different drainage scenarios. China Rural Water Hydropower (8), 1–5. (in Chinese with English abstract).

Google Scholar

Wang, H., Lei, X. H., Khu, S. T., and Song, L. (2019). Optimization of pump start-up depth in drainage pumping station based on SWMM and PSO. Water 11 (5), 1002. doi:10.3390/w11051002

CrossRef Full Text | Google Scholar

Wang, M. M., Zheng, S., and Sweetapple, C. (2022). A framework for comparing multi-objective optimization approaches for a stormwater drainage pumping system to reduce energy consumption and maintenance costs. Water 14 (8), 1248. doi:10.3390/w14081248

CrossRef Full Text | Google Scholar

Wu, P., Lai, Z., Wu, D., and Wang, L. (2015). Optimization research of parallel pump system for improving energy efficiency. J. Water Resour. Plan. Manag. 141 (8), 04014094. doi:10.1061/(ASCE)WR.1943-5452.0000493

CrossRef Full Text | Google Scholar

Wu, W. Y., Maier Holger, R., and Simpson Angus, R. (2010). Single-objective versus multiobjective optimization of water distribution systems accounting for greenhouse gas emissions by carbon pricing. J. Water Resour. Plan. Manag. 136 (5), 555–565. doi:10.1061/(asce)wr.1943-5452.0000072

CrossRef Full Text | Google Scholar

Xu, Z., Wu, L. Y., Zhang, X. T., and Xue, A. (2011). Fuzzy optimal control of sewage pumping station with flow concentration. Commun. Comput. Inf. Sci. 215 (2), 259–266. PART. doi:10.1007/978-3-642-23324-1_42

CrossRef Full Text | Google Scholar

Yang, S., Li-Chiu, C., and Chang, F. (2019). AI-based design of urban stormwater detention facilities accounting for carryover storage. J. Hydrology 575, 1111–1122. doi:10.1016/j.jhydrol.2019.06.009

CrossRef Full Text | Google Scholar

Yazdi, J., Choi, H. S., and Kim, J. H. (2016). A methodology for optimal operation of pumping stations in urban drainage systems. J. Hydro-environment Res. 11, 101–112. doi:10.1016/j.jher.2015.09.001

CrossRef Full Text | Google Scholar

Yazdi, J., and Kim, J. H. (2015). Intelligent pump operation and river diversion systems for urban storm management. J. Hydrol. Eng. 20 (11), 04015031. doi:10.1061/(asce)he.1943-5584.0001226

CrossRef Full Text | Google Scholar

Zhao, K. Y. (2004). Numerical model of unsteady flow in natural river. J. Water Resour. Water Eng. 15 (1), 38–41. (in Chinese with English abstract). doi:10.3969/j.issn.1672-643X.2004.01.008

CrossRef Full Text | Google Scholar

Zheng, J., Yang, K., Ni, F. Q., and Liu, G. S. (2013). Research on overall improved genetic algorithm applied in optimal generation dispatching of multi-reservoir system. J. Hydraulic Eng. 44 (2), 205–211. (in Chinese with English abstract).

Google Scholar

Zhou, X. L., Liu, J., Luo, Q. S., and Liu, S. H. (2010). Further research of 1 D numerical simulation of unsteady channel flow. Eng. J. Wuhan Univ. 43 (4), 443–445450. (in Chinese with English abstract).

Google Scholar

Zhu, Z., Lin, Y., Li, X., Zhai, L., and Tong, L. (2022). Axial thrust instability analysis and estimation theory of high speed centrifugal pump. Phys. Fluids 34, 075118. doi:10.1063/5.0098194

CrossRef Full Text | Google Scholar