Optimal placement and capacity sizing of energy storage systems via NSGA-II in active distribution network

In recent years, with the rapid development of renewable energy, the penetration rate of renewable energy generation in the active distribution network (ADN) has increased. Because of the instability of renewable energy generation, the operation stability of ADN has decreased. Due to the ability to cut peak load and fill valley load, battery energy storage systems (BESSs) can enhance the stability of the electric system. However, the placement and capacity of BESSs connected to ADN are extremely significant, otherwise, it will lead to a further decline in the stability of ADN. To ensure the effectiveness of the BESSs connected to the grid, this work uses the fuzzy kernel C-means (FKCM) method for scene clustering. Meanwhile, a multi-objective optimization model of BESS configuration is established with the objective of BESS configuration cost, voltage fluctuation, and load fluctuation, and solved by non-dominated sorting genetic algorithm-II (NSGA-II). In this work, the grey target decision method based on the entropy weight method (EWM) is used to obtain the optimal compromise solution from the Pareto non-dominated set. Moreover, the proposed method is tested and verified in the extended IEEE-33 node system and the extended IEEE-69 node system. The results show that the BESSs configuration scheme obtained by NSGA-II can effectively reduce the fluctuation of voltage and load, and improve the stability of ADN operation.

1 Introduction

With the continuous development and progress of society and technology, traditional energy sources based on fossil fuels have become difficult to meet the needs of human society. Nowadays, thermal power generation is still the main way for people to obtain electric energy. However, the harmful gases emitted by the combustion of fossil fuels have become a problem, and the combustion of fossil fuels is aggravating environmental pollution and global warming (Company, 2021; Zandalinas et al., 2021). At present, energy storage and environmental pollution issues have become two serious challenges to the sustainable development of society. It is urgent to reduce carbon emissions and build a new type of power system with renewable energy sources as the main body (He et al., 2021; Dong et al., 2022).

The new power grid with photovoltaic and wind energy as the main energy structure has the advantage of a flexible power supply, so it is a better solution to the power supply problem of the grid (Bin et al., 2019; Li et al., 2022a). However, photovoltaic, wind power has obvious characteristics of randomness, volatility, and intermittency, its intermittency, and volatility will harm the quality of the power supply. And photovoltaic, wind power needs to go through the power electronic equipment to achieve energy control and does not have the power grid frequency, voltage regulation, and other functions. Renewable energy also has the characteristics of dispersion, when the renewable energy to a high penetration rate into the grid will aggravate the impact caused by the volatility, such as voltage deviation, power loss, etc. (Hu et al., 2022; Xiao and Pan, 2022).

Distributed generation (DG) and energy storage systems (ESSs) play an important role in power grids with high renewable energy generation penetration rates (Wu et al., 2021a; Shi et al., 2022). On the one hand, as an independent power supply compatible with the environment on the user side, DG can meet the peaking demand of the power system and supply power to remote users, and commercial and residential areas, it also can save transmission investment and reduce transmission losses. On the other hand, because the DG is mostly renewable energy generation, its output has obvious randomness and intermittency, which affects the voltage stability of the active distribution network (ADN), changes the direction of the ADN power flow, and causes the system power flow to be random. When large-scale renewable energy generation access to ADN will cause power flow and voltage over-limit, change the voltage characteristics, and reduce the stability of ADN. Furthermore, the role of DG in ADN is mostly used as a backup power supply, which is easy to cause the voltage and frequency of the ADN to drop and exceed the limit during the power switching process. Even so, DG is still considered by many energy and power system experts as the main way to increase the utilization of renewable energy and improve the stability and flexibility of ADN (Yang et al., 2021; Wu et al., 2022).

ESSs can effectively solve various energy supply and demand balance problems and improve energy utilization efficiency through their peak-shaving and flexible energy management capabilities. Meanwhile, the ESSs can effectively solve serious problems such as power flow reverse and voltage over-limit which occur in the ADN after DG access, and ensure the normal operation of the distribution network (Li et al., 2018). Battery energy storage systems (BESSs), which use batteries as energy storage carriers, have become a hot topic of current research due to their high energy density, fast response time, and modularity (Das et al., 2018; Wu et al., 2021b). BESS can effectively solve various supply-demand imbalance and power quality problems by using high energy density to cut peaks and fill valleys on the network and using high power density to smooth out random power fluctuation (Liu et al., 2016; Zheng, 2018; Ren et al., 2019; Yang et al., 2020).

After the ESSs are connected to the ADN, the operating state of the ADN and the ability of peak cutting are affected by the access mode, location, and capacity. In recent years, many scholars have studied the planning of ESSs, however, most of the research models are single-objective models, and these models are difficult to consider the stability of the network and the economics of energy storage at the same time. Reference (Yan et al., 2013) established an optimal value assessment model of BESSs with net income as the objective function. The reference (Su et al., 2016) established a planning model for the location and capacity of distributed power and energy storage devices with the cost input of ADN as the objective function. Literature (Lee and Chen, 1995) constructed an energy storage planning model with the cost of electricity purchased by customers as the objective function. Reference (Ghatak et al., 2019) established an energy storage planning model with battery storage life as the objective function and quantified the battery characteristic parameters by combining three characteristics of battery discharge depth, discharge rate, and effective discharge volume. In reference (Chen, 2020), an energy storage planning model has been established with the objective function of accurately tracking real-time meteorological conditions, and an improved logistic regression model was used to evaluate the impact of real-time numerical meteorological conditions on the device. All the above research models are single-objective planning models, which do not consider the coupling problem between ESSs planning and network operation conditions. The reference (Fu et al., 2022) established a multi-objective optimal configuration model with the economic benefits of ESSs and voltage quality as the optimization objectives. However, the voltage quality does not fully reflect the real operating condition of the network after accessing ESSs. Therefore, building a multi-objective optimal allocation model for ESSs can not only fully exploit the potential of ESSs, but also achieve a better balance between the economic benefits of ESSs and network stability.

In most papers, the multi-objective optimization problem is weighted into a single objective problem by the weighting method. However, it is difficult to guarantee the objectivity of the planning scheme solved by this method. In this regard, some studies used a bi-level planning model to solve the different problems of BESSs location and capacity sizing (Li et al., 2022b). The reference (Meng et al., 2021) proposed a bi-layer BESSs planning scheme considering renewable energy and load uncertainties. The optimal solution of this model can solve the problem of objectivity in the single-objective model, but the two-layer model is complex, and difficult to obtain the optimal solution. ESSs location and capacity sizing is a high-dimensional, multi-objective, complex constraints problem. The solution process of traditional planning methods is complex and easy to fall into local optimum. Therefore, it is very important to establish a Pareto-based multi-objective model. This model can well adjust the balance between various optimization variables in multi-objective optimization problems and ensure that the results have good objectivity.

This work is based on the non-dominated sorting genetic algorithm-II (NSGA-II), which shows a high optimization performance under several standard function test environments. The main content of this work is as follows:

(1) A multi-objective planning optimal location and capacity model based on the Pareto of BESSs is established with three objectives, and NSGA-II is used to solve this multi-objective model;

(2) The clustering algorithm is used to cluster the daily load, wind power, and photovoltaic (PV) output curves of the whole year, and the typical scenarios are obtained based on the combination of time series characteristics. Simulation calculations are performed in different typical scenarios to obtain the sum of each objective function throughout the year;

(3) The simulation based on the extended IEEE-33 node system and the extended IEEE-69 node system verifies that the proposed method can effectively obtain the optimal BESSs configuration method.

2 Battery energy storage systems configuration model

2.1 Objective function

In this work, the total investment operating cost of the BESSs, the total load fluctuation of ADN, the total voltage fluctuation of ADN, and the BESSs configuration optimization model based on Pareto can be established as follows:

$\min \mathit{F}\left(\mathit{x}\right)=\min \left\{F_1,\right.\left.F_2,F_3\right\}(1)$

where $\mathit{F}\left(\mathit{x}\right)$ consists of objective functions $\left\{F_1,\right.\left.F_2,F_3\right\}$, which are the total investment operating cost of the BESSs, total load fluctuation of ADN, and total voltage fluctuation of ADN; $\mathit{x}$ represents the decision space consisting of the optimal installation node location, capacity, and hourly power optimization variables of BESSs and HESSs.

2.1.1 Total investment operating cost

The research object of this work is the ADN that has been built, so the total investment cost of BESS can be described as follow:

$\min F_1=\min \left(c_{\mathrm{T}\mathrm{C}\mathrm{C}}+c_{\mathrm{O}\mathrm{M}}-I_{\mathrm{s}\mathrm{u}\mathrm{b}}+\left(c_{\mathrm{c}}+I_{\mathrm{d}}\right)+c_{\mathrm{a}\mathrm{b}}+c_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}+c_{\mathrm{C}\mathrm{E}}\right)(2)$

where $c_{\mathrm{T}\mathrm{C}\mathrm{C}}$ and $c_{\mathrm{O}\mathrm{M}}$ are the investment cost, operation cost and maintenance cost of BESS respectively; $c_{\mathrm{c}}$, $I_{\mathrm{d}}$ and $I_{\mathrm{s}\mathrm{u}\mathrm{b}}$ represent the electricity purchase cost, electricity sales revenue, and government subsidies respectively; $c_{\mathrm{a}\mathrm{b}}$, $c_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}$ and $c_{\mathrm{C}\mathrm{E}}$ represent the wind power and solar power abandonment cost, the cost of ADN loss, and the cost of carbon emissions from peak shaving of conventional power sources.

(1) Equivalent investment cost

$c_{\mathrm{T}\mathrm{C}\mathrm{C}}=\left[c_{\mathrm{i}\mathrm{n}\mathrm{v}}\bullet N_{\mathrm{B}\mathrm{E}\mathrm{S}\mathrm{S}}+{\displaystyle \sum }_{n=1}^{N_{\mathrm{B}\mathrm{E}\mathrm{S}\mathrm{S}}}\left(a\bullet P_{\mathrm{B}\mathrm{E}\mathrm{S}\mathrm{S}\mathrm{s},n}+b\bullet E_{\mathrm{B}\mathrm{E}\mathrm{S}\mathrm{S}\mathrm{s},n}\right)\right]\bullet \frac{r\bullet {\left(1+r\right)}^y}{{\left(1+r\right)}^y-1}(3)$

where $c_{\mathrm{i}\mathrm{n}\mathrm{v}}$ represents a fixed investment construction cost of one BESSs; $N_{\mathrm{B}\mathrm{E}\mathrm{S}\mathrm{S}}$ represents the number of BESS installed; $E_{\mathrm{B}\mathrm{E}\mathrm{S}\mathrm{S}\mathrm{s},n}$ and $P_{\mathrm{B}\mathrm{E}\mathrm{S}\mathrm{S}\mathrm{s},n}$ represent the configuration rated capacity and rated power of the $n$ th BESS respectively; $a$ and $b$ represent the power cost of BESS and the capacity cost under different charging rates respectively; $y$ represents the service life of BESSs. In this work $y$ is 15 years; $r$ represents the discount rate, which value is 6.332%.

(2) Operation and maintenance cost

$c_{\mathrm{O}\mathrm{M}}=\left[{\displaystyle \sum }_{n=1}^{N_{\mathrm{B}\mathrm{E}\mathrm{S}\mathrm{S}}}\left(a\bullet P_{\mathrm{B}\mathrm{E}\mathrm{S}\mathrm{S}\mathrm{s},n}+b\bullet E_{\mathrm{B}\mathrm{E}\mathrm{S}\mathrm{S}\mathrm{s},n}\right)\right]\bullet {\epsilon }_{\mathrm{O}\mathrm{M}}(4)$

where ${\epsilon }_{\mathrm{O}\mathrm{M}}$ represents the coefficient of operation and maintenance. ${\epsilon }_{\mathrm{O}\mathrm{M}}$ takes 5% in this work.

(3) Government subsidies

$c_{\mathrm{c}\mathrm{h}\mathrm{a}}={\displaystyle \sum }_{m=1}^{M_{\mathrm{d}}}{D}_m\bullet \left[{\displaystyle \sum }_{n=1}^{N_{\mathrm{B}\mathrm{E}\mathrm{S}\mathrm{S}\mathrm{s}}}{\displaystyle \sum }_{t=1}^T\left({\epsilon }_{\mathrm{p}}\left(t\right)\bullet P_{\mathrm{c},n}\left(t\right)\right)\right](5)$

$I_{\mathrm{d}\mathrm{i}\mathrm{s}}={\displaystyle \sum }_{m=1}^{M_{\mathrm{d}}}{D}_m\bullet \left[{\displaystyle \sum }_{n=1}^{N_{\mathrm{B}\mathrm{E}\mathrm{S}\mathrm{S}\mathrm{s}}}{\displaystyle \sum }_{t=1}^T\left({\epsilon }_{\mathrm{s}}\left(t\right)\bullet P_{\mathrm{d},n}\left(t\right)\right)\right](6)$

$I_{\mathrm{d}\mathrm{i}\mathrm{s}}={\displaystyle \sum }_{m=1}^{M_{\mathrm{d}}}{D}_m\bullet \left[{\displaystyle \sum }_{n=1}^{N_{\mathrm{B}\mathrm{E}\mathrm{S}\mathrm{S}\mathrm{s}}}{\displaystyle \sum }_{t=1}^T\left(\rho \bullet P_{\mathrm{d}\mathrm{i}\mathrm{s},n}\left(t\right)\right)\right](7)$

where $M_{\mathrm{d}}$ represents the number of scenarios; $D_m$ represents the number of days corresponding to scenario $m$; ${\epsilon }_{\mathrm{p}}\left(t\right)$ and ${\epsilon }_{\mathrm{s}}\left(t\right)$ represent the electricity purchase and sale prices of BESSs in period $t$, respectively; $P_{\mathrm{c},n}\left(t\right)$ and $P_{\mathrm{d},n}\left(t\right)$ represent the charging and discharging power of the $n$ th BESSs in period $t$, respectively; $T$ represents the dispatching cycle, which is taken 24 h. $\rho$ represents the operating subsidy given by the government for the electricity sales of BESSs.

(4) Wind and solar abandonment cost

$c_{\mathrm{a}\mathrm{b}}={\displaystyle \sum }_{m=1}^{M_{\mathrm{d}}}{D}_m\bullet \left[\left.{\displaystyle \sum }_{t=1}^T\left(P_{\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{d}}\left(t\right)+P_{\mathrm{P}\mathrm{V}}\left(t\right)-P_{\mathrm{c}/\mathrm{d}}\left(t\right)-\right.|P_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}|\left(t\right)|-|P_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}|\left(t\right)\right)\right]\bullet \delta (8)$

where $P_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}\left(t\right)$, $P_{\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{d}}\left(t\right)$ and $P_{\mathrm{P}\mathrm{V}}\left(t\right)$ represent the load demand, wind power output, and PV output at time $t$, respectively; $P_{\mathrm{c}/\mathrm{d}}\left(t\right)$ represents the charge/discharge power of BESSs in period $t$; $P_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}\left(t\right)$ represents the line loss of power in $t$ period; $\delta$ represents the cost of wind and solar abandonment on the renewable energy side of the ADN.

(5) Cost of power loss

$c_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}={\displaystyle \sum }_{m=1}^{M_{\mathrm{d}}}{D}_m\bullet \left[{\displaystyle \sum }_{n=1}^{N_{\mathrm{B}\mathrm{E}\mathrm{S}\mathrm{S}\mathrm{s}}}{\displaystyle \sum }_{t=1}^T\left({\epsilon }_{\mathrm{s}}\left(t\right)\bullet P_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}\left(t\right)\right)\right](9)$

(6) Cost of carbon emissions from peak shaving of conventional power sources

$c_{\mathrm{C}\mathrm{E}}={\displaystyle \sum }_{m=1}^{M_{\mathrm{d}}}{D}_m\bullet \left[{\displaystyle \sum }_{t=1}^T{P}_{\mathrm{g}\mathrm{r}\mathrm{i}\mathrm{d}}\left(t\right)\bullet {\displaystyle \sum }_{p=1}^P\left(U_p\bullet u_p\right)\right],\mathrm{i}\mathrm{f}\cdots P_{\mathrm{g}\mathrm{r}\mathrm{i}\mathrm{d}}\left(t\right)>0(10)$

where $P_{\mathrm{g}\mathrm{r}\mathrm{i}\mathrm{d}}\left(t\right)$ represents the amount of electricity purchased from the ADN at time $t$; $P$ represents the number of pollutant types; $U_p$ represents the pollutant $p$ discharge penalty coefficient; $u_p$ represents the emission penalty price of pollutant $p$.

2.1.2 Total load fluctuation of active distribution network

$\min F_2=\min {\displaystyle \sum }_{m=1}^{M_{\mathrm{d}}}{D}_m\bullet \left[{\displaystyle \sum }_{t=1}^T\sqrt{{\left(F_{\mathrm{L}}\left(t\right)-F_{\mathrm{L}}\left(t-1\right)\right)}^2}\right](11)$

where $F_{\mathrm{L}}\left(t\right)$ represents the equivalent load power at time $t$.

2.1.3 Total voltage fluctuation of active distribution network

$\min F_3=\min {\displaystyle \sum }_{m=1}^{M_{\mathrm{d}}}{D}_m\bullet \left[{\displaystyle \sum }_{j=1}^{N_{\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{s}}}{\displaystyle \sum }_{t=1}^T\left|V_j\left(t\right)-V_{\mathrm{R}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{d}}\right|\right](12)$

where $V_j\left(t\right)$ represents the voltage per unit value of $j$ th node at time $t$; $V_{\mathrm{R}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{d}}$ represents the node-rated voltage, which is 1p.u.

3 Constraints

3.1 Node voltage

$U_i^{\min }\le U_i\le U_i^{\max }(13)$

where $U_i^{\max }$ and $U_i^{\min }$ represent the maximum and minimum of the node voltage respectively.

$E_{\mathrm{B}\mathrm{E}\mathrm{S}\mathrm{S}\mathrm{s}}^{\min }\le E_{\mathrm{B}\mathrm{E}\mathrm{S}\mathrm{S}\mathrm{s}}\le E_{\mathrm{B}\mathrm{E}\mathrm{S}\mathrm{S}\mathrm{s}}^{\max }(14)$

where, $E_{\mathrm{B}\mathrm{E}\mathrm{S}\mathrm{S}\mathrm{s}}^{\max }$ and $E_{\mathrm{B}\mathrm{E}\mathrm{S}\mathrm{S}\mathrm{s}}^{\min }$ represent the maximum and minimum of the installed capacity of the BESSs, respectively.

3.2 Installation node

$N_{\mathrm{B}\mathrm{E}\mathrm{S}\mathrm{S}\mathrm{s}}^{\min }\le N_{\mathrm{B}\mathrm{E}\mathrm{S}\mathrm{S}\mathrm{s}}\le N_{\mathrm{B}\mathrm{E}\mathrm{S}\mathrm{S}\mathrm{s}}^{\max },\cdots N_{\mathrm{B}\mathrm{E}\mathrm{S}\mathrm{S},1}\ne N_{\mathrm{B}\mathrm{E}\mathrm{S}\mathrm{S},2}(15)$

where $N_{\mathrm{B}\mathrm{E}\mathrm{S}\mathrm{S}\mathrm{s}}^{\max }$ and $N_{\mathrm{B}\mathrm{E}\mathrm{S}\mathrm{S}\mathrm{s}}^{\min }$ represent the maximum and minimum of the location of the BESSs installation node, respectively.

3.3 Wind and solar abandonment

$R_a=\frac{{\displaystyle \sum }_{m=1}^{M_{\mathrm{d}}}{D}_m\bullet \left[{\displaystyle \sum }_{t=1}^T\left(P_{\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{d}}\left(t\right)+P_{\mathrm{P}\mathrm{V}}\left(t\right)-P_{\mathrm{c}/\mathrm{d}}\left(t\right)-P_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}\left(t\right)-P_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}\left(t\right)\right)\right]}{{\displaystyle \sum }_{m=1}^{M_{\mathrm{d}}}{D}_m\bullet \left[{\displaystyle \sum }_{t=1}^T\left(P_{\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{d}}\left(t\right)+P_{\mathrm{P}\mathrm{V}}\left(t\right)\right)\right]}(16)$

$R_a\le R_{a,\max }(17)$

where $R_a$ represents the rate of wind and solar abandonment, which can be calculated by Eq. 16; $R_{a,\max }$ represents the maximum rate of wind and solar abandonment.

4 Non-dominated sorting genetic algorithm-II for optimal battery energy storage systems placement and sizing

4.1 Non-dominated sorting genetic algorithm-II

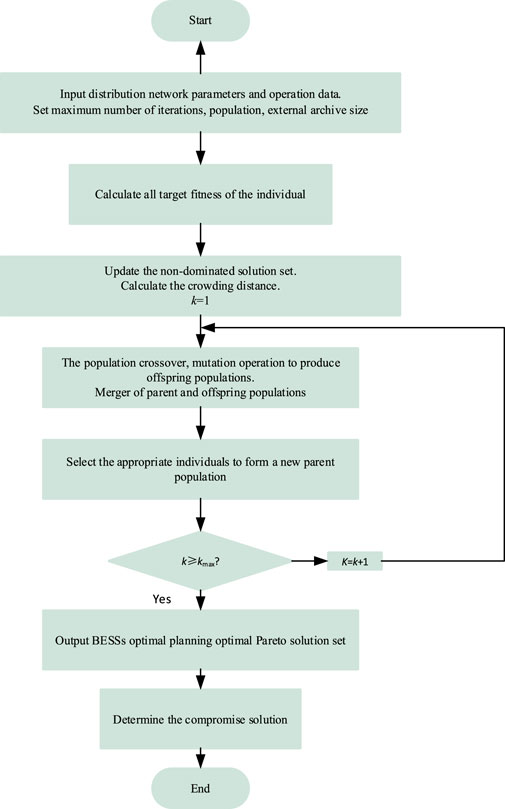
NSGA-II has diverse populations and high-accuracy optimization results. Firstly, the algorithm uses a fast non-dominated sorting method to classify the population into different ranking levels. Secondly, the crowding distance between individuals with the same ranking level is calculated, and individuals with a larger crowding distance are selected. The results can be evenly distributed in the target space, thus maintaining the diversity of the population. Finally, the optimal solution in the Pareto solution set is effectively saved by the elite strategy (Wu et al., 2014).

(1) Non-dominated solution set ranking

The non-dominated solution in the population can be determined by calculating the value of the objective function. According to the non-dominated level of each individual in the population, the whole population is sorted hierarchically.

(2) Calculate the crowding distance

To further select individuals at the same non-dominated level, the crowding distance between individuals needs to be calculated.

$L_{\mathrm{d}}=L_{\mathrm{d}}+\frac{\left[f_n\left(i+1\right)-f_n\left(i-1\right)\right]}{\left(f_n^{\max }-f_n^{\min }\right)}(18)$

where $L_{\mathrm{d}}$ represents the crowding distance; $f_n\left(i+1\right)$ and $f_n\left(i-1\right)$ represent the nth fitness value of the $\left(i+1\right)$ th and $\left(i-1\right)$ th individual at the same level, respectively; $f_n^{\max }$ and $f_n^{\min }$ represent the maximum and minimum value of the nth fitness function.

Then through the binary tournament selection method, two individuals are randomly selected, and the individuals with higher non-dominated levels can enter the next population. If the level is the same, choose the more crowded population.

(3) Elite strategy selection method

The simulated binary method is used to cross and polynomially mutate the population. Finally, the parent population and offspring population are combined to form a new population. The above steps should be repeated until the maximum number of iterations is reached, and output the Pareto optimal solution set.

4.2 Pareto solution set processing

In the process of NSGA-II algorithm optimization, the Pareto solution set will be continuously updated and put into a limited scale storage pool. When the algorithm iteratively obtains a new non-dominated solution, it needs to compare it with the non-dominated solution set in the storage pool, and then determine whether the new non-dominated solution is liberated into the storage pool. The judgment process is as follows (Faramarzi et al., 2020):

(1) If the new solution dominates the storage pool, it is replaced with the new solution;

(2) If the new solution is dominated by at least one solution in the storage pool, the new solution is discarded;

(3) If there is no dominant relationship between the new solution and the storage pool, the new solution is liberated into the storage pool.

To increase the diversity of solutions, when the number of non-dominated solutions in the archive set is higher than the upper limit, the redundant solutions must be removed. In this work, we use the crowded distance ranking method to select a densely distributed set of non-dominated solutions and eliminate redundant solutions by the roulette wheel method.

4.3 Multi-objective gray target decision based on entropy weight method

A multi-objective gray target decision based on the entropy weight method (EWM) is designed. Firstly, the evaluation indexes of each solution are set to build the sample matrix, and the decision matrix can be built by normalizing the sample matrix. Then, the weights of evaluation indexes of all Pareto non-dominated solutions and their distances from the target are obtained based on EWM and their distances from the target, and the solution with the closest distance to the target is determined as the best compromise solution for the BESS optimal allocation scheme (He et al., 2021).

(1) Establishing the sample matrix

To evaluate the similarity and equilibrium of each solution, this method adds two indicators in the sample matrix. One is the Euclidean distance (ED) between each solution and the ideal point, and the other is the Mahalanobis distance (MD) between each solution and the equilibrium point. Therefore, the sample matrix of effects containing five evaluation metrics can be expressed as:

$\mathbf{Z}={\left(v_g^k\right)}_{n\times \left(m+2\right)}=\left[\mathbf{F},\mathbf{E},\mathbf{M}\right]=\left[\begin{array}{ccc}{F}_1^1& \cdots & \begin{array}{ccc}{F}_m^1& E^1& M^1\end{array}\\ F_1^2& \cdots & \begin{array}{ccc}{F}_m^2& E^2& M^2\end{array}\\ \begin{array}{c}\cdots \\ F_1^n\end{array}& \begin{array}{c}\ddots \\ \cdots \end{array}& \begin{array}{ccc}\begin{array}{c}\cdots \\ F_m^n\end{array}& \begin{array}{c}\cdots \\ E^n\end{array}& \begin{array}{c}\cdots \\ M^n\end{array}\end{array}\end{array}\right](19)$

where E and M denote the ideal point distance matrix and equilibrium point distance matrix of all solutions, respectively. The ED between the $k$ th solution and the ideal point can be calculated by Eq. 20, and the MD between the $k$ th solution and the equilibrium point can be calculated by Eq. 21.

$E^k=\sqrt{{\sum }_{g+1}^{m+2}{\left(F_g^k-P_g\right)}^2}(20)$

$M^k=\sqrt{{\sum }_{g=1}^m{\left(F_g^k-u_g\right)}^{\mathrm{T}}{\sum }^{-1}\left(F_g^k-u_g\right)}(21)$

where $P_g$ denotes the ideal point of the $g$ th objective; $u_g$ represents the average of all solutions under the $g$ th objective; ${\sum }^{-1}$ is the covariance matrix.

(2) Design of decision matrix

According to the principle of rewarding good and punishing bad, the following operator is designed:

$q_g=\frac{1}{n}{\sum }_{g=1}^n{X}_g^k(22)$

where $X_g^k$ represents the evaluation index of the $k$ th solution at the $g$ th objective.

Then the decision matrix is established, as follows:

$\mathbf{V}={\left(v_g^k\right)}_{n\times \left(m+2\right)}=\frac{q_g-F_g^k}{\max \left\{\underset{1\le k\le n}{\max }\left\{F_g^k\right\}-q_g,q_g-\underset{1\le k\le n}{\min }\left\{F_g^k\right\}\right\}}(23)$

The target is identified in the gray decision region formed by the decision matrix as follows:

$v_g^0=\max \left\{v_g^k\left|1\le k\le n\right.\right\}(24)$

(3) Grey target decision based on EWM

First, the target weight of the $k$ th scenario under the $g$ th objective can be calculated by Eq. 25

$w_g^k=\frac{F_g^k}{{\sum }_{k=1}^n{Z}_g^k},\mathrm{i}\mathrm{f}{F}_g^k\ge 0(25)$

Next, the entropy values of the $g$ targets can be calculated as follows:

${EV}_g=\frac{1}{\ln n}{\sum }_{k=1}^n\left(w_g^k\bullet \ln w_g^k\right),\mathrm{i}\mathrm{f}{EV}_g>0(26)$

Among them, the smaller the entropy value of the indicator tends to contain more information, so the entropy weight is larger. The entropy weight of the $g$ th target is calculated as follows.

$w_g=\frac{1-{EV}_g}{{\sum }_{g=1}^{m+2}\left(1-{EV}_g\right)}(27)$

Then, the distance of each solution to the target can be calculated as follows:

${MDB}^k=\left|v^k-v^0\right|=\sqrt{{\sum }_{g=1}^{m+2}{w}_g{\left(F_g^k-u_g\right)}^{\mathrm{T}}{\sum }^{-1}\left(F_g^k-u_g\right)}(28)$

Finally, the target distance of each solution is sorted, and the solution closest to the target is selected as the best decision. The specific process of Table 1 NSGA-II solving the optimization problem of BESSs is shown in Figure 1. The basic principles and procedures of NSGA-II are as follows:

TABLE 1

TABLE 1. The basic principles and procedures of NSGA-II.

FIGURE 1

FIGURE 1. The flowchart diagram of the NSGA-II used for BESSs.

5 Fuzzy kernel C-means-based scene clustering

The most well-known and commonly used clustering methods are the K-means (Kanungo et al., 2002) clustering algorithm and the fuzzy C-means (FCM) clustering algorithm (Pal and Bezdek, 1995), (Askari, 2021). The K-means is simpler and more efficient, with the advantages of fast convergence and low linear complexity, but it is not applicable when the data set size is large and is sensitive to the initial clustering center. Moreover, its membership degree is either 0 or 1, which is a hard classification. In contrast, the membership degree of the FCM takes any value in the range of [0,1], and the criterion function is differentiable, which can The FCM clustering algorithm has any value in the range of [0, 1], and the criterion function is differentiable so that it can accurately cluster data with the non-convex distribution. To avoid the influence of non-uniform sample distribution on clustering results, this work uses a fuzzy kernel C-means (FKCM) clustering algorithm based on the Mercer kernel function to cluster ADN source-load scenarios.

The clustering principle of the FKCM clustering algorithm in the feature space is to minimize the weighted distance squared between a sample and its clustering center squared sum, which is described as follows:

$J_m\left(U,v\right)={\displaystyle \sum }_{i=1}^c{\displaystyle \sum }_{k=1}^n{u}_{ik}^m{\parallel \mathrm{\Phi }\left(x_k\right)-\mathrm{\Phi }\left(v_i\right)\parallel }^2,\cdots i=\mathrm{1,2},\dots ,c;k=\mathrm{1,2},\dots ,n(29)$

where $m$ represents a constant whose value is greater than 1; c and n are the numbers of clusters and the number of samples; $x_k$ represents the $k$ th sample; $v_i$ represents the center of the $i$ th cluster; $u_{ik}^m$ represents the membership degree function of the $k$ th sample in the $i$ th cluster, which satisfies the $0\le u_{ik}^m\le 1$ and $0<{\displaystyle \sum }_{k=1}^n{u}_{ik}<1$; $U$ represents the membership degree matrix.

The typical days of wind power and photovoltaic in each season can be obtained by the FKCM clustering algorithm, and then the clustering results of typical days in each season are combined. Therefore, there are a total of 36 source-load combination scenario sets in the four seasons (for example, spring wind power output 1, spring photovoltaic output 2, and spring load can be combined into one scenario set). Although various ADN operation scenarios can make the planning results more reasonable, it will significantly increase the solution time of the configuration model. Therefore, this paper uses the probability distribution method to reduce the large number of operation scenarios generated based on the FKCM clustering algorithm, and finally fits out the source-load scenarios of four seasons.

First, the probability of each scenario in each season can be calculated as follows:

${\rho }_m=\frac{D_m}{{\displaystyle \sum }_{m=1}^M{D}_m}(30)$

where $M$ represents the total number of all scenes in each season; $D_m$ represents the number of days the $m$ th scenario occurs during the season.

Then, based on the probability distribution of each scenario, the typical scenarios of each season are fitted to obtain four scenarios of spring, summer, autumn, and winter considering source-load uncertainty. The scenario fitting for each season is as follows:

$\left\{\begin{array}{c}{\mathit{P}}_{\mathrm{F}}=\left[P_{\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{d},\mathrm{F}},P_{\mathrm{P}\mathrm{V},\mathrm{F}},P_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d},\mathrm{F}}\right]={\displaystyle \sum }_{m=1}^M{\rho }_m\bullet {\mathit{P}}_m\\ {\mathit{P}}_m=\left[P_{\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{d},m},P_{\mathrm{P}\mathrm{V},m},P_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d},m}\right]\end{array}\right.(31)$

where ${\mathit{P}}_{\mathrm{F}}$ represents the fitted source-load timing power set; $P_{\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{d},\mathrm{F}}$, $P_{\mathrm{P}\mathrm{V},\mathrm{F}}$ and $P_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d},\mathrm{F}}$ represent the wind power, photovoltaic output, and load power of the season after fitting, respectively. ${\mathit{P}}_m$ represents the source-load sequential power set for scenario $m$; $P_{\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{d},m}$, $P_{\mathrm{P}\mathrm{V},m}$, $P_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d},m}$ represent the wind power, PV output, and load power in m scenarios, respectively.

The fitted wind, photovoltaic, and load curves of four typical scenarios in spring, summer, autumn, and winter are shown in Figure 2.

FIGURE 2

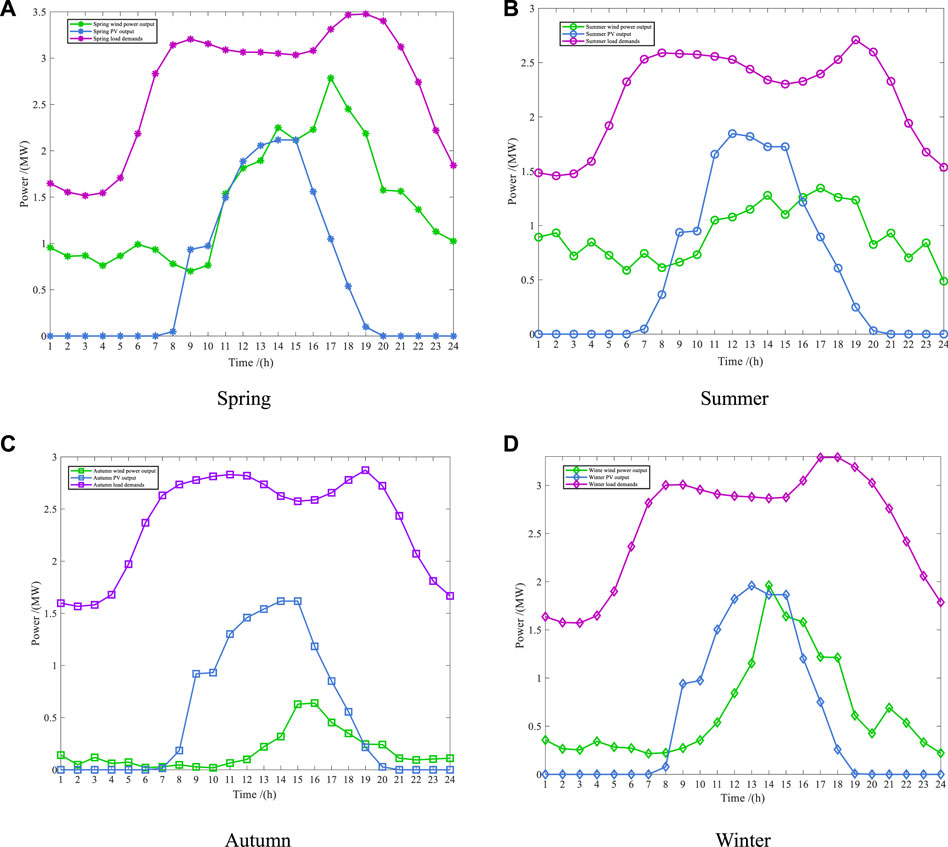
FIGURE 2. Typical diurnal curves of load, wind and PV power. (A) Spring. (B) Summer. (C) Autumn. (D) Winter.

6 Case studies

In this work, the extended IEEE-33 node test system and the extended IEEE-69 node test system are used to prove that NSGA-II can get the correct BESSs configuration scheme. And this scheme can effectively improve the voltage quality problem in ADN caused by the high renewable energy generation penetration rate. Table 2 shows the main parameters of the ADN.

TABLE 2

TABLE 2. Main parameters of ADN.

6.1 IEEE-33 node test system

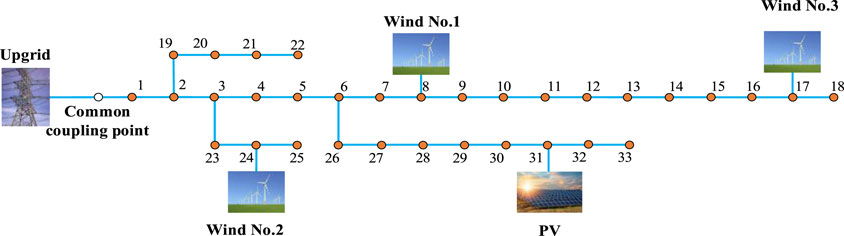
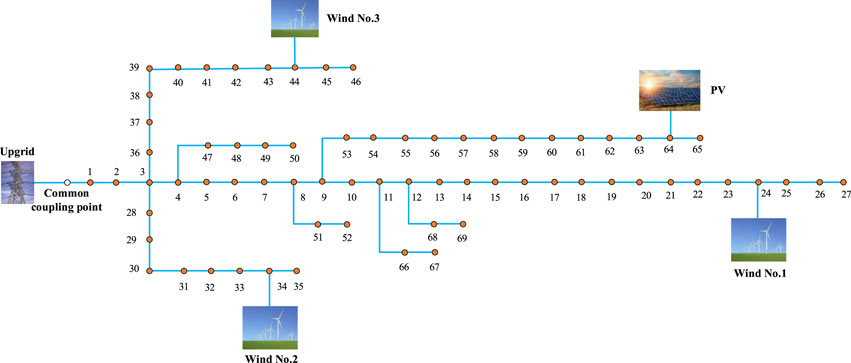
The extended IEEE-33 node test system topology is shown in Figure 3. Wind power No. 1, No. 2, and No. 3 are connected at nodes 8, 24, and 17, respectively, and PV is connected at node 31. Table 1 shows the main parameters of ADN.

FIGURE 3

FIGURE 3. Topology of the extended IEEE-33 node test system.

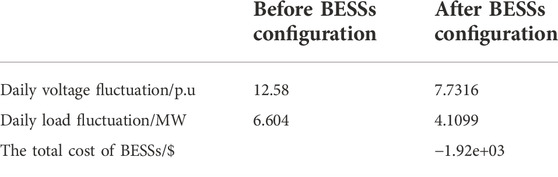
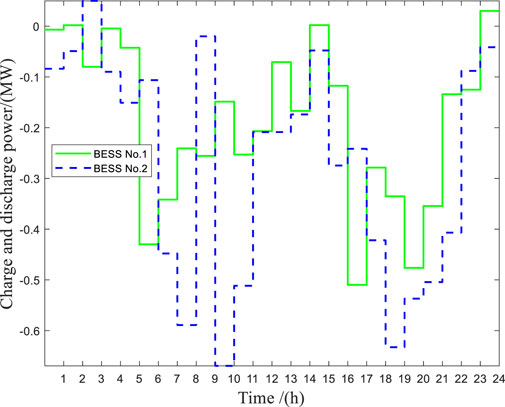
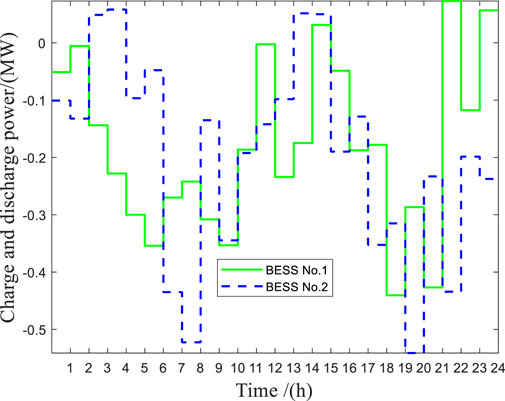
Table 3 shows the specific configuration scheme of BESSs. Table 4 shows the numerical changes of specific indicators in ADN before and after the access of the BESSs configuration scheme obtained by NSGA-II. By comparing the data in Table 4, after accessing BESSs, specifically, daily voltage fluctuation decreased by 4.8484 p. u. (the improvement rate is 38.54%), and the load fluctuation decreased by 2.4941 MW (the improvement rate is 37.77%). The total cost of BESSs is $-1.92e+03, which means a profit of $ 1.92e+03 a year after BESSs configuration. Moreover, Figure 4 compares the changes of three technical indicators of the ADN before and after the access of BESSs. As shown in Figure 4A, after BESSs is connected to the active distribution network, the node voltage level generally has an upward trend (at 1p.u. nearby). Meanwhile, it can be seen from Figure 4B that the average voltage fluctuation of nodes in the ADN decreases in 1 day. This means that BESSs can effectively improve the voltage quality of ADN. At last Figure 5 shows the charge and discharge power of BESSs in a day.

TABLE 3

TABLE 3. BESSs optimal configuration scheme.

TABLE 4

TABLE 4. Comparison before and after BESSs configuration.

FIGURE 4

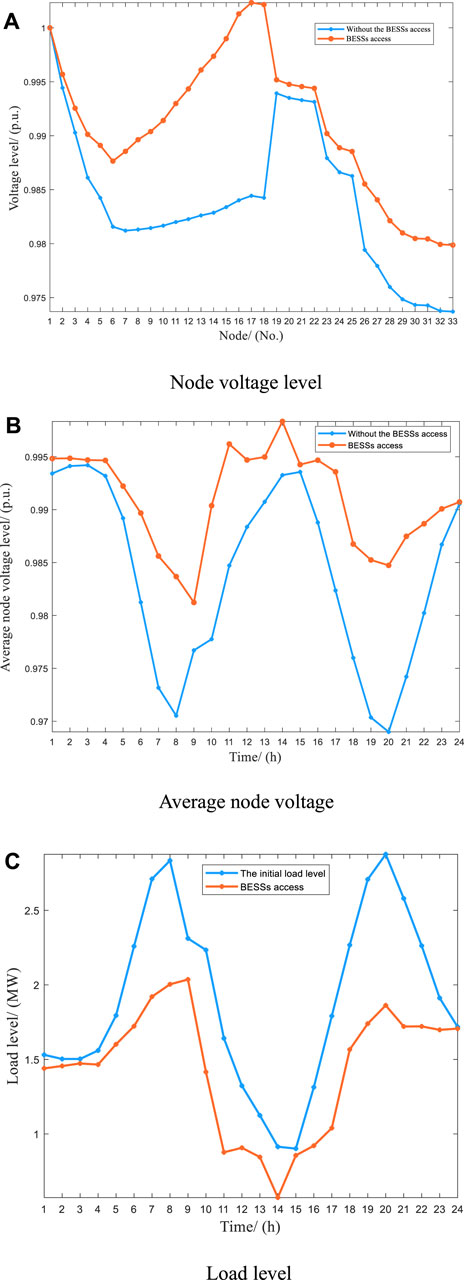
FIGURE 4. Optimization results of network obtained by NSGA-II in the extended IEEE-33 node test system. (A) Node voltage level. (B) Average node voltage. (C) Load level.

FIGURE 5

FIGURE 5. BESSs charge and discharge power in a day under IEEE-33 node system.

6.2 IEEE-69 node test system

The extended IEEE-69 node test system topology is shown in Figure 6. Wind power No. 1, No. 2, and No. 3 are connected at nodes 24, 34, and 44, respectively, and PV is connected at node 64.

FIGURE 6

FIGURE 6. Topology of the extended IEEE-69 bus system.

Table 5 shows the specific configuration scheme of BESSs. By comparing the data in Table 6, after accessing BESSs, specifically, the daily voltage fluctuation decreased by 8.095 p. u. (the improvement rate is 22.058%), and the load fluctuation decreased by 2.4481 MW (the improvement rate is 37.07%). Moreover, Figure 7 compares the changes in three technical indicators of the ADN before and after the access of BESSs. The total cost of BESSs is $ -1.2e+03. Figure 7 shows the three technical indicators before and after the access of BESSs. In Figure 7A, the node voltage level of node 57-node 65 has been greatly improved, and the curve in Figure 7B also shows that the voltage fluctuation of ADN has been effectively reduced after BESSs access. It can be concluded that by installing BESSs in the ADN, the power quality in the ADN has been improved, and the revenue can be $1.2e+03. And Figure 8 shows the charge and discharge power in a day under the extended IEEE-69 node system.

TABLE 5

TABLE 5. BESSs optimal configuration scheme.

TABLE 6

TABLE 6. Comparison before and after BESSs configuration.

FIGURE 7

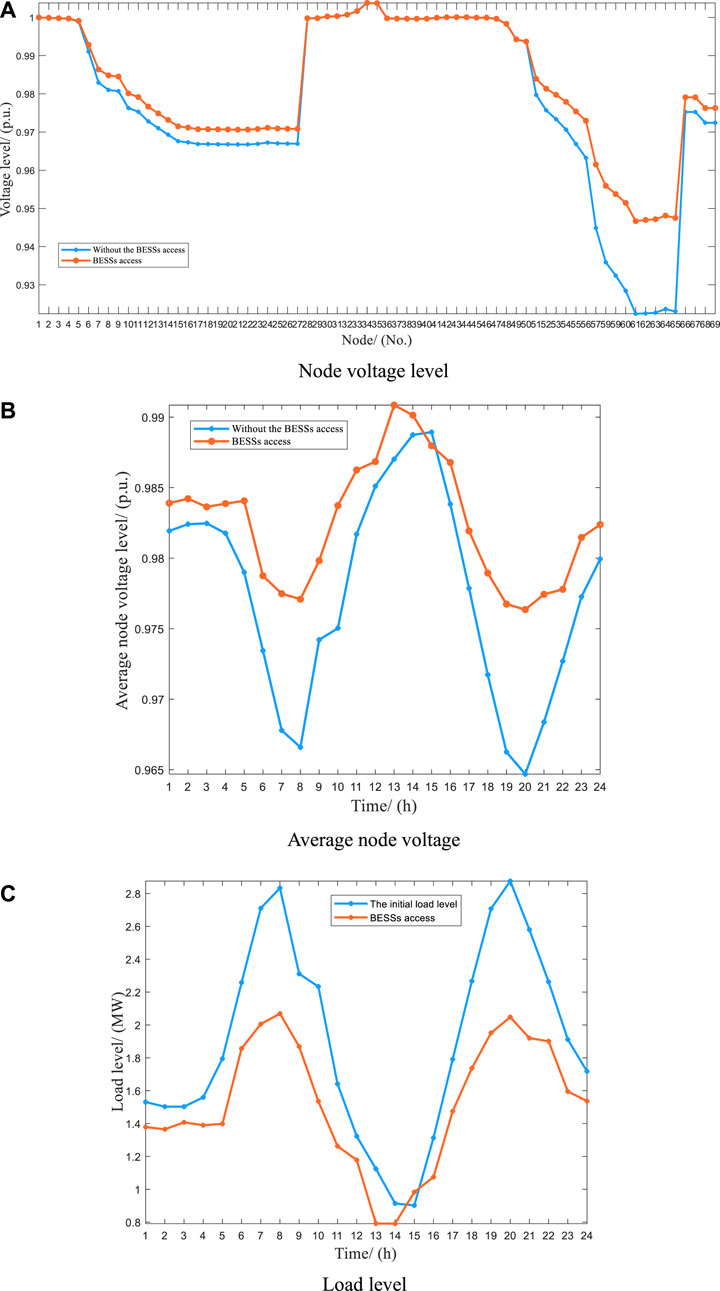
FIGURE 7. Optimization results of network obtained by NSGA-II under the extended IEEE-69 node test system. (A) Node voltage level. (B) Average node voltage. (C) Load level.

FIGURE 8

FIGURE 8. BESSs charge and discharge power in a day under the extended IEEE-69 node test system.

6.3 Comparison of algorithms

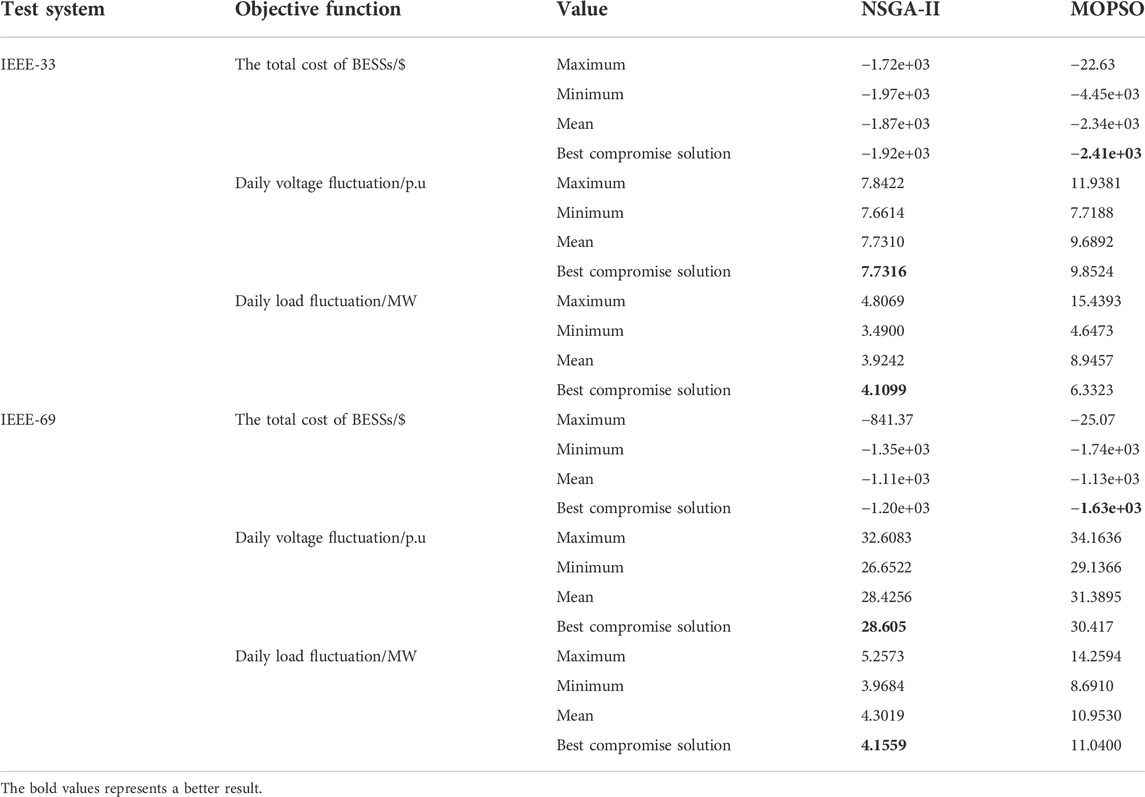
In this section, we use multi-objective particle swarm optimization (MOPSO) as a comparison algorithm to verify the superiority of NSGA-II. Table 7 shows the result obtained by two algorithms.

TABLE 7

TABLE 7. Pareto optimization results of the model obtained by two algorithms.

By comparing the results in Table 7, it can be seen that NSGA-II has the smallest daily voltage fluctuation and daily load fluctuation except for the total cost of BESSs. Meanwhile, the cost results obtained by the two algorithms are not much different. Therefore, it can be concluded that NSGA-II can obtain a more reasonable Pareto non-dominated solution set and provide the best candidate for decision makers.

6.4 Discussion

Figure 9 shows the Pareto front distribution obtained by NSGA-II in the simulation experiments based on the extended IEEE-33 node test system and the extended IEEE-69 node test system. It can be seen from Figure 9 that the NSGA-II can obtain a widely distributed Pareto front. This proves the effectiveness and powerful optimizing ability of NSGA-II algorithm.

FIGURE 9

FIGURE 9. The Pareto front distribution obtained by NSGA-II. (A) The Pareto front distribution based on the extended IEEE-33-node test system. (B) The Pareto front distribution based on the extended IEEE-69-node test system.

To verify the rationality of the EWM-based grey target decision, this work uses the method in Reference (Hu et al., 2014) to map the $a$ th objective function corresponding to the $b$ th non-dominated solution to the two-dimensional plane of ($a$ ×$i$). The equation is as follows:

$L_{i,a}=K\frac{f_{b,a}-f_a^{\min }}{f_a^{\max }-f_a^{\min }}(32)$

where $K$ is a random parameter; $f_{b,a}$ represents the $a$ th objective function of the $b$ th non-dominated solution.

Figure 10 shows a two-dimensional plane ($a$ ×$i$) mapped the Pareto front of the extend IEEE-33 node system and the extended IEEE-69 node system through the high-dimensional Cartesian coordinates. The abscissa is the optimized objective function, and the ordinate is the mapped objective function value. The objective functions are connected by a virtual line. The optimal compromise solution of the grey target decision based on EWM is represented by the red solid line. It can be seen that the compromise solution is in a reasonable range, which can avoid a greater preference for a certain goal due to subjective weight. And the distribution of the non-dominated solution set is more extensive, which indicates that NSGA-II algorithm has excellent optimization ability.

FIGURE 10

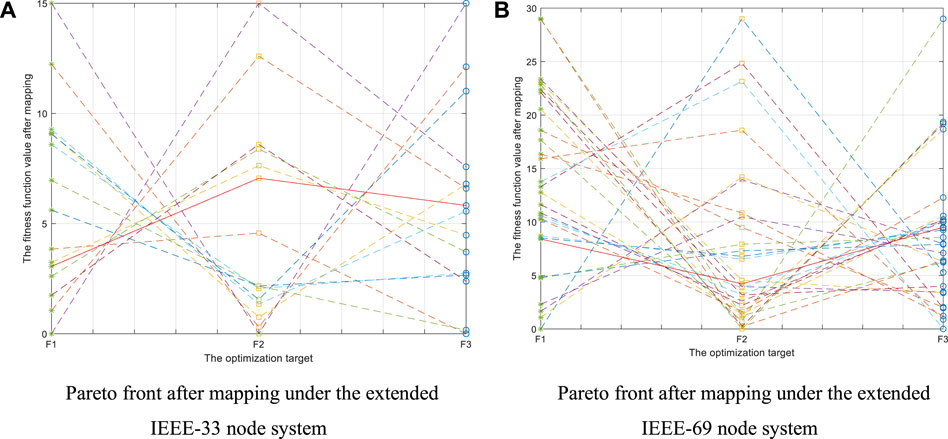
FIGURE 10. The Pareto front of the parallel coordinate system under the extended IEEE-33 node system and the extended IEEE-69 node system. (A) Pareto front after mapping under the extended IEEE-33 node system. (B) Pareto front after mapping under the extended IEEE-69 node system.

It should be noted that at 1 p.m. of Figure 4C and 1 and 2 p.m. of Figure 7C, the load level of the ADN with BESS drops to a very low level. This is because when configuring BESSs, the cost of configuring BESSs is considered an important factor. At 1 and 2 p.m. every day, it is in the peak load period. At this time, the load of the ADN increases, and the BESSs will deliver more electricity to the ADN to obtain more benefits while ensuring the stability of the ADN. The net load $P_{\mathrm{L}}$ of the ADN can be calculated by Eq. 33. As shown in Eq. 33, the increase of electric energy transmitted by BESSs to ADN will lead to a decrease in the net load level of the ADN.

$P_{\mathrm{L}}=P_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}-P_{\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{d}}-P_{\mathrm{P}\mathrm{V}}+P_{\mathrm{B}\mathrm{E}\mathrm{S}\mathrm{S}\mathrm{s}}(33)$

where $P_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}$, $P_{\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{d}}$ and $P_{\mathrm{P}\mathrm{V}}$ represent the load demand, wind poaxwer output, and PV output; $P_{\mathrm{B}\mathrm{E}\mathrm{S}\mathrm{S}\mathrm{s}}$ represents the power of BESSs, and its value is negative when it outputs electricity to the ADN.

7 Conclusion

To deal with the low stability of the ADN caused by the high proportion of renewable energy generations, this work proposes a configuration method of a Pareto multi-objective battery ESSs based on NSGA-II to improve the stability of the ADN. The main contributions of this work are:

(1) The clustering algorithm based on FKCM is used to cluster the load and wind-solar output, and four clustering scenarios are obtained.

(2) The grey target decision based on EWM is used to obtain the optimal compromise solution from the Pareto front, to get rid of the unreasonable favoritism caused by weighting multiple objectives with subjective weights.

(3) The extended IEEE-33 node system and the extended IEEE-69 node system are used for simulation experiments. The experimental results show that NSGA-II can balance the economy of BESSs configuration and stabilize the power and voltage levels of the ADN. Therefore, the BESSs configuration scheme obtained by the method described in this work is effective and can improve the stability of ADN operation.

In practice, the scale of ADN is large and more constraints need to be considered, which is a great challenge to the performance of the algorithm. At the same time, the heuristic algorithm has strong randomness, and the best compromise solution obtained each time is different. Therefore, it is more subjective to select the final solution from multiple optimal compromise solutions. However, compared with traditional optimization methods, heuristic algorithms do not require accurate models and a large amount of data. The algorithm structure is simple and efficient, which greatly improves the calculation speed and efficiency, and it is easier to obtain the global optimal solution, making the configuration of ESSs more reasonable. Therefore, considering the accuracy, effectiveness and time cost of the algorithm, the heuristic algorithm has more advantages than other traditional methods.

In future research, the NSGA-II algorithm will be applied to the BESSs planning problem considering the demand side response and the optimization problem of the electricity-hydrogen hybrid ESSs.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

RS: writing the manuscript; GH: discussion of the objective functions; SS: discussion of the constrains; YD: discussion of the algorithm; JC and HC: completion of the experimental test; KW: editing; CZ: discussion of the topic.

Acknowledgments

The authors gratefully acknowledge the support of Enhancement Strategy of Multi-type Energy Integration of Active Distribution Network (YNKJXM20220113).

Conflict of interest

RS, GH, SS, YD, JC, HC, KW, and CZ were employed by Dali Power Supply Bureau of Yunnan Power Grid Co., Ltd., Electric Power Research Institute of Yunnan Power Grid Co., Ltd., Grid Planning Research Center of Yunnan Power Grid Co., Ltd.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Askari, S. (2021). Fuzzy C-Means clustering algorithm for data with unequal cluster sizes and contaminated with noise and outliers: Review and development. Expert Syst. Appl. 165, 113856. doi:10.1016/j.eswa.2020.113856

CrossRef Full Text | Google Scholar

Bin, Y., Xu, L., Wang, J., Zhu, S. Y., Qiu, X. F., Yin, C. X., et al. (2019). Research on investment input-output benefit of distribution network planning considering micro-grid and multi-load development under the new power reform. IOP Conf. Ser. Earth Environ. Sci. 237 (6), 062013–62013. doi:10.1088/1755-1315/237/6/062013

CrossRef Full Text | Google Scholar

Chen, X. L. (2020). Operational reliability evaluation of power generation and transmission combined system considering multiple meteorological elements and retired battery energy storage. Chongqin, China: Chongqing University, doi:10.27670/d.cnki.gcqdu.2020.000145

CrossRef Full Text | Google Scholar

Company, B. P. (2021). Statistical review of world energy 2021. https://www.bp.com/en/global/corporate/energy-economics/statistical-review-of-world energy. html.[R/OL]. [2021-07-09]

Google Scholar

Das, C. K., Bass, O., Kothapalli, G., Mahmoud, T. S., Habibi, D., Hu, D. C., et al. (2018). Overview of energy storage systems in distribution networks: Placement, sizing, operation, and power quality. Renew. Sustain. Energy Rev. 91, 1205–1230. doi:10.1016/J.RSER.2018.03.068

CrossRef Full Text | Google Scholar

Dong, X., Wu, J., Xu, Z. B., Liu, K., and Guan, X. (2022). Optimal coordination of hydrogen-based integrated energy systems with combination of hydrogen and water storage. Appl. energy 308, 118274. doi:10.1016/j.apenergy.2021.118274

CrossRef Full Text | Google Scholar

Faramarzi, A., Heidarinejad, M., Stephens, B., and Mirjalili, S. (2020). Equilibrium optimizer: A novel optimization algorithm. Knowl. Based. Syst. 191, 105190. doi:10.1016/j.knosys.2019.105190

CrossRef Full Text | Google Scholar

Fu, L., Dong, L. T., and Zhang, Y. (2022). Research on optimal configuration of energy storage system in distribution network considering voltage quality. Electr. Autom. 44 (1), 24–26. doi:10.3969/j.issn.1000-3886.2022.01.008

CrossRef Full Text | Google Scholar

Ghatak, S. R., Sannigrahi, S., and Acharjee, P. (2019). Multi-objective approach for strategic incorporation of solar energy source, battery storage system, and DSTATCOM in a smart grid environment. IEEE Syst. J. 13, 3038–3049. doi:10.1109/JSYST.2018.2875177

CrossRef Full Text | Google Scholar

He, T. Y., Li, S. N., Wu, S. J., Li, C., and Xu, B. (2021). Biobjective optimization-based frequency regulation of power grids with highparticipated renewable energy and energy storage systems. Math. Problems Eng. 2021, 1–16. doi:10.1155/2021/5526492

CrossRef Full Text | Google Scholar

Hu, D. C., Zhang, S., Han, T., et al. (2022). Low-carbon transition path of power generation sector under carbon neutral target. Clean. Coal Technol. 28, 23–33. doi:10.13226/j.issn.1006-6772.cn22032102

CrossRef Full Text | Google Scholar

Hu, W., Yen, G. G., and Zhang, X. (2014). Multiobjective particle swarm optimization based on Pareto entropy. J. Softw. 25 (5), 1025–1050. doi:10.13328/j.cnki.jos.004496

CrossRef Full Text | Google Scholar

Kanungo, T., Mount, D. M., Netanyahu, N. S., Piatko, C., Silverman, R., and Wu, A. (2002). An efficient k-means clustering algorithm: Analysis and implementation. IEEE Trans. Pattern Anal. Mach. Intell. 24 (7), 881–892. doi:10.1109/TPAMI.2002.1017616

CrossRef Full Text | Google Scholar

Lee, T. Y., and Chen, N. M. (1995). Determination of optimal contract capacities and optimal sizes of battery energy storage systems for time-of-use rates industrial customers. IEEE Trans. energy Convers. 10 (3), 562–568. doi:10.1109/60.464883

CrossRef Full Text | Google Scholar

Li, J. L., Guo, Z. D., Ma, S. L., et al. (2022). Summary of "Source-Network-Load Storage" architecture and evaluation system in new power system. High. Volt. Eng., 1003–6520. doi:10.13336/j.1003-6520.hve.20220532

CrossRef Full Text | Google Scholar

Li, Y., Feng, B., Li, G. Q., Qi, J., Zhao, D., and Mu, Y. (2018). Optimal distributed generation planning in active distribution networks considering integration of energy storage. Appl. Energy 210, 1073–1081. doi:10.1016/j.apenergy.2017.08.008

CrossRef Full Text | Google Scholar

Li, Y., Feng, B., Wang, B., and Sun, S. (2022). Joint planning of distributed generations and energy storage in active distribution networks: A Bi-level programming approach. Energy 245, 123226. doi:10.1016/j.energy.2022.123226

CrossRef Full Text | Google Scholar

Liu, M. J., Li, W. R., and Wang, S. C. (2016). Reliability evaluation of microgrid with tidal power generation and battery storage in islanded mode. Power Autom. Equip. 36 (11), 33–39. doi:10.16081/j.issn.1006-6047.2016.11.005

CrossRef Full Text | Google Scholar

Meng, Q. Q., Li, X. Q., Yu, H. F., et al. (2021). Optimal planning of energy storage power station considering source-charge uncertainty. Acta Energiae Solaris Sin. 42 (10), 415–423. doi:10.19912/j.0254-0096.tynxb.2019-1023

CrossRef Full Text | Google Scholar

Pal, N. R., and Bezdek, J. C. (1995). On cluster validity for the fuzzy c-means model. IEEE Trans. Fuzzy Syst. 3 (3), 370–379. doi:10.1109/91.413225

CrossRef Full Text | Google Scholar

Ren, Z. P., Lu, B. C., Zhao, Y. L., et al. (2019). Modeling and simulation of photovoltaic virtual synchronous generator. Power Syst. Prot. Control 47 (13), 92–99. doi:10.19783/j.cnki.pspc.180963

CrossRef Full Text | Google Scholar

Shi, W. H., Qu, J. X., Luo, K., et al. Grid-integration and operation of high-proportioned new energy. Strategic Study CAE 2022, 1–12. doi:10.15302/J-SSCAE-2022.07.006

CrossRef Full Text | Google Scholar

Su, H. F., Hu, M. J., and Liang, Z. R. (2016). Distributed power planning with energy storage device based on timing characteristics. Power Autom. Equip. 36 (6), 56–63. doi:10.16081/j.issn.1006-6047.2016.06.009

CrossRef Full Text | Google Scholar

Wu, Q., Luo, J., and Lin, J. (2014). Production job multi-objective scheduling optimization based on set pair analysis and NSGA-II. Appl. Res. Comput. 31 (5), 1414–1417. doi:10.3969/j.issn.1001-3695.2014.05.031

CrossRef Full Text | Google Scholar

Wu, Y. J., Liang, X. Y., Huang, T., Lin, Z., Li, Z., and Hossain, M. F. (2021). A hierarchical framework for renewable energy sources consumption promotion among microgrids through two-layer electricity prices. Renew. Sustain. Energy Rev. 145, 111140. doi:10.1016/j.rser.2021.111140

CrossRef Full Text | Google Scholar

Wu, Y. J., Lin, Z. W., Liu, C. J., Chen, Y., and Uddin, N. (2021). A demand response trade model considering cost and benefit allocation game and hydrogen to electricity conversion. IEEE Trans. Ind. Appl. 58, 2909–2920. doi:10.1109/TIA.2021.3088769

CrossRef Full Text | Google Scholar

Wu, Y. J., Lin, Z. W., Liu, C. J., Huang, T., Chen, Y., Ru, Y., et al. (2022). Resilience enhancement for urban distribution network via risk-based emergency response plan amendment for ice disasters. Int. J. Electr. Power & Energy Syst. 141, 108183. doi:10.1016/j.ijepes.2022.108183

CrossRef Full Text | Google Scholar

Xiao, L. Y., and Pan, J. F. Suggestions on building a wide area virtual power plant based on photovoltaic power generation and physical energy storage. Bull. Chin. Acad. Sci. 2022, 549–558. doi:10.16418/j.issn.1000-3045.20220120001

CrossRef Full Text | Google Scholar

Yan, Z. M., Wang, C. M., Zheng, J., et al. (2013). Value assessment model of battery energy storage system in distribution network. Electr. Power Autom. Equip. 33 (2), 57–61. doi:10.3969/j.issn.1006-6047.2013.02.010

CrossRef Full Text | Google Scholar

Yang, B., Wang, J. T., Chen, Y. X., Li, D., Zeng, C., et al. (2020). Optimal sizing and placement of energy storage system in power grids: A state-of-the-art one-stop handbook. J. Energy Storage 32, 101814. doi:10.1016/j.est.2020.101814

CrossRef Full Text | Google Scholar

Yang, B., Yu, L., Chen, Y. H., Ye, H., Shao, R., Shu, H., et al. (2021). Modelling, applications, and evaluations of optimal sizing and placement of distributed generations: A critical state-of-the-art survey. Int. J. Energy Res. 45 (3), 3615–3642. doi:10.1002/er.6104

CrossRef Full Text | Google Scholar

Zandalinas, S. I., Fritschi, F. B., and Mittler, R. (2021). Global warming, climate change, and environmental pollution: Recipe for a multifactorial stress combination disaster. Trends Plant Sci. 26 (6), 588–599. doi:10.1016/j.tplants.2021.02.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Zheng, Z. D. (2018). Analysis of application mode and control strategy of battery energy storage system to reduce light abandonment in photovoltaic power station. Electr. Energy Effic. Manag. Technol. 23, 58–61–78. doi:10.16628/j.cnki.2095-8188.2018.23.011

CrossRef Full Text | Google Scholar