Investigation of high-speed deep well pump performance with different outlet setting angle of space diffuser

As one of the important equipment for pumping groundwater, how to improve the operation performance of deep well pump has been a research hotspot. At present, most of the deep well pump hydraulic design research mainly focuses on the low speed condition, and there is still a lack of systematic research on the internal flow theory and design method of the high speed deep well pump. In this paper, numerical simulation is used to investigate the performance change law of high speed deep well pump under different space diffuser blade outlet setting angles, and the performance test of the design scheme model is used to verify the accuracy of numerical simulation. The hydraulic loss inside the space diffuser and the velocity moment at the outlet are quantitatively analyzed. The results shown that the outlet setting angle of 90° is a relatively optimal solution. Under the designed outlet setting angle, the hydraulic loss in the first-stage space diffuser decreases with the increase of the flow rate, and the average hydraulic loss in the space diffuser at all levels fluctuates between 16% and 20%. With the increase of the number of stages, the velocity moment at the outlet of the space diffuser also increases gradually, and the change trend of the velocity moment at the outlet of the first-stage space diffuser under different outlet setting angles is relatively consistent. This research can provide reference for the optimal design and application of high speed deep well pump.

Introduction

As the core equipment for pumping groundwater, multistage deep well pumps are widely used in factories, railways, geothermal research, water companies, agricultural irrigation, mining and other fields due to their advantages of small diameter, high head, light weight, convenient transportation and reasonable price (Sontake et al., 2020). Therefore, the increasing number of energy-saving strategies and users has prompted industry and researchers to focus on the performance changes of deep well pumps (Zhou et al., 2022).

In order to investigate the flow pattern of the fluid inside the deep well pump and optimize the hydraulic performance of the deep well pump, scholars have carried out a large number of numerical simulations and experiments on the deep well pump, and have achieved a lot of research results (El-Emam et al., 2022). Gölcü et al. (Gölcü et al., 2006) analyzed the effect of splitter vanes on the performance of the deep well pump with different blade numbers, and continued to study the effect of splitter vane length on the performance of the deep well pump under the optimal scheme. The study shown that when the number of vanes is 6 and 7, the performance of the deep well pump is negatively increased by the splitter vanes. When the number of vanes is 5, the efficiency of the deep well pump is improved, and when the splitter vanes are 80% of the length of the main vane, the deep well pump can reach the best efficiency point. Zhang et al. (Zhang et al., 2016) proposed an axial diffuser, which has improved efficiency and higher economy than radial blades, and is suitable for deep well pumps with medium and high specific speeds. Goel et al. (Goel et al., 2008) optimized the blade shape and found that it can reduce the internal pressure loss of the pump. Shi et al. (Shi et al., 2013) analyzed the influence of different impeller outlet width on the deep well centrifugal pump, and found that with the increase of the impeller outlet width, the hydraulic performance of the pump also became worse, and the shaft power also gradually increased. Lin et al. (Lin et al., 2022) explored the influence of diffuser on the centrifugal pump at different inlet setting angles, and found that the increase of the inlet setting angle is beneficial to reduce the strength of the vortex in the impeller, but the large inlet setting angle will lead to a higher energy loss in the inlet pipe, which reduces the hydraulic performance of the pump. Tan et al. (Lei et al., 2014) proposed an optimal design scheme for blade wrap angle, and proved the superiority of the design method through experiments. Peng et al. (Peng et al., 2020) analyzed the effect of the blade outlet setting angle on the performance of the low specific speed multistage deep well pump, and found that increasing the blade outlet setting angle would lead to more cavitation on the impeller. Tanaka et al. (Tanaka et al., 2021) used a simulation method to study the transient characteristics of a centrifugal pump during rapid start-up, and compared with the experimental results; Zheng et al. (Zheng et al., 2020) found that under the condition of small flow, the gap flow will lead to the performance degradation of centrifugal pump. Cheng et al. (Cheng et al., 2019) found that appropriately increasing the wrap angle of the space diffuser can improve the flow characteristics within the space diffuser. Xu et al. (Xu et al., 2022) studied whether it will affect the centrifugal pump by changing the thickness of the blade, and found that under the constant thickness of blade condition, when the blade thickness exceeds 6 mm, the pump head and efficiency will drop rapidly; and under the variable thickness of blade condition, the minimum thickness of the pump blades should be 4 mm, and a maximum thickness of 60% of the chord length is proposed to improve pump performance.

In the deep well pump, the space diffuser is an important energy conversion flow component, and its hydraulic design greatly affects the performance of the deep well pump (Benghanem et al., 2013; Yang et al., 2021). At present, the research on the influence of the outlet setting angle of the space diffuser of the 6,000 r/min high speed deep well pump on its performance has not been reported yet. In this paper, under the condition that other hydraulic parameters of the space diffuser remain unchanged, the numerical simulation method is used to investigate the effect of the space diffuser, when the blade outlet setting angles are 40°, 50°, 60°, 70°, 80°, 90° and 100°. The influence of deep well pump performance provides a theoretical basis for optimizing the hydraulic parameters of space diffusers.

Physical models

The research object is the ZQSY100-2.2 YG high-speed deep well pump (hereinafter referred to as the deep well pump), which has four stages, and the main components are the motor, impeller, diffuser, etc. Design flow rate Q_d = 4 m³/h, design rated head H = 65 m, designed rotating speed n = 6,000 r/min, specific speed n_s = 83. The main design parameters of the overcurrent components of the deep well pump are shown in Table 1, and the assembly diagram of the overcurrent components is shown in Figure 1. Considering the smoothness of the outflow of the last stage diffuser, the space diffuser adopts two design schemes, A and B. The first three stages adopt the space diffuser A, and the last stage adopts the space diffuser B. The three-dimensional models of the impeller and two kinds of diffusers are shown in Figure 2. In order to study the influence of the outlet setting angle of the space diffusers on the performance of the deep well pump, seven different schemes are adopted, namely 40°, 50°, 60°, 70°, 80°, 90° and 100°.

TABLE 1

TABLE 1. Main parameters of flow-through components of the deep well pump.

FIGURE 1

FIGURE 1. Assembly diagram of overflow parts of the deep well pump.

FIGURE 2

FIGURE 2. Three-dimensional models of impeller and diffusers.

Numerical methods

Computational domain

CFturbo software is used to design spatial diffusers and impellers with different outlet setting angles, and the three-dimensional (3D) water body diagram is derived. UG12.0 is used to carry out 3D modeling of the computational domain of the remaining components of the deep well pump, including the cavity, the inlet pipe, and the outlet pipe. Considering the gap between the orifice ring to the impeller inlet and set its value is 0.5 mm. In order to reduce the influence of the inlet and outlet boundaries on the numerical simulation results and obtain more stable simulation data with good convergence characteristics, the inlet and outlet pipes of the deep well pump are extended.

Mesh generation

In the numerical simulation of the high speed multistage deep well pump, the structural mesh division of the computational domain of each component should be carried out first. The TurboGrid software is used to mesh the impellers and space diffusers at all levels of the high speed multistage deep well pump, and the ICEM software is used to mesh the inlet and outlet sections and cavity parts. The meshes near the blades of the diffusers are locally refined in order to better capture the complex flow in these areas. The specific mesh is shown in Figure 3.

FIGURE 3

FIGURE 3. Meshes of the calculation domain.

Boundary conditions

The full flow field structured meshes are imported into ANSYS Fluent software, and each mesh computing domain is defined (Benghanem et al., 2013). The four impeller computational domains are set as rotating domains, the impeller rotational speed is set as 6,000 r/min, and the inlet and outlet sections, cavity and space diffuser fluid domains are set as static domains. The inlet boundary condition is set to total pressure inlet and relative pressure to 0. The outlet boundary condition is set as the mass flow outlet, which selects seven different values according to the rated flow to simulate and calculate the corresponding performance. The impeller is situated in the rotating reference frame, the diffuser is in the fixed reference frame, and they are related to each other through the frozen rotor. The surface roughness is set to 0.06 mm, the wall is set to a non-slip wall. The turbulence model is set to the SST k-ω model, which is widely used in the prediction of internal flow in deep well pumps (Ji et al., 2013).

Mesh independence study

The number of overall meshes will affect the calculation results, and eight groups of meshes with different numbers are selected to provide mesh independence verification. Selecting the rated operating point of the deep well pump at 4 m³/h for numerical calculation, eight groups of different heads are obtained. The relationship between the head and the number of meshes is shown in Figure 4. It can be seen that with the increase of the number of meshes, the change of the head tends to be gentle. When the total number of meshes is greater than nine million, the head of the high speed multistage deep well pump is gradually stabilized. In order to ensure the calculation accuracy and save calculation time, the total number of meshes finally selected is 10 million. The y⁺ values are generally around 30 for all calculational domains, which meets the simulation needs of the SST k-ω model (Han et al., 2021).

FIGURE 4

FIGURE 4. Mesh independence verification.

Results and discussion

Verification of simulation

This pump performance experiment was carried out in the open experimental bench of the National Pump Comprehensive Laboratory of Jiangsu University. The schematic diagram of the experimental bench is shown in Figure 5. It mainly consists of high speed multistage deep well pump, frequency converter, outlet pipeline, outlet regulating valve, outlet pressure sensor, flow meters, data acquisition instruments, etc. The speed of the deep well pump is adjusted by the frequency converter, the flow is adjusted by the valve on the pipeline, and the outlet pressure of the deep well pump is monitored by the pressure sensor. The diameter of the outlet pipeline is 50mm, the pressure sensor adopts the WT2000 pressure sensor, the measurement range is 0–1.6MPa, and the comprehensive accuracy is 0.5%. The turbine flowmeter adopts the LWGY-50A0A3T turbine flowmeter, and the test accuracy is ±0.5%. The data are collected using a comprehensive hydro-mechanical tester of type TPA-3A developed by Jiangsu University.

FIGURE 5

FIGURE 5. Schematic diagram of the experimental test device.

Figure 6 is a comparison diagram of the experimental data and the simulated data of the high speed multistage deep well pump under the design speed of 6,000 r/min and different flow conditions. It can be seen that the simulation value of the external characteristics of the high speed multistage deep well pump is in good agreement with the experimental value. Under the working condition of rated flow of 4 m³/h, the head tends to be equal to the experimental value, and the difference between the efficiency and the experimental value is small. Under different flow conditions, the errors of the simulated and experimental values of head and efficiency are all within the acceptable range, indicating that the numerical simulation results have relatively high reliability and reference value.

FIGURE 6

FIGURE 6. Comparison of external characteristic curves.

External characteristics

The outlet setting angle of the space diffuser is changed and matched with the same impeller. Keeping the pre-processing settings unchanged, numerical simulations are performed for seven sets of outlet setting angles of the space vane. The relationship between the space diffuser outlet setting angle and the head and efficiency of the deep well pump at rated flow rate is obtained and the results are shown in Figure 7. With the increase of the outlet setting angle of the space diffuser, the head of the deep well pump gradually increases. When the outlet setting angle of the space diffuser is 90°, the head of the deep well pump is the largest, and then decreases. And the efficiency of the deep well pump shows an upward trend of oscillation, when the space diffuser outlet setting angle is 50°. The efficiency of the deep well pump at rated flow is the lowest, and when the space diffuser outlet setting angle is 80°, the deep well pump has the highest efficiency at rated flow. Considering the head and efficiency performance of the deep well pump comprehensively, the optimal space diffuser with the outlet setting angle of 90° is selected (Gonzalez et al., 2002).

FIGURE 7

FIGURE 7. The characteristic curve of the head and efficiency with different outlet setting angle.

Figure 8A is the head characteristic curve of the deep well pump under the space diffusers with different outlet setting angles. The head change trends of the deep well pump under the space diffusers with different outlet setting angles are basically the same, and they all decrease with the increase of the flow rate. When the flow rate is 2 m³/h, the head of the deep well pump is the largest when the setting angle of the space diffuser outlet is 100°, and the head of the deep well pump is the smallest when the space diffuser outlet setting angle is 40°. When the flow rate is 8 m³/h, the head of the deep well pump is the largest when the outlet setting angle of the space diffuser is 100°, and the head of the deep well pump is the smallest when the outlet setting angle of the space diffuser is 40°. On the whole, from small flow rate to large flow rate, the head of the deep well pump is the largest when the space diffuser outlet setting angle is 100°, and the smallest when the outlet setting angle is 40°. Figure 8B is the efficiency characteristic curve of the deep well pump under the space diffusers with different outlet setting angles. The efficiency changing trend with different outlet setting angles is basically the same. The efficiency of the pump increases first and then decreases as the flow rate increases. Under the condition of small flow rate of 2 m³/h, the efficiency of the deep well pump is the highest when the space diffuser outlet setting angle is 60°, and the efficiency of the deep well pump is the lowest when the space diffuser outlet setting angle is 50°. When the flow rate is 8 m³/h, the efficiency of the deep well pump is the largest when the space diffuser outlet setting angle is 100°, and the deep well pump efficiency is the lowest when the space diffuser outlet setting angle is 40°.

FIGURE 8

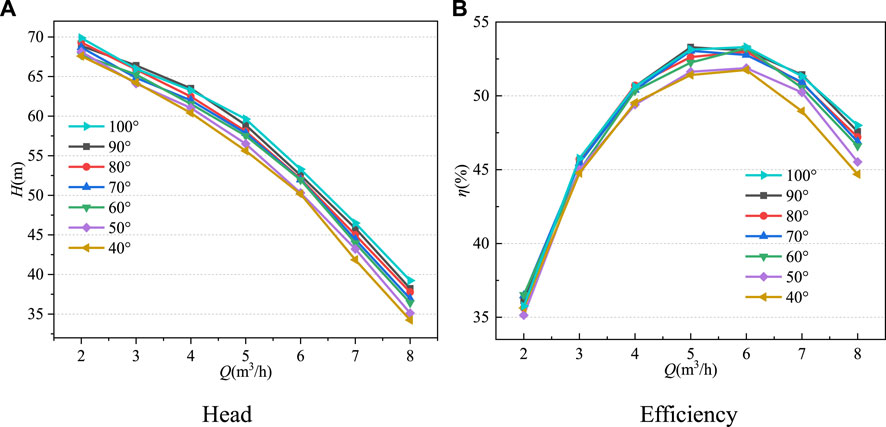
FIGURE 8. Comparison of external characteristics at different outlet setting angles of space diffusers.

Hydraulic loss

When the deep well pump is running, due to factors such as the roughness of the wall surface of the over-flow part and the viscosity of the fluid itself, the fluid will have collision and friction when flowing in the deep-well pump, which will cause the phenomenon of fluid de-flow and backflow in the flow channel of the over-flow component (Zhang et al., 2021). The loss of head and efficiency of the deep well pump is called hydraulic loss, and the calculation formula of the hydraulic loss in each stage of the space diffuser is as follows:

$\delta =\frac{p_1-p_2}{\Delta p}\times 100\%(1)$

where δ is the hydraulic loss ratio in the space diffuser; p₁ is the total pressure at the inlet of the space diffuser; p₂ is the total pressure at the outlet of the space diffuser; Δp is the pressure boost value of the impeller at all levels. The following will analyze the hydraulic loss inside the space diffuser under different outlet setting angles and different flow rates.

Figure 9A shows the hydraulic loss in the first-stage space diffuser under different outlet setting angles. The hydraulic loss in the first-stage space diffuser increases first, then decreases and then increases with the increase of the outlet setting angle. When the diffuser outlet setting angle is 90°, the hydraulic loss in the first-stage space diffuser is the largest, and when the space diffuser outlet setting angle is 70°, the hydraulic loss in the first-stage space diffuser is the smallest. Figure 9B shows the average hydraulic loss in the space diffusers at all levels under different outlet setting angles. The hydraulic loss in the space diffusers at all levels decreases first and then increases with the increase of the outlet setting angle. When the outlet setting angle is 90°, the hydraulic loss in the space diffusers at all levels is the largest. When the outlet setting angle of the space diffuser is 60°, the hydraulic loss in the space diffusers at all levels is the smallest, but the relative difference in the size of the hydraulic loss is not very large. The hydraulic loss cannot fully represent the level of efficiency, because the setting angle of the diffuser outlet will affect the internal flow and pressure distribution of the next-stage impeller, and the blade load will change. For multistage pumps, the factors affecting efficiency are complex.

FIGURE 9

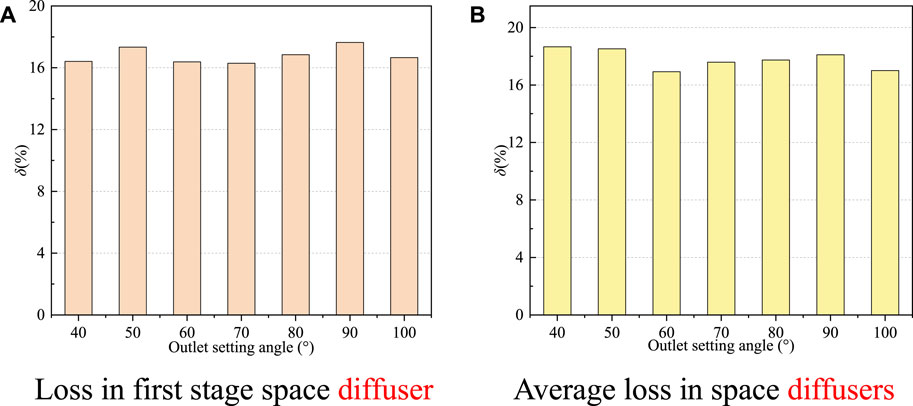
FIGURE 9. Hydraulic loss in the first stage space diffuser and the average hydraulic loss in space diffusers with different outlet setting angles.

Figure 10 shows the hydraulic loss in the first-stage space diffusers and the average hydraulic loss in the diffusers at all levels at different flow rates under the design outlet setting angle. With the increase of the flow rate, the hydraulic loss in the first-stage space diffusers gradually decreases, when the flow rate is 8 m³/h, the hydraulic loss in the first-stage space diffuser reaches the minimum. The average hydraulic loss in the space diffusers at all levels fluctuates between 16% and 20%. At 7 m³/h, the average hydraulic loss in the space diffusers at all levels reaches the minimum. At 2 m³/h, the average hydraulic loss in the space diffusers at all levels reaches the maximum. Starting from the rated flow rate of 4 m³/h, the hydraulic loss in the first-stage space diffusers is less than the average hydraulic loss in the space diffusers at all levels. The gap gradually widens with the increase of flow rate, indicating that under large flow conditions, the first stage hydraulic loss in the space diffuser is relatively small in the four-stage space diffuser.

FIGURE 10

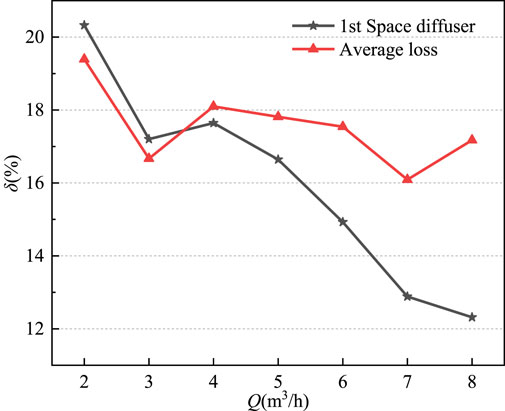
FIGURE 10. The hydraulic loss in the first-stage space diffusers and the average hydraulic loss in the space diffusers at different flow rates.

Outlet velocity moment

The space diffuser plays the role of rectification in the deep well pump (Iskenderli et al., 2013). In order to compare the rectification effect of the space diffuser under different outlet setting angles, the velocity moment is introduced, which represents the size of the general trend of the fluid particles moving along the direction of the closed surface. It is specified that the counterclockwise direction along the curve is the positive direction, and the clockwise direction along the curve is the negative direction. The specific formula is as follows:

$\mathrm{\Gamma }=\underset{L}{\oint }\overrightarrow{v}\cdot d\overrightarrow{l}(2)$

where Γ is the velocity moment, L is the closed curve, $\overrightarrow{v}$ is the velocity vector, and $d\overrightarrow{l}$ is the arc element vector of the curve L.

The absolute value of the velocity moment represents the size of the rectification capability of the space diffuser, and the smaller the absolute value, the stronger the rectification capability. Now define ε as the dimensionless radial position, and its calculation formula is as follows:

$\epsilon =\frac{R-R_D}{R_d-R_D}(3)$

where R_D is the outer diameter of the space diffuser outlet, R_d is the inner diameter of the space diffuser outlet, and R is the radius of a point between the inner diameter and the outer diameter of the space diffuser. The following will analyze the velocity moment of the space diffuser outlet under different outlet setting angles and different flow rates.

Figure 11 shows the outlet velocity moment of the space diffusers at the rated flow rate under the designed outlet setting angle. The variation trend of the velocity moment of the four-stage space diffusers are basically same. The overall magnitude is not large and the outlet velocity moments of the space diffusers at all levels are all positive values, among which the velocity moment at the exit of the fourth-stage space diffuser is much larger than the other three-stage space diffusers, and the exit velocity moment of the first-stage space diffuser is the smallest, indicating that the rectification effect of the first-stage space diffuser is better. On the whole, from the inner diameter to the outer diameter of the space diffuser outlet, the outlet circulation of the space diffusers at all levels shows an upward trend. However, near the outer diameter of the space diffuser outlet, the velocity moment of the space diffusers at all levels will decrease.

FIGURE 11

FIGURE 11. Outlet velocity moment of space diffusers at each level at design outlet setting angle.

Figure 12 shows the outlet velocity moment of the first-stage space diffuser at different outlet setting angles under rated flow. The variation trend of the first-stage space diffuser outlet velocity moment under different outlet setting angles is basically the same. From the inner diameter of the first-stage space diffuser outlet to the outer diameter, the velocity moment first increases and then decreases. When ε is between 0 and 0.54, the outlet setting angle is 90°, and the velocity moment at the first-stage space diffuser is the smallest. When ε is between 0.54 and 1, the outlet setting angle is 100°, the velocity moment of the first-stage space diffuser is the smallest. It means that the space diffuser has better rectification capability and can eliminate the rotational component of fluid better, when the space diffuser outlet setting angle is 90° and 100°. When the outlet setting angle is 40°, the outlet velocity moment of the first stage space diffuser is the largest. It means that when the outlet setting angle is 40°, the rectification capability of the space diffuser is poor, and it is not able to better eliminate the rotational component of the fluid. It leads to unstable flow pattern when the fluid enters the next stage impeller, which affects the overall performance of the deep well pump.

FIGURE 12

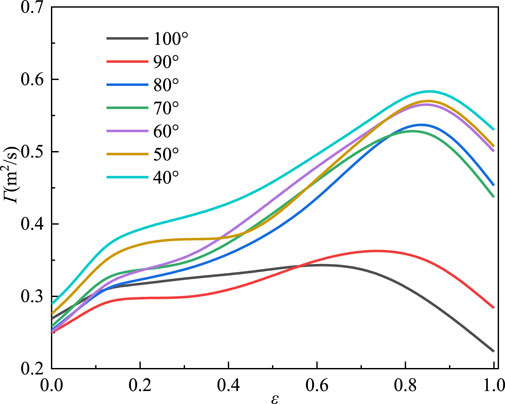
FIGURE 12. The velocity moment of the first-stage space diffuser at different outlet setting angles.

Figure 13 shows the outlet velocity moment of the first-stage space diffuser at different flow rates under the design outlet setting angle. The change trend of the outlet velocity moment of the first-stage space diffuser under different flow rates is relatively consistent, from the inner diameter of the first-stage space diffuser outlet to the outer diameter and the velocity moment both increase first and then decrease. With the increase of the flow rate, the outlet circulation volume of the first-stage space diffusers also gradually increases. When the flow rate is 8 m³/h, the outlet velocity moment of the first-stage space diffusers is the largest, and the rectification capacity of the space diffusers is the worst. This is because under large flow conditions, the rotational component of the fluid at the outlet of the space diffuser is very large. The space diffuser can only eliminate part of the rotational component, and the remaining rotational component leads to a large velocity moment. Under the condition of small flow, the velocity moment near the outlet diameter of the first-stage space diffuser changes drastically, which has exceeded the outlet velocity moment under the rated flow. It shows that the internal flow of the deep well pump is unstable under small flow conditions, and the rectification ability of the space diffuser is also poor.

FIGURE 13

FIGURE 13. The velocity moment of the first-stage space diffuser at different flow rates.

Conclusion

Based on the numerical simulation method, the performance comparison of the deep well pump with different outlet setting angles of the space diffuser was carried out, and the hydraulic loss inside the space diffuser and the outlet velocity moment were quantitatively analyzed. The main findings and conclusions are as follows:

(1) The head of the high-speed deep well pump at rated flow increases with the increase of the outlet setting angle of the space diffuser. When the outlet setting angle is 90°, the head is the largest. When the outlet setting angle is 80°, the efficiency is the largest. Compared with the space diffusers with different outlet setting angles, it is a relatively optimal solution to design the space diffuser outlet setting angle to 90°.

(2) When the outlet setting angle of the space diffuser is 90°, the hydraulic loss in the first-stage space diffuser and the average hydraulic loss in the space diffusers at all levels are relatively the largest. Under the design outlet setting angle, the hydraulic loss of first-stage space diffuser decreases with the increase of the flow rate, and the hydraulic loss in the first-stage space diffuser is the smallest at 8 m³/h. The average hydraulic loss in the space diffusers at all levels fluctuates between 16% and 20%. At 7 m³/h, the average hydraulic loss in the space diffusers at all levels is the smallest, and at 2 m³/h, the average hydraulic loss in the space diffusers at all levels is the largest.

(3) Under rated operating conditions, the variation trend of the velocity moment at the outlet of the space diffusers at all levels is relatively consistent. With the increase of the number of stages, the velocity moment at the exit of the diffuser also increases gradually. The variation trend of the outlet velocity moment under the setting angle is relatively consistent. When the outlet setting angle is 90° and 100°, the outlet velocity moment of the first-stage space diffuser is smaller, and the rectification capability of the space diffuser is stronger. When the outlet setting angle is 40°, the velocity moment of the first-stage space diffuser outlet is the largest, and the rectification capacity of the space diffuser is poor. Under different flow rates, the velocity moment of the first-stage space diffuser outlet increases with the increase of the flow rate, and when the flow rate is 8 m³/h, the velocity moment at the exit of the first-stage space diffuser is the largest.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

YG contributed to the design of the study. WC, YZ performed the numerical simulation. YG, WC, GC organized the experimental test. YZ, XZ wrote the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work was supported by Scientific Research and Technology Development Project of CNPC (Grant Nos. 2021DJ4603) and Jiangsu Provincial Key Research and Development Program (Grant Nos. BE2020330).

Conflict of interest

Authors YG, GC and XZ were employed by Research Institute of Petroleum Exploration and Development, PetroChina.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Benghanem, M., Daffallah, K., Joraid, A., Alamri, S., and Jaber, A. (2013). Performances of solar water pumping system using helical pump for a deep well: A case study for madinah, Saudi arabia. Energy Convers. Manag. 65, 50–56. doi:10.1016/j.enconman.2012.08.013

CrossRef Full Text | Google Scholar

Cheng, X., Chen, H., and Wang, X. (2019). Analysis of the impact of the space guide vane wrap angle on the performance of a submersible well pump. Fluid Dyn. Mater. Process. 15 (3), 271–284. doi:10.32604/fdmp.2019.07250

CrossRef Full Text | Google Scholar

El-Emam, M. A., Zhou, L., Yasser, E., Bai, L., and Shi, W. (2022). Computational methods of erosion wear in centrifugal pump: A state-of-the-art review. Arch. Comput. Methods Eng. 22, 3789–3814. doi:10.1007/s11831-022-09714-x

CrossRef Full Text | Google Scholar

Goel, T., Dorney, D. J., Haftka, R. T., and Shyy, W. (2008). Improving the hydrodynamic performance of diffuser vanes via shape optimization. Comput. Fluids 37 (6), 705–723. doi:10.1016/j.compfluid.2007.10.002

CrossRef Full Text | Google Scholar

Gölcü, M., Pancar, Y., and Sekmen, Y. (2006). Energy saving in a deep well pump with splitter blade. Energy Convers. Manag. 47 (5), 638–651. doi:10.1016/j.enconman.2005.05.001

CrossRef Full Text | Google Scholar

Gonzalez, J., Fernandez, J., Blanco, E., and Santolaria, C. (2002). Numerical simulation of the dynamic effects due to impeller-volute interaction in a centrifugal pump. J. Fluids Eng. 124 (2), 348–355. doi:10.1115/1.1457452

CrossRef Full Text | Google Scholar

Han, Y., Zhou, L., Bai, L., Shi, W., and Agarwal, R. (2021). Comparison and validation of various turbulence models for U-bend flow with a magnetic resonance velocimetry experiment. Phys. Fluids 33 (12), 125117. doi:10.1063/5.0073910

CrossRef Full Text | Google Scholar

Iskenderli, I., Kuliev, I., Narimanov, V., and Kel’biev, F. M. (2013). Analysis of efficiency of methods for improving sucker-rod deep-well pump plungers and choice of an alternative method. Chem. Pet. Eng. 49 (7), 536–538. doi:10.1007/s10556-013-9788-3

CrossRef Full Text | Google Scholar

Ji, B., Luo, X., Wu, Y., Peng, X., and Duan, Y. (2013). Numerical analysis of unsteady cavitating turbulent flow and shedding horse-shoe vortex structure around a twisted hydrofoil. Int. J. Multiph. Flow 51, 33–43. doi:10.1016/j.ijmultiphaseflow.2012.11.008

CrossRef Full Text | Google Scholar

Lei, T., Baoshan, Z., Shuliang, C., Bing, H., and Wang, Y. (2014). Influence of blade wrap angle on centrifugal pump performance by numerical and experimental study. Chin. J. Mech. Eng. 27 (1), 171–177. doi:10.3901/cjme.2014.01.171

CrossRef Full Text | Google Scholar

Lin, P., Yang, T., Xu, W., and Zhu, Z. (2022). Influence of different offset angles of inlet guide vanes on flow characteristics of centrifugal pump. Front. Energy Res. 10, 818244. doi:10.3389/fenrg.2022.818244

CrossRef Full Text | Google Scholar

Peng, G., Chen, Q., Zhou, L., Pan, B., and Zhu, Y. (2020). Effect of blade outlet angle on the flow field and preventing overload in a centrifugal pump. Micromachines 11 (9), 811. doi:10.3390/mi11090811

PubMed Abstract | CrossRef Full Text | Google Scholar

Shi, W., Zhou, L., Lu, W., Pei, B., and Lang, T. (2013). Numerical prediction and performance experiment in a deep-well centrifugal pump with different impeller outlet width. Chin. J. Mech. Eng. 26 (1), 46–52. doi:10.3901/cjme.2013.01.046

CrossRef Full Text | Google Scholar

Sontake, V., Tiwari, A., and Kalamkar, V. (2020). Performance investigations of solar photovoltaic water pumping system using centrifugal deep well pump. Therm. Sci. 24, 2915–2927. doi:10.2298/tsci180804282s

CrossRef Full Text | Google Scholar

Tanaka, T., Toyomoto, T., Nasu, K., and Tabaru, M. (2021). Transient characteristics of a centrifugal pump at rapid startup. J. Phys. Conf. Ser. 1909 (1), 012032. doi:10.1088/1742-6596/1909/1/012032

CrossRef Full Text | Google Scholar

Xu, Z., Kong, F., Tang, L., Liu, M., Wang, J., and Qiu, N. (2022). Effect of blade thickness on internal flow and performance of a plastic centrifugal pump. Machines 10 (1), 61. doi:10.3390/machines10010061

CrossRef Full Text | Google Scholar

Yang, Y., Zhou, L., Hang, J., Du, D., Shi, W., and He, Z. (2021). Energy characteristics and optimal design of diffuser meridian in an electrical submersible pump. Renew. Energy 167, 718–727. doi:10.1016/j.renene.2020.11.143

CrossRef Full Text | Google Scholar

Zhang, Q., Xu, Y., Cao, L., Shi, W., and Lu, W. (2016). Design and performance research of a mixed-flow submersible deep well pump. Int. J. Fluid Mach. Syst. 9 (3), 256–264. doi:10.5293/ijfms.2016.9.3.256

CrossRef Full Text | Google Scholar

Zhang, Y., Zang, W., Zheng, J., Cappietti, L., Zhang, J., Zheng, Y., et al. (2021). The influence of waves propagating with the current on the wake of a tidal stream turbine. Appl. Energy 290, 116729. doi:10.1016/j.apenergy.2021.116729

CrossRef Full Text | Google Scholar

Zheng, L., Chen, X., Dou, H. S., Zhang, W., Zhu, Z., and Cheng, X. (2020). Effects of clearance flow on the characteristics of centrifugal pump under low flow rate. J. Mech. Sci. Technol. 34 (1), 189–200. doi:10.1007/s12206-019-1220-2

CrossRef Full Text | Google Scholar

Zhou, L., Hang, J., Bai, L., Krzemianowski, Z., El-Emam, M. A., Yasser, E., et al. (2022). Application of entropy production theory for energy losses and other investigation in pumps and turbines: A review. Appl. Energy 318, 119211. doi:10.1016/j.apenergy.2022.119211

CrossRef Full Text | Google Scholar