An electrical vehicle-assisted demand response management system: A reinforcement learning method

With the continuous progress of urbanization, determining the charging and discharging strategy for randomly parked electric vehicles to help the peak load shifting without affecting users’ travel is a key problem. This paper design a reinforcement learning-based method for the electric vehicle-assisted demand response management system. Specifically, we formalize the charging and discharging sequential decision problem of the parking lot into the Markov process, in which the state space is composed of the state of parking spaces, electric vehicles, and the total load. The charging and discharging decision of each parking space acts as the action space. The reward comprises the penalty term that guarantees the user’s travel and the sliding average value of the load representing peak load shifting. After that, we use a Deep Q-Network (DQN)-based reinforcement learning architecture to solve this problem. Finally, we conduct a comprehensive evaluation with real-world power usage data. The results show that our proposed method will reduce the peak load by 10% without affecting the travel plan of all electric vehicles. Compared with random charging and discharging scenarios, we have better performance in terms of state-of-charge (SoC) achievement rate and peak load shifting effect.

1 Introduction

With the continuous progress of urbanization, the population is constantly funneled into large- and medium-sized cities, and it brings great power load pressure to most cities (Lin and Zhu, 2020). Considering the fact that the speed of power infrastructure construction cannot keep up with the speed of load growth, time-sharing power supply is the most commonly used method to deal with the electricity outage. For example, from 2020 to the present, major cities in China have experienced limited electricity consumption due to excessive load, such as Guangzhou, Shenyang, Xi’an, and Chengdu. Evidently, this coercive method will seriously affect people’s daily life. Therefore, when the power infrastructure cannot be rapidly deployed to improve the power generation/supply capacity, it becomes urgent to find a more effective way to relieve the power consumption pressure.

Smart grid (Fang et al., 2012; Gungor et al., 2011), which supports bi-directional information and energy transformation, can attract users to adjust their electricity consumption habits and actively participate in the dispatch of the power grid, that is, demand response (Medina et al., 2010; Palensky and Dietrich, 2011). Therefore, the wide application of smart grid technology can ensure the safe, reliable, and efficient operation of the power grid by introducing distributed energy storage equipment and distributed power users into the demand response process when the power grid load supply cannot be rapidly increased. Great research effort has been devoted to leveraging energy storage equipment to assist demand response management (Cui et al., 2017; Tang et al., 2019). For instance, it has to be mentioned that the unrestricted deployment of electrical energy storage devices will bring great economic burden, which is impractical.

Recently, with the increasingly severe global energy shortage and environmental pollution, the automobile industry has been undergoing major changes, and electric vehicles (EVs) have become a new direction for the development of various automobile companies (Emadi et al., 2008; Lopes et al., 2011). The EV industry has been developing rapidly in recent years, with the total value of the global EV market growing from $18 billion in 2018 to $22.42 billion in 2019 and an annual growth rate of more than 7.5%. Statistical studies show that most electric vehicles are in shutdown state 90% of the time, during which the on-board battery of electric vehicles can be regarded as a distributed energy storage device to participate in the demand side management of the microgrid, which is called V2G technology (vehicle-to-grid) (Madawala and Thrimawithana, 2011; Ota et al., 2012).

Electric vehicles have been widely used as a load-balancing tool in academic circles because of their good power storage capacity and flexibility. However, due to the uncertainty of vehicle owners’ commuting behavior, electricity power demand and load, etc., reasonably planning the charging and discharging strategy of electric vehicles to help the power grid carry out peak load filling and demand response is a key problem. Scholars have made great efforts in designing an EV charging/discharging strategy, which can be mainly divided into two categories: optimization scheduling (Karapetyan et al., 2021; Zhang et al., 2022) and trading-based method (Li et al., 2019; Yang et al., 2020). However, these two mainstream approaches have their drawbacks. The scheduling-based method is suitable for the offline environment, that is, decision-makers need to obtain some prior knowledge, such as the EV owners’ travel plan and the future electricity supply/demand. At the same time, this method will ignore the needs of EV owners in pursuit of higher power conversion efficiency. Regarding the trading-based method, it can be used in an online environment and fully meets the needs of EV owners, but it has limited help for demand response because it is a completely free market with limited incentives for EV owners.

As introduced earlier, it is necessary to find a novel optimization algorithm to satisfy the aforementioned requirements (online, demand response, and EV owners’ travel plan and enthusiasm). Reinforcement learning (RL) (Kaelbling et al., 1996) is a new artificial intelligence method to obtain optimal strategies for sequential decision problems. In the energy trading market, each participant can be regarded as an agent, while the trading market is formed as a multi-agent cooperation model (Wu et al., 2007). In such a multi-agent model, the purpose of each agent is to improve its own utility and meet its own needs, which causes great difficulty in constructing and solving the decision-making model of such a multi-agent-based energy trading market. Since RL can formulate effective coordination strategies for the agent without explicitly building a complete decision model, it can adapt the agent’s behavior to the uncertain and changing dynamic environment and improve the agent’s performance through interaction. Thus, RL can often achieve good results in the scenario of multi-agent cooperation, such as energy trading, which has aroused extensive research by scholars (Liu et al., 2017; Hua et al., 2019). Nowadays, there exist many RL-based energy management methods; for example, Qian et al. (2020) proposed a reinforcement learning-based EV charging strategy focusing on the intelligent transportation system, and it can minimize the total travel distance and charging cost. Zhang et al. (2022) proposed a multi-agent reinforcement learning method to make an optimal energy purchase schedule for charging stations and a long short-term memory (LSTM) neural network to predict the EV’s charging demand. Although the existing research studies are focused on power scheduling, different scenarios have different problems, and the existing reinforcement learning method cannot be applied to the EV-assisted demand response scenario studied in our study. Specifically, in this scenario, there are electric vehicles with uncertain quantities and uncertain charging/discharging requirements. This scenario is evidently a multi-agent scenario, considering that the policy trained by multi-agent reinforcement learning is only for one agent. However, in this scenario, EV entry and exit are not restricted, and the strategy for an agent will not be practical after the EV leaves. So in the EV-assisted demand response system with uncertain EVs, determining the strategy of EVs’ charging/discharging behavior is a challenge.

To this end, in this paper, we will study an EV-assisted demand response management system to relieve the power consumption pressure in urban peak hours by planning EV charging/discharging behaviors. Considering the efficiency of decision-making, we aim to design a reinforcement learning method for an EV-assisted demand response management system. The main contribution of this paper is as follows: we first formalize the EV charging/discharging strategy as an MDP model. Electric vehicles can enter and exit at any time; we focus on making decisions for parking spaces, and the action space is the charging and discharging strategy of each parking space. Considering that too many electric vehicles lead to too much action space, we classify electric vehicles, and similar electric vehicles share one action. The state space includes the state of parking spaces, EVs, and total demand. Because our system is a multi-objective optimization problem, we use a penalty item to ensure that the departure SoC will be enough for the next travel, and we use a moving average reward to ensure the peaking load shifting effect. After that, we design a DQN reinforcement learning architecture to solve the MDP model. Finally, comprehensive evaluations are conducted with real-world data to verify the effectiveness of our method.

The remainder of this paper is organized as follows: in Section 2, we briefly review the research efforts related to EV charging/discharging strategy and reinforcement learning method. In Section 3, we introduce the models of our EV-assisted demand response management system and build the EV charging and discharging scheduling optimization model. In Section 4, the background of deep reinforcement learning is proposed, and the MDP process of the EV charging/discharging behavior is modeled. In Section 5, the DQN reinforcement learning method is introduced, and we propose a DQN-based EV charging/discharging strategy algorithm. In Section 6, we evaluate the performances of the proposed method and compare our method with other methods, concluding the effectiveness of the proposed method in peak load shifting. Finally, we conclude this paper in Section 7.

2 Related work

With the rapid growth of electric users, the imbalance between power supply and demand in the power grid becomes more prominent. Many scholars have focused on alleviating the imbalance of power supply through demand response technology without increasing power infrastructure (Althaher et al., 2015; Eksin et al., 2015; Wang et al., 2018). For example, Jeddi et al. (2021) proposed a coordinated load scheduling method for each home customer in order to optimize their energy consumption at the neighborhood level. Under such a load scheduling method, the home customers will be rewarded, and demand response will be implemented. Similarly, facing the residential demand response problem, Liu et al. (2019) proposed an energy trading method based on game theory, in which the householder with renewable resources will transfer energy through a peer-to-peer (P2P) trading market. It can be seen that the demand response mechanism has been widely used in electric energy scheduling, especially in residential areas.

Moreover, electric vehicles (EVs) equipped with large capacity batteries can be used as distributed energy storage devices to participate in demand response. Therefore, scholars have also carried out research on demand response methods involving EVs by vehicle-to-grid technology. Kikusato et al. (2019) proposed an EV charge–discharge management framework, in which the home energy management system (HEMS) decides the EV charge–discharge plan with information from the grid energy management system, aiming to reduce the residential operation cost. Li et al. (2020) proposed an auction market that allows electric vehicles with surplus energy to sell their energy to those with insufficient energy. (Li et al., 2019). Yang et al. (2020) proposed the auction-based EV energy trading market, in which EVs with insufficient energy act as buyers and EVs with surplus energy act as sellers. This mechanism can help peak-load shifting to a certain extent. Thus, using EVs as energy storage equipment for demand response has become a new direction in the academic world. However, the traditional scheduling and transaction methods are not enough in terms of efficiency and user satisfaction for flexible energy storage devices such as EVs.

Reinforcement learning, as an optimal strategy solution, has been widely used in energy scheduling and trading. Compared with previous non-artificial intelligence scheduling or trading methods, the RL method has a good effect in coping with environmental changes, so it has a better performance in the scenario involving EVs. For example, Wan et al. (2019) proposed a model-free approach to determine the real-time optimal schedules based on deep reinforcement learning. The approach contains a representation network to extract discriminative features from the electricity prices and a Q network to approximate the optimal action-value function. Zhang et al. (2020) proposed a DQN-based method to manage the EV charging behavior in order to improve the income of EV owners and to reduce the pressure on the power grid as much as possible.

3 EV-assisted demand response management system

In this section, we will introduce the EV-assisted demand response management system in detail. First, we will give the system model, and then we will introduce the EVs’ model and the optimization formulation.

3.1 System model

The proposed EV-assisted demand response management system will be considered to be deployed in a small area which often has a lot of electricity users, such as a residential area and shopping mall. In such an area, there exists a parking lot for electric vehicles (EVs) to charge and discharge. Notably, EVs with high state-of-charge (SoC) can be regarded as the energy storage unit and supply electric power to the electric users within this area via V2G technology. So, the V2G EV-assisted demand response management system will greatly help to reduce the load pressure on the grid and enable more power users to use electricity. Meanwhile, since the position between the EVs and the electricity user is very close, the power transfer will not undergo multiple voltage changes, so the power loss is assumed to be 0. The system model is shown in Figure 1, and the important notations are shown in Table 1. The symbolic expression and some assumptions are as follows:

FIGURE 1

FIGURE 1. Market structure.

TABLE 1

TABLE 1. Key notations.

The EVs are saved into set P, and the m parking spaces are saved into set G. Furthermore, the EVs with insufficient energy are saved into set P_b, and the EVs with extra energy are saved into set P_s. The time is slotted and is denoted by an integer set T = [1, 2, 3, … ], and 1 day is divided into 24 slots. For an EV i ∈ P, when he/she enters the parking lot, he/she will upload some status and requirements information to the platform, including the arrival and departure time, arrival SoC, and departure SoC. The arrival and departure times are denoted as ta_i and td_i, respectively. The arrival SoC is denoted as $So{C}_i^a$ and represents the state-of-charge when the EV i arrives into the system at ta_i. The departure SoC is denoted as $So{C}_i^d$ and represents the minimum state-of-charge when the EV i departs at td_i. Notably, the departure SoC is determined by their travel plans. The management system is responsible for making decisions about the charging and discharging behavior of EVs. In each time slot t, the platform will make a decision to determine the charging and discharging behavior of each EV in this time slot and charge or pay according to the real-time electricity bill at that time. The system makes full use of the capability of EVs for scheduling while ensuring the departure SOC.

3.2 Electric vehicle model

As introduced before, in our paper, EVs act as both load and supply. Generally speaking, an electric vehicle can be considered as a mobile chemical energy storage unit. When it is parked in the parking lot and connected to the EV-assisted demand response management system, it is no different from the conventional chemical energy storage unit. However, electric vehicles need to assume the responsibility of vehicles and cannot always be parked in the parking lot as a power dispatching tool. So, the EVs can only be dispatched to discharge during their parking time, especially for the EVs that need to be charged. Specifically, the EV i’s parking time period is denoted as T_i = [ta_i, td_i]. Notably, the EV must be parked in a parking space, so i also denotes the ID of parking space i ∈ G. At the same time, different models of electric vehicles also have differences in battery capacity and charging and discharging speed. We use the symbols C_i and q_i to represent the battery capacity and charging/discharging speed of EV i. Notably, for convenience of calculation, we assume that the charging/discharging speed (q_i) of EV i is determined by the parking pile that they park. Then, we construct the following constraints to model electric vehicles:

$So{C}_i^t=So{C}_i^{t-1}+\frac{q_i}{C_i},t\in T_i=\left[t{a}_i,t{d}_i\right],(1)$

where $So{C}_i^t$ represents the SoC of EV i at time slot t. This equation reflects the linear transfer formula of battery state when energy loss is ignored.

$So{C}_i^{\min }\le So{C}_t^i\le So{C}_i^{\max },t\in T_i=\left[t{a}_i,t{d}_i\right],(2)$

where $So{C}_i^{\min }$ and $So{C}_i^{\max }$ represent the lower and upper bounds of SoC. This equation constrains the state of the battery according to its physical properties so that it can maintain a better performance.

$q_i=0,t\notin T_i.(3)$

This equation means that charging and discharging scheduling cannot be carried out when electric vehicles are not in the parking lot.

3.3 EV charging/discharging scheduling problem formulation

In the traditional demand response management system, the EV charging/discharging scheduling problem is always formulated as an optimization problem. The system collects the information of all EVs in the future for a period of time to make a comprehensive charging and discharging decision so that a certain index can reach the optimum. In our paper, we consider that the optimization goal is maximization of peak load shifting, that is, to help the power grid to cut peak and fill valley as much as possible. Then, the EV charging/discharging scheduling problem can be expressed as a mixed-integer linear program (MILP) model as follows:

$\max \sum _{t=1}^{t_n}\Vert \sum _{i=1}^m{x}_i^{t}So{C}_i^t-\frac{{\sum }_{t=1}^{t_n}{Q}^t}{t_n}\Vert ,(4)$

subject to:

$So{C}_i^t=So{C}_i^{t-1}+\frac{q_i}{C_i},t\in \left[t{a}_i+1,t{a}_i\right],i\in G,(5)$

$x_i^t\left(So{C}_i^{t-1}-So{C}_i^t\right)=q_i,t\in \left[t{a}_i+1,t{a}_i\right],i\in G,(6)$

$So{C}_i^{t{d}_i}\ge So{C}_i^d,i\in G,(7)$

$So{C}_i^{\min }\le So{C}_t^i\le So{C}_i^{\max },t\in T_i=\left[t{a}_i,t{d}_i\right],i\in P,(8)$

$x_i^t=\mathrm{0,1},-1i\in G,(9)$

where $x_i^t$ is the optimization parameters, and it represents the charging/discharging status of the EV which is parked at parking space i (we call it EV i for convenience). When $x_i^t=1,-\mathrm{1,0}$, they mean that at time slot t, EV i will charge, discharge, or stop, respectively.

Here, we will briefly introduce the aforementioned optimization model. First, the objective function represents that we want to maximize the effect of peak load shifting for a period of time. Constrain 1 shows the calculation rules of power transmission and SoC. Constraint 2 specifies that the charging and discharging speed shall satisfy the physical limits of parking piles. Constraint 3 specifies that the SoC of all EVs will have enough SoC when the EVs leave the parking lot. Constraint 4 specifies the constraint of optimization parameters.

To solve such an optimization equation, it is evident that an optimal charging and discharging strategy will be obtained, but considering many practical factors, it cannot be really used in practice. First, solving such a model requires the system to obtain accurate future information in advance, which is evidently impossible in practice. Second, even if the system obtains future information, the optimal matching strategy is obtained by solving the optimization problem. But once the future environment changes, the strategy will no longer be optimal. Therefore, in order to deal with this uncertain electric vehicle charging and discharging problem, it is necessary to design a method that can obtain the optimal strategy according to the current conditions.

4 MDP model of EV-assisted demand response strategy

In this section, we will introduce the Markov decision process (MDP) model of our proposed EV-assisted demand response system. First, we will introduce the rational of introducing the MDP model. Then, the background of deep reinforcement learning is proposed. Finally, the MDP model of charging/discharging strategy is given.

4.1 Rational

As introduced in Section 3.3, we have formulated the EV charging/discharging management as an MILP problem. However, this method has a high demand for future state and is too sensitive to environmental changes, which makes it unable to be deployed in actual scenarios. Reinforcement learning can obtain the best strategies in different environments through continuous exploration, and it has natural advantages in the face of such complex and changeable scenes.

But in our proposed EV-assisted demand response system, there still exists the following challenges: 1) there exist multiple EVs with different states and targets: different EVs have different SoC and different charging and discharging requirements, so it is necessary to learn different strategies for them. 2) EVs enter and exit the parking lot at any time; therefore, if each specific EV is given a learning strategy, the learned strategy will not be used after it leaves. 3) Considering that parking spaces are fixed, we can set strategies based on them. However, with the increase in the number of parking spaces, the dimension of action space is too large, which often leads to failure to learn useful strategies. To address the aforementioned problem, we divide EVs into several categories according to the SoC and charging and discharging requirements and provide learning strategies for each, respectively. In this way, we only need to classify the new EVs to get the related strategy.

4.2 Deep reinforcement learning

Deep reinforcement learning (DRL) combines the perceptual capability of deep learning (DL) with the decision-making capability of reinforcement learning (RL), where the agent perceives information through a higher dimensional space and applies the obtained information to make decisions for complex scenarios. Deep reinforcement learning is widely used because it can achieve direct control from original input to output through end-to-end learning. Existing research mainly classifies deep reinforcement learning algorithms into three main categories: one based on value functions, one based on policy gradients, and one based on multiple agents.

Mnih of DeepMind proposed Deep Q-Networks (DQNs) (Mnih et al., 2013), and people gradually started to study them at a deeper level while applying them to a wider range of fields. In recent years, research in deep reinforcement learning has focused on DQN, which combines convolutional neural networks with Q-learning and introduces an experience replay mechanism that allows algorithms to learn control policies by directly sensing high-dimensional inputs. The Deep Q-Network uses a Q-value function Q (s, a, θ) with parameters θ to approximate the value function. Under environment ϵ, when the number of iterations is i, the definition of the loss function L_i (θ_i) is expressed as follows:

$L_i\left({\theta }_i\right)=E_{s,a\rho \left(.\right)}\left[{\left(y_i-Q\left(s,a,{\theta }_i\right)\right)}^2\right],(10)$

where ρ(.) denotes the probability distribution of s choosing action a in a given environment, and y_i denotes the objective of the ith iteration Q-value function, which is defined as follows:

$y_i=E_{s^{\prime }ϵ}\left[r+\gamma \max Q\left(s^{\prime },a^{\prime },{\theta }_{i-1}|s,a\right)\right],(11)$

where r is the reward value fed to the agent by the environment, and γ is the discount factor. The goal of learning depends on the network weights, and the update formula of network weights is

$\begin{array}{ll}\hfill {\nabla }_{{\theta }_i}{L}_i\left({\theta }_i\right)& =E\left[\left(r+\gamma \max Q\left(s^{\prime },a^{\prime },{\theta }_{i-1}\right)\right.\right.\hfill \\ \hfill & -\left.\left.Q\left(s,a,{\theta }_i\right)\right)\nabla Q\left(s,a,{\theta }_i\right)\right].\hfill \end{array}(12)$

Although DQN based on the Q-learning algorithm has achieved good results in many fields, DQN is no longer applicable when facing continuous action space. Therefore, policy gradient methods have been introduced to deep reinforcement learning. Lillicrap et al. (2015) proposed the deep deterministic policy gradient (DDPG) algorithm in 2015. DDPG is an algorithm for deep reinforcement learning applied to continuous action space, which combines a deterministic policy gradient (DPG) algorithm with an actor–critic framework. In the DDPG, the objective function is defined as the sum of the awards with discounts:

$J\left({\theta }^u\right)=E_{{\theta }^u}\left[r_1+\gamma r_2+{\gamma }^2{r}_3+\cdots \right].(13)$

Then, the stochastic gradient descent method is used for end-to-end optimization of the objective function. Through a series of experiments, it is shown that DDPG not only performs stably in the continuous action space but is also much faster than DQN in terms of solution speed.

A multi-agent system (MAS) is a collection of multiple agents whose goal is to build complex systems into easily manageable systems. Multi-agent reinforcement learning (MARL) is the application of reinforcement learning ideas and algorithms to multi-agent systems. In the 1990s, Littman (1994) proposed MARL with a Markov decision process (MDP) as the environmental framework, which provided a template for solving most reinforcement learning problems. The environment of MARL is an MDP-based casuistic game framework with the following tuple:

$<S,A_1,\dots A_n,R_1,\dots ,R_n,P>,(14)$

where n is the number of agents and A is the set of joint action spaces of all agents:

$A=A_1\times \cdots \times A_n,(15)$

where R_i is the reward function for each agent:

$R_i:S\times A\times S\to R,(16)$

where P is the state transfer function:

$P:S\times A\times S\to \left[\mathrm{0,1}\right].(17)$

In the case of multiple agents, the state transfer is the result of all agents acting together, so the reward of the agents depends on the joint policy. The policy H is defined as the joint policy of agents, and accordingly, the reward of each agent is

$R_i^H=E\left[R_{t+1}|S_t=s,A_t=a,H\right].(18)$

Its Bellman equation is

$v_i^H\left(s\right)=E_i^H\left[R_{t+1}+\gamma V_i^H\left(S_{t+1}\right)|S_t=s\right],(19)$

$Q_i^H\left(s,a\right)=E_i^H\left[R_{t+1}+\gamma Q_i^H\left(S_{t+1},A_{t+1}\right)|S_t=s,A_t=a\right].(20)$

Depending on the type of task, MARL can be classified as fully cooperative, fully competitive, or hybrid, using different algorithms for different problems.

4.3 MDP for EV-assisted demand response management

First, to address the EV-assisted demand response problem via reinforcement learning, the main goal is to design a central agent to achieve peak and valley filling in the area, taking into account the individual economic benefits of EVs. Considering that the charging and discharging behavior of EVs are implemented at regular intervals, so the EV-assisted demand response problem can be regarded as a sequential decision problem. Therefore, we introduce an MDP model with discrete time steps to establish the charging and discharging behavior of EVs in the EV-assisted demand response system. Briefly, the agent represents a community electric company, and it observes the environmental status s_t, including the electricity demand in the current region and the battery status of each electric vehicle. Then, the charging/discharging action a_t is selected for the EVs, and the environment provides a corresponding reward r_t for the replacement. After that, the aforementioned process will be repeated in the time series. Finally, we can obtain the best execution strategy π* by repeating the aforementioned process (training process) many times. Furthermore, the transition relationship between states is no longer internal but is determined by both states and actions. In the following, we will introduce the elements of the proposed Markov model in detail, including agent, state space, action space, observation space, transition, and reward.

In the model, the agent is the parking lot provider, and the responsibility of the agent can be expressed as follows: they give charging or discharging instructions to EVs in each parking space according to the state at each moment. It can help the power grid to cut peak load and fill valley load and, at the same, time try to satisfy the power demand of EVs.

We denote S as the state space in our MDP model and s^t is the state at time slot t. Specifically, s^t can be expressed as

$s^t=\left\{l_1^t,l_2^t,\dots ,l_m^t,Q^{t-1}\right\},(21)$

where $l_i^t$ represents the state of parking space i ∈ G, m represents the number of total parking spaces, and Q^t−1 represents the total demand of this area at time slot t−1. Furthermore, $l_i^t$ can be expressed as

$l_i^t=\left\{spee{d}_i,work,classif{y}^t,t{d}_i,So{C}_i^t,So{C}_i^d,C_i\right\},(22)$

where speed_i represents the charging/discharging speed of charging pile i. work represents the dispatch demand of charging pile i, and when there is no EV in this parking space or it does not need to be dispatched, the value is 0; otherwise, it is 1. classify^t, td_i, $So{C}_i^t$, $So{C}_i^d$, and C_i represent the category, departure time, current SoC, departure SoC, and battery capacity of the EV in parking space i, and when there is no car in the parking space, these values are all 0.

We denote A as the action space in our MDP model and a^t as the action at time slot t. As introduced before, we will classify EVs into five categories to help the agent to learn strategies more effectively and reduce the dimension of the action space:

• Case A: The EV i’ SoC at time slot t is within the following range:

$So{C}_i^t-So{C}_i^d\le 5\%.(23)$

These EVs will not give action at this moment.

• Case B: The EV i’ SoC at time slot t is within the following range, and the charging piles are the DC model (7 KW in our paper):

$So{C}_i^t-So{C}_i^d>5\%.(24)$

• Case C: The EV i’ SoC at time slot t is within the following range, and the charging piles are AC model (30 KW in our paper):

$So{C}_i^t-So{C}_i^d>5\%.(25)$

• Case D: The EV i’ SoC at time slot t is within the following range, and the charging piles are DC model (7 KW in our paper):

$So{C}_i^t<So{C}_i^d.(26)$

• Case E: The EV i’ SoC at time slot t is within the following range, and the charging piles are AC model (30 KW in our paper):

$So{C}_i^t<So{C}_i^d.(27)$

Specifically, a^t can be expressed as

$a^t=\left\{a_1^t,a_2^t,a_3^t,a_4^t\right\},(28)$

where m represents the number of charging piles. $a_1^t$ to $a_4^t$ represents the action of the aforementioned categories from Case B to E at time slot t. When the value is 0, it means that the EV in the parking space will not be charged or discharged; when the value is 1, it means that the EV in the parking space will be charged; and when the value is −1, it means that the EV in the parking space will be discharged.

Considering the state s^t and action a^t, at time slot t+1, each parking space will update its status according to the charging/discharging decision at the last time slot and read the new status if a new EV enters.

Finally, considering the two goals of peak load reduction and satisfying the SoC demand of EV as much as possible, the reward will consist of two parts: 1) the reward represents the peak shifting and 2) the penalty item represents the SoC demand of EV. Specifically, the reward space R can be expressed as

$R^t=\left\{r_1^t,r_2^t,\dots ,r_m^t,r_{\mathit{load}}^t\right\},(29)$

where $r_i^t$ represents the penalty item which is calculation at each time slot.

$r_i^t=\left\{\begin{array}{cc}\hfill 0\hfill & \hfill So{C}_i^t\ge So{C}_i^d\hfill \\ \hfill -1\hfill & \hfill So{C}_i^t<So{C}_i^d\hfill \end{array}\right.(30)$

While r_load represents the reward of peak shifting, and we express it in the form of moving average:

$r_{\mathit{load}}^t=1-\Vert \frac{Av{e}_{\mathit{power}}^t-Q^t}{Av{e}_{\mathit{power}}^t}\Vert ,(31)$

where $Av{e}_{\mathit{power}}^t$ represents the total power of the last o time slot before time slot t:

$Av{e}_{\mathit{power}}^t=\frac{Q^{t-o+1}+\cdots +Q^t}{o}.(32)$

Notably, in our paper, o is set as 4.

Overall, the total reward at time slot t can be expressed as

$r^t=\frac{1}{m}\sum _{i=1}^m{r}_i^t+r_{\mathit{load}}^t.(33)$

5 Solutions via deep reinforcement learning

In this section, we design a value-based reinforcement learning method to adaptively learn the policy of the agent, which can obtain the algorithm performance while effectively lightening the attack success rate. The diagram of the proposed method is illustrated in Figure 2.

FIGURE 2

FIGURE 2. Deep reinforcement learning.

5.1 Network structure

Two neural networks are introduced for different objectives in this paper: 1) a value evaluation network Q (s^t, a^t; θ) for evaluating the performance of employed action policy under state given and 2) a target network Q′(s^t, a^t; θ′) for stabilizing the policy training process.

Specifically, the output of the value evaluation network is an estimation of cumulative reward function $E\left[{\sum }_{\tau =t}^T{\gamma }^{\tau -1}{r}^t|s^t,a^t\right]$. The estimation methodology using neural networks prevents the reinforcement learning method from the curse of dimensionality that traditional tabular reinforcement learning methods face.

Recalling the Bellman equation in Eq. 20, the update target of the value evaluation network includes the evaluation network itself. It leads to the problem of instability when updating the evaluation network. To address this problem, the target network Q′(s^t, a^t; θ′) is proposed. When updating the evaluation network, the fixed target network is used to replace the Q-value estimation on the right side of Eq. (20). Furthermore, after certain times of evaluation network update, the parameters of the target network will be reset as the parameters of the value evaluation network. The details of the update mechanism will be introduced in Section 5.3.

5.2 Action selection

During each time step, the agent needs to first observe the state of the environment, and based on this, the agent selects the action with the aim to maximize the future cumulative reward. The critical part is to balance the relationship between the exploration and exploitation in action selection. If the agent explores the environment more, the convergence speed of the policy learning process will be inevitably reduced. Nevertheless, if the agent chooses to exploit existing knowledge deeply, it may be trapped in the sub-optimal policy.

To balance between the exploration and exploitation well, an annealing ϵ-greedy is used in this paper. At each time step t, the action chosen is determined based on a parameter ϵ, which varies from (0,1). The agent will choose a random action from the action space with probability ϵ to explore the environment. Otherwise, the agent selects the action $a^t=\underset{a}{argmax}Q(s^t,a;\theta )$ with probability 1 − ϵ for exploiting existing knowledge. During the early stage of optimal policy learning, the agent has relatively less knowledge about the environment, so the agent should explore the environment more than exploiting. Thus, the value of ϵ is set as a high value during the early stage. As the agent possesses more knowledge about the environmental dynamics, the weight of exploitation should be enlarged when selecting an action, and the value of ϵ should be reduced gradually. In implementation, the value of ϵ is initialized as ϵ_ini which is a relatively high value before the policy learning. At each training step, the value of ϵ minus an annealing parameter ϵ_dec until the value of ϵ is not larger than a small value ϵ_min.

5.3 Policy iteration mechanism

At each time step t, the interaction information between the agent and environment [s^t, a^t, r^t, s^t+1] is stored in an experience replay memory with size E_r. When updating, to ensure the property of independently identically distribution (i.i.d) of training data, a mini-batch of interaction data ${[s^{\tau },a^{\tau },r^{\tau },s^{\tau +1}]}_{\tau =1}^{N_p}$ is randomly selected from the experience replay memory as training data to update the network. N_p is the size of the mini-batch.

The value evaluation network Q (s^t, a^t; θ) is updated according to loss function as follows:

$L=\frac{1}{N_p}\sum _{i=1}^{N_p}\left[{\left(y-Q\left(s_{\tau },a_t;\theta \right)\right)}^2\right],(34)$

$y=r_{\tau }+\gamma \underset{a}{\max }Q\left(s_{\tau },a_{\tau };\theta \right).(35)$

In order to keep the stability of the policy learning process, the target network is updated via tracking the value evaluation network slowly. Specifically, the parameters of the target network are reset as the parameters of the value evaluation network at every D time step.

The training process of the DQN-based load hiding algorithm is summarized in Algorithm 1.

6 Performance evaluation

In this section, we conduct several comprehensive evaluations to verify the performance of our proposed method. In the following, at first, the evaluation settings are given. Then, the results of our proposed method are introduced. Finally, the comparison results are shown.

6.1 Evaluation settings

In the following evaluations, the EV-assisted demand response environment follows the following settings and assumptions. First, we assume that the method is deployed in a community [randomly selected 40 electricity users in the REDD dataset (Kelly and Knottenbelt, 2015)] in 1 day (24 time slots). In addition, there exists a parking lot to help with the demand response, which contains 20 parking spaces. The parking lot is equipped with V2G charging piles to satisfy the charging and discharging between EVs. There exist twelve 7-kWh charging piles and eight 30-kWh charging piles. The electric vehicle models and their proportions are shown in Table 2. Their electric power varies from 55 kWh to 100 kWh. The proportion is also reasonably assumed according to the sales of electric vehicles. Then, when a parking space is free, there is the probability of ɛ = .85 that an EV will enter the parking lot and park at that location at the next time slot. The model of EVs will follow the assumption of Table 2, and its arrival SoC follows the uniform distribution from 0 to 100, while the departure SoC follows the normal distribution from 15% to 85%.

TABLE 2

TABLE 2. EV models.

6.2 Reinforcement learning performance

First, we will show the performance of the reinforcement learning training process. As shown in Figure 3, we can see that when the training episode reaches about 1,000 rounds, the reward will converge quickly. Regarding Figures 3B, C, these two figures show the changes in two main components of reward. Similarly, we can see that the convergence speed is very fast. The reason for the fast convergence speed is that we simplify the action space so that the training process becomes simpler. In fact, we have tried to give each parking space an action. In this large-scale action space, there is no trend of convergence after 10,000 times of training. Meanwhile, after convergence, there still exists little penalty term. The reason behind this is the setting of the trade-off coefficient between the two awards. In order to completely eliminate the behaviors prohibited by the penalty term, we can appropriately increase the coefficient of the penalty term. From these results, we can see that our MDP model and reinforcement learning method can effectively solve the charging/discharging decision problem of EVs.

FIGURE 3

FIGURE 3. (A) Training process, (B) peak load shifting reward, and (C) penalty term.

6.3 Power grid performance

After verifying the feasibility and effectiveness of the proposed method in training, we will verify the actual performance of the proposed method in the power grid. In Figure 4A, we can see that the proposed method is likely to allow the electric vehicle to charge at a low load and discharge at a high load. Therefore, the effect of peak load shifting can be achieved. Specifically, in the area introduced before, our proposed method can reduce 10% of the peak load and improve over 50% of the valley load. Moreover, Figures 4B, C show the charging/discharging power in each time slot. The results show that in daily time, the charging behavior will be strictly limited. While during the night, in order to increase the valley load, the discharging behavior will be completely prohibited. Therefore, our method can effectively learn effective strategies to cut peak and fill valley.

FIGURE 4

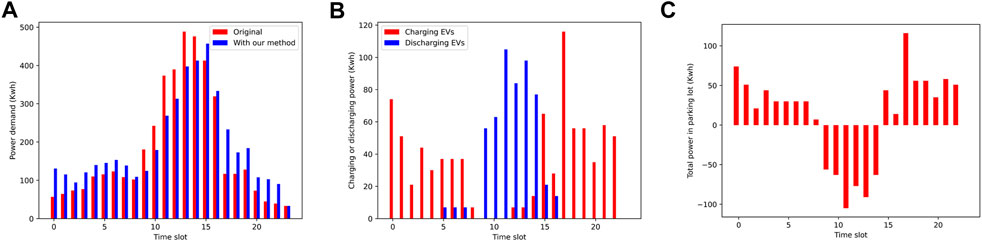
FIGURE 4. (A) Load curve, (B) charging/discharging volume, (C) and the difference between charging and discharging.

The aforementioned results show that at the overall level of the power grid, our method is conducive to achieving peak load shifting. Next, we will discuss the performance of our method in ensuring the future travel of individual EV owners. As shown in Table 3, we have verified the proportion of EVs that can leave the parking lot with enough SoC (satisfaction ratio) and the final SoC achievement rate of EVs that need to be charged under different numbers of parking spaces. It can be seen that almost all EVs can leave the parking lot with the target SoC, and almost all EVs that need to be recharged can satisfy their charging requirements. In addition, our method has similar efficiency in dealing with parking spaces of different sizes because we have classified and simplified the action space, thus reducing the coupling between each action and increasing the effectiveness of the strategy.

TABLE 3

TABLE 3. Satisfaction ratio and SoC achievement rate.

In conclusion, our method achieves the effect of peak load shifting while ensuring individual demand.

6.4 Comparison

Finally, we will compare our method with other methods, such as the offline optimization method and the random method (i.e., freely charging and discharging). Regarding Figure 5, it can be demonstrated that the offline optimization method has a certain peak shaving effect but does not perform as well as our proposed method. For the random method, it will not greatly change the demand response of the grid because there are electric vehicles that need to be charged or discharged at every moment, and their loads will offset each other. While regarding the satisfaction ratio, the result of the offline optimization method is similar to that of the proposed method. The random method has no restriction on the user’s behavior, so it will be equal to 1. It is not very different from the 90% achieved by our method, and it is completely acceptable.

FIGURE 5

FIGURE 5. Comparison: load curve.

All in all, our proposed method has a good effect in terms of convergence speed, load-shifting performance, and EV satisfaction ratio, and it also performs better than other methods.

7 Conclusion

In our paper, addressing the problem of demand response in a small area, we proposed a reinforcement learning-based method for an EV-assisted demand response management system to determine the best charging/discharging strategy. Specifically, we formalized the EV charging/discharging strategy determination problem as a Markov decision process (MDP), and the MDP model is constructed as follows: the state space mainly consists of occupation and charging speed of charging piles, current SoC, departure SoC, battery capacity, departure time of EVs, etc. The action refers to the EV charging/discharging behavior in each charging pile. We use a sliding average load method to represent the reward about the peak load shifting effect, and we set a series of penalty terms to ensure the departure SoC is enough for the next travel. Then, we proposed a DQN-based reinforcement learning architecture to solve this problem. Finally, the evaluation based on the real world shows that our method can effectively help regional peak load shifting and has better performance than the random scheduling and offline optimization methods.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

DL (first author): conceptualization, methodology, investigation, results analysis, and writing—original draft; QY (corresponding author): conceptualization, supervision, and writing—review and editing; YW: survey of methods and simulation; YZ: simulation; XL: analysis of results; LM: data processing and writing—review and editing.

Funding

The work was supported in part by the Key Research and Development Program of Shaanxi under Grant 2022GY-033, in part by the National Science Foundation of China under Grants 61973247, 62203350, and 61673315, in part by China Postdoctoral Science Foundation 2021M692566, and in part by the operation expenses for universities’ basic scientific research of central authorities xzy012021027.

Conflict of interest

Authors LM and XL were employed by State Grid Information & Telecommunication Group Co., LTD., China.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Althaher, S., Mancarella, P., and Mutale, J. (2015). Automated demand response from home energy management system under dynamic pricing and power and comfort constraints. IEEE Trans. Smart Grid 6, 1874–1883. doi:10.1109/TSG.2014.2388357

CrossRef Full Text | Google Scholar

Cui, B., Gao, D.-c., Xiao, F., and Wang, S. (2017). Model-based optimal design of active cool thermal energy storage for maximal life-cycle cost saving from demand management in commercial buildings. Appl. Energy 201, 382–396. doi:10.1016/j.apenergy.2016.12.035

CrossRef Full Text | Google Scholar

Eksin, C., Deliç, H., and Ribeiro, A. (2015). Demand response management in smart grids with heterogeneous consumer preferences. IEEE Trans. Smart Grid 6, 3082–3094. doi:10.1109/TSG.2015.2422711

CrossRef Full Text | Google Scholar

Emadi, A., Lee, Y. J., and Rajashekara, K. (2008). Power electronics and motor drives in electric, hybrid electric, and plug-in hybrid electric vehicles. IEEE Trans. Ind. Electron. 55, 2237–2245. doi:10.1109/TIE.2008.922768

CrossRef Full Text | Google Scholar

Fang, X., Misra, S., Xue, G., and Yang, D. (2012). Smart grid — the new and improved power grid: A survey. IEEE Commun. Surv. Tutorials 14, 944–980. doi:10.1109/SURV.2011.101911.00087

CrossRef Full Text | Google Scholar

Gungor, V. C., Sahin, D., Kocak, T., Ergut, S., Buccella, C., Cecati, C., et al. (2011). Smart grid technologies: Communication technologies and standards. IEEE Trans. Ind. Inf. 7, 529–539. doi:10.1109/TII.2011.2166794

CrossRef Full Text | Google Scholar

Hua, H., Qin, Y., Hao, C., and Cao, J. (2019). Optimal energy management strategies for energy internet via deep reinforcement learning approach. Appl. energy 239, 598–609. doi:10.1016/j.apenergy.2019.01.145

CrossRef Full Text | Google Scholar

Jeddi, B., Mishra, Y., and Ledwich, G. (2021). Distributed load scheduling in residential neighborhoods for coordinated operation of multiple home energy management systems. Appl. Energy 300, 117353. doi:10.1016/j.apenergy.2021.117353

CrossRef Full Text | Google Scholar

Kaelbling, L. P., Littman, M. L., and Moore, A. W. (1996). Reinforcement learning: A survey. J. Artif. Intell. Res. 4, 237–285. doi:10.1613/jair.301

CrossRef Full Text | Google Scholar

Karapetyan, A., Khonji, M., Chau, S. C.-K., Elbassioni, K., Zeineldin, H., El-Fouly, T. H. M., et al. (2021). A competitive scheduling algorithm for online demand response in islanded microgrids. IEEE Trans. Power Syst. 36, 3430–3440. doi:10.1109/TPWRS.2020.3046144

CrossRef Full Text | Google Scholar

Kelly, J., and Knottenbelt, W. (2015). “Neural nilm: Deep neural networks applied to energy disaggregation,” in Proceedings of the 2nd ACM international conference on embedded systems for energy-efficient built environments, 55–64.

Google Scholar

Kikusato, H., Mori, K., Yoshizawa, S., Fujimoto, Y., Asano, H., Hayashi, Y., et al. (2019). Electric vehicle charge–discharge management for utilization of photovoltaic by coordination between home and grid energy management systems. IEEE Trans. Smart Grid 10, 3186–3197. doi:10.1109/TSG.2018.2820026

CrossRef Full Text | Google Scholar

Lange, S., and Riedmiller, M. (2010). “Deep auto-encoder neural networks in reinforcement learning,” in The 2010 international joint conference on neural networks (IJCNN) (IEEE), 1–8.

CrossRef Full Text | Google Scholar

Li, D., Yang, Q., Yu, W., An, D., Zhang, Y., and Zhao, W. (2019). Towards differential privacy-based online double auction for smart grid. IEEE Trans. Inf. Forensic. Secur. 15, 971–986. doi:10.1109/tifs.2019.2932911

CrossRef Full Text | Google Scholar

Li, D., Yang, Q., Yu, W., An, D., Zhang, Y., and Zhao, W. (2020). Towards differential privacy-based online double auction for smart grid. IEEE Trans. Inf. Forensic. Secur. 15, 971–986. doi:10.1109/TIFS.2019.2932911

CrossRef Full Text | Google Scholar

Lillicrap, T. P., Hunt, J. J., Pritzel, A., Heess, N., Erez, T., Tassa, Y., et al. (2015). Continuous control with deep reinforcement learning. arXiv preprint arXiv:1509.02971.

Google Scholar

Lin, B., and Zhu, J. (2020). Chinese electricity demand and electricity consumption efficiency: Do the structural changes matter? Appl. Energy 262, 114505. doi:10.1016/j.apenergy.2020.114505

CrossRef Full Text | Google Scholar

Littman, M. L. (1994). “Markov games as a framework for multi-agent reinforcement learning,” in Machine learning proceedings 1994. Editors W. W. Cohen, and H. Hirsh (San Francisco (CA): Morgan Kaufmann), 157–163. doi:10.1016/B978-1-55860-335-6.50027-1

CrossRef Full Text | Google Scholar

Liu, T., Hu, X., Li, S. E., and Cao, D. (2017). Reinforcement learning optimized look-ahead energy management of a parallel hybrid electric vehicle. Ieee. ASME. Trans. Mechatron. 22, 1497–1507. doi:10.1109/tmech.2017.2707338

CrossRef Full Text | Google Scholar

Liu, W., Qi, D., and Wen, F. (2019). Intraday residential demand response scheme based on peer-to-peer energy trading. IEEE Trans. Ind. Inf. 16, 1823–1835. doi:10.1109/tii.2019.2929498

CrossRef Full Text | Google Scholar

Lopes, J. A. P., Soares, F. J., and Almeida, P. M. R. (2011). Integration of electric vehicles in the electric power system. Proc. IEEE 99, 168–183. doi:10.1109/JPROC.2010.2066250

CrossRef Full Text | Google Scholar

Madawala, U. K., and Thrimawithana, D. J. (2011). A bidirectional inductive power interface for electric vehicles in v2g systems. IEEE Trans. Ind. Electron. 58, 4789–4796. doi:10.1109/TIE.2011.2114312

CrossRef Full Text | Google Scholar

Medina, J., Muller, N., and Roytelman, I. (2010). Demand response and distribution grid operations: Opportunities and challenges. IEEE Trans. Smart Grid 1, 193–198. doi:10.1109/TSG.2010.2050156

CrossRef Full Text | Google Scholar

Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A., Antonoglou, I., Wierstra, D., et al. (2013). Playing atari with deep reinforcement learning. arXiv preprint arXiv:1312.5602.

Google Scholar

Ota, Y., Taniguchi, H., Nakajima, T., Liyanage, K. M., Baba, J., and Yokoyama, A. (2012). Autonomous distributed v2g (vehicle-to-grid) satisfying scheduled charging. IEEE Trans. Smart Grid 3, 559–564. doi:10.1109/TSG.2011.2167993

CrossRef Full Text | Google Scholar

Palensky, P., and Dietrich, D. (2011). Demand side management: Demand response, intelligent energy systems, and smart loads. IEEE Trans. Ind. Inf. 7, 381–388. doi:10.1109/TII.2011.2158841

CrossRef Full Text | Google Scholar

Qian, T., Shao, C., Wang, X., and Shahidehpour, M. (2020). Deep reinforcement learning for ev charging navigation by coordinating smart grid and intelligent transportation system. IEEE Trans. Smart Grid 11, 1714–1723. doi:10.1109/TSG.2019.2942593

CrossRef Full Text | Google Scholar

Tang, R., Li, H., and Wang, S. (2019). A game theory-based decentralized control strategy for power demand management of building cluster using thermal mass and energy storage. Appl. Energy 242, 809–820. doi:10.1016/j.apenergy.2019.03.152

CrossRef Full Text | Google Scholar

Wan, Z., Li, H., He, H., and Prokhorov, D. (2019). Model-free real-time ev charging scheduling based on deep reinforcement learning. IEEE Trans. Smart Grid 10, 5246–5257. doi:10.1109/TSG.2018.2879572

CrossRef Full Text | Google Scholar

Wang, S., Bi, S., and Zhang, Y.-J. A. (2018). Demand response management for profit maximizing energy loads in real-time electricity market. IEEE Trans. Power Syst. 33, 6387–6396. doi:10.1109/TPWRS.2018.2827401

CrossRef Full Text | Google Scholar

Wu, Q., Liu, W., Yang, Y., Zhao, C., and Yong, L. (2007). “Intelligent decision support system for power grid dispatching based on multi-agent system,” in International Conference on Power System Technology.

Google Scholar

Yang, Q., Li, D., An, D., Yu, W., Fu, X., Yang, X., et al. (2020). Towards incentive for electrical vehicles demand response with location privacy guaranteeing in microgrids. IEEE Trans. Dependable Secure Comput. 19, 131–148. doi:10.1109/tdsc.2020.2975157

CrossRef Full Text | Google Scholar

Zhang, F., Yang, Q., and An, D. (2020). Cddpg: A deep-reinforcement-learning-based approach for electric vehicle charging control. IEEE Internet Things J. 8, 3075–3087. doi:10.1109/jiot.2020.3015204

CrossRef Full Text | Google Scholar

Zhang, D., Zhu, H., Zhang, H., Goh, H. H., Liu, H., and Wu, T. (2022). Multi-objective optimization for smart integrated energy system considering demand responses and dynamic prices. IEEE Trans. Smart Grid 13, 1100–1112. doi:10.1109/TSG.2021.3128547

CrossRef Full Text | Google Scholar

Zhang, Y., Yang, Q., An, D., Li, D., and Wu, Z. (2022). “Multistep multiagent reinforcement learning for optimal energy schedule strategy of charging stations in smart grid,” in IEEE Transactions on Cybernetics, 1–14. doi:10.1109/TCYB.2022.3165074

PubMed Abstract | CrossRef Full Text | Google Scholar