A review of time reversal-based methods applied to fault location in power networks

Electromagnetic time reversal (EMTR)-based methods have been applied to the problem of fault location in power networks since 2012. Over the past decade, considerable theoretical investigations have led to a continuous improvement of the EMTR method in terms of fault location accuracy and efficiency. Meanwhile, different full-scale experiments, including pilot tests, were carried out, demonstrating the applicability and robustness of the EMTR method when applied to real power-system environments. This paper presents a review of the foregoing theoretical and experimental studies. Furthermore, suggestions for future studies are propounded, along with discussing various challenging research questions that still need to be addressed.

1 Introduction

Time reversal has received increased attention during the past three decades as a method for source location/identification and has been successfully applied to various areas of engineering [e.g., Blomgren et al. (2002), Fink et al. (2003), Lerosey et al. (2007), Lemoult et al. (2011), Bacot et al. (2016), Rachidi et al. (2017)]. One of the areas in which the electromagnetic time reversal (EMTR) technique is applied is the problem of fault location in electrical power systems Manesh et al. (2012).

Electricity transmission and distribution networks are prone to various types of faults (e.g., single/three phase-to-ground faults) due to various potential causes, such as weather-related events (e.g., lightning, storms, freezing rain) or technical failures (e.g., insulation deterioration or breakdown). In this regard, reliable and efficient fault location techniques are of vital importance in electrical power systems to ensure the security and quality of electricity supply Saha et al. (2009), IEEE Std C37.114-2004 (2015), Furse et al. (2021). Within this context, various solutions have been proposed for the fault location problem since the 1950s Stringfield et al. (1957). They can be clustered in two main categories of fault location methods: 1) impedance- (or phasor-) based methods [e.g., Izykowski et al. (2011), Majidi and Etezadi-Amoli (2018)] and 2) traveling wave- (or high-frequency component-) based methods [e.g., Lopes et al. (2019), Naidu et al. (2019), de Magalhaes Junior and Lopes (2022)].

In 2012, the time-reversal technique was for the first time applied to address the fault location problem Manesh et al. (2012). Thanks to significant worldwide studies since then, the EMTR-based fault location method is nowadays considered as a reliable method that belongs to the category of traveling wave-based methods. By virtue of the inherent focusing property of the time-reversed back-injected waves (e.g., those associated with the fault-originated transients) onto the original source, the EMTR method has been shown to possess a number of advantages over classical traveling wave-based methods, such as its straightforward applicability to inhomogeneous media (i.e., mixed overhead and coaxial power cable lines), the potential use of a single observation (measurement) point, and no need for dedicated processing applied to fault-originated transients for wavefront arrival time detection.

The present paper covers both theoretical investigations and experimental activities. We first present for the novice reader the basics of the theoretical foundations of time reversal (Section 2). The application of EMTR to the fault location problem in power networks is discussed in Section 3. In particular, the specificities of the EMTR method compared to other traveling wave-based methods are discussed. Also, two subcategories of EMTR-based fault location methods (considering matched and mismatched media, respectively) are introduced. In Section 4 and Section 5, the two subcategories of EMTR methods are respectively reviewed, presenting their general features and discussing the metrics used to locate the focal point of the backward-propagated waves (which corresponds to the fault location). Experimental studies of the EMTR method using realistic-scale power networks are summarized in Section 6. Finally, Section 7 presents a discussion about the outstanding challenges of EMTR when applied to the fault location problem, mainly including: 1) the effect of imperfect knowledge of power network parameters (e.g., soil electrical parameters), 2) the effect of losses, 3) the need for appropriate signal processing to quantify the refocusing of the backward-propagating wave to the fault location, and 4) the need of further theoretical investigation for the EMTR method in mismatched media.

2 Time reversal operation and its focusing property

The concept of time reversal can be interpreted from different perspectives. It involves a fundamental operation consisting of reversing in time a given time-dependent physical quantity s(t), namely

$s\left(t\right)\stackrel{\mathrm{T}\mathrm{R}}{⟼}s\left(-t\right).(1)$

s(t) is a real and causal function with compact support in the sense that it is defined on a finite time interval $\left[0,T_s\right]$ such that

$s\left(t\right)=0,\left(t<0,\mathrm{a}\mathrm{n}\mathrm{d}t>T_s\right).(2)$

The time-domain operation of reversing s(t) corresponds to the complex conjugate operation in the frequency domain (denoted by the symbol *):

$S\left(j\omega \right)\stackrel{\mathrm{T}\mathrm{R}}{⟼}{\left[S\left(j\omega \right)\right]}^{*},(3)$

with S (jω) being the Fourier transform of s(t).

Note that, to ensure causality, the time-reversal operation in the time domain is more practically carried out through

$s\left(t\right)\stackrel{\mathrm{T}\mathrm{R}}{⟼}s\left(T-t\right),(4)$

where T is the temporal length of the time window over which s(t) is observed, satisfying T⩾T_s.

The spread of time reversal in contemporary scientific and engineering communities largely stems from the comprehensive theoretical and experimental study on the time-reversal inherent focusing property in the early 1990s Cassereau and Fink (1992), Fink (1992), Fink (1993), Wu et al. (1992). Specifically, for waves (e.g., acoustic or electromagnetic) generated by a point source and possibly reflected, scattered, and distorted in given propagative media, the focusing property states that time-reversed measured waves, being back injected into the same medium where the forward propagation occurred, would retrace the originally followed paths and eventually converge in synchrony on the initial source location as if the time goes backward.

A time-reversal cavity is proposed as a two-step procedure to achieve the time reversal focusing property Fink (1992). As illustrated in Figure 1A, a closed surface in three dimensions is assumed to enclose a point-like source (red circle) and its surrounding medium, which can be inhomogeneous (the green region illustrates the presence of scatterers)¹. In the forward-propagation stage (also named the recording step or direct time²), the source-generated and distorted (by the surrounding inhomogeneous medium) waves are recorded by an infinite number of elementary transducers located on the imaginary surface of the cavity. In the backward-propagation stage (also named the reconstructing step or reversed time, see Figure 1B), those recorded waves are time reversed and back injected to propagate inward from the respective elementary transducers at the cavity surface. The resulting wave is a time-reversed copy of the original one and would finally converge back to the source location.

FIGURE 1

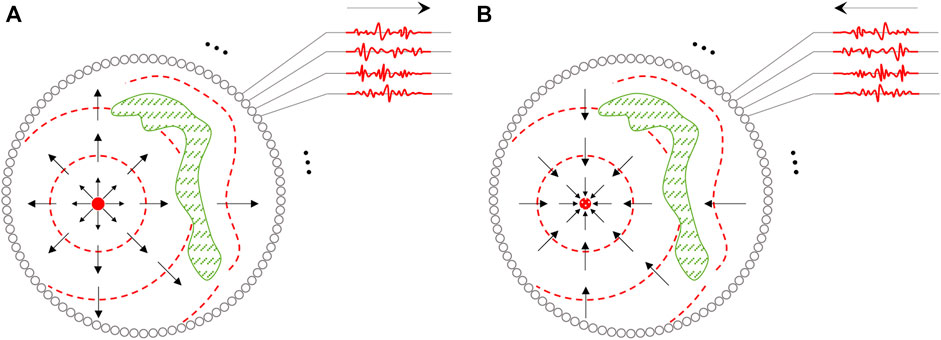
FIGURE 1. Two-dimensional illustration of a time-reversal cavity for (A) forward-propagation stage: recording step and (B) backward-propagation stage: reconstructing step [adopted from Fink (1992)].

It can be noticed that a time-reversal cavity is a conceptual description that appears quite challenging to be implemented in reality since it theoretically requires an infinite number of measurements over the surface of the cavity. In practice, a time-reversal cavity is alternatively realized by means of a one/two-dimensional transducer array constituting the so-called time-reversal mirror Fink (1992), Fink (1993). As a consequence, a time-reversal mirror makes use of a limited number of transducers. It is shown that proper spatial distribution of the transducers on a limited angular aperture to sample sufficient wavefronts renders the focusing property achievable in practice Wu et al. (1992).

3 Electromagnetic time reversal applied to fault location in power networks

After the foundation studies in the field of acoustics, time reversal was later introduced into the field of electromagnetic waves under the general denomination of electromagnetic time reversal (EMTR) Lerosey et al. (2004), Carminati et al. (2007), de Rosny et al. (2010) and has been regarded as a promising technique in localizing electromagnetic transient sources Rachidi et al. (2017). Representative applications of EMTR include medical imaging [e.g., Kosmas and Rappaport (2005)], target detection [e.g., Mukherjee et al. (2017)], lightning discharge localization [e.g., Lugrin et al. (2014), Mostajabi et al. (2019)], soft fault location in wires [e.g., Kafal et al. (2016)], localization of electromagnetic interference sources [e.g., Karami et al. (2021a), Karami et al. (2021b), Li et al. (2021)], localization of partial discharges [e.g., Azadifar et al. (2020), Ragusa et al. (2022)], and locating faults in electrical power systems [e.g., Manesh et al. (2012)].

The EMTR-based fault location method is carried out in two steps corresponding to the forward- and backward-propagation stages, respectively. The procedure is described in detail below.

1) Forward-propagation stage: a fault occurrence generates traveling waves that propagate from the fault location towards power network terminals. The fault-originated transients are measured at a number of observation points situated at the terminals (i.e., sensors are generally distributed at the substations located at the power network terminals) or, in case, at other user-defined points.

2) Backward propagation stage: first, the measured transients are time reversed. Then, the backward propagation is numerically simulated by back injecting the time-reversed transients into a model of the targeted power network. The modeling and simulation can be performed either in the frequency domain using analytical formulae [e.g., BLT equations Tesche et al. (1996)] or in the time domain using time-domain simulation tools [e.g., the EMTP-RV as done in Mahseredjian et al. (2007)] or the finite-difference time-domain (FDTD) method [e.g., Sun et al. (2022a)]. Finally, the unknown fault location is determined using an appropriate criterion or metric to quantify the refocusing of the backward-propagating waves.

It is evident that the EMTR-based fault location method is, in essence, dependent on post-fault traveling wave processes. Consequently, it keeps the advantages of traveling wave-based fault location methods, such as insensitivity to fault characteristics (i.e., fault type and impedance) and robustness against power-frequency boundary conditions (e.g., current transformers saturation and power-frequency injections from dispersed energy resources). Meanwhile, the EMTR method benefits from the inherent focusing property of time reversal, thus bringing additional advantages that are briefly summarized and explained in what follows.

Firstly, the EMTR method can be applied using a single observation point even with the presence of inhomogeneity and multiple branches in power networks. Draeger and Fink (1997) demonstrated the possibility of achieving the time-reversal focusing property using a single-channel (end) measurement in a closed reflective cavity. A power network is conventionally connected at its terminals to electrical equipment (e.g., power transformers) featuring high input impedance Greenwood (1991). Therefore, those terminals behave approximately as open circuits for the incident traveling waves initiated by a fault, resulting in the boundary conditions being quasi-fully reflective. Moreover, the more complex the propagative medium, such as a high degree of inhomogeneity or multiple scattering, the better the time-reversal focusing quality (e.g., a higher resolution) Derode et al. (1995), Derode et al. (2003). It is worth mentioning that power networks consisting of multiple conductors (e.g., three-phase systems) are generally configured in a topology involving multiple laterals and junctions. Moreover, power networks are increasingly constructed in a mixed pattern of overhead lines and underground cables and thus are inherently inhomogeneous media.

Another noticeable feature of the EMTR method lies in its wide applicability to different power networks. According to the existing publications, the EMTR method has been applied to both electrical power transmission and distribution systems, including diverse application scenarios, such as high-voltage direct current (HVDC) networks [e.g., Razzaghi et al. (2014), Zhang et al. (2017), Li et al. (2018), Tailor and Ukil (2019)], series-compensated transmission lines [e.g., Razzaghi et al. (2013b)], medium-voltage (MV) underground cable networks [e.g., da Costa et al. (2020), Kafal et al. (2021b)], and radial distribution networks [e.g., Razzaghi et al. (2013a), He et al. (2020a), Wang et al. (2020a)].

Lastly, as explained earlier, the EMTR method can be classified into the category of traveling wave-based fault location methods. It is worth further clarifying that the focus of the EMTR method is the processing of the full waveform of fault-originated transients rather than the wavefront arrival time as in classical time-of-arrival (ToA) methods. The precise estimation of the arrival instants of the reflected waves (either from the fault location or other line terminals) can be challenging in some realistic fault scenarios, such as the case featuring a small fault inception angle or high fault impedance. The EMTR method, on the other hand, has been proven to be effective in such cases [e.g., Wang et al. (2020b), An et al. (2021), Wang et al. (2022)].

During the past decade, the EMTR-based fault location methodology has been largely enriched with various fault location metrics, which can be classified into two main subcategories: 1) the matched EMTR-based fault location method, in which the medium in the direct time and reversed time are identical (see Section 4), and 2) the mismatched EMTR method, which involve a reversed-time medium with characteristics being (to a certain extent) different from the ones of the (original) medium in the direct time (see Section 5). The latter is motivated to eliminate the need for multiple simulations of fault currents at guessed fault locations and, thus, to reduce the computational time required in the backward-propagation stage. Furthermore, different types of full-scale experimental studies have been conducted, taking the initial step to incorporate the EMTR method into the daily operation of electrical power systems as a reliable and efficient fault location technique (see Section 6).

4 Matched electromagnetic time reversal-based fault location method

4.1 General considerations

One of the fundamental hypotheses of time reversal is the so-called matched media condition, which states that the propagative media in the stages of forward (direct time) and backward (reversed time) propagation are identical Fink (1992). Within the context of fault location, the matched-media condition entails simulating a fault event at a guessed fault location x_g in the backward-propagation stage, as schematically delineated in Figures 2A,B. If the guessed fault location x_g coincides with the true fault location x_f, then the two media are matched. Given this, a set of a priori guessed fault locations are first defined to allow simulating a fault occurrence at each of those locations. The spatial reciprocity then determines that the matched-media condition is satisfied if and only if x_g coincides with x_f.

FIGURE 2

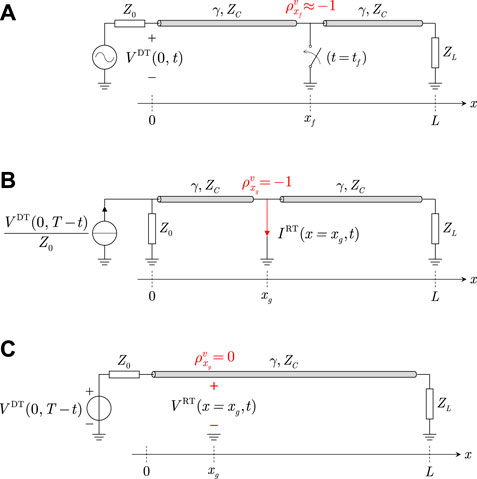
FIGURE 2. Schematic representation of (A) a fault occurrence along transmission lines and the application of EMTR to locate the fault based on the conditions of: (B) matched media and (C) mismatched media. ${\rho }_{x_f}^v$ and ${\rho }_{x_g}^v$ are the voltage reflection coefficients at the fault location x = x_f and the guessed fault location x = x_g, respectively. Z₀ (Z_L) is the input impedance of terminal power equipment [adapted from (Wang et al. (2022)].

From another perspective, the matched-media condition is, in essence, aimed at achieving the match or identity between the respective transfer functions in the frequency domain (or impulse responses in the time domain) pertaining to the forward- and backward-propagation stages. Consider the two-port representation of a fault event in Figure 3A. A fault occurrence at an assumed fault location x_f is simulated by injecting a voltage V_f(jω), which is proposed to be a step or double-exponential function Razzaghi et al. (2013a), He et al. (2020a). Then, the transfer function in the forward propagation stage H^DT (jω) is the ratio of the measured response V^DT (0, jω) to the excitation V_f(jω):

$H^{\text{DT}}\left(j\omega \right)=V^{\text{DT}}\left(0,j\omega \right)/V_f\left(j\omega \right).(5)$

FIGURE 3

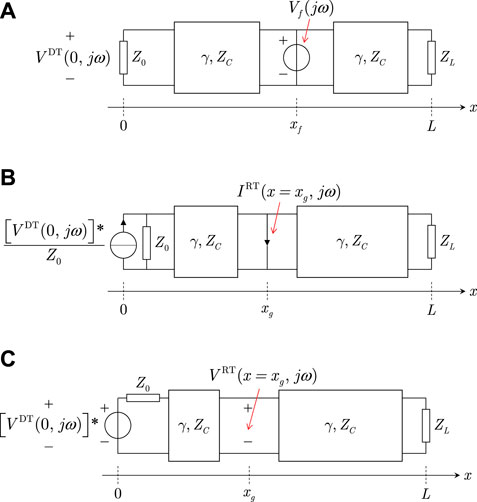
FIGURE 3. Two-port representation of (A) a fault occurrence along transmission lines and the application of EMTR to locate the fault based on the conditions of: (B) matched media and (C) mismatched media.

Similarly, in the backward propagation stage (see Figure 3B), the transfer function corresponding to a guessed fault location H^RT(x = x_g, jω) is the output-input ratio of I^RT(x = x_g, jω) to ${[V^{\text{DT}}(0,j\omega )]}^{*}/Z_0$:

$H^{\text{RT}}\left(x=x_g,j\omega \right)=I^{\text{RT}}\left(x=x_g,j\omega \right)/\left\{{\left[V^{\text{DT}}\left(0,j\omega \right)\right]}^{*}/Z_0\right\}.(6)$

The matched-media condition, namely

$H^{\text{DT}}\left(j\omega \right)=H^{\text{RT}}\left(x=x_g,j\omega \right),(7)$

holds for x_g = x_f.

4.2 Focusing/location metrics

As mentioned in Section 3, the backward-propagation stage of EMTR requires an appropriate metric to quantify the refocusing of the backward-propagating waves. The proposed metrics in the context of the matched EMTR-based fault location method explore certain features pertaining to the fault current to estimate a most-likely fault location. They are briefly described in what follows.

The fault current signal energy (FCSE) was proposed by Razzaghi et al. (2013a) in the earliest systematic application of EMTR to the fault location problem in power networks. The FCSE metric utilizes the maximum energy concentration of the fault current signal to identify the true fault location. Razzaghi et al. (2013a), Razzaghi et al. (2013b), Razzaghi et al. (2014) performed comprehensive simulations considering different power networks, which not only validated the broad applicability of the FCSE metric but also revealed the earlier-mentioned advantages provided by the EMTR-based fault location method.

He et al. (2018) presented a comparison of two time-reversal focusing metrics, namely the 2-norm (energy) and ∞-norm (maximum amplitude). They proposed the maximum amplitude of the fault current signal as an alternative fault location metric, which stems from the dual spatial and temporal focus of fault-originated transients at the original fault location He et al. (2018). The maximum amplitude metric was shown to be more robust against noise in measurements in comparison with the FCSE metric.

He et al. (2020a) proposed a correlation metric to identify the fault location. The correlation metric consists of a direct quantitative evaluation of the similarity between H^DT (jω) and H^RT(x, jω) by means of a linear inner product of the two transfer functions, being aimed at improving the location reliability in complex power networks He et al. (2020a). This metric takes into account that the signal energy might notably reduce when the back-injected transients propagate through line junctions (this issue was also observed by Razzaghi et al. in their first publications). In 2021, Cozza et al. (2021b) proposed an inverse filtering surge compression method, which was shown to be capable of using a relatively low sampling rate (can be as low as 100 ksps) to estimate the transfer functions from fault transient signals. Besides, He et al. (2020b) discussed the spatial resolution of the correlation metric, which was defined using the theory of Fabry-Pérot interferometers as the minimum shift from the true fault location to an adjacent guessed fault location induced by the minimum variation between their corresponding resonance frequencies. They analyzed the spatial resolution from the perspective of resonance systems regarding fault location sensitivity and coherence bandwidth, and proved that using the entire frequency bandwidth of fault-originated transient signal would limit the spatial resolution. A careful selection of resonance frequencies involved in the calculation of the metric thus improves its fault location accuracy and spatial resolution.

Wang et al. (2020a), Wang et al. (2018b) elucidated the similarity between H^DT (jω) and H^RT(x, jω) with a particular focus on the components intrinsic to the fault-switching frequency (which depends on the propagative path from the fault location to a given observation point) and its odd harmonics (also named natural or resonance frequencies) Chen et al. (2019). An integrated time-frequency analysis indicated that the similarity between the transfer functions implies that the fault current signal at the true fault location behaves as a quasi-scaled and lagged copy of the time-reversed fault-originated transients. A cross-correlation metric was proposed to quantify the degree of the time-domain similarity and, thus, identify the true fault location. The similarity metric was numerically validated and later applied in a live pilot test (see Section 6).

5 Mismatched electromagnetic time reversal-based fault location method

5.1 General considerations

Relative to the classical implementation of time reversal (i.e., in matched media), the concept of mismatched media refers to the condition where time-reversed waves are back injected and propagate through a medium that is partly different from the original medium in the forward-propagation stage Liu et al. (2007), Wang et al. (2021).

As illustrated in Figure 2C, the fundamental consideration of the EMTR-based fault location method in lumped mismatched media lies in assuming that the targeted power network remains non-faulty in the backward-propagation stage, therefore excluding the need for multiple simulations of fault events at guessed fault locations. The absence of the transverse branch associated with the fault results in a mismatch between the forward- and backward-propagation media. Specifically, the boundary condition at the fault location changes from the state of fault (i.e., ${\rho }_{x_g}^v=-1$) to that of non-fault (i.e., ${\rho }_{x_g}^v=0$). This also constitutes a lumped mismatch in the sense that the propagative parameters and the boundary conditions at the line terminals of the targeted power network remain intact.

Such lumped mismatched media also serves the purpose of a computationally efficient fault location process, given that the multiple independent simulations (at guessed fault locations) are no longer required in the backward-propagation stage. Therefore, instead of evaluating the fault current as in the matched EMTR method, the voltage V^RT(x, jω) is processed as the characteristic quantity to infer the true fault location (see Figure 2C).

Within the framework mentioned above, a direct-reversed-time transfer function H (x, jω) is formulated to relate the output function V^RT(x, jω) in the backward-propagation stage to the input V_f(jω) that emulates a fault occurrence in the forward-propagation stage Wang et al. (2022). More specifically,

$H\left(x,j\omega \right)=H^{\text{DT}}\left(j\omega \right){\left[H^{\mathrm{R}\mathrm{T},v}\left(x,j\omega \right)\right]}^{*},(8)$

with H^RT,v (x, jω) being the ratio of V^RT(x, jω) to ${[V^{\text{DT}}(0,j\omega )]}^{*}$ (see Figure 3C):

$H^{\mathrm{R}\mathrm{T},v}\left(x,j\omega \right)=V^{\text{RT}}\left(x,j\omega \right)/{\left[V^{\text{DT}}\left(0,j\omega \right)\right]}^{*}.(9)$

The superscript ‘v’ is added to distinguish H^RT,v (x, jω) from H^RT(x, jω) in Eq. 6 defined in the matched EMTR method.

5.2 Focusing/location metrics

By extending the focusing property of EMTR in lumped mismatched media to locate faults in power networks, Codino et al. (2017), Wang et al. (2017), Wang et al. (2022) reported a series of frequency- and time-domain properties of H (x, jω) that enable the determination of the true fault location.

First, Codino et al. (2017) mathematically proved a theorem that introduces the so-called bounded phase property. This property states that the phase angle of H (x, jω) is confined in the open interval (−π/2, π/2) exclusively when the observation point is exactly at the true fault location x_f. In other words, the real part of H (x_f, jω) is constantly positive over frequencies. By simulation case studies, the applicability of the bounded phase property to inhomogeneous and branched transmission line networks was demonstrated.

Wang et al. (2017), Wang et al. (2022) proposed and proved two other theorems related to the mirrored minimum squared modulus and energy of H (x, jω). The theorems state that, in correspondence of the fault switching frequency and its odd harmonics, the squared modulus of H (x, jω) reaches its minimum always at the mirror-image point of the true fault location with respect to the line center and, thus, the mirror-image point further corresponds to a global minimum of the energy of H (x, jω). Based on these theorems, the energy of V^RT(x, jω) was proposed as a fault location metric calculated through a data-driven algorithm. The algorithm contains a procedure to be executed prior to a fault event. It relies on constructing a database to index over a normalized copy of H^RT,v (x, jω) at a set of guessed fault locations. Wang et al. (2022) presented both numerical and experimental validations of the metric. Also, the data-driven algorithm was verified to be capable of accomplishing the fault location task online quasi-instantaneously after acquiring fault-originated transients.

Note that, in parallel with the data-driven algorithm proposed by Wang et al., He et al. (2020a), Wang and Zhuang (2022) also put forward, as an alternative to the conventional mode of offline stimulating the backward propagation, pre-calculating the corresponding transfer functions or fault current signals, which are independent of the physical measurements of fault-generated transients. In this way, the fault location metric can be evaluated using accumulated transfer functions or fault currents, thus dramatically accelerating the EMTR-based fault location process.

With respect to the challenging task of locating high-impedance faults, An et al. (2021), Sun et al. (2021), Sun et al. (2022b) proposed a modified algorithm to calculate the mirrored minimum energy metric. The algorithm requires two observation points to synchronously measure fault-originated transients at both ends of a targeted transmission line. The simulation of the backward propagation follows the conventional procedure involving the time reversal and back injection of both measured transient signals, with one of them multiplied by −1. The energy of either V^RT(x, jω) [i.e., An et al. (2021)] or the current flowing through a 1000-Ω grounding resistance [i.e., Sun et al. (2021), Sun et al. (2022b)] is calculated as a fault location metric. The results of simulation case studies suggested that the double-ended metric is more effective in locating high-impedance faults (impedances higher than 100 Ω) compared to the FCSE metric and the original mirrored minimum energy metric.

A similar effort to accelerate the backward-propagation process led to the so-called FasTR method Kafal et al. (2021a). The method returns to the essence of the time-reversal focusing property, characterizing the original source with the maximum spatial and temporal coherence using multiple synchronous measurements (i.e., no less than two). More specifically, the FasTR method constructs a cost function (e.g., voltage signal) at each guessed fault location resulting from the superposition of time-reversed measured signals being back-injected from the selected observations. The extremum or peak amplitude of the constructed signal is defined as a fault location metric. The FasTR method was shown to accurately identify the assumed fault location in a single/double Y-junction network of coaxial cables, at which a double-exponential voltage pulse was injected to emulate a fault event.

6 Experimental study of electromagnetic time reversal-based fault location method

Different types of full-scale experiments, including field experiments and pilot tests, have been performed worldwide in the past years, with particular attention to assessing the fault location performance of the EMTR method in real power-system environments. So far, three experimental studies have been reported in the literature Wang et al. (2018a), Wang et al. (2020b), Kafal et al. (2021a). Note that a series of reduced-scale experiments in laboratory environments were also conducted during the same period, providing a preliminary validation of some of the foregoing EMTR fault location metrics [e.g., Razzaghi et al. (2013a), He et al. (2018)]. It should be noted that the focus of this section is to review experimental studies conducted on real power networks (see Table 1).

TABLE 1

TABLE 1. Full-scale experiments validating the EMTR-based fault location method.

In 2016, EPFL and XJTU jointly conducted the first field experiment on a 677-m long overhead-line section of a 10-kV double-circuit power distribution network in Yuncheng city, Shanxi province, China Wang et al. (2018a). The experiment emulated a single-phase-to-ground fault by injecting a voltage pulse into one of the phase conductors when the targeted line was unenergized, whose set-up is schematically described in Figure 4A. The pulse waveform was designed to dominate a wide enough frequency band to cover the typical frequency spectrum of fault-generated transients. The experiment served to validate the EMTR-FCSE and -amplitude peak metrics. According to Wang et al. (2018a), He et al. (2018), both metrics are capable of accurately identifying the true fault location (i.e., Phase c of Tower No. 23).

FIGURE 4

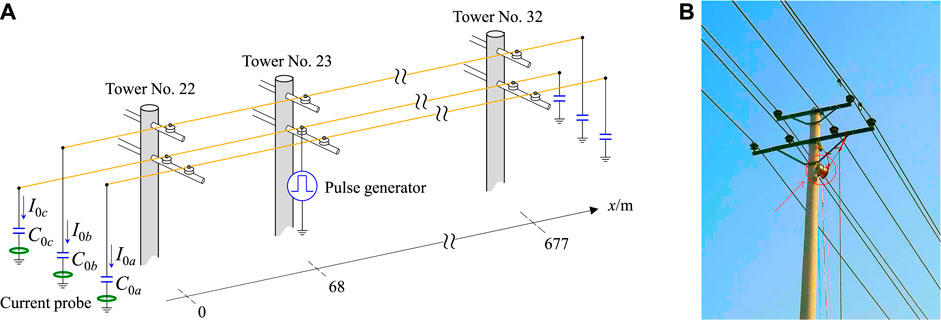
FIGURE 4. (A) Schematic description of the field experimental set-up configured using a 677-m long 10-kV overhead line spanning 11 towers (numbered 22–32). At the two terminal towers, the overhead lines were grounded through lumped capacitors (e.g., C_0a to C_0c), which were designed to emulate high-frequency impedance of power transformers. (B) Picture of Tower No. 23, where a pulse generator (marked with the red circle) was connected to one of the phase conductors [adapted from (Wang et al. (2018a)].

The full-scale experimental study carried out in Wang et al. (2018a) was focused on assessing the applicability of the EMTR method in real power network environments. The fact remains that a fault event in the experiment was considered equivalent to injecting a voltage pulse to emulate post-fault transient processes. Also, to acquire the transient signal, a measurement chain composed of discrete instruments (e.g., broadband current probes and oscilloscopes, as illustrated in Figure 4A) was used.

In 2017, Wang et al. (2020b) conducted a series of pilot tests on a radial MV distribution feeder in Switzerland, as illustrated in Figure 5. Wang et al. (2020b) realized the deployment of the EMTR method into a National Instruments CompactRIO embedded controller coupled with sensing and triggering units. The fault location system integrated the functions of fault detection, data acquisition, electromagnetic transients (EMT) simulations (through demanding the EMTP-RV), and EMTR-based fault location processing. A range of faults of very different natures was intentionally triggered when the pilot distribution network was under normal operating conditions. Specifically, both solid and resistive fault cases (with fault impedance up to 30 Ω) were included in the test. In addition to permanent faults consequent upon a short circuit (realized by a switching maneuver using MV switchgear), single and intermittent arcing discharges were triggered (using spark gaps), emulating transient fault events.

FIGURE 5

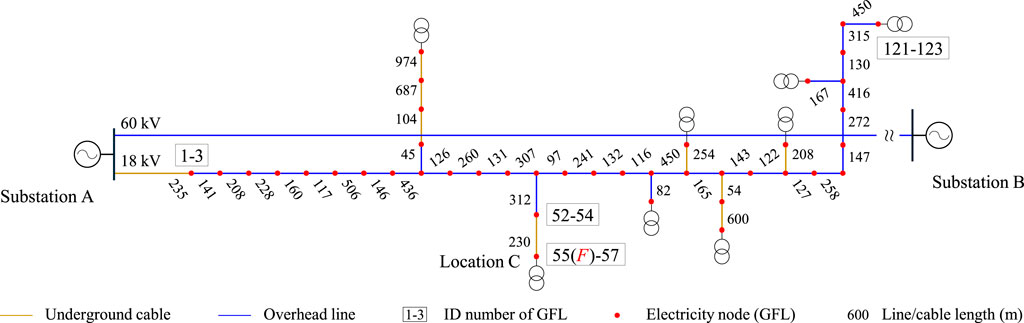
FIGURE 5. Schematic description of the pilot test set-up configured using a radial MV distribution feeder [adopted from (Wang et al. (2020b)]. The pilot network consisted of 11.9-km long double-circuit lines (overhead lines) operating at 18/60 kV and eight 18-kV three-phase laterals (overhead lines, underground cables, or mixed configuration). The MV side of the primary substation A served as the single observation point. The assumed fault location was the line-cable mixed lateral terminal indicated as Location C.

The EMTR-FCSE and cross-correlation metrics were validated in the experiments, effectively locating both the fault location and the faulty phase in all the tested fault cases especially reaching a resolution of 10 m, namely distinguishing the true fault location from its adjacent guessed locations when they are 10 m apart Wang et al. (2020a), Wang et al. (2020b), as shown in Figure 6.

FIGURE 6

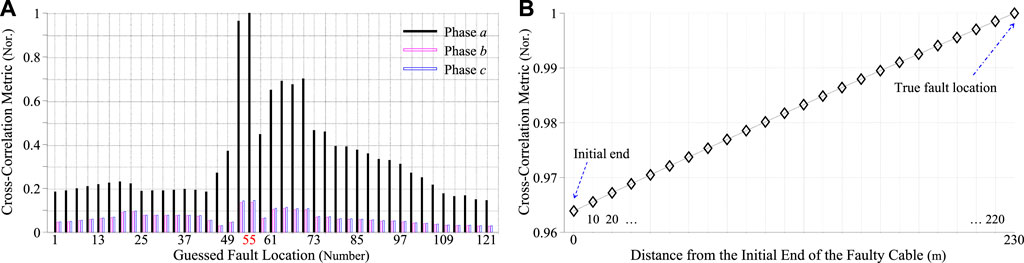
FIGURE 6. Normalized cross-correlation metric calculated for the solid phase (a)-to-ground fault in the pilot test as a function of (A) the guessed fault location and (B) the distance from the initial end (i.e., the guessed fault location numbered 52) of the 230-m faulty cable. The true fault location is numbered 55.

In 2021, Kafal et al. (2021b) reported a pilot test designed to validate the FasTR method in a realistic MV underground cable network in Switzerland. The pilot test utilized a 2.5-km long Y-shaped section of the cable network. Fault transient signals were generated by a manual switch operation of a circuit breaker. A fault location framework was also developed, coordinating distributed sensors (sharing a clock reference under the GPS protocol) and a fault location platform. The latter integrated a remote server communicating with the sensors to read measured transient signals and a computing unit executing the FasTR algorithm. The pilot test employed transient signals acquired by two sensors to construct the cost function, showing that the FasTR method provided an acceptable fault location accuracy with a minimum error of 27 m and a maximum of 54 m.

7 Outstanding challenges and suggestions for future research

In summary, the theoretical studies on the EMTR-based fault location method over the past decade successfully demonstrated the effective use of the time-reversal focusing property for the fault location problem by proposing various metrics and algorithms. Also, the applicability of the EMTR method in real fault scenarios was validated in real-scale pilot tests.

Despite the achieved significant results demonstrating the performance of the EMTR method, we identify in what follows some of the most salient research questions, which are still not fully addressed in the literature so far, and future directions for research are indicated.

It is essential to reiterate that the EMTR method belongs to the category of traveling-wave methods. The simulation of the backward propagation is based on an accurate numerical representation of the targeted power network with reference to its actual configuration and parameters. However, a complete knowledge of a power network is not always attainable. For example, soil parameters (e.g., resistivity) can vary in time (in light of weather conditions) and in space (along the geographical span of the network and/or horizontal stratification), and are a function of the frequency. The problem of inferring the line parameters, either from actual measurements or through applying appropriate parameter estimation techniques, is therefore of capital importance and should be the subject of future investigation.

In the strict sense, the Telegrapher’s equations governing voltage/current wave propagation along transmission lines are time-reversal invariant under the assumption of either lossless or inverted-lossy media Razzaghi et al. (2014). Razzaghi et al. showed that a lossy backward-propagation model can be used in the EMTR-based fault location method. Recently, Cozza et al. (2021a) studied the influence of both propagation and termination losses on the fault location performance of full transient-based traveling wave methods. It was concluded that a biased fault location result could be yielded when propagation losses become comparable to dissipation in termination impedances. It is therefore important to consider the issue of losses more thoroughly, especially when the targeted power network is characterized by salient topological complexity or/and lengthy transmission lines, such as a distribution system composed of multiple main feeders or a point-to-point long-distance HVDC transmission system.

One of the important steps in every EMTR-based algorithm for source location is the choice of an appropriate metric to quantify the refocusing of the backward-propagating waves. As discussed earlier, several metrics have been proposed in the literature for this purpose. The metrics involve the evaluation of the fault signal parameters (energy, peak, etc.) or the similarity between two transfer functions or waveforms. Prior to applying the metric, the fault-originated transients should undergo appropriate signal processing to extract the resonance-frequency components and remove other parts, such as the main steady-state low-frequency signal. Furthermore, the combined effect of propagation losses and strong inhomogeneity might pose a problem for some metrics, such as the correlation estimator and cross-correlation metrics, to extract the transfer functions and recognize the resonance frequency from fault-originated traveling waves. This issue requires further attention and needs to be addressed in future studies.

The traditional approach using the time reversal process is to apply its time correlation properties that are valid if and only if the wave propagation can be represented by a linear system of differential equations with time-invariant parameters. In case this hypothesis is no longer verified, there are no theorems that identify the conditions that, if satisfied, guarantee the existence and uniqueness of the time-reversal operation. In view of that, future research is needed to identify these conditions. The consequence of these findings is of universal value: it will be possible not only to improve the existing time reversal methods targeting the precise source location in inhomogeneous and non-linear media but also to solve the problem of the optimum sensing placement that maximizes the energy focalization in the reversed time and thus increases the accuracy of the source location.

The concept of EMTR in mismatched media has been shown to be promising because it requires only one single simulation for the backward propagation, therefore, reducing significantly the computational burden of running multiple independent backward simulations as it is in the matched methods. However, the proposed properties and metrics are valid for specific and relatively simple topologies. For example, the scope of applying the mirrored minimum energy metric is limited in non-branched transmission lines. Further research is needed to apply EMTR in mismatched media to topologically-complex power networks.

Lastly, further experimental studies are necessary to pave the way for implementing the EMTR technique in different power networks. For example, pilot tests can be conducted in point-to-point or meshed HVDC systems.

Author contributions

Writing, original draft preparation: ZW and SH; writing, review, and editing: RR, MP, YX, and FR.

Funding

This work was supported by the Postdoc.Mobility Fellowship (P500PT_206941/1) of the Swiss National Science Foundation (SNSF).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹The inhomogeneous medium is composed of sub media characterized by different wave propagation characteristics (e.g., wave propagation velocity).

²The superscript “DT” and “RT” are used hereafter to indicate signals/functions present in the forward- and backward-propagation stages, respectively.

References

An, J., Zhuang, C., Rachidi, F., and Zeng, R. (2021). An effective EMTR-based high-impedance fault location method for transmission lines. IEEE Trans. Electromagn. Compat. 63, 268–276. doi:10.1109/TEMC.2020.2991862

CrossRef Full Text | Google Scholar

Azadifar, M., Karami, H., Wang, Z., Rubinstein, M., Rachidi, F., Karami, H., et al. (2020). Partial discharge localization using electromagnetic time reversal: A performance analysis. IEEE Access 8, 147507–147515. doi:10.1109/ACCESS.2020.3015973

CrossRef Full Text | Google Scholar

Bacot, V., Labousse, M., Eddi, A., Fink, M., and Fort, E. (2016). Time reversal and holography with spacetime transformations. Nat. Phys. 12, 972–977. doi:10.1038/nphys3810

CrossRef Full Text | Google Scholar

Blomgren, P., Papanicolaou, G., and Zhao, H. (2002). Super-resolution in time-reversal acoustics. J. Acoust. Soc. Am. 111, 230–248. doi:10.1121/1.1421342

PubMed Abstract | CrossRef Full Text | Google Scholar

Carminati, R., Pierrat, R., de Rosny, J., and Fink, M. (2007). Theory of the time reversal cavity for electromagnetic fields. Opt. Lett. 32, 3107. doi:10.1364/ol.32.003107

PubMed Abstract | CrossRef Full Text | Google Scholar

Cassereau, D., and Fink, M. (1992). Time reversal of ultrasonic fields - Part III: Theory of the closed time-reversal cavity. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 39, 579–592. doi:10.1109/58.156176

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Z., Wang, Z., Paolone, M., and Rachidi, F. (2019). Properties of direct-time and reversed-time transfer functions to locate disturbances along power transmission lines. In Proceedings of the 2019 IEEE Milan PowerTech, PowerTech 2019 (IEEE), 23-27 June 2019, Milan, Italy, 1–8. doi:10.1109/PTC.2019.8810552

CrossRef Full Text | Google Scholar

Codino, A., Wang, Z., Razzaghi, R., Paolone, M., and Rachidi, F. (2017). An alternative method for locating faults in transmission line networks based on time reversal. IEEE Trans. Electromagn. Compat. 59, 1601–1612. doi:10.1109/TEMC.2017.2671369

CrossRef Full Text | Google Scholar

Cozza, A., He, S., and Xie, Y. (2021a). Impact of propagation losses on fault location accuracy in full transient-based methods. IEEE Trans. Power Deliv. 36, 383–396. doi:10.1109/TPWRD.2020.2983323

CrossRef Full Text | Google Scholar

Cozza, A., He, S., and Xie, Y. (2021b). Surge compression for improved fault location accuracy in full transient-based methods. IEEE Sens. J. 21, 995–1008. doi:10.1109/JSEN.2020.2989202

CrossRef Full Text | Google Scholar

da Costa, L. A., Gazzana, D. S., Leborgne, R. C., and Thomas, D. W. P. (2020). Incipient Fault location in underground distribution networks using electromagnetic time reversal. In Proceedings of the 2020 IEEE International Conference on Environment and Electrical Engineering and 2020 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), 09-12 June 2020, Madrid, Spain. 1–6. doi:10.1109/EEEIC/ICPSEurope49358.2020.9160622

CrossRef Full Text | Google Scholar

de Magalhaes Junior, F. M., and Lopes, F. V. (2022). Mathematical study on traveling waves phenomena on three phase transmission lines Part I: Fault-launched waves. IEEE Trans. Power Deliv. 37, 1151–1160. doi:10.1109/TPWRD.2021.3077769

CrossRef Full Text | Google Scholar

de Rosny, J., Lerosey, G., and Fink, M. (2010). Theory of electromagnetic time-reversal mirrors. IEEE Trans. Antennas Propag. 58, 3139–3149. doi:10.1109/TAP.2010.2052567

CrossRef Full Text | Google Scholar

Derode, A., Roux, P., and Fink, M. (1995). Robust acoustic time reversal with high-order multiple scattering. Phys. Rev. Lett. 75, 4206–4209. doi:10.1103/PhysRevLett.75.4206

PubMed Abstract | CrossRef Full Text | Google Scholar

Derode, A., Tourin, A., de Rosny, J., Tanter, M., Yon, S., and Fink, M. (2003). Taking advantage of multiple scattering to communicate with time-reversal antennas. Phys. Rev. Lett. 90, 014301/1–014301/4. doi:10.1103/PhysRevLett.90.014301

PubMed Abstract | CrossRef Full Text | Google Scholar

Draeger, C., and Fink, M. (1997). One-Channel time reversal of elastic waves in a chaotic 2D-silicon cavity. Phys. Rev. Lett. 79, 407–410. doi:10.1103/PhysRevLett.79.407

CrossRef Full Text | Google Scholar

Fink, M., Montaldo, G., and Tanter, M. (2003). Time-reversal acoustics in biomedical engineering. Annu. Rev. Biomed. Eng. 5, 465–497. doi:10.1146/annurev.bioeng.5.040202.121630

PubMed Abstract | CrossRef Full Text | Google Scholar

Fink, M. (1992). Time reversal of ultrasonic fields - Part I: Basic principles. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 39, 555–566. doi:10.1109/58.156174

PubMed Abstract | CrossRef Full Text | Google Scholar

Fink, M. (1993). Time-reversal mirrors. J. Phys. D. Appl. Phys. 26, 1333–1350. doi:10.1088/0022-3727/26/9/001

CrossRef Full Text | Google Scholar

Furse, C. M., Kafal, M., Razzaghi, R., and Shin, Y. (2021). Fault diagnosis for electrical systems and power networks: A review. IEEE Sens. J. 21, 888–906. doi:10.1109/JSEN.2020.2987321

CrossRef Full Text | Google Scholar

Greenwood, A. (1991). Electrical transients in power systems. Hoboken, New Jersey, United States: John Wiley & Sons.

Google Scholar

He, S., Cozza, A., and Xie, Y. (2020a). Electromagnetic time reversal as a correlation estimator: Improved metrics and design criteria for fault location in power Grids. IEEE Trans. Electromagn. Compat. 62, 598–611. doi:10.1109/TEMC.2019.2904841

CrossRef Full Text | Google Scholar

He, S., Cozza, A., and Xie, Y. (2020b). On the spatial resolution of fault-location techniques based on full-fault transients. IEEE Trans. Power Deliv. 35, 1527–1540. doi:10.1109/TPWRD.2019.2949914

CrossRef Full Text | Google Scholar

He, S., Xie, Y., Wang, Z., Rachidi, F., Liu, B., Li, Q., et al. (2018). Norm criteria in the electromagnetic time reversal technique for fault location in transmission lines. IEEE Trans. Electromagn. Compat. 60, 1240–1248. doi:10.1109/TEMC.2018.2806892

CrossRef Full Text | Google Scholar

IEEE Std C37.114-2004 (2015). IEEE guide for determining fault location on AC transmission and distribution lines. Tech. Rep, 1–61. doi:10.1109/IEEESTD.2015.7024095

CrossRef Full Text | Google Scholar

Izykowski, J., Rosolowski, E., Balcerek, P., Fulczyk, M., and Saha, M. M. (2011). Accurate noniterative fault-location algorithm utilizing two-end unsynchronized measurements. IEEE Trans. Power Deliv. 26, 547–555. doi:10.1109/TPWRD.2009.2031440

CrossRef Full Text | Google Scholar

Kafal, M., Cozza, A., and Pichon, L. (2016). Locating multiple soft faults in wire networks using an alternative DORT implementation. IEEE Trans. Instrum. Meas. 65, 399–406. doi:10.1109/TIM.2015.2498559

CrossRef Full Text | Google Scholar

Kafal, M., Gregis, N., Benoit, J., and Ravot, N. (2021a). An effective method based on time reversal and optimization techniques for locating faults on power Grids. IEEE Sens. J. 21, 1092–1099. doi:10.1109/JSEN.2020.3000301

CrossRef Full Text | Google Scholar

Kafal, M., Gregis, N., Benoit, J., Ravot, N., Lagomarsini, C., and Gobat, G. (2021b). Pilot tests of FasTR method for locating transient faults in medium voltage underground power networks. IEEE Sens. J. 21, 8510–8519. doi:10.1109/JSEN.2020.3034465

CrossRef Full Text | Google Scholar

Karami, H., Azadifar, M., Mostajabi, A., Favrat, P., Rubinstein, M., and Rachidi, F. (2021a). Localization of electromagnetic interference sources using a time-reversal cavity. IEEE Trans. Ind. Electron. 68, 654–662. doi:10.1109/TIE.2019.2962460

CrossRef Full Text | Google Scholar

Karami, H., Azadifar, M., Wang, Z., Rubinstein, M., and Rachidi, F. (2021b). Single-sensor EMI source localization using time reversal: An experimental validation. Electronics 10, 2448. doi:10.3390/electronics10192448

CrossRef Full Text | Google Scholar

Kosmas, P., and Rappaport, C. M. (2005). Time reversal with the FDTD method for microwave breast cancer detection. IEEE Trans. Microw. Theory Tech. 53, 2317–2323. doi:10.1109/TMTT.2005.850444

CrossRef Full Text | Google Scholar

Lemoult, F., Fink, M., and Lerosey, G. (2011). Acoustic resonators for far-field control of sound on a subwavelength scale. Phys. Rev. Lett. 107, 064301–064305. doi:10.1103/PhysRevLett.107.064301

PubMed Abstract | CrossRef Full Text | Google Scholar

Lerosey, G., de Rosny, J., Tourin, A., Derode, A., Montaldo, G., and Fink, M. (2004). Time reversal of electromagnetic waves. Phys. Rev. Lett. 92, 193904–193921. doi:10.1103/PhysRevLett.92.193904

PubMed Abstract | CrossRef Full Text | Google Scholar

Lerosey, G., de Rosny, J., Tourin, A., and Fink, M. (2007). Focusing beyond the diffraction limit with far-field time reversal. Science 315, 1120–1122. doi:10.1126/science.1134824

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, M., Zhou, C., Zhou, W., Wang, C., Yao, L., Su, M., et al. (2018). A novel fault location method for a cross-bonded HV cable system based on sheath current monitoring. Sensors 18, 3356. doi:10.3390/s18103356

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Q., Wang, Z., Xie, Y., Rachidi, F., and Rubinstein, M. (2021). A correlation-based electromagnetic time reversal technique to locate indoor transient radiation sources. IEEE Trans. Microw. Theory Tech. 69, 3945–3957. doi:10.1109/TMTT.2021.3086826

CrossRef Full Text | Google Scholar

Liu, D., Vasudevan, S., Krolik, J., Bal, G., and Carin, L. (2007). Electromagnetic time-reversal source localization in changing media: Experiment and analysis. IEEE Trans. Antennas Propag. 55, 344–354. doi:10.1109/TAP.2006.889807

CrossRef Full Text | Google Scholar

Lopes, F. V., Lima, P., Ribeiro, J. P. G., Honorato, T. R., Silva, K. M., Leite, E. J. S., et al. (2019). Practical methodology for two-terminal traveling wave-based fault location eliminating the need for line parameters and time synchronization. IEEE Trans. Power Deliv. 34, 2123–2134. doi:10.1109/TPWRD.2019.2891538

CrossRef Full Text | Google Scholar

Lugrin, G., Parra, N. M., Rachidi, F., Rubinstein, M., and Diendorfer, G. (2014). On the location of lightning discharges using time reversal of electromagnetic fields. IEEE Trans. Electromagn. Compat. 56, 149–158. doi:10.1109/TEMC.2013.2266932

CrossRef Full Text | Google Scholar

Mahseredjian, J., Dennetière, S., Dubé, L., Khodabakhchian, B., and Gérin-Lajoie, L. (2007). On A new approach for the simulation of transients in power systems. Electr. Power Syst. Res. 77, 1514–1520. doi:10.1016/j.epsr.2006.08.027

CrossRef Full Text | Google Scholar

Majidi, M., and Etezadi-Amoli, M. (2018). A new fault location technique in Smart distribution networks using synchronized/nonsynchronized measurements. IEEE Trans. Power Deliv. 33, 1358–1368. doi:10.1109/TPWRD.2017.2787131

CrossRef Full Text | Google Scholar

Manesh, H. M., Lugrin, G., Razzaghi, R., Romero, C., Paolone, M., and Rachidi, F. (2012). A new method to locate faults in power networks based on electromagnetic time reversal. In Proceedings of the 2012 IEEE 13th Int. Work. Signal Process. Adv. Wirel. Commun. (SPAWC), 17-20 June 2012, Cesme, Turkey, 469–474. doi:10.1109/SPAWC.2012.6292952

CrossRef Full Text | Google Scholar

Mostajabi, A., Karami, H., Azadifar, M., Ghasemi, A., Rubinstein, M., and Rachidi, F. (2019). Single-sensor source localization using electromagnetic time reversal and deep transfer learning: Application to lightning. Sci. Rep. 9 (17372), 1–14. doi:10.1038/s41598-019-53934-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Mukherjee, S., Udpa, L., Udpa, S., and Rothwell, E. J. (2017). Target localization using microwave time-reversal mirror in reflection mode. IEEE Trans. Antennas Propag. 65, 820–828. doi:10.1109/TAP.2016.2627011

CrossRef Full Text | Google Scholar

Naidu, O. D., Pradhan, A. K., and Member, S. (2019). A traveling wave-based fault location method using unsynchronized current measurements. IEEE Trans. Power Deliv. 34, 505–513. doi:10.1109/tpwrd.2018.2875598

CrossRef Full Text | Google Scholar

Rachidi, F., Rubinstein, M., and Paolone, M. (2017). Electromagnetic time reversal: Application to electromagnetic compatibility and power systems. Hoboken, New Jersey, United States: John Wiley & Sons.

Google Scholar

Ragusa, A., Sasse, H. G., and Duffy, A. (2022). On-line partial discharge localization in power cables based on electromagnetic time reversal theory - numerical validation. IEEE Trans. Power Deliv. 37, 2911–2920. doi:10.1109/TPWRD.2021.3119236

CrossRef Full Text | Google Scholar

Razzaghi, R., Lugrin, G., Manesh, H., Romero, C., Paolone, M., and Rachidi, F. (2013a). An efficient method based on the electromagnetic time reversal to locate faults in power networks. IEEE Trans. Power Deliv. 28, 1663–1673. doi:10.1109/TPWRD.2013.2251911

CrossRef Full Text | Google Scholar

Razzaghi, R., Lugrin, G., Paolone, M., and Rachidi, F. (2013b). On the use of electromagnetic time reversal to locate faults in series-compensated transmission lines. In Proceedings of the 2013 IEEE Grenoble Conference. 16-20 June 2013, Grenoble, France, doi:10.1109/PTC.2013.6652101

CrossRef Full Text | Google Scholar

Razzaghi, R., Paolone, M., Rachidi, F., Descloux, J., Raison, B., and Retière, N. (2014). fault location in multi-terminal HVDC networks based on electromagnetic time reversal with limited time reversal window. In Proceedings of the 2014 Power Systems Computation Conference. 18-22 Aug. 2014, Wroclaw, Poland, doi:10.1109/PSCC.2014.7038411

CrossRef Full Text | Google Scholar

Saha, M. M., Izykowski, J. J., and Rosolowski, E. (2009). fault location on power networks. New York, United States: Springer.

Google Scholar

Stringfield, T. W., Marihart, D. J., and Stevens, R. F. (1957). fault location methods for overhead lines. Trans. AIEE. Part III Power Appar. Syst. 76, 518–529. doi:10.1109/AIEEPAS.1957.4499601

CrossRef Full Text | Google Scholar

Sun, J., Yang, Q., Cui, H., Ran, J., and Liu, H. (2021). Distribution line fault location with unknown fault impedance based on electromagnetic time reversal. IEEE Trans. Electromagn. Compat. 63, 1921–1929. doi:10.1109/TEMC.2021.3097105

CrossRef Full Text | Google Scholar

Sun, J., Yang, Q., Xu, W., and He, W. (2022a). A distribution line fault location estimation algorithm based on electromagnetic time-reversal method calculated in the finite difference time domain. IEEE Trans. Electromagn. Compat. 64, 865–873. doi:10.1109/TEMC.2021.3140170

CrossRef Full Text | Google Scholar

Sun, J., Zhang, X., Wei, S., Luo, Q., Hu, Y., and Yang, Q. (2022b). High-impedance fault location method of three-phase distribution lines based on electromagnetic time reversal. Electr. Power Syst. Res. 212, 108629. doi:10.1016/j.epsr.2022.108629

CrossRef Full Text | Google Scholar

Tailor, K., and Ukil, A. (2019). fault detection and locating using electromagnetic time reversal (EMTR) technique for HVDC transmission network. In Proceedings of the 2019 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC). 1–5. doi:10.1109/APPEEC45492.2019.8994683

CrossRef Full Text | Google Scholar

Tesche, F. M., Ianoz, M., and Karlsson, T. (1996). EMC analysis methods and computational models. Hoboken, New Jersey, United States: Wiley.

Google Scholar

Wang, G., and Zhuang, C. (2022). a fault location method using direct convolution: Electromagnetic time reversal or not reversal. IEEE Trans. Electromagn. Compat. 64, 1112–1116. doi:10.1109/TEMC.2022.3168012

CrossRef Full Text | Google Scholar

Wang, Z., Chen, Z., and Paolone, M. (2022). A data-driven fault location algorithm based on the electromagnetic time reversal in mismatched media. IEEE Trans. Power Deliv. 37, 3709–3721. doi:10.1109/TPWRD.2021.3135429

CrossRef Full Text | Google Scholar

Wang, Z., Codino, A., Razzaghi, R., Paolone, M., and Rachidi, F. (2017). Using electromagnetic time reversal to locate faults in transmission lines: Definition and application of the ”mirrored minimum energy” property. In Proceedings of the 2017 International Symposium on Electromagnetic Compatibility - EMC EUROPE. 04-07 Sep. 2017, Angers, France, doi:10.1109/EMCEurope.2017.8094641

CrossRef Full Text | Google Scholar

Wang, Z., He, S., Li, Q., Liu, B., Razzaghi, R., Paolone, M., et al. (2018a). A full-scale experimental validation of electromagnetic time reversal applied to locate disturbances in overhead power distribution lines. IEEE Trans. Electromagn. Compat. 60, 1562–1570. doi:10.1109/TEMC.2018.2793967

CrossRef Full Text | Google Scholar

Wang, Z., Karami, H., Lowenstein, A., Rahimi, S., Dehkhoda, P., Sadeghi, S. H. H., et al. (2021). An experimental study on electromagnetic time reversal focusing property in mismatched media. In Proceedings of the 2021 XXXIVth General Assembly and Scientific Symposium of the International Union of Radio Science (URSI GASS). 28 Aug. 2021-04 Sep. 2021, 1–4. doi:10.23919/URSIGASS51995.2021.9560282

CrossRef Full Text | Google Scholar

Wang, Z., Razzaghi, R., Paolone, M., and Rachidi, F. (2018b). Electromagnetic time reversal applied to fault location: On the properties of back-injected signals. In Proceedings of the 20th Power Syst. Comput. Conf. PSCC 2018 Power Systems Computation Conference. 11-15 June 2018, Dublin, Ireland, doi:10.23919/PSCC.2018.8449024

CrossRef Full Text | Google Scholar

Wang, Z., Razzaghi, R., Paolone, M., and Rachidi, F. (2020a). Electromagnetic time reversal similarity characteristics and its application to locating faults in power networks. IEEE Trans. Power Deliv. 35, 1735–1748. doi:10.1109/TPWRD.2019.2952207

CrossRef Full Text | Google Scholar

Wang, Z., Razzaghi, R., Paolone, M., and Rachidi, F. (2020b). Time reversal applied to fault location in power networks pilot test results and analyses. Int. J. Electr. Power & Energy Syst. 114, 105382. doi:10.1016/j.ijepes.2019.105382

CrossRef Full Text | Google Scholar

Wu, F., Thomas, J.-L., and Fink, M. (1992). Time reversal of ultrasonic fields - Part II: Experimental results. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 39, 567–578. doi:10.1109/58.156175

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, X., Tai, N., Wang, Y., and Liu, J. (2017). EMTR-based fault location for DC line in VSC-mtdc system using high-frequency currents. IET Gener. Transm. &amp. Distrib. 11, 2499–2507. doi:10.1049/iet-gtd.2016.1215

CrossRef Full Text | Google Scholar

Nomenclature

Abbreviation

EMTR Electromagnetic time reversal

DT Direct time (i.e., forward propagation stage)

RT Reversed time (i.e., backward-propagation stage)

FCSE Fault current signal energy

Function and variable

x_f,x_g True fault location, guessed fault location

V_f(jω) Fault simulation voltage

Z₀ Terminal impedance at the location x = 0

V^DT(x, jω) Voltage in the direct time at the location x

I^RT(x, jω) Current in the reversed time at the location x

V^RT(x, jω) Voltage in the reversed time at the location x

H^DT(jω) Transfer function in the direct time

H^RT(x, jω) Matched media-based transfer function in the reversed time at the location x

H^RT,v(x, jω) Mismatched media-based transfer function in the reversed time at the location x

H(x, jω) Mismatched media-based direct-reversed-time transfer function at the location x