Parameter estimation of harmonics arising in electrical instruments of smart grids using cuckoo search heuristics

The accurate estimation of power signal parameters allows smart grids to optimize power delivery efficiency, improve equipment utilization, and control power flow among generation nodes and loads. However, practically it becomes a challenging task because of the presence of harmonic distortions. In this study, a parameter estimation of the power system harmonics is investigated through swarm intelligence–based optimization strength of the cuckoo search algorithm. The performance evaluation is conducted in detail for different generations and particle sizes and for different signal-to-noise ratios. The simulation results reveal that the cuckoo search optimization heuristic accurately estimates the amplitude and phase parameters of the power system harmonics and is robust against different signal-to-noise ratios.

1 Introduction

The control of the power systems and synchronization of grid-connected electrical devices require parameters of voltage and current signals, such as amplitude, frequency, and phase (Baradarani et al., 2014; Jafarpisheh et al., 2016). Accurate information on these signal parameters allows smart grids to optimize power delivery efficiency, improve equipment utilization, and control power flow among generation nodes and loads (Sun et al., 2019). However, practically the presence of harmonics and inter-harmonic distortions in power signals complicates the situation because the amplitude and phase estimations of harmonics is challenging for evaluating the quality of service characteristics in smart grids (Rivas et al., 2020). Thus, it is imperative to investigate the development of accurate, robust, and stable estimation methods to mitigate the adverse effects of harmonics in smart grid efficiency.

Different researchers have investigated the domain of estimating power system harmonics and proposed various techniques. For example, Das et al. (2020) developed the ADALINE-based least mean square (LMS) algorithm and compared its performance with the recursive least square, while Elnady et al. (2020) presented the novel smooth variable structure filters for voltage harmonics and voltage imbalance. Santos et al. (2020) introduced the filter bank–based ESPRIT approach for increased efficiency in harmonics detection and estimation. Enayati and Moravej (2017) developed a hybrid estimation scheme by combining recursive least squares with the iterated extended Kalman filter, and Shuai et al. (2018) presented the frequency shifting/filtering method. Xu et al. (Xu and Ding, 2018; Xu and Song, 2020) investigated the parameter estimation of power signals using iterative/recursive methods, such as multi-innovation stochastic gradient (Xu and Ding, 2017), separable multi-synchronous multi-innovation gradient (Xu et al., 2022), separable Newton recursive (Xu, 2022a), separable multi-innovation Newton iterative (Xu, 2022b), and hierarchical principle-based recursive least squares (Xu et al., 2021). Chaudhary et al. introduced fractional gradient-based estimation algorithms for power signals, such as fractional LMS (Chaudhary et al., 2017) and innovative fractional order LMS (Chaudhary et al., 2020), while Zubair et al. (2018) presented the momentum term–based fractional scheme. Mehmood et al. (2020), Mehmood et al. (2021) had applied evolutionary and swarming heuristics for parameter estimation of power signals.

The schemes based on swarm and evolutionary heuristics have established their significance through effective application in solving various challenging optimization tasks (Francesca and Birattari, 2016; Jana et al., 2019; Sabir et al., 2020; AbdelAty et al., 2022; Altaf et al., 2022) such as power system harmonics estimation (Ray and Subudhi, 2012; Elvira-Ortiz et al., 2020; Ray and Subudhi, 2015; Kabalci et al., 2018; doNascimentoSepulchro et al., 2014; Singh et al., 2016). Yang and Deb (2009), Yang and Deb (2014) introduced a metaheuristic inspired by the search mechanism of cuckoo called the cuckoo search optimization (CSO) algorithm. The CSO has been used extensively for effective solutions in a number of engineering and applied problems with many variants (Li and Yin, 2015; Cuong-Le et al., 2021), such as photovoltaic model (Gude and Jana, 2020), social media sentiment analysis (Pandey et al., 2017), path planning (Song et al., 2020), power control in salt reactors (Karahan, 2021), damage detection infrastructures (Tran-Ngoc et al., 2019), chemoinformatics (Houssein et al., 2020), economic load dispatch (Yu et al., 2020), and many others. The effective performance of CSO in illustrated applications motivated us to explore parameter estimation power system harmonics through well-established optimization strength of the CSO. In this study, parameters of power system harmonics are estimated through CSO for different generation and particle size. Detailed and in-depth performance analyses are conducted to check the accuracy, diversity, and robustness of the CSO for harmonics estimation.

The remaining article is set as follows: the estimation model for power system harmonics along with the optimization procedure of CSO is described in Section 2. The results of simulation studies are elaborated in Section 3. The conclusions and future works are listed in Section 4.

2 Materials and methods

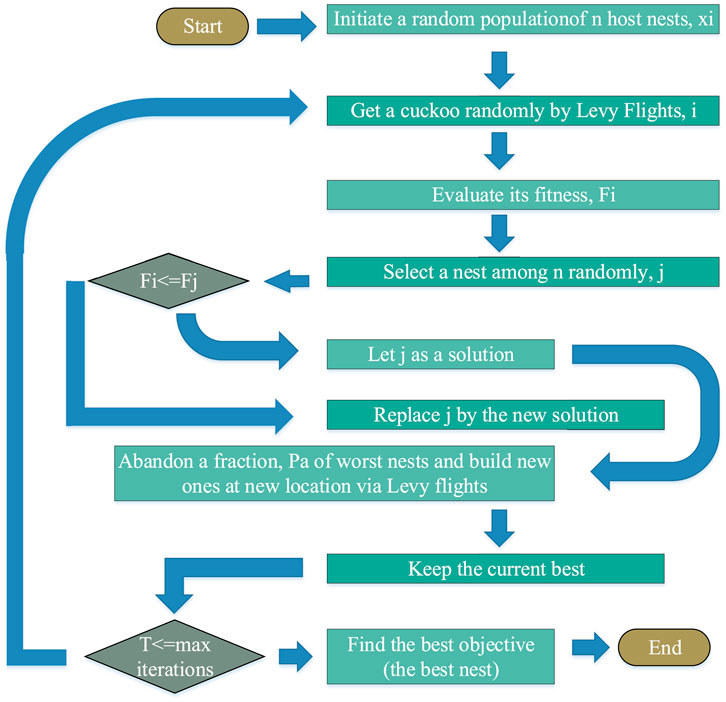
The system model for power harmonics signal is first introduced, then the proposed methodology for optimization of the fitness function for the estimation of the harmonic signal is presented in this section. The overall flow diagram of the proposed scheme is presented in Figure 1 by means of different process block structures.

FIGURE 1

FIGURE 1. Process flow structure of the CSO algorithm.

2.1 System model

The general harmonic signal in terms of its constituent parameters (Malik et al., 2022) is defined as

$s\left(t\right)={\displaystyle \sum }_{k=1}^K{\alpha }_k\sin \left({\beta }_{k}t+{\gamma }_k\right)+\delta \left(t\right)h\left(t\right)={\displaystyle \sum }_{j=1}^J{a}_j\sin \left(b_{j}t+c_j\right)+d\left(t\right),(1)$

and the variables in Eq. 1 are defined as J represents harmonic order, $a_j$ is amplitude, $b_j$ is angular frequency represented as $b_j=2\pi f_0$ with $f_0$ as fundamental frequency, $c_j$ is phase, and d is AWGN. Then, by writing a discrete version of Eq. 1 after sampling with period p, $t_n=np$, and by assuming $h\left(t_n\right)=h\left(n\right)$, Eq. 1 is rewritten as

$\begin{array}{l}h\left(t_n\right)={\displaystyle \sum }_{j=1}^J{a}_j\sin \left(b_j{t}_n+{\gamma }_k\right)+d\left(t_n\right),\\ h\left(n\right)={\displaystyle \sum }_{j=1}^J{a}_j\sin \left({\beta }_{j}n+c_k\right)+d\left(n\right).\end{array}(2)$

Expanding Eq. 2 through the fundamental trigonometric identity

$h\left(n\right)={\displaystyle \sum }_{j=1}^J\left[a_j\cos \left(b_{j}n\right)\sin c_j+a_j\sin \left(b_{j}n\right)\cos c_j\right]+d\left(n\right),(3)$

with the assumption that

$u_j=a_j\cos c_j \mathrm{a}\mathrm{n}\mathrm{d}{v}_j=a_j\sin c_j,(4)$

using the assumptions given in Eq. 4 into Eq. 3 gives Eq. 5:

$h\left(n\right)={\displaystyle \sum }_{j=1}^J\left[u_j\sin \left(b_{j}n\right)+v_j\cos \left(b_{j}n\right)\right]+d\left(n\right).(5)$

The harmonics estimation model with information-vector $\mathbf{\psi }$ and parameter-vector $\mathbf{\zeta }$ is written as

$\begin{array}{c}h\left(n\right)={\mathbf{\psi }}^T\left(n\right)\mathbf{\zeta }+d\left(n\right),\\ \mathbf{\psi }\left(n\right)=\left[\sin \left(b_{1}n\right),\cos \left(b_{1}n\right),\sin \left(b_{2}n\right),\cos \left(b_{2}n\right),...,\sin \left(b_{j}n\right),\cos \left(b_{j}n\right)\right],\\ \mathbf{\zeta }=\left[u_1,v_1,u_2,v_2,...,u_j,v_j\right].\end{array}(6)$

The aim is to estimate the amplitude and phase parameters of the harmonics through minimizing the error-based criterion function defined as

$\delta \left(n\right)=\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}{\left[h\left(n\right)-\stackrel{\sim }{h}\left(n\right)\right]}^2={\left[h\left(n\right)-{\mathbf{\psi }}^T\left(n\right)\stackrel{\sim }{\mathbf{\zeta }}\right]}^2,(7)$

$h\left(n\right)$ is the actual signal, $\stackrel{\sim }{h}\left(n\right)$ is an estimated harmonic signal calculated through estimated parameter-vector $\stackrel{\sim }{\mathbf{\zeta }}$ by using the proposed CSO-based heuristic. The relationship between the intermediate variables and the actual parameters is given by

$a_j=\sqrt{{\left(u_j\right)}^2+{\left(v_j\right)}^2},c_j={\tan }^{-1}\frac{v_j}{u_j}.(8)$

2.2 Optimization method: Cuckoo search optimization algorithm

Yang and Deb (2009), Yang and Deb (2014) introduced a metaheuristic inspired by the search mechanism of cuckoo called CSO with exhaustive applications in different fields of engineering design and optimization. The formulation of the CSO is based on three fundamental concepts: firstly, each cuckoo lays a single egg in a single instance of time, while dumping the respective egg in an arbitrary selected nest; secondly, the nests with the best fitness, i.e., having the best quality of eggs, proceed to the next generations; and thirdly, the number of host nests is fixed, and the probability of discovery of next by the host cuckoo is set between 0 and 1. The basis of these three fundamental steps in the CSO is proposed with the process flow structure as shown in Figure 1.

Proceeding by the actual behavior of the cuckoo, mathematical models were introduced by Yang et al.; by taking the new candidate solution x_i(t+1) that represents an i-th cuckoo at t flight/iteration index and considering the Levy flight, we have the following expression iterative update of CSO as

$x_i\left(t+1\right)=x_i\left(t\right)+\alpha \odot Levy\left(\lambda \right),(9)$

here α represents the step size based on the scale of the optimization problem, and generally its value is set equal to unit value in most of the cases and the Levy flight is represented with a random walk procedure on the basis of Levy distribution as

$Levy\left(\lambda \right)\sim u=t^{\left(-\lambda \right)},(10)$

here λ is a constant taken between 1 and 3, and the Levy flight has an infinite mean and variance. Further details on the mathematical terms, convergence proofs, and applications can be referred from citations mentioned therein: Yang and Deb (2009); Yang and Deb (2014); Li and Yin (2015); Pandey et al. (2017); Tran-Ngoc et al. (2019); Gude and Jana (2020); Houssein et al. (2020); Song et al. (2020); Yu et al. (2020); Cuong-Le et al. (2021); Karahan (2021). Inspired by the optimization performance of the CSO algorithm, we have implemented the CSO for optimization of parameters of the system models presented in Eqs. 1–8. The CSO algorithm was implemented in the presented research based on the routine available at the MATLAB Central File Exchange (Yang, 2022). The optimization strength of the CSO may be enhanced by integrating it with the kernel theory (Arqub, 2016; Arqub, 2018; Arqub, 2020; Arqub and Al-Smadi, 2020; Sweis et al., 2022).

3 Results and discussion

Harmonics estimation of power systems is carried out in this research work by applying the CSO algorithm to two examples, and the results are given in a tabular form with the necessary discussion along with graphs. The simulations are conducted using MATLAB with a sampling frequency of 2 KHz. Three levels of additive white Gaussian noise d with 30 DB, 60 DB, and 90 DB are introduced in the system to check the heftiness of the proposed scheme. The investigation is carried out by considering four generation (G) sizes and three particle (P) sizes in the CSO. The considered values of G are 500, 1000, 1,500, and 2000, while the values of P are 50, 100, and 150.

Example 1. The harmonic signal (Malik et al., 2022) considered in the first simulation study is

$h\left(t\right)=\left[\begin{array}{l}1.5\sin \left(2\pi f_{1}t+1.396\right)+0.5\sin \left(2\pi f_{3}t+1.047\right)+0.2\sin \left(2\pi f_{5}t+0.785\right)\\ +0.15\sin \left(2\pi f_{7}t+0.628\right)+0.1\sin \left(2\pi f_{11}t+0.523\right)\end{array}\right].(11)$

Ten parameters are taken under consideration in this problem. Five phase and five amplitude parameters that were taken are given below, while, $f_1$, $f_3$, $f_5$, $f_7$, and $f_{11}$ are the frequencies with values 50 Hz, 150 Hz, 250 Hz, 350 Hz, and 550 Hz, respectively:

$\begin{array}{l}\mathbf{\zeta }=\left[a_1,a_2,a_3,a_4,a_5,c_1,c_2,c_3,c_4,c_5\right]\\ =\left[\mathrm{1.50,0.50,0.20,0.15,0.10,1.396,1.047,0.785,0.628,0.523}\right].\end{array}(12)$

Example 2. The harmonic signal considered in the second simulation study is

$h\left(t\right)=\left[\begin{array}{l}1.2\sin \left(2\pi f_{1}t+1.309\right)+0.8\sin \left(2\pi f_{3}t+0.959\right)+0.2\sin \left(2\pi f_{5}t+0.785\right)\\ +0.18\sin \left(2\pi f_{7}t+0.698\right)+0.1\sin \left(2\pi f_{11}t+0.523\right)\end{array}\right].(13)$

The parameter-vector consisting of five amplitude and five phase parameters is

$\begin{array}{l}\mathbf{\zeta }=\left[a_1,a_2,a_3,a_4,a_5,c_1,c_2,c_3,c_4,c_5\right]\\ =\left[\mathrm{1.20,0.80,0.20,0.18,0.10,1.309,0.959,0.785,0.698,0.523}\right].\end{array}(14)$

The results of Example 1 in terms of parameter estimates through the CSO along with the MSE value are given in Tables 1–4 for G = 500, 1,000, 1,500, and 2,000, respectively. While the respective results in the case of Example 2 are presented in Tables 5–8. The learning curves for Example 1 are given in Figure 2, while for Example 2, the convergence plots are provided in Figure 3. The results clearly indicate that the CSO gives a better accuracy for 90 dB SNR than it does for 60 dB and 30 dB. Moreover, the accuracy of the CSO for harmonics estimation increases by increasing the generation size.

TABLE 1

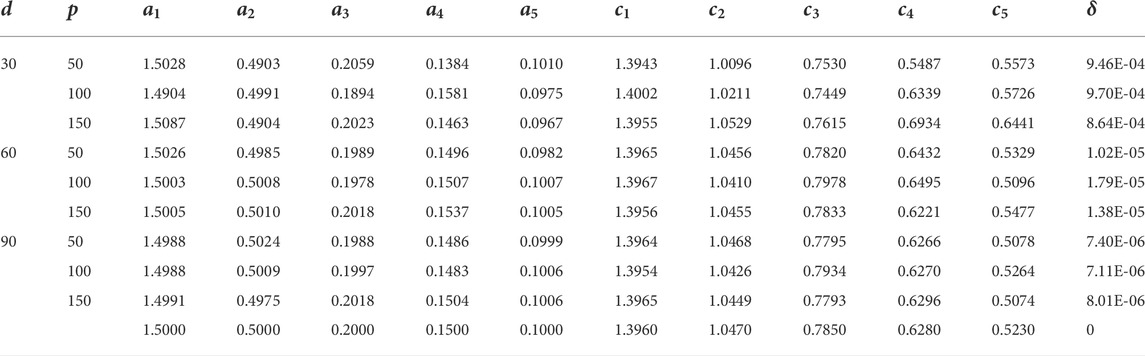
TABLE 1. Results of parameter estimates of Example 1 for G = 500.

TABLE 2

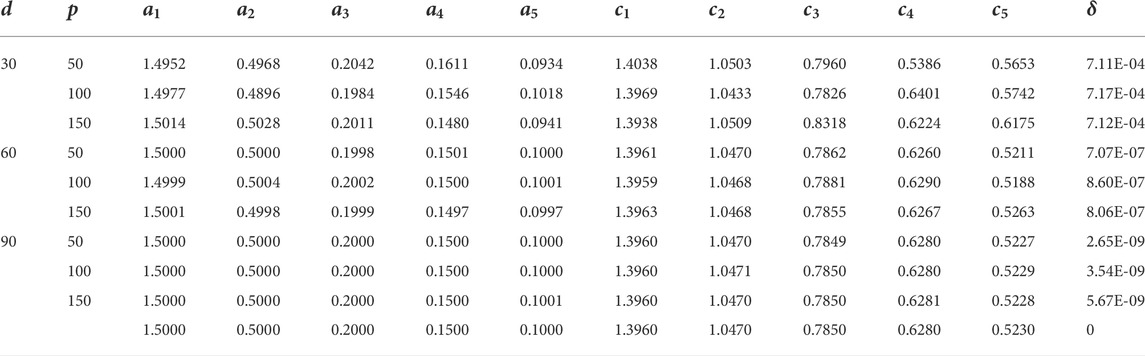
TABLE 2. Results of parameter estimates of Example 1 for G = 1,000.

TABLE 3

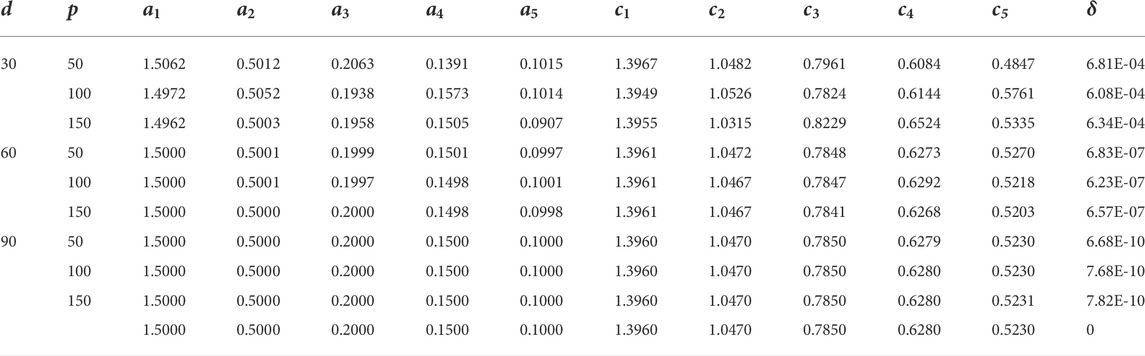
TABLE 3. Results of parameter estimates of Example 1 for G = 1,500.

TABLE 4

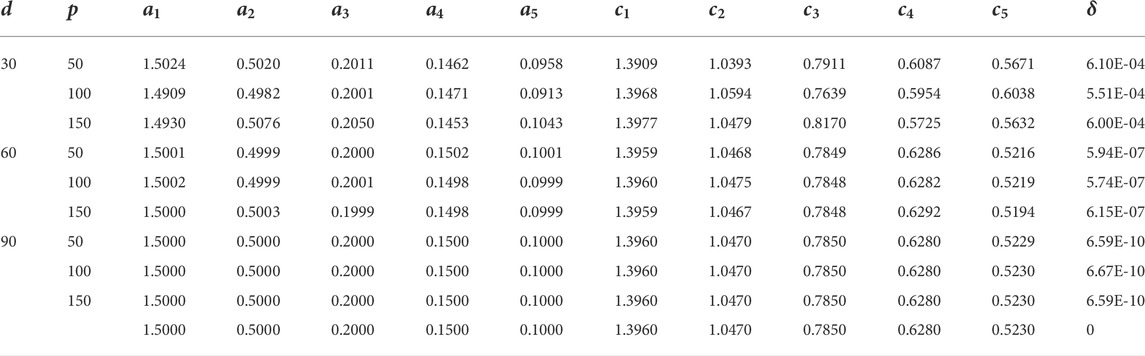
TABLE 4. Results of parameter estimates of Example 1 for G = 2000.

TABLE 5

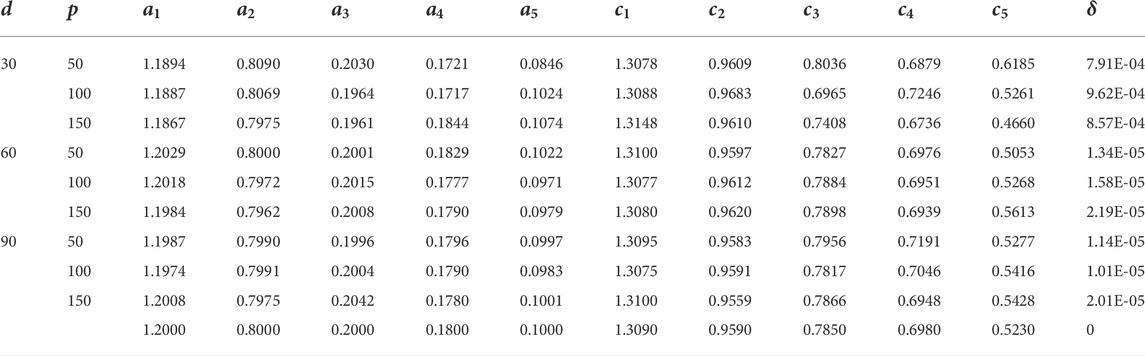
TABLE 5. Results of parameter estimates of Example 2 for G = 500.

TABLE 6

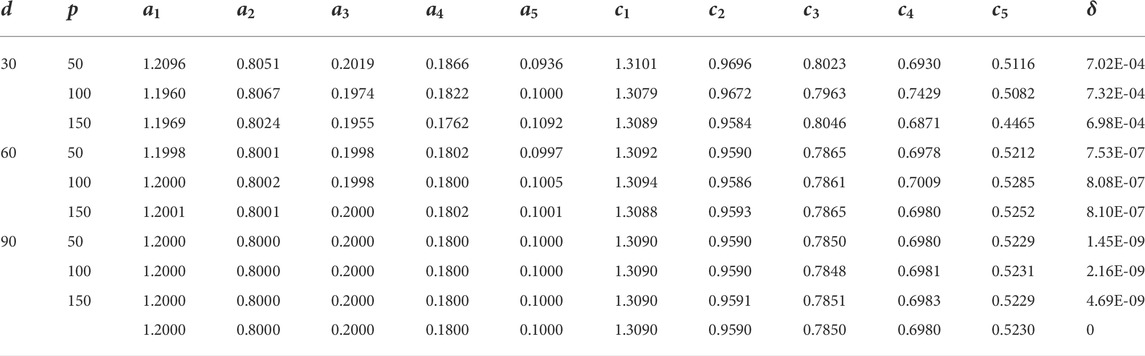
TABLE 6. Results of parameter estimates of Example 2 for G = 1,000.

TABLE 7

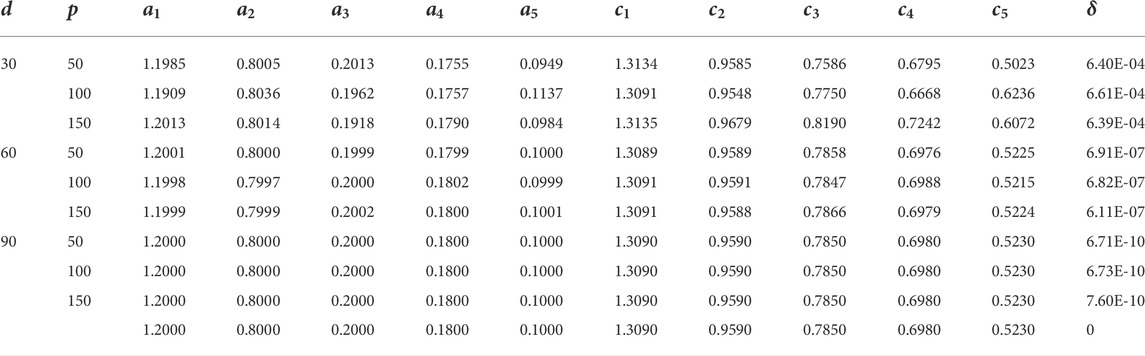
TABLE 7. Results of parameter estimates of Example 2 for G = 1,500.

TABLE 8

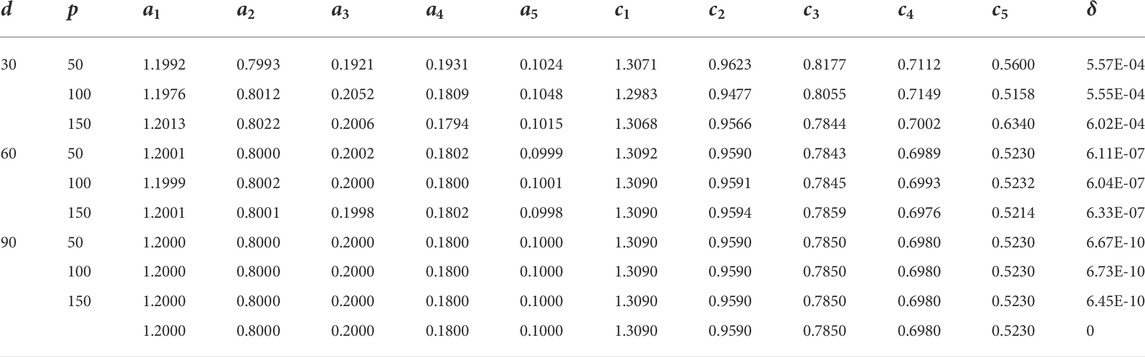
TABLE 8. Results of parameter estimates of Example 2 for G = 2000.

FIGURE 2

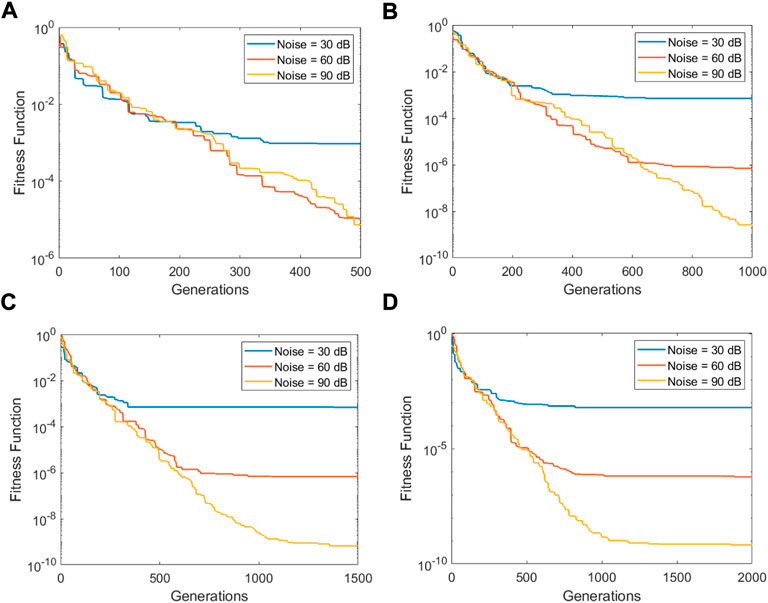
FIGURE 2. Convergence plots of Example 1: (A) G = 500, (B) G = 500, (C) G = 500, and (D) G = 500.

FIGURE 3

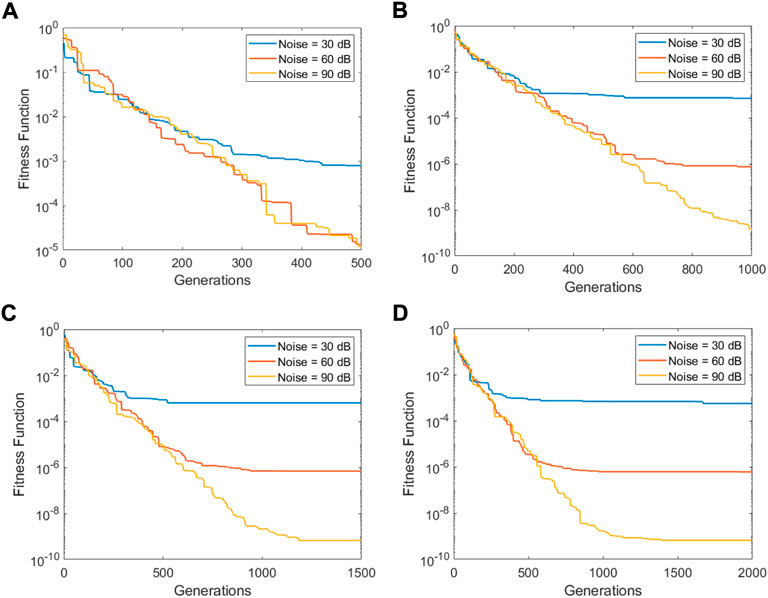
FIGURE 3. Convergence plots of Example 1: (A) G = 500, (B) G = 500, (C) G = 500, and (D) G = 500.

4 Conclusion

This study exploits a swarm intelligence–based cuckoo search optimization, CSO, heuristic for parameter estimation of power system harmonics. The CSO accurately estimates the amplitude and phase parameters associated with the first, third, fifth, and eleventh harmonic components. Simulation studies conducted on the mean square error–based evaluation metric indicate that the accuracy of the CSO increases with an increase in the generation size, while increasing particle size has not shown a significant rise in the accuracy level. Moreover, the CSO has shown a robust performance in estimating the parameters of power system harmonics for different scenarios of additive white Gaussian noise.

Future studies may investigate the applying of the CSO algorithm for real-time harmonics estimation and for other engineering optimization problems (Phannil et al., 2018; Montoya et al., 2019; Beleiu et al., 2020; Yang et al., 2020; Chaudhary et al., 2021).

Data availability statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

Conceptualization: NC and MZ; methodology: NM, NC, and MZ; software: NM; validation: ZK, AK, MZ, and NC; resources: AK and CC; writing—original draft preparation: NM; writing—review and editing: NC, ZK, AK, and MZ; supervision: CC and NC; project administration: AM and AA; funding acquisition: AM and AA.

Funding

The Deanship of Scientific Research (DSR) at King Abdulaziz University (KAU), Jeddah, Saudi Arabia has funded this project, under grant no. (KEP-MSc: 122-135-1443).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, editors, and reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

AbdelAty, A. M., Fouda, M. E., and Eltawil, A. (2022). Parameter estimation of two spiking neuron models with meta-heuristic optimization algorithms. Front. Neuroinform. 16, 771730. doi:10.3389/fninf.2022.771730

PubMed Abstract | CrossRef Full Text | Google Scholar

Altaf, F., Chang, C. L., Chaudhary, N. I., Raja, M. A. Z., Cheema, K. M., Shu, C. M., et al. (2022). Adaptive evolutionary computation for nonlinear hammerstein control autoregressive systems with key term separation principle. Mathematics 10 (6), 1001. doi:10.3390/math10061001

CrossRef Full Text | Google Scholar

Arqub, O. A., and Al-Smadi, M. (2020). Numerical solutions of Riesz fractional diffusion and advection-dispersion equations in porous media using iterative reproducing kernel algorithm. J. Porous Media 23 (8), 783–804. doi:10.1615/jpormedia.2020025011

CrossRef Full Text | Google Scholar

Arqub, O. A. (2016). Approximate solutions of DASs with nonclassical boundary conditions using novel reproducing kernel algorithm. Fundam. Inf. 146 (3), 231–254. doi:10.3233/fi-2016-1384

CrossRef Full Text | Google Scholar

Arqub, O. A. (2020). Numerical simulation of time-fractional partial differential equations arising in fluid flows via reproducing Kernel method. Int. J. Numer. Methods Heat. Fluid Flow. 30, 4711–4733. doi:10.1108/hff-10-2017-0394

CrossRef Full Text | Google Scholar

Arqub, O. A. (2018). Numerical solutions for the Robin time-fractional partial differential equations of heat and fluid flows based on the reproducing kernel algorithm. Int. J. Numer. Methods Heat. Fluid Flow. 28, 828–856. doi:10.1108/hff-07-2016-0278

CrossRef Full Text | Google Scholar

Baradarani, F., Zadeh, M. R. D., and Zamani, M. A. (2014). A phase-angle estimation method for synchronization of grid-connected power-electronic converters. IEEE Trans. Power Deliv. 30 (2), 827–835. doi:10.1109/tpwrd.2014.2362930

CrossRef Full Text | Google Scholar

Beleiu, H. G., Maier, V., Pavel, S. G., Birou, I., Pică, C. S., and Dărab, P. C. (2020). Harmonics consequences on drive systems with induction motor. Appl. Sci. 10 (4), 1528. doi:10.3390/app10041528

CrossRef Full Text | Google Scholar

Chaudhary, N. I., Latif, R., Raja, M. A. Z., and Machado, J. T. (2020). An innovative fractional order LMS algorithm for power signal parameter estimation. Appl. Math. Model. 83, 703–718. doi:10.1016/j.apm.2020.03.014

CrossRef Full Text | Google Scholar

Chaudhary, N. I., Zubair, S., and Raja, M. A. Z. (2017). A new computing approach for power signal modeling using fractional adaptive algorithms. ISA Trans. 68, 189–202. doi:10.1016/j.isatra.2017.03.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Chaudhary, N. I., Raja, M. A. Z., He, Y., Khan, Z. A., and Tenreiro Machado, J. (2021). Design of multi innovation fractional LMS algorithm for parameter estimation of input nonlinear control autoregressive systems. Appl. Math. Model. 93, 412–425. doi:10.1016/j.apm.2020.12.035

CrossRef Full Text | Google Scholar

Cuong-Le, T., Minh, H. L., Khatir, S., Wahab, M. A., Tran, M. T., and Mirjalili, S. (2021). A novel version of Cuckoo search algorithm for solving optimization problems. Expert Syst. Appl. 186, 115669. doi:10.1016/j.eswa.2021.115669

CrossRef Full Text | Google Scholar

Das, S. R., Ray, P. K., Sahoo, A. K., Balasubramanian, K., and Reddy, G. S. (2020). Improvement of power quality in a three-phase system using an adaline-based multilevel inverter. Front. Energy Res. 8, 23. doi:10.3389/fenrg.2020.00023

CrossRef Full Text | Google Scholar

do Nascimento Sepulchro, W., Encarnação, L. F., and Brunoro, M. (2014). Harmonic state and power flow estimation in distribution systems using evolutionary strategy. J. Control Autom. Electr. Syst. 25 (3), 358–367. doi:10.1007/s40313-014-0110-1

CrossRef Full Text | Google Scholar

Elnady, A., Al-Shabi, M., and Adam, A. A. (2020). Novel filters based operational scheme for five-level diode-clamped inverters in microgrid. Front. Energy Res. 8, 11. doi:10.3389/fenrg.2020.00011

CrossRef Full Text | Google Scholar

Elvira-Ortiz, D. A., Jaen-Cuellar, A. Y., Morinigo-Sotelo, D., Morales-Velazquez, L., Osornio-Rios, R. A., and Romero-Troncoso, R. d. J. (2020). Genetic algorithm methodology for the estimation of generated power and harmonic content in photovoltaic generation. Appl. Sci. 10 (2), 542. doi:10.3390/app10020542

CrossRef Full Text | Google Scholar

Enayati, J., and Moravej, Z. (2017). Real‐time harmonics estimation in power systems using a novel hybrid algorithm. IET Gener. Transm. &amp. Distrib. 11 (14), 3532–3538. doi:10.1049/iet-gtd.2017.0044

CrossRef Full Text | Google Scholar

Francesca, G., and Birattari, M. (2016). Automatic design of robot swarms: Achievements and challenges. Front. Robot. AI 3, 29. doi:10.3389/frobt.2016.00029

CrossRef Full Text | Google Scholar

Gude, S., and Jana, K. C. (2020). Parameter extraction of photovoltaic cell using an improved cuckoo search optimization. Sol. Energy 204, 280–293. doi:10.1016/j.solener.2020.04.036

CrossRef Full Text | Google Scholar

Houssein, E. H., Hosney, M. E., Elhoseny, M., Oliva, D., Mohamed, W. M., and Hassaballah, M. (2020). Hybrid Harris hawks optimization with cuckoo search for drug design and discovery in chemoinformatics. Sci. Rep. 10 (1), 14439–14522. doi:10.1038/s41598-020-71502-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Jafarpisheh, B., Madani, S. M., and Shahrtash, S. M. (2016). A new DFT-based phasor estimation algorithm using high-frequency modulation. IEEE Trans. Power Deliv. 32 (6), 1–2423. doi:10.1109/tpwrd.2016.2629762

CrossRef Full Text | Google Scholar

Jana, G., Mitra, A., Pan, S., Sural, S., and Chattaraj, P. K. (2019). Modified particle swarm optimization algorithms for the generation of stable structures of carbon clusters, Cn (n= 3–6, 10). Front. Chem. 7, 485. doi:10.3389/fchem.2019.00485

PubMed Abstract | CrossRef Full Text | Google Scholar

Kabalci, Y., Kockanat, S., and Kabalci, E. (2018). A modified ABC algorithm approach for power system harmonic estimation problems. Electr. power Syst. Res. 154, 160–173. doi:10.1016/j.epsr.2017.08.019

CrossRef Full Text | Google Scholar

Karahan, O. (2021). Design of optimal fractional order fuzzy PID controller based on cuckoo search algorithm for core power control in molten salt reactors. Prog. Nucl. Energy 139, 103868. doi:10.1016/j.pnucene.2021.103868

CrossRef Full Text | Google Scholar

Li, X., and Yin, M. (2015). Modified cuckoo search algorithm with self adaptive parameter method. Inf. Sci. 298, 80–97.doi:10.1016/j.ins.2014.11.042

CrossRef Full Text | Google Scholar

Malik, N. A., Chang, C. L., Chaudhary, N. I., Raja, M. A. Z., Cheema, K. M., Shu, C. M., et al. (2022). Knacks of fractional order swarming intelligence for parameter estimation of harmonics in electrical systems. Mathematics 10 (9), 1570. doi:10.3390/math10091570

CrossRef Full Text | Google Scholar

Mehmood, A., Raja, M. A. Z., Zameer, A., and Chaudhary, N. I. (2021). Design of backtracking search heuristics for parameter estimation of power signals. Neural comput. Appl. 33 (5), 1479–1496. doi:10.1007/s00521-020-05029-9

CrossRef Full Text | Google Scholar

Mehmood, A., Chaudhary, N. I., Zameer, A., and Raja, M. A. Z. (2020). Novel computing paradigms for parameter estimation in power signal models. Neural comput. Appl. 32 (10), 6253–6282. doi:10.1007/s00521-019-04133-9

CrossRef Full Text | Google Scholar

Montoya, F. G., Baños, R., Alcayde, A., and Arrabal-Campos, F. M. (2019). Analysis of power flow under non-sinusoidal conditions in the presence of harmonics and interharmonics using geometric algebra. Int. J. Electr. Power & Energy Syst. 111, 486–492. doi:10.1016/j.ijepes.2019.04.032

CrossRef Full Text | Google Scholar

Pandey, A. C., Rajpoot, D. S., and Saraswat, M. (2017). Twitter sentiment analysis using hybrid cuckoo search method. Inf. Process. Manag. 53 (4), 764–779. doi:10.1016/j.ipm.2017.02.004

CrossRef Full Text | Google Scholar

Phannil, N., Jettanasen, C., and Ngaopitakkul, A. (2018). Harmonics and reduction of energy consumption in lighting systems by using LED lamps. Energies 11 (11), 3169. doi:10.3390/en11113169

CrossRef Full Text | Google Scholar

Ray, P. K., and Subudhi, B. (2012). BFO optimized RLS algorithm for power system harmonics estimation. Appl. Soft Comput. 12 (8), 1965–1977. doi:10.1016/j.asoc.2012.03.008

CrossRef Full Text | Google Scholar

Ray, P. K., and Subudhi, B. (2015). Neuro-evolutionary approaches to power system harmonics estimation. Int. J. Electr. Power & Energy Syst. 64, 212–220. doi:10.1016/j.ijepes.2014.07.035

CrossRef Full Text | Google Scholar

Rivas, A. E. L., da Silva, N., and Abrão, T. (2020). Adaptive current harmonic estimation under fault conditions for smart grid systems. Electr. Power Syst. Res. 183, 106276. doi:10.1016/j.epsr.2020.106276

CrossRef Full Text | Google Scholar

Sabir, Z., Raja, M. A. Z., Guirao, J. L., and Shoaib, M. (2020). A neuro-swarming intelligence-based computing for second order singular periodic non-linear boundary value problems. Front. Phys. 8, 224. doi:10.3389/fphy.2020.00224

CrossRef Full Text | Google Scholar

Santos, E., Khosravy, M., Lima, M. A., Cerqueira, A. S., and Duque, C. A. (2020). ESPRIT associated with filter bank for power-line harmonics, sub-harmonics and inter-harmonics parameters estimation. Int. J. Electr. Power & Energy Syst. 118, 105731. doi:10.1016/j.ijepes.2019.105731

CrossRef Full Text | Google Scholar

Shuai, Z., Zhang, J., Tang, L., Teng, Z., and Wen, H. (2018). Frequency shifting and filtering algorithm for power system harmonic estimation. IEEE Trans. Ind. Inf. 15 (3), 1554–1565. doi:10.1109/tii.2018.2844191

CrossRef Full Text | Google Scholar

Singh, S. K., Sinha, N., Goswami, A. K., and Sinha, N. (2016). Robust estimation of power system harmonics using a hybrid firefly based recursive least square algorithm. Int. J. Electr. Power & Energy Syst. 80, 287–296. doi:10.1016/j.ijepes.2016.01.046

CrossRef Full Text | Google Scholar

Song, P. C., Pan, J. S., and Chu, S. C. (2020). A parallel compact cuckoo search algorithm for three-dimensional path planning. Appl. Soft Comput. 94, 106443. doi:10.1016/j.asoc.2020.106443

CrossRef Full Text | Google Scholar

Sun, J., Aboutanios, E., Smith, D. B., and Fletcher, J. E. (2019). Robust frequency, phase, and amplitude estimation in power systems considering harmonics. IEEE Trans. Power Deliv. 35 (3), 1158–1168. doi:10.1109/tpwrd.2019.2936885

CrossRef Full Text | Google Scholar

Sweis, H., Shawagfeh, N., and Arqub, O. A. (2022). Fractional crossover delay differential equations of Mittag-Leffler kernel: Existence, uniqueness, and numerical solutions using the Galerkin algorithm based on shifted Legendre polynomials. Results Phys. 41, 105891. doi:10.1016/j.rinp.2022.105891

CrossRef Full Text | Google Scholar

Tran-Ngoc, H., Khatir, S., De Roeck, G., Bui-Tien, T., and Wahab, M. A. (2019). An efficient artificial neural network for damage detection in bridges and beam-like structures by improving training parameters using cuckoo search algorithm. Eng. Struct. 199, 109637. doi:10.1016/j.engstruct.2019.109637

CrossRef Full Text | Google Scholar

Xu, L., Chen, F., Ding, F., Alsaedi, A., and Hayat, T. (2021). Hierarchical recursive signal modeling for multifrequency signals based on discrete measured data. Int. J. Adapt. Control Signal Process. 35 (5), 676–693. doi:10.1002/acs.3221

CrossRef Full Text | Google Scholar

Xu, L., and Ding, F. (2018). Iterative parameter estimation for signal models based on measured data. Circuits Syst. Signal Process. 37 (7), 3046–3069. doi:10.1007/s00034-017-0705-4

CrossRef Full Text | Google Scholar

Xu, L., and Ding, F. (2017). Recursive least squares and multi-innovation stochastic gradient parameter estimation methods for signal modeling. Circuits Syst. Signal Process. 36 (4), 1735–1753. doi:10.1007/s00034-016-0378-4

CrossRef Full Text | Google Scholar

Xu, L., Ding, F., and Zhu, Q. (2022). Separable synchronous multi-innovation gradient-based iterative signal modeling from on-line measurements. IEEE Trans. Instrum. Meas. 71, 1–13. doi:10.1109/tim.2022.3154797

CrossRef Full Text | Google Scholar

Xu, L. (2022). Separable multi-innovation Newton iterative modeling algorithm for multi-frequency signals based on the sliding measurement window. Circuits Syst. Signal Process. 41 (2), 805–830. doi:10.1007/s00034-021-01801-x

CrossRef Full Text | Google Scholar

Xu, L. (2022). Separable Newton recursive estimation method through system responses based on dynamically discrete measurements with increasing data length. Int. J. Control Autom. Syst. 20 (2), 432–443. doi:10.1007/s12555-020-0619-y

CrossRef Full Text | Google Scholar

Xu, L., and Song, G. (2020). A recursive parameter estimation algorithm for modeling signals with multi-frequencies. Circuits Syst. Signal Process. 39 (8), 4198–4224. doi:10.1007/s00034-020-01356-3

CrossRef Full Text | Google Scholar

Yang, X. S. (2022). MATLAB Central File Exchange. Avaliable at: https://www.mathworks.com/matlabcentral/fileexchange/29809-cuckoo-search-cs-algorithm September 30, 2022).

Google Scholar

Yang, X. S., and Deb, S. (2009). “Cuckoo search via Lévy flights,” in Proceedings of the 2009 World congress on nature & biologically inspired computing (NaBIC), Coimbatore, India, December 2009 (IEEE), 210–214. doi:10.1109/NABIC.2009.5393690

CrossRef Full Text | Google Scholar

Yang, X. S., and Deb, S. (2014). Cuckoo search: Recent advances and applications. Neural comput. Appl. 24 (1), 169–174. doi:10.1007/s00521-013-1367-1

CrossRef Full Text | Google Scholar

Yang, X., Yang, Y., Liu, Y., and Deng, Z. (2020). A reliability assessment approach for electric power systems considering wind power uncertainty. IEEE Access 8, 12467–12478. doi:10.1109/access.2020.2966275

CrossRef Full Text | Google Scholar

Yu, J., Kim, C. H., and Rhee, S. B. (2020). Clustering cuckoo search optimization for economic load dispatch problem. Neural comput. Appl. 32 (22), 16951–16969. doi:10.1007/s00521-020-05036-w

CrossRef Full Text | Google Scholar

Zubair, S., Chaudhary, N. I., Khan, Z. A., and Wang, W. (2018). Momentum fractional LMS for power signal parameter estimation. Signal Process. 142, 441–449. doi:10.1016/j.sigpro.2017.08.009

CrossRef Full Text | Google Scholar