Deep learning model-transformer based wind power forecasting approach

The uncertainty and fluctuation are the major challenges casted by the large penetration of wind power (WP). As one of the most important solutions for tackling these issues, accurate forecasting is able to enhance the wind energy consumption and improve the penetration rate of WP. In this paper, we propose a deep learning model-transformer based wind power forecasting (WPF) model. The transformer is a neural network architecture based on the attention mechanism, which is clearly different from other deep learning models such as CNN or RNN. The basic unit of the transformer network consists of residual structure, self-attention mechanism and feedforward network. The overall multilayer encoder to decoder structure enables the network to complete modeling of sequential data. By comparing the forecasting results with other four deep learning models, such as LSTM, the accuracy and efficiency of transformer have been validated. Furthermore, the migration learning experiments show that transformer can also provide good migration performance.

1 Introduction

Wind energy is an economical, efficient and environment friendly renewable energy source that plays an important role in reducing global carbon emissions (Lin and Liu, 2020). According to Global Wind Report 2022, total installed WP capacity had reached 837 GW by the end of 2021 (Council, 2022). As the proportion of installed wind turbines (WTs) increases year by year, the strong randomness, volatility and intermittency of WP lead to the contradiction between the safe operation of the power grid and the efficient consumption of WP (Yang et al., 2022). Accurate forecasting can reduce the uncertainty and increase the penetration rate of WP.

The WPF mentioned in this paper refers to the forecasting of specific point values of future wind speed or WP. It is called the deterministic forecasting model, which mainly includes physical forecasting models, statistical forecasting models and hybrid forecasting models (Hanifi et al., 2020; Sun et al., 2021).

Physical forecasting modeling obtains wind speed forecasting information based on numerical weather forecast data with mathematical models, and then predicts WP with the help of relevant WP curves using the wind speed forecasts (Li et al., 2013). Therefore improving the accuracy of the NWP model directly affects the forecasting accuracy of the physical model (Cassola and Burlando, 2012).

Statistical forecasting modeling is establishing a mapping relationship between historical data and forecasted data. Statistical models can be classified into traditional statistical models, time series models, traditional machine learning models and deep learning models. The persistence method, known as the most classical traditional statistical method, uses the wind power at the current moment as the forecasted value. This method is simple but limited to the use of ultra-short-term forecasting (Wu and Hong, 2007). Commonly used time series models include AutoreGressive (AR) (Poggi et al., 2003), Auto Regression Moving Average (ARMA) (Huang et al., 2012), Autoregressive Integrated Moving Average (ARIMA) (Hodge et al., 2011), etc. Time series models are difficult to explore the non-linear relationship in the data. So such models are only suitable for static data analysis. Traditional machine learning models can predict future wind power value adaptively based on historical WP data. Machine learning models are widely used in wind power forecasting and related fields. The popular methods include artificial neuro network (ANN) (Hu et al., 2016), support vector machine (SVM) (Li et al., 2020), Piecewise support vector machine (PSVM) (Liu et al., 2009), Least Square support vector machine (LSSVM) (Chen et al., 2016), Random Forest (RF) (Lahouar and Slama, 2017), Bayesian Additive RegressionTrees (Alipour et al., 2019), K-Nearest-Neighbors (KNN) (Yesilbudak et al., 2017), etc. These machine learning models require additional time to extract features from multidimensional data with good accuracy and relevance. Optimization algorithms can effectively solve this problem (Shahid et al., 2021). Li et al. (2021) proposed a hybrid improved cuckoo search algorithm to optimize the hyperparameters of support vector machines for short-term wind power forecasting.

In recent years, deep learning models have provided promising performance in natural language processing (NLP), computer vision and other fields, while related techniques are also applied to wind power forecasting. Among them, two recurrent neural networks (RNN), Long Short Term Memory (LSTM) and Gated Recurrent Unit (GRU), are mainly utilized for wind power forecasting research (Lu et al., 2018; Deng et al., 2020; Wang et al., 2020). used wavelet decomposition to reduce the volatility of the original series. They transformed non-stationary time series into stable and predictable series to forecast by LSTM Liu et al. (2020). enhanced the effect of forgetting gate in LSTM, optimized the convergence speed, and filtered the feature data within a certain distance based on correlation. The forecasting permance was futher improved by clustering Yu et al. (2019). used variable mode decomposition to stratify wind power sequences according to different frequencies. Then similar fluctuating patterns were identified in each layer by K-means clustering algorithm. Furthermore, the unstable features were captured in each set by LSTM Sun et al. (2019). To address the overfitting problem, employed multi-level residual networks and DenseNet to improve the overall performance Ko et al. (2020). introduced the attention mechanism into the GRU to obtain a novel sequence-to-sequence model Niu et al. (2020). The combination of multiple deep learning models can also improve the accuracy of WPF. proposed a novel spatio-temporal correlation model (STCM) for ultra-short-term wind power forecasting Wu et al. (2021). proposed a hybrid deep learning algorithm, which consists of GRU, LSTM, and fully connected neural networks, to accurately predict ultra-short-term wind power generation at the Boco Rock wind farm in Australia, Hossain et al. (2020). The RNN model is unable to capture the long periods temporal correlation due to the gradient disappearance problem. To address this problem, Lai et al. (2018) developed an RNN-skip structure with time-hopping connections to extend the time span of the information flow. RNN also suffers from the inability of recursive computation to parallelize problem. The transformer is the first sequence transcription model based solely on the attention mechanism, which has been proved that it can solve the aforementioned problems (Vaswani et al., 2017). The transformer was first proposed in NLP. BERT (Devlin et al., 2018), GPT-2 (Radford et al., 2019), RoBERTa (Liu et al., 2019), T5 (Raffel et al., 2020) and BART (Lewis et al., 2019) based on transformer have made a huge impact in the NLP field. Recently, almost all advanced NLP models have been adapted from one of above basic models (Bommasani et al., 2021). Transformer made a big splash in the field of computer visiona along with the publication of the VIT (Dosovitskiy et al., 2020), CvT (Wu et al., 2021), CaiT (Touvron et al., 2021), DETR (Carion et al., 2020), and Swin Transformer (Liu et al., 2021). Transformer was also applied to the field of power system time series forecasting. Lin et al. employed the Spring DWT attention layer to measure the similarity of query-key pairs of sequences (Lin et al., 2020). Santos et al. and Phan et al. employed the transformer-based time series forecasting model to predict the PV power generation for each hour (López Santos et al., 2022; Phan et al., 2022). L'Heureux et al. proposed a transformer-based architecture for load forecasting (L’Heureux et al., 2022).

Transformer architecture has become a mainstream technology in NLP which performs better than RNN or Seq2Seq algorithms. For this reason, this paper used the transformer as the basic model for wind power forecasting research.

The remainder of the paper is organized as follows. Section 2 presents the forecasting problem. Section 3 introduces Data-driven model of wind power forecasting. Section 4 shows the analysis and discussion of the numerical simulation results. Section 5 concludes this paper.

2 Problem description

In this paper, wind power forecasting refers to making speculations about the possible levels of wind power in several future periods.

Suppose $\mathit{D}=\left\{{\mathit{D}}_1,{\mathit{D}}_2,\cdots ,{\mathit{D}}_{\mathit{n}}\right\}$ is the historical information collected from WPAPs, where $\mathit{n}$ is the number of WPAPs. ${\mathit{D}}_{\mathit{i}}=\left\{{\mathit{P}}_{\mathit{i}},{\mathit{F}}_{\mathit{i}}\right\}$ is the historical information of $\mathit{i}$ th WPAP, where ${\mathit{P}}_{\mathit{i}}$. is the power output of the $\mathit{i}$ th WPAP and ${\mathit{F}}_{\mathit{i}}$ is other characteristic information of the $\mathit{i}$ th WPAP. For each ${\mathit{P}}_{\mathit{i}}^{\mathit{t}}$ in ${\mathit{P}}_{\mathit{i}}=\left\{{\mathit{P}}_{\mathit{i}}^1,{\mathit{P}}_{\mathit{i}}^2,\cdots ,{\mathit{P}}_{\mathit{i}}^{\mathit{t}}\right\}$ is the power outputs of the $\mathit{i}$ th WPAP at timestamp $\mathit{t}$. For each ${\mathit{F}}_{\mathit{i},\mathit{j}}^{\mathit{t}}$ in ${\mathit{F}}_{\mathit{i}}=\left\{{\mathit{F}}_{\mathit{i},1}^1,{\mathit{F}}_{\mathit{i},1}^2,\cdots ,{\mathit{F}}_{\mathit{i},1}^{\mathit{t}},{\mathit{F}}_{\mathit{i},2}^1,{\mathit{F}}_{\mathit{i},2}^2,\cdots ,{\mathit{F}}_{\mathit{i},2}^{\mathit{t}},\cdots ,{\mathit{F}}_{\mathit{i},\mathit{j}}^1,{\mathit{F}}_{\mathit{i},\mathit{j}}^2,\cdots ,{\mathit{F}}_{\mathit{i},\mathit{j}}^{\mathit{t}}\right\}$ is the $\mathit{j}$ th feature data of the $\mathit{i}$ th WPAP at timestamp $\mathit{t}$. Common characteristics are wind speed and WPAP ambient temperature, etc. The one-step ahead wind power sequence forecasting model $\mathit{f}$ can be denoted as:

$P_i^{pre}=f\left(D_i\right),i\in \left[0,n\right]$

Where $P_i^{pre}$ denotes the power forecasting sequence of the $i$ th WPAP.

3 Deep learning model for wind power forecasting

In this paper, the transformer is chosen as the basic deep learning model for wind power forecasting because it is considered to use a broader inductive bias compared to RNN, allowing it to handle more generalized information. The inductive bias of a learning algorithm is the set of assumptions that the learner uses to predict outputs of given inputs that it has not encountered. For example, the loop structure and gate structure are the inductive bias of RNNs. The transformer model mainly includes self-attentive mechanisms, position-wise feed-forward networks and residual connections. These three neural network structures do not rely on strong assumptions on the objective function. Furthermore, they do not have the inductive bias as translation invariance or the time invariance. So, a much more general form makes the transformer model applicable to more subjects. In this section, we introduce the structure of the transformer.

3.1 Encoder to decoder structure

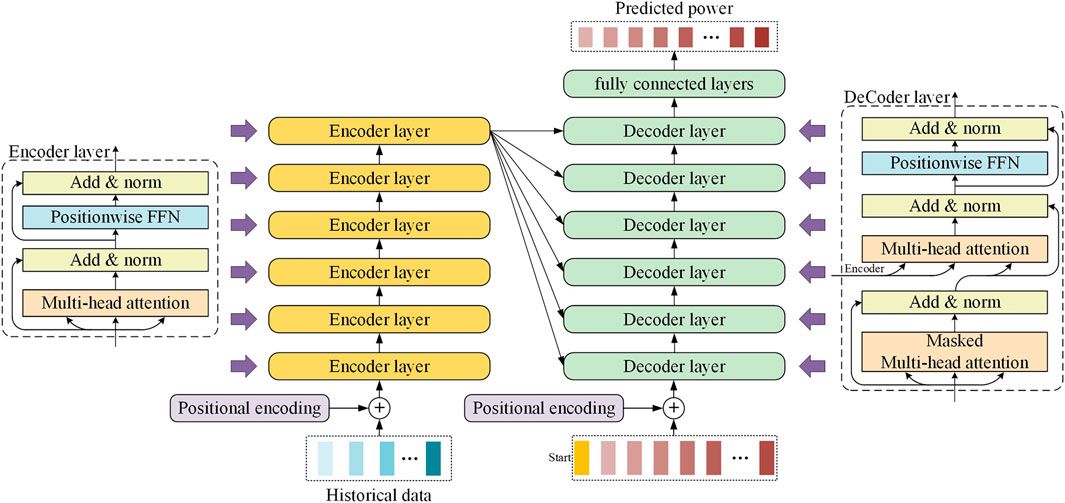
Numerous wind power sequence forecasting models follow the encoder to decoder structure (Lu et al., 2018; Niu et al., 2020; Li and Armandpour, 2022), which is illustrated in Figure 1. The encoder maps the WPAP historical sequence data $D=\left\{D_1,D_2,\cdots ,D_n\right\}$ to the hidden state $\mathrm{H}=\left\{{\mathrm{H}}_1,{\mathrm{H}}_2,\cdots ,{\mathrm{H}}_n\right\}$. The decoder then outputs the forecasted power sequence $P^{pre}=\left\{P_1^{pre},P_2^{pre},\cdots ,P_n^{pre}\right\}$ based on the hidden state $\mathrm{H}$. As shown in Figure 2, transformer architecture also follows this architecture and uses stacked self-attentive mechanisms, pointwise fully connected layers and the RetNet structure (He et al., 2016) to build the decoder and encoder. Encoder consist of a self-defined number of identical encoder layers stacked on top of each other. Each encoder layer has two sub-layers: multi-head self-attention mechanism and position-wise fully connected feed-forward network. Each sub-layer uses a residual structure and then the output data is layer-normalized which can be expressed as:

$O_{sub}=\mathit{LN}\left(x+SL\left(x\right)\right)$

Where $O_{sub}$ is the output of sub-layer, $x$ is the input of the sub-layer, LN is the layer normalization function, SL is the function employed in the sub-layer.

FIGURE 1

FIGURE 1. Encoder to decoder structure.

FIGURE 2

FIGURE 2. Encoder and decoder stacks of transformer.

To facilitate residual connectivity, outputs produced from all sublayers in the model as well as the embedding layer have the same self-defined dimension $d_{model}$.

The decoder has the same number of stack layers as the encoder. each decoder layer consists of three sub-layers. The first sublayer is the Masked Multi-head attention layer, whose main function is to ensure that the forecasting of position $i$ only depends on the known outputs of positions smaller than $i$. The last two layers use the same sub-layers as the encoder layer. Each sub-layer has a residual architecture and layer normalization of the output.

3.2 Self-attentive mechanism

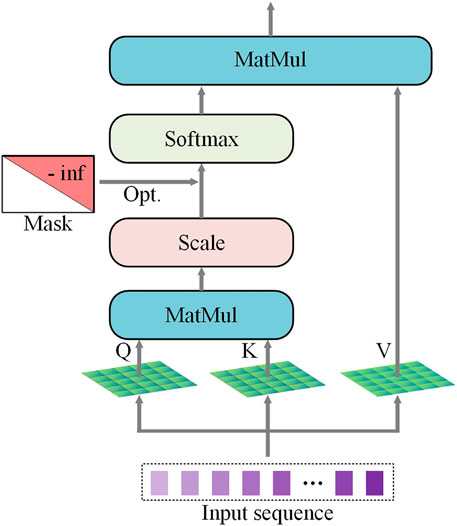
The attention mechanism (AM) is a resource allocation scheme that allocates computational resources to more important tasks while solving the information overload problem in the presence of limited computational power. The input information of AM can be represented by key vector -value vector pairs [$\left(k_1,v_1\right),\left(k_2,v_2\right),\dots ,\left(k_m,v_m\right)$]. The target value information can be represented by query vector. The weight of the value vectors are calculated based on the similarity of query vector and key vector. And then, the final attention value can be obtained by weighted summation of value vector. The core idea of the attention mechanism can be expressed as the following equation.

$\begin{array}{c}{S}_{att}=\mathrm{W}\times \mathrm{V}\\ \mathrm{W}=\mathrm{f}\mathrm{u}\mathrm{n}\mathrm{c}\left(\mathrm{Q},\mathrm{K}\right)\end{array}$

Where $S_{att}$ is the attention value, V is the value vector of key-value pairs, K is the key vector of key-value pairs, Q is the query vector, W is the corresponding weight of V and $\mathrm{f}\mathrm{u}\mathrm{n}\mathrm{c}$ is the weight transformation function.

The self-attentive mechanism (SAM) uses three learnable parameter matrices $W_q$, $W_k$ and $W_v$ to transform the input sequence X into the query vector $Q_s$, key vector $K_s$ and value vector $V_s$. The model uses a SoftMax function as the weight transformation function. The weights of the $V_s$ are obtained by calculating the dot product of $Q_s$ and $K_s$ divided by $\sqrt{d_k}$. The output of SAM is obtained by weighted summation of $V_s$, as depicted in Figure 3.

$\begin{array}{c}{Q}_s=W_{Q}X\in {\mathbb{R}}^{d_k\times N}\\ K_s=W_{K}X\in {\mathbb{R}}^{d_k\times N}\\ V_s=W_{V}X\in {\mathbb{R}}^{d_v\times N}\\ \mathrm{A}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\left(Q,K,V\right)=\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)V\end{array}$

Where $d_k$ is the dimension of $K_s$.

FIGURE 3

FIGURE 3. Self-attention with masking function.

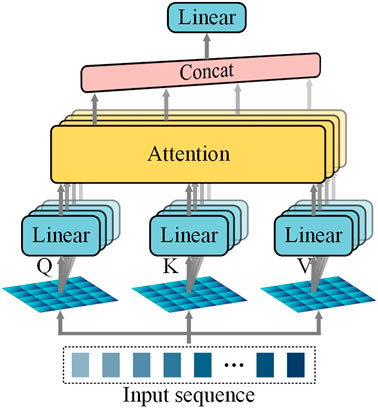
3.3 Multi-head attention and masked multi-head attention

Multi-head attention mechanism uses different weight matrices to project the single attention head input sequence into different subspaces, which allows the model to focus on different aspects of information. The different weight matrices $W_i^Q$, $W_i^K$ and $W_i^V$ transform the vectors $Q$, $K$ and $V$ of dimension $d_{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}$ into $h$ vectors $Q_i$, $K_i$ and $V_i$ of dimensiond $d_{model}/h$ and input them into the corresponding parallel attention layers, where h is the number of parallel layers. Then the outputs of each layer are concatenated and the results output via the linear layer, as depicted in Figure 4.

$\begin{array}{c}\mathrm{M}\mathrm{u}\mathrm{l}\mathrm{t}\mathrm{i}\mathrm{H}\mathrm{e}\mathrm{a}\mathrm{d}\left(Q,K,V\right)=\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{a}\mathrm{t}\left({\mathrm{h}\mathrm{e}\mathrm{a}\mathrm{d}}_1,\dots ,{\mathrm{h}\mathrm{e}\mathrm{a}\mathrm{d}}_h\right)W^O\\ \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}{head}_i=\mathrm{A}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\left(Q_i,K_i,V_i\right)\\ Q_i=Q{W}_i^Q\\ K_i=K{W}_i^K\\ V_i=V{W}_i^V\end{array}i=\mathrm{1,2},\dots ,h$

Where $W_i^Q\in {\mathbb{R}}^{d_{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}\times d_k}$, $W_i^K\in {\mathbb{R}}^{d_{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}\times d_k}$, $W_i^V\in {\mathbb{R}}^{d_{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}\times d_v}$, $W^O\in {\mathbb{R}}^{h{d}_v\times d_{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}}$, and $d_k=d_v=d_{model}/h$

FIGURE 4

FIGURE 4. Multi-head attention.

Masked multi-head attention mechanism is proposed to prevent the decoder from seeing future information. An upper triangular matrix with all values of "-inf” is added to the dot product matrix before it is softmaxed, as depicted in Figure 3.

3.4 Position-wise feed-forward networks and positional encoding

Each encoder and decoder layer contains a position-wise feed-forward networks, which is composed of two linear transformations and uses the ReLu function as the activation function. Due to the existence of two linear transformations, the inner layer dimension can be adjusted while the input and output dimensions are guaranteed to be equal to $d_{model}$. The formula is as follows.

$\begin{array}{c}\mathrm{F}\mathrm{F}\mathrm{N}\left(x\right)=ReLu\left(x{W}_1+b_1\right)W_2+b_2\\ \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}ReLu\left(x\right)=\mathit{max}\left(0,x\right)\end{array}$

where $W_1$ and $W_2$ are the two linear transformation matrixes, $b_1$ and $b_2$ are biases of the two linear transformations and $x$ is the input data.

Since transformer architecture does not contain recursion and there is no relative or absolute position information of each value in the inputs of the transformer, it is necessary to there is no relative or absolute position information of each value in the inputs of the transformer so that the model can make use of the sequential information. Transformer uses sine and cosine functions of different frequencies.

$\begin{array}{c}P{E}_{\left(pos,2id\right)}=\sin \left(pos/{10000}^{2id/d_{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}}\right)\\ P{E}_{\left(pos,2id+1\right)}=\cos \left(pos/{10000}^{2id/d_{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}}\right)\end{array}$

where $pos$ is the position and $id$ is the dimension.

3.5 Power forecasting and model migration

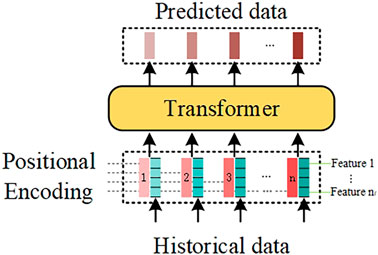
In this paper, transformer is used as the power prediction model. The historical feature data needs to be processed before it can be input into transformer. The transformation of historical data into feature vectors and positional encoding are shown in the Figure 5. The feature vector at each timestamp consists of different WPAP feature values in the specified order. Each encoder layer extracts features from the input data using the multi-head attention mechanism, position-wise feed-forward networks, normalization layer and residual structure. The last encoder layer passes the feature information to each decoder layer. The first sub-layer of each decoder layer extracts the sequence feature information from the predicted data. Finally, the predicted data of the specified length is processed by the fully-connected layer and output.

FIGURE 5

FIGURE 5. Data input.

Migrating the trained model parameters to another model for a related task can effectively speed up the model convergence and reduce the overfitting problem. The data between different WPAPs has some similarity. This paper proposes to train untrained WPAP prediction models which we migrate the trained WPAP power prediction model parameters to.

4 Experimental results and discussion

To verify the effectiveness of transformer for wind power forecasting, we conducted a case study using areal-world wind farm operation dataset.

4.1 Dataset preparation

In this paper, experiments are conducted by using the Spatial Dynamic Wind Power Forecasting (SDWPF) dataset, which is constructed based on real-world wind farm data from Longyuan Power Group Corp. Ltd. (Zhou et al., 2022). SDWPF contains 134 WPAPs output power, wind speed, ambient temperature and other characteristic information, which is sampled at 10-min intervals and covers 245 days of data. From them, we selected the power, wind speed and ambient temperature of eight WPAPs data as the feature information used for single turbine one-step ahead wind power prediction. Three data subsets are used in the evaluation: training set, validation set, and test set, and the three subsets are assigned in the ratio of 6:2:2 as shown in Figure 6. The training set is used to update the model parameters. First, the results of the forward calculation are stored for each parameter. Then, the partial derivatives of each parameter can be calculated through loss function based on the chain rule subsequently. At last, the partial derivatives are multiplied with the learning rate to obtain the optimized values of the parameters. The validation set is used for hyperparameter tuning during the model training, and the test set is used to evaluate the generalization ability of the model.

FIGURE 6

FIGURE 6. Data subset allocation ratio.

4.2 Data processing

The input variables used in this study are normalized in order to speed up the gradient descent for optimal solutions and to improve the accuracy of the model after training. The feature information is scaled to the range (0, 1) by min-max normalization, and the model output is denormalized.

$\begin{array}{c}{x}_{inp}^{\prime }=\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{l}\left(x_{inp}\right)\\ \mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{l}\left(x_{inp}\right)=\frac{x_{inp}-\mathit{max}\left(x_{inp}\right)}{\mathit{max}\left(x_{inp}\right)-\mathit{min}\left(x_{inp}\right)}\end{array}$

Where $x_{inp}^{\prime }$ is the normalized output of the model input data $x_{inp}$

$\begin{array}{c}{x}_{out}^{\prime }=de\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{l}\left(x_{out}\right)\\ \mathrm{d}\mathrm{e}\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{l}\left(x_{out}\right)=\frac{x_{out}-\mathit{max}\left(x_{in}\right)}{\mathit{max}\left(x_{in}\right)-\mathit{min}\left(x_{in}\right)}\end{array}$

Where $x_{out}^{\prime }$ is the denormalized output of the model output data $x_{out}$

4.3 Performance evaluation

In this paper, we use four metrics to evaluate the prediction performance of transformer, namely mean squared error (MSE), mean absolute error (MAE), mean square root error (RMSE), r2score, and explained variance (EV). They can be expressed mathematically as:

$\begin{array}{c}MSE=\frac{1}{l}{\displaystyle \sum }_{i=1}^l{\left(p-\widehat{p}\right)}^2\\ MAE=\frac{1}{l}{\displaystyle \sum }_{i=1}^l\left|p-\widehat{p}\right|\\ RMSE=\sqrt{\frac{1}{l}{\displaystyle \sum }_{i=1}^l{\left(p-\widehat{p}\right)}^2}\\ \mathrm{r}2\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}=1-\frac{\sum \left|p-\widehat{p}\right|}{\sum \left|p-p^{\prime }\right|}\end{array}$

Where p denotes the original power, $\widehat{p}$ denotes the forecasted power, $l$ denotes the length of the forecast series and $p^{\prime }$ denotes the mean value of original power.

The better the fit between the prediction structure and the actual results, the better $MSE$, $MAE$ and $RMSE$ tend to 0 and $\mathrm{r}2\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}$ tend to one

4.4 Experimental numerical results

In this paper, the experiments performed by all the models use the historical wind power data of the 40 h to predict the wind power value of the next 8 h.

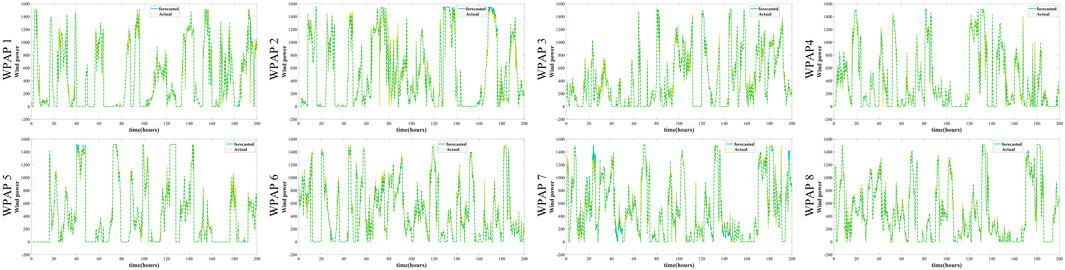
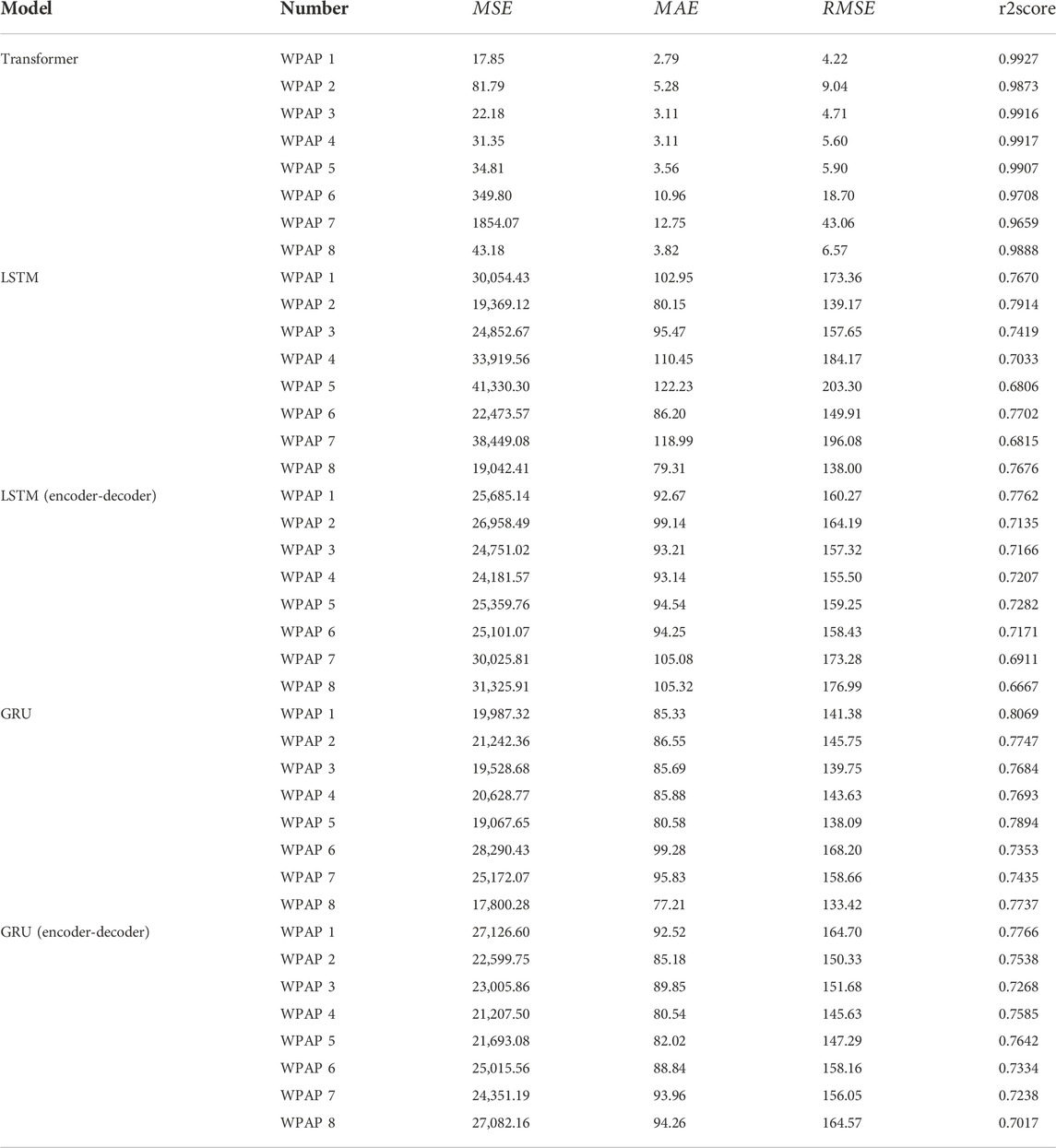
First, we use transformer to perform a one-step power forecasting on eight WPAPs datasets. A comparison of the predicted and actual power curves for each WPAP is shown in Figure 7. It can be seen that the predicted power of each WPAP can match the actual power well, and the two curves have similar trends. This power comparison graph shows that transformer has good prediction capability. Also, we perform the same experiments using LSTM, GRU models and LSTM and GRU models with encoder-decoder structure. The performance indexes for each WPAP power forecasting using the five models are shown in Table 1. It can be seen that the forecasting performance of transformer on this dataset is much better than the four models. The mean MSE, MAE and RMSE of transformer prediction results are 304.38, 5.67 and 12.23 respectively. They are small compared to the mean power output value of 393.47 and the maximum value of 1552.76. The mean r2score of transformer forecasting results is 0.9849, which is 33.47%, 37.50%, 27.88% and 32.66% improvement compared to 0.7379, 0.7163, 0.7702 and 0.7424 of the other four models. It can be seen that transformer forecasts very accurately, thanks to the structure of encoder-decoder, the design of multi-headed self-attentiveness, the ability of masked multi-headed self-attentiveness to extract sequence information and the structure of residuals, etc.

FIGURE 7

FIGURE 7. One-step power forecasting experimental results of NO.1-NO.8 WPAP.

TABLE 1

TABLE 1. Each prediction model corresponds to the performance index of each WPAP.

Transformer has certain generalization performance, and we randomly selected 12 WPAPs datasets, using the model parameters already trained by WPAP 1, to train the model and complete the prediction task. The experimental results are shown in Figure 8, and the prediction performance indexes of transformer migration learning on each t WPAP dataset and the distance of relative location between each WPAP and WPAP1 are shown in Table 2. The MSE, MAE and RMSE of forecasting results are 34.87, 3.35 and 5.57, which are also small. The r2score of 0.9904 is likewise very close to 1. Transformer has a better model migration effect due to its minimal inductive bias. It can be seen that other WPAPs within the same area can use the trained transformer model parameters for model training and achieve good prediction accuracy.

FIGURE 8

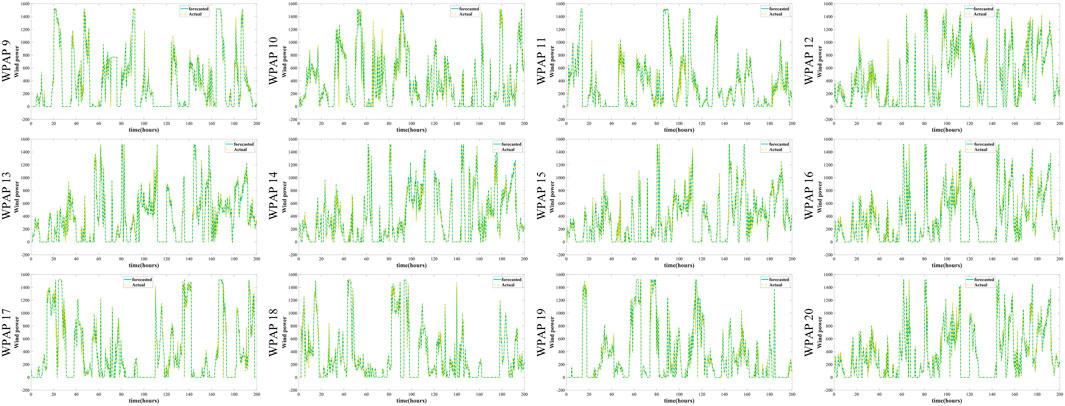
FIGURE 8. Transformer model migration based one-step power forecasting experimental results of NO.9-NO.20 WPAP.

TABLE 2

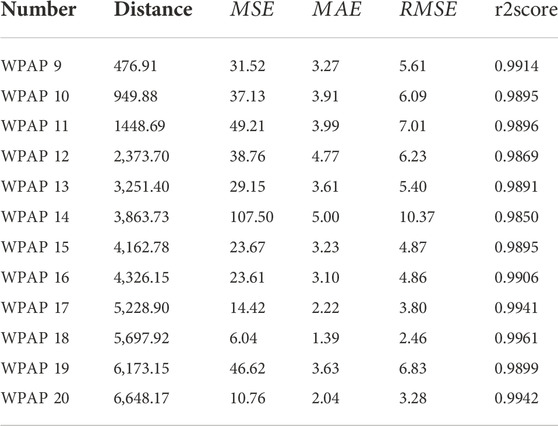
TABLE 2. Performance indicators of WPAPs 9 to 20 and the distance of relative location between each WPAP and WPAP one.

5 Conclusion

In this paper, we illustrate the principle of transformer with powerful sequence modeling capabilities such as encoder to decoder architecture, self-attentive mechanism, multi-headed attention, and sequence modeling using masks, and use it for WPAP power forecasting. We use 40 h of historical power data, wind speed data and ambient temperature data to predict the output power of WPAPs for the next 8 h. The mean values of MSE, MAE and RMSE of the transformer model prediction results are 304.38, 5.67 and 12.23, respectively, which are relative small compared to the mean power output value and the maximum value. The r2score is 0.9849 which is very close to 1. We then use the 12 WPAPs dataset for transformer’s migration learning experiment. The predicted results show that the MSE, MAE and RMSE are also small and the r2score is also very close to 1. The transformer can have good migration performance within the same area.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can bedirected to the corresponding author.

Author contributions

SH proposed the concept of the study and reviewed the manuscript. YQ designed the project and revised the manuscript. CY completed the experiments and wrote the original draft.

Funding

This work was supported by the National Key Research and Development Program of China (No. 2022YFE0118500), the National Natural Science Foundation of China (No. 52207095) and Natural Science Foundation of Hunan Province (No. 2022JJ40075).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alipour, P., Mukherjee, S., and Nateghi, R. (2019). Assessing climate sensitivity of peak electricity load for resilient power systems planning and operation: A study applied to the Texas region. Energy 185, 1143–1153. doi:10.1016/j.energy.2019.07.074

CrossRef Full Text | Google Scholar

Bommasani, R., Hudson, D. A., Adeli, E., Altman, R., Arora, S., von Arx, S., et al. (2021). On the opportunities and risks of foundation models. arXivhttps://arxiv.org/abs/2108.07258.

Google Scholar

Carion, N., Massa, F., Synnaeve, G., Usunier, N., Kirillov, A., and Zagoruyko, S. (2020)., 12346. Springer, 213–229. End-to-end object detection with transformersEur. Conf. Comput. Vis.

Google Scholar

Cassola, F., and Burlando, M. (2012). Wind speed and wind energy forecast through Kalman filtering of Numerical Weather Prediction model output. Appl. energy 99, 154–166. doi:10.1016/j.apenergy.2012.03.054

CrossRef Full Text | Google Scholar

Chen, T., Lehr, J., Lavrova, O., and Martinez-Ramonz, M. (2016). “Distribution-level peak load prediction based on bayesian additive regression trees,” in Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM): IEEE), Boston, MA, USA, 1–5.

Google Scholar

Council, G. W. E. (2022). GWEC global wind Report 2022. Bonn, Germany: Global Wind Energy Council.

Google Scholar

Deng, X., Shao, H., Hu, C., Jiang, D., and Jiang, Y. (2020). Wind power forecasting methods based on deep learning: A survey. Comput. Model. Eng. Sci. 122 (1), 273–301. doi:10.32604/cmes.2020.08768

CrossRef Full Text | Google Scholar

Devlin, J., Chang, M.-W., Lee, K., and Toutanova, K. (2018). Bert: Pre-training of deep bidirectional transformers for language understanding. arXivhttps://arxiv.org/abs/1810.04805.

Google Scholar

Dosovitskiy, A., Beyer, L., Kolesnikov, A., Weissenborn, D., Zhai, X., Unterthiner, T., et al. (2020). An image is worth 16x16 words: Transformers for image recognition at scale. https://arxiv.org/abs/2010.11929.

Google Scholar

Hanifi, S., Liu, X., Lin, Z., and Lotfian, S. (2020). A critical review of wind power forecasting methods—Past, present and future. Energies 13 (15), 3764. doi:10.3390/en13153764

CrossRef Full Text | Google Scholar

He, K., Zhang, X., Ren, S., and Sun, J. (2002). “Deep residual learning for image recognition,” in Proceedings of the IEEE conference on computer vision and pattern recognition, San Juan, PR, USA, 770–778.

Google Scholar

Hodge, B.-M., Zeiler, A., Brooks, D., Blau, G., Pekny, J., and Reklatis, G. (2011)., 29. Elsevier, 1789–1793. Improved wind power forecasting with ARIMA modelsComput. Aided Chem. Eng.

CrossRef Full Text | Google Scholar

Hossain, M. A., Chakrabortty, R. K., Elsawah, S., and Ryan, M. J. (2020). “Hybrid deep learning model for ultra-short-term wind power forecasting,” in Proceedings of the 2020 IEEE International Conference on Applied Superconductivity and Electromagnetic Devices (ASEMD): IEEE, Tianjin, China, 1–2.

CrossRef Full Text | Google Scholar

Hu, Q., Zhang, R., and Zhou, Y. (2016). Transfer learning for short-term wind speed prediction with deep neural networks. Renew. Energy 85, 83–95. doi:10.1016/j.renene.2015.06.034

CrossRef Full Text | Google Scholar

Huang, R., Huang, T., Gadh, R., and Li, N. (2012). “Solar generation prediction using the ARMA model in a laboratory-level micro-grid,” in Proceedings of the 2012 IEEE third international conference on smart grid communications (SmartGridComm): IEEE, Tainan, Taiwan, 528–533.

Google Scholar

Ko, M.-S., Lee, K., Kim, J.-K., Hong, C. W., Dong, Z. Y., and Hur, K. (2020). Deep concatenated residual network with bidirectional LSTM for one-hour-ahead wind power forecasting. IEEE Trans. Sustain. Energy 12 (2), 1321–1335. doi:10.1109/tste.2020.3043884

CrossRef Full Text | Google Scholar

Lahouar, A., and Slama, J. B. H. (2017). Hour-ahead wind power forecast based on random forests. Renew. energy 109, 529–541. doi:10.1016/j.renene.2017.03.064

CrossRef Full Text | Google Scholar

Lai, G., Chang, W.-C., Yang, Y., and Liu, H. (2018). “Modeling long-and short-term temporal patterns with deep neural networks,” in Proceedings of the The 41st international ACM SIGIR conference on research & development in information retrieval), Ann Arbor MI USA, 95–104.

CrossRef Full Text | Google Scholar

Lewis, M., Liu, Y., Goyal, N., Ghazvininejad, M., Mohamed, A., Levy, O., et al. (2019). Bart: Denoising sequence-to-sequence pre-training for natural language generation, translation, and comprehension. arXivhttps://arxiv.org/abs/1910.13461.

Google Scholar

L’Heureux, A., Grolinger, K., and Capretz, M. A. (2022). Transformer-based model for electrical load forecasting. Energies 15 (14), 4993. doi:10.3390/en15144993

CrossRef Full Text | Google Scholar

Li, J., and Armandpour, M. (2022). “Deep spatio-temporal wind power forecasting,” in Proceedings of the ICASSP 2022-2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP): IEEE), Singapore, 4138–4142.

CrossRef Full Text | Google Scholar

Li, L.-l., Cen, Z.-Y., Tseng, M.-L., Shen, Q., and Ali, M. H. (2021). Improving short-term wind power prediction using hybrid improved cuckoo search arithmetic-Support vector regression machine. J. Clean. Prod. 279, 123739. doi:10.1016/j.jclepro.2020.123739

CrossRef Full Text | Google Scholar

Li, L.-L., Zhao, X., Tseng, M.-L., and Tan, R. R. (2020). Short-term wind power forecasting based on support vector machine with improved dragonfly algorithm. J. Clean. Prod. 242, 118447. doi:10.1016/j.jclepro.2019.118447

CrossRef Full Text | Google Scholar

Li, L., Liu, Y.-q., Yang, Y.-p., Shuang, H., and Wang, Y.-m. (2013). A physical approach of the short-term wind power prediction based on CFD pre-calculated flow fields. J. Hydrodyn. 25 (1), 56–61. doi:10.1016/s1001-6058(13)60338-8

CrossRef Full Text | Google Scholar

Lin, Y., Koprinska, I., and Rana, M. (2020)., 12534. Springer, 616–628.SpringNet: Transformer and Spring DTW for time series forecastingInt. Conf. Neural Inf. Process.

CrossRef Full Text | Google Scholar

Lin, Z., and Liu, X. (2020). Assessment of wind turbine aero-hydro-servo-elastic modelling on the effects of mooring line tension via deep learning. Energies 13 (9), 2264. doi:10.3390/en13092264

CrossRef Full Text | Google Scholar

Liu, B., Zhao, S., Yu, X., Zhang, L., and Wang, Q. (2020). A novel deep learning approach for wind power forecasting based on WD-LSTM model. Energies 13 (18), 4964. doi:10.3390/en13184964

CrossRef Full Text | Google Scholar

Liu, Y., Ott, M., Goyal, N., Du, J., Joshi, M., Chen, D., et al. (2019). Roberta: A robustly optimized bert pretraining approach. arXivhttps://arxiv.org/abs/1907.11692.

Google Scholar

Liu, Y., Shi, J., Yang, Y., and Han, S. (2009). Piecewise support vector machine model for short-term wind-power prediction. Int. J. Green Energy 6 (5), 479–489. doi:10.1080/15435070903228050

CrossRef Full Text | Google Scholar

Liu, Z., Lin, Y., Cao, Y., Hu, H., Wei, Y., Zhang, Z., et al. (2021). “Swin transformer: Hierarchical vision transformer using shifted windows,” in Proceedings of the IEEE/CVF International Conference on Computer Vision), Montreal, BC, Canada, 10012–10022.

CrossRef Full Text | Google Scholar

López Santos, M., García-Santiago, X., Echevarría Camarero, F., Blázquez Gil, G., and Carrasco Ortega, P. (2022). Application of temporal fusion transformer for day-ahead PV power forecasting. Energies 15 (14), 5232. doi:10.3390/en15145232

CrossRef Full Text | Google Scholar

Lu, K., Sun, W. X., Wang, X., Meng, X. R., Zhai, Y., Li, H. H., et al. (2018)., 186. IOP Publishing, 012020.Short-term wind power prediction model based on encoder-decoder LSTM, IOP Conf. Ser. Earth Environ. Sci.

CrossRef Full Text | Google Scholar

Niu, Z., Yu, Z., Tang, W., Wu, Q., and Reformat, M. (2020). Wind power forecasting using attention-based gated recurrent unit network. Energy 196, 117081. doi:10.1016/j.energy.2020.117081

CrossRef Full Text | Google Scholar

Phan, Q.-T., Wu, Y.-K., and Phan, Q.-D. (2022). “An approach using transformer-based model for short-term PV generation forecasting,” in Proceedings of the 2022 8th International Conference on Applied System Innovation (ICASI): IEEE, Nantou, Taiwan, 17–20.

CrossRef Full Text | Google Scholar

Poggi, P., Muselli, M., Notton, G., Cristofari, C., and Louche, A. (2003). Forecasting and simulating wind speed in Corsica by using an autoregressive model. Energy Convers. Manag. 44 (20), 3177–3196. doi:10.1016/s0196-8904(03)00108-0

CrossRef Full Text | Google Scholar

Radford, A., Wu, J., Child, R., Luan, D., Amodei, D., and Sutskever, I. (2019). Language models are unsupervised multitask learners. OpenAI blog 1 (8), 9.

Google Scholar

Raffel, C., Shazeer, N., Roberts, A., Lee, K., Narang, S., Matena, M., et al. (2020). Exploring the limits of transfer learning with a unified text-to-text transformer. J. Mach. Learn. Res. 21 (140), 1–67.

PubMed Abstract | Google Scholar

Shahid, F., Zameer, A., and Muneeb, M. (2021). A novel genetic LSTM model for wind power forecast. Energy 223, 120069. doi:10.1016/j.energy.2021.120069

CrossRef Full Text | Google Scholar

Sun, R., Zhang, T., He, Q., and Xu, H. (2021). Review on key technologies and applications in wind power forecasting. High. Volt. Eng. 47, 1129–1143.

Google Scholar

Sun, Z., Zhao, S., and Zhang, J. (2019). Short-term wind power forecasting on multiple scales using VMD decomposition, K-means clustering and LSTM principal computing. IEEE Access 7, 166917–166929. doi:10.1109/access.2019.2942040

CrossRef Full Text | Google Scholar

Touvron, H., Cord, M., Sablayrolles, A., Synnaeve, G., and Jégou, H. (2021). “Going deeper with image transformers,” in Proceedings of the IEEE/CVF International Conference on Computer Vision), Montreal, BC, Canada, 32–42.

CrossRef Full Text | Google Scholar

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., et al. (2017). Attention is all you need. Adv. neural Inf. Process. Syst. 30.

Google Scholar

Wang, Y., Gao, J., Xu, Z., and Li, L. (2020). A short-term output power prediction model of wind power based on deep learning of grouped time series. Eur. J. Electr. Eng. 22 (1), 29–38. doi:10.18280/ejee.220104

CrossRef Full Text | Google Scholar

Wu, H., Xiao, B., Codella, N., Liu, M., Dai, X., Yuan, L., et al. (2021). “Cvt: Introducing convolutions to vision transformers,” in Proceedings of the IEEE/CVF International Conference on Computer Vision), Montreal, BC, Canada, 22–31.

CrossRef Full Text | Google Scholar

Wu, Q., Guan, F., Lv, C., and Huang, Y. (2021). Ultra-short-term multi-step wind power forecasting based on CNN-LSTM. IET Renew. Power Gen. 15 (5), 1019–1029. doi:10.1049/rpg2.12085

CrossRef Full Text | Google Scholar

Wu, Y.-K., and Hong, J.-S. (2007). A literature review of wind forecasting technology in the world. IEEE Lausanne Power Tech. 2007, 504–509.

CrossRef Full Text | Google Scholar

Yesilbudak, M., Sagiroglu, S., and Colak, I. (2017). A novel implementation of kNN classifier based on multi-tupled meteorological input data for wind power prediction. Energy Convers. Manag. 135, 434–444. doi:10.1016/j.enconman.2016.12.094

CrossRef Full Text | Google Scholar

Yu, R., Gao, J., Yu, M., Lu, W., Xu, T., Zhao, M., et al. (2019). LSTM-EFG for wind power forecasting based on sequential correlation features. Future Gener. Comput. Syst. 93, 33–42. doi:10.1016/j.future.2018.09.054

CrossRef Full Text | Google Scholar

Zhou, J., Lu, X., Xiao, Y., Su, J., Lyu, J., Ma, Y., et al. (2022). Sdwpf: A dataset for spatial dynamic wind power forecasting challenge at kdd cup 2022. arXiv https://arxiv.org/abs/2208.04360.

Google Scholar