Large-scale power inspection: A deep reinforcement learning approach

Power inspection plays an important role in ensuring the normal operation of the power grid. However, inspection of transmission lines in an unoccupied area is time-consuming and labor-intensive. Recently, unmanned aerial vehicle (UAV) inspection has attracted remarkable attention in the space-ground collaborative smart grid, where UAVs are able to provide full converge of patrol points on transmission lines without the limitation of communication and manpower. Nevertheless, how to schedule UAVs to traverse numerous, dispersed target nodes in a vast area with the least cost (e.g., time consumption and total distance) has rarely been studied. In this paper, we focus on this challenging and practical issue which can be considered as a family of vehicle routing problems (VRPs) with regard to different constraints, and propose a Diverse Trajectory-driven Deep Reinforcement Learning (DT-DRL) approach with encoder-decoder scheme to tackle it. First, we bring in a threshold unit in our encoder for better state representation. Secondly, we realize that the already visited nodes have no impact on future decisions, and then devise a dynamic-aware context embedding which removes irrelevant nodes to trace the current graph. Finally, we introduce multiply decoders with identical structure but unshared parameters, and design a Kullback-Leibler divergence based regular term to enforce decoders to output diverse trajectories, which expands the search space and enhances the routing performance. Comprehensive experiments on five types of routing problems show that our approach consistently outperforms both DRL and heuristic methods by a clear margin.

1 Introduction

UAV power inspection is a promising approach for transmission line detection and maintenance due to the immunity from limited manpower and adverse environments Alhassan et al. (2020). UAVs are utilized to provide full coverage of all transmission line segments defined by the pylons, where each segment is considered as a target node to be traversed. Accordingly, UAV power inspection can be modeled as a traveling salesman problem (TSP) with the purpose of minimizing the total traversal distance. Recently, with the rapid development of the smart grid industry, the total length of transmission lines of 220 kV and above in China has reached 0.84 million kilometers by the end of 2021 with an annual growth rate of 3.8% Duan et al. (2022); Prabhu et al. (2022). The tremendous growth poses new challenges to power inspection, among which, how to schedule UAVs to traverse such numerous target nodes on transmission lines with high precision and high efficiency is the most essential issue.

In this paper, we concentrate on solving large-scale TSP. TSP, a class of vehicle routing problems (VRPs), is defined to find the shortest possible tour traversing all cities exactly once and back to the starting city. It has attracted considerable attention in recent years due to its profound impact on theoretical computer science and operational research, and extensive real-world applications in robotics Guan et al. (2021), logistics Baniasadi et al. (2020), electricity Sun et al. (2022), etc. Nevertheless, TSP is generally an NP-hard combinatorial optimization problem, and it is intractable and time-consuming to apply an exhaustive search to obtain the optimal solution via exact algorithms Vásquez et al. (2021). In contrast, heuristic algorithms, such as ant colony optimization Ebadinezhad (2020) and genetic algorithm Baniamerian et al. (2019), are able to yield near-optimal solutions in polynomial time. However, such heuristics methods are often guided by hand-designed rules, which rely heavily on intuition and domain prior knowledge Wei et al. (2022), and may lead to unsatisfactory solutions occasionally.

In the last decade, deep learning methods have achieved great success in a variety of artificial intelligence fields Huang et al. (2022); Yan et al. (2022); Tang et al. (2022). Among them, deep reinforcement learning (DRL) methods have been leveraged to learn the underlying patterns from numerous instances, and solve routing problems in an end-to-end framework without the need of prior knowledge Francois-Lavet et al. (2018). Most DRL methods follow the encoder-decoder scheme Kool et al. (2018) and learn constructive heuristics by adding unvisited nodes into the partial tour step-by-step until completion. Specifically, the encoder maps the node information into feature embeddings, and the decoder generates the probability of selecting the next valid node at each time step. In comparison with exact and heuristic algorithms, DRL models achieve high computational speed and superior routing performance.

Though showing promising results, there are still several limitations of existing constructive DRL methods. First, prevailing DRL methods do not obey the Bellman’s Principle of Optimality Jones and Peet (2021) completely. To be more specific, the constructive routing process can be considered as a series of sequential node-selection sub-tasks. The already visited nodes are irrelevant to the current decision. However, prevailing DRL methods utilize a fixed context embedding which can not reflect the dynamics of state transitions well. Hence, such a rigid embedding over the whole graph is not suitable for all sub-tasks and may deteriorate the solution quality. The second limitation is that the solutions (i.e., trajectories) generated by DRL models are not diverse enough. Conceptually, generating a group of more diverse traversing trajectories will expand the search space and lead to better routing results Kwon et al. (2020). However, existing methods train one policy merely and the only source of diversity derives from the relatively determined probability distribution of selecting nodes, which is far from sufficient.

To tackle the above limitations, we propose a Diverse Trajectory-driven Deep Reinforcement Learning approach, named as DT-DRL. First, to reflect the dynamics of state transitions, we develop an attentive context embedding by means of exploiting the recursive attribute of routing problems. The DRL-based TSP can be formulated as a Markov Decision Process (MDP) abiding by existing works Kool et al. (2018); Xin et al. (2020); Li et al. (2021a). Based on the nature of MDP that past decisions have no effect on future decisions given the present Song et al. (2000), if the current node and the depot (i.e., start point and end point of the current sub-task) are known, the nodes already visited in the past have no effect on the traversing order of the unvisited nodes in the future Xu et al. (2021). To this end, we explicitly remove them in the context embedding. And our proposed context contains the embeddings of the current node, depot, and unvisited graph, and adjusts over time continuously. Hence, such an informative context embedding for selecting the next node to visit is able to boost the routing performance. Secondly, to output diverse trajectories, we bring in multiply decoders with identical structures but independent network parameters to learn distinct routing patterns. During training, a Kullback-Leibler divergence based cross entropy loss is introduced to enforce the decoders to generate dissimilar probability distribution of node selection. The modification is analogous to guiding a student to approach the same problem from diverse perspectives, and teaching him different problem-solving thoughts. Consequently, such a student is able to solve unseen problems better according to Bransford et al. (1986); Kwon et al. (2020).

In order to verify the effectiveness of our proposed approach, we conduct comprehensive experiments on five types of routing problems: 1) TSP; 2) capacitated VRP (CVRP); 3) orienteering problem (OP); 4) prize collecting TSP (PCTSP); and 5) split delivery VRP (SDVRP). The experimental results show that our DT-DRL outperforms both DRL and heuristic methods by a clear margin, regardless of the size and type of problems. For example, DT-DRL achieves an average reduction of 4.64% in the optimality gap, compared to the landmark DRL method AM Kool et al. (2018). Moreover, we also perform generalization analysis on TSPs and CVRPs. The comparison results demonstrate that our DT-DRL generalizes better on larger scale problems in comparison with state-of-the-art methods.

The main contributions of our approach are summarized as follows:

• We realize the importance of capturing the dynamics of state transitions in constructive routing problems. Based on the nature of Markov decision process that past decisions have no effect on future decisions, we introduce an attentive, dynamic-aware context embedding for graph representation, which facilitates improving the accuracy of route planning.

• We bring in multiply decoders with the same structure but unshared parameters, and design a Kullback-Leibler divergence based regularization term to output diverse trajectories, which expands the search space significantly.

• We perform extensive experiments on five types of routing problems, and the results illustrate that our proposed method achieves highly competitive performance in route planning.

The remainder of this paper is organized as follows. Section 2 gives a brief review of existing mainstream works. Section 3 elaborates the framework and training policy of our proposed approach. Section 4 provides the comprehensive comparison experiments, generalization analysis, and ablation study. Finally, Section 5 concludes the paper.

2 Related work

In this section, we briefly review the mainstream methods for solving vehicle routing problems, including TSPs, CVRPs, etc. The prevalent routing methods can be categorized into three types: exact methods, heuristic methods, and reinforcement learning-based methods.

2.1 Exact methods

Over the past decades, exact methods are the most well-known ones to solve vehicle routing problems, as they are guaranteed to find the optimal solution. Exact solvers, such as branch-and-bound Arigliano et al. (2018), branch-and-price Akca et al. (2009), and Concorde Hitte et al. (2003), apply brute-force search to traverse all possible paths throughout the entire solution space. However, they can only get satisfactory results when the problem size is moderate. The execution time for tackling large-scale routing problems is unacceptable due to the extremely high computational complexity. Therefore, how to search the path efficiently is an important research topic.

2.2 Heuristic methods

In contrast, heuristic methods are able to reduce the search space and computational complexity significantly by designing elaborated, hand-crafted rules to guide the search process. Heuristic methods are divided into three categories as follows.

2.2.1 Evolutionary-based heuristics

Inspired by biological evolution in nature, evolutionary-based heuristics, including genetic algorithm (GA), constructs a population of feasible solutions first and then optimize it progressively based on ‘the survival of the fittest’. The authors in Baniamerian et al. (2019) update the individual solutions with crossover and mutation operators, and retain the competitive ones according to the roulette wheel selection. The authors in Sethanan and Jamrus (2020) design a hybrid differential evolutionary router involving genetic operators with the fuzzy logic controller.

2.2.2 Swarm intelligence-based heuristics

Swarm intelligence-based heuristic methods, such as particle swarm optimization (PSO) and ant colony optimization (ACO), are illuminated by group behaviors of various organisms. The authors in Duan et al. (2021) incorporate the encoder-decoder scheme and robustness metric, and develop a robust PSO approach to solve VRPs with time windows. The authors in Ebadinezhad (2020) propose a novel ACO algorithm with dynamic evaporation strategy to enhance the convergence speed.

2.2.3 Solver-based heuristics

Mathematical linear programming solvers, such as Gurobi Muley (2021), LKH-3 Helsgaun (2017), and Google OR Tools Gunjan et al. (2012), are also able to handle combinatorial optimization problems including VRPs, with the advantages of generality and portability. However, such heuristic paradigms all rely heavily on the domain prior knowledge and engineering experience, and can not receive superior performance on large-scale, complex problems.

2.3 Reinforcement learning-based methods

Illuminated by the recent advances in deep learning, the exploration of utilizing deep reinforcement learning methods to tackle routing problems has been emerging vigorously. Without the need of hand-crafted rules and domain prior knowledge Li et al. (2021b), DRL methods can be adapted to solve varied and flexible routing scenarios Bao et al. (2020); Yang et al. (2022). We classify the DRL methods into two flavours according to the solution process.

2.3.1 Construction-based deep reinforcement learning

Construction-based DRL methods choose one of the unvisited nodes to join the current part at each step, and provide a complete solution eventually. Constructive models are trained to learn a probability distribution of selecting nodes to form paths with minimum length from scratch. Attention model (AM) Kool et al. (2018) is a landmark achievement, which introduces a transformer-based encoder-decoder architecture as the policy network and receives excellent results. Besides, the authors in Kwon et al. (2020) further improve the state-of-the-art performance by exploring diverse rollouts and data augmentation strategies.

2.3.2 Improvement-based deep reinforcement learning

Unlike the constructive DRL, the improvement-based DRL models continuously refine the existing path in order to obtain a more optimal solution. Most studies on improvement DRL usually hinge on local search algorithms, including node swap Chen and Tian (2019), 2-opt Wu et al. (2021) and so forth. Dual-Aspect Collaborative Transformer (DACT) Ma et al. (2021) learns characteristics of the nodes and positions separately, and thus incompatible correlations can be eliminated. Nevertheless, both construction and improvement DRL methods suffer from several problems, like weak generalization ability.

3 Methodology

In this section, we first introduce the common objective function of routing problems and reformulate it as a Markov Decision Process. Second, we propose a novel deep reinforcement learning-based router, namely DT-DRL, and detail the framework of the elaborated encoder and decoder. Finally, we describe the training policy of our approach.

3.1 Formulation

We introduce the proposed DT-DRL model in terms of TSP. For other routing problems, the model is the same, while the input and mask are supposed to be modified slightly, which is discussed in Kool et al. (2018). Suppose x_i be the coordinate of the ith node and x₀ be the coordinate of the depot. Thus, the input to the model is the coordinate matrix of all nodes X = [x₀; x₁; ⋯ ; x_N], where N is the number of all non-depot nodes. The output A can be viewed as a permutation of nodes (a₁, a₂, …, a_N), where a_i represents the index of the selected node at step i. Departing from the original depot x_o, the objective of routing problems is to minimize the total traversal length L(A|s) of instance s.

$L\left(A|s\right)={‖{\mathit{x}}_{a_N}-{\mathit{x}}_{a_0}‖}_2+\sum _{i=1}^N{‖{\mathit{x}}_{a_i}-{\mathit{x}}_{a_{i-1}}‖}_2,(1)$

where ${‖\cdot ‖}_2$ denotes L2-Norm. Accordingly, this kind of path optimization issue can be regarded as a node-selection problem with N time steps.

Deep reinforcement learning has received a broad range of attention because of its excellent sequential decision-making capability in the past decade. Thus it is suitable to tackle such routing problems. Here, we reformulate the representative TSP as a Markov decision process, which is defined by a 5-tuple $M=\left\{\mathit{S},\mathcal{A},\tau ,R,\mathit{\theta }\right\}$. The descriptions of the state space $\mathit{S}=\left(s_0,s_1,\dots ,s_N\right)$, action sequence $\mathcal{A}=\left(a_1,\dots ,a_N\right)$, transition rule τ, cumulative reward R, and policy parameters θ are detailed below.

State: The state s_t of MDP describes a partial tour of TSP at the current step t, i.e., a sequence of previously selected nodes a_1:t.

Action: The action $a_t\in \left\{\left\{\mathrm{1,2},\dots ,N\right\}\backslash \left\{{\mathit{a}}_{1:t-1}\right\}\right\}$ represents selecting one of the unvisited nodes at time step t. How nodes are selected at each time step depends on the policy network of the model, which is one of the most important parts of DRL.

Transition: The current action a_t converts the precious state a_t−1 to the current state s_t according to the transition rule τ. In the MDP, the state transition rule we use is deterministic, i.e., p(s_t|a_t, s_t−1) = 1.

Reward: Following the existing works Kool et al. (2018); Kwon et al. (2020); Ma et al. (2021), we define the cumulative reward for instance s as the opposite of the total length: $R=-L(\mathcal{A}|s)$.

Policy: In our DRL-based approach, we focus on learning a constructive stochastic policy network, parameterized by θ, to generate a complete path from the initial state s₀. Accordingly, the joint probability of this MDP can be expressed based on the chain rule:

$p_{\mathit{\theta }}\left(\mathcal{A}|s_0\right)=\prod _{t=1}^N{p}_{\mathit{\theta }}\left(a_t|s_{t-1}\right)p_{\mathit{\theta }}\left(s_t|a_t,s_{t-1}\right),(2)$

where we omit the subscript θ afterwards for brevity.

3.2 Overall framework of our approach

We build on the milestone AM Kool et al. (2018) and design a Diverse Trajectory-driven DRL approach to learn better route planning from multiply perspectives. Our DT-DRL leverages a transformer-based neural network to maximize the cumulative reward of the MDP, which consists of three components: 1) multi-head self-attention encoder; 2) diverse trajectory-driven decoder; and 3) cross entropy loss-based training policy. The overall framework of our DT-DRL is illustrated in Figure 1. The encoder embeds the node coordinate matrix into node embeddings. Then, the decoder execute N steps and select the best node per time step, based on the node embeddings and the current context embedding. The whole model is optimized via policy gradient.

FIGURE 1

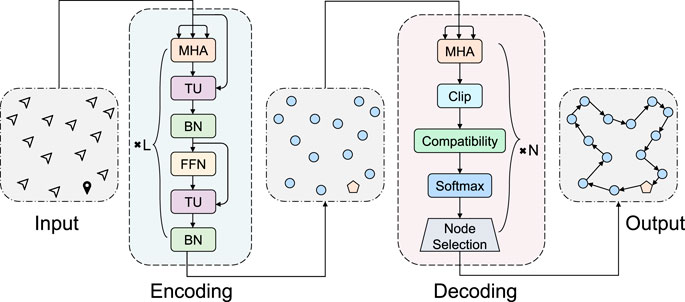
FIGURE 1. Overall framework of our proposed approach. The square pentagon represents the depot and the circle represents the non-depot node to be traversed. MHA, TU, BN, and FFN are short for the multi-head attention, threshold unit, batch normalization, and feed-forward network, which will be detailed in Sections 3.3, 3.4.

To better capture the dynamics of state transfer, our DT-DRL makes three branches of modifications: 1) we bring in a threshold unit to enhance the traditional encoder for high-quality node mapping; 2) we depict a attentive context in the decoder, which removes the irrelevant impact of visited nodes; 3) we introduce a regularization to encourage decoders to output diverse trajectories and learn distinct routing strategies. In the following, we describe how to implement node embedding during encoding in Section 3.3; how to construct the context in the process of decoding in Section 3.4; and how to optimize our model via policy gradient in Section 3.5.

3.3 Encoder

The encoder takes the two-dimensional node coordinate matrix X as input and maps them into high-dimensional node embeddings through a linear projection:

${\mathit{E}}^{\left(0\right)}=\mathit{X}{\mathit{W}}^{\text{x}}+{\mathit{B}}^{\text{x}},(3)$

where W^x and B^x are learnable parameters. The initial node embeddings ${\mathit{E}}^{(0)}=\left[{\mathit{e}}_1^{(0)};\cdots ;{\mathit{e}}_N^{(0)}\right]\in {\mathbb{R}}^{N\times d_{\text{e}}}$ are updated using L attention layers, each of which contains a multi-head attention (MHA) sublayer and a node-wise feed-forward network (FFN) sublayer. The core of MHA sublayer is expressed as follows:

${\mathit{Q}}_h,{\mathit{K}}_h,{\mathit{V}}_h=\mathit{E}{\mathit{W}}_h^{\text{Q}},\mathit{E}{\mathit{W}}_h^{\text{K}},\mathit{E}{\mathit{W}}_h^{\text{V}},(4)$

${\mathit{A}}_h=\mathrm{S}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}\left(\frac{{\mathit{Q}}_h{\mathit{K}}_h^{\text{T}}}{\sqrt{d_{\text{k}}}}\right){\mathit{V}}_h,(5)$

$\mathrm{M}\mathrm{H}\mathrm{A}\left(\mathit{E}\right)=\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{a}\mathrm{t}\left({\mathit{A}}_1,{\mathit{A}}_2,\dots ,{\mathit{A}}_H\right){\mathit{W}}^O,(6)$

where ${\mathit{W}}_h^{\text{Q}}$, ${\mathit{W}}_h^{\text{K}}\in {\mathbb{R}}^{d_{\text{e}}\times d_{\text{k}}}$, and ${\mathit{W}}_h^{\text{V}}\in {\mathbb{R}}^{d_{\text{e}}\times d_v}$ are trainable query, key, amd value matrices, ${\mathit{W}}^O\in {\mathbb{R}}^{H{d}_v\times d_{\text{e}}}$ is a learnable parameter matrix to calculate the output of MHA sublayer, H is the number of multi-head attention.

Inspired by the gate-like aggregation Parisotto et al. (2020) in vision tasks, we propose a novel threshold unit (TU) for better state representation learning, compared to the direct skip connection He et al. (2016). In our DT-DRL, we replace the residual operation with a threshold-based connection. Specifically, the weight coefficient calculated from the input matrix E_in is assigned to the output matrix E_out:

$\mathrm{T}\mathrm{U}\left({\mathit{E}}_{\text{in}},{\mathit{E}}_{\text{out}}\right)={\mathit{E}}_{\text{in}}+\mathrm{S}\mathrm{i}\mathrm{g}\mathrm{m}\mathrm{o}\mathrm{i}\mathrm{d}\left({\mathit{E}}_{\text{in}}{\mathit{W}}^{\text{G}}+{\mathit{B}}^{\text{G}}\right)\odot {\mathit{E}}_{\text{out}},(7)$

where W^G and B^G are trainable matrices, and ⊙ denotes the Hadamard product. Let E^(l−1) be the output of the (l − 1)-th layer. Hence, the output of the lth MHA sublayer can be calculated as:

${\mathit{E}}_{\text{MHA}}^{\left(l\right)}=\mathrm{B}\mathrm{N}\left(\mathrm{T}\mathrm{U}\left({\mathit{E}}^{\left(l-1\right)},\mathrm{M}\mathrm{H}\mathrm{A}\left({\mathit{E}}^{\left(l-1\right)}\right)\right)\right),(8)$

where BN(⋅) is the batch normalization operator. The operations are similar in the FFN sublayer. Given the input E^(l) to the lth FFN sublayer, the output E^(l) is defined as follows:

${\mathit{E}}^{\left(l\right)}=\mathrm{B}\mathrm{N}\left(\mathrm{T}\mathrm{U}\left({\mathit{E}}_{\text{MHA}}^{\left(l\right)},\mathrm{F}\mathrm{F}\mathrm{N}\left({\mathit{E}}_{\text{MHA}}^{\left(l\right)}\right)\right)\right),(9)$

where FFN(⋅) is the feed-forward operator, containing two learnable linear projections and a ReLU activation in between. Therefore, the output of our encoder are node embeddings ${\mathit{E}}^{(L)}=\left[{\mathit{e}}_0^{(L)};{\mathit{e}}_1^{(L)};\cdots ;{\mathit{e}}_N^{(L)}\right]$, where we omit the superscript (L) in the process of decoding below.

3.4 Decoder

In order to output diverse trajectories, our DT-DRL features M decoders with the same structure but independent parameters. Each decoder, indexed by m, generates the probability p^m(a_t = i|s_t−1) of selecting the next valid node i at time t. Traditional methods Kool et al. (2018); Kwon et al. (2020) usually leverage the entire graph embedding $\bar{\mathit{e}}={\sum }_{i=1}^N\frac{1}{N}{\mathit{e}}_i$ as the map information in the context, which can not capture the state transfer dynamics. In contrast, our proposed approach ignores the extraneous effects of nodes that have already been visited and proposes a more informative time-varying context embedding c_t:

${\mathit{c}}_t=\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{a}\mathrm{t}\left(\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\left\{{\mathit{e}}_{a_{t:N}}\right\},\mathrm{m}\mathrm{a}\mathrm{x}\left\{{\mathit{e}}_{a_{t:N}}\right\},{\mathit{e}}_0,{\mathit{e}}_{t-1}\right){\mathit{W}}^{\text{C}},(10)$

$\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\left\{{\mathit{e}}_{a_{t:N}}\right\}={\bar{\mathit{e}}}_{a_{t:N}}=\frac{1}{N-t+1}\sum _{i=t}^N{\mathit{e}}_i,(11)$

$\mathrm{m}\mathrm{a}\mathrm{x}\left\{{\mathit{e}}_{a_{t:N}}\right\}=\max {\mathit{e}}_i,i\in \left\{t,\dots ,N\right\},(12)$

where ${\mathit{W}}^{\text{C}}\in {\mathbb{R}}^{4d_{\text{e}}\times d_{\text{e}}}$ is a learnable parameter matrix for dimension transformation, e₀ and e_t−1 are embeddings of the depot and current node, and the superscript (L) for node embeddings is omitted for brevity.

Afterwards, we compute a new context ${\widehat{\mathit{c}}}_t^m$ for decoder m at time t through a MHA block, which is motivated by the glimpse layer in Bello et al. (2016). Unlike the MHA in our encoder, the keys and queries in the decoder are calculated from the node embeddings e_i, and the only query comes from the context embedding c_t. And then, we calculate the compatibilities $u_i^m$ via a single attention head and clip the results within $\left[-\mathcal{C},\mathcal{C}\right]$ for better exploration according to Eq. 15. Finally, we obtain the final output probability $p_{\mathit{\theta }}^m(a_t=i|s_{t-1})$ of selecting node i for decoder m at time t through a softmax function:

${\widehat{\mathit{c}}}_t^m=\mathrm{M}\mathrm{H}\mathrm{A}\left({\mathit{E}}^{\left(L\right)}\right),(13)$

${\mathit{q}}^m,{\mathit{k}}^m,{\mathit{v}}^m={\mathit{c}}_t{\mathit{W}}_m^{\text{Q},\mathrm{C}},{\mathit{e}}_i{\mathit{W}}_m^{\text{K},\mathrm{C}},{\mathit{e}}_i{\mathit{W}}_m^{\text{V},\mathrm{C}},(14)$

$u_i^m=\mathcal{C}\tanh \left(\left({\widehat{\mathit{c}}}_t^m{\mathit{W}}_m^{\text{Q},\mathrm{G}}\right){\left({\mathit{e}}_i{\mathit{W}}_m^{\text{K},\mathrm{G}}\right)}^{\text{T}}/\sqrt{d_{\text{k}}}\right),(15)$

$p_{\mathit{\theta }}^m\left(a_t=i|s_{t-1}\right)=\frac{e^{u_i^m}}{{\sum }_j{e}^{u_j^m}},(16)$

where ${\mathit{W}}_m^{\text{Q},\mathrm{C}}$, ${\mathit{W}}_m^{\text{K},\mathrm{C}}$, ${\mathit{W}}_m^{\text{Q},\mathrm{G}}$, ${\mathit{W}}_m^{\text{K},\mathrm{G}}\in {\mathbb{R}}^{d_{\text{e}}\times d_{\text{k}}}$, and ${\mathit{W}}_m^{\text{V},\mathrm{C}}\in {\mathbb{R}}^{d_{\text{e}}\times d_{\text{v}}}$ are learnable matrices in our decoder. The constructive path searching process during decoding is illustrated in Figure 2.

FIGURE 2

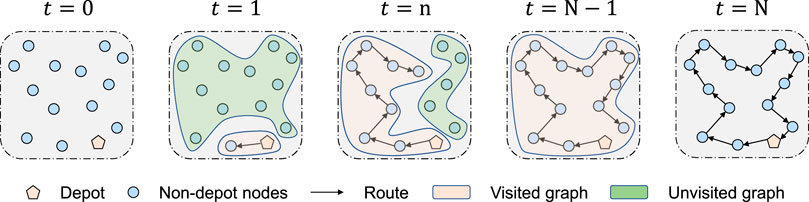
FIGURE 2. Constructive path searching process of our DT-DRL. After encoding, the node coordinates are projected to node embeddings, which remain unchanged throughout the entire decoding process. Afterwards, for each time step of decoding, one of the unvisited nodes will be selected. The resulting output is a sequence of nodes, representing the final route. In our approach, we seek to capture the dynamics of state transitions by means of modeling visited and unvisited graph. And the future traveling order depends merely on the current node, depot and unvisited graph.

3.5 Training policy

3.5.1 Exploration with multiply trajectories

Our DT-DRL starts with sampling M solution trajectories $\left\{{\mathcal{A}}^1,{\mathcal{A}}^2,\dots ,{\mathcal{A}}^M\right\}$, each of which can be considered as a set of action sequences generated by a decoder:

${\mathcal{A}}^m=\left(a_0^m,a_1^m,\dots ,a_N^m\right),m=\mathrm{1,2},\dots ,M.(17)$

For all trajectories, the depot node a₀ is fixed. Therefore, we aim to design a regularization to encourage different decoders to generate diverse non-depot starting nodes a₁, and thus the model is able to learn distinct routing patterns and output diverse trajectories. A Kullback-Leibler divergence based cross entropy (CE) loss ${\mathcal{L}}_{\text{CE}}$ is imposed to diversify each pair of the output probability distributions from M decoders:

${\mathcal{L}}_{\text{CE}}=-D_{\text{KL}}=-\sum _{i=1}^M\sum _{j=1}^M\sum _{a_1}{p}_{\mathit{\theta }}^i\left(a_1|s_0\right)\log \frac{p_{\mathit{\theta }}^i\left(a_1|s_0\right)}{p_{\mathit{\theta }}^j\left(a_1|s_0\right)}.(18)$

Such exploration is only computed on the selection of the first non-depot node, and thus the increase in computational time is small compared to the routing gain. Conceptually, the core idea of our DT-DRL is analogous to guiding a student to approach the same problem from diverse perspectives, and teaching him different problem-solving thoughts.

3.5.2 Reinforcement with greedy rollout baseline

Given an input instance s, each decoder individually generates a trajectory ${\mathcal{A}}^m$ with the probability distribution $p_{\mathit{\theta }}\left({\mathcal{A}}^m|s\right)$. To maximize the expected reward $R=L\left(\mathcal{A}|s\right)$, we define the reinforcement loss ${\mathcal{L}}_{\text{RL}}\left(\mathit{\theta }|s\right)={\sum }_{m=1}^M{\mathbb{E}}_{p_{\mathit{\theta }}\left({\mathcal{A}}^m|s\right)}\left[L\left({\mathcal{A}}^m|s\right)\right]$ and optimize it by gradient descent with the greedy rollout baseline b(s):

$\nabla {\mathcal{L}}_{\text{RL}}\left(\mathit{\theta }|s\right)=\sum _{m=1}^M{\mathbb{E}}_{p_{\mathit{\theta }}\left({\mathcal{A}}^m|s\right)}\left[\left(L\left({\mathcal{A}}^m|s\right)-b\left(s\right)\right)\nabla \log p_{\mathit{\theta }}\left({\mathcal{A}}^m|s\right)\right].(19)$

we adopt the same baseline as A^m Kool et al. (2018) in order to reduce the gradient variance and boost the convergence speed.

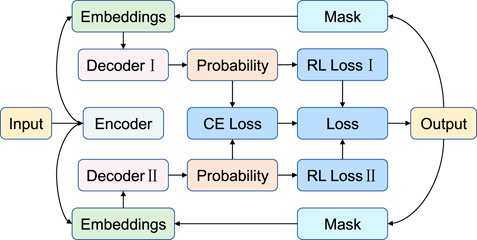
Overall, the training policy is illustrated in Figure 3. And our DT-DRL model can be optimized as follows:

$\nabla \mathcal{L}\left(\mathit{\theta }\right)=\nabla {\mathcal{L}}_{\text{RL}}\left(\mathit{\theta }|s\right)+{\psi }_{\text{CE}}\nabla {\mathcal{L}}_{\text{CE}}.(20)$

where ψ_CE is the hyperparameter to balance the effect of CE loss.

FIGURE 3

FIGURE 3. Training policy of our DT-DRL. We adopt two (multiply) decoders for demonstration.

4 Experiments

In this section, we first introduce the experimental setup, evaluation metric, and implementation details. Second, we conduct sufficient comparative experiments with exact, heuristic, and learning-based algorithms to verify the effectiveness of our DT-DRL. Finally, we perform generalization and ablation analysis to evaluate the proposed DRL approach more comprehensively.

4.1 Experiment setting

We focus on five types of routing problems: 1) TSP; 2) CVRP; 3) OP; 4) PCTSP; and 5) SDVRP. They provide researchers with various objectives and challenges, and are traditionally solve by different problem-specific methods. Among which, TSP and CVRP are the most extensively studied ones. We describe the settings of TSP and CVRP, and the details of other variants are shown in Supplementary Material.

For each problem, we follow the current popular practice Kool et al. (2018); Kwon et al. (2020); Wu et al. (2021); Ma et al. (2021) to generate instances on the fly with N = 20, 50, and 100 nodes, where we call them TSP20, CVRP20, etc. for convenience. The coordinates of each node are sampled randomly from the uniform distribution in a [0, 1] × [0, 1] unit square. Pertaining to CVRP, the vehicle capacities are set to 30, 40, and 50 for problems with 20, 50, and 100 nodes, respectively. The demand of each non-depot node is selected randomly from the set of integers {1, …, 9}.

All DRL-based models are trained on 100,000 randomly generated instances on the fly and tested on 10,000 other instances with the same distribution. For evaluation metric, we measure the performance of our DT-DRL and other baselines via the mean tour length L_mean, optimality gap, and total computation time.

$\mathrm{G}\mathrm{a}\mathrm{p}=\frac{L_{\text{mean}}-L_{\text{opt}}}{l_{\text{opt}}}\times 100\%,(21)$

where L_opt indicates the optimal result. More concretely, Concorde is leveraged to obtain the shortest length for TSP, and the optimality gaps for other VRPs are calculated based on Gurobi and LKH-3. In order to eliminate the influence of the computational platform on the experimental results, all algorithms are implemented in Python 3.8.0 and all experiments are conducted on an Intel Core i7-12700 KF CPU and an NVIDIA GeForce RTX 3070 GPU.

The node elements are embedded into 128-dimensional vectors through a learnable linear projection. The encoder of DT-DRL consists of three layers, each of which has eight attention heads and 512-dimensional hidden features. The number of decoders is selected to be five and each decoder takes 128-dimensional vectors and 8-head attention. The tanh clip is utilized with $\mathcal{C}=10$. Abiding by existing works Kool et al. (2018); Kwon et al. (2020), we train the model with 50 epochs, each with 2,500 iterations. We set the batch size to 512. To contribute to fairer comparisons and mitigate the effects of hyperparameters, we use the same training parameters as those for DRL. To be more specific, we apply Adam optimizer to train the policy network. And the initial learning rate is set to 10^–4 and decays 0.96 per epoch. The coefficient of CE loss ψ_CE = 0.01 in Eq. 20.

4.2 Comparison results

We compare our DT-DRL with a variety of exact, heuristic, and DRL-based methods, including:

1) Concorde Hitte et al. (2003): a specialized exact routing solver;

2) Gurobi Muley (2021): a commercial linear programming optimizer;

3) LKH-3 Helsgaun (2017): a heuristic optimization solver achieve state-of-the-art performance on numerous VRPs;

4) Google OR Tools Gunjan et al. (2012): Mature tools for solving combinatorial optimization problems developed by Google;

5) GA Baniamerian et al. (2019): an evolutionary-based genetic algorithm for solving routing problems;

6) ACO Duan et al. (2021): a swarm intelligence-based ant colony optimization approach for tackling VRPs;

7) Wu et al. (2021): an improvement-based DRL router;

8) DACT Ma et al. (2021): an improvement-based dual-aspect collaborative transformer for solving VRPs;

9) AM Kool et al. (2018): a landmark DRL model with attention mechanism and encoder-decoder scheme;

10) POMO Kwon et al. (2020): a competitive DRL approach achieving state-of-the-art performance on various routing problems;

The comparison results with baseline methods on two most representative VRPs (i.e., TSP and CVRP) are shown in Table 1 and the results of other routing problems are also reported in Table 2. We summarize the comparative study as follows:

TABLE 1

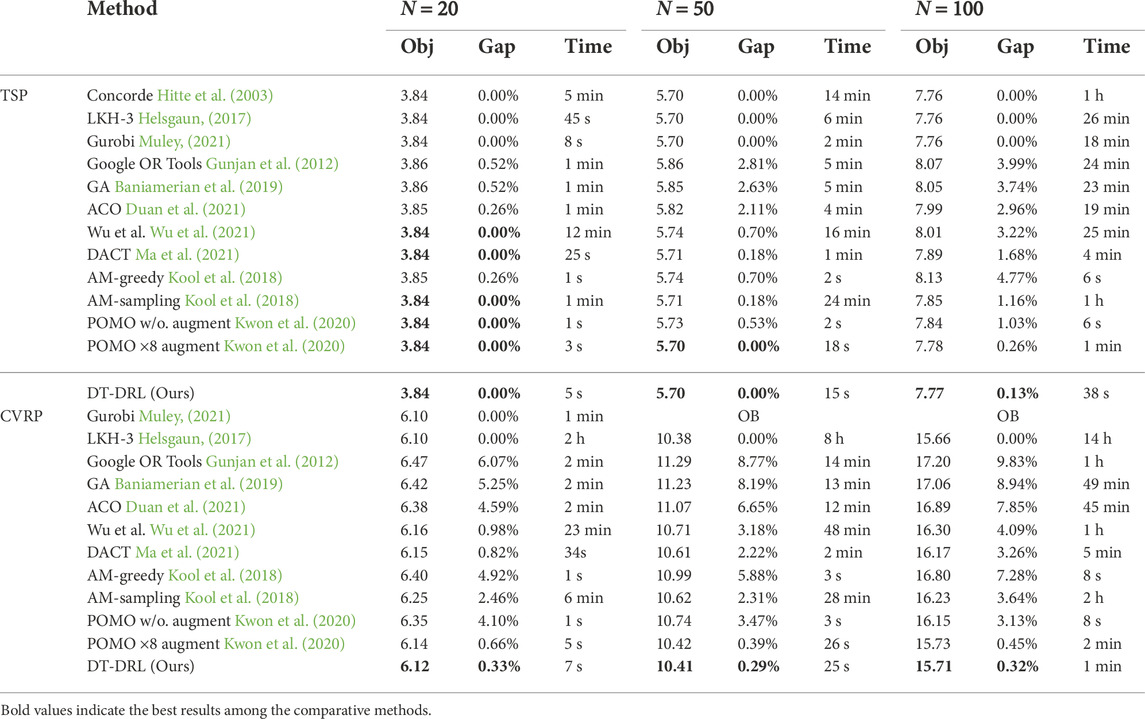
TABLE 1. Comparison results with exact, heuristic, and DRL-based baselines on TSP and CVRP. Bold numbers indicate the best results among learning-based methods. OB means out of budget and “w/o.” is short for without.

TABLE 2

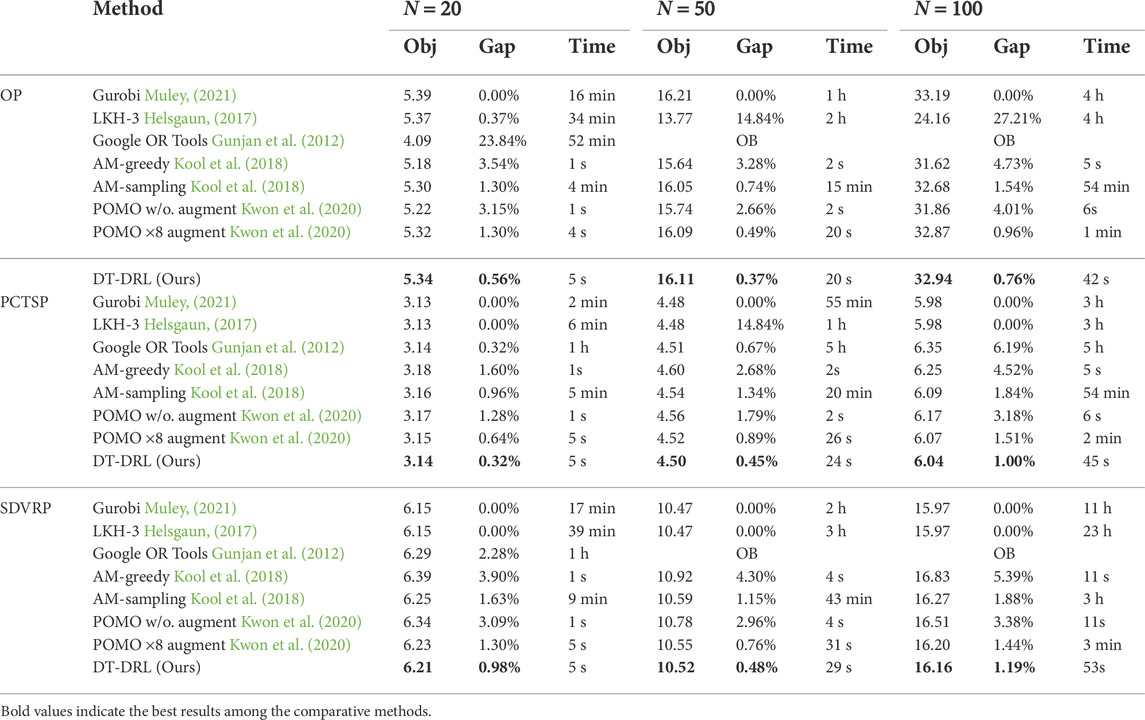
TABLE 2. Comparison results with baselines on other routing problems including OP, PCTSP, and SDVRP. While for OP, the smaller the value of the objective, the better, which is contrast to other problems.

• On all five types of routing problems, our proposed DT-DRL consistently outstrips other state-of-the-art baseline methods by a clear margin in terms of both solution quality and computational time. It favourably demonstrate the superiority of our algorithm for striking a better balance between effectiveness and efficiency.

• Table 1 compares the routing performance of different baselines on TSP and CVRP. Take a challenging TSP100 as an example, our method achieves an average (optimality) gap of 0.13%, which outperforms the milestone routing model, AM-greedy, by an reduction of 4.64%. Compared with the second-best method (i.e., POMO with × 8 instance augmentation), the optimality gap of our DT-DRL is reduced by half and the computational time consumed is decreased by 36.67% at the same time.

• Pertaining to CVRP, our approach achieves the best optimality gap of 0.33%, 0.29%, and 0.32% with 20, 50, and 100 nodes, respectively. Take CVRP50 as an example, our DT-DRL achieves an reduction of 5.59%, 3.18%, 2.89%, and 1.93% in comparison with construction-based methods (i.e., AM and POMO) and improvement-based ones (i.e., Wu et al. and DACT). Furthermore, on both TSP and CVRP, as the problem size grows continually, it is clear that the superiority of our algorithm becomes more and more significant.

• Table 2 reports the comparison results on other routing problems. It can be easily observed that our DT-DRL gets the best objective function values, i.e., 5.34, 16.11, and 32.94, on OP20, OP50, and OP100 severally, which outperforms other DRL-based methods by a clear margin. AS for PCTSP, the optimality gap of our approach is reduced by 0.32%, 0.44%, and 0.51% with 20, 50, and 100 nodes, compared to the state-of-the-art POMO with × 8 instance augmentation. Moreover, DT-DRL outstrips the elaborated DRL-based methods, AM-sampling and POMO with augmentation, by up to 0.69% and 0.25% in terms of the optimality gap. Meanwhile, the computational time of our model for inferring 10,000 test instances is decreased by at least an order of magnitude.

4.3 Generalization analysis

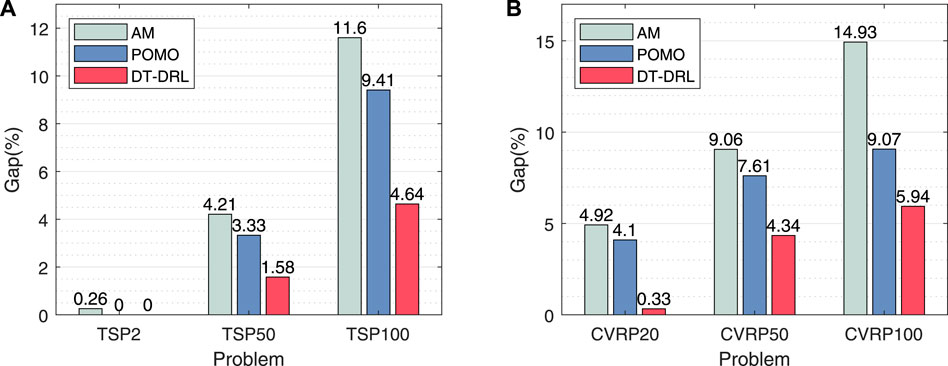
In real-world scenarios, the number of nodes is changing constantly. It is impractical to train a model that is suitable to a specific case. Hence, the model should be robust enough to changes in the number of tasks. Here we verify the generalization ability of our proposed approach on two representative routing problems, TSP and CVRP. Specifically, we train the DRL-based model on TSP20 and test on 10,000 TSP20, TSP50, and TSP100 instances, respectively. Similarly, we also train the model on CVRP20 and deploy it CVRP20, CVRP50, and CVRP100. The average optimality gaps of our DT-DRL and other constructive DRL methods are recorded in Figure 4.

FIGURE 4

FIGURE 4. Generalization results between AM, POMO, and our DT-DRL on (A) TSPs and (B) CVRPs.

It is clearly observed that the generalization results of our DT-DRL are consistently better than those of DRL methods regardless the number of nodes. Compared to AM and POMO, our DT-DRL significantly reduces the optimality gap by 2.63% and 1.75% on TSP50, and 6.96% and 4.77% on TSP100, respectively. As for CVRP, the generalization advantage of our algorithm becomes more significant. Our model achieves an average gap of 0.33%, 4.34%, and 5.96% on instances with 20, 50, and 100 nodes, respectively, which outperforms the state-of-the-art method POMO by up to 3.77%, 3.27%, and 3.13%.

4.4 Ablation study

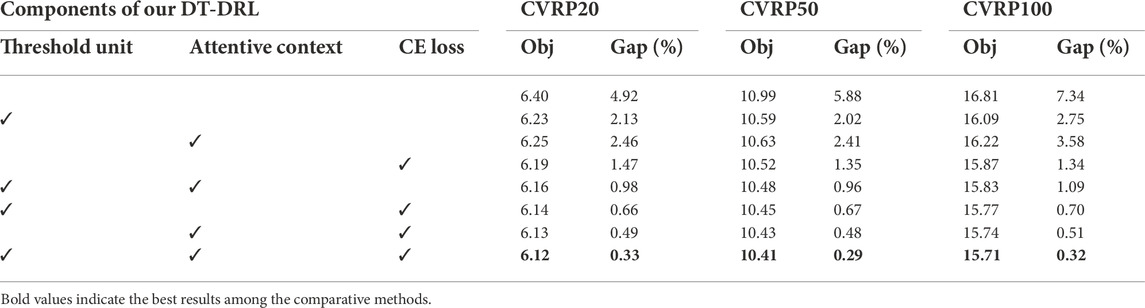
4.4.1 Effect of each component

Our proposed DT-DRL has three creative components: 1) the threshold unit; 2) attentive context; and 3) diverse-trajectory driven CE loss for improving route planning performance. Tables 3, 4 record the effect of gradually integrating these three components on TSP and CVRP. For TSP100, it can be seen that the optimality gap of the vanilla baseline with the addition of threshold unit, attentive context, and CE loss alone, respectively, is 1.03%, 1.16%, and 0.77%, which has a reduction of 0.90%, 0.77%, and 1.16% compared to the vanilla one. As for CVRP100, our approach with three components alone severally achieves an optimality gap of 2.75%, 3.58%, and 1.34%, which boosts the routing performance of the naïve approach by 4.59%, 3.76%, and 6.00%. In addition, the pair-wise combination of components further improves the effectiveness of path planning. Overall, our DT-DRL with three innovative components achieves the best results on all problems.

TABLE 3

TABLE 3. Ablation study of different components of our DT-DRL on TSP.

TABLE 4

TABLE 4. Ablation study of different components of our DT-DRL on CVRP.

4.4.2 Effect of the number of trajectories/decoders

We propose a Diverse Trajectory-driven DRL method to boost the routing performance significantly. The number of trajectories generated by different decoders has a crucial impact on the final results. Here we compare the objective values of DT-DRL with 1, 3, and 5 trajectories on two representative VRPs, TSP and CVRP. The results are shown in Figure 5. We can clearly observe that the performance of path planning keeps getting better as the number of trajectories/decoders increases. Take CVRP as an example, our method with five diverse trajectories achieves an reduction of 3.01%, 2.62%, and 2.60% in the value of objective function on CVRP20, CVRP50, and CVRP100, respectively. It also implies that the routing performance could be improved slightly when the number of diverse trajectories is further increased. Therefore, how to explore a more flexible way to determine the number of trajectories is a difficult point for future research.

FIGURE 5

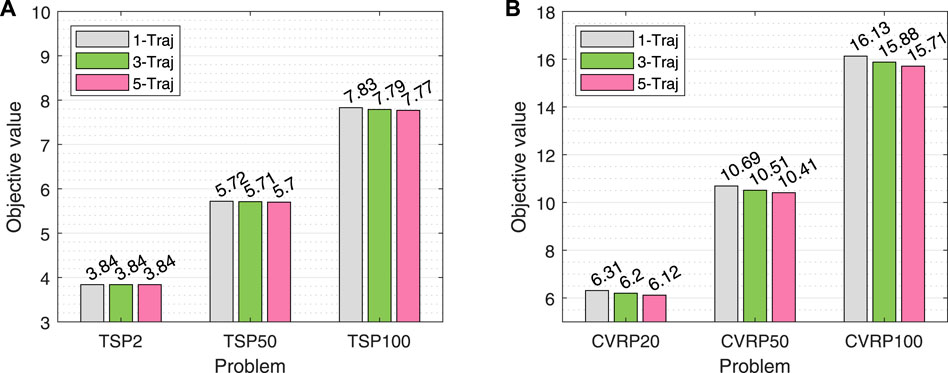
FIGURE 5. Comparison results of our proposed approach with different (1, 3, and 5) trajectories on (A) TSPs and (B) CVRPs.

4.4.3 Effect of hyperparameters

Following the current study Kool et al. (2018), we perform sensitivity studies of combinations of different learning rates and random seeds. The results in objective value as well as optimality gap for all runs with seeds 1,234 and 1,235 and two different learning rate strategies are listed in Table 5. It can be observed that the results with different seeds are almost the same, except for the large-scale scenes involving TSP100 and CVRP100. Furthermore, the different ways of learning rate variation have little effect on the final routing performance, which also proves the robustness of our algorithm. Take CVRP100 as an example, the difference between the optimal gaps of DT-DRL with different settings does not exceed 0.19%.

TABLE 5

TABLE 5. Routing performance of our approach with different learning rate strategies and seeds for TSP and CVRP.

5 Conclusion

In this paper, we concentrate on the large-scale power inspection with UAVs, and formulate this challenging issue as a family of VRPs when considering different constraints and scenarios. We adopt a constructive routing strategy, which selects the next node to visit and add it to the current, partial tour step-by-step. We regard this constructive, sequential node-selection process as a Markov decision process, and propose a novel deep reinforcement learning approach for routing, which avoids manually designed rules and does not require domain prior knowledge.

We make three branches of modifications to enhance the routing performance of our DRL approach. First, we introduce a threshold unit in the encoder for more informative node embeddings. Secondly, we design an attentive context embedding which removes the irrelevant nodes to better reflect the dynamics of state transitions. Finally, we bring in multiply decoders with the same structure but independent parameters, and devise a KL divergence based regular term to enforce them to learn distinct routing patterns and generate diverse trajectories.

We perform extensive experiments on five types of routing problems: TSP, CVRP, OP, PCTSP, and SDVRP. The comparison results illustrate that our proposed DT-DRL outstrips both DRL and heuristic ones by a clear margin. Moreover, our model generalizes well on larger scale problems compared to state-of-the-art DRL methods. Last but nor least, the ablation study demonstrates the effectiveness of our elaborated modifications.

Pertaining to future works, we note that there is still a gap between the effect of our DRL algorithm and that of the exact algorithm. On the one hand, we realize that the first-time-visitation may not be the best solution for the whole graph, and try to develop different relational encoder-decoder frameworks to improve the flexibility and accuracy of DRL models. On the other hand, besides construction-type routing method, we can also attempt an improvement-type method to boost the routing performance, where the model optimizes the initial complete solution iteratively with trial-and-error. In the near future, we would like to apply our model to a broader range of smart grids.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

QG: Conceptualization, Methodology, Coding, Validation, Formal Analysis, Investigation, Data curation, Writing-original manuscript. XZ: Conceptualization, Methodology, Formal Analysis, Investigation, Resources, Data curation. MX: Methodology, Validation, Formal Analysis, Resources, Writing-review and editing. JN: Conceptualization, Methodology, Data curation, Resources, Visualization. HC: Conceptualization, Methodology, Coding, Validation, Formal Analysis, Writing-review and editing. ZC: Methodology, Formal Analysis, Investigation, Resources, Data curation. ZH: Methodology, Data curation, Resources.

Funding

The research work was funded by State Grid Corporation of China (SGCC) Science and Technology Research Project 5700-202233182A-1-1-ZN.

Conflict of interest

Authors XZ, JN, ZC, and ZH were employed by State Grid Gansu Electric Power Company. The authors declare that this study received funding from the State Grid Corporation of China. The funder had the following involvement in the study: (1) data collection; (2) data analysis; (3) manuscript preparation.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2022.1054859/full#supplementary-material

References

Akca, Z., Berger, R., and Ralphs, T. (2009). “A branch-and-price algorithm for combined location and routing problems under capacity restrictions,” in Operations research and cyber-infrastructure (Berlin, Germany: Springer), 309–330.

CrossRef Full Text | Google Scholar

Alhassan, A. B., Zhang, X., Shen, H., and Xu, H. (2020). Power transmission line inspection robots: A review, trends and challenges for future research. Int. J. Electr. Power & Energy Syst. 118, 105862. doi:10.1016/j.ijepes.2020.105862

CrossRef Full Text | Google Scholar

Arigliano, A., Calogiuri, T., Ghiani, G., and Guerriero, E. (2018). A branch-and-bound algorithm for the time-dependent travelling salesman problem. Networks 72, 382–392. doi:10.1002/net.21830

CrossRef Full Text | Google Scholar

Baniamerian, A., Bashiri, M., and Tavakkoli-Moghaddam, R. (2019). Modified variable neighborhood search and genetic algorithm for profitable heterogeneous vehicle routing problem with cross-docking. Appl. Soft Comput. 75, 441–460. doi:10.1016/j.asoc.2018.11.029

CrossRef Full Text | Google Scholar

Baniasadi, P., Foumani, M., Smith-Miles, K., and Ejov, V. (2020). A transformation technique for the clustered generalized traveling salesman problem with applications to logistics. Eur. J. Operational Res. 285, 444–457. doi:10.1016/j.ejor.2020.01.053

CrossRef Full Text | Google Scholar

Bao, Z., Zhang, Q., Wu, L., and Chen, D. (2020). Cascading failure propagation simulation in integrated electricity and natural gas systems. J. Mod. Power Syst. Clean Energy 8, 961–970. doi:10.35833/mpce.2019.000455

CrossRef Full Text | Google Scholar

Bello, I., Pham, H., Le, Q. V., Norouzi, M., and Bengio, S. (2016). Neural combinatorial optimization with reinforcement learning. Available at http://arXiv.org/abs/1611.09940.

Google Scholar

Bransford, J., Sherwood, R., Vye, N., and Rieser, J. (1986). Teaching thinking and problem solving: Research foundations. Am. Psychol. 41, 1078–1089. doi:10.1037/0003-066x.41.10.1078

CrossRef Full Text | Google Scholar

Chen, X., and Tian, Y. (2019). Learning to perform local rewriting for combinatorial optimization. Adv. Neural Inf. Process. Syst. 32.

Google Scholar

Duan, C., Nishikawa, T., Eroglu, D., and Motter, A. E. (2022). Network structural origin of instabilities in large complex systems. Sci. Adv. 8, eabm8310. doi:10.1126/sciadv.abm8310

PubMed Abstract | CrossRef Full Text | Google Scholar

Duan, J., He, Z., and Yen, G. G. (2021). Robust multiobjective optimization for vehicle routing problem with time windows. IEEE Trans. Cybern. 52, 8300–8314. doi:10.1109/tcyb.2021.3049635

PubMed Abstract | CrossRef Full Text | Google Scholar

Ebadinezhad, S. (2020). Deaco: Adopting dynamic evaporation strategy to enhance aco algorithm for the traveling salesman problem. Eng. Appl. Artif. Intell. 92, 103649. doi:10.1016/j.engappai.2020.103649

CrossRef Full Text | Google Scholar

Francois-Lavet, V., Henderson, P., Islam, R., Bellemare, M. G., and Pineau, J. (2018). An introduction to deep reinforcement learning. FNT. Mach. Learn. 11, 219–354. doi:10.1561/2200000071

CrossRef Full Text | Google Scholar

Guan, Q., Hong, X., Ke, W., Zhang, L., Sun, G., and Gong, Y. (2021). “Kohonen self-organizing map based route planning: A revisit,” in 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September 2021 - 01 October 2021 (IEEE), 7969–7976.

CrossRef Full Text | Google Scholar

Gunjan, V. K., Pooja, , Kumari, M., Kumar, A., and Rao, A. A. (2012). Search engine optimization with Google. Int. J. Comput. Sci. Issues (IJCSI) 9, 206.

Google Scholar

He, K., Zhang, X., Ren, S., and Sun, J. (2016). “Deep residual learning for image recognition,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27-30 June 2016, 770–778.

CrossRef Full Text | Google Scholar

Helsgaun, K. (2017). An extension of the lin-kernighan-helsgaun tsp solver for constrained traveling salesman and vehicle routing problems. Roskilde: Roskilde University, 24–50.

Google Scholar

Hitte, C., Lorentzen, T., Guyon, R., Kim, L., Cadieu, E., Parker, H., et al. (2003). Comparison of multimap and tsp/concorde for constructing radiation hybrid maps. J. Hered. 94, 9–13. doi:10.1093/jhered/esg012

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, Y., Li, G., Chen, C., Bian, Y., Qian, T., and Bie, Z. (2022). Resilient distribution networks by microgrid formation using deep reinforcement learning. IEEE Trans. Smart Grid 13, 4918–4930. doi:10.1109/tsg.2022.3179593

CrossRef Full Text | Google Scholar

Jones, M., and Peet, M. M. (2021). A generalization of bellman’s equation with application to path planning, obstacle avoidance and invariant set estimation. Automatica 127, 109510. doi:10.1016/j.automatica.2021.109510

CrossRef Full Text | Google Scholar

Kool, W., Van Hoof, H., and Welling, M. (2018). Attention, learn to solve routing problems!. Available at http://arXiv.org/abs/1803.08475.

Google Scholar

Kwon, Y.-D., Choo, J., Kim, B., Yoon, I., Gwon, Y., and Min, S. (2020). Pomo: Policy optimization with multiple optima for reinforcement learning. Adv. Neural Inf. Process. Syst. 33, 21188–21198.

Google Scholar

Li, J., Ma, Y., Gao, R., Cao, Z., Lim, A., Song, W., et al. (2021a). Deep reinforcement learning for solving the heterogeneous capacitated vehicle routing problem. IEEE Trans. Cybern. 2021, 1–14. doi:10.1109/tcyb.2021.3111082

CrossRef Full Text | Google Scholar

Li, Y., Gao, W., Huang, S., Wang, R., Yan, W., Gevorgian, V., et al. (2021b). Data-driven optimal control strategy for virtual synchronous generator via deep reinforcement learning approach. J. Mod. Power Syst. Clean Energy 9, 919–929. doi:10.35833/mpce.2020.000267

CrossRef Full Text | Google Scholar

Ma, Y., Li, J., Cao, Z., Song, W., Zhang, L., Chen, Z., et al. (2021). Learning to iteratively solve routing problems with dual-aspect collaborative transformer. Adv. Neural Inf. Process. Syst. 34, 11096–11107.

Google Scholar

Muley, V. Y. (2021). “Mathematical linear programming to model micrornas-mediated gene regulation using gurobi optimizer,” in Modeling transcriptional regulation (Berlin, Germany: Springer), 287–301.

CrossRef Full Text | Google Scholar

Parisotto, E., Song, F., Rae, J., Pascanu, R., Gulcehre, C., Jayakumar, S., et al. (2020). “Stabilizing transformers for reinforcement learning,” in International conference on machine learning, Wienna, Austria, July 12, 2020–July 18, 2020 (PMLR), 7487–7498.

Google Scholar

Prabhu, P., Subramani, M., and Kwak, K.-s. (2022). Analysis of integrated uwb mimo and cr antenna system using transmission line model with functional verification. Sci. Rep. 12, 14128–14218. doi:10.1038/s41598-022-17550-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Sethanan, K., and Jamrus, T. (2020). Hybrid differential evolution algorithm and genetic operator for multi-trip vehicle routing problem with backhauls and heterogeneous fleet in the beverage logistics industry. Comput. Industrial Eng. 146, 106571. doi:10.1016/j.cie.2020.106571

CrossRef Full Text | Google Scholar

Song, H., Liu, C.-C., Lawarrée, J., and Dahlgren, R. W. (2000). Optimal electricity supply bidding by markov decision process. IEEE Trans. Power Syst. 15, 618–624. doi:10.1109/59.867150

CrossRef Full Text | Google Scholar

Sun, M., Zhao, X., Tan, H., and Li, X. (2022). Coordinated operation of the integrated electricity-water distribution system and water-cooled 5g base stations. Energy 238, 122034. doi:10.1016/j.energy.2021.122034

CrossRef Full Text | Google Scholar

Tang, W., Zhao, W., Qian, T., Zhao, B., Lin, Z., and Xin, Y. (2022). Learning-accelerated asynchronous decentralized optimization for integrated transmission and distribution systems over lossy networks. Sustain. Energy, Grids Netw. 31, 100724. doi:10.1016/j.segan.2022.100724

CrossRef Full Text | Google Scholar

Vásquez, S. A., Angulo, G., and Klapp, M. A. (2021). An exact solution method for the tsp with drone based on decomposition. Comput. Operations Res. 127, 105127. doi:10.1016/j.cor.2020.105127

CrossRef Full Text | Google Scholar

Wei, W., Gu, H., Deng, W., Xiao, Z., and Ren, X. (2022). Abl-tc: A lightweight design for network traffic classification empowered by deep learning. Neurocomputing 489, 333–344. doi:10.1016/j.neucom.2022.03.007

CrossRef Full Text | Google Scholar

Wu, Y., Song, W., Cao, Z., Zhang, J., and Lim, A. (2021). Learning improvement heuristics for solving routing problems. IEEE Trans. Neural Netw. Learn. Syst. 33, 5057–5069. doi:10.1109/tnnls.2021.3068828

PubMed Abstract | CrossRef Full Text | Google Scholar

Xin, L., Song, W., Cao, Z., and Zhang, J. (2020). Step-wise deep learning models for solving routing problems. IEEE Trans. Ind. Inf. 17, 4861–4871. doi:10.1109/tii.2020.3031409

CrossRef Full Text | Google Scholar

Xu, Y., Fang, M., Chen, L., Xu, G., Du, Y., and Zhang, C. (2021). Reinforcement learning with multiple relational attention for solving vehicle routing problems. IEEE Trans. Cybern. 52, 11107–11120. doi:10.1109/tcyb.2021.3089179

PubMed Abstract | CrossRef Full Text | Google Scholar

Yan, X., Jia, L., Cao, H., Yu, Y., Wang, T., Zhang, F., et al. (2022). Multitargets joint training lightweight model for object detection of substation. IEEE Trans. Neural Netw. Learn. Syst. 2022, 1–12. doi:10.1109/tnnls.2022.3190139

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, L., Sun, Q., Zhang, N., and Li, Y. (2022). Indirect multi-energy transactions of energy internet with deep reinforcement learning approach. IEEE Trans. Power Syst. 37, 4067–4077. doi:10.1109/tpwrs.2022.3142969

CrossRef Full Text | Google Scholar