
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Energy Res. , 14 November 2022
Sec. Process and Energy Systems Engineering
Volume 10 - 2022 | https://doi.org/10.3389/fenrg.2022.1047984
This article is part of the Research Topic Design, Simulation and Optimization of Hydraulic Machinery, Volume II View all 9 articles
The synergy of cavitation and sediment erosion is the most severe destruction in hydraulic machinery in sediment-laden rivers, and currently the physics and mechanism are still lack of understanding. The synergy effects of cavitation and sediment erosion not only reduce the efficiency and life of hydraulic machinery but also cause costs in operation and maintenance. With the rapid development of renewable clean energy and the transformation of water resources, an increasing number of new hydropower stations and water diversion projects are currently planned or under construction, where most of them are in sediment-laden rivers. In the present paper, the research work, including theory, experiment, and simulation, in this field carried out by various investigators are presented and discussed. Physical mechanisms involved in the synergy of cavitation and sediment erosion which is responsible for material damage as investigated by researchers have also been discussed, and would help to identify gaps for future studies.
Hydraulic machineries (i.e., pump, turbine, and reversible pump-turbine) must be often operated in cavitation conditions. Cavitation is one of the major challenges limiting the safe and stable operation of electric power systems (i.e., pumps, turbines), especially in sediment-laden flows where the synergy of cavitation and sediment erosion will cause even more severe damages. According to the literature (Naidu, 2016; Sharma and Singh, 1987; Naidu, 1996; Wang et al., 2022), cavitation has shown to be the major cause of metal loss at pump/hydropower stations, particularly in South Asian countries belonging to Himalayan regions (such as India, China, and Nepal), where large contents of quartz exist in the sediment especially during the monsoon season (Singhal and Ratnendra, 2017). The synergy effects of cavitation and sediment erosion are important and result in more severe damage (Thapa et al., 2007; Teran et al., 2018), as shown in Figures 1, 2. In China, the total annual sediment yield of the main rivers was 4.77 × 109 tons in 2020 (Ministry of Water Resources of the People’s Republic of China, 2020), and pumps or turbines are prone to experience cavitation and thus even serious erosion due to the synergistic effects of cavitation and sediment erosion (Huang, 1991) when operated in sediment-laden rivers. This problem is a major concern in the case of small and mini hydropower plants, which have been developed quickly in recent years. According to the literature, 40% of the turbines in the built hydropower station in China experience serious synergistic effects of cavitation and sediment erosion (Yang, 2012), ultimately leading to economic losses (i.e., the efficiency and life reduction and operation and maintenance costs of the turbine).

FIGURE 1. Erosion in the hydro turbine for (A) the needle with pure cavitation erosion, (B) the needle with synergy of cavitation and sand erosion, and (C) turbine runner with synergy of cavitation and sand erosion shown in the enlarged picture (Thapa et al., 2007).
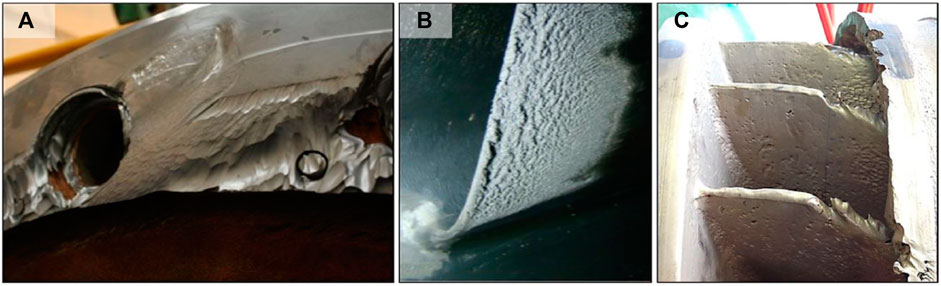
FIGURE 2. Erosion damage in the components of three Francis turbines: (A) hard-particle erosion in one of the covers, (B) cavitation damage at the trailing edge of one of the runner blades, and (C) synergistic damage of the hard particles and cavitation at the leading edge of the runner blades (Teran et al., 2018).
Hydrodynamic cavitation generally occurs if the local static pressure drops below the saturated vapor pressure, and consequently, the negative pressures are relieved by means of forming gas-filled or gas- and vapor-filled cavities (i.e., evaporation) (Knapp et al., 1970; Arndt, 1981; Brennen, 1995). Vapor structures are transported into high static pressure areas by the flow, and the subsequent collapse of vapor regions will generate shock waves, which can cause vibrations and noise (Brennen, 1994). Near solid boundaries, the collapse of vapor structures often leads to severe damage of surface material, i.e., pitting or erosion (Knapp et al., 1970; Arndt, 1981; Brennen, 1994; Brennen, 1995). The synergism of cavitation and sediment erosion, which occurs in high-speed regions, including guide vanes and runner blade inlet of a turbine and pump in hydraulic machinery, generally consists of two interrelated processes: 1) high-speed impact on the solid walls of sediment particles carrying kinematic energy and 2) the collapse of cavitation bubbles, and their combined effects, such as cavitation-induced acceleration of the solid particles impinging the surface (Arndt et al., 1989; Kumar and Saini, 2010). Cavities in liquid flows will experience unsteady processes, i.e., cavity formation, growth, and collapse, which could significantly change the motions of nearby sediment particles, acting on the sediment erosion process known as cavitation enhancement. Meanwhile, the existence of sediment particles alters the cavity behaviors from cavity inception and development to the cavity collapse process, influencing the cavitation erosion. This is a challenging problem, and complex phenomena including gas/vapor-liquid-solid three-phase flows, mass transfer, compressibility, turbulence, unsteadiness, and material properties as well, where the physical understanding is very limited and requires further investigation. With the development of modern hydraulic machinery toward large-scale, large-capacity, high-speed, and high-performance directions, the synergistic effects of cavitation and sediment erosion are becoming a serious problem, and the lack of physics and mechanisms involved significantly limits the reliability, stability, and safe operation of hydraulic machinery in sediment-laden flows.
Cavitation in sediment-laden flows is complex gas/vapor-liquid-solid three-phase turbulent flows. So far, despite plenty of research work on cavitation erosion (Tomita and Shima, 1986; Berchiche et al., 2002; Sreedhar et al., 2017) and sediment erosion (Padhy and Saini, 2008; Padhy and Saini, 2009), theoretical work on the synergy mechanism of cavitation and sediment erosion is very scarce. For example, Rao and Buckley (Rao and Buckley, 1984) reviewed erosion models for both long-term cavitation and liquid impingement proposed by different investigators, including the curve fitting approach and a power-law relationship. They also evaluated the importance of the different modeling methods using data from cavitation fields and a liquid impingement device. As for the prediction of synergy effects of cavitation and sediment erosion. Ni and He (Ni and He, 1994) theoretically investigated the impact of shock waves generated by the bubble collapse on the solid particles considering the liquid compressibility, and the maximum velocities of solid particles were obtained. The Gilmore equation was used to calculate the bubble radius and the particle motion was calculated by solving the Newton equation. Their study showed that the shockwave-induced speed of particles was large enough to cause damage to the concretes used in hydraulic structures. Duan (Duan, 1998) carried out experimental and theoretical work to investigate the erosion performance under different flow velocities, and found that when above certain flow rate, cavitation would protect the solid walls of flow passage from being eroded, thus weakening the erosion process. Inspired by this experiment, Li (Li, 2006) proposed a microscopic model based on the assumption that the particle near the cavitation bubbles will be trapped by the microjet of the collapsing bubble and accelerated to an extremely high velocity towards the solid walls, resulting in potential damage. That is,
here, V is the characteristic velocity of the flow and L is the characteristic length of the flow. The predictions by this microscopic model show that the acceleration rate is so high that the particle could acquire a velocity up to several hundred meters per second within microseconds. Following, this theoretical microscopic model was validated by the numerical simulation work by (Dunstan and Li, 2010).
Recently, based on an effective-medium approach where the influence of effective suspension viscosity on bubble/particle dynamics and the impact energy of erosive particles were incorporated, (Su et al., 2021) developed a theoretical model to predict the synergistic erosion of cavitation and sediment particles by taking into account the dual effects of sediment particles (i.e., viscosity effect of small particles and inertial effects of large particles) in a large range of sediment sizes. Good agreement between the model prediction and experimental data was found. This theoretical model could predict the opposing effects of sediment parties on the cavitation erosion as well, and showed that the viscous effect of sediment-sized particles (STP, < 50 μm) could mitigate or even override the impact of impinging microjets and sand-sized particles (SDP, > 50 μm).
and
where μem and ρem are the effective viscosity and density of the STP suspension, respectively; ρp and ρlm are the density of the particles and liquid medium, respectively; and
here, A denotes vpsep and B = (2ρp + ρem)Rp2/9μem. Then, according to the study by Bitter, (1963), the deformation wear (WD) can be expressed as
here, ε is an empirical constant related to the specific energy for deformation wear, depending on the material properties of the particles and the exposed target surface.
Teran et al., (2021) developed a synergy model to predict the wear behavior of combined effect of cavitation and particle erosion where the impact velocity of a particle trapped by the microjet of a collapsing bubble near a solid wall was estimated, and implemented this model into the CFD software. Their model was validated with the experimental results obtained by a slurry pot erosion tester and showed good agreement. In this model, the impact velocity of the particle (Vp) which is accelerated towards the wall by a collapsing bubble is as follows
where, mp = the particle mass, Rb = the maximum bubble radius, S = is the position of the particle with respect to the wall, Pc = is the collapse pressure, k1 = 200 m/s and k2 = -6 m/s are the constants, and k3 = -5.647, k4 = -1358, k5 = -6.373, and k6 = 1.798 are the fitting constants. Based on the Grant-Tabakoff erosion model (Grant and Tabakoff, 1973), the dimensionless erosion rate E is
where,
here, E is the ratio of the mass loss due to the impact of one particle on the surface to the particle’s mass, Vpf is the final impact velocity of the particle, α is the impact angle, α0 is the angle of maximum erosion, RT is the tangential restitution ratio, and k7 and k12, are fitting coefficients of the model, and V1, V2, and V3 are the reference speeds.
In summary, the above theoretical studies reveal that the accurate prediction of impact loads generated by the collapsing cavitation bubbles or cavity structures and maximum sediment particle velocity is critical for the evaluation of synergy of cavitation and sediment erosion. Physical models have been mainly established on the dynamics, such as pressure loads, of the collapsing bubbles and its influence on nearby particle motions, such as microscopic model. In addition, the gas/vapor-liquid-solid three-phase cavitation mixture properties (i.e., viscosity) provides interesting perspective for the understanding and prediction of synergy of cavitation and sediment erosion in sediment-laden flows. On the basis of theoretical results, an in-depth and detailed knowledge on cavitation in sediment-laden flows could be obtained, which greatly contributes to the suppression of synergy of cavitation and sediment erosion and improvement of hydraulic machine performance.
Experiment has always been an important way for understanding the physics and mechanism behind the synergy of cavitation and sediment erosion. Experimental investigations of synergistic effects of cavitation and sediment erosion have been designed and conducted by using both laboratory and field experiments. So far, the laboratory studies on synergy of cavitation and sediment erosion are generally based on small-scale models (i.e., foil, cylinder, venturi, rotating risk, and impeller) to accelerate cavitation erosion testing with vibratory apparatus (i.e., Figure 3) (Huang et al., 1996; Wu and Gou, 2013; Zhao et al., 2017; Teran et al., 2018; Wang et al., 2018; Stella and Alcivar, 2019; Su et al., 2021), rotating disc systems (i.e., Figure 4) (Rasmussen, 1956; Lichtman, 1967; Wood et al., 1967; Thapa et al., 2007; Hong et al., 2013; Steller and Gireń, 2015), slurry pot testers (i.e., Figure 5) (Amarendra et al., 2012; Peng et al., 2020), and water tunnel (i.e., Figure 6) (Liu, 1983; Gregorc et al., 2011; Gregorc et al., 2012). In the following, these devices used in the laboratory studies are explained briefly.
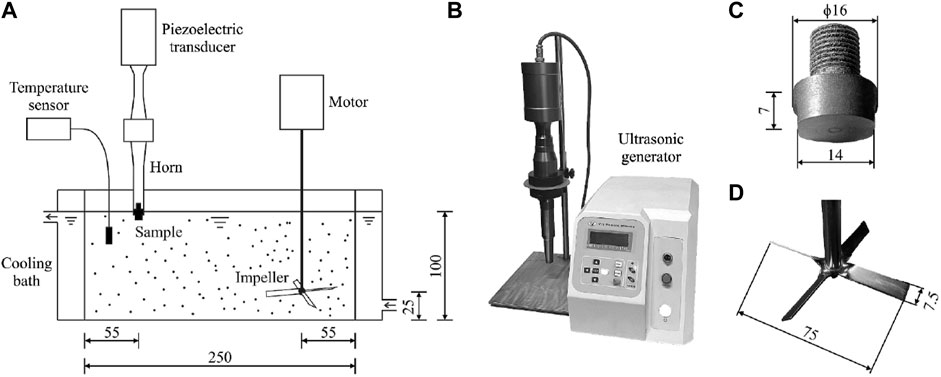
FIGURE 3. Vibratory test facility (Su et al., 2021). (A) Schematic diagram of the experimental setup; (B) ultrasonic device; (C) sample dimensions; (D) impeller dimensions (mm).
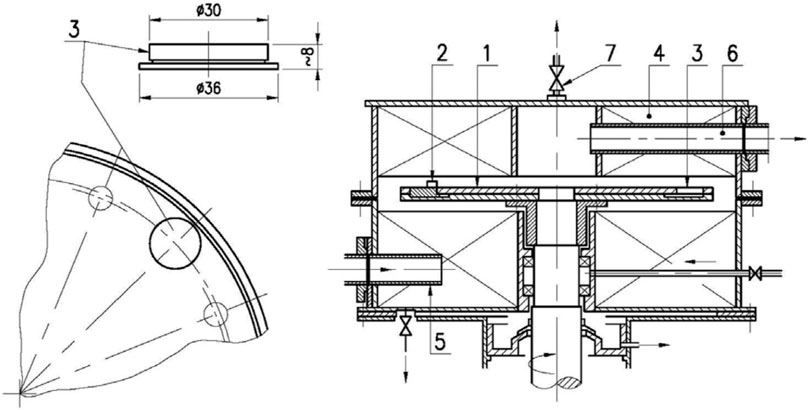
FIGURE 4. Rotating disk device (Steller and Gireń, 2015) at the IMP PAN lab in Gdansk, Poland. 1-disk; 2-cavitator (pin); 3-specimen; 4-stagnator vane; 5, 6-liquid inlet, outlet; 7-de-aerating valve.
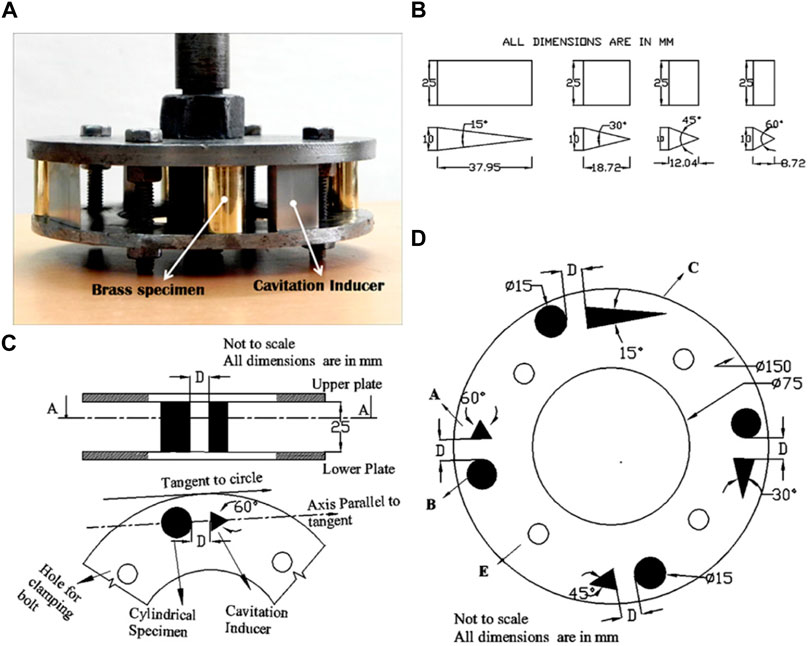
FIGURE 5. Slurry pot test (Amarendra et al., 2012). (A) Photograph of the specimen holder of the modified slurry pot test setup; (B) drawing of the cavitation inducers; (C) schematic diagram of the specimen holder with section at A-A; (D) positioning of the CIs and the specimen. A—CI, B—cylindrical specimen, C—lower base plate, D—distance between specimen and cavitation inducer and E—hole for clamping the bolt.
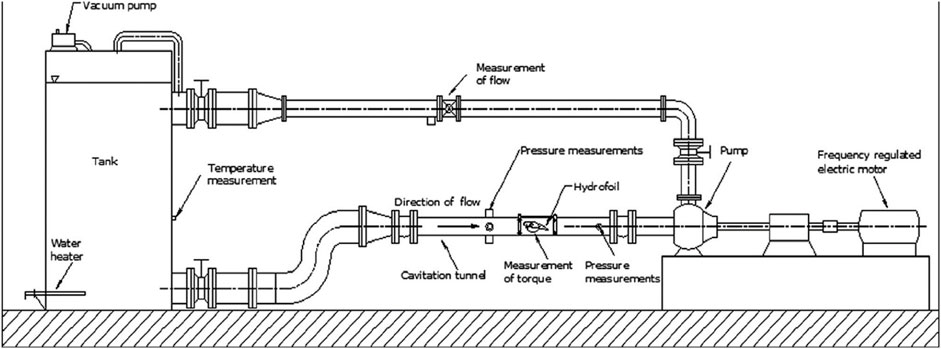
FIGURE 6. Cavitation tunnel sketch (Gregorc et al., 2011; Gregorc et al., 2012).
Using vibratory test facilities, a number of studies have provided detailed quantification of the synergistic effects of cavitation and sediment erosion. For example, Huang et al. (Huang et al., 1996) conducted systematic experiments to study the effects of particle properties on cavitation and sediment erosion to understand the synergy mechanism in solid-water mixtures using vibratory test facilities. The damaged patterns of specimen surfaces were measured by SEM photographs, and the vibratory cavitation erosion test was guided by ASTM D32-77 (ASTM D32-77, 1977). Su et al., (2021) employed the vibratory test facility to investigate the effects of microparticles in synergistic cavitation-particle erosion in a flat-bottomed Perspex vessel as shown in Figure 3. In this study, the test samples including vibrating horn tip and four-bladed impeller were all fabricated from medium carbon steel (AISI 1045, density 7.87 × 103 kg m−3). The microparticle with median diameters of approximately 45 μm and 90 μm were tested. Romero et al., (2019) experimentally investigated the effects of particle sizes and sediment concentrations on the synergy between cavitation and solid particle erosion with a modified ultrasonic cavitation tribometer. The test material was AISI 316 stainless steel with a hardness of 223.3 ± 4.9 HV, and the optical stereoscopy and scanning electron microscopy were used to analyze the surface wear. The sand particles used were from the penstock of the Amaime 152 hydroelectric plant with the size distribution ranging between 50 μm and 150 μm, and the hardness of 775.9 ± 124.2 HV. Chen et al., (2022b) investigated the erosion characteristics of 6063 aluminum specimens in sandy water containing quartz sand which has sharp edges and irregular shapes under different sediment sizes and concentrations using the ultrasonic vibration cavitation apparatus to understand the mechanism involved in the synergy of cavitation and sediment erosion. Chen et al., (2007) investigated the effects of microparticles with different sizes on cavitation erosion using the tip surface testing and free radical detection where after the experiment, the tip surface was examined by the Wyko MHT-III optical interferometer. The rotating speed was 15,000 r/min for 10 min. Their study showed that particles at a certain size would increase the number of heterogeneous nucleation while weaken bubble-particle interactions.
The cavitating rotating disk resembles the pump impeller that is well suitable for the study of cavitation erosion in hydraulic machinery, and high intensity cavitating flows can be obtained. As presented in Figure 4, the rotating disk device consists of a disk with pins or holes at various radii (Steller and Gireń, 2015), and cavitation bubbles are generated and collapsed by the movement of the pins or holes in the disk through the ambient stationary liquid. Using the rotary disk cavitation system which can consider the centrifugal force in rotary hydraulic machines (i.e., pump and turbine), Wang et al., (2008) investigated the microparticles and their size on cavitation erosion process. In this study, the dimensions of the sample were 40 × 30 × 6 mm, and material of the sample was the Q235 steel without heat treatment. The diameter of the rotating disk was 300 mm, and the rotating speed of the disk was 2800 r/min in the experiments at room temperature.
Amarendra et al., (2012) studied the synergy of slurry erosion and cavitation erosion using a slurry pot tester. A schematic of this test is shown in Figure 5. The slurry pot has a circular section with a diameter of 282 mm and a height of 286 mm, with the diameters of the upper and lower circular ring plates of 150 mm and a thickness of 4 mm. The size of the sand particles is between 210 μm and 354 μm, and the concentration is 10 wt%. Weight loss was measured using a Mettler Toledo electronic balance (model AB-104S) with a least count of 0.1 mg. Sato et al., (1991) experimentally studied coupled damage caused by sediment erosion (i.e., artificial sediment (Al2O3)) and cavitation erosion using the submerged cavitating jet experimental apparatus. The magnitude of the acoustic emission energy, impact pressure and material damage rate caused by cavitating jet impingement were carefully examined.
Gregorc et al., (2011); Gregorc et al., (2012) investigated the impact of particles on cavitating flows around a hydrofoil in water tunnel at the University of Maribor as schematically shown in Figure 6, and the influence of particle concentration on hydrodynamic performance (lift and drag forces) was quantified. The particles of material FR 240/F were used with a density of 1700 kg/m3, and a mean diameter of 30 μm.
In addition to the synergy effects of cavitation and sediment erosion experiments using simple geometry models, experiments have also been conducted on proto pumps and turbines (Zhou et al., 2013; Lu et al., 2014; Wang et al., 2014; Zhao et al., 2017; Liu et al., 2019), and even the field experiments have been conducted in hydroelectric power and pump stations (Yang et al., 2005; Lu et al., 2019). Specifically, Takagi et al., (1978) experimentally studied the influence of alumina concentration on the performance and cavitation characteristics of turbines. Mei and Wu, (1996) conducted experiments to study the effect of solid particles on different model Francis turbines and observed earlier cavitation inception in sandy water. Jin et al., (1986) carried out an experiment to investigate the role of sand particles on the combined effects of cavitation and sediment erosion of hydraulic turbines, and the 18Cr-8Ni steel was tested in a venturi device at a hydroelectric power station in the flood season. In their work, two types of damage: 1) smooth erosion in the area of regular fluid flow and 2) in the regions where cavitation occurred, were studied, and the sand particles, cavities, cracks, and cutting scar sand fatigue patterns on the sponge-like worn surface were observed. Thapa et al. (Thapa et al., 2007) investigated the combined effects of cavitation and sediment erosion in hydraulic turbines on a rotary disk apparatus. Their study showed that the combined effects of cavitation and sediment erosion were stronger than the individual effects. Using the hydraulic machinery erosion testing system at the China Institute of Water Resources and Hydropower Research (CIWRH), China, which has three test modes including venturi-section water tunnel, rotating disc and rotating disc with jet nozzle (Lu et al., 2014; Liu et al., 2019; Hydraulic Machinery, 2021), as shown in Figures 7, 8, Lu et al., (2014) experimentally studied the synergetic erosion caused by cavitation and sand erosion in hydraulic machinery. A high-precision electronic analytical balance (maximum capacity: 220 g, readability: 0.1 mg) was used to measure the weight loss, and a 3D surface profiler was used to image the erode surface as well as the volume loss. Furthermore, Figure 9 shows the Francis turbine test rig under construction at Turbine Testing Tab (TTL) at Kathmandu University, which has been used for hydropower development, especially the problem of sediments in the design and operation of hydraulic machineries in the Himalayan region (Thapa et al., 2007; Thapa et al., 2012a; Thapa et al., 2012b).

FIGURE 7. Photograph of the hydraulic machinery abrasion testing system at the China Institute of Water Resources and Hydropower Research (Hydraulic Machinery, 2021).
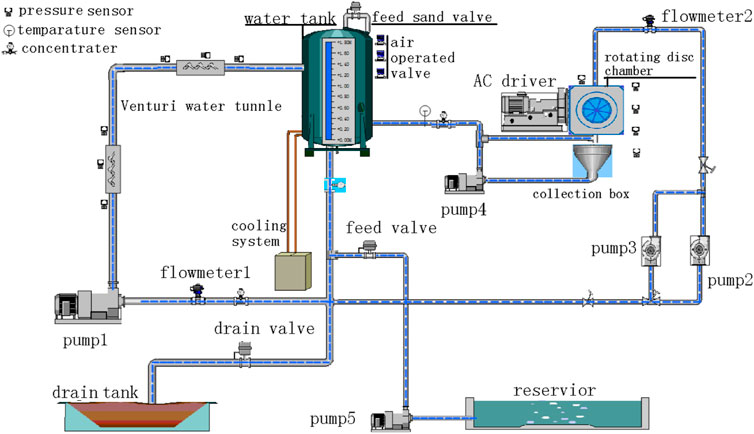
FIGURE 8. The layout of the integrated test rigs at CIWRH (Lu et al., 2014).

FIGURE 9. Francis turbine test rig under construction at Turbine Testing Laboratory (TTL) at Kathmandu University in Nepal (Thapa, 2019).
The majority of abovementioned experimental work in the synergy of cavitation and sediment erosion is summarized in Table 1. Here we come up with a brief summary of these experiment work. These results show that the synergy of cavitation and sediment erosion causes more severe damages than the individual effects of pure cavitation or pure sediment erosion, respectively. The dual effects of sediment on cavitation erosion (i.e., acceleration and inhibition) are observed on both laboratory and field studies, and mainly depend on the sediment size, concentration, and material properties. Research has illustrated that with increasing sediment size and concentration, the synergy of cavitation and sediment erosion experiences a plateau value, which indicates a critical sediment size and concentration value in terms of synergy of cavitation and sediment erosion. Furthermore, the coexistence of sediment and bubbles will alter significantly the local flow structures, i.e., high pressure region, faster bubble collapse, moments and noises in cavitating flows, and bubble-particle collisions also reduce the number of free bubbles, which could change the cavity structures. The detailed discussion about the influence of sediment on synergy of cavitation and sediment erosion will be presented in the following section.
Compared with experimental measurements and theoretical modelings, the numerical simulations can predict local flow structures and dynamics associated with synergistic effects of cavitation and sediment particles, and promote the understanding of combined effects of cavitation and sediment erosion. Up to now, the prediction and prevention of the combined effects of cavitation and sediment erosion in hydraulic practice are still limited by the lack of physical understanding of flow structures and dynamics of cavitation in sediment-laden flows, and the corresponding responses of solid materials. With the advancement in computational power, computational fluid dynamics (CFD) method has been extensively used to predict and design the cavitating flows to prevent the potential erosion in hydraulic machinery in sediment-laden rivers (i.e., Figure 10).
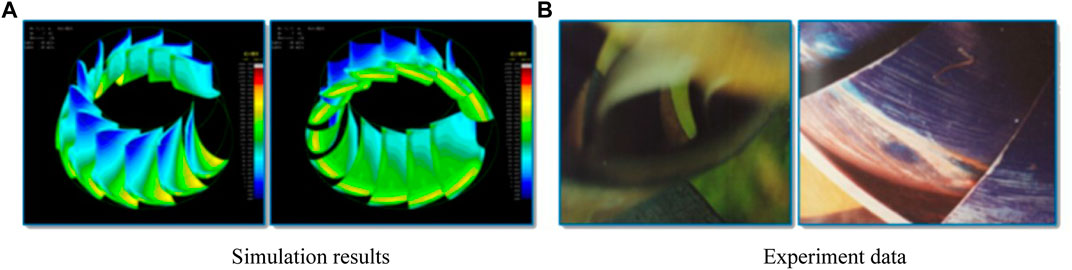
FIGURE 10. Comparisons of the erosion distribution on blades of turbines at Liujiaxia Hydropower station for (A) numerical results, and (B) experiment data (Lu et al., 2019).
Specifically, Dunstan and Li, (2010) carried out a numerical study on cavitation enhancement of sediment erosion using commercial code STAR-CCM+ and a simplified analytical approach in MATLAB. The micromodel proposed by Li, (2006) which considered a single sediment particle entrained in the micro-jet of collapsing cavitation bubbles was used to calculate the particle energy potential gained from the collapsing bubble and thus the erosion distribution. Simulation results supported the mechanism of the Li’s micromodel (Li, 2006) that the particle damage potential would be enhanced by the microjet generated in the process of bubble collapse, and further showed that this enhancement is mainly associated with the mass of particle and ratio between the distance from the collapsing bubble to a solid boundary and its radius upon collapse.
Weili et al., (2010) numerically studied cavitation characteristics in both pure water and solid-liquid two-phase flow conditions in a Kaplan turbine. The Singhal cavitation model (Singhal et al., 2002) was used to calculate the phase change between vapor phase and liquid phase. In their study, a particle trajectory model was used to investigate the region and degree of runner blade erosion in different operation conditions. The study found that compared with the efficiency with two phases cavitation in clean water of 89.52%, the efficiency was 87.84% in sediment flow, decreasing by 1.68%.
Gregorc et al., (2011) studied the impact of solid particles on the development of cavitation flow around a hydrofoil using an inhomogeneous model where an addition phase particle dispersion model (Euler-Euler) was used. Numerical modeling was performed using the commercial CFD program ANSYS-CFX 12.1 while considering the impact of particles. The results showed that the hydrodynamic forces on the hydrofoil were significantly influenced by mass fraction of particles in water, and the changes in the mass fraction of particles ξ = 0.0032 led to a change of the ratio of moments Mt/Mt0 up to 11%. The increase in the vapor phase in the case of the dispersed phase mass fraction is 0.0032 and the shear velocity is 0.876 compared with pure water. Figure 11 presents a comparison of the vapor volume fraction simulation without particles and with particles under different conditions.

FIGURE 11. (A) Comparison of vapor volume fraction simulation without particles (left) and with particles (right ξ = 0.0032) at equal Δp = 50.02 bars, Qi = 15 kg/s, and (B) comparison of vapor volume fraction simulation without particles (left) and with particles (right ξ = 0.0032, μd = 0.87) at equal Δp = 0.35 bars (Gregorc et al., 2011).
Wang et al., (2014) numerically investigated the influence of the solid particle content on the cavitation characteristics of a centrifugal pump by combining the numerical calculations and the test results, and revealed that with an increase in the solid particle content, the cavitation would be worsened. The simulations were conducted on ANSYS-CFX using an inhomogeneous mixture multiphase model and Singhal cavitation model (Singhal et al., 2002) to calculate the solid-liquid-vapor three-phase flows. The particle size is 100 μm with different particle concentrations of 10%, 20%, and 30%.
Kumar and Bhingole, (2015) employed numerical simulations to investigate the combined erosion in a Kaplan turbine rated capacity of 7 MW using ANSYS 14 software. The computational domain was constructed from the casing inlet to the draft tube outlet, where 15 aero wicket gates and five runner blades were used, and the unstructured tetrahedral mesh was generated. The 3D viscous flow simulation with the SST k-ɷ turbulence model has been conducted. The operation conditions used in the simulation including pure water, cavitation erosion, sediment erosion and a combined erosion model at 100% wicket gate opening with varying sediment size and sediment concentration were investigated. The results showed that under the combined erosion operation, the combined erosion rate and nonuniformity increased with the increasing in sediment diameter and sediment concentration. The maximum efficiency drop of 4.31 pct and the maximum normalized average combined erosion of 0.00329 g g−1 were found at 100 μm sediment diameter and 10,000 ppm sediment concentration.
Sun et al., (2022) numerically investigated the effects of sediment diameter and concentration on synergistic cavitation and sediment erosion mechanisms in cavitating flows around a rotating disk using ANSYS-CFX code. The non-homogeneous multiphase flow model with the modified RNG k-ε turbulence model and Zwart-Gerber-Belamri cavitation model was employed to simulate the bubble-particles interaction of solid-liquid-gas three-phase flow. In the simulation, sediment is considered as the dispersed solid particles, and water and vapor are regarded as continuous fluids. The sediment size is in the range of 20–400 μm and sediment concentration is in the range of 1%–10%. They concluded that with an increase in sediment particle size, the cavitation is first inhibited and then promoted where both the cavitation area and intensity are enhanced, and with increasing sediment particle concentration, the cavitation is always promoted where the cavitation area is expanded and cavitation intensity remains the same.
Although few numerical studies have been conducted on the synergy effects of cavitation and sediment erosion of cavitation in sediment-laden flows, the cavitation or air bubble behaviors when interacting with solid walls and particles have been studied using CFD numerical simulations (Johnsen and Colonius, 2009; Jayaprakash et al., 2012; Zhang et al., 2016; Teran et al., 2018; Chen et al., 2022a). For example, Johnsen and Colonius, (2009) numerically simulated the collapsing behaviors of a non-spherical gas bubble induced by a shock wave in a free field near a solid surface, and showed that the shock induced collapse would generate a high velocity reentrant jet, which created a water hammer shock and produced high pressures on the neighboring walls, leading to potential damage. In their study, they used a high-order WENO scheme for the accurate shock- and interface-capturing, and the numerical results were validated by the available theory and experiments. Teran et al., (2018) employed the combined experiments and numerical simulations to investigate the interactive behavior of hard particles and cavitation bubbles near a solid wall to deepen the understanding of synergistic effects of particle erosion and cavitation damage using the commercial software ANSYS-FLUENT solver. In their simulation, the Volume-Of-Fluid (VOF) model was used to capture the evolution of the interface between air and liquid water, and the six degree-of-freedom solver coupled with a dynamic mesh was used to model the interaction between the particle and the fluid. Figure 12 shows the comparisons of an image sequence obtained experimentally and the contour lines of air volume fraction showing the bubble interface obtained using CFD simulations. Red represents air, while blue color represents water. The data were obtained for a maximum bubble size (Rb) of 2.5 mm, distance to wall of 1.5 mm, particle diameter of 60 μm, and particle material sand.
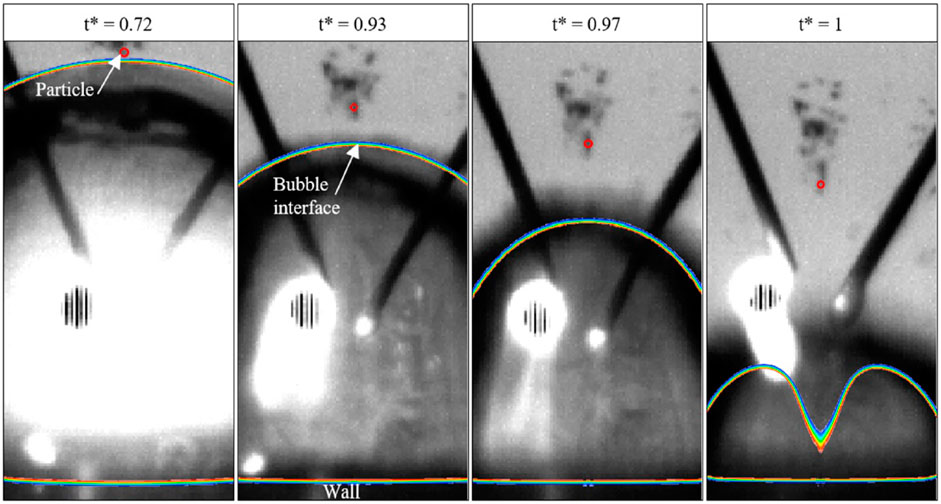
FIGURE 12. Comparison of experimentally observed and numerically predicted time evolution of bubble radius and nearby particle motions (Teran et al., 2018).
The abovementioned simulation work illustrates the state-of-art of numerical approaches and physical models describing the gas/vapor-liquid-solid complex three-phase flows, showing that simulation is an important tool to deepen the knowledge and understanding of cavitation in sediment-laden flows. The complex turbulence flows are mainly calculated using Reynolds-Averaged Navier-Stokes Equations (i.e., RNG k-ε, SST k-ɷ). The multiphase models includes both homogeneous models using Euler method (i.e., VOF interface capturing), and discrete models using Lagragian method to track the trajectories of sediment particles are adopted. The cavitation models to describe the mass transfer between liquid and its vapor including Singhal cavitation model and Zwart-Gerber-Belamri cavitation model are employed. Simulation work provide further insight into the physics involved in the cavitation in sediment-laden flows. However, these models are mainly developed based on single phase flows or pure cavitating flows without suspended sediment particles. It is required to develop high-fidelity numerical models, i.e., advanced turbulence models, cavitation models, three-phase multiphase models. Due to its complexity in nature, it also possesses difficulties where high quality experiment data is need for the model validation and hard to obtain.
The synergy of cavitation and sediment erosion where the two are seen to mutually induce, has been shown to be more serious and not the simply linear superposition of the individual erosion. The unique features of cavitation erosion, as well as sediment erosion and the complex interaction between cavitation and sediment particles, lead to great challenges in understanding the physical mechanism of synergy between cavitation and sediment erosion. Specifically, the typical cavitation erosion curves (volume loss in time and volume loss rate of erosion) show four stages: incubation stage, acceleration, deceleration, and equilibrium (Thiruvengadam and Preseir, 1964; ASTM G32-16, 2016; ASTM G134-17, 2017), while sand erosion has no incubation period and damage is proportional to time. Sediment erosion alone which is approximately the 3rd power of velocity causes 4 times more weight loss than cavitation erosion alone which is approximately the 6th power or higher of velocity, and combined action causes 16 times weight loss (Mei and Wu, 1996). In this section, the effects of sediment particles on cavitating flows and cavitation enhancement on sediment erosion are discussed in detail.
Many studies have shown that the existence of sediment particles in sediment-laden flows will significantly alter the mixture fluid properties (i.e., viscosity, turbulence fluctuations) and flow structures, changing the cavity behaviors including the inception cavitation number, cavity length, and cavity dimension fluctuations (Lian et al., 2018). The sediment particles mainly have two opposite effects, i.e., inhibition and acceleration, on cavitation damage, depending on the particle concentration, size, shape, density, hardness, and so on, where all these properties are supposed to be essentially equal. Generally, the existence of sediment particles will increase the number of cavitation nuclei, accelerating the cavitation inception process, while on the other hand, the viscosity of fluid is increased and vapor pressure is raised, inhibiting the formation of cavitation bubbles. These two completing mechanisms together determine the cavity behaviors, particle trajectories, and thus erosion process.
Till now, due to the lack of understanding of the physics and mechanisms of the effects of sediment particles on cavitation, there is no consensus on how particle properties, especially the particle size and concentration, influence cavitation, consequently leading to the synergy of the cavitation and sediment erosion, and the corresponding critical particle parameter values. The studies by Zhao et al. (Zhao et al., 1993) and Huang et al. (Huang et al., 2006) showed that the cavitation damage increases with increasing particle concentration due to the abrasion wear of the sands. However, in another study, Huang et al. (Huang et al., 1996) found that the cavitation damage was relieved when the particle concentration was above a certain value.
In the early, using a vibratory cavitation erosion facility, Ashworth and Procter, (1975) reported that the addition of small quantities of high molecular weight polyacrylamide into water could increase the rate of vibratory cavitation erosion of copper, as shown in Figures 13, 14. In a circulating water tunnel, Liu (Wood et al., 1967) first measured the inception cavitation number σin as a function of sediment concentration over a cylinder with diameter D = 15 mm. The sand used was made from Huanghe (Yellow River) with a grain size of 14–18 μm and a sand concentration of 1–87 kg/m3. Another experiment was also conducted in water tunnel around a NASA 4412 airfoil with plastic sand of effective diameter D = 0.165 mm and density ρ = 1070 kg/m3. These two experimental studies showed that there exists a critical concentration of approximately Scr = 10–13 kg/m3 for the NASA 4412 airfoil at which the incipient cavitation number reaches a maximum value. In the following, lots of researches on cavitation erosion in sediment-laden flows have been conducted.
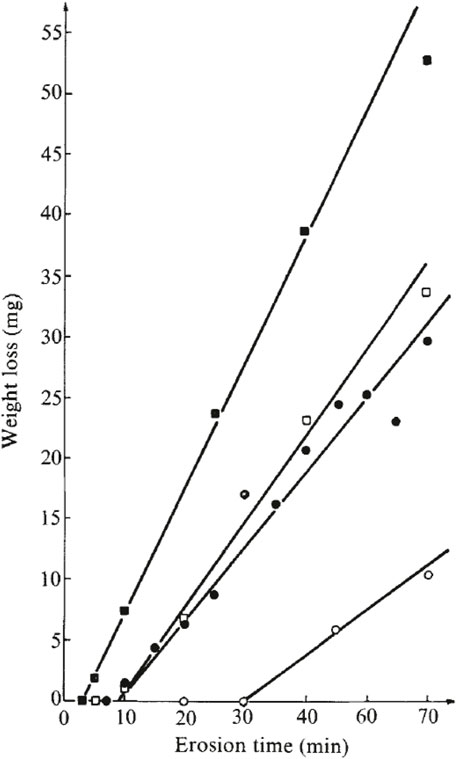
FIGURE 13. Curves of vibratory cavitation erosion weight loss as a function of time for copper secimens (Ashworth and Procter, 1975) in: ●, distlled water; □, equilibrated 100 w. p.p.m polyacrylamide solution; ■, equilibrated 1,000 w. p.p.m polyacrylamide solution; ○, 2:3 v/v glycerol-distilled water mixture.
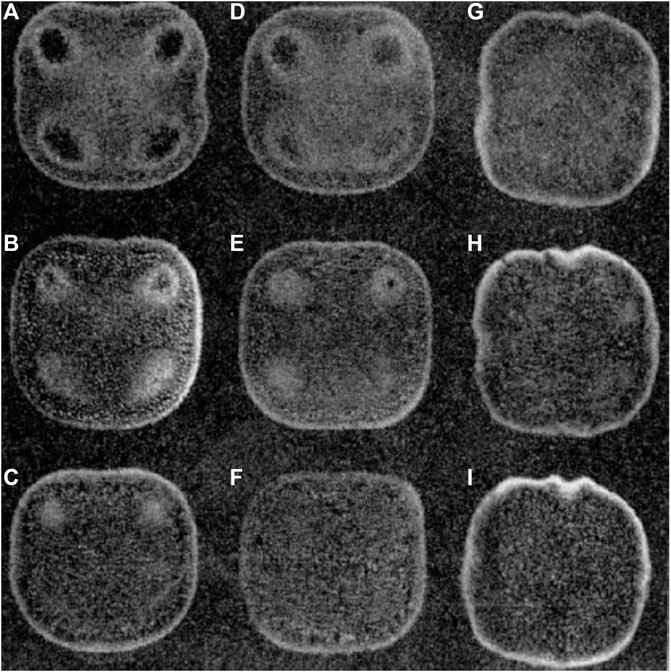
FIGURE 14. Surface appearance of copper specimens after vibratory cavitation erosion in: (A), distilled water for 10 min; (B), distilled water for 20 min; (C), distilled water for 60 min; (D), equilibrated 100 w. p.p.m. polyacrylamide solution for 10 min; (E), equilibrated 100 w. p.p.m. polyacrylamide solution for 20 min; (F), equilibrated 100 w. p.p.m. polyacrylamide solution for 60 min; (G), equilibrated 1000 w. p.p.m. polyacrylamide solution for 10 min; (H), equilibrated 1,000 w. p.p.m. polyacrylamide solution for 20 min; (I), equilibrated 1,000 w. p.p.m. polyacrylamide solution for 60 min (Ashworth and Procter, 1975). Magnification ×2.2.
For example, Du, (1994) conducted experiments to investigate the erosion mechanisms in hydraulic machinery, and made detailed comparisons among the sediment erosion, cavitation erosion, and the combined effects of cavitation and sediment erosion. Their work showed that the combined effects of cavitation and sediment erosion would accelerate the erosion process, and pits, such as fish-scale pits along the flow directions, were caused by this effect, while only pure sediment erosion would lead to smoother flow surface. Cheng, (1990) conducted systematic experimental investigations of the effects of sediment particles on cavitation, and showed that at low particle concentrations below the critical value Scr (Scr = 10–15 kg/m3), the cavitation erosion is enhanced, while at large particle concentrations above Scr, cavitation erosion is suppressed. This work indicated that the increase in particle concentration would increase liquid viscosity and drag force, reduce local velocity and turbulence intensity level, and so on. Han and Huang, (2021) employed the magneto-strictive instrument test to study the combined effects of cavitation and sediment erosion, and found that the critical particle volume concentration is about 5%, and small particle shows high erosive potential. Tie et al., (2000) experimentally examined the damage location and relative degree of sand and water cavitation on the impeller (i.e., 40% design flow rate, 3% head drop) using the test loop for solid and liquid two phases, and showed that under the synergy effects of cavitation and sediment erosion, the erosion on the pressure side at the blade inlet and rear cover plate is less than that under the pure sand wear. The sand used came from the Yangtze River in summer, with diameter of sand of 90 μm, the density of 2720 kg/m3, and the concentration of 32 kg/m3. Zhao et al., (2017) employed CFD tools to study the effects of sand particles on the cavitation flow in a centrifugal pump, and indicated that large particles and high sand concentrations could inhibit cavitation with the size range of 5–15 μm and 0.5%–1.5% in concentration. Moreover, Deng et al., (2000) observed that sediment particles could trigger coherent structures near walls during the turbulence initiation process and thus change the cavitation process and the erosion characteristics. Mei and Wu, (1996) experimentally observed that the particle concentration will change the cavity length. Ladouani and Nemdili, (2005) carried out experiments to investigate the effect of solid-mixture on the cavitation characteristics of a centrifugal pump, and showed that at low flow rates, the NPSH curve is insensitive to sediment concentration, while at large flow rates, the NPSH curve of solid-mixture is higher than that of the clear water. The intensity of cavitation increases with the increasing sediment concentration. Gregorc et al., (2011) combined the experimental and numerical studies and pointed out that the particle concentration will change the hydrodynamic performance. Wu and Gou, (2013) experimentally found that when the particle size is larger than the critical size, further increasing particle size and concentration will promote the cavitation erosion.
Investigations of the particle properties, such as particle size and concentration, on cavitation erosion have been conducted using both experimental measurements and numerical simulations. A very rough general idea about the particle size of sand is that the “critical value” is about 50 μm diameter, above which it will cause substantial damage to the operation of hydraulic machinery. However, some researches have shown that this ‘critical value’ could be different and much lower than approximately 20 μm, as shown in Figure 15.
For example, Huang et al., (1996) experimentally investigated the influence of particle size, hardness, and concentration on cavitation damage in solid-water mixtures using vibratory facilities. The particles used are aluminum (D = 4 μm), molybdenum (D = 4 μm), nickel (D = 4 μm), and quartz (D = 0.8, 4 and 50 μm), and the concentration is c = 10–15%. They found that solid particles play significant roles in cavitation erosion by means of two ways: 1) aggravating abrasive wear of materials by the effects of particle size, concentration, and hardness, and 2) relieving the damage of collapse bubble pressure because of the variation of the physical properties in mixtures. Their study also pointed out that above a certain particle concentration, a declining tendency of damage was observed in mixtures of aluminum-water, nickel-water, and molybdenum-water. Chen et al., (2007) systematically investigated the effects of microparticle size (CeO2 particles with diameters of D = 0.1, 0.5, 0.8–1.2 μm), where abrasive wear is not as important as cavitation erosion does, on cavitation erosion, and showed that the critical particle size is 0.5 μm. A physical model is also proposed and indicates that the existence of solid particles will increase the number of heterogeneous nucleation and reduce the number of bubble-particle combinations, leading to the cavitation erosion process together. Using a rotary disk cavitation system and numerical simulations as well, Wang et al., (2008) investigated the effects of microparticles on cavitation erosion, and the particles were made of CeO2 with diameters, such as 0.1, 0.5, 1.2, 1.8, 2.6, and 4 μm. This work revealed that existence of particles with proper size that play important roles in the generation of cavitation erosion, and the micro shockwave is critical to cavitation erosion. Wu and Gou, (2013) experimentally investigated the critical particle size on cavitation damage using the vibratory apparatus. The sands came from the Nanjing reach of the Yangtze River, and three concentrations of sand were tested including 25 kg/m3, 50 kg/m3, and 85 kg/m3 for five sand sizes with effective diameter of D = 531 μm, 253 μm, 63 μm, 42 μm, and 26 μm. Their work showed that the critical size of the sand particles was D = 48 μm, and attributed the effects of the particle sizes to the changes of liquid viscosity and thus the action of microjet on the solid surfaces. Lian et al., (2018) experimentally studied the cavitation erosion and abrasive wear in a vibratory apparatus with mean particle diameters of 26–531 μm at concentrations of 25 kg/m3, 50 kg/m3, and 85 kg/m3, and observed that the critical particle size for synergistic effects of cavitation and sediment erosion is about 35–48 μm, and small particle will significantly increase fluid viscosity, suppressing the cavitation process. Figure 16 shows the SEM photographs of specimen surfaces with and without sediments. Chen et al. (Chen et al., 2022b) carried out the ultrasonic vibration cavitation experiment, and measured that the critical size was as high as approximately 120 μm and the particle concentration was approximately 10 kg/m3. In their experiment, the density of sediment is 2.65 g/cm3 and the mean sand particle sizes d50 are 660.1, 302.2, 158.3, 80.4, 35.2, and 1.8 μm at several sediment concentrations of 1 kg/m3, 7 kg/m3, 20 kg/m3, 50 kg/m3, and 85 kg/m3 respectively. Gou et al., (2018) found that when the particle size is less than 40 μm and the concentration is in the range of 30–300 kg/m3, the particles have an inhibitory effect on cavitation, where the solid-liquid mixtures contain six particle sizes (10–100 μm) mixed in nine concentrations (6–300 kg/m3) with tap water. Hu and Zheng, (2017) found that the critical conditions are as follows: the particles size is 152 μm, and the concentration is below 3 wt% using silica sands of 75–150# with an irregular shape with sharp edges which are the main ingredients of sediment harmful to fluid machinery in high sediment rivers and the sand concentrations are 0.5, 1, 3, 5 and 10 wt%, as shown in Figure 17. However, Zhong and Minemura, (1996) suggested that when the sediment size is less than 1000 μm, the sediment-laden flow will not cause damage. Xie et al., (2002) thought that damage inhibition would occur only when the sediment size was less than 250 μm.

FIGURE 16. SEM photographs of specimen surfaces in distilled water (B) and mixtures with sediments at a concentration of 85 kg/m3 and various sizes (26 μm (A), and 253 μm (C)) at 240 min (Lian et al., 2018).

FIGURE 17. SEM morphologies of material surfaces after CE for 10 h in (A) pure water (B,C) 0.5 wt% (D,E) 1 wt% (F,G) 3 wt%, (H) 5 wt% and (I) 10 wt% sand suspensions, where b, d and f are obtained in the ring-like region, and c, e and g are from the center regions. The inserted images are local magnification for the representative morphologies (Hu and Zheng, 2017).
Compared with sediment-laden flows under non-cavitation conditions, in addition to the cavitation bubble collapse induced loads on walls, the presence of cavitation bubbles in sediment-laden flows will change the particle motions (i.e., trajectories, velocity, and direction), and thus influence the sediment erosion process such as the impact of particles on solid walls, resulting in more severe damage, referred to cavitation enhancement on sediment erosion (Li, 2006). However, despite intense research efforts in past decades, as reviewed by a number of publications (Singh et al., 2012; Gohil and Saini, 2014; Kumar and Bhingole, 2015), the physical mechanism remains poorly understood. Basically, cavitation in sediment-laden flows is a complex solid-vapor-liquid three-phase turbulent flow phenomenon. On one hand, as for the cavitation phenomenon, the shock wave and microjet generated during the collapse of cavitation bubbles are the main causes of cavitation erosion. The unsteady cavity behaviors (growth, fluctuations, breakup, shedding, and collapse) will directly act on sediment particles, changing the sediment particle motions and thus erosion process. Cavitating flows is highly compressible and could reach sonic and even supersonic flows. According to the research, in cavitating flows, large-scale cavity collapse will induce shockwave and cause strong cavitation instabilities (Schnerr et al., 2008). Wang et al. used high-frequency dynamic surface pressure measurements, and captured the local strong impact load in the transient process of cavity breakup and shedding, leading to cavitation erosion (Wang et al., 2017). On the other hand, as for the cavitation in sediment-laden flows, the occurrence of cavitation bubbles will significantly change the flow fields including the particle motions, and alter the sediment erosion process. In the research of cavitation enhancement on erosion process in sediment-laden flows, one of the most important studies is the physical model established based on the cavitation bubble collapse induced microjet dynamics. Jin et al., (1986) first observed that cavitation bubbles would accelerate the sediment particle, increasing the particle kinematic energy, and then the high-speed impact of sediment particles on walls would cause more severe destruction. Sato et al., (1991) carried out an erosion experiment to study the coupled damage of cavitation and sediment erosion using submerged water jets, and showed that the occurrence of cavitation would change the locations and intensities of cavitation and sediment erosion associated with the unsteadiness at cavity closure with strong vortices, along with the vortex shedding and collapse dynamics. Based on Sato’s experimental data (Sato et al., 1991); (Li, 2006) established the microscale model where microjets induced by cavitation bubble collapse will bring the sediment particles and cause erosion. Dunstan and Li, (2010) further validated this micro model using numerical simulations. In this micro model (Li, 2006), the cavitation enhancement of sediment erosion can be divided into three stages: 1) the particles are captured and held in the jet center, 2) the particles are accelerated to an extremely high velocity and 3) the particles are turned to their sharpest (i.e., the cutting) edge towards the material. Consequently, the cavitating jet causes material pits first and subsequently entrained particles further cut into the center of the already damaged area, resulting in the synergetic damage.
Although the understanding of the interactions between sediment particles and cavity structures in sediment-laden flows is very limited, lots of researchers have investigated the interactions between sediment particle and cavitation bubble, and made significant progress, providing detailed and fundamental information to improve the understanding of the synergism of cavitation and sediment erosion (Borkent et al., 2008; Kumar and Bhingole, 2015; Wu et al., 2017; Zhang et al., 2019). Borkent et al., (2008) observed that the growth process of cavitation bubbles attached to particle surface will accelerate the sediment particle, as shown in Figure 18, and thus the cavitation and sediment erosion is more severe than sediment erosion alone caused by the direct impact of the rotating particles on the material surface. Wu et al., (2017) experimentally studied the interactions between laser-induced bubbles and a free settling particle, and observed the particle ejection behavior and bubbles at the rear of sediment particles. Based on the force balance model, the maximum particle velocity and flow conditions are well predicted. Zhang et al., (2019) conducted systematic studies of the interactions of sediment particles and the collapse of sphere laser induced bubbles near walls. Several researches have shown that the synergistic effects of cavitation and sediment erosion will enhance the cavitation erosion process. For example, Thapa et al., (2007) found that under the synergistic effects of cavitation and sediment erosion, the cavitation erosion intensity is enhanced, and the cavitation region moves towards the wake region of the side parts of the cavitator. Zhang et al., (2006) conducted experiments to study the cavitation around foils in sediment-laden flows, and showed two interaction modes between sediment particle and cavity behaviors, where in the process of the cavity cloud shedding and collapse, the sediment particle was accelerated to impact on the foil surface at a large angle, and in the process of the cavity growth, the sediment particle was accelerated to impact on the foil surface in a small angle. The combined effects of these two modes results in more serious destruction than the individual effect. From above, it is shown that researchers have qualitatively observed the enhanced erosion process under the synergistic effects of cavitation and sediment erosion, however, there is still a lack of understanding of the influence of cavity collapse induced microjets/shockwaves and their propagation on sediment particle motions. Furthermore, more attention should be paid on the influence of sediment particle parameters (size, concentration) on cavity induced pressure fluctuations and shockwaves.

FIGURE 18. Examples of a cavitation event on a particle and the successive dynamics (Borkent et al., 2008).
The above results show the interactions between sediment particles and cavity structures in sediment-laden flows. It is shown that sediment particle parameters (i.e., size, concentration) can significantly influence the synergy of cavitation and sediment erosion, and at the same time, the influence of cavity behaviors on sediment particles. The dual role of sediment particles (i.e., acceleration and inhibition) is discussed in detail, where the critical sediment size and concentration measured by different investigators are presented. In addition, the unsteady cavity behaviors, such as cavity formation, development, and collapse, could change the sediment particle motions, and accelerate the sediment particles to extreme a high velocity, leading to large impact on near solid walls and material erosion.
The literature review summarizes recent results and highlights the synergy mechanism of cavitation and sediment erosion in hydraulic machinery. The effects of particle properties on cavitation erosion process, and the effects of cavitation behaviors on sediment erosion process are discussed in detail to further understand the synergy mechanism of cavitation and sediment erosion, and help for the optimal anti-cavitation optimal designs for hydraulic machinery. The following conclusions can be drawn:
1) Investigations of synergy between cavitation and sediment erosion have been conducted using experiments, theoretical studies, and numerical simulations. The experiments have been carried out with vibratory apparatus, rotating disc systems, slurry pot testers, and water tunnel on both small-scale models (cylinder, hydrofoil, rotating disc, venturi, and impellers) and large-scale fields (proto turbine or pumps in hydropower or pump stations) and are the main research methods.
2) The theoretical and numerical studies are currently limited and are scarce. The theoretical work is mainly based on the understanding of microjets and shockwaves generated by cavitation bubble collapse and their interactions with sediment particles, i.e., acceleration effects. The current numerical studies are conducted on commercial software such as ANSYS-CFX, ANSYS-FLUENT, and STAR-CCM + using RANS turbulence models (i.e., RNG k-ε and SST k-ɷ). The solid particles are calculated using discrete models, using one-way or two-way coupling between fluid phase and particles where the particle forces can be modeled.
3) The effects of sediment particles on cavitation damage mainly have two opposite effects, i.e., inhibition and acceleration. Generally, at low particle concentrations and large particle sizes the cavitation erosion is enhanced, while at high particle concentrations and small particle sizes, cavitation erosion is suppressed. However, the critical particle concentration and size are usually case dependent, and there is no consensus.
4) The synergy of cavitation and sediment erosion is complex and can be probed from the perspectives of sediment particles and cavitation, respectively. Specifically, the effects of sediment particles on cavitation are mainly dependent on particle size, concentration, shapes, hardness, including: 1) increasing the cavitation nuclei size, numbers, and distribution, increasing the vapor pressure; 2) changing the local pressure distributions where owing to the particle motion or rotation, the pressure distribution on a particle is not uniform and the low-pressure side prefers to cavitate earlier; 3) enhancing the cavitation erosion due to the additional washing out effect of particles on solid walls. The cavitation enhancement of sediment erosion is caused by the microjet or shockwave dynamics in the process of cavitation bubble collapse which could accelerate the nearby particle to an extremely high velocity, resulting in serious damage.
According to the above results and discussion, the understanding, and prospects for the synergy of cavitation and sediment erosion on future research lines are proposed as follows:
1) Advanced experiments are required for the investigations of synergy of cavitation and sediment erosion. Cavitation in sediment-laden flows is complex turbulent flows, and the employment and development of advanced flow diagnostic techniques such as a high-resolution 3D laser scanner, high-speed imaging, particle image velocity (PIV), and MESM sensors, are recommended. Sediment-laden flows are usually not transparent, and traditional PIV techniques cannot reach the flow fields in the center region. It is suggested to develop a PIV technique that can be used underwater to obtain detailed flow field information.
2) It is necessary to establish high-fidelity physical and mathematical models for solid-liquid-vapor three-phase flows. For example, the current particle force models are mainly established in single-phase flows. For cavitating flow which is highly nonuniform, unsteady, transient, and density-variable, the improvement of particle force model inside cavitation region is critical for the prediction of particle trajectories, and the corresponding impact on solid walls. It is suggested to develop new physical models to predict the synergy of cavitation and sediment erosion, improving the model accuracy and performance under different flow conditions
3) The understanding of multiscale interactions between vapors structures and particles would promote the understanding of synergy of cavitation and sediment erosion. Cavitation in sediment-laden flows is a multiscale flow phenomenon. Previous work is based on the understanding of microstructure (i.e., microjet and shockwave) on the acceleration of particle speed. However, different from the interactions between cavitation bubbles and particles, the understanding of the actions of macroscale cavity structures on microscale particles brings new challenges and requires multiscale properties. It is necessary to investigate the synergy of cavitation and sediment erosion using multi-scale models and approaches. In addition, plenty of work has been conducted on the interaction between shockwave generated by collapsing cavitation bubbles. However, to the best of our knowledge, no studies on the interaction between shockwave dynamics (Wang et al., 2020a, 2020b) generated by collapsing large scale cavity structure which could be more common and erosive than a single bubble in practical engineering and sediment has been conducted. Future work on large scale cavity collapse induced shockwave dynamics and and its synergy with sediment erosion is suggested to be provided using improved multi-scale simulation tools.
4) Effective measures are needed to suppress the erosion from synergy of cavitation and sediment erosion. The synergy of cavitation and sediment erosion is even more serious than their individual effects. Consequently, in addition to traditional active (i.e., air injection) and passive prevention methods (i.e., coating), it would be effective to study the synergy effects of cavitation and sediment erosion using methods such as bionics techniques (i.e., microstructures at leading edge), optimization design methods for wide operation conditions, and advanced composite materials for hydraulic machineries.
CW: Methodology, Data Analysis, Writing–Reviewing and Editing; LT: Methodology, Data Analysis, Writing–Reviewing and Editing; MC: Methodology, Writing–Reviewing and Editing; HF: Methodology, Writing–Reviewing and Editing; DL: Methodology, Writing–Reviewing and Editing.
This work has been supported by the National Key Research and Development Program of China (2020YFB1901401), the Guoqiang Institute of Tsinghua University (2021GQG1003), the State Key Laboratory of Hydroscience and Engineering (2021-KY-04, sklhse-2022-Iow06), the Creative Seed Fund of Shanxi Research Institute for Clean Energy of Tsinghua University.
DL was employed by the company Dongfang Electric Corporation.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Amarendra, H. J., Chaudhari, G. P., and Nath, S. K. (2012). Synergy of cavitation and slurry erosion in the slurry pot tester. Wear 290, 25–31. doi:10.1016/j.wear.2012.05.025
Arndt, E. R. A., Voigt, R. L., Sinclair, J. P., Rodrique, P., and Ferreira, A. (1989). Cavitation erosion in hydro turbines. J. Hydraul. Eng. 115, 1297–1315. doi:10.1061/(asce)0733-9429(1989)115:10(1297)
Arndt, R. E. (1981). Cavitation in fluid machinery and hydraulic structures. Annu. Rev. Fluid Mech. 13 (1), 273–326. doi:10.1146/annurev.fl.13.010181.001421
Ashworth, V., and Procter, R. P. M. (1975). Cavitation damage in dilute polymer solutions. Nature 258, 64–66. doi:10.1038/258064a0
ASTM D32-77 (1977). Standard method of vibratory cavitation erosion test. Philadelphia, United States: ASTM Stand.
ASTM G134-17 (2017). G134-17 Standard test method for erosion of solid materials by a cavitating liquid jet. Philadelphia, United States: ASTM Stand, 1–17.
ASTM G32-16 (2016). G32-16 Standard test method for cavitation erosion using vibratory apparatus1. Philadelphia, United States: ASTM Stand, 1–20.
Berchiche, N., Franc, J. P., and Michel, J. M. (2002). A cavitation erosion model for ductile materials. J. Fluids Eng. 124, 601–606. doi:10.1115/1.1486474
Bitter, J. G. A. (1963). A study of erosion phenomena: Part I. Wear 6, 5–21. doi:10.1016/0043-1648(63)90003-6
Borkent, B. M., Arora, M., Ohl, C., De Hong, N., Versluis, M., Lohse, D., et al. (2008). The acceleration of solid particles subjected to cavitation nucleation. J. Fluid Mech. 610, 157–182. doi:10.1017/s002211200800253x
Chen, H., Liu, S., Wang, J., and Chen, D. (2007). Study on effect of microparticle’s size on cavitation erosion in solid-liquid system. J. Appl. Phys. 101, 103510. doi:10.1063/1.2734547
Chen, M., Tan, L., Fan, H., Wang, C., and Liu, D. (2022a). Solid-liquid multiphase flow and erosion characteristics of a centrifugal pump in the energy storage pump station. J. Energy Storage 56, 105916.
Chen, S., Xu, W., and Luo, J. (2022b). Experimental study on the mesoscale causes of the effect of sediment size and concentration on material cavitation erosion in sandy water. Wear 488–489, 204114. doi:10.1016/j.wear.2021.204114
Cheng, Z. (1990). Experimental study on critical sediment concentration in cavitation and abrasion. Hydropower Technol. 2, 57–63.
Deng, J., Yang, Y., Shen, H., Xu, W., and Dong, J. (2000). The influence to abrasion of sediment concentration. J. Sediment Res. 4, 65–68.
Du, T. (1994). A new solution to the causes of pump damage in sand laden water. Water Pump. Technol. 1, 7.
Duan, C. G. (1998). “Approach to the demand on anti-abrasive erosion from hydraulic machinery project, hydraulic machinery and cavitation,” in Proceedings of XIX IAHR symposium (Singapore: World Science), 59–69.
Dunstan, P. J., and Li, S. (2010). Cavitation enhancement of silt erosion: Numerical studies. Wear 268, 946–954. doi:10.1016/j.wear.2009.12.036
Gohil, P. P., and Saini, R. P. (2014). Coalesced effect of cavitation and silt erosion in hydro turbines-A review. Renew. Sustain. Energy Rev. 33, 280–289. doi:10.1016/j.rser.2014.01.075
Gou, W., Zhang, H., Li, H., Liu, F., and Lian, J. (2018). Effects of silica sand on synergistic erosion caused by cavitation, abrasion, and corrosion. Wear 412–413, 120–126. doi:10.1016/j.wear.2018.07.023
Grant, G., and Tabakoff, W. (1973). An experimental investigation of the erosive characteristics of 2024 Aluminum Alloy. Cincinnati, OH: Department of Aerospace Engineering, University of Cincinnati.
Gregorc, B., Hriberšek, M., and Predin, A. (2011). The analysis of the impact of particles on cavitation flow development. J. Fluids Eng. 133, 111304. doi:10.1115/1.4005315
Gregorc, B., Predin, A., Fabijan, D., and Klasinc, R. (2012). Experimental analysis of the impact of particles on the cavitating flow. J. Mech. Eng. 58 (4), 238–244. doi:10.5545/sv-jme.2011.062
Han, D., and Huang, J. (2021). Experimental study on oscillation cavitation and sediment abrasion simulation. J. Water Conservancy 1, 34–3757.
Hong, S., Wu, Y., Wang, Q., Ying, G., Li, G., Gao, W., et al. (2013). Microstructure and cavitation–silt erosion behavior of high-velocity oxygen–fuel (HVOF) sprayed Cr3C2–NiCr coating. Surf. Coat. Technol. 225, 85–91. doi:10.1016/j.surfcoat.2013.03.020
Hu, H., and Zheng, Y. (2017). The effect of sand particle concentrations on the vibratory cavitation erosion. Wear 384-385, 95–105. doi:10.1016/j.wear.2017.05.003
Huang, J. (1991). Principle and application of cavitation and cavitation erosion [M]. Beijing: Tsinghua University Press, 113–115.
Huang, S., Ihara, A., Waranabe, H., and Hashimoto, H. (1996). Effects of solid particle properties on cavitation erosion in solid-water mixtures. J. Fluids Eng. 118, 749–755. doi:10.1115/1.2835505
Huang, X., Yuan, Y., and Wang, S. (2006). Mechanism of abrasion to material by high-velocity sediment-laden flow and effect of aeration on abrasion resistance. J. Water Resour. Archit. Eng. 4 (1), 1–5. (in Chinese)
Hydraulic Machinery (2021). The hydraulic machinery abrasion testing system in China Institute of Water Resources and Hydropower Research. AvaliableAt: http://www.iwhr.com/zgskywwnew/kypt/syjd/webinfo/2018/04/1524331217683592.htm.
Jayaprakash, A., Hsiao, C. T., and Chahine, G. (2012). Numerical and experimental study of the interaction of a spark-generated bubble and a vertical wall. J. Fluids Eng. 134, 031301. doi:10.1115/1.4005688
Jin, H., Zheng, F., Li, S., and Hang, C. (1986). The role of sand particles on the rapid destruction of the cavitation zone of hydraulic turbines. Wear 112, 199–205. doi:10.1016/0043-1648(86)90240-1
Johnsen, E., and Colonius, T. (2009). Numerical simulations of non-spherical bubble collapse. J. Fluid Mech. 629, 231–262. doi:10.1017/s0022112009006351
Kumar, D., and Bhingole, P. P. (2015). CFD based analysis of combined effect of cavitation and silt erosion on Kaplan turbine. Mater. Today Proc. 2, 2314–2322. doi:10.1016/j.matpr.2015.07.276
Kumar, P., and Saini, R. P. (2010). Study of cavitation in hydro turbines-A review. Renew. Sustain. Energy Rev. 14, 374–383. doi:10.1016/j.rser.2009.07.024
Ladouani, A., and Nemdili, A. (2005). Experimental investigation of the effect of solid-mixture on the cavitation characteristic of a centrifugal pump. WIT Trans. Built Environ. 84, 7. doi:10.2495/FSI050081
Li, S. (2006). Cavitation enhancement of silt erosion-An envisaged micro model. Wear 260, 1145–1150. doi:10.1016/j.wear.2005.07.002
Lian, J., Gou, W., Li, H., and Zhang, H. (2018). Effect of sediment size on damage caused by cavitation erosion and abrasive wear in sediment-water mixture. Wear 398-399, 201–208. doi:10.1016/j.wear.2017.12.010
Lichtman, J. Z. (1967). Cavitation erosion performance and related properties of cured-sheet elastomeric coating systems. J. Mater. 2 (3), 638–660.
Liu, J., Yu, J., and Jiang, C. (2019). Evaluation on sediment erosion of Pelton turbine flow passage component. IOP Conf. Ser. Earth Environ. Sci. 240, 022027. doi:10.1088/1755-1315/240/2/022027
Lu, L., Pan, L., Peng, Z., Xu, H., Meng, X., and Gao, Z. (2019). Construction and application of hydraulic machinery R&D platform. J. China Inst. Water Resour. Hydropower Res. 17 (6), 432–438445. (in Chinese). doi:10.13244/j.cnki.jiwhr.2019.06.005
Lu, L., Zhang, J., Zhu, L., Xu, H., Meng, X., Yu, J., et al. (2014). An experiment system for testing synergetic erosion caused by sand abrasion and cavitation. 27th IAHR Symposium on Hydraulic Machinery and Systems (IAHR 2014). IOP Conf. Ser. Earth Environ. Sci. 22, 052017.
Mei, Z., and Wu, Y. (1996). “Review of research on abrasion and cavitation of silt laden flow through hydraulic turbine runner in China,” in Hydraulic machinery and cavitation (Dordretcht: Springer), 641–650.
Ministry of Water Resources of the People's Republic of China (2020). China river sediment bulletin. Beijing: China Water&Power Press.
Naidu, B. S. K. (2016). Renovation and modernization of silt prone hydropower stations in India, workshop on silting problems in hydroelectric power stations. New Delhi: Indian Institute of Technology Roorkee, 13–16.
Naidu, B. S. K. (1996). Silt damages to equipment in hydro power stations and remedial measures. New Delhi: CBIP Workshop.
Ni, H., and He, Z. (1994). Impact of shock waves of bubble collapse on solid particles carried by flow fields. J. Dalian Univ. Technol. 34 (6), 727–731.
Padhy, M. K., and Saini, R. P. (2008). A review on silt erosion in hydroturbines. Renew. Sustain. Energy Rev. 12, 1974–1987. doi:10.1016/j.rser.2007.01.025
Padhy, M. K., and Saini, R. P. (2009). Effect of size and concentration of silt particles on erosion of Pelton turbine buckets. Energy 34, 1477–1483. doi:10.1016/j.energy.2009.06.015
Peng, C., Tian, S., Li, G., and Wei, M. (2020). Enhancement of cavitation intensity and erosion ability of submerged cavitation jet by adding micro-particles. Ocean Eng. 209, 107516.
Rao, P. V., and Buckley, D. H. (1984). Predictive capability of long-term cavitation and liquid impingement erosion models. Wear 94, 259–274. doi:10.1016/0043-1648(84)90131-5
Rasmussen, R. E. H. (1956). “Some experiments on cavitation erosion in water mixed with air,” in Proceedings, symposium on cavitation in hydrodynamics, NPL (teddington) (H.M.S.O. Publication), 20.
Romero, R., Teran, L. A., Coronado, J. J., Ladino, J. A., and Rodríguez, S. A. (2019). Synergy between cavitation and solid particle erosion in an ultrasonic tribometer. Wear 428-429, 395–403. doi:10.1016/j.wear.2019.04.007
Sato, J., Usami, K., and Okamura, T. (1991). Basic study of coupled damage caused by silt abrasion and cavitation erosion: Experiments with submerged water jets. JSME Int. J. 34 (3), 292–297. doi:10.1299/jsmeb1988.34.3_292
Schnerr, G. H., Sezal, I. H., and Schmidt, S. J. (2008). Numerical investigation of three-dimensional cloud cavitation with special emphasis on collapse induced shock dynamics. Phys. Fluids 20, 040703. doi:10.1063/1.2911039
Sharma, D. P., and Singh, S. (1987). Operational problems of water turbine in UP - with special reference to Tiloth Power Station. Lucknow: All India Seminar on Metallurgical Problems in Power Projects, 18–35.
Singh, R., Tiwari, S. K., and Mishra, S. K. (2012). Cavitation erosion in hydraulic turbine components and mitigation by coatings: Current status and future needs. J. Mat. Eng. Perform. 21, 1539–1551. doi:10.1007/s11665-011-0051-9
Singhal, A. K., Athavale, M. M., Li, H., and Yu, J. (2002). Mathematical basis and validation of the full cavitation model. J. Fluids Eng. 124, 617–624. doi:10.1115/1.1486223
Singhal, S. K., and Ratnendra, S. (2017). Proceedings of the Himalayan small hydropower summit. Report, 200–207.
Sreedhar, B. K., Albert, S. K., and Pandit, A. B. (2017). Cavitation damage: Theory and measurements-A review. Wear 372-373, 177–196. doi:10.1016/j.wear.2016.12.009
Stella, J., and Alcivar, R. (2019). Influence of addition of microsized alumina particles on material damage induced by vibratory cavitation erosion. Wear. 436–437, 203027.
Su, K., Wu, J., and Xia, D. (2021). Dual role of microparticle in synergistic cavitation-particle erosion: Modeling and experiments. Wear 203633, 470–471. doi:10.1016/j.wear.2021.203633
Sun, J., Ge, X., Chu, D., Zhang, L., Meng, H., and Zheng, Y. (2022). Effects of sediment diameter and concentration on cavitation characteristics and mechanism. Tribol. Int. 171, 107543. doi:10.1016/j.triboint.2022.107543
Takagi, T., Okamura, T., and Toshima, M. (1978). Effects of suspended solid on performance of a model hydraulic turbine. Xi’an: The 2nd China-Japan Joint Conference on Fluid Machinery, 302–309.
Teran, L. A., Laín, S., and Rodríguea, S. A. (2021). Synergy effect modeling of cavitation and hard particle erosion: Implementation and validation. Wear 478–479, 203901. doi:10.1016/j.wear.2021.203901
Teran, L. A., Rodríguez, S. A., Laín, S., and Jung, S. (2018). Interaction of particles with a cavitation bubble near a solid wall. Phys. Fluids 30, 123304. doi:10.1063/1.5063472
Thapa, B., Chaudhary, P., Dahlhaug, O. G., and Upadhyay, P. (2007). “Study of combined effect of sand erosion and cavitation in hydraulic turbines,” in International conference on small hydropower (Hydro Sri Lanka: Fluid Dynamics), 22–24.
Thapa, B. (2019). Contribution of FranSed project to the research at turbine testing laboratory at Kathmandu university in Nepal. FranSed Q. Newsl. 3. AvaliableAt: https://www.ntnu.edu/hydrocen/newsletter-3.
Thapa, B. S., Thapa, B., and Dahlhaug, O. G. (2012). Current research in hydraulic turbines for handling sediments. Energy 47, 62–69. doi:10.1016/j.energy.2012.05.014
Thapa, B. S., Thapa, B., and Dahlhaug, O. G. (2012). Empirical modelling of sediment erosion in Francis turbines. Energy 41, 386–391. doi:10.1016/j.energy.2012.02.066
Thiruvengadam, A., and Preseir, H. S. (1964). On testing materials for cavitation damage resistance. J. Ship Res. 8, 39–56. doi:10.5957/jsr.1964.8.5.39
Tie, Z., Jiao, Z., and Huang, J. (2000). Damage test and research of sand and water cavitation for centrifugal pumps. Process Equip. Pip. 37 (3), 42–44.
Tomita, Y., and Shima, A. (1986). Mechanisms of impulsive pressure generation and damage pit formation by bubble collapse. J. Fluid Mech. 160, 535–564. doi:10.1017/s0022112086000745
Wang, C., Huang, B., Wang, G., Zhang, M., and Ding, N. (2017). Unsteady pressure fluctuation characteristics in the process of breakup and shedding of sheet/cloud cavitation. Int. J. Heat Mass Transf. 114, 769–785. doi:10.1016/j.ijheatmasstransfer.2017.06.005
Wang, J., Chen, H., Qin, L., Li, Y., and Chen, D. (2008). Key roles of micro-particles in water on occurrence of cavitation-erosion of hydro-machinery. Sci. Bull. (Beijing). 53 (10), 1603–1607. doi:10.1007/s11434-008-0089-8
Wang, X., Zhang, J., Zhu, R., and Fu, Q. (2014). Analysis of the influence of the solid particle content on the cavitation characteristics of a centrifugal pump. J. Eng. Therm. Energy Power 29 (2), 202–212. (in Chinese). doi:10.16146/j.cnki.rndlgc.2014.02.006
Wang, Y., Wu, J., and Ma, F. (2018). Cavitation-silt erosion in sand suspensions. J. Mech. Sci. Technol. 32 (12), 5697–5702. doi:10.1007/s12206-018-1116-6
Wang, C., Wang, G., and Huang, B. (2020a). Dynamics of unsteady compressible cavitating flows associated with the cavity shedding. Ocean Eng. 209, 107025.
Wang, C., Wang, G., and Huang, B. (2020b). Characteristics and dynamics of compressible cavitating flows with special emphasis on compressibility effects. Int. J. Multiphase Flow 130, 103357.
Wang, C., Wang, G., Zhang, M., and Huang, B. (2022). Experimental investigation of wall-pressure fluctuations in compressible turbulent cavitating flows with emphasis on non-Gaussian features. Exp. Therm. Fluid Sci. 139, 110726.
Weili, L., Jinling, L., Xingqi, L., and Yuan, L. (2010). Research on the cavitation characteristic of Kaplan turbine under sediment flow condition. IOP Conf. Ser. Earth Environ. Sci. 12, 012022. doi:10.1088/1755-1315/12/1/012022
Wood, G. M., Knudsen, L. K., and Hammitt, F. G. (1967). Cavitation damage studies with rotating disk in water. J. Basic Eng. 89, 98–109. doi:10.1115/1.3609577
Wu, J., and Gou, W. (2013). Critical size effect of sand particles on cavitation damage. J. Hydrodyn. 25 (1), 165–166. doi:10.1016/s1001-6058(13)60350-9
Wu, S., Zuo, Z., Stone, H. A., and Liu, S. (2017). Motion of a free-settling spherical particle driven by a laser-induced bubble. Phys. Rev. Lett. 119, 084501. doi:10.1103/physrevlett.119.084501
Xie, C., Duan, W., Xie, B., and Yang, G. (2002). Study on sand erosion of hydroturbines. Hubei Water Power, 37–40. (in Chinese). doi:10.13622/j.cnki.cn42-1800/tv.2002.01.014
Yang, J. (2012). Abrasion Causes and protective measures of hydraulic turbines in hydropower stations. Technol. Enterp. 12, 310. (in Chinese). doi:10.13751/j.cnki.kjyqy.2012.12.125
Yang, J., Wang, J., and Chang, J. (2005). Effect of sand-contained water on the cavitation pressure in Wanjiazhai Hydropower Station. Water Conservation Hydropower Technol. 36 (05), 64–67. (in Chinese). doi:10.13928/j.cnki.wrahe.2005.05.021
Zhang, T., Chen, C., and Chen, F. (2006). Research progress in cavitation, wear and their combined effects. J. Drainage Irrigation Mech. Eng. 24 (4), 47–53.
Zhang, Y., Xie, X., Zhang, Y., and Du, X. (2019). Experimental study of influences of a particle on the collapsing dynamics of a laser-induced cavitation bubble near a solid-wall. Exp. Therm. Fluid Sci. 105, 289–306. doi:10.1016/j.expthermflusci.2019.04.005
Zhang, Y., Zhang, Y., Qian, Z., Ji, B., and Wu, Y. (2016). A review of microscopic interactions between cavitation bubbles and particles in silt-laden flow. Renew. Sustain. Energy Rev. 56, 303–318. doi:10.1016/j.rser.2015.11.052
Zhao, K., Gu, C., Shen, F., and Lou, B. (1993). Study on mechanism of combined action of abrasion and cavitation erosion on some engineering steels. Wear 162-164, 811–819. doi:10.1016/0043-1648(93)90082-w
Zhao, W., Han, X., Li, R., Zheng, Y., and Pan, X. (2017). Effects of silt diameter and silt concentration on cavitation flow in centrifugal pump. Trans. Chin. Soc. Agric. Eng. 33 (4), 117–124. (in Chinese). doi:10.11975/j.issn.1002-6819.2017.04.017
Zhong, Y., and Minemura, K. (1996). Measurement of erosion due to particle impingement and numerical prediction of wear in pump casing. Wear 199, 36–44. doi:10.1016/0043-1648(96)06974-8
Keywords: cavitation, sediment-laden flows, cavitation erosion, sediment erosion, synergy effects
Citation: Wang C, Tan L, Chen M, Fan H and Liu D (2022) A review on synergy of cavitation and sediment erosion in hydraulic machinery. Front. Energy Res. 10:1047984. doi: 10.3389/fenrg.2022.1047984
Received: 19 September 2022; Accepted: 31 October 2022;
Published: 14 November 2022.
Edited by:
Enhua Wang, Beijing Institute of Technology, ChinaReviewed by:
Mauricio Frota, Pontifical Catholic University of Rio de Janeiro, BrazilCopyright © 2022 Wang, Tan, Chen, Fan and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lei Tan, dGFubGVpQG1haWwudHNpbmdodWEuZWR1LmNu
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.