A united credible capacity evaluation method of distributed generation and energy storage based on active island operation

Cooperating with distributed energy storage, distributed generation is with the potential of supply load stably under both normal and failure periods of distribution network. Therefore, distributed generation has not only electricity value, but also capacity value. The capacity value can be characterized by credible capacity index. However, the uncertainty of the distributed generation output and the sequential characteristics of energy-storage operation must be considered during a united credible capacity evaluation. A united credible capacity evaluation method of distributed generation and energy storage based on active island operation is proposed. The proposed method carries out day-ahead economic dispatching under a normal state and island partition under a fault state, alternately, to realize accurate reliability calculation, which is the key link of credible capacity searching. The main work is as follows. First, a day-ahead economic dispatching model under normal state is established to obtain the sequential remaining electricity information of energy storage. Second, the models of maximum island partition and optimal island rectification are established based on electricity sufficiency and power balance information. By solving the maximum island partition and optimal island rectification models alternately, optimal island partition schemes under the fault state could be achieved. Then, the convergence criterion based on variance coefficients instead of artificial selection is designed in reliability calculation. Finally, the united credible capacity of distributed generation and energy storage is evaluated in the PG&E 69-bus system. It is found that credible capacity value increases by 23%, 53%, and 61%, respectively, under the energy storage allocation ratios of 20%, 30%, and 40%. It can be seen that the integration of energy storage makes a significant impact on distributed generation credible capacity value.

1 Introduction

In order to achieve the goal of carbon peaking and carbon neutralization, wind turbine, photovoltaic equipment (PV), and other renewable power generation equipment will be vigorously developed in China. Distributed generation (DG) is an important development direction of renewable power generation (Sun et al., 2021). However, the output of wind turbine and PV fluctuates strongly and the integration of DG will bring great challenges to the safety and stability of the power system. Therefore, it is suggested that a certain proportion of energy storage (ES) should be configured to stabilize the DG output fluctuation when renewable power generation is invested in the future by National Energy Administration of China (Sun et al., 2017). DG and ES are gradually integrated into the distribution network (DN) located in the load center. The electricity load demand can be satisfied locally and the upstream power system can be saved or delayed (Bagheri et al., 2015). In addition, the power restoration potential of DG plays an important role in supporting the reliable operation of DN. For example, the uninterrupted power supply of important loads with high priority can be achieved by active island operation (Hamidan and Borousan., 2022). It can be seen that the integration of DG can reduce the electricity sufficiency dependence on the superior grid and increase the load carrying capacity of DN, i.e., DG has a capacity value. However, the capacity value cannot be simply measured by installed capacity. It is necessary to fully consider the fluctuation of DG and the sequential characteristics of ES in a scientific capacity value evaluation (Tapetado and Usaola, 2019).

Renewable power generation has strong intermittency and uncertainty and it is difficult to accurately measure the contribution to power supply reliability after the integration of DG. In 1966, the concept of credible capacity (CC) was firstly proposed by L. L. Garver based on effective load-carrying capacity (Garver, 1966). Since then, CC has gradually become the main index to measure the capacity value of renewable power generation. However, the evaluation method of CC has not made an agreement and the method can be divided into two categories according to whether it is based on reliability calculation. Load duration curve (LDC) method is a common non-reliability CC evaluation method. The LDC before and after the integration of renewable power generation are compared in reference (Frew et al., 2017), and the average load decrease in the first 100 h is regarded as the CC value. A CC index can be quickly obtained by this method from a macro perspective. However, the effect of power grid-scheduling strategy and other factors on CC value is not considered. The guidance on further exploring the capacity value of renewable power generation is not analyzed. In addition, the calculation formula of CC can be obtained approximately through probability modeling methods, function fitting, and neural network training. A Garver approximation method is proposed in the reference (D'Annunzio and Santoso, 2008) and a wind turbine is established as a discrete output level model in the method. The CC of the wind turbine is deducted under the assumption that power supply reliability decreases exponentially with the increase of load demand. A Z-statistic method is proposed in the reference (Dragoon and Dvortsov, 2006). The approximate calculation formula of CC is derived under the assumption that the redundant capacity follows normal distribution with the fluctuation of DG and load demand. A reliability function method is proposed in the reference (Zhang et al., 2013). The power supply reliability function of the power system with the load demand as the variable is established in this article. Then, the formula of wind turbine CC is deduced and this method is applicable to scenarios where the permeability of renewable energy is relatively low. A large number of empirical samples are used to train the artificial neural networks in the reference (Ding and Xu, 2016) and the CC value can be calculated directly based on empirical formulas. However, strong assumptions are required for the derivation of formulas on the aforementioned methods and they can only be applied in specific scenarios.

CC evaluation based on equal power supply reliability criterion is a more mature and accurate calculation method (Paik et al., 2021), where the load demand increases after the integration of wind turbine and PV under the premise of equal power supply reliability. The main work of a reliability-based CC evaluation method is reliability calculation of DN with the integration of DG. A lot of research studies have been explored in this field. A fault-recovery optimization algorithm based on sequential load demand fluctuation is established in the reference (Zou et al., 2019) and the reliability of hybrid DG systems is calculated. However, the transfer capability of DN is ignored in reliability calculation, without repeated searching under the fault state, switching, and DN connectivity discrimination by traditional reliability calculation methods. An algorithm based on s binary matrix operation set is proposed in the reference (Arefi et al., 2020), the switching moment information is matched and associated with the load node. Thus, the direct method can be used to evaluate DN reliability efficiently, but the load transfer is also not considered in reliability calculation. In order to reconcile the calculation efficiency and accuracy, an optimization method for DN reliability calculation considering load transfer between feeders is proposed in the reference (Li et al., 2019). However, the reverse transmission of power flow caused by DN reconfiguration under the fault state is ignored. In addition, the selection of a reliability index is a significant link in reliability calculation. Most research studies select expected energy not served (EENS) as the comparison standard of power supply reliability in the process of searching the CC value (Rathore and Patidar, 2019), while there are also some references that use such indices as loss of load frequency (Silva et al., 2022), loss of load duration (Zeng et al., 2020), well-being framework (Wangdee, 2018), and value at risk index (Rayati et al., 2019). Finally, since the CC searching process belongs to one-dimensional searching, the common methods such as dichotomy and secant method (Cai and Xu, 2021) can ensure calculation accuracy.

Failure effects analysis is the main work of DN reliability calculation. The restoration potential of DG and the topology flexibility of DN can be fully utilized to maintain uninterrupted power supply for important loads with high priority. The realization of power supply restoration under the fault state depends on the formulation of the island partition scheme (Zhao et al., 2019). In order to make full use of the power supply potential of DG, the IEEE 1547.4-2011 standard encourages conscious island operation and points out that action strategy of switching should be considered in island operation planning (Photovoltaics and Storage, 2011). Starting from island optimization objective, the reference (Guimaraes et al., 2021) assigns different priorities to each objective item. A linear programming model is established and multiple factors such as EENS, power-line loss, and switching operation state are considered. However, the power loss of customers caused by secondary outage constraint and the characteristics of DN topology flexibility are not considered. The island partition model of DN under severe disturbance environment is established in the reference (Hosseinnezhad et al., 2018). Load-demand restoration, load priority, and power balance are considered in the model. However, the expansion on the power supply restoration path by DN interconnection switch is ignored.

Island partition is a typical NP hard problem, which is very difficult to solve. In reference (Xu et al., 2017), the active power of the load node is regarded as priority and a Dijkstra algorithm is used to search the optimal DG restoration path. In reference (Chen et al., 2015), the connection relationship between each load node and each DG is constrained based on the upstream and downstream relationship of radial DN topology. And then, the final island schemes with each DG as the root node are obtained. The deep searching method is used to find the restoration path between each DG and important loads with high priority in the reference (Gao et al., 2016). The topology of island is determined by evaluating the power supply security and fault duration time. The main idea of the graph theory partition method based on an undirected graph model (Slota et al., 2020) is to transform the island partition problem into a minimum spanning-tree problem. Prim algorithm (Sinishaw et al., 2021) can generate radial topology quickly by considering the information of edges weight and it is suitable for solving the island partition problem involving intersection switches. However, in the existing island partition research studies, the DG output under the fault state is usually taken as an average-rated power or the output at a certain moment, while the fault duration of the power system in reality is random and varied. If the DG output and load demand are regarded as fixed values and the sequential fluctuation under the fault state is ignored, the final island partition effect will make a huge deviation. The safe and reliable operation of island operation under the fault state cannot be guaranteed. At present, there are few research studies on dynamic island partition methods for multi-period time and the research studies in this area are still at the initial stage.

Due to the fluctuation of the DG output, there are great differences in the island partition schemes at various moments. The integration of ES can significantly reduce the impact of DG output fluctuation on the island partition effect and improve the island efficiency (Jin et al., 2017; Zhou et al., 2017). However, establishing the island partition model considering the sequential characteristics of ES remaining electricity will significantly increase the complexity of the problem. There are still few research studies on island partition considering the operation of ES. A power supply restoration strategy for active DN under the fault state is proposed in the reference (Li et al., 2020). DN topology reconfiguration, island operation of DG, the support function of transportable energy storage, and other factors are considered in the model to minimize relevant costs. In reference (Yao et al., 2018), the effect of transportable energy storage on load restoration under the fault state is considered in the island partition model. The transportable path and integration location of transportable energy storage are analyzed emphatically in this article. The power-supply restoration scheme of a mobile emergency generator under emergency condition is researched in the reference (Lei et al., 2016). However, the integration of mobile emergency generators in the active DN is required to meet the constraint, and not all load nodes are candidates for the integration location of mobile emergency generators. In addition, the scheduling strategy of mobile emergency generators is not properly discussed.

To sum up, the existing research studies on the united CC assessment of DG and ES is not enough and the shortcomings of these research studies on CC evaluation can be given as follows. 1) Only the capacity value of DG is considered in the existing CC evaluation research studies and the ability of stabilizing the DG output after the integration of ES is ignored. The effective scheduling method of energy storage under the fault state requires further research and analysis. Aiming at this problem, a united CC evaluation method of both DG and ES based on active island operation is proposed in this article. The characteristic is that the united CC indices of DG and ES are first brought forward. The ability of ES to stabilize the DG output under is fully considered under the fault state and the day-ahead economic dispatching is conducted to determine the remaining electricity of ES under the normal state. 2) The flexibility of DN topology is always ignored when searching for feasible island partition schemes. Since there is no interconnection switch in DN topology, the radial constraint is not required to be considered in the model. The secondary outage constraint is not considered in most of the existing references. In order to overcome this problem, a complex island partition model considering the introduction of interconnection switch, secondary outage constraint, sequential operation of ES, fluctuation of DG and load demand, and other significant factors is established. The major contributions of this article can be highlighted as follows:

(1) United CC index is defined to measure the capacity value of DG and ES in DN. Day-ahead economic dispatching under normal state and island partition under fault state are conducted alternately to realize an accurate CC evaluation.

(2) The island partition model is decoupled into maximum island partition and optimal island rectification based on electricity sufficiency and power-balance information. The solving speed is improved significantly.

(3) The variance coefficient instead of a fixed value is designed for the convergence criterion of SMCS and the CC evaluation error can be adjusted flexibly according to the variance coefficient.

2 Credible capacity evaluation method

2.1 The credible capacity evaluation process based on equivalent load-carrying capacity concept

The CC evaluation based on the reliability calculation result is able to reflect the capacity value of DG under the fault state and it is a more accurate evaluation method. The CC evaluation based on ELCC concept is carried out in this article and the EENS index is regarded as the power supply reliability index. The EENS index E_NS of the power system can be calculated as follows:

$E_{\mathrm{N}\mathrm{S}}={\displaystyle \sum }_{t=1}^T{\displaystyle \sum }_{a=1}^A{\displaystyle \sum }_{i\in \mathit{N}/{\mathit{\Omega }}_a}{P}_{i,t}^{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}(1)$

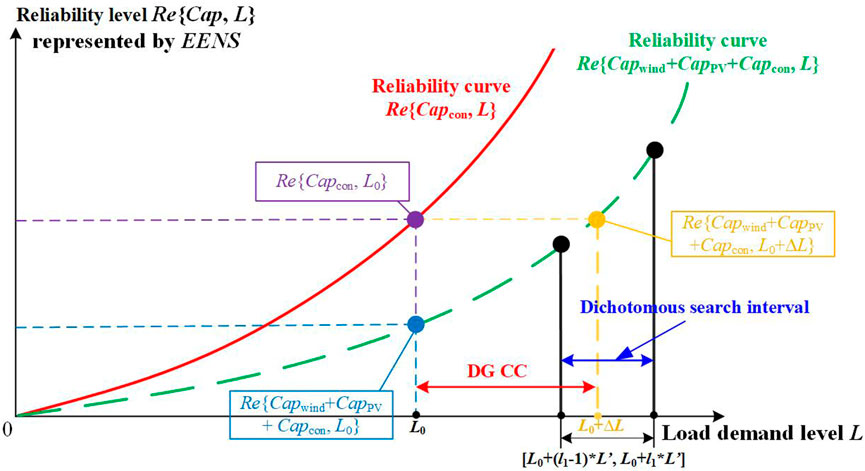
It is assumed that the capacity of the conventional unit in the power system is Cap_con and the load demand level is L₀. The reliability level can be denoted as Re (Cap_con, L₀) and the reliability level of the system is inversely proportional to the Re (Cap_con, L₀) value. When the wind turbine (with Cap_wind capacity) and PV (with Cap_PV capacity) are integrated into DN, the power supply reliability level is increased to Re (Cap_con + Cap_wind + Cap_PV, L₀). The capacity value of the integrated DG can be denoted by the load demand increase. When the load demand level is increased to L₀+∆L, the load demand increase, denoted as ∆L, is regarded as DG CC with the integrated capacity of Cap_wind + Cap_PV if the equal reliability criterion is met. The equal power supply reliability criterion can be denoted as follows:

$Re\left\{Ca{p}_{\mathrm{c}\mathrm{o}\mathrm{n}},L_0\right\}=Re\left\{Ca{p}_{\mathrm{c}\mathrm{o}\mathrm{n}}+Ca{p}_{\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{d}}+Ca{p}_{\mathrm{p}\mathrm{v}},L_0+∆L\right\}(2)$

In addition, the capacity credit rate r_CC is a significant index to measure the confidence proportion of DG-integrated capacity. The confidence level of different DG types can be reflected by the r_CC index. The index can be calculated as follows:

$r_{CC}=\frac{∆L}{Ca{p}_{\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{d}}+Ca{p}_{\mathrm{p}\mathrm{v}}}\times 100\%(3)$

The physical meaning of capacity credit rate r_CC is the proportion of CC value to DG-installed capacity and the r_CC index is between 0 and 1. The DG capacity value is directly proportional to the value of capacity credit rate r_CC.

2.2 Credible capacity evaluation method based on sequential Monte Carlo simulation

Reliability calculation is the main work of DG CC evaluation. However, the randomness of system-component failure, the fluctuation and uncertainty of the DG output, and ES-remaining electricity makes reliability calculation a huge problem. The SMCS method can be used for various failure scenario samplings during the evaluation period. The fluctuation of the DG output and the sequential characteristics of ES are fully considered and the island partition scheme can be formulated in turn for various failure scenarios. The EENS index is calculated as the power supply reliability index.

2.2.1 Sequential operation state vector-generation method

The sequential operation state vector of system components is sampled during the evaluation period T. The potential failure components include DGs, distribution feeders, circuit breakers, and transformers. It should be noted that the active power output is 0 when DG is under the fault state while the failure of other components will lead to an open circuit. The two-state model is adopted to each component in the system and all components are in operation at the initial time. It is assumed that the normal operation time of the kth component is subject to the exponential distribution of failure rate ${\lambda }_k$. The uncertainty of the operation state is simulated by random-number sampling which obeys 0–1 uniform distribution. Then, the normal operation time of the kth component $t_k^{\mathrm{o}\mathrm{p}}$ is obtained. Similarly, the fault duration time of the kth component is subject to the exponential distribution of repair rate ${\mu }_k$. The fault duration time of the kth component $t_k^{\mathrm{r}\mathrm{e}\mathrm{p}}$ can be obtained. The normal operation time $t_k^{\mathrm{o}\mathrm{p}}$ and fault duration time $t_k^{\mathrm{r}\mathrm{e}\mathrm{p}}$ obtained by sampling shall be arranged in order. The sequential operation state vector of the kth component ${\mathit{S}\mathit{Q}}_{\mathit{k}}=\left[t_{k,1}^{\mathrm{o}\mathrm{p}},t_{k,1}^{\mathrm{r}\mathrm{e}\mathrm{p}},t_{k,2}^{\mathrm{o}\mathrm{p}},t_{k,2}^{\mathrm{r}\mathrm{e}\mathrm{p}},\cdots \cdots \right]$ is obtained when the following equation is satisfied:

$T<{\displaystyle \sum }_j\left(t_{k,j}^{\mathrm{o}\mathrm{p}}+t_{k,j}^{\mathrm{r}\mathrm{e}\mathrm{p}}\right)(4)$

2.2.2 Failure effects analysis based on island partition model

For the fault of some components located in DN downstream, part of load nodes can be transferred to other feeders through interconnection switch operation. But, the downstream load nodes cannot obtain electricity from the superior grid when the components near the root node are under the fault state. The switching operation will not be able to maintain the continuous power supply of the downstream load nodes, and it is necessary to formulate island partition schemes for different failure scenarios.

The island partition model can be established as a 0–1 mixed-integer programming model. The difficulty is that load priority, secondary outage constraint, fluctuation of load demand, and DG and other factors are required to be considered. The coupling of multiple constraints makes island partition an NP hard problem. In addition, the DN topology flexibility and radial operation constraints of the interconnection switches are also required to be taken into account, and it is very difficult for solving the island model. In this study, the island benefit is regarded as the optimization objective, which aims to maximize the restoration potential of DG and ES and reduce the EENS index of important loads with high priority in DN. The island partition model is shown as follows:

$\mathrm{s}.\mathrm{t}.\{\begin{array}{c}\min {\displaystyle \sum }_{i\in \mathit{N}}[\left(1-S{T}_i\right)*{\displaystyle \sum }_{t=t_1}^{t_2}{B}_{i,t}]\\ \begin{array}{c}\begin{array}{cc}{B}_{i,t}=P_{i,t}^{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}*P{R}_i& \begin{array}{cc}\forall i\in \mathit{N},\forall t\in \left[t_1,t_2\right]& \left(5.1\right)\end{array}\end{array}\\ \begin{array}{cc}S{T}_i=\{\begin{array}{l}\begin{array}{ccc}1& if& \begin{array}{cc}s{t}_{i,t}=1& \forall i\in \mathit{N},\forall t\in \left[t_1,t_2\right]\end{array}\end{array}\\ \begin{array}{ccc}0& if& \begin{array}{cc}s{t}_{i,t}=0& \forall i\in \mathit{N},\forall t\in \left[t_1,t_2\right]\end{array}\end{array}\end{array}& \left(5.2\right)\end{array}\\ \begin{array}{cc}s{t}_{i,t}=\{\begin{array}{c}\begin{array}{ccc}1& if& \begin{array}{cc}i\in \stackrel{A}{\underset{a=1}{\cup }}{\mathit{\Omega }}_a& \forall i\in \mathit{N},\forall t\in \left[t_1,t_2\right]\end{array}\end{array}\\ \begin{array}{ccc}0& if& \begin{array}{cc}i\notin \stackrel{A}{\underset{a=1}{\cup }}{\mathit{\Omega }}_a& \forall i\in \mathit{N},\forall t\in \left[t_1,t_2\right]\end{array}\end{array}\end{array}& \left(5.3\right)\end{array}\end{array}\\ \begin{array}{c}\begin{array}{cc}{\beta }_{ij}+{\beta }_{ji}={\omega }_{ij}& \begin{array}{cc}\forall i\in {\mathit{\Omega }}_a,j\in {\mathit{N}\mathit{B}}_i,\forall a\in \left[1,A\right]& \left(5.4\right)\end{array}\end{array}\\ \begin{array}{cc}{\beta }_{ij}=0& \begin{array}{cc}\forall i\in {\mathit{\Lambda }}_a,\forall a\in \left[1,A\right]& \left(5.5\right)\end{array}\end{array}\\ \begin{array}{cc}{\beta }_{ij}\in \left\{0,1\right\}& \begin{array}{cc}\forall i\in {\mathit{\Omega }}_a/{\mathit{\Lambda }}_a,j\in {\mathit{N}\mathit{B}}_i,\forall a\in \left[1,A\right]& \left(5.6\right)\end{array}\end{array}\end{array}\\ \begin{array}{c}\begin{array}{cc}{\displaystyle \sum }_{j\in {\mathit{N}\mathit{B}}_i}{\beta }_{ij}=1& \begin{array}{cc}\forall i\in {\mathit{\Omega }}_a,\forall i\notin {\mathit{\Lambda }}_a,\forall a\in \left[1,A\right]& \left(5.7\right)\end{array}\end{array}\\ \begin{array}{cc}0\le {\omega }_{ij}\le 1& \begin{array}{cc}\forall i\in {\mathit{\Omega }}_a,j\in {\mathit{N}\mathit{B}}_i,\forall a\in \left[1,A\right]& \left(5.8\right)\end{array}\end{array}\\ \begin{array}{cc}{\mathit{\Omega }}_a\cap {\mathit{\Omega }}_b=\varnothing & \begin{array}{cc}\forall a\in \left[1,A\right],b\in \left[1,A\right],a\ne b& \left(5.9\right)\end{array}\end{array}\end{array}\\ \begin{array}{c}\begin{array}{cc}{\mathit{\Lambda }}_a\cap {\mathit{\Lambda }}_b=\varnothing & \begin{array}{cc}\forall a\in \left[1,A\right],b\in \left[1,A\right],a\ne b& \left(5.10\right)\end{array}\end{array}\\ \begin{array}{cc}P{G}_{i,t}\le P{G}_{i,t}^{\max }& \begin{array}{cc}\forall i\in {\mathit{\Lambda }}_a,\forall a\in \left[1,A\right],\forall t\in \left[t_1,t_2\right]& \left(5.11\right)\end{array}\end{array}\\ \begin{array}{cc}{\displaystyle \sum }_{i\in {\mathit{\Omega }}_a}{P}_{i,t}^{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}*s{t}_{i,t}={\displaystyle \sum }_{j\in {\mathit{\Lambda }}_a}{P}_{j,t}^{\mathrm{d}\mathrm{i}\mathrm{s}}-P_{j,t}^{\mathrm{c}\mathrm{h}\mathrm{a}}+P{G}_{j,t}& \begin{array}{cc}\forall a\in \left[1,A\right],\forall t\in \left[t_1,t_2\right]& \left(5.12\right)\end{array}\end{array}\end{array}\\ \begin{array}{c}\begin{array}{cc}{E}_{\min }⩽E_{i,t}⩽E_{\max }& \begin{array}{cc}\forall i\in {\mathit{\Lambda }}_a,\forall t\in \left[t_1,t_2\right]& \left(5.13\right)\end{array}\end{array}\\ \begin{array}{cc}{E}_{i,t_1}=E_0& \begin{array}{cc}\forall i\in {\mathit{\Lambda }}_a& \left(5.14\right)\end{array}\end{array}\\ \begin{array}{cc}{E}_{i,t}=E_{i,t-1}-P_{i,t}^{\mathrm{d}\mathrm{i}\mathrm{s}}+P_{i,t}^{\mathrm{c}\mathrm{h}\mathrm{a}}& \begin{array}{cc}\forall i\in {\mathit{\Lambda }}_a,\forall t\in \left[t_1,t_2\right]& \left(5.15\right)\end{array}\end{array}\end{array}\\ \begin{array}{c}\begin{array}{cc}0\le u_{i,t}^{\mathrm{c}\mathrm{h}\mathrm{a}}+u_{i,t}^{\mathrm{d}\mathrm{i}\mathrm{s}}\le 1& \begin{array}{cc}\forall i\in {\mathit{\Lambda }}_a,\forall t\in \left[t_1,t_2\right]& \left(5.16\right)\end{array}\end{array}\\ \begin{array}{cc}{E}_{\max }*u_{i,t}^{\mathrm{c}\mathrm{h}\mathrm{a}}*{\beta }_{\min }\le P_{i,t}^{\mathrm{c}\mathrm{h}\mathrm{a}}\le E_{\max }*u_{i,t}^{\mathrm{c}\mathrm{h}\mathrm{a}}*{\beta }_{\max }& \begin{array}{cc}\forall i\in {\mathit{\Lambda }}_a,\forall t\in \left[t_1,t_2\right]& \left(5.17\right)\end{array}\end{array}\\ \begin{array}{cc}{E}_{\max }*u_{i,t}^{\mathrm{d}\mathrm{i}\mathrm{s}}*{\beta }_{\min }\le P_{i,t}^{\mathrm{d}\mathrm{i}\mathrm{s}}\le E_{\max }*u_{i,t}^{\mathrm{d}\mathrm{i}\mathrm{s}}*{\beta }_{\max }& \begin{array}{cc}\forall i\in {\mathit{\Lambda }}_a,\forall t\in \left[t_1,t_2\right]& \left(5.18\right)\end{array}\end{array}\end{array}\end{array}(5)$

2.2.3 Convergence criterion of sequential Monte Carlo simulation based on confidence level

If the absolute error is selected artificially as the calculation accuracy in SMCS, the calculation speed or convergence accuracy may not meet expectations. The variance coefficients can be used as the convergence criterion of SMCS.

$\chi =\frac{\sqrt{Var\left(\overline{y}\right)}}{\overline{y}}=\frac{\sigma }{\overline{y}\sqrt{n}}(6)$

The SMCS converges and the sampling stops when the variance coefficients are small enough. The standard normal distribution can be constructed as shown in Eq. 7.

$\frac{1}{\chi }-\frac{y\sqrt{n}}{\sigma }=\frac{\left(\overline{y}-y\right)}{\raisebox{1ex}{$\sigma $}\!\left/ \!\raisebox{-1ex}{$\sqrt{n}$}\right.}\sim N\left(\mathrm{0,1}\right)(7)$

For the population subject to the standard normal distribution, it satisfies the following equation:

$P\left(-{\mu }_{\frac{\alpha }{2}}<\frac{1}{\chi }-\frac{y}{\raisebox{1ex}{$\sigma $}\!\left/ \!\raisebox{-1ex}{$\sqrt{n}$}\right.}<{\mu }_{\frac{\alpha }{2}}\right)=2\varphi \left({\mu }_{\frac{\alpha }{2}}\right)-1=1-\alpha (8)$

Then, Eq. 9 can be obtained by mathematical statistics:

$P\left[\left(1-\chi {\mu }_{\frac{\alpha }{2}}\right)\overline{y}<y<\left(1+\chi {\mu }_{\frac{\alpha }{2}}\right)\overline{y}\right]=1-\alpha (9)$

If α = 0.05, the corresponding upper quantile $\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$2$}\right.=1.96$. The variance coefficients $\chi \le 0.05$. The error accuracy under α = 0.05 can be obtained according to the following equation:

$P\left[\left(1-0.05\times 1.96\right)\overline{y}<y<\left(1+0.05\times 1.96\right)\overline{y}\right]=0.95(10)$

It can be seen from the aforementioned equation that the error between true value y and estimated value $\overline{y}$ is within ± 10% at a reasonable confidence level and variance coefficients.

2.2.4 Credible capacity searching method based on dichotomy

CC searching is a one-dimensional searching process which requires repeated iterations to obtain the load demand increase based on equal power supply reliability criterion. Dichotomy is an effective method to realize one-dimensional searching process. The specific steps of CC searching are as follows:

(1) Before DG integration, the load demand level of the system is L₀. Evaluate the power supply reliability level Re (Cap_con, L₀), and it is represented by EENS under the fault state.

(2) The wind turbine and PV with the capacity of Cap_wind and Cap_PV is integrated into DN and the load demand level is maintained in L₀. The power-supply reliability level is improved and denoted as Re (Cap_wind + Cap_PV + Cap_con, L₀). Set the initial value l₁ = 1.

(3) Increase the load demand level of the system to L₀+l₁*L’. Evaluate the power supply reliability level Re (Cap_wind + Cap_PV + Cap_con, L₀+l₁*L’). Judge whether Re (Cap_wind + Cap_PV + Cap_con, L₀+l₁*L’) > Re (Cap_con, L₀) can be satisfied. If it is not, turn to step (4). Otherwise, turn to step (5).

(4) Let l₁ = l₁+1, return to step (3).

(5) The load demand level increase corresponding to CC is considered to be between [L₀+(l₁-1)*L′, L₀+l₁*L’]. Search the DG CC value based on dichotomy until equal power supply reliability criterion, as shown in Eq. 2, is satisfied. The obtained ∆L is the DG CC value. The schematic diagram of CC searching is shown in Figure 1.

FIGURE 1

FIGURE 1. The schematic diagram of CC searching.

3 Solution method of island partition

3.1 Calculation method of initial remaining electricity of energy storage

The ES initial remaining electricity constraint shown as Eq. 5 (5.14) is required in the island partition model. The integration of ES makes a significant impact on DN operation and the power supply reliability. The main dispatching objective of ES operation under the normal state is to achieve peak load-shifting and utilize the difference between peak and valley electricity prices to obtain profits. The objective function of the day-ahead economic dispatching model proposed in this article is divided into three parts. The first part is the cost of electricity purchasing and the income from selling electricity in DN. The second part is the cost of network loss. The third part is the cost of ES equipment loss. The ES optimal operation model can be established as follows:

$\min {\displaystyle \sum }_{t=1}^T\left(C_{t,\mathrm{b}\mathrm{u}\mathrm{y}}{P}_{t,\mathrm{b}\mathrm{u}\mathrm{y}}^{\mathrm{t}\mathrm{r}\mathrm{a}}-C_{t,\mathrm{s}\mathrm{e}\mathrm{l}\mathrm{l}}{P}_{t,\mathrm{s}\mathrm{e}\mathrm{l}\mathrm{l}}^{\mathrm{t}\mathrm{r}\mathrm{a}}\right)+C_t{\displaystyle \sum }_{t=1}^T{\displaystyle \sum }_{ij\in \mathit{E}}{I}_{ij,t}^2{R}_{ij}+C_{\mathrm{E}\mathrm{S}}{\displaystyle \sum }_{t=1}^T{\displaystyle \sum }_{i=1}^{N_{\mathrm{E}\mathrm{S}}}\max \left\{P_{i,t}^{\mathrm{d}\mathrm{i}\mathrm{s}},P_{i,t}^{\mathrm{c}\mathrm{h}\mathrm{a}}\right\}$

$\{\begin{array}{c}\begin{array}{cc}{P}_{ji,t}-R_{ij}{I}_{ij,t}^2-{\displaystyle \sum }_{k\in \mathit{H}\left(i\right)}{P}_{ik,t}=P_{i,t}^{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}-P{G}_{i,t}-P_{i,t}^{\mathrm{d}\mathrm{i}\mathrm{s}}+P_{i,t}^{\mathrm{c}\mathrm{h}\mathrm{a}}& \left(11.1\right)\end{array}\\ \begin{array}{c}\begin{array}{cc}{Q}_{i,t}^{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}=Q_{ji,t}-x_{ij}{I}_{ij,t}^2-{\displaystyle \sum }_{k\in \mathit{H}\left(i\right)}{Q}_{ik,t}& \left(11.2\right)\end{array}\\ \begin{array}{c}\begin{array}{cc}{U}_{j,t}^2=U_{i,t}^2-2\left(r_{ij}{P}_{ij,t}+x_{ij}{Q}_{ij,t}\right)+\left(r_{ij}^2+x_{ij}^2\right)I_{ij,t}^2& \left(11.3\right)\end{array}\\ \begin{array}{cc}{I}_{ij,t}^2=\frac{P_{ij,t}^2+Q_{ij,t}^2}{U_{i,t}^2}& \left(11.4\right)\end{array}\\ \begin{array}{c}\begin{array}{cc}{I}_{ij,t}^2\le I_{ij,\max }^2& \left(11.5\right)\end{array}\\ \begin{array}{cc}{U}_{i,\min }\le U_{i,t}\le U_{i,\max }& \left(11.6\right)\end{array}\end{array}\end{array}\end{array}\end{array}(11)$

For the constraints in the day-ahead economic dispatching model, Eq. 11 (11.1)–(11.2) denotes that the injected power of nodes shall satisfy the power-balance constraint. Eq. 11 (11.3) denotes that the voltage between adjacent nodes satisfies the voltage amplitude constraints. Equation (11.4) denotes the calculation method of the current in the branch. The branch current and node voltage constraints are established in Eq. 11 (11.5)–(11.6) in order to guarantee DN operation state within the security region.

In addition, the charging and discharging processes of ES are shown in Eq. 15 (5.13)–(5.18). For the established day-ahead economic dispatching model of DN, it can be transformed into a second-order cone optimization problem (Ding et al., 2017) by variable equivalent substitution method. Then, the initial remaining electricity of ES is the solution of the cone programming problem and the solving process will not be expanded in detail here.

3.2 Maximum island partition and optimal island rectification

Multiple constraints shall be coupled in the island partition model and the direct solving is very difficult. The island partition model in Section 2.2.2 is decoupled into the MIP and OPR models. The MIP scheme is formulated based on electricity sufficiency information and the final island scheme can be quickly obtained after OPR based on the power-balance information. The MIP model can be decoupled as follows:

$\min {\displaystyle \sum }_{i\in \mathit{N}}[\left(1-S{T}_i\right)*{\displaystyle \sum }_{t=t_1}^{t_2}{B}_{i,t}]$

$s.t.\{\begin{array}{c}\begin{array}{cc}Eq.\left(5.1\right)\sim Eq.\left(5.2\right)& \mathrm{S}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{a}\mathrm{r}\mathrm{y}\mathrm{o}\mathrm{u}\mathrm{t}\mathrm{a}\mathrm{g}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{t}\end{array}\\ \begin{array}{c}\begin{array}{cc}Eq.\left(5.3\right)& \mathrm{C}\mathrm{a}\mathrm{l}\mathrm{c}\mathrm{u}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{o}\mathrm{f}\mathrm{b}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{f}\mathrm{i}\mathrm{t}\end{array}\\ \begin{array}{c}\begin{array}{cc}Eq.\left(5.4\right)\sim Eq.\left(5.8\right)& \mathrm{R}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{l}\mathrm{o}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{o}\mathrm{f}\mathrm{D}\mathrm{N}\end{array}\\ \begin{array}{c}\begin{array}{cc}Eq.\left(5.9\right)\sim Eq.\left(5.10\right)& \mathrm{I}\mathrm{s}\mathrm{l}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{j}\mathrm{o}\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{t}\end{array}\\ \begin{array}{c}\begin{array}{cc}Eq.\left(5.11\right)& \mathrm{D}\mathrm{G}\mathrm{o}\mathrm{u}\mathrm{t}\mathrm{p}\mathrm{u}\mathrm{t}\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{t}\end{array}\\ \begin{array}{cc}Eq.\left(5.14\right)& \mathrm{Remaining}\mathrm{power}\mathrm{state}\mathrm{of}\mathrm{ES}\end{array}\\ \begin{array}{cc}Eq.\left(13\right)& \mathrm{E}\mathrm{l}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{y}\mathrm{s}\mathrm{u}\mathrm{f}\mathrm{f}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{y}\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{t}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}(12)$

It should be noted that the solution of the MIP model is only a pre-scheme which satisfies the electricity sufficiency constraint. The constraint can be denoted as follows.

${\displaystyle \sum }_{t=t_1}^{t_2}{\displaystyle \sum }_{i\in {\mathit{\Omega }}_a}{P}_{i,t}^{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}\ast s{t}_{i,t}\le E_{i,t_1}+{\displaystyle \sum }_{t=t_1}^{t_2}{\displaystyle \sum }_{i\in {\mathit{\Lambda }}_a}P{G}_{i,t}^{\max }\forall a\in \left[1,A\right](13)$

The electricity sufficiency constraint denotes that the sum power output of DG- and ES-remaining electricity is greater than the total load demand during the fault period. Otherwise, the final island scheme will not satisfy the electricity sufficiency constraint. The purpose of MIP is to determine the optimal range of the final island and guarantee more important loads with high priority which can be restored under the fault state.

A heuristic prospective greedy algorithm is proposed for solving the MIP model (Chen et al., 2022) (Yu and Ma, 2014). The proposed algorithm avoids repeated iterations of existing intelligent algorithms and improves the solving speed of island partition significantly. In addition, the power supply restoration path is expanded by the introduction of a prospective neighborhood. The single-step blindness of the common greedy algorithm was effectively overcome, which reduces the power outage loss to a greater extent and brings greater benefits. It is assumed that the system fails during [t₁, t₂]. The pseudocode of the MIP based on the heuristic perspective greedy algorithm is shown in Table 1.

Step 1: Determine the downstream power outage area according to the sampling failure scenario. Save the topology of the DN power outage area and record it as figure G.

Step 2: Select a DG integration node as the initial node to formulate the MIP scheme. Judge whether the maximum electricity $C_{\mathrm{R}}^{\max }$ of DG output and ES-remaining electricity is greater than the load demand $P_{{\mathit{\Lambda }}_a\left(d\right)}$ of the DG-integrated node. If it is not, turn to Step 6. Otherwise, the integrated DG node is drawn into island set V.

$C_{\mathrm{R}}^{\max }=E_{i,t_1}+{\displaystyle \sum }_{t=t_1}^{t_2}{\displaystyle \sum }_{i\in {\mathit{\Lambda }}_a}P{G}_{i,t}^{\max }\forall a\in \left[1,A\right](14)$

$P_{{\mathit{\Lambda }}_a\left(d\right)}^{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}={\displaystyle \sum }_{t\in \left[t_1,t_2\right]}{P}_{{\mathit{\Lambda }}_a\left(d\right),t}^{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}(15)$

TABLE 1

TABLE 1. The prospective greedy algorithm pseudo-code.

Step 3: Update the parameters of island set V. The parameters of the island include the sum of active power load demand P_V, the island benefit B_V, and remaining electricity C_R.

$P_V={\displaystyle \sum }_{i\in \mathit{V}}{P}_{i,t}^{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}\forall t\in \left[t_1,t_2\right](16)$

$B_V={\displaystyle \sum }_{i\in \mathit{V}}{P}_{i,t}^{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}\ast P{R}_i\forall t\in \left[t_1,t_2\right](17)$

$C_{\mathrm{R}}=C_{\mathrm{R}}^{\max }-P_V\forall a\in \left[1,A\right](18)$

Step 4: Search the neighborhood set NE¹ and prospective neighborhood set NE_m². Calculate the value ratio Va¹(m) and Va_m(n). If the value ratio is not 0, the schemes with the best value ratio are drawn into island set V, and then turn to Step 3. If the value ratio is 0, turn to Step 5. It should be noted that there is a topological connection relationship with at least one node in set V for the nodes in neighborhood set NE¹. However, the intersection of neighborhood set NE¹ and set V is an empty set. For the nodes in the prospective neighborhood set NE_m², there is a topological connection relationship with at least one node in neighborhood set NE¹. The intersection of neighborhood set NE¹ and prospective neighborhood set NE_m² is an empty set. In addition, the intersection of set V and prospective neighborhood set NE_m² is also an empty set.

$V{a}^1\left(m\right)=\{\begin{array}{cc}\frac{B_V\left(N{E}^1\left(m\right)\right)}{P_V\left(N{E}^1\left(m\right)\right)},if{P}_V\left(N{E}^1\left(m\right)\right)\le C_{\mathrm{R}}& \forall m\in \left\{1,2,\dots ,N_0\right\}\\ 0,if{P}_V\left(N{E}^1\left(m\right)\right)>C_{\mathrm{R}}& \forall m\in \left\{1,2,\dots ,N_0\right\}\end{array}(19)$

$V{a}_m\left(n\right)=\{\begin{array}{c}\frac{B_V\left(N{E}^1\left(m\right)\right)+B_V\left(N{E_m}^2\left(n\right)\right)}{P_V\left(N{E}^1\left(m\right)\right)+P_V\left(N{E_m}^2\left(n\right)\right)},if{P}_V\left(N{E}^1\left(m\right)\right)+P_V\left(N{E_m}^2\left(n\right)\right)\le C_{\mathrm{R}}\\ 0,if{P}_V\left(N{E}^1\left(m\right)\right)+P_V\left(N{E_m}^2\left(n\right)\right)>C_{\mathrm{R}}\end{array}(20)$

Step 5: Mark the corresponding DG and the island set V is compressed into a new node s_a. Update the figure G.

Step 6: The compressed node s_a is restored to the original form of figure G. Judge whether the DN is with a ring network and Prim algorithm of the minimum spanning tree is applied to disconnect the ring network, and the MIP scheme with a radial structure is obtained.

A possible maximum island scheme based on the electricity sufficiency information is obtained by using the MIP model. However, due to the fluctuation of the DG output and sequential characteristics of ES-remaining electricity in an actual operation, the scheme is only a potential optimal power restoration scheme with blindness and inaccuracy. In order to obtain the final island scheme, it is necessary to carry out OPR on the MIP scheme based on the power-balance information. The OPR model based on the power-balance information can be established as follows:

$\min {\displaystyle \sum }_{i\in \mathit{V}}[\left(1-S{T}_i\right)\ast {\displaystyle \sum }_{t=t_1}^{t_2}{B}_{i,t}]$

$s.t.\{\begin{array}{c}\begin{array}{cc}Eq.\left(5.1\right)\sim Eq.\left(5.2\right)& \mathrm{S}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{a}\mathrm{r}\mathrm{y}\mathrm{o}\mathrm{u}\mathrm{t}\mathrm{a}\mathrm{g}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{t}\end{array}\\ \begin{array}{c}\begin{array}{cc}Eq.\left(5.3\right)& \mathrm{C}\mathrm{a}\mathrm{l}\mathrm{c}\mathrm{u}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{o}\mathrm{f}\mathrm{b}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{f}\mathrm{i}\mathrm{t}\end{array}\\ \begin{array}{c}\begin{array}{cc}Eq.\left(5.4\right)\sim Eq.\left(5.8\right)& \mathrm{R}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{l}\mathrm{o}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{o}\mathrm{f}\mathrm{D}\mathrm{N}\end{array}\\ \begin{array}{c}\begin{array}{cc}Eq.\left(5.11\right)& \mathrm{D}\mathrm{G}\mathrm{o}\mathrm{u}\mathrm{t}\mathrm{p}\mathrm{u}\mathrm{t}\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{t}\end{array}\\ \begin{array}{c}\begin{array}{cc}Eq.\left(5.12\right)& \mathrm{P}\mathrm{o}\mathrm{w}\mathrm{e}\mathrm{r}\mathrm{b}\mathrm{a}\mathrm{n}\mathrm{l}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{t}\end{array}\\ \begin{array}{cc}Eq.\left(5.13\right)\sim Eq.\left(5.18\right)& \mathrm{E}\mathrm{n}\mathrm{e}\mathrm{r}\mathrm{g}\mathrm{y}\mathrm{s}\mathrm{t}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{g}\mathrm{e}\mathrm{o}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{s}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}(21)$

It should be noted that the scheme optimized by the OPR model is the solution of MIP rather than the load nodes in set N. The final island scheme is obtained based on both electricity sufficiency and power-balance information. In addition, it is also required to satisfy the node voltage constraint and branch power flow constraint to ensure a safe and stable operation under the fault state.

4 Case study

4.1 The parameters of distribution network

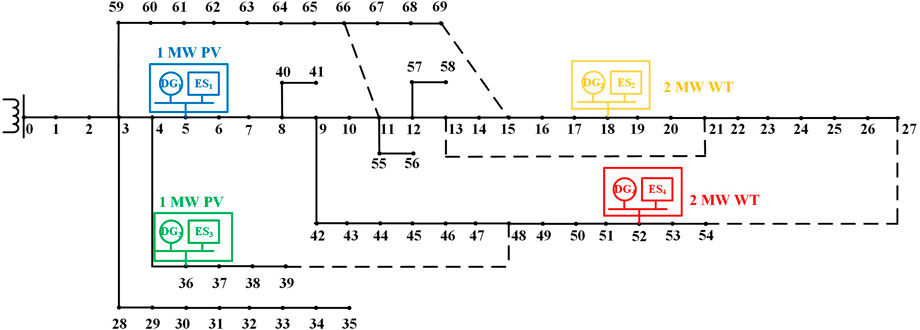
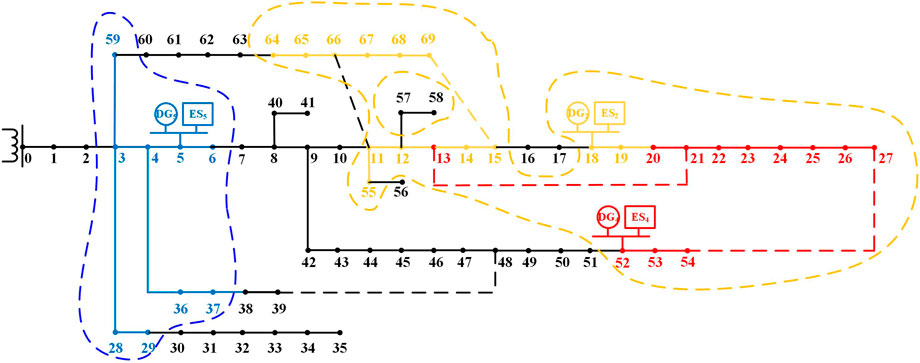
The island partition of DN with DG and distributed ES is analyzed for PG&E 69-bus system in this study. The DN topology of the PG&E 69-bus system is shown in Figure 2. The superior grid is regarded as a special DG with sufficient electricity. 1 MV PV is integrated into load node 5 and node 36 and 2 MV wind turbine is integrated into load node 18 and node 52. In addition, ES is integrated into nodes 5, 18, 36, and 52 under the allocation ratio of 20%. The failure components considered in DN include the buses, circuit breakers, transformers, and feeders. The components of DN are established as two-state models and the failure rate is 0.2 times per year, while the repair rate is 1,000 times per year. There are intersection switches 11–66, 13–21, 15–69, 27–54, and 39–48 in DN and they are regarded as normally open switches under a normal operation state. Therefore, the fault of the intersection switches is not considered in the reliability calculation. The load-demand values and priority of the PG&E 69-bus system is shown in Supplementary Appendix SA1. The computation was conducted in MATLAB with the aid of CPLEX. The simulation platform is a 64-bit server with AMD Ryzen seven CPU @3.20 GHz and 16 GB RAM.

FIGURE 2

FIGURE 2. The DN topology of the PG&E 69-bus system.

4.2 The formulation of island partition scheme

4.2.1 The solution of maximum island partition based on prospective greedy algorithm

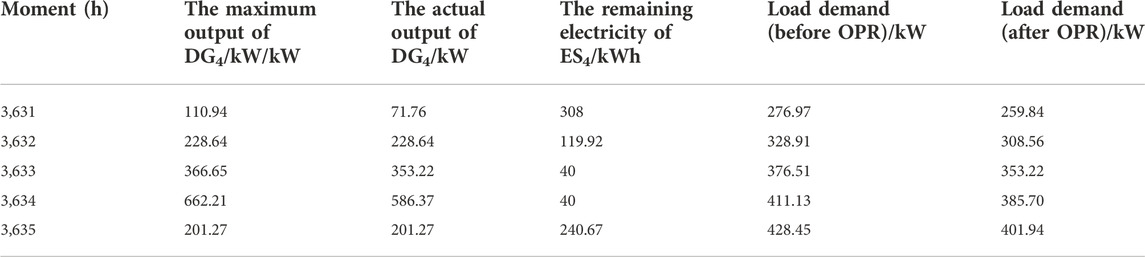
During the period of 3,631 h–3635 h, the branch 0–1 breaks down and may last for 5 h. The downstream load cannot obtain electricity from the superior grid. It is required to formulate a MIP scheme of DN based on the DG output and ES-remaining electricity information of each moment. Then, sequential ES operation simulation based on the day ahead economic dispatching model is carried out from 3,625 h to 3,648 h. The ES remaining electricity at each moment is obtained as shown in Supplementary Appendix SA2. Power supply restoration scheme is formulated by the descending order of DG integration capacity.

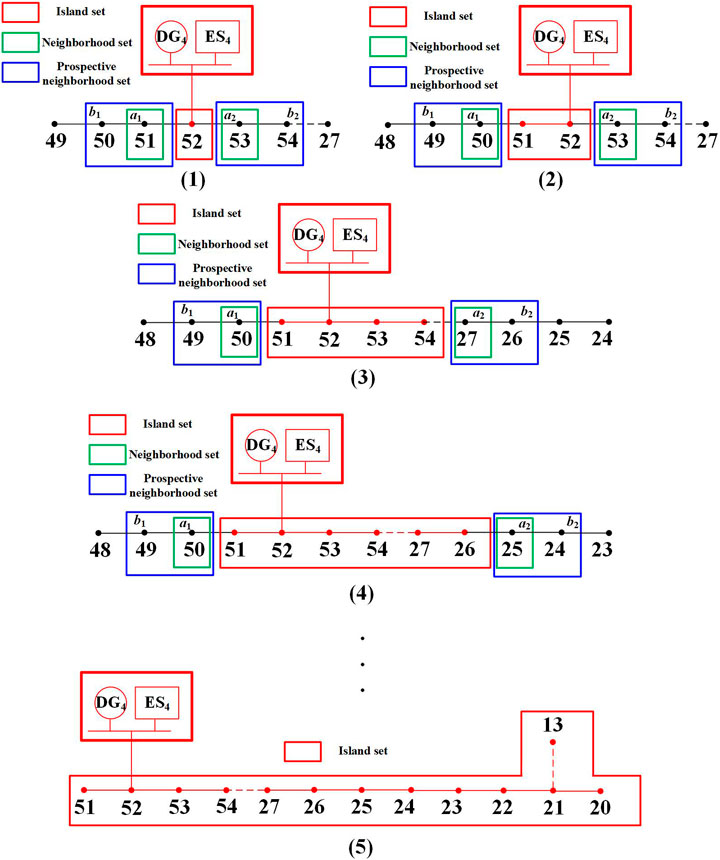
Taking DG₄ and ES₄ as examples, the MIP scheme based on the prospective greedy algorithm is formulated as follows. The sum of ES₄ remaining electricity at 3,631 h and the total DG₄ output from 3,631 h to 3,635 h is 1,837.73 kWh, which is the accessible electricity for MIP. Then, judge whether the node 52 can be drawn into the island according to the electricity sufficiency information. If the node 52 can be restored, search the neighborhood set of the island based on the prospective greedy algorithm and the searching process is shown in Figure 3. The neighborhood set of the island a₁ and a₂ is shown by the green square and the prospective neighborhood set b₁ and b₂ is shown by the blue square. Calculate the values of Va¹(m) and Va_m(n). In the first searching, the value ratio of scheme a₁ is the highest and the benefit is 1761.04. Therefore, the corresponding node 51 is drawn into the island. Search the scheme combination continuously and update the neighborhood set and prospective neighborhood set respectively until the values of Va¹(m) and Va_m(n) are all 0. The obtained island will be compressed into a new node 70. That is because the unrestored load nodes may not be searched when other DGs are selected as the initial node. These nodes cannot obtain electricity from other DGs due to the break of topological relationship after the islands are formed.

FIGURE 3

FIGURE 3. The searching process by using the prospective greedy algorithm.

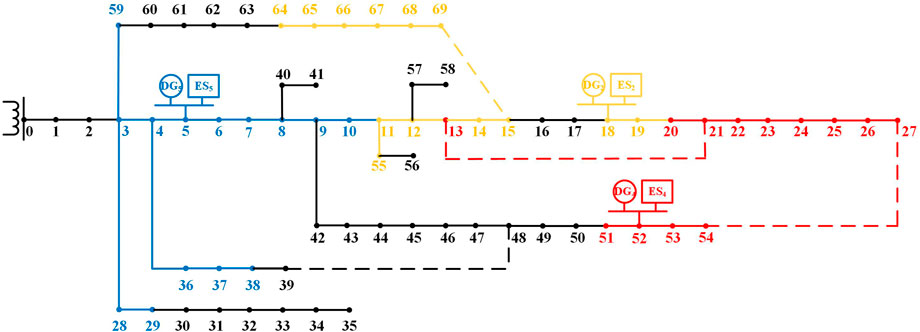
Similarly, the MIP schemes starting from other DGs can be obtained and the final MIP scheme is shown in Figure 4. It should be noted that in the searching process starting from DG₁, node 36 is drawn into the island and DG₁ and DG₃ should be merged. The new DG is denoted as DG₅ and the new ES is ES₅.

FIGURE 4

FIGURE 4. The island partition scheme based on the MIP model.

4.2.2 The verification of the maximum island partition solution based on the optimal island rectification model

The power supply restoration scheme obtained based on the MIP model is only a potential optimal power restoration scheme with blindness and inaccuracy. The final island should satisfy the power balance constraint and OPR is required to be carried out to guarantee the continuous power supply in the island at all moments under the fault state. The information of DG output, ES-remaining electricity, and load demand from 3,631 h to 3,635 h is shown in Table 2. The maximum active power output of DG₄ in 3,633 h is 366.65 kWh while the total load demand is 376.51 kWh of the MIP scheme as shown in Figure 4. Therefore, node 51 is drawn out of the island scheme. The OPR results indicate that the solution obtained by MIP does not satisfy the power-balance constraint from 3,631 h to 3,635 h. It can be found that the output of DG is less than the total load demand corresponding to the MIP scheme in the first 2 h. Therefore, the remaining electricity of ES₄ decreases to the minimum value and cannot support the power supply of the last 3 h. The final island scheme after OPR is shown in Figure 5. It is found that there is a deviation of the island scheme before and after the process of OPR. OPR is a necessary step to accurately formulate the island partition scheme.

TABLE 2

TABLE 2. The DG output and load demand from 3,631 h to 3,635 h.

FIGURE 5

FIGURE 5. Final island partition scheme.

4.2.3 The comparison of key factors

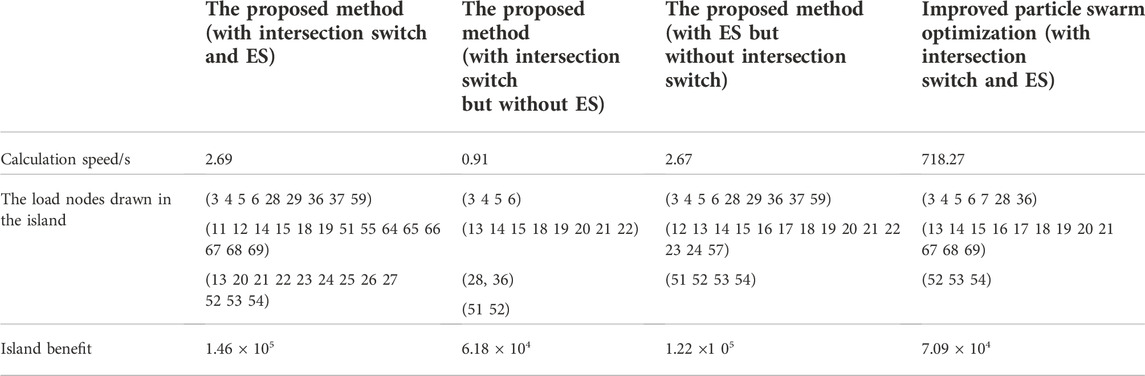
In order to clear the effect of key factors on the benefit of island partition, three comparative analyses from the aspects of ES integration, intersection switch, and solution algorithm are conducted. The comparison results are shown in Table 3. First, the integration of ES is able to shift the peak load demand and the potential of DG power supply restoration can be fully exploited under the fault state. It is found that the integration of ES makes a significant impact on the island partition scheme and the island benefit is improved. Then, the introduction of intersection switch is able to expand the searching path of the prospective greedy algorithm and improve the probability of obtaining the island scheme with better benefits. DN topology flexibility realized by the intersection switch must be considered in island partition. Finally, an improved particle swarm optimization (Tawfeek et al., 2018) is compared with the proposed method. It is found that the proposed method can overcome the low convergence speed caused by iterative calculation of intelligent algorithms. The solution speed of the island scheme is significantly improved on the premise of the island scheme.

TABLE 3

TABLE 3. The comparison of key factors on the benefit of island partition.

4.3 Credible capacity evaluation results

4.3.1 Sequential Monte Carlo simulation convergence criterion

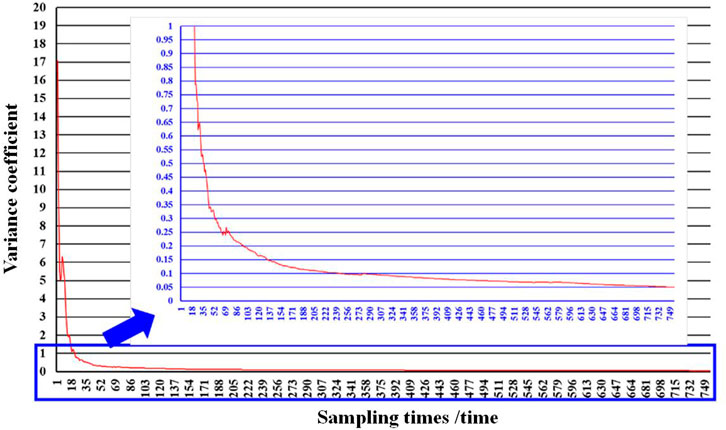
The convergence criterion based on variance coefficients is used in SMCS. The variance coefficients decrease gradually with the increase of sampling times and the diagram of SMCS convergence process is shown in Figure 6. When the sampling times reach 751 (i.e., 7,510 years), the variance coefficients decrease to 0.05. At a given reasonable confidence level α = 0.05, the difference between the true value of the reliability level and the estimated $\overline{y}$ obtained by SMCS is small and the error is within 10%. Instead of selecting a fixed value as the convergence criterion, the reliability and computational efficiency have been significantly improved by proposed method.

FIGURE 6

FIGURE 6. The diagram of the SMCS convergence process.

4.3.2 Credible capacity evaluation results under different energy storage allocation ratio

The impact of ES integration on the island benefit is analyzed in Section 4.2.3 and it is found that the power supply reliability can be improved after the integration of ES. In order to explore the impact on the DG CC value, four different scenarios with ES allocation ratios of 0%, 20%, 30%, and 40% are analyzed. The united CC value under different scenarios with ES allocation ratio is shown in Figure 7A. The detailed CC searching result under different allocation ratios of ES is shown in Supplementary Appendix SA3. The united CC value is 831.8 kW under the scenario without ES integration and the CC rate index is 13.86%. When the ES allocation ratio is increased to 20%, 30%, and 40%, the CC rate index is 17.08%, 21.29%, and 22.29%, respectively. The DG CC value is increased by 23%, 53%, and 61%. It can be seen that the united CC value gradually increases with the improvement of ES allocation ratio and appropriate configuration of ES is able to improve the DG capacity value.

FIGURE 7

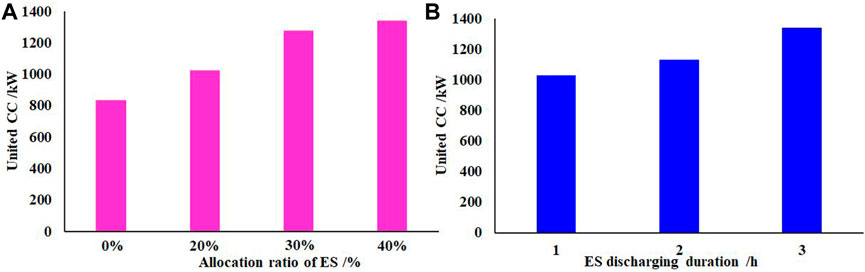
FIGURE 7. The CC value under different scenarios (A) United CC value under different scenarios with ES allocation ratio (B) The united CC value under different full-charging or discharging periods of ES.

In order to explore the impact of ES discharging duration, the united CC value is evaluated when ES can be charged or discharged continuously for 1, 2, and 4 h. The installation ratio of ES is set to 20%. For the wind turbine, the rated power of ES is 0.4 MW and the maximum electricity of ES is 0.4 MWh, 0.8 MWh, and 1.6 MWh. For PV equipment, the rated power of ES is 0.2 MW and the maximum electricity of ES is 0.2 MWh, 0.4 MWh, and 0.8 MWh, respectively. The CC values under different ES discharging durations are shown in Figure 7B. When ES can discharge continuously for 2 h, the united CC value is 1,127.94 kW. When ES can discharge continuously for 4 h, the united CC value is improved to 1,335.17 kW. It can be seen that the ES discharging duration makes an effect on the CC value. In this article, the whole process of once CC evaluation takes about 50 h.

4.3.3 Comparison between the proposed method and non-reliability method

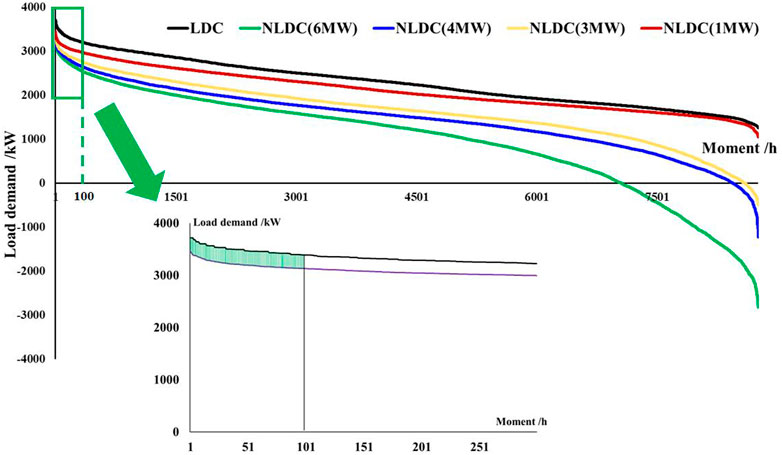
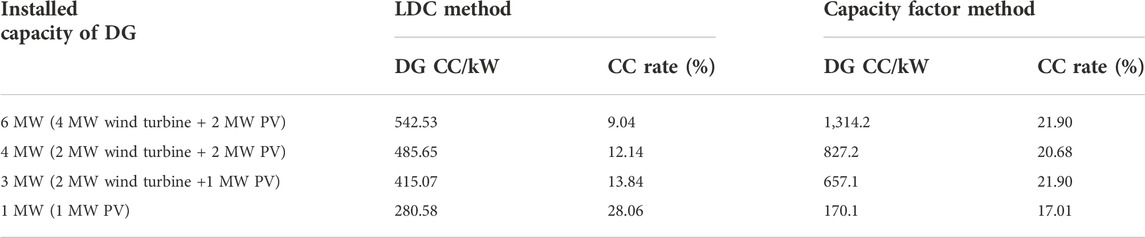
The non-reliability methods based on the capacity factor and the LDC method are compared with the proposed method. The capacity factor is the proportion of DG maximum active power output to the installed capacity of DG, which can be used to roughly measure capacity value. The CC rate value of PV is 17.01% and the value of the wind turbine is 24.35%. The CC is a constant value based on capacity factor, irrelevant with the permeability of DG. According to the LDC method, the CC value is the average value of the difference between the original LDC and net LDC of the first 100 h. The diagram of the LDC-based method is shown in Figure 8 and the CC evaluation result is shown in Table 4. When DG permeability is high, the evaluation result based on the LDC method is seriously lower than the actual CC value. This is because the LDC method focuses on the DG output under the normal state when the load demand is high. Differently, the fault-recovery ability of DG under the fault state can be fully measured by the proposed method, which is more suitable to the engineering practice.

FIGURE 8

FIGURE 8. The diagram of the LDC-based method.

TABLE 4

TABLE 4. DG CC evaluation results by using different methods.

5 Discussion

In this article, a united credible capacity evaluation method of distributed generation and energy storage based on active island operation is proposed. A united credible capacity index based on the equivalent load carrying capacity concept is put forward to measure the capacity value of renewable power generation accurately. The main work of united credible capacity evaluation is reliability calculation of the distribution network. The sequential Monte Carlo simulation, conducting day-ahead economic dispatching under the normal state and active island operation under the fault state alternately, is used to calculate power supply reliability. What’s more, the convergence criterion based on variance coefficients is introduced for sequential Monte Carlo simulation. The difficulty of the distribution network reliability calculation is island partition under the fault state with the fluctuation of distributed generation output and energy storage remaining electricity. The problem is decoupled into maximum island partition and optimal island rectification model and they can be quickly solved by using the prospective greedy algorithm. Based on the proposed method in this article, the case study of PG&E 69-bus system is analyzed. It is found that:

1) An appropriate configuration of energy storage is able to improve the capacity value of distributed generation. United credible capacity increases by 23%, 53%, and 61%, respectively, under the energy storage allocation ratio of 20%, 30%, and 40%.

2) The distribution network topology flexibility brought by the intersection switches makes great influence on the island partition effect and it cannot be ignored in distributed generation credible capacity evaluation.

3) The proposed united credible capacity index can account for power supply reliability under the fault state. It is suitable for high distributed generation permeability scenarios.

To realize power recovery, DG is required to be observable and controllable. In fact, some DGs are integrated into the low-voltage distribution network and they are invested and built by users or third parties. The distribution system operator may be unable to control them at some moment, which may reduce the value of DG CC to a certain extent. In addition, there will be increasing flexible resources from all sides of the source–network–load–storage, e.g., demand response and reactive equipment, which are not yet considered in this article.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

The paper is completed with the joint efforts of six authors; each of them has made their own contributions from the model, algorithm, data, and other aspects. CJ: Conceptualization and Methodology. SB: Supervision. ZY: Writing–Original Draft. LY: Software. JR: Translation. MS: Resources.

Funding

This work was supported by the State Grid scientific and technological projects of China (SGZJDK00DWJS2100256), Tianjin Science and technology planning project (22ZLGCGX00050), the 67th Postdoctoral Fund and Independent innovation fund of Tianjin University in 2021.

Conflict of interest

LY and MS are employed by the State Grid Tianjin Electric Power Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2022.1043229/full#supplementary-material

References

Arefi, A., Ledwich, G., Nourbakhsh, G., and Behi, B. (2020). A fast adequacy analysis for radial distribution networks considering reconfiguration and DGs. IEEE Trans. Smart Grid 11 (5), 3896–3909. doi:10.1109/TSG.2020.2977211

CrossRef Full Text | Google Scholar

Bagheri, A., Monsef, H., and Lesani, H. (2015). Renewable power generation employed in an integrated dynamic distribution network expansion planning. Electr. Power Syst. Res. 127, 280–296. doi:10.1016/j.epsr.2015.06.004

CrossRef Full Text | Google Scholar

Cai, J., and Xu, Q. (2021). Capacity credit evaluation of wind energy using a robust secant method incorporating improved importance sampling. Sustain. Energy Technol. Assessments 43, 100892. in press. doi:10.1016/j.seta.2020.100892

CrossRef Full Text | Google Scholar

Chen, C., Wang, J., Qiu, F., and Zhao, D. (2015). Resilient distribution system by microgrids formation after natural disasters. IEEE Trans. Smart Grid 7 (2), 958–966. doi:10.1109/TSG.2015.2429653

CrossRef Full Text | Google Scholar

Chen, J., Sun, B., Li, Y., Jing, R., Zeng, Y., and Li, M. (2022). An evaluation method of distributed generation credible capacity based on island partition. Energy Rep. 8, 11271–11287. doi:10.1016/j.egyr.2022.08.251

CrossRef Full Text | Google Scholar

D'Annunzio, C., and Santoso, S. (2008). Noniterative method to approximate the effective load carrying capability of a wind plant. IEEE Trans. Energy Convers. 23 (2), 544–550. doi:10.1109/TEC.2008.918597

CrossRef Full Text | Google Scholar

Ding, M., and Xu, Z. (2016). Empirical model for capacity credit evaluation of utility-scale PV plant. IEEE Trans. Sustain. Energy 8 (1), 94–103. doi:10.1109/TSTE.2016.2584119

CrossRef Full Text | Google Scholar

Ding, T., Liu, S., Wu, Z., and Bie, Z. (2017). Sensitivity-based relaxation and decomposition method to dynamic reactive power optimisation considering DGs in active distribution networks. IET Gener. Transm. &amp. Distrib. 11 (1), 37–48. doi:10.1049/iet-gtd.2016.0303

CrossRef Full Text | Google Scholar

Dragoon, K., and Dvortsov, V. (2006). Z-method for power system resource adequacy applications. IEEE Trans. Power Syst. 21 (2), 982–988. doi:10.1109/TPWRS.2006.873417

CrossRef Full Text | Google Scholar

Frew, A., Cole, J., Sun, Y., Mai, T., and Richards, J. (2017). 8760-based method for representing variable generation capacity value in capacity expansion models. Golden, CO (United States): National Renewable Energy Lab.

Google Scholar

Gao, H., Chen, Y., Xu, Y., and Liu, C. C. (2016). Resilience-oriented critical load restoration using microgrids in distribution systems. IEEE Trans. Smart Grid 7 (6), 2837–2848. doi:10.1109/TSG.2016.2550625

CrossRef Full Text | Google Scholar

Garver, L. (1966). Effective load carrying capability of generating units. IEEE Trans. Power Apparatus Syst. PAS-85 (8), 910–919. doi:10.1109/TPAS.1966.291652

CrossRef Full Text | Google Scholar

Guimaraes, G., Bernardon, P., Garcia, J., Schmitz, M., and Pfitscher, L. L. (2021). A decomposition heuristic algorithm for dynamic reconfiguration after contingency situations in distribution systems considering island operations. Electr. Power Syst. Res. 192, 106969. in press. doi:10.1016/j.epsr.2020.106969

CrossRef Full Text | Google Scholar

Hamidan, A., and Borousan, F. (2022). Optimal planning of distributed generation and battery energy storage systems simultaneously in distribution networks for loss reduction and reliability improvement. J. Energy Storage 46, 103844. in press. doi:10.1016/j.est.2021.103844

CrossRef Full Text | Google Scholar

Hosseinnezhad, V., Rafiee, M., Ahmadian, M., and Siano, P. (2018). Optimal Island partitioning of smart distribution systems to improve system restoration under emergency conditions. Int. J. Electr. Power & Energy Syst. 97, 155–164. doi:10.1016/j.ijepes.2017.11.003

CrossRef Full Text | Google Scholar

JinMuJia, X. Y. H., Jia, H., Wu, J., Jiang, T., and Yu, X. (2017). Dynamic economic dispatch of a hybrid energy microgrid considering building based virtual energy storage system. Appl. energy 194, 386–398. doi:10.1016/j.apenergy.2016.07.080

CrossRef Full Text | Google Scholar

Lei, S., Wang, J., Chen, C., and Hou, Y. (2016). Mobile emergency generator pre-positioning and real-time allocation for resilient response to natural disasters. IEEE Trans. Smart Grid 9 (3), 1–2041. doi:10.1109/TSG.2016.2605692

CrossRef Full Text | Google Scholar

Li, Z., Khrebtova, T., Zhao, N., Zhang, Z., and Fu, Y. (2020). Bi-level service restoration strategy for active distribution system considering different types of energy supply sources. IET Gener. Transm. &amp. Distrib. 14 (19), 4186–4194. doi:10.1049/iet-gtd.2020.0047

CrossRef Full Text | Google Scholar

Li, Z., Wu, W., Zhang, B., and Tai, X. (2019). Analytical reliability assessment method for complex distribution networks considering post-fault network reconfiguration. IEEE Trans. Power Syst. 35 (2), 1457–1467. doi:10.1109/TPWRS.2019.2936543

CrossRef Full Text | Google Scholar

Paik, C., Chung, Y., and Kim, J. (2021). ELCC-based capacity credit estimation accounting for uncertainties in capacity factors and its application to solar power in Korea. Renew. Energy 164, 833–841. doi:10.1016/j.renene.2020.09.129

CrossRef Full Text | Google Scholar

Photovoltaics, G., and Storage, E. (2011). IEEE guide for design, operation, and integration of distributed resource island systems with electric power systems (United State: IEEE). doi:10.1109/IEEESTD.2011.5960751

CrossRef Full Text | Google Scholar

Rathore, A., and Patidar, P. (2019). Reliability assessment using probabilistic modelling of pumped storage hydro plant with PV-Wind based standalone microgrid. Int. J. Electr. Power & Energy Syst. 106, 17–32. doi:10.1016/j.ijepes.2018.09.030

CrossRef Full Text | Google Scholar

Rayati, M., Goodarzi, H., and Ranjbar, M. (2019). Optimal bidding strategy of coordinated wind power and gas turbine units in real-time market using conditional value at risk. Int. Trans. Electr. Energy Syst. 29 (1), 2645. doi:10.1002/etep.2645

CrossRef Full Text | Google Scholar

Silva, A., Lf, A., and Jg, C. (2022). Reliability evaluation of generating systems considering aging processes. Electr. Power Syst. Res. 202, 107589. in press. doi:10.1016/j.epsr.2021.107589

CrossRef Full Text | Google Scholar

Sinishaw, Y., Bantyirga, B., and Abebe, K. (2021). Analysis of smart grid technology application for power distribution system reliability enhancement: A case study on bahir dar power distribution. Sci. Afr. 12, e00840. in press. doi:10.1016/j.sciaf.2021.e00840

CrossRef Full Text | Google Scholar

Slota, M., Root, C., Devine, K., Madduri, K., and Rajamanickam, S. (2020). Scalable, multi-constraint, complex-objective graph partitioning. IEEE Trans. Parallel Distrib. Syst. 31 (12), 2789–2801. doi:10.1109/TPDS.2020.3002150

CrossRef Full Text | Google Scholar

Sun, B., Li, Y., Zeng, Y., Yang, T., and Dong, S. (2021). The total social cost evaluation of two wind and PV energy development modes: A study on henan of China. Energy Rep. 7, 6565–6580. doi:10.1016/j.egyr.2021.09.121

CrossRef Full Text | Google Scholar

Sun, B., Yu, Y., and Qin, C. (2017). Should China focus on the distributed development of wind and solar photovoltaic power generation? A comparative study. Appl. Energy 185, 421–439. doi:10.1016/j.apenergy.2016.11.004

CrossRef Full Text | Google Scholar

Tapetado, P., and Usaola, J. (2019). Capacity credits of wind and solar generation: The Spanish case. Renew. Energy 143, 164–175. doi:10.1016/j.renene.2019.04.139

CrossRef Full Text | Google Scholar

Tawfeek, S., Ahmed, H., and Hasan, S. (2018). Analytical and particle swarm optimization algorithms for optimal allocation of four different distributed generation types in radial distribution networks. Energy Procedia 153, 86–94. doi:10.1016/j.egypro.2018.10.030

CrossRef Full Text | Google Scholar

Wangdee, W. (2018). Deterministic-based power grid planning enhancement using system well-being analysis. J. Mod. Power Syst. Clean. Energy 6 (3), 438–448. doi:10.1007/s40565-018-0390-8

CrossRef Full Text | Google Scholar

Xu, Y., Liu, C., Wang, Z., Mo, K., Schneider, K. P., Tuffner, F. K., et al. (2017). DGs for service restoration to critical loads in a secondary network. IEEE Trans. Smart Grid 10 (1), 435–447. doi:10.1109/TSG.2017.2743158

CrossRef Full Text | Google Scholar

Yao, S., Wang, P., and Zhao, T. (2018). Transportable energy storage for more resilient distribution systems with multiple microgrids. IEEE Trans. Smart Grid 10 (3), 3331–3341. doi:10.1109/TSG.2018.2824820

CrossRef Full Text | Google Scholar

Yu, Y., and Ma, S. (2014). 1-Neighbour knapsack problem and prospective greedy algorithm of intentional islanding in active distribution network. Sci. China Technol. Sci. 57, 568–577. doi:10.1007/s11431-014-5460-1

CrossRef Full Text | Google Scholar

Zeng, B., Sun, B., Wei, X., Gong, D., Zhao, D., and Singh, C. (2020). Capacity value estimation of plug-in electric vehicle parking-lots in urban power systems: A physical-social coupling perspective. Appl. Energy 265, 114809. in press. doi:10.1016/j.apenergy.2020.114809

CrossRef Full Text | Google Scholar

Zhang, N., Kang, C., Kirschen, S., and Xia, Q. (2013). Rigorous model for evaluating wind power capacity credit. IET Renew. Power Gener. 7 (5), 504–513. doi:10.1049/iet-rpg.2012.0037

CrossRef Full Text | Google Scholar

Zhao, J., Zhang, M., Yu, H., Ji, H., Song, G, Lia, P., et al. (2019). An islanding partition method of active distribution networks based on chance-constrained programming. Appl. Energy 242, 78–91. doi:10.1016/j.apenergy.2019.03.118

CrossRef Full Text | Google Scholar

Zhou, Y., Wang, C., Wu, J., Wang, J., Cheng, M., and Li, G. (2017). Optimal scheduling of aggregated thermostatically controlled loads with renewable generation in the intraday electricity market. Appl. energy 188, 456–465. doi:10.1016/j.apenergy.2016.12.008

CrossRef Full Text | Google Scholar

Zou, K., Agalgaonkar, P., Muttaqi, M., Muttaqi, K. M., and Perera, S. (2019). Distribution system restoration with renewable resources for reliability improvement under system uncertainties. IEEE Trans. Ind. Electron. 67 (10), 8438–8449. doi:10.1109/TIE.2019.2947807

CrossRef Full Text | Google Scholar

Nomenclature

Abbreviations

$C_{\mathrm{E}\mathrm{S}}$ the loss cost equivalent to 1 kWh of ES charging or discharging

$C_{\mathrm{R}}^{\max }$ the maximum electricity

$C_{t,\mathrm{b}\mathrm{u}\mathrm{y}}$ electricity purchase price between DN and superior grid at time t

$C_{t,\mathrm{s}\mathrm{e}\mathrm{l}\mathrm{l}}$ electricity-selling price between DN and the superior grid at time t

$I_{ij,\max }$ the upper limit of branch current

$I_{ij,t}$ the branch current at time t

${NE}_m^2\left(n\right)$ the nth neighborhood node of NE¹(m)

$P_{i,t}^{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}$ the active power of node i at time t

$P_{j,t}^{\mathrm{c}\mathrm{h}\mathrm{a}}$ the charging electricity with ES integration of node j at time t.

$P_{j,t}^{\mathrm{d}\mathrm{i}\mathrm{s}}$ the discharging electricity with ES integration of node j at time t.

$P_{ji,t}$ the active branch composed of nodes i and j at time t

$P_{t,\mathrm{b}\mathrm{u}\mathrm{y}}^{\mathrm{t}\mathrm{r}\mathrm{a}}$ the power purchased by the DN operator from the superior grid at time t

$P_{t,\mathrm{s}\mathrm{e}\mathrm{l}\mathrm{l}}^{\mathrm{t}\mathrm{r}\mathrm{a}}$ the power sold by the DN operator from the superior grid at time t

$Q_{i,t}^{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}$ the reactive load demand of customer node i at time t

$Q_{ji,t}$ the reactive power of branch composed of nodes i and j at time t

$R_{ij}$ the resistance of the branch composed of nodes i and j

$U_{i,\max }$ the upper voltage limits of node i

$U_{i,\min }$ the lower voltage limits of node i

$U_{i,t}$ the voltage of node i at time t

$t_{k,j}^{\mathrm{o}\mathrm{p}}$ the normal operation time of the kth component under the jth sampling

$t_{k,j}^{\mathrm{r}\mathrm{e}\mathrm{p}}$ the fault duration time of the kth component under the jth sampling

$t_k^{\mathrm{o}\mathrm{p}}$ the normal operation time of the kth component

$t_k^{\mathrm{r}\mathrm{e}\mathrm{p}}$ the fault duration time of the kth component

$u_{i,t}^{\mathrm{c}\mathrm{h}\mathrm{a}}$ The variable is 1 when the ES of node i is charging at time t, otherwise it is 0

$u_{i,t}^{\mathrm{d}\mathrm{i}\mathrm{s}}$ the variable is 1 when the ES of node i is charging at time t, otherwise it is 0

$x_{ij}$ the reactance of branch composed of nodes i and j

$\overline{y}$ the mean value of samples

${NE}_m^2$ the neighborhood node set of the mth node NE¹(m) in NE¹

${\Lambda }_a$ the set of DG integration nodes in the ath island

${\beta }_{ij}$ variable set to 1 if node i is the parent of node j and to 0 otherwise.

${\mu }_k$ the repair rate of the kth component

${\omega }_{ij}$ variable set to 1 if the line between node i and node j is connected and to 0 if the line is disconnected

${\Omega }_a$ the island set corresponding to the ath island

∆L the load demand increase

A the number of island

B_i,t the benefit value of node i at time t

B_V the total load benefits in set V

Cap_con the capacity of the conventional unit in the power system

Cap_PV the capacity of the PV in the power system

Cap_wind the capacity of wind turbine in the power system

CC credible capacity

C_t the loss cost of the network

DG distributed generation

DN LDC distribution network load duration curve

E the branches set of DN

EENS expected energy not served

E_i,t the remaining electricity of node i at time t

ELCC equivalent load-carrying capacity

E_max the upper limits of ES-remaining electricity

E_min the lower limits of ES-remaining electricity

E_NS the EENS index under fault state during evaluation period T

ES energy storage

G the updated undirected graph of the distribution network

H(i) the set of branches associated with node i

L₀ the load level of the system

MIP maximum island partition

n the number of samples

N the set of load nodes in DN

N₀ the number of nodes in NE¹

NB_i the neighborhood node set of node i

NE¹ the neighborhood node set of set V

NE¹(m) the mth node in NE¹

N_ES the number of ES integration nodes

OPR optimal island rectification

Parameter

PG_i,t DG power output of node i at time t

PR_i the priority of load node i

PV photovoltaic equipment

P_V the total active power of all nodes in set V

r_CC the capacity credit rate

Re( ) the reliability level

s_a the compressed node of the ath island

SMCS sequential Monte Carlo simulation

SQ_k the sequence operation state vector of the kth component

ST_i a 0–1 variable denoting whether node i can be restored under the fault state

st_i,t a 0–1 variable denoting whether node i can be restored at time t

T the evaluation period

t₁ the initial time of the fault

t₂ the end time of the fault

V island set

Va¹(m) the value ratio of node NE¹(m)

Va_m(n) the combination value ratio of neighborhood node NE¹(m) and prospective neighborhood node NE_m²(n)

α the confidence level

β_max relevant parameters of upper limits of charging and discharging

β_min relevant parameters of lower limits of charging and discharging

λ_k the failure rate of the kth component

σ the standard deviation of samples

$P{G}_{i,t}^{\max }$ the maximum DG power output of node i at time t

$Var\left(\overline{y}\right)$ the variance of samples

$\chi$ the variance coefficients

$\varphi$ the probability at the upper quantile in the normal distribution