Multi-objective optimal scheduling of charging stations based on deep reinforcement learning

With the green-oriented transition of energy, electric vehicles (EVs) are being developed rapidly to replace fuel vehicles. In the face of large-scale EV access to the grid, real-time and effective charging management has become a key problem. Considering the charging characteristics of different EVs, we propose a real-time scheduling framework for charging stations with an electric vehicle aggregator (EVA) as the decision-making body. However, with multiple optimization objectives, it is challenging to formulate a real-time strategy to ensure each participant’s interests. Moreover, the uncertainty of renewable energy generation and user demand makes it difficult to establish the optimization model. In this paper, we model charging scheduling as a Markov decision process (MDP) based on deep reinforcement learning (DRL) to avoid the afore-mentioned problems. With a continuous action space, the MDP model is solved by the twin delayed deep deterministic policy gradient algorithm (TD3). While ensuring the maximum benefit of the EVA, we also ensure minimal fluctuation in the microgrid exchange power. To verify the effectiveness of the proposed method, we set up two comparative experiments, using the disorder charging method and deep deterministic policy gradient (DDPG) method, respectively. The results show that the strategy obtained by TD3 is optimal, which can reduce power purchase cost by 10.9% and reduce power fluctuations by 69.4%.

1 Introduction

In recent years, the global energy structure (Tian et al., 2018; Peng et al., 2021) is transforming into clean energy (Fu et al., 2018; Rajendran et al., 2022), which provides an incentive for the development of EVs. According to research, the exhaust gas emitted by fuel vehicles is one of the main causes of global warming (Purushotham Reddy et al., 2021). Against the background of carbon neutrality (Duan, 2021), some countries have introduced relevant policies promoting EVs (Yang et al., 2020) to replace traditional fuel vehicles. A smart grid is a new type of modern grid that is stable, efficient, and economical. However, with the large-scale charging demand of EVs, the smart grid faces many challenges (Choi et al., 2017; Brenna et al., 2018), such as increasing exchange power fluctuations and degrading power quality. Therefore, the stable access of EVs to the smart grid is a key issue that must be solved.

EVs have the advantages of flexibility and adjustability due to the power battery. Taking advantage of these features, people can control the charging or discharging of EVs to realize grid stability. At present, various optimization approaches have been proposed to manage the charge or discharge of EVs, that is, convex-optimum methods, programming-based methods (Hu et al., 2013; Ordoudis et al., 2019), and heuristic-based methods (Megantoro et al., 2017; Li et al., 2019). Shi et al. (2017) optimized the day-ahead scheduling of EVs by Lyapunov optimization, which can realize real-time management but relies on precise objective functions. Based on mixed integer programming, Koufakis et al. (2020) minimized EV charging costs and load fluctuations, which also relies on accurate predictions of environmental information. Combining genetic algorithms and dynamic programming algorithms, Ravey et al. (2012) formulated energy management strategies for EVs, but the method shows poor robustness. Therefore, the uncertainty of renewable energy generation and user demand makes it difficult to establish the optimization model based on traditional methods.

There are two ways to deal with the uncertainty in charge and discharge management of EVs. One is to predict uncertain values before optimization through physical models or probability distributions (Kabir et al., 2020). However, this method is only suitable for scenarios with low accuracy requirements, such as day-ahead prediction. Another solution benefits from the development of DRL (Franaois-Lavet et al., 2018). DRL includes two types of methods, model-based and model-free. Model-free DRL (Wan et al., 2019) has attracted great attention in this field due to the following two advantages: 1) neural network as a function approximator (Zhang et al., 2021) can extract more data features based on data history. The data features are input into the policy network to learn the optimal policy. This process does not rely on the predicted values. 2) This method makes decisions according to the current state, so it is suitable for real-time decision scenarios with high precision requirements.

Based on DRL, Chis et al. (2017) and Li et al. (2022) combined neural networks and DRL, which effectively reduced the charging cost. Zhao and Lee (2022) and Su et al. (2020) proposed a dynamic pricing mechanism based on DRL to minimize charging costs. Abdalrahman and Zhuang (2022) improved user satisfaction by maximizing the quality of the charging service. Qian et al. (2022) proposed a pricing mechanism based on multi-agent reinforcement learning and reduced the cost of charging stations. However, the afore-mentioned works in the literature only consider the benefits of the demand side while ignoring the benefits of the supply side. In the electricity market, EVA (Okur et al., 2020; Kong et al., 2021) plays an important role in integrating demand, participating in bidding, and purchasing resources. Qiu et al. (2020) and Tao et al. (2022) studied the efficient pricing problem from the perspective of EVA. Considering the operation cost of microgrids and the purchasing cost of EVs, Zhaoxia et al. (2019) reduced overall costs through day-ahead optimized scheduling. Kandpal and Verma (2021) and Mahmud et al. (2019) considered the microgrid benefits by minimizing grid peaks, but they still used inefficient traditional methods. As an important part of the electricity market, the role of EVA participating in electricity ancillary services (Yang et al., 2017; Yuan et al., 2021) is neglected. Meanwhile, there are few works in the literature (Wang and Cui, 2020; Zhou et al., 2021) that consider the behavioral characteristics of different cars such as taxis, buses, and private cars. Most of them are about path planning or pricing issues.

To sum up, at present, EV charging scheduling based on DRL is used and the following problems still exist: 1) As one of the most effective mechanisms to integrate the market, the benefits and the electric ancillary service functions of EVA are neglected. 2) When applying DRL, it is difficult to learn a strategy that can balance multiple optimization objectives. 3) In the charging model, the characteristics of different types of EVs are not taken into account. Aiming to fill the research gaps, this paper proposes a real-time charging scheduling framework with EVA as the decision-making body. We build a scheduling model with continuous action space, which is solved based on TD3. Our optimization objectives are set to minimize the cost of EVA and minimize the fluctuations of microgrids. The main contributions of this paper are as follows:

• A real-time charging scheduling framework with EVA as a decision-making body is proposed. Considering multiple optimization objectives, the EVA cost and the microgrid exchange power fluctuations are minimized.

• Considering the charging characteristics of taxis and private cars, the charging scheduling process is established as an MDP model. EVA is an agent that interacts with the environment to maximize accumulated rewards.

• The MDP model is solved by TD3. Compared with the disorder charging method and DDPG, the TD3 achieves lower EVA costs and lower microgrid fluctuations.

The remainder of this paper is organized as follows. In Section 2, we introduce the system model, constraints, and optimization objectives in detail. In Section 3, we introduce the main elements of the design of the MDP model. In Section 4, we briefly introduce the TD3 method. In Section 5, we perform groups of experiments and analyze the results. Finally, in Section 6, we conclude this paper.

2 System model

2.1 System framework

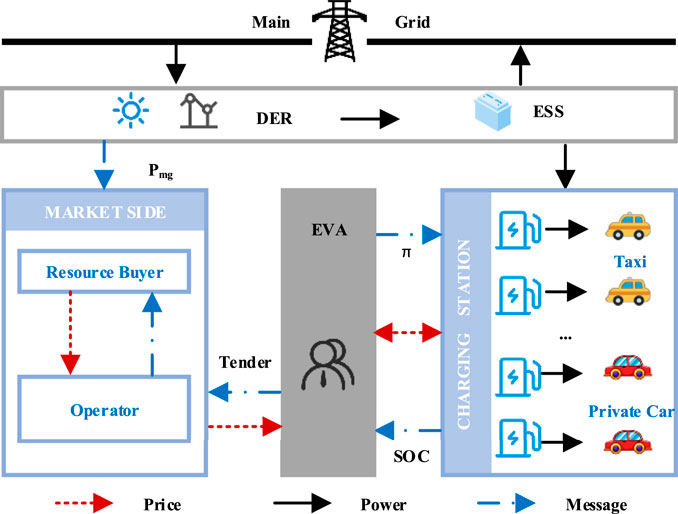
In this paper, the framework of charging station scheduling is shown in Figure 1. First, the power supplier microgrid is composed of DER, an energy storage system (ESS), a micro-power dispatching center (MDC), and a load. Microgrid stability is affected by output power P_DER and load power P_L. DER is a electricity-generating unit, and its excess energy is stored or sent to the main grid. We assume that P_DER includes two types of output sources, photovoltaic power and wind force. EVA mainly sends charging strategy π to the charging station according to the physical information and economic information. The physical information includes the microgrid exchange power and the state of charge (SOC) of the charging stations. Economic information is determined by the market side, including resource buyers and market operators. The market operator acts as a middleman, matching tenders and resource buyers. On the market side, EVA minimizes the purchase cost of resources. On the grid side, EVA minimizes power fluctuations.

FIGURE 1

FIGURE 1. Scheduling framework of the EV charging station in a microgrid.

When the EVs arrive at the station, EVA will obtain their maximum charging power and charging demand. According to the day-ahead exchange power P_mg and the electricity price from the market side, EVA formulates the charging strategy π. According to the strategy, DER supplies energy for EVs in charging stations. Meanwhile, the charging station feeds back the SOC to EVA, which provides a reference for its decision-making.

2.2 Constraint model

This paper considers two types of vehicles, taxis and private cars. We divided the 24-h scheduling time into T time steps, that is, t = {1, 2, ⋯T}. One time step is denoted as τ.

At time t, the number of taxis and private cars is X_t and Y_t, respectively. When updating the number of cars at the next moment, we need to remove the cars that meet the charging expectations and add new cars. We assumed that the number of newly added taxis and private cars at each moment is M_t and N_t, and the proportion with fast-charging demand is σ₁ and σ₂. In the scheduling process, the charging or discharging power is limited to the following two conditions.

2.2.1 Power limitations of charging station

$P_t^{\min }\le P_t\le P_t^{\max }(1)$

where $P_t^{\min }$ and $P_t^{\max }$ are the maximum and minimum charging power of the charging station at time t. The positive P_t represents the charging power, while the negative P_t represents the discharging power of EVs. $P_t^{\min }$ and $P_t^{\max }$ are limited by two conditions, which can be expressed as

$P_t^{\min }=\max \left\{-P_t^{\mathit{station}},-{\eta }_{\mathit{dis}}\frac{S_t^{\mathit{SOC}}c}{\tau }\right\}(2)$

$P_t^{\max }=\min \left\{P_t^{\mathit{station}},\frac{1}{{\eta }_{\mathit{dis}}}\cdot \frac{\left(X_t+Y_t-S_t^{\mathit{SOC}}\right)c}{\tau }\right\}(3)$

where the first term represents the maximum or minimum power of the charging station during time τ. The second term represents the remaining available capacity of the battery. $P_t^{\mathit{station}}$ is the maximum charging power of the charging station. c, η_dis, and η_ch are the battery capacity, discharging efficiency, and charging efficiency, respectively. $S_t^{\mathit{SOC}}$ is the sum SOC of the EVs at time t.

2.2.2 State of charge limitations of electric vehicles

$0\le S_t^{\mathit{SOC}}\le {\mathrm{X}}_t+{\mathrm{Y}}_t(4)$

$\left|S_t^{\mathit{SOC}}-E_t^{\mathit{SOC}}\right|\le \delta (5)$

where δ is the allowable difference factor between the SOC expected value $E_t^{\mathit{SOC}}$ and the actual value $S_t^{\mathit{SOC}}$. Eq. 4 expresses the total SOC range of EVs. Eq. 5 is the judgment condition for whether EVs reach the expected values.

At time t, the maximum power of the charging station is

$P_t^{\mathit{station}}=P_t^{f,\max }+P_t^{s,\max }(6)$

where $P_t^{f,\max }$ and $P_t^{s,\max }$ are the maximum power for fast charging and slow charging at time t.

$P_t^{f,\max }=P_f\cdot n_t^{\mathit{fast}}\cdot \tau (7)$

$P_t^{s,\max }=P_s\cdot n_t^{\mathit{slow}}\cdot \tau (8)$

where P_f and P_s are a fast power and slow power of the charging station, which are fixed values. $n_t^{\mathit{fast}}$ and $n_t^{\mathit{slow}}$ are the number of fast-charging vehicles and the slow-charging vehicles at time t, respectively.

For the total power P_t allocated to the charging station, the power distributed to each fast-charging and slow-charging vehicle is

$P_{t,i}^{\mathit{fast}}=\frac{P_t^{f,\max }}{P_t^{\mathit{station}}\cdot n_t^{\mathit{fast}}}\cdot P_t(9)$

$P_{t,i}^{\mathit{slow}}=\frac{P_t^{s,\max }}{P_t^{\mathit{station}}\cdot n_t^{\mathit{slow}}}\cdot P_t(10)$

The SOC update satisfies the following equation:

$S_{t+1,i}^{\mathit{SOC}}=\left\{\begin{array}{c}\hfill S_{t,i}^{\mathit{SOC}}+\frac{1}{{\eta }_{\mathit{dis}}}\cdot \frac{P_{t,i}\cdot \tau }{\mathrm{c}},P_{t,k,i}\le 0\hfill \\ \hfill S_{t,i}^{\mathit{SOC}}+{\eta }_{ch}\cdot \frac{P_{t,i}\cdot \tau }{\mathrm{c}},P_{t,k,i}>0\hfill \end{array}\right.(11)$

Note that for each time step, we need to remove the cars that have reached the expected values and add the new cars. Therefore, the total value of SOC at the next moment can be expressed as

$S_{t+1}^{\mathit{SOC}}=\sum S_{t+1,i}^{\mathit{SOC}}+\sum S_{t+1,i}^{\mathit{SOC,M+N}}-\sum S_{t,i}^{\mathit{ESOC}}(12)$

where the first item is the sum of the updated SOC of all vehicles at time t. The second term is the sum of the SOC of newly added M_t+1 + N_t+1 vehicles at time t + 1. The third term is the sum of the SOC that reaches the expected values at time t.

2.3 Optimization objective

According to the system model in Section 2.1, we set two optimization objectives, namely, maximizing the benefits of EVA and minimizing power fluctuations.

Assuming that the service cost of EVA is a fixed value, reducing the power purchase cost can maximize EVA’s profit. The first optimization objective can be set as follows:

$\mathrm{m}\mathrm{i}\mathrm{n}{F}_a={\sum }_{t=1}^T{\lambda }_t{P}_t\cdot \tau (13)$

where λ_t is the time-of-use electricity price at time t. P_t is limited by Eq. 1.

We define F_P as the exchange power fluctuation of the microgrid. The second optimization objective can be set as follows:

$\mathrm{m}\mathrm{i}\mathrm{n}{F}_P=\sum _{t=1}^T\left(P_{MG,t}-\frac{1}{T}\sum _{t=1}^T{\widehat{P}}_{MG,t}\right)(14)$

where P_MG,t is the microgrid real-time power including EVs at time t. ${\widehat{P}}_{MG,t}$ is the day-ahead forecasting value of the microgrid power without EVs at time t.

$P_{MG,t}=P_{EV,t}+P_{L,t}-P_{\mathit{DER,t}}(15)$

${\widehat{P}}_{MG,t}={\widehat{P}}_{L,t}-{\widehat{P}}_{\mathit{DER,t}}(16)$

where P_EV,t, P_L,t, and P_DER,t are the real-time values of EVs, other loads, and DER, respectively. ${\widehat{P}}_{L,t}$ and ${\widehat{P}}_{\mathit{DER,t}}$ are the day-head predicted values of other loads and DER, respectively.

3 Model design of Markov decision process

3.1 Markov decision process

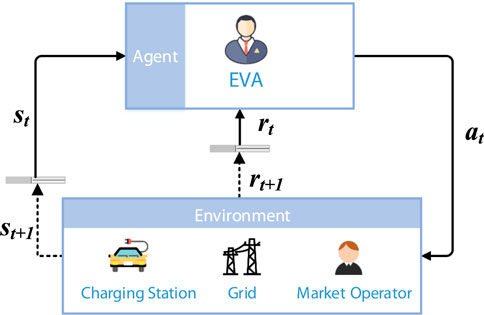
For reinforcement learning (RL), the agent and environment are two main interacting objects, as shown in Figure 2. The agent perceives the state and reward from the environment to learn and make decisions, while the environment updates the state and reward at the next moment based on the current action from the agent. The purpose of this process is to learn a strategy that satisfies the optimization objectives through continuous interactions.

FIGURE 2

FIGURE 2. RL structure for charging scheduling.

The learning process of RL is usually described by MDP. We set the EVA as an agent and information such as price and power as the environment. At time t, the agent interacts with the environment to give a policy π and implement action a_t within the action range. The environment reacts to a_t and updates the state s_t+1. The state transition function P determines the update from s_t to s_t+1. The environment feedbacks to the agent a reward $r_t=R\left(s_t,a_t\right)$ to guide the agent to achieve the optimization objectives. To express this process, we need four elements, state, action, state transition function, and reward function, which are denoted as a tuple $⟨\mathrm{S},\mathrm{A},\mathrm{P},\mathrm{R}⟩$.

3.2 Model design

State space S is the set of state values. S is a description of the current situation and should not contain redundant information. Therefore, in this paper, s_t ∈ S contains four variables, time-of-use electricity price, the sum of charging station SOC, the output power of DER, and the power of other loads, denoted as $s_t=\left\{{\lambda }_t,S_t^{\mathit{SOC}},P_{\mathit{DER,t}},P_{L,t}\right\}$.

Action space A is the set of action values. We set the total charging or discharging power of the charging station as the action. Limited by the maximum and minimum charging power, a_t can be expressed as

$a_t=\left\{\begin{array}{cc}\hfill P_t^{\min }\hfill & \hfill ,P_t<P_t^{\min }\hfill \\ \hfill P_t^{\max }\hfill & \hfill ,P_t>P_t^{\max }\hfill \\ \hfill P_t\hfill & \hfill ,others\hfill \end{array}\right.(17)$

where $P_t^{\min }$ and $P_t^{\max }$ are determined by Eqs. 2, 3, respectively.

State transition function P is the rule for state update, denoted as

$\mathrm{P}:s_t\times a_t\to s_{t+1}(18)$

In Eq. 18, it can be seen that s_t+1 is determined by the action and state s_t. The probability of taking action a_t in state s_t is denoted as p (s_t+1|s_t, a_t).

Reward function $R\left(s_t,a_t\right)$ represents the optimization objectives of the model. In order to maximize the benefits of EVA, the reward function can be designed as

$r_{t,1}=-{\lambda }_t{a}_t\cdot \tau (19)$

At time t, in order to minimize the exchange power fluctuations of the microgrid, the reward function can be designed as

$r_{t,2}=-\left|P_{MG,t}-{\widehat{P}}_{MG,t}\right|(20)$

At time t, in order to encourage the agent to charge and satisfy the needs of users, the reward function can be designed as

$r_{t,3}=\left\{\begin{array}{cc}\hfill 1\hfill & \hfill \left|S_t^{\mathit{SOC}}-E_t^{\mathit{SOC}}\right|<\delta \hfill \\ \hfill 0\hfill & \hfill \left|S_t^{\mathit{SOC}}-E_t^{\mathit{SOC}}\right|>\delta \hfill \end{array}\right.(21)$

where $E_t^{\mathit{SOC}}$ is the sum of the expected SOC values at time t.

In order to balance these three rewards, the total reward function can be expressed as

$r_t={\beta }_1{r}_{t,1}+{\beta }_2{r}_{t,2}+{\beta }_3{r}_{t,3}(22)$

where β₁, β₂, and β₃ are the balance coefficients of three rewards, respectively.

4 Proposed approach

TD3 is a type of deterministic strategy gradient algorithm, which is a relatively advanced method. In Section 3, the action is continuously adjustable. Therefore, it is necessary to select a type of RL method with continuous action space. Compared with traditional RL methods, such as Q-learning, TD3 can handle decision problems with continuous action space and continuous state space. The training process has fast convergence speed and good stability. The following is the principle and training process of TD3.

4.1 TD3 algorithm

TD3 is an optimization method of DDPG, which is based on the actor-critic framework. Methods based on the actor-critic framework consist of critic networks and actor networks. The purpose of the actor networks is to establish a relational mapping of s_t and a_t, while the purpose of the critic networks is to evaluate this mapping relationship and output the value function Q. Its mapping relationship can be described as

$\begin{array}{c}Actor:s_t\to a_t\hfill \\ Critic:\left[s_t,a_t\right]\to Q\hfill \end{array}(23)$

DDPG uses the experience replay of Deep Q-learning (Gao and Jin, 2022), and adds two target networks, namely, the target-actor network and the target-critic network. The loss function L of the critic network is defined as

$L\left({\theta }_Q\right)=\frac{1}{M}{\sum }_{i=1}^M{\left[Q^{t\arg et}-Q\left(s_t,a_t,{\theta }_Q\right)\right]}^2(24)$

where θ_Q is the critic network parameter. M is the number of learning samples selected from the experience replay buffer. $Q_t^{t\arg et}$ is the value function of the target-critic network, which is calculated as follows:

$Q_t^{t\arg et}=r_t+\gamma Q^{\prime }\left[s_{t+1},{\mu }^{2032;}\left(s_{t+1},{\theta }_{{\mu }^{2032;}}\right),{\theta }_{Q^{2032;}}\right](25)$

where γ is the discount factor. μ′ and θ_μ′ represent the target-actor network and its parameter, respectively. Q′ and θ_Q′ represent the target-critic network and its parameter, respectively.

The current state is mapped to action by the function μ(s_t, θ_μ). The actor-network parameter is updated through the gradient back-propagation algorithm. Its loss gradient is

${\nabla }_{{\theta }_{\mu }}J\approx \frac{1}{M}\sum _{i=1}^M\left[{\nabla }_{a}Q\left(s_t,a,{\theta }_Q\right){|}_{a=\mu \left(s_t,{\theta }_{\mu }\right)}\cdot {\nabla }_{{\theta }_{\mu }}\mu \left(s_t,{\theta }_{\mu }\right)\right](26)$

where ∇ is the gradient. μ and θ_μ are the output value and parameters of the actor-network.

The target network parameters θ_Q′ and θ_μ′ can be updated by smoothing exponentials

${\theta }_{Q^{2032;}}=\tau {\theta }_Q+\left(1-\tau \right){\theta }_{Q^{2032;}}(27)$

${\theta }_{{\mu }^{2032;}}=\tau {\theta }_{\mu }+\left(1-\tau \right){\theta }_{{\mu }^{2032;}}(28)$

where τ is the update factor.

When updating the Q value of the critic network, it can be expressed as

$Q=r+\gamma \max Q\left(s_{t+1},a_{t+1}\right)(29)$

However, if the value function is estimated by maximum, the DDPG method will overestimate, which causes slow convergence and a suboptimal solution. In order to overcome these shortcomings, TD3 has been improved in the following three aspects.

First, in order to overcome the over-estimation problem, TD3 establishes two independent critic networks and two target-critic networks. The target network Q value is updated by the minimum Q value, as follows:

$Q_t^{t\arg et}=r_t+\gamma \underset{k=\mathrm{1,2}}{\min }{Q_k}^{2032;}\left[s_{t+1},{\mu }^{2032;}\left(s_{t+1},{\theta }_{{\mu }^{2032;}}\right),{\theta }_{Q_k^{2032;}}\right](30)$

where ${Q_k}^{2032;}$ and ${\theta }_{Q_k^{2032;}}$ (k = 1, 2) represent two target-critic networks and their parameters.

The loss function can be improved as

$L\left({\theta }_{Q_k}\right)=\frac{1}{M}\sum _{i=1}^M{\left[Q^{t\arg et}-Q_k\left(s_t,a_t,{\theta }_{Q_k}\right)\right]}^2,k=\mathrm{1,2}(31)$

where Q_k and ${\theta }_{Q_k}$ (k = 1, 2) represent two critic networks and their parameters, respectively.

Second, if we update the actor-network μ and critic networks Q_k in each loop, the training process will be unstable. Fixing μ and only training the Q-function can converge faster and get better results. Therefore, TD3 adds the concept of actor-network training frequency, which is less than the update frequency of the critic network. That is also the meaning of “delay.”

Finally, to avoid overfitting, TD3 adds a target-actor smoothing step. The action output by the actor-network is improved as

${\tilde{a}}_{t+1}={\mu }^{2032;}\left(s_{t+1},{\theta }_{{\mu }^{2032;}}\right)+\epsilon ,\epsilon \sim clip\left(0,\sigma ,-d,d\right),d>0(32)$

where ɛ is the noise obeying the truncated normal distribution. σ is the variance, and d is the truncated amplitude.

4.2 Training process

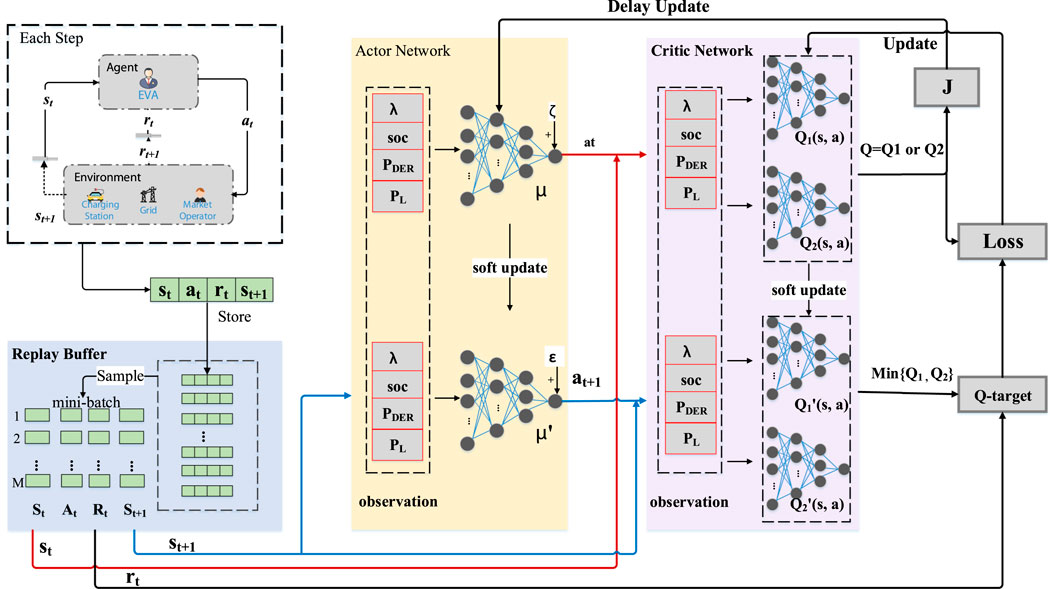
Based on TD3, the training framework for optimal scheduling of charging stations is shown in Figure 3. The detailed training steps of the agent are as follows.

FIGURE 3

FIGURE 3. Training framework of TD3.

First, as shown by the red line in Figure 3, the agent interacts with the environment to get s_t and uses the actor-network to get μ(s_t, θ_μ). To increase the exploratory effect, we add random noise to the action, which is ${\tilde{a}}_t=\mu (s_t,{\theta }_{\mu })+(1-\zeta )\cdot N(\mathrm{0,1})$. In the environment, get the next moment state s_t+1 and reward r_t. The tuple [s_t, a_t, r_t, s_t+1] is stored in the experience replay buffer for sampling. When the data in the buffer reach a certain amount, M samples for training are randomly selected.

Then, as shown by the blue line in Figure 3, the target networks get target action by Eq. 32. Through the critic networks, value functions Q₁ (s_t, a_t) and Q₂ (s_t, a_t) are calculated. Through the target-critic networks, the target value functions ${Q_1}^{2032;}(s_t,a_t)$ and ${Q_2}^{2032;}(s_t,a_t)$ are calculated. Then, the target value function $Q_t^{t\arg et}$ is obtained by Eq. 30.

Finally, as shown by three gray squares on the right in Figure 3, the critic network parameters ${\theta }_{Q_1}$ and ${\theta }_{Q_2}$, are updated, which are determined by Eq. 31. The actor-network parameter θ_μ is delay updated, which is determined by Eq. 26. Three target network parameters θ_μ′, ${\theta }_{Q_1^{2032;}}$, and ${\theta }_{Q_2^{2032;}}$, are soft updated, which are determined by Eqs 27, 28. The next training loop is continued until the reward curve converges.

Algorithm 1 outlines the process of learning the optimal policy based on TD3.

Algorithm 1. Training procedure of the TD3.

5 Experiment

5.1 Experimental settings

In this paper, we simulate charging station scheduling in a complex park during a working day. This type of park includes offices, residences, and commercial shops. The microgrid contains wind force, photovoltaic outputs, charging stations, and other household loads. The detailed parameter settings are as follows.

5.1.1 Environmental parameters

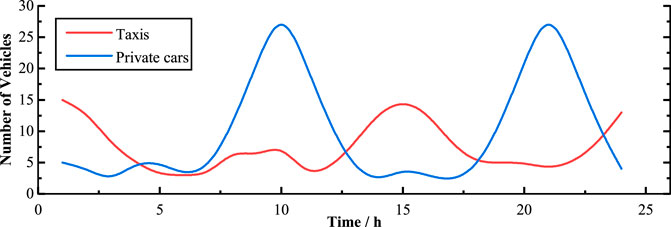
We consider two types of vehicles, taxis and private cars. Figure 4 shows the number distributions of taxis and private cars. Taxis usually use a two-shift system, with shifts at 6:00 and 18:00, respectively. Therefore, we assumed that the taxi charging peak occurs at 1:00 and 15:00. The private car charging peaks are affected by two groups of people, employees and residents. Therefore, it is assumed that the charging peaks occur at 10:00 and 21:00, respectively. The fast-charging ratios of taxis and private cars are set to σ₁ = 0.7 and σ₂ = 0.1, respectively. The initial SOC distributions of taxis and private cars are N(0.35, 1) and N(0.45, 1), respectively, and the expected SOC distributions are N(0.95, 1) and N(0.90, 1), respectively.

FIGURE 4

FIGURE 4. Number distributions of taxis and private cars.

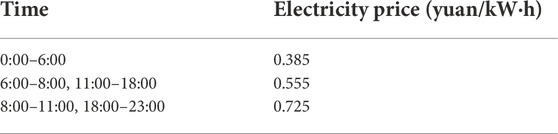
The charging station power is divided into four gears: −30, −7, +7, and +30 kw. When each vehicle leaves the charging pile, the deviation of SOC from the expected value is less than the tolerance factor δ = 0.05. The time step is set to τ = 1h and the time-of-use electricity price is listed in Table 1.

TABLE 1

TABLE 1. Time-of-use electricity price.

Figure 5 shows the day-ahead power curves that are output forecast curves (Figure 5A) and household load forecast curves (Figure 5B). Assuming that this working day is an ordinary sunny day, the photovoltaic output power reaches the peak about at 12:00, and the wind-force output power fluctuates randomly. According to Eq. 16, we can obtain the forecast curve of microgrid exchange power (Figure 5C), which shows that there are evident peaks and valleys in some periods. To rule out the possibility that the method depends on the distribution, we set the uncertain power to be ±10% of the forecast power.

FIGURE 5

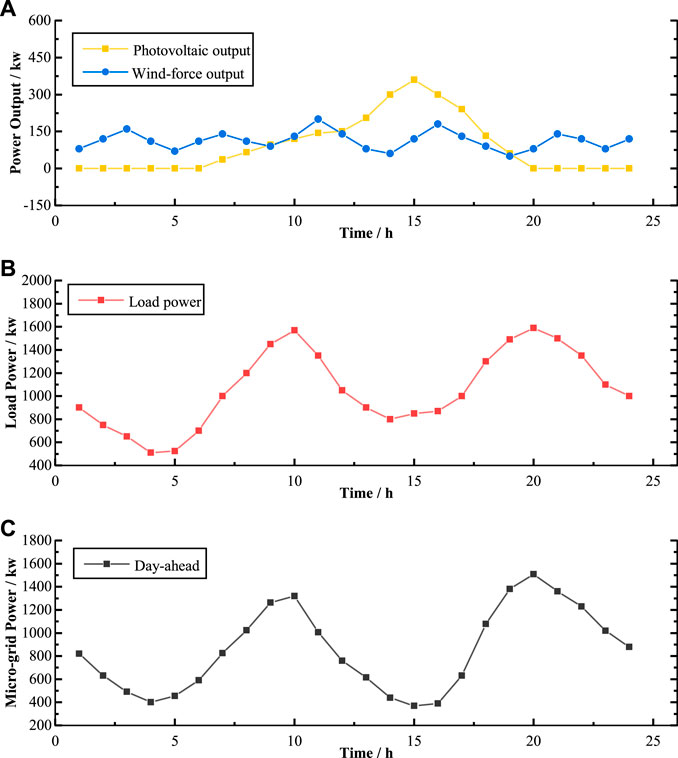
FIGURE 5. Day-ahead power curves for microgrid: (A) output power; (B) load power; (C) microgrid exchange power.

5.1.2 Algorithm settings

To evaluate the performance of the TD3, we set up two different methods, the disorder charging method and DDPG. The parameters and rule settings of these three methods are as follows:

• TD3: The detailed parameters of TD3 are shown in Table 2. In Eq. 24, we set the number M of learning samples from the experience replay buffer to 256. When updating the Q value of two critic networks, the discount factor γ set to 0.99 (Zhang et al., 2021) works best. In Eqs 27, 28, the soft update factor τ is set to 0.005. In Eq. 32, the added noise is set to ɛ ∼ clip (0.2, 1, −0.5, 0.5). For better exploration, set th initial value of greedy coefficient ς is set to zero and its increment for each episode to 0.00002. Note that when setting the reward functions, each reward is normalized by its maximum values.

• DDPG: Compared with TD3, DDPG uses one critic network and does not add noise ɛ when the actor-target network updates the action. In order to compare the performance of different algorithms, other training parameters of DDPG keep the same as that of TD3.

• Disorder charging: To provide a quantitative reference for the performance of the DRL methods, we set up a disordered charging experiment. When one EV arrives at the station, the charging station starts to continuously supply power with P_f = 30kw or P_f = 7kw until its SOC reaches the expected value.

TABLE 2

TABLE 2. Training parameters of TD3.

5.1.3 Metrics

To quantitatively evaluate the performance of the three methods, we set the following three metrics.

• Average price: ${\bar{F}}_a={\sum }_{t=1}^{24}{\lambda }_t{a}_t/{\sum }_{t=1}^{24}{a}_t$ represents the average cost of EVA in one day. The lower ${\bar{F}}_a$ is, the greater the benefits EVA can get.

• Fluctuation: $F_P={\sum }_{t=1}^{24}(P_{MG,t}-{\sum }_{t=1}^{24}{P}_{MG,t}/24)$ represents the total fluctuations of microgrid changing power in one day. The lower the F_P, the better the charging strategy is in reducing the fluctuations of the microgrid.

• Satisfaction: $\xi ={\sum }_{t=1}^{24}{a}_t/A_{\max }$, where A_max represents the maximum charging demand in one day. In order to ensure the user’s experience, we set the satisfaction coefficient ξ. The higher the ξ, the better the charging strategy performs in improving the users’ experience.

5.2 Training results

We evaluate three groups of experiment results and training processes by the three metrics in Section 5.1.3. The following are the analysis results.

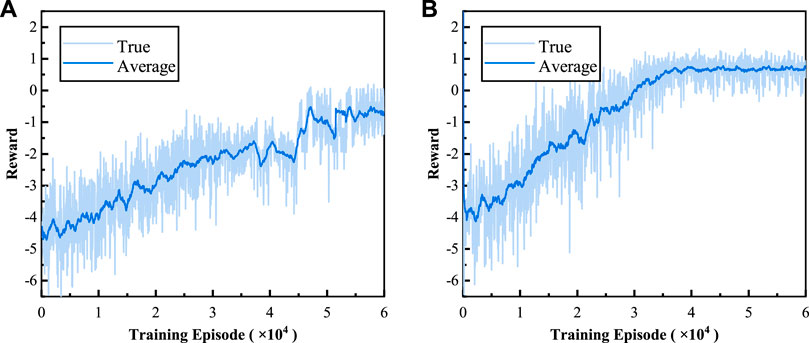
Figure 6 shows the training process of two DRL methods. To be more intuitive, we average the rewards every 30 episodes, the results of which are shown as the dark blue curve in Figure 6. It can be seen that at the beginning, the reward of both methods is low. When the reward curve tends to stabilize, it means that the agent has explored the optimal strategy. Compared with DDPG (Figure 6A), the convergence point of TD3 (Figure 6B) is 28% earlier and the reward value is 1.5 (Table 3). Therefore, TD3 has notable advantages of better stability, faster convergence, and higher reward in solving the model proposed in this paper.

FIGURE 6

FIGURE 6. Reward curves in the training process: (A) DDPG and (B) TD3.

TABLE 3

TABLE 3. Experimental results of charging strategies under different methods.

Figure 7 shows the results of charging or discharging strategies obtained by three experiments. The gray curves represent the time-of-use price, and the red columns represent the charging or discharging power in each time step. Positive values represent electricity purchased and negative values represent electricity sold by EVA. In Figure 7A, it is evident that the disorder charging method does not respond to price. Its charging strategy is to meet the maximum charging demand in each time step. In Figure 7B, the scheduling strategy obtained by DDPG is to charge less during the high-price hours and charge more during other hours. In Figure 7C, the TD3-based strategy has evident discharge behaviors during high-price hours, which indicates a more adequate response to price. From the perspective of the overall benefit, the TD3-based strategy can reduce the electricity price by 10.90% (Table 3), which performs better than DDPG.

FIGURE 7

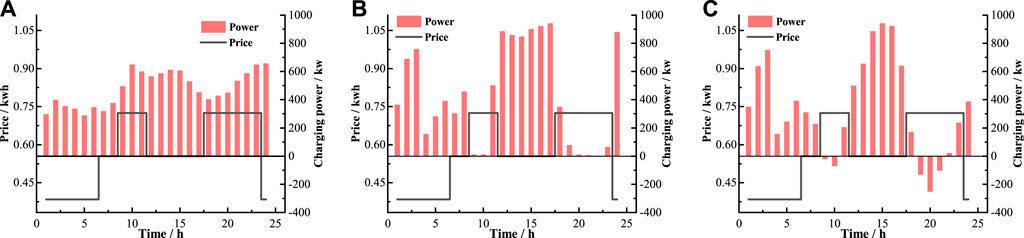
FIGURE 7. Charging or discharging strategies obtained by (A)disorder charging, (B) DDPG, and (C) TD3.

Figure 8 shows the results of the microgrid exchanging power. Compared with the day-ahead values, it is evident that the average exchanging power of all experiments increases, which is the result of balancing the charging satisfaction. As shown by the red line in Figure 8, if the charging behavior of EVs is not managed, a large number of EV loads will increase the peak-to-valley difference. In addition, compared with DDPG, the strategy obtained by TD3 can drastically reduce the power fluctuation by 69.40% (Table 3), which is almost twice that of DDPG. Note that in the hours of 3:00–7:00, there is a valley for both RL methods. Combined with Figure 7, during this low-price period, the agent sacrifices certain power fluctuations, which can not only reduce the charging cost but also improve the charging satisfaction.

FIGURE 8

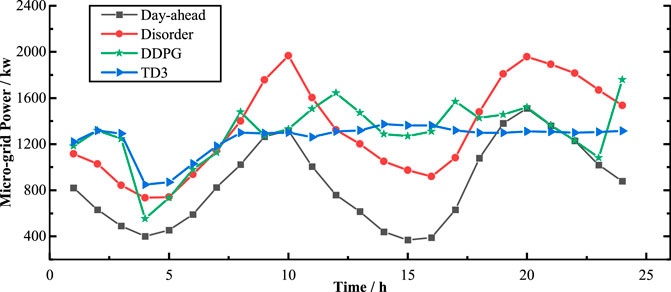
FIGURE 8. Exchange power of the microgrid in one day obtained by day-ahead prediction; disorder charging, DDPG; TD3.

Table 3 summarizes the results of the three groups of experiments. In terms of charging satisfaction, compared with the other two methods, TD3 sacrifices a certain degree of satisfaction. However, compared to DDPG’s results, it is worth sacrificing 24% satisfaction to reduce 51% cost and 84% power fluctuations. Therefore, for the charging model in this paper, the strategy based on TD3 is optimal, which can obtain the real-time scheduling strategy faster and higher overall benefits.

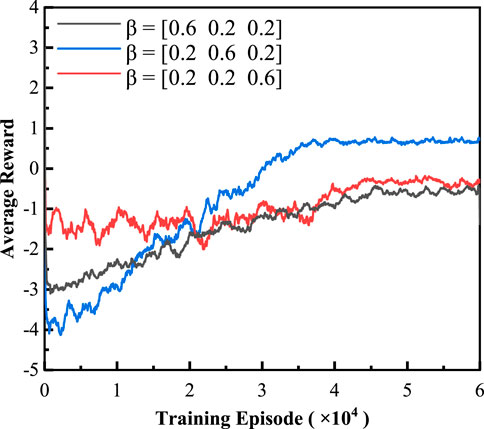
5.3 Impact of model parameters

In the training process of TD3, the balance coefficient β = [β₁, β₂, β₃] has an important influence on the exploration of optimal strategy. Figure 9 shows the training curves for three different groups of balance coefficients. In order to explore the influence on strategy formulation, experiments are conducted with β₁, β₂, β₃ as the dominant factors, respectively. From Figure 9, it can be seen that the reward dominated by β₂ is the largest. Table 4 summarizes the experiment results, from which we can see that the strategies dominated by β₁ and β₃ are two extreme cases. The former reduces costs with maximum discharging, while the latter improves satisfaction with maximum charging. On the whole, when dominated by β₂, the strategy can guarantee both low cost and low power fluctuations. Therefore, for the training in Section 5.2, the balance coefficient is set to be [0.2, 0.6, 0.2] dominated by β₂.

FIGURE 9

FIGURE 9. Training curves under different balance coefficient β based on TD3.

TABLE 4

TABLE 4. Experimental results of charging strategies under different balance coefficient β.

6 Conclusion

In the current EV charging management market, balancing the interests of each participant will be an important part in improving the market structure. Therefore, it is necessary to formulate a charging management strategy that considers the interests of each participant. Considering the participation of EVA, microgrids, and users, this paper provides a reference for solving this problem.

Based on DRL, we propose a charging scheduling framework with EVA as the decision-making body. Considering the charging characteristics of electric taxis and private cars, we formulate a charging strategy for charging stations based on TD3. Compared with the disorder charging method and DDPG, TD3 can reduce power purchase costs by 10.9% and reduce power fluctuations by 69.4% on the basis of ensuring certain user satisfaction.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

FC performed the experiment and wrote the manuscript, XL contributed to the analysis and manuscript preparation, RZ helped perform the analysis with constructive discussions, and QY contributed to the conception of the study.

Funding

This work was supported in part by the National Natural Science Foundation of China under Grant 62173268, Grant 61803295, Grant 61973247, and Grant 61673315; in part by the Major Research Plan of the National Natural Science Foundation of China under Grant 61833015; in part by the National Postdoctoral Innovative Talents Support Program of China under Grant BX20200272; in part the National Key Research and Development Program of China under Grant 2019YFB1704103; and in part by the China Postdoctoral Science Foundation under Grant 2018M643659.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdalrahman, A., and Zhuang, W. (2022). Dynamic pricing for differentiated pev charging services using deep reinforcement learning. IEEE Trans. Intell. Transp. Syst. 23, 1415–1427. doi:10.1109/tits.2020.3025832

CrossRef Full Text | Google Scholar

Brenna, M., Foiadelli, F., Soccini, A., and Volpi, L. (2018). “Charging strategies for electric vehicles with vehicle to grid implementation for photovoltaic dispatchability,” in 2018 International Conference of Electrical and Electronic Technologies for Automotive, Milan, Italy, July 09–11, 2018 (IEEE), 1–6.

CrossRef Full Text | Google Scholar

Chis, A., Lund’en, J., and Koivunen, V. (2017). Reinforcement learning-based plug-in electric vehicle charging with forecasted price. IEEE Trans. Veh. Technol. 66, 3674–3684. doi:10.1109/TVT.2016.2603536

CrossRef Full Text | Google Scholar

Choi, W., Wu, Y., Han, D., Gorman, J., Palavicino, P. C., Lee, W., et al. (2017). “Reviews on grid-connected inverter, utility-scaled battery energy storage system, and vehicle-to-grid application - challenges and opportunities,” in 2017 IEEE Transportation Electrification Conference and Expo (ITEC), Chicago, IL, June 22–24, 2017 (IEEE), 203–210.

CrossRef Full Text | Google Scholar

Duan, P. (2021). “Research on the transaction and settlement mechanism of yunnan clean energy’s participation in the west to east power transmission for the goal of “carbon peak” and “carbon neutral,” in 2021 IEEE Sustainable Power and Energy Conference (iSPEC), Nanjing, China, December 23–25, 2021 (IEEE), 1843–1850.

Google Scholar

Franaois-Lavet, V., Henderson, P., Islam, R., Bellemare, M. G., and Pineau, J. (2018). An introduction to deep reinforcement learning. Hanover, United States: Now Foundations and Trends.

Google Scholar

Fu, G., Liu, J., Liu, J., and Liu, R. (2018). “Quantitative analysis of the feasibility of realizing the transformation to clean energy for China’s energy increment by 2035,” in 2018 International Conference on Power System Technology (POWERCON), Guangzhou, China, November 06–08, 2018 (IEEE), 510–515.

Google Scholar

Gao, G., and Jin, R. (2022). “An end-to-end flow control method based on dqn,” in 2022 International Conference on Big Data, Information and Computer Network, Sanya, China, January 20–22, 2022 (IEEE), 504–507.

CrossRef Full Text | Google Scholar

Hu, W., Su, C., Chen, Z., and Bak-Jensen, B. (2013). Optimal operation of plug-in electric vehicles in power systems with high wind power penetrations. IEEE Trans. Sustain. Energy 4, 577–585. doi:10.1109/tste.2012.2229304

CrossRef Full Text | Google Scholar

Kabir, M. E., Assi, C., Tushar, M. H. K., and Yan, J. (2020). Optimal scheduling of ev charging at a solar power-based charging station. IEEE Syst. J. 14, 4221–4231. doi:10.1109/jsyst.2020.2968270

CrossRef Full Text | Google Scholar

Kandpal, B., and Verma, A. (2021). Demand peak reduction of smart buildings using feedback-based real-time scheduling of evs. IEEE Syst. J. 16, 1–12. doi:10.1109/JSYST.2021.3113977

CrossRef Full Text | Google Scholar

Kong, W., Luo, F., Jia, Y., Dong, Z. Y., and Liu, J. (2021). Benefits of home energy storage utilization: An Australian case study of demand charge practices in residential sector. IEEE Trans. Smart Grid 12, 3086–3096. doi:10.1109/tsg.2021.3054126

CrossRef Full Text | Google Scholar

Koufakis, A.-M., Rigas, E. S., Bassiliades, N., and Ramchurn, S. D. (2020). Offline and online electric vehicle charging scheduling with v2v energy transfer. IEEE Trans. Intell. Transp. Syst. 21, 2128–2138. doi:10.1109/tits.2019.2914087

CrossRef Full Text | Google Scholar

Li, H., Yang, D., Su, W., Lv, J., and Yu, X. (2019). An overall distribution particle swarm optimization mppt algorithm for photovoltaic system under partial shading. IEEE Trans. Ind. Electron. 66, 265–275. doi:10.1109/tie.2018.2829668

CrossRef Full Text | Google Scholar

Li, S., Hu, W., Cao, D., Dragicevic, T., Huang, Q., Chen, Z., et al. (2022). Electric vehicle charging management based on deep reinforcement learning. J. Mod. Power Syst. Clean Energy 10, 719–730. doi:10.35833/mpce.2020.000460

CrossRef Full Text | Google Scholar

Mahmud, K., Hossain, M. J., and Ravishankar, J. (2019). Peak-load management in commercial systems with electric vehicles. IEEE Syst. J. 13, 1872–1882. doi:10.1109/jsyst.2018.2850887

CrossRef Full Text | Google Scholar

Megantoro, P., Danang Wijaya, F., and Firmansyah, E. (2017). “Analyze and optimization of genetic algorithm implemented on maximum power point tracking technique for pv system,” in 2017 international seminar on application for technology of information and communication (iSemantic) (New Jersey, United States: IEEE), 79–84.

CrossRef Full Text | Google Scholar

Okur, O., Heijnen, P., and Lukszo, Z. (2020). “Aggregator’s business models: Challenges faced by different roles,” in 2020 IEEE PES innovative smart grid technologies europe (ISGT-Europe) (New Jersey, United States: IEEE), 484–488.

Google Scholar

Ordoudis, C., Pinson, P., and Morales, J. M. (2019). An integrated market for electricity and natural gas systems with stochastic power producers. Eur. J. Operational Res. 272, 642–654. doi:10.1016/j.ejor.2018.06.036

CrossRef Full Text | Google Scholar

Peng, L., Jinyu, X., Jiawei, W., Zhengxi, C., and Shining, Z. (2021). “Development of global wind and solar resource to cope with global climate change,” in 2021 IEEE Sustainable Power and Energy Conference (iSPEC), Nanjing, China, December 23–25, 2021 (IEEE), 986–996.

CrossRef Full Text | Google Scholar

Purushotham Reddy, M., Aneesh, A., Praneetha, K., and Vijay, S. (2021). “Global warming analysis and prediction using data science,” in 2021 Fifth International Conference on I-SMAC (IoT in Social, Mobile, Analytics and Cloud) (I-SMAC), Palladam, India, November 11–13, 2021 (IEEE), 1055–1059.

CrossRef Full Text | Google Scholar

Qian, T., Shao, C., Li, X., Wang, X., Chen, Z., and Shahidehpour, M. (2022). Multi-agent deep reinforcement learning method for ev charging station game. IEEE Trans. Power Syst. 37, 1682–1694. doi:10.1109/tpwrs.2021.3111014

CrossRef Full Text | Google Scholar

Qiu, D., Ye, Y., Papadaskalopoulos, D., and Strbac, G. (2020). A deep reinforcement learning method for pricing electric vehicles with discrete charging levels. IEEE Trans. Ind. Appl. 56, 5901–5912. doi:10.1109/tia.2020.2984614

CrossRef Full Text | Google Scholar

Rajendran, A., Jayan, P. P., Mohammed Ajlif, A., Daniel, J., Joseph, A., and Surendran, A. (2022). “Energy performance improvement in house boat tourism through clean energy route interfaced with energy efficient power conversion techniques and energy storage,” in 2022 IEEE International Conference on Power Electronics, Smart Grid, and Renewable Energy (PESGRE), Trivandrum, India, January 02–05, 2022 (IEEE), 1–7.

CrossRef Full Text | Google Scholar

Ravey, A., Roche, R., Blunier, B., and Miraoui, A. (2012). “Combined optimal sizing and energy management of hybrid electric vehicles,” in 2012 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, June 18–20, 2012 (IEEE), 1–6.

CrossRef Full Text | Google Scholar

Shi, W., Li, N., Chu, C.-C., and Gadh, R. (2017). Real-time energy management in microgrids. IEEE Trans. Smart Grid 8, 228–238. doi:10.1109/tsg.2015.2462294

CrossRef Full Text | Google Scholar

Su, Z., Lin, T., Xu, Q., Chen, N., Yu, S., and Guo, S. (2020). “An online pricing strategy of ev charging and data caching in highway service stations,” in 2020 16th International Conference on Mobility, Sensing and Networking (MSN), Tokyo, Japan, December 17–19, 2020 (IEEE), 81–85.

CrossRef Full Text | Google Scholar

Tao, Y., Qiu, J., and Lai, S. (2022). Deep reinforcement learning based bidding strategy for evas in local energy market considering information asymmetry. IEEE Trans. Ind. Inf. 18, 3831–3842. doi:10.1109/tii.2021.3116275

CrossRef Full Text | Google Scholar

Tian, Y., Yu, Z., Zhao, N., Zhu, Y., and Xia, R. (2018). “Optimized operation of multiple energy interconnection network based on energy utilization rate and global energy consumption ratio,” in 2018 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, October 20–22, 2018 (IEEE), 1–6.

CrossRef Full Text | Google Scholar

Wan, Z., Li, H., He, H., and Prokhorov, D. (2019). Model-free real-time ev charging scheduling based on deep reinforcement learning. IEEE Trans. Smart Grid 10, 5246–5257. doi:10.1109/tsg.2018.2879572

CrossRef Full Text | Google Scholar

Wang, G., and Cui, D. (2020). “Research on vehicle routing branch pricing algorithm for multi-model electric vehicles based on board testing,” in 2020 IEEE International Conference on Power, Intelligent Computing and Systems (ICPICS), Shenyang, China, July 28–30, 2020 (IEEE), 954–959.

CrossRef Full Text | Google Scholar

Yang, J., Fei, F., Xiao, M., Pang, A., Zeng, Z., Lv, L., et al. (2017). “A noval bidding strategy of electric vehicles participation in ancillary service market,” in 2017 4th International Conference on Systems and Informatics (ICSAI), Hangzhou, China, November 11–13, 2017 (IEEE), 306–311.

CrossRef Full Text | Google Scholar

Yang, Y., Zhang, B., Wang, W., Wang, M., and Peng, X. (2020). “Development pathway and practices for integration of electric vehicles and internet of energy,” in 2020 IEEE Sustainable Power and Energy Conference (iSPEC), Chengdu, China, November 23–25, 2020 (IEEE), 2128–2134.

CrossRef Full Text | Google Scholar

Yuan, H., Lai, X., Wang, Y., and Hu, J. (2021). “Reserve capacity prediction of electric vehicles for ancillary service market participation,” in 2021 IEEE 2nd China International Youth Conference on Electrical Engineering (CIYCEE), Chengdu, China, December 15–17, 2021 (IEEE), 1–7.

CrossRef Full Text | Google Scholar

Zhang, F., Yang, Q., and An, D. (2021). Cddpg: A deep-reinforcement-learning-based approach for electric vehicle charging control. IEEE Internet Things J. 8, 3075–3087. doi:10.1109/jiot.2020.3015204

CrossRef Full Text | Google Scholar

Zhao, Z., and Lee, C. K. M. (2022). Dynamic pricing for ev charging stations: A deep reinforcement learning approach. IEEE Trans. Transp. Electrific. 8, 2456–2468. doi:10.1109/tte.2021.3139674

CrossRef Full Text | Google Scholar

Zhaoxia, X., Hui, L., Tianli, Z., and Huaimin, L. (2019). “Day-ahead optimal scheduling strategy of microgrid with evs charging station,” in 2019 IEEE 10th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Xi'an, China, June 03–06, 2019 (IEEE), 774–780.

CrossRef Full Text | Google Scholar

Zhou, J., Zhao, Y., Li, Y., Kong, J., Yang, C., and Tian, Z. (2021). “A heterogeneous network for electric vehicle charging station communication,” in 2021 6th International Conference on Power and Renewable Energy (ICPRE), Shanghai, China, September 17–20, 2021 (IEEE), 1204–1208.

CrossRef Full Text | Google Scholar