- 1CNNC Key Laboratory on Nuclear Reactor Thermal Hydraulics Technology, Nuclear Power Institute of China, Chengdu, China
- 2Department of Engineering Physics, Tsinghua University, Beijing, China
- 3Key Laboratory of Energy Thermal Conversion and Control of Ministry of Education, School of Energy and Environment, Southeast University, Nanjing, China
For the special phenomena of heat transfer deterioration or enhancement in supercritical fluid heat transfer, existing research still presents inconsistent opinions. In this study, we perform an analysis of the property changes, and present new understandings for pseudo-boiling theory. More importantly, essential differences between subcritical boiling and supercritical pseudo-boiling are highlighted; the critical factors being thermodynamic instability and stability. For isothermal heating cases, pseudo film boiling can be regarded as an extension of near-critical boiling. Moreover, pseudo nucleate boiling only appears in non-isothermal heating cases and is strongly dependent on the heater geometry, materials, etc. A coupled level-set and volume-of-fluid method is used to simulate the near-critical film boiling of carbon dioxide at pressures of 7.0 and 7.37 MPa. In comparison, supercritical cases at a pressure of 7.5 MPa are the natural convections of single-phase fluid with variable physical properties. The numerical results indicate the similar motions of low-density fluids in subcritical and supercritical cases. All results are consistent with prior experiments, providing a better understanding of the special features of supercritical fluid heat transfer.
1 Introduction
Fourth-generation nuclear energy systems are safer and more economical, and their use has gradually spread worldwide. Among different reactor designs, system simplification and the realization of a higher core outlet temperature is easier in gas-cooled reactors. Recently, supercritical carbon dioxide cooled reactors have aroused widespread attention because of advantages in efficiency, small size, and weight (Ahn et al., 2015). These advantages are due to the peculiar physicochemical properties of supercritical fluids (SCF), especially in the pseudo-critical region (Brun et al., 2017). However, special heat transfer mechanisms have also been found, which pose numerous risks to the system (Duffey and Pioro, 2005) and should be carefully studied. Similar problems exist in supercritical water reactors.
In the vicinity of the critical point, SCFs are very compressible and dense. For such fluids in heated enclosures, the rapid establishment of thermal equilibration, observed in microgravity experiments, cannot be explained by convection and conduction (Shen and Zhang, 2013). Onuki et al. (1990) (Boukari et al., 1990; Zappoli et al., 1990) studied dominant thermo-acoustic heating (piston effect) and successfully explained microgravity experiments through numerical models. However, for most industrial applications of SCF heat transfer, systems are maintained at a constant pressure using a pressurizer. In this condition, expansion of the thermal boundary layer cannot cause adiabatic compression of bulk materials, unlike a moving piston. Meanwhile, unlike the study of the piston effect at small temperature differences (dozens of milli Kelvins), fluid states are usually much removed from the critical point. These factors together make the piston effect negligible.
Therefore, buoyancy driven convection, including natural convection and mixed convection, is still the key driver of SCF heat transfer. Large-scale variations of SCF properties within the pseudo-critical region make the transfer mechanism complex, indicated by various experimental studies (Swenson et al., 1965; Li et al., 2010; Jiang et al., 2013). For heat transfer of SCFs flowing inside channels, Pioro and Duffey (2005) (Duffey and Pioro, 2005) reviewed more than 450 experimental papers on supercritical water and supercritical carbon dioxide spanning from the 1950s to the 2000s. The results verify that three different heat transfer modes dominate (Mokry et al., 2010): normal heat transfer, improved heat transfer, and deteriorated heat transfer. These modes are mainly influenced by the pressure, pipe diameter, mass flow rate, heat flux, bulk temperature, and flow direction. Similar phenomena are also observed in other SCFs, for example, methane (Gu et al., 2013) and kerosene (Fu et al., 2017). For natural convection of SCFs, Knapp and Sabersky (Knapp and Sabersky, 1966) designed an experiment employing horizontal wires heated in supercritical carbon dioxide. In the experiment, three general types of flow modes were observed: laminar flow, oscillation flow, and bubble-like flow, which are similar to subcritical pool boiling. Since then, many studies (Goldstein and Aung, 1968; Nishkawa and Ito, 1969; Abadzic and Goldstein, 1970; Neumann and Hahne, 1980) have attempted to repeat Knapp’s work, and it was finally determined that the last two modes only appear in experiments that heat thin, low thermal diffusivity wires (Hahne and Neumann, 1981).
From a theoretical perspective, the mechanisms for improved heat transfer and deteriorated heat transfer are still controversial. According to observations of bubble-like structures and flow noise such as subcritical boiling, some studies (Ackerman, 1970; Banuti and Hannemann, 2014; Nasuti and Pizzarelli, 2020; Xu et al., 2020) proposed a pseudo-boiling theory and likened the improved heat transfer to nuclear boiling, and the deteriorated heat transfer to film boiling. Another theory focused on the buoyancy and flow acceleration effects caused by changes in the properties (McEligot et al., 1970; Petukhov et al., 1972; Hiroaki et al., 1973; Liu et al., 2017; Xu et al., 2017). This theory considers the force on near-wall fluids and explains experiment results very well. Nevertheless, the two theories have limitations. Existing research still presents inconsistent results, especially regarding the onset of heat transfer deterioration. For the pseudo-boiling theory, differences between the subcritical gas-liquid transition and pseudo-critical phenomena should be carefully considered. For the buoyancy and flow acceleration theory, effects of peculiar properties on the boundary layer are important and difficult to elucidate, requiring further studies.
Many researchers have carried out both experimental and theoretical studies on SCF heat transfer, particularly on flow and heat transfer in tubes. However, the existing research still yields inconsistent results due to complex turbulence flows. In contrast, it is much simpler to conduct visual experiments on, and to analyze the mechanism in pool heating cases; rarely reported in existing SCF studies. Moreover, basic analyses of the property distortions, especially comparisons of the subcritical gas-liquid transition, can also provide important information. Therefore, in the present study, the similarities of, and differences between the subcritical gas-liquid transition and pseudo-critical phenomena are studied using theoretical analyses and numerical simulations. A coupled level-set and volume-of-fluid method is used to analyze bubble growth in the film boiling of carbon dioxide near its critical point. For cases above the critical point, the natural convection of single-phase fluid with variable properties is considered. Through comparisons of these cases, the pseudo-boiling heat transfer mechanism in supercritical fluids has been improved.
2 Analysis of heat transfer characteristics of supercritical fluid in pool heating cases
The original pseudo-boiling theory was advanced by experimental observations, and can partly be proved by comparing gas-liquid transitions and pseudo-critical transitions, especially similarities in property changes. However, more importantly, the discrepancies in thermodynamic stabilities between these transitions lead to essential differences; thus, the original pseudo-boiling theory must be modified.
2.1 Similarities between the subcritical gas-liquid transition and the pseudo-critical transition
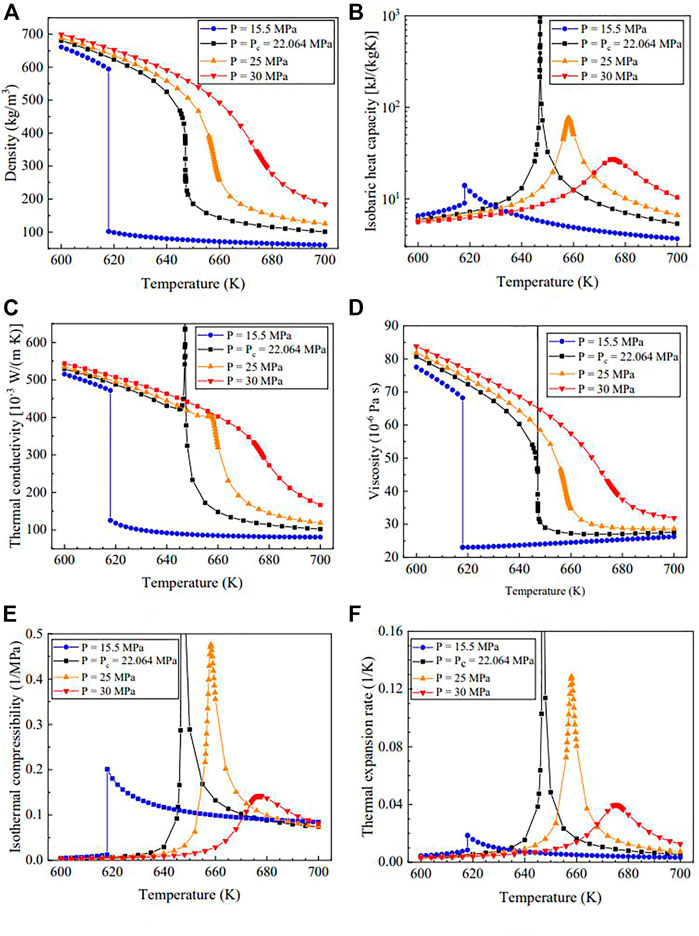
Taking water as an example, Figure 1 displays several properties at different pressures, including the density ρ, isobaric heat capacity
Similar to the stepwise change during the subcritical gas-liquid transition, the fluid density changes dramatically in the pseudo-critical region. At a constant pressure of
For the isobaric heat capacity
The isothermal compressibility,
The changes in the thermal conductivity,
In the supercritical region, the maximum of the isobaric specific heat,
These phenomena are also present in other fluids, indicating the correlation between the subcritical gas-liquid transition and the pseudo-critical transition. Meanwhile, inelastic X-ray scattering experiments (Gorelli et al., 2006; Simeoni et al., 2010; Fomin et al., 2015) confirm the transitions between liquid-like and gas-like structures in SCFs, which are well reproduced by molecular dynamics simulations. Many studies (Ha et al., 2018; Yoon et al., 2019; Maxim et al., 2020) have examined structure-property correlations and have proposed the theory “supercritical gas-liquid coexistence” on a micro level. For different fluids in different states, intermolecular attraction and repulsion leads to different macro behaviors.
2.2 Differences between the subcritical gas-liquid transition and the pseudo-critical transition
Although many similarities between the two phenomena are presented above, the subcritical gas-liquid transition is still fundamentally different from the pseudo-critical transition (Liu et al., 2022). In the subcritical gas-liquid transition, phase separation occurs between gas and liquid phases and surface tension plays an important role in boiling. However, in the whole supercritical region, the two phases are indistinguishable, and phase separation does not occur. These differences can be explained by the thermodynamic stability theory and different heat transfer mechanisms.
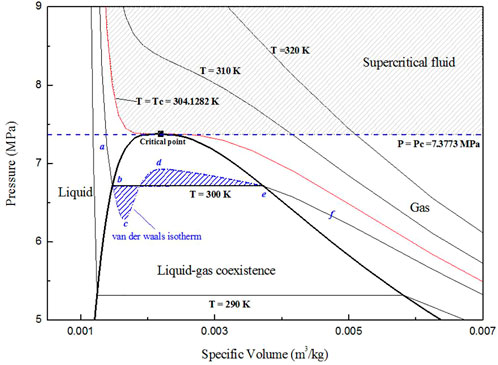
According to the well-known van der Waals model, the isotherm is represented by “abcdef” in Figure 2. For cd,
In the subcritical pool boiling case, with heating from the bottom, the temperature of the heated wall is higher than the saturated temperature. At this condition, fluid near the wall is superheated. However, most of the superheated liquid cannot transform into gas as the formation of bubbles is conditional and random. The appearance of the gas phase in superheated liquid originates from density fluctuations caused by random movement of molecules. As illustrated in Figure 3A, density fluctuations cause a pressure increase,
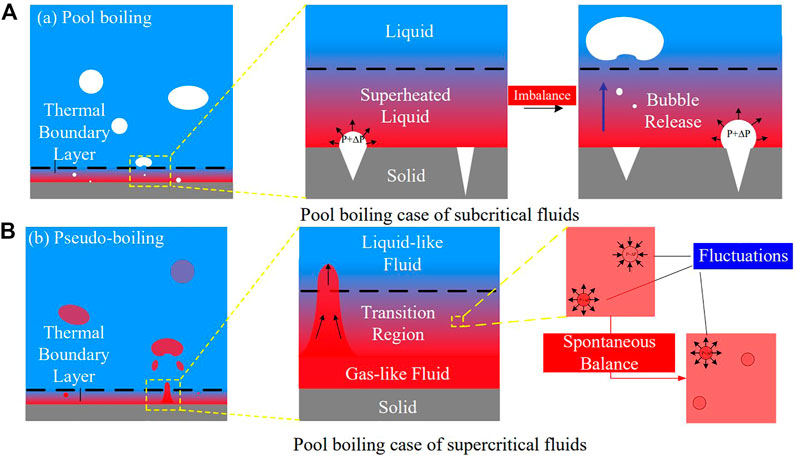
FIGURE 3. Different heat transfer mechanisms of the (A) subcritical gas-liquid transition and (B) pseudo-critical transition.
The pseudo-boiling case is referred to as the subcritical boiling case, where the bulk temperature is less than the pseudo-critical temperature,
Subcritical gas-liquid transition depends on two key parameters: temperature and nucleation sites. Bubble formation is a stochastic process, dominated by density fluctuations and thermodynamic instability. Further, different modes of bubble formation and movement lead to different boiling modes, including nucleate boiling, transition boiling, and film boiling. The pseudo-critical transition depends on the temperature, and gas-like fluid formation is a deterministic process, although the movements of gas-like fluids are still stochastic. Different modes of gas-like fluid formation and movement also cause different pseudo-boiling modes. According to the prior similarity analyses, the pseudo-boiling modes are similar to the boiling modes. Natural convection induced by buoyancy, with a large density difference, is the common feature.
2.3 Mathematical description of hydraulic instability
For a typical subcritical horizontal film boiling case, a layer of vapor fully covers the heated wall and a layer of liquid is present above the vapor layer. The temperature of the heated wall is constant and higher than the saturation temperature. Due to density differences under gravity, the liquid-vapor interface is unstable, which is called Rayleigh-Taylor instability. Meanwhile, evaporation of the liquid and the generation of fresh vapor cause changes at the gas-liquid interface.
According to Taylor’s theory (Taylor, 1950), the interface disturbance can be expressed through first-order perturbation analysis using the following equation:
The growth coefficient,
Therefore, the interface disturbance is divided into several sub-disturbances with a particular wavelength
For the horizontal film boiling with no forced convection, the irrotational flow kinematic equation, which yields the relations between wave number, gravity, surface tension, and the fluid properties, can be simplified to the following equation (Berenson, 1961):
If the vapor velocity,
According to the previous analysis, the larger the value of
As shown in Eq. 5, the value of
However, the surface tension,
3 Numerical methods and models
To prove the prior theories, several numerical simulations are performed for both the subcritical and supercritical fluids. This section aims to demonstrate the numerical methods and models.
3.1 Horizontal film boiling of subcritical fluids
3.1.1 Macro-scale model
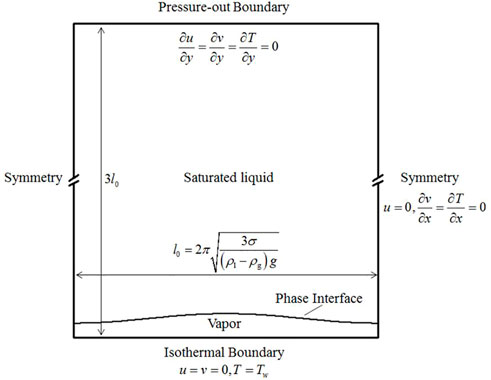
For the subcritical cases, the computational domain is a rectangular region. The domain width is the most dangerous wavelength,
In the initial condition, the liquid temperature is set as the saturated temperature. The gas-liquid interface is initialized as the original disturbance, which satisfies
Meanwhile, the vapor temperature increases linearly from the interface to the bottom, along the negative
3.1.2 Numerical methods
In order to simulate horizontal film boiling, the coupled level-set and volume-of-fluid method in FLUENT 17.2 is used to capture and track the interface. The continuum surface force model (CSF) (Brackbill et al., 1992) is used to consider the effect of surface tension in the momentum equation. As the fluid velocity is small, these cases only consider the laminar model. The governing equations for these models can be found in the help manual of Fluent.
The evaporation model is presented by Sun et al. (2012), and is developed specially for film boiling. In this model, heat transfer in the saturated liquid is ignored. Therefore, the thermal conductivity of the saturated liquid,
The mass transfer from the gas to liquid,
Finally, through the used defined functions (UDFs) of FLUENT,
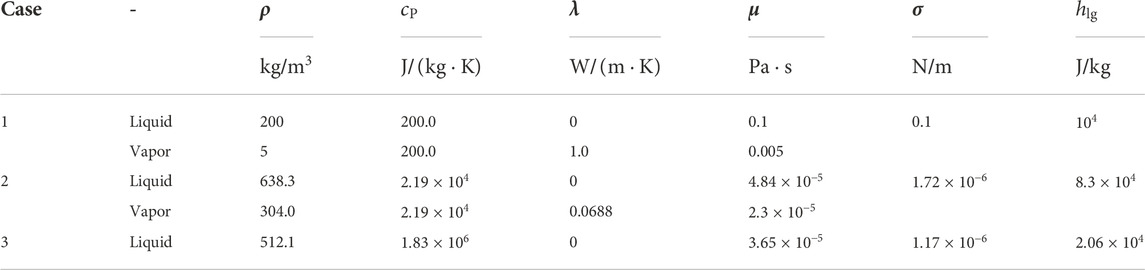
The numerical simulations of the cases are shown in Table 1 and the properties of the saturated liquid and vapor are listed in Table 2.
3.1.3 Grid independence tests
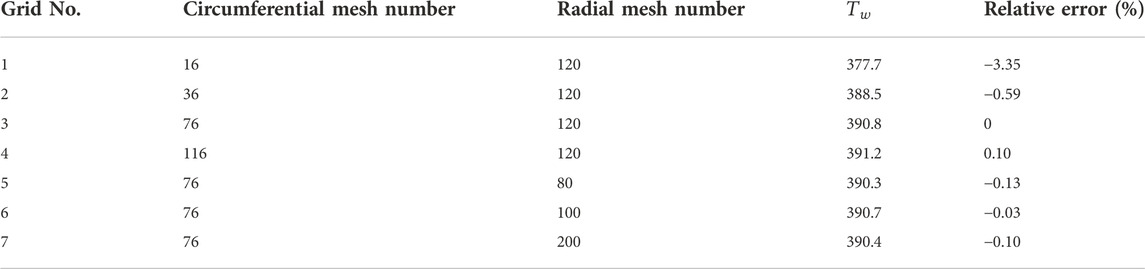
To obtain grid-independent results, three different grid systems of
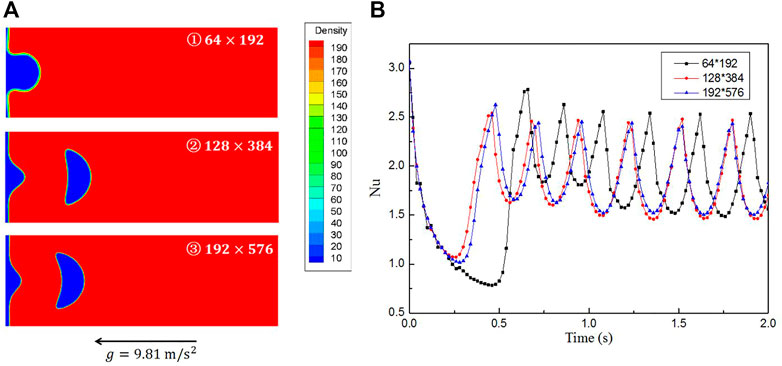
FIGURE 5. Results for three grid systems. (A) Bubble shapes at
As a verification, the results are compared with Klimenko’s analyses (dashed line in Figure 5B). In Case 1, the space- and time-averaged Nusselt number is 1.70, whereas it is 1.91 according to Klimenko’s correlation. The difference between them is 10% and thus the results are comparable and consistent with the prior work.
3.2 Pseudo-boiling of supercritical fluids
3.2.1 Macro-scale model
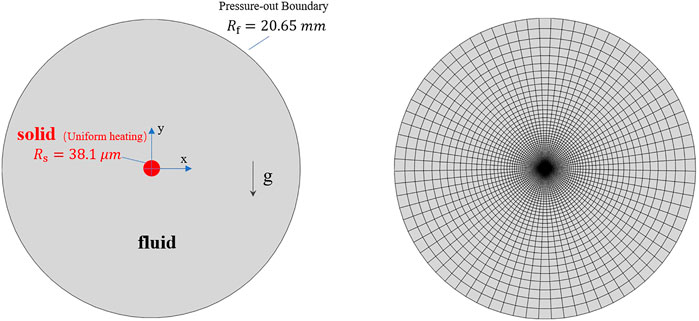
In the pseudo-boiling cases, the bulk temperature and the heating wall temperature are below and above the pseudo-critical temperature,
In the model, a uniformly heated wire is present in the center, and the outer boundary is free. The computational domain is large enough so as to not affect the flow field near the wire. The radius of the wire and the domain are 38.1
3.2.2 Numerical methods
According to the statement in Section 2, supercritical fluids are always homogeneous with no phase transition. However, property changes with temperature in the pseudo-critical region, especially the density change, are not linear. The density can be doubled within a small temperature range, and the density change is certainly not small. Therefore, distinct from normal, natural convection simulations of single-phase fluids, the two main assumptions that the well-known Boussinesq approximation relied on are no longer valid in pseudo-boiling cases. It is thus necessary to solve the Navier-Stokes equations directly, with variable properties.
The change of the carbon dioxide properties with pressure is ignored, and only the effect of temperature is considered. The properties are described by a piecewise-linear profile consisting of 50 data points given by REFPROP. In the region where physical properties change dramatically, the temperature interval between adjacent data points is small. Similar to the subcritical boiling cases, only the laminar model is considered.
3.2.3 Independence tests
The independence tests study the effects of the number of circumferential and radial meshes and time steps. As shown in Table 3, the
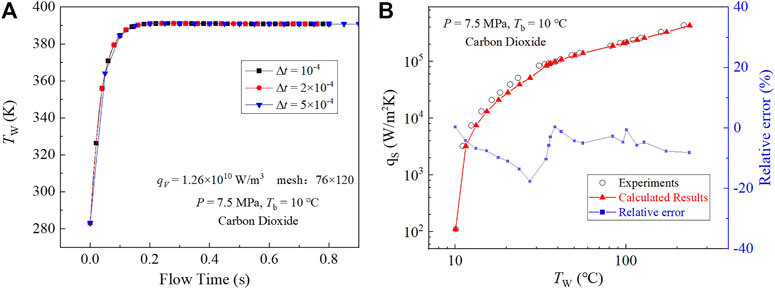
FIGURE 7. Independence tests and verifications. (A) Time step independence tests. (B) Comparisons with the experiments (Rousselet et al., 2013).
As a verification, the results are compared with Rousselt’s experiments (dots in Figure 7B). For the 22 calculated conditions, the maximum relative difference of the wall temperature is approximately 18% and the mean relative difference is only 6%. Therefore, the model used in this section is reliable.
4 Results and discussions
4.1 Results of horizontal film boiling cases
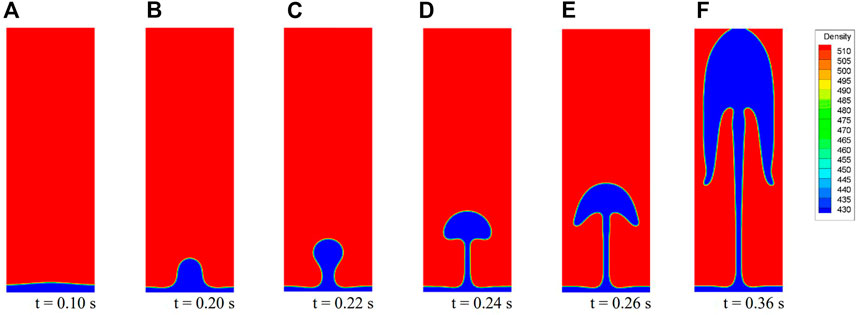
Figure 8 presents six typical bubble shapes during the bubble release process for Case 2. For saturated carbon dioxide at 7 MPa, when the overheat temperature is high enough, the generated gas gathers into a stable film and film boiling occurs. With a given initial interface, the bubble formed at the center rises under the effect of buoyancy. The neck of the bubble becomes thinner until detachment. After detaching, the bubble continues to rise and leaves a packet at the detachment point (Figure 8C). This packet is pulled back into the gas film under the effect of surface tension. Further, the packet is finally absorbed and becomes a disturbance that propagates to both sides (Figure 8D). Meanwhile, the shape of the rising bubble constantly changes. As shown in Figures 8E,F, new bubble release processes occur at the original antinodes. If the flow field is undisturbed, this cycle is periodic. These results are consistent with experimental observations (Figure 9A). The photos are reproduced with permission from Abadzic and Goldstein (1970).

FIGURE 9. Film boiling experimental results for carbon dioxide at different cases. (A) 80 K overheat; (B) 110 K overheat; (C) 400 K overheat.
In this process, the overheat condition provides the necessary energy for bubble formation and affects the frequency of bubble detachment. Specifically, when the overheat temperature is low, the whole gas film may form a bubble and the bubble then detaches from the wall. At this time, the wall is no longer covered by the vapor, and the boiling mode is nucleate boiling. The surface tension effect tends to generate a “smooth” interface as the surface energy decreases. According to Eq. 4, a larger value of
When approaching the critical point, the differences between the two phases, in terms of latent heat and surface tension decrease rapidly. In Case 3, for saturated carbon dioxide at 7.37 MPa, the interface (Figure 10) is a slender column rather than individual bubbles as seen in Case 2, although the overheat temperature in the two cases are identical. At this condition, vapor formation becomes easier and numerous vapors are generated at a moderate overheat temperature. The slender vapor column becomes taller and accumulates most of the vapor at the top. Upon disturbance, the top of the vapor column may break into many small bubbles (Figure 9B). In this context, the numerical result is too idealistic to observe.
If the vapor is produced faster, the vapor columns may converge to form a vapor sheet, which has been verified by experiment (Figure 9C).
4.2 Results of the pseudo-boiling cases
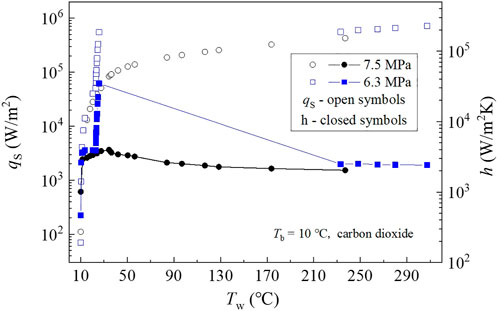
Figure 11 compares the surface heat flux,
When the bulk is liquid-like, the heat transfer curve,
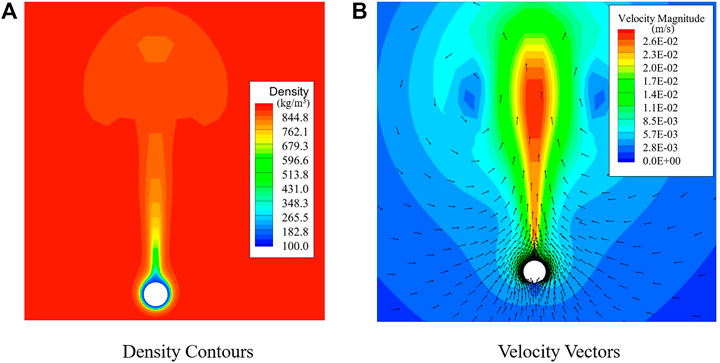
Figure 12 presents the density and velocity contours of the fully-developed pseudo-boiling case. The surface heat flux
The density profile displays a three-layer structure: the gas-like fluid layer, the transition layer, and the liquid-like fluid layer. Owing to the hydrodynamic instability, a number of initial disturbances appear in the transition layer and develop into the thermal plumes.
Thermal plumes are the key and are similar to bubbles in the subcritical cases. A typical plume exhibits a mushroom-like structure, consisting of a central rising column with vortexes on both sides. In the growth process, the upper high-density fluids are pushed away by the plume and flow downward along the sides. Some of the high-density fluid flows into the bottom low-density layer and is then heated, finally rising along the central column. The plumes may collide and merge with one another. The plumes cool as they rise, and their shapes change constantly. Specifically, the vertexes on both sides of the plumes are easily broken away, while the generated disturbances further affect the flow field.
4.3 Comparison of the pseudo-boiling and boiling cases
Thermal plumes in pseudo-boiling cases act like bubbles and vapor columns, and the near-wall low-density fluid layer is similar to the vapor film. Significant similarities exist between pseudo-boiling cases and film boiling cases, especially for the near-critical film boiling cases (Figure 10). However, in supercritical conditions, phase interfaces are non-existent, and the surface tension,
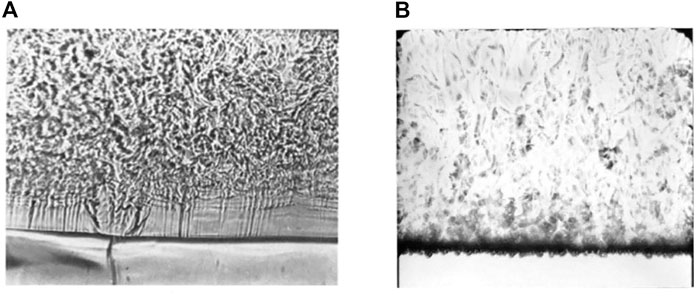
FIGURE 13. Pseudo-boiling experiments on a wire. (A) Pseudo film boiling (B) Pseudo nucleate boiling.
Heat transfer in these two cases is enhanced by convection as the boundary layers are disturbed by the rising vapor or gas-like fluids. Certainly, the degree of heat transfer enhancement is much lower than for nucleate boiling. The low-density, near-wall fluid layer severely limits heat transfer. In applications, film boiling is regarded as the cause of heat transfer deterioration. It is desirable to avoid the transition from nucleate boiling to film boiling, which is called boiling crisis.
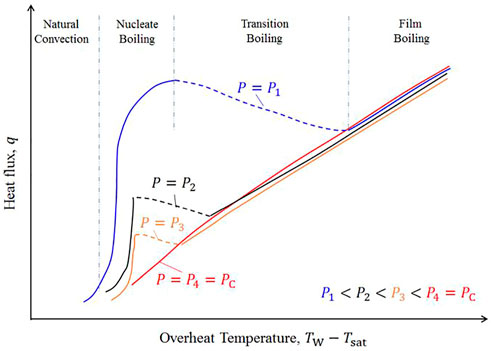
Many experiments have verified that heat fluxes when nucleate boiling occurs are reduced as the critical point is approached, and film boiling occurs more readily (Figure 14) (Hall and Jackson, 1978). The nucleate boiling and transition boiling areas in the boiling curve shrink, while the film boiling area expands. In this context, if only these isothermal heating cases are considered, pseudo film boiling can be regarded as an extension of near-critical boiling.
In subcritical boiling, an isothermal heating wall may lead to different boiling modes, which also depend on the heat flux, the number of vaporized cores, etc. However, according to the above analyses, pseudo film boiling is the only likelihood for an isothermal heating wall in pseudo-boiling cases. In order to prevent the formation of a low-density fluid layer, a heating wall with an inhomogeneous temperature profile is required.
Prior experiments have proved pseudo nucleate boiling, which is called bubble-like flow, and corresponds to a considerable increase in the heat transfer coefficient (Figure 13B). Pseudo nucleate boiling in the horizontal heating cases is only observed when the heaters are very fine wires with low thermal diffusion coefficients, for example, a nichrome wire with diameter of 0.1 mm (Knapp and Sabersky, 1966). Theoretically, a material with a low thermal diffusion coefficient is more likely to have an inhomogeneous surface temperature. Bubble-like structures are generated and released from hotspots. The hotspots are then covered and cooled by the high-density and low-temperature bulk. Nevertheless, the explanation provided in this paper is not insufficient. More experiments with wires of different diameters and materials are required to provide further evidence for our theory.
5 Conclusion
This paper theoretically analyses the similarities and differences between the subcritical gas-liquid transition and the pseudocritical transition. The heat transfer characteristics in the subcritical gas-liquid transition and the pseudocritical transition are compared through theory and numerical simulations.
Property changes during the subcritical phase transition and the pseudocritical transition are similar, leading to similar heat transfer characteristics. The similarities are the result of the hydraulic instability of the low-density bulk under the effects of gravity. However, thermodynamic stability prevents the phase separation of supercritical fluids. Pseudocritical transition only depends on the temperature; the formation of low-density bulk in supercritical cases is a deterministic process. On the contrary, vapor formation in subcritical cases is a stochastic process which relies on the initial nucleation sites.
The random distribution of nucleation sites means that the heating wall may not necessarily be completely covered by the low-density fluid during boiling. For an isothermal heating wall, different boiling modes may appear in subcritical cases, whereas only pseudo film boiling is observed in supercritical cases. For isothermal heating cases, pseudo-boiling cases can be regarded as an extension of near-critical boiling. However, pseudo nucleate boiling may appear in non-isothermal cases, which strongly depends on the heater geometry, materials, etc.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
ML: software, methodology, writing-original draft; SL: methodology; DX: analysis; SH: methodology, supervision, YH: conceptualization, funding acquisition, supervision.
Funding
This work was supported by the National Natural Science Foundation of China (Grant No. U1867218) and the Nuclear Power Technology Innovation Center in the National Defense Science and Technology Industry of China.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abadzic, E., and Goldstein, R. J. (1970). Film boiling and free convection heat transfer to carbon dioxide near the critical state. Int. J. Heat Mass Transf. 13 (7), 1163–1175. doi:10.1016/0017-9310(70)90006-2
Ackerman, J. (1970). Pseudoboiling heat transfer to supercritical pressure water in smooth and ribbed tubes. J. Heat. Transf. 92 (3), 490–497. doi:10.1115/1.3449698
Ahn, Y., Bae, S. J., Kim, M., Cho, S. K., Baik, S., Lee, J. I., et al. (2015). Review of supercritical CO2 power cycle technology and current status of research and development. Nucl. Eng. Technol. 47 (6), 647–661. doi:10.1016/j.net.2015.06.009
Banuti, D. T., and Hannemann, K. (2014). “Supercritical pseudo-boiling and its relevance for transcritical injection,” in 50th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Cleveland, OH, July 28-30, 2014.
Berenson, P. J. (1961). Film-boiling heat transfer from a horizontal surface. J. Heat Transf. 83 (3), 351–356. doi:10.1115/1.3682280
Boukari, H., Shaumeyer, J. N., Briggs, M. E., and Gammon, R. W. (1990). Critical speeding up in pure fluids. Phys. Rev. A . Coll. Park. 41 (4), 2260–2263. doi:10.1103/physreva.41.2260
Brackbill, J. U., Kothe, D. B., and Zemach, C. (1992). A continuum method for modeling surface tension. J. Comput. Phys. 100 (2), 335–354. doi:10.1016/0021-9991(92)90240-y
Brun, K., Friedman, P., and Dennis, R. (2017). Fundamentals and applications of supercritical carbon dioxide (sCO2) based power cycles. Sawston, United Kingdom: Woodhead publishing.
Cardy, J. (1996). Scaling and renormalization in statistical physics. NewYork: Cambridge University Press.
Duffey, R. B., and Pioro, I. L. (2005). Experimental heat transfer of supercritical carbon dioxide flowing inside channels (survey). Nucl. Eng. Des. 235 (8), 913–924. doi:10.1016/j.nucengdes.2004.11.011
Fomin, Y. D., Ryzhov, V., Tsiok, E., and Brazhkin, V. (2015). Dynamical crossover line in supercritical water. Sci. Rep. 5, 14234. doi:10.1038/srep14234
Fu, Y., Huang, H., Wen, J., Xu, G., and Zhao, W. (2017). Experimental investigation on convective heat transfer of supercritical RP-3 in vertical miniature tubes with various diameters. Int. J. Heat Mass Transf. 112, 814–824. doi:10.1016/j.ijheatmasstransfer.2017.05.008
Goldstein, R. J., and Aung, W. (1968). Heat transfer by free convection from a horizontal wire to carbon dioxide in the critical region. J. Heat Transf. 90 (1), 51–55. doi:10.1115/1.3597459
Gorelli, F., Santoro, M., Scopigno, T., Krisch, M., and Ruocco, G. (2006). Liquidlike behavior of supercritical fluids. Phys. Rev. Lett. 97 (24), 245702. doi:10.1103/PhysRevLett.97.245702
Gu, H., Li, H., Wang, H., and Luo, Y. (2013). Experimental investigation on convective heat transfer from a horizontal miniature tube to methane at supercritical pressures. Appl. Therm. Eng. 58 (1-2), 490–498. doi:10.1016/j.applthermaleng.2013.04.049
Ha, M. Y., Yoon, T. J., Tlusty, T., Jho, Y., and Lee, W. B. (2018). Widom delta of supercritical gas–liquid coexistence. J. Phys. Chem. Lett. 9 (7), 1734–1738. doi:10.1021/acs.jpclett.8b00430
Hahne, E., and Neumann, R. (1981). Boiling-like phenomena in free-convection heat transfer at supercritical pressures. Warme- Stoffubertragung 15 (3), 171–180. doi:10.1007/BF01376829
Hall, W. B., and Jackson, J. D. (1978). Heat transfer near the critical point. Adv. Heat. Transf. 7, 1–86. doi:10.1016/S0065-2717(08)70016-9
Hiroaki, T., Ayao, T., Masaru, H., and Nuchi, N. (1973). Effects of buoyancy and of acceleration owing to thermal expansion on forced turbulent convection in vertical circular tubes—Criteria of the effects, velocity and temperature profiles, and reverse transition from turbulent to laminar flow. Int. J. Heat Mass Transf. 16 (6), 1267–1288. doi:10.1016/0017-9310(73)90135-x
Jiang, P., Liu, B., Zhao, C., and Luo, F. (2013). Convection heat transfer of supercritical pressure carbon dioxide in a vertical micro tube from transition to turbulent flow regime. Int. J. heat mass Transf. 56 (1-2), 741–749. doi:10.1016/j.ijheatmasstransfer.2012.08.038
Kadanoff, L. P., Götzes, W., Hamblen, D., Hecht, R., Kane, J., Palciauskas, V. V., et al. (1967). Static phenomena near critical points: Theory and experiment. Rev. Mod. Phys. 39 (2), 395–431. doi:10.1103/RevModPhys.39.395
Knapp, K. K., and Sabersky, R. H. (1966). Free convection heat transfer to carbon dioxide near the critical point. Int. J. Heat Mass Transf. 9 (1), 41–51. doi:10.1016/0017-9310(66)90055-x
Li, Z., Jiang, P., Zhao, C., and Zhang, Y. (2010). Experimental investigation of convection heat transfer of CO2 at supercritical pressures in a vertical circular tube. Exp. Therm. fluid Sci. 34 (8), 1162–1171. doi:10.1016/j.expthermflusci.2010.04.005
Liu, M., Tang, J., Liu, S., Xi, D., Min, L., Zang, J., et al. (2022). Modified landau model for fluids: A rethink of pseudoboiling theory for supercritical fluids. J. Supercrit. Fluids 183, 105554. doi:10.1016/j.supflu.2022.105554
Liu, S., Huang, Y., Liu, G., Wang, J., and Leung, L. K. (2017). Improvement of buoyancy and acceleration parameters for forced and mixed convective heat transfer to supercritical fluids flowing in vertical tubes. Int. J. Heat Mass Transf. 106, 1144–1156. doi:10.1016/j.ijheatmasstransfer.2016.10.093
Maxim, F., Karalis, K., Boillat, P., Banuti, D. T., Marquez Damian, J. I., Niceno, B., et al. (2020). Thermodynamics and dynamics of supercritical water pseudo-boiling. Adv. Sci. (Weinh). 8, 2002312. doi:10.1002/advs.202002312
McEligot, D., Coon, C., and Perkins, H. (1970). Relaminarization in tubes. Int. J. Heat Mass Transf. 13 (2), 431–433. doi:10.1016/0017-9310(70)90118-3
Mokry, S., Pioro, I., Kirillov, P., and Gospodinov, Y. (2010). Supercritical-water heat transfer in a vertical bare tube. Nucl. Eng. Des. 240 (3), 568–576. doi:10.1016/j.nucengdes.2009.09.003
Nasuti, F., and Pizzarelli, M. (2020). Pseudo-boiling and heat transfer deterioration while heating supercritical liquid rocket engine propellants. J. Supercrit. Fluids 168, 105066. doi:10.1016/j.supflu.2020.105066
Neumann, R. J., and Hahne, E. W. (1980). Free convective heat transfer to supercritical carbon dioxide. Int. J. Heat Mass Transf. 23 (12), 1643–1652. doi:10.1016/0017-9310(80)90223-9
Nishkawa, K., and Ito, T. (1969). An analysis of free-convective heat transfer from an isothermal vertical plate to supercritical fluids. Int. J. Heat Mass Transf. 12 (11), 1449–1463. doi:10.1016/0017-9310(69)90027-1
Onuki, A., Hao, H., and Ferrell, R. A. (1990). Fast adiabatic equilibration in a single-component fluid near the liquid-vapor critical point. Phys. Rev. A . Coll. Park. 41 (4), 2256–2259. doi:10.1103/physreva.41.2256
Petukhov, B., Protopopov, V., and Silin, V. (1972). Experimental investigation of worsened heat-transfer conditions with the turbulent flow of carbon dioxide at supercritical pressure. High. Temp. 10 (2), 304–310.
Pioro, I. L., and Duffey, R. B. (2005). Experimental heat transfer in supercritical water flowing inside channels (survey). Nucl. Eng. Des. 235 (22), 2407–2430. doi:10.1016/j.nucengdes.2005.05.034
Rousselet, Y., Warrier, G. R., and Dhir, V. K. (2013). Natural convection from horizontal cylinders at near-critical pressures—part I: Experimental study. J. Heat Transf. 135 (2). doi:10.1115/1.4007672
Shen, B., and Zhang, P. (2013). An overview of heat transfer near the liquid–gas critical point under the influence of the piston effect: Phenomena and theory. Int. J. Therm. Sci. 71, 1–19. doi:10.1016/j.ijthermalsci.2013.04.010
Simeoni, G., Bryk, T., Gorelli, F., Krisch, M., Ruocco, G., Santoro, M., et al. (2010). The Widom line as the crossover between liquid-like and gas-like behaviour in supercritical fluids. Nat. Phys. 6 (7), 503–507. doi:10.1038/nphys1683
Sun, D., Xu, J., and Wang, L. (2012). A vapor-liquid phase change model for two-phase boiling and condensation. J. Xi'an Jiaot. Univ. 46 (7), 7–11.
Swenson, H., Carver, J., and Kakarala, C. d. (1965). Heat transfer to supercritical water in smooth-bore tubes. J. Heat Transf. 87 (4), 477–483. doi:10.1115/1.3689139
Taylor, G. I. (1950). “The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. I,” in Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, Taylor, Geoffrey, March 1950.
Wilson, K. G. (1971). Renormalization group and critical phenomena. I. Renormalization group and the kadanoff scaling picture. Phys. Rev. B 4 (9), 3174–3183. doi:10.1103/PhysRevB.4.3174
Xu, J., Zhang, H., Zhu, B., and Xie, J. (2020). Critical supercritical-boiling-number to determine the onset of heat transfer deterioration for supercritical fluids. Sol. Energy 195, 27–36. doi:10.1016/j.solener.2019.11.036
Xu, R.-N., Luo, F., and Jiang, P.-X. (2017). Buoyancy effects on turbulent heat transfer of supercritical CO2 in a vertical mini-tube based on continuous wall temperature measurements. Int. J. heat mass Transf. 110, 576–586. doi:10.1016/j.ijheatmasstransfer.2017.03.063
Yoon, T. J., Ha, M. Y., Lee, W. B., and Lee, Y.-W. (2019). A corresponding-state framework for the structural transition of supercritical fluids across the Widom delta. J. Chem. Phys. 150 (15), 154503. doi:10.1063/1.5086467
Zappoli, B., Bailly, D., Garrabos, Y., Neindre, B. L., Guenoun, P., and Beysens, D. (1990). Anomalous heat transport by the piston effect in supercritical fluids under zero gravity. Phys. Rev. A . Coll. Park. 41 (4), 2264–2267. doi:10.1103/physreva.41.2264
Nomenclature
n wave frequency,
b -in growth coefficient,
q heat flux,
h heat transfer coefficient
Subscripts
pc pseudocritical
C critical
l liquid
g vapor or gas
b bulk
w wall
sat saturation
Keywords: supercritical fluids, pseudo-boiling, boiling, natural convection, heat transfer
Citation: Liu M, Liu S, Xi D, Huang S and Huang Y (2023) Analysis of heat transfer mechanism in supercritical fluids from the aspect of pool heating. Front. Energy Res. 10:1042391. doi: 10.3389/fenrg.2022.1042391
Received: 12 September 2022; Accepted: 14 November 2022;
Published: 13 January 2023.
Edited by:
Mingjun Wang, Xi’an Jiaotong University, ChinaReviewed by:
Haochun Zhang, Harbin Institute of Technology, ChinaZhuqiang Yang, Dalian University of Technology, China
Copyright © 2023 Liu, Liu, Xi, Huang and Huang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Shanfang Huang, c2ZodWFuZ0BtYWlsLnRzaW5naHVhLmVkdS5jbg==
 Minyun Liu
Minyun Liu Shenghui Liu
Shenghui Liu Dapeng Xi
Dapeng Xi Shanfang Huang
Shanfang Huang Yanping Huang
Yanping Huang