Hierarchical entropy analysis for flow pattern of steam-liquid two phase flow in a rod bundle

Introduction

The two-phase flow in the rod bundle is widely found in modern industrial fields such as energy, chemical refrigeration and other modern industrial fields. The flow of coolant through the fuel rod bundle assembly of the boiling water reactor core in the nuclear reactor belongs to the common phenomenon of steam-liquid two-phase flow in the longitudinal arrangement rod bundle (Enrique et al., 2009; Arai et al., 2012; Yang et al., 2012). Since the two-phase flow is a complex nonlinear dynamical system, no theoretical model and numerical simulation method have fully revealed the dynamic characteristics of the two-phase flow mechanics. Therefore, it is necessary to effectively characterize the dynamics of the two-phase flow in the rod bundle.

In recent years, some scholars have applied methods such as chaos theory, fractal theory, complex network and time-frequency domain analysis to reveal the dynamic characteristics of two-phase flow to a certain extent (Du et al., 2012; Karimi et al., 2011; Gao et al., 2011; Lee et al., 2008). Li et al. (2013) applied the smooth Wigner three-spectral slice spectrum, contour line and secondary slice method to analyze the pressure difference fluctuation signal of nitrogen-water two-phase flow, and found that the above method can not only reveal the evolution law of different flow patterns, but also provide new method for the other study of multiphase flow patterns. Sun et al. (2011) applied wavelet transform, Hilbert-Huang transform and adaptive optimal kernel to process the dynamic differential pressure signal of steam-liquid two-phase flow, and studied the dynamic characteristics of different flow types of steam-liquid two-phase flow. Zheng et al. (2009) applied multi-scale entropy to analyze the conductance signal of steam-liquid two-phase flow and revealed the dynamic characteristics of each flow pattern through the dynamic characteristics of sample entropy at different scales. Du et al. (2012) applied the multi-scale arrangement entropy algorithm to study the oil-water two-phase flow in the vertical pipe, and quantitatively described the dynamic complexity of the oil-in-water flow pattern according to the multi-scale arrangement entropy rate and mean value. Zhu et al. (2014) applied the hierarchical entropy to analyze the bearing fault signal, and found that the layered entropy can more effectively reflect the information in the fault signal than the multi-scale entropy, especially to effectively overcome the disadvantage of the information in the high-frequency part of the multi-scale entropy loss signal. Jiang et al. (2011) also adopted the hierarchical entropy to analyze biological signals, and found that layering can effectively reduce the impact of noise on signal analysis. Zhang et al. (2017) studied single-phase convection and steam-water two-phase flow boiling in a vertical rod bundle, and developed new correlations to predict single-phase heat transfer and two-phase flow boiling heat transfer coefficients. Zhou et al. (2015) used the differential pressure signal of the steam-liquid two-phase flow, multi-scale entropy algorithm is employed to reveal the dynamic characteristics of the different flow patterns in the rod bundle. Li et al. (2014) analyzed the flow characteristics of vertical upward two-phase flow in small rectangular channels, and proposed two time-frequency representation-based methods (i.e., AOK TFR and DA SFBW) to characterize quantitatively the dynamics behavior of different nitrogen-water two-phase flow patterns. Zhang et al. (2018a) studied theoretically the flow patterns of two-phase vertically upward flow across horizontal tube bundles based on the Kanizawa flow regime criteria and Hibiki flow regime criteria. Liu et al. (2022) conducted experimental studies on the gas-liquid flow patterns and spatial-temporal of each phase in the PWR prototype 5 × 5 rod bundle channel based on the void fraction data, evaluated the existing drift-flux correlations and proposed a new correlation for void fraction of prototype rod bundle channel with its reliability verified. Han et al. (2021) studied five flow regimes (bubbly, finely dispersed bubbly, cap-bubbly, churn and annular flows) and their transitions in upward gas-liquid flows in vertical rod bundle flow channels. Zhang et al. (2018b) investigated on single-phase convection and steam-water two-phase flow boiling heat transfer in an electrically heated staggered inclined rod bundle at atmospheric pressure, and developed new correlations to predict local flow boiling heat transfer coefficients in the inclined rod buddle. Although hierarchical entropy (HE) has been widely used in the analysis of signal complexity and dynamic characteristics, there are few reports on its application in the field of two-phase flow. In this paper, hierarchical entropy is firstly applied to four typical signals to prove its ability to characterize complex signals, and then stratified entropy algorithm is applied to fluctuation signal of pressure difference signal of steam-liquid two-phase flow in rod bundle to study the evolution law and dynamic characteristics of steam-liquid two-phase flow.

Theoretical basis

Sample entropy method

Given a signal of length N: $\mathrm{x}=\{x\left(1\right),...,x\left(i\right),...,x\left(N\right)\}$.Its sample entropy is calculated as follows (Ramdani et al., 2009):

(1) Constructing template vectors in m dimensions ${\mathrm{x}}_m\left(i\right)$:

${\mathrm{x}}_m\left(i\right)=\left\{\mathrm{x}\left(i\right),\mathrm{x}\left(i+1\right),...,\mathrm{x}\left(i+m-1\right)\right\},1\le i\le N-m+1(1)$

(2) The distance between the two vectors was defined as:

$d\left[x_m\left(i\right),x_m\left(j\right)\right]=\underset{k\in \left[1,m-1\right]}{\max }\left|x_m\left(i+k\right)-x_m\left(j+k\right)\right|(2)$

(3) Given the capacity limit r (r > 0), Count the number of $\left[x_m\left(i\right),x_m\left(j\right)\right]<\mathrm{r}$ $A_i$, the ratio of $A_i$to the total number of vectors is recorded as $B_i^m\left(\mathrm{r}\right)$:

$B_i^m\left(\mathrm{r}\right)=\frac{A_i}{N-m+1},1\le i\le N-m(3)$

(4) The mean of $B_i^m\left(\mathrm{r}\right)$ is defined as$B^m\left(\mathrm{r}\right)$:

$B^m\left(\mathrm{r}\right)=\frac{1}{N-m}{\sum }_{i=1}^{N-m}{B}_i^m\left(r\right)(4)$

(5) Increase the dimension of the vector from m to m+1, repeat the above steps 2–4, get $B^{m+1}\left(\mathrm{r}\right)$.Calculate the sample entropy. Its formula is:

$SampEn\left(m,\mathrm{r},n\right)=-\ln \frac{B^{m+1}\left(\mathrm{r}\right)}{B^m\left(\mathrm{r}\right)}(5)$

Hierarchical entropy method

Hierarchical entropy method is a new method to characterize the complexity of signal. It can represent both the information contained in the low frequency part of signal and the information contained in the high frequency part of signal. At the same time, it has good anti-noise performance to the signal containing noise (Costa et al., 2002; Costa et al., 2005; Costa et al., 2003).

Firstly, for a signal $\mathrm{x}=\{x\left(1\right),...,x\left(i\right),...,x\left(N\right)\}$, average signal $Q_0$and difference signal $Q_1$ are constructed as follows:

$Q_0\left(\mathrm{x}\right)=\frac{x\left(2j\right)+x\left(2j+1\right)}{2},j=\mathrm{0,1,2},...,2^{n-1}(6)$

$Q_0\left(\mathrm{x}\right)=\frac{x\left(2j\right)+x\left(2j+1\right)}{2},j=\mathrm{0,1,2},...,2^{n-1}(7)$

Where: Signal $Q_0$ with length$2^{\mathrm{n}-1}$represents the low-frequency part of signal $\mathrm{x}$ on scale 2, signal $Q_1$ with length$2^{\mathrm{n}-1}$represents the high-frequency part of signal $\mathrm{x}$ on scale 2. The original signal $\mathrm{x}$ can be represented by $Q_0$ and $Q_1$ as follows:

$\mathrm{x}=\{Q_0{\left(x\right)}_j+Q_1{\left(x{)}_j,Q_0(x\right)}_j-Q_1{\left(x\right)}_j\},j=\mathrm{0,1,2},...,2^{n-1}(8)$

Therefore, $Q_0$ and $Q_1$ constitute a 2-scale analysis of the original signal $\mathrm{x}$. For j = 0 or 1, the operation of Q can be expressed by a matrix:

$Q={\left(\begin{array}{l}\frac{1}{2}\frac{{\left(-1\right)}^j}{2}00\cdot \cdot \cdot 00\\ 00\frac{1}{2}\frac{{\left(-1\right)}^j}{2}\cdot \cdot \cdot 00\\ 0000\cdot \cdot \cdot \frac{1}{2}\frac{{\left(-1\right)}^j}{2}\end{array}\right)}_{2^{n-1}\times 2^n}(9)$

Secondly, in order to describe the multi-scale analysis of signal $\mathrm{x}$, a non-negative integer is defined as follows for $n\in N$ and vector ${[\mathrm{v}}_1{,\mathrm{v}}_2{,...,\mathrm{v}}_{\mathrm{n}}]\in \left\{\mathrm{0,1}\right\}$:

$e={\displaystyle \sum }_{j=1}^n{v}_j{2}^{n-j}(10)$

The stratified part of signal $\mathrm{x}$ is defined as follows:

${\mathrm{x}}_{n,e}=Q_{v_1},Q_{v_2},...,Q_{v_n}\left(\mathrm{x}\right)(11)$

It can be seen that ${\mathrm{x}}_{n,0}$ and ${\mathrm{x}}_{n,1}$ are respectively the high-frequency part and low-frequency part of signal $\mathrm{x}$ on scale n +1. ${\mathrm{x}}_{\mathrm{0,0}}$is the original signal. For different n and e, ${\mathrm{x}}_{n,e}$ consists of hierarchical decomposition of signal $\mathrm{x}$ at different scales. Figure 1 shows the hierarchical decomposition of signal $\mathrm{x}$ with three scales in the form of tree graph.

FIGURE 1

FIGURE 1. Hierarchical decomposition of signal x with three scales.

Finally, calculate the sample entropy for each ${\mathrm{x}}_{n,e}$. This process is called hierarchical entropy analysis. In the process of sample entropy calculation, the matching length of sequence m = 2, threshold r = 0.25$\sigma$(signal standard deviation), and data length is 2048 (Pincus et al., 2001).

Method evaluation

To verify the wide application of hierarchical entropy theory, four typical signals, namely sinusoid and sine+noise mixing, Lorenz and Lorenz+noise mixing, are selected for analysis and calculation. Generation conditions for several signals are as follows (Ge et al., 2009):

(1) Sine signal

$y=3\mathit{sin}\left(x\right)(12)$

(2) Sine + white gaussian noise

$y=3\mathit{sin}\left(x\right)+P\cdot y1(13)$

Where: y1 is the white gaussian noise sequence, p is the proportion of random components, and here take p = 0.2.

(3) Lorenz equation

$\begin{array}{l}\frac{\mathrm{d}x}{\mathrm{d}t}=10\left(x-y\right),\\ \frac{\mathrm{d}y}{\mathrm{d}t}=-y+28x-xz,\\ \frac{\mathrm{d}z}{\mathrm{d}t}=xy-\frac{8}{3}z\\ \end{array}(14)$

The initial conditions x = 1, y = 0, z = 1, using the fourth order Runge-Kutta methods iteration, take the variable y as the simulation sequence;

(4) Lorenz + gaussian noise

The variable y+30 dB noise obtained in (3)

Figure 2 shows the hierarchical entropy analysis of the Lorenz + gaussian noise signal. It can be seen from the figure that when n is constant, the entropy value of ${\mathrm{x}}_{n,0}$ is the largest; as n increases, the entropy value of ${\mathrm{x}}_{n,0}$ tends to rise. Figure 3 shows the anti-noise detection of the four typical signals, showing that either the sine signal or the Lorenz signal agree with the original complex sequence after adding white gaussian noise, which shows that hierarchical entropy is very effective in dealing with noise of periodic and complex sequences. Therefore, hierarchical entropy can be applied to signal containing noise, and its results are not affected by noise.

FIGURE 2

FIGURE 2. Hierarchical entropy analysis for Lorenz signals added white gaussian noise.

FIGURE 3

FIGURE 3. HE values of the 16 hierarchical decomposition nodes for four typical signals.

Hierarchical entropy and dynamic characteristics of two-phase flow

Figure 4 shows the experimental system of a rod bundle steam-liquid two-phase flow. It is mainly composed of water tank, centrifugal pump, turbine flowmeter, preheater, test section, steam liquid separator, condenser, high-speed camera and so on. Deionized water was selected as the working medium in the test. At the beginning of the test, the deionized water in the experimental loop was circulated by the centrifugal pump and then carried to the flowmeter and flow regulating valve. The deionized water was heated by the pre-heater to ensure that the temperature of the deionized water at the inlet of the test section meets the test requirements. When the deionized water flows through the test section, AC power was directly added to the preheating section and the heating rod bundle in the test section, and the heating power was continuously adjusted by the voltage regulator. After the deionized water was heated and boiled in the test section, the two-phase mixture flowing from the outlet of the test section enters the separator for separation. The steam phase was condensed and combined with the separated liquid phase. Finally, it flows into the water tank, forming a closed cycle.

FIGURE 4

FIGURE 4. Schematic of experimental apparatus.

The experimental section consists of two parts, namely, electric heating rod bundle and casing, as shown in Figure 5. Nine stainless steel heating rod bundles with a $3\times 3$ array were placed in a circular casing to form the experimental channel. The length of the heating rod bundle is 1000 mm, the bottom 300 mm and the top 100 mm are the non-heating section, and the middle 600 mm is the effective heating section; the outer diameter of the heating rod bundle is 10 mm, and the distance between adjacent rods is 15 mm. The casing is 1.33 m long, with an inner diameter of 60 mm and an outer diameter of 70 mm.

FIGURE 5

FIGURE 5. Structure of the test section.

The main data collected in the experiment are the differential pressure signal and the mass flow velocity of the liquid. The differential pressure signal was measured by the Rosemount 3051S capacitive differential pressure transmitter with a measurement accuracy of 0.05%, the update response time was 100 ms/time, and the differential pressure calibration range was 0.5 in H2O-2000 psi. In the experiment, the sampling frequency of differential pressure signal was 400 Hz, and the sampling time was 10 s. In the experiment, WYLWGY-4 intelligent turbine flowmeter was used to measure the mass flow velocity of liquid, and the accuracy grade was $\pm 1.0\%$ (Zhou et al., 2014; Meng et al., 2014).

The test procedure was summarized as follows: 1) The water tank was filled deionized water. The deionized water was used to filled the entire experimental loop driven by a centrifugal pump; 2) The power supply of the preheater and the experimental section were switched. 3) The data acquisition system was stared; 4) The experimental loop valve was adjust so that the flowmeter was reached a predetermined value; 5) The inlet temperature of test section was keep the specified temperature by adjusting the voltage of pre-heat; 6) When the voltage of the test section was adjusted, the experimental data was recorded after reaching the stable working condition; 7) After one working condition is completed, repeat 4–6 until all experimental working conditions are completed; 8) The power supply of the preheater and the experimental section were cut off. After a period of the deionized water circulation, the test section and the preheating section were cooled and then the centrifugal pump and condenser were turned off.

In the experimental process, four typical flow patterns were observed in the rod bundle flow, bubble-churn flow, churn flow and annular flow, as shown in Figure 6. Differential pressure signals corresponding to four typical flow patterns are collected. The results of hierarchical entropy calculation of differential pressure signals are shown in Figure 7.

FIGURE 6

FIGURE 6. Flow patterns in the vertical rod-bundle.

FIGURE 7

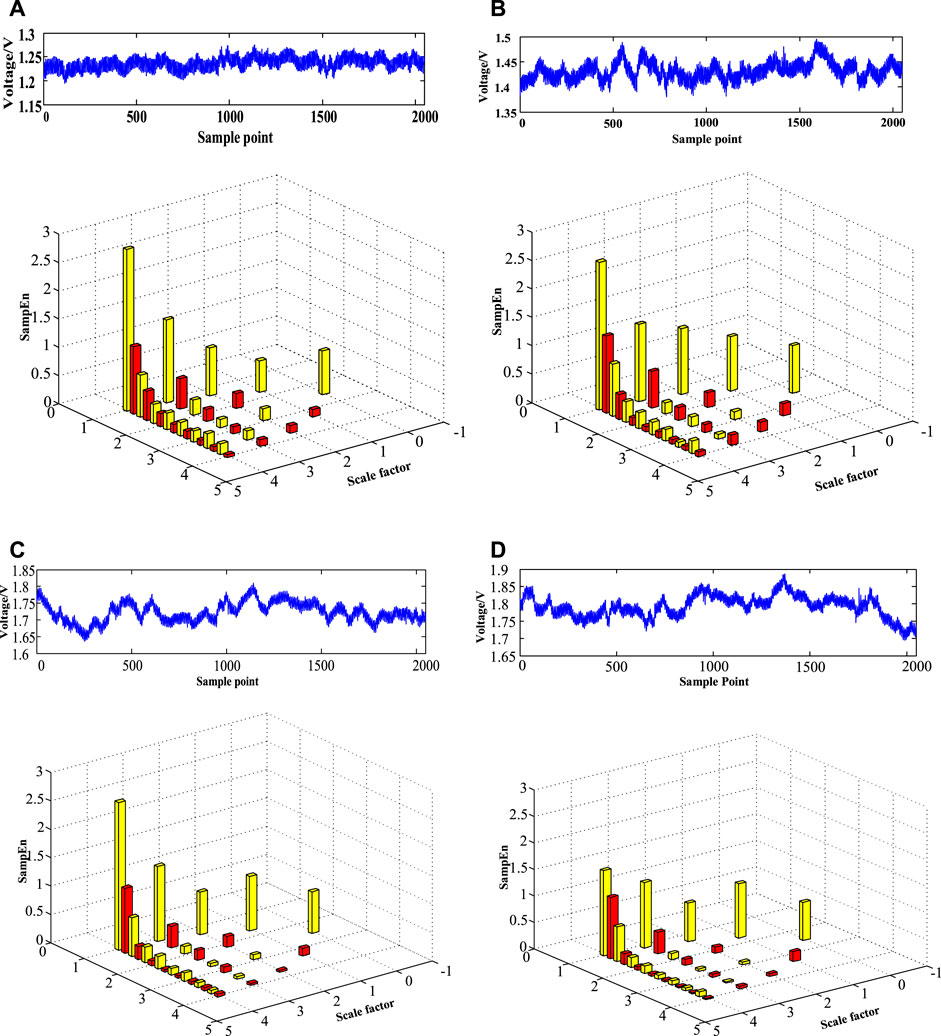
FIGURE 7. Hierarchical entropy analysis for differential pressure signal of typical flow patterns; (A) bubble flow, (B) bubble-churn flow, (C) churn flow, (D) annular flow.

As can be seen from Figure 6, several typical flow patterns in rod bundle channels have the following physical characteristics:

(1) Bubble flow: The liquid phase dominates. Discrete small bubbles are randomly distributed in the continuous liquid phase. Most of the bubbles move up along the flow direction with the main flow in its sub-channels (sub-channels 1,2 and 3 divided as shown in Figure 5), and only a few bubbles drift between adjacent sub-channels, and in the diameter of the bubbles in the bubble flow pattern is approximately 2–10 mm.

(2) Bubble-churn flow: The small bubbles continue to gather and move in adjacent channels, so that the aggregated bubbles in the channel continue to grow. When they grow to a certain size, the bubbles deform into an oval or hat shape. However, as the polymerization bubbles are disturbed and segmented by the rod bundles, the state of the polymerization bubbles is unstable and the bubbles break quickly. In the experimental section, it is difficult to distinguish the cap bubbles from the elastic bubbles.

(3) Churn flow: Bubbles aggregate and twist in the rod bundle. Usually, the twisted bubble spans 1–2 sub-channels. Because the aggregated bubble is disturbed and divided by the rod bundle, the state of the aggregated bubble is unstable and ruptures quickly. At this time, many irregular bubbles are generated after the collapse of the polymerized bubbles, which are mixed and distributed in the liquid flow. This flow pattern shows the characteristics of oscillation, and with the drag of the large upward moving bubble, the liquid produces alternating up and down movement, and exists for a long time in a wide range of working conditions. When the churn flow pattern appears, the steam phase and liquid phase are strongly disturbed in the rod bundle channel, which causes strong scouring on the inner wall and sleeve wall of the heated rod bundle tube.

(4) Annular flow: The massive liquid flow in the channel is broken, and the bubbles unite and form a continuous column along the rod bundle. The liquid phase flows upward in the form of a liquid film in the sub-channel, and a large amount of liquid is entrained in the steam column in the form of small water droplets. However, when the liquid film is scoured by the steam body, ripples appear, and the two phases form a toothed interface, which may cause the rupture of the liquid film due to the action of fluctuations.

It can be seen from Figure 7 that the hierarchical entropy values of differential pressure signals of the four typical flow patterns are different at different scales, which is caused by the different proportions of dynamic information and dynamic information in low frequency and high frequency of different flow patterns. On the whole, the entropy of the hierarchical entropy root node ${\mathrm{x}}_{n,0}$ of the four flow patterns increases with the increase of scale. For the same scale, regardless of the high frequency part or the low frequency part, the entropy value of stratification decreases rapidly with the increase of e. In detail, the entropy value of bubble flow at the root node ${\mathrm{x}}_{\mathrm{0,0}}$ is the largest (0.79), followed by bubble-churn flow (0.74) and churn flow (0.74), and the annular flow is the smallest (0.71). However, with the increase of scale, the difference becomes larger and larger. For example, on scale 4, the entropy value of ${\mathrm{x}}_{\mathrm{5,0}}$ is 2.86, 2.65, 2.60 and 1.61 successively. In the high frequency part, at scale 1, the annular flow has the maximum entropy and the bubble flow has the minimum entropy. When the scale exceeds 1, the high frequency part is similar to white gaussian noise. The characteristics of hierarchical entropy of each flow pattern reflect the evolution characteristics of each flow pattern. In the bubble flow, the liquid phase dominates, and the steam bubbles are randomly distributed in the continuous liquid phase. Macroscopically, it appears to move upward with the main flow in its sub-channels (sub-channels 1, 2 and 3 divided as shown in Figure 5). Therefore, the differential pressure signal of the flow pattern is similar to random signal with small fluctuation, and the information occupies a large proportion in the low-frequency part, so the entropy value is the highest at the root node of the hierarchical tree graph. In the annular flow, the bubbles unite and form steam column in the channel of the rod bundle. The liquid phase flows along the rod bundle in the form of liquid film, and a wavy interface is formed between the steam phase and the liquid phase. In addition, a liquid bridge is formed between adjacent steam columns. The rupture of the liquid bridge and the fluctuation interface results in a large fluctuation range of differential pressure signal and a large proportion of information in the high frequency part, so it shows a low entropy value. For churn flow and bubble-churn flow, the oscillating random flow phenomenon exhibited by the steam and liquid phases in adjacent channels is less intense than that of bubble flow due to the enhancement of lateral and turbulent churn in adjacent channels. Especially for churn flow, with the drag of the upward moving large bubbles, the liquid will move up and down alternately, resulting in obvious vibration characteristics. Therefore, its entropy value is between bubble flow and annular flow, but the entropy value of hierarchical entropy has little difference between bubble-churn flow and churn flow, and cannot effectively distinguish these two flow patterns. It can be seen from the above analysis that the application of hierarchical entropy can reveal the dynamic information of different flow patterns well.

Figure 8 shows the hierarchical entropy values of the four flow pattern differential signals on the 16 hierarchical decomposition nodes. As can be seen from the figure, at the first three nodes, there are obvious differences in the entropy values: the bubble flow is the largest, and the annular flow is the smallest. In other nodes, the law of the largest bubble flow and the smallest circulation flow is also followed, but the difference is not obvious. This is because the signal will inevitably be doped with noise during the experiment, and the layered noise is separated, and the difference in entropy value calculated by the sample entropy is small. For bubble-churn flow and churn flow, the entropy values of each node are basically overlapped, and the difference between the entropy values is very small, so the two flow types cannot be effectively distinguished. This is mainly because the differential pressure fluctuation signals of the two flow patterns are very similar.

FIGURE 8

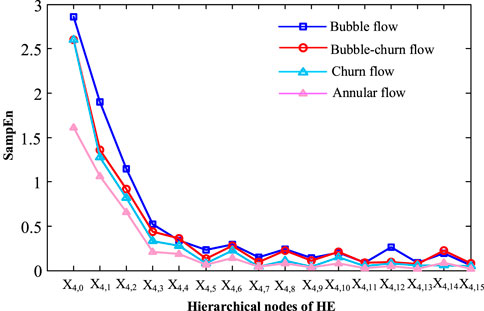
FIGURE 8. HE values of the 16 hierarchical decomposition nodes for the four differential pressure signal.

Conclusion

As a nonlinear analysis method, hierarchical entropy can represent the complexity of high and low frequency signals, and can effectively de-noise the signals with a lot of noise, reveal their internal characteristics, and has good robustness. The application of hierarchical entropy to differential pressure signals of two-phase flow in the rod bundle shows that hierarchical entropy can effectively reveal dynamic information of bubble flow, bubble-churn flow, churn flow and annular flow. Among them, the entropy value of bubble flow at the root node ${\mathrm{x}}_{\mathrm{0,0}}$ is the largest (0.79), followed by bubble-churn flow (0.74) and churn flow (0.74), and annular flow is the smallest (0.71). In the high frequency part, at scale 1, the annular flow has the maximum entropy and the bubble flow has the minimum entropy. When the scale exceeds 1, the high frequency part is similar to the white gaussian noise. It can effectively remove the noise mixed in the experimental process, but it cannot effectively distinguish between the bubble-churn flow and the churn flow.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

Chao Zhang: Conceptualization, Software, Writing- Original draft preparation.Xinyue Liu: Methodology, Data curation. Yandong Hou: Reviewing and Editing. Weicaho Li: Investigation, Reviewing and Editing. Benan Cai: Visualization. Weihua Cai: Supervision, Project Administration.

Funding

This study has been financially supported by Natural Science Foundation of Jilin Province (Grant No. 20220101245JC).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Arai, T., Furuya, M., Kanai, T., and Shirakawa, K. (2012). Development of a subchannel void sensor and two-phase flow measurement in 10×10 rod bundle. Int. J. Multiph. Flow 47, 183–192. doi:10.1016/j.ijmultiphaseflow.2012.07.012

CrossRef Full Text | Google Scholar

Costa, M., Goldberger, A. L., and Peng, C. K. (2005). Multiscale entropy analysis of biological signals. Phys. Rev. E 71 (2), 021906. doi:10.1103/physreve.71.021906

PubMed Abstract | CrossRef Full Text | Google Scholar

Costa, M., Goldberger, A. L., and Peng, C. K. (2002). Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 89 (6), 068102. doi:10.1103/physrevlett.89.068102

PubMed Abstract | CrossRef Full Text | Google Scholar

Costa, M., Peng, C. K., Goldberger, A. L., and Hausdorff, J. M. (2003). Multiscale entropy analysis of human gait dynamics. Phys. A Stat. Mech. its Appl. 330 (1), 53–60. doi:10.1016/j.physa.2003.08.022

PubMed Abstract | CrossRef Full Text | Google Scholar

Du, M., Jin, N. D., Gao, Z. K., Wang, Z-Y, and Chen, P (2012a). Time-frequency analysis of vertical upward oil-water two phase flow. AIR Conference Proceedings 1428, 107–114. doi:10.1063/1.3694695

CrossRef Full Text | Google Scholar

Du, M., Sun, B., Jin, N. D., and Gao, Z. K. (2012b). Analysis of total energy and time-frequency entropy of gas–liquid two-phase flow pattern. Chem. Eng. Sci. 82, 144–158. doi:10.1016/j.ces.2012.07.028

CrossRef Full Text | Google Scholar

Enrique, J. J., Hibiki, T., Ishii, M., Yun, B. J., and Park, G. C. (2009). Drift-flux model in a sub-channel of rod bundle geometry. Int. J. Heat Mass Transf. 52 (13-14), 3032–3041. doi:10.1016/j.ijheatmasstransfer.2009.02.012

CrossRef Full Text | Google Scholar

Gao, Z. K., and Jin, N. D. (2011). Nonlinear characterization of oil–gas–water three-phase flow in complex networks. Chem. Eng. Sci. 66 (12), 2660–2671. doi:10.1016/j.ces.2011.03.008

CrossRef Full Text | Google Scholar

Ge, J. Y., Zhou, P., Zhao, X., et al. (2009). Multiscale entropy analysis of EEG signal. Comput. Eng. Appl. 45 (10), 13–15.

Google Scholar

Han, X., Shen, X. Z., Yamamoto, T., Nakajima, K., Sun, H., Hibiki, T., et al. (2021). Flow regime and void fraction predictions in vertical rod bundle flow channels. Int. J. Heat Mass Transf. 178, 121637. doi:10.1016/j.ijheatmasstransfer.2021.121637

CrossRef Full Text | Google Scholar

Jiang, Y., Peng, C. K., and Xu, Y. (2011). Hierarchical entropy analysis for biological signals. J. Comput. Appl. Math. 236 (5), 728–742. doi:10.1016/j.cam.2011.06.007

CrossRef Full Text | Google Scholar

Karimi, M., Mostoufi, N., Zarghami, R., and Sotudeh-Gharebagh, R. (2011). Nonlinear dynamics of a gas–solid fluidized bed by the state space analysis. Chem. Eng. Sci. 66 (20), 4645–4653. doi:10.1016/j.ces.2011.06.022

CrossRef Full Text | Google Scholar

Lee, J. Y., Kim, N. S., and Ishii, M. (2008). Flow regime identification using chaotic characteristics of two-phase flow. Nucl. Eng. Des. 238 (4), 945–957. doi:10.1016/j.nucengdes.2007.09.005

CrossRef Full Text | Google Scholar

Li, H. W., Zhou, Y. L., Hou, Y. D., Sun, B., and Yang, Y. (2014). Flow pattern map and time–frequency spectrum characteristics of nitrogen–water two-phase flow in small vertical upward noncircular channels. Exp. Therm. Fluid Sci. 54, 47–60. doi:10.1016/j.expthermflusci.2014.01.017

CrossRef Full Text | Google Scholar

Li, H. W., Zhou, Y. L., Wang, S. Y., and Sun, B. (2013). The sliced trispectrum fluctuation characteristics and flow pattern representation of the nitrogen-water two-phase flow of small channel. Acta Phys. Sin. 62 (14), 140505. doi:10.7498/aps.62.140505

CrossRef Full Text | Google Scholar

Liu, S., Liu, L., Gu, H. Y., and Wang, K. (2022). Experimental study of gas-liquid flow patterns and void fraction in prototype 5×5 rod bundle channel using wire-mesh sensor. Ann. Nucl. Energy 171 (1), 109022. doi:10.1016/j.anucene.2022.109022

CrossRef Full Text | Google Scholar

Meng, Z. M., Dong, B., Wang, L. S., Fu, X., Tian, W., Yang, Y., et al. (2014). Experimental research of liquid entrainment through ADS-4 in AP1000. Ann. Nucl. Energy 72, 428–437. doi:10.1016/j.anucene.2014.06.012

CrossRef Full Text | Google Scholar

Pincus, S. M. (2001). Assessing serial irregularity and its implications for health. Ann. N. Y. Acad. Sci. 954 (1), 245–267. doi:10.1111/j.1749-6632.2001.tb02755.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Ramdani, S., Bouchara, F., and Lagarde, J. (2009). Influence of noise on the sample entropy algorithm Chaos 19 (1):013123 doi:10.1063/1.3081406

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, B., Wang, E. P., Zheng, Y. J., et al. (2011). Time-frequency spectral analysis of gas-liquid two-phase flow's fluctuations. Acta Phys. Sin. 60 (1), 014701. doi:10.7498/aps.60.014701

CrossRef Full Text | Google Scholar

Yang, X., Schlegel, J. P., Hibiki, T., Ishii, M., Liu, Y., and et, al. (2012). Measurement and modeling of two-phase flow parameters in scaled 8×8 BWR rod bundle. Int. J. Heat Fluid Flow 34, 85–97. doi:10.1016/j.ijheatfluidflow.2012.02.001

CrossRef Full Text | Google Scholar

Zhang, K., Hou, Y. D., Tian, W. X., Fan, Y., Su, G., and Qiu, S. (2017). Experimental investigations on single-phase convection and steam-water two-phase flow boiling in a vertical rod bundle. Exp. Therm. Fluid Sci. 80, 147–154. doi:10.1016/j.expthermflusci.2016.08.018

CrossRef Full Text | Google Scholar

Zhang, K., Hou, Y. D., Tian, W. X., Zhang, Y., Su, G., and Qiu, S. (2018a). Experimental investigations on single-phase convection and two-phase flow boiling heat transfer in an inclined rod bundle. Appl. Therm. Eng. 148, 340–351. doi:10.1016/j.applthermaleng.2018.11.067

CrossRef Full Text | Google Scholar

Zhang, K., Hou, Y. D., Tian, W. X., Zhang, Y., Su, G., and Qiu, S. (2018b). Flow pattern effect on two-phase pressure drops in vertical upward flow across a horizontal tube bundle. Ann. Nucl. Energy 120, 253–264. doi:10.1016/j.anucene.2018.05.059

CrossRef Full Text | Google Scholar

Zheng, G. B., and Jin, N. D. (2009). Multiscale entropy and dynamic characteristics of two-phase flow patterns. Acta Phys. Sin. 58, 4485–4492. doi:10.7498/aps.58.4485

CrossRef Full Text | Google Scholar

Zhou, Y. L., Hou, Y. D., Li, H. W., et al. (2014). Experiment study on onset of nucleate boiling in rod bundle channel. Atomic energy Sci. Technol. 48 (8), 1416–1420.

Google Scholar

Zhou, Y. L., Hou, Y. D., Li, H. W., Sun, B., and Yang, D. (2015). Flow pattern map and multi-scale entropy analysis in 3×3 rod bundle channel. Ann. Nucl. Energy 80, 144–150. doi:10.1016/j.anucene.2015.02.006

CrossRef Full Text | Google Scholar

Zhu, K., Song, X., and Xue, D. (2014). A roller bearing fault diagnosis method based on hierarchical entropy and support vector machine with particle swarm optimization algorithm. Measurement 47, 669–675. doi:10.1016/j.measurement.2013.09.019

CrossRef Full Text | Google Scholar