Pin-resolved ultra-fine-group with correction method and its application to plate-type fuel reactor analysis

In order to perform the resonance calculation efficiently and accurately, several pin-resolved ultra-fine-group methods combining the ultra-fine-group method and Dancoff factor have been developed recently. The ultra-fine-group method is used to consider the self-shielding effect accurately in the 1-D fuel model, and the Dancoff factor is used to consider the shadowing effect in a lattice system. The pin-resolved ultra-fine-group with correction method, combining the ultra-fine-group method and Dancoff factor, is implemented in a transport code using the method of characteristic. In order to expand the application range, the pin-resolved method is extended for the plate-type fuel. Numerical results show good accuracy for the plate-type fuel reactor analysis.

Introduction

The calculation in which effective multi-group cross sections for the problem are estimated from the cross section library is called the resonance treatment or resonance calculation. Effective cross sections are used in subsequent calculations and their accuracy is the guarantee for subsequent calculations. On the other hand, it is difficult to obtain accurate effective cross sections due to the resonance self-shielding effect. Much effort has been devoted to the study of resonance calculation and many resonance calculation methods have been proposed.

Effective cross sections can be estimated accurately in the ultra-fine-group method where the transport equation or slowing-down equation is solved with ultra fine energy groups (Sugimura and Yamamoto, 2007; Zhang et al., 2018). However, it is impractical to use the ultra-fine-group method in real-world problems with large and complex geometries. The equivalence theory is a simple and fast method and is widely used in many codes (Knott and Yamamoto, 2010). Due to many assumptions in the derivation process, the accuracy of the equivalence theory is limited and the equivalence theory cannot deal with the space-dependent self-shielding effect in the fuel dump and the resonance interference effect among resonant nuclides. The Stamm’ler’s method (Stamm’ler and Abbate, 1983) was proposed for a lattice system and the space-dependent Dancoff method (Matsumoto et al., 2012) was proposed to consider the space-dependent self-shielding effect in the fuel dump. The resonance interference factor table is used to consider the interference effect (Choi et al., 2017). As for the subgroup method (Chiba and Unesaki, 2006; He et al., 2018), Tone’s method (Tone, 1975; Lee and Yang, 2012; Mao, 2017; Zheng et al., 2018) and Embedded Self-Shielding Method (ESSM; Hong and Kim, 2011; Williams and Kim, 2012), the neutron slowing-down equation is solved directly with multi-group cross sections instead of being simplified in the equivalence theory, which means these method can be used in general geometries and the computation time is longer and the result is more accurate than the equivalence theory. However, in order to obtain highly accurate cross sections, the neutron slowing-down equation is solved with hundreds of energy groups. Compared with the Tone’s method and ESSM, the subgroup method can reduce the number of energy groups by subdividing energy groups by the magnitude of cross sections. On the other hand, the use of subgroup parameters results in an inability to handle the temperature distribution effect.

In order to efficiently obtain highly accurate cross sections, pin-resolved resonance self-shielding methods have been proposed recently. Yamamoto et al., 2010 used the ultra-fine-group method to prepare a table of the effective cross section and the Dancoff factor for various fuel pins and estimated the effective cross section by interpolation with the Dancoff factor. Liu et al., 2015, Liu et al., 2017) used the ESSM to consider the shadowing effect in a lattice system and correct the escape cross section in an isolated fuel pin where the effective cross section was calculated with the ultra-fine-group method. Choi et al., 2016 used the Enhance Neutron Current Method (ENCM; Yamamoto, 2012) to calculate the Dancoff factor for each fuel pin and used the Stamm’ler’s method to correct the collision probability in an isolated fuel pin where the effective cross section was calculated with the ultra-fine-group method. Liu et al., 2017 used the neutron current method to calculate the Dancoff factor for each fuel pin and built the equivalent 1-D cylindrical model by preserving the Dancoff factor. And the effective cross section was calculated by the pseudo-resonant-nuclide subgroup method in the equivalent 1-D cylindrical model. Yamaji et al., 2018 used the ENCM to calculate the Dancoff factor for each fuel pin and also built the equivalent 1-D cylindrical model in which the effective cross section was calculated with the ultra-fine-group method. Zu et al., 2018 prepared a table of the escape cross section and the pin pitch, and used the one-group ESSM to calculate the escape cross section for each fuel pin and built the equivalent 1-D cylindrical model by interpolating the table. The effective cross section was calculated by the ultra-fine-group method in the equivalent 1-D cylindrical model. Rao et al, (2022) proposed a new pin-resolved resonance self-shielding method where the effective cross section was calculated in the infinite lattice system and corrected by the equivalence theory with Dancoff factor. These pin-resolved resonance self-shielding methods use the Dancoff factor to consider the shadowing effect and use the ultra-fine-group method to accurately estimate the effective cross section. Since the one-group neutron slowing-down calculation is performed to calculate Dancoff factor and the ultra-fine-group calculation for each fuel pin can be parallel, the computation time for the pin-resolved resonance self-shielding method is short.

These methods are currently applied to fuel rods. In order to expand the application range, the Pin-resolved Ultra-fine-group with Correction Method (PUCM) was extended for the plate-type fuel and implemented in a transport code using the Method of Characteristics (MOC) (Zhao et al., 2021, Zhao et al., 2022). In subsequent sections, we will review the equivalence theory and the PUCM, and present the results calculated by the PUCM for the plate-type fuel reactor analysis.

Theory

Equivalence theory

A neutron slowing-down equation in a two-region heterogeneous system is

${\mathrm{\Sigma }}_{t,f}\left(E\right){\varphi }_f\left(E\right)V_f=P_{f\to f}\left(E\right)V_f{Q}_{s,f}\left(E\right)+P_{m\to f}\left(E\right)V_m{Q}_{s,m}\left(E\right)(1)$

where ${\mathrm{\Sigma }}_{t,f}\left(E\right)$ is the macroscopic total cross section in the fuel; ${\varphi }_f\left(E\right)$ is the neutron flux in the fuel; $V_f$ and $V_m$ are the volumes of the fuel and moderator, respectively; $P_{f\to f}\left(E\right)$ and $P_{m\to f}\left(E\right)$ are the fuel-to-fuel and moderator-to-fuel collision probabilities, respectively; $Q_{s,f}\left(E\right)$ and $Q_{s,m}\left(E\right)$ are scattering sources in the fuel and moderator, respectively.

By neglecting anisotropic, inelastic and up scatterings, scattering sources are simplified to

$Q_{s,f}\left(E\right)={\displaystyle \sum }_{k\in f}{\int }_E^{E/{\alpha }_k}\frac{N_k{\sigma }_{s,k}\left(E^{\prime }\right){\varphi }_f\left(E^{\prime }\right)}{\left(1-{\alpha }_k\right)E^{\prime }}d{E}^{\prime }(2)$

$Q_{s,m}\left(E\right)={\displaystyle \sum }_{k\in m}{\int }_E^{E/{\alpha }_k}\frac{N_k{\sigma }_{s,k}\left(E^{\prime }\right){\varphi }_m\left(E^{\prime }\right)}{\left(1-{\alpha }_k\right)E^{\prime }}d{E}^{\prime }(3)$

where $N_k$ is the number density of nuclide k; ${\sigma }_{s,k}\left(E^{\prime }\right)$ is the scattering cross section of nuclide k; ${\alpha }_k$ = ${\left(1-{\mathrm{A}}_k\right)}^2/{\left(1+{\mathrm{A}}_k\right)}^2$; ${\mathrm{A}}_k$ is the mass of nuclide k.

The shape of the neutron spectrum is assumed as 1/E in the slowing-down source calculation, that is,

${\varphi }_i\left(E\right)\approx \frac{1}{E}\left(i=f,m\right)(4)$

The scattering cross sections of nuclides in the fuel and moderator are considered as constant, and assumed to be equal to potential scattering cross sections. With these assumptions and the narrow resonance approximation, scattering sources in the fuel and moderator are simplified to

$\begin{array}{l}{Q}_{s,i}\left(E\right)={\displaystyle \sum }_{k\in i}{\int }_E^{E/{\alpha }_k}\frac{N_k{\sigma }_{s,k}\left(E^{\prime }\right){\varphi }_i\left(E^{\prime }\right)}{\left(1-{\alpha }_k\right)E^{\prime }}d{E}^{\prime }\\ ={\displaystyle \sum }_{k\in i}{N}_k{\sigma }_{p,k}{\int }_E^{E/{\alpha }_k}\frac{1}{\left(1-{\alpha }_k\right)E^{\prime }}\frac{d{E}^{\prime }}{E^{\prime }}\left(i=f,m\right)\\ =\frac{1}{E}{\displaystyle \sum }_{k\in i}{N}_k{\sigma }_{p,k}\\ =\frac{1}{E}{\Sigma }_{p,i}\end{array}(5)$

where ${\Sigma }_{p,i}$ is the macroscopic potential scattering cross section in region i.

In the two-region system, the fuel-to-fuel collision probability can be written as the fuel-to-moderator collision probability

$P_{f\to f}\left(E\right)=1-P_{f\to m}\left(E\right)(6)$

By substituting Eqs. 5, 6 into Eq. 1, it becomes

${\mathrm{\Sigma }}_{t,f}\left(E\right){\varphi }_f\left(E\right)V_f=\frac{1}{E}\left(\left(1-P_{f\to m}\left(E\right)\right)V_f{\mathrm{\Sigma }}_{p,f}+P_{m\to f}\left(E\right)V_m{\mathrm{\Sigma }}_{p,m}\right)(7)$

To simplify Eq. 7, the reciprocity theorem is considered:

$P_{m\to f}\left(E\right)V_m{\mathrm{\Sigma }}_{p,m}=P_{f\to m}\left(E\right)V_f{\mathrm{\Sigma }}_{t,f}(8)$

In Eq. 8, the total cross section of the moderator is assumed to be equal to the potential scattering cross section.

By substituting Eq. 8 into Eq. 7, the flux in the fuel becomes

${\varphi }_f\left(E\right)=\frac{1}{E}\left(\left(1-P_{f\to m}\left(E\right)\right)\frac{{\mathrm{\Sigma }}_{p,f}}{{\mathrm{\Sigma }}_{t,f}\left(E\right)}+P_{f\to m}\left(E\right)\right)(9)$

With the Wigner’s rational approximation for the escape probability, the fuel-to-moderator collision probability becomes

$P_{f\to m}\left(E\right)=\frac{{\mathrm{\Sigma }}_e}{{\mathrm{\Sigma }}_{t,f}\left(E\right)+{\mathrm{\Sigma }}_e}(10)$

where ${\Sigma }_e$ is the macroscopic escape cross section.

However, the actual reactor core is a lattice system instead of two-region system. There are many fuel regions in a core. And the neutron that should have entered the fuel region in the two-region system may enter other fuel regions in a lattice system. In order to consider the spatial shadowing effect in a lattice system, the fuel-to-moderator collision probability is corrected to

$P_{f\to m}\left(E\right)=\frac{D{\mathrm{\Sigma }}_e}{{\mathrm{\Sigma }}_{t,f}\left(E\right)+D{\mathrm{\Sigma }}_e}(11)$

where D is the Dancoff factor.

By substituting Eq. 11 into Eq. 9, the flux becomes

$\begin{array}{l}{\varphi }_f\left(E\right)=\frac{1}{E}\frac{{\mathrm{\Sigma }}_{p,f}+D{\mathrm{\Sigma }}_e}{{\mathrm{\Sigma }}_{t,f}\left(E\right)+D{\mathrm{\Sigma }}_e}\\ =\frac{1}{E}\frac{{\sigma }_{p,r}+\left({\displaystyle \sum }_{k\ne r}{N}_k{\sigma }_{p,k}+D{\mathrm{\Sigma }}_e\right)/N_r}{{\sigma }_{t,r}+\left({\displaystyle \sum }_{k\ne r}{N}_k{\sigma }_{p,k}+D{\mathrm{\Sigma }}_e\right)/N_r}\end{array}(12)$

The background cross section for nuclide r is given by

${\sigma }_{b,r}=\left({\displaystyle \sum }_{k\ne r}{N}_k{\sigma }_{p,k}+D{\mathrm{\Sigma }}_e\right)/N_r(13)$

In the pressurized water reactor analysis, the intermediate resonance (IR) approximation is used instead of the narrow resonance (NR) approximation. With the IR approximation, the background cross section for nuclide r becomes

${\sigma }_{b,r}=\left({\displaystyle \sum }_{k\ne r}{\lambda }_k{N}_k{\sigma }_{s,k}+D{\mathrm{\Sigma }}_e\right)/N_r(14)$

The Dancoff factor can be calculated by using the ENCM and the background cross sections are calculated. Then, effective cross sections can be evaluated from pre-tabulated self-shielded cross section tables. Background cross sections are updated by using new effective cross sections. The process is repeated until convergence.

1-D pin-resolved ultra-fine-group with correction method

From the review, it can be seen that several assumptions are used in the equivalence theory:

(1) The neutron slowing down is dominated by the elastic scattering. The scattering source can be simplified by assuming no anisotropic and inelastic scatterings, no up-scattering and only elastic scattering.

(2) The shape of the neutron spectrum is assumed as 1/E in the slowing-down source calculation.

(3) A nonresonant nuclide has a constant scattering cross section which is assumed to be equal to the potential scattering cross section. And the total cross section of a nonresonant nuclide is also assumed to be equal to the potential scattering cross section.

(4) NR and IR approximations.

(5) The escape probability from a fuel is simplified with the rational approximation. And the material composition and temperature in the fuel are assumed to be spatially constant.

In order to improve the resonance calculation accuracy, assumptions (2–5) are eliminated and the ultra-fine-group slowing-down equation for the 1-D plate-type model is used. And assumption (1) is still used to simplify the scattering source in the slowing-down equation. Reflective boundary conditions are used in the 1-D plate-type model. To consider the shadowing effect in the actual lattice system, the effective cross section calculated by the ultra-fine-group method in the 1-D plate-type model is corrected with the shadowing effect correction factor as follows:

${\sigma }_{r,i}={\sigma }_{r,i}^{\mathrm{i}\mathrm{n}\mathrm{f}}\frac{{\sigma }_{r,F}\left(D_{lat}\right)}{{\sigma }_{r,F}\left(D_{\mathrm{i}\mathrm{n}\mathrm{f}}\right)}(15)$

where ${\sigma }_{r,i}$is the effective cross section of resonant nuclide r in region i; ${\sigma }_{r,i}^{\mathrm{i}\mathrm{n}\mathrm{f}}$is the cross section estimated in the 1-D plate-type model with the ultra-fine-group calculation; $D_{lat}$is the position-dependent Dancoff factor for the fuel pin in the actual lattice system; $D_{\mathrm{i}\mathrm{n}\mathrm{f}}$is the Dancoff factor for the 1-D plate-type model; ${\sigma }_{r,F}\left(D_{lat}\right)$ and ${\sigma }_{r,F}\left(D_{\mathrm{i}\mathrm{n}\mathrm{f}}\right)$ are cross sections in the fuel plate calculated by using the equivalence theory with $D_{lat}$ and $D_{\mathrm{i}\mathrm{n}\mathrm{f}}$, respectively. In Eq. 15, the shadowing effect of region i in the fuel plate is assumed to be equal to that of the fuel plate and the assumption has no significant impact on effective cross sections (Rao et al., 2022).

This pin-resolved ultra-fine-group with correction method is implemented with a MOC code. And the collision probability method for 1-D slab geometry is also implemented to perform the 1-D ultra-fine-group calculation. The cross section library is based on ENDF/B-VII.0 and its energy structure is WIMS-69 group structure (IAEA, 2007). The resonance energy range is from 0.625 eV to 24.78 keV (13th group to 45th group), which is divided into 50,000 groups by equal division for lethargy in the 1-D ultra-fine-group slowing-down calculation.

The calculation process of the PUCM is as follows:

(1) $D_{lat}$ for each fuel plate is calculated by the ENCM.

(2) $D_{\mathrm{i}\mathrm{n}\mathrm{f}}$ in the 1-D plate-type model is evaluated by the ENCM with reflective boundary conditions.

(3) The ultra-fine-group calculation is performed to calculate the cross sections ${\sigma }_{r,i}^{\mathrm{i}\mathrm{n}\mathrm{f}}$ in the 1-D plate-type model.

(4) Effective cross sections from the ultra-fine-group method are corrected as shown in Eq. 15.

(5) Repeat Steps (2–4) for each fuel plate.

Numerical results

Plate cell with spatially constant material composition and temperature

In this section, a plate cell with the uniform material composition and temperature distribution was calculated. The geometry of the plate cell is shown in Figure 1 and compositions of materials are from the Mosteller benchmark problem (Mosteller, 2007), given in Table 1. The temperature in all regions is 600 K.

FIGURE 1

FIGURE 1. The geometry of the plate cell problem, unit in cm.

TABLE 1

TABLE 1. Material compositions.

Reference results were calculated by a continuous-energy Monte Carlo code RMC (Wang et al., 2015). The statistic errors of cross sections are less than 0.05%. Detailed total and absorption cross sections of main resonant nuclides for 15 energy groups from 4 eV to 24.78 keV are compared in Figures 2, 3. The errors for total cross sections of all nuclides are less than 2.5%. In particular, the errors for ²³⁵U, ²³⁸U, ²³⁹Pu and ²⁴¹Pu total cross sections are less than 1.5%. As for absorption cross sections, the errors for ²³⁵U, ²³⁸U, ²³⁹Pu and ²⁴¹Pu are also less than 1.5%. The maximum error of ²⁴⁰Pu absorption cross sections is 3.65%. The absolute values of errors for ²⁴²Pu absorption cross sections in Groups 16–19 (906.898 eV-5.53 keV) exceed 3% and the minimum error is −7.22% in Group 17 (2.23945 keV–3.5191 keV). However, because ²⁴²Pu absorption cross sections in Groups 16–19 are relatively small and the number density of ²⁴²Pu is also small, the deviation of ²⁴²Pu absorption reaction rates may also be small. Table 2 shows the comparison of the k_eff. The relative error of k_eff is -70.7 pcm, which means the k_eff calculated by the PUCM agree well with the reference result.

FIGURE 2

FIGURE 2. Comparison of resonant nuclides’ total cross sections.

FIGURE 3

FIGURE 3. Comparison of resonant nuclides’ absorption cross sections.

TABLE 2

TABLE 2. k_eff for the plate cell.

Plate cell with spatially dependent material composition and temperature

To verify the ability to deal with the space-dependent self-shielding effect in the fuel dump, a plate cell with the spatially dependent material composition and temperature was calculated in this section. The geometry of the plate cell is shown in Figure 4 and compositions of materials are from the Mosteller benchmark problem, given in Tables 1, 3. The temperature in the fuel region filled with 6 wt% PuO₂ is 900 K, and that in other regions is 600 K.

FIGURE 4

FIGURE 4. The geometry of the plate cell with non-uniform material composition, unit in cm.

TABLE 3

TABLE 3. Material compositions.

Total and absorption cross sections of main resonant nuclides are compared in Figures 5–8. In the 6 wt% PuO₂ fuel, errors for total cross sections of all nuclides are less than 2.5%. In particular, errors for ²³⁵U, ²³⁸U, ²³⁹Pu and ²⁴¹Pu total cross sections are less than 1.5%. The errors for ²³⁵U, ²³⁸U, ²³⁹Pu and ²⁴¹Pu absorption cross sections are also less than 2.5%. The errors for ²⁴⁰Pu and ²⁴²Pu absorption cross sections are relatively large. The maximum error of ²⁴⁰Pu absorption cross sections is 3.61% and the minimum error of ²⁴²Pu absorption cross sections is −7.25%.

FIGURE 5

FIGURE 5. Comparison of resonant nuclides’ total cross sections in 6 wt% PuO₂.

FIGURE 6

FIGURE 6. Comparison of resonant nuclides’ absorption cross sections in 6 wt% PuO₂.

FIGURE 7

FIGURE 7. Comparison of resonant nuclides’ total cross sections in 8 wt% PuO₂.

FIGURE 8

FIGURE 8. Comparison of resonant nuclides’ absorption cross sections in 8 wt% PuO₂.

The errors of ²³⁸U total and absorption cross sections in Groups 24–25 for the 6 wt% PuO₂ fuel are larger than that for the 8 wt% PuO₂ fuel. In Group 25 (15.968 eV–27.7 eV), errors of ²³⁸U total and absorption cross sections in the 6 wt% PuO₂ fuel are 1.24% and 2.18%, respectively. Table 4 shows the comparison of the k_eff. The relative error of k_eff is −72.7 pcm.

TABLE 4

TABLE 4. k_eff for the plate cell with non-uniform material composition.

MTR plate-type fuel assembly

In this section, a standard plate-type fuel assembly was calculated. The geometry and compositions of materials are from the MTR benchmark problem (IAEA, 1980; Margulis and Gilad, 2016), given in Figure 9; Table 5. There are 23 fuel plates in the assembly. The length and width of the fuel assembly are 7.7 cm and 8.1 cm. The thickness and length of fuel dump is 0.051 cm and 6.30 cm. In order to perform the calculation accurately, each fuel plate was divided into 15 blocks and the length of each block is 0.42 cm. The fuel used in this calculation is LEU and the enrichment of ²³⁵U is 20 wt%. The material of the support frame is aluminum and its density is 2.7 g/cm³. The temperature in all regions is 600 K.

FIGURE 9

FIGURE 9. The geometry of the MTR fuel assembly.

TABLE 5

TABLE 5. Material compositions for MTR fuel assembly.

The k_eff is shown in Table 6. The k_eff produced by the PUCM agrees well with the reference result. Total and absorption cross sections in Regions 1–4 shown in Figure 9 are compared in Figures 10–13. Since the resonance self-shielding effect of ²³⁵U is relatively weak and errors of ²³⁵U cross sections are less than 0.5% as shown in previous sections, only ²³⁸U total and absorption cross sections are presented. The maximum error of ²³⁸U total and absorption cross sections in Regions 1–2 is around 1.5%, while that in Regions 3–4 is around 2.5%. The number of energy groups with a²³⁸U absorption cross section error greater than 1% in Regions 3–4 is 9 and in Regions 1–2 is 1.²³⁸U total and absorption cross sections in Regions 3–4 become more inaccurate than that in Regions 1–2. Since there are cladding and moderator in the right side of Regions 3–4 instead of fuel, the approximation of 1-D plate-type model in Regions 3–4 may cause more errors. The relative errors of fission rates in the assembly are presented in Figure 14. The maximum error is less than 0.22% and occurs in peripheral fuel blocks.

TABLE 6

TABLE 6. k_eff for MTR fuel assembly.

FIGURE 10

FIGURE 10. Comparison of ²³⁸U total and absorption cross sections in Region 1.

FIGURE 11

FIGURE 11. Comparison of ²³⁸U total and absorption cross sections in Region 2.

FIGURE 12

FIGURE 12. Comparison of ²³⁸U total and absorption cross sections in Region 3.

FIGURE 13

FIGURE 13. Comparison of ²³⁸U total and absorption cross sections in Region 4.

FIGURE 14

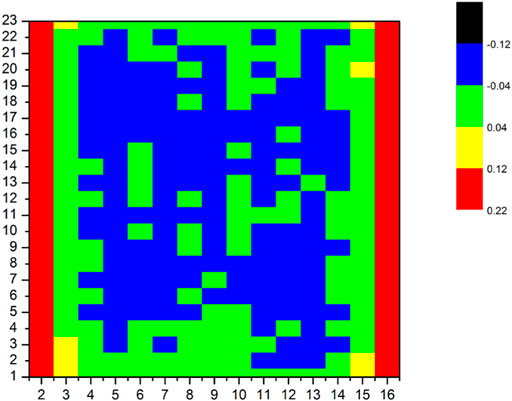
FIGURE 14. Relative error of fission rates distribution in the assembly, unit in %. Fuel blocks are numbered starts from 2.

MTR plate-type fuel cores

Both LEU and HEU MTR cores were calculated in this section. The geometry is presented in Figure 15. There are 21 standard fuel assemblies and 4 control assemblies surrounded by the water and graphite in the core. The fuel assembly in the core center is divided into two parts. The upper part consists of 12 fuel plates and the lower part consists of 11 fuel plates. The enrichment of ²³⁵U in HEU is 93 wt%. The density of graphite is 1.7 g/cm³. The material compositions are given in Tables 5, 7. The temperature in all regions is 600 K.

FIGURE 15

FIGURE 15. The geometry of the MTR core.

TABLE 7

TABLE 7. Material compositions for MTR core.

The k_eff results for LEU and HEU cores are presented in Tables 8, 9, respectively. The deviation of k_eff between the PUCM and RMC is around 200 pcm. The assembly-wise and plate-wise fission rates for both LEU and HEU cores are presented in Figures 16–19. The relative errors of assembly-wise fission rates are less than 1% in both LEU and HEU cores. Most plate-wise fission rate errors are less than 1.5%. However, fission rates of peripheral fuel plates are underestimated by more than 2% or even 5%. The root mean square (RMS) of plate-wise fission rate errors is around 1%.

TABLE 8

TABLE 8. k_eff for MTR core (LEU).

TABLE 9

TABLE 9. k_eff for MTR core (HEU).

FIGURE 16

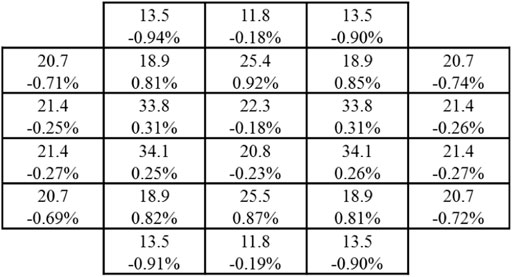
FIGURE 16. Fission rates in assemblies of MTR core (LEU). The number above is the fission rate calculated by the PUCM and the number below is the relative error.

FIGURE 17

FIGURE 17. The relative error of plate-wise fission rates in MTR core (LEU), unit in %.

FIGURE 18

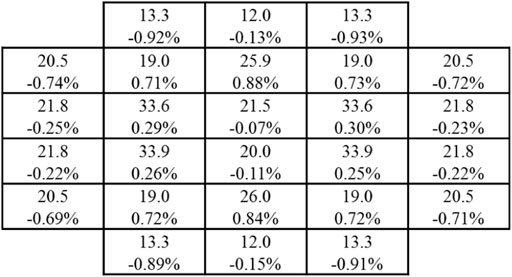
FIGURE 18. Fission rates in assemblies of MTR core (HEU). The number above is the fission rate calculated by the PUCM and the number below is the relative error.

FIGURE 19

FIGURE 19. The relative error of plate-wise fission rates in MTR core (HEU), unit in %.

Conclusion

The pin-resolved ultra-fine-group with correction method combining the ultra-fine-group method and equivalence theory is reviewed in this work. To eliminated errors introduced by several assumptions, for example, the escape probability from a fuel is simplified with the rational approximation, the ultra-fine-group slowing-down equation for the 1-D plate-type model is used. Meanwhile, to consider the shadowing effect in the actual lattice system, the effective cross section calculated by the ultra-fine-group method in the 1-D plate-type model is corrected with the shadowing effect correction factor calculated by the equivalence theory. And the pin-resolved ultra-fine-group with correction method is implemented in a MOC transport code and extended for the plate-type fuel. The collision probability method for 1-D slab geometry is also implemented to perform the 1-D ultra-fine-group calculation. The resonance energy range (0.625 eV–24.78 keV) is divided into 50,000 groups in the 1-D ultra-fine-group slowing-down calculation. The plate cell, assembly and core problems are calculated. Results produced by the PUCM show good consistency with reference results produced by RMC. The deviation of k_eff is less than 100 pcm for pin cell and assembly problems. And the relative error of ²³⁸U cross sections is less than 3%.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

JR: Main researcher and manuscript writer, XP: Researcher, YY: Advisor and director, QL: Advisor and director, KW: Advisor and director.

Funding

This work is supported by National Natural Science Foundation of China (Grant No. 11905214) and China Association for Science and Technology (Young Elite Scientists Sponsorship Program 2019QNRC001).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chiba, G., and Unesaki, H. (2006). Improvement of moment-based probability table for resonance self-shielding calculation. Ann. Nucl. Energy 33 (13), 1141–1146. doi:10.1016/j.anucene.2006.05.013

CrossRef Full Text | Google Scholar

Choi, S., Khassenov, A., and Lee, D. (2016). Resonance self-shielding method using resonance interference factor library for practical lattice physics computations of LWRs. J. Nucl. Sci. Technol. 53 (8), 1142–1154. doi:10.1080/00223131.2015.1095686

CrossRef Full Text | Google Scholar

Choi, S., Lee, C., and Lee, D. (2017). Resonance treatment using pin-based pointwise energy slowing-down method. J. Comput. Phys. 330, 134–155. doi:10.1016/j.jcp.2016.11.007

CrossRef Full Text | Google Scholar

He, Q. M., Cao, L. Z., Wu, H. C., Forget, B., and Smith, K. (2018). Predicting spatially dependent reaction rate for problem with nonuniform temperature distribution by subgroup method. Ann. Nucl. Energy 111, 188–203. doi:10.1016/j.anucene.2017.08.054

CrossRef Full Text | Google Scholar

Hong, S. G., and Kim, K.-S. (2011). Iterative resonance self-shielding methods using resonance integral table in heterogeneous transport lattice calculations. Ann. Nucl. Energy 38, 32–43. doi:10.1016/j.anucene.2010.08.022

CrossRef Full Text | Google Scholar

IAEA (1980). Research reactor core conversion from the use of high-enriched uranium to the use of low enriched uranium fuels guidebook, 233. TECDOCIAEA.

Google Scholar

International Atomic Energy Agency (2007). WIMS-D library update. Vienna: Non-serial Publications, IAEA.

Google Scholar

Knott, D., and Yamamoto, A. (2010). Lattice physics computation, volume II of handbook of nuclear engineering, 913–1239.

Google Scholar

Lee, C. H., and Yang, W. S. (2012). MC2-3: Multigroup cross section generation code for fast reactor analysis. January. ANL/NE-11-41.

Google Scholar

Liu, Y., and Martin, W. (2017). Pin-resolved resonance self-shielding methods in LWR direct transport calculations. Ann. Nucl. Energy 110, 1165–1175. doi:10.1016/j.anucene.2017.08.050

CrossRef Full Text | Google Scholar

Liu, Y., Martin, W., Williams, M., and Kim, K. S. (2015). A full-core resonance self-shielding method using a continuous-energy quasi–one-dimensional slowing-down solution that accounts for temperature-dependent fuel subregions and resonance interference. Nucl. Sci. Eng. 180, 247–272. doi:10.13182/nse14-65

CrossRef Full Text | Google Scholar

Liu, Z., He, Q., Zu, T., Cao, L., Wu, H., and Zhang, Q. (2017). The pseudo-resonant-nuclide subgroup method based global-local self-shielding calculation scheme. J. Nucl. Sci. Technol. 55, 217–228. doi:10.1080/00223131.2017.1394232

CrossRef Full Text | Google Scholar

Margulis, M., and Gilad, E. (2016). Monte Carlo and nodal neutron physics calculations of the IAEA MTR benchmark using Serpent/DYN3D code system. Prog. Nucl. Energy 88, 118–133. doi:10.1016/j.pnucene.2015.12.008

CrossRef Full Text | Google Scholar

Matsumoto, H., Ouisloumen, M., and Takeda, T. (2012). Development of spatially dependent resonance shielding method. J. Nucl. Sci. Technol. 42, 688–694. doi:10.1080/18811248.2004.9726438

CrossRef Full Text | Google Scholar

Mosteller, R. D. (2007). Monterey, California.The Doppler-defect benchmark: Overview and summary of results. Joint international topical meeting on mathematics & computational and supercomputing in nuclear applications (M&C + SNA 2007).

Google Scholar

Rao, J. J., Peng, X. J., Y, Y. R., Li, Q., and Wang, K. (2022). A new pin-resolved ultra-fine-group method based on global-local resonance treatment framework. Ann. Nucl. Energy 170, 108954. doi:10.1016/j.anucene.2021.108954

CrossRef Full Text | Google Scholar

Stamm’ler, R. J. J., and Abbate, M. J. (1983). Methods of steady-state reactor physics in nuclear design. London: Academic Press.

Google Scholar

Sugimura, N., and Yamamoto, A. (2007). Resonance treatment based on ultra-fine-group spectrum calculation in the AEGIS code. J. Nucl. Sci. Technol. 44 (7), 958–966. doi:10.1080/18811248.2007.9711335

CrossRef Full Text | Google Scholar

Tone, T. (1975). A numerical study of heterogeneity effects in fast reactor critical assemblies. J. Nucl. Sci. Technol. 12 (8), 467–481. doi:10.1080/18811248.1975.9733139

CrossRef Full Text | Google Scholar

Wang, K., Li, Z., She, D., Liang, J. G., Xu, Q., Qiu, Y. S., et al. (2015). Rmc – a Monte Carlo code for reactor core analysis. Ann. Nucl. Energy 82, 121–129. doi:10.1016/j.anucene.2014.08.048

CrossRef Full Text | Google Scholar

Williams, M. L., and Kim, K. S. (2012). The embedded self-shielding method. PHYSOR-2012. Knoxville, TN. April 15–20, 2012.

Google Scholar

Yamaji, K., Koike, H., Kamiyama, Y., Kirimura, K., and Kosaka, S. (2018). Ultra-fine-group resonance treatment using equivalent Dancoff-factor cell model in lattice physics code GALAXY. J. Nucl. Sci. Technol. 55, 756–780. doi:10.1080/00223131.2018.1439416

CrossRef Full Text | Google Scholar

Yamamoto, A., Endo, T., Tabuchi, M., Sugimura, N., Ushio, T., Mori, M., et al. (2010). Aegis: An advanced lattice physics code for light water reactor analysis. Nucl. Eng. Technol. 42, 500–519. doi:10.5516/net.2010.42.5.500

CrossRef Full Text | Google Scholar

Yamamoto, A. (2012). Evaluation of background cross section for heterogeneous and complicated geometry by the enhanced neutron current method. J. Nucl. Sci. Technol. 45, 1287–1292. doi:10.1080/18811248.2008.9711916

CrossRef Full Text | Google Scholar

Zhang, Q., Jiang, R., Zhao, Q., Cao, L. Z., and Wu, H. C. (2018). Accurate resonance absorption calculation for fuel pins with nonuniform intra-pellet temperature profile based on ultra-fine-group slowing-down calculations. Ann. Nucl. Energy 120, 392–401. doi:10.1016/j.anucene.2018.06.005

CrossRef Full Text | Google Scholar

Zhao, C., Peng, X. J., Zhang, H. B., Zhao, W., Chen, Z., and Li, Q. (2021). A linear source scheme for the 2D/1D transport method in SHARK. Ann. Nucl. Energy 161, 108479. doi:10.1016/j.anucene.2021.108479

CrossRef Full Text | Google Scholar

Zhao, C., Peng, X. J., Zhang, H. B., Zhao, W., Li, Q., and Chen, Z. (2022). Analysis and comparison of the 2D/1D and quasi-3D methods with the direct transport code SHARK. Nucl. Eng. Technol. 54, 19–29. doi:10.1016/j.net.2021.07.038

CrossRef Full Text | Google Scholar

Zheng, Y. Q., Du, X. N., Xu, Z. T., Zhou, S. C., Liu, Y., Wan, C. H., et al. (2018). Sarax: A new code for fast reactor analysis part I: Methods. Nucl. Eng. Des. 340, 421–430. doi:10.1016/j.nucengdes.2018.10.008

CrossRef Full Text | Google Scholar

Zu, T. J., Li, J. K., Yin, W., and Cao, L. Z. (2018). Accurate resonance calculation method coupling simplified embedded self-shielding method and ultra-fine group method. Ann. Nucl. Energy 120, 198–206. doi:10.1016/j.anucene.2018.05.040

CrossRef Full Text | Google Scholar