Methodology for updating GO-FLOW model to handle scenario changes in nuclear power plants

Introduction

Ensuring nuclear safety is the premise and foundation of nuclear power development (Wang et al., 2021). Before a nuclear power plant is put into commercial operation, it must be confirmed by safety review that the nuclear power plant is well designed to be safe enough under various hypothetical operation scenarios, even under accidents. However, in the process of operation, a nuclear power plant will inevitably experience various changes in configuration, success criteria, and even system design, resulting in various assumptions made in the safety analysis at the design stage may not remain valid and the operational risk in the actual operation of the nuclear power plant may rise and exceed the limit (Kafka, 1997).

Risk management is an activity which integrates recognition of risk, risk assessment, developing strategies to manage it, and mitigation of risk using managerial resources (Berg, 2010). One of the important tasks of operational risk management in a nuclear power plant is to evaluate whether any configuration change of the nuclear power plant can still achieve its expected safety and economic goals. Probabilistic Safety Assessment (PSA) is an effective means to assist nuclear power plants in risk management. Different from the PSA in the design stage, the PSA used in the operation stage of the nuclear power plant is called living PSA (Johanson and Holmberg, 1994).

The PSA in nuclear industry mainly relies on the so-called Fault Tree/Event Tree (FT/ET) method (Ibáñez-Llano et al., 2010). A fault tree conducts deductive analysis around the unexpected events of a system, such as system failure or loss of function, and identifies the causes of the unexpected events of the system level by level until the analysis boundary or the lowest level is reached (Lambert, 2004). One of the major advantages of this deductive analysis is that it is not easy to omit any failure modes, which ensures the transparency of the analysis process and the credibility of the analysis results. However, one disadvantage is that a FTA model in engineering is generally large, and different people may understand and describe the fault logic of a system in different ways, which is not easy to be understood by others. For this reason, each nuclear power design company generally forms a special department, and the works of PSA modeling and analysis are performed by professional personnel and it is difficult for operators of a nuclear power plant to modify the PSA model according to the changes of the nuclear power plant.

In recent years, some studies (Zhang et al., 2015; Chen et al., 2020) have attempted to establish PSA models that can be updated automatically or semi automatically according to the changes in a nuclear power plant. These studies use the modular approach to construct fault trees, and each module contains a group of states of a component. When a component state changes, only the corresponding component module needs to be updated, without changing the logical structure of the overall fault trees. In other words, these studies are based on a common basic assumption that the changes of a component state or system configuration will not affect the success/failure criteria of the system. This assumption is valid in most cases, but not always. When the system success/failure criteria or functional requirements change, the fault tree needs to be rebuilt manually.

GO-FLOW methodology is a success-oriented system reliability analysis method (Matsuoka and Kobayashi, 1991a; Matsuoka and Kobayashi, 1991b). GO-FLOW methodology was developed from GO methodology (Williams, 1978; Keley, 1983). However, GO-FLOW introduces the concept of signal which describes various flows in the industrial systems including mass, energy and control commands and the phased missions of a system at different time points can be described and analyzed. Therefore, a GO-FLOW model is to calculate the probability that a system can provide a specific flow at a specific time. This characteristic is particularly suitable for risk analysis of nuclear power plants, because the safety of nuclear power plants is closely related to the ability of relevant systems to provide and transfer coolant. Furthermore, because GO-FLOW describes the nature of flow in the system, a GO-FLOW model is very similar to the system structure, which lays a foundation for this paper to propose updating the GO-FLOW model to calculate the system reliability/risk under different scenarios.

The following sections are arranged as follows: section II provides a brief introduction of GO-FLOW methodology; section III introduces a new updating method of GO-FLOW model; section IV presents a case study for demonstrating the proposed GO-FLOW model update method, and summary and main conclusions are given in last section.

GO-FLOW methodology and its applications in nuclear industry

Basic principle of GO-FLOW methodology

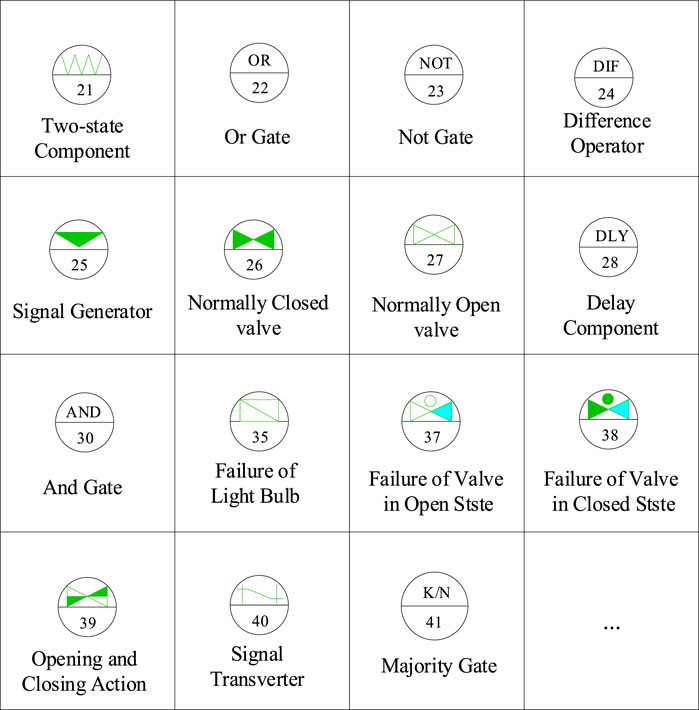
The GO-FLOW (Matsuoka and Kobayashi, 1993; Matsuoka and Kobayashi, 1997; Matsuoka, 2009) analyzes the reliability/availability of a system according to the GO-FLOW diagram of the system. As shown in Figure 1, a GO-FLOW diagram is composed of standard GO-FLOW operators and signal lines for connecting GO-FLOW operators.

FIGURE 1

FIGURE 1. Basic GO-FLOW operators.

A GO-FLOW operator indicates a function of a physical component, or a logic gate or a signal generator. A signal line represents the input-output relationship of two GO-FLOW operators. A signal flow represents a physical quantity or information, such as water flow, current, trigger signal, time interval, etc.

A GO-FLOW method measures a signal by intensity which represents the probability of the actual or potential existence of a physical quantity/information. In addition to indicating the probability of signal existence, an intensity can also indicate time information, such as the sub-input signals of GO-FLOW operators 35, 37, and 38 where the meaning of signal flow indicates the time interval between two time points.

GO-FLOW modeling approach

The steps of system analysis by GO-FLOW methodology are as follows (Matsuoka and Kobayashi, 1997):

1. System modeling with GO-FLOW chart;

2. Set relevant GO-FLOW operator parameters;

3. Perform GO-FLOW program analysis;

4. System result analysis.

GO-FLOW modeling assumptions include:

1. Systems and components have two states;

2. Component states are statistically independent;

3. Failure rate of a component is constant;

4. Repair rate of a component is constant

During the GO-FLOW modeling of a system, first one or more GO-FLOW operators are selected according to the characteristics of each element of the system. For example, Operator 21 is used for the transmission type of components, Operator 26 is used for the normally closed type of components and Operator 27 is used for the normally open type of components. Then corresponding logical operators are selected according to the structure of the system and the functional requirements of the system under a specific scenario to connect the components together to form a GO-FLOW chart. A GO-FLOW chart is therefore similar to the structure of the system. Next, a GO-FLOW operator is connected to a final signal, indicating that the output of the component corresponding to this operator is an object of system reliability/risk analysis. Finally, time points are set for operators. The sequence of time points reflects the dynamic time sequence characteristics of the components. The number of time points can be set according to the needs of analysis.

Applications of GO-FLOW methodology in reliability/risk monitoring of nuclear industry

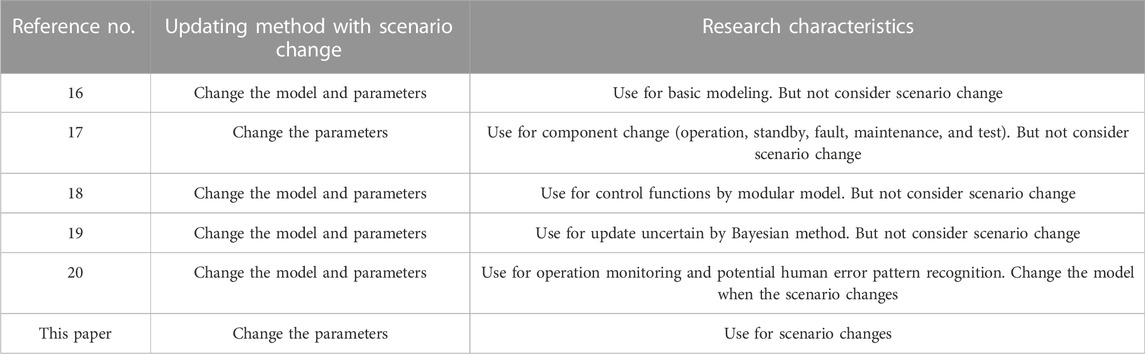
In the field of reliability analysis and risk monitoring of nuclear power plants, the authors proposed a hierarchical modeling method to improve the efficiency of GO-FLOW method in modeling, model updating and model calculation (Xinyu et al., 2017). Yang et al. (June 2016) proposed a dynamic PSA method for modeling and updating the typical states of components, including operation, standby, fault, maintenance, and test. The state of components can be updated as appropriate without changing the model. Lu et al. (Hongxin et al., 2019) extended the GO-FLOW methodology by introducing new GO-FLOW operators to describe the control functions for the usage of GO-FLOW for reliability/risk monitoring of nuclear power systems. Further, Lu et al. proposed a method to update the uncertainty states of component according to the human operator’s cognitive process (Hongxin et al., 2021). Yang et al. (Jun et al., 2022) recently proposed a comprehensive operation feasibility analysis framework based on GO-FLOW, in which a pattern matching algorithm based on process action library is used for operation monitoring and potential human error pattern recognition. Table 1 Provides an evolution process of the GO-FLOW model.

TABLE 1

TABLE 1. Representative GO-FLOW model updating method.

The traditional GO-FLOW models focus on the systems operating in a single scenario based on the following two assumptions:

a) the goal of a system is fixed: in other words, the change of success criteria does not need to be considered;

b) the components that achieve the system goal are also fixed, that is, the model does not include any components that do not contribute to the system objectives.

However, when the operating scenario changes, the above two modeling assumptions may change.

Moreover, with the development of nuclear power technology, the new generation of nuclear power plant is developing towards miniaturization and modularization. Some nuclear power systems are designed to be more compact and provide different functions for different operation conditions and scenarios. How to update the system reliability/risk model in time to reflect the scenario changes of a nuclear power plant has become a current research interest on the online reliability/risk analysis and monitoring of nuclear power plants.

Taking the Residual Heat Removal (RHR) system of a typical pressurized water reactor nuclear power plant as an example, it provides the different functions under the following typical scenarios (Matsuoka and Kobayashi, 1997):

■ Providing cooling during reactor startup and shutdown under normal operation conditions, and provides temperature regulation function for the reactor coolant system under low pressure operation conditions.

■ providing the redundant low-temperature overpressure protection channel for RCS.

■ Cool down the core by Recirculation Water Storage Tank (RWST) in the early state of Loss of Coolant Accident (LOCA).

■ Cool down the core using the water from the sump in LOCA after the RWST becomes empty.

■ Providing core cooling during refueling outage (mid-loop operation).

Because the temperature and capacity of water source are different in different scenarios, the RHR system is designed to use different components to provide cooling water with different flows and temperatures in different scenarios to ensure the safe operation of the nuclear power plant. If a system such as RHR is modeled separately by scenario in the reliability/risk monitoring model of the nuclear power plant, the following technical problems will arise.

■ The scale of the overall reliability/risk monitoring model will increase significantly.

■ When the design of a system changes or the state of a component changes, all relevant models need to be updated, which will make more efforts in the maintenance of GO-FLOW models.

In view of this, this paper proposes a general GO-FLOW modeling method to adapt the GO-FLOW model to various working conditions.

GO-FLOW modeling for scenario change

For a system, the following typical changes may occur when the scenario changes:

■ Configuration change: refers to the change of system configuration, including any component being out of service (e.g., in fault or maintenance state), switching from running to standby or vice versa, however, the success criteria of the system have not changed.

■ Success criteria change: refers to the change of the functional requirements of a system. For example, the components or ways of realizing the system functions have changed.

Assumed that the reliability (success probability) of a system to realize a specific task i is Ri:

${\mathit{R}}_{\mathit{i}}\left(\mathit{t}\right)={\mathit{f}}_{\mathit{i}}\left[{\mathit{C}}_{\mathbf{1}}\left(\mathit{t}\right),{\mathit{C}}_{\mathbf{2}}\left(\mathit{t}\right),\cdot \cdot \cdot ,{\mathit{C}}_{\mathit{n}}\left(\mathit{t}\right)\right](1)$

where Ci(t) refers to the i component of the system, t is the operation time of the system, fi is the reliability logic (function) of the components to realize the task i. The configuration change of the system refers to the change of Ci(t), but Ri or fi has not changed. The change of success criteria corresponds to the change of Ri or fi, and therefore includes the following two categories:

Category I: corresponds to the change of fi, i.e., the changes in system tasks.

Category II: corresponds to the change of Ci(t), i.e., the changes of the reliability logic of the components to realize a specific system task.

At present, most of the research on the application of GO-FLOW to the reliability/risk monitoring of nuclear power plants is focused on the configuration changes (June 2016; Xinyu et al., 2017; Hongxin et al., 2019). This paper focuses on how to build a GO-FLOW model to make it adaptable for the scenarios where the success criteria have changed.

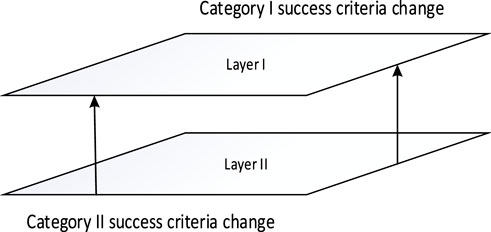
In this paper, a two-layer structure GO-FLOW method is proposed, which corresponds to the change of the success criteria of Category I (at Layer I) and Category II (at Layer II) respectively. Figure 2.

FIGURE 2

FIGURE 2. Two layers of GO-FLOW structure corresponding to the success criteria changes.

Category I success criteria change

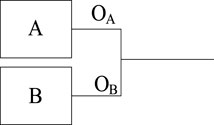
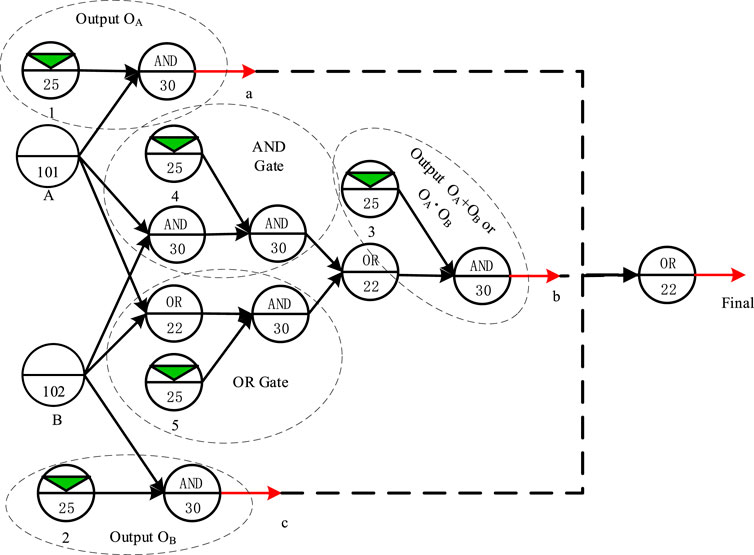
Without losing generality, the task change of a system composed of two components A and B is studied below, such as Figure 3. The output of component A is OA and the output of component B is OB. The system may be used for the following five scenario tasks.

■ Only component A is required to function.

■ Only component B is required to function.

■ Both components A and B are required to provide to function.

■ Either component A or B is required to function.

■ No component is required to function.

FIGURE 3

FIGURE 3. Two components system composed of (A) and (B).

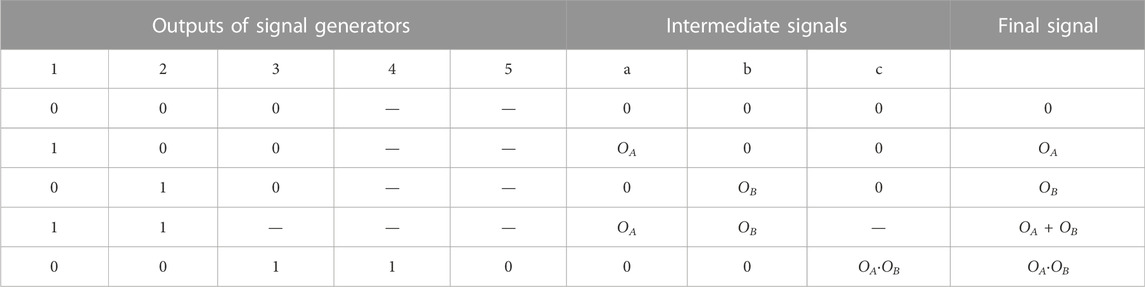
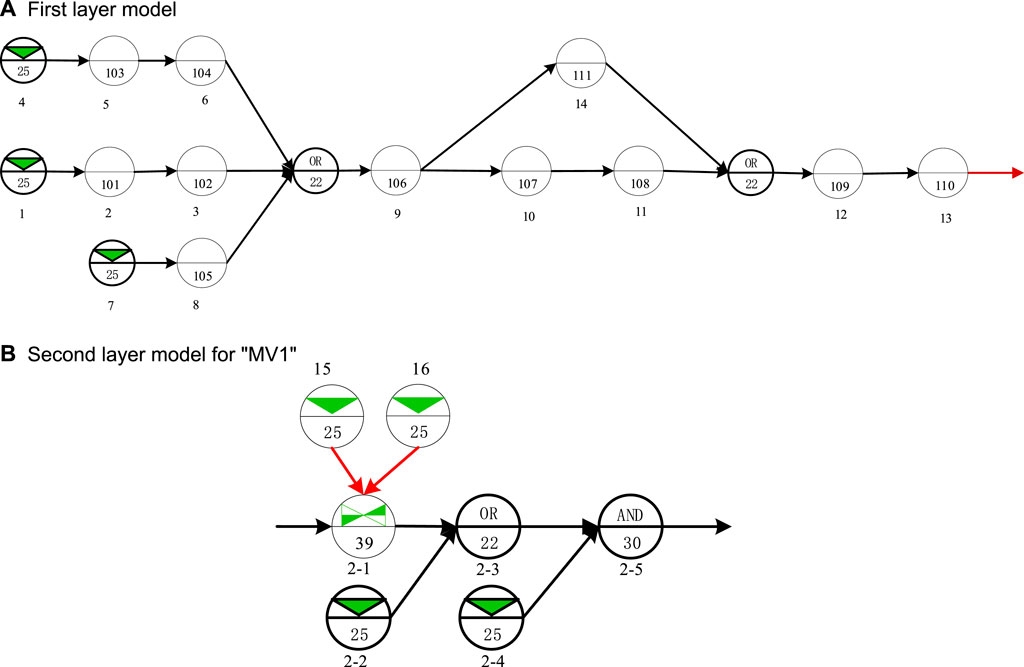
The GO-FLOW model of the system at Layer I is shown in Figure 4. The GO-FLOW operators 101 and 102 are two user-defined modules, respectively corresponding to components A and B, and the component characteristics of components A and B are defined by the models at Layer II. The final signal of the model integrates three intermediate signals, namely a, b and c. According to different scenarios, the final signal provides 0 (corresponding to no output), OA (The probability that only component A works), OB (The probability that only component B works), OA·OB. (The probability that both A and B work), and OA + OB. (The probability that either A or B works). In this model, five signal generators (Operators 25) are used to adjust the logic of the final signal generation. The signal combinations of the five signal generators and the corresponding final signals are shown in Table 2. Other signal combinations listed in the table are considered repetitive or meaningless. Since most complex logic can be combined by AND and OR logic, the change of the system success logic under the condition that the system configuration is unchanged can be controlled through the change of the signal combination.

FIGURE 4

FIGURE 4. GO-FLOW model at Layer I.

TABLE 2

TABLE 2. Final signal under various signal combinations at the 1st layer.

Category II success criteria change

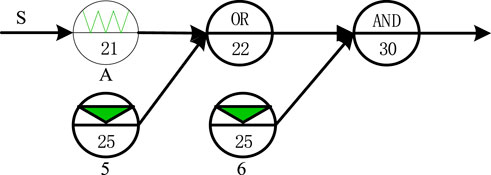
The 2nd layer of the model describes the changes of the success criteria caused by the characteristics and reliability logic of the components. Taking the GO-FLOW operator 101 in Figure 4 as an example, a model describing the characteristics of its component is shown in Figure 5. In this model, it is assumed that the operator 101 describes a conductive component, such as a pump. The characteristics of the component are described by the on a GO-FLOW operator 21, an AND gate, an OR gate and two signal generators (corresponding to the GO-FLOW operators 25). The signal combinations of the two signal generators and the corresponding final signals are shown in Table 3. It can be seen from the table that the model provides three states of the component, namely blocked, running and bypassed. “Running” is the working state of the component. “Blocked” means that the component blocks the flow. For example, when a pump is stuck, the function of the pump is changed from transport to barrier, resulting in cutting off the flow path. “Bypassed” means that the component is bypassed or the function of the component is ignored. For example, after a pump loses power supply, its function of providing the pressure head of fluid is lost, but the fluid can still pass through.

FIGURE 5

FIGURE 5. Modelling component characteristics at the second layer.

TABLE 3

TABLE 3. Final signal under various signal combinations at the second layer.

Case study

Scenario analysis of residual heat removal system

A RHR system of Pressurized Water Reactor (PWR) is taken as a study case to show the modeling and analysis of a system for reliability/risk analysis based on proposed new technology. The RHR is expected to be put into operation to provide cooling water for removing the heat from the Reactor Coolant System (RCS) in the case that the reactor is over-heating during the reactor shutdown.

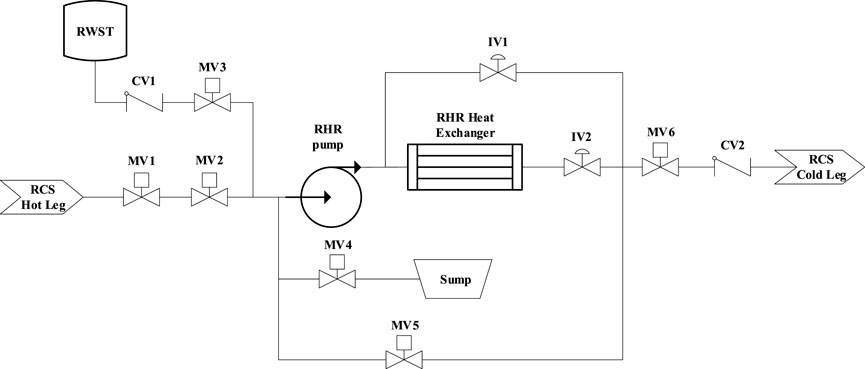
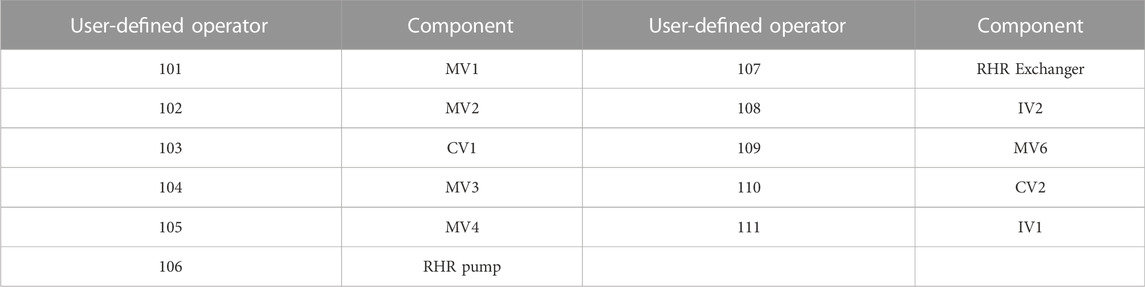
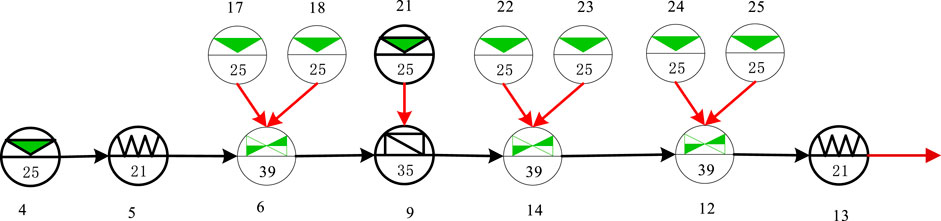
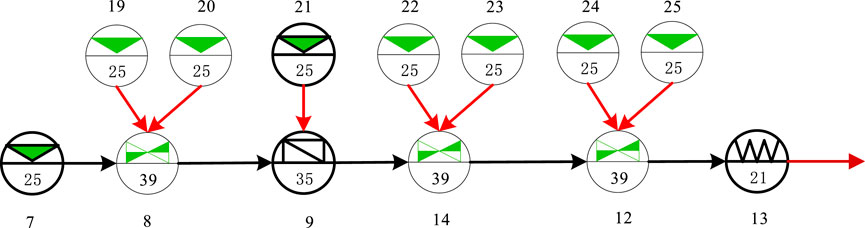
The structure of the RHR is shown in Figure 6. The system is composed of one RWST, one RHR pump, one RHR Heat Exchanger, six Motorized Valves (MV), two Check Valves (CV), and two Isolation Valves (IV). The RHR system may experience the following three scenarios:

■ Scenario 1: during the normal operation of nuclear power plant, water is taken from the hot leg of RCS, which is powered by the RHR pump and cooled by the RHR heat exchanger, and finally injected into the RCS cold leg. In this scenario, three Motorized Valves (MV1, MV2, MV6), one Isolation Valve (IV2) and one Check Valve (CV2) are put into use.

■ Scenario 2: After LOCA occurs, low temperature water is provided from RWST and directly injected into the cold leg of RCS by the RHR pump. In this scenario, two Motorized Valves (MV3, MV6), one Isolation Valve (IV1), and two Check Valve (CV1, CV2) are put into use.

■ Scenario 3: In case that the water supply from RWST is insufficient, water is taken from the sump and injected into the cold leg of RCS by the RHR pump for the purpose of 24 h cooling. In this scenario, Two Motorized Valves (MV4, MV6), one Isolation Valve (IV1), and one Check Valve (CV2) are put into use.

FIGURE 6

FIGURE 6. Structure of the RHR system.

If too much water flow into the cold leg of RCS, the cooling water can be refluxed by opening MV5 to slow down the cooling rate.

GO-FLOW modeling in traditional way

In this case study, the following assumptions are made for modeling the RHR system with the GO-FLOW methodology. The water source will supply enough cooling water during each situation.

■ The failures of all pipelines are not considered.

■ The failures of the start signal for pumps and valves are not considered.

■ MV5 is only involved in system regulation and is considered to be available at any time.

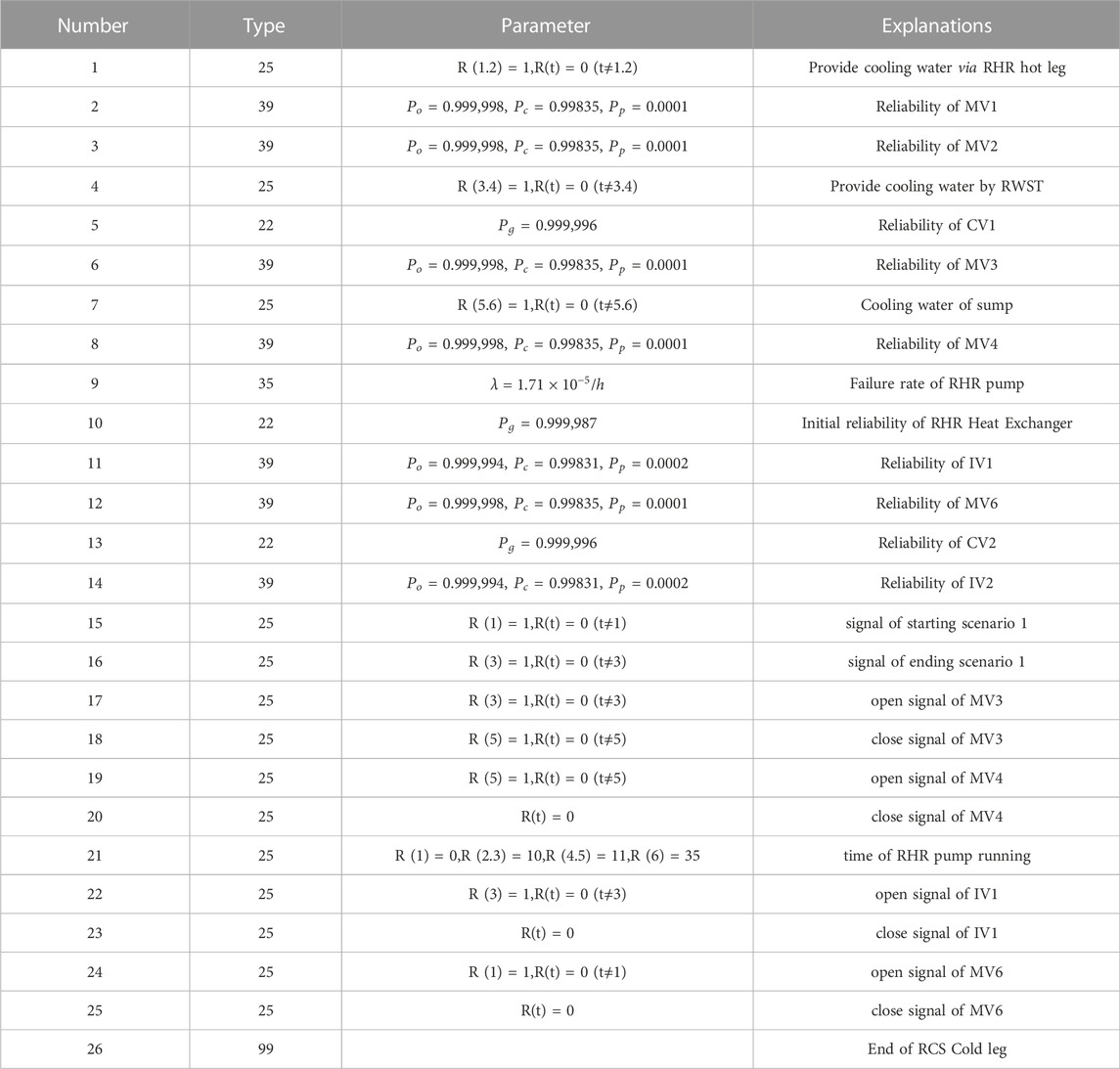
The GO-FLOW model parameters of RHR system are listed in Table 4. In order to demonstrate the application of GO-FLOW model in different scenarios, the following time points are set in the GO-FLOW model.

■ Time point 1: The RHR system works in scenario 1. No accident occurred in the reactor. The MV1, MV2, IV2, and MV6 are open, while the other valves are closed.

■ Time point 2: The RHR system works in scenario one for 10 h.

■ Time point 3: LOCA accident occurs. The RHR system works in scenario 2. The MV3 and IV1 are open, and the MV1, MV2 and IV2 are closed.

■ Time point 4: The RHR system work in scenario two for 1 h.

■ Time point 5: The RHR system works in scenario 3. The water in RWST becomes insufficient to supply the coolant of reactor. The MV4 is open and the MV3 is closed.

■ Time point 6: The RHR system works in scenario three for 24 h.

TABLE 4

TABLE 4. User-defined operators and corresponding components.

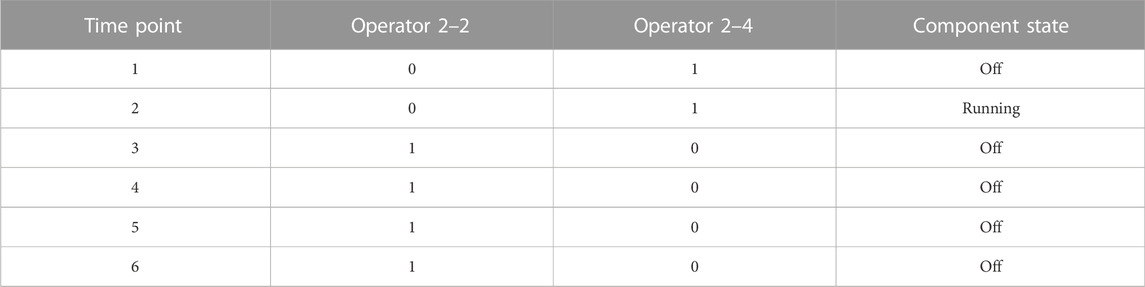
Figure 7 Figure 8 Figure 9 present the GO-FLOW models built in a traditional way for each different scenario. The GO-FLOW model established by the adaptive system success criterion updating method proposed in this paper is shown in Figure 10, where Figure 10A is the first layer model and Figure 10B is the MV1 model as an example of the component model at the second layer. Table 4 shows the user-defined operators and corresponding components in the first layer GO-FLOW model. Table 5 shows the control signals (2–2) of MV1 at each time point and the corresponding component states. Table 6 provides the reliability data for the RHR system reliability calculation and the calculation results by the traditional modeling way and new way are given in Table 7. In the traditional modeling way, the result of time1,2 come from scenario one; the result of time3,4 come from scenario two; the result of time5,6 come from scenario 3.

FIGURE 7

FIGURE 7. GO-FLOW model for scenario 1.

FIGURE 8

FIGURE 8. GO-FLOW model for scenario 2.

FIGURE 9

FIGURE 9. GO-FLOW model for scenario 3.

FIGURE 10

FIGURE 10. New GO-FLOW model.

TABLE 5

TABLE 5. Changes with time of signal.

TABLE 6

TABLE 6. Parameters of the GO-FLOW model.

TABLE 7

TABLE 7. Final result.

Discussion

Nuclear power plants include more compact designs and can perform a variety of tasks depending on the scenarios. A recent area of research on the online reliability/risk analysis and monitoring of nuclear power plants is how to update the system reliability/risk model in time to reflect scenario changes of a nuclear power plant. For modeling a system operating in multiple scenarios by the traditional GO-FLOW method, each scenario needs to be modeled separately, which often leads to an annoying repetitive modeling and analysis burden. This paper provides a practical GO-FLOW modeling approach to describe the variation of the model probability in different scenarios.

While convenient, this model adopts several issues. The method will be examined further in this research by looking at its applicability, flexibility, uncertainty, and consistency.

Since this method is based on the GO-FLOW model for modeling, the overall direct reliability calculation in conjunction with a quick fault tree algorithm is used to address the shared signal problem. As a result, the model can be configured to match the system configuration without the need to describe the system failure logic starting from various equipment failure modes as in a fault tree, preventing the model from growing out of control. The flexibility of utilizing hierarchical modeling, which does not need to reevaluate the overall system dependability logic while making local alterations, is another advantage of the technique. With this model, just the parameters need to be changed when the scenario changes rather than having to re-construction the layer. The model provides flexibility while increasing its complexity of the model. Its model size is larger than the original model in any single scenario but smaller than the sum of all original models. So, the approach is more suitable for modeling systems with variable scenarios.

Probabilistic estimates used in risk assessment do not accurately capture the system’s utmost reality. The nature of various situations has led to a variety of definitions for uncertainty. Simply said, there are three primary places where uncertainties might come from quality uncertainty, model uncertainty, and data uncertainty. While “Parameter Uncertainties” depend on the type of calculations and study parameters, “Model Uncertainty,” and “Completeness Uncertainty” depend on the expert’s experience, knowledge, and attitude (Lim, 2018; Mohammad, 2022). On the one hand, this paper offers a procedural GO-FLOW modeling approach that standardizes the modeling process for staff and may be utilized to reduce “Model Uncertainty” and “Completeness Uncertainty.” But on other hand, complex modeling will increase the uncertainty of the model. As the methods can be logically equivalent to the traditional model, “Parameter Uncertainties” are essentially equivalent to the traditional GO-FLOW method, which is taken into account in Ref. 14 and is not extensively discussed in this study. (He and Mohammad, 2022).

As a whole, In Table 8, a benchmarking with the traditional GO-FLOW method is provided.

TABLE 8

TABLE 8. Benchmarking with the traditional GO-FLOW method.

Conclusions

In this paper, a new GO-FLOW modeling approach is proposed to analyze the reliability of a system of which success criteria may change in different scenarios. A two-layer hierarchical modeling framework is adopted. The first layer uses user-defined operators to avoid the model being too complicated due to the detailed description of component characteristics. At the same time, the main line of the model is highly similar to the system schematic diagram. The second layer describes the dynamic characteristics of the elements. Because of the independence of the components, independent calculation can be carried out for each element, and the calculation results are summarized into the first layer model, which will significantly improve the calculation efficiency. The consistency of the calculation results of the new and old methods is verified by a case. The method proposed in this paper is suitable for online system reliability/risk analysis based on the GO-FLOW method. It is possible to avoid difficulties in model modification and upgrading caused by using multiple models.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

DX substantial contributions to the conception or design of the work; or the acquisition, analysis, or interpretation of data for the work. YM drafting the work or revising it critically for important intellectual content and provide approval for publication of the content XZ and WH agree to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. WJ provides article polish.

Funding

This work was supported by Shenzhen Natural Science Fund (the Stable Support Plan Program 20220810124935001). This work was also supported by the Stable Support Plan Program under Shenzhen Natural Science Fund Contract No. 20220811012323001.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Berg, H. P. (2010). Risk management: Procedures, methods and experiences. Reliab. Theory Appl. 5 (17), 79–95.

Google Scholar

Chen, S., Zhang, Z., Zhang, H., Zhang, M., Wang, H., Ma, Y., et al. (2020). Research on living PSA method based on time-dependent MFT for real-time online risk monitoring. Ann. Nucl. Energy 143, 107406. doi:10.1016/j.anucene.2020.107406

CrossRef Full Text | Google Scholar

He, L., and Mohammad, Y. (2022). Advanced decision-making methods and applications in system safety and reliability problems. Switzerland: Springer Cham.

Google Scholar

Hongxin, L., Ming, Y., Xinyu, D., Li, W., and Yang, J. (2019). Reliability modeling by extended GO-FLOW methodology for automatic control component and system at NPP. Nucl. Eng. Des. 342, 264–275. doi:10.1016/j.nucengdes.2018.11.030

CrossRef Full Text | Google Scholar

Hongxin, L., Ming, Y., and Zhihui, X. (2021). Study on evidence-based LPSA method in nuclear power plant under abnormal operating conditions. Ann. Nucl. Energy 151, 264–275. doi:10.1016/j.anucene.2020.107874

CrossRef Full Text | Google Scholar

Ibáñez-Llano, C., Rauzy, A., Meléndez, E., and Nieto, F. (2010). Hybrid approach for the assessment of PSA models by means of binary decision diagrams. Reliab. Eng. Syst. Saf. 95 (10), 1076–1092. doi:10.1016/j.ress.2010.04.016

CrossRef Full Text | Google Scholar

Johanson, G., and Holmberg, J. (1994). Safety evaluation by living probabilistic safety assessment. procedures and applications for planning of operational activities and analysis of operating experience. Swed. Nucl. Power Insp. 94, 2.

Google Scholar

Jun, Y. (2016). Research on reliability analysis techniques used for risk monitoring at NPPs. Harbin, China: Harbin Engineering University.

Google Scholar

Jun, Y., Xue, Y., Xinyu, D., Lu, H., and Yang, M. (2022). An intelligent operational supervision system for operability and reliability analysis of operators manual actions in Task Implementation. Process Saf. Environ. Prot. 158, 340–359. doi:10.1016/j.psep.2021.12.023

CrossRef Full Text | Google Scholar

Kafka, P. (1997). Living PSA-risk monitoring—Current use and developments. Nucl. Eng. Des. 175 (3), 197–204. doi:10.1016/s0029-5493(97)00037-x

CrossRef Full Text | Google Scholar

Keley, A. P. (1983). Go methodology. Washington: Electric Power Research Institute.

Google Scholar

Lambert, H. E. (2004). Use of fault tree analysis for automotive reliability and safety analysis. SAE Trans. 2004, 690–696. doi:10.4271/2004-01-1537

CrossRef Full Text | Google Scholar

Lim, J. (2018). Temperature limit in the RHR system when aligned to the ECCS. Ann. Nucl. Energy 118, 400–405. doi:10.1016/j.anucene.2018.04.038

CrossRef Full Text | Google Scholar

Matsuoka, T. (2009). An exact method for solving logical loops in reliability analysis. Reliab. Eng. Syst. Saf. 94, 1282–1288. doi:10.1016/j.ress.2009.01.007

CrossRef Full Text | Google Scholar

Matsuoka, T., and Kobayashi, M. (1991). “Development of the GO-FLOW reliability analysis support system,” in Proceedings of an international symposium probabilistic safety assessment (Vienna: International Atomic Energy Agency IAEA), 677–688.

Google Scholar

Matsuoka, T., and Kobayashi, M. (1991). GO-FLOW: A system reliability analysis methodology. Probability Safety Assessment and Management, 525–532.

Google Scholar

Matsuoka, T., and Kobayashi, M. (1997). The GO-FLOW reliability analysis methodology-analysis of common cause failures with uncertainty. Nucl. Eng. Des. 175, 205–214. doi:10.1016/S0029-5493(97)00038-1

CrossRef Full Text | Google Scholar

Matsuoka, T., and Kobayashi, M. (1993). “The incorporation of common cause failures into the GO-FLOW methodology,” in Proceedings of the probabilistic safety assessment international topical meeting (Florida: IAEA), 811–817.

Google Scholar

Mohammad, Y. (2022). Linguistic methods under fuzzy information in system safety and reliability analysis. Switzerland: Springer.

Google Scholar

Wang, Z., Zhang, L., and WangCNPO, J. (2021). Exploring a new safety management and control mode for nuclear power in-service inspection//IOP conference series: Earth and environmental science. IOP Publ. 651 (2), 022002. doi:10.1088/1755-1315/651/2/022002

CrossRef Full Text | Google Scholar

Williams, R. L. (1978). Go methodology-overview. Washington: Electric Power Research Institute.

Google Scholar

Xinyu, D., Ming, Y., and Bowen, Z. (2017). “Hierarchical modeling of go-flow models for online risk monitoring of nuclear power plants,” in Proceedings of the 2017 25th international conference on nuclear engineering (Shanghai, China: ASME), 67543.

CrossRef Full Text | Google Scholar

Zhang, M., Zhang, Z., and Chen, S. (2015). Living PSA modeling and updating for online risk monitoring. Int. Electron. J. Nucl. Saf. Simul. 6 (1), 20–29.

Google Scholar