Research on security-constrained unit commitment based on an improved ordinal optimization algorithm

It is of great significance for the development of intermittent renewable energy and the marketization of electricity to study an efficient and accurate algorithm for solving the unit commitment problem with security constraints. Based on the existing constrained ordinal optimization (COO) algorithm, an improved ordinal optimization (OO) algorithm is proposed, which can be applied to solve SCUC problems. In order to solve the rough model and the accurate model, the discrete variable identification strategy and the effective safety constraint reduction strategy are adopted, respectively. Compared with the traditional object-oriented algorithm, the improved object-oriented algorithm not only gives full play to the computational efficiency of the traditional object-oriented algorithm but also further improves the compactness and reduces the computational redundancy. IEEE 118 simulation results verify the correctness and effectiveness of the algorithm.

Introduction

Under the background of large-scale wind power integration, SCUC considering the uncertainty of wind power has become not only the main basis for making a day-ahead generation schedule but also an important basis for day-ahead power market decision-making (Shi et al., 2016). On the one hand, SCUC is a large-scale mixed-integer planning problem with constraints and nonlinearity in math (Zhang et al., 2013). On the other hand, it is a typical non-deterministic polynomial hard problem in solving. With the scale of a power grid being increasingly enlarged and more intermittent renewable energy integration, the difficulty of solving SCUC problems has been increasing daily (Yang et al., 2022a). Therefore, how to solve the SCUC problems with the uncertainty of wind power quickly and effectively has become a research focus (Nan et al., 2018).

For solving the uncertain SCUC models, the recent mainstream method is based on Benders decomposition (BD). With the help of BD, the SCUC model can be decomposed into two subproblems which are unit commitment and network security constraint check. Then, the Lagrangian relaxation method (Zhang et al., 2012), dynamic programming method (Chen et al., 2015), branch and bound method (Hussin and Hassan, 2014), and different kinds of intelligent optimization algorithms (Lee and Lin, 2012; Chen et al., 2021; Li et al., 2021; Ma et al., 2021; Yang et al., 2022b; Yang et al., 2022c; Wang et al., 2022; Zhou et al., 2022; Zhu et al., 2022) can be used to solve each subproblem. The first three methods have a strict mathematical model, but the Lagrangian relaxation method is affected by the sensitivity of the unit to the Lagrangian multiplier, and the oscillation phenomenon is easy to occur in the iterative process of the algorithm. The dynamic programming method is easy to cause a “dimension disaster” problem; if the bound estimation of the branch and bound method is wrong, it is no different from an exhaustive search in extreme cases. The intelligent optimization algorithm is used for uncertain optimization problems with complex constraints, and an iterative calculation is used to deal with constraint subproblems in various scenarios, which requires a lot of calculation time. In short, the solving efficiency has been difficult to meet the needs of engineers (Lee and Lin, 2012).

In recent years, as one of the efficient methods which can solve complicated optimization problems, the theory of OO (Jia, 2006) has attracted more and more attention. In Wu and Shahidehpour (2014), this method was first introduced into the field of solving uncertain SCUC problems. Considering the situation of actual engineering, OO abandons any attempt to find the optimal solutions but seeks for good enough solutions. Compared with traditional BD, this method has successfully increased the solving efficiency by nearly 30 times, which proves the advantages of the OO theory in the field of solving uncertain SCUC problems. From the existing research, OO has been proved that it is a kind of efficient method to solve uncertain SCUC problems. However, the traditional OO theory starts from the solution space, reducing the scale of model feasible regions by constructing several rough models, which makes the redundant information of the model itself to be ignored and eliminated. Therefore, in the aspect of solving efficiency, the OO theory still has much need for improvement and advancement. It is mainly shown in the following paragraph. In this study, an improved adaptive Prony method is proposed to accurately describe the changes in electrical parameters when power system faults occur. The variable step size strategy is used to search the points of the subsegment, and MSRFE is used as the criterion. The simulation results on a given fault signal show that the improved Prony algorithm has higher accuracy and efficiency than the traditional method.

Step 1: although the SCUC model is solved by OO, a rough model should be constructed at first, which could select the feasible solution space of startup/shutdown states. Nonetheless, there are many units in large-scale power systems. If the feasible solution of the startup/shutdown states is selected for all units, the efficiency of the rough model will be greatly affected. For the actual large-scale power grid, the maximum load usually reaches more than 70% of the installed capacity, which means that some units are in a normally open circuit or shutdown state. Thus, there is no need to do state combinations for all units (Gao et al., 2008) if the normally open or stopped units could be first identified in the OO rough model, which will effectively improve the solving efficiency of it.

Step 2: the computational complexity of network security constraint checking and calculation is the largest calculation amount in solving SCUC problems. In Wu and Shahidehpour (2014), the strategy is to check all lines one by one in an accurate OO-based model because the number of nodes and lines which need to be checked will increase rapidly with the expansion of the grid scale. Therefore, the calculation efficiency of OO will be seriously affected by this strategy. In Mogo and Kamwa (2019), the research illustrates that there is only a little part of numerous network security constraints that could restrict the feasible regions. A fast identification method for identifying invalid security constraints is proposed, which successfully reduces the invalid security constraints by more than 85% without affecting the calculation accuracy of the model. Introducing the identification method of invalid security constraints into the COO-based exact model can effectively reduce the redundancy of the exact model and improve the computational efficiency.

In order to solve SCUC problems with wind power fast and effectively, an improved stochastic COO method is proposed in this study. The main contributions of this method are as follows.

A discrete variable identification strategy is proposed and introduced into the rough model, which lays a foundation for constructing a rough model based on COO. This improvement reduces the scale of solution space of a rough model and improves the compactness and solving efficiency of the rough model.

The non-effective security constraint reduction strategy in Wu and Shahidehpour (2014) is introduced into the accurate model, which forms the basis of building the accurate OO-based model for continuous variables. This improvement could greatly reduce the number of security constraints in the OO-based model, which will promote the efficiency of the solution effectively. The correctness and effectiveness of the proposed method can be verified by numerical experiments on an IEEE 118-bus system.

The structure of this study is shown in the following sections. A mathematical model of SCUC is introduced in chapter 2. The improved COO algorithm is shown in chapter 3. The numerical test and simulation results are set in chapter 4. The conclusion is in chapter 5.

Uncertain unit commitment model considering security constraints

In the security-constrained unit commitment problem considering wind power uncertainty, not only the constraints of system power balance, generator capacity, and network security should be considered but also the risk constraints of positive and negative rotation should be considered. In this study, the opportunity constraint is used to characterize the rotation risk constraint, and the model is established with the objective function of minimizing the total operating cost.

Objective function and conventional constraints

The SCUC problem of the wind power-integrated power system usually includes two parts (Gao et al., 2008): first, considering the uncertainty of the wind power output and second, to ensure the safe and stable operation of the system. In that proposition, the total operation costs should be minimized. The objective function of this model can be abstracted as follows:

$\min F_{Gt}={\displaystyle \sum }_{t=1}^{24}{\displaystyle \sum }_{i=1}^M\left[U_{Git}{Y}_{it}\left(P_{Git}\right)+U_{Git}\left(1-U_{Git-1}\right)S_{Git}\right],(1)$

where F_Gt is the total operation cost. P_Git, t is time and i is the number of units. U_Git are the active power output and startup/shutdown status. Y_it(P_Git) is the operation cost of unit, and $S_{it}\left({\tau }_i\right)$ is the startup/shutdown cost of the unit.

The operation cost of the unit and startup/shutdown cost of the unit can be represented as follows:

$Y_{it}\left(P_{Git}\right)={\alpha }_i+{\beta }_i{P}_{Git}+{\gamma }_i{P}_{Git}^2,(2)$

$S_{it}\left({\tau }_i\right)=S_{0i}+S_{1i}\left(1-e^{{\tau }_i/{\omega }_i}\right),(3)$

where ${\alpha }_i$,${\beta }_i$,${\gamma }_i$are the operation cost parameters of units and ${\varpi }_i$ is the parameter of the startup/shutdown cost.

The constraint condition of decision variables in an SCUC model is the key to ensure the safe and reliable operation of the system.

i) The system power balance constraint is defined as follows:

${\displaystyle \sum }_{i=1}^M{U}_{Git}{P}_{Git}+P_{Wt}=P_{Lt}+P_{Dt},(4)$

where $P_{Dt}$ is the active load of the system at time t. $P_{Lt}$ is the network active power loss at time t. $P_{Wt}$ is the active output power of the wind turbine at time t.

ii) The capacity constraints of generators can be expressed as follows:

$P_{Gi\min }\le P_{Git}\le P_{Gi\max },(5)$

where P_Gimin and P_Gimax are the upper limit and lower limit of active power generation of unit i at time interval t, respectively.

iii) Minimum up and down time constraints are defined as follows:

${\displaystyle \sum }_{t=1}^{24}\left|U_{Git}-U_{Git-1}\right|\le n_i,(6)$

where ni is the maximum startup/shutdown times of unit i in a scheduling cycle.

iv) Minimum startup/shutdown time constraints are as follows:

$\left(U_{Git-1}-U_{Git}\right)\left(X_{Git}^{on}-T_{Git}^{on}\right)\ge 0,(7)$

$\left(U_{Git}-U_{Git-1}\right)\left(X_{Git}^{off}-T_{Git}^{off}\right)\ge 0,(8)$

where $X_{Git}^{on}$ and $X_{Git}^{off}$ are the startup and shutdown time of unit i at time interval t, respectively. $T_{Git}^{on}$ and $T_{Git}^{off}$ are the minimum startup/shutdown time available.

v) Ramping up and down constraints are as follows:

$-\mathrm{\Delta }{P}_{Gi}^{down}\le P_{Gi}-P_{Git-1}\le \mathrm{\Delta }{P}_{Gi}^{up},(9)$

where $\Delta P_{Gi}^{up}$ and $\Delta P_{Gi}^{down}$ are the maximum ramping up/down limits of unit i in an hour, respectively.

vi) Network security constraints are defined as follows:

$A\cdot P_t\le B_t,(10)$

among which

$A=\left(\begin{array}{l}T\times K_p\\ -T\times K_p\end{array}\right),(11)$

$B_t=\left(\begin{array}{l}{P}_{L\max }+T\times K_D\times D_t\\ P_{L\max }-T\times K_D\times D_t\end{array}\right),(12)$

where P_t is the unit active output power matrix at time t. T is the shift factor matrix. K_p is the node-generator correlation matrix. K_D is the bus-load correlation matrix, and D_t is the load matrix at time t. P_Lmax is the transmission capacity of the line L.

Risk constraints of positive and negative rotation

The chance-constrained method (Wang et al., 2012) is adopted to appropriately add the uncertainty factors caused by wind power to the SCUC model in this study.

Considering the random UC of wind power, if the deterministic method is used to obtain the spinning reserve, the influence of wind power uncertainty on the system cannot be measured accurately (Wu et al., 2016; Roald et al., 2017). Therefore, based on the opportunity constraint theory, an index reflecting the system operation risk is constructed. The deterministic constraint of a traditional rotating reserve is transformed into the uncertainty constraint, considering the operation risk, and the UC model, considering the uncertainty of wind power generation, is constructed.

System positive and negative rotation reserve risk indicators should be established as follows.

$Q_{\mathrm{d}t}=q\left\{P_{\mathrm{W}t}|P_{\mathrm{W}t}\mathbf{<}{\overline{P}}_{\mathrm{W}t}\&R_{\mathrm{Gp}}\mathbf{<}{\overline{P}}_{\mathrm{W}t}-P_{\mathrm{W}t}+R_{\mathrm{Lp}}\right\},(13)$

$Q_{\mathrm{u}t}=q\left\{P_{\mathrm{W}t}\mathbf{|}{P}_{\mathrm{W}t}>{\overline{P}}_{\mathrm{W}t}\&R_{\mathrm{Gn}}\mathbf{<}{P}_{\mathrm{W}t}-{\overline{P}}_{\mathrm{W}t}+R_{\mathrm{Ln}}\right\},(14)$

where Q_dt and Q_ut are the probability of positive and negative rotation reserve of the system at time t. q(PW) is the probability density function of wind power. ${\overline{P}}_{\mathrm{W}t}$ is the average wind power output at time t. R_Gp and R_Gn are provided by the positive and negative rotation standby systems, respectively. R_Lp and R_Ln are positive and negative spinning reserve demands for conventional units, respectively.

Using the chance constraint theory in an uncertain environment, the rotation reserve of wind power integration is changed from the deterministic inequality constraint to the uncertain inequality constraint. It is necessary to ensure that the probability of shortage of the positive and negative spinning reserve capacity is less than a certain risk threshold. Therefore, (13) and (14) can be transformed as follows:

$Q_{dt}\left(R_{Gp}\right)={\int }_{-\infty }^{P_{Wt}+R_{Lp}-R_{Gp}}q\left(P_{Wt}\right)d{P}_{Wt}\le \lambda ,(15)$

$Q_u\left(R_{Gn}\right)={\int }_{{\overline{P}}_W+R_{Gn}-R_{\mathit{Ln}}}^{+\infty }q\left(P_W\right)d{P}_W\le \lambda .(16)$

This study assumes that the probability of the short-term wind speed follows normal distribution (Bian et al., 2018). The derivation processes of relations (13–16) and the introduction of the wind power uncertainty in the model are described in Appendix. The effectiveness of using the chance-constrained method to describe the uncertainty of wind power generation in a power dispatching problem has been used for Yang et al. (2013).

SCUC model solved by an improved COO algorithm

Ordered optimization (OO) is compared with the traditional optimization method; the OO method is not to find the global optimal solution but to find the “good enough” solution to meet the project requirements. The process called target softening (Ho et al., 1992) has good efficiency and compatibility and can be combined with other optimization methods.

Since the SCUC model is a mixed-integer programming problem with relatively independent decision variables, a rough model and accurate model are, respectively, constructed for the discrete decision variable U_Git and continuous decision variable P_Git, which can be decoupled during the ordinal comparison process.

The general framework of the improved COO algorithm

The improvement is based on the existing COO algorithm, which is as follows.

i) By adding discrete variable identification to the rough model, the normally open/normally closed elements in the discrete space can be identified. Then, the remaining elements are filtered by the rough model to reduce the calculation dimension of the rough model and improve the efficiency of the rough model.

ii) Adding non-effective security constraints to the accurate model can reduce the network security constraints in the accurate model and eliminate the invalid security constraints. It can reduce the number of network security constraints that need to be identified, thus reducing the complexity of solving.

The following three steps of implementing the algorithm are as follows.

Step 1: a rough model is established, and N feasible solutions are preselected from the unit startup/shutdown solution space according to the normal distribution. The number of these N feasible solutions is closely related to the size of the solution space and constitutes a feature set Ω. When the size of the solution space is less than 108, N is usually set to 1000.

Step 2: s solutions from Ω are selected, and specific rules are used to form a set s that contains at least k solutions good enough with a probability of α%. Blind selection (BP) (Lau and Ho, 1997) is used to determine the selected collection s. Its mathematical model is as follows.

$P\left(\left|G\cap S\right|\ge k\right)={\displaystyle \sum }_{j=k}^{\min \left(g,s\right)}{\displaystyle \sum }_{i=0}^{s-j}\frac{C_g^j{C}_{N-g}^{s-i-j}}{C_N^{s-i}}{C}_s^{\mathrm{i}}{q}^{s-i}{\left(1-q\right)}^i\ge \eta ,(17)$

where $P\left(\cdot \right)$ is the alignment probability. g is the size of feasible solutions in set G. s is the number of solutions in the selected set S. k represents the alignment level that is measured by counting how many good enough solutions exist in the set S. $\eta$ is the probability criteria, representing that it contains at least k good enough solutions in the selected set S. $\eta$ is usually set as 0.95. q is the probability that an observed feasible decision is truly feasible.

Step 3:an accurate model is created to obtain the continuous P_Git variable. Minimizing the total cost of ownership with performance constraints considered is the goal of the model. Then, according to the state of each unit, the operation cost and output of each unit are calculated according to the selected quantity s. Finally, the solutions of the selected set are sorted to obtain the optimal solution.

The construction of the rough models

Discrete variable identification model

The feasible region space is reduced by using the rough model to perform prescreening; this may reduce the computational complexity of an accurate model. Considering the time scale of the late dispatch being short, in this period, there are always some units that are normally open/stopped, owing to the impact of the load level and the scale of the install generations. Therefore, if the normally open/stopped units can be identified before prescreening the rough model, the scale of the SCUC solution space can be efficiently reduced so that it may increase the calculation efficiency.

A quadratic optimization model for identifying normally open/stopped units is first constructed in this study. Assuming the units of the system are all open in the model and then considering the main constraints which are related to the output of generators, the minimum operating cost is considered as the optimization objective; the mathematical model is shown as follows:

$\{\min F_{Gt}={\displaystyle \sum }_{t=1}^{24}\begin{array}{l}{\displaystyle \sum }_{i=1}^M{Y}_{it}\left(P_{Git}\right)\\ s.t.{\displaystyle \sum }_{i=1}^M{P}_{Git}+P_{Wt}=P_{Dt}+R\\ A\cdot P_t\le B_t\\ 0\le P_{Git}\le P_{Gi\max }\\ -\mathrm{\Delta }{P}_{Gi}^{down}\le P_{Git}-P_{Git-1}\le \mathrm{\Delta }{P}_{Gi}^{up}.\end{array}(18)$

According to the solution result of the model, for all time period t = 1, 2, 3,...., T. If P_Git satisfies $P_{Git}>P_{Gi\min }$, the unit i is a normally open unit. If P_Git satisfies $P_{Git}<\delta P_{Gi\min }$, the unit i is a normally stopped unit, and $\delta$ is the identification parameter which is set at 0.05.

The normally open/stop generators can be effectively identified by the model, and the main reason is as follows.

The power generation rights, equal opportunity, and free competition ideas are integrated into the design of the model, which may give all units the opportunity of opening. Then, the operation cost is used as the target to perform optimal calculation. If the unit output power in the whole scheduling period is in the low level, which means the units cannot obtain the share of electricity by competition in the previous load level. Therefore, they can be treated as normally stopped units. On the contrary, if the unit output is higher than the minimum output in the entire scheduling period, it can be considered that the units can always get more power in the competition. Thus, they can be considered as normally open units.

Although the optimization model with constraints belonging to the quadratic optimization model and the solution is complex, it only needs to be solved once. It is very effective in reducing the dimensions of the solution space. Overall, adding that model into the rough COO model can improve the overall computational efficiency.

The construction of a COO-based rough model

In order to realize the decoupling process of discrete and continuous variables in solution, according to the startup/shutdown state of the constraints, the rough model is built and the solution space of unit commitment is screened out. These are power balance constraints, ramping up constraints, and minimum up and down constraints. The mathematical description is as follows.

$\{\begin{array}{l}{\displaystyle \sum }_{i=1}^M{U}_{Git}{P}_{Gi\max }+P_{Wt}\ge P_{Dt}+R_{Dp},\\ {\displaystyle \sum }_{i=1}^M{U}_{Git}{P}_{Gi\min }+P_{Wt}\le P_{Dt}-R_{Dn},\\ {\displaystyle \sum }_{i=1}^M\left[U_{Git}\Delta P_{Gi}^{up}+P_{Gi\min }\left(U_{Git}-U_{Git-1}\right)\right]\ge \left|P_{Dt}-P_{Dt-1}\right|,\\ {\displaystyle \sum }_{i=1}^M\left[U_{Git}\Delta P_{Gi}^{down}+P_{Gi\min }\left(U_{Git}-U_{Git-1}\right)\right]\ge \left|P_{Dt}-P_{Dt-1}\right|,\\ {\displaystyle \sum }_{t=1}^{24}\left|U_{Git}-U_{Git-1}\right|\le N_i.\end{array}(19)$

The parameters in the aforementioned formula are mentioned previously and will not be repeated here.

The solution of the rough model

The solving ideas of this study used a discrete variable to identify the normally open/stopped units and to optimize those in the model. After that, the COO-based rough model is used to perform the prescreening for optimizing units, which may form the solution space. The pseudo-code is shown as follows.

The discrete variable identification model is constructed and solved; t=1; s=1; i=1; while $i\le M$do:

if $t\in \left[\mathrm{1,24}\right],P_{Git}>P_{G\min }$; then, optimization normally open units;

else if $t\in \left[\mathrm{1,24}\right],P_{Git}<\delta P_{G\min }$; then, optimization normally stopped units;

else add to the set of units that are not optimized, i=i+1;

end if

while $s\le N$do:

Randomly generating one-time unit startup/shutdown plan that the constraint is not optimized. Formula (19) is the constraint, and the branch and bound method is used to solve the unit startup/shutdown state matrix of the following time;

s=s+1

end if

End algorithm

The construction of an accurate model

Non-effective security constraint reduction

A modern power system has a large scale and many nodes. Therefore, the solution of a power flow equation and checking of network security constraints are the two most time-consuming steps in solving SCUC problems. However, research shows that only a small part of network constraints is effective and can limit the formation of feasible regions (Gao et al., 2008). Therefore, if ineffective constraints can be identified quickly, the model will greatly enhance the compactness and reduce the difficulty of solving.

In this study, the definition of non-effective security constraints is that if a constraint is removed, the feasible region of the model is the same as the previous one. The constraint is a non-effective constraint. According to the definition, the necessary and sufficient conditions for the identification of non-effective security constraints, which are the non-effective constraint and feasible regions, do not have any intersection or the intersection is just a vertex of the simple form. According to the sufficient and necessary conditions mentioned previously, constructing the feasible region optimization model after cutting security constraint condition $A^{\left\{j\right\}}{\left(P_{G1t},P_{G2t},\cdots P_{GMt}\right)}^T\le B_t^{\left\{j\right\}}$is shown as follows.

Using Eq. 20, it can identify the non-effective security constraints precisely. Due to the requirement of solving a constrained optimization model, the calculation is much more complex. Therefore, the constraints of Eq. 20 can be relaxed to construct a sufficient rather than a necessary condition for identifying ineffective security constraints.

$\{\begin{array}{l}{Z}_2=\max {\displaystyle \sum }_{i=1}^M{a}_{ji}{P}_{Git},\\ s.t.0\le P_{Git}\le P_{Gi\max },\\ {\displaystyle \sum }_{i=1}^M{P}_{Git}+P_{Wt}=P_{Dt}+R.\end{array}(20)$

Due to the fact that $Z_1\le Z_2$, it can be considered that when $Z_2\le B_{j,t}$, the constraint $A^{-\left\{j\right\}}{\left(P_{G1t},P_{G2t},\cdots P_{GMt}\right)}^T\le B_t^{-\left\{j\right\}}$ is a non-effective one. In order to carry out further simplification of the calculation, formula (20) is solved analytically. Thus, the abandoned solution model can be proposed; the sufficient but not necessary condition used the known parameters to identify the non-effective constraints, which are shown as follows.

$\{\begin{array}{l}{\displaystyle \sum }_{i=1}^{k-1}{\overline{P}}_i\le D_t-P_{w,t}\le {\displaystyle \sum }_{i=1}^k{\overline{P}}_i,\\ {\displaystyle \sum }_{m=1}^{k-1}\left(a_{j,i_m}-a_{j,i_k}\right){\overline{P}}_{i_m}+a_{j,i_k}\left(P_{Dt}-P_{Wt}\right)\le B_{j,t}.\end{array}(21)$

Accurate model construction

A model based on exact COO can accurately sort the solutions in the selected set while ensuring that all solutions satisfy the model constraints. Identifying and reducing invalid security constraints is the foundation. An accurate COO-based model is constructed based on the objective function of the SCUC model and the constraints associated with continuous variables P_Git, which is shown as follows:

$\{\begin{array}{l}\min F_{Gt}={\displaystyle \sum }_{t=1}^{24}{\displaystyle \sum }_{i=1}^M{Y}_{it}\left(P_{Git}\right)\\ s.t,\\ A·P_t\le B_t,\\ P_{Gi\min }\le P_{Git}\le P_{Gi\max },\\ {\displaystyle \sum }_{i=1}^M{U}_{Git}{P}_{Git}+P_{Wt}=P_{Dt}.\end{array}(22)$

The parameters in the aforementioned formula are mentioned previously and will not be repeated here.

Numerical simulation

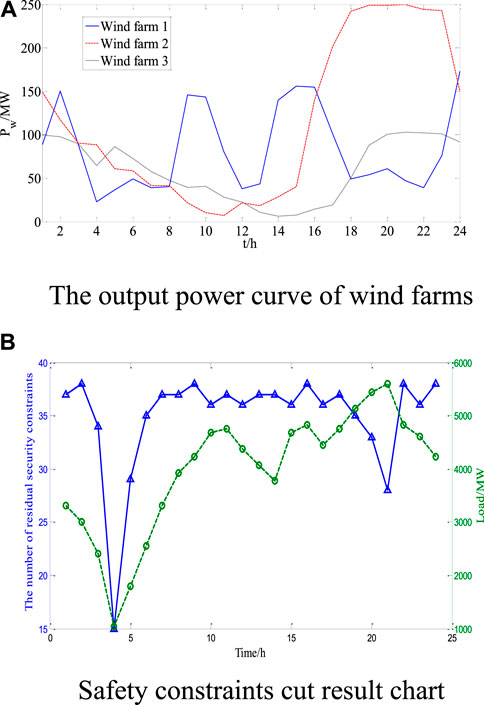
The numerical tests were conducted on a modified IEEE 118-bus system consisting of 54 thermal generators, 91 demand sides, and three wind farms. Wind farms with a rated power of 100 MW, 200 MW, and 250 MW are located at buses 144, 54, and 95, respectively, and their active power curves are shown in Figure 1A. The positive rotating standby of traditional units accounts for 8% of the maximum load of the system, the negative rotating standby accounts for 2% of the minimum load of the system, and the risk index of the rotating standby is 0.01. The network structure, generator parameters, and loads can be obtained with reference to Chen et al. (2015). The numerical test is realized on the computer by MATLAB 8.0 and the optimizer CPLEX 12.5. First, the rough model is established by MATLAB programming and then solved by CPLEX. The MATPOWER toolbox is used to solve nonlinear programming problems in exact models.

FIGURE 1

FIGURE 1. (A) The output power curve of wind farms and (B) Safety constraints cut result chart.

The opportunity-constrained method is used to obtain the system rotational standby. The wind farm is shown in Table 1A. In order to verify the validity of a discrete identification model, it is used to identify unit commitment states, and the results are compared with the final results that are based on traditional BD. The results are shown in Table 1B.

TABLE 1A

TABLE 1A. Spinning reserve of each wind farm (MW).

By comparing the results, in 20 normally open units, the discrete variable identification model has identified three; the recognition rate is 15%. However, in the 31 normally stopped units, the model identifies 20; the identification rate is 64.5%. There are no identification errors that occurred during the whole recognition process.

The comparison shows that the discrete variable recognition model proposed in this study not only has the high rate of identifying normally stopped units but also has high recognition accuracy. When it is incorporated into the COO-based rough model, the computational dimension of the rough model can be reduced, and the solving efficiency can be improved.

In order to verify the validity of the proposed security constraint reduction strategies, formula (22) is used to cut the non-effective security constraints. The remaining security constraints after cutting are shown in Figure 1B.

Figure 1B shows that the IEEE 118 system in each period has 372 security constraints, so there are 8928 security constraints in 24 h. Through the non-effective security constrained cut model, there are 8090 non-effective security constraints that have been cut in a total of 24 h. The cutting proportion reached above 90%. The aforementioned results show that there is a large amount of redundant information in the security constraints of the existing SCUC model, and the non-effective security constraint reduction strategy can effectively eliminate them.

From each time interval, the number of remaining security constraints is between 15 and 38. The trend of variation is related to the load change. The reason is that when the load is heavy, the safety margin of the whole system will drop. Thus, there are more lines that need to be checked, which may produce much more effective security constraints. On the contrary, if the load is light, the number of effective security constraints will reduce.

To verify the validity of the ineffective security constraints introduced in the COO-based accurate model, each start/close scenario for the selected set S is solved using the improved COO-based accurate model and the traditional COO-based model. The operating time is shown in Table 2B. It is necessary to point out that the simulation is carried out on the basis of the improved COO-based rough model proposed in this study.

TABLE 1B

TABLE 1B. Result of discrete variable identification.

It is necessary to point out that the simulation is carried out on the basis of the improved COO-based rough model proposed in Table 2A, which shows that the time to solve the rough model is increased by 40 s after the discrete variable identification strategy is added to the COO-based rough model. Although the discrete variable recognition model requires 2.89 s, the whole dimension of the rough model is decreased. Therefore, as a result, the solving efficiency of the improved COO-based rough model has been improved.

TABLE 2B

TABLE 2B. Accurate model performance.

Table 2B also shows the non-effective security constraint reduction strategy in this study can effectively identify non-effective security constraints. The whole calculation process takes only 0.09 s, and the total time is reduced by nearly 42.43 s. It can be seen that incorporating an ineffective security constraint reduction strategy into an accurate COO-based model can effectively improve the computational efficiency.

The correctness and validity of the whole algorithm

In this study, the improved COO algorithm is used to solve the SCUC model to verify the correctness and effectiveness of the proposed method. The cost of the optimal solution and the start–stop state of the conventional unit are shown in Table 3A.

TABLE 2A

TABLE 2A. Rough model performance.

TABLE 3A

TABLE 3A. Start–stop scheme.

To compare the validity and correctness of the proposed methods, we use the following two methods to solve SCUC problems.

Method 1 is a sequential optimization algorithm of a document (Lee and Lin, 2012).

Method 2 is a mixed-integer programming based on BD.

The calculation results and computation time of the three methods are shown in Table 3B.

TABLE 3B

TABLE 3B. Performance tables of each algorithm.

As shown in Table 3B, compared with the Benders decomposition method, the COO method has obvious advantages both in calculating the efficiency and accuracy. Compared with the method in Wu and Shahidehpour (2014), the improved COO algorithm reduces the total cost by about 0.45% but increases the computational efficiency by nearly 18.85%.

There are some reasons for the solving efficiency of the improved COO algorithms being increased. The COO-based rough model uses a discrete variable identification strategy, which reduces the dimension of the solution. An ineffective security constraint reduction strategy is introduced in the exact model based on collaborative work, eliminating the ineffective security constraints in the exact model. The aforementioned improvements improve the compactness of the algorithm and further improve the efficiency of the algorithm.

Summary

In order to reach the goal of solving the uncertain SCUC problems with wind power fast and effectively. Based on the traditional COO theory, this model introduces discrete variable identification and ineffective security constraint reduction strategies. This study proposes an improved stochastic COO method. The simulation results based on standard examples show some advantages of this method.

i) Although solving the discrete variable identification model needs some time, it can reduce the dimension of rough model’s solution space. Therefore, as a result, introducing the discrete variable identification strategy can improve the calculation efficiency of the COO-based rough model.

ii) The invalid security constraint reduction strategy can identify more than 90% of invalid security constraints in the short term. Introducing it into the precise model based on COO can effectively reduce the computational redundancy and improve the computational efficiency.

iii) The improvement strategy in this study has improved the compactness of the COO algorithm. Compared with the traditional COO algorithm, the improved random COO algorithm improves the solving efficiency greatly. At the same time, compared with other methods, it has obvious advantages both in accuracy and efficiency.

A discrete variable recognition strategy is proposed and incorporated into the rough model, which is the foundation of building a COO-based rough model. This improvement reduces the scale of solution space of the rough model, which could promote the compactness of the rough model and the efficiency of the solution. The non-effective security constraint reduction strategy [12] is introduced into the accurate model, which is the base of building the accurate OO-based model for continuous variables. This improvement could greatly reduce the number of security constraints in the OO-based model, which will promote the efficiency of the solution effectively. The correctness and effectiveness of the proposed method in this study can be tested from the numerical test on the IEEE 118-bus system.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

ZZ put forward the main research points; GX completed manuscript writing , revision and simulation research; NY collected relevant background information and revised grammar and expression. All authors contributed to manuscript revision, read, and approved the submitted version.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bian, Q. Y., Qiu, Y. T., Wu, W. L., Xin, H. H., and Fu, X. H. (2018). Generation dispatch method based on maximum entropy principle for power systems with high penetration of wind power. J. Mod. Power Syst. Clean. Energy 6 (6), 1213–1222. doi:10.1007/s40565-018-0419-z

CrossRef Full Text | Google Scholar

Chen, Z., Wu, L., and Shahidehpour, M. (2015). Effective load carrying capability evaluation of renewable energy via stochastic long-term hourly based SCUC. IEEE Trans. Sustain. Energy 6 (1), 188–197. doi:10.1109/tste.2014.2362291

CrossRef Full Text | Google Scholar

Chen, J. J., Qi, B. X., Rong, Z. K., Peng, K., Zhao, Y., and Zhang, X. (2021). Multi-energy coordinated microgrid scheduling with integrated demand response for flexibility improvement. Energy 217, 119387. doi:10.1016/j.energy.2020.119387

CrossRef Full Text | Google Scholar

Gao, Z., Gen, J., and Zhang, X. (2008). Monthly unit commitment and security assessment algorithm for large-scale power system[J]. Automation Electr. Power Syst. 32 (23), 28–30. doi:10.3321/j.issn:1000-1026.2008.23.007

CrossRef Full Text | Google Scholar

Ho, Y., and Michael, E. (1995). Ordinal optimization approach to rare event probability problems. Discrete Event Dyn. Syst. 5 (2-3), 281–301. doi:10.1007/bf01439043

CrossRef Full Text | Google Scholar

Ho, Y. C., Serenivas, R. S., and Vkaili, P. (1992). Ordinal optimization of DEDS. Discret. Event Dyn. Syst. 2 (2), 61–88. doi:10.1007/bf01797280

CrossRef Full Text | Google Scholar

Hussin, S. M., and Hassan, M. Y. (2014). “Coordination of short-term maintenance scheduling with hourly security-constrained unit commitment[C],” in Proceedings of the 2014 IEEE 8th International Power Engineering and Optimization Conference (PEOCO), MALAYSIA, 73–78.

Google Scholar

Jia, Q. (2006). Enhanced ordinal OPtimization: A theoretical study and applications [D]. Beijing: Tsinghua University.

Google Scholar

Lau, T. W. E., and Ho, Y. C. (1997). Universal alignment probabilities and subset selection for ordinal optimization. J. Optim. Theory Appl. 93 (3), 455–489. doi:10.1023/a:1022614327007

CrossRef Full Text | Google Scholar

Lee, G., and Lin, G. (2012). Unit commitment with security assessment using chaotic pso algorithm[J]. J. Circuits Syst. Comput. 20 (7), 1357–1376.

Google Scholar

Li, Z., Yu, C., Abu-Siada, A., Li, Z., and Zhang, T. (2021). An online correction system for electronic voltage transformers. Int. J. Electr. Power & Energy Syst. 126, 106611. doi:10.1016/j.ijepes.2020.106611

CrossRef Full Text | Google Scholar

Ma, H., Zheng, K., Jiang, H., and Yin, H. (2021). A family of dual-boost bridgeless five-level rectifiers with common-core inductors. IEEE Trans. Power Electron. 36 (11), 12565–12578. doi:10.1109/tpel.2021.3078533

CrossRef Full Text | Google Scholar

Mogo, J. B., and Kamwa, I. (2019). Improved deterministic reserve allocation method for multi-area unit scheduling and dispatch under wind uncertainty. J. Mod. Power Syst. Clean. Energy 7 (5), 1142–1154. doi:10.1007/s40565-019-0499-4

CrossRef Full Text | Google Scholar

Nan, Y., Di, Y., Zhou, Z., Jiazhan, C., Daojun, C., and Xiaoming, W. (2018). Research on modelling and solution of stochastic SCUC under AC power flow constraints. IET Gener. Transm. &amp. Distrib. 12 (15), 3618–3625. doi:10.1049/iet-gtd.2017.1845

CrossRef Full Text | Google Scholar

Roald, L., Misra, S., Krause, T., et al. (2017). Corrective control to handle forecast uncertainty: A chance constrained optimal power flow[J]. IEEE Trans. Power Syst. 32 (2), 1626–1637.

Google Scholar

Shi, T., Gao, S., and Zhang, N. (2016). Two-stage stochastic model of unit commitment with wind farm and an improved algorithm [J]. Trans. China Electrotech. Soc. 31 (16), 172–180.

Google Scholar

Wang, Q., Guan, Y., and Wang, J. (2012). A chance-constrained two-stage stochastic program for unit commitment with uncertain wind power output. IEEE Trans. Power Syst. 27 (1), 206–215. doi:10.1109/tpwrs.2011.2159522

CrossRef Full Text | Google Scholar

Wang, C., Chu, S., Ying, Y., Wang, A., Chen, R., Xu, H., et al. (2022). Underfrequency load shedding scheme for islanded microgrids considering objective and subjective weight of loads. IEEE Trans. Smart Grid, 1. doi:10.1109/TSG.2022.3203172

CrossRef Full Text | Google Scholar

Wu, H., and Shahidehpour, M. (2014). Stochastic SCUC solution with variable wind energy using constrained ordinal optimization. IEEE Trans. Sustain. Energy 5 (2), 379–388. doi:10.1109/tste.2013.2289853

CrossRef Full Text | Google Scholar

Wu, Z., Zeng, P., Zhang, X. P., and Zhou, Q. (2016). A solution to the chance-constrained two-stage stochastic program for unit commitment with wind energy integration. IEEE Trans. Power Syst. 31 (6), 4185–4196. doi:10.1109/tpwrs.2015.2513395

CrossRef Full Text | Google Scholar

Yang, N., Wang, B., and Liu, D. (2013). Large-scale wind power stochastic optimization scheduling method considering flexible load peaking[J]. Trans. China Electrotech. Soc. 28 (11), 231–238.

Google Scholar

Yang, N., Yang, C., Wu, L., Shen, X., Jia, J., Li, Z., et al. (2022). Intelligent data-driven decision-making method for dynamic multisequence: An E-Seq2Seq-based SCUC expert system. IEEE Trans. Ind. Inf. 18 (5), 3126–3137. doi:10.1109/tii.2021.3107406

CrossRef Full Text | Google Scholar

Yang, N., Dong, Z., Wu, L., Zhang, L., Shen, X., Chen, D., et al. (2022). A comprehensive review of security-constrained unit commitment. J. Mod. Power Syst. Clean Energy 10 (3), 562–576. doi:10.35833/mpce.2021.000255

CrossRef Full Text | Google Scholar

Yang, N., Yang, C., Xing, C., Ye, D., Jia, J., Chen, D., et al. (2022). Deep learning-based SCUC decision-making: An intelligent data-driven approach with self-learning capabilities. IET Generation Trans. Dist. 16 (4), 629–640. doi:10.1049/gtd2.12315

CrossRef Full Text | Google Scholar

Zhang, N., Gao, S., and Zhao, X. (2012). A fast Lagrangian relaxation method for unit commitment[J]. Power Syst. Prot. Control 40 (19), 47–53.

Google Scholar

Zhang, N., Gao, S., and Zhao, X. (2013). An unit commitment model and algorithm with randomness of wind power[J]. Trans. China Electrotech. Soc. 28 (05), 22–29.

Google Scholar

Zhou, Y., Zhai, Q., and Wu, L. (2022). Optimal operation of regional microgrids with renewable and energy storage: solution robustness and nonanticipativity against uncertainties. IEEE Trans. Smart Grid, 1. doi:10.1109/TSG.2022.3185231

CrossRef Full Text | Google Scholar

Zhu, B., Wang, H., Zhang, Y., and Chen, S. (2022). Buck-based active-clamp circuit for current-fed isolated DC–DC converters. IEEE Trans. Power Electron. 37 (4), 4337–4345. doi:10.1109/tpel.2021.3121704

CrossRef Full Text | Google Scholar