Remaining useful life prognostics of lithium-ion batteries based on a coordinate reconfiguration of degradation trajectory and multiple linear regression

Lithium battery has been widely applied as new energy to cope with pressures in both form environment and energy. The remaining useful life (RUL) prognostics of lithium-ion batteries have become more critical. Convenient battery life prediction allows early detection of performance deficiencies to help maintain the battery system promptly. This paper proposes a RUL prognostics model of lithium-ion batteries based on a coordinate reconfiguration of degradation trajectory and multiple linear regression. First, a new sampling rule is used to reconfigure the coordinates of degradation data of new batteries and truncated similar batteries. Then, the relationship between similar and new lithium-ion batteries is established by using the reconfiguration data. Moreover, a new RUL prognostics model based on a coordinate reconfiguration of degradation trajectory and multiple linear regression is established by considering the influence of time-varying factors, which can improve prediction accuracy with small sample data and significantly reduce product development time and cost.

1 Introduction

To cope with the dual pressure in the field of environment and energy, most countries in the world regard the exploitation and utilization of new energy as a significant strategy for sustainable development (Fan et al., 2021a). With the gradual improvement of energy storage systems, equipment with batteries as the primary energy supply or energy storage component is widely applied. Lithium-ion batteries are commonly used in aerospace, electric vehicles, and electronic products to relieve environmental pressure (Ren et al., 2019; Zhang et al., 2021; Li et al., 2022c), such as Contemporary Amperex Technology Co., Limited (CATL), which is a global leader of new energy innovative technologies, Tesla, which is the global leader in electric vehicles. The battery performance directly affects the safety of system operation, mission completion, and the lifestyle of consumers (Chen et al., 2021; Li et al., 2022b). In order to extend the service life of batteries, new electrode and electrolyte materials, new battery structures, and battery performance degradation mechanisms are continuously studied. Lithium-ion battery manufacturers must conduct extensive life testing to obtain the design formulations, structural parameters, and operating environments that maximize battery life. Predicting the life of newly developed batteries based on the full-life degradation data of similar batteries (reference batteries) can significantly reduce product development time and cost (Finegan and Cooper, 2019; Fan et al., 2021b; Ge et al., 2022). Therefore, the remaining useful life (RUL) prognostics of lithium-ion batteries are beneficial for properly using and maintaining batteries and assisting in designing new products during the R&D phase. The RUL of a battery is influenced by multiple factors such as current health status, historical data, and failure mechanisms. Therefore, predicting battery RUL is both exciting and challenging.

Many reviews has discussed the RUL of lithium-ion batteries, such as papers (Han et al., 2019; Li et al., 2019; Hu et al., 2020; Ge et al., 2021). Ge et al. (2021) organized four public battery data sets and gave the advantages and limitations of different state of health (SOH) estimations and RUL prognostics methods of lithium-ion batteries. Han et al. (2019) reviewed the aging mechanisms, degradation characteristics, and the influence factors of lithium-ion battery degradation along with the whole cycle life. Wang et al. (2021) gave a critical review of RUL prognostics of lithium-ion batteries based on deep learning algorithms, which compared different adaptive mathematical models. Lipu et al. (2018) analyzed challenges and recommendations about SOH and RUL estimation methods for lithium-ion batteries in electric vehicles. Wu et al. (2016) reviewed the RUL prognostics and analyzed the practical application problems of vehicle lithium-ion batteries using data-driven methodologies. Li et al. (2019) summarized the benefits and drawbacks of data-driven approaches for battery SOH estimations. Hu et al. (2020) reviewed RUL prediction methods and provided some challenges: battery data sets, first principle-based prognostics, early prediction algorithms, and engineering applications. The RUL prognostics approach for lithium-ion batteries is mainly divided into mechanical models and data-driven methods. The mechanism model needs to establish a mathematical system dynamics or degradation mechanism model.

In recent years, many researchers have used Kalman filters or particle filters based on degradation modelling to predict the RUL of lithium-ion batteries. However, it is usually not economical or feasible to build a physical model when the degradation mechanism of the battery is unknown. In addition, mechanical models are generally applicable only to specific battery models. When historical degradation data is known, data-driven methods can predict the lifetime of a lithium battery without a degradation model (Zhao et al., 2021). Data-driven prediction methods are divided into two categories: data extrapolation methods and knowledge-based methods. Zhang et al. (2021) established a hybrid prediction model, which integrates a random forest, artificial bee colony, and general regression neural network, to predict the RUL of lithium-ion batteries in an early-cycle stage. Nuhic et al. (2013) presented a data-driven method for SOH and RUL prognostics of lithium-ion batteries based on a support vector machine (SVM) and training and testing data processing. Jianfang et al. (2021) proposed a multi-scale prediction approach for RUL and SOH based on Wavelet neural network and unscented particle filter model. A new hybrid RUL method for lithium-ion batteries, which can fully use historical information, is proposed by combining the algorithms of unscented Kalman filters, ensemble empirical mode decomposition, and relevance vector machine (Chang et al., 2017). Lu et al. (2020) predicted the RUL of lithium-ion batteries with high accuracy based on the autoregressive integrated moving average model time series algorithm. Lui et al. (2021) presented a physics-based RUL prognostics method by considering multiple degradation mechanisms applicable to lithium-ion batteries, and it has been used in implantable applications. Wu et al. (2022) explored a RUL prognostics method for lithium-ion batteries by improving particle filter algorithm from the perspective of reweighting the particles, which can improve the accuracy of the prediction results of its remaining service life. Lyu et al. (2021) established a model-data-fusion method for battery SOH estimation and RUL prognostics by combining a data-driven battery degradation model and a particle filter, and battery aging tests verified the proposed model-data-fusion method. Li et al. (2022a) built a novel health indicator for online health estimation of lithium-ion batteries by combining an interpolation method and incremental capacity curve filtering. Ma et al. (2021) built a new framework for capacity regeneration point detection and RUL prognostics through the particle filter and autoregressive model. Yu et al. (2022) presented an improved Euclidean distance method and a cosine similarity method from the perspective of similarity for online diagnosis of multi-fault in-series connected battery packs. Ge et al. (2022) established a comprehensive lithium-ion battery SOH estimation method based on variable mode decomposition, particle filter, and long short-term memory with a self-attention mechanism. Hu and Zhao (2022) presented a RUL prognostics method for lithium-ion batteries based on the wavelet threshold denoising and transformer neural network. Wang and Feng (2021) proposed a new RUL prognostics approach for lithium-ion batteries using a novel health indicator and relevance vector machine. The data extrapolation method firstly predicts the lithium-ion battery capacity or health index sequence and then determines whether it reaches the failure threshold or calculates the RUL. Data extrapolation methods are only suitable for short-term state prediction and late-remaining life prediction due to iteration errors. The knowledge-based approach establishes the mapping relationship between data and life without any iteration error and is widely adopted in practice.

In this paper, we established a new RUL prognostics model based on a coordinate reconfiguration of degradation trajectory and multiple linear regression. The main contributions of this study are summarized as follows:

(1) This paper proposes a coordinate reconfiguration of degradation trajectory to transform the battery performance degradation data of different lengths into the same size, revealing the relationship between the performance degradation patterns of different battery samples.

(2) We consider the influence of time-varying factors when building the RUL prognostics model to improve prediction accuracy.

(3) The prognostics model can achieve high prediction accuracy with small sample data and significantly reduce product development time and cost.

The remainder of this paper is organized as follows. Section 2 introduces the coordinate reconfiguration of degradation trajectory and multiple linear regression. An analysis of the results is discussed in Section 3. Finally, some concluding remarks from this study are presented in Section 4.

2 Materials and methods

Lithium-ion batteries usually have different degradation model parameters at different life degradation stages and different degradation models. Data-driven lithium-ion battery lifetime prediction methods mainly include data extrapolation and knowledge-based approaches. Meanwhile, the data extrapolation method can only generalize the historical degradation trend to the future. The life prediction results obtained by using this method have considerable errors in the case of small sample data. In contrast, the knowledge-based approach still has high prediction accuracy in the case of small sample data. Therefore, this section proposes a new knowledge-based method for the life prediction of lithium-ion batteries.

2.1 Coordinate reconfiguration of degradation trajectory

The performance degradation trajectories of new batteries and their similar reference batteries are shown in Figure 1. It is shown that the performance degradation trajectories of the new battery and each reference battery are widely different due to the different formulations. Both data extrapolation and similarity-based methods cannot achieve good prediction accuracy. Degraded data are usually sampled at equal time intervals. Meanwhile, the performance degradation data are time-based and collected at equal time intervals. However, different formulation batteries have different lifetimes, and the sampling points of performance degradation sequences are different, which made it extremely difficult to explore the correlation between the evolution of different battery performance degradation laws.

FIGURE 1

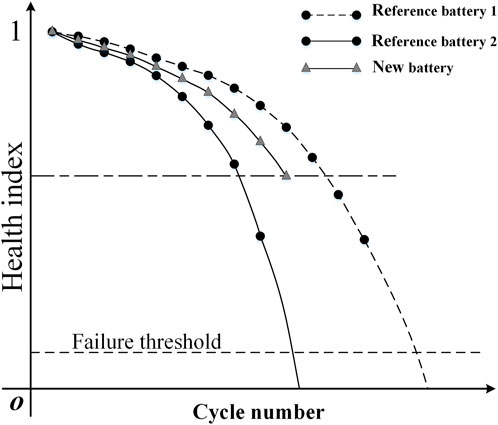
FIGURE 1. The performance degradation trajectories of the new battery and similar reference batteries.

Based on above problem, we rotate degradation trajectory and coordinate system simultaneously by 90 degrees counterclockwise. The time-based degradation data is transformed into the degradation amount as the base, which achieves the coordinate reconstruction of the original performance degradation trajectory. Since all battery samples are defined with the same degradation amount of functional failure, the sampling benchmark is unified among the samples after the reconfiguration, which is beneficial for mining the interrelationship between the data. The principle and process of the coordinate reconfiguration of the performance degradation trajectory are shown in Figure 2.

FIGURE 2

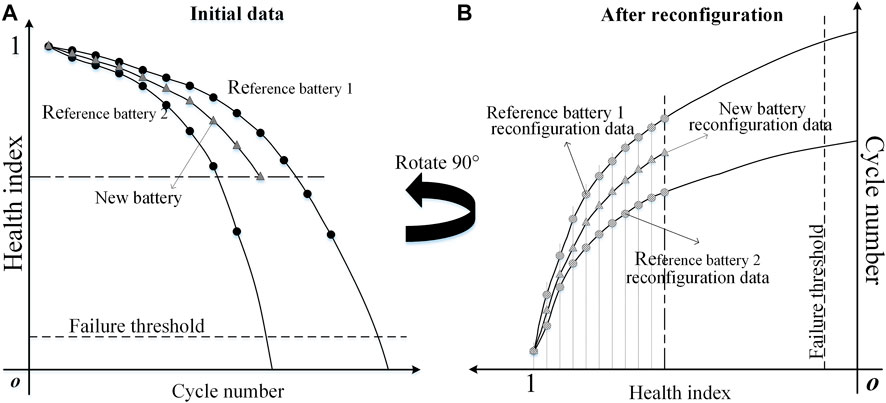
FIGURE 2. The coordinate reconfiguration of the performance degradation trajectory of lithium-ion batteries.

Data-based and knowledge-based life prognostic methods are mathematically regression problems. Regression problems are divided into two categories: prediction (which is different from “prediction” in the sense of “life prognostics”) and control. Prediction in mathematics is defined as mathematical methods to obtain a functional relationship between the independent and dependent variables. Control in mathematics is defined as determining the range of independent variables by ensuring that the dependent variables are within the specified range. Prediction is a forward calculation process, while control is an inverse solution process, so the prediction problem is more accessible than the control problem. The predictive life problem in system health management is a control problem in mathematical terms. The product life is predicted by controlling the health index of the product.

This paper proposes a method to reconfigure the performance degradation trajectory coordinates to use the performance degradation data of similar batteries. The coordinate reconfiguration transforms the performance degradation data sampled with equal time intervals into the cycle number data sampled with equal degradation amount, which is the same performance degradation trajectory from two different dimensions. After reconfiguration, the RUL prognostic problem is transformed into a predictive problem with the health index as the independent variable and the number of cycles experienced as the dependent variable, which is much easier to solve.

The lithium-ion battery performance degradation trajectory is obtained by connecting several discrete columns of data. The original performance degradation trajectory is donated by$\left\{\left(t_1,H{I}_1\right),\left(t_1+\mathit{\Delta }t,H{I}_2\right),\left(t_1+2\Delta t,H{I}_3\right),...,\left(t_1+\left(N-1\right)\Delta t,H{I}_N\right)\right\},$where $t_1$ is the initial test time; $\Delta t$ is the time interval of the test, which is a cycle for lithium-ion battery performance degradation; $N$ is the total number of tests, which is the length of the degradation sequence; $H{I}_i,i=\mathrm{1,2},...,N$ is the lithium-ion battery health index at different times. The original performance degradation trajectory can be simplified as

$\left\{\left(1,H{I}_1\right),\left(2,H{I}_2\right),\left(3,H{I}_3\right),...,\left(N,H{I}_N\right)\right\}(1)$

First, the health index series are smoothed to be strictly monotonic using the empirical modal decomposition (EMD) method. The degenerate trajectory is represented as$\left\{\left(1,H{I}_1^{*}\right),\left(2,H{I}_2^{*}\right),\left(3,H{I}_3^{*}\right),...,\left(N,H{I}_N^{*}\right)\right\}$ with $H{I}_1^{*}>H{I}_2^{*}>H{I}_3^{*}>...>H{I}_N^{*}$. Let $H{I}_i^{*},i=\mathrm{1,2},..,N$ be the smoothed health index value. It is known that the smoothed health index series are strictly monotonic according to the properties of EMD.

Then, the health index sampling interval and sequence were determined. Let $\Delta HI$ be the difference in health index between adjacent sampling points. $H{I}_1^{*}$ and $H{I}_N^{*}$ denote the initial (maximum) and termination (minimum) values of the sampling sequence. Therefore, the reconfigured sampling sequence is $\left\{H{I}_1^{*},H{I}_1^{*}-\Delta HI,H{I}_1^{*}-2\Delta HI,...,H{I}_N^{*}\right\}$, where $H{I}_1^{*}$ is the first value of the smoothed health index sequence, and $H{I}_N^{*}$ may not be at the sampling point. Now suppose $\left(H{I}_1^{*}-H{I}_N^{*}\right)/\mathit{\Delta }HI$ is a positive integer.

We exchange the degradation trajectory coordinates, so $\left\{\left(1,H{I}_1^{*}\right),\left(2,H{I}_2^{*}\right),\left(3,H{I}_3^{*}\right),...,\left(N,H{I}_N^{*}\right)\right\}$ becomes $\left\{\left(H{I}_1^{*},1\right),\left(H{I}_2^{*},2\right),\left(H{I}_3^{*},3\right),...,\left(H{I}_N^{*},N\right)\right\}$. Then, by using the piecewise cubic Hermite interpolating polynomial (PCHIP) algorithm, the sequence of cycle numbers for the reconfigured sampling sequence is calculated as $\left\{C_1,C_2,C_3,...,C_M\right\}$. Thus, the performance degradation trajectory after reconfiguration is given by

$\left\{\left(H{I}_1^{*},C_1\right),\left(H{I}_1^{*}-\Delta HI,C_2\right),\left(H{I}_1^{*}-2\Delta HI,C_3\right),...,\left(H{I}_1^{*}-\left(M-1\right)\Delta HI,C_M\right)\right\}(2)$

where $H{I}_1^{*}$ is the health index of the first cycle, $\Delta HI$ is the reconfigured health index sampling interval, $M$ is the number of sampling points after reconfiguration.

The PCHIP interpolation algorithm is as follows.

Let $I=\left[a,b\right]$ be $a=x_0<x_1<...<x_n=b$, $f_k$ is the value of the function at the split point, denote $h_k=x_{k+1}-x_k,p_k=f^{\prime }\left(x_k\right)$, where $k=\mathrm{0,1},..,n-1$. The PCHIP function $I_h\left(x\right)$ satisfies the following conditions:

(1) The definition domain is $I=\left[a,b\right]$;

(2) $I_k=\left[x_k,x_{k+1}\right],k=\mathrm{0,1},...,n-1$ is represented as a subset of $I$, $I_h\left(x\right)$ can be represented as a cubic spline polynomial equation $I_k\left(x\right)$;

(3) The $I_h\left(x\right)$ satisfy the interpolation condition: $I_h\left(x_k\right)=f_k,I_h^{\prime }\left(x_k\right)=p_k,k=\mathrm{0,1,2},...,n-1$.

In each subinterval $\left[x_k,x_{k+1}\right]$, the PCHIP function can be expressed as

$I_k\left(x\right)=f_k+c_{k,1}\left(x-x_k\right)+c_{k,2}{\left(x-x_k\right)}^2+c_{k,3}{\left(x-x_k\right)}^3(3)$

where

$\{\begin{array}{l}{c}_{k,1}=p_k\\ c_{k,2}=\left(\frac{3}{h_k}\left(f_{k+1}-f_k\right)-2p_k-p_{k-1}\right)\frac{1}{h_k}\\ c_{k,3}=\left(p_{k+1}+p_k-2\frac{f_{k+1}-f_k}{h_k}\right)\frac{1}{h_k^2}\\ h_k=x_{k+1}-x_k,p_k=f^{\prime }\left(x_k\right)\\ x\in \left[x_k,x_{k+1}\right],k=\mathrm{0,1},...,n-1\end{array}(4)$

2.2 Multiple linear regression

After coordinate reconfiguration, the reconfiguration data of the new and the reference battery is achieved. The newly developed battery reconfiguration data is noted as

$\left\{\left(H{I}_1,C_1^p\right),\left(H{I}_1-\Delta HI,C_2^p\right),\left(H{I}_1-2\Delta HI,C_3^p\right),...,\left(H{I}_1-\left(M-1\right)\Delta HI,C_M^p\right)\right\}(5)$

where $C_i^p,i=\mathrm{1,2},...,M$ is the number of charge cycles for each new battery sampling point. The data after reconfiguration of the jth reference battery is noted as:

$\left\{\left(H{I}_1,C_1^{r,j}\right),\left(H{I}_1-\Delta HI,C_2^{r,j}\right),\left(H{I}_1-2\Delta HI,C_3^{r,j}\right),...,\left(H{I}_1-\left(M-1\right)\Delta HI,C_M^{r,j}\right)\right\},j=\mathrm{1,2},...,Q(6)$

where $j$ indicates the $j$th type of reference battery and $Q$ is the total number of reference battery types.

The mapping between the cycle number and health index of the new and reference batteries was established by multiple linear regression, which is shown in Figure 3. Note that

$\left(HI,C^{r,1},C^{r,2},...,C^{r,Q}\right)\stackrel{f}{{\displaystyle \to }}{C}^p(7)$

where $C^p$ is the number of cycles of a new battery at a health index of $HI$.

FIGURE 3

FIGURE 3. Schematic diagram of life prediction modeling.

The multiple linear regression model is as follows:

$\begin{array}{l}{C}^p=f\left(C^{r,1},...,C^{r,Q},HI;\mathit{\theta }\right)={\theta }_0+{\theta }_1\cdot C^{r,1}+,...,+{\theta }_Q\cdot C^{r,Q}+{\theta }_{Q+1}\cdot HI\\ =\left[1,C^{r,1},...,C^{r,Q},HI\right]{\left[{\theta }_0,{\theta }_1,...,{\theta }_Q,{\theta }_{Q+1}\right]}^T\end{array}(8)$

where $\mathit{\theta }={\left[{\theta }_0,{\theta }_1,...,{\theta }_Q,{\theta }_{Q+1}\right]}^T$is $Q+2$ regression parameters, which can be determined from the training data.

The objective function is determined by the least square method, and the parameters of the regression model were estimated using the data shown in Figure 4, where $\widehat{\mathit{\theta }}={\left[{\widehat{\theta }}_0,{\widehat{\theta }}_1,...,{\widehat{\theta }}_Q,{\widehat{\theta }}_{Q+1}\right]}^T$.

FIGURE 4

FIGURE 4. Lithium-ion battery health index degradation sequence.

Let $H{I}_{threshold}$ be the failure threshold, suppose the life of reference batteries is $\left\{L^{r,1},L^{r,2},...,L^{r,Q}\right\}$, then the life ${\widehat{L}}^p$ of the newly developed battery is estimated as

${\widehat{L}}^p=\left[1,L^{r,1},...,L^{r,Q},H{I}_{threshold}\right]{\left[{\widehat{\theta }}_0,{\widehat{\theta }}_1,...,{\widehat{\theta }}_Q,{\widehat{\theta }}_{Q+1}\right]}^T(9)$

3 Case study

In this case study, the effectiveness and feasibility of the proposed method are verified using data from different lithium-ion battery life cycle tests under laboratory conditions. Five different lithium-ion batteries are cyclically charged and discharged under the same conditions (room temperature). The voltage, current, and capacity data of the charging and discharging process are recorded during the test. The discharge capacity is used as a performance index to quantify the SOH of lithium-ion batteries. The battery fails when the capacity of the test battery degrades to 82% of the rated capacity. The discharge capacity of lithium-ion batteries gradually decreases, and the failure threshold is 82%. The cycle life test data of the five test batteries are shown in Table 1.

TABLE 1

TABLE 1. Battery life data.

First, the SOH of lithium-ion batteries is evaluated using capacity data to obtain a sequence of health indices reflecting the health of lithium-ion batteries.

$HI\left(t\right)=\frac{C\left(t\right)}{C_{rated}}(10)$

where $C\left(t\right)$ is the real-time capacity and $C_{rated}$ is the rated capacity.

The health index degradation sequences of the five test batteries are shown in Figure 4. The relative length ($RL$) of the known data is defined as

$RL=\frac{1-H{I}_{end}}{1-H{I}_{threshold}}\times 100\%(11)$

where $H{I}_{end}$ is the last health index in the known data and $H{I}_{threshold}$ is the failure threshold of the health index.

One of the five test batteries was selected as the predictive battery. The remaining four batteries were used as reference batteries for life prediction analysis under different known data length conditions. The results are shown in Figure 5. For battery 1, the relative error of prediction is less than the limited value 0.2 after the relative length of known data is greater than 30%; for batteries 3 and 5, the relative error of prediction is less than the limited value 0.2 after the relative length of known data is greater than 20%. With the gradual increase of known data, the life prediction results are closer to real life. The above illustrates that the proposed life prediction method can constrain the relative error of prediction to less than 0.2 with little data.

FIGURE 5

FIGURE 5. Battery life prediction results under different data conditions.

In order to verify the applicability of the proposed method to different batteries, batteries 1, 2, 3, 4, and 5 were taken in turn as the predictive batteries under the condition of 50% known data length, and the remaining four batteries were used as the reference batteries. The prediction results are shown in Table 2.

TABLE 2

TABLE 2. Life prediction results of different batteries.

According to Table 2, the average absolute error of the prediction results is 25, and the average relative error is 9.5% under the condition of 50% known data length. The RUL prognostics model based on a coordinate reconfiguration of degradation trajectory and multiple linear regression has high accuracy for different batteries. It is suitable for life inference analysis of newly developed batteries in the product design stage and gives a reference for manufacturers when developing new batteries.

4 Conclusion

Fastly and accurately predicting the RUL of lithium-ion batteries in an early-cycle stage can speed up battery improvement and optimization. This paper established a new RUL prognostics model based on a coordinate reconfiguration of degradation trajectory and multiple linear regression, which can improve prediction accuracy with small sample data. Firstly, we proposed a coordinate reconfiguration of the degradation trajectory, revealing the relationship between performance degradation patterns of different battery samples. Then, a RUL prognostics model of lithium-ion batteries is presented to improve prediction accuracy by considering the influence of time-varying factors. Finally, a practical case was examined by a RUL prognostics model. Through five different lithium-ion battery test data analyses, we obtained the prediction life and error, which can decrease the life test time while ensuring the prediction accuracy, thus reducing the cost in the R&D phase.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author contributions

ZC: conceptualization, methodology, funding acquisition, investigation; LL: supervision, funding acquisition, writing-review and editing; WC: project administration, writing-review and editing; SY: methodology, validation, formal analysis; YW: methodology, project administration; DW: supervision, resources, validation.

Funding

This work was supported by the National Natural Science Foundation of China under Grant 72101270; the Foundation Strengthening Program of China (Grant No. 2020-JCJQ-JJ-215, 2019-JCJQ-ZD-199).

Acknowledgments

We thank the associate editor and the reviewers for their helpful feedback that improved this paper.

Conflict of interest

Authors LL, WC, SY, YW, and DW were employed by China Academy of Launch Vehicle Technology.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chang, Y., Fang, H., and Zhang, Y. (2017). A new hybrid method for the prediction of the remaining useful life of a lithium-ion battery. Appl. Energy 206, 1564–1578. doi:10.1016/j.apenergy.2017.09.106

CrossRef Full Text | Google Scholar

Chen, T., Song, M., Hui, H., and Long, H. (2021). Battery electrode mass loading prognostics and analysis for lithium-ion battery–based energy storage systems. Front. Energy Res. 9, 754317. doi:10.3389/fenrg.2021.754317

CrossRef Full Text | Google Scholar

Fan, D., Ren, Y., Feng, Q., Liu, Y., Wang, Z., and Lin, J. (2021a). Restoration of smart grids: Current status, challenges, and opportunities. Renew. Sustain. Energy Rev. 143, 110909. doi:10.1016/j.rser.2021.110909

CrossRef Full Text | Google Scholar

Fan, D., Zhang, A., Feng, Q., Cai, B., Liu, Y., and Ren, Y. (2021b). Group maintenance optimization of subsea Xmas trees with stochastic dependency. Reliab. Eng. Syst. Saf. 209, 107450. doi:10.1016/j.ress.2021.107450

CrossRef Full Text | Google Scholar

Finegan, D. P., and Cooper, S. J. (2019). Battery safety: Data-driven prediction of failure. Joule 3, 2599–2601. doi:10.1016/j.joule.2019.10.013

CrossRef Full Text | Google Scholar

Ge, M.-F., Liu, Y., Jiang, X., and Liu, J. (2021). A review on state of health estimations and remaining useful life prognostics of lithium-ion batteries. Measurement 174, 109057. doi:10.1016/j.measurement.2021.109057

CrossRef Full Text | Google Scholar

Ge, Y., Zhang, F., and Ren, Y. (2022). Lithium ion battery health prediction via variable mode decomposition and deep learning network with self-attention mechanism. Front. Energy Res. 10. doi:10.3389/fenrg.2022.810490

CrossRef Full Text | Google Scholar

Han, X., Lu, L., Zheng, Y., Feng, X., Li, Z., Li, J., et al. (2019). A review on the key issues of the lithium ion battery degradation among the whole life cycle. eTransportation 1, 100005. doi:10.1016/j.etran.2019.100005

CrossRef Full Text | Google Scholar

Hu, W., and Zhao, S. (2022). Remaining useful life prediction of lithium-ion batteries based on wavelet denoising and transformer neural network. Front. Energy Res. 10. doi:10.3389/fenrg.2022.969168

CrossRef Full Text | Google Scholar

Hu, X., Xu, L., Lin, X., and Pecht, M. (2020). Battery lifetime prognostics. Joule 4, 310–346. doi:10.1016/j.joule.2019.11.018

CrossRef Full Text | Google Scholar

Jianfang, J. I. A., Keke, W., Xiaoqiong, P., Yuanhao, S. H. I., Jie, W. E. N., and Jianchao, Z. (2021). Multi-scale prediction of RUL and SOH for lithium-ion batteries based on WNN-UPF combined model. Chin. J. Electron. 30, 26–35. doi:10.1049/cje.2020.10.012

CrossRef Full Text | Google Scholar

Li, L., Li, Y., Cui, W., Chen, Z., Wang, D., Zhou, B., et al. (2022a). A novel health indicator for online health estimation of lithium-ion batteries using partial incremental capacity and dynamic voltage warping. J. Power Sources 545, 231961. doi:10.1016/j.jpowsour.2022.231961

CrossRef Full Text | Google Scholar

Li, W., Zhong, X., Shao, H., Cai, B., and Yang, X. (2022b). Multi-mode data augmentation and fault diagnosis of rotating machinery using modified ACGAN designed with new framework. Adv. Eng. Inf. 52, 101552. doi:10.1016/j.aei.2022.101552

CrossRef Full Text | Google Scholar

Li, X., Shao, H., Lu, S., Xiang, J., and Cai, B. (2022c). Highly efficient fault diagnosis of rotating machinery under time-varying speeds using LSISMM and small infrared thermal images. IEEE Trans. Syst. Man. Cybern. Syst., 1–13. doi:10.1109/TSMC.2022.3151185

CrossRef Full Text | Google Scholar

Li, Y., Liu, K., Foley, A. M., Zülke, A., Berecibar, M., Nanini-Maury, E., et al. (2019). Data-driven health estimation and lifetime prediction of lithium-ion batteries: A review. Renew. Sustain. Energy Rev. 113, 109254. doi:10.1016/j.rser.2019.109254

CrossRef Full Text | Google Scholar

Lipu, M. S. H., Hannan, M. A., Hussain, A., Hoque, M. M., Ker, P. J., Saad, M. H. M., et al. (2018). A review of state of health and remaining useful life estimation methods for lithium-ion battery in electric vehicles: Challenges and recommendations. J. Clean. Prod. 205, 115–133. doi:10.1016/j.jclepro.2018.09.065

CrossRef Full Text | Google Scholar

Lu, C., Gu, Z. J., and Yan, Y. (2020). RUL prediction of lithium ion battery based on ARIMA time series algorithm. Mat. Sci. Forum 999, 117–128. doi:10.4028/www.scientific.net/MSF.999.117

CrossRef Full Text | Google Scholar

Lui, Y. H., Li, M., Downey, A., Shen, S., Nemani, V. P., Ye, H., et al. (2021). Physics-based prognostics of implantable-grade lithium-ion battery for remaining useful life prediction. J. Power Sources 485, 229327. doi:10.1016/j.jpowsour.2020.229327

CrossRef Full Text | Google Scholar

Lyu, Z., Gao, R., and Chen, L. (2021). Li-ion battery state of health estimation and remaining useful life prediction through a model-data-fusion method. IEEE Trans. Power Electron. 36, 6228–6240. doi:10.1109/TPEL.2020.3033297

CrossRef Full Text | Google Scholar

Ma, Q., Zheng, Y., Yang, W., Zhang, Y., and Zhang, H. (2021). Remaining useful life prediction of lithium battery based on capacity regeneration point detection. Energy 234, 121233. doi:10.1016/j.energy.2021.121233

CrossRef Full Text | Google Scholar

Nuhic, A., Terzimehic, T., Soczka-Guth, T., Buchholz, M., and Dietmayer, K. (2013). Health diagnosis and remaining useful life prognostics of lithium-ion batteries using data-driven methods. J. Power Sources 239, 680–688. doi:10.1016/j.jpowsour.2012.11.146

CrossRef Full Text | Google Scholar

Ren, Y., Fan, D., Feng, Q., Wang, Z., Sun, B., and Yang, D. (2019). Agent-based restoration approach for reliability with load balancing on smart grids. Appl. Energy 249, 46–57. doi:10.1016/j.apenergy.2019.04.119

CrossRef Full Text | Google Scholar

Wang, R., and Feng, H. (2021). Remaining useful life prediction of lithium-ion battery using a novel health indicator. Qual. Reliab. Eng. Int. 37, 1232–1243. doi:10.1002/qre.2792

CrossRef Full Text | Google Scholar

Wang, S., Jin, S., Bai, D., Fan, Y., Shi, H., and Fernandez, C. (2021). A critical review of improved deep learning methods for the remaining useful life prediction of lithium-ion batteries. Energy Rep. 7, 5562–5574. doi:10.1016/j.egyr.2021.08.182

CrossRef Full Text | Google Scholar

Wu, L., Fu, X., and Guan, Y. (2016). Review of the remaining useful life prognostics of vehicle lithium-ion batteries using data-driven methodologies. Appl. Sci. (Basel). 6, 166. doi:10.3390/app6060166

CrossRef Full Text | Google Scholar

Wu, T., Zhao, T., and Xu, S. (2022). Prediction of remaining useful life of the lithium-ion battery based on improved particle filtering. Front. Energy Res. 10. doi:10.3389/fenrg.2022.863285

CrossRef Full Text | Google Scholar

Yu, Q., Li, J., Chen, Z., and Pecht, M. (2022). multi-fault diagnosis of lithium-ion battery systems based on correlation coefficient and similarity approaches. Front. Energy Res. 10. doi:10.3389/fenrg.2022.891637

CrossRef Full Text | Google Scholar

Zhang, Y., Peng, Z., Guan, Y., and Wu, L. (2021). Prognostics of battery cycle life in the early-cycle stage based on hybrid model. Energy 221, 119901. doi:10.1016/j.energy.2021.119901

CrossRef Full Text | Google Scholar

Zhao, X., Kim, J., Warns, K., Wang, X., Ramuhalli, P., Cetiner, S., et al. (2021). Prognostics and health management in nuclear power plants: An updated method-centric review with special focus on data-driven methods. Front. Energy Res. 9, 696785. doi:10.3389/fenrg.2021.696785

CrossRef Full Text | Google Scholar