Decentralized robust optimal dispatch of user-level integrated electricity-gas-heat systems considering two-level integrated demand response

With the change of users’ energy consumption concept, the users are no longer rigid as the traditional inelasticity but can be flexible to carry out integrated demand response (IDR). The load has also been transformed from a traditional purely consumptive load to a new type of load that combines production and consumption with the improvement and popularization of renewable energy production technologies such as wind power and photovoltaic. In this paper, considering the IDR of loads and the uncertainty of renewable energy output, a decentralized robust optimal dispatch study is conducted on user-level integrated electricity-gas-heat systems (IEGHSs) composed of energy hubs (EHs) and some users. This paper firstly developed the comprehensive model of the user-level IEGHS, including the detailed mathematical model of EH, IDR, and users. Then, based on the established model, an optimal dispatching model is established with the goal of the lowest operating cost for the system. In order to cope with the uncertainty of the output of renewable energy equipment while protecting the security and privacy of different participants in the integrated energy system (IES), a decentralized robust algorithm is used to solve the model. Finally, the proposed model is analyzed and verified by an IES example composed of one EH and three users with the ability of IDRs, and the feasibility of the proposed model and algorithm is verified.

1 Introduction

Climate problems are becoming increasingly serious, and energy conservation and emission reduction are imperative. The IESs play a significant role in promoting renewable energy accommodation and improving energy utilization efficiency by virtue of their advantages of multi-energy complementation and energy cascade utilization. It is exactly because of the above advantages of the IES that the reliability of users’ energy use can be guaranteed and the IDR at the user level can be implemented (Ma et al., 2021).

With the increasingly severe energy situation, the role of the energy hub of the integrated energy system has become increasingly prominent (Jia et al., 2021; Ma et al., 2021; Li et al., 2022). References (Liu et al., 2022) and (Zhang et al., 2021) established an energy sharing framework for a two-layer Heat–Electricity integrated energy system including EHs and prosumers, aiming to maximize the EH profits. Reference (Schick et al., 2022) studied the role and influence of prosumers in integrated energy systems and pointed out that distributed energy storage can provide key flexibility under high renewable energy shares. Reference (Liu N et al., 2019) studied multi-microgrid energy sharing considering combined heat and power and demand response and used a distributed optimization algorithm to solve it. References (Nunna et al., 2020) and (Ding et al., 2022a) established an energy storage market model and considered energy storage systems as multi-agent energy transactions. Reference (Peng et al., 2021) pointed out the shortcomings of the traditional single energy centralized optimization and introduced a distributed multi-energy sharing mechanism centered on EHs. Reference (Qin et al., 2020) studied the multi-objective optimization and game of electric-gas integrated energy system considering the demand characteristics of distributed energy stations and energy users. Reference (Martinez Cesena et al., 2020) carried out the simulation and optimization of integrated electricity–heat–gas systems in flexible MEDs and considers the support services of the multi-energy network. Reference (Wang et al., 2021) conducted a research analysis on the optimized operation and demand response of integrated community energy systems to reduce costs. Reference (Sangswang and Konghirun, 2020) introduced a home energy system including solar energy, energy storage, and electric vehicles, and conducted demand response analysis and demand response program development.

The coupling and substitution of multiple energy enhance the flexibility of the energy consumption method, and the demand side can change the energy consumption method according to the supply side price and the system feature to implement IDR (Liu P et al., 2019). Reference (Shao et al., 2021) introduced an IDR optimization model for EHs and enabled interaction with integrated electrical-gas systems. Reference (Zhang et al., 2022) studied the relationship between demand response and dynamic prices and established a two-dimensional demand response model of spatio-temporal coupling. Reference (Bahrami and Sheikhi, 2016) called an EH capable of implementing IDR a smart EH and studied an ordered potential game with a unique Nash equilibrium among multiple smart EHs. Reference (Bukhsh et al., 2016) utilized demand-side flexibility to cope with the uncertainty of renewable energy generation to optimize the cost of generation. Reference (Gao et al., 2021) studied the IDR of residential users and pointed out its characteristics of incomplete rationality and strong randomness. Reference (Dababneh and Li, 2019) studied the relationship between manufacturers’ electricity and natural gas demand and established a production scheduling model considering integrated electricity and natural gas demand response. Reference (Huang et al., 2021) developed an intelligent demand response program to address practical challenges in microgrids, such as the uncertainty of photovoltaics. Reference (Hassan et al., 2020) brought together residential, commercial, and industrial consumers to implement demand responses to reduce energy consumption. Reference (Han et al., 2022) established a data-driven demand response model and pointed out that edge computing is beneficial to shorten the optimal scheduling time.

Renewable energy is a powerful pillar for addressing the energy crisis and achieving carbon neutrality, but it is characterized by uncertainties that can be handled through robust optimization (Zang et al., 2018; Zang et al., 2020; Wang et al., 2022). Reference (Sharma et al., 2021) developed a two-stage robust optimization model for multiple uncertainties in multi-energy buildings. References (Zhao et al., 2018; He et al., 2019; Ding et al., 2022b) established a distributionally robust scheduling model to deal with load uncertainty in integrated gas-electricity systems and AC/DC hybrid microgrids, respectively. References (Ding et al., 2017) and (Ding et al., 2021) established a two-stage robust centralized optimal scheduling model to deal with the inverter setting problem caused by photovoltaic intermittency. References (Xu et al., 2018) and (Liu et al., 2021) investigated robust scheduling methods for highly variable and stochastic wind power generation. Reference (Lara et al., 2019) proposed a robust energy management system and modeled it in detail.

Distributed optimization is more realistic than centralized, and can protect user privacy and security, which is the future development trend (Mu et al., 2020; Qu et al., 2021). Reference (Wei et al., 2022) proposed a decentralized demand energy management approach for industrial parks and protected private data. Reference (Chen et al., 2021) studied the distributed robust dynamic economic dispatch for transmission and distribution network coordination. Reference (Lilla et al., 2020) adopts the alternating direction multiplier method (ADMM) for day-ahead scheduling among multiple users who have their characteristic confidentiality requirements. Reference (Zheng et al., 2018) proposed an asynchronous distributed ADMM to solve the convergence problem of optimal operation of multi-agent systems.

However, few research has considered the decentralized robust optimal dispatch and two-level IDR in the user-level IEGHS. To make up for this gap, the main contributions of this paper are summarized as follows:

1) A detailed mathematical model is established for the user-level IEGHS based on the comprehensive modeling of EH, users, and IDR mechanisms. The user-level IEGHS is divided into two levels: node load and user load, corresponding to the implementation of the two-level IDR.

2) A decentralized robust optimal dispatch model is proposed for the user-level IEGHS, where the two-level IDR is incorporated to cope with the uncertainty of renewable energy while protecting the user’s privacy. Moreover, the multi-agent decentralized robust optimization solution method is developed to adapt to the multi-agent multiple energy interaction architectures.

The rest of the paper is organized as follows. Section 2 presents the comprehensive model of the user-level IEGHS. Section 3 proposes the centralized optimal dispatch model of the user-level IEGHS. Section 4 develops the decentralized robust optimal dispatch model of the user-level IEGHS. Section 5 introduces the multi-agent decentralized robust optimization solution method. Section 6 presents the simulation results of the proposed model. Finally, conclusions are drawn in Section 7.

2 Modeling of the user-level IEGHS

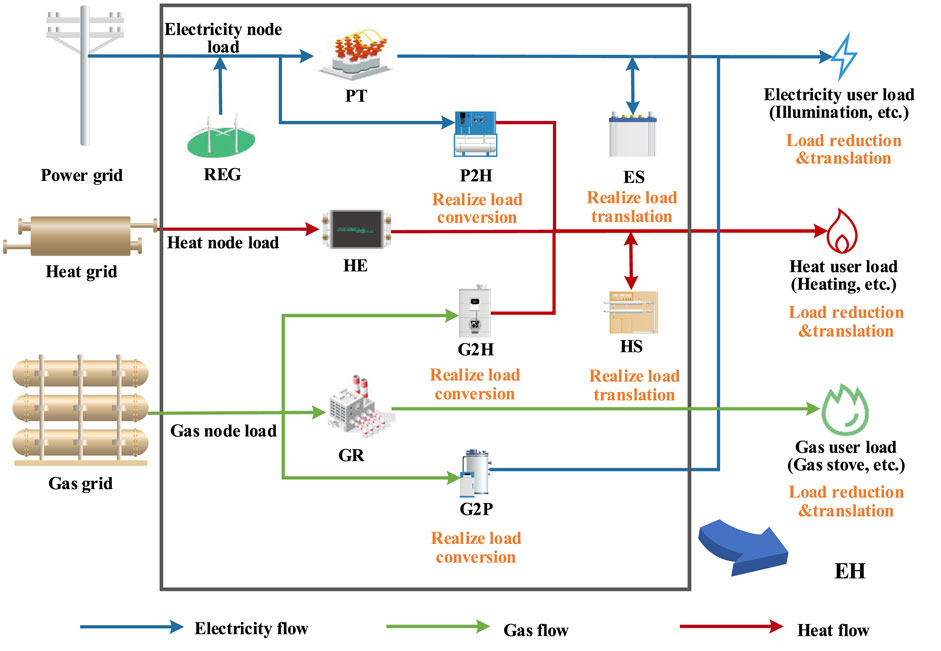
The schematic diagram of a typical user-level IEGHS is shown in Figure 1, where the two ends are the distribution network side and the user side, respectively providing energy supply and energy demand for the integrated energy system, and the middle is the EH, which realizes the generation, conversion, and storage of various forms of energy and is the key to the implementation of IDR. Moreover, EH contains renewable energy generation (REG) equipment, adjustment equipment between distribution networks and users such as power transformers (PT), heat exchangers (HE), gas regulators (GR), energy conversion equipment such as electricity-to-heat (P2H), gas-to-heat (G2H), gas-to-electricity (G2P) equipment, and energy storage equipment such as electricity storage (ES) and heat storage (HS) devices.

FIGURE 1

FIGURE 1. The schematic diagram of a typical user-level IEGHS.

The user-level IEGHS can be divided into two layers: one is node load, which is the output of the distribution network node and the input of EH, and the other is user load, which is the output of EH and the input of users. From the distribution network side, part of the node loads in the electricity, heat, and gas networks are directly used by the users through PT, HE, and GR, while another part is transformed by the energy conversion and storage equipment in the EH and then used by the users. So the node loads are essentially the same as the user loads.

Due to the existence of two types of loads, node loads and user loads, the IDR of loads can be viewed at two levels: first, the IDR of user loads, where users’ electricity, heat, and gas loads actively or passively cut and shift according to energy sales prices and incentive policies; second, the IDR of node loads, where the cut and shift of user loads constitutes a part of the cut and shift of node loads, and in addition nodal electricity, heat, and gas loads can converse and shift through the energy conversion and storage equipment in the EH respectively.

2.1 EH

The EH is the hub for coupling different types of energy and is key to implementing IDR. The EH can break down energy barriers, consisting of renewable energy generation equipment to produce green electricity, and energy conversion equipment and storage equipment to break through the limitations of energy use in form and time.

2.1.1 Renewable energy generation

The REG mainly includes wind power and photovoltaic power generation, which are the current mainstream REG methods. The technical route has been quite mature and is clean, zero carbon, and sustainable, but both wind power and photovoltaic power generation have a direct relationship with the weather, featuring uncertainty. The mathematical model of REG in the EH is

$\begin{array}{c}\mathbf{0}\le {\mathit{E}}_{\mathit{R}\mathit{E},\mathit{t}}\le {\mathit{E}}_{\mathit{R}\mathit{E},\mathit{t}}^{\mathbf{max}},\forall \mathit{t}\in \mathit{T}\end{array}(1)$

where ${\mathit{E}}_{\mathit{R}\mathit{E},\mathit{t}}$ and ${\mathit{E}}_{\mathit{R}\mathit{E},\mathit{t}}^{\mathbf{max}}$ are the actual power output and maximum predicted output of REG at tth time period.

2.1.2 Energy conversion equipment

The energy conversion equipment under the EH mainly includes G2P, G2H, and P2H. These devices are important for breaking energy barriers, increasing the flexibility of energy use at the load side of root nodes, improving energy utilization efficiency, and realizing energy cascade utilization.

The G2P, such as gas turbines, converts the chemical energy in natural gas into electrical energy and supplies it to the users with electrical load. The unified mathematical model of G2P is

$\begin{array}{c}{\mathit{E}}_{\mathit{G}\mathbf{2}\mathit{P},\mathit{t}}={\mathit{\eta }}_{\mathit{G}\mathbf{2}\mathit{P}}{\mathit{G}}_{\mathit{G}\mathbf{2}\mathit{P},\mathit{t}},\forall \mathit{t}\in \mathit{T}\end{array}(2)$

$\begin{array}{c}{\mathit{G}}_{\mathit{G}\mathbf{2}\mathit{P}}^{\mathbf{min}}\le {\mathit{G}}_{\mathit{G}\mathbf{2}\mathit{P},\mathit{t}}\le {\mathit{G}}_{\mathit{G}\mathbf{2}\mathit{P}}^{\mathbf{max}},\forall \mathit{t}\in \mathit{T}\end{array}(3)$

$\begin{array}{c}\Delta {\mathit{G}}_{\mathit{G}\mathbf{2}\mathit{P}}^{\mathbf{min}}\le {\mathit{G}}_{\mathit{G}\mathbf{2}\mathit{P},\mathit{t}}-{\mathit{G}}_{\mathit{G}\mathbf{2}\mathit{P},\mathit{t}-\mathbf{1}}\le {\Delta \mathit{G}}_{\mathit{G}\mathbf{2}\mathit{P}}^{\mathbf{max}},\forall \mathit{t}\in \mathit{T}\end{array}(4)$

where ${\mathit{G}}_{\mathit{G}\mathbf{2}\mathit{P},\mathit{t}}$ is the gas consumed by the G2P on tth time period; ${\mathit{E}}_{\mathit{G}\mathbf{2}\mathit{P},\mathit{t}}$ is the electrical power output of the G2P on tth time period; ${\mathit{\eta }}_{\mathit{G}\mathbf{2}\mathit{P}}$ is the conversion efficiency of the G2P; ${\mathit{G}}_{\mathit{G}\mathbf{2}\mathit{P}}^{\mathbf{min}}$ and ${\mathit{G}}_{\mathit{G}\mathbf{2}\mathit{P}}^{\mathbf{max}}$ are the lower and upper limits of the gas consumption at all times; $\Delta {\mathit{G}}_{\mathit{G}\mathbf{2}\mathit{P}}^{\mathbf{min}}$ and ${\Delta \mathit{G}}_{\mathit{G}\mathbf{2}\mathit{P}}^{\mathbf{max}}$ are the lower and upper limits of gas consumption fluctuations between two consecutive time periods.

The G2H, such as gas boilers, converts the chemical energy in natural gas into heat energy to supply the users with heat load. The unified mathematical model of G2H is

$\begin{array}{c}{\mathit{H}}_{\mathit{G}\mathbf{2}\mathit{H},\mathit{t}}={\mathit{\eta }}_{\mathit{G}\mathbf{2}\mathit{H}}{\mathit{G}}_{\mathit{G}\mathbf{2}\mathit{H},\mathit{t}},\forall \mathit{t}\in \mathit{T}\end{array}(5)$

$\begin{array}{c}{\mathit{G}}_{\mathit{G}\mathbf{2}\mathit{H}}^{\mathbf{min}}\le {\mathit{G}}_{\mathit{G}\mathbf{2}\mathit{H},\mathit{t}}\le {\mathit{G}}_{\mathit{G}\mathbf{2}\mathit{H}}^{\mathbf{max}},\forall \mathit{t}\in \mathit{T}\end{array}(6)$

$\begin{array}{c}\Delta {\mathit{G}}_{\mathit{G}\mathbf{2}\mathit{H}}^{\mathbf{min}}\le {\mathit{G}}_{\mathit{G}\mathbf{2}\mathit{H},\mathit{t}}-{\mathit{G}}_{\mathit{G}\mathbf{2}\mathit{H},\mathit{t}-\mathbf{1}}\le {\Delta \mathit{G}}_{\mathit{G}\mathbf{2}\mathit{H}}^{\mathbf{max}},\forall \mathit{t}\in \mathit{T}\end{array}(7)$

where ${\mathit{G}}_{\mathit{G}\mathbf{2}\mathit{H},\mathit{t}}$ is the gas consumed by the G2H on tth time period; ${\mathit{H}}_{\mathit{G}\mathbf{2}\mathit{H},\mathit{t}}$ is the thermal power output of the G2H at tth time period; ${\mathit{\eta }}_{\mathit{G}\mathbf{2}\mathit{H}}$ is the conversion efficiency of the G2H; ${\mathit{G}}_{\mathit{G}\mathbf{2}\mathit{H}}^{\mathbf{min}}$ and ${\mathit{G}}_{\mathit{G}\mathbf{2}\mathit{H}}^{\mathbf{max}}$ are the lower and upper limits of the gas consumption at all times; $\Delta {\mathit{G}}_{\mathit{G}\mathbf{2}\mathit{H}}^{\mathbf{min}}$ and ${\Delta \mathit{G}}_{\mathit{G}\mathbf{2}\mathit{H}}^{\mathbf{max}}$ are the lower and upper limits of gas consumption fluctuations between two consecutive time periods.

The P2H, such as electrical boilers, converts the electrical energy into heat energy, supplying the users with heat load. The unified mathematical model of P2H is

$\begin{array}{c}{\mathit{H}}_{\mathit{P}\mathbf{2}\mathit{H},\mathit{t}}={\mathit{\eta }}_{\mathit{P}\mathbf{2}\mathit{H}}{\mathit{E}}_{\mathit{P}\mathbf{2}\mathit{H},\mathit{t}},\forall \mathit{t}\in \mathit{T}\end{array}(8)$

$\begin{array}{c}{\mathit{E}}_{\mathit{P}\mathbf{2}\mathit{H}}^{\mathbf{min}}\le {\mathit{E}}_{\mathit{P}\mathbf{2}\mathit{H},\mathit{t}}\le {\mathit{E}}_{\mathit{P}\mathbf{2}\mathit{H}}^{\mathbf{max}},\forall \mathit{t}\in \mathit{T}\end{array}(9)$

$\begin{array}{c}\Delta {\mathit{E}}_{\mathit{P}\mathbf{2}\mathit{H}}^{\mathbf{min}}\le {\mathit{E}}_{\mathit{P}\mathbf{2}\mathit{H},\mathit{t}}-{\mathit{E}}_{\mathit{P}\mathbf{2}\mathit{H},\mathit{t}-\mathbf{1}}\le {\Delta \mathit{E}}_{\mathit{P}\mathbf{2}\mathit{H}}^{\mathbf{max}},\forall \mathit{t}\in \mathit{T}\end{array}(10)$

where ${\mathit{E}}_{\mathit{P}\mathbf{2}\mathit{H},\mathit{t}}$ is the electricity consumed by the P2H at tth time period; ${\mathit{H}}_{\mathit{P}\mathbf{2}\mathit{H},\mathit{t}}$ is the thermal power output of the P2H at tth time period; ${\mathit{\eta }}_{\mathit{P}\mathbf{2}\mathit{H}}$ is the conversion efficiency of the P2H; ${\mathit{E}}_{\mathit{P}\mathbf{2}\mathit{H}}^{\mathbf{min}}$ and ${\mathit{E}}_{\mathit{P}\mathbf{2}\mathit{H}}^{\mathbf{max}}$ are the lower and upper limits of the electricity consumption at all times; $\Delta {\mathit{E}}_{\mathit{P}\mathbf{2}\mathit{H}}^{\mathbf{min}}$ and ${\Delta \mathit{E}}_{\mathit{P}\mathbf{2}\mathit{H}}^{\mathbf{max}}$ are the lower and upper limits of electricity consumption fluctuations between two consecutive time periods.

2.1.3 Energy storage equipment

The energy storage equipment under the EH is ES and HS. These devices break the limitation of matching supply and demand in real time, making the load transferable in time and enhancing the flexibility and economy of the whole system operation.

The HS can be modeled as

$\begin{array}{c}{\mathit{H}\mathit{S}}_{\mathit{t}}=\mathit{H}{\mathit{S}}_{\mathit{t}-\mathbf{1}}+{\mathit{H}}_{\mathit{c},\mathit{t}}{\mathit{\zeta }}_{\mathit{c},\mathit{H}}-{\mathit{H}}_{\mathit{d}\mathit{c},\mathit{t}}/{\mathit{\zeta }}_{\mathit{d}\mathit{c},\mathit{H}},\forall \mathit{t}\in \mathit{T}\end{array}(11)$

$\begin{array}{c}{\displaystyle \sum }_{\mathit{t}=\mathbf{1}}^{\mathit{T}}{\mathit{H}}_{\mathit{c},\mathit{t}}={\displaystyle \sum }_{\mathit{t}=\mathbf{1}}^{\mathit{T}}{\mathit{H}}_{\mathit{d}\mathit{c},\mathit{t}}\end{array}(12)$

$\begin{array}{c}{\mathit{H}\mathit{S}}_{\mathbf{min}}\le \mathit{H}{\mathit{S}}_{\mathit{t}}{\le \mathit{H}\mathit{S}}_{\mathbf{max}},\forall \mathit{t}\in \mathit{T}\end{array}(13)$

$\begin{array}{c}{\mathit{H}}_{\mathit{c},\mathbf{min}}\le {\mathit{H}}_{\mathit{c},\mathit{t}}{\le \mathit{H}}_{\mathit{c},\mathbf{max}},\forall \mathit{t}\in \mathit{T}\end{array}(14)$

$\begin{array}{c}{\mathit{H}}_{\mathit{d}\mathit{c},\mathbf{min}}\le {\mathit{H}}_{\mathit{d}\mathit{c},\mathit{t}}{\le \mathit{H}}_{\mathit{d}\mathit{c},\mathbf{max}},\forall \mathit{t}\in \mathit{T}\end{array}(15)$

where ${\mathit{H}\mathit{S}}_{\mathit{t}}$ , ${\mathit{H}}_{\mathit{c},\mathit{t}}$ , and ${\mathit{H}}_{\mathit{d}\mathit{c},\mathit{H}}$ represent the heat-containing state, heat storage power, and heat release power of the HS at tth time period; ${\mathit{\zeta }}_{\mathit{c},\mathit{H}}$ and ${\mathit{\zeta }}_{\mathit{d}\mathit{c},\mathit{H}}$ are the charging and discharging efficiencies of the HS; ${\mathit{H}\mathit{S}}_{\mathbf{min}}$ and ${\mathit{H}\mathit{S}}_{\mathbf{max}}$ indicate the lower and upper limits of the capacity of the HS; ${\mathit{H}}_{\mathit{c},\mathbf{min}}$ and ${\mathit{H}}_{\mathit{c},\mathbf{max}}$ indicate the lower and upper limits of HS input; ${\mathit{H}}_{\mathit{d}\mathit{c},\mathbf{min}}$ and ${\mathit{H}}_{\mathit{d}\mathit{c},\mathbf{max}}$ indicate the lower and upper limits of HS output.

The ES can be modeled as

$\begin{array}{c}{\mathit{E}\mathit{S}}_{\mathit{t}}=\mathit{E}{\mathit{S}}_{\mathit{t}-\mathbf{1}}+{\mathit{E}}_{\mathit{c},\mathit{t}}{\mathit{\zeta }}_{\mathit{c},\mathit{E}}-{\mathit{E}}_{\mathit{d}\mathit{c},\mathit{t}}/{\mathit{\zeta }}_{\mathit{d}\mathit{c},\mathit{E}},\forall \mathit{t}\in \mathit{T}\end{array}(16)$

$\begin{array}{c}{\displaystyle \sum }_{\mathit{t}=\mathbf{1}}^{\mathit{T}}{\mathit{E}}_{\mathit{c},\mathit{t}}={\displaystyle \sum }_{\mathit{t}=\mathbf{1}}^{\mathit{T}}{\mathit{E}}_{\mathit{d}\mathit{c},\mathit{t}}\end{array}(17)$

$\begin{array}{c}{\mathit{E}\mathit{S}}_{\mathbf{min}}\le \mathit{E}{\mathit{S}}_{\mathit{t}}{\le \mathit{E}\mathit{S}}_{\mathbf{max}},\forall \mathit{t}\in \mathit{T}\end{array}(18)$

$\begin{array}{c}{\mathit{E}}_{\mathit{c},\mathbf{min}}\le {\mathit{E}}_{\mathit{c},\mathit{t}}{\le \mathit{E}}_{\mathit{c},\mathbf{max}},\forall \mathit{t}\in \mathit{T}\end{array}(19)$

$\begin{array}{c}{\mathit{E}}_{\mathit{d}\mathit{c},\mathbf{min}}\le {\mathit{E}}_{\mathit{d}\mathit{c},\mathit{t}}{\le \mathit{E}}_{\mathit{d}\mathit{c},\mathbf{max}},\forall \mathit{t}\in \mathit{T}\end{array}(20)$

where ${\mathit{E}\mathit{S}}_{\mathit{t}}$ , ${\mathit{E}}_{\mathit{c},\mathit{t}}$ , and ${\mathit{E}}_{\mathit{d}\mathit{c},\mathit{H}}$ represent the electricity-containing state, the charging power, and the discharging power of the ES at tth time period; ${\mathit{\zeta }}_{\mathit{c},\mathit{E}}$ and ${\mathit{\zeta }}_{\mathit{d}\mathit{c},\mathit{E}}$ are the charging and discharging efficiencies of the ES; ${\mathit{E}\mathit{S}}_{\mathbf{min}}$ and ${\mathit{E}\mathit{S}}_{\mathbf{max}}$ indicate the lower and upper limits of the capacity of the ES; ${\mathit{E}}_{\mathit{c},\mathbf{min}}$ and ${\mathit{E}}_{\mathit{c},\mathbf{max}}$ indicate the lower and upper limits of ES input; ${\mathit{E}}_{\mathit{d}\mathit{c},\mathbf{min}}$ and ${\mathit{E}}_{\mathit{d}\mathit{c},\mathbf{max}}$ indicate the lower and upper limits of ES output.

2.2 Users

In addition to energy usage equipment, users can also possess small-scale distributed energy production equipment, such as rooftop photovoltaics (RPVs), rooftop solar heatings (RSHs), etc. Due to the existence of these apparatuses, users do not have to rely entirely on upper-level energy suppliers, and even have the possibility to interact with other users.

The RPV can be modeled as

$\begin{array}{c}\mathbf{0}\le {\mathit{E}}_{\mathit{P}\mathit{V},\mathit{n},\mathit{t}}\le {\mathit{E}}_{\mathit{P}\mathit{V},\mathit{n},\mathit{t}}^{\mathbf{max}},\forall \mathit{t}\in \mathit{T}\end{array}(21)$

where ${\mathit{E}}_{\mathit{P}\mathit{V},\mathit{n},\mathit{t}}$ and ${\mathit{E}}_{\mathit{P}\mathit{V},\mathit{n},\mathit{t}}^{\mathbf{max}}$ are the actual power output and maximum predicted output of the RPV of nth user at tth time period.

The RSH can be modeled as

$\begin{array}{c}\mathbf{0}\le {\mathit{H}}_{\mathit{S}\mathit{P},\mathit{n},\mathit{t}}\le {\mathit{H}}_{\mathit{S}\mathit{P},\mathit{n},\mathit{t}}^{\mathbf{max}},\forall \mathit{t}\in \mathit{T}\end{array}(22)$

where ${\mathit{H}}_{\mathit{S}\mathit{P},\mathit{n},\mathit{t}}$ and ${\mathit{H}}_{\mathit{S}\mathit{P},\mathit{n},\mathit{t}}^{\mathbf{max}}$ are the actual power output and maximum predicted output of the RSH of nth user at tth time period.

2.3 IDR

The IDR is a derivation and expansion of traditional electricity demand response, with coordinated optimization of energy coupling, storage, and redistribution on the user-level IEGHS. The mathematical model of the IDR is established for the adjustable load, which is classified as the translatable load, the curtailable load, and the convertible load to represent the shift in time and conversion in energy type.

2.3.1 The translatable load

The translatable load refers to the load whose use time can be advanced or delayed. However, the total translatable load should not change after the adjustment. The mathematical model of the translatable load is stated as

$\begin{array}{c}{\displaystyle \sum }_{\mathit{t}\in {\mathbf{\Omega }}_{\mathit{T}+}}{\mathit{D}}_{\mathit{s}\mathit{h}\mathit{i}\mathit{f}\mathit{t}+,\mathit{n},\mathit{t}}={\displaystyle \sum }_{\mathit{t}\in {\mathbf{\Omega }}_{\mathit{T}-}}{\mathit{D}}_{\mathit{s}\mathit{h}\mathit{i}\mathit{f}\mathit{t}-,\mathit{n},\mathit{t}},\forall \mathit{n}\in {\mathbf{\Omega }}_{\mathit{U}\mathit{S}\mathit{E}}\end{array}(23)$

$\begin{array}{c}{\mathit{D}}_{\mathit{s}\mathit{h}\mathit{i}\mathit{f}\mathit{t}+,\mathit{n},\mathit{min}}\le {\mathit{D}}_{\mathit{s}\mathit{h}\mathit{i}\mathit{f}\mathit{t}+,\mathit{n},\mathit{t}}\le {\mathit{D}}_{\mathit{s}\mathit{h}\mathit{i}\mathit{f}\mathit{t}+,\mathit{n},\mathit{max}},\forall \mathit{n}\in {\mathbf{\Omega }}_{\mathit{U}\mathit{S}\mathit{E}}\mathit{t}\in {\mathbf{\Omega }}_{\mathit{T}+}\end{array}(24)$

$\begin{array}{c}{\mathit{D}}_{\mathit{s}\mathit{h}\mathit{i}\mathit{f}\mathit{t}-,\mathit{n},\mathit{min}}\le {\mathit{D}}_{\mathit{s}\mathit{h}\mathit{i}\mathit{f}\mathit{t}-,\mathit{n},\mathit{t}}\le {\mathit{D}}_{\mathit{s}\mathit{h}\mathit{i}\mathit{f}\mathit{t}-,\mathit{n},\mathit{max}},\forall \mathit{n}\in {\mathbf{\Omega }}_{\mathit{U}\mathit{S}\mathit{E}}\mathit{t}\in {\mathbf{\Omega }}_{\mathit{T}-}\end{array}(25)$

Where ${\mathbf{\Omega }}_{\mathit{U}\mathit{S}\mathit{E}}$ represents the set of users of IEGHS; ${\mathbf{\Omega }}_{\mathit{T}+}$ and ${\mathbf{\Omega }}_{\mathit{T}-}$ represent the set of time periods during which the loads are moved in and out, respectively; ${\mathit{D}}_{\mathbf{s}\mathbf{h}\mathbf{i}\mathbf{f}\mathbf{t}+,\mathit{n},\mathit{t}}$ and ${\mathit{D}}_{\mathbf{s}\mathbf{h}\mathbf{i}\mathbf{f}\mathbf{t}-,\mathit{n},\mathit{t}}$ indicate the amount of load moved in and out of nth user at tth time period; ${\mathit{D}}_{\mathbf{s}\mathbf{h}\mathbf{i}\mathbf{f}\mathbf{t}+,\mathit{n},\mathbf{min}}$ and ${\mathit{D}}_{\mathbf{s}\mathbf{h}\mathbf{i}\mathbf{f}\mathbf{t}+,\mathit{n},\mathbf{max}}$ are the lower and upper limits of the load moved in of nth user; ${\mathit{D}}_{\mathbf{s}\mathbf{h}\mathbf{i}\mathbf{f}\mathbf{t}-,\mathit{n},\mathbf{min}}$ and ${\mathit{D}}_{\mathbf{s}\mathbf{h}\mathbf{i}\mathbf{f}\mathbf{t}-,\mathit{n},\mathbf{max}}$ are the lower and upper limits of the load moved out of nth user.

2.3.2 The curtailable load

The curtailable load refers to the load that can be directly interrupted within a limited range and within a specific time period, which is to ensure the safe operation of the system during peak hours. The mathematical model of the curtailable load is stated as

$\begin{array}{c}{\mathit{D}}_{\mathbf{c}\mathbf{u}\mathbf{t},\mathit{n},\mathbf{min}}\le {\mathit{D}}_{\mathbf{c}\mathbf{u}\mathbf{t},\mathit{n},\mathit{t}}\le {\mathit{D}}_{\mathbf{c}\mathbf{u}\mathbf{t},\mathit{n},\mathbf{max}},\forall \mathit{n}\in {\mathbf{\Omega }}_{\mathit{U}\mathit{S}\mathit{E}}\mathit{t}\in {\mathbf{\Omega }}_{\mathit{T}\mathit{c}\mathit{u}\mathit{t}}\end{array}(26)$

where ${\mathbf{\Omega }}_{\mathit{T}\mathbf{c}\mathbf{u}\mathbf{t}}$ represents the set of time periods during which loads are curtailed; ${\mathit{D}}_{\mathbf{c}\mathbf{u}\mathbf{t},\mathit{n},\mathit{t}}$ indicates the amount of load curtailed of nth user at tth time period; ${\mathit{D}}_{\mathbf{c}\mathbf{u}\mathbf{t},\mathit{n},\mathbf{min}}$ and ${\mathit{D}}_{\mathbf{c}\mathbf{u}\mathbf{t},\mathit{n},\mathbf{max}}$ are the lower and upper limits of the load curtailed of nth user.

2.3.3 The convertible load

The convertible load mainly represents the substitution of different energy forms, e.g. energy demand can be flexibly met by converting one energy source to another through energy conversion equipment in EH. The mathematical model of the convertible load is stated as

$\begin{array}{c}{\mathit{E}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v}+,\mathit{n},\mathit{t}}={\mathit{\omega }}_{\mathit{H}\mathbf{2}\mathit{E}}{\mathit{\mu }}_{\mathit{H}\mathbf{2}\mathit{E}}{\mathit{H}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v}-,\mathit{n},\mathit{t}}+{\mathit{\omega }}_{\mathit{G}\mathbf{2}\mathit{E}}{\mathit{\mu }}_{\mathit{G}\mathbf{2}\mathit{E}}{\mathit{G}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v}-,\mathit{n},\mathit{t}},\forall \mathit{n}\in {\mathbf{\Omega }}_{\mathit{U}\mathit{S}\mathit{E}}\mathit{t}\in \mathit{T}\end{array}(27)$

$\begin{array}{c}{\mathit{H}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v}+,\mathit{n},\mathit{t}}={\mathit{\omega }}_{\mathit{E}\mathbf{2}\mathit{H}}{\mathit{\mu }}_{\mathit{E}\mathbf{2}\mathit{H}}{\mathit{E}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v}-,\mathit{n},\mathit{t}}+{\mathit{\omega }}_{\mathit{G}\mathbf{2}\mathit{H}}{\mathit{\mu }}_{\mathit{G}\mathbf{2}\mathit{H}}{\mathit{G}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v}-,\mathit{n},\mathit{t}},\forall \mathit{n}\in {\mathbf{\Omega }}_{\mathit{U}\mathit{S}\mathit{E}}\mathit{t}\in \mathit{T}\end{array}(28)$

$\begin{array}{c}{\mathit{G}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v}+,\mathit{n},\mathit{t}}={\mathit{\omega }}_{\mathit{E}\mathbf{2}\mathit{G}}{\mathit{\mu }}_{\mathit{E}\mathbf{2}\mathit{G}}{\mathit{E}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v}-,\mathit{n},\mathit{t}}+{\mathit{\omega }}_{\mathit{H}\mathbf{2}\mathit{G}}{\mathit{\mu }}_{\mathit{H}\mathbf{2}\mathit{G}}{\mathit{H}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v}-,\mathit{n},\mathit{t}},\forall \mathit{n}\in {\mathbf{\Omega }}_{\mathit{U}\mathit{S}\mathit{E}}\mathit{t}\in \mathit{T}\end{array}(29)$

$\begin{array}{c}{\mathit{E}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v}-,\mathit{n},\mathbf{min}}\le {\mathit{E}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v}-,\mathit{n},\mathit{t}}\le {\mathit{E}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v}-,\mathit{n},\mathbf{max}},\forall \mathit{n}\in {\mathbf{\Omega }}_{\mathit{U}\mathit{S}\mathit{E}}\mathit{t}\in {\mathbf{\Omega }}_{\mathit{T}\mathit{c}\mathit{o}\mathit{n}\mathit{v},\mathit{E}}\end{array}(30)$

$\begin{array}{c}{\mathit{H}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v}-,\mathit{n},\mathbf{min}}\le {\mathit{H}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v}-,\mathit{n},\mathit{t}}\le {\mathit{H}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v}-,\mathit{n},\mathbf{max}},\forall \mathit{n}\in {\mathbf{\Omega }}_{\mathit{U}\mathit{S}\mathit{E}}\mathit{t}\in {\mathbf{\Omega }}_{\mathit{T}\mathit{c}\mathit{o}\mathit{n}\mathit{v},\mathit{H}}\end{array}(31)$

$\begin{array}{c}{\mathit{G}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v}-,\mathit{n},\mathit{min}}\le {\mathit{G}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v}-,\mathit{n},\mathit{t}}\le {\mathit{G}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v}-,\mathit{n},\mathit{max}},\forall \mathit{n}\in {\mathbf{\Omega }}_{\mathit{U}\mathit{S}\mathit{E}}\mathit{t}\in {\mathbf{\Omega }}_{\mathit{T}\mathit{c}\mathit{o}\mathit{n}\mathit{v},\mathit{G}}\end{array}(32)$

$\begin{array}{c}{\mathit{\mu }}_{\mathit{E}\mathbf{2}\mathit{H}}+{\mathit{\mu }}_{\mathit{E}\mathbf{2}\mathit{G}}=\mathbf{1},{\mathit{\mu }}_{\mathit{H}\mathbf{2}\mathit{E}}+{\mathit{\mu }}_{\mathit{H}\mathbf{2}\mathit{G}}=\mathbf{1},{\mathit{\mu }}_{\mathit{G}\mathbf{2}\mathit{E}}+{\mathit{\mu }}_{\mathit{G}\mathbf{2}\mathit{H}}=\mathbf{1}\end{array}(33)$

where ${\mathbf{\Omega }}_{\mathit{T}\mathit{c}\mathit{o}\mathit{n}\mathit{v},\mathit{E}}$, ${\mathbf{\Omega }}_{\mathit{T}\mathit{c}\mathit{o}\mathit{n}\mathit{v},\mathit{H}}$ and ${\mathbf{\Omega }}_{\mathit{T}\mathit{c}\mathit{o}\mathit{n}\mathit{v},\mathit{G}}$ represent the set of time periods during which the electricity, heat and gas load are converted in and out; ${\mathit{E}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v}-,\mathit{n},\mathit{t}}$, ${\mathit{H}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v}-,\mathit{n},\mathit{t}}$ and ${\mathit{G}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v}-,\mathit{n},\mathit{t}}$ indicate the amount of the electricity, heat and gas load converted out of nth user at tth time period; ${\mathit{E}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v}+,\mathit{n},\mathit{t}}$, ${\mathit{H}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v}+,\mathit{n},\mathit{t}}$ and ${\mathit{G}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v}+,\mathit{n},\mathit{t}}$ indicate the amount of the electricity, heat and gas load converted in of nth user at tth time period; ${\mathit{\omega }}_{\mathit{H}\mathbf{2}\mathit{E}}$, ${\mathit{\omega }}_{\mathit{G}\mathbf{2}\mathit{E}}$, ${\mathit{\omega }}_{\mathit{E}\mathbf{2}\mathit{H}}$, ${\mathit{\omega }}_{\mathit{G}\mathbf{2}\mathit{H}}$, ${\mathit{\omega }}_{\mathit{E}\mathbf{2}\mathit{G}}$ and ${\mathit{\omega }}_{\mathit{H}\mathbf{2}\mathit{G}}$ are the conversion efficiency of the convertible load; ${\mathit{\mu }}_{\mathit{H}\mathbf{2}\mathit{E}}$, ${\mathit{\mu }}_{\mathit{G}\mathbf{2}\mathit{E}}$, ${\mathit{\mu }}_{\mathit{E}\mathbf{2}\mathit{H}}$, ${\mathit{\mu }}_{\mathit{G}\mathbf{2}\mathit{H}}$, ${\mathit{\mu }}_{\mathit{E}\mathbf{2}\mathit{G}}$ and ${\mathit{\mu }}_{\mathit{H}\mathbf{2}\mathit{G}}$ are the conversion ratio of the convertible load. If there is no conversion form among users, the corresponding conversion efficiency and conversion ratio are equal to 0. ${\mathit{E}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v}-,\mathit{n},\mathbf{min}}$ and ${\mathit{E}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v}-,\mathit{n},\mathbf{max}}$ are the lower and upper limits of the electric load converted out of nth user; ${\mathit{H}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v}-,\mathit{n},\mathbf{min}}$ and ${\mathit{H}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v}-,\mathit{n},\mathbf{max}}$ are the lower and upper limits of the heat load converted out of nth user; ${\mathit{G}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v}-,\mathit{n},\mathbf{min}}$ and ${\mathit{G}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v}-,\mathit{n},\mathbf{max}}$ are the lower and upper limits of the gas load converted out of nth user.

3 Centralized optimal dispatch model of the user-level IEGHS

3.1 Objective function

The objective function of the optimal dispatch model is to minimize the cost of EHs and users in the day-ahead integrated energy dispatch of the user-level IEGHS, which is related to the supply-side energy prices, the operation and maintenance costs of energy conversion and storage facilities, and the cost of distributed energy production by users. The objective function is shown below.

$\begin{array}{l}\mathbf{min}\mathit{C}\mathit{o}\mathit{s}\mathit{t}={\displaystyle \sum }_{\mathit{t}=\mathbf{1}}^{\mathit{T}}{\mathit{E}}_{\mathit{R}\mathit{E},\mathit{t}}{\mathit{\gamma }}_{\mathit{R}\mathit{E},\mathit{t}}+{\displaystyle \sum }_{\mathit{t}=\mathbf{1}}^{\mathit{T}}{\mathit{E}}_{\mathit{G}\mathbf{2}\mathit{P},\mathit{t}}{\mathit{\gamma }}_{\mathit{G}\mathbf{2}\mathit{P},\mathit{t}}+{\displaystyle \sum }_{\mathit{t}=\mathbf{1}}^{\mathit{T}}{\mathit{H}}_{\mathit{G}\mathbf{2}\mathit{H},\mathit{t}}{\mathit{\gamma }}_{\mathit{G}\mathbf{2}\mathit{H},\mathit{t}}\\ +{\displaystyle \sum }_{\mathit{t}=\mathbf{1}}^{\mathit{T}}{\mathit{H}}_{\mathit{P}\mathbf{2}\mathit{H},\mathit{t}}{\mathit{\gamma }}_{\mathit{P}\mathbf{2}\mathit{H},\mathit{t}}+{\displaystyle \sum }_{\mathit{t}=\mathbf{1}}^{\mathit{T}}\left({\mathit{H}}_{\mathit{c},\mathit{t}}+{\mathit{H}}_{\mathit{d}\mathit{c},\mathit{t}}\right){\mathit{\gamma }}_{\mathit{H}\mathit{S},\mathit{t}}\\ +{\displaystyle \sum }_{\mathit{t}=\mathbf{1}}^{\mathit{T}}\left({\mathit{E}}_{\mathit{c},\mathit{t}}+{\mathit{E}}_{\mathit{d}\mathit{c},\mathit{t}}\right){\mathit{\gamma }}_{\mathit{E}\mathit{S},\mathit{t}}+{\displaystyle \sum }_{\mathit{t}=\mathbf{1}}^{\mathit{T}}\left({\mathit{E}}_{\mathit{B},\mathit{t}}{\mathit{p}}_{\mathit{B},\mathit{E},\mathit{t}}+{\mathit{H}}_{\mathit{B},\mathit{t}}{\mathit{p}}_{\mathit{B},\mathit{H},\mathit{t}}+{\mathit{G}}_{\mathit{B},\mathit{t}}{\mathit{p}}_{\mathit{B},\mathit{G},\mathit{t}}\right)\\ +{\displaystyle \sum }_{\mathit{n}=\mathbf{1}}^{\mathit{N}}{\displaystyle \sum }_{\mathit{t}=\mathbf{1}}^{\mathit{T}}\left(({\mathit{E}}_{\mathit{P}\mathit{V},\mathit{n},\mathit{t}}{\mathit{\gamma }}_{\mathit{P}\mathit{V},\mathit{n},\mathit{t}}+{\mathit{H}}_{\mathit{S}\mathit{P},\mathit{n},\mathit{t}}{\mathit{\gamma }}_{\mathit{S}\mathit{P},\mathit{n},\mathit{t}}\right)\end{array}(34)$

where ${\mathit{\gamma }}_{\mathit{R}\mathit{E},\mathit{t}}$, ${\mathit{\gamma }}_{\mathit{G}\mathbf{2}\mathit{P},\mathit{t}}$, ${\mathit{\gamma }}_{\mathit{G}\mathbf{2}\mathit{H},\mathit{t}}$, ${\mathit{\gamma }}_{\mathit{P}\mathbf{2}\mathit{H},\mathit{t}}$, ${\mathit{\gamma }}_{\mathit{H}\mathit{S},\mathit{t}}$ and ${\mathit{\gamma }}_{\mathit{E}\mathit{S},\mathit{t}}$ are the operation and maintenance cost coefficients of the REG, G2P, G2H, P2H, HS, and ES, respectively; ${\mathit{E}}_{\mathit{B},\mathit{t}}$, ${\mathit{H}}_{\mathit{B},\mathit{t}}$ and ${\mathit{G}}_{\mathit{B},\mathit{t}}$ are electricity, heat and gas energy purchased from the distribution network side; ${\mathit{p}}_{\mathit{B},\mathit{E},\mathit{t}}$, ${\mathit{p}}_{\mathit{B},\mathit{H},\mathit{t}}$ and ${\mathit{p}}_{\mathit{B},\mathit{G},\mathit{t}}$ are the prices of electricity, heat and gas energy purchased; ${\mathit{\gamma }}_{\mathit{P}\mathit{V},\mathit{n},\mathit{t}}$ and ${\mathit{\gamma }}_{\mathit{S}\mathit{P},\mathit{n},\mathit{t}}$ are the operation and maintenance cost coefficients of the RPV and RSH of nth user.

3.2 Root node constraints

The root node constraint, i.e., the energy limit of the electricity distribution network, heat distribution network, and gas distribution network to supply electricity, heat, and gas to the EH, can be expressed by the following equations.

$\begin{array}{c}\mathbf{0}\le {\mathit{E}}_{\mathit{B},\mathit{t}}\le {\mathit{E}}_{\mathit{B},\mathit{t}}^{\mathbf{max}},\forall \mathit{t}\in \mathit{T}\end{array}(35)$

$\begin{array}{c}\mathbf{0}\le {\mathit{H}}_{\mathit{B},\mathit{t}}\le {\mathit{H}}_{\mathit{B},\mathit{t}}^{\mathbf{max}},\forall \mathit{t}\in \mathit{T}\end{array}(36)$

$\begin{array}{c}\mathbf{0}\le {\mathit{G}}_{\mathit{B},\mathit{t}}\le {\mathit{G}}_{\mathit{B},\mathit{t}}^{\mathbf{max}},\forall \mathit{t}\in \mathit{T}\end{array}(37)$

where ${\mathit{E}}_{\mathit{B},\mathit{t}}^{\mathbf{max}}$, ${\mathit{H}}_{\mathit{B},\mathit{t}}^{\mathbf{max}}$ , ${\mathit{G}}_{\mathit{B},\mathit{t}}^{\mathbf{max}}$ are the upper limits of energy supply from the distribution network to the EH at tth time period, respectively.

3.3 EH constraints

The operation constraints of the energy production, conversion, and storage equipment in the EH are already formulated as Eqs 1–20.

3.4 Users constraints

The operation constraints of the RPV and RSH in the users are already presented in Eqs 21, 22.

3.5 IDR constraints

The constraints related to the three types of IDR, translatable, curtailable, and convertible, when the user loads perform the IDR are shown in Eqs 23–33.

3.6 Energy balance constraints

The energy balance constraint consists of two parts, namely, the energy balance constraints of electric energy, heat energy, and gas energy in the EH, and the energy balance constraints of the users' electricity, heat, and gas loads before and after the IDR. Based on the refined mathematical model of the EH, the energy balance constraints of electric energy, heat energy, and gas energy inside the EH are formulated as

$\begin{array}{c}{\displaystyle \sum }_{\mathit{n}=\mathbf{1}}^{\mathit{N}}{\mathit{E}}_{\mathit{D},\mathit{n},\mathit{t}}={\mathit{E}}_{\mathit{B},\mathit{t}}+{\mathit{E}}_{\mathit{R}\mathit{E},\mathit{t}}+{\mathit{E}}_{\mathit{G}\mathbf{2}\mathit{P},\mathit{t}}-{\mathit{E}}_{\mathit{P}\mathbf{2}\mathit{H},\mathit{t}}-{\mathit{E}}_{\mathit{c},\mathit{t}}+{\mathit{E}}_{\mathit{d}\mathit{c},\mathit{t}}\end{array}(38)$

$\begin{array}{c}{\displaystyle \sum }_{\mathit{n}=\mathbf{1}}^{\mathit{N}}{\mathit{H}}_{\mathit{D},\mathit{n},\mathit{t}}={\mathit{H}}_{\mathit{B},\mathit{t}}+{\mathit{H}}_{\mathit{G}\mathbf{2}\mathit{H},\mathit{t}}+{\mathit{H}}_{\mathit{P}\mathbf{2}\mathit{H},\mathit{t}}-{\mathit{H}}_{\mathit{c},\mathit{t}}+{\mathit{H}}_{\mathit{d}\mathit{c},\mathit{t}}\end{array}(39)$

$\begin{array}{c}{\displaystyle \sum }_{\mathit{n}=\mathbf{1}}^{\mathit{N}}{\mathit{G}}_{\mathit{D},\mathit{n},\mathit{t}}={\mathit{G}}_{\mathit{B},\mathit{t}}-{\mathit{G}}_{\mathit{G}\mathbf{2}\mathit{P},\mathit{t}}-{\mathit{G}}_{\mathit{G}\mathbf{2}\mathit{H},\mathit{t}}\end{array}(40)$

The energy balance constraints of the user’s electricity load before and after the IDR can be expressed as

$\begin{array}{c}{\mathit{E}}_{\mathit{D},\mathit{n},\mathit{t}}+{\mathit{E}}_{\mathit{P}\mathit{V},\mathit{n},\mathit{t}}={\mathit{E}}_{\mathit{D}\mathbf{0},\mathit{n},\mathit{t}}-{\mathit{E}}_{\mathit{s}\mathit{h}\mathit{i}\mathit{f}\mathit{t},\mathit{n},\mathit{t}}-{\mathit{E}}_{\mathit{c}\mathit{u}\mathit{t},\mathit{n},\mathit{t}}-{\mathit{E}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v},\mathit{n},\mathit{t}}+{\displaystyle \sum }_{\mathit{j}=\mathbf{1},\mathit{j}\ne \mathit{n}}^{\mathit{N}}{\mathit{E}}_{\mathit{S},\mathit{n}\mathit{j},\mathit{t}}\end{array}(41)$

$\begin{array}{c}{\mathit{E}}_{\mathit{S},\mathit{i}\mathit{j},\mathit{t}}+{\mathit{E}}_{\mathit{S},\mathit{j}\mathit{i},\mathit{t}}=\mathbf{0}\end{array}(42)$

$\begin{array}{c}{\mathit{E}}_{\mathit{s}\mathit{h}\mathit{i}\mathit{f}\mathit{t},\mathit{n},\mathit{t}}={\mathit{E}}_{\mathit{s}\mathit{h}\mathit{i}\mathit{f}\mathit{t}-,\mathit{n},\mathit{t}}-{\mathit{E}}_{\mathit{s}\mathit{h}\mathit{i}\mathit{f}\mathit{t}+,\mathit{n},\mathit{t}}\end{array}(43)$

$\begin{array}{c}{\mathit{E}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v},\mathit{n},\mathit{t}}={\mathit{E}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v}-,\mathit{n},\mathit{t}}-{\mathit{E}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v}+,\mathit{n},\mathit{t}}\end{array}(44)$

where ${\mathit{E}}_{\mathit{D}\mathbf{0},\mathit{n},\mathit{t}}$ is the electricity load of users before IDR; ${\mathit{E}}_{\mathit{D},\mathit{n},\mathit{t}}$ is the electricity load of users after IDR; ${\mathit{E}}_{\mathit{S},\mathit{n}\mathit{j},\mathit{t}}$ denotes the electricity transferred from the n-th user to the j-th user at t-th time period.

The energy balance constraints of the users' heat load before and after the IDR can be expressed as

$\begin{array}{c}{\mathit{H}}_{\mathit{D},\mathit{n},\mathit{t}}+{\mathit{H}}_{\mathit{S}\mathit{P},\mathit{n},\mathit{t}}={\mathit{H}}_{\mathit{D}\mathbf{0},\mathit{n},\mathit{t}}-{\mathit{H}}_{\mathit{s}\mathit{h}\mathit{i}\mathit{f}\mathit{t},\mathit{n},\mathit{t}}-{\mathit{H}}_{\mathit{c}\mathit{u}\mathit{t},\mathit{n},\mathit{t}}-{\mathit{H}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v},\mathit{n},\mathit{t}}+{\displaystyle \sum }_{\mathit{j}=\mathbf{1},\mathit{j}\ne \mathit{n}}^{\mathit{N}}{\mathit{H}}_{\mathit{S},\mathit{n}\mathit{j},\mathit{t}}\end{array}(45)$

$\begin{array}{c}{\mathit{H}}_{\mathit{S},\mathit{i}\mathit{j},\mathit{t}}+{\mathit{H}}_{\mathit{S},\mathit{j}\mathit{i},\mathit{t}}=\mathbf{0}\end{array}(46)$

$\begin{array}{c}{\mathit{H}}_{\mathit{s}\mathit{h}\mathit{i}\mathit{f}\mathit{t},\mathit{n},\mathit{t}}={\mathit{H}}_{\mathit{s}\mathit{h}\mathit{i}\mathit{f}\mathit{t}-,\mathit{n},\mathit{t}}-{\mathit{H}}_{\mathit{s}\mathit{h}\mathit{i}\mathit{f}\mathit{t}+,\mathit{n},\mathit{t}}\end{array}(47)$

$\begin{array}{c}{\mathit{H}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v},\mathit{n},\mathit{t}}={\mathit{H}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v}-,\mathit{n},\mathit{t}}-{\mathit{H}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v}+,\mathit{n},\mathit{t}}\end{array}(48)$

where ${\mathit{H}}_{\mathit{D}\mathbf{0},\mathit{n},\mathit{t}}$ is the heat load of users before IDR; ${\mathit{H}}_{\mathit{D},\mathit{n},\mathit{t}}$ is the heat load of users after IDR; ${\mathit{H}}_{\mathit{S},\mathit{n}\mathit{j},\mathit{t}}$ denotes the heat transferred from the n-th user to the j-th user at t-th time period.

The energy balance constraints of the users' gas load before and after the IDR can be expressed as

$\begin{array}{c}{\mathit{G}}_{\mathit{D},\mathit{n},\mathit{t}}={\mathit{G}}_{\mathit{D}\mathbf{0},\mathit{n},\mathit{t}}-{\mathit{G}}_{\mathit{s}\mathit{h}\mathit{i}\mathit{f}\mathit{t},\mathit{n},\mathit{t}}-{\mathit{G}}_{\mathit{c}\mathit{u}\mathit{t},\mathit{n},\mathit{t}}-{\mathit{G}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v},\mathit{n},\mathit{t}}\end{array}(49)$

$\begin{array}{c}{\mathit{G}}_{\mathit{s}\mathit{h}\mathit{i}\mathit{f}\mathit{t},\mathit{n},\mathit{t}}={\mathit{G}}_{\mathit{s}\mathit{h}\mathit{i}\mathit{f}\mathit{t}-,\mathit{n},\mathit{t}}-{\mathit{G}}_{\mathit{s}\mathit{h}\mathit{i}\mathit{f}\mathit{t}+,\mathit{n},\mathit{t}}\end{array}(50)$

$\begin{array}{c}{\mathit{G}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v},\mathit{n},\mathit{t}}={\mathit{G}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v}-,\mathit{n},\mathit{t}}-{\mathit{G}}_{\mathit{c}\mathit{o}\mathit{n}\mathit{v}+,\mathit{n},\mathit{t}}\end{array}(51)$

where ${\mathit{G}}_{\mathit{D}\mathbf{0},\mathit{n},\mathit{t}}$ is the gas load of users before IDR; ${\mathit{G}}_{\mathit{D},\mathit{n},\mathit{t}}$ is the gas load of users after IDR.

4 Decentralized robust optimal dispatch model of the user-level IEGHS

4.1 robust optimal dispatch model

In the user-level IEGHS in this paper, the renewable energy production equipment consists of REG in the EH and distributed energy production equipment of the users. The output of these energy production facilities is highly dependent on the weather and has certain uncertainties. Although the current renewable energy output forecast has reached a certain accuracy, there is still a certain error between the forecast and the actual output. There are various ways to consider the prediction error, and robust optimization is one of the typical ways.

The solution of the robust optimization strictly satisfies all the constraints corresponding to all the values of the uncertain parameters in the uncertain set. The uncertain set includes box, ellipsoid, polyhedron, and other forms. Among them, the box uncertainty set is used because it is more convenient to calculate. The renewable energy output uncertainty constraints in EH and users are as follows

$\begin{array}{c}\forall {\mathit{E}}_{\mathit{R}\mathit{E},\mathit{t}}\in {\mathit{U}}_{\mathit{R}\mathit{E}},\forall {\mathit{E}}_{\mathit{P}\mathit{V},\mathit{n},\mathit{t}}\in {\mathit{U}}_{\mathit{P}\mathit{V},\mathit{n}},\forall {\mathit{H}}_{\mathit{S}\mathit{P},\mathit{n},\mathit{t}}\in {\mathit{U}}_{\mathit{S}\mathit{P},\mathit{n}}\end{array}(52)$

$\begin{array}{c}{\mathit{U}}_{\mathit{R}\mathit{E}}=\left\{{\mathit{E}}_{\mathit{R}\mathit{E},\mathit{t}}|{\mathit{E}}_{\mathit{R}\mathit{E}\mathbf{0},\mathit{t}}-{∆\mathit{E}}_{\mathit{R}\mathit{E},\mathit{t}}{\le \mathit{E}}_{\mathit{R}\mathit{E},\mathit{t}}\le {\mathit{E}}_{\mathit{R}\mathit{E}\mathbf{0},\mathit{t}}+{∆\mathit{E}}_{\mathit{R}\mathit{E},\mathit{t}},\forall \mathit{t}\in \mathit{T}\right\}\end{array}(53)$

$\begin{array}{c}{\mathit{U}}_{\mathit{P}\mathit{V},\mathit{n}}=\left\{{\mathit{E}}_{\mathit{P}\mathit{V},\mathit{n},\mathit{t}}|{\mathit{E}}_{\mathit{P}\mathit{V}\mathbf{0},\mathit{n},\mathit{t}}-{∆\mathit{E}}_{\mathit{P}\mathit{V},\mathit{n},\mathit{t}}{\le \mathit{E}}_{\mathit{P}\mathit{V},\mathit{n},\mathit{t}}\le {\mathit{E}}_{\mathit{P}\mathit{V}\mathbf{0},\mathit{n},\mathit{t}}+{∆\mathit{E}}_{\mathit{P}\mathit{V},\mathit{n},\mathit{t}},\forall \mathit{t}\in \mathit{T}\right\}\end{array}(54)$

$\begin{array}{c}{\mathit{U}}_{\mathit{S}\mathit{P},\mathit{n}}=\left\{{\mathit{H}}_{\mathit{S}\mathit{P},\mathit{n},\mathit{t}}|{\mathit{H}}_{\mathit{S}\mathit{P}\mathbf{0},\mathit{n},\mathit{t}}-{∆\mathit{H}}_{\mathit{S}\mathit{P},\mathit{n},\mathit{t}}{\le \mathit{H}}_{\mathit{S}\mathit{P},\mathit{n},\mathit{t}}\le {\mathit{H}}_{\mathit{S}\mathit{P}\mathbf{0},\mathit{n},\mathit{t}}+{∆\mathit{H}}_{\mathit{S}\mathit{P},\mathit{n},\mathit{t}},\forall \mathit{t}\in \mathit{T}\right\}\end{array}(55)$

where ${\mathit{E}}_{\mathit{R}\mathit{E},\mathit{t}}$, ${\mathit{E}}_{\mathit{P}\mathit{V},\mathit{n},\mathit{t}}$ , and ${\mathit{H}}_{\mathit{S}\mathit{P},\mathit{n},\mathit{t}}$ are the actual output of the renewable energy production equipment; ${\mathit{E}}_{\mathit{R}\mathit{E}\mathbf{0},\mathit{t}}$, ${\mathit{E}}_{\mathit{P}\mathit{V}\mathbf{0},\mathit{n},\mathit{t}}$ , and ${\mathit{H}}_{\mathit{S}\mathit{P}\mathbf{0},\mathit{n},\mathit{t}}$ are the mean value of the fluctuation interval of the output of renewable energy production equipment; ${∆\mathit{E}}_{\mathit{R}\mathit{E},\mathit{t}}$, ${∆\mathit{E}}_{\mathit{P}\mathit{V},\mathit{n},\mathit{t}}$ , and $∆{\mathit{H}}_{\mathit{S}\mathit{P},\mathit{n},\mathit{t}}$ are the radius of the fluctuation interval of the output of renewable energy production equipment.

The above uncertainty constraints on renewable energy output in EH and users are written in a uniform mathematical form as follows

$\begin{array}{c}\mathit{y}\left(\mathit{\xi }\right)=\mathit{y}+\mathit{\xi }\end{array}(56)$

$\begin{array}{c}\forall \mathit{\xi }\in \mathit{U}=\left\{\mathit{\xi }|-∆\mathit{\xi }\le \mathit{\xi }\le ∆\mathit{\xi }\right\}\end{array}(57)$

where $\mathit{y}\left(\mathit{\xi }\right)$ is the actual output of the renewable energy production equipment; $\mathit{y}$ is the predicted output of the renewable energy production equipment; $\mathit{\xi }$ is the deviation of actual output from the predicted output; $∆\mathit{\xi }$ is the radius of the fluctuation interval of the deviation.

A robust optimal dispatch model is developed by considering uncertainty constraints on renewable energy output in EH and users. The proposed robust optimal dispatch model is a min-max two-layer robust optimization model, which aims to promote the accommodation of renewable energy as much as possible while minimizing the system cost. In addition, the two-layer robust optimization model is different from the two-stage robust optimization model which is essentially a min-max-min three-layer robust optimization model. And to simplify the narrative, the robust optimal dispatch model is described in a compact format as follows

$\begin{array}{c}\mathbf{min}\left({\mathit{a}}^{\mathit{T}}\mathit{x}+\underset{\mathit{\xi }\mathit{\in }\mathit{U}}{\mathbf{max}}{\mathit{b}}^{\mathit{T}}\mathit{y}\left(\mathbf{\xi }\right)\right)\\ \mathit{s}.\mathit{t}.\mathit{A}\mathit{x}\le \mathit{c}\\ \mathit{B}\mathit{y}\left(\mathit{\xi }\right)\le \mathit{d},\forall \mathbf{\xi }\in \mathit{U}\\ \mathit{G}\mathit{x}+\mathit{H}\mathit{y}\left(\mathit{\xi }\right)\le \mathit{g},\forall \mathbf{\xi }\in \mathit{U}\end{array}(58)$

where $\mathit{x}$ and $\mathit{y}\left(\mathit{\xi }\right)$ denote the decision variables of the first stage and the second stage, respectively; $\mathit{\xi }$ indicates uncertainty variables; A, B, G, and H are the corresponding coefficient matrices; a, b, c, d, and g are the corresponding vectors. In equation (58), the first line of the constraint includes equations (2)-(20), equations (23)-(33), equations (35)-(37), equations (39)-(40), equations (42)-(44), and equations (46)-(51); the second line of the constraint includes equation (1), equations (21)-(22), and equations (52)-(55); and the third line of the constraint includes equation (38), equation (41), and equation (45).

4.2 Multi-agent decentralized optimization framework

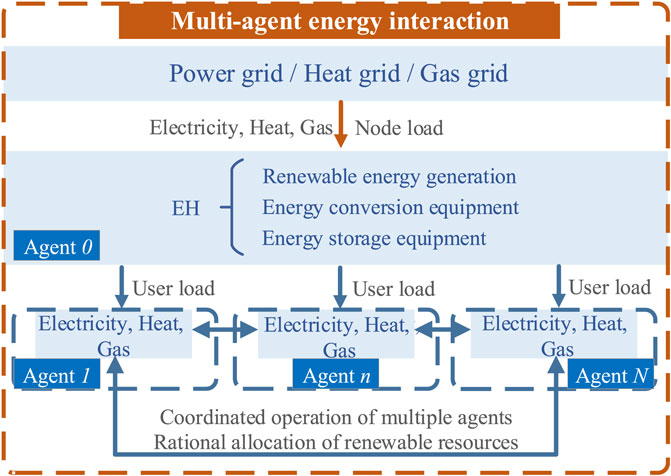
The user-level IEGHS includes multiple agents of EH and different users, with information and energy interactions between the agents. Although the traditional centralized optimal dispatching can yield the optimal dispatching operation plan for the entire system, it requires the equipment operation information within each agent, which cannot protect privacy and security. Some studies have already used the alternating direction multiplier method (ADMM) for different participating agents to coordinate the solution alternately, and each participating agent performs the optimal dispatching on its own, in addition to providing a small amount of necessary interaction information to ensure the normal inter-agent energy interaction, without sharing the internal information, which protects the privacy and security of each agent.

The multi-agent decentralized optimization framework is shown in Figure 2, with the EH as subject 1 and the different users as the remaining agents. The EH, i.e., agent 1, purchases electricity, heat, and gas energy from the distribution network for users, and is the hub for realizing energy production, conversion, and storage, as well as the bridge between the distribution network and the users. The different users, i.e., the remaining agents, are the direct users of electricity, heat, and gas energy, and also the demand side of the EH, which can perform IDR according to the real-time energy prices.

FIGURE 2

FIGURE 2. The multi-agent decentralized optimization framework.

Moreover, different users have different energy-using equipment and different energy-using characteristics, and some users even have small-scale distributed energy production equipment, such as rooftop photovoltaics, solar water heaters, biogas tanks, etc. The existence of these distributed energy production equipment makes the user load not exactly a user of energy, but also a producer of energy, so energy interaction is feasible between different users.

The coordinated operation of multiple agents is conducive to the rational allocation of renewable resources such as wind power and photovoltaic, as well as the optimal allocation of each energy flow within the node load.

5 Multi-agent decentralized robust optimization solution method

The ADMM is used for the decentralized solution of the proposed robust optimization model to form a decentralized robust optimization solution method. Since the two-layer robust optimization model is difficult to be solved directly, it is necessary to convert the two-layer robust optimization model into a single-layer robust optimization model by a robust counterpart, and then split the objective function and constraints of the built robust optimization model by agent to realize the decoupling among agents and form multiple sub-problems, and finally solve multiple sub-problems alternately by the decentralized solution algorithm ADMM. The decentralized robust optimization solution framework is shown in Figure 3.

FIGURE 3

FIGURE 3. The decentralized robust optimization solution framework.

5.1 Robust counterpart

The two-layer robust optimization model shown in Eq. 58 is an NP-hard problem, which is difficult to solve directly, and the mainstream solution methods can be divided into two categories: the affine strategy and the decomposition method. In this paper, the affine function is used to establish the affine relationship between the second-stage decision variables and the uncertain parameters, i.e., it is assumed that the second-stage decision variables can be automatically adjusted according to the corresponding uncertain parameters to solve the established two-layer robust optimization model. The affine function is defined as (Ben-Tal et al., 2009)

$\begin{array}{c}\mathit{y}\left(\mathit{\xi }\right)={\mathit{y}}_{\mathbf{0}}+{\displaystyle \sum }_{\mathit{k}=\mathbf{1}}^{\mathit{K}}{\mathit{y}}_{\mathit{k}}{\mathit{\xi }}_{\mathit{k}}\end{array}(59)$

Where K is the number of renewable energy units in the system; ${\mathit{y}}_{\mathbf{0}}$ and ${\mathit{y}}_{\mathit{k}}$ are the newly introduced auxiliary variables, the values of which can be obtained by solving the model.

By substituting the affine function into the robust optimization model and introducing the auxiliary variable Q, the original model can be transformed into

$\begin{array}{c}\mathbf{min}\left({\mathit{a}}^{\mathit{T}}\mathit{x}+\mathit{Q}\right)\\ \mathit{s}.\mathit{t}.\mathit{A}\mathit{x}\le \mathit{c}\\ \underset{\mathit{\xi }\in \mathit{U}}{\mathbf{max}}{\mathit{b}}^{\mathit{T}}\left({\mathit{y}}_{\mathbf{0}}+{\displaystyle \sum }_{\mathit{k}=\mathbf{1}}^{\mathit{K}}{\mathit{y}}_{\mathit{k}}{\mathit{\xi }}_{\mathit{k}}\right)\le \mathit{Q}\\ \underset{\mathit{\xi }\in \mathit{U}}{\mathbf{max}}\left\{\mathit{B}\left({\mathit{y}}_{\mathbf{0}}+{\displaystyle \sum }_{\mathit{k}=\mathbf{1}}^{\mathit{K}}{\mathit{y}}_{\mathit{k}}{\mathit{\xi }}_{\mathit{k}}\right)-\mathit{d}\right\}\le \mathbf{0}\\ \underset{\mathit{\xi }\in \mathit{U}}{\mathbf{max}}\left\{\mathit{G}\mathit{x}+\mathit{H}\left({\mathit{y}}_{\mathbf{0}}+{\displaystyle \sum }_{\mathit{k}=\mathbf{1}}^{\mathit{K}}{\mathit{y}}_{\mathit{k}}{\mathit{\xi }}_{\mathit{k}}\right)-\mathit{g}\right\}\le \mathbf{0}\end{array}(60)$

Taking the second equation in the constraints as an example to illustrate the transformation process of the model solution, the original problem represented by the second equation is as follows

$\begin{array}{c}\underset{\mathbf{\xi }}{\mathbf{max}}{\mathit{b}}^{\mathit{T}}\left({\mathit{y}}_{\mathbf{0}}+{\displaystyle \sum }_{\mathit{k}=\mathbf{1}}^{\mathit{K}}{\mathit{y}}_{\mathit{k}}{\mathit{\xi }}_{\mathit{k}}\right)\\ \mathit{s}.\mathit{t}.{\mathit{\xi }}_{\mathit{k}\mathbf{0}}-∆{\mathit{\xi }}_{\mathit{k}}\le {\mathit{\xi }}_{\mathit{k}}\le {\mathit{\xi }}_{\mathit{k}\mathbf{0}}+∆{\mathit{\xi }}_{\mathit{k}}\end{array}(61)$

The dual problem is as follows

$\begin{array}{c}\mathbf{min}{\mathit{b}}^{\mathit{T}}{\mathit{y}}_{\mathbf{0}}+{\displaystyle \sum }_{\mathit{k}=\mathbf{1}}^{\mathit{K}}\left[\left({\mathit{\lambda }}_{\mathit{k}}-{\mathit{\nu }}_{\mathit{k}}\right){\mathit{\xi }}_{\mathit{k}\mathbf{0}}+\left({\mathit{\lambda }}_{\mathit{k}}+{\mathit{\nu }}_{\mathit{k}}\right)\Delta {\mathit{\xi }}_{\mathit{k}}\right]\\ \mathbf{s}.\mathit{t}.{\mathit{\lambda }}_{\mathit{k}}-{\mathit{\nu }}_{\mathit{k}}={\mathit{b}}^{\mathit{T}}{\mathit{y}}_{\mathit{k}}\end{array}(62)$

Where ${\mathit{\lambda }}_{\mathit{k}}$ and ${\mathit{\nu }}_{\mathit{k}}$ are nonnegative dual variables. According to the strong dual theory, the objective value of the original problem is guaranteed to be less than or equal to Q when and only when the objective value of the dual problem is less than or equal to Q. Therefore, the second equation in the constraints can be transformed into the following linear form.

$\begin{array}{c}{\mathit{b}}^{\mathit{T}}{\mathit{y}}_{\mathbf{0}}+{\displaystyle \sum }_{\mathit{k}=\mathbf{1}}^{\mathit{K}}\left[\left({\mathit{\lambda }}_{\mathit{k}}-{\mathit{\nu }}_{\mathit{k}}\right){\mathit{\xi }}_{\mathit{k}\mathbf{0}}+\left({\mathit{\lambda }}_{\mathit{k}}+{\mathit{\nu }}_{\mathit{k}}\right)\Delta {\mathit{\xi }}_{\mathit{k}}\right]\le \mathit{Q}\end{array}(63)$

$\begin{array}{c}{\mathit{\lambda }}_{\mathit{k}}-{\mathit{\nu }}_{\mathit{k}}={\mathit{b}}^{\mathit{T}}{\mathit{y}}_{\mathit{k}}\end{array}(64)$

The transformation process of the third and fourth equation in the constraints is similar to the second equation. Up to this point, the adjustable robust optimization model is transformed into a single layer optimization problem.

5.2 The ADMM algorithm

The main idea of the ADMM with both decomposition and convergence is that the independent variables are decomposed into blocks of sub-independent variables according to the idea of blocking, and when solving one block of sub-independent variables, the form of the extended Lagrangian objective function is maintained, and the other block of sub-independent variables in its objective function are substituted into the latest optimization result (or the initial value) and used as constants in this optimization. This solves the problem of cross terms between the independent variables from different blocks in the quadratic penalty term and ensures fast convergence from the quadratic penalty term (Mu et al., 2020).

In order to use the ADMM for the decentralized solution of the proposed robust optimization model, it is first necessary to decouple the association between agents, i.e., to split the objective function and constraints of the proposed robust optimization model by agents. For the centralized optimal dispatch model in which two agents use the same variable representation, the replica variable method is used to decouple and add the corresponding equation constraints, as shown in equations (65)-(67); the energy interaction constraints between different users are shown in equations (68)-(69).

$\begin{array}{c}{\mathit{E}}_{\mathit{D},\mathit{n},\mathit{t}}^{\mathit{E}\mathit{H}}-{\mathit{E}}_{\mathit{D},\mathit{n},\mathit{t}}^{\mathit{U}\mathit{S}\mathit{E}}=\mathbf{0},\forall \mathit{n}\in {\mathbf{\Omega }}_{\mathit{U}\mathit{S}\mathit{E}}\mathit{t}\in \mathit{T}\end{array}(65)$

$\begin{array}{c}{\mathit{H}}_{\mathit{D},\mathit{n},\mathit{t}}^{\mathit{E}\mathit{H}}-{\mathit{H}}_{\mathit{D},\mathit{n},\mathit{t}}^{\mathit{U}\mathit{S}\mathit{E}}=\mathbf{0},\forall \mathit{n}\in {\mathbf{\Omega }}_{\mathit{U}\mathit{S}\mathit{E}}\mathit{t}\in \mathit{T}\end{array}(66)$

$\begin{array}{c}{\mathit{G}}_{\mathit{D},\mathit{n},\mathit{t}}^{\mathit{E}\mathit{H}}-{\mathit{G}}_{\mathit{D},\mathit{n},\mathit{t}}^{\mathit{U}\mathit{S}\mathit{E}}=\mathbf{0},\forall \mathit{n}\in {\mathbf{\Omega }}_{\mathit{U}\mathit{S}\mathit{E}}\mathit{t}\in \mathit{T}\end{array}(67)$

$\begin{array}{c}{\mathit{E}}_{\mathit{S},\mathit{i}\mathit{j},\mathit{t}}-{\mathit{E}}_{\mathit{S},\mathit{j}\mathit{i},\mathit{t}}=\mathbf{0},\forall \mathit{i},\mathit{j}\in {\mathbf{\Omega }}_{\mathit{U}\mathit{S}\mathit{E}},\mathit{i}\ne \mathit{j},\mathit{t}\in \mathit{T}\end{array}(68)$

$\begin{array}{c}{\mathit{H}}_{\mathit{S},\mathit{i}\mathit{j},\mathit{t}}-{\mathit{H}}_{\mathit{S},\mathit{j}\mathit{i},\mathit{t}}=\mathbf{0},\forall \mathit{i},\mathit{j}\in {\mathbf{\Omega }}_{\mathit{U}\mathit{S}\mathit{E}},\mathit{i}\ne \mathit{j},\mathit{t}\in \mathit{T}\end{array}(69)$

The robust optimization model where the objective function and constraints have been split is shown below.

$\begin{array}{c}\mathbf{min}{\mathit{f}}_{\mathbf{0}}\left({\mathit{x}}_{\mathbf{0}},{\mathit{y}}_{\mathbf{0}}\left({\mathit{\xi }}_{\mathbf{0}}\right)\right)+{\displaystyle \sum }_{\mathit{n}=\mathbf{1}}^{\mathit{N}}{\mathit{g}}_{\mathit{n}}\left({\mathit{x}}_{\mathit{n}},{\mathit{y}}_{\mathit{n}}\left({\mathit{\xi }}_{\mathit{n}}\right)\right)\\ \mathit{s}.\mathit{t}.{\mathit{A}}_{\mathit{i}}{\mathit{x}}_{\mathit{i}}\le {\mathit{c}}_{\mathit{i}},\mathit{i}=\mathbf{0,1},\cdots \mathit{N}\\ {\mathit{B}}_{\mathit{i}}{\mathit{y}}_{\mathit{i}}\left({\mathit{\xi }}_{\mathit{i}}\right)\le {\mathit{d}}_{\mathit{i}},\forall {\mathit{\xi }}_{\mathit{i}}\in {\mathit{U}}_{\mathit{i}},\mathit{i}=\mathbf{0,1},\cdots \mathit{N}\\ {\mathit{G}}_{\mathit{i}}{\mathit{x}}_{\mathit{i}}+{\mathit{H}}_{\mathit{i}}{\mathit{y}}_{\mathit{i}}\left({\mathit{\xi }}_{\mathit{i}}\right)\le {\mathit{g}}_{\mathit{i}},\forall {\mathit{\xi }}_{\mathit{i}}\in {\mathit{U}}_{\mathit{i}},\mathit{i}=\mathbf{0,1},\cdots \mathit{N}\\ {\mathit{E}}_{\mathit{i}}{\mathit{x}}_{\mathit{i}}+{\mathit{F}}_{\mathit{j}}{\mathit{x}}_{\mathit{j}}=\mathbf{0},\mathit{i}\ne \mathit{j},\mathit{i}=\mathbf{0,1},\cdots \mathit{N},\mathit{j}=\mathbf{0,1},\cdots \mathit{N}\end{array}(70)$

Where the fourth line of the constraints includes Eqs 65–69, indicating the coupling constraints among the agents.

Using the extended lagrangian relaxation technique, the extended lagrangian function of the optimization problem can be obtained as shown in Eq. 71

$\begin{array}{c}{\mathit{L}=\mathit{f}}_{\mathbf{0}}\left({\mathit{x}}_{\mathbf{0}},{\mathit{y}}_{\mathbf{0}}\left({\mathit{\xi }}_{\mathbf{0}}\right)\right)+{\displaystyle \sum }_{\mathit{n}=\mathbf{1}}^{\mathit{N}}{\mathit{g}}_{\mathit{n}}\left({\mathit{x}}_{\mathit{n}},{\mathit{y}}_{\mathit{n}}\left({\mathit{\xi }}_{\mathit{n}}\right)\right)\\ +{\displaystyle \sum }_{\mathit{i}=\mathbf{0}}^{\mathit{N}}{\displaystyle \sum }_{\mathit{j}=\mathbf{0},\mathit{j}\ne \mathit{i}}^{\mathit{N}}{\mathit{\lambda }}_{\mathit{i}\mathit{j}}^{\mathit{T}}\left({\mathit{E}}_{\mathit{i}}{\mathit{x}}_{\mathit{i}}+{\mathit{F}}_{\mathit{j}}{\mathit{x}}_{\mathit{j}}\right)\\ +{\displaystyle \sum }_{\mathit{i}=\mathbf{0}}^{\mathit{N}}{\displaystyle \sum }_{\mathit{j}=\mathbf{0},\mathit{j}\ne \mathit{i}}^{\mathit{N}}\frac{\mathit{\rho }}{\mathbf{2}}\parallel {{\mathit{E}}_{\mathit{i}}{\mathit{x}}_{\mathit{i}}+{\mathit{F}}_{\mathit{j}}{\mathit{x}}_{\mathit{j}}\parallel }^{\mathbf{2}}\end{array}(71)$

Following the idea of the dual ascent method, the solution is solved for the split independent variables in alternating iterations in turn, as shown below.

$\begin{array}{c}\left({\mathit{x}}_{\mathit{i}}^{\mathit{k}+\mathbf{1}},{\mathit{y}}_{\mathit{i}}^{\mathit{k}+\mathbf{1}}\right)=\mathbf{arg}\underset{{\mathit{x}}_{\mathit{i}}}{\mathbf{min}}{\mathit{L}}_{\mathit{i}}\left({\mathit{x}}_{\mathit{i}},{\mathit{y}}_{\mathit{i}},{\mathit{x}}_{\mathit{j}}^{\mathit{k}},{\mathit{y}}_{\mathit{j}}^{\mathit{k}},{\mathit{\lambda }}_{\mathit{i}\mathit{j}}^{\mathit{k}}\right),\mathit{i}\ne \mathit{j},\mathit{i}=\mathbf{0,1},\cdots \mathit{N},\mathit{j}=\mathbf{0,1},\cdots \mathit{N}\end{array}(72)$

$\begin{array}{c}{\mathit{\lambda }}_{\mathit{i}\mathit{j}}^{\mathit{k}+\mathbf{1}}={\mathit{\lambda }}_{\mathit{i}\mathit{j}}^{\mathit{k}}+\mathit{\rho }\left({\mathit{E}}_{\mathit{i}}{\mathit{x}}_{\mathit{i}}+{\mathit{F}}_{\mathit{j}}{\mathit{x}}_{\mathit{j}}\right),\mathit{i}\ne \mathit{j},\mathit{i}=\mathbf{0,1},\cdots \mathit{N},\mathit{j}=\mathbf{0,1},\cdots \mathit{N}\end{array}(73)$

Convergence to the optimal solution can be achieved by increasing the number of iterations of optimization k. The residuals converge as shown in (74), the objective function converges as shown in (75), and the dual variables converge as shown in (76).

$\begin{array}{c}\mathit{k}\to \mathit{\infty },{\mathit{E}}_{\mathit{i}}{\mathit{x}}_{\mathit{i}}^{\mathit{k}}+{\mathit{F}}_{\mathit{j}}{\mathit{x}}_{\mathit{j}}^{\mathit{k}}\to \mathbf{0},\mathit{i}\ne \mathit{j},\mathit{i}=\mathbf{0,1},\cdots \mathit{N},\mathit{j}=\mathbf{0,1},\cdots \mathit{N}\end{array}(74)$

$\begin{array}{c}\mathit{k}\to \mathit{\infty },{\mathit{f}}_{\mathbf{0}}\left({\mathit{x}}_{\mathbf{0}}^{\mathit{k}},{\mathit{y}}_{\mathbf{0}}^{\mathit{k}}\right)+{\displaystyle \sum }_{\mathit{n}=\mathbf{1}}^{\mathit{N}}{\mathit{g}}_{\mathit{n}}\left({\mathit{x}}_{\mathit{n}}^{\mathit{k}},{\mathit{y}}_{\mathit{n}}^{\mathit{k}}\right)\to {\mathit{p}}^{*}\end{array}(75)$

$\begin{array}{c}\mathit{k}\to \mathit{\infty },{\mathit{\lambda }}_{\mathit{i}\mathit{j}}^{\mathit{k}}\to {\mathit{\lambda }}_{\mathit{i}\mathit{j}}^{*}\mathit{i}\ne \mathit{j},\mathit{i}=\mathbf{0,1},\cdots \mathit{N},\mathit{j}=\mathbf{0,1},\cdots \mathit{N}\end{array}(76)$

The convergence stop iteration condition of ADMM is based on the original residuals and dual residuals being less than a set threshold ( ${\epsilon }^{pri}$ is the convergence threshold of the original residuals). The original residuals in the kth iteration are calculated as shown in (77).

$\begin{array}{c}\parallel {\mathit{r}}^{\mathit{k}}{\parallel }_{\mathbf{2}}=\parallel \mathit{E}{\mathit{x}}^{\mathit{k}}+\mathit{F}{\mathit{x}}^{\mathit{k}}{\parallel }_{\mathbf{2}}\le {\mathit{\epsilon }}^{\mathit{p}\mathit{r}\mathit{i}}\end{array}(77)$

Where ${\mathit{x}}^{\mathit{k}}$ represents $\left({\mathit{x}}_{\mathbf{0}}^{\mathit{k}};{\mathit{x}}_{\mathbf{1}}^{\mathit{k}};\cdots ;{\mathit{x}}_{\mathit{N}}^{\mathit{k}}\right)$; E and F are the corresponding coefficient matrices.

The mathematical analysis of the convergence rate of ADMM is more difficult than the analysis of other optimization algorithms (e.g., the interior point method). However, after several examples, it can be found that the convergence rate of ADMM is between linear and sublinear (closer to sublinear), which can converge quickly to low medium accuracy, while it takes longer to converge to high accuracy. Therefore, when we use the ADMM for optimization, we can set the accuracy to meet the engineering application, and the residual convergence threshold can usually be 10^-3 or 10^-4, without deliberately pursuing ultra-high accuracy.

In addition, it is necessary to explain the iterative step size when the alternate direction multiplier is updated. Selecting different values will affect the convergence effect. If it is too large or too small, the number of iterations will increase, so it is usually enough to choose $\rho =0.05\sim 1.5$.

6 Case study

6.1 Case description

In this paper, there are four agents in the setting case, which are an EH and three users. The structural relationship among the four agents is shown in Figure 2, and these three users have IDR capability. In this case, the day is divided into 24 time periods for decentralized robust optimal dispatching of each agent on an hourly basis. Considering the uncertainty of renewable energy output in each agent and different flexible load ratios in user load, four uncertainties (0, 0.1, 0.2, 0.3) and five flexible load ratios (0.3, 0.4, 0.5, 0.6, 0.7) are set to compare and analyze the results of decentralized robust optimal dispatch under different uncertainties and different flexible load ratios. The contribution of IDR to renewable energy accommodation, the mutual influence of different demand response markets for electricity, heat, and gas, and the convergence effect of the decentralized robust algorithm are also analyzed.

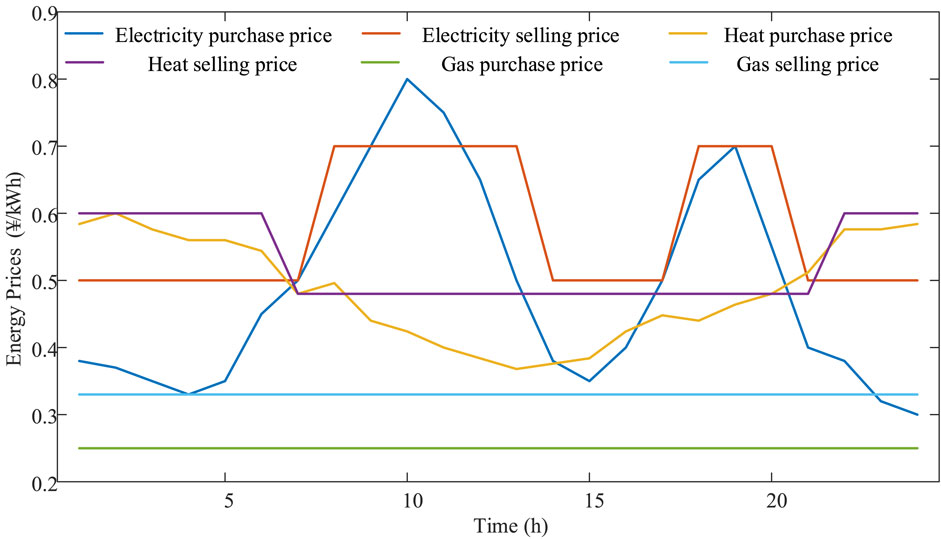
Energy prices are shown in Figure 4. The price of purchasing electricity and heat from the distribution network is a real-time price mechanism, and the price of selling electricity and heat to customers is a peak and valley price mechanism; the purchase and sale prices of natural gas are both fixed price mechanisms.

FIGURE 4

FIGURE 4. Energy prices.

6.2 The results of the decentralized robust optimal dispatch

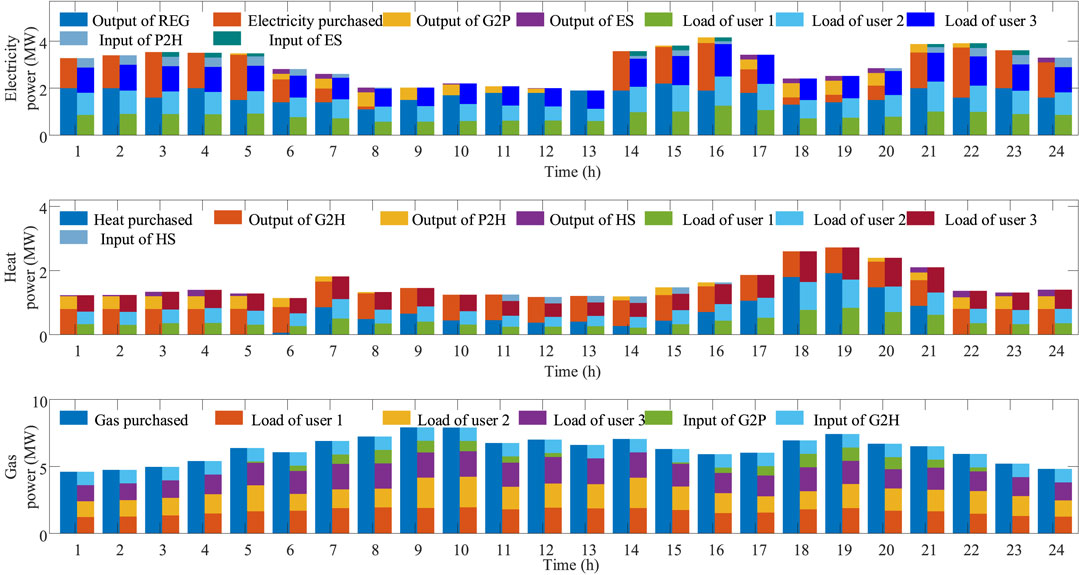
Considering the uncertainty of 0.1 and the flexible load ratio of 0.5, the results of the decentralized robust optimal dispatching of the three energy flows in the EH are shown in Figure 5. There are four ways of supplying electricity, which are REG, G2P, discharging of ES, and electricity purchase from the distribution network; there are three ways of consuming electricity, user consumption, P2H, and charging of ES. The original peak hours of electricity load are 8:00–13:00 and 18:00–20:00, which are also the peak periods of electricity price. ES charges in non-peak hours and discharges in peak hours, which realizes the transfer of electricity consumption in time. In addition, the G2P generates electricity mainly during peak hours, which realizes the conversion from electricity to gas in the form of energy utilization, thus effectively reducing the energy purchase cost. The supply of heat is mainly produced by P2H, G2H, discharging of HS, and heat purchase from the distribution network during low heat price hours, while the heat is only consumed by users, except for the charging of HS. Since there is no equipment to produce gas in the EH, the supply of gas is completely dependent on the distribution network. Part of the gas is directly consumed by the users, and the remaining part is converted into electricity and heat by the G2P and G2H to reduce energy costs.

FIGURE 5

FIGURE 5. The results of the decentralized robust optimal dispatching in the EH.

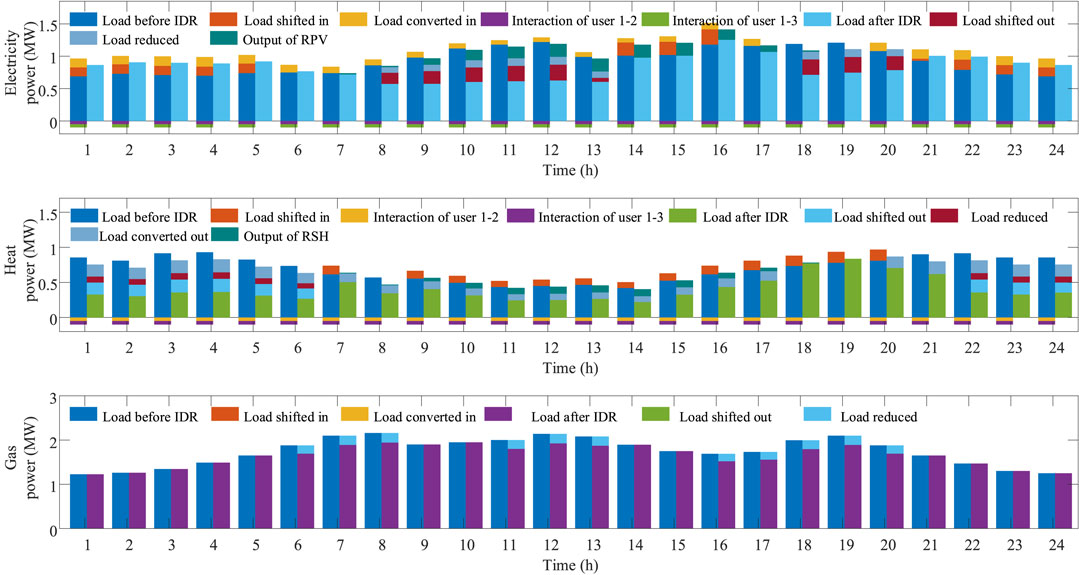
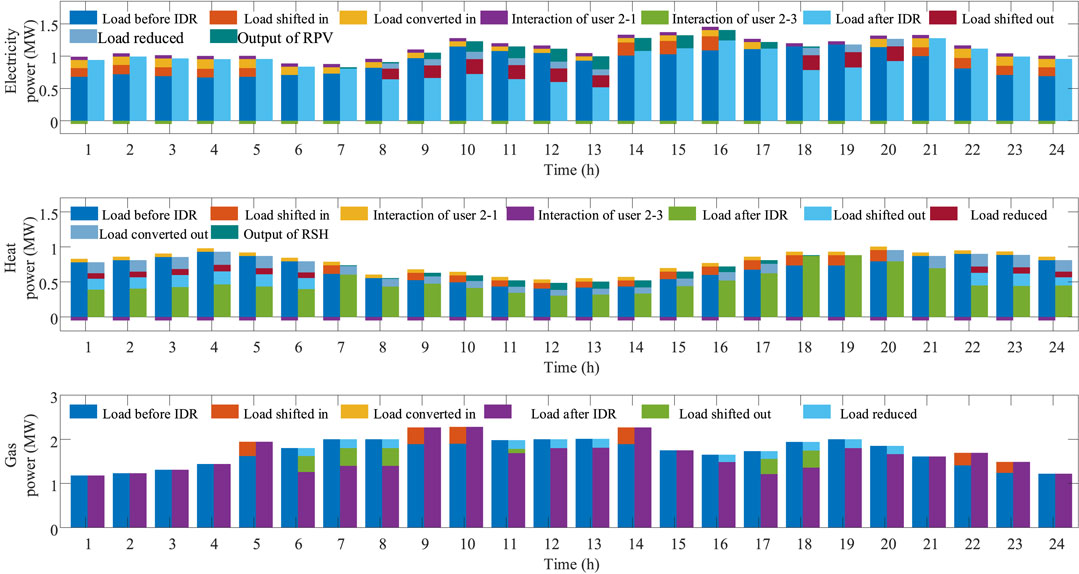
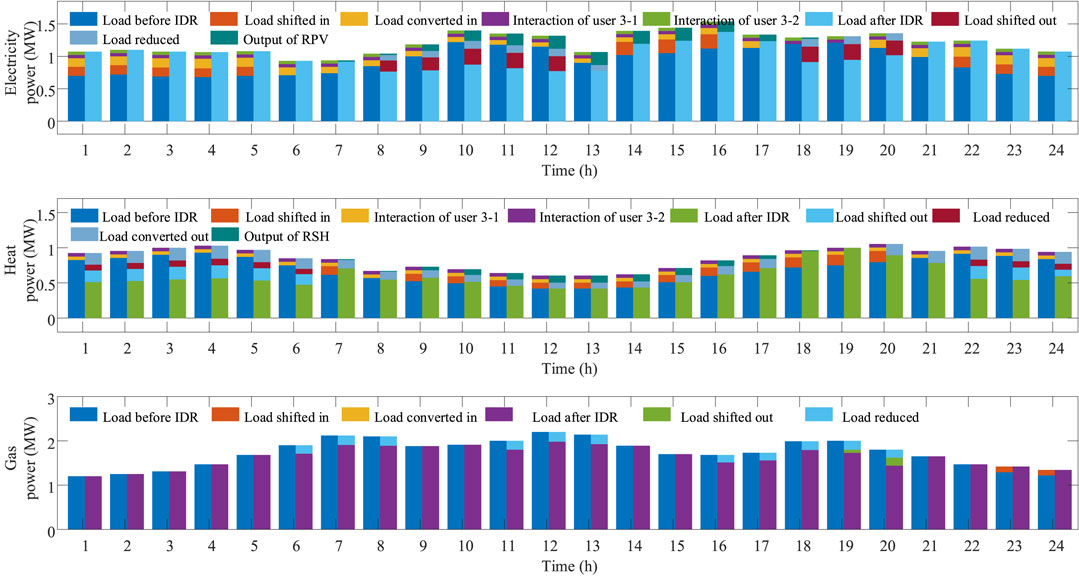
The results of users participating in IDR are shown in Figures 6–8, respectively. The mechanism of IDR is the price mechanism, i.e., based on energy prices, IDR is carried out by shifting load use periods, transferring load use users, transforming load use energy forms, and cutting unnecessary loads.

FIGURE 6

FIGURE 6. The results of user 1 participating in IDR.

FIGURE 7

FIGURE 7. The results of user 2 participating in IDR.

FIGURE 8

FIGURE 8. The results of user 3 participating in IDR.

For electricity, the peak hours of electricity load before IDR are 8:00–13:00 and 18:00–20:00. User 1, user 2, and user 3 participate in load shifting and load cutting during the peak hours, in addition to the contribution of distributed energy production equipment such as RPV, 8:00–13:00 and 18:00–20:00 are no longer peak hours, which plays a role in peak shaving and valley filling as well as reducing the cost of electricity purchase. For heat, the peak hours for heat loads before IDR are 1:00–6:00 and 22:00–24:00. The main way of IDR for the heat loads of user 1, user 2, and user 3 is load shifting and load conversion during peak hours, i.e., shifting heat loads to non-peak hours and converting heat loads to electric loads during peak hours. Moreover, there is a small amount of curtailment during peak hours. For gas, the peak hours of gas loads before IDR are 6:00–8:00, 11:00–13:00, and 16:00–20:00. Since the price of gas is constant, gas loads participate little in IDR, mainly in load cutting and shifting, but the participation of gas loads can serve the optimal use of the other two energy flows.

In addition to load shifting, cutting, and converting within users, there are interactions among users, namely, the load can be transferred between different users from the perspective of IDR. In this case, only electricity and heat can interact, and gas is not available for interaction because it is all supplied by the distribution network. According to the result shown in the figure below, user 3 outputs electricity and heat to user 1 and user 2, and user 2 also outputs electricity and heat to user 1. In other words, part of a load of user 1 is transferred to user 2 and user 3, and a load of user 2 is also transferred to user 3.

6.3 The comparison of different IDR scenarios

The consideration of IDR can decrease the operating cost of integrated energy systems and promote the accommodation of renewable energy. In order to study the impact of considering IDR, three different scenarios are set, namely, without considering IDR (No IDR), considering IDR without energy coupling of electricity, heat, and gas (IDR without coupling), and considering IDR with energy coupling of electricity, heat, and gas (IDR with coupling). The cost of decentralized robust optimal dispatch for each agent under different IDR scenarios is shown in Table 1. It can be noted that accounting for IDR has a significant improvement on the revenue of the EH as well as the cost of energy use for each user. The total cost under IDR without coupling is ¥60,167.1, which is ¥7,889.7, or 11.59%, lower compared to the total cost of ¥68,056.8 under No IDR. The scenario IDR with coupling has a cost of ¥54,162.0, which is $13,894.8, or 20.42%, lower compared to the total cost of ¥68,056.8 under No IDR.

TABLE 1

TABLE 1. The cost of decentralized robust optimal dispatch for each agent under different IDR scenarios.

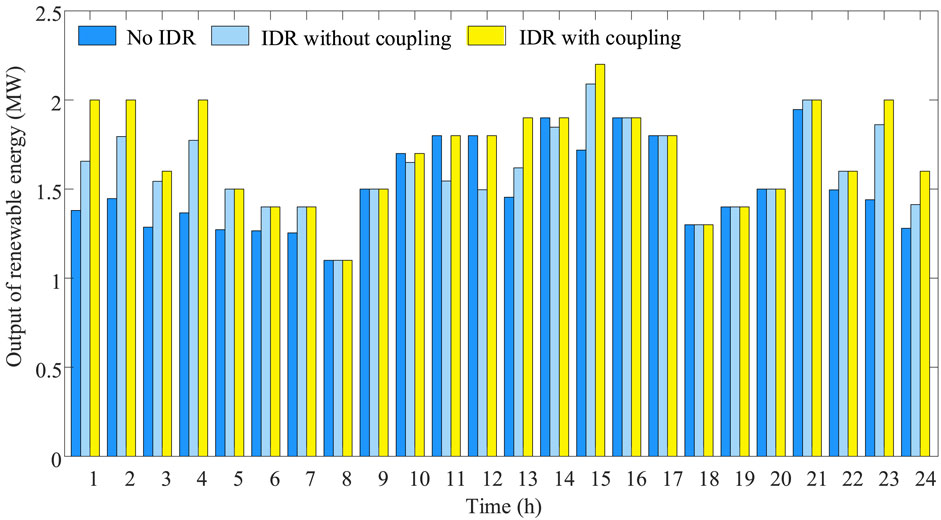
The renewable energy accommodation under No IDR, IDR without coupling, and IDR with coupling in 1 day is 36.31 MW, 38.69 MW, and 40.9 MW, respectively. Taking IDR into account, there is a significant improvement in the accommodation of renewable energy in the EH, which is mainly reflected in the accommodation of nighttime wind power. The renewable energy accommodation under different IDR scenarios is shown in Figure 9.

FIGURE 9

FIGURE 9. The renewable energy accommodation under different IDR scenarios.

Specifically, compared to No IDR, in the IDR without coupling scenario, energy can be shifted on the time axis due to the consideration of energy storage devices and the translatable load. The load level of the original daytime peak hours is reduced, so the accommodation of daytime PV during 10:00–12:00 and 14:00 h is insufficient and there is an abandonment phenomenon. However, the load level in the nighttime hours has increased, and the accommodation of nighttime wind power is enhanced in the hours of 1:00–7:00 and 21:00–24:00. Overall, the accommodation of renewable energy has increased and promoted to some extent. Compared with IDR without coupling scenario, in the IDR with coupling scenario, in addition to the existence of the shift of energy in the time axis, there is also the transformation of energy between different forms, which not only compensates for the abandonment phenomenon in the uncoupled scenario but also further enhances the accommodation of nighttime wind power, thus achieving the complete accommodation of renewable energy.

6.4 The comparison of different modes of demand response market

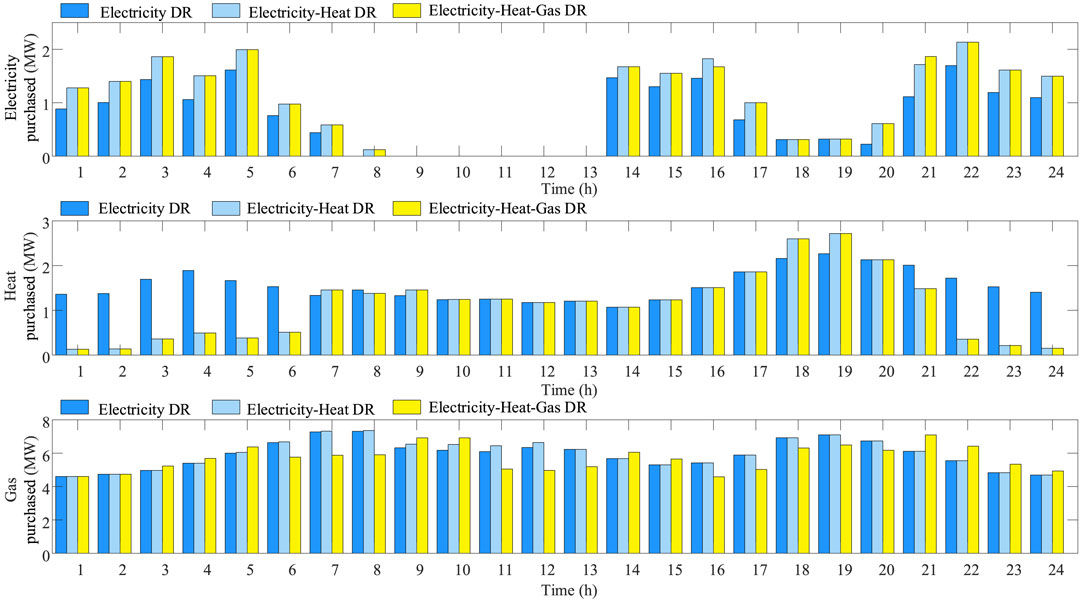
A comparative analysis is made of the purchase of energy by EH from the distribution network under the three modes of the user-level electricity demand response market, electricity-heat demand response market, and electricity-heat-gas demand response market. Figure 10 shows the energy purchases in different demand response markets.

FIGURE 10

FIGURE 10. The energy purchases in different demand response markets.

When considering the electricity demand response market, due to the load reduction and load shift out of peak hours, and the need to accommodate renewable energy as much as possible, the electricity purchase period is mainly distributed in off-peak hours, and the peak hours of the original electricity load, 8:00–13:00 and 18:00–20:00 are the valleys of electricity purchases. And because the coupling between electricity and heat and electricity and gas is not involved, it has little impact on the purchase of heat energy and gas energy.

The electricity-heat demand response market, based on the electricity demand response market, introduces the heat demand response market and takes into account the coupling between electricity and heat. For the part of the heat, the load is converted into electricity load, and the peak hours of heat load are cut and shifted out, so that the heat energy purchased during the peak hours of the original heat load, i.e., 1:00–6:00 and 22:00–24:00, decreases significantly, while the purchases of electricity and gas increase. In addition, during the off-peak period of heat, because the user’s solar thermal equipment is at its peak output, and there is a conversion of thermal load to an electrical load, as well as the support of gas-to-heat equipment at the EH level, although the heat load shifts in, the heat energy purchases do not change much.

When considering the electricity-heat-gas demand response market, the purchases of electrical energy and heat energy are almost unchanged compared to the electricity-heat demand response market. This is because the gas energy price is constant, so the mechanism of the gas energy participating in the demand response is not a real-time price response mechanism, but is coupled with electricity and heat through G2P equipment and G2H equipment at the EH. The function of gas demand response is to provide another form of energy support for electricity and heat, which can be understood as a capacity market for another form of energy, which can play a huge role in the sudden emergency failure of the power system and thermal system.

6.5 The comparison of different uncertainties and elastic load ratios

Table 2 shows the decentralized robust optimal dispatch cost of each agent under different uncertainties. When the uncertainty is 0, it means that the uncertainty of renewable energy output is not considered, and the result is a deterministic optimal dispatch, with a total cost of ¥52,045.7, and the economy is optimal. When the uncertainty is 0.1, 0.2, and 0.3, it means that the uncertainty of renewable energy output of 10%, 20%, and 30% are considered respectively, which is a robust optimal dispatch. The total cost is ¥54162.0, ¥56292.0, and ¥58482.8 respectively. Compared with the deterministic optimal dispatch cost, the cost increases by ¥2116.3, ¥4246.3, and ¥6437.1 respectively, accounting for 4.07%, 8.16%, and 12.37%. The economy is weakened, but the optimization results have certain robustness.

TABLE 2

TABLE 2. The cost of decentralized robust optimal dispatch for each agent under different uncertainties.

With the increase in uncertainty, the revenue of the EH decreases, and the cost of 3 users increases. The reason should be that in order to cope with the uncertainty of renewable energy, each agent will increase the dependence on reliable energy, that is, increase the purchase of energy. And the greater the uncertainty, the greater the purchase of energy and the higher the cost. Robust optimization sacrifices some economies to deal with uncertainty. Since the output forecast of renewable energy has reached a certain accuracy, considering the robustness and economy comprehensively, it can be considered that under the uncertainty of 0.1, the deviation of the output forecast of renewable energy can be satisfied.

The decentralized robust optimal dispatch cost of each agent under different elastic load ratios of users is shown in Figure 11. It can be seen from the figure that the total cost of the integrated energy system decreases with the increase of the user’s elastic load ratio. The reason is that the higher the ratio of the user’s elastic load, the greater the degree that the user can participate in the IDR, and the more flexible the user’s load is, so the user’s own energy consumption cost can be reduced. In addition, the upper-level EH has more options for operating modes, and the adjustable range is larger, so the income of the EH will also increase. The reduction of the cost of the users and the increase of the income of the EH will reduce the final operating cost of the integrated energy system.

FIGURE 11

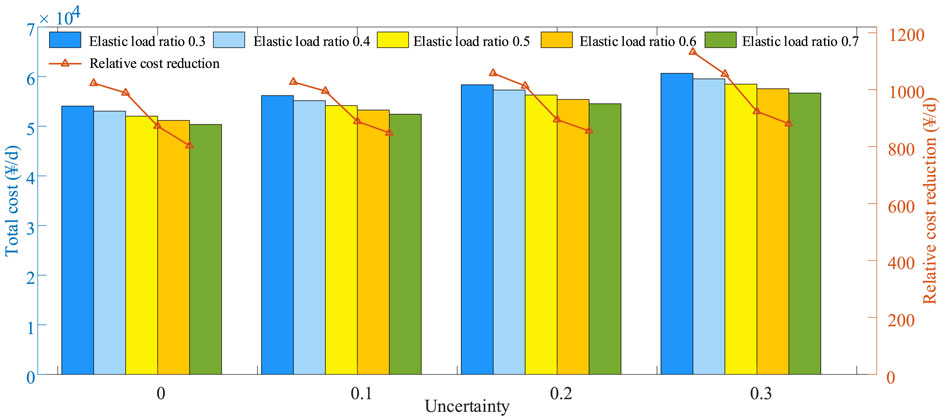
FIGURE 11. The decentralized robust optimal dispatch cost of each agent under different elastic load ratios.

In addition, it is worth noting that although the total operating cost of the system decreases with the increase of the user’s elastic load ratio, due to the user’s participation in the demand response, it will cause discomfort in energy consumption and pay a certain price. The more the user participates in the IDR, the higher the discomfort, so the relative cost reduction caused by the increase in the elastic load ratio gradually decreases.

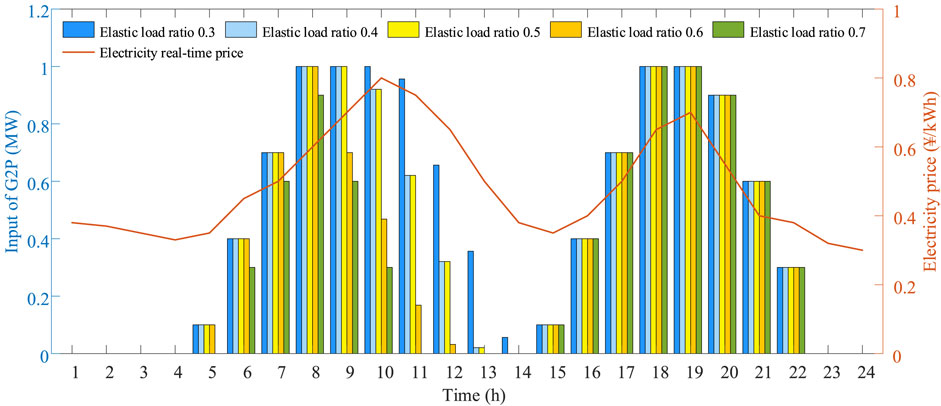
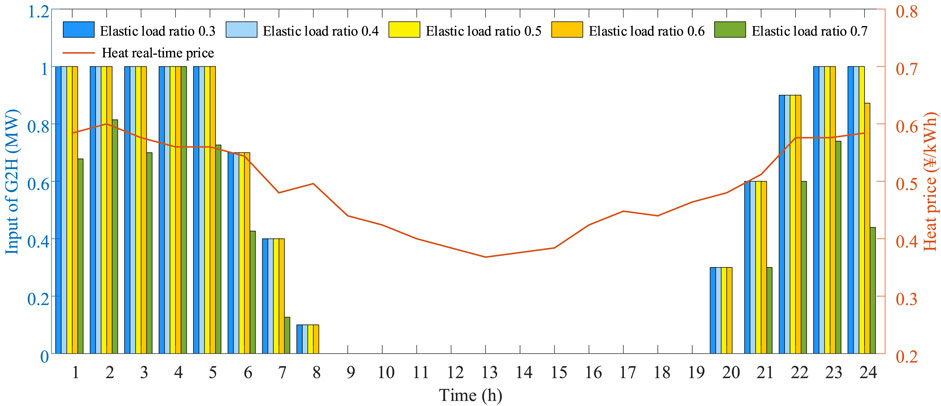
The input conditions of G2P equipment, G2H equipment, and P2H equipment under different elastic load ratios are shown in Figures 12, 13, 14, respectively. For G2P equipment, the conversion efficiency is 0.6, the upper limit of gas consumption in each period is 1MW, and the upper limit of gas consumption fluctuation between two periods is 0.3MW; for G2H equipment, the conversion efficiency is 0.5, and the gas consumption in each period is 1MW, and the upper limit of gas consumption fluctuation between two periods is 0.3MW; for P2H equipment, its conversion efficiency is 0.95, the upper limit of power consumption in each period is 0.4MW, and the upper limit of power consumption fluctuation between two periods is 0.12 MW.

FIGURE 12

FIGURE 12. The input conditions of G2P.

FIGURE 13

FIGURE 13. The input conditions of G2H.

FIGURE 14

FIGURE 14. The input conditions of P2H.

Firstly, it can be seen from the figure that the input peak and valley conditions of G2P equipment and G2H equipment are consistent with the peak and valley conditions of the real-time price of electric energy and the real-time price of heat energy respectively, while the input peak and valley conditions of P2H equipment is opposite to the real-time price of electric energy. This is the response of the energy coupling equipment to the real-time price mechanism, but it is also restricted by the equipment output constraints and ramp constraints at the same time. Secondly, as the ratio of elastic load increases, the degree of load participating in IDR increases, especially the coupling effect between electricity load and heat load increases, so the output of G2P equipment and G2H equipment decreases, and the output of P2H equipment increases. In addition, it should be noted that when the elastic load ratio is 0.3, 0.4, and 0.5, the output of each energy conversion equipment is almost unchanged because it is constrained by the equipment output constraints and ramp constraints. The above conclusions are not reflected until the elastic load ratio rises to 0.6 and 0.7.

6.6 Result analysis of the decentralized robust optimization algorithm

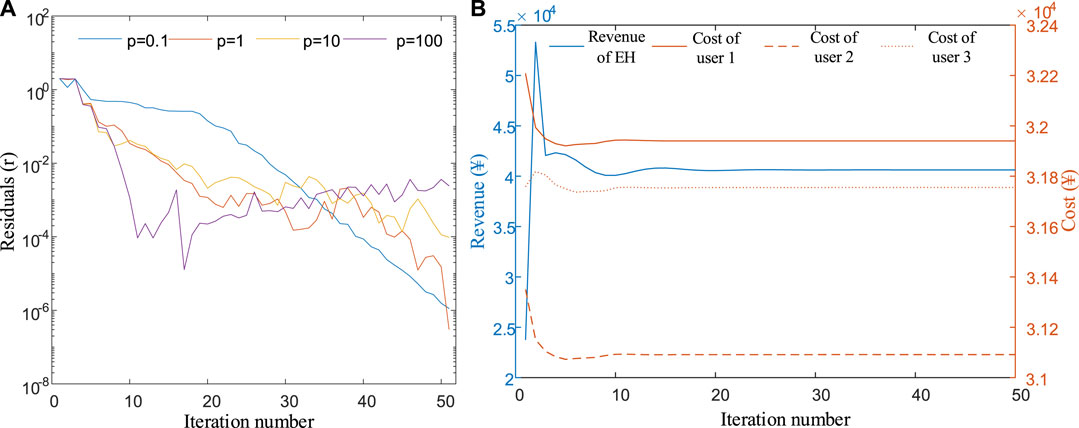
The convergence effect of the decentralized robust optimization algorithm is shown in Figure 15. It can be seen from (a) that when the value is large, such as $\rho =100$, the residual converges faster in the initial iteration process, but fluctuates greatly in the later iteration, and the convergence effect is poor; When the value is small, such as $\rho =0.1$, the residual converges slowly in the initial iteration process, but the fluctuation is small in the later iteration, and the convergence effect is good. As shown in (b), the convergence of the benefits and costs of the decentralized robust optimal dispatch of each agent. The EH benefits finally converge to ¥40624.6, the costs of user 1 finally converge to ¥31940.1, the costs of user 2 finally converge to ¥31091.6, and the costs of user 3 finally converge to ¥31755.2. Compared with the centralized robust optimal dispatch, the errors shown in Table 3 are 0.039%, 0.033%, 0.026%, and 0.041% respectively, which can be regarded as no deviation.

FIGURE 15

FIGURE 15. The convergence effect of the decentralized robust optimization algorithm.

TABLE 3

TABLE 3. The comparision of the results of centralized and decentralized approaches.

7 Conclusion

In this paper, the following conclusions can be obtained by conducting a decentralized robust optimal dispatch study on a user-level IEGHS composed of EH and multiple users under the consideration of IDR. Users can carry out IDR by responding to price signals, and actively adjusting their own energy consumption methods. On the one hand, through the translation, reduction, and conversion of internal loads, and on the other hand, through energy interaction between users, they can cut peaks and fill valleys, and reduce energy purchase costs to optimize resource allocation. For three different IDR scenarios (No IDR, IDR without coupling, and IDR with coupling), IDR without coupling has promoted the accommodation of renewable energy to some extent, but there is an abandonment phenomenon of light. And IDR with coupling makes up for the abandonment phenomenon of light, and further promotes the accommodation of renewable energy. For the three modes of demand response market (electricity, electricity-heat, and electricity-heat-gas), the purchase of electricity increases, and the purchase of heat decreases under electricity-heat compared to the electricity-only demand response market due to the conversion of heat load to electricity load. In addition, the mechanism by which gas participates in the electricity-heat-gas demand response market can be understood as a capacity market of another energy form, which has little impact on the purchase of electricity and heat. With the increase of the elastic load ratio of users, the decentralized robust optimal dispatching cost of each agent gradually decreases, but the relative cost reduction between different elastic load ratios also gradually decreases. In addition, with the increase of uncertainty, the dispatching cost of each agent increases, which needs to be considered comprehensively with robustness and economy. Finally, compared with the centralized robust optimal dispatching, the multi-agent decentralized robust optimal dispatching has a very small result error, which can be regarded as unbiased.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

ZM: Writing-original draft, Validation. MY: Investigation, Software, Data curation. WJ: Conceptualization, Methodology. TD: Writing-review and editing.

Funding

This work is supported by the Science and Technology Project of State Grid Corporation of China(5400-202199524A-0-5-ZN).

Conflict of interest

Author ZM was employed by the company State Grid Jiangsu Electric Power Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bahrami, S., and Sheikhi, A. (2016). From demand response in smart grid toward integrated demand response in smart energy hub. IEEE Trans. Smart Grid 7 (2), 1–658. doi:10.1109/tsg.2015.2464374

CrossRef Full Text | Google Scholar

Ben-Tal, A., El Ghaoui, L., and Nemirovski, A. (2009). Robust optimization. Princeton university press. Princeton, New Jersey,US.

Google Scholar

Bukhsh, W. A., Zhang, C., and Pinson, P. (2016). An integrated multiperiod OPF model with demand response and renewable generation uncertainty. IEEE Trans. Smart Grid 7 (3), 1495–1503. doi:10.1109/tsg.2015.2502723

CrossRef Full Text | Google Scholar

Chen, Z., Guo, C., Dong, S., Ding, Y., and Mao, H. (2021). Distributed robust dynamic economic dispatch of integrated transmission and distribution systems. IEEE Trans. Ind. Appl. 57 (5), 4500–4512. doi:10.1109/tia.2021.3091663

CrossRef Full Text | Google Scholar

Dababneh, F., and Li, L. (2019). Integrated electricity and natural gas demand response for manufacturers in the smart grid. IEEE Trans. Smart Grid 10 (4), 4164–4174. doi:10.1109/tsg.2018.2850841

CrossRef Full Text | Google Scholar

Ding, T., Li, C., Yang, Y., Jiang, J., Bie, Z., and Blaabjerg, F. (2017). A two-stage robust optimization for centralized-optimal dispatch of photovoltaic inverters in active distribution networks. IEEE Trans. Sustain. Energy 8 (2), 744–754. doi:10.1109/tste.2016.2605926

CrossRef Full Text | Google Scholar

Ding, T., Qu, M., Huang, C., Wang, Z., Du, P., and Shahidehpour, M. (2021). Multi-period active distribution network planning using multi-stage stochastic programming and nested decomposition by SDDIP. IEEE Trans. Power Syst. 36 (3), 2281–2292. doi:10.1109/TPWRS.2020.3032830

CrossRef Full Text | Google Scholar

Ding, T., Jia, W., Shahidehpour, M., Han, O., Sun, Y., and Zhang, Z. (2022). Review of optimization methods for energy hub planning, operation, trading, and control. IEEE Trans. Sustain. Energy 13 (3), 1802–1818. doi:10.1109/TSTE.2022.3172004

CrossRef Full Text | Google Scholar

Ding, T., Zhang, X., Lu, R., Qu, M., Shahidehpour, M., He, Y., et al. (2022). Multi-stage distributionally robust stochastic dual dynamic programming to multi-period economic dispatch with virtual energy storage. IEEE Trans. Sustain. Energy 13 (1), 146–158. doi:10.1109/TSTE.2021.3105525

CrossRef Full Text | Google Scholar

Gao, B., Chen, C., Qin, Y., Liu, X., and Zhu, Z. (2021). Evolutionary game-theoretic analysis for residential users considering integrated demand response. J. Mod. Power Syst. Clean Energy 9 (6), 1500–1509. doi:10.35833/mpce.2019.000030

CrossRef Full Text | Google Scholar

Han, J., Liu, N., and Shi, J. (2022). Optimal scheduling of distribution system with edge computing and data-driven modeling of demand response. J. Mod. Power Syst. Clean Energy 10 (4), 989–999. doi:10.35833/MPCE.2020.000510

CrossRef Full Text | Google Scholar

Hassan, A., Acharya, S., Chertkov, M., Deka, D., and Dvorkin, Y. (2020). A hierarchical approach to multienergy demand response: From electricity to multienergy applications. Proc. IEEE 108 (9), 1457–1474. doi:10.1109/jproc.2020.2983388

CrossRef Full Text | Google Scholar

He, C., Zhang, X., Liu, T., and Wu, L. (2019). Distributionally robust scheduling of integrated gas-electricity systems with demand response. IEEE Trans. Power Syst. 34 (5), 3791–3803. doi:10.1109/tpwrs.2019.2907170

CrossRef Full Text | Google Scholar

Huang, C., Zhang, H., Song, Y., Wang, L., Ahmad, T., and Luo, X. (2021). Demand response for industrial micro-grid considering photovoltaic power uncertainty and battery operational cost. IEEE Trans. Smart Grid 12 (4), 3043–3055. doi:10.1109/tsg.2021.3052515

CrossRef Full Text | Google Scholar

Jia, W., Ding, T., Huang, C., Wang, Z., Zhou, Q., and Shahidehpour, M. (2021). Convex optimization of integrated power-gas energy flow model with applications to probabilistic energy flow. IEEE Trans. Power Syst. 36 (2), 1432–1441. doi:10.1109/tpwrs.2020.3018869

CrossRef Full Text | Google Scholar

Lara, J. D., Olivares, D. E., and Canizares, C. A. (2019). Robust energy management of isolated microgrids. IEEE Syst. J. 13 (1), 680–691. doi:10.1109/jsyst.2018.2828838

CrossRef Full Text | Google Scholar

Li, S., Ding, T., Jia, W., Huang, C., Catalao, J. P. S., and Li, F. (2022). A machine learning-based vulnerability analysis for cascading failures of integrated power-gas systems. IEEE Trans. Power Syst. 37 (3), 2259–2270. doi:10.1109/tpwrs.2021.3119237

CrossRef Full Text | Google Scholar

Lilla, S., Orozco, C., Borghetti, A., Napolitano, F., and Tossani, F. (2020). Day-ahead scheduling of a local energy community: An alternating direction method of multipliers approach. IEEE Trans. Power Syst. 35 (2), 1132–1142. doi:10.1109/tpwrs.2019.2944541

CrossRef Full Text | Google Scholar

Liu, R.-P., Hou, Y., Li, Y., Lei, S., Wei, W., and Wang, X. (2021). Sample robust scheduling of electricity-gas systems under wind power uncertainty. IEEE Trans. Power Syst. 36 (6), 5889–5900. doi:10.1109/tpwrs.2021.3081557

CrossRef Full Text | Google Scholar

Liu, N., Tan, L., Sun, H., Zhou, Z., and Guo, B. (2022). Bilevel heat-electricity energy sharing for integrated energy systems with energy hubs and prosumers. IEEE Trans. Ind. Inf. 18 (6), 3754–3765. doi:10.1109/tii.2021.3112095

CrossRef Full Text | Google Scholar

Liu, N., Wang, J., and Wang, L. (2019). Hybrid energy sharing for multiple microgrids in an integrated heat-electricity energy system. IEEE Trans. Sustain. Energy 10 (3), 1139–1151. doi:10.1109/tste.2018.2861986

CrossRef Full Text | Google Scholar

Liu, P., Ding, T., Zou, Z., and Yang, Y. (2019). Integrated demand response for a load serving entity in multi-energy market considering network constraints. Appl. Energy 250, 512–529. doi:10.1016/j.apenergy.2019.05.003

CrossRef Full Text | Google Scholar

Ma, Z., Zheng, Y., Mu, C., Ding, T., and Zang, H. (2021). Optimal trading strategy for integrated energy company based on integrated demand response considering load classifications. Int. J. Electr. Power and Energy Syst. 128, 106673. doi:10.1016/j.ijepes.2020.106673

CrossRef Full Text | Google Scholar

Martinez Cesena, E. A., Loukarakis, E., Good, N., and Mancarella, P. (2020). Integrated electricity- heat-gas systems: Techno-economic modeling, optimization, and application to multienergy districts. Proc. IEEE 108 (9), 1392–1410. doi:10.1109/jproc.2020.2989382

CrossRef Full Text | Google Scholar

Mu, C., Ding, T., Qu, M., Zhou, Q., Li, F., and Shahidehpour, M. (2020). Decentralized optimization operation for the multiple integrated energy systems with energy cascade utilization. Appl. Energy 280, 115989. doi:10.1016/j.apenergy.2020.115989

CrossRef Full Text | Google Scholar

Nunna, H. S. V. S. K., Sesetti, A., Rathore, A. K., and Doolla, S. (2020). Multiagent-based energy trading platform for energy storage systems in distribution systems with interconnected microgrids. IEEE Trans. Ind. Appl. 56 (3), 3207–3217. doi:10.1109/tia.2020.2979782

CrossRef Full Text | Google Scholar

Peng, Q., Wang, X., Kuang, Y., Wang, Y., Zhao, H., Wang, Z., et al. (2021). Hybrid energy sharing mechanism for integrated energy systems based on the stackelberg game. CSEE J. Power Energy Syst. 7 (5), 911–921. doi:10.17775/cseejpes.2020.06500

CrossRef Full Text | Google Scholar

Qin, Y., Wu, L., Zheng, J., Li, M., Jing, Z., Wu, Q. H., et al. (2020). Optimal operation of integrated energy systems subject to the coupled demand constraints of electricity and natural gas. CSEE J. Power Energy Syst. 6 (2), 444–457. doi:10.17775/cseejpes.2018.00640

CrossRef Full Text | Google Scholar

Qu, M., Ding, T., Jia, W., Zhu, S., Yang, Y., and Blaabjerg, F. (2021). Distributed optimal control of energy hubs for micro-integrated energy systems. IEEE Trans. Syst. Man. Cybern. Syst. 51 (4), 2145–2158. doi:10.1109/TSMC.2020.3012113

CrossRef Full Text | Google Scholar

Sangswang, A., and Konghirun, M. (2020). Optimal strategies in home energy management system integrating solar power, energy storage, and vehicle-to-grid for grid support and energy efficiency. IEEE Trans. Ind. Appl. 56 (5), 5716–5728. doi:10.1109/tia.2020.2991652

CrossRef Full Text | Google Scholar

Schick, C., Klempp, N., and Hufendiek, K. (2022). Role and impact of prosumers in a sector-integrated energy system with high renewable shares. IEEE Trans. Power Syst. 37 (4), 3286–3298. doi:10.1109/tpwrs.2020.3040654

CrossRef Full Text | Google Scholar

Shao, C., Ding, Y., Siano, P., and Song, Y. (2021). Optimal scheduling of the integrated electricity and natural gas systems considering the integrated demand response of energy hubs. IEEE Syst. J. 15 (3), 4545–4553. doi:10.1109/jsyst.2020.3020063

CrossRef Full Text | Google Scholar

Sharma, S., Verma, A., Xu, Y., and Panigrahi, B. K. (2021). Robustly coordinated Bi-level energy management of a multi-energy building under multiple uncertainties. IEEE Trans. Sustain. Energy 12 (1), 3–13. doi:10.1109/tste.2019.2962826

CrossRef Full Text | Google Scholar

Wang, L., Hou, C., Ye, B., Wang, X., Yin, C., and Cong, H. (2021). Optimal operation analysis of integrated community energy system considering the uncertainty of demand response. IEEE Trans. Power Syst. 36 (4), 3681–3691. doi:10.1109/tpwrs.2021.3051720

CrossRef Full Text | Google Scholar

Wang, Y., Gao, S., Jia, W., Ding, T., Zhou, Z., and Wang, Z. (2022). Data-driven distributionally robust economic dispatch for park integrated energy systems with coordination of carbon capture and storage devices and combined heat and power plants. IET Renew. Power Gen. 16 (12), 2617–2629. doi:10.1049/rpg2.12436

CrossRef Full Text | Google Scholar

Wei, J., Zhang, Y., Wang, J., Wu, L., Zhao, P., and Jiang, Z. (2022). Decentralized demand management based on alternating direction method of multipliers algorithm for industrial park with CHP units and thermal storage. J. Mod. Power Syst. Clean Energy 10 (1), 120–130. doi:10.35833/mpce.2020.000623

CrossRef Full Text | Google Scholar

Xu, Y., Yin, M., Dong, Z. Y., Zhang, R., Hill, D. J., and Zhang, Y. (2018). Robust dispatch of high wind power-penetrated power systems against transient instability. IEEE Trans. Power Syst. 33 (1), 174–186. doi:10.1109/tpwrs.2017.2699678

CrossRef Full Text | Google Scholar

Zang, H., Cheng, L., Ding, T., Cheung, K. W., Liang, Z., Wei, Z., et al. (2018). Hybrid method for short-term photovoltaic power forecasting based on deep convolutional neural network. IET Gener. Transm. &amp. Distrib. 12 (20), 4557–4567. doi:10.1049/iet-gtd.2018.5847

CrossRef Full Text | Google Scholar

Zang, H., Cheng, L., Ding, T., Cheung, K. W., Wei, Z., and Sun, G. (2020). Day-ahead photovoltaic power forecasting approach based on deep convolutional neural networks and meta learning. Int. J. Electr. Power & Energy Syst. 118, 105790. doi:10.1016/j.ijepes.2019.105790

CrossRef Full Text | Google Scholar

Zhang, Z., Ding, T., Zhou, Q., Sun, Y., Qu, M., Zeng, Z., et al. (2021). A review of technologies and applications on versatile energy storage systems. Renew. Sustain. Energy Rev. 148, 111263. doi:10.1016/j.rser.2021.111263

CrossRef Full Text | Google Scholar

Zhang, D., Zhu, H., Zhang, H., Goh, H. H., Liu, H., and Wu, T. (2022). Multi-objective optimization for smart integrated energy system considering demand responses and dynamic prices. IEEE Trans. Smart Grid 13 (2), 1100–1112. doi:10.1109/tsg.2021.3128547

CrossRef Full Text | Google Scholar

Zhao, B., Qiu, H., Qin, R., Zhang, X., Gu, W., and Wang, C. (2018). Robust optimal dispatch of AC/DC hybrid microgrids considering generation and load uncertainties and energy storage loss. IEEE Trans. Power Syst. 33 (6), 5945–5957. doi:10.1109/tpwrs.2018.2835464

CrossRef Full Text | Google Scholar

Zheng, Y., Song, Y., Hill, D. J., and Zhang, Y. (2018). Multiagent system based microgrid energy management via asynchronous consensus ADMM. IEEE Trans. Energy Convers. 33 (2), 886–888. doi:10.1109/tec.2018.2799482

CrossRef Full Text | Google Scholar

Nomenclature

Abbreviation

IEGHS Integrated electricity-gas-heat system

IDR Integrated demand response

EH Energy hub

ADMM Alternating direction multiplier method

REG Renewable energy generation

PT Power transformer

HE Heat exchanger

GR Gas regulator

P2H Electricity-to-heat equipment

G2H Gas-to-heat equipment

G2P Gas-to-electricity equipment

ES Electricity storage equipment

HS Heat storage equipment

RPV rooftop photovoltaics

RSH rooftop solar heatings

Matrices

ABEFGH The corresponding coefficient matrices in a compact format

Vectors

abcdg The corresponding coefficient vectors in a compact format

Sets

T Set of dispatch periods

U Set of uncertainty