
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res. , 21 September 2022
Sec. Process and Energy Systems Engineering
Volume 10 - 2022 | https://doi.org/10.3389/fenrg.2022.1027439
This article is part of the Research Topic Planning and Operation of Hybrid Renewable Energy Systems, Volume II View all 12 articles
The paper studies the estimation of state of charge (SOC) of batteries. Firstly, the research status of battery management system, battery equivalent model and SOC estimation algorithm is introduced, and the performance of common equivalent circuit model and SOC estimation algorithm in complexity and accuracy is compared and analyzed. On this basis, this paper proposes an extended Kalman filter (EKF) algorithm based on the first-order RC model, and optimizes it by piecewise fitting. The accuracy of the optimized EKF algorithm is greatly improved. Finally, the modeling and simulation are completed through MATLAB/SIMULINK, and the experimental platform is designed and built to test the SOC estimation algorithm based on EKF. The simulation and experimental results verify the accuracy of the estimation algorithm.
The energy situation in today’s world is facing a core contradiction, that is, the contradiction between growing demand and increasingly tight supply. In the traditional energy, the reserves of non-renewable energy represented by coal and fossil fuels are limited, and it is more and more difficult to explore. With the emission of carbon dioxide and various harmful gases, it seriously endangers the safety of the earth’s environment. Facing the disharmonious development of global climate caused by energy problems, as of 12 June 2020, 125 countries in the world have promised to achieve the goal of carbon neutrality by the middle of the 21st century (Chenic et al., 2022). Therefore, streamlining the energy structure and improving energy utilization have become the joint efforts of scholars and researchers all over the world. The research on renewable clean energy such as photovoltaic and wind energy has objectivity and inevitability, and electrochemical power supply has become the focus of research because of its high energy conversion and storage efficiency.
As a key technology, energy storage technology not only promotes the intelligence of large-scale distributed power grid (Yan et al., 2021; Sridhar and Salkuti, 2022), but also relates to the large-scale grid connection of renewable energy. It is of great significance to improve the efficiency of clean energy power generation. It is a key research object of countries all over the world, especially developed countries (Luo et al., 2015). At present, pumped storage is still the main energy storage means in the world, with the largest installed capacity, accounting for 98% of the total global energy storage capacity by 2015. However, at the same time, energy storage technologies such as compressed air, flywheel, superconductivity, lead-acid battery and lithium-ion battery are also developing rapidly. Different energy storage technologies have different characteristics.
Among them, lithium battery energy storage has become a research hotspot because of its safety and efficiency, short energy storage cycle and high energy density. The voltage and capacity of a single lithium-ion battery are limited, so that multiple batteries need to be cascaded to form a battery module to adapt to the application in the scenario of high voltage and high power level. Therefore, the management system for battery module has been further developed.
The core function of battery management system (BMS) is to reasonably estimate the battery parameters and give different solutions for different situations, so as to ensure the safe and stable operation of battery energy storage system. The technology development of BMS has been paid attention by more and more manufacturers. General Motors Corporation of the United States has developed a BMS serving EV1 of electric vehicle, which has the functions of live monitoring, shunt adoption, thermal management and so on. It can realize the power-off protection of abnormal voltage, and support the application on the battery module cascaded with up to 26 batteries (Lee and Cheng, 2005). Germany has also independently developed BADICHE system and BATTMAN system (Garcia et al., 2010); Toyota Motor Corporation of Japan has developed Prius system for hybrid electric vehicles; Tesla Motors has independently developed the corresponding battery management system for pure electric vehicles. It is a general trend that traditional vehicles are constantly replaced by new energy vehicles.
Lithium-ion battery is the main energy storage element in the energy storage system. Its various parameters usually change in actual working conditions, and need to be measured indirectly by certain means. At present, the commonly used method is to establish the equivalent model of the battery, and then determine the various states of the battery at a certain time through the study of the equivalent model. At present, the equivalent models of batteries are roughly divided into three categories: electrochemical model, mathematical model and equivalent circuit model. In this paper, the equivalent circuit model is used to study, and its accuracy is between electrochemical model and mathematical model. It is easy to model the equivalent circuit model and predict the SOC, so it is widely used in all kinds of automotive BMS.
It is the key and difficult point of BMS system to realize the accurate estimation of battery SOC based on equivalent model and corresponding estimation algorithm. At present, the commonly used SOC estimation algorithms mainly include traditional algorithm, filtering algorithm, learning algorithm and hybrid algorithm.
Two typical traditional algorithms are ampere hour integration method (Liu et al., 2019) and open circuit voltage method (Zhang et al., 2016). The ampere hour integration method is calculated by adding the initial value of SOC and the integral value of current during charging and discharging process. This method is simple and easy to understand, but there are obvious shortcomings. Before SOC estimation, the initial value of SOC is usually unknown. Moreover, this method has high requirements for the accuracy of current sampling, and SOC estimation is easily affected by the inaccurate initial value and cumulative error of integration (LI et al., 2013; Xiong et al., 2020). As an open-loop estimation method (Caumont et al., 2000; Zhu et al., 2004), its estimation accuracy is difficult to ensure.
The open circuit voltage method establishes the corresponding relationship between SOC and open circuit voltage (OCV) by measuring the OCV of the battery, and then determines the SOC by looking up the table (Xiong et al., 2018). This method also has high requirements for the accuracy of voltage sampling, and the battery needs to stand for several hours before OCV measurement which is difficult to meet the requirements of on-line calculation which means SOC cannot be estimated in real time (Li et al., 2017).
Common filtering algorithms include Kalman filtering algorithm (KF) (Rakhmatov et al., 2003; Xing et al., 2011), particle filtering (PF)algorithm (Zhou et al., 2016) and synovial observer (Chen et al., 2016; Chen et al., 2017) algorithm. Among several filtering algorithms, KF can give consideration to both computational complexity and estimation accuracy, so it is widely used in automobile, energy storage, navigation and other fields.
In 1960, Rudolph E. Kalman proposed the concept of standard Kalman filter (SKF). This method is widely used in discrete linear systems because of its recursive iteration of predicted and measured values and continuous convergence to obtain accurate results. Moreover, it needs less computing space and has rapidity and accuracy which make it suitable for online computing. The accuracy of Kalman filter depends on the accuracy of modeling. When the model is inaccurate, the accuracy of the algorithm will be greatly affected (Zhang et al., 2017).However, linear Kalman filter can only be used in linear battery model. Because it sacrifices part of the accuracy, the estimation is not accurate enough. On this basis, an extended Kalman filter suitable for nonlinear systems is proposed. This method linearizes the nonlinear system by ignoring the higher-order term through the Taylor expansion of the function, which greatly improves the application scope of the algorithm and improves the accuracy to a certain extent. In order to further improve convergence and robustness, scholars have proposed a series of derivative algorithms, such as adaptive extended Kalman filter (AEKF) (Dong et al., 2018), unscented Kalman filter (UKF) (He et al., 2013) and cubature Kalman filter (CKF) (Arasaratnam et al., 2010).
Neural network (NN) (Wang and Zhou, 2018) and fuzzy logic (FL) (Zheng et al., 2019) are typical learning algorithms. NN is a mathematical model that analyzes the system by simulating the synaptic connection of human brain. By training NN with a large amount of data, the relationship between input and output of nonlinear system can be simulated with high accuracy. When the training data is sufficient, the output accuracy is high. However, when the amount of data is too large, it will also lead to overfitting. At this time, the estimation accuracy of NN will decline. The disadvantage of NN is that it relies on a large number of training data, and different training strategies will have a great impact on the estimation results. FL refers to a mathematical method that simulates the thinking mode of the human brain for judging uncertain things with the help of the concept of membership function, so as to deal with nonlinear and large lag objects. Common FL algorithms include mean blur and Gaussian blur.
Hybrid algorithm combines two or more algorithms. Literature (Guo et al., 2016) combines the least square method and adaptive unscented Kalman filter (AUKF). Through simulation experiments, it is verified that the proposed algorithm has higher SOC estimation accuracy and convergence than the single AUKF. Literature (Xu et al., 2020) proposes a hybrid algorithm PF-CKF that combines PF and CKF. This hybrid algorithm significantly improves the SOC estimation accuracy by updating the battery model parameters in real time. Although the hybrid algorithm can achieve better results, its computational complexity is greatly increased, which is higher than the single algorithm.
The paper uses the extended Kalman filter algorithm based on equivalent circuit model to estimate the battery SOC and optimizes it by piecewise fitting which improves the accuracy and stability of the estimation.
As an energy storage element, lithium-ion battery has precise internal structure and complex working principle. Due to the influence of its own service state and external environment, the internal characteristics of the battery often change. These factors mainly include the internal discharge depth, charge and discharge rate, life aging degree and external environment temperature. In the process of predicting the battery state of charge, the battery management system needs to monitor and collect the changing internal parameters of the battery in real time, so as to analyze and calculate the internal characteristics of the battery in different states and realize the real-time estimation of the battery state of charge.
The packaging of lithium-ion battery is highly integrated, so the lithium-ion battery looks like a black box system. For the external monitoring system, only the two battery parameters of battery port voltage and load current can be obtained directly through detection. However, the relevant parameters characterizing the battery characteristics inside the battery cannot be obtained intuitively through monitoring, which makes it difficult for the battery management system to estimate the battery SOC. Therefore, it is necessary to establish the equivalent circuit model inside the battery and realize the quantitative description of the actual circuit characteristics inside the battery through modeling, so as to meet the needs of BMS for reliable estimation of battery SOC. Modeling battery is difficult as it is actually a non-linear model depending on various changing variables like temperature, discharging, and charging states (Sher and Addoweesh, 2012). The establishment of the internal equivalent circuit model of the battery needs to be able to accurately simulate the actual working characteristics of the battery, including static and dynamic characteristics. At the same time, the amount of calculation and complexity should be moderate to ensure the response speed of the estimation process. The establishment of accurate battery internal equivalent model is the basis of the accuracy and rapidity of the subsequent estimation algorithm in this paper.
When the battery is in an open circuit state, the potential value on the electrode is called the equilibrium electrode potential. When the battery is in a dynamic state and there is current flowing in the closed circuit, the potential value on the electrode is called the actual electrode potential. The actual electrode potential is not invariable. With the current passing through the battery, its value will gradually deviate from the equilibrium potential. This phenomenon is the polarization phenomenon of the battery. The difference between the equilibrium electrode potential and the actual electrode potential is called the overvoltage difference, and the magnitude of the overvoltage difference reflects the degree of polarization of the battery. Generally speaking, the deviation degree of electrode potential is positively correlated with the current flowing through the unit electrode, and large current will aggravate the polarization phenomenon. According to the different causes of polarization, battery polarization can be divided into three categories: ohmic polarization, electrochemical polarization and concentration polarization. The corresponding battery internal resistance are ohmic internal resistance, electrochemical polarization internal resistance and concentration polarization internal resistance. Therefore, the internal resistance of the battery can be divided into ohmic internal resistance and polarization internal resistance. The value of ohmic internal resistance is related to temperature, SOC and other variables (Zhongbao et al., 2017).
The polarization of the battery represents the offset of the battery port voltage to the open circuit voltage after power on. In order to simulate this phenomenon, a variety of internal equivalent circuit models of the battery have appeared. At present, several common equivalent circuit topologies are Rint model, first-order RC model, second-order RC model and PNGV model, as shown in Figure 1.
The Rint model consists of an ideal voltage source and a resistor in series. Its advantages lie in simple topology, easy determination of parameter values and easy realization of modeling and simulation. However, this modeling method simply equates the internal resistance of the battery with a constant resistance. This is equivalent to assuming that the internal resistance of the battery is constant during charging and discharging which deviates from the actual situation. In practice, the internal structure and chemical mechanism of the battery are complex. Affected by the state of charge, working temperature, current and other factors, the internal resistance of the battery is in a dynamic state. Therefore, using an internal resistance with a constant resistance value for equivalence will produce large errors.
The first-order RC model, also known as Thevenin model, adds a first-order RC parallel circuit composed of polarization resistance and polarization capacitance to the topology of Rint model. This resistance-capacitance circuit can simulate the dynamic process of the generation and elimination of battery polarization effect (Rakhmatov et al., 2003). In the Rint equivalent circuit model, the polarization phenomenon is linearly simplified as a kind of instantaneous polarization, while in practical work, the battery usually has a more complex polarization process. For example, when the battery begins to have current, its port voltage will not change instantaneously, but change slowly with time. After the current path is disconnected, the polarization process will not stop instantaneously, but will decay slowly with time. Therefore, in order to more accurately simulate the polarization characteristics of the battery, an RC parallel circuit is added to the first-order RC circuit. By adjusting the value of RC, the nonlinear change process of voltage with time can be approximately simulated, so that the external characteristics of the battery port are more in line with the actual external characteristic curve. Due to the addition of resistance capacitance parallel circuit, the accuracy of the first-order RC model is improved. At the same time, the circuit is relatively simple and the parameters are easy to measure.
The second-order RC model consists of an ohmic resistor and two RC polarization circuits in series. A group of RC parallel circuits are added to the topology of the first-order RC model. This further improves the accuracy of the simulation. Similarly, connecting more RC parallel circuits in series in the circuit can continuously improve the accuracy of the equivalent model, but the complexity of the model also increases, the rapidity of the algorithm is difficult to guarantee, and there are high requirements for hardware.
PNGV model is formed by adding a capacitor on the basis of the second-order RC model to describe the cumulative effect of load current, that is, the change of open circuit voltage caused by external load. PNGV model can truly simulate the charge and discharge behavior of battery, and is widely used in transient analysis. However, PNGV is not suitable for long-time simulation, otherwise the current accumulation effect will cause a large change of open circuit voltage.
It should be noted that in the process of charge and discharge, the internal parameters of the battery are not constant, but constantly changing, and the specific value is related to the SOC in the current state. In order to make the prediction results more accurate, in the application process of the equivalent model, the parameter value of the equivalent model should be corrected in real time according to the estimated value of the current SOC, that is, the battery equivalent circuit model with dynamic parameters should be established.
Through the analysis of the above models, the relationship between the complexity and accuracy of the model is roughly positively correlated, that is, the higher the accuracy of the model, the higher the complexity, and the higher the complexity means the decrease of the calculation speed. Therefore, how to balance the relationship between calculation speed and calculation accuracy is the key point to be considered when selecting the equivalent model. As for SOC estimation algorithm, there are two aspects to consider. On the one hand, in order to reduce the error, the equivalent model is supposed to simulate the actual working state as much as possible. On the other hand, the algorithm based on the equivalent model will be embedded in the battery management system. Therefore, the equivalent model should not be too complex and the order should not be too high. It should occupy less memory and be easy to implement. After comprehensive consideration, the first-order RC model is selected as the equivalent model of EKF algorithm.
Combined with relevant circuit theoretical knowledge, the state equations of first-order RC model can be deduced. The state equations are listed based on the voltage current relationship of the complete circuit and the resistance-capacitance parallel circuit, as shown in Eq. 1.
In the above formula, Uoc is the open circuit voltage of the battery in the static state, Uo is the port voltage, Up is the voltage on the polarization resistance, Ro is the ohmic internal resistance, Rp is the polarization internal resistance, Cp is the polarization capacitance, Ip is the current flowing through the polarization capacitance and IL is the load current. The model is a nonlinear system which takes the load current IL as the input variable and the port voltage Uo as the output variable.
SOC estimation is one of the important functions of battery management system. The accurate prediction of SOC is an important guarantee to realize the functions of battery monitoring and equalization. Kalman filter is an algorithm that uses the monitored data related to the predicted data to correct the estimated value of the predicted data, and finally realizes the accurate estimation of the predicted data through continuous iteration. Kalman filter can be divided into two parts: prediction and correction. It makes a priori estimation and a posteriori estimation on the predicted data respectively. The EKF method is more widely used in engineering because most systems are nonlinear in practical application, The basic idea of EKF is to linearize the nonlinear equation by using Taylor expansion. In this way, the nonlinear system is approximated as a linear time-varying system, so the EKF method can be used (Garcia et al., 2010). When the predicted object is a nonlinear system, its state space expression is shown in Eq. 2.
In the above equation, F1 (XN,UN) and F2 (XN,UN) are the state equation function and observation equation function of the system respectively.Expand F1 (XN,UN) and F2 (XN,UN) with first-order Taylor formula respectively:
The recurrence formula of EKF is shown in Eqs 5–8:
The state space expression of the predicted object:
The priori estimate of state variables:
The priori estimate of error covariance matrix:
Gain matrix:
The posteriori estimate of state variables:
The posteriori estimate of error covariance matrix:
In the EKF method, Q and R are the variance of process noise and observation noise respectively. The state transition matrix GN and the observation matrix CN are the real-time first-order derivative of the state equation function and the observation equation function respectively to ensure the prediction accuracy.
The circuit relation equations of the first-order RC model are shown in Eq. 1. Taking SOC and up as state variables, combined with the state expression of EKF predicted system, the state space equation of first-order RC model based on EKF algorithm in discrete system can be deduced, as shown in Eq. 11.
Discretize (11) to obtain the discrete state space equation, as shown in Eq. 12.
In the formula, Δt represents the sampling period of the discrete system, and the system coefficient matrices GN、HN、CN、DN are respectively shown in Eq. 13.
It should be noted that Ro、Rp、Cp and other parameters in Eqs 12, 13 are functions of SOC, which means they have mapping relationship with SOC. Therefore, when using EKF algorithm to estimate SOC, it is necessary to make data table and linear programming the corresponding relationship between Ro、Rp、Cp and SOC. During each iteration, update the equivalent circuit parameters of the first-order RC model according to the latest estimated value of SOC. The SOC calculation process based on EKF is shown in Figure 2.
The linear fitting method for the data table is ordinary least squares. According to the known data points in the data table, the one-to-one mapping curve of SOC and Ro、Rp、Cp is fitted. The slope and intercept of the curve are shown in Eq. 14.
When SOC is at different levels, the variation degree of internal parameters such as internal resistance and capacitance varies greatly. If the data table is fitted as a whole, it is easy to produce large errors and deviate from the real situation. Therefore, in the data processing of the data table, the original algorithm is optimized by piecewise fitting to improve the accuracy of estimation as shown in Figure 3.
The simulation software used in this paper is Matlab/Simulink. The discharge current decreases as a linear function from 1C, as shown in Figure 4. The SOC estimation curve and the SOC estimation error is shown in Figure 5 and Figure 6 respectively. The simulation results show that EKF method still has good follow-up to SOC. The estimation error is within ±0.5%, and the estimation accuracy is high.
The internal parameters of the battery will be affected by the changes of various environmental factors. Therefore, parameter identification is needed in SOC estimation. In this paper, in order to improve the accuracy of SOC estimation, the battery discharge state is tracked and corrected in real time by establishing a data table. NCR18650BF lithium-ion battery is selected for the experiment. In order to get the data table, HPPC tests was carried out on the battery. Conduct a charge and discharge pulse test on every SOC step and the SOC step is 0.1. The amplitude of charge and discharge pulses is 1C, lasting for 20s. The standing interval between charge and discharge pulses is 80s. After that, SOC is adjusted with a charge and discharge current of 0.2C. After standing for 1 hour, conduct the next charge and discharge pulse test and repeat this cycle. The experimental temperature is 25 ± 2°C. Through HPPC tests, the data table of internal parameters of lithium-ion battery can be obtained. It is shown in Tables 1 and 2.
NCR18650BF battery was used to build the experimental prototype, and the SOC estimation experiment was carried out in constant current discharge mode.
The experimental platform is shown in Figure 7. It mainly includes the battery discharge link, sampling link and calculation link. In the figure, from top to bottom, there are electronic load, sampling circuit board, battery, battery holder and Hall current sensor. The load used in the experiment is the 63200A series programmable electronic load of Chroma company, which has various modes such as constant current (CC), constant resistance (CR), constant voltage (CV), constant power (CP), etc. In the experiment, the constant current discharge of the battery can be controlled by adjusting the electronic load in the CC working mode. At the same time, the electronic load used in the experiment can measure the SOC of the battery and display it in real time as shown in Figure 8. The measured value is taken as the real-time actual value of SOC for reference.
The calculation link processes and calculates the sampled voltage and current data to obtain the real-time SOC prediction value. The program flow chart is shown in Figure 9.
In the program, timer interrupt and main loop are carried out in parallel. Timer interrupt is used to collect port voltage and load current to track the change of detectable value. The main cycle is responsible for EKF calculation according to the collected data to realize SOC prediction. Due to the large fluctuation range of the actually measured data table, if the overall linear programming of the data table is carried out, the prediction result error is very large. Therefore, it is decided to carry out the linear programming in sections, and the linear programming coefficient of each function is different. The SOC is divided into ten levels, and each level is stepped by 0.1. When the program is running, the specific linear programming coefficient should be judged according to the level where the SOC iteration value is located. It should be noted that the sampled data and the data used for EKF calculation should be stored separately, so as not to change the data used for calculation before the EKF calculation in the main cycle is completed. In this program, set the sampling frequency to 1 kHz and the frequency of parameter update to 5Hz.
Figure 10A shows the comparison between the SOC estimation curve measured in the experiment before optimization and the actual curve. At the beginning of the iteration, the SOC estimated value can quickly follow the real value in a short time. Then with the passage of time, the estimation error becomes larger and larger. And because of the disturbance and noise in the actual experiment, the estimation result has a small amplitude oscillation.
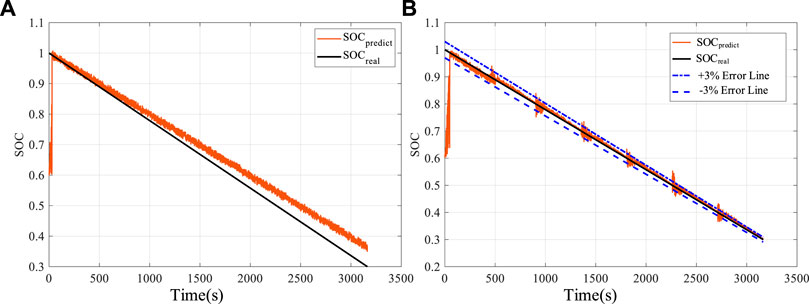
FIGURE 10. (A) Comparison between actual SOC curve and estimated SOC curve before optimization. (B) Comparison between actual SOC curve and estimated SOC curve after optimization.
After analysis, this may be due to the deviation error caused by the overall linear fitting when identifying the data table in the algorithm. Therefore, piecewise fitting is adopted for the data table instead of overall fitting. When SOC is at different levels, different calculation coefficients are used. Figure 11 shows the comparison of different fitting methods of the data table. The optimized experimental results are shown in Figure 10B. It can be seen that although there are still oscillations and offsets in the estimation results, a correction will be made whenever entering a new level. As time goes on, the estimated results will not deviate significantly from the true value. Compared with the results before optimization, the estimation accuracy is significantly improved.
Aiming at the problem of battery SOC estimation, this paper proposes an EKF estimation algorithm based on piecewise fitting. The traditional EKF algorithm directly fits various parameters based on the full SOC segment, which is easy to cause the problem of parameter overfitting and then lead to the deviation of estimation results. The proposed method can achieve SOC tracking in the whole SOC range, has strong self-correction ability, and the estimation error in actual working conditions is basically less than 3%. Subsequently, the author will further optimize the algorithm to optimize the oscillation of SOC estimation value caused by switching state matrix parameters in different SOC sections, so as to further reduce the maximum estimation error.
The original contributions presented in the study are included in the article/supplementary materials, further inquiries can be directed to the corresponding author.
BY contributed to methodology and original draft. GJ organized the data curation. WC performed the visualization of the manuscript. HY contributed to review and editing. All authors contributed to manuscript revision, read, and approved the submitted version.
This work was supported in part by the Supported by the Open Fund of Jiangsu Engineering Technology Research Center for Energy Storage Conversion and Application (China Electric Power Research Institute) under Grant NY80-21-001.
Author BY, GL, and, HL were employed by the company China Electric Power Research Institute Co, Ltd.
The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Arasaratnam, I., Haykin, S., and Hurd, T. R. (2010). Cubature Kalman filtering for continuous-discrete systems: Theory and simulations. IEEE Trans. Signal Process. 58 (10), 4977–4993. doi:10.1109/tsp.2010.2056923
Caumont, O., Le Moigne, P., Rombaut, C., Muneret, X., and Lenain, P. (2000). Energy gauge for lead-acid batteries in electric vehicles. IEEE Trans. energy Convers. 15, 354–360. doi:10.1109/60.875503
Chen, Q., Jiang, J., Liu, S., and Zhang, C. (2016). A novel sliding mode observer for state of charge estimation of EV lithium batteries. J. Power Electron. 16 (3), 1131–1140. doi:10.6113/jpe.2016.16.3.1131
Chen, Q., Jiang, J., Ruan, H., and Zhang, C. (2017). Simply designed and universal sliding mode observer for the SOC estimation of lithium-ion batteries. IET Power Electron. 10 (6), 697–705. doi:10.1049/iet-pel.2016.0095
Chenic, A. Ș., Cretu, A. I., Burlacu, A., Moroianu, N., Vîrjan, D., Huru, D., et al. (2022). Logical analysis on the strategy for a sustainable transition of the world to green energy—2050. Smart cities and villages coupled to renewable energy sources with low carbon footprint. Sustainability 14, 8622. doi:10.3390/su14148622
Dong, X., Zhang, C., and Jiang, J. (2018). Evaluation of SOC estimation method based on EKF/AEKF under noise interference. Energy Procedia 152 (1), 520–525. doi:10.1016/j.egypro.2018.09.204
Garcia, P., Fernandez, L. M., Garcia, C. A., and Jurado, F. (2010). Energy management system of fuel-cell-battery hybrid tramway. IEEE Trans. Ind. Electron. 57 (12), 4013–4023. doi:10.1109/tie.2009.2034173
Guo, X., Kang, L., Yao, Y., Huang, Z., and Li, W. (2016). Joint estimation of the electric vehicle power battery state of charge based on the least squares method and the Kalman filter algorithm. Energies 9 (2), 100–116. doi:10.3390/en9020100
He, H., Qin, H., Sun, X., and Shui, Y. (2013). Comparison study on the battery so C estimation with EKF and UKF algorithms. Energies 6 (10), 5088–5100. doi:10.3390/en6105088
Lee, Y. S., and Cheng, M. W. (2005). Intelligent control battery equalization for series connected lithium-ion battery strings. IEEE Trans. Ind. Electron. 52 (5), 1297–1307. doi:10.1109/tie.2005.855673
Li, Jiahao, Barillas, J. K., Guenther, C., and Danzer, M. A. (2013). A comparative study of state of charge estimation algorithms for LiFePO4 batteries used in electric vehicles. J. Power Sources 230, 244–250. doi:10.1016/j.jpowsour.2012.12.057
Li, Z., Huang, J., Liaw, B. Y., and Zhang, J. (2017). On state-of-charge determination for lithium-ion batteries. J. Power Sources 348, 281–301. doi:10.1016/j.jpowsour.2017.03.001
Liu, Z., Li, Z., Zhang, J., Su, L., and Ge, H. (2019). Accurate and efficient estimation of lithium-ion battery state of charge with alternate adaptive extended kalman filter and ampere-hour counting methods. Energies 12, 757. doi:10.3390/en12040757
Luo, X., Wang, J., Dooner, M., and Clarke, J. (2015). Overview of current development in electrical energy storage technologies and the application potential in power system operation. Appl. Energy 137, 511–536. doi:10.1016/j.apenergy.2014.09.081
Rakhmatov, D., Vrudhula, S., and Wallach, D. A. (2003). A model for battery lifetime analysis for organizing applications on a pocket computer. IEEE Trans. VLSI. Syst. 11 (6), 1019–1030. doi:10.1109/tvlsi.2003.819320
Sher, H. A., and Addoweesh, K. E. (2012). Power storage options for hybrid electric vehicles—a survey. J. Renew. Sustain. Energy 4 (5), 1588–1593.
Sridhar, S., and Salkuti, S. R. (2022). Development and future scope of renewable energy and energy storage systems. Smart Cities 5, 668–699. doi:10.3390/smartcities5020035
Wang, H., and Zhou, G. (2018). State of charge prediction of supercapacitors via combination of Kalman filtering and backpropagation neural network. IET Electr. Power Appl. 12 (4), 588–594. doi:10.1049/iet-epa.2017.0242
Xing, Y., Ma, E., Tsui, K. L., and Pecht, M. (2011). Battery management systems in electric and hybrid vehicles. Energies 4 (12), 1840–1857. doi:10.3390/en4111840
Xiong, R., Cao, J., Yu, Q., He, H., and Sun, F. (2018). Critical review on the battery state of charge estimation methods for electric vehicles. IEEE Access 6, 1832–1843. doi:10.1109/access.2017.2780258
Xiong, X., Wang, S. L., Fernandez, C., Yu, C., Zou, C., and Jiang, C. (2020). A novel practical state of charge estimation method: An adaptive improved ampere-hour method based on composite correction factor. Int. J. Energy Res. 44 (14), 11385–11404. doi:10.1002/er.5758
Xu, W., Xu, J., and Yan, X. (2020). Lithium-ion battery state of charge and parameters joint estimation using cubature Kalman filter and particle filter. J. Power Electron. 20 (1), 292–307. doi:10.1007/s43236-019-00023-4
Yan, X., Wang, C., Wang, Z., Ma, H., Liang, B., and Wei, X. (2021). A united control strategy of photovoltaic-battery energy storage system based on voltage-frequency controlled VSG. Electronics 10, 2047. doi:10.3390/electronics10172047
Zhang, C., Jiang, J., Zhang, L., Liu, S., Wang, L., and Loh, P. (2016). A generalized SOC-OCV model for lithium-ion batteries and the SOC estimation for LNMCO battery. Energies 9 (11), 900. doi:10.3390/en9110900
Zhang, Y., Xiong, R., He, H., and Shen, W. (2017). Lithium-Ion battery pack state of charge and state of energy estimation algorithms using a hardware-in-the-loop validation. IEEE Trans. Power Electron. 32 (6), 4421–4431. doi:10.1109/tpel.2016.2603229
Zheng, W., Xia, B., Wang, W., Lai, Y., Wang, M., and Wang, H. (2019). State of charge estimation for power lithium-ion battery using a fuzzy logic sliding mode observer. Energies 12 (13), 2491. doi:10.3390/en12132491
Zhongbao, Wei, Meng, Shujuan, Tseng, K. J., Lim, T. M., Soong, B. H., and Skyllas-Kazacos, M. (2017). An adaptive model for vanadium redox flow battery and its application for online peak power estimation. J. Power Sources 344, 195–207. doi:10.1016/j.jpowsour.2017.01.102
Zhou, D., Zhang, K., Ravey, A., Gao, F., and Miraoui, A. (2016). Online estimation of lithium polymer batteries state-of-charge using particle filter-based data fusion with multimodels approach. IEEE Trans. Ind. Appl. 52 (3), 2582–2595. doi:10.1109/tia.2016.2524438
Keywords: state of charge, estimation algorithm, extended kalman filter nomenclature: simulink (RRID:SCR_014744), matlab (RRID:SCR_001622), kalman filter
Citation: Yang B, Li G, Tang W and Li H (2022) Research on optimized SOC estimation algorithm based on extended kalman filter. Front. Energy Res. 10:1027439. doi: 10.3389/fenrg.2022.1027439
Received: 25 August 2022; Accepted: 06 September 2022;
Published: 21 September 2022.
Edited by:
Liansong Xiong, Xi’an Jiaotong University, ChinaReviewed by:
Da Xu, China University of Geosciences Wuhan, ChinaCopyright © 2022 Yang, Li, Tang and Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Bo Yang, eWFuZ2JvQGVwcmkuc2djYy5jb20uY24=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.