MHD Eyring–Powell nanofluid flow across a wedge with convective and thermal radiation

In this research, a theoretical investigation into the heat transport characteristics of an Eyring–Powell nanomaterial boundary layer flow on a wedge surface with passively controlled nanoparticles is carried out. In this model, thermal convective boundary conditions, thermal radiation, heat production, and absorption are also studied. The non-Newtonian Eyring–Powell fluid’s features are predicted using the model under consideration. The Buongiorno model is used to study how a temperature gradient affects thermophoresis and how nanoparticles affect the Brownian motion. The prevailing nonlinear boundary layer equations are derived and then renewed in an ordinary differential boundary value problem (ODBVP) by substituting apt similarity transformations. The acquired nonlinear ODBVP is then resolved using the bvp4c method to explore the fields of nanofluid velocity, nanofluid temperature, and nanoparticle concentration. A mathematical examination of the surface drag force coefficients and Nusselt number is carried out using various physical parameters. The Eyring–Powell fluid parameter ($K_1)$ reduces the thickness of the momentum boundary layer thickness. The thermophoresis aspect $\left(Nt\right)$ enhances the thermal field and solutal field. The Nusselt number ($NuR{e}_x^{-0.5}$) reduces the need for a stronger internal heat source mechanism.

1 Introduction

The physical characteristics of carrier liquids and those of nanoparticles have recently generated an exciting and never-ending research activity. Nanomaterials offer a wide range of uses in manufacturing as well as in other fields like heat exchangers, combustion, microelectronics, solar thermal exchanges, transportation, and energy conservation. All of these applications have the common challenge of heat transformation problems. For example, the cooling of electronic instruments is the most serious industrial concern because of the high amount of heat generated and the surface temperature of the devices. Previously, motor oil, water, kerosene, and ethylene glycol having low heat transport rates have been recognized as coolants in these applications. Studies involving nanoparticles have shown that adding these particles to base fluids enhances the thermal conductivity of liquids. The nanomaterial makes it easier for refrigerants to transfer heat, cuts down on process time, and makes machinery work better.

Choi and Eastman, (1995) developed the idea of nanofluids and demonstrated the superior thermal characteristics of nanomaterials. A two-component inhomogeneous nanoliquid model was proposed by Buongiorno (2006) to study the heat transfer of nanomaterials. This model suggests employing thermophoresis by the thermal gradient and Brownian motion by nanoparticles’ arbitrary movement mechanisms. Khan and Pop, (2010) used the Buongiorno model to address the boundary layer heat transfer of a nanofluid caused by the elongation of the plate. They found that both Brownian motion and thermophoresis are mechanisms that increase the energy of the system. Khan and Pop, (2010) extended to nonlinear elongation of the plate by Rana and Bhargava, (2012) and reconfirmed the results of Khan and Pop, (2010). Nield and Kuznetsov, (2009) conducted a theoretical study of the Cheng–Minkowycz problem by employing the nanofluid model proposed by Buongiorno. Tayebi et al. (2021) performed a numerical investigation of the thermo-natural convection and entropy generation of an $A{l}_2{O}_3$-$H_{2}O$ nanofluid confined by two circular cylinders in the presence of magnetic fields. A Sattar Dogonchi et al. (2021) analyzed the natural convection heat transfer of $A{l}_2{O}_3$-$H_{2}O$ nanoliquid within a crown cavity with a circular cylinder inside it. The natural convection of the $CuO-water$ nanoliquid in a rectangular chamber with fins attached to the insulated wall and porous medium was investigated in the work of Sadegh Sadeghi et al. (2021). Subsequently, Kuznetsov and Nield, (2013) revised the model proposed by Buongiorno by considering the passive control of nanoparticles. The revised model of Kuznetsov and Nield was appreciated and used by several researchers, to name a few, Hayat et al. (2017), Halim et al. (2017), Tripathi et al. (2017), Macha et al. (2017), Srinivas Reddy and Naikoti, (2016), Vijaya Bhasker Reddy et al. (2019), Rauf et al. (2019), Giri et al. (2017), Kalaivanan et al. (2020), Weera et al. (2022), Abbasi et al. (2021), and Acharya (2021). They concluded that the revised Buongiorno model (RBM) is relevant for studying the heat transport of nano liquids. Furthermore, studies related to heat transport on a wedge surface using RBM are limited. Therefore, we incorporated the revised Buongiorno model into the analysis in this study.

The abundant materials used in applications and everyday life, including polymers, dyes, low shear blood, lubricants, and molten plastics, have non-Newtonian behavior. The heat transport of non-Newtonian materials has a central purpose in the processing of composites, in the production of devolatilization of polymers, in the processing of plastic foam, fermentation, boiling, and absorption of bubbles. Therefore, great devotion has been devoted to the study of several non-Newtonian fluid models as a single constitutive expression, which is not suitable for representing the relationship between stress and shear rates of different fluids. Researchers are currently very interested in non-Newtonian fluid models and have been examined in a variety of contexts (Ali et al., 2020; Azam, 2022a; Ali et al., 2022; Azam et al., 2022; Azam, 2022b). The Eyring–Powell material model has several advantages: 1) it is a model based on the kinetic theory; 2) it describes the characteristics of shear-thinning fluids; and 3) the characteristics of Newtonian materials can be recovered for high shear rates.

Therefore, Gireesha et al. (2015) used the Eyring–Powell fluid model to investigate the three-dimensional flow with thermal convective boundary surface and thermal radiation. The stretching surface-driven flow of non-Newtonian material subjected to the magnetic field was analyzed by Akbar et al. (2015) using the Eyring–Powell fluid model. Patel and Timol, (2009) explored the features of Eyring–Powell fluid dynamics by incorporating the asymptotic boundary constraints. Ramana et al. (2021) investigated a hydromagnetic transverse flow of an Oldroyd-B-type liquid using a Cattaneo–Christov model heat flux with varying thicknesses. The effects of hall and ion slip on an unstable laminar MHD convective rotating flow of heat-generating or -absorbing second-grade fluid across a semi-infinite vertical-moving permeable surface have been studied theoretically by Veera Krishna et al. (2021).

The radiation-supported dynamics and heat transfer of the Eyring–Powell material over an elongated plate were analyzed by Araa et al. (2014). Khan et al. (2018) explored the homogenous–heterogeneous chemical reactions on Eyring–Powell fluid conveying nanoparticles. Recently, several researchers, such as Jalil et al. (2013), Hayat et al. (2015), Hayat et al. (2016), Rehman et al. (2016), Khan et al. (2017a), Muhammad et al. (2021), Riaz et al. (2021) Chu et al. (2021), Sreenivasulu et al. (2021)), and Haldar et al. (2021), studied the features of the Eyring–Powell fluid subjected to diverse physical aspects. However, the convective conditions, magnetic field, and active control of nanoparticles on the Eyring–Powell fluid flow on a wedge surface are yet to be explored.

To the best of our knowledge, the fluid flow of Eyring–Powell nanomaterials over a wedge-shaped surface with convective and zero mass flux boundary conditions are yet to be investigated. The Eyring–Powell fluid model has more applications than Oldroyd-B, Maxwell, and other fluid models. The main objective of the present study is to analyze the flow characteristics of Eyring–Powell nanomaterials and heat transport involving the convective thermal condition and the thermal radiation process. The characteristics of the thermal gradient caused by thermophoresis and Brownian motion are determined using the Buongiorno model. The bvp4c approach is used to construct the solutions of the resulting nonlinear differential equations. The impact on velocity, temperature, volume fraction of the nanoparticles, friction factors, and Nusselt number fields of the associated physical parameters are accessible through graphs and tables.

2 Formulation of the problem

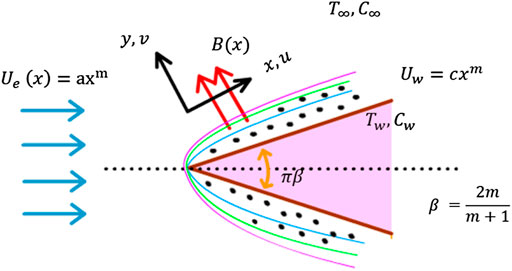
We examine the steady two-dimensional Falkner–Skan flow of a non-Newtonian Eyring–Powell fluid. Brownian motion and thermophoresis effects are used to investigate the properties of heat and mass transfer. A stretching wedge with a stretching velocity $U_w=c{x}^m$ induces fluid flow. $U_w$>0 denotes a stretching wedge surface velocity, while $U_w<0$ denotes a contracting wedge surface velocity (see Figure 1). The problem-free stream velocity is $U_e=a{x}^m$, and the constants a, c, and m are all positive. The wedge angle parameter is $\beta =\frac{2m}{m+1}$. Thermal radiation is also considered. A convective heating analysis referred to as the heat transfer coefficient regulates the temperature at the wedge’s surface. The surface flux of the nanoparticle volume fraction is zero.

FIGURE 1

FIGURE 1. Physical diagram of the problem.

The expression for stress tensor in the Eyring–Powell model is

${\rho }_{ij}=\mu \frac{\partial u_i}{\partial x_j}+\frac{1}{d}{\mathit{sinh}}^{-1}\left(\frac{1}{E}\frac{\partial u_i}{\partial x_j}\right),(1)$

where $\mu$ is the dynamic viscosity of the fluid,

${\mathit{sinh}}^{-1}\left(\frac{1}{E}\frac{\partial u_i}{\partial x_j}\right)\cong \frac{1}{E}\frac{\partial u_i}{\partial x_j}-\frac{1}{6}{\left(\frac{1}{E}\frac{\partial u_i}{\partial x_j}\right)}^3,\left|\frac{1}{E}\frac{\partial u_i}{\partial x_j}\right|\ll 1,(2)$

and $d$ and ${\rm E}$ are Eyring–Powell and rheological fluid parameters. Using the boundary layer approximation for Eyring–Powell, the governing equations can be rendered as (Kuznetsov and Nield, 2013; Macha et al., 2017; Vijaya Bhaskar Reddy et al., 2019)

$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,(3)$

$u\frac{\partial u}{\partial x}+v\frac{\partial v}{\partial y}=\left(v+\frac{1}{\rho dE}\right)\frac{{\partial }^{2}u}{\partial y^2}-\frac{1}{2\rho d{E}^3}{\left(\frac{\partial u}{\partial y}\right)}^2\frac{{\partial }^{2}u}{\partial y^2}+U_e\frac{\partial U_e}{\partial x}+\frac{\sigma B^2}{\rho }\left(U_e-u\right),(4)$

$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\alpha \frac{{\partial }^{2}T}{\partial y^2}+\tau \left[D_B\frac{\partial C}{\partial y}\frac{\partial T}{\partial y}+\left(\frac{D_T}{T_{\infty }}\right){\left(\frac{\partial T}{\partial y}\right)}^2\right]-\frac{1}{{\left(\rho c\right)}_f}\frac{\partial q_r}{\partial y}+\frac{Q_0\left(T-T_{\infty }\right)}{{\left(\rho c\right)}_f},(5)$

$u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}=D_B\frac{{\partial }^{2}C}{\partial y^2}+\frac{D_T}{T_{\infty }}\left(\frac{{\partial }^{2}T}{\partial y^2}\right).(6)$

The relative boundary conditions are (Kuznetsov and Nield, 2013; Macha et al., 2017),

$u=U_w,v=0,-k\frac{\partial T}{\partial y}=h_f\left(T_f-T\right),{\mathrm{D}}_B\frac{\partial C}{\partial y}+\frac{D_T}{T_{\infty }}\frac{\partial T}{\partial y}=0\mathrm{a}\mathrm{t}y=0,u=U_e,T\to T_{\infty },C\to C_{\infty }\mathrm{a}\mathrm{t}y\to \infty .(7)$

By using the similarity transformation,

$\eta =y\sqrt{\frac{\left(m+1\right)U_e}{2vx}},\psi \left(x,y\right)=\sqrt{\frac{2vx{U}_e}{\left(m+1\right)}}f\left(\eta \right),\theta \left(\eta \right)=\frac{T-T_{\infty }}{T_f-T_{\infty }},\varphi \left(\eta \right)=\frac{C-C_{\infty }}{C_{\infty }}.(8)$

From (8), Eq. 4–Eq. 6 are being converted to

$\left(1+K_1-K_1{K}_2{f^{″}}^2\right)f^{‴}+\beta \left(1-{\left(f^{\prime }\right)}^2\right)+f{f}^{″}+M\left(2-\beta \right)\left(1-f^{\prime }\right)=0,(9)$

$\left(1+Rd\right){\theta }^{″}+Nb{\theta }^{\prime }{\varphi }^{\prime }\mathit{Pr}+Prf\theta \prime +PrNt{\left({\theta }^{\prime }\right)}^2+QPr\theta =0,(10)$

${\varphi }^{″}+Scf{\varphi }^{\prime }+{\theta }^{″}\frac{Nt}{Nb}=0.(11)$

The converted boundary conditions are

$f\left(\eta \right)=0,f^{\prime }\left(\eta \right)=\lambda ,{\theta }^{\prime }=-\gamma \sqrt{\left(2-\beta \right)}\left(1-\theta \left(\eta \right)\right),Nb{\theta }^{\prime }\left(\eta \right)=0\mathrm{a}\mathrm{t}\eta =0,(\mathrm{12a})$

$f^{\prime }\left(\eta \right)\to 1,\theta \left(\eta \right)\to 0,\varphi \left(\eta \right)\to 0\mathrm{a}\mathrm{s}\eta \to \infty ,(\mathrm{12b})$

where primes point out the differential with respect to $\eta$. The dimensionless constants $\mathit{Pr}$, $Nb$, $Nt$,$Sc,\gamma ,\lambda$, $K_1,M,Q,\mathrm{a}\mathrm{n}\mathrm{d}{K}_2$ represent the Prandtl number, the Brownian motion parameter, the thermophoresis parameter, the Schmidt number, the convective parameter, stretching parameter, fluid parameters, magnetic parameter heat generation/absorption, and local Eyring fluid parameter, which are defined as

$\mathit{Pr}=\frac{v}{\alpha },Nb=\frac{\tau D_B{C}_{\infty }}{v},Nt=\frac{\tau D_T\left(T_w-T_{\infty }\right)}{T_{\infty }v},\lambda =\frac{c}{a},Sc=\frac{v}{D_B},$

$\gamma =\frac{h_f}{k}\sqrt{\frac{v}{a}},K_2=\frac{U_e^3}{2xv{E}^2}\frac{m+1}{2},K_1=\frac{1}{\mu Ed},M=\frac{\sigma B_0^2}{\rho a},Q=\frac{Q_0}{\rho C_{p}a}.$

3 Quantities of physical interest

The significant physical quantities are described as

$C_f=\frac{{\tau }_w^{″}}{\rho U_e^2},N{u}_x=\frac{x{q}_w^{″}}{k\left(T_f-T_{\infty }\right)}.(13)$

Here, ${\tau }_w^{″}$ is the shear stress and $q_w^{″}$ is the heat flux and are written as

${\tau }_w^{″}=\left(\mu +\frac{1}{Ed}\right)\frac{\partial u}{\partial y}-\frac{1}{6d}{\left(\frac{1}{E}\frac{\partial u}{\partial y}\right)}^3,q_w^{″}={\left(-k\frac{\partial T}{\partial y}+q_r\right)}_{y=0}.(14)$

Then, 13) and 14) have been converted to

$C_f{Re}_x^{\frac{1}{2}}=\left(1+K_1\right)f^{″}\left(0\right)-\frac{K_1{K}_2}{3}{f}^{\prime {\prime }^3}\left(0\right),\sqrt{\left(2-\beta \right)}N{u}_x{Re}_x^{-\frac{1}{2}}=-\left(1+Rd\right){\theta }^{\prime }\left(0\right),(15)$

where ${Re}_x$ is the Reynolds number.

4 Numerical procedure

The MATLAB solver “bvp4c” is used to solve the non-dimensional Eq. (9)–Eq. (12b). It has been applied by several experts to tackle boundary layer flow problems. The numerical solution is found using this package by fixing the convergence criteria to 0.000001. We used the following substitutions to convert Eq. 9 to Eq. 11 into a collection of first-order ODEs.

$y_1=f,y_2=f^{\prime },y_3=f^{″},\theta =y_4,{\theta }^{\prime }=y_5,\varphi =y_6,{\varphi }^{\prime }=y_7.$

The system of first-order ODEs is represented in the following matrix form:

${\left(\begin{array}{c}{y}_1\\ y_2\\ \begin{array}{c}{y}_3\\ y_4\\ \begin{array}{c}{y}_5\\ y_6\\ y_7\end{array}\end{array}\end{array}\right)}^{\prime }=\left(\begin{array}{c}{y}_2\\ y_3\\ \begin{array}{c}-\frac{\beta \left(1-y_2^2\right)+y_1{y}_3+M\left(2-\beta \right)\left(1-y_2\right)}{\left(1+K_1-K_1{K}_2{y}_3^2\right)}\\ y_5\\ \begin{array}{c}-\frac{NbPr{y}_5{y}_7+\mathit{Pr}{y}_1{y}_5+PrNt{y}_5^2+QPr{y}_4}{\left(1+Rd\right)}\\ y_7\\ -Sc{y}_1{y}_7-\frac{Nt}{Nb}{y}_5^{\prime }\end{array}\end{array}\end{array}\right).$

Subjected to the following boundary conditions

$\left(\begin{array}{c}{y}_1\left(0\right)\\ y_2\left(0\right)\\ \begin{array}{c}{y}_3\left(0\right)\\ y_4\left(0\right)\\ \begin{array}{c}{y}_5\left(0\right)\\ y_6\left(0\right)\\ y_7\left(0\right)\end{array}\end{array}\end{array}\right)=\left(\begin{array}{c}0\\ \lambda \\ \begin{array}{c}{S}_1\\ S_2\\ \begin{array}{c}-\gamma \sqrt{2-\beta }\left(1-S_2\right)\\ S_3\\ \frac{Nt}{Nb}\left\{\gamma \sqrt{2-\beta }\left(1-S_2\right)\right\}\end{array}\end{array}\end{array}\right),$

where $S_1,S_2,S_3$ are guesses until the desired outcome is achieved. Other boundary conditions are $y_2\left(\infty \right)=1,y_4\left(\infty \right)=0,{\mathrm{a}\mathrm{n}\mathrm{d}y}_6\left(\infty \right)=0$. The accuracy of the implemented numerical method has been validated by comparing the limiting case of the present problem (see Table 1) with the previously published results by Khan et al. (2017b). An excellent achievement has been found with previously published result.

TABLE 1

TABLE 1. Comparison values of $-f^{\prime \prime }\left(0\right)$ for different values of $\beta$ when $K_1=K_2=M=0$.

5 Results and discussion

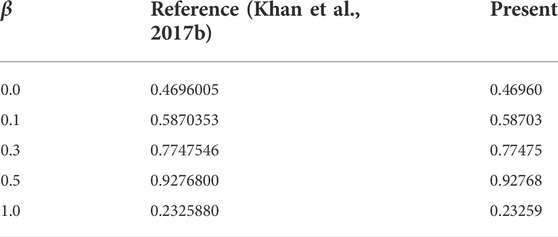
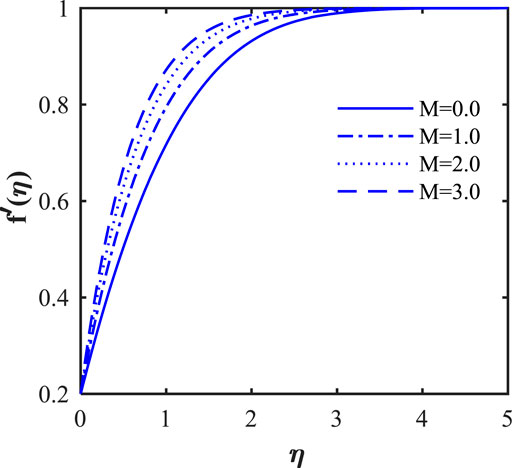
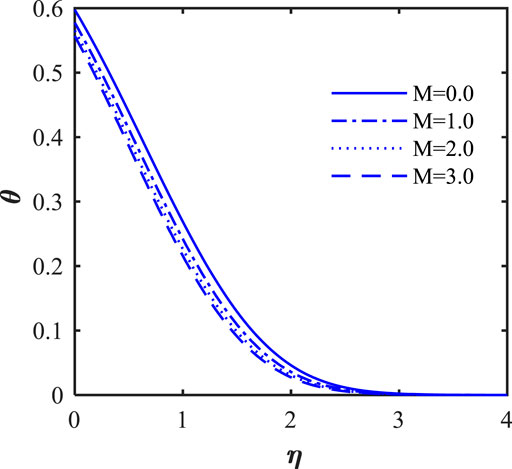
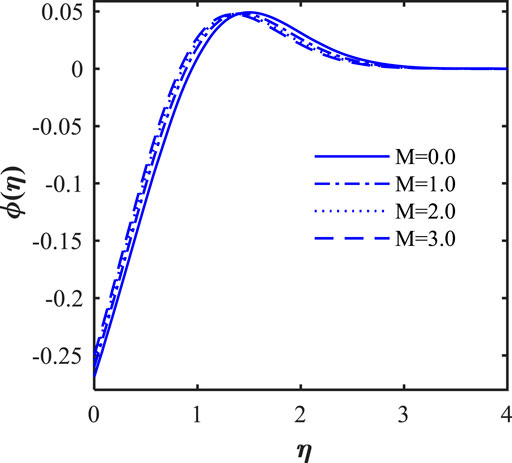
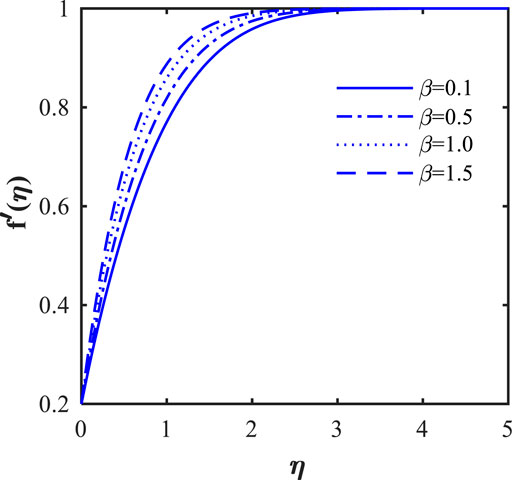
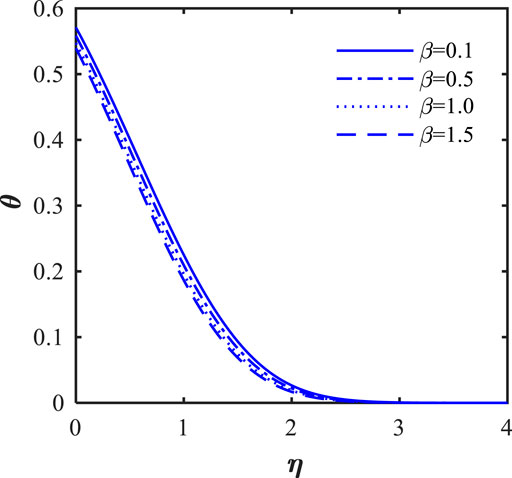
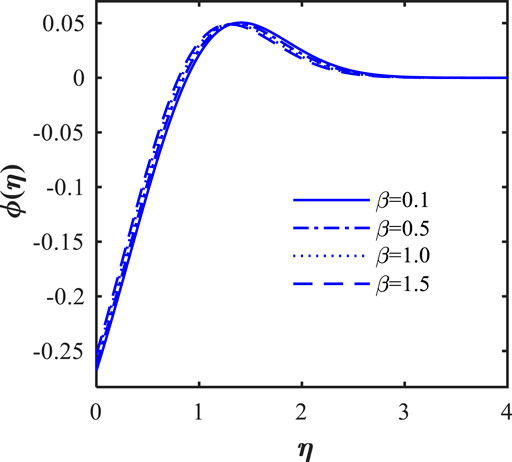
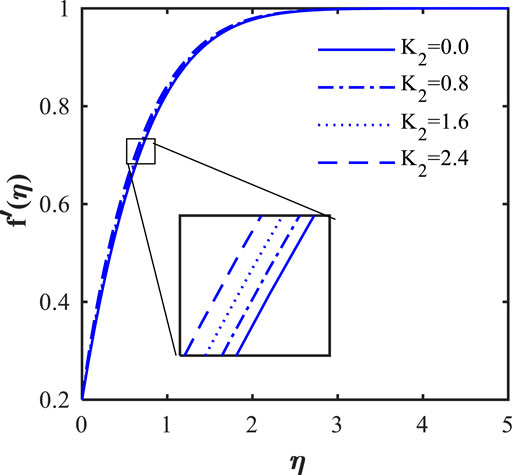
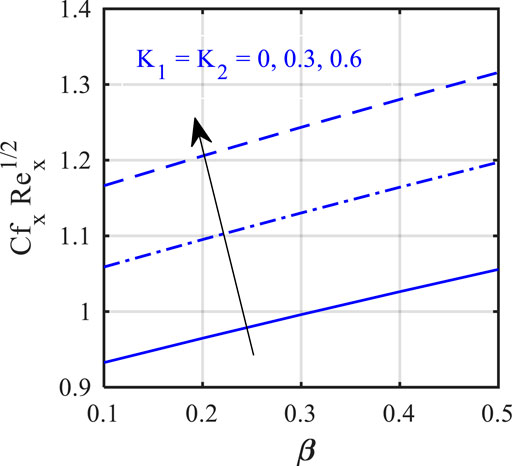
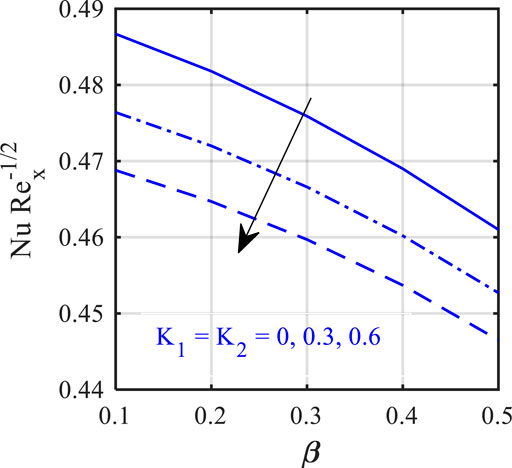
In this section, we will illustrate the solutions obtained with the influence of various influence parameters, such as magnetic field parameter ($M$), stretching ratio parameter ($\lambda$), pressure gradient parameter ($\beta$), Eyring–Powell fluid parameters ($K_1$ and $K_2$), Biot number ($\gamma$), internal heat source parameter ($Q$), radiation parameter ($Rd$), Brownian motion parameter ($Nb$), and thermophoresis parameter ($Nt$) on the dimensionless nanoliquid velocity $f^{\prime }\left(\eta \right)$, temperature $\theta \left(\eta \right)$, nanoparticle concentration $\varphi \left(\eta \right)$, skin friction coefficient ($C{f}_{x}R{e}_x^{0.5}$), and Nusselt number ($NuR{e}_x^{-0.5}$) and presented in graphs (2)–(28). We set the default values for physical parameters to $K_1=0.6,K_2=0.3,M=1.5,\beta =0.2,Rd=0.3,\lambda =0.2,Nt=0.5,Nb=0.5,\gamma =0.6,\mathrm{a}\mathrm{n}\mathrm{d}Q=0.2$ during our simulations.

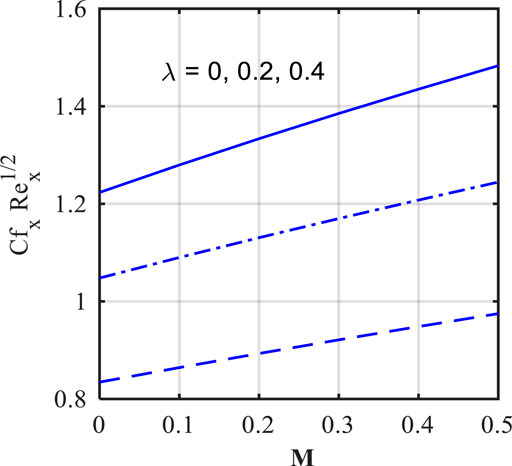
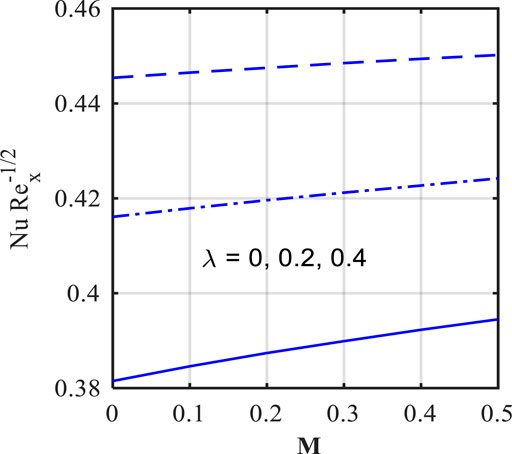
The impact of the Lorentz force, that is, in terms of magnetic field parameter ($M$) on the fields of velocity $f^{\prime }\left(\eta \right)$, temperature $\theta \left(\eta \right)$, and nanoparticle concentration $\varphi \left(\eta \right)$ fields is depicted in Figures 2–4, respectively. We perceive that the velocity $f^{\prime }\left(\eta \right)$ and the associated boundary layer thickness show positive behaviors for $M$. This unexpected result may be due to the impact of the wedge surface and the pressure gradient parameter in the flow domain. However, the thermal field $\theta \left(\eta \right)$ is maximum in the absence of a magnetic field. Furthermore, the nanoparticle concentration $\varphi \left(\eta \right)$ profile increases near the surface of the wedge but reduces away from the surface of the wedge.

FIGURE 2

FIGURE 2. Variations $f^{\prime }$ via $M$.

FIGURE 3

FIGURE 3. Variations $\theta$ via $M$.

FIGURE 4

FIGURE 4. Variations of $\varphi$ via $M$.

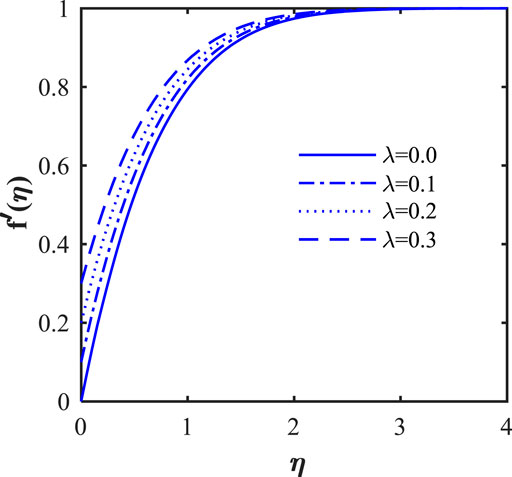
The influence of the stretching ratio ($\lambda$) on dimensionless velocity $f^{\prime }\left(\eta \right)$, temperature $\theta \left(\eta \right)$, and nanoparticle concentration $\varphi \left(\eta \right)$ profiles is illustrated in Figures 5–7, respectively. In Figure 5, for increasing the values of $\lambda$, the velocity field and the thickness of the boundary layer are improved. As we know, the stretching ratio parameter is directly proportional to the stretching rate of the wedge surface. Therefore, an increase in the stretching ratio parameter leads to a stronger stretching process of the surface and thus increases the fluid movement. It is evident from Figure 6 that an improvement in the stretching ratio parameter $\lambda$ reduces $\theta \left(\eta \right)$. From Figure 7, it is evident that the $\varphi \left(\eta \right)$ field increases near the surface of the wedge, while $\varphi \left(\eta \right)$ field decreases when away from the surface.

FIGURE 5

FIGURE 5. Variations of $f^{\prime }$ via $\lambda$.

FIGURE 6

FIGURE 6. Variations of $\theta$ via $\lambda$.

FIGURE 7

FIGURE 7. Variations of $\varphi$ via $\lambda$.

The variation of pressure gradient number ($\beta$) on dimensionless $f^{\prime }\left(\eta \right)$, $\theta \left(\eta \right)$, and $\varphi \left(\eta \right)$ can be obtained, respectively, in Figures 8–10. Here, in Figure 8, the velocity $f^{\prime }\left(\eta \right)$ and its allied thickness of the boundary layer are enriched for the growing values of $\beta$. Physically, because the pressure gradient number descends the fluid viscosity, such viscosity establishes an increase in the velocity field $f^{\prime }\left(\eta \right)$. Figure 9 depicts that the thermal layer thickness enhances with $\beta$. However, the $\varphi \left(\eta \right)$ shows the double behavior for the influence of $\beta$ (see Figure 10). Figure 11 shows that the velocity is an increasing function of $K_2$.

FIGURE 8

FIGURE 8. Variations of $f^{\prime }$ via $\beta$.

FIGURE 9

FIGURE 9. Variations of $\theta$ via $\beta$.

FIGURE 10

FIGURE 10. Variations of $\varphi$ via $\beta$.

FIGURE 11

FIGURE 11. Variations of $f^{\prime }$ via $K_2$.

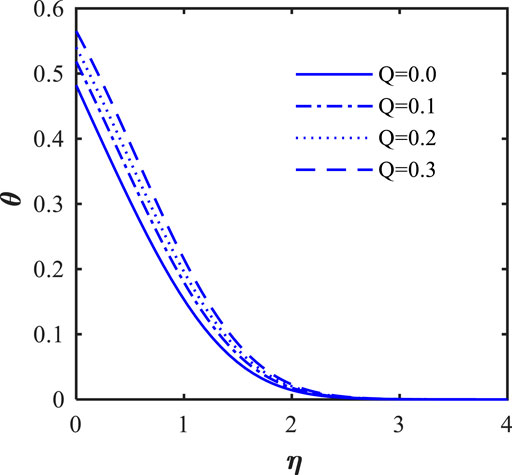
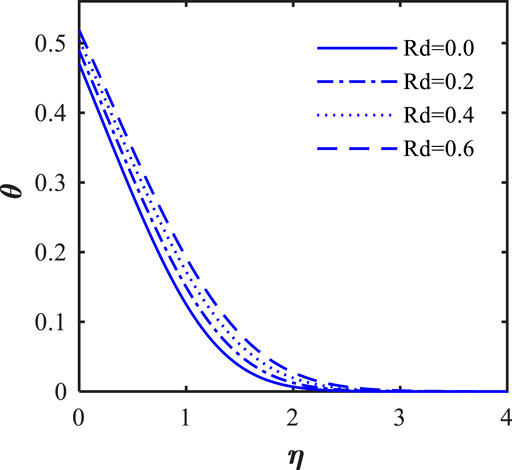
Figures 12–14 illustrate the variation in $f^{\prime }\left(\eta \right)$, $\theta \left(\eta \right)$, and $\varphi \left(\eta \right)$ for a higher estimation of the Eyring–Powell fluid number ($K_1$). It is evident from Figure 12 that an improvement in $K_1$ diminishes the velocity. Physically, this infers that those larger values of $K_1$ improve the nonlinear relationship between shear stress and the shear rate, which condenses the velocity field $f^{\prime }\left(\eta \right)$. The thermal field enhanced with $K_1$ can be seen in Figure 13. However, the nanoparticle concentration field decreases in the region $\eta \in \left[\mathrm{0,1.3}\right]$, increases in the region $\eta \in \left[1.4,3\right]$, and approaches zero for $\eta >3$ for increasing values of $K_1$ (see Figure 14). The higher values of the Biot number ($\gamma$), internal heat source parameter ($Q$), and radiation parameter ($Rd$) cause an enhancement in the temperature distribution $\theta \left(\eta \right)$, which is shown in Figures 15–17, respectively. Physically, the convective heating process adds supplementary heat to the surface of the wedge, so the thermal layer thickness increases with the Biot number ($\gamma$). Both internal heat source and thermal radiation mechanisms integrate the thermal energy due to which the temperature field increases significantly.

FIGURE 12

FIGURE 12. Variations of $f^{\prime }$ via $K_1$.

FIGURE 13

FIGURE 13. Variations of $\theta$ via $K_1$.

FIGURE 14

FIGURE 14. Variations of $\varphi$ via $K_1$.

FIGURE 15

FIGURE 15. Variations of $\theta$ via $\gamma$.

FIGURE 16

FIGURE 16. Variations of $\theta$ via $Q$.

FIGURE 17

FIGURE 17. Variations of $\theta$ via $Rd$.

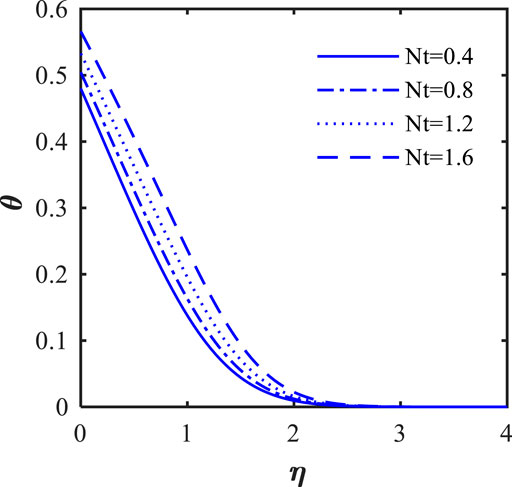
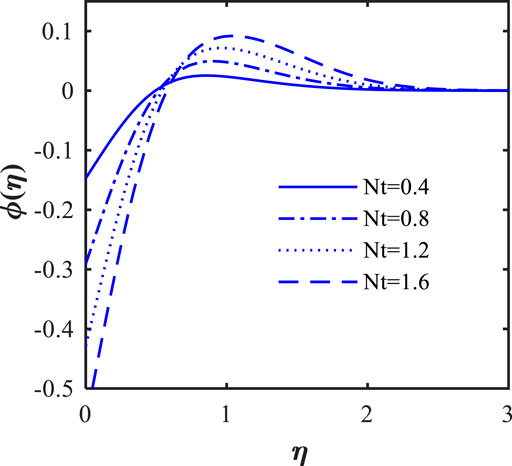
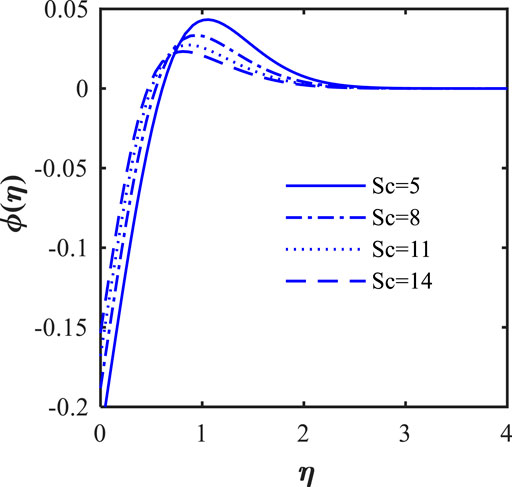
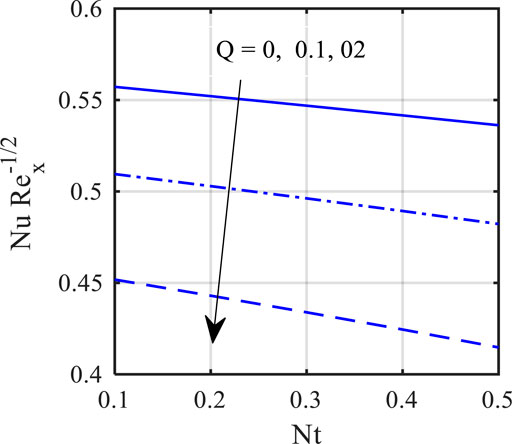
The effects of the thermophoresis parameter ($Nt$) on dimensionless $\theta \left(\eta \right)$ and $\varphi \left(\eta \right)$ are presented, respectively, in Figures 18, 19. Figure 18 signifies that $\theta \left(\eta \right)$ and its allied thickness of the boundary layer are improved with $Nt$. Materially, since the nanoparticles migration improves the fluid thermal conductivity and establishes an increase in the temperature profile, the solutal layer thickness increases with $Nt$ (see Figure 19). It is also observed that the impact of $Nt$ is more evident on the wedge surface. The effects of $Sc$ and $Nb$ are qualitatively similar on the nanoparticle’s volume fraction field, as shown in Figures 20, 21. The variability of the concentration field for different $Nb$ values are shown in Figure 21. When there is a greater input of Nb, both the thickness of the boundary layer and the concentration profile decrease. The cause of this is because it accelerates the rate at which minute particles move at diverse speeds in numerous unexpected directions.

FIGURE 18

FIGURE 18. Variations of $\theta$ via $Nt$.

FIGURE 19

FIGURE 19. Variations of $\varphi$ via $Nt$.

FIGURE 20

FIGURE 20. Variations of $\varphi$ via $Sc$.

FIGURE 21

FIGURE 21. Variations of $\varphi$ via $Nb$.

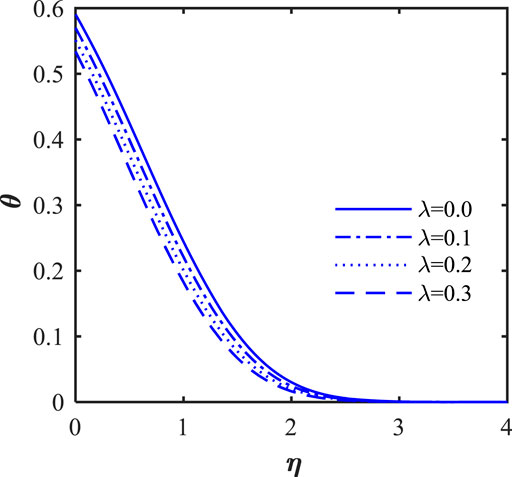
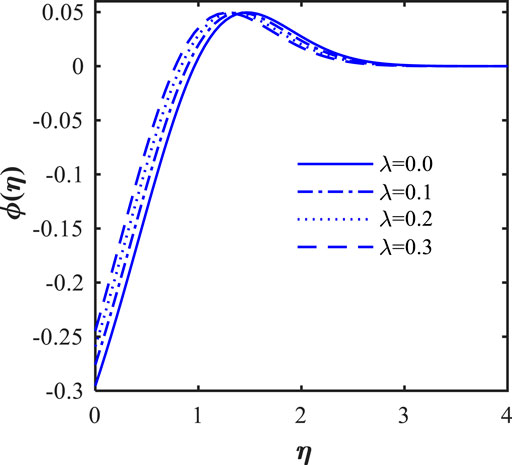
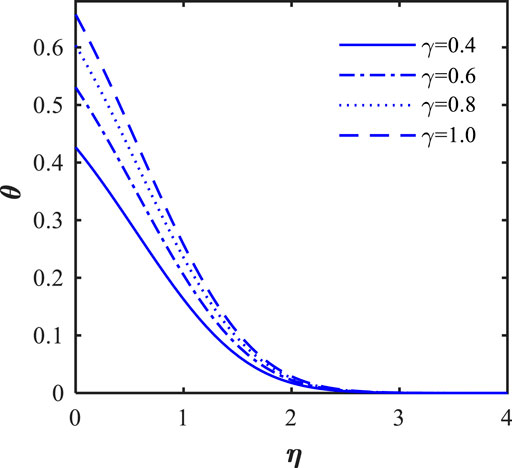
Figures 22, 23 illustrate the role of the stretching ratio parameter ($\lambda$) on the skin friction coefficient ($C{f}_{x}R{e}_x^{0.5}$) and the Nusselt number ($NuR{e}_x^{-0.5}$). The skin friction coefficient ($C{f}_{x}R{e}_x^{0.5}$) is a descending function of $\lambda$; this is because the momentum layer is thicker for larger values of $\lambda$. Figure 23 depicts that $NuR{e}_x^{-0.5}$ is an ascending function of $\lambda$. As we noted, the thermal layer thickness increases with $\lambda$, and subsequently $NuR{e}_x^{-0.5}$ increases. Figures 24, 25 present the consequence of $K_1$ and $K_2$ on $C{f}_{x}R{e}_x^{0.5}$ and $NuR{e}_x^{-0.5}$. $C{f}_{x}R{e}_x^{0.5}$ is an increasing function of $K_1$ and $K_2$, while $NuR{e}_x^{-0.5}$ is a diminishing function of $K_1$ and $K_2$. The role of $Q$ and $Rd$ on $NuR{e}_x^{-0.5}$ is demonstrated in Figures 26, 27, respectively. The thermal boundary layer thickness increases with $Q$; as a result, $NuR{e}_x^{-0.5}$ reduces by enlarging the values of $Q$, while $NuR{e}_x^{-0.5}$ is an increasing function of $Rd$. Finally, Figures 28A,B present the streamlined patterns for different values of $\lambda$.

FIGURE 22

FIGURE 22. Variations of ${Cf}_x{Re}_x^{1/2}$ via $M$ and $\lambda$.

FIGURE 23

FIGURE 23. Variations of ${\text{Nu}}_{\text{x}}{Re}_x^{-1/2}$ via $M$ and $\lambda$.

FIGURE 24

FIGURE 24. Variations of ${Cf}_x{Re}_x^{1/2}$ via $K_{1,}{K}_{2,}$ and $\beta$.

FIGURE 25

FIGURE 25. Variations of ${Nu}_x{Re}_x^{-1/2}$ via $K_{1,}{K}_{2,}$ and $\beta$.

FIGURE 26

FIGURE 26. Variations of ${NU}_x{Re}_x^{1/2}$ via $Nt$ and $Q$.

FIGURE 27

FIGURE 27. Variations of ${Nu}_x{Re}_x^{-1/2}$ via $Nb$ and $Rd$.

FIGURE 28

FIGURE 28. Streamline patterns for different values of $\lambda$ (A) $\lambda =0$ (B) $\lambda =0.2$.

6 Concluding remarks

The theoretical analysis conducted for the Eyring–Powell nanofluid flow with convective boundary condition, internal heat source, and thermal radiation is created by stretching the surface of the wedge. Passive control of the nanoparticle mechanism is also accounted for. The chief outcomes are summarized as follows:

• The stretching ratio number enhances the velocity field, while the thermal field reduces for a higher stretching ratio number.

• The pressure gradient number tends to enhance the velocity and reduces the temperature.

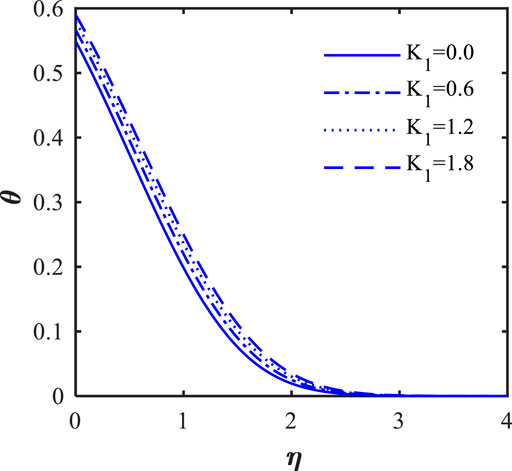
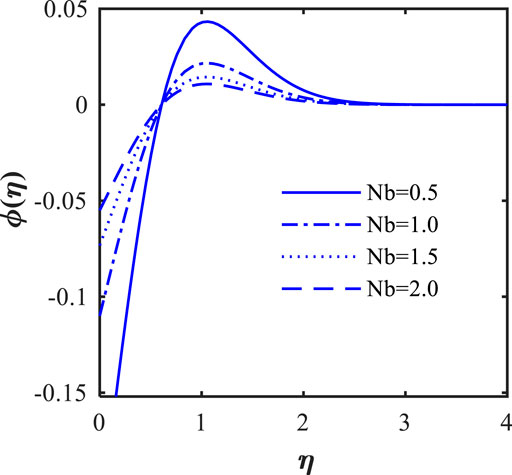
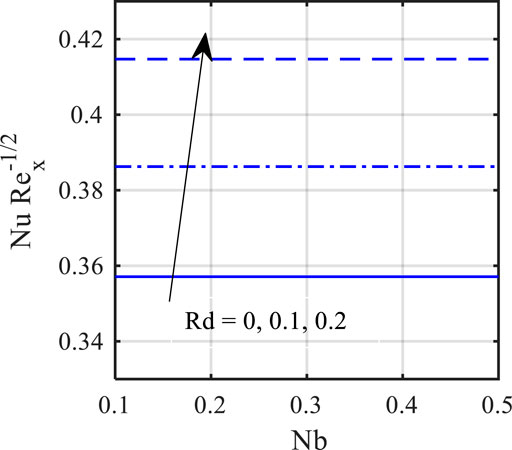
• Thermal field fluctuation is more pronounced for changing Brownian motion parameters close to the wedge’s surface.

• The thermal field is higher for larger thermophoresis parameters, radiation parameter, heat source parameter, and Biot number.

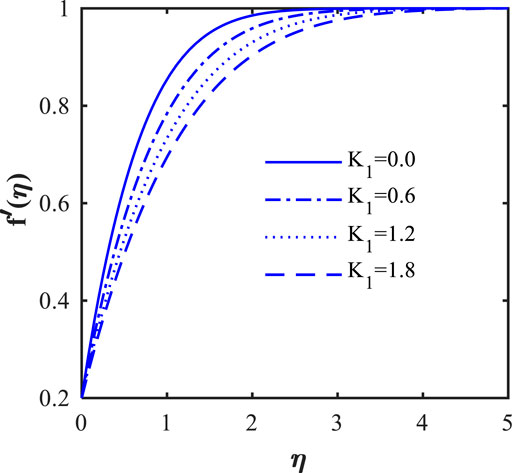
• An increase in the Eyring–Powell fluid number decreases the velocity field.

• The Nusselt number reduces the heat source mechanism.

• The friction factor is an increasing function of $K_1$ and $K_2$, while the Nusselt number is a diminishing function of $K_1$ and $K_2$.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abbasi, A., Mabood, F., Farooq, W., and Hussain, Z. (2021). Non-orthogonal stagnation point flow of Maxwell nanomaterial over a stretching cylinder. Int. Commun. Heat Mass Transf. 120, 105043. doi:10.1016/j.icheatmasstransfer.2020.105043

CrossRef Full Text | Google Scholar

Acharya, N. (2021). Spectral simulation to investigate the effects of active passive controls of nanoparticles on the radiative nanofluidic transport over a spinning disk. J. Therm. Sci. Eng. Appl. 13 (3), 031023. doi:10.1115/1.4048677

CrossRef Full Text | Google Scholar

Akbar, N. S., Ebaid, A., and Khan, Z. H. (2015). Numerical analysis of magnetic field effects on Eyring-Powell fluid flow towards a stretching sheet. J. Magnetism Magnetic Mater. 382, 355–358. doi:10.1016/j.jmmm.2015.01.088

CrossRef Full Text | Google Scholar

Ali, F., Hou, Y., Zahid, M., Rana, M., and Usman, M. (2022). Influence of magnetohydrodynamics and heat transfer on the reverse roll coating of a Jeffrey fluid: A theoretical study. J. Plastic Film Sheeting 38 (1), 72–104. doi:10.1177/87560879211029693

CrossRef Full Text | Google Scholar

Ali, F., Hou, Y., Zahid, M., and Rana, M. A. (2020). Theoretical study of the reverse roll coating of non-isothermal magnetohydrodynamics viscoplastic fluid. Coatings (Basel). 10 (10), 940. doi:10.3390/coatings10100940

CrossRef Full Text | Google Scholar

Ara, A., Khan, N. A., Khan, H., and Sultan, F. (2014). Radiation effect on boundary layer flow of an Eyring–Powell fluid over an exponentially shrinking sheet. Ain Shams Eng. J. 5 (4), 1337–1342. doi:10.1016/j.asej.2014.06.002

CrossRef Full Text | Google Scholar

Azam, M. (2022). Bioconvection and nonlinear thermal extrusion in development ofchemically reactive Sutterby nano-material due to gyrotactic microorganisms. Int. Commun. Heat Mass Transf. 130, 105820. doi:10.1016/j.icheatmasstransfer.2021.105820

CrossRef Full Text | Google Scholar

Azam, M. (2022). Effects of Cattaneo-Christov heat flux and nonlinear thermal radiation on MHD Maxwell nanofluid with Arrhenius activation energy. Case Stud. Therm. Eng. 34, 102048. doi:10.1016/j.csite.2022.102048

CrossRef Full Text | Google Scholar

Azam, M., Abbas, N., Ganesh Kumar, K., and Wali, S. (2022). Transient bioconvection and activation energy impacts on Casson nanofluid with gyrotactic microorganisms and nonlinear radiation. Waves in Random and Complex Media, 1–20. doi:10.1080/17455030.2022.2078014

CrossRef Full Text | Google Scholar

Buongiorno, J. (2006). Convective transport in nanofluids. J. Heat. Transf. 128, 240–250. doi:10.1115/1.2150834

CrossRef Full Text | Google Scholar

Choi, S. U. S., and Eastman, J. A. (1995). Enhancing thermal conductivity of fluids with nanoparticals. United States: ASME international mechanical engineering congress and exposition.

Google Scholar

Chu, Y. M., Ahmad, F., Khan, M. I., Nazeer, M., Hussain, F., Khan, N. B., et al. (2021). Numerical and scale analysis of non-Newtonian fluid (Eyring-Powell) through pseudo-spectral collocation method (PSCM) towards a magnetized stretchable Riga surface. Alexandria Eng. J. 60 (2), 2127–2137. doi:10.1016/j.aej.2020.12.017

CrossRef Full Text | Google Scholar

Dogonchi, A. S., Sadeghi, M. S., Ghodrat, M., Chamkha, A. J., Elmasry, Y., and Alsulami, R. (2021). Natural convection and entropy generation of a nanoliquid in a crown wavy cavity: Effect of thermo-physical parameters and cavity shape. Case Stud. Therm. Eng. Volume 27, 101208. doi:10.1016/j.csite.2021.101208

CrossRef Full Text | Google Scholar

Gireesha, B. J., Gorla, R. S. R., and Mahanthesh, B. (2015). Effect of suspended nanoparticles on three-dimensional MHD flow, heat and mass transfer of radiating Eyring-Powell fluid over a stretching sheet. J. Nanofluids 4 (4), 474–484. doi:10.1166/jon.2015.1177

CrossRef Full Text | Google Scholar

Giri, S. S., Das, K., and Kundu, P. K. (2017). Stefan blowing effects on MHD bioconvection flow of a nanofluid in the presence of gyrotactic microorganisms with active and passive nanoparticles flux. Eur. Phys. J. Plus 132 (2), 101–114. doi:10.1140/epjp/i2017-11338-7

CrossRef Full Text | Google Scholar

Haldar, S., Mukhopadhyay, S., and Layek, G. C. (2021). Effects of thermal radiation on Eyring–Powell fluid flow and heat transfer over a power-law stretching permeable surface. Int. J. Comput. Methods Eng. Sci. Mech. 22, 366–375. doi:10.1080/15502287.2021.1887403

CrossRef Full Text | Google Scholar

Halim, N. A., Haq, R. U., and Noor, N. F. M. (2017). Active and passive controls of nanoparticles in Maxwell stagnation point flow over a slipped stretched surface. Meccanica 52 (7), 1527–1539. doi:10.1007/s11012-016-0517-9

CrossRef Full Text | Google Scholar

Hayat, T., Ali, S., Alsaedi, A., and Alsulami, H. H. (2016). Influence of thermal radiation and Joule heating in the Eyring–Powell fluid flow with the Soret and Dufour effects. J. Appl. Mech. Tech. Phy. 57 (6), 1051–1060. doi:10.1134/s0021894416060122

CrossRef Full Text | Google Scholar

Hayat, T., Ali, S., Farooq, M. A., and Alsaedi, A. (2015). On comparison of series and numerical solutions for flow of Eyring-Powell fluid with Newtonian heating and internal heat generation/absorption. PLoS One 10 (9), e0129613. doi:10.1371/journal.pone.0129613

PubMed Abstract | CrossRef Full Text | Google Scholar

Hayat, T., Aziz, A., Muhammad, T., and Alsaedi, A. (2017). Active and passive controls of Jeffrey nanofluid flow over a nonlinear stretching surface. Results Phys. 7, 4071–4078. doi:10.1016/j.rinp.2017.10.028

CrossRef Full Text | Google Scholar

Jalil, M., Asghar, S., and Imran, S. M. (2013). Self similar solutions for the flow and heat transfer of Powell-Eyring fluid over a moving surface in a parallel free stream. Int. J. Heat Mass Transf. 65, 73–79. doi:10.1016/j.ijheatmasstransfer.2013.05.049

CrossRef Full Text | Google Scholar

Kalaivanan, R., Ganesh, N. V., and Al-Mdallal, Q. M. (2020). An investigation on Arrhenius activation energy of second grade nanofluid flow with active and passive control of nanomaterials. Case Stud. Therm. Eng. 22, 100774. doi:10.1016/j.csite.2020.100774

CrossRef Full Text | Google Scholar

Khan, I., Khan, M., Malik, M. Y., Salahuddin, T., and Shafquatullah, H. (2017). Mixed convection flow of Eyring-Powell nanofluid over a cone and plate with chemical reactive species. Results Phys. 7, 3716–3722. doi:10.1016/j.rinp.2017.08.042

CrossRef Full Text | Google Scholar

Khan, I., Malik, M. Y., Salahuddin, T., Khan, M., and Rehman, K. U. (2018). Homogenous–heterogeneous reactions in MHD flow of Powell–Eyring fluid over a stretching sheet with Newtonian heating. Neural comput. Appl. 30 (11), 3581–3588. doi:10.1007/s00521-017-2943-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Khan, M., Azam, M., and Muni, A. (2017). On unsteady Falkner-Skan flow of MHD Carreau nanofluid past a static/moving wedge with convective surface condition. J. Mol. Liq. 230, 48–58. doi:10.1016/j.molliq.2016.12.097

CrossRef Full Text | Google Scholar

Khan, W. A., and Pop, I. (2010). Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. heat mass Transf. 53 (11-12), 2477–2483. doi:10.1016/j.ijheatmasstransfer.2010.01.032

CrossRef Full Text | Google Scholar

Kuznetsov, A. V., and Nield, D. A. (2013). The cheng–minkowycz problem for natural convective boundary layer flow in a porous medium saturated by a nanofluid: A revised model. Int. J. Heat Mass Transf. 65, 682–685. doi:10.1016/j.ijheatmasstransfer.2013.06.054

CrossRef Full Text | Google Scholar

Macha, M., Cherlacola, S. R., and Naikoti, K. (2017). Magnetohydrodynamic flow and heat transfer to Sisko nanofluid over a wedge. Inter. J. Fluid Mech. Res. 44 (1)–13. doi:10.1615/InterJFluidMechRes.2017015861

CrossRef Full Text | Google Scholar

Muhammad, T., Waqas, H., Khan, S. A., Ellahi, R., and Sait, S. M. (2021). Significance of nonlinear thermal radiation in 3D Eyring–Powell nanofluid flow with Arrhenius activation energy. J. Therm. Anal. Calorim. 143 (2), 929–944. doi:10.1007/s10973-020-09459-4

CrossRef Full Text | Google Scholar

Nield, D. A., and Kuznetsov, A. V. (2009). The Cheng–Minkowycz problem for natural convective boundary-layer flow in a porous medium saturated by a nanofluid. Int. J. Heat Mass Transf. 52 (25-26), 5792–5795. doi:10.1016/j.ijheatmasstransfer.2009.07.024

CrossRef Full Text | Google Scholar

Patel, M., and Timol, M. G. (2009). Numerical treatment of Powell–Eyring fluid flow using method of satisfaction of asymptotic boundary conditions (MSABC). Appl. Numer. Math. 59 (10), 2584–2592. doi:10.1016/j.apnum.2009.04.010

CrossRef Full Text | Google Scholar

Ramana, K. V., Gangadhar, K., Kannan, T., and Chamkha, A. J. (2021). Cattaneo–Christov heat flux theory on transverse MHD Oldroyd-B liquid over nonlinear stretched flow. J. Therm. Analysis Calorim. 147, 2749–2759. doi:10.1007/s10973-021-10568-x

CrossRef Full Text | Google Scholar

Rana, P., and Bhargava, R. (2012). Flow and heat transfer of a nanofluid over a nonlinearly stretching sheet: A numerical study. Commun. Nonlinear Sci. Numer. Simul. 17 (1), 212–226. doi:10.1016/j.cnsns.2011.05.009

CrossRef Full Text | Google Scholar

Rauf, A., Abbas, Z., and Shehzad, S. A. (2019). Interactions of active and passive control of nanoparticles on radiative magnetohydrodynamics flow of nanofluid over oscillatory rotating disk in porous medium. J. nanofluids 8 (7), 1385–1396. doi:10.1166/jon.2019.1705

CrossRef Full Text | Google Scholar

Rehman, K. U., Malik, M. Y., Salahuddin, T., and Naseer, M. (2016). Dual stratified mixed convection flow of Eyring-Powell fluid over an inclined stretching cylinder with heat generation/absorption effect. AIP Adv. 6 (7), 075112. doi:10.1063/1.4959587

CrossRef Full Text | Google Scholar

Riaz, A., Ellahi, R., and Sait, S. M. (2021). Role of hybrid nanoparticles in thermal performance of peristaltic flow of Eyring–Powell fluid model. J. Therm. Anal. Calorim. 143, 1021–1035. doi:10.1007/s10973-020-09872-9

CrossRef Full Text | Google Scholar

SadeghSadeghi, M., Dogonchi, A. S., Ghodrat, M., Chamkha, A. J., and NaderKarimi, H. A. (2021). Natural convection of cuo-water nanofluid in a conventional oil/water separator cavity: Application to combined-cycle power plants. J. Taiwan Inst. Chem. Eng. 124, 307–319. doi:10.1016/j.csite.2021.101208

CrossRef Full Text | Google Scholar

Sreenivasulu, P., Poornima, T., Malleswari, B., Reddy, N. B., and Souayeh, B. (2021). Internal energy activation stimulus on magneto-bioconvective Powell-Eyring nanofluid containing gyrotactic microorganisms under active/passive nanoparticles flux. Phys. Scr. 96 (5), 055221. doi:10.1088/1402-4896/abeb33

CrossRef Full Text | Google Scholar

Srinivas Reddy, C., and Naikoti, Kishan (2016). MHD boundary layer flow of Casson nanofluid over a non linear stretching sheet with viscous dissipation and convective condition. J. nanofluids 5 (6), 870–879. doi:10.1166/jon.2016.1271

CrossRef Full Text | Google Scholar

Tayebi, T., Sattar Dogonchi, A., Karimi, N., Ge-JiLe, H., Chamkha, A. J., and Elmasry, Y. (2021). Thermo-economic and entropy generation analyses of magnetic natural convective flow in a nanofluid-filled annular enclosure fitted with fins. Sustain. Energy Technol. Assessments 46, 101274. doi:10.1016/j.seta.2021.101274

CrossRef Full Text | Google Scholar

Tripathi, R., Seth, G. S., and Mishra, M. K. (2017). Double diffusive flow of a hydromagnetic nanofluid in a rotating channel with Hall effect and viscous dissipation: Active and passive control of nanoparticles. Adv. Powder Technol. 28 (10), 2630–2641. doi:10.1016/j.apt.2017.07.015

CrossRef Full Text | Google Scholar

Veera Krishna, M., Ameer Ahamad, N., and Chamkha, Ali J. (2021). Hall and ion slip impacts on unsteady MHD convective rotating flow of heat generating/absorbing second grade fluid. Alexandria Eng. J. 60, 845–858. doi:10.1016/j.aej.2020.10.013

CrossRef Full Text | Google Scholar

Vijaya Bhaskar Reddy, N., Kishan, N., and Srinivas Reddy, C. (2019). Melting heat transfer and MHD boundary layer flow of eyring-powell nanofluid over a nonlinear stretching sheet with slip. Int. J. Appl. Mech. Eng. 24 (1), 161–178. doi:10.2478/ijame-2019-0011

CrossRef Full Text | Google Scholar

Weera, W., Maneengam, A., Saeed, A. M., Aissa, A., Guedri, K., Younis, O., et al. (2022). Effects of branched fins on alumina and N-octadecane melting performance inside energy storage system. Front. Phys. 10, 957025. doi:10.3389/fphy.2022.957025

CrossRef Full Text | Google Scholar

Glossary

$x,y$ space coordinates ($s^{-1})$

$u,v$ velocity components($m{s}^{-1})$

$C$ fluid concentration$\left(kg{m}^{-3}\right)$

$C_{\infty }$ ambient concentration $\left(kg{m}^{-3}\right)$

$T_f$ wall temperature ($K)$

$T_{\infty }$ ambient temperature ($K)$

$T$ fluid temperature ($K)$

$k$ fluid thermal conductivity $\left(Wm⁻¹K⁻¹\right)$

$D_B$ Brownian diffusion ($m^2{s}^{-1})$

$D_T$ thermophoretic diffusion ($m^2{s}^{-1})$

$K_1,K_2$ Eyring–Powell fluid parameter

$\mathit{Pr}$ Prandtl number

$Sc$ Schmidt number

$Nb$ Brownian motion parameter

$Nt$ thermophoresis parameter

$Q$ heat source parameter

$U_e$ free stream velocity

$U_w$ wedge surface velocity ($m{s}^{-1})$

$Re$ Reynolds number

$d,{\rm E}$ fluid parameters

$Nu$ Nusselt number

$C_f$ skin friction

$Rd$ thermal radiation

$M$ magnetic parameter

$\gamma$ Biot number

$\beta$ pressure gradient parameter

$\tau$ ratio of specific heat

${\tau }_w^{″}$ wall shear stress $\left(kg{s}^{-2}{m}^{-1}\right)$

$q_w^{″}$ heat flux $\left(W\cdot m^{-2}\right)$

$\lambda$ stretching ratio parameter

$\mu$ dynamic viscosity $\left(kg{s}^{-1}{m}^{-1}\right)$

$\nu$ kinematic viscosity ($m^2{s}^{-1})$

$\rho$ density of the fluid $\left(kg{m}^{-3}\right)$

$\theta$ dimensionless temperature

$\psi$ stream function

$\eta$ dimensionless similarity variable

$C_p$ specific heat $\left(Jk{g}^{-1}K\right)$

$a,c$ constants