Assessment of solar load models for bifacial PV panels

Solar load is one of the key inputs in thermal analysis of all solar based applications using ray tracing. Commercial and academic Computational Fluid Dynamics (CFD) codes incorporate different solar load models for ray tracing, i.e., Solar Position and Intensity (SOPLOS) theoretical maximum function, American Society of Heating, Refrigeration, and Airconditioning Engineers (ASHRAE) fair weather and constant solar load models. However, solar load depends largely on weather conditions of the site whereas the solar load models in CFD software do not accommodate changing weather patterns and hence the CFD simulation results obtained are not representative of an extended period of time. This paper studies the effect of changing weather patterns on solar load assessment, using bifacial solar panels as a case study. In this study, on-site data of a humid sub-tropical region for monsoon season, mid-June to mid-August, has been used as an input for solar ray tracing due to large temperature variations and cloud cover for longer duration. Comparative study of SOPLOS and ASHRAE models with in situ model shows that they over predict front side solar load, with only 0.5% and 13% matching in situ data respectively, while both models under predict rear side solar load in the studied time period, with 2% and 24% solar load estimation agreeing with in situ data respectively.

Introduction

The use of hydrocarbons in energy sector has resulted in unprecedented amount of emissions of greenhouse gases which is leading to irreversible changes in our eco-system. These drastic changes have compelled researchers to focus on renewable energy resources, particularly solar energy as it is one of the cleanest and most abundant sources of renewable energy. Earth’s atmosphere receives 3.85 million exajoules (EJ) of solar energy per year, and rooftop solar panels have the potential of producing 27 PWh of energy per annum (Joshi et al., 2021). A significant disadvantage of conventional solar panels is insufficient energy production on cloudy days, resulting in a low return on investment in regions that receive less direct sun light, necessitating solar irradiance studies. Additionally, the growing focus on solar energy research has significantly increased thermal analysis of solar based applications e.g., solar heaters, solar dryers, solar chimneys, solar panels etc. Thermal analysis involves the computation of incident solar radiations, their absorption and reflection to calculate radiative flux and their corresponding radiation temperatures.

The efficiency of commercial PV cells is rated between 10 and 20% with $0.1–0.24/kwh (Photovoltaic Energy Factsheet, 2021) (Soomar et al., 2022) while the remaining incident solar energy is mostly wasted as heat, which further reduces their overall efficiency by decreasing the voltage generated. In addition, there are shading losses in a solar panel when every cell in the panel has to operate at the reduced current set by shaded cells which may be remedied by installing panels on the roof or in open lots (Iqbal et al., 2022). Alternatively, there are ways to increase overall energy yield of solar panels. In terms of technological and economic viability, bifacial solar module technology, which is projected to dominate PV installations in the near future, represents an emerging trend in rooftop PV systems for energy generation (Desai et al., 2022). One of them is by using bifacial solar panels, which produce power from both sides of the panel. They are particularly suitable for climatic regions with higher diffused light since no shading effects are caused by direct sun light and bifacial solar panels can exploit light from all available direction. In studies by Sun et al. (2018) and Kopecek and Libal (2021), bifacial solar panels are claimed to increase energy yield by 10%–30% when used on highly reflecting light-colored surfaces. Coupled with an efficient Maximum Power Point Tracking (MPPT) algorithm such as learning-based real-time hybrid global search adaptive approach of Wang et al. (2022) can yield greater energy extracting efficiency. Furthermore, different approaches can be used to reduce the inherent noise of the system (Arshad et al., 2022; Chen et al., 2022). Given the significance of bifacial solar modules in increasing energy capture and the importance of rear side solar load in its numerical analysis, it is used as a case study in our assessment.

Several models are present to estimate solar irradiance and insolation on front and rear faces of tilted surfaces, specially tilted bifacial solar panels. Danks (2014) calculated annual solar insolation for different cities of the world by using solar position algorithm developed by the National Renewable Energy Laboratory (Reda and Andreas, 2004), diffused light obtained from Perez sky model (Perez et al., 1990) and integrated both of them for solar ray tracing in OpenFoam (OpenFoam.com, 2022). In 2015, Yusufoglu et al. (2015) elaborated individual and combined effect of several site-specific conditions of bifacial solar panels, such as albedo, reflective surface size, module elevation, and tilt angle. They utilized Perez model (Perez et al., 1990) to calculate diffuse solar irradiance, while albedo coefficient was calculated using the method proposed by Ineichen et al. (1990). A ray tracing method was then used in (Yusufoglu et al., 2015) to measure the rear side and average irradiance of bifacial solar panel on a summer day in Cairo for different elevations and albedo coefficients. To model energy yield in bifacial solar panels through simulations, Wang et al. (2015) provided guidelines for the modelling process, calculated total solar power received in Germany and Singapore throughout a particular day in July and compared it with power received on other days in January, April, and October. They also calculated bifacial module power with different panel elevations and background reflectivity values for Konstanz, Germany, and equinox of Singapore. To assess the performance of bifacial modules in every region of the world, Sun et al. (2018) derived a set of empirical design rules, which optimize bifacial solar modules across the world and provide the groundwork for rapid assessment of the location-specific performance. The study used National Renewable Energy Laboratory (NREL) solar position algorithm (Reda and Andreas, 2004) in PV Sandia modelling toolbox (Holmgren et al., 2018) to calculate solar path. It combined irradiance values at the interval of 1 minute using Haurwitz clear-sky model (Haurwitz, 1945; Haurwitz, 1946), implemented in PVLIB tool box (Holmgren et al., 2018) with NASA monthly Surface Meteorology database to calculate irradiance for each climatic region with a spatial resolution of 1 × 1° (latitude). Sun et al. (2018) concluded that the NASA satellite derived insolation database is suitable for preliminary estimation, while detailed local meteorological data is essential for actual installation. Models like Isotropic Sky Diffuse Model, Simple Sandia Sky Diffuse Model, Hay and Davies Sky Diffuse Model, Reindl Sky Diffuse Model, and Perez Sky Diffuse Model do not use real weather conditions and additionally are not included in popular commercial software.

A coupled optical-electrical-thermal model of bifacial solar panels was presented by Gu et al. (2020) using database from solarGIS to obtain Global Horizontal Irradiance (GHI) and Diffuse Horizontal Irradiance (DHI). These two values were used in equations developed by Yang (2016), Sun et al. (2012), and Noorian et al. (2008) to calculate front and rear side irradiance of bifacial solar panel along with view factors which accommodate diffuse surface to surface radiation. To model bifacial illumination of full photovoltaic systems using ray tracing annually, Ernst et al. (2022) utilized acceleration strategies that reduced heavy ray tracing requirements by nearly 90%. In Zhao et al. (2021)used DIVA for Rhino, a program that uses backward ray tracing method based on Perez model (Perez et al., 1990) and a cumulative sky approach (Robinson and Stone, 2004) to analyze shading and mismatch loss. An open source python toolkit bifacial radiance (Pelaez and Deline, 2020) was developed in 2020 to automate PV systems performance in ray tracing software tool called RADIANCE (Ward, 1994). Altan et al. (Haider et al., 2022a; Haider et al., 2022b) used deep learning algorithms to forecast short- and long-term solar irradiance. Performance evaluation and enhancement of solar panels has also been the subject of several researches leading to different types of solar simulators. Shah et al. (2020) designed a solar simulator using 1,000 W metal halide lamp coupled with a truncated ellipsoidal reflector optimized through parametric iterations.

Absorptivity and emissivity of all surfaces in the domain along with spectral distribution are required for solar load calculation in thermal analysis, while the irradiance tools discussed above calculate incident radiations. Solar load models first calculate the direction of sun with respect to the domain followed by calculation of radiative flux on surface obtained via solar ray tracing. The radiative flux includes primary solar hits on the object, reflective fluxes and diffusive sky radiative fluxes. This solar load is used as a heat source in energy equation for heat transfer. The present radiance models e.g., Hay and Davies, Perez, Reindl etc. calculate plane of array irradiance but they require an interface for coupling the calculated irradiance values with surface absorptivity and emissivity to calculate solar loads for thermal analysis. Different commercial and opensource Computational Fluid Dynamics (CFD) software have embedded solar load models to predict illumination energy source that results from incident solar radiation via solar ray tracing. These solar load models include theoretical maximum model derived from Solar Position and Intensity (SOPLOS), American Society of Heating, Refrigeration, and Airconditioning Engineers (ASHRAE) fair weather model, and constant solar load models. However, solar load depends largely on weather conditions of the site whereas the solar load models that CFD software use for thermal analysis do not accommodate changing weather patterns; hence the CFD simulation results obtained are not representative of an extended period of time. A number of studies on solar applications have used SOPLOS theoretical maximum and ASHRAE-fair weather models primarily using commercial CFD software ANSYS to predict solar loads. Table 1 provides a summary of works with the solar load models.

TABLE 1

TABLE 1. Research studies that utilize solar load models.

A constant solar load model was used by Jonsson (2007), Patidar (2009), and Kuharat and Anwar Bég (2019) for solar ray tracing to simulate car cabin climate and solar collector performance. They employed a constant Direct Normal Irradiance value and found that the temperature distribution is strongly dependent on the accurate estimation of solar load.

In Table 1, “solar calculator” indicates that the ASHRAE-Fair-weather or SOPLOS theoretical maximum model was used to calculate DNI and DHI. Moon et al. (2016) and Hadi et al. (2022) used solar calculator in ANSYS to estimate solar load and analyze thermal comfort for a passenger compartment of vehicle. Similarly, Jain et al. (2019), used solar calculator to calculate solar load parameters of Ludhiana on 21st November for CFD study of solar dryer. In 2022, Zeeshan et al. (2022) predicted thermal comfort effect of trees in streets of Karachi, Pakistan by using P1 radiation modelling along with fair weather solar ray tracing for solar irradiation and radiative transfer. In these studies, it was mostly assumed that weather was clear and sunny in the studied period to support the solar calculator model.

ASHRAE-Fair weather model uses extraterrestrial solar irradiance data from ASHRAE handbook to calculate DHI and DNI values. Potgieter et al. (2020) used fair-weather model for solar ray tracing and compared numerical results with experimental ones for solar air heater on a particular time in day. Another study by Xu et al. (2022) used ASHRAE fair-weather solar radiation model to get temperature distribution inside a greenhouse throughout a day. Fairweather model has also been used by Zhong and Calautit (2020) for thermal modelling of a stadium in Doha. Attig-Bahar et al. (2019) used solar load calculator in 3D numerical analysis of solar chimney power plant, but for longer period of simulations, they used one dimensional mathematical model coupled with real weather data. Al-Nehari et al. (2021) applied solar load model in solar cooker analysis via two methods: first by using experimental values of DNI and DHI and second where ANSYS solar calculator is used for solar ray tracing throughout the day. However, the percentage difference in results is minor because the experiment was carried out on a fairly clear day.

Solar load estimation using CFD tools is often used to assess potential of a site for installation of solar PV and solar thermal systems. These estimates are based on models often derived from theoretical considerations and overlook actual weather patterns. Therefore, this paper focuses on solar load estimation based on actual weather patterns by comparing the radiative heat fluxes obtained from in situ solar load model (using experimental DNI and DHI) with the ASHRAE fair weather model and theoretical maximum model used for solar ray tracing in CFD codes.

The focus of this study is a humid subtropical region because of the diversity and severity of weather patterns fluctuating from clear skies, regularly cloudy, particularly during monsoon season. The frequent variations in cloud cover can have a significant impact on solar load, whereas in other climatic conditions such a critical impact is not expected. In this work, the differences between experimental input based solar ray tracing and existing solar calculator, including SOPLOS theoretical maximum and ASHRAE-fair-weather models, for humid sub-tropical regions is analyzed so that the accuracy of models can be checked, and the results can be generalized for all similar climatic regions. It was observed that the ASHRAE fair weather model and SOPLOS theoretical maximum model overpredict front side solar load with only 0.5% and 13% of those predictions matching actual data respectively, while both models under predict rear side solar load with 2% and 24% of those predictions matching actual data, respectively.

Methodology

To perform a comparative study of SOPLOS theoretical maximum, ASHRAE fair weather model and in situ DNI and DHI values for numerical solar ray tracing on a bifacial solar panel, OpenFoam solar load model with reflected rays was used. Solar ray tracing method in the solar load model is used to estimate the direct solar energy produced from incident solar radiations by using a face shading algorithm. Radiative flux from the first reflected rays can be optionally included in OpenFoam. To account for diffuse surface to surface radiative flux, view factor model needs to be used along with solar load model.

Sun direction coordinates for the domain were calculated from 15th June to 15th August with half hourly interval, using solar calculator code (OpenFoam.com). This period is selected for study because the weather changes from dry and hot to humid and hot, with the arrival of rainy season in most sub tropical regions. Experimental values of DHI and DNI were measured from a shaded pyranometer mounted at a location in Islamabad, Pakistan. Steady state numerical simulation was performed for each time interval. The total computations for one model with half hour interval from 15th June to 15th August sums up to 1,678 number of simulations per model with a total 5,034 simulations for the three models. To automate the computations, a parametric tool was developed in python that takes values of start time, start Day, sun direction coordinates, experimental DNI and DHI with half hourly interval and integrates it in the OpenFoam case files. Probes are defined on the front and rear sides of solar panel which record radiative flux values for each time interval. The python script for automation then runs the 5,034 simulations for all of the three models and stores results in separate folders for each time step. Specifications of the server used to perform the simulations are: 64 cores and 128 threads, 384 GB RAM, Ubuntu 20.04 operating system, NVIDIA Tesla v100 GPU and CUDA 11.2. The total time taken for 2 months simulation of all models is 10 days. Front and back radiative flux values of bifacial solar panel from each simulation were extracted and graphs were drawn for comparative study.

Data collection and processing

The in situ data of Global Horizontal Irradiance (GHI), Diffuse Horizontal Irradiance (DHI) and Direct Normal irradiance (DNI) were recorded at regular intervals at a single location in Islamabad. The specifications of instruments used are given in Table 2. The daily uncertainty for DNI and GHI/DHI values is approximately 1% and less than 2% respectively.

TABLE 2

TABLE 2. Instrument specifications.

Data was collected with time intervals of 10 min, however, the instantaneous data at every half an hour interval was used in simulation so that the changing weather pattern can be accommodated along with manageable computational resources.

Simulation framework

All three models were applied on a south facing bifacial solar panel, tilted at 30° the optimal year-around tilt angle for the location, and covering approximately 5% of the ground domain. Average elevation of the panel was kept constant at 1.6 m for all models with dimensions of 1.68 m × 1.02 m × 0.04 m for the panel. In the domain shown in Figure 1, north and east directions are taken along y-axis and x-axis respectively.

FIGURE 1

FIGURE 1. Computational domain considered in the study.

Opaque reflective boundary condition was defined for panel and ground, while transparent boundary condition was applied on the remaining boundaries of the computational domain. Spectral distribution was defined for two bands i.e., visible and infra-red, with specific absorption emission values for concrete and glass (Engineering ToolBox, 2009).

Three models were used in solar load to calculate direct normal and diffuse horizontal irradiance. First is the user defined solar load model in which insitu DNI and DHI data obtained from instruments mentioned in Table 2 was utilized in solar load radiation model for solar ray tracing. The second is fair weather model, integrated in OpenFoam and commercial CFD software. It is derived from Eq. 1 and extraterrestrial solar irradiance and related data from ASHRAE Handbook (Curcija, 2001).

$E_{DN}=\frac{A}{\exp \left(B/\sin \beta \right)},(1)$

where.

A = apparent solar irradiation at air mass m = 0.

B = atmospheric extinction coefficient β = Solar altitude above horizontal (in degrees).

Albedo value of 0.35 for grey concrete of roof top was taken from (Marceau and Vangeem, 2008). In OpenFoam, a cloud cover fraction is also incorporated in the above equation as shown in Eq. 2:

$E_{DN}=\left(1-0.75\times {\mathit{s}\mathit{k}\mathit{y}\mathit{C}\mathit{l}\mathit{o}\mathit{u}\mathit{d}\mathit{C}\mathit{o}\mathit{v}\mathit{e}\mathit{r}\mathit{F}\mathit{r}\mathit{a}\mathit{c}\mathit{t}\mathit{i}\mathit{o}\mathit{n}}^3\right)\times \frac{A}{\exp \left(B/\sin \beta \right)}(2)$

Where, (Spark, 2016) provides monthly average cloud coverage values of Islamabad, Pakistan. To keep fair weather model realistic, average values of 10%, 20%, and 25% cloud cover for the months of June, July and August respectively, were taken instead of using a constant fraction.

The third is theoretical maximum model developed by National Renewable Energy Laboratory (NREL), integrated in OpenFoam. It calculates the maximum possible values of solar irradiance which are unlikely to be experienced due to atmospheric conditions. The equation for theoretical maximum model is shown in equation Eq. 3

$EDN=\mathit{S}\mathit{e}\mathit{t}\mathit{r}\mathit{n}*\mathit{S}\mathit{u}\mathit{n}\mathit{p}\mathit{r}\mathit{i}\mathit{m}\mathit{e},(3)$

where S_etrn is the direct normal solar irradiance at the top of the atmosphere and S_unprime is correction factor to account for attenuation in solar load through the atmosphere. Both theoretical maximum and fair weather models use Eq. 4 (Curcija, 2001) for calculating diffuse radiations on a tilt surface.

$E_D=C{E}_{DN}\frac{\left(1+\cos ϵ\right)}{2},(4)$

where ϵ = tilt angle of surface from horizontal plane C= Solar diffusivity constant.

The ground reflected solar irradiance on a tilt surface is calculated using Eq. 5 (Moon et al., 2016).

$E_R=E_{DN}\left(C+\sin \beta \right){\rho }_g\frac{\left(1-\cos ϵ\right)}{2},(5)$

where ρ_g is the ground reflectivity. The total diffuse irradiation on a surface is calculated to be the sum of E_D and E_R. Simulations were automated using basic python libraries such as shutil, OS, numpy and pandas. Each test case value was read from excel file database and written to radiation properties file which was then read by the simulator to process on pre-built mesh. After OpenFoam processing, the output values were extracted from probe folder of each case recursively into a csv file. The simulations were run parallel on 64 cores. The script also wrote time taken by all set of simulations on a text file.

Results and discussion

The data collected through probes on front and rear side of the south facing panel was extracted from each steady state simulation performed. Solar ray tracing of calculated solar loads resulted in radiative heat flux, hence the radiative heat flux is also used as a parameter for comparison as it is a direct result of solar load models employed. The results of solar ray tracing for the south facing panel are shown in Figure 2. While Figure 2 shows four instances in a day, which are indicative, simulations for all daylight hours at half hour intervals averaging ∼28 simulations for each day are represented in Figures 3, 4.

FIGURE 2

FIGURE 2. Solar ray tracing with radiative heat flux (W/m²) on 25th June in Islamabad, Pakistan.

FIGURE 3

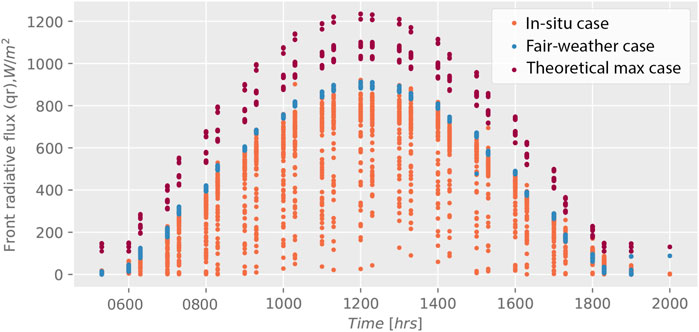
FIGURE 3. Graphical representation of half hourly front-side radiative flux (qr) for 15th June-15th Aug.

FIGURE 4

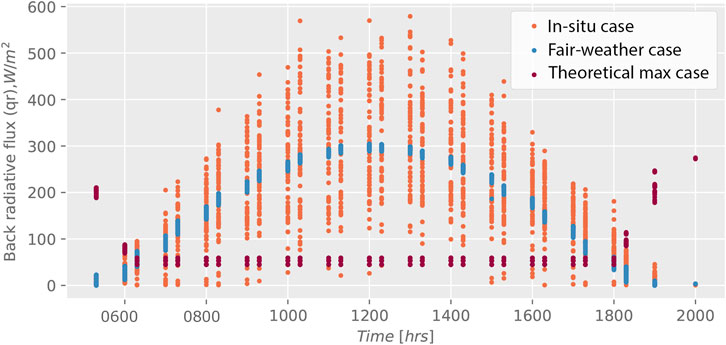
FIGURE 4. Graphical representation of half hourly back-side radiative flux (qr) for 15th June-15th August.

Using results drawn from the three models, graphs were plotted for front and rear side radiative heat flux as shown in Figures 3, 4. These graphs show distribution of radiative heat flux on front and rear side of panels for a total of 5,034 data points spread across 5:30 a.m. to 7:30 p.m. from 15th June to 15th August.

From the graphs, it can be noted that although fair weather and theoretical maximum models over-predict front side radiative heat flux, they under-predict solar load on the rear side of bifacial solar panel. The solar loads calculated with in situ based input show greater dispersion because of changing weather patterns. The graphs also display how theoretical maximum and fair-weather models match only a small percentage of actual solar loads obtained over extended period of time through in situ model. In situ based solar load calculations were compared with theoretical maximum and fair-weather solar loads by applying a tolerance of ±15%. It was found that for front side, fair-weather model overlaps with only 13% of in situ data while theoretical maximum gives non-realistic solar loads, with only 0.5% of its values overlapping in situ data. Similarly, for rear side, fair-weather covers 24% of in situ solar loads while theoretical maximum covers only 2% of in situ rear side solar load. Moreover, Islamabad has a weather pattern that receives a high direct irradiance components during sunny days while it receives high diffuse component for the rainy monsoon season. This study also indicates that in regions which have hot summers with humid rainy weather patterns in between, bifacial modules have higher gains.

The plots in Figures 5, 6, 7 show that radiative transfer from in situ case has the greatest amount of dispersion across days, with a standard deviation of 91.24 against an average of 560 W/m² in daily averages over 2 months. Total radiative flux of theoretical maximum model shows little variation across days, with a standard deviation of 43.18 against an average of 740 W/m² while fair weather model shows almost no variation of total radiative flux with days, with a standard deviation of 20.03 against an average of 683 W/m².

FIGURE 5

FIGURE 5. In situ total radiative flux (qr).

FIGURE 6

FIGURE 6. Fair weather total radiative flux.

FIGURE 7

FIGURE 7. Theoretical maximum total radiative flux.

A comparative graph showing difference between solar ray tracing of fair-weather model and theoretical maximum model with the solar ray tracing of in situ data is drawn in Figure 8.

FIGURE 8

FIGURE 8. Total radiative transfer comparison.

The angular deviation and offset of theoretical maximum total radiative flux from in situ case is 13° and 300W/m² respectively while angular deviation and offset of fair weather total radiative flux from in situ case is 8° and 170W/m² respectively in Figure 8. Although total radiative transfer comparison shows small deviations, the breakdown of total radiative transfer into front and back radiative transfer shows large differences as shown in Figures 9, 10. The reason for large differences between theoretical maximum model and in situ model is the lesser attenuation applied by theoretical maximum model on the normal solar irradiance reaching the atmosphere. Using this model for solar thermal analysis of solar panels can lead to highly inaccurate results. The radiative heat fluxes obtained from fair weather model for the front side are comparable with the ones obtained from in situ data but for a particular time period only i.e., near sun rise and sun set. There is large discrepancy for the rear side solar loads gained through fair-weather model. This is because the fair-weather model, derived from ASHRAE handbook and integrated in commercial and open source software, is based on the data obtained for 21st day of each month during the base year of 1964 (Curcija, 2001).

FIGURE 9

FIGURE 9. Front side radiative transfer comparison.

FIGURE 10

FIGURE 10. Back side radiative transfer comparison.

Two sample z-test was performed in which in situ model was compared against fair weather and theoretical maximum models. The significant value was taken to be 0.01 and p values were calculated for each sample set. The details of two sets are given in Table 3.

TABLE 3

TABLE 3. z-test results.

Since the p-value is less than 0.01 for both sample sets, we have sufficient evidence to reject null hypothesis. In other words, the total radiation transfer is significantly different between the two models. The details of different radiative fluxes calculated from all three models are shown in Table 4.

TABLE 4

TABLE 4. Statistical properties of radiative transfer for different models.

It can be observed that although average total radiative transfer of theoretical maximum and fair-weather cases is more than in situ case, the rear side gain from in situ model is the highest. The average difference between in situ and fair-weather model, from Table 4, for front and rear side radiative flux is approximately 6% and 26% respectively. Similarly, for total radiative flux, the average fair weather radiative flux varies from in situ radiative flux by 18%. As evident through the differences, using both models in solar thermal analysis that expands over long periods of time can lead to large inaccuracies in the results. The theoretical maximum solar load model is seldom used in literature, while the frequent use of fair weather model employed by studies such as Potgieter et al. (2020); Xu et al. (2022) and Zhong and Calautit (2020) is correct only across a limited number of cases. Most of the studies that used fair weather model or solar calculator assumed clear sky conditions in the studied time periods. While such results are accurate for shorter period of times, they are not accurate for an extended period of time, especially in humid-sub tropical regions where summers are marked by the arrival of heavy rainfall season. In such climatic conditions where the weather is often changing from sunny to overcast in a single day, the assumption of clear skies for calculating solar loads can introduce increased errors in the CFD results.

Conclusion

Solar load estimation leading to radiative heat flux, on a bifacial solar panel with constant elevation and albedo, was carried out using three methods over a period of 2 months starting from mid-June to mid -August. The three methods included SOPLOS theoretical maximum and ASHRAE-fair weather solar load models, which are often used in commercial and opensource CFD software. Both methods were compared with the third method, the in situ solar load approach that relies on on-site weather data and which has rarely been employed in previous research. It was found that SOPLOS theoretical maximum and ASHRAE fair weather models over predict front side load, with only 0.5% and 13% matching in situ data respectively while under predict rear side solar load, with 2% and 24% solar load aligning with in situ data respectively. The focus of this study is monsoon season as it is more diverse in solar loads, this can be expanded to a whole year. Additionally, only one albedo for concrete as was considered and tilt angle was maintained at 30°, as both are optimal configurations, however different albedo may be considered for vegetation as well as a broader range of tilt angles.

It was observed that using theoretical maximum and fair-weather models in studies can lead to high inaccuracies during analysis of solar thermal systems. Standard deviation of in situ daily averages was found to be 91.24 against an average of 560 W/m². Therefore, the approach of using daily averages from in situ data is also not accurate since the daily average is not consistent throughout the month. Consequently, the results obtained through these models cannot be generalized for longer time periods, extending over months or years. The use of in situ data in conjunction with solar ray tracing will provide more accurate assessment of irradiance on solar photovoltaic panels.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

BR: Concept, Coding, Calculations, Initial Draft, revision. AS: Coding, Calculations, Initial Draft. MS: Concept, Funding, Data, Resources, Supervision, Initial Draft, Revision. SA: Supervision, Revisions. YA: Supervision, Funding.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Al-Nehari, H. A., Mohammed, M. A., Odhah, A. A., Al-attab, K., Mohammed, B. K., Al-Habari, A. M., et al. (2021). Experimental and numerical analysis of tiltable box-type solar cooker with tracking mechanism. Renew. Energy 180, 954–965. doi:10.1016/j.renene.2021.08.125

CrossRef Full Text | Google Scholar

Arshad, S. M. N., Ayaz, Y., Ali, S., Ansari, A. R., and Nawaz, R. (2022). Experimental study on slosh dynamics estimation in a partially filled liquid container using a low-cost measurement system. IEEE Sens. J. 22, 16212–16222. doi:10.1109/JSEN.2022.3188114

CrossRef Full Text | Google Scholar

Attig-Bahar, F., Sahraoui, M., Guellouz, M. S., and Kaddeche, S. (2019). Effect of the ground heat storage on solar chimney power plant performance in the South of Tunisia: Case of Tozeur. Sol. Energy 193, 545–555. doi:10.1016/j.solener.2019.09.058

CrossRef Full Text | Google Scholar

Chen, M., Zhang, Y., Wang, S., Ali, S., Wang, X., Yang, X., et al. (2022). Bearing-based distributed formation control of unmanned aerial vehicle swarm by quaternion-based attitude synchronization in three-dimensional space. Drones 6 (9), 227. doi:10.3390/DRONES6090227

CrossRef Full Text | Google Scholar

Curcija, D. C. (2001). Chapter 30: Fenestration. ASHRAE HVAC fundamentals-handbook, 674–677.

Google Scholar

Danks, R. (2014). “Applications of large scale solar modeling in the built environment,” in Proceeding. of eSim Conference, Ottawa, Canada, 562–574.

Google Scholar

Desai, A., Mukhopadhyay, I., and Ray, A. (2022). Feasibility assessment of bifacial rooftop photovoltaic systems in the state of Gujarat in India. Front. Energy Res. 10, 620. doi:10.3389/fenrg.2022.869890

CrossRef Full Text | Google Scholar

Ernst, M., Conechado, G. E. J., and Asselineau, C.-A. (2022). Accelerating the simulation of annual bifacial illumination of real photovoltaic systems with ray tracing. iScience 25 (1), 103698. doi:10.1016/j.isci.2021.103698

PubMed Abstract | CrossRef Full Text | Google Scholar

Gu, W., Ma, T., Li, M., Shen, L., and Zhang, Y. (2020). A coupled optical-electrical-thermal model of the bifacial photovoltaic module. Appl. Energy 258, 114075. doi:10.1016/j.apenergy.2019.114075

CrossRef Full Text | Google Scholar

Hadi, J. M., Alturaihi, M. H., Jasim, N. Y., and Habeeb, L. J. (2022). Numerical study of airflow and temperature variations inside car at different solar intensity angles. Mater. Today Proc. 60, 1689–1695. doi:10.1016/j.matpr.2021.12.225

CrossRef Full Text | Google Scholar

Haider, S. A., Sajid, M., Sajid, H., Uddin, E., and Ayaz, Y. (2022). Deep learning and statistical methods for short- and long-term solar irradiance forecasting for Islamabad. Renew. Energy 198, 51–60. doi:10.1016/J.RENENE.2022.07.136

CrossRef Full Text | Google Scholar

Haider, S. A., Sajid, M., Sajid, H., Uddin, E., and Ayaz, Y. (2022). Deep learning and statistical methods for short- and long-term solar irradiance forecasting for Islamabad. Renew. Energy 198, 51–60. doi:10.1016/j.renene.2022.07.136

CrossRef Full Text | Google Scholar

Haurwitz, B. (1946). Insolation in relation to cloud type. J. Meteor. 3 (4), 123–124. doi:10.1175/1520-0469(1946)003<0123:iirtct>2.0.co;2

CrossRef Full Text | Google Scholar

Haurwitz, B. (1945). Insolation in relation to cloudiness and cloud density. J. Meteor. 2 (3), 154–166. doi:10.1175/1520-0469(1945)002<0154:iirtca>2.0.co;2

CrossRef Full Text | Google Scholar

Holmgren, W. F., Hansen, C. W., and Mikofski, M. A. (2018). Pvlib python: a python package for modeling solar energy systems. J. Open Source Softw. 3 (29), 884. doi:10.21105/joss.00884

CrossRef Full Text | Google Scholar

Ineichen, P., Guisan, O., and Perez, R. (1990). Ground-reflected radiation and albedo. Sol. Energy 44 (4), 207–214. doi:10.1016/0038-092x(90)90149-7

CrossRef Full Text | Google Scholar

Iqbal, S., Khan, S. N., Sajid, M., Khan, J., Ayaz, Y., and Waqas, A. (2022). Impact and performance efficiency analysis of grid-tied solar photovoltaic system based on installation site environmental factors. Energy & Environ., 0958305X2211066. doi:10.1177/0958305X22110661810.1177/0958305X221106618

CrossRef Full Text | Google Scholar

Jain, A., Sharma, M., Kumar, A., Sharma, A., and Palamanit, A. (2019). Computational fluid dynamics simulation and energy analysis of domestic direct-type multi-shelf solar dryer. J. Therm. Anal. Calorim. 136 (1), 173–184. doi:10.1007/s10973-018-7973-5

CrossRef Full Text | Google Scholar

Jonsson, J. (2007). “Including solar load in CFD analysis of temperature distribution in a car passenger compartment master of science programme mechanical engineering,” (Lulea, Sweden: Lulea University of Technology). MASTER’S THESIS.

Google Scholar

Joshi, S., Mittal, S., Holloway, P., Shukla, P. R., Ó Gallachóir, B., and Glynn, J. (2021). High resolution global spatiotemporal assessment of rooftop solar photovoltaics potential for renewable electricity generation. Nat. Commun. 12 (1), 5738. doi:10.1038/s41467-021-25720-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Kopecek, R., and Libal, J. (2021). Bifacial photovoltaics 2021: Status, opportunities and challenges. Energies 14 (8). doi:10.3390/en14082076

CrossRef Full Text | Google Scholar

Kuharat, S., and Anwar Bég, O. (2019). Computational fluid dynamics simulation of a nanofluid-based annular solar collector with different metallic nano-particles Kuharat. S Beg. OA Title Comput. fluid Dyn. Simul. a nanofluid-based Annu. Sol. Collect. Differ. me 61 (11), 8943–8953.

Google Scholar

Marceau, M. L., and Vangeem, M. G. (2008). PCA R&D SN2982a solar reflectance values of concrete. skokie illinois: permission of Concrete International 2008.

Google Scholar

Moon, J. H., Lee, J. W., Jeong, C. H., and Lee, S. H. (2016). Thermal comfort analysis in a passenger compartment considering the solar radiation effect. Int. J. Therm. Sci. 107, 77–88. doi:10.1016/j.ijthermalsci.2016.03.013

CrossRef Full Text | Google Scholar

Noorian, A. M., Moradi, I., and Kamali, G. A. (2008). Evaluation of 12 models to estimate hourly diffuse irradiation on inclined surfaces. Renew. energy 33 (6), 1406–1412. doi:10.1016/j.renene.2007.06.027

CrossRef Full Text | Google Scholar

OpenFoam.com, (2022). OpenFOAM: API Guide: OpenFOAM: Open source CFD: API. https://www.openfoam.com/documentation/guides/v2112/api/index.html (Accessed November 4, 2022).

Google Scholar

Patidar, A. (2009). “Simulation and validation of passenger compartment soaking and cooling under solar load,” in International Mobility Engineering Congress and Exposition, Chennai , India.

CrossRef Full Text | Google Scholar

Pelaez, S. A., and Deline, C. (2020). bifacial\_radiance: a python package for modeling bifacial solar photovoltaic systems. J. Open Source Softw. 5 (50), 1865. doi:10.21105/joss.01865

CrossRef Full Text | Google Scholar

Perez, R., Ineichen, P., Seals, R., Michalsky, J., and Stewart, R. (1990). Modeling daylight availability and irradiance components from direct and global irradiance. Sol. Energy 44 (5), 271–289. doi:10.1016/0038-092X(90)90055-H

CrossRef Full Text | Google Scholar

Photovoltaic Energy Factsheet, (2021). Photovoltaic energy Factsheet. Ann Arbor, MI: Center for Sustainable Systems, University of Michigan.

Google Scholar

Potgieter, M. S. W., Bester, C. R., and Bhamjee, M. (2020). Experimental and CFD investigation of a hybrid solar air heater. Sol. Energy 195, 413–428. doi:10.1016/j.solener.2019.11.058

CrossRef Full Text | Google Scholar

Reda, I., and Andreas, A. (2004). Solar position algorithm for solar radiation applications. Sol. Energy 76 (5), 577–589. doi:10.1016/j.solener.2003.12.003

CrossRef Full Text | Google Scholar

Robinson, D., and Stone, A., “Irradiation modelling made simple: The cumulative sky approach and its applications,” in PLEA conference, 2004. 19–22. Santiago, Chile

Google Scholar

Shah, M. A. H., Butt, H., Farooq, M., Ihsan, M. N., Sajid, M., and Uddin, E. (2020). Development of a truncated ellipsoidal reflector-based metal halide lamp solar simulator for characterization of photovoltaic cells. Energy Sources Part A Recovery Util. Environ. Eff. 43 (20), 1–15. doi:10.1080/15567036.2020.184255710.1080/15567036.2020.1842557

CrossRef Full Text | Google Scholar

Soomar, A. M., Hakeem, A., Messaoudi, M., Musznicki, P., Iqbal, A., and Czapp, S. (2022). Solar photovoltaic energy optimization and challenges. Front. Energy Res. 10, 445. doi:10.3389/fenrg.2022.879985

CrossRef Full Text | Google Scholar

Spark, W. (2016). Cloud cover categories in the summer in Islamabad. Islamabad, Pakistan: Weather Spark.

Google Scholar

Sun, L., Lu, L., and Yang, H. (2012). Optimum design of shading-type building-integrated photovoltaic claddings with different surface azimuth angles. Appl. Energy 90 (1), 233–240. doi:10.1016/j.apenergy.2011.01.062

CrossRef Full Text | Google Scholar

Sun, X., Khan, M. R., Deline, C., and Alam, M. A. (2018). Optimization and performance of bifacial solar modules: A global perspective. Appl. Energy 212, 1601–1610, Nov. doi:10.1016/j.apenergy.2017.12.041

CrossRef Full Text | Google Scholar

Engineering ToolBox (2009). Absorbed Solar Radiation. Available at: https://www.engineeringtoolbox.com/solar-radiation-absorbed-materials-d_1568.html (Accessed November 4, 2022).

Google Scholar

Wang, S., Wilkie, O., Lam, J., Steeman, R., Zhang, W., Khoo, K. S., et al. (2015). Bifacial photovoltaic systems energy yield modelling. Energy Procedia 77, 428–433. doi:10.1016/j.egypro.2015.07.060

CrossRef Full Text | Google Scholar

Wang, Y., Yanarates, C., and Zhou, Z. (2022). External current source–based unilluminated PV partial shading emulation system verified through the hybrid global search adaptive perturb and observe MPPT algorithm. Front. Energy Res. 10, 281. doi:10.3389/fenrg.2022.868951

CrossRef Full Text | Google Scholar

Ward, G. J. (1994). “The RADIANCE lighting simulation and rendering system,” in 21st annual conference on Computer graphics and interactive techniques, New York, N.Y, United States, 459–472. doi:10.1145/192161.192286

CrossRef Full Text | Google Scholar

Xu, K., Guo, X., He, J., Yu, B., Tan, J., and Guo, Y. (2022). A study on temperature spatial distribution of a greenhouse under solar load with considering crop transpiration and optical effects. Energy Convers. Manag. 254, 115277. doi:10.1016/j.enconman.2022.115277

CrossRef Full Text | Google Scholar

Yang, D. (2016). Solar radiation on inclined surfaces: Corrections and benchmarks. Sol. Energy 136, 288–302. doi:10.1016/j.solener.2016.06.062

CrossRef Full Text | Google Scholar

Yusufoglu, U. A., Pletzer, T. M., Koduvelikulathu, L. J., Comparotto, C., Kopecek, R., and Kurz, H. (2015). Analysis of the annual performance of bifacial modules and optimization methods. IEEE J. Photovoltaics 5 (1), 320–328. doi:10.1109/JPHOTOV.2014.2364406

CrossRef Full Text | Google Scholar

Zeeshan, M., Ali, Z., and Din, E. U. (2022). Thermal performance prediction of street trees inside isolated open spaces – evaluations from real scale retrofitting project. J. Build. Perform. Simul. 0 (0), 1–17. doi:10.1080/19401493.2022.2038270

CrossRef Full Text | Google Scholar

Zhao, C., Xiao, J., Yu, Y., and Jaubert, J.-N. (2021). Accurate shading factor and mismatch loss analysis of bifacial HSAT systems through ray-tracing modeling. Sol. Energy Adv. 1, 100004. doi:10.1016/j.seja.2021.100004

CrossRef Full Text | Google Scholar

Zhong, F., and Calautit, J. (2020). An integrated cooling jet and air curtain system for stadiums in hot climates. Atmos. (Basel). 11 (5), 546. doi:10.3390/atmos11050546

CrossRef Full Text | Google Scholar