Prabhakar fractional derivative model of sodium alginate (C6H9NaO7) for accelerated plate motions

The Prabhakar fractional derivative model is not studied in the open literature for the Casson fluid model when the vertical plate exhibits linear and quadratic translations with constant heating. Therefore, this study deals with the thermal transport of sodium alginate (C₆H₉NaO₇) over a vertical plate with a constant temperature. Since the classical PDEs are incapable of analyzing and investigating the physical impact of flow variables with memory effects, a fractional derivative model is developed using the Prabhakar fractional derivative approach. Two different types of plate translations (linear and quadratic) are considered. The non-dimensional governing equations are transformed into a fractional model and solved using the Laplace transformation (L.T) technique. The effects and behavior of significant physical parameters and fractional order parameters are studied graphically and discussed. As a consequence, it is found that as fractional limitations are increased, the thermal and momentum profiles drop. In addition, the momentum profile in the case of quadratic translation (variable acceleration) shows a higher magnitude than the case of linear translation (constantly accelerated plate).

Introduction

When it comes to non-Newtonian fluid flow mechanics, engineers, physicists, and mathematicians face a unique challenge. Because these fluids are so complex, no constitutive equation can depict all of their features. Instead, various non-Newtonian fluid models have been planned as part of the process. Viscoelastic fluids, in particular, have attracted researchers’ interest. This category includes the great majority of non-Newtonian fluids discussed in the collected works, such as the power law and grade two or three fluids (Andersson et al., 1992; Hassanien, 1996; Sadeghy and Sharifi, 2004; Sajid et al., 2007). These basic fluid models include flaws that cause them to provide findings that do not correspond to actual fluid flows. Power-law fluids are the most often used model for modeling non-Newtonian fluid dynamics. The model predicts shear-thinning and shear-thickening behaviors. However, it is insufficient for demonstrating the typical stress behavior in various non-Newtonian fluids, such as die swelling and the rod-climbing behavior. The second-grade fluid model is the simplest subclass of viscoelastic fluids for which an analytic solution is likely. Normal stress effects may be depicted in a second-grade fluid model, which is a subset of Rivlin–Ericksen fluids, albeit shear thinning/thickening is not supported (Aksoy et al., 2007). Non-Newtonian fluids are classified into three types: differential, rate, and integral fluids. The Maxwell model, which can predict stress relaxation, is the most fundamental subclass of rate-type fluids. As a result, this rheological model avoids the need for boundary layer analysis when dealing with the complicated consequences of shear-dependent viscosity (Hayat et al., 2011). Non-Newtonian fluids include the Casson fluid. The Casson fluid has a high yield stress. It is a shear-thinning liquid with an infinite viscosity at zero rates of shear, a yield stress below which no flow occurs, and a zero viscosity at an infinite rate of shear, which means that if shear stress is less, then the yield stress is applied to the fluid; it behaves like a solid, but if shear stress is greater than the yield stress is applied to the fluid, it begins to move. Casson fluids include jelly, tomato sauce, honey, soup, concentrated fruit liquids, and similar goods. Casson fluids may also be made from human blood. Because of several components in the aqueous base plasma such as protein, fibrinogen, and globulin, human red blood cells can form a chainlike structure known as aggregates or rouleaux. If the rouleaux act like a plastic solid, the yield stress corresponds to Casson fluids’ constant yield stress (Chuong and Fung, 1986). The Casson fluid is a shear-thinning liquid with a zero at the zero shear rate, an infinite viscosity at the zero shear rate, and yield stress below which no flow occurs (Dash et al., 1996). (Archana et al. 2017) studied the effect of nonlinear thermal radiation, Joule heating, and magnetic field on a spinning Casson nano liquid stream. When considering the stream of non-Newtonian micro liquids due to heat transfer in the presence of a permeable surface, (Nadeem et al. 2014) explored the stagnation point problem. (Li et al. 2022) investigated the rotating stream of the Casson nano liquid due to the impacts of MHD and the Cattaneo–Christov heat flux in the presence of double diffusion heat flux using a finite element model. (Haq et al. 1988) investigated the flow of the Casson nano liquid with the effects of heat transfer and MHD in the presence of a shrinking sheet while accounting for the convective boundary. (Alwawi et al. 2009) examined the flow of the Casson micro liquid with heat transfer induced by Lorentz force coupled convection using KBM while taking CMC water into account. (Sivaraj et al. 2019) investigated cross-diffusion effects on the Casson fluid flow using variable fluid properties. (Durairaj et al. 2017) examined the strong effects of the heat generating or absorbing and chemically reacting Casson fluid flow over a vertical cone and flat plate saturated in a non-Darcy porous medium. (Jasmine Benazir et al. 2016) studied a deep comparison between the Casson fluid flow when heat and mass transfer are taken over a vertical cone and a flat plate. (Mythili and Sivaraj 2016) considered two geometries of the vertical cone and flat plate and studied the effects of higher-order chemical reactions and the non-uniform heat source/sink on the non-Newtonian Casson fluid flow.

Numerous studies have broadly carried out fractional calculus in recent years because of its capability to explain the reminiscence effects of different physical processes. Nowadays, fractional calculus has been efficiently implemented in many science fields, including rheology, viscoelasticity, biophysics, bioengineering, sign principle, picture processing, physics, and control ideas(Raza et al., 2022; Wang et al., 2022). Many theoretical and practical problems described by mathematical models with fractional differential equations have been investigated. Among the several functions in the fractional calculus, the Mittag–Leffler function is considered the important one. In 1971, Tilak Raj Prabhakar proposed a three-parameter generalization of the Mittag–Leffler function, also known as the Prabhakar function. Recently, the Prabhakar fractional derivative along with the non-singular Mittag–Leffler kernel has influenced many authors (Panchal et al., 2016; Polito and Tomovski, 2016; Sandev, 2017; Giusti and Colombaro, 2018; Garrappa and Kaslik, 2020; Asjad et al., 2021; Basit et al., 2021), working with fractional derivatives due to its applications in many real-world problems. Fractional differential classifications through the Prabhakar derivative with a solid discipline were investigated by (Alidousti and Ghafari 2020). (Derakhshan et al. 2019) described a new numerical technique for solving variable-order fractional integro-differential equations in (Samraiz et al., 2020) fractional derivatives of non-Newtonian fluids in the convection channel with hybrid nanoparticles, which have been mentioned in (Asjad et al. 2020). A few other interesting studies on fractional derivatives are given in the literature (Khan et al., 2017; Ali, 2018; Khan et al., 2020; Saqib et al., 2020). However, (Abdal et al. 2021), (Bilal et al. 2022), and (Qureshi et al. 2022) investigated different fluid models and reported very interesting results.

The aforementioned literature shows that the Prabhakar fractional derivative model, by taking into account linear translation and quadratic translation, is not studied for the Casson fluid model. Therefore, in this work, an attempt is made. More exactly, in this work, the Casson-type fluid flow is considered over a vertical plate with a constant temperature. Both constant and variable acceleration cases are discussed. The momentum and temperature equations are first transformed into a fractional model with an excellent fractional definition known as the Prabhakar fractional derivative and then solved via L.T. The results are obtained for both types of translations (linear and quadratic) and then computed in tables and plotted in various graphs.

Problem description

Consider an unsteady, incompressible free-convection Casson fluid’s flow on an infinite vertical plate. It is supposed that at $\tau \le 0$, the system is at rest with constant temperature ${\theta }_{\infty }$. At the time $\tau >0$, the stationary plate starts to move with a translation velocity $v\left(0,\tau \right)=A\tau$, and the temperature of the plate raised from ${\theta }_{\infty }\mathrm{to}{\theta }_w$. The flow is incompressible, one-dimensional, and one-directional and depends on time. The initial fluid motion is vertical and regulated by the partial differential equations (velocity and energy equations) (Sandev, 2017; Derakhshan et al., 2019; Alidousti and Ghafari, 2020; Asjad et al., 2020; Garrappa and Kaslik, 2020).

$\rho \frac{\partial v_{\left(\eta ,\tau \right)}}{\partial \tau }=\mu \left(1+\frac{1}{{\beta }_o}\right)\frac{{\partial }^2{v}_{\left(\eta ,\tau \right)}}{\partial {\eta }^2}+g\rho {\beta }_{\theta }\left({\theta }_{\left(\eta ,\tau \right)}-{\theta }_{\infty }\right)(1)$

$\rho C_p\frac{\partial {\theta }_{\left(\eta ,\tau \right)}}{\partial \tau }=-\frac{\partial {\delta }_{\left(\eta ,\tau \right)}}{\partial \eta },(2)$

${\delta }_{\left(\eta ,\tau \right)}=-k\frac{\partial {\theta }_{\left(\eta ,\tau \right)}}{\partial \eta }.(3)$

The imposed initial and boundary conditions are as follows:

$\begin{array}{c}v\left(\eta ,0\right)=0,\theta \left(\eta ,0\right)={\theta }_{\infty }\\ \\ v\left(0,\tau \right)=A\tau ,\theta \left(0,\tau \right)={\theta }_w\\ \\ v\left(\infty ,\tau \right)=0,\theta \left(\infty ,\tau \right)={\theta }_{\infty }\\ \end{array}\},(4)$

where $\rho$ is the density, $v\left(\eta ,\tau \right)$ is the x-component of the velocity vector, $\mu$ is the dynamic viscosity, $g$ is the gravitational acceleration, ${\beta }_{\theta }$ is the volumetric thermal expansion, $\theta \left(\eta ,\tau \right)$ is the x-component of the temperature vector, $c_p$ is the heat capacitance, and k is the thermal conductivity of the fluid. It should be noted that the constitutive equation for an incompressible Casson fluid is given in Eq. 2 of (Alidousti and Ghafari 2020); therefore, it is not included in this study to avoid similarity.

To eliminate the units, the dimensionless variables listed as follows are put into Eqs. 1–4.

$v^{*}=\frac{v}{{vA}^{1/3}},{\eta }^{*}=\frac{\eta A^{1/3}}{v^{2/3}},{\tau }^{*}=\frac{\tau A^{2/3}}{v^{1/3}},{\theta }^{*}\left(\eta ,\tau \right)=\frac{\theta -{\theta }_{\infty }}{{\theta }_w-{\theta }_{\infty }}=\frac{\theta -{\theta }_{\infty }}{∆\theta }.$

${\delta }_{\left(\eta ,\tau \right)}^{*}=\frac{v^{2/3}}{k{A}^{1/3}∆\theta }{\delta }_{\left(\eta ,\tau \right)}.(5)$

Our dimensionless problem takes the form ($*\mathrm{s}\mathrm{y}\mathrm{m}\mathrm{b}\mathrm{o}\mathrm{l}\mathrm{i}\mathrm{s}\mathrm{d}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{p}\mathrm{e}\mathrm{d}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{s}\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{y}$)

$\frac{\partial v_{\left(\eta ,\tau \right)}}{\partial \tau }=\left(1+\frac{1}{{\beta }_o}\right)\frac{{\partial }^2{v}_{\left(\eta ,\tau \right)}}{\partial {\eta }^2}+Gr{\theta }_{\left(\eta ,\tau \right)},(6)$

$\mathrm{Pr}\frac{\partial {\theta }_{\left(\eta ,\tau \right)}}{\partial \tau }=-\frac{\partial {\delta }_{\left(\eta ,\tau \right)}}{\partial \eta },(7)$

$-\frac{\partial {\theta }_{\left(\eta ,\tau \right)}}{\partial \eta }={\delta }_{\left(\eta ,\tau \right)},(8)$

$v_{\left(\eta ,0\right)}=0,v_{\left(0,\tau \right)}=\tau ,v_{\left(\infty ,\tau \right)}=0,$

${\theta }_{\left(\eta ,0\right)}=0,{\theta }_{\left(0,\tau \right)}=1,{\theta }_{\left(\infty ,\tau \right)}=0,$

where $\mathrm{Pr}=\mu C_p/k,Gr=g{\beta }_{\theta }\Delta \theta /A$.

We presented an effective fractional mathematical model for the calculation of momentum and heat equations with the help of the Prabhakar fractional derivative, which can be expressed mathematically as (Asjad et al., 2020; Wang et al., 2022)

${}_{}{}^C{\mathfrak{D}}_{\alpha ,\beta ,\alpha }^{\gamma }h\left(t\right)=E_{\alpha ,n,-\beta ,\alpha }^{-\gamma }{h}^n\left(t\right)=e_{\alpha ,n,-\beta }^{-\gamma }\left(\alpha ;t\right)*h^n\left(t\right),$

$={{\displaystyle \int }}_0^t{\left(t-\tau \right)}^{n-\beta -1}{E}_{\alpha ,n,-\beta }^{-\gamma }\left(\alpha {\left(t-\tau \right)}^{\alpha }\right)h^n\left(\tau \right)d\tau ,$

where ${}_{}{}^C{\mathfrak{D}}_{\alpha ,\beta ,\alpha }^{\gamma },h^{\left(n\right)}$ represents the Prabhakar fractional operator with the nth derivative of $h\left(t\right)\in A{C}^n\left(0,b\right),A{C}^n\left(0,b\right),$ respectively, and

$E_{\alpha ,\beta ,\alpha }^{\gamma }h\left(t\right)={{\displaystyle \int }}_0^t{\left(t-\tau \right)}^{\beta -1}{E}_{\alpha ,\beta }^{-\gamma }\left(\alpha {\left(t-\tau \right)}^{\alpha }\right)h\left(\tau \right)d\tau$

is identified as the Prabhakar integral with

$E_{\alpha ,\beta }^{\gamma }\left(z\right)={\displaystyle \sum }_{m=0}^{\infty }\frac{\mathrm{\Gamma }\left(\gamma +m\right)z^m}{m!\mathrm{\Gamma }\left(\gamma \right)\mathrm{\Gamma }\left(\alpha m+\beta \right)}$

which is of the three-parametric Mittag–Leffler function, and $e_{\alpha ,\beta }^{\gamma }\left(\alpha ;t\right)=t^{\beta -1}{E}_{\alpha ,\beta }^{\gamma }\left(\alpha t^{\alpha }\right)$ is the Prabhakar kernel. The L.T of the Prabhakar fractional derivative operator ${}_{}{}^C{\mathfrak{D}}_{\alpha ,\beta ,\alpha }^{\gamma }$ is

$\mathcal{L}\left[{}_{}{}^C{\mathfrak{D}}_{\alpha ,\beta ,\alpha }^{\gamma }\mathrm{h}\left(t\right)\right]=\mathcal{L}\left[h^m\left(t\right)*e_{\alpha ,m-\beta }^{-\gamma }\left(\alpha ;t\right)\right]=\mathcal{L}\left\{h^m\left(t\right)\right\}\mathcal{L}\left\{e_{\alpha ,m-\beta }^{-\gamma }\left(\alpha ;t\right)\right\}$

$=\mathcal{L}\left\{h^m\left(t\right)\right\}{s}^{\beta -m}{\left(1-\alpha s^{-\alpha }\right)}^{\gamma }.(9)$

Then, by taking $\beta =\gamma =0$, we may derive the traditional Fourier’s law. Also, because the Prabhakar fractional derivative is primarily dependent on Fourier’s law of thermal conductivity, the Fourier law in the form of the Prabhakar fractional derivative is

${\delta }_{\left(\eta ,\tau \right)}=-k{}_{}{\mathfrak{D}}_{\alpha ,\beta ,\alpha }^{-\gamma }\frac{\partial {\theta }_{\left(\eta ,\tau \right)}}{\partial \eta }.(10)$

Solution to the problem

a. Solution to the temperature field

As the energy equation involves Fourier’s thermal flux law, by utilizing the L.T scheme to Eqs. 7–10 for the solution to the temperature profile and its matching conditions, we obtain

$\mathrm{Pr}q{\overline{\theta }}_{\left(\eta ,q\right)}=-\frac{\partial {\overline{\delta }}_{\left(\eta ,q\right)}}{\partial \eta },(11)$

${\overline{\delta }}_{\left(\eta ,q\right)}=-q^{\beta }{\left(1-\alpha q^{-\alpha }\right)}^{\gamma }\frac{\partial {\overline{\theta }}_{\left(\eta ,q\right)}}{\partial \eta },(12)$

${\overline{\theta }}_{\left(0,q\right)}=\frac{1}{q},{\overline{\theta }}_{\left(\eta ,s\right)}\to 0;\eta \to \infty .(13)$

Inserting Eq. 12 into Eq. 11, for the solution to the temperature field, we have

$\frac{{\partial }^2{\overline{\theta }}_{\left(\eta ,q\right)}}{\partial {\zeta }^2}-\frac{\mathit{Pr}q}{q^{\beta }{\left(1-\alpha q^{-\alpha }\right)}^{\gamma }}{\overline{\theta }}_{\left(\eta ,q\right)}=0.(14)$

By introducing the aforementioned conditions 13) in Eq. 14, the solution of the thermal profile takes the form as follows:

${\overline{\theta }}_{\left(\eta ,q\right)}=\frac{1}{q}{e}^{-\eta \sqrt{\frac{\mathit{Pr}q}{q^{\beta }{\left(1-\alpha q^{-\alpha }\right)}^{\gamma }}}}.(15)$

The aforementioned exponential equation in the summation form is as follows:

${\overline{\theta }}_{\left(\eta ,q\right)}=\frac{1}{q}+{\displaystyle \sum }_{i=1}^{\infty }{\displaystyle \sum }_{J=0}^{\infty }\left(\begin{array}{c}-\frac{i\gamma }{2}\\ \\ J\end{array}\right)\frac{{\left(-\eta \right)}^i{\left(\mathit{Pr}\right)}^{i/2}}{i!}\frac{q^{-i\left(\beta -1\right)/2}}{{\alpha }^J{q}^{\left(1+\alpha J\right)}},$

with its Laplace inverse as follows:

${\theta }_{\left(\eta ,\tau \right)}=1+{\sum }_{i=1}^{\infty }{\sum }_{J=0}^{\infty }\left(\begin{array}{c}-\frac{i\gamma }{2}\\ \\ J\end{array}\right)\frac{{\left(-\eta \right)}^i{\left(\mathit{Pr}\right)}^{i/2}}{i!{\alpha }^J}\frac{{\tau }^{-1+\left(1+\alpha J\right)+i\left(\beta -1\right)/2}}{\mathrm{\Gamma }\left(\left(1+\alpha J\right)+i\left(\beta -1\right)/2\right)}.$

b. Classical solution to the temperature field $\left(\mathit{\beta }=\mathit{\gamma }=\mathbf{0}\right)$

For the classical thermal profile, take $\beta =\gamma =0$, so

$\mathcal{L}\left[e_{\alpha ,0}^0\left(\alpha ;t\right)\right]=1=\delta \left(t\right).$

$\delta \left(t\right)$ denotes the Dirac’s delta distribution. Using this connection, generalized Fourier’s law will be turned into classical Fourier’s law and

${\overline{\theta }}_{\left(\eta ,q\right)}=\frac{1}{q}{e}^{-\eta \sqrt{\mathit{Pr}q}},(16)$

with its Laplace inverse

${\theta }_{\left(\eta ,\tau \right)}=\mathrm{E}\mathrm{r}\mathrm{f}\mathrm{c}\left[\frac{\sqrt{\mathrm{Pr}}\eta }{2\sqrt{t}}\right],\sqrt{\mathrm{Pr}}\eta >0.$

c. Solution to the velocity field

First case

The solution to the velocity profile will be determined in this section using the same approach as the approach to the energy equation. We obtain this by applying the L.T technique to Eq. 6 and its accompanying conditions.

$q{\overline{v}}_{\left(\eta ,q\right)}={\beta }_1\frac{{\partial }^2{\overline{v}}_{\left(\eta ,q\right)}}{\partial {\eta }^2}+Gr{\overline{\theta }}_{\left(\eta ,q\right)};{\beta }_1=1+\frac{1}{{\beta }_o},(17)$

${\overline{v}}_{\left(0,q\right)}=\frac{1}{q^2},{\overline{v}}_{\left(\eta ,\tau \right)}=0,\eta \to \infty .(18)$

Using the aforementioned conditions of Eq. 18, the solution of the momentum equation is as follows:

${\overline{v}}_{\left(\eta ,q\right)}=\frac{1}{q^2}{e}^{-\eta \sqrt{\frac{q}{{\mathrm{\beta }}_1}}}+\frac{Gr}{{\mathrm{\beta }}_{1}q}\frac{1}{\mathit{Pr}q/q^{\beta }{\left(1-\alpha q^{-\alpha }\right)}^{\gamma }-q/{\mathrm{\beta }}_1}\left(\frac{e^{-\eta \sqrt{\frac{q}{{\mathrm{\beta }}_1}}}}{q}-\frac{e^{-\eta \sqrt{\frac{\mathit{Pr}q}{q^{\beta }{\left(1-\alpha q^{-\alpha }\right)}^{\gamma }}}}}{q}\right).(19)$

Inverting the exponential form into the summation form, the velocity becomes as follows:

${\overline{v}}_{\left(\eta ,q\right)}={\displaystyle \sum }_{n=0}^{\infty }\frac{{\left(-y\right)}^n{\left({\beta }_1\right)}^{-n/2}}{n!}{q}^{n/2-1}-B_1{\displaystyle \sum }_{n=1}^{\infty }{\displaystyle \sum }_{m=0}^{\infty }\left(\begin{array}{c}-\frac{n\gamma }{2}\\ \\ m\end{array}\right)\frac{{\left(-y\right)}^n{\left(\mathit{Pr}\right)}^{n/2}}{n!}\frac{q^{n\left(\beta -1\right)/2}}{{\alpha }^m{q}^{1+\alpha m}},(20)$

with its Laplace inverse

$v_{\left(\eta ,\tau \right)}={\displaystyle \sum }_{n=0}^{\infty }\frac{{\left(-y\right)}^n{\left({\beta }_1\right)}^{-n/2}}{n!}\frac{{\tau }^{-n/2}}{\mathrm{\Gamma }\left(1-\frac{n}{2}\right)}-B_1{\displaystyle \sum }_{n=1}^{\infty }{\displaystyle \sum }_{m=0}^{\infty }\left(\begin{array}{c}-\frac{n\gamma }{2}\\ \\ m\end{array}\right)\frac{{\left(-y\right)}^n{\left(\mathit{Pr}\right)}^{n/2}}{n!}\frac{{\tau }^{\alpha m-n\left(\beta -1\right)/2}}{\mathrm{\Gamma }\left(1+\alpha m-n\left(\beta -1\right)/2\right)}.(21)$

Second case

In this case, the imposed initial and boundary conditions are as follows:

$\begin{array}{c}v\left(\eta ,0\right)=0,\theta \left(\eta ,0\right)={\theta }_{\infty }\\ \\ v\left(0,\tau \right)=B{\tau }^2,\theta \left(0,\tau \right)={\theta }_w\\ \\ v\left(\infty ,\tau \right)=0,\theta \left(\infty ,\tau \right)={\theta }_{\infty }\\ \end{array}\}.(22)$

By introducing the following dimensionless variables

$v^{*}=\frac{v}{{\left(v^{2}B\right)}^{1/5}},{\eta }^{*}=\frac{\eta B^{1/5}}{v^{3/5}},{\tau }^{*}=\frac{\tau B^{2/5}}{v^{1/5}},Gr=\frac{g{\beta }_{\theta }\Delta \theta }{B^{1/5}{v}^{1/5}},{\delta }_{\left(\eta ,\tau \right)}^{*}=\frac{v^{3/5}}{k{B}^{1/5}∆\theta }{\delta }_{\left(\eta ,\tau \right)}(23)$

into the governed Eqs. 1–3 and respective conditions in Eq. 22, in which the only condition of quadratic translation transforms to $v\left(0,\tau \right)={\tau }^2,$ rest of the conditions in Eq. 22 remain the same. After Laplace transformation, the momentum equation takes the form:

$\frac{{\partial }^2{\overline{v}}_{\left(\eta ,q\right)}}{\partial {\eta }^2}-\frac{q}{{\beta }_1}{\overline{v}}_{\left(\eta ,q\right)}=-\frac{Gr}{{\beta }_1}{\overline{\theta }}_{\left(\eta ,q\right)}$

with

$\overline{v}\left(0,q\right)=\frac{2}{q^3},\overline{v}\left(\infty ,q\right)=0.$

By utilizing these conditions, the solution to the momentum profile will become

${\overline{v}}_{\left(\eta ,q\right)}=\frac{2}{q^3}{e}^{-\eta \sqrt{\frac{q}{{\mathrm{\beta }}_1}}}+\frac{Gr}{{\mathrm{\beta }}_{1}q}\frac{1}{\frac{\mathit{Pr}q}{q^{\beta }{\left(1-\alpha q^{-\alpha }\right)}^{\gamma }}-\frac{q}{{\mathrm{\beta }}_1}}\left(\frac{e^{-\eta \sqrt{\frac{q}{{\mathrm{\beta }}_1}}}}{q}-\frac{e^{-\eta \sqrt{\frac{\mathit{Pr}q}{q^{\beta }{\left(1-\alpha q^{-\alpha }\right)}^{\gamma }}}}}{q}\right),(24)$

with its Laplace inverse

$v_{\left(\eta ,\tau \right)}=2{\tau }^2+{\displaystyle \sum }_{n=0}^{\infty }\frac{{\left(-y\right)}^n{\left({\beta }_1\right)}^{-n/2}}{n!}\frac{1}{\Gamma \left(1-n/2\right){\tau }^{n/2+1}}-B_1{\displaystyle \sum }_{n=1}^{\infty }{\displaystyle \sum }_{m=0}^{\infty }\left(\begin{array}{c}-\frac{n\gamma }{2}\\ \\ m\end{array}\right)\frac{{\left(-y\right)}^n{\left(\mathit{Pr}\right)}^{n/2}}{n!}\frac{{\tau }^{\alpha m}}{\mathrm{\Gamma }\left(1+\alpha m-n\left(\beta -1\right)/2\right){\tau }^{n\left(\beta -1\right)/2}}.(25)$

Skin friction and Nusselt number

The skin friction for the Casson fluid is given by

$C_f={\beta }_1{\frac{\partial v\left(\eta ,\tau \right)}{\partial \eta }|}_{\eta =0}.(26)$

Similarly, the Nusselt number, which is the heat transfer rate, can be written as follows:

$Nu=-{\frac{\partial \theta \left(\eta ,\tau \right)}{\partial \eta }|}_{\eta =0}.(27)$

Discussion of results

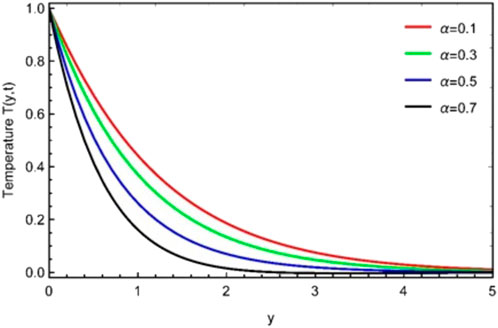
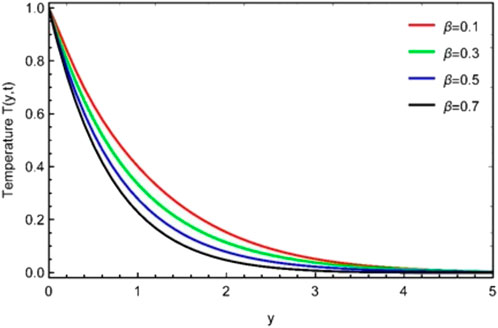
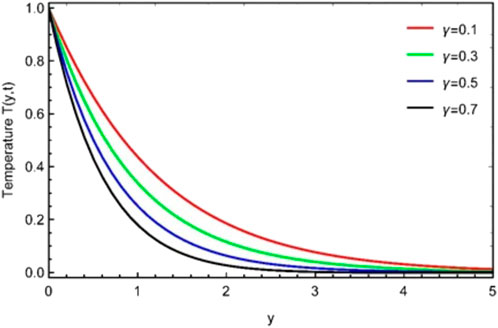
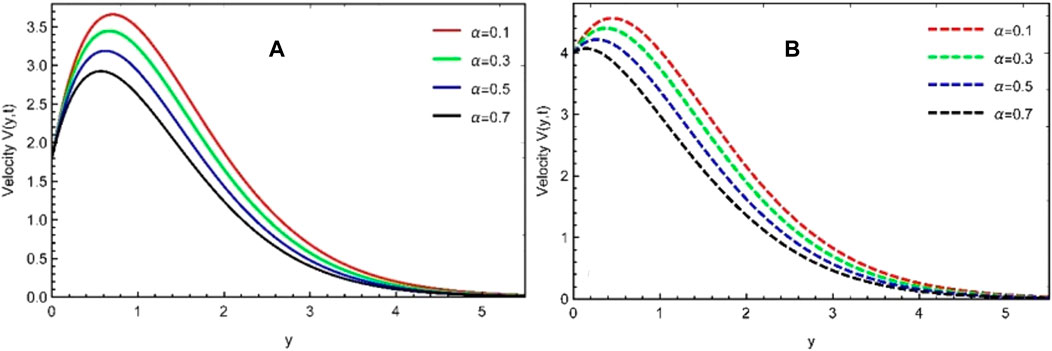
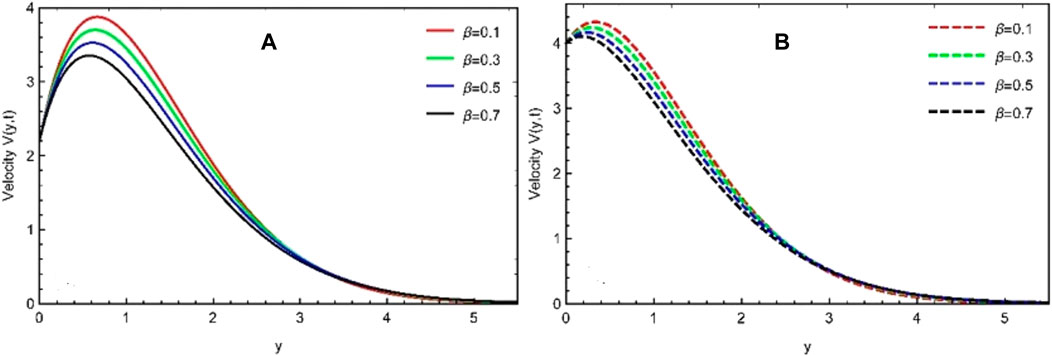
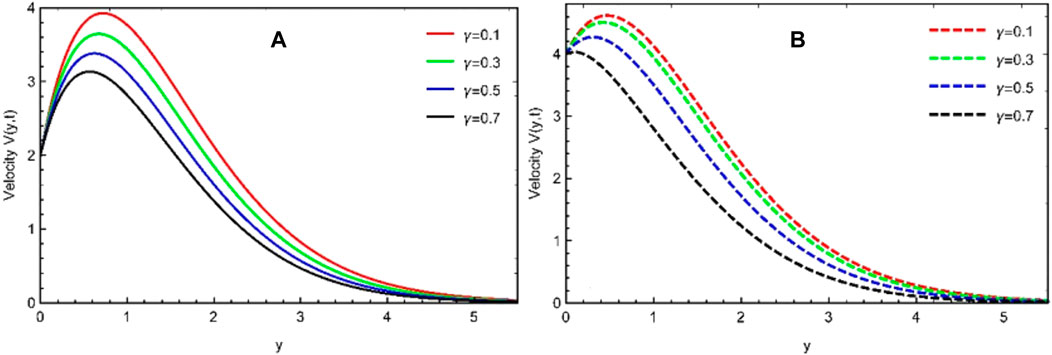
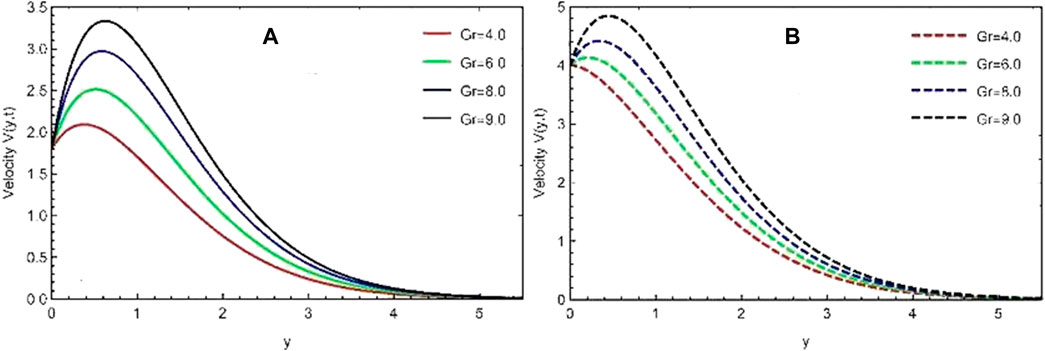
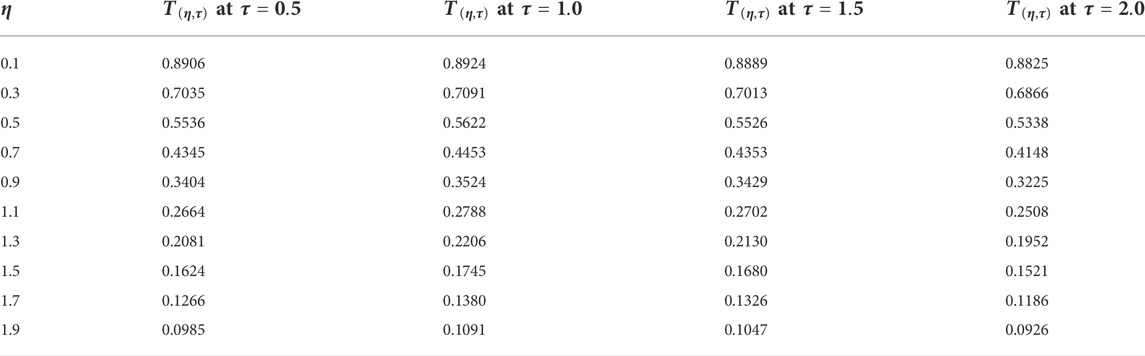
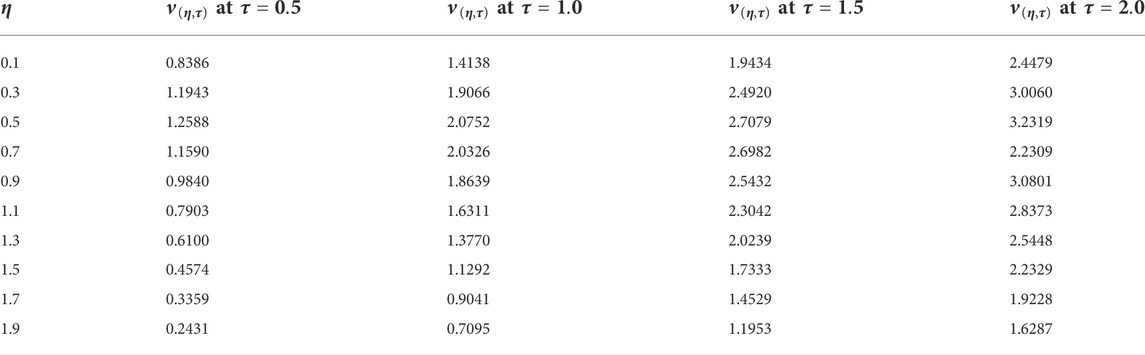
This study examines the unsteady, viscous, and incompressible flow of the Casson fluid over an erected vertical plate. The plate is given a translation motion, whereas the temperature is kept constant. The problem is first converted into the fractional form using an efficient mathematical fractional definition, known as the Prabhakar fractional derivative, and then solved by the Laplace transform technique. The results are displayed graphically and in tabular form for various flow parameters and fractional order parameters, as shown in Figures 1–8. The impacts of fractional parameters α, β, and γ for the temperature profile are explored in Figures 1–3. It is shown that by increasing the values of fractional parameters α, β, and γ, velocity decreases in each case. It should be noted that, due to the non-Newtonian behavior of sodium alginate (C₆H₉NaO₇), the Prandtl number is chosen as Pr = 11.4. It should be noted that in these Figures 4–8, in the first velocity profile (a), the graph is plotted for the constantly accelerated plate (linear translation), and in the second velocity profile (b), the graph is plotted for the variable accelerated plate (quadratic translation). Figures 4–6 are plotted to investigate the effects of fractional parameters α, β, and γ on the momentum profile, and again, it is noted that by varying the estimations of α, β, and γ, velocity is reduced, an identical behavior that is observed in the case of the temperature profile (Figures 1–3). It is further noted that in the case of linear translation (constantly accelerated plate), the magnitude of velocity is less than the quadratic translation (variable accelerated plate). Furthermore, the behavior of both velocity profiles (a) and (b) is analyzed in Figure 7 for the thermal Grashof number. The higher velocity profile due to larger $Gr$ is seen from the curve. The physical examination for such influences is due to the buoyancy forces, and an increase in the Grashof number means a greater buoyancy effect, which increases the velocity field. In this figure, it is also noted that in the case of linear translation (constantly accelerated plate), the magnitude of velocity is less than the quadratic translation (variable accelerated plate).

FIGURE 1

FIGURE 1. Temperature plot for $\alpha$ when $\beta =\gamma =0.8,\mathrm{Pr}=11.4,\mathrm{a}\mathrm{n}\mathrm{d}t=1.0.$

FIGURE 2

FIGURE 2. Temperature plot for $\beta \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{n}\alpha =\gamma =0.8,\mathrm{Pr}=11.4,\mathrm{a}\mathrm{n}\mathrm{d}t=1.0.$

FIGURE 3

FIGURE 3. Temperature plot for $\gamma$ when $\alpha =\beta =0.8,\mathrm{Pr}=11.4,\mathrm{a}\mathrm{n}\mathrm{d}t=1.0.$

FIGURE 4

FIGURE 4. Velocity plot for $\alpha$ when $\beta =\gamma =0.8,\mathrm{Pr}=11.4,Gr=8.0,{\beta }_1=1.4,\left(a\right):t=2.0;\mathrm{a}\mathrm{n}\mathrm{d}\left(b\right):t=4.$

FIGURE 5

FIGURE 5. Velocity plot for $\beta$ with $\alpha =\gamma =0.8,\mathrm{Pr}=11.4,Gr=8.0,{\beta }_1=1.4,\left(a\right):t=2.25;\mathrm{a}\mathrm{n}\mathrm{d}\left(b\right):t=4$.

FIGURE 6

FIGURE 6. Velocity plot for $\gamma$ with $\alpha =\beta =0.8,\mathrm{Pr}=11.4,Gr=8.0,{\beta }_1=1.4,\left(a\right):t=2.0;\mathrm{a}\mathrm{n}\mathrm{d}\left(b\right):t=4$.

FIGURE 7

FIGURE 7. Velocity plot for $Gr$ with $\alpha =\beta =\gamma =0.8,\mathrm{Pr}=11.4,{\beta }_1=1.4,\left(a\right):t=1.97;\mathrm{a}\mathrm{n}\mathrm{d}\left(b\right):t=4$.

FIGURE 8

FIGURE 8. Velocity plot for ${\beta }_1$ with $\alpha =\beta =\gamma =0.8,\mathrm{Pr}=11.4,Gr=8.0,\left(a\right):t=2.0;\mathrm{a}\mathrm{n}\mathrm{d}\left(b\right):t=4$.

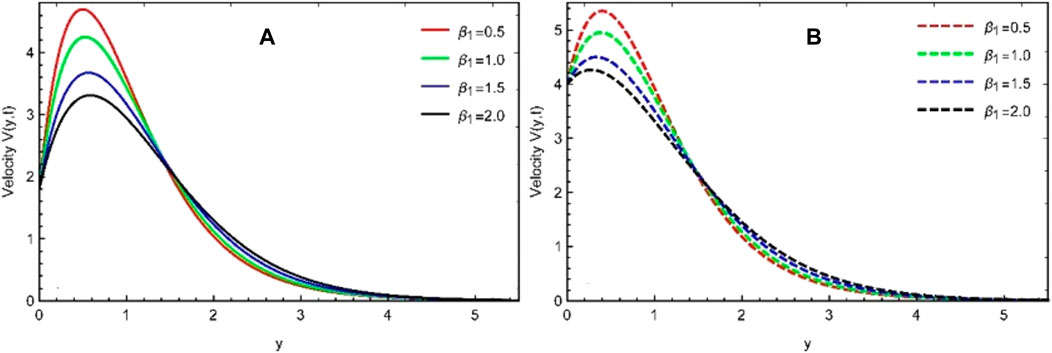
The behavior of the non-Newtonian Casson fluid parameter ${\beta }_1$ versus $\eta$ is plotted in Figure 8 for both types of velocity profiles. It is found that for the fluid velocity for different estimations of the Casson fluid parameter ${\beta }_1,$ the velocity is reduced by raising the estimations of the Casson fluid parameter ${\beta }_1.$ This figure also indicates that in the case of linear translation (constantly accelerated plate), in this study also the magnitude of velocity is less than the quadratic translation (variable accelerated plate). Finally, Table 1 shows a numerical analysis of the temperature field at different times for different values of the space variable. It is found that with increasing time (time from 0.5 to 1.5), the temperature increases; however, at time equal to 2, temperature shows a decrease. However, with the increasing space variable, temperature increases for all times. Table 2 shows simulations of the velocity profile at different times. It is noticed that initially, for small values of time, the momentum profile increases with the increasing time and space variable. The increase here is continuous. Finally, the numerical investigations of the Nusselt number and skin friction are presented in Table 3 at different values of time. It is examined from this table that the rate of heat transfer decreases with increasing time, whereas skin friction has the opposite behavior, i.e., increases with increasing time.

TABLE 1

TABLE 1. Numerical analysis of the temperature field at different times.

TABLE 2

TABLE 2. Numerical analysis velocity profile at different times.

TABLE 3

TABLE 3. Numerical analysis of the Nusselt number and skin friction.

Conclusion

The Casson fluid model is not studied in the literature via the Prabhakar fractional derivative approach when the vertical plate exhibits linear and quadratic translations with constant heating. Therefore, in this work, an attempt is made. This work considers an unsteady incompressible flow over a vertical plate with a constant temperature. The non-dimensional fractional equations are solved using the L.T technique. The impacts of various restrictions on leading equations are quantitatively investigated. The key points of this work are the following:

• By increasing the values of the fractional parameters, the temperature profile drops and asymptotically grows with time.

• The momentum field diminishes as the fractional constraint values grow.

• Due to increases in the buoyancy effect, the velocity profile accelerates by increasing the value of the Grashof number Gr.

• Velocity and temperature profiles both grow asymptotically with time.

• The Nusselt number decreases with time, whereas skin friction presents an increasing behavior with an increase in time values.

• In the future, this work can be extended to other non-Newtonian fluid models with various types of plate motions such as translations and oscillations.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

IK: formulation, solution, and writing the manuscript.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdal, S., Habib, U., Siddique, I., Akgul, A., and Ali, B. (2021). Attribution of multi-slips and bioconvection for micropolar nanofluids transpiration through porous medium over an extending sheet with PST and PHF conditions. Int. J. Appl. Comput. Math. 7, 235. doi:10.1007/s40819-021-01137-9

CrossRef Full Text | Google Scholar

Aksoy, Y. I., Pakdemirli, M., and Khalique, C. M. (2007). Boundary layer equations and stretching sheet solutions for the modified second grade fluid. Int. J. Eng. Sci. 45 (10), 829–841. doi:10.1016/j.ijengsci.2007.05.006

CrossRef Full Text | Google Scholar

Ali, A. (2018). A novel method for a fractional derivative with non-local and non-singular kernel, Chaos. Solit. Fractals 114, 478–482. doi:10.1016/j.chaos.2018.07.032

CrossRef Full Text | Google Scholar

Alidousti, J., and Ghafari, E. (2020). Dynamic behavior of a fractional order prey-predator model with group defense. Chaos, Solit. Fractals 134, 109688. doi:10.1016/j.chaos.2020.109688

CrossRef Full Text | Google Scholar

Alwawi, E. A., Krulig, E., and Gordon, K. B. (2009). Long‐term efficacy of biologics in the treatment of psoriasis: What do we really know? Dermatol. Ther. 22 (5), 431–440. doi:10.1111/j.1529-8019.2009.01259.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Andersson, H., Bech, K., and Dandapat, B. (1992). Magnetohydrodynamic flow of a power-law fluid over a stretching sheet. Int. J. Non-Linear Mech. 27 (6), 929–936. doi:10.1016/0020-7462(92)90045-9

CrossRef Full Text | Google Scholar

Archana, M., Gireesha, B., Venkatesh, P., and Reddy, M. G. (2017). Influence of nonlinear thermal radiation and magnetic field on three-dimensional flow of a Maxwell nanofluid. J. nanofluids 6 (2), 232–242. doi:10.1166/jon.2017.1320

CrossRef Full Text | Google Scholar

Asjad, M. I., Aleem, M., Ahmadian, A., Salahshour, S., and Ferrara, M. (2020). New trends of fractional modeling and heat and mass transfer investigation of (SWCNTs and MWCNTs)-CMC based nanofluids flow over inclined plate with generalized boundary conditions. Chin. J. Phys. 66, 497–516. doi:10.1016/j.cjph.2020.05.026

CrossRef Full Text | Google Scholar

Asjad, M. I., Muhammad, Z., Chu, Y. M., and Baleanu, D. (2021). Prabhakar fractional derivative and its applications in the transport phenomena containing nanoparticles. Therm. Sci. 25 (2), 411–416. doi:10.2298/TSCI21S2411A

CrossRef Full Text | Google Scholar

Basit, A., Asjad, M. I., and Akgül, A. (2021). Convective flow of a fractional second grade fluid containing different nanoparticles with Prabhakar fractional derivative subject to non‐uniform velocity at the boundary. Math. Methods Appl. Sci. 2021, 1–12. doi:10.1002/mma.7461

CrossRef Full Text | Google Scholar

Bilal, S., Ali Shah, I., Ali, A., Nisar, K. S., Khan, I., Motawi Khashan, M., et al. (2022). Finite difference simulations for magnetically effected swirling flow of Newtonian liquid induced by porous disk with inclusion of thermophoretic particles diffusion. Alexandria Eng. J. 61 (6), 4341–4358. doi:10.1016/j.aej.2021.09.054

CrossRef Full Text | Google Scholar

Chuong, C.-J., and Fung, Y.-C. (1986). “Residual stress in arteries,” in Frontiers in biomechanics, (Berlin, Germany: Springer), 117–129.

CrossRef Full Text | Google Scholar

Dash, R., Mehta, K., and Jayaraman, G. (1996). Casson fluid flow in a pipe filled with a homogeneous porous medium. Int. J. Eng. Sci. 34 (10), 1145–1156. doi:10.1016/0020-7225(96)00012-2

CrossRef Full Text | Google Scholar

Derakhshan, R., Turner, R., and Mancini, M. (2019). Project governance and stakeholders: A literature review. Int. J. Proj. Manag. 37 (1), 98–116. doi:10.1016/j.ijproman.2018.10.007

CrossRef Full Text | Google Scholar

Durairaj, M., Ramachandran, S., and Mehdi, R. M. (2017). Heat generating/absorbing and chemically reacting Casson fluid flow over a vertical cone and flat plate saturated with non-Darcy porous medium. Int. J. Numer. Methods Heat. Fluid Flow. 27 (1), 156–173. doi:10.1108/HFF-08-2015-0318

CrossRef Full Text | Google Scholar

Garrappa, R., and Kaslik, E. (2020). Stability of fractional-order systems with Prabhakar derivatives. Nonlinear Dyn. 102 (1), 567–578. doi:10.1007/s11071-020-05897-9

CrossRef Full Text | Google Scholar

Giusti, A., and Colombaro, I. (2018). Prabhakar-like fractional viscoelasticity. Commun. Nonlinear Sci. Numer. Simul. 56, 138–143. doi:10.1016/j.cnsns.2017.08.002

CrossRef Full Text | Google Scholar

Haq, B. U., Hardenbol, J., and Vail, P. R. (1988). Mesozoic and Cenozoic chronostratigraphy and cycles of sea-level change,” in Sea-Level Changes: An Integrated Approach, (Tulsa: SEPM Special Publication).

CrossRef Full Text | Google Scholar

Hassanien, I. (1996). Flow and heat transfer on a continuous flat surface moving in a parallel free stream of power-law fluid. Appl. Math. Model. 20 (10), 779–784. doi:10.1016/0307-904x(96)00082-0

CrossRef Full Text | Google Scholar

Hayat, T., Awais, M., and Sajid, M. (2011). Mass transfer effects on the unsteady flow of UCM fluid over a stretching sheet. Int. J. Mod. Phys. B 25 (21), 2863–2878. doi:10.1142/s0217979211101375

CrossRef Full Text | Google Scholar

Jasmine Benazir, A., Sivaraj, R., and Rashidi, M. M. (2016). Comparison between Casson fluid flow in the presence of heat and mass transfer from a vertical cone and flat plate. J. Heat. Transf. 138 (11), 112005. doi:10.1115/1.4033971

CrossRef Full Text | Google Scholar

Khan, I., Saqib, M., and Ali, F. (2017). Application of time-fractional derivatives with non-singular kernel to the generalized convective flow of Casson fluid in a microchannel with constant walls temperature. Eur. Phys. J. Spec. Top. 226 (16-18), 3791–3802. doi:10.1140/epjst/e2018-00097-5

CrossRef Full Text | Google Scholar

Khan, I., Saqib, M., and Alqahtani, A. M. (2020). Channel flow of fractionalized H2O-based CNTs nanofluids with Newtonian heating. Discrete Continuous Dyn. Syst. - S 13 (3), 769–779. doi:10.3934/dcdss.2020043

CrossRef Full Text | Google Scholar

Li, P., Raza, A., El-Zahar, E. R., Al-Khaled, K., Khan, S. U., Ijaz Khan, M., et al. (2022). Applications of fractional derivatives in MHD free-convective oscillating flow of a blood based CNTs nanofluid across a porous medium. Proc. Institution Mech. Eng. Part E J. Process Mech. Eng. 0 (0), 095440892210824. doi:10.1177/09544089221082489

CrossRef Full Text | Google Scholar

Mythili, D., and Sivaraj, R. (2016). Influence of higher order chemical reaction and non-uniform heat source/sink on Casson fluid flow over a vertical cone and flat plate. J. Mol. Liq. 216, 466–475. doi:10.1016/j.molliq.2016.01.072

CrossRef Full Text | Google Scholar

Nadeem, S. M., Ahmad, M., Zahir, Z. A., Javaid, A., and Ashraf, M. (2014). The role of mycorrhizae and plant growth promoting rhizobacteria (PGPR) in improving crop productivity under stressful environments. Biotechnol. Adv. 32 (2), 429–448. doi:10.1016/j.biotechadv.2013.12.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Panchal, S., Khandagale, A. D., and Dole, P. V. (2016). K-hilfer-prabhakar fractional derivatives and applications. arXiv preprint arXiv:1609.05696.

Google Scholar

Polito, F., and Tomovski, Z. (2016). Some properties of Prabhakar-type fractional calculus operators. Fract. Differ. Calc. 6, 73–94. doi:10.7153/fdc-06-05

CrossRef Full Text | Google Scholar

Qureshi, Z. A., Bilal, S., Khan, U., Ali, A., Sultana, M., Botmart, T., Zahran, H. Y., et al. (2022). Mathematical analysis about influence of Lorentz force and interfacial nano layers on nanofluids flow through orthogonal porous surfaces with injection of SWCNTs. Alexandria Eng. J. 61 (12), 12925–12941. doi:10.1016/j.aej.2022.07.010

CrossRef Full Text | Google Scholar

Raza, A., Khan, S. U., Farid, S., Ijaz Khan, M., Khan, M. R., Haq, A. U., et al. (2022). Transport properties of mixed convective nano-material flow considering the generalized Fourier law and a vertical surface: Concept of Caputo-Time Fractional Derivative. Proc. Institution Mech. Eng. Part A J. Power Energy 236, 974–984. doi:10.1177/09576509221075110

CrossRef Full Text | Google Scholar

Samraiz, M., Perveen, Z., Rahman, G., Sooppy Nisar, K., and Kumar, D. (2020). Hilfer-Prabhakar fractional derivative with applications to mathematical physics. Front. Phys. 23, 309. doi:10.3389/fphy.2020.00309

CrossRef Full Text | Google Scholar

Sadeghy, K., and Sharifi, M. (2004). Local similarity solution for the flow of a “second-grade” viscoelastic fluid above a moving plate. Int. J. Non-Linear Mech. 39 (8), 1265–1273. doi:10.1016/j.ijnonlinmec.2003.08.005

CrossRef Full Text | Google Scholar

Sajid, M., Hayat, T., and Asghar, S. (2007). Non-similar analytic solution for MHD flow and heat transfer in a third-order fluid over a stretching sheet. Int. J. Heat Mass Transf. 50 (9-10), 1723–1736. doi:10.1016/j.ijheatmasstransfer.2006.10.011

CrossRef Full Text | Google Scholar

Sandev, T. (2017). Generalized Langevin equation and the Prabhakar derivative. Mathematics 5 (4), 66. doi:10.3390/math5040066

CrossRef Full Text | Google Scholar

Saqib, M., Kasim, A. R. M., Mohammad, N. F., Ching, D. L. C., and Shafie, S. (2020). Application of fractional derivative without singular and local kernel to enhanced heat transfer in CNTs nanofluid over an inclined plate. Symmetry 12 (5), 768. doi:10.3390/sym12050768

CrossRef Full Text | Google Scholar

Sivaraj, R., Benazir, A. J., Srinivas, S., and Chamkha, A. J. (2019). Investigation of cross-diffusion effects on Casson fluid flow in existence of variable fluid properties. Eur. Phys. J. Spec. Top. 228, 35–53. doi:10.1140/epjst/e2019-800187-3

CrossRef Full Text | Google Scholar

Wang, Y., Mansir, I. B., Al-Khaled, K., Raza, A., Khan, S. U., Khan, M. I., et al. (2022). Thermal outcomes for blood-based carbon nanotubes (SWCNT and MWCNTs) with Newtonian heating by using new Prabhakar fractional derivative simulations. Case Stud. Therm. Eng. 32, 101904. doi:10.1016/j.csite.2022.101904

CrossRef Full Text | Google Scholar