A capacitor-based DC circuit breaker for HVDC power grid

DC circuit breakers (DCCBs) are the critical equipment to isolate faults in high-voltage DC grids. The improvement of interruption performances of capacitor-based DCCBs (C-DCCBs) has been widely researched. However, in previous papers, the adaptive reclosing of C-DCCBs is less considered and requires further research. In this paper, a novel C-DCCB with adaptive reclosing ability is proposed. The interruption and adaptive reclosing processes of the proposed C-DCCB are presented. The fault current is interrupted by charging the internal capacitor to a voltage higher than the system voltage. The fault property identification is key to adaptive reclosing and is achieved using the capacitor discharge characteristic. The parameter designs are analyzed to guarantee successful interruptions, and the identification criteria are proposed to serve the adaptive reclosing. On the one hand, the proposed C-DCCB has good interruption performances; on the other hand, an adaptive reclosing strategy is designed for the proposed C-DCCB to restore the power transmission whereas avoiding a second fault shock, which is the main contribution of this paper. Finally, the interruption and adaptive reclosing performances of the proposed C-DCCB are validated using PSCAD/EMTDC simulations.

1 Introduction

High-voltage DC (HVDC) grids have great application potential in renewable energy integration, island power supply and AC grid interconnection (Hertem and Ghandhari, 2010)- (An et al., 2017). However, after a DC fault occurs, the DC fault current quickly increases and the DC voltage rapidly drops, which seriously affects the safe and stable operation of HVDC grids. DC circuit breakers (DCCBs) can soon isolate the fault area and maintain the normal operation of the nonfault area. Traditionally, DCCBs are divided into mechanical, solid-state and hybrid DCCBs (Bucher and Franck, 2016)- (Chen et al., 2021). Several mechanical DCCBs use semiconductors such as thyristors to improve the interruption performance, obscuring the boundary between mechanical and hybrid DCCBs (Wen et al., 2018)- (Wu et al., 2020a). In this paper, DCCBs that interrupt the fault current by semiconductors with turn-off ability are called semiconductor-based DCCBs (S-DCCBs); DCCBs that interrupt the fault current by charging the internal capacitor to a voltage higher than the system voltage are called capacitor-based DCCBs (C-DCCBs).

In S-DCCBs, the main breaker (MB), which is composed of insulated-gate bipolar transistors (IGBTs) or integrated gate commutated thyristors (IGCTs), can interrupt the fault current. In (Hafner and Jacobson, 2011; Hassanpoor et al., 2015; Wen et al., 2016; Jovcic et al., 2019), S-DCCBs conduct the system current with small conduction losses during a normal state. During interruptions, the system current is commutated into the MB and then interrupted by the MB. S-DCCBs have attracted considerable attention because of good interruption performances. In China, S-DCCBs with different topologies have been applied to the Zhoushan DC project and Zhangbei DC grid project, respectively (Jovcic et al., 2019). However, the interruption capacity of S-DCCBs is limited by the turn-off capacity of IGBT and IGCT, and IGBT and IGCT bring high construction costs.

For C-DCCBs, the system current is commutated into the internal capacitor during the interruption. It gradually decreases to 0 after the capacitor is charged to a voltage higher than the system voltage. C-DCCBs usually use semiconductors without turn-off ability to save the construction cost, such as thyristors and diodes. C-DCCBs with different topologies in China have been applied to the Zhangbei DC grid project and the Nan’ao DC grid project, respectively (Liu, 2019)- (Chen et al., 2018). Many topologies have been proposed to improve the C-DCCB performances regarding bidirectional interruption, interruption speed, pre-activation ability, etc. The C-DCCB in (Wu et al., 2020b) achieves bidirectional current commutation using bridge-type branches. In (Jamshidifar and Jovcic, 2018), the C-DCCB uses fast thyristors to quickly interrupt large fault currents. In (Sima et al., 2019), the capacitor is inserted into a bridge composed of spark gap switches, and this topology guarantees that the C-DCCB can consecutively interrupt the fault current. The pre-activation of DCCB achieves that the DCCB operation time overlaps with the protection time, which effectively reduces the fault interruption time (Hafner and Jacobson, 2011). However, the C-DCCBs in (Chen et al., 2018; Jamshidifar and Jovcic, 2018; Liu, 2019; Sima et al., 2019; Wu et al., 2020b) do not have the pre-activation ability. For C-DCCBs in (Wu et al., 2019) and (Guo et al., 2020), the thyristors in the MB can temporarily conduct the load current, thus achieving the pre-activation ability. In (Augustin et al., 2021), a C-DCCB family consisting of one unidirectional and six bidirectional concepts is presented, and all concepts have the pre-activation ability. Nevertheless, the reclosing of C-DCCBs is not considered in (Liu, 2019)- (Augustin et al., 2021).

Considering that most overhead line faults are transient, the DCCB should reclose in time to restore the power transmission after isolating (Wang et al., 2203). However, in case of a permanent fault, the direct reclosing will bring a second fault shock, which is harmful to the HVDC grid. To solve this problem, the permanent and transient faults should be discriminated, and the DCCB only reconnects the HVDC grid to the isolated line when the fault is transient, which is called adaptive reclosing.

The fault property identification is key to the adaptive reclosing strategy. Because the permanent and transient faults result in different boundary conditions, the fault property can be identified according to the traveling wave characteristics (Wang et al., 2203)- (Mei et al., 2021). In (Wang et al., 2203), the voltage pulse is produced by the hybrid MMC on the healthy pole. However, considering the construction and conduction cost, the half-bridge MMC is more attractive than the hybrid MMC for HVDC grids. In (Song et al., 2019)- (Zhang et al., 2020), the voltage pulse is injected into the fault line by controlling the MB of S-DCCBs. The MMC and S-DCCB are simultaneously controlled to produce the voltage pulse in (Yang et al., 1123). In (Mei et al., 2021), the voltage pulse comes from the energy absorption module of S-DCCB. In (Li et al., 2020), the HVDC grid charges the fault line through the arrester of S-DCCB, and the fault property is identified using the fault line voltage. In (Pei et al., 2019), the fault property can be identified using the fault current, and the fault current is limited because the MB modules are sequentially turned on. However, the methods in (Wang et al., 2203)- (Pei et al., 2019) do not consider the C-DCCBs.

For C-DCCBs, most previous papers consider the direct reclosing and the consecutive interruption ability rather than the fault property identification is focused on. For example (Sima et al., 2019),- (Augustin et al., 2021) use different methods to quickly restore the interruption ability of C-DCCBs before the direct reclosing. Nevertheless, the fault property identification and adaptive reclosing of C-DCCBs are worth studying to improve the reclosing performance. In (Wen et al., 2021), for HVDC grids adopting C-DCCBs, the fault property is identified by comparing the residual voltages at two ends of the isolated fault line. However, this method only applies to symmetrical monopole DC systems and requires long-distance communication. In (Torwelle et al., 2021), a grounded branch is added to the C-DCCB, which enables the internal capacitor charges the fault line, and the fault property is identified using the line voltage. However, the capacitor may need to charge the fault line multiple times, which obviously increases the reclosing time.

Although several C-DCCBs with good interruption performances have been proposed, the C-DCCB with adaptive reclosing ability needs further research. In this paper, a novel C-DCCB is proposed to serve HVDC grids. On the one hand, the proposed C-DCCB achieves good interruption performances; on the other hand, it has the ability of adaptive reclosing, which is the main contribution of this paper. The adaptive reclosing ability avoids the second fault shock in case of permanent faults and the voltage oscillations in case of transient faults. The paper is structured as follows. Section 2 describes the topology and operation of the proposed C-DCCB. Section 3 analyzes the parameter design and fault property identification. Section 4 shows the simulation results, which validate the performance of the proposed C-DCCB. Finally, Section 5 concludes this paper.

2 Proposed DC circuit breaker

2.1 Topology of the proposed C-DCCB

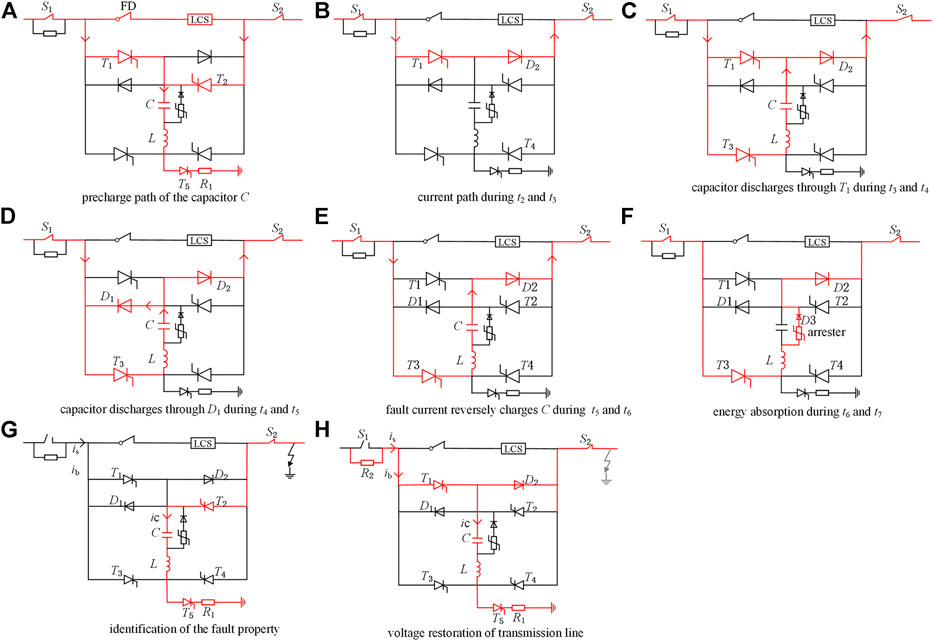
As shown in Figure 1, the proposed C-DCCB contains the main conductor (MC), MB, energy absorber (EA) and precharge branch. The MC is composed of a fast disconnector (FD) and a load commutation switch (LCS), and the LCS only endures the commutation voltage. The MB is composed of an inductor L, capacitor C, diodes D₁–D₂, and thyristors T₁–T₄. The EA is composed of an arrester and diode D₃. The precharge branch is composed of a resistor R₁ and thyristor T₅. Both sides of the C-DCCB are equipped with residual current breakers (RCBs). The RCB can interrupt residual DC currents of up to 10 A, and the interruption time is 30 ms. After a current zero occurs, the FD can restore its dielectric strength within a few milliseconds to withstand the peak transient interruption voltage (TIV). In practical engineering, the FD can be composed of several vacuum circuit breakers to achieve operation performance (Shi et al., 2015).

FIGURE 1

FIGURE 1. Topology of the capacitor-based DC circuit breaker.

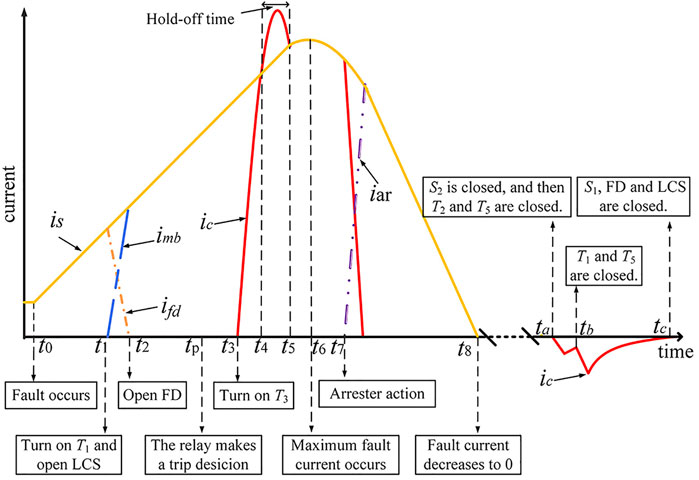
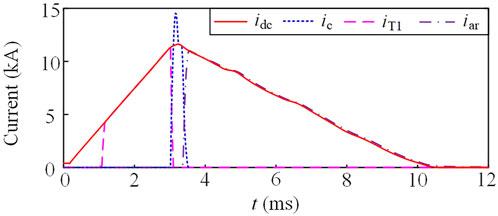
To clarify the operation processes, the current curves in C-DCCB during interrupting fault currents and reclosing with transient faults are shown in Figure 2, where i_s, i_mb, i_fd, i_c and i_ar are the currents of the DC system, MB, FD, capacitor C and arrester, respectively. The reference directions of currents and capacitor voltage u_c are marked in Figure 1. During operations, the main switching events and time labels are given in Figure 2.

FIGURE 2

FIGURE 2. Current curves during interrupting fault currents and reclosing with a transient fault.

2.2 Operation processes of the C-DCCB

2.2.1 Capacitor precharge

Initially, the HVDC grid precharges the capacitor C by turning on T₁, T₂ and T₅, and the current path is shown in Figure 3A. After the capacitor voltage u_c is charged to the system voltage, T₁, T₂ and T₅ naturally turn off. Because of the leakage discharge, u_c slowly decreases during the normal state. Once u_c decreases to a preset value, T₁, T₂ and T₅ are turned on to precharge the capacitor. Thus, u_c is always no less than the preset value during the normal state.

FIGURE 3

FIGURE 3. Operation procedures of the C-DCCB.

2.2.2 Current commutation

During the normal state, the MC conducts the load current with small conduction losses. Considering the pre-activation strategy, once the protection detects a potential fault at t = t₁, the C-DCCB commutates the current into the MB by turning on T₁ and turning off the LCS. At t = t₂, i_fd decreases to 0, and the FD begins to open. After that, the current path in the C-DCCB is shown in Figure 3B. If the protection decides not to interrupt the current at t = t_p, the C-DCCB successively closes the FD and LCS; thus, the current naturally commutates into the MC, and the thyristor T₁ turns off naturally after the current of T₁ is smaller than the holding current; Otherwise, the C-DCCB performs the following interruption operations.

During t₁–t_p, the voltage drop in the C-DCCB is equal to the on-state voltages of T₁ and D₂; thus, the disturbance caused by the pre-activation is insignificant. By pre-commutating the system current from the MC into the MB, the C-DCCB operation time overlaps with the protection time. Thus, the pre-activation effectively reduces the fault clearing time.

2.2.3 Capacitor discharge

As shown in Figure 3C, during t₃ and t₄ the system provides the fault current to the fault point through S₁, T₁, D₂ and S₂. At the same time, the capacitor discharges through the following loop: C—T₁—T₃—L. As shown in Figure 3D, after i_c exceeds the fault current at t = t₄, T₁ is reversely blocked, and the discharging loop is changed as: C—D₁—T₃—L. After i_c decreases to the fault current at t = t₅, D₁ is reversely blocked, and T₁ begins to endure the forward voltage stress, as shown in Figure 3E. To reliably turn off T₁, the time interval between t₄ and t₅, which is the reverse-bias time of T₁ and marked as t_R, should be greater than the turn-off time t_q. The turn-off time t_q, which can be found in the datasheet, is the minimum reverse-bias time to ensure the turn-off of the thyristor (Technical Information, 2012).

During t₂ and t₅, the voltage drop in the C-DCCB is rather small compared with the system voltage. After t = t₅, the voltage drop in the C-DCCB is approximately equal to the capacitor voltage and quickly charged to the system voltage. We mark the FD operation time as t_FD. The value of t₃ should meet the following two constraints: 1) t₃ should not be earlier than t_p, and 2) the FD recovers its dielectric strength at t = t₂+ t_FD, which time instant should be earlier than t₅ to avoid the interruption failure. Considering that the interval between t₃ and t₅ is greater than t_q, these two constraints can be satisfied when t₃ is selected as:

$t_3=\max \left(t_p,t_2+t_{FD}-t_q\right)(1)$

2.2.4 Energy absorption

After the capacitor is charged to the arrester reference voltage, the fault current commutates into the EA and gradually decreases, as shown in Figure 3F. The arrester releases the residual energies stored in the system, and the peak TIV usually is limited to 1.5 times the system voltage. After the fault current decreases to 10 A, S₁, and S₂ are opened to isolate the fault totally. After the isolation, the capacitor voltage u_c is opposite to its initial state.

2.2.5 Adaptive reclosing

To guarantee that the DC line recovers its insulation characteristic, the reclosing is usually hundreds of milliseconds later than the isolation (Yang et al., 1123). After receiving the adaptive reclosing command, the C-DCCB closes S₂ and turns on T₂ and T₅. If the fault is permanent, the capacitor C significantly discharges through the following loop: C—L—T₅—R₁—fault point—S₂—T₂, as shown in Figure 3G. If the fault is transient, the capacitor slightly discharges through the equivalent grounded capacitance of the DC line.

After identifying the permanent fault, S₂ is opened to isolate the fault when the discharging current is smaller than 10 A. After identifying the transient fault, the C-DCCB turns on T₁ and T₅; thus, the capacitor C and the DC line are charged to the system voltage, as shown in Figure 3H; after that, the C-DCCB successively closes S₁, FD and LCS, and the reclosing is completed.

After reclosing the C-DCCB located on one side of the DC line, if the fault is transient, the line voltage is close to the system voltage; otherwise, the line voltage is much less than the system voltage. Thus, the C-DCCB located on the other side of the DC line directly identifies the fault property using the line voltage.

3 Parameter design and fault property identification of the C-DCCB

3.1 Turning T₁ off

During t₃ and t₄, the capacitor discharging loop is equivalent to the circuit shown in Figure 4A, where u_Ti is the voltage drop in T_i, i = 1, 2, 3, 4. Assume that thyristors have the same voltage drops of u_T, then we can obtain:

$\left[\begin{array}{c}\stackrel{•}{u_c}\\ \stackrel{•}{i_c}\end{array}\right]=\left[\begin{array}{cc}0& -1/C\\ -1/L& 0\end{array}\right]\left[\begin{array}{c}{u}_c\\ i_c\end{array}\right](2)$

where the initial values of i_c and u_c are 0 and u_c0, respectively, and u_c0 is negative under the reference direction in Figure 1.

FIGURE 4

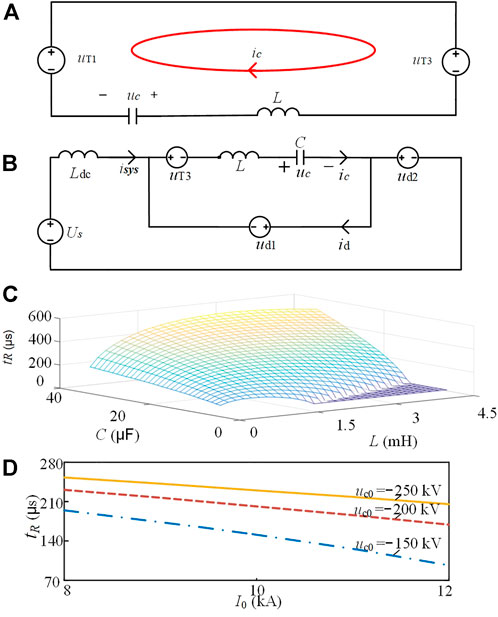
FIGURE 4. (A) Equivalent circuit of the capacitor discharging during t3 and t4. (B) equivalent discharge circuit of the capacitor during t4 and t5; (C) relations of tR, L, and C (D) relations of IR. Io. and uc0.

After a metallic fault occurs at the load side of the C-DCCB, the system side of the C-DCCB is equivalent to a voltage source connected in series with an inductor L_dc. The equivalent capacitor discharge circuit during t₄ and t₅ is shown in Figure 4B, where i_sys is the system current, i_d is the current flowing through D₁, u_di is the voltage drop in D_i, i = 1, 2. Assume that the diodes have the same voltage drop of u_d, then we can obtain:

$\left[\begin{array}{cccc}0& 0& 0& -L\\ L_{dc}& 0& 0& L\\ 1& 1& 0& -1\\ 0& 0& 1& 0\end{array}\right]\left[\begin{array}{c}\stackrel{•}{i_{sys}}\\ \stackrel{•}{i_d}\\ \stackrel{•}{u_c}\\ \stackrel{•}{i_c}\end{array}\right]=\left[\begin{array}{c}{u}_c+u_T+u_{\mathrm{d}}\\ U_s-u_c-u_T-u_{\mathrm{d}}\\ 0\\ i_c/C\end{array}\right](3)$

In Eq. 3, the initial values of u_c and i_c can be obtained from those final values in Eq. 2; i_sys and i_c have the same initial value, and i_d has an initial value of 0.

In this analysis, U_s = 200 kV, L_dc = 0.04 H, u_c0 = −200 kV, and the fault current at t₃ has a value of I₀ = 10 kA. Substituting these parameters into (2) and (3), the relations of the reverse-bias time t_R, L and C can be obtained. As shown in Figure 4C, t_R increases with C, because the larger capacitor stores more energy to maintain the reverse-bias of T₁. When L is small, t_R increases with L. However, when L exceeds a critical value L_C, t_R decreases with L. When C is too small and L is too large, t_R is 0. When C = 9 μF and L = 1.2 mH, the relations of t_R, I₀ and u_c0 are shown in Figure 4D. The value of t_R decreases with I₀ and increases with the absolute value of u_c0.

According to the relations of t_R and system parameters, the parameter design principles of the C-DCCB are as follows: 1) the values of L and C should guarantee that t_R is greater than the turn-off time t_q under the worst interruption condition, i.e., the C-DCCB interrupts the maximum fault current when the initial capacitor voltage u_c0 has a minimum absolute value; 2) the value of L should be close to the critical value L_c to improve the utilization efficiency of L and C.

3.2 Fault property identification

3.2.1 Analysis model:

This section takes the reclosing after a positive pole fault as an example. As shown in Figure 5A, the systems on both sides of the negative pole are represented by the Thevenin equivalent circuits; U_eq1 and U_eq2 are Thevenin voltages; Z_eq1 and Z_eq2 are Thevenin impedances; u_r is the capacitor voltage at the beginning of reclosing. Taking the fault point as a boundary, the DC line is divided into two parts. If the fault is permanent, the switch k₁ is closed; otherwise, k₁ is opened. The turn-on commands of thyristors T_L and T_R represent the reclosing commands of C-DCCBs on the left and right sides, respectively.

FIGURE 5

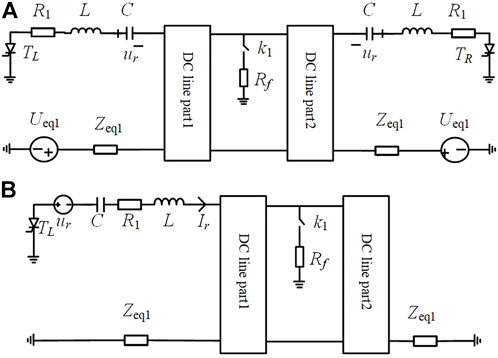
FIGURE 5. (A)Schematic of the system circuit after isolating the fault pole; (B)equivalent system circuit during the reclosing.

We assume that the C-DCCB on the left side closes S₂, T₂ and T₅, which is equivalent to that T_L is turned on in Figure 5A. According to the superposition theorem, during the reclosing, the system response change is caused by the excitation of the voltage source u_r. Considering only the excitation of u_r, the equivalent system circuit is shown in Figure 5B.

Using the DC line’s frequency-dependent parameter, the nodal admittance matrix of the DC line can be obtained, and then the bus admittance matrix of the circuit in Figure 5B can be established. The self-impedance of the node connecting the voltage source u_r and the capacitor C is marked as Z_self, then the current injected into the DC line, marked as I_r, is:

$I_r=u_r/\left(s{Z}_{self}\right)(4)$

where s is the Laplace operator.

During reclosing, the capacitor voltage u_c is:

$u_c=u_r+I_r/\left(sC\right)(5)$

The value of u_c in the frequency domain can be calculated by combining (4) and (5). The value of u_c in the time domain can be obtained using the numerical inversion of the Laplace transform (Gómez and Uribe, 2009). The detailed calculation process can refer to the method in (Guo et al., 2021) and is not repeated in this paper.

3.2.2 Transient fault:

At the beginning of reclosing, the voltage source u_r generates a current traveling wave on the DC line. When the fault is transient, because the DC line end is an open circuit, the current traveling wave is totally reflected at the DC line end, and the reflection wave is in the opposite direction of the original traveling wave. When the reflection current wave transmits to the DC line head, I_r decreases to 0, and the thyristor T_L is reversely biased, causing the capacitor voltage u_c keeps unchanged.

According to the system parameters in Section 4, we take u_r = 1 pu, C = 9 μF, L = 1.2 mH, R₁ = 150 Ω, Z_eq1 = Z_eq2 = 100 Ω. As shown in Figure 6A, the capacitor discharges through the DC line during reclosing without fault, and u_c gradually decreases. Because of the current reflection wave, the thyristor T_L is turned off and u_c keeps unchanged after 1.36 ms. The deviation between the calculation and simulation values of u_c is relatively small, which validates the accuracy of the analysis model.

FIGURE 6

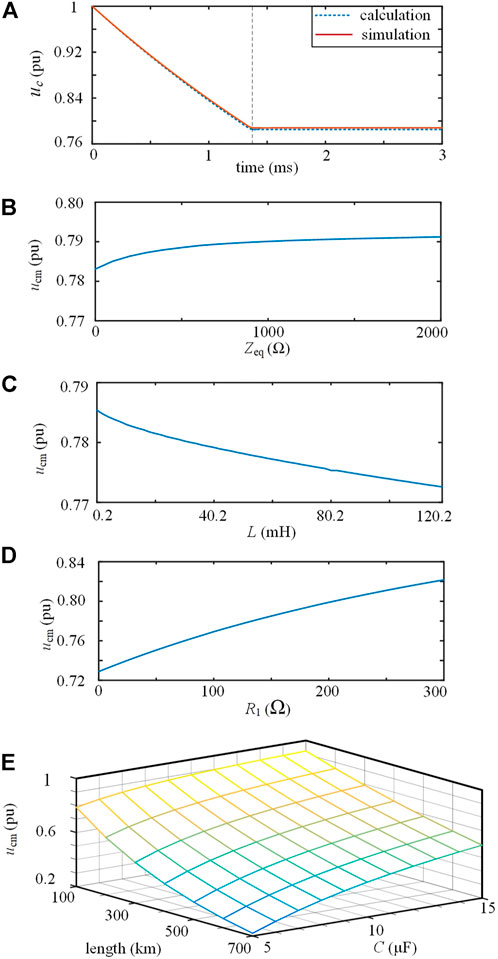
FIGURE 6. (A) Simulation and calculation values of Δu during reclosing without fault; (B) relation between ucm and Zeq (C) relation between ucm and L (D) relation between ucm and R1 (E) relations of ucm, C and line length.

During reclosing, the minimum value of u_c is marked as u_cm. The relations of u_cm and the system parameters are discussed using the above analysis model. The values of Z_eq1 and Z_eq2 are related to the non-fault area of the DC grid. When Z_eq1 = Z_eq2 = Z_eq, the relation between u_cm and Z_eq is shown in Figure 6B. When Z_eq increases from 0 to 2 kΩ, u_cm only increases by 1.0%, indicating that the non-fault area of the DC grid has little influence on u_cm.

As shown in Figure 6C, when L increases from 0.2 to 120.2 mH, u_cm only decreases by 1.6%, indicating that the influence of L on u_cm is not significant. As shown in Figure 6D, u_cm increases with increasing R₁, because R₁ limits the amplitude of the current traveling wave, thus limiting the discharge of capacitor C. As shown in Figure 6E, u_cm increases with the increasing C. With the DC line length increase, the arrival time of the current reflection wave increases, causing the increase in capacitor discharge time and the decrease of u_cm.

3.2.3 Permanent fault:

After reclosing the C-DCCB with a permanent fault, the current traveling wave will be reflected at the fault point. If the fault resistance is less than the line wave impedance, the current reflection wave has the same polarity as the original current traveling wave; otherwise, compared to the original current traveling wave, the current reflection wave has an opposite polarity and smaller amplitude. Therefore, the traveling wave effect will not cause the capacitor current to cross zero during reclosing with a permanent fault.

As shown in Figure 3G, the capacitor significantly discharges through R₁, L and the fault line during reclosing with a permanent fault. The equivalent parallel admittance of the DC line has little effect on the discharge. Using the lumped parameter model of the DC line, the equivalent capacitor discharge circuit is shown in Figure 7A, where R_eq and L_eq are the equivalent resistance and inductance of the DC line, respectively. For this second-order circuit, when $\left(R_1+R_{eq}\right)>2\sqrt{\left(L+L_{eq}\right)/C}$, the discharge process is overdamped, and u_c gradually decreases to 0. When $\left(R_1+R_{eq}\right)<2\sqrt{\left(L+L_{eq}\right)/C}$, the discharge process is underdamped, and u_c decreases to a negative value when the discharge current crosses zero. After the discharge current crosses zero, the thyristor T_L is turned off, and u_c maintains the negative value.

FIGURE 7

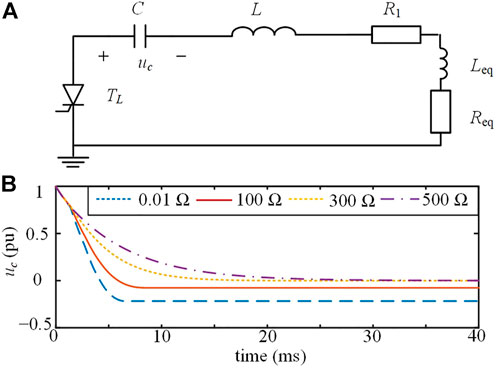
FIGURE 7. (A) Equivalent discharge circuit during reclosing with a permanent fault; (B) waveforms of uc, when the permanent fault has different fault resistances.

As shown in Figure 7B, for a permanent fault located at the DC line end, when the fault resistance is 0 and 100 Ω, the discharge is underdamped, and the minimum value of u_c is less than 0. When the fault resistance is 300 and 500 Ω, the discharge process is overdamped, and u_c decreases to 0. These results are consistent with the above analysis.

3.2.4 Criteria for identifying the fault property:

According to the above analysis, during reclosing with transient faults, u_c decreases to a positive value u_cm, which can be calculated using Eq. 4 and Eq. 5. During reclosing with permanent faults, u_c decreases to be no more than 0. A permanent fault is identified using the following criterion:

$u_c\left(t\right)\le u_{th}=u_{cm}-u_{mar1}(6)$

where u_th is the voltage threshold, and u_mar1 is a positive safety margin.

A transient fault is identified using the following criterion:

$\begin{array}{ccc}{u}_c\left(t\right)>u_{th}& \&& \left|u_c\left(t-\Delta t\right)-u_c\left(t\right)\right|<u_{error}\end{array}(7)$

A slighter fault causes a slower capacitor discharge rate during reclosing with a permanent fault. The values of u_error and ∆t should satisfy the following conditions: 1) the criterion in Eq. 7 is not true in the case of the slightest permanent fault, which occurs at the end of DC line and has the largest fault resistance; and 2) u_error is greater than the maximum measurement error.

In addition, to correctly identify the transient fault that lasts longer than hundreds of milliseconds, the following method is adopted: after identifying a permanent fault, the C-DCCB will perform another reclosing attempt to identify the fault property again unless the number of reclosing attempts reaches the maximum value allowed by the system.

4 Simulation results

4.1 Simulation parameters

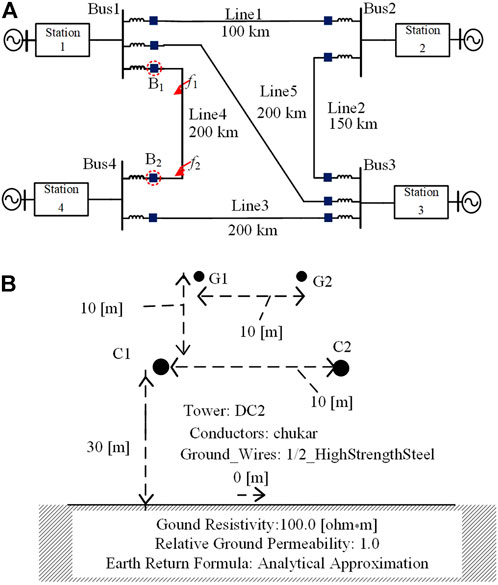
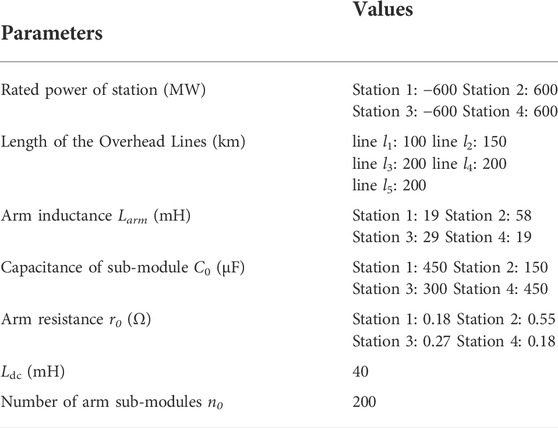
As shown in Figure 8A, a four-terminal bipolar DC grid is established in PSCAD/EMTDC, and the rated voltage is ±200 kV. In the DC grid, each station contains 2 MMCs, and its neutral point is directly earthed. For the equivalent model, all sub-modules in each MMC arm are equivalent to a Thevenin equivalent circuit; thus, the simulation efficiency is greatly improved. The DC grid is bipolar and has a rated voltage of ±200 kV, and the detailed equivalent model of MMC in (Cigré, 2014) is used. Both ends of the DC line are equipped with C-DCCBs and current-limiting inductors of 0.04 H. The C-DCCB located on the Bus1 side of Line 4 is marked as B₁ and taken as an example. For simplicity, only simulation results of the positive pole are shown in this paper. The parameters of the C-DCCB and simulation model are shown in Table 1 and Table 2, and the design of reclosing parameters is presented as follows.

FIGURE 8

FIGURE 8. (A) Topology of the DC grid; (B) configuration of transmission line.

TABLE 1

TABLE 1. Parameters of the C-DCCB.

TABLE 2

TABLE 2. Main parameters of the HVDC Grid.

During the interruption, the internal capacitor voltage u_c is charged to the peak TIV of 300 kV. After the interruption, the capacitor C slowly discharges through the arrester and D₃. After a time delay of 300 ms, the capacitor voltage is discharged to u_r = 192 kV at the beginning of reclosing. The transmission line is based on the frequency-dependent model, and the line configuration is shown in Figure 8B. Substituting the C-DCCB and line parameters into (4) and (5), we can obtain that u_cm = 0.785 u_r. In this paper, the safety margin u_mar1 is taken as 10 kV. Then, the voltage threshold u_th in (6) and (7) has a value of 0.785 × 192–10 = 140.7 kV.

For DC grid protections, the maximum value of fault resistance is usually hundreds of ohm. In simulations, even if the permanent fault located on the B₂ side of Line 4 has a fault resistance of up to 1 kΩ, u_c decreases to u_th within 3 ms during the reclosing process. Thus, as long as ∆t is greater than 3 ms and u_error is less than (u_r−u_th), the permanent fault will not cause malfunctions of criterion in Eq. 7. We assume that the capacitor voltmeter has a voltage range of 350 kV and an accuracy ratio of 0.1%; thus, the maximum measurement error of the voltmeter is 0.35 kV. Considering these above conditions, we select u_error and ∆t as 0.5 kV and 5 ms, respectively.

4.2 Interruption of fault current

As shown in Figure 8A, considering the most serious fault condition, a metallic fault occurs at the line side of B₁ at t = 0 ms, and the initial capacitor voltage is −180 kV. After the fault is detected at t = 1 ms, the interruption results are shown in Figure 9, where i_dc, i_T1, i_c and i_ar are the currents flowing through Line 4, T₁, C and arrester, respectively.

FIGURE 9

FIGURE 9. Current waveforms during the interruption.

We assume that the protection detects the fault at t = 1 ms. As shown in Figure 9, after t = 1 ms, T₁ is turned on and then the LCS is turned off. At t = 1.16 ms, i_dc is commutated into the MB, and the FD is opened without arc. Substituting system parameters into (1), T₃ is turned on at t = 3.1 ms. After that, i_c rapidly exceeds the fault current; thus, T₁ is reversely biased. The reverse-bias of T₁ continues until i_dc exceeds i_c. The reverse-bias time is 120 μs and two times t_q, which is sufficient to turn off T₁. With the charging of the capacitor, i_dc reaches the maximum value of 11.7 kA at t = 3.29 ms and then gradually decreases. At t = 3.42 ms, i_dc is commutated into the arrester. At t = 10.3 ms, i_dc falls to below 10 A.

For the typical hybrid DCCB in (Hafner and Jacobson, 2011), the fault current decreases almost immediately after the FD recovers the dielectric strength. For the C-DCCB, the fault current begins to fall at t = 3.29 ms, which is only 0.13 ms later than the instant that the FD recovers the dielectric strength at t = 3.16 ms. The time interval from the fault inception to the moment that the fault current begins to decrease is defined as the fault neutralization time. The fault neutralization time of C-DCCB is only a few hundred microseconds longer than that of typical hybrid DCCB, indicating a quick interruption speed.

4.3 Reclosing with a permanent fault

4.3.1 Permanent metallic fault

We set a permanent fault at the midpoint of Line 4 at t = 0 ms, and the fault resistance is 0.01 Ω. At t = 300 ms, B₁ begins to reclose, i.e., T₂ and T₅ are turned on. As shown in Figure 10A, u_c gradually decreases during reclosing and is smaller than u_th = 140.7 kV after t = 301.08 ms. Thus, B₁ identifies the permanent fault. During reclosing, the capacitor discharges through R₁, L and the fault line, and this second-order discharge circuit is underdamped because the fault resistance is small. As shown in Figure 10A, when i_c crosses 0 at t = 305.08 ms, u_c decreases to a negative value, and T₂ and T₅ are turned off. After that, S₂ is opened to isolate the permanent fault.

FIGURE 10

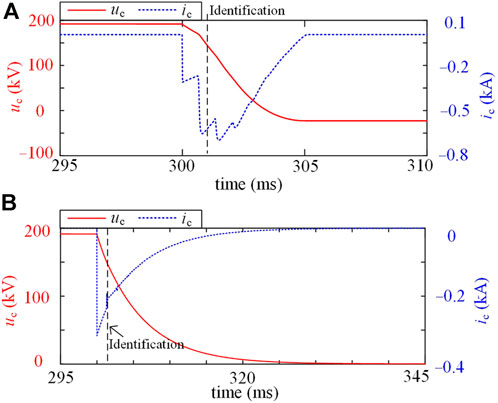
FIGURE 10. Simulation results during reclosing: (A) permanent metallic fault: (B) permanent high resistance fault.

At the initial stage of reclosing, i_c undergoes multiple abrupt changes because of the traveling wave effect. The traveling impact decreases over time and is not significant after 302.5 ms. At t = 305.08 ms, the zero crossing of i_c is caused by the underdamped discharge process rather than the traveling effect, which is consistent with the analysis in Section 3.2.

4.3.2 Permanent high-resistance fault

We set a permanent fault at the B₂ side of Line 4, and the fault resistance is 500 Ω. After the interruption, B₁ begins to reclose at t = 300 ms. As shown in Figure 10B, u_c decreases to u_th = 140.7 kV at t = 301.76 ms; thus, the permanent fault is identified. Because the fault resistance is large, the capacitor discharge process is overdamped. At t = 320 ms, u_c decreases to 6.7 kV and i_c is smaller than 10 A. Then, S₂ begins to be opened, and the fault is totally isolated at t = 340 ms.

4.4 Reclosing with a transient fault

After isolating a transient fault on Line 4, B₁ begins to reclose at t = 300 ms; thus, a current traveling wave is injected into Line 4. The current traveling wave transmits along Line 4 and is totally reflected at the end of Line 4. As shown in Figure 11A, at t = 301.40 ms, the current reflection wave arrives at the head of Line 4 and causes i_c to cross 0, because the reflected wave is in the opposite polarity of the original traveling wave. After that, u_c maintains at 151 kV. At t = 306.36 ms, the criterion in Eq. 7 is activated, indicating that the fault on Line 4 has disappeared. After that, B₁ turns on T₁ and T₅; thus, the DC grid charges the capacitor C and Line 4 through the resistor R₂. Finally, the capacitor C is charged to the system voltage.

FIGURE 11

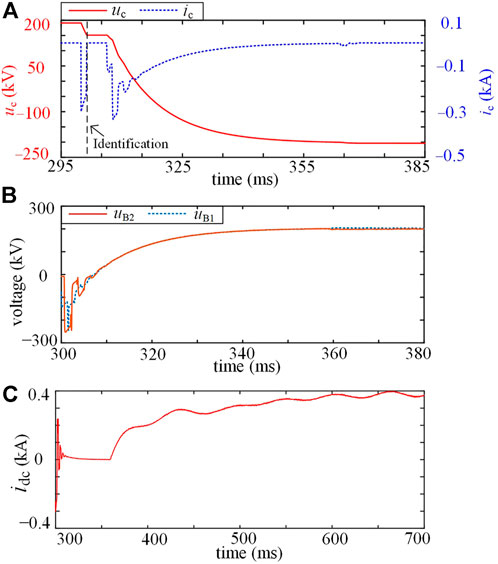
FIGURE 11. Simulation results during reclosing with a transient fault: (A) the value of uc and ic; (B) line voltages uB1 and uB2; (C) line current idc.

As shown in Figure 11B, the voltage of Line 4 on B₁ side, marked as u_B1, increases to 190 kV at t = 339.20 ms, and B₁ begins to close S₁. At t = 339.24 ms, the voltage of Line 4 on B₂ side, marked as u_B2, increases to 190 kV; thus, B₂ directly identifies that the line fault has disappeared, and S₁, S₂, FD and LCS in B₂ are successively closed. After that, u_B1 and u_B2 gradually recover to close to 200 kV.

During the reclosing process, the discharging of the capacitor and charging of Line 4 cause negative and positive abrupt changes in i_dc, respectively, as shown in Figure 11C. After t = 360 ms, MCs of B₁ and B₂ have been closed; thus, i_dc begins to restore to the normal value. Line 4 begins to restore the power transmission. This restoration process takes hundreds of milliseconds. A special control strategy can be used to improve the restoration speed, which will be considered in future work.

4.5 Comparisons

In this section, the C-DCCBs in (Liu, 2019), (Wu et al., 2019) and (Guo et al., 2020) are compared with the proposed C-DCCB.

4.5.1 Interruption performance

In these C-DCCBs, only the C-DCCB in (Liu, 2019) opens the FD with arcing, which increases the FD operation time. Thus, when the same FD is used, the C-DCCB in (Liu, 2019) has a longer interruption time than the other three C-DCCBs. For the other three C-DCCBs, the fault current decreases within a few hundred microseconds after the FD recovers the dielectric strength, indicating a quick interruption speed.

Except for the MC, the C-DCCB in (Liu, 2019) cannot provide another current path to conduct the load current, whereas the other three C-DCCBs can conduct the load current using the thyristors in the MB. Therefore, the C-DCCB in (Liu, 2019) does not have the pre-activation ability, whereas the other three C-DCCBs have the pre-activation ability. Combining the protection and pre-activation, these three C-DCCBs can further reduce the interruption time.

During the interruption of backward direction currents, the C-DCCB in (Liu, 2019) cannot decrease the FD current to 0 until the capacitor discharge current is reversed, causing a larger interruption time. In (Wu et al., 2019), the C-DCCB interrupts only the forward direction currents and cannot interrupt the backward direction fault currents. Because of the symmetry of topology, the proposed C-DCCB can interrupt bidirectional currents with the same performance, and the C-DCCB in (Guo et al., 2020) also has this interruption characteristic.

4.5.2 Semiconductor cost

The peak TIV of these C-DCCBs, marked as U_p, is selected as 300 kV to compare the semiconductor cost. For the proposed C-DCCB, T₁ and T₂ are turned off during the interruption of the forward direction and backward direction currents, respectively. They should be composed of fast thyristor modules to maintain a short interruption time. The thyristors T₃ and T₄ are naturally turned off after the interruption, and the thyristor T₅ is naturally turned off after the precharge process; thus, thyristors T₃, T₄ and T₅ can be composed of phase-control thyristor modules. Then, the proposed C-DCCB contains phase-control thyristor modules with a voltage rating of 3U_p, fast thyristor modules with a voltage rating of 2U_p, and diode modules of 3U_p.

For the C-DCCB in (Liu, 2019), a triggered spark gap or reverse-conducting thyristor can be used to trigger the capacitor discharge during the interruption. The reverse-conducting thyristor comprises phase-control thyristor modules with a voltage rating of U_p and diode modules with a voltage rating of U_p. In (Wu et al., 2019), three thyristors need to be turned off during the interruption process. They should be composed of fast thyristor modules with a voltage rating of 3U_p; one thyristor is naturally turned off after the interruption and can be composed of phase-control thyristor modules with a voltage rating of U_p. In (Guo et al., 2020), one thyristor is turned off during the interruption process and composed of fast thyristor modules with a voltage rating of U_p. In addition, phase-control thyristor modules with a voltage rating of 5U_p and diode modules with a voltage rating of 5U_p are also needed in (Guo et al., 2020).

We assume that the thyristor module N2825TE400 (4 kV, ¥ 3,723 (findic and digikey, 2021)), fast thyristor module 5STF 28H2060 (2 kV, ¥ 2,755 (findic and digikey, 2021)) and diode module W3082MC450 (4.5 kV, ¥ 1,610 (findic and digikey, 2021)) are used, and a safety voltage margin of 2 is maintained. Then, the device costs of these C-DCCBs are given in Table 3, and the unit of device costs is RMB. The C-DCCBs in (Liu, 2019) and (Guo et al., 2020) have the smallest and largest semiconductor costs, respectively, and the proposed C-DCCB has a higher semiconductor cost than the C-DCCB in (Wu et al., 2019).

TABLE 3

TABLE 3. Semiconductor costs of C-DCCBs.

According to the evaluation method in (Evans et al., 2019), the capacitor C of 9 μF in the proposed C-DCCB has a cost of ¥ 2,231,323, which is more than half of the total semiconductor cost of ¥ 3,975,570. Thus, the capacitor cost is vital for evaluating the construction cost of C-DCCBs. For C-DCCBs, the capacitor value is related to the interruption conditions, such as voltage rating and interruption capacity. Comparing capacitor costs of C-DCCBs should be based on the same interruption conditions. Considering that the capacitor values in (Liu, 2019), (Wu et al., 2019), (Guo et al., 2020) and this paper are selected based on different interruption conditions, the capacitor costs are not compared to avoid injustice.

4.5.3 Reclosing performance

For the C-DCCB in (Liu, 2019), the polarities of the capacitor voltage are in the opposite directions before and after the interruption. The C-DCCB in (Liu, 2019) requires additional circuits to restore the normal state of the capacitor before reclosing, which increases the construction cost and is not conducive to fast reclosing. The C-DCCB in (Wu et al., 2019) has the same polarity of capacitor voltage before and after the interruption, and the C-DCCB in (Guo et al., 2020) can quickly restore the initial capacitor voltage using the grounded branch. Thus, these two C-DCCBs have a fast reclosing ability.

However, direct reclosing rather than adaptive reclosing is considered in previous papers. The direct reclosing strategy directly recloses the C-DCCB to reconnect the HVDC grid to the isolated line, and the C-DCCB interrupts the fault current in case of permanent faults. Considering that these C-DCCBs have similar performances during the direct reclosing, the proposed C-DCCB is used to perform the direct reclosing to validate the advantage of the proposed adaptive reclosing strategy.

For the first direct reclosing method, which is marked as DR1, the proposed C-DCCB successively closes S₁, S₂ and FD. For the second direct reclosing method, which uses the pre-activation ability and is marked as DR2, the proposed C-DCCB successively closes S₁—S₂ and turns on T₁—T₂, and then the system current is commutated into the MC by closing FD and turning on LCS. Compared with the DR1, the DR2 effectively reduces the interruption time during the permanent fault because the process of commutating the fault current from MC into MB is avoided. The proposed adaptive reclosing strategy is marked as AR.

We set a permanent metallic fault at the head of Line 4. For DR1 and DR2, we assume that the fault detection time is only 0.2 ms. As shown in Figure 12, compared with DR1, DR2 reduces the maximum value of i_dc from 9.73 to 2.11 kA because DR2 has a much shorter interruption time. For the proposed adaptive reclosing strategy, the maximum absolute value of i_dc is only 1.22 kA. Therefore, compared with direct reclosing strategies, the proposed adaptive reclosing strategy effectively limits the fault current during the permanent fault.

FIGURE 12

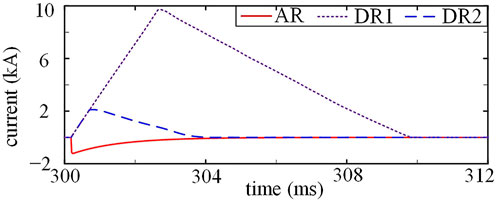
FIGURE 12. Waveforms of idc when the C-DCCB recloses with a permanent fault using different reclosing strategies.

We set a transient fault at Line 4, and B₁ recloses using different reclosing strategies. The simulation results are shown in Figure 13. For DR1 and DR2, the HVDC grid directly charges the positive pole of Line 4, causing oscillations in the Bus1 voltage u_bus1, and DR1 and DR2 almost have the same waveforms of u_bus1. For the adaptive reclosing strategy, the HVDC grid charges the positive pole of Line 4 and the internal capacitor of C-DCCB through the resistor R₂ at 301.6 ms; thus, u_bus1 drops to 168 kV and then quickly returns to the normal value without significant oscillations. Compared with direct reclosing strategies, the adaptive reclosing strategy effectively reduces the voltage oscillations in HVDC grids.

FIGURE 13

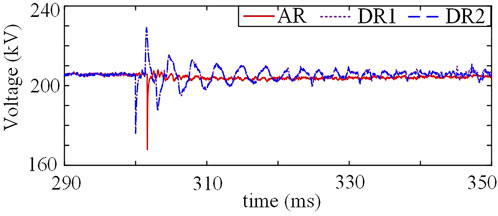
FIGURE 13. Waveforms of ubus1 when the C-DCCB recloses with a transient fault using different reclosing strategies.

5 Conclusion

This paper proposes a novel C-DCCB with adaptive reclosing ability. The parameter design is analyzed to ensure the reliable turn-off of the thyristor, which is key to the successful interruption. The transient process during adaptive reclosing is analyzed to identify the fault property. The semiconductor cost, interruption and reclosing performances of the proposed C-DCCB are compared with those of previous C-DCCBs. The main conclusions are summarized as follows.

1) The proposed C-DCCB achieves good interruption performances, such as quick interruption speed and pre-activation ability. During interruptions, the fault current decreases within a few hundred microseconds after the FD restores the dielectric strength. Using the pre-activation, the fault current is commutated into the MB during the protection time, thus effectively reducing the interruption time.

2) During the adaptive reclosing, the internal capacitor has a large initial voltage and discharges through the grounded branch. The capacitor voltage decreases to a positive value when the fault is transient, and the capacitor voltage is no more than 0 when the fault is permanent; thus, the fault property is identified using the capacitor voltage.

3) The adaptive reclosing of C-DCCBs is less considered in previous papers. An adaptive reclosing strategy is designed for the proposed C-DCCB, which is the main contribution of this paper. Using the adaptive reclosing strategy, the proposed C-DCCB avoids the second fault shock in case of permanent faults, and the power transmission is restored without significant voltage oscillations in transient faults.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

ZX: Writing-Original Draft, Visualization. JL: Writing–Review and Editing, Supervision. YG: Conceptualization, Methodology, Writing-Original Draft. YW: Supervision.

Funding

This work is supported by the National Natural Science Foundation of China (52107130).

Acknowledgments

This is a brief acknowledgement of the contributions of individual colleagues, institutions, or agencies that assisted the writers’ efforts in the writing of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

An, T., Tang, G., and Wang, W. (2017). Research and application on multi-terminal and DC grids based on VSC-HVDC technology in China. High. Volt. 2, 1–10. doi:10.1049/hve.2017.0010

CrossRef Full Text | Google Scholar

Augustin, T., Becerra, M., and Nee, H.-P. (2021). Enhanced active resonant DC circuit breakers based on discharge closing switches. IEEE Trans. Power Deliv. 36 (3), 1735–1743. doi:10.1109/tpwrd.2020.3014084

CrossRef Full Text | Google Scholar

Bucher, M. K., and Franck, C. M. (2016). fault current interruption in multiterminal HVDC networks. IEEE Trans. Power Deliv. 31 (1), 87–95. doi:10.1109/tpwrd.2015.2448761

CrossRef Full Text | Google Scholar

Chen, M., Xu, H., and Zhang, Z. (2018). Design and simulation of coupling mechanical high voltage DC circuit breaker. High. Volt. Eng. 44 (2), 380–387.

Google Scholar

Chen, W., Zeng, R., He, J., Wu, Y., Wei, X., Fang, T., et al. (2021). Development and prospect of direct-current circuit breaker in China. High. Volt. 6, 1–15. doi:10.1049/hve2.12077

CrossRef Full Text | Google Scholar

Cigré (2014). TB604—guide for the development of models for HVDC converters in a HVDC grid joint working group B4.57.

Google Scholar

Evans, N., Dworakowski, P., Al-Kharaz, M., Hegde, S., Perez, E., and Morel, F. (2019). “Cost-performance framework for the assessment of Modular Multilevel Converter in HVDC transmission applications,” in IECON 2019- 45th annual conference of the (Lisbon, Portugal: IEEE Industrial Electronics Society), 4793–4798.

CrossRef Full Text | Google Scholar

findic and digikey (2021). findic digikey. Available: https://www.findic.com/https://www.digikey.com/(accessed on Aug. 19, 2021).

Gómez, P., and Uribe, F. A. (2009). The numerical Laplace transform: An accurate technique for analyzing electromagnetic transients on power system devices. Int. J. Electr. Power & Energy Syst. 31 (2–3), 116–123. doi:10.1016/j.ijepes.2008.10.006

CrossRef Full Text | Google Scholar

Guo, Y., Li, H., Liang, Y., and Wang, G. (2021). A method to calculate short-circuit faults in high-voltage DC grids. IEEE Trans. Power Deliv. 36 (1), 267–279. doi:10.1109/tpwrd.2020.2978625

CrossRef Full Text | Google Scholar

Guo, Y., Wang, G., Zeng, D., Li, H., and Chao, H. (2020). A thyristor full-bridge-based DC circuit breaker. IEEE Trans. Power Electron. 35 (1), 1111–1123. doi:10.1109/tpel.2019.2915808

CrossRef Full Text | Google Scholar

Hafner, J., and Jacobson, B. (2011). “Proactive hybrid HVDC breakers—a key innovation for reliable HVDC grids,” in CIGRE bologna conf, 1–8.

Google Scholar

Hassanpoor, A., Hafner, J., and Jacobson, B. (2015). Technical assessment of load commutation switch in hybrid HVDC breaker. IEEE Trans. Power Electron. 30 (10), 5393–5400. doi:10.1109/tpel.2014.2372815

CrossRef Full Text | Google Scholar

Hertem, V., and Ghandhari, M. (2010). “Multi-terminal VSC HVDC for the European supergrid: Obstacles. Renew. Sustain. Energy Rev. 14, 3156–3163.

Google Scholar

Jamshidifar, A., and Jovcic, D. (2018). Design, modeling and control of hybrid DC circuit breaker based on fast thyristors. IEEE Trans. Power Deliv. 33 (2), 919–927. doi:10.1109/tpwrd.2017.2761022

CrossRef Full Text | Google Scholar

Jovcic, D., Tang, G., and Pang, H. (2019). Adopting circuit breakers for high-voltage dc networks: Appropriating the vast advantages of dc transmission grids. IEEE Power Energy Mag. 17 (3), 82–93. doi:10.1109/mpe.2019.2897408

CrossRef Full Text | Google Scholar

Li, B., He, J., Li, Y., and Wen, W. (2020). A novel DCCB reclosing strategy for the flexible HVDC grid. IEEE Trans. Power Deliv. 35 (1), 244–257. doi:10.1109/tpwrd.2019.2938594

CrossRef Full Text | Google Scholar

Liu, C., (2019). “535kV high voltage DC circuit breaker insulation test analysis,” in 2019 5th international conference on electric power equipment - switching technology (Kitakyushu, Japan: ICEPE-ST), 580–584.

Google Scholar

Mei, J., Ge, R., Zhu, P., Fan, G., Wang, B., and Yan, L. (2021). An adaptive reclosing scheme for MMC-HVDC systems based on pulse injection from parallel energy absorption module. IEEE Trans. Power Deliv. 36 (3) 1809–1818. doi:10.1109/tpwrd.2020.3015311

CrossRef Full Text | Google Scholar

Pei, X., Tang, G., and Zhang, S. (2019). Sequential auto-reclosing strategy for hybrid HVDC breakers in VSC-based DC grids. J. Mod. Power Syst. Clean. Energy 7 (3), 633–643. doi:10.1007/s40565-018-0486-1

CrossRef Full Text | Google Scholar

Shi, Z., Zhang, Y., Jia, S., Song, X., Wang, L., and Chen, M. (2015). Design and numerical investigation of a HVDC vacuum switch based on artificial current zero. IEEE Trans. Dielectr. Electr. Insul. 22 (1), 135–141. doi:10.1109/tdei.2014.004533

CrossRef Full Text | Google Scholar

Sima, W., Fu, Z., Yang, M., Yuan, T., Sun, P., Han, X., et al. (2019). A novel active mechanical HVDC breaker with consecutive interruption capability for fault clearances in MMC-HVDC systems. IEEE Trans. Ind. Electron. 66 (9), 6979–6989. doi:10.1109/tie.2018.2878115

CrossRef Full Text | Google Scholar

Song, G., Wang, T., and Hussain, K. S. T. (2019). DC line fault identification based on pulse injection from hybrid HVDC breaker. IEEE Trans. Power Deliv. 34 (1), 271–280. doi:10.1109/tpwrd.2018.2865226

CrossRef Full Text | Google Scholar

Technical Information (2012). Bipolar semiconductors. Infineon. Available: https://www.infineon.com/cms/de/product/power/high-power-diodes-thyristors/thyristor-diode-discs/?redirId=28573#! documents.

Google Scholar

Torwelle, P., Bertinato, A., Grieshaber, W., Yang, Y., Raison, B., Le, T. D., et al. (2021). Pre-energization concept for overhead lines in MTDC grids using DCCB internal capacitor. IEEE Trans. Power Deliv. 37 (1–1), 155–164. doi:10.1109/tpwrd.2021.3054599

CrossRef Full Text | Google Scholar

Wang, T., Song, G., and Hussain, K. S. T. (22032019). Adaptive single-Pole auto-reclosing scheme for hybrid MMC-HVDC systems. IEEE Trans. Power Deliv. 34 (6), 2194–2203. doi:10.1109/tpwrd.2019.2921674

CrossRef Full Text | Google Scholar

Wen, W., Huang, Y., Sun, Y., Wu, J., Al-Dweikat, M., and Liu, W. (2016). Research on current commutation measures for hybrid DC circuit breakers. IEEE Trans. Power Deliv. 31 (4), 1456–1463. doi:10.1109/tpwrd.2016.2535397

CrossRef Full Text | Google Scholar

Wen, W., Liu, H., Li, B., Li, P., Zhang, N., Gao, C., et al. (41332021). Novel reclosing strategy based on transient operating voltage in pseudobipolar DC system with mechanical DCCB. IEEE Trans. Power Electron. 36 (4), 4125–4133. doi:10.1109/tpel.2020.3022070

CrossRef Full Text | Google Scholar

Wen, W., Wang, Y., Li, B., Huang, Y., Li, R., and Wang, Q. (94312018). Transient current interruption characteristics of a novel mechanical DC circuit breaker. IEEE Trans. Power Electron. 33 (11), 1. doi:10.1109/tpel.2018.2797243

CrossRef Full Text | Google Scholar

Wu, Y., Wu, Y., Rong, M., and Yang, F. (2019). Development of a novel HVdc circuit breaker combining liquid metal load commutation switch and two-stage commutation circuit. IEEE Trans. Ind. Electron. 66 (8), 6055–6064. doi:10.1109/tie.2018.2870387

CrossRef Full Text | Google Scholar

Wu, Y., Wu, Y., Yang, F., Rong, M., and Hu, Y. (2020). A novel current injection DC circuit breaker integrating current commutation and energy dissipation. IEEE J. Emerg. Sel. Top. Power Electron. 8 (3), 2861–2869. doi:10.1109/jestpe.2019.2911103

CrossRef Full Text | Google Scholar

Wu, Y., Wu, Y., Yang, F., Rong, M., and Hu, Y. (2020). Bidirectional current injection MVDC circuit breaker: Principle and analysis. IEEE J. Emerg. Sel. Top. Power Electron. 8 (2), 1536–1546. doi:10.1109/jestpe.2018.2888590

CrossRef Full Text | Google Scholar

Yang, S., Xiang, W., Lu, X., Zuo, W., and Wen, J. (11232020). An adaptive reclosing strategy for MMC-HVDC systems with hybrid DC circuit breakers. IEEE Trans. Power Deliv. 35 (3), 1111–1123. doi:10.1109/tpwrd.2019.2935311

CrossRef Full Text | Google Scholar

Zhang, S., Zou, G., Xu, C., and Sun, W. (2020). A reclosing scheme of hybrid DC circuit breaker for MMC-HVDC systems. IEEE J. Emerg. Sel. Top. Power Electron. 9, 7126–7137. doi:10.1109/jestpe.2020.3025598

CrossRef Full Text | Google Scholar