Accelerating transmission-constrained unit commitment via a data-driven learning framework

As a fundamental task in power system operations, transmission-constrained unit commitment (TCUC) decides ON/OFF state (i.e., commitment) and scheduled generation for each unit. Generally, TCUC is formulated as a mixed-integer linear programming (MILP) and must be resolved within a limited time window. However, due to the NP-hard property of MILP and the increasing complexity of power systems, solving the TCUC within a limited time is computationally challenging. Regarding the computation challenge, the availability of historical TCUC data and the development of the machine learning (ML) community are potentially helpful. To this end, this paper designs an ML-aided framework that can leverage historical data in enabling computation improvement of TCUC. In the offline stage, ML models are trained to predict the commitments based on historical TCUC data. In the online stage, the commitments are quickly predicted using the well-trained ML. Furthermore, a feasibility checking process is conducted to ensure the commitment feasibility. As a result, only a reduced TCUC with fewer binary variables needs to be solved, leading to computation acceleration. Case studies on an IEEE 24-bus and a practical 5655-bus system show the effectiveness of the presented framework.

1 Introduction

The transmission-constrained unit commitment (TCUC) problem has been widely regarded as one of the most fundamental applications in power system operations Li et al. (2022, 2021a,b, 2020); Wu J. et al. (2021); Liu et al. (2021b). In practice, the TCUC is routinely implemented by Independent System Operators (ISO) to clear the day-ahead electricity market within 4–6 h Chen et al. (2022a, 2016); Liu et al. (2020, 2021a); Chen et al. (2021); Ma et al. (2021). Toward a specific power system consisting of massive transmission lines and units, TCUC is mathematically formulated as a mixed-integer linear programming (MILP) with massive binary and continuous variables, as well as prevailing constraints. Aiming at least operation cost, the MILP-based TCUC determines the optimal ON/OFF state (i.e., commitment) and scheduled generation of each unit to clear the electricity market. Typically, ISOs apply powerful commercial solvers (e.g., Gurobi) to solve the MILP-based TCUC problem on a daily basis Zhang et al. (2020).

Due to the rapid development of modern power systems, the size and the complexity of TCUC increased significantly. For example, 42,705 buses and 1,258 units exist in the Midcontinent ISO Chen et al. (2013), resulting in a MILP-based TCUC model with hundreds of thousands of variables and constraints. Moreover, it is well known that the MILP problems belong to the class of NP-hard problems. Consequently, an ongoing challenge in ISOs is how to efficiently solve such a large-size MILP problem within a limited time window.

Regarding the computation challenge, developments in the machine learning (ML) community enable various ML algorithms [e.g., deep neural network (DNN), decision tree (DT), random forest (RF), and k-nearest neighbors (k-NN)] to be practically helpful Nair et al. (2020). For example, Google Research Team successfully developed a DNN-based framework that can quickly solve large-size MILP problems without optimality loss. The core is leveraging the massive historical MILP instances to train an array of sophisticated heuristic processes in the DNN. As long as the new features are available, the well-trained DNN can quickly yet accurately predict the binary solutions. However, even though the DNN in Nair et al. (2020) shows remarkable ability to solve MILP, it is still difficult to convince ISOs to replace mathematical-programming-based commercial solvers with the black-box ML algorithms. This is because the black-box solutions may not satisfy all the physical constraints. Indeed, Álinson et al. Xavier et al. (2021) pointed out that combining ML algorithms and off-the-shelf solvers is more practical and reliable regarding improving TCUC computation.

Inspired by the above problems, this paper presents a data-driven ML-aided framework for improving the TCUC computation while maintaining enough solution quality. First, the historical TCUC optimal solutions and their corresponding features are collected. Furthermore, the unit generation pattern is analyzed, so that a target set ${\mathcal{I}}^{\mathit{tar}}$ consisting of units to be predicted can be identified. Under the lens of ML, determining the commitments is essentially a multi-label classification problem. Therefore, ML algorithms (i.e., DNN, DT, RF, and k-NN) with remarkable multi-label classification ability are trained to predict the commitments for the target units. Moreover, a feasibility checking process is conducted to ensure the physical feasibility of the predicted commitments. The corresponding variables are fixed if the commitments are feasible; otherwise, they are utilized as warm-starting solutions for Branch-and-Bound algorithm. As a result, Gurobi could solve a MILP-based TCUC with fewer binaries, which is computationally easier than the original version.

The main works of this paper are summarized as follows:

• A data-driven ML-aided framework is presented for improving the TCUC computation. The framework possesses general and plug-and-play properties. That is, it is compatible with various ML classification algorithms and the ISOs’ practice. Most importantly, the feasibility checking process ensures that the predicted commitments satisfy all the constraints.

• Taking DNN, DT, RF, and k-NN as core, case studies are conducted on an IEEE 24-bus system and a practical 5655-bus system, showing the computation benefits of the framework. In addition, our results report an interesting observation: the most naive k-NN significantly outperforms DNN, DT, and RF under the framework. This observation implies that learning TCUC could be a low-hanging fruit Pineda and Morales (2021) not requiring sophisticated methods. To improve the transparency of this paper, the datasets and the ML codes have been uploaded at Lin (2022).

The remaining parts are organized as follows: Section 2 reviews related works; Section 3 introduces the mathematical model of TCUC; Section 4 expounds the presented framework; Section 5 shows the experimental results; Section 6 concludes this paper.

2 Related works

Leveraging the black-box ML algorithms to solve TCUC can be traced back to the 90s when Huang et al. Huang and Huang (1997) combined neural networks and dynamic programming for solving TCUC. After the 20th century, the breakthroughs of commercial solvers enabled the mathematical programming (white-box methods) to be mainstream in solving TCUC.

In recent years, the significant progress of the ML community has awakened the interest in applying ML to TCUC Yang and Wu (2021). Typically, the main applications can be categorized into 1) explicitly describing the operation rules that are difficult to describe in the TCUC model mathematically Li et al. (2019); Zhang et al. (2021); Hou et al. (2020); Chen et al. (2022b); Ye et al. (2019), 2) simplifying the TCUC model Mohammadi et al. (2021); Yang et al. (2020); Wu T. et al. (2021); Pineda et al. (2020), and 3) accelerating the TCUC computation performance de Mars and O’Sullivan (2021); Nikolaidis and Chatzis (2021); Pineda and Morales (2021); Xavier et al. (2021); Yang et al. (2021); Zhou et al. (2018); Zhou et al. (2021).

Explicitly describing the operation rules. Li et al. Li et al. (2019) applied a centralized Q-learning-based method that requires no prior information on the actual cost functions, thus can handle the cases that TCUC cost functions are indescribable mathematically. Similarly, Zhang et al. (2021) utilized DNN to encode the complicated frequency response as constraints in the TCUC model. In Hou et al. (2020), a sparse oblique DT was deployed to extract security rules as sparse constraints. As a matter of fact, learning to approximate the mathematically indescribable rules of TCUC explicitly has been gradually recognized as an excellent alternative to improve the TCUC performance. In Chen et al. (2022b), Chen et al. employed a closed-loop predict-and-optimize method to learn the RES prediction that can lead to better TCUC economics. In addition, one desirable byproduct of such learning is the better TCUC computation performance. For example, Ye et al. (2019) combined deep learning and reinforcement learning to handle the computation intractability caused by the non-convexity in a bi-level electricity market model.

Simplifying the TCUC model. An important reason for the difficulty of TCUC computation is the massive physical constraints. In fact, a large part of the constraints is redundant. Thus, ISOs can remove these constraints without affecting the optimal solution. For example, Midcontinent ISO governs a system with 42,705 buses but only considers about 20 transmission constraints in TCUC. As a result, leveraging ML to filter out the redundant constraints is valuable. In Mohammadi et al. (2021), a tree method was employed to relieve the heavy computation burden by removing redundant constraints (most of them are transmission constraints) from the original MILP-based TCUC model. In Yang et al. (2020), support vector machine, RF, and neural network were applied to classify whether a TCUC problem is a hard case. If identified as a hard case, the decision variables are aggregated and reduced, leading to a computationally easier TCUC. In Wu T. et al. (2021), the commitment variables were directly decided by a convolutional neural network. Thus the operators only need to solve a small-scale convex optimization, leading to remarkable computation improvement. Furthermore, Pineda et al. Pineda et al. (2020) designed a simple yet effective k-NN-based method to learn the congestion status of transmission lines so that the redundant and inactive transmission constraints can be removed. According to the experiments in Mohammadi et al. (2021); Pineda et al. (2020); Yang et al. (2020); Wu T. et al. (2021), simplifying the TCUC model by filtering out certain constraints is valuable for practical TCUC.

Accelerating the TCUC computation performance. This paper falls in this category, which is to accelerate TCUC computation while trying to avoid quality losses as much as possible. This category can be further divided into two sub-categories 1) using ML for solving TCUC directly Nikolaidis and Chatzis (2021); Zhou et al. (2018); de Mars and O’Sullivan (2021); Yang et al. (2021) and 2) using ML to aid commercial solvers for solving TCUC Xavier et al. (2021); Zhou et al. (2021); Pineda and Morales (2021). In Nikolaidis and Chatzis (2021), the authors developed a Gaussian-process-based Bayesian optimization for quickly solving TCUC and showed the effectiveness in the medium system. In Zhou et al. (2018), reinforcement learning was deployed to enable multi-objective TCUC solutions to bypass local optimum. In de Mars and O’Sullivan (2021), a purely data-driven method that can simulate experts was presented to solve TCUC, which shows remarkable ability in a practical system. Moreover, Yang et al. (2021) designed a guided tree to solve TCUC, which computationally outperforms the unguided tree. Even though experimental results in Nikolaidis and Chatzis (2021); Zhou et al. (2018); de Mars and O’Sullivan (2021); Yang et al. (2021) highlighted certain preferable advantages of these black-box ML algorithms, they lack comprehensive comparisons to the state-of-the-art solvers. On the other hand, Zhou et al. (2021) leveraged the classification-based method to identify useful TCUC instances, of which binary variables are strategically utilized to fix that in the new TCUC instance. According to their experiments, the method leads to 58.82% computation improvement in a Polish 2382-bus system while guaranteeing good solution quality. Furthermore, Álinson et al. Xavier et al. (2021) designed a framework involving k-NN and support vector machine for boosting the computation performance of the commercial solvers. According to their comprehensive experiments in 9 large-size systems, the speedup achieves 17.47x without loss in solution optimality. As a result, Pineda and Morales (2021) concluded that even a naive ML algorithm could significantly boost the computation performance in solver-based TCUC solving.

Instead of focusing on a single ML algorithm, this paper presents a general ML-aided framework compatible with various ML classification algorithms (i.e., DNN, DT, RF, and k-NN). Additionally, the ML-aided framework is compared to the traditional way based entirely on the commercial solvers. As a result, case studies in IEEE 24-bus and practical 5655-bus systems show the computation benefits.

3 Mathematical model of transmission-constrained unit commitment

The TCUC is modeled as in Eqs 1–13. The objective Eq. 1 is to minimize the total operation cost z, including start-up, shut-down, and generation costs. Regarding the unit constraints, Eqs 2, 3 indicate the minimum ON/OFF constraints; Eqs 4, 5 describe the linearized generation cost using $|\mathcal{K}|$ segments; Eq. 6 limits the generation for each segment; Eq. 7 expresses the generation limitations; Eq. 8 represents the logical relationship of the binary variables; Eqs 9, 10 are the ramping constraints; Eq. 11 limits the scheduled RES power within its availability. The system constraints include power balance Eq. 12 and transmission capabilities Eq. 13. Generally, ISOs solve TCUC Eqs 1–13 as long as the load demand $\widehat{\mathit{L}}$ and RES power $\widehat{\mathit{W}}$ are accessible. Therefore, the TCUC cost $z(\widehat{\mathit{L}},\widehat{\mathit{W}})$ is represented as the function of $\widehat{\mathit{L}}$ and $\widehat{\mathit{W}}$.

$z\left(\widehat{\mathit{L}},\widehat{\mathit{W}}\right)≔\underset{\mathit{x}}{\min }\sum _{t\in \mathcal{T}}\sum _{i\in \mathcal{I}}\left(C_i^{su}{I}_{ti}^{su}+C_i^{sd}{I}_{ti}^{sd}+C_{ti}^p\right).(1)$

$\begin{array}{lll}\hfill & \mathit{\text{Unit}}\mathit{\text{constraints:}}\hfill & \hfill \\ \hfill & {\sum }_{t^{\prime }=t-T_i^u+1}^t{I}_{t^{\prime }i}^{su}\le I_{ti}\hfill & \hfill & \forall t\in {\mathcal{T}}_i^u,i\in \mathcal{I}\hfill \end{array}(2)$

${\sum }_{t^{\prime }=t-T_i^d+1}^t{I}_{t^{\prime }i}^{sd}\le 1-I_{ti}\forall t\in {\mathcal{T}}_i^d,i\in \mathcal{I}(3)$

$C_{ti}^p=N_i{I}_{ti}+{\sum }_{k\in \mathcal{K}}{C}_{ik}^{\mathit{seg}}{P}_{\mathit{tik}}^{\mathit{seg}}\forall t\in \mathcal{T},i\in \mathcal{I}(4)$

$P_{ti}={\sum }_{k\in \mathcal{K}}{P}_{\mathit{tik}}^{\mathit{seg}}\forall t\in \mathcal{T},i\in \mathcal{I}(5)$

$0\le P_{\mathit{tik}}^{\mathit{seg}}\le I_{ti}{\bar{P}}_{ik}^{\mathit{seg}}\forall t\in \mathcal{T},i\in \mathcal{I},k\in \mathcal{K}(6)$

$I_{ti}{P}_i^{\mathit{min}}\le P_{ti}\le I_{ti}{P}_i^{\mathit{max}}\forall t\in \mathcal{T},i\in \mathcal{I}(7)$

$I_{ti}^{su}-I_{ti}^{sd}=I_{ti}-I_{t-1,i}\forall t\in \mathcal{T},i\in \mathcal{I}(8)$

$\begin{array}{c}{P}_{ti}-P_{t-1,i}\le P_i^{\mathit{max}}\left(1-I_{ti}\right)+R_i^{up}{I}_{t-1,i}+R_i^{su}\left(I_{ti}-I_{t-1,i}\right)\\ \forall t\in \mathcal{T},i\in \mathcal{I}\end{array}(9)$

$\begin{array}{c}{P}_{t-1,i}-P_{ti}\le P_i^{\mathit{max}}\left(1-I_{t-1,i}\right)+R_i^{dn}{I}_{t,i}+R_i^{sd}\left(I_{t-1,i}-I_{ti}\right)\\ \forall t\in \mathcal{T},i\in \mathcal{I}\end{array}(10)$

$0\le W_{tj}\le {\widehat{W}}_{tj}\forall t\in \mathcal{T},j\in \mathcal{J}(11)$

$\begin{array}{llll}\hfill & \mathit{\text{System}}\mathit{\text{constraints:}}\hfill & \hfill & \hfill \\ \hfill & {\sum }_{i\in \mathcal{I}}{P}_{ti}+{\sum }_{j\in \mathcal{J}}{W}_{tj}={\sum }_{q\in \mathcal{Q}}{\widehat{L}}_{tq}\hfill & \hfill & \forall t\in \mathcal{T}\hfill \end{array}(12)$

$\begin{array}{c}-B_b\le {\sum }_{i\in \mathcal{I}}{\tau }_{ib}{P}_{ti}+{\sum }_{j\in \mathcal{J}}{\tau }_{jb}{W}_{tj}-{\sum }_{q\in \mathcal{Q}}{\tau }_{qb}{\widehat{L}}_{tq}\le B_b\\ \forall t\in \mathcal{T},b\in \mathcal{B}\end{array}(13)$

The computation intractability of MILP-based TCUC mainly stems from the binary variables I_ti, $I_{ti}^{su}$, and $I_{ti}^{sd}$. If the number of the binary variables is reduced, the model could be computationally easier. As a result, this paper aims to present a ML-aided framework for identifying the binary variables I_ti quickly, so that the computation burden of TCUC model can be relieved. However, the ML algorithms cannot consider the physical feasibility especially the minimum ON/OFF requirement Eqs 2, 3. Therefore, a feasibility checking stage is also designed.

4 The ML-Aided framework

First, this section describes the dataset processing. And then, the utilized ML algorithms and the tuned hyper-parameters are briefly introduced. Finally, the steps to implement the framework are expounded.

4.1 Construction of dataset

The construction of the dataset is shown as in Figure 1.

• A raw dataset is downloaded from Chen (2021). The dataset includes load demand ${\widehat{\mathit{L}}}_n$ and RES power ${\widehat{\mathit{W}}}_n$, ranging from 01/01/2018 to 12/31/2020 (1,096 dispatch days). The RES/load data of each dispatch day has 3 more variants. Therefore, 4384 RES/load instances exist and $|\mathcal{N}|=$ 4,384.

• Taking ${\widehat{\mathit{L}}}_n$ and ${\widehat{\mathit{W}}}_n$ as inputs, Gurobi is applied to solve TCUC Eqs 1–13 for each dispatch day $n\in \mathcal{N}$. As a result, $|\mathcal{N}|$ instances ${\mathcal{S}}_n^{\prime \prime }$ as in Eq. 14 are obtained.

${\mathcal{S}}_n^{\prime \prime }=\left\{{\widehat{\mathit{L}}}_n,{\widehat{\mathit{W}}}_n,{\mathit{I}}_n^{\star },z_n^{\star },o_n^{cs}\right\}\forall n\in \mathcal{N}(14)$

FIGURE 1

FIGURE 1. Steps to construct dataset.

For a system with $|\mathcal{Q}|$ load buses, $|\mathcal{J}|$ RES farms, and $|\mathcal{I}|$ units, the corresponding ${\widehat{\mathit{L}}}_n$, ${\widehat{\mathit{W}}}_n$, and ${\mathit{I}}_n^{\star }$ are $|\mathcal{T}|\times |\mathcal{Q}|$, $|\mathcal{T}|\times |\mathcal{J}|$, and $|\mathcal{T}|\times |\mathcal{I}|$ matrices, respectively.

• The row-sum operation is applied on ${\widehat{\mathit{L}}}_n$, resulting in a $|\mathcal{T}|\times$1 vector ${\tilde{\mathit{L}}}_n$. The tth element in ${\tilde{\mathit{L}}}_n$ represents the total system load at hour t of day n. As a result, ${\mathcal{S}}_n^{\prime \prime }$ Eq. 14 is converted into ${\mathcal{S}}_n^{\prime }$ Eq. 15. It should be noted that the row-sum operation is only applied on ${\widehat{\mathit{L}}}_n$. This is because ${\widehat{\mathit{L}}}_n$ includes overly redundant elements, which may result in the over-fitting issue.

${\mathcal{S}}_n^{\prime }=\left\{{\tilde{\mathit{L}}}_n,{\widehat{\mathit{W}}}_n,{\mathit{I}}_n^{\star },z_n^{\star },o_n^{cs}\right\}\forall n\in \mathcal{N}(15)$

• In the presented framework, each unit corresponds to a predictor. Thus, ${\mathcal{S}}_n^{\prime }$ is further divided for unit i, leading to ${\mathcal{S}}_{n,i}$ as in Eq. 16.

${\mathcal{S}}_{n,i}=\left\{{\tilde{\mathit{L}}}_n,{\widehat{\mathit{W}}}_n,{\mathit{I}}_{n,i}^{\star },z_n^{\star },o_n^{cs}\right\}\forall n\in \mathcal{N},i\in \mathcal{I}(16)$

Here, ${\mathit{I}}_{n,i}^{\star }$ is the optimal commitment decision of unit i at day n, which is a $|\mathcal{T}|\times$1 vector.

Taking $\{{\tilde{\mathit{L}}}_n,{\widehat{\mathit{W}}}_n\}$ as feature and ${\mathit{I}}_{n,i}^{\star }$ as label, the commitment predictor ${\mathcal{P}}_i$ as in Eq. 17 can be trained for unit i.

${\mathcal{P}}_i:{\mathbb{R}}^{\left(|\mathcal{T}|\cdot |\mathcal{Q}|+|\mathcal{T}|\cdot |\mathcal{J}|\right)\times 1}\to {\mathbb{R}}^{|\mathcal{T}|\times 1}(17)$

Under the lens of ML, this mapping is essentially a multi-label classification.

Finally, the dataset is divided into two parts for creating training and testing sets: 1) Training set (83%) ranging from 01/01/2018 to 06/30/2020, which is treated as historical dispatch days indexed by $h\in \mathcal{H}$. 2) Testing set (17%) ranging from 07/01/2020 to 12/31/2020, which is regarded as the upcoming days indexed by $d\in \mathcal{D}$. Eq. 18 states the relationship for the datasets.

$\mathcal{H}\cup \mathcal{D}=\mathcal{N}\mathcal{H}\cap \mathcal{D}=\varnothing (18)$

4.2 Machine learning algorithms

Among the various ML algorithms, DNN, DT, RF, and k-NN are utilized as the predictor.

4.2.1 Deep neural network

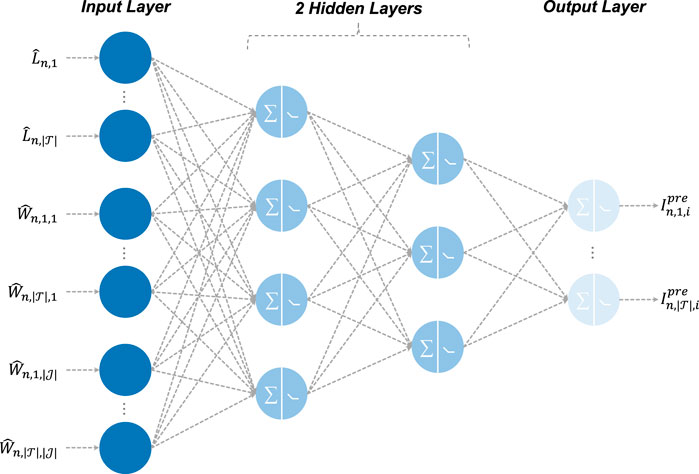
Essentially, DNN is an artificial neural network containing two or more hidden layers, which has been recognized as a powerful supervised ML algorithm. In the case of TCUC, a simple DNN with 2 hidden layers for unit i is sketched as in Figure 2.

FIGURE 2

FIGURE 2. Structure of an illustrative DNN.

The neurons in the hidden layers are based on certain activation functions, such as rectified linear unit Eq. 19 and threshold logic unit Eq. 20.

$ReLU=\max \left\{w_0+w_1{f}_1+\cdots +w_m{f}_m,0\right\}(19)$

$TLU=w_0+w_1{f}_1+\cdots +w_m{f}_m(20)$

Here, w₀ is a bias term and the remaining w indicate the weights assigned for the gray arrows; f indicates the inputs for the neurons. By combining many hidden layers, DNN has potential to approximate the complex mapping from RES/load to the optimal unit commitment.

Fine-tuning hyper-parameters, especially those for the hidden layer structure, are the key to obtaining a high-performance DNN. This paper utilizes a 10-fold grid search to identify the best combination of hidden layer structure hidden_layer_sizes = {(150, 150, 150), (150, 100, 50), (150, 150, 150, 150, 150, 150), (150, 125, 100, 75, 50, 25)} and coefficient of the norm-2 regularization alpha = {0.000001, 0.001, 1}. The adaptive moment estimation algorithm Pedregosa et al. (2011) is utilized for the weight optimization, due to its robustness. The rectified linear unit Eq. 19 is deployed as the activation functions, which can lead to faster training. DNN is sensitive to scaling, thus the features $\{{\tilde{\mathit{L}}}_n,{\widehat{\mathit{W}}}_n\}$ are normalized into [0,1].

4.2.2 Decision tree

DT is a supervised ML algorithm that good at multi-label classification. The most preferable property of DT is the interpretability, which can visualize the map from the features to the decisions. One byproduct caused by the interpretability is feature selection. That is, DT can show which attribute of feature has the most significant impact on the label. In the case of TCUC, the visualization can show which RES/load bus has the greatest impact on the commitment.

Additionally, DT can handle contextual data conveniently. For example, the weather information (e.g., sunny or rainy) can be utilized for training without digitization and normalization. Instead, this is somehow difficult for DNN.

The training of DT is essentially a process of minimizing Gini Impurity Eq. 21 or Entropy Eq. 22 for each node in a DT.

$G_e=1-\sum _{z\in \mathcal{Z}}{R_{e,z}}^2\forall e\in \mathcal{E}(21)$

$E_e=-\sum _{z\in \mathcal{Z},R_{e,z}\ne 0}{R}_{n,z}{\log }_2\left(R_{n,z}\right)\forall e\in \mathcal{E}(22)$

Here, $z/\mathcal{Z}$ indicates the index/set of commitment classes; $e/\mathcal{E}$ represents the index/set of the DT nodes; R_e,z means the ratio of commitment class z instances among the training instances in the node e.

According to Pedregosa et al. (2011), the Gini Impurity Eq. 21 and Entropy Eq. 22 generally lead to similar DT predictor. However, the former could be faster in terms of training. Therefore, Gini Impurity Eq. 21 is utilized. In DT, 4 hyper-parameters could affect the performance significantly, including the maximum depth of DT max_depth = {5, 6, 7, 8, 9}, the minimum number of samples required to split an internal node min_samples_split = {2, 4}, the minimum number of samples required to be at a leaf node min_samples_leaf = {2, 4}, the maximum number of leaf nodes max_leaf_nodes = {5, 25}. The best combination of these hyper-parameters are identified via a 10-fold grid search.

4.2.3 Random forest

Ensembling a number of DTs results in a RF. The RF makes predictions by comprehensively considering the voting results of the DTs. Thus, RF is regarded as a boosting version of DT. The RF and DT share similar properties (e.g., using Gini Impurity or Entropy for measuring quality), except the interpretability. This is because visualizing a tree is easy, but visualizing a forest is difficult and meaningless.

Regarding the hyper-parameters of RF, the number of DTs in the RF n_estimators = {5, 25, 50}, the maximum depth of the trees max_depth = {3, 5, 9}, the minimum number of samples required to split an internal node min_samples_split = {2, 4} are tuned via a 10-fold grid search. The quality measurement is set as Gini Impurity that is consistent with DT.

4.2.4 K-nearest neighbor

Compared to DNN, DT, and RF, k-NN is a naive ML algorithm. Essentially, k-NN conducts classification by identifying the closest instances from historical instances. In this paper, the following variant of k-NN with k = 1 is designed.

First, the most closest historical instances $h^{\prime }\in \mathcal{H}$ to dispatch day d is identified, as shown in Eq. 23.

$h^{\prime }≔\underset{h\in \mathcal{H}}{\mathrm{arg\; min}}{‖Vec\left({\tilde{\mathit{L}}}_d,{\widehat{\mathit{W}}}_d\right)-Vec\left({\tilde{\mathit{L}}}_h,{\widehat{\mathit{W}}}_h\right)‖}_2(23)$

Here, Vec (⋅) indicates the vectorizing operation that can adaptively reformulate the matrices as a vector. Finally, historical commitment solution ${\mathit{I}}_{h^{\prime },i}^{\star }$ is directly utilized as the prediction ${\mathit{I}}_{d,i}^{\mathit{pre}}$.

4.3 Implementation steps

The process of implementing the presented ML-aided framework is shown as in Figure 3, which can be summarized as following:

• Based on a specified ML algorithm, a predictor ${\mathcal{P}}_i$ is trained for unit $i\in \mathcal{I}$ using the training set $\mathcal{H}$.

• Taking $\{{\tilde{\mathit{L}}}_d,{\widehat{\mathit{W}}}_d\}$ as input features, the trained predictor ${\mathcal{P}}_i$ predicts the commitment solution ${\mathit{I}}_{d,i}^{\mathit{pre}}$ for unit $i\in {\mathcal{I}}^{\mathit{tar}}$.

• Given the predictions ${\mathit{I}}_{d,i}^{\mathit{pre}}$, feasibility checking process is conducted. Specifically, it checks whether ${\mathit{I}}_{d,i}^{\mathit{pre}}$ satisfies the constraints Eqs 2–11. If satisfy, the corresponding commitment decisions are fixed as ${\mathit{I}}_{d,i}^{\mathit{pre}}$, and then Gurobi is utilized to solve Eqs 1–13 with less binary variables. Otherwise, ${\mathit{I}}_{d,i}^{\mathit{pre}}$ are utilized as warm-start solution for solving Eqs 1–13.

FIGURE 3

FIGURE 3. Implementation steps of the ML-aided framework.

After solving Eqs 1–13, record the computation time o^ml and the optimal TCUC cost z^ml,⋆ under the presented ML-aided framework. Furthermore, evaluating the computation improvement Eq. 24 and optimality loss Eq. 25 compared to o^cs (computation time of being solved by commercial solvers directly) and z^⋆ (optimal TCUC cost provided by commercial solvers).

${\text{Computation\hspace{0.17em}Improvement}}_d=\frac{|o_d^{ml}-o_d^{cs}|}{o_d^{cs}}\forall d\in \mathcal{D}(24)$

${\text{Optimality\hspace{0.17em}Loss}}_d=\frac{|z_d^{ml,\star }-z_d^{\star }|}{z_d^{\star }}\forall d\in \mathcal{D}(25)$

5 Case studies

Based on a small-size IEEE 24-bus system and a large-size 5655-bus system, case studies are conducted to evaluate the presented framework. Both the systems are tuned following Chen et al. (2022b). The ML algorithms are carried out via scikit-learn Pedregosa et al. (2011) based on Python 3.8. The commercial solver is Gurobi 9.5.

5.1 Cases on 24-bus system

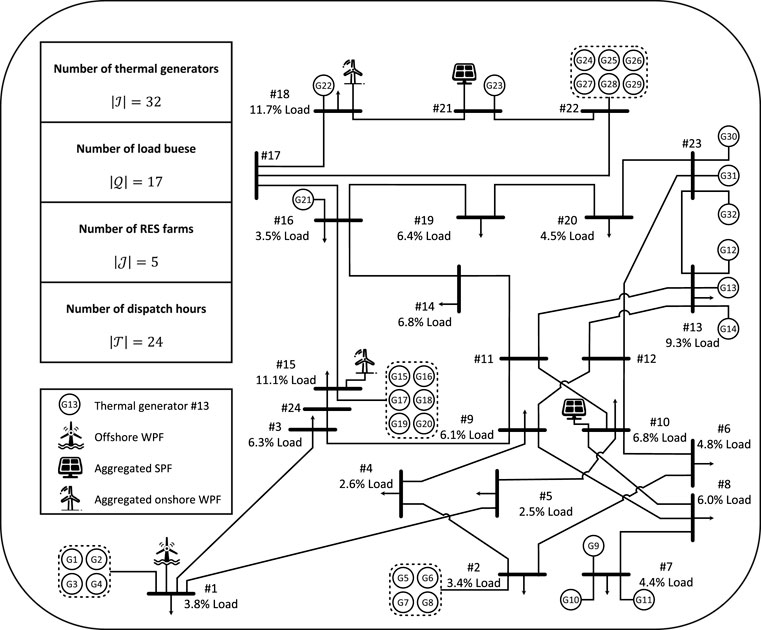
The IEEE 24-bus is sketched in Figure 4, in which 32 generators are involved.

FIGURE 4

FIGURE 4. The structure of the IEEE 24-bus system.

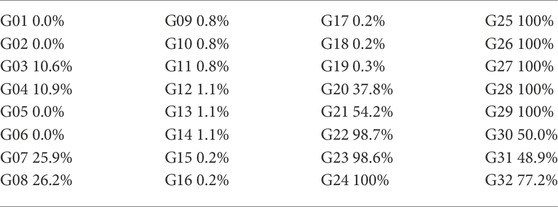
The ON-state ratios of the generators are computed using their historical datasets and listed in Table 1. According to Table 1, some generators never startup (e.g., G01 and G02) or shutdown (e.g., G28 and G29), leading to overly unbalanced historical data. Therefore, only the generators with ON-state ratios fall within [5%, 95%] are relatively suitable for being predicted, resulting in set ${\mathcal{I}}^{\mathit{tar}}$ = {G03, G04, G07, G08, G20, G21, G30, G31, G32}.

TABLE 1

TABLE 1. ON-state ratio of generators in IEEE 24-bus system.

5.1.1 Overall performance

Table 2 compares the computation improvement and the optimality loss, in which the column label Feasible/Infeasible indicates the performance on feasible/infeasible TCUC cases. Regarding the computation improvement, k-NN surprisingly outperforms other algorithms with 83.27% improvement. This is due to the fact that the k-NN essentially picks an optimal commitment result from the historical days, which can satisfy all constraints of TCUC. Also, since the RES and load information of the picked historical day and the upcoming dispatch day is similar, the commitment results are mutually feasible. Additionally, it should be pointed out that the warm-start strategy for infeasible predictions may not lead to positive computation improvement. This is because the infeasible commitment could induce the Branch-and-Bound algorithm to search from a bad initial node, thus worsening the computation performance.

TABLE 2

TABLE 2. Computation improvement and optimality loss in IEEE 24-bus system.

In terms of the optimality loss, only k-NN achieves ignorable loss. The other ML algorithms suffer noticeable optimality loss in the feasible cases. This point indicates that the predicted commitments provided by DNN, DT, and RF are mathematically far from the optimal commitment. As a result, about half of these predicted commitments are infeasible. On the other hand, k-NN directly identifies the mathematically similar and feasible commitments from historical data, in which the physical requirements are preserved entirely. Even though the commitments are not exactly the same as the optimal commitment, TCUC can still adjust scheduled power p to achieve the optimal cost. As a result, k-NN achieves significant computation improvement without optimality loss in all the cases.

5.1.2 Prediction performance

Even though the prediction performance is not the main concern of this paper, it is of interest to observe the relationship between the accuracy and the computation improvement.

This section introduces accuracy Eq. 26, receiver operating characteristic curve (ROC) score Géron (2019), precision Eq. 27, and recall Eq. 28 to evaluate the prediction performance. The ROC score is the area under the ROC curve, which can be regarded as a comprehensive evaluation tool combining precision and recall.

$\text{Accuracy}=\frac{\text{Correct\hspace{0.17em}Predictions}}{\text{All\hspace{0.17em}Predictions}}(26)$

$\text{Precision}=\frac{\text{True\hspace{0.17em}ON}}{\text{True\hspace{0.17em}ON}+\text{False\hspace{0.17em}ON}}(27)$

$\text{Recall}=\frac{\text{True\hspace{0.17em}ON}}{\text{True\hspace{0.17em}ON}+\text{False\hspace{0.17em}OFF}}(28)$

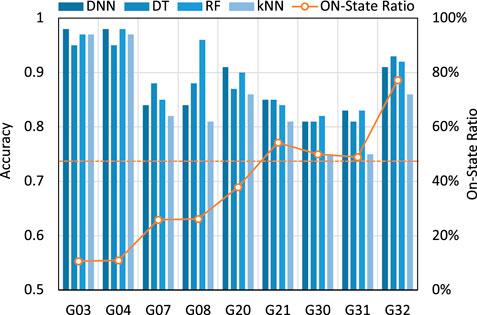
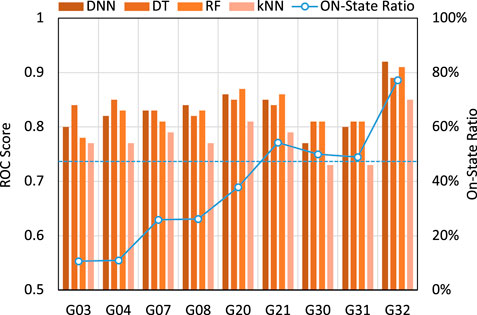
Figure 5 shows that DNN, DT, and RF are comparable regarding accuracy. Additionally, Figure 5 utilizes a dashed line to indicate the 50% ON-state ratio, which means an ideally balanced dataset. Figure 5 illustrates that the closer to the 50% line, the worse accuracy. This is because invariably predicting ON/OFF can achieve good accuracy for the units always stay ON/OFF state. On the other hand, when the ON-state ratio is around 50% (e.g., G30 and G31), it is challenging to maintain high accuracy.

FIGURE 5

FIGURE 5. Accuracy in IEEE 24-bus system.

Furthermore, Figure 6 shows that DNN, DT, and RF are comparable and significantly outperform k-NN in terms of ROC score. As a result, it can be concluded that DNN, DT, and RF perform better than k-NN regarding prediction. This is due to the sophisticated prediction mechanisms of these three algorithms.

FIGURE 6

FIGURE 6. ROC score in IEEE 24-bus system.

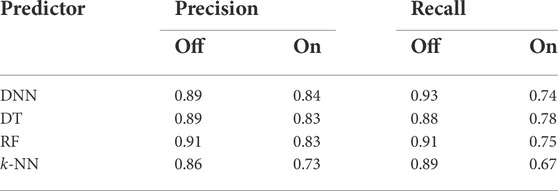
Furthermore, Table 3 lists the precision and recall. The precision indicates the accuracy of the ON-state predictions; the recall represents the ratio of ON states that the predictors correctly detect. Clearly, these algorithms only perform well in the OFF-state cases, which are more frequent state than the ON state. Therefore, Table 3 implies that all the algorithms struggle to predict the less-frequent state.

TABLE 3

TABLE 3. Precision and recall in IEEE 24-bus system.

5.2 Cases on 5655-bus system

This section investigates the ML-aided framework in the 5655-bus system Chen et al. (2022b). The system possesses 461 generators, 6,630 transmission lines, 5 aggregated RES farms. The predictors merely predict the 246 generators with a 5%–95% ON-state ratio. Since our results show that the 5655-bus prediction comparisons have the same trends as the 24-bus comparisons, the prediction results for the 5655-bus are not specifically analyzed in this section for better readability.

5.2.1 Overall performance

Table 4 compares the computation improvement and optimality loss on a large-size 5655-bus system. Regarding the computation improvement, k-NN still outperforms other algorithms with a 64.62% improvement, of which all the predictions are feasible. DNN, DT, and RF also achieve a computation improvement of about 40%.

TABLE 4

TABLE 4. Computation improvement and optimality loss in 5655-Bus system.

In terms of optimality loss, all the algorithms result in a loss within 1%, which is acceptable because the computation benefits are at least 40%.

In sum, except for k-NN, Table 4 indicates that DNN, DT, and RF are comparable in the 5655-bus system regarding the overall performance. However, DT has the fastest training speed among the three algorithms, and DNN is the slowest. Therefore, DT could be more preferable.

5.2.2 Comparing performances in 24-bus and 5655-bus systems

Furthermore, it is worth comparing the framework performances in the 24-bus and 5655-bus systems.

Regarding the computation improvement, the margin between k-NN and the other three algorithms is smaller in the 5655-bus. This is because, in such a large-size system, the massive transmission constraints Eq. 13 are also the primary cause of computational burden. Therefore, even though fixing the binaries I can relieve the computational burden, the accelerations cannot be as significant as the small-size 24-bus system. Additionally, due to the remarkable adjusting ability (i.e., massive online generator fleet) of the 5655-bus system, the predicted commitments are more likely to be feasible, leading to a lower infeasibility ratio in the 5655-bus system. Moreover, it should be pointed out that the adverse effects of infeasible predictions on TCUC instances also become more noticeable in the 5655-bus system. The reason is that the Branch-and-Bound algorithm is more sensitive to the initial node in the large-size system. However, the infeasible predictions generally make the Branch-and-Bound algorithm start from a bad initial node.

It is also worth pointing out that the optimality losses of DNN, DT, and RF become acceptable in the 5655-bus system. This is also due to the fact that the 5655-bus system possesses remarkable adjusting ability. Thus given different commitments I, the TCUC can still achieve a solution that is mathematically close to the optimal solution.

In summary, comparisons between the two systems demonstrate that the presented ML-aided framework is suitable for the large-size system with significant adjustment ability.

6 Conclusion and discussions

6.1 Conclusion

This paper designs an ML-aided framework for improving the TCUC computation performance. Specifically, DNN, DT, RF, and k-NN are leveraged to predict and fix the commitment decisions of the TCUC models, so that Gurobi can solve a reduced TCUC problem with fewer binary variables. To evaluate the effectiveness of the framework, case studies are conducted on a 24-bus system and a 5655-bus system. The following conclusions are obtained:

• The presented ML-aided framework achieves significant TCUC computation improvement, especially in the large-size system, but at the expense of certain optimality loss. In the small-size 24-bus system, the optimality loss could be 6%–17%. In the large-size 5655-bus system, the optimality loss is merely within 1%, but the computation improvement achieves as much as 64.62%.

• Our results report that the simplest k-NN outperforms the other ML algorithms (DT, RF, and DNN) in terms of computation improvement. Interestingly, the k-NN leads to the worst prediction accuracy. This point indicates that learning and accelerating TCUC could be a low-hanging fruit Pineda and Morales (2021). In such a case, naive algorithms could be more preferable than sophisticated algorithms since pursuing the ultimate task improvement is our primary goal.

6.2 Discussions

It is noteworthy that using infeasible predictions for the warm start could adversely affect the computation, as shown in Table 2 and Table 4. This adverse effect is even worse in the 5655-bus system. There are three potential options for relieving this problem: 1) discarding the infeasible solution and solving TCUC directly with the solver; 2) fixing the infeasible solution (especially for constraints Eqs 2, 3) and then performing the warm start; and 3) using k-NN to find the nearest feasible solution to the infeasible solution and replacing it.

Although the presented framework cannot achieve the impressive effectiveness as the mentioned references [e.g., 17.47x in Xavier et al. (2021) and 215.9x in Pineda and Morales (2021)], it is more general, more exploratory, and more transparent. Specifically, Pineda and Morales (2021) only considers the k-NN method and does not discuss the data processing; in comparison, the presented framework is compatible with DNN, DT, and RF in addition to the k-NN, and is designed with a data-processing stage. Moreover, this paper has open-sourced all the datasets and code, which can facilitate the further exploration of the presented framework.

Additionally, it is worth pointing out that the TCUC model in this paper does not yet consider the security constraints (e.g., N-1 feasibility constraints) commonly used in practical applications. This is because considering these constraints may require decomposition algorithms to solve the TCUC model, while this paper intends to focus on the most fundamental TCUC problem, so that it is convenient to obtain a clear and intuitive conclusion regarding the acceleration. However, this may raise a question: is the presented framework still effective in extreme scenarios? In light of this, future works will further refine the TCUC model and discuss the effectiveness of the presented framework in different scenarios.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/Supplementary Material.

Author contributions

Conceptualization: ZL, LiL, and CM; methodology: ZL and YL; software: ZL; validation: YC and JY; formal analysis: HL; investigation: LWL; writing—original draft preparation: ZL and YL; writing—review and editing: ZL and YL; visualization: YL; supervision: ZL; funding acquisition: ZL. All authors have read and agreed to the published version of the manuscript.

Funding

This paper is supported by the project entitled The Operation Service of Distributed Resource Aggregators in the Park under the Background of the Opening of the Energy Market (2021YFSY0019) from State Grid Sichuan Comprehensive Energy Service Co. Ltd.

Conflict of interest

ZL, YC, JY, CM, LWL, and YL were employed by the company State Grid Sichuan Comprehensive Energy Service Co. Ltd.; HL was employed by the company State Grid Chengdu Power Supply Co. Ltd. and LiL was employed by the comany Sichuan Yongjing Investment Co. Ltd.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chen, T., Liu, Y., Li, W., and Ma, T. (2021). Adaptive microgrid price-making strategy and economic dispatching method based on blockchain technology. Electr. Power Constr. 42, 17–28. doi:10.12204/j.issn.1000-7229.2021.06.003

CrossRef Full Text | Google Scholar

Chen, X. (2021). Closed-loop ncuc dataset. Available at: https://github.com/asxadf/closed_loop_ncuc_dataset.GitHub.

Google Scholar

Chen, X., Liu, Y., and Wu, L. (2022a). Improving electricity market economy via closed-loop predict-and-optimize. arXiv preprint arXiv:2208.13065. Available at: https://arxiv.org/abs/2208.13065 (Accessed Aug 27, 2022).

Google Scholar

Chen, X., Yang, Y., Liu, Y., and Wu, L. (2022b). Feature-driven economic improvement for network-constrained unit commitment: A closed-loop predict-and-optimize framework. IEEE Trans. Power Syst. 37, 3104–3118. doi:10.1109/tpwrs.2021.3128485

CrossRef Full Text | Google Scholar

Chen, Y., Casto, A., Wang, F., Wang, Q., Wang, X., and Wan, J. (2016). Improving large scale day-ahead security constrained unit commitment performance. IEEE Trans. Power Syst. 31, 4732–4743. doi:10.1109/tpwrs.2016.2530811

CrossRef Full Text | Google Scholar

Chen, Y., Gribik, P., and Gardner, J. (2013). Incorporating post zonal reserve deployment transmission constraints into energy and ancillary service co-optimization. IEEE Trans. Power Syst. 29, 537–549. doi:10.1109/tpwrs.2013.2284791

CrossRef Full Text | Google Scholar

de Mars, P., and O’Sullivan, A. (2021). Applying reinforcement learning and tree search to the unit commitment problem. Appl. Energy 302, 117519. doi:10.1016/j.apenergy.2021.117519

CrossRef Full Text | Google Scholar

Géron, A. (2019). Hands-on machine learning with Scikit-Learn, Keras, and TensorFlow: Concepts, tools, and techniques to build intelligent systems. California, United States: O’Reilly Media.

Google Scholar

Hou, Q., Zhang, N., Kirschen, D. S., Du, E., Cheng, Y., and Kang, C. (2020). Sparse oblique decision tree for power system security rules extraction and embedding. IEEE Trans. Power Syst. 36, 1605–1615. doi:10.1109/tpwrs.2020.3019383

CrossRef Full Text | Google Scholar

Huang, S., and Huang, C. (1997). Application of genetic-based neural networks to thermal unit commitment. IEEE Trans. Power Syst. 12, 654–660. doi:10.1109/59.589634

CrossRef Full Text | Google Scholar

Li, F., Qin, J., and Zheng, W. (2019). Distributed q-learning-based online optimization algorithm for unit commitment and dispatch in smart grid. IEEE Trans. Cybern. 50, 4146–4156. doi:10.1109/tcyb.2019.2921475

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Z., Wu, L., Xu, Y., Moazeni, S., and Tang, Z. (2022). Multi-stage real-time operation of a multi-energy microgrid with electrical and thermal energy storage assets: A data-driven mpc-adp approach. IEEE Trans. Smart Grid 13, 213–226. doi:10.1109/tsg.2021.3119972

CrossRef Full Text | Google Scholar

Li, Z., Wu, L., and Xu, Y. (2021a). Risk-averse coordinated operation of a multi-energy microgrid considering voltage/var control and thermal flow: An adaptive stochastic approach. IEEE Trans. Smart Grid 12, 3914–3927. doi:10.1109/tsg.2021.3080312

CrossRef Full Text | Google Scholar

Li, Z., Xu, Y., Fang, S., Wang, Y., and Zheng, X. (2020). Multiobjective coordinated energy dispatch and voyage scheduling for a multienergy ship microgrid. IEEE Trans. Ind. Appl. 56, 989–999. doi:10.1109/tia.2019.2956720

CrossRef Full Text | Google Scholar

Li, Z., Xu, Y., Wu, L., and Zheng, X. (2021b). A risk-averse adaptively stochastic optimization method for multi-energy ship operation under diverse uncertainties. IEEE Trans. Power Syst. 36, 2149–2161. doi:10.1109/tpwrs.2020.3039538

CrossRef Full Text | Google Scholar

Lin, Z. (2022). Codes of ml-aided framework. Available at: https://github.com/linzhaohang11/data_mluc.GitHub.

Google Scholar

Liu, Y., Chen, X., Li, B., Li, H., and Ye, Y. (2020). Wks-type distributionally robust optimisation for optimal sub-hourly look-ahead economic dispatch. IET Gener. Transm. &amp. Distrib. 14, 2237–2246. doi:10.1049/iet-gtd.2019.1344

CrossRef Full Text | Google Scholar

Liu, Y., Chen, X., Wu, L., and Ye, Y. (2021a). An idm-based distributionally robust economic dispatch model for iehg-mg considering wind power uncertainty. CSEE J. Power Energy Syst. 1–11. Early access. doi:10.17775/CSEEJPES.2021.03940

CrossRef Full Text | Google Scholar

Liu, Y., Li, L., Liu, Z., Miao, S., Zhang, S., and Zhang, L. (2021b). Cooperative control strategy of distribution network considering generalized energy storage cluster participation. Electr. Power Constr. 42, 89–98. doi:10.12204/j.issn.1000-7229.2021.08.011

CrossRef Full Text | Google Scholar

Ma, T., Liu, Y., Liu, J., Jiang, Z., and Xu, L. (2021). Distributed transaction model of electricity in multi-microgrid applying smart contract technology. Electr. Power Constr. 42, 41–48. doi:10.12204/j.issn.1000-7229.2021.01.005

CrossRef Full Text | Google Scholar

Mohammadi, F., Sahraei-Ardakani, M., Trakas, D., and Hatziargyriou, N. (2021). Machine learning assisted stochastic unit commitment during hurricanes with predictable line outages. IEEE Trans. Power Syst. 36, 5131–5142. doi:10.1109/tpwrs.2021.3069443

CrossRef Full Text | Google Scholar

Nair, V., Bartunov, S., Gimeno, F., von Glehn, I., Lichocki, P., Lobov, I., et al. (2020). Solving mixed integer programs using neural networks. arXiv preprint arXiv:2012.13349. Available at: https://arxiv.org/abs/2012.13349 (Accessed Dec 23, 2020).

Google Scholar

Nikolaidis, P., and Chatzis, S. (2021). Gaussian process-based bayesian optimization for data-driven unit commitment. Int. J. Electr. Power & Energy Syst. 130, 106930. doi:10.1016/j.ijepes.2021.106930

CrossRef Full Text | Google Scholar

Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., et al. (2011). Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 12, 2825–2830. doi:10.5555/1953048.2078195

CrossRef Full Text | Google Scholar

Pineda, S., and Morales, J. (2021). Is learning for the unit commitment problem a low-hanging fruit? arXiv preprint arXiv:2106.11687. Available at: https://arxiv.org/pdf/2106.11687.pdf (Accessed Jun 22, 2021).

Google Scholar

Pineda, S., Morales, J., and Jiménez-Cordero, A. (2020). Data-driven screening of network constraints for unit commitment. IEEE Trans. Power Syst. 35, 3695–3705. doi:10.1109/tpwrs.2020.2980212

CrossRef Full Text | Google Scholar

Wu, J., Liu, Y., Xu, L., Ma, T., Guo, J., and Yang, Q. (2021a). Robust game transaction model of multi-microgrid system applying blockchain technology considering wind power uncertainty. Electr. Power Constr. 42, 10–21. doi:10.12204/j.issn.1000-7229.2021.09.002

CrossRef Full Text | Google Scholar

Wu, T., Zhang, Y., and Wang, S. (2021b). Deep learning to optimize: Security-constrained unit commitment with uncertain wind power generation and besss. IEEE Trans. Sustain. Energy 99, 1. doi:10.1109/TSTE.2021.3107848

CrossRef Full Text | Google Scholar

Xavier, Á. S., Qiu, F., and Ahmed, S. (2021). Learning to solve large-scale security-constrained unit commitment problems. Inf. J. Comput. 33, 739–756. doi:10.48550/arXiv.1902.01697

CrossRef Full Text | Google Scholar

Yang, N., Yang, C., Wu, L., Shen, X., Jia, J., Li, Z., et al. (2021). Intelligent data-driven decision-making method for dynamic multi-sequence: An e-seq2seq based scuc expert system. IEEE Trans. Ind. Inf. 18, 3126–3137. doi:10.1109/tii.2021.3107406

CrossRef Full Text | Google Scholar

Yang, Y., Lu, X., and Wu, L. (2020). Integrated data-driven framework for fast scuc calculation. IET Gener. Transm. &amp. Distrib. 14, 5728–5738. doi:10.1049/iet-gtd.2020.0823

CrossRef Full Text | Google Scholar

Yang, Y., and Wu, L. (2021). Machine learning approaches to the unit commitment problem: Current trends, emerging challenges, and new strategies. Electr. J. 34, 106889. doi:10.1016/j.tej.2020.106889

CrossRef Full Text | Google Scholar

Ye, Y., Qiu, D., Sun, M., Papadaskalopoulos, D., and Strbac, G. (2019). Deep reinforcement learning for strategic bidding in electricity markets. IEEE Trans. Smart Grid 11, 1343–1355. doi:10.1109/tsg.2019.2936142

CrossRef Full Text | Google Scholar

Zhang, S., Ye, H., Wang, F., Chen, Y., Rose, S., and Ma, Y. (2020). Data-aided offline and online screening for security constraint. IEEE Trans. Power Syst. 36, 2614–2622. doi:10.1109/tpwrs.2020.3040222

CrossRef Full Text | Google Scholar

Zhang, Y., Cui, H., Liu, J., Qiu, F., Hong, T., Yao, R., et al. (2021). Encoding frequency constraints in preventive unit commitment using deep learning with region-of-interest active sampling. arXiv preprint arXiv:2102.09583. Available at: https://arxiv.org/abs/2102.09583 (Accessed Feb 18, 2021).

Google Scholar

Zhou, M., Wang, B., Li, T., and Watada, J. (2018). A data-driven approach for multi-objective unit commitment under hybrid uncertainties. Energy 164, 722–733. doi:10.1016/j.energy.2018.09.008

CrossRef Full Text | Google Scholar

Zhou, Y., Zhai, Q., and Wu, L. (2021). A data-driven variable reduction approach for fast unit commitment of large-scale systems. J. Mod. Power Syst. Clean Energy, 1–12. Early access. doi:10.35833/MPCE.2021.000382

CrossRef Full Text | Google Scholar

Nomenclature

Sets and indices

$\mathit{i}/\mathcal{I}$ Index/set of units.

${\mathcal{I}}^{\mathit{tar}}$ Set of target units to be predicted

$\mathit{t},{\mathit{t}}^{\mathit{\prime }}/\mathcal{T}$ Indexes/set of dispatch horizon

${\mathcal{T}}_{\mathit{i}}^{\mathit{u}}$ ON-time set $\{T_i^u,\dots ,T\}$ of unit i

${\mathcal{T}}_{\mathit{i}}^{\mathit{d}}$ OFF-time set $\{T_i^d,\dots ,T\}$ of unit i

$\mathit{j}/\mathcal{J}$ Index/set of RES farms

$\mathit{q}/\mathcal{Q}$ Index/set of load buses

$\mathit{b}/\mathcal{B}$ Index/set of transmission branches

$\mathit{k}/\mathcal{K}$ Index/set of generation segments.

$\mathit{n}/\mathcal{N}$ Index/set of dispatch days in raw dataset.

$\mathit{h}/\mathcal{H}$ Index/set of historical dispatch days for training.

$\mathit{d}/\mathcal{D}$ Index/set of upcoming dispatch days for testing.

${\mathcal{S}}_{\mathit{n}}$ Instance of dispatch day n.

Decision variables

x Vector of TCUC decisions. x = {I, I^su, I^sd, P^seg, P, W, C^p}

I_ti Commitment of unit i at hour t

${\mathit{I}}_{\mathit{t}\mathit{i}}^{\mathit{s}\mathit{u}}$ Start-up decision of unit i at hour t

${\mathit{I}}_{\mathit{t}\mathit{i}}^{\mathit{s}\mathit{d}}$ Shut-down decision of unit i at hour t

$P_{\mathit{tik}}^{\mathit{seg}}$ The k^th-segment generation of unit i at hour t

P_ti Total scheduled generation of unit i at hour t

W_tj Scheduled generation of RES farm j at hour t

${\mathit{C}}_{\mathit{t}\mathit{i}}^{\mathit{p}}$ Generation cost of unit i at hour t

z_n TCUC cost of dispatch day n

⋅^⋆/⋅^pre Optimal/Predicted solution for a variable

Constant parameters

${\mathit{C}}_{\mathit{i}}^{\mathit{s}\mathit{u}}/{\mathit{C}}_{\mathit{i}}^{\mathit{s}\mathit{d}}$ Start-up/Shut-down cost of unit i

T The last hour in set $\mathcal{T}$

${\mathit{T}}_{\mathit{i}}^{\mathit{u}}/{\mathit{T}}_{\mathit{i}}^{\mathit{d}}$ Minimum ON-time/OFF-time of unit i

${\mathit{P}}_{\mathit{i}}^{\mathit{min}}/{\mathit{P}}_{\mathit{i}}^{\mathit{max}}$ Minimum/Maximum generation unit of i

${\stackrel{\mathit{̄}}{\mathit{P}}}_{\mathit{i}\mathit{k}}^{\mathit{seg}}$ Limitation of k^th-segment generation of unit i

${\widehat{\mathit{W}}}_{\mathit{j}}$ Available power of RES farm j

${\mathit{R}}_{\mathit{i}}^{\mathit{u}\mathit{p}}/{\mathit{R}}_{\mathit{i}}^{\mathit{d}\mathit{n}}/{\mathit{R}}_{\mathit{i}}^{\mathit{s}\mathit{u}}/{\mathit{R}}_{\mathit{i}}^{\mathit{s}\mathit{d}}$ Upward/Downward/Start-up/Shut-down ramping capacity of unit i

${\widehat{\mathit{L}}}_{\mathit{t}\mathit{q}}$ Load demand of load bus q at hour t

B_b Transmission limitation of branch b

τ_qb Power shifting factor from bus q to branch q

Others

|⋅| Cardinality of a set

o^cs/o^ml TCUC solving time of the commercial solver/ML-aided framework

z^ml,⋆ TCUC cost of the ML-aided framework

TCUC Transmission-constrained unit commitment

MILP Mixed-integer linear programming

ML Machine learning

DT Decision tree

RF Random forest

DNN Deep neural network

k-NN k-nearest neighbors

RES Renewable energy source

ISO Independent System Operator

ROC Receiver operating characteristic