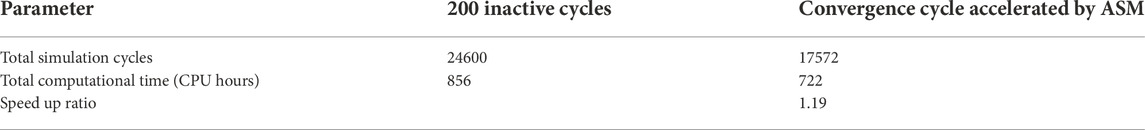- 1Institute of Nuclear Physics and Chemistry, China Academy of Engineering Physics, Mianyang, China
- 2Department of Engineering Physics, Tsinghua University, Beijing, China
The safety analysis of nuclear systems such as nuclear reactors requires transient calculation. The Monte Carlo (MC) method has grown rapidly in recent years because of its high-fidelity modelling and simulation capability. The predictor-corrector quasi-static (PCQS) MC method has been investigated for kinetic calculation. However, the approach to shorten the computational time required to solve the transient fixed source equation (TFSE) is still under development. The convergence characteristic of the neutron source iteration algorithm of the PCQS MC method is analyzed in this study with a simplified model. It is found that the convergence rate of the iteration algorithm is governed by the effective spectral radius (ESR). The lower the ESR is, the faster the convergence is. In order to reduce the ESR, the asymptotic superhistory method (ASM) is developed for the PCQS MC method in the RMC code. The performance of ASM is evaluated by the C5G7-TD benchmark. Results show that the reduction in the number of inactive cycles is more than 85%, and over 15% of computational time including active cycles is saved. It is demonstrated how ASM speeds up the iterations using the Wasserstein distance measure.
1 Introduction
High-fidelity simulations for nuclear systems such as nuclear reactors and spent fuel reprocessing solutions have been developed rapidly in the last decade. In particular, the exponential increase of high-performance computing accelerates the implementation of high-fidelity simulations in engineering fields. Among many high-fidelity simulation methods, the Monte Carlo (MC) method is widely regarded as the most accurate method and is usually used for validations of other methods. The MC method has two major advantages: one is the usage of accurate continuous-energy cross-sections, and another is the precise 3-dimensional (3D) geometry modeling based on constructive solid geometry (CSG) or computer-aided design (CAD) geometry (Wilson et al., 2010; Davis et al., 2020; Deng et al., 2022). MC codes such as MCNP (Goorley et al., 2012), Serpent (Leppänen et al., 2015), OpenMC (Romano et al., 2015), and RMC (Wang et al., 2015) are widely used in new reactor designs, which have disparate features from normal nuclear reactors in geometry, material, and spectra.
Typically, the MC method is capable of steady state simulations, including criticality calculation and shielding calculation, etc. Kinetic simulation functions are not as well-developed as steady state simulation functions for many MC codes. However, transient behaviors are fundamental and essential in the safety analysis of nuclear systems. The lack of kinetic simulation functions severely limits MC codes’ further applications. Therefore, many studies concerning kinetic simulation methods are under development.
Generally, kinetic MC methods could be divided into two kinds: one is the direct MC kinetic simulation method, and another is the hybrid MC kinetic simulation method with deterministic methods. The direct MC kinetic simulation method includes Dynamic Monte Carlo (DMC) method (Sjenitzer and Hoogenboom, 2013; Jia et al., 2022) and similar methods which implement acceleration skills such as quasi-static treatments (Trahan, 2019). The direct method simulates the neutron flight and delayed neutron precursors variation with a continuous-in-time model, which is very accurate but causes massive computational consumption. The hybrid MC kinetic simulation method with deterministic methods include the time-dependent coarse mesh finite difference method (TD-CMFD) based on the multi-group cross-sections tallied from a MC solver (Shaner, 2018; Kreher et al., 2022), the transient fission matrix method (TFM) (Heuer et al., 2015), the time-dependent response matrix (TDRM) method (Mickus et al., 2020), and the predictor-corrector quasi-static (PCQS) method (Jo et al., 2016). Among the above methods, the TD-CMFD, TFM and TDRM methods require extra treatment on space meshing before calculation. As a result, the suited geometries are limited. By comparison, the PCQS method is still based on continuous-energy cross-sections and arbitrary complex geometries, and thus has an advantage in modelling flexibility.
A complete PCQS MC calculation consists of a series of single MC calculations at successive time steps. Every single MC calculation solves a transient fixed-source equation (TSFE), except for the first time step at which the eigenvalue equation is solved. Usually, solving the fixed-source equation by MC method does not need any iteration algorithm, but the neutron tracking may not terminate when calculating transient supercritical problems with a large time step (Jo et al., 2016). Therefore, the neutron source iteration algorithm is used to solve both the TFSEs and the eigenvalue equation. Figure 1 shows the flow chart of a complete PCQS MC calculation. Consequently, the computational cost of a complete PCQS MC calculation is tens of or even hundreds of times of a single MC criticality calculation, depending on the number of time steps. It is necessary then to accelerate the calculation, especially to reduce iterations for fission source and external source convergence.
Jo et al. (2016) proposed a partial current-based CMFD (p-CMFD) acceleration method, which has been the only acceleration method for PCQS MC calculation. As mentioned before, the CMFD method requires space meshing, which limits the capability to solve problems with irregular geometries.
Many previous studies have proposed methods to accelerate neutron source iterations. There are two kinds of acceleration methods. The first kind uses space meshing, including the fission matrix method (Kuroishi and Nomura, 2003; Dufek and Gudowski, 2009), the CMFD method (Lee et al., 2010; Yun and Cho, 2010), the functional Monte Carlo (FMC) method (Larsen and Yang, 2011), etc. These methods are all sensitive to the meshing methods, which are highly dependent on the users’ experience. Besides, some methods need a vast footprint, and some are only suited for nuclear systems with regular shapes, which eliminates the MC method’s advantage in free 3D modeling. The second kind is independent of space meshing, including the Wielandt’s method (Yamamoto and Miyoshi, 2004; Brown, 2007; She et al., 2015; Pan et al., 2022c), the superhistory method (Brissenden and Garlick, 1986; She et al., 2015; Mickus and Dufek, 2018; Pan et al., 2022c), the neutron population growth method (Mickus and Dufek, 2018; Pan et al., 2022a), and the source extrapolation method (Pan et al., 2022b). Wielandt’s method is based on the shifted inverse power method (Bronson et al., 2013). Other methods are based on the property that iteration computational cost is directly proportional to the neutron history number while the statistical error is in reverse proportion to the square root of the neutron history number. However, the above methods have only been applied to criticality problems where the eigenvalue equation is solved.
In this study, the asymptotic superhistory method (ASM) is developed to accelerate the neutron source iterations in solving TFSE. The basic theory is introduced in Section 2. Section 3 shows the numerical simulations and performance. Section 4 makes the conclusion.
2 Methodology
2.1 Transient fixed source equation of the predictor-corrector quasi-static method and the neutron source iteration algorithm
Before introducing the asymptotic superhistory method for TFSE, the deduction of TFSE is provided herein, and the iteration algorithm is discussed.
The TFSE is the key equation of the PCQS method. The fundamental equations of the PCQS method were firstly developed for deterministic codes (Dulla et al., 2008). The PCQS equations are derived from the time-dependent Boltzmann neutron transport equation:
and the delayed precursor transport equation:
where r is the neutron position, Ω is the neutron flying angle, E is the neutron energy, t is the time, Φ is the neutron flux, v is the neutron speed, χp is the prompt neutron energy spectra, i is the delayed neutron family, χi is the delayed neutron energy spectra of family i, βi is the delayed neutron fraction of family i, λi is the delayed constant of family i, Ci is the delayed neutron precorsor concentration of family i. LΦ is the leakage operator, TΦ is the collision operator, SΦ is the scattering operator, and FΦ is the fission operator. Definitions of the operators in Eqs. 1, 2 could be found in Rao et al. (2019).
In the PCQS method, the implicit backward difference time discretization strategy is applied. At time step tn+1, the partial differential terms in Eqs. 1, 2 are expressed as follows:
where Δtn+1 = tn+1 − tn.
Replace all t in Eqs. 1, 2 with tn+1 except the partial item, substituting Eq. 3 into Eqs. 1, 2, and rearranging gives the predicted neutron flux equation:
where T′Φ is the PCQS leakage operator and Sn is the external source (PCQS source). Denote that
and
and then Eq. 4 becomes:
which is obviously a fixed-source equation. Therefore, Eq. 4 is the TFSE of the PCQS method.
The MC codes usually use a direct method to solve Eq. 7:
however, there are several problems to use Eq. 8 to solve TFSE:
• As Jo et al. (2016) stated, the neutron history may not terminate when Δtn+1 is not sufficiently small, which means that Eq. 8 does not have solutions. This characteristics will also be shown in Section 2.2.
• Code users cannot control statistical errors conveniently. Due to the variation of the geometries or materials during the transient process, the neutron multiplication characteristics differs at each time step. Consequently, the simulated neutron history number varies at different time steps. The estimated statistical errors may be significant in deep sub-critical conditions and minor in super-critical states.
Thus, the neutron source iteration algorithm is used instead, which is similar to that used in deterministic methods (Turinsky et al., 1994):
where (j) is the serial number of iterations.
2.2 Convergence characteristics of the neutron source iteration algorithm
Before developing the acceleration algorithm, it is necessary to analyze the convergence characteristics of Eq. 9. Because Eq. 9 is closely related to the model complexity and does not have a common analytical solution, a 0-dimensional and mono-energy model with single family delayed neutron precorsor is used herein, which can also reveal the essence.
For the simplified model, Eqs. 1, 2 become:
and
To obtain the PCQS fixed source equation corresponding to Eqs.10, 11 the implicit difference strategy is implemented:
Substituting Eq. 12 into Eqs. 10, 11 and rearranging gives:
where sn is the external source:
and gn+1 is a coefficient:
where keff,n+1 is the effective multiplication factor of the simplified model at t = tn+1 without external sources:
Eq. 13 is the TFSE of this simplified model. When solving Eq. 13 using the fixed-point iteration method, the iteration format is:
Therefore, this paper called gn+1 the equivalent spectral radius (ESR) of the TFSE. The condition that Eq. 17 is converged is:|gn+1| < 1. Obviously, gn+1 > 0, and thus the convergence condition is:
Besides, the closer to 1 the gn+1 is, the lower the convergence rate is.
It is found that keff,n+1 ≤ 1 sets up Eq. 18, which means that the iteration is converged if the model at t = tn+1 is critical or subcritical without external sources. When the model is supercritical, substituting Eq. 15 into Eq. 18 and rearranging yields a quadratic inequality:
where
and
Because keff,n+1 > 1, a > 0, and thus b2 + 4a > 0. Therefore, the quadratic fucntion
is a parabola going upwards, and Eq. 19 has analytical solution:
Eq. 23 shows that when the model is supercritical without external sources, the time step should be sufficiently small to make sure that the iteration is converged. Besides, direct solution by Φn+1 = sn/(1 − gn+1) will give meaningless results that Φn+1 < 0 when gn+1 > 1, which is consistent with the discussion in Section 2.1.
Extrapolating from the study of the simplified model, the time step should be small enough when the model is supercritical, and the neutron source iteration is unconditional convergence when the model is subcritical or critical without external sources. The convergence rate can be increased by a lower ESR, which can be used to speed up TFSE iterations. The asymptotic superhistory approach is used in this paper to reduce ESR.
2.3 The asymptotic superhistory acceleration method
The superhistory method was proposed by Brissenden and Garlick (1986) to accelerate the MC criticality calculation. The MC criticality calculation solves the eigenvalue equation by neutron source iterations:
The convergence rate of Eq. 24 is determined by the dominance ratio
and the dominance ratio is reduced to
Similarly, the superhistory method is applied to the TFSE as follows:
and the ESR ρ(M−1F) is reduced to
Note that the Wielandt method is not applicable, because the Wielandt method is based on the shifted inverse power method, which is only suitable for solving the eigenvalue problems. However, the TFSE is a nonhomogeneous equation and thus only the ASM method is suitable.
Based on the effective DR measure, a metric of the computational burden, She et al. (2015) proved, however, that the superhistory method could not shorten the calculation time because every cycle requires additional time. The ASM (She et al., 2015), which lowers each generation’s neutron history number by a set of predetermined factors, is suggested as a remedy, and used in this paper:
1) Given the neutron population of each cycle m.
2) Input the asymptotic factors N1, N2, … , Nn and asymptotic period p. Notably, N1 > N2 > ⋯ > Nn.
3) Starting from the first cycle, the neutron population is changed to m/N1. Then, one cycle consists of N1 generations.
4) After p cycles, change the neutron population to m/N2 and run p cycles.
5) Repeat until finishing n × p cycles.
6) Change the neutron population back to m and execute the simulation as usual.
The algorithm is implemented in the RMC code (Wang et al., 2015). The asymptotic factors are 16, 8, 4, 2 and the asymptotic periods are 5, by default, and thus the acceleration lasts for 20 cycles. Default asymptotic parameters are used in Section 3, however user-defined parameters are also allowed.
3 Results and discussion
The ASM’s performance is evaluated in this section. In order to more effectively compare the convergence characteristic with and without the superhistory method, this work uses the Wasserstein distance (WD) measure (Guo et al., 2022) as defined by Eq. 27, which is similar to the progress relative entropy but performs better:
where WDr,j is WD of cycle j in the r direction (r can be x, y or z), i is the neutron index, and
Besides, an experience-based convergence criterion is employed:
where jmax = max (WDr,2, WDr,3, … , WDr,j) and
3.1 The C5G7-TD benchmark and the TD4-4 case
The C5G7-TD benchmark consists of a set of kinetic and transient test cases. Figure 2 depicts a quarter of its geometry model, with Figures 2A,B showing the 2-dimensional (2D) geometry and the 3D geometry’s expansion down the z-axis, respectively. Guo et al. (2021) simulated all subcritical kinetic cases using the RMC code.
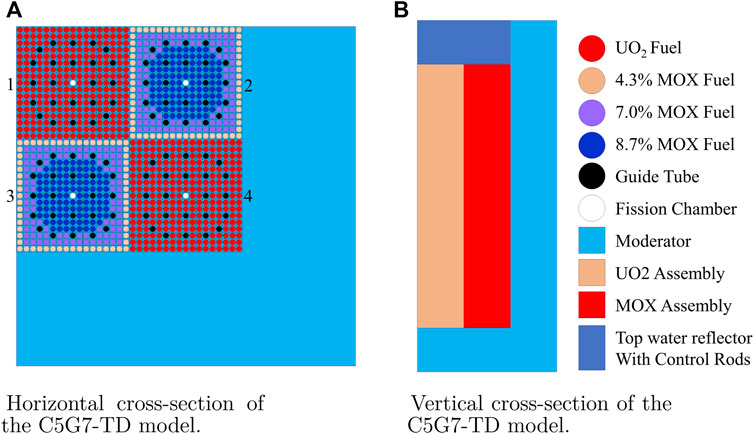
FIGURE 2. Geometry configuration of the C5G7-TD benchmark. (A) Horizontal and (B) vertical cross-section of the C5G7-TD model.
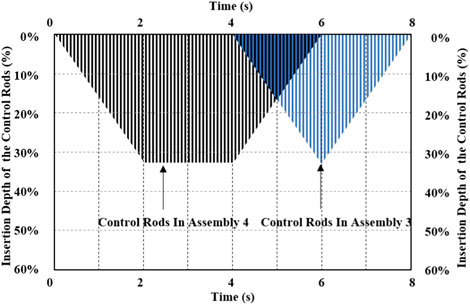
The C5G7-TD benchmark has 28 subcritical kinetic cases. The TD4-4 case is a 3D transient, driven by the control rod (CR) movement shown in Figure 3. Initially, the CRs in assembly 4 are inserted. After 2 s the insertion stops at one-third depth of the assembly, and then the CRs stay in the position. At the end of 4 s, the CRs in assembly 4 are withdrawn, meanwhile the CRs in assembly 3 are inserted. After 2 s, the CRs in assembly 4 are fully out of the core, and the CRs in assembly 3 stops insertion and are withdrawn until the end of 8 s.
3.2 Validation of the convergence criterion
The previous study (Guo et al., 2021) employed 200 inactive cycles and 400 active cycles for TD4-4’s convergence at all time steps, and the results showed good agreement with other codes. The reason for a global inactive cycle configuration throughout the transient is that the convergence is unknown in advance, and thus a conservative value is required. Using Eq. 28, the cycles at which the neutron source iteration achieves convergence are displayed in Figure 4.
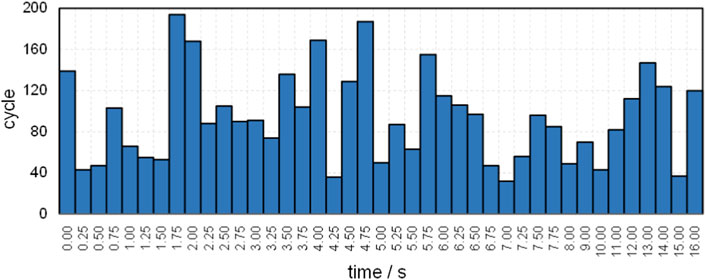
FIGURE 4. The convergence cycles of TD4-4, given by Eq. 28.
Nearly half of the time steps require over 100 iterations to converge. Especially, time step t = 1.75 s requires a maximum of 194 iterations, and time step t = 4.75 s requires a second maximum of 187 iterations. Both are close to but still less than 200. Therefore, the convergence criterion demonstrates the conservatism of the previous configuration.
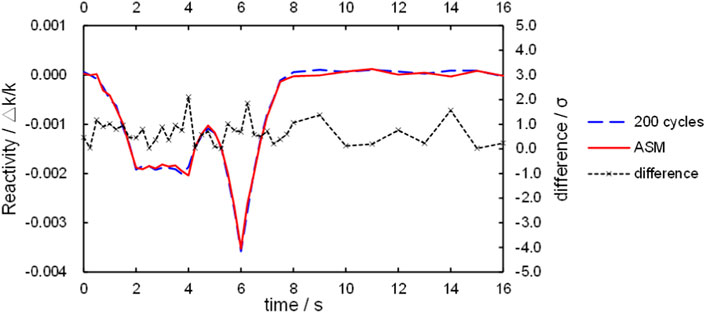
A comparative calculation is performed to further validate the convergence criterion, in which the inactive cycle configurations are set as the declared convergence iterations shown in Figures 4, 5 compares the reactivity results. It is found that the reactivity profile obtained by fewer iterations given by Eq. 28 is in good agreement with that obtained by 200 iterations, with all time-steps’ deviation less than 3 times the standard deviation. Therefore, the convergence criterion can be used to determine the convergence iteration. At least, it is valid for the TD4-4 case.
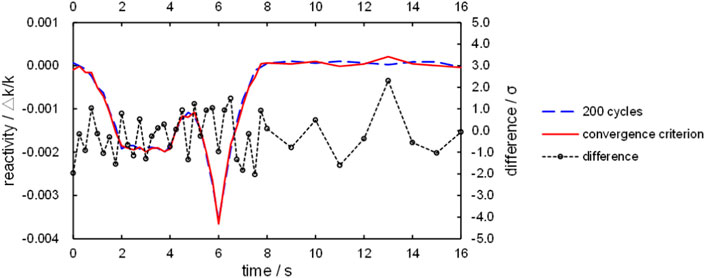
FIGURE 5. Comparison of reactivity profiles, obtained by setting 200 inactive cycles and using Eq. 28.
3.3 Performance of the asymptotic superhistory method
To accelerate the entire TD4-4 transient calculation, the ASM is used. After acceleration, the convergence iterations given by Eq. 28 are shown in Figure 6. When compared to Figure 4, the asymptotic super history method significantly speeds up the neutron source iteration. Notably, the convergence cycles are reduced at every time step.
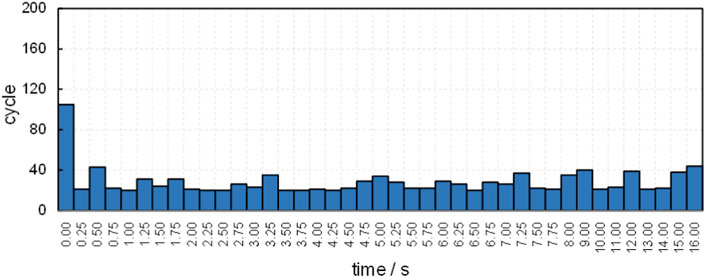
FIGURE 6. The convergence cycles given by Eq. 28, after accelerating TD4-4’s transient calculation by ASM.
Figure 7 provides the comparison of reactivity profiles obtained with and without ASM. It is observed that two reactivity curves agree well statistically. Therefore, implementation of ASM does not reduce the accuracy of the result.
The whole TD4-4 transient consists of 41 time steps, and the previous study used a total of 8,200 inactive cycles. Applying the asymptotic super history method reduces the number of inactive cycles to 1,172, a reduction of more than 85%. Considering that a complete MC calculation consists of both inactive and active cycles, the total simulation cycles and the total computational time are compared, and the results are listed in Table. 1. It is found that over 15% of the total computational cost is saved.
3.4 Inspection of the convergence process
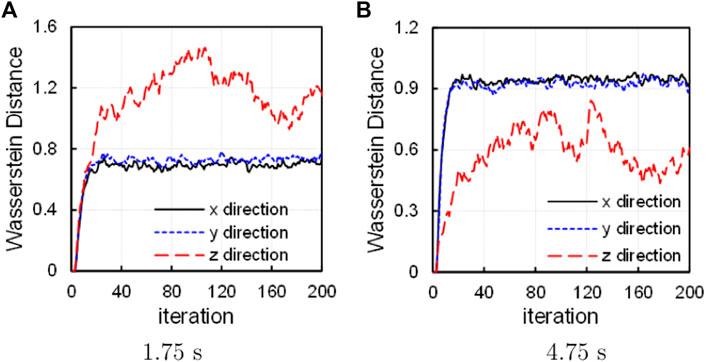
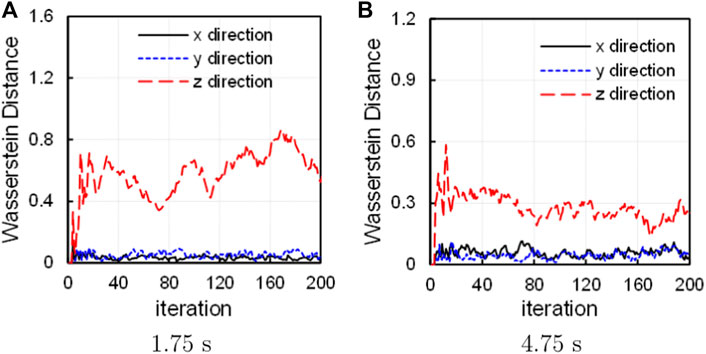
A detailed inspection into the convergence process is studied using WD curves. Since the slowest convergence occurs at t = 1.75 s and t = 4.75 s as Figure 4 shows, the two time steps are selected to apply WD diagnostics. The Wasserstein diagnostics curves are depicted in Figures 8A,B at the two time steps.
In the x and y direction, the WD curves exhibit steep rising edge and rapidly reaches stable after less than 20 cycles. However, in the z direction, the WD curves rise slowly, which slows down the convergence. Besides, the WDz curves show distinct fluctuation, which indicates that the neutron source distribution is oscillating along the z direction. One of the reason is that the length of the active region along the z direction is 128.52 cm, three times of that along the x and y directions (42.84 cm). Another reason is that this study uses a quarter core model, in which the left and up boundary conditions in Figure 2A are reflective along x and y directions, while the up and down boundary conditions in Figure 2B are crossing along z directions. Therefore, the neutron source distribution trends to oscillate around the axis of symmetry along the z direction.
It is also noted that the WDz curve is higher than the WDx and WDy curves at t = 1.75 s, while the WDz curve is lower at t = 4.75 s. Only the CRs in assembly 4 is moving vertically at t = 1.75 s, which causes larger changes of the neutron source distribution along the z direction. However, at t = 4.75 s the CRs in both assembly 3 and 4 are moving oppositely, and thus the neutrons are flowing from assembly 3 into assembly 4, causing larger changes in the horizontal direction.
After applying ASM, the WD curves exhibit significant changes, as shown in Figure 9. The curves in the x and y direction stable at much faster speed and lower level (WD < 0.1) than the curves in Figure 8. Considering the first asymptotic factor is 16, the neutron source distribution in the x and y direction is accelerated by 16 times the original convergence speed as revealed by Eq. 26. Because the neutron source distribution along the x and y directions converges at less than 20 cycles in Figure 8, the curves in the x and y direction after applying the ASM method stable after 2 cycles theoretically. Because WD uses the second cycle as the reference, the WDx and WDy values are as small as their fluctuation range.
In the z direction, however, the WD curves stable at a little higher level than those in the x and y direction. Figure 10 compares the WDz curves with and without ASM. It is found that the WDz curves obtained with ASM are lower than those without ASM, which indicates that the convergence is accelerated in the first cycle because the neutrons of next cycles become closer to those of the second cycle. Therefore, the WD results also proves the acceleration capability of ASM.
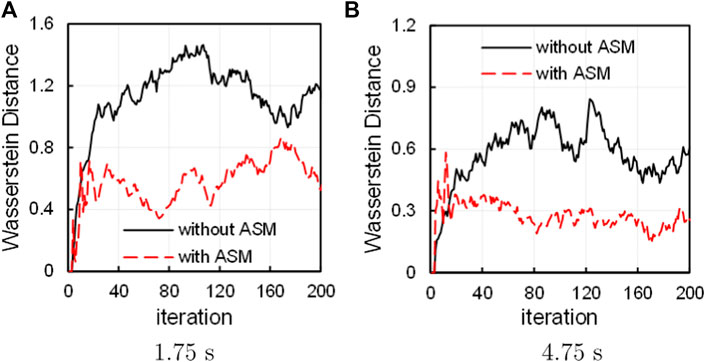
FIGURE 10. Comparison of Wasserstein distance curves in the z direction at (A) 1.75 s and (B) 4.75 s.
4 Conclusion
The acceleration problem in the MC PCQS calculation is studied in this paper. TFSE and the corresponding neutron source iteration algorithm are introduced, as well as the reason to use iterations. A simplified model is used to analyze the iteration convergence features of TFSE. It is found that reducing ESR is capable of accelerating the iteration convergence. Therefore, ASM is developed for MC PCQS to decrease inactive cycle numbers and lower the computational cost. The performance is tested with the TD4-4 case of the C5G7-TD benchmark. Results show that the number of inactive cycles is reduced by more than 85% compared with the previous study, and over 15% of the total computational cost is saved. Using the Wasserstein distance measure, it is found that ASM considerably speeds up the convergence of the neutron source distributions along the x and y directions. The iteration is also accelerated along the z direction. As predicted by the convergence characteristic analysis using the simplified model, the time step affects the convergence, which will be studied in the future.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
XG: Conceptualization, Modeling, Formal Analysis, Writing-original draft and revising. GW: Conceptualization, Supervision, Writing-review and editing. KW: Funding Acquistion.
Funding
This work was supported by the National Key Research and Development Project of China (Grant No: 2020YFB1901700).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Brissenden, R. J., and Garlick, A. R. (1986). Biases in the estimation of keff and its error by Monte Carlo methods. Ann. Nucl. Energy 13, 63–83. doi:10.1016/0306-4549(86)90095-2
Bronson, R., Costa, G. B., and Saccoman, J. T. (2013). Linear algebra: Algorithms, applications, and techniques.
Davis, A., Shriwise, P., and Zhang, X. (2020). “Dag-openmc: Cad-based geometry in openmc,” in Transactions - 2020 Virtual Conference.
Deng, L., Li, G., Zhang, B.-Y., Li, R., Zhang, L.-Y., Wang, X., et al. (2022). A high fidelity general purpose 3-d Monte Carlo particle transport program jmct3. 0. Nucl. Sci. Tech. 33, 108–118. doi:10.1007/s41365-022-01092-0
Dufek, J., and Gudowski, W. (2009). Stability and convergence problems of the Monte Carlo fission matrix acceleration methods. Ann. Nucl. Energy 36, 1648–1651. doi:10.1016/j.anucene.2009.07.020
Dulla, S., Mund, E. H., and Ravetto, P. (2008). The quasi-static method revisited. Prog. Nucl. Energy 50, 908–920. doi:10.1016/j.pnucene.2008.04.009
Goorley, T., James, M., Booth, T., Brown, F., Bull, J., Cox, L., et al. (2012). Initial mcnp6 release overview. Nucl. Technol. 180, 298–315. doi:10.13182/nt11-135
Guo, X., Li, Z., Huang, S., and Wang, K. (2022). Convergence diagnostics for Monte Carlo fission source distributions using the wasserstein distance measure. Nucl. Eng. Des. 389, 111675. doi:10.1016/j.nucengdes.2022.111675
Guo, X., Shang, X., Song, J., Shi, G., and Wang, K. (2021). Kinetic methods in Monte Carlo code rmc and its implementation to c5g7-td benchmark. Ann. Nucl. Energy 151, 107864. doi:10.1016/j.anucene.2020.107864
Laureau, A., Aufiero, M., Rubiolo, P. R., Merle-Lucotte, E., Heuer, D., et al. (2015). Transient fission matrix: Kinetic calculation and kinetic parameters beta(eff) and lambda(eff) calculation. Ann. Nucl. energy 85, 1035–1044.
Hou, J. J., Ivanov, K. N., Boyarinov, V. F., and Fomichenko, P. A. (2017). Oecd/nea benchmark for time-dependent neutron transport calculations without spatial homogenization. Nucl. Eng. Des. 317, 177–189. doi:10.1016/j.nucengdes.2017.02.008
Jia, C., Jian, L., Guo, X., Wang, K., Huang, S., and Liang, J. (2022). Development of an improved direct kinetic simulation capability in rmc code. Ann. Nucl. Energy 173, 109110. doi:10.1016/j.anucene.2022.109110
Jo, Y., Cho, B., and Cho, N. Z. (2016). Nuclear reactor transient analysis by continuous-energy Monte Carlo calculation based on predictor-corrector quasi-static method. Nucl. Sci. Eng. 183, 229–246. doi:10.13182/nse15-100
Kreher, M. A., Shaner, S., Forget, B., and Smith, K. (2022). Frequency transform method for transient analysis of nuclear reactors in Monte Carlo. Nucl. Sci. Eng. 2022, 1–12. doi:10.1080/00295639.2022.2067739
Kuroishi, T., and Nomura, Y. (2003). Development of fission source acceleration method for slow convergence in criticality analyses by using matrix eigenvector applicable to spent fuel transport cask with axial burnup profile. J. Nucl. Sci. Technol. 40, 433–440. doi:10.1080/18811248.2003.9715377
Larsen, E. W., and Yang, J. (2011). A functional Monte Carlo method for k-eigenvalue problems. Nucl. Sci. Eng. 159, 107–126. doi:10.13182/nse07-92
Lee, M. J., Joo, H. G., Lee, D., and Smith, K. (2010). “Investigation of cmfd accelerated Monte Carlo eigenvalue calculation with simplified low dimensional multigroup formulation,” in PHYSOR 2010.
Leppänen, J., Pusa, M., Viitanen, T., Valtavirta, V., and Kaltiaisenaho, T. (2015). The serpent Monte Carlo code: Status, development and applications in 2013. Ann. Nucl. Energy 82, 142–150. doi:10.1016/j.anucene.2014.08.024
Mickus, I., and Dufek, J. (2018). Optimal neutron population growth in accelerated Monte Carlo criticality calculations. Ann. Nucl. Energy 117, 297–304. doi:10.1016/j.anucene.2018.03.046
Mickus, I., Roberts, J. A., and Dufek, J. (2020). Stochastic-deterministic response matrix method for reactor transients. Ann. Nucl. Energy 140, 107103. doi:10.1016/j.anucene.2019.107103
Pan, Q., An, N., Zhang, T., Liu, X., Cai, Y., Wang, L., et al. (2022a). Single-step Monte Carlo criticality algorithm. Comput. Phys. Commun. 279, 108439. doi:10.1016/j.cpc.2022.108439
Pan, Q., Cai, Y., Wang, L., Zhang, T., Liu, X., and Wang, K. (2022b). Source extrapolation scheme for Monte Carlo fission source convergence based on rmc code. Ann. Nucl. Energy 166, 108737. doi:10.1016/j.anucene.2021.108737
Pan, Q., Zhang, T., Liu, X., Cai, Y., Wang, L., and Wang, K. (2022c). Optimal batch size growth for wielandt method and superhistory method. Nucl. Sci. Eng. 196, 183–192. doi:10.1080/00295639.2021.1968223
Rao, J., Shang, X., Yu, G., and Wang, K. (2019). Coupling rmc and cfd for simulation of transients in treat reactor. Ann. Nucl. Energy 132, 249–257. doi:10.1016/j.anucene.2019.04.039
Romano, P. K., Horelik, N. E., Herman, B. R., Nelson, A. G., Forget, B., and Smith, K. (2015). Openmc: A state-of-the-art Monte Carlo code for research and development. Ann. Nucl. Energy 82, 90–97. doi:10.1016/j.anucene.2014.07.048
Shaner, S. C. (2018). Development of high fidelity methods for 3d Monte Carlo transient analysis of nuclear reactors.
She, D., Wang, K., and Yu, G. (2015). Asymptotic wielandt method and superhistory method for source convergence in Monte Carlo criticality calculation. Nucl. Sci. Eng. 172, 127–137. doi:10.13182/NSE11-44
Sjenitzer, B. L., and Hoogenboom, J. E. (2013). Dynamic Monte Carlo method for nuclear reactor kinetics calculations. Nucl. Sci. Eng. 175, 94–107. doi:10.13182/nse12-44
Trahan, T. J. (2019). A quasi-static Monte Carlo algorithm for the simulation of sub-prompt critical transients. Ann. Nucl. Energy 127, 257–267. doi:10.1016/j.anucene.2018.11.055
Turinsky, P. J., Al-Chalabi, R. M., Engrand, P., Sarsour, H. N., Faure, F. X., and Guo, W. (1994). “NESTLE: Few-group neutron diffusion equation solver utilizing the nodal expansion method for eigenvalue, adjoint, fixed-source steady-state and transient problems,” in Tech. rep. (Idaho Falls, Idaho: Idaho National Lab., USA).
Wang, K., Li, Z., She, D., Xu, Q., Qiu, Y., Yu, J., et al. (2015). Rmc–a Monte Carlo code for reactor core analysis. Ann. Nucl. Energy 82, 121–129. doi:10.1016/j.anucene.2014.08.048
Wilson, P., Tautges, T. J., Kraftcheck, J. A., Smith, B. M., and Henderson, D. L. (2010). Acceleration techniques for the direct use of cad-based geometry in fusion neutronics analysis. Fusion Eng. Des. 85, 1759–1765. doi:10.1016/j.fusengdes.2010.05.030
Yamamoto, T., and Miyoshi, Y. (2004). Reliable method for fission source convergence of Monte Carlo criticality calculation with wielandt’s method. J. Nucl. Sci. Technol. 41, 99–107. doi:10.1080/18811248.2004.9715465
Keywords: PCQS, Monte Carlo, fixed-source equation, asymptotic superhistory method, convergence
Citation: Guo X, Wang G and Wang K (2023) Convergence characteristics and acceleration of the transient fixed source equation solved by Monte Carlo method. Front. Energy Res. 10:1010482. doi: 10.3389/fenrg.2022.1010482
Received: 03 August 2022; Accepted: 20 September 2022;
Published: 09 January 2023.
Edited by:
Shichang Liu, North China Electric Power University, ChinaReviewed by:
Qingquan Pan, Shanghai Jiao Tong University, ChinaJiankai Yu, The University of Tennessee, Knoxville, United States
Copyright © 2023 Guo, Wang and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Guanbo Wang, d2diMDRkZXBAaG90bWFpbC5jb20=
 Xiaoyu Guo
Xiaoyu Guo Guanbo Wang1*
Guanbo Wang1*