A prior knowledge-embedded reinforcement learning method for real-time active power corrective control in complex power systems

With the increasing uncertainty and complexity of modern power grids, the real-time active power corrective control problem becomes intractable, bringing significant challenges to the stable operation of future power systems. To promote effective and efficient active power corrective control, a prior knowledge-embedded reinforcement learning method is proposed in this paper, to improve the performance of the deep reinforcement learning agent while maintaining the real-time control manner. The system-level feature is first established based on prior knowledge and cooperating with the equipment-level features, to provide a thorough description of the power network states. A global-local network structure is then constructed to integrate the two-level information accordingly by introducing the graph pooling method. Based on the multi-level representation of power system states, the Deep Q-learning from Demonstrations method is adopted to guide the deep reinforcement learning agent to learn from the expert policy along with the interactive improving process. Considering the infrequent corrective control actions in practice, the double-prioritized training mechanism combined with the λ-return is further developed to help the agent lay emphasis on learning from critical control experience. Simulation results demonstrate that the proposed method prevails over the conventional deep reinforcement learning methods in training efficiency and control effects, and has the potential to solve the complex active power corrective control problem in the future.

1 Introduction

Security control is a critical method to ensure the safe and reliable operation of power systems. The blackouts in recent years show that successive outages of transmission lines are the main cause of cascading failures and even system crashes. Therefore, it is of great significance to perform real-time and effective active power corrective control in the complex power system, to efficiently eliminate line overloads, prevent cascading failures and ensure the stable operation of the power grid.

Scholars have conducted extensive research on this topic. In the early days, generation rescheduling and load shedding are carried out to mitigate the transmission line congestion based on the sensitivity matrices (Talukdar et al., 2005). Fuzzy logic control is also utilized to alleviate the line overloads (Lenoir et al., 2009). As the power system becomes increasingly complex, the security-constrained optimal power flow (SCOPF) approaches considering N-1 contingencies are widely adopted. Based on linear network compression, a preventive SCOPF problem is solved to avoid all possible overloads by pre-schedule (Karbalaei et al., 2018). Considering the large cost to satisfy all N-1 constraints in the preventive control method, corrective control is introduced in the SCOPF approach to mitigate overloads in contingencies. A corrective SCOPF approach is proposed in (Cao et al., 2015) with the help of multi-terminal VSC-HVDC. By introducing the unified power flow controller as the fast corrective control measure, a three-stage corrective SCOPF approach is proposed in (Yan et al., 2020a) based on Benders decomposition and sequential cone programming. A real-time distributed OPF approach is also proposed to perform robust corrective control (Ding et al., 2020). Efforts are also made to make full use of the preventive method and the corrective method. In (Waseem and Manshadi, 2021), contingencies are filtered and divided for preventive actions and corrective actions, and the SCOPF problem is solved based on a decomposed convex relaxation algorithm. The combination of preventive SCOPF and corrective SCOPF is proposed in (Xu et al., 2013) to promote system security, while the evolutionary algorithm and the interior-point method are adopted for optimal solutions. Besides, considering the open-loop feature of the OPF-based methods, the model-predictive control method is also developed to alleviate overloads based on the model-based linear power flow model (Martin and Hiskens, 2016).

The existing methods provide enlightening solutions to realize the effective corrective control of power systems. However, with the high penetration of renewable energy and the wide interconnection of power grids, the power system’s operation mode and stability characteristics become more complex (Yan et al., 2019; Yan et al., 2020b; Yan et al., 2021). The strong complexity and uncertainty of the new-type power system aggravate the modeling difficulty of the active power corrective control problem. Correspondingly, the model-based methods will face great challenges in promoting the effectiveness and efficiency of the corrective control strategy. Meanwhile, the swiftly developed deep reinforcement learning (DRL) method can deal with complicated problems in a model-free manner with high computational efficiency. These features make the DRL method suitable for the real-time active power corrective control problem. In our previous work, by introducing the simulation assistance, graph neural networks, and the multi-agent framework, we have proposed basic methods for the application of deep reinforcement learning in modern power system corrective control and verified the efficiency, feasibility, and adaptability of the DRL method (Xu et al., 2020; Chen et al., 2021; Xu et al., 2021).

However, the active power corrective control in new-type power systems demands the efficient and accurate alleviation of line overloads under the highly dynamic and strongly uncertain network operation states, which is of great complexity. The interactive learning of the conventional DRL method usually requires a lot of time, and the performance of the final strategy explored in the complex power system with massive constraints can be difficult to guarantee. At the same time, as aforementioned, there are plenty of model-based methods, as well as human experience, in the field of active power corrective control. If we can make full use of the prior knowledge, it will be of great help to apply the DRL method to active power corrective control more efficiently and effectively. In recent years, researchers begin to study the fusion of prior knowledge in DRL methods. A deep Q-learning from demonstrations (DQfD) method is proposed in (Hester et al., 2018), where human experience is collected as demonstration data to pre-train the DRL agent and further join its interactive learning process. Based on this idea, some researchers focus on improving the performance of the DQfD method by introducing soft expert guidance or behavioral cloning (Gao et al., 2018; Li et al., 2022a). Most recently, attempts of applying the prior knowledge guided DRL in power systems have been made, where the emergency voltage control is conducted (Li et al., 2022b).

Enlightened by the above work, a prior knowledge-embedded reinforcement learning (PKE-RL) method for active power corrective control is proposed in this paper, to improve the exploration efficiency and control performance of DRL methods in complex corrective control problems. The contributions of this paper are as follows:

1) According to the multi-level characteristics of the power system, the differential integration method of the real-time power grid state based on graph convolution and graph pooling is proposed, to fully represent and fuse the system operation indexes and fine-grained equipment features at global and local levels.

2) Based on the idea of Deep Q-learning from Demonstrations, the prior experience is introduced to the initial strategy optimization and whole-process guidance of the agent training. Considering the sparsity of the corrective control action, a double-prioritized DQfD(λ) training mechanism is further developed to focus the training process on critical control trajectories.

3) The simulation results in the modified 36-bus system demonstrate that the proposed method can effectively utilize the prior knowledge to further improve the DRL training performance and optimize the operation stability of power grids.

The remainder of this paper is organized as follows: Section 2 describes the active power corrective problem and formulates it as a Markov decision process (MDP). Section 3 illustrates the proposed prior knowledge-embedded reinforcement learning method. In Section 4, case studies are given to verify the proposed method. Section 5 summarizes our work and provides future directions for our research.

2 Problem formulation

2.1 Objective and constraints

The goal of the conventional active power corrective control is generally described as:

$\{\begin{array}{c}\min f\left(\left|\Delta {\mathbf{P}}_{\mathbf{G}}\right|,\text{Δ}{\mathbf{P}}_{\mathbf{L}},\text{Δ}\mathbf{{\rm N}}\right)\\ \mathrm{s}.\mathrm{t}.\left|P_{ij}\right|\le {\overline{P}}_{ij}\end{array}(1)$

where $f\left(\cdot \right)$ denotes the function related to the control cost, $\Delta {\mathbf{P}}_{\mathbf{G}}$ and $\Delta {\mathbf{P}}_{\mathbf{L}}$ represent the amount of generator redispatch and load shedding, respectively. $\Delta \mathbf{{\rm N}}$ represents the adjustment of the topology, such as line switching or bus-bar splitting. Notably, topological changes are assumed to be cost-free in this paper. $P_{ij}$ and ${\overline{P}}_{ij}$ denote the current power and capacity of the transmission line $l_{ij}$.

Along with the traditional constraints, to guide the corrective control actions to the feasible region and minimize their disturbance to the power grid, the number of topological control actions and redispatch amounts of generators are also restricted.

$X_{line}+X_{bus}\le N_{\text{limit}}(2)$

$\{\begin{array}{c}\left|\Delta {\mathbf{P}}_{\mathbf{G}}\right|\le \min \left({\mathbf{P}}_{\mathbf{G}\max }-{\mathbf{P}}_{\mathbf{G}},{\mathbf{R}}_{\mathbf{u}\mathbf{p}}\right)\\ \left|\Delta {\mathbf{P}}_{\mathbf{G}}\right|\le \min \left({\mathbf{P}}_{\mathbf{G}}-{\mathbf{P}}_{\mathbf{G}\min },{\mathbf{R}}_{\mathbf{d}\mathbf{o}\mathbf{w}\mathbf{n}}\right)\end{array}(3)$

where $X_{line}$, $X_{bus}$, $N_{\text{limit}}$ represent the number of line switching actions, bus-bar switching actions, and the limited topological actions, respectively. ${\mathbf{P}}_{\mathbf{G}\max }$ , ${\mathbf{P}}_{\mathbf{G}\min }$ , ${\mathbf{R}}_{\mathbf{u}\mathbf{p}}$ , ${\mathbf{R}}_{\mathbf{d}\mathbf{o}\mathbf{w}\mathbf{n}}$ denote the upper and lower bounds of the generator outputs, as well as the bidirectional ramping rates of the generators.

As the active power corrective control aims to avoid cascading failures by mitigating overloads, same as (Xu et al., 2021), the problem is extended to a time-series control problem as illustrated in Eq. 4. The goal can transform into securing the system operation while minimizing the overall cost during the control period, where corrective actions are carried out to alleviate overloads, preventive actions can also be considered to promote the system stability in advance:

$\min {\displaystyle \sum }_{t=\mathit{0}}^T\left[f\left(\left|\Delta {\mathit{P}}_{\mathit{G}}\left(t\right)\right|,\text{Δ}{\mathit{P}}_{\mathit{L}}\left(t\right),t\right)+f_{net}\left(t\right)+E_{loss}\left(t\right)\cdot p\left(t\right)\right](4)$

where T denotes the control duration, $f_{net}\left(t\right)$ represents the network loss cost, which can reflect the economic influence of corrective actions. $E_{loss}\left(t\right)$ symbolizes the energy loss at time t when a blackout strikes and $p\left(t\right)$ represents the marginal price of the generators’ outputs.

Furthermore, considering the practical constraints, the reaction time and the recovery time of power equipment are adopted, to reflect the available time for mitigating the overloads and the time requirements for reactivating the power equipment.

2.2 Problem formulated as MDP

According to the objective function presented in Eq. 4, the active power corrective control can be modeled as MDP in the form of a 5-element tuple $=\left\{\mathcal{S},\mathcal{A},\mathcal{P},\mathcal{R},\gamma \right\}$ . Where $\gamma$ symbolizes the discounting factor and $\mathcal{P}$ represents the state transition probability matrix. The details of other elements are elaborated as follows:

State space $\mathcal{S}$: The state $s_t\in \mathcal{S}$ represents the observation collected by the dispatch center from the power grid. As topological adjustments and node injections are addressed to mitigate line overloads, the features of generators, loads, and transmission lines are considered. Thus, the state is consisted of the active power status of power equipment and the load ratio of each line, i.e.,

$s_t=\left(\mathbf{P},\mathbf{\rho }\right)(5)$

where $\mathbf{P}$ denote the active power status of the power equipment, including outputs of generators, consumption of loads, and power flow at both ends of the lines. $\mathbf{\rho }$ represents the load ratio of each transmission line, i.e., the current flow divided by the thermal limit of each line.

Action space $\mathcal{A}$: To avoid damaging the interest of consumers, the action space comprises generator redispatch, line switching, bus-bar switching, and do-nothing actions. Notably, the line switching and bus-bar switching actions change the topology of the power grid in different ways. The bus-bar switching intervenes in the bus selection of the connected power equipment in one substation, while the line switching action alters the operating status of lines.

Reward function $\mathcal{R}$: As the control agent aims to secure the long-term operation of the power grid under strong uncertainties, the available transmission capacity (ATC) must be maintained to promote the flexibility of the power system with considering the risks brought by the heavy-loaded lines and overload lines. Thus, the modified available transmission capacity is introduced to represent the flexibility of the grid (Nacional de Colombia, Universidad, 2020):

$o_t={\displaystyle \sum }_{i=\mathit{1}}^{N_L}[\mathit{max}\left(\mathit{0},\left(\mathit{1}-{\rho }_i^{\mathit{2}}\right)\right)-\alpha \cdot \mathit{max}\left(\mathit{0},{\rho }_i-\mathit{1}\right)-\beta \cdot \mathit{max}\left(\mathit{0},{\rho }_i-\mathit{0.9}\right))(6)$

where $N_L$ denotes the number of lines, $\alpha$ and $\beta$ represent the penalty factors of overload and heavy load, respectively.

Based on MDP, the current system flexibility reflects the immediate effect of the action at the last time step, then the reward $r_t$ can be defined as:

$r_t=sign\left(o_{t+\mathit{1}}\right)\log \left(\mathit{1}+\left|o_{t+\mathit{1}}\right|\right)(7)$

where $sign\left(\cdot \right)$ produces a plus or minus sign according to the positive elements or the negative elements. Equation 7 can maintain the reward over a reasonable scale for the DRL agent to learn (Hester et al., 2018).

3 The prior knowledge-embedded reinforcement learning method

Although the deep reinforcement learning method can handle various problems with high computation efficiency, the effectiveness of the learned policy depends on its interaction with the environment. For the active power corrective control in new-type power systems, the existence of massive constraints, the strong uncertainty of power grid disturbances, and the selection of the proper measure from huge candidate strategies should be considered simultaneously. Thus, it can be challenging for the self-evolving reinforcement learning method to learn a high-quality corrective control strategy in such complex power networks.

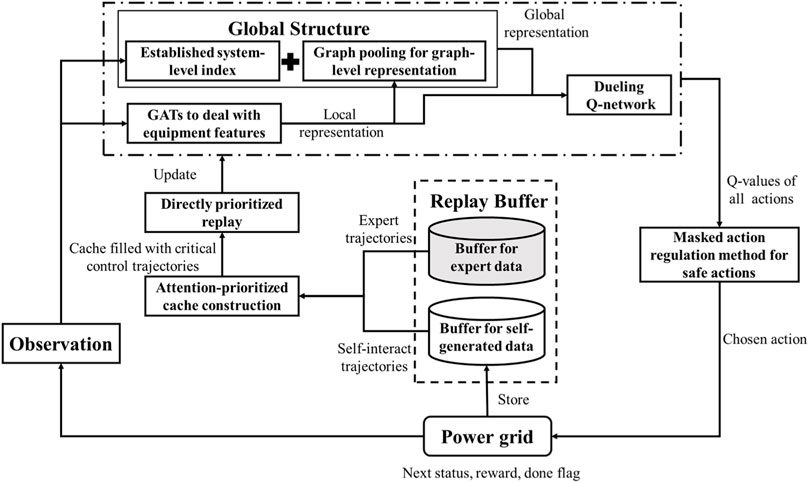
To promote the effectiveness of the reinforcement learning method in active power corrective control problems, a prior knowledge-embedded reinforcement learning method is developed in this paper. The architecture is illustrated in Figure 1. The system-level power network feature is constructed to merge domain knowledge into the observation of the DRL agent. Based on the graph pooling method, a global-local network structure is established to assist the agent deal with the system-level information and equipment-level features accordingly. Then, with the perception ability enhanced, the deep Q-learning from demonstrations method is introduced to improve the DRL agent’s capability with the guidance of expert knowledge. Besides, a double-prioritized DQN(λ) algorithm is utilized to facilitate the training process by focusing on the evaluation of key corrective control trajectories. The dueling deep Q-network is utilized as the basic DRL framework.

FIGURE 1

FIGURE 1. The overall architecture of the proposed PKE-RL method.

3.1 The multi-level differential integration of environment features

As the power grid is a high-dimensional dynamic system with strong complexity, a multi-level differential integration approach for environment features is proposed to aid the agent to realize a better perception of the status.

In the bulk power system, there are plenty of features provided for the agent at the moment of decision, and the key information can be difficult to extract since the features are from various equipment in a wide area. Hence, the global-level feature is established on the current modified ATC of the grid to provide an additional holistic perspective as in Eq. 8:

$s_{t,global}=o_t(8)$

According to Eq. 7 and Eq. 8, it can be easily found that the global-level feature represents $r_{t-\mathit{1}}$ in another form.

To coordinate with the multi-level features, in our network architecture, a differential integration strategy for global and local features is proposed. For the local features, graph attention networks (GATs) are introduced to perform representation learning due to the network-structure data format. The power equipment can be regarded as nodes of a graph. Thus, the adjacency matrix can be constructed based on the connections between the power equipment, i.e., the origin and extremity of lines, generators, and loads. The feature matrix is formed by combining the common and the unique features of the above equipment. The details of graph formulation for local features are shown in (Xu et al., 2021). Thus, the adjacency matrix and feature matrix in this problem can be elaborated as:

${\mathbf{A}}_{ij}=\{\begin{array}{c}1,\mathrm{i}\mathrm{f}\mathrm{e}\mathrm{q}\mathrm{u}\mathrm{i}\mathrm{p}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}i\mathrm{a}\mathrm{n}\mathrm{d}j\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{a}\mathrm{m}\mathrm{e}\mathrm{b}\mathrm{u}\mathrm{s}\mathrm{o}\mathrm{r}\mathrm{s}\mathrm{a}\mathrm{m}\mathrm{e}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}\\ 0,\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\end{array}(9)$

${\mathbf{X}}_{equipment-type}\{\begin{array}{c}\text{Origin}\\ \text{Extremity}\\ \text{Load}\\ \text{Generator}\end{array}\left[\begin{array}{c}{P}_{OR}\\ P_{EX}\\ P_L\\ P_G\end{array}\begin{array}{c}\rho \\ \rho \\ \mathit{0}\\ \mathit{0}\end{array}\right](10)$

where $P_{OR}$ and $P_{EX}$ denote the active power flow at the origin and the extremity of the transmission line, respectively. $P_L$ represents the active consumption value of the load, and $P_G$ stands for the active power output of the generator. $\rho$ denotes the load ratio of the transmission line.

Then, GATs can be utilized to conduct graph convolution. The graph attention layer with multi-head attention for transformed features of the ith node ${\mathit{h}}_i$ can be defined in Eq. 11 as (Veličković et al., 2017):

${\mathit{h}}_{\mathit{i}}^{\prime }=\sigma \left(\frac{\mathit{1}}{K}{\displaystyle \sum }_{k=\mathit{1}}^K{\displaystyle \sum }_{j\in {\mathcal{N}}_i}{\alpha }_{ij}^k{\mathbf{W}}^k{\mathit{h}}_{\mathit{j}}\right)(11)$

Where $\sigma$ symbolizes the non-linear activation function, ${\mathcal{N}}_i$ denotes the neighboring node set of the ith node, K represents the number of independent attention mechanisms, ${\alpha }_{ij}^k$ symbolizes the normalized attention coefficients computed by the kth attention mechanism (Vaswani et al., 2017), and ${\mathbf{W}}^k$ is the kth weight matrix. Notably, the initial transformed features of nodes H⁰ equals the feature matrix X.

After the graph convolution, the transformed node-level vectors of the local features are obtained to serve as the concrete representation of the current status. To get a comprehensive environment perception, a self-learning graph-level representation is acquired by introducing graph pooling on the transformed node-level vectors. Specifically, a self-attention graph pooling method is adopted to efficiently extract important information from node-level vectors, while nodal features and graph topology are both considered. In (Lee et al., 2019), the attention score of each node is obtained by adopting graph convolution:

$V=\delta \left(GAT\left(\mathbf{H},\mathbf{A}\right)\right)(12)$

where $\delta$ represents the activation function and $GAT\left(\cdot \right)$ denotes the graph attention layer with multi-head attention as shown in Eq. 11.

Then, the most important nodes based on the attention score will be preserved as in Eq. 13.

$\text{id}=top-rank\left(V,\left|\zeta N\right|\right)(13)$

where $\text{id}$ denotes the indexes of the preserved nodes, $top-rank$ represents the function of obtaining those indexes, $\zeta$ controls the ratio of preserved nodes, and $N$ denotes the number of nodes.

The graph pooling can then be realized according to Eq. 14:

$\{\begin{array}{c}{\mathbf{H}}_{out}={\mathbf{H}}_{\text{id}}\odot V\text{id}\\ {\mathbf{A}}_{out}={\mathbf{A}}_{\text{id},\text{id}}\end{array}(14)$

Thus, the important nodes are preserved to assist the agent address on fewer nodes with critical information maintained, which can prevent the distraction from the redundant signals in the bulk power system. Based on features of the important nodes, a readout layer is further adopted to aggregate the critical information and make graph-level representation as shown in Eq. 15 (Cangea et al., 2018):

$\mathit{G}=\frac{{\displaystyle \sum }_{i=\mathit{1}}^{N_C}{\mathit{g}}_i}{N_C}\parallel \stackrel{N_c}{\underset{i=\mathit{1}}{\max }}{\mathbf{g}}_i(15)$

where ${\mathbf{g}}_i$ represents the features of the ith important node, $N_C$ represents the number of the important nodes, and $\parallel$ is the concatenation function.

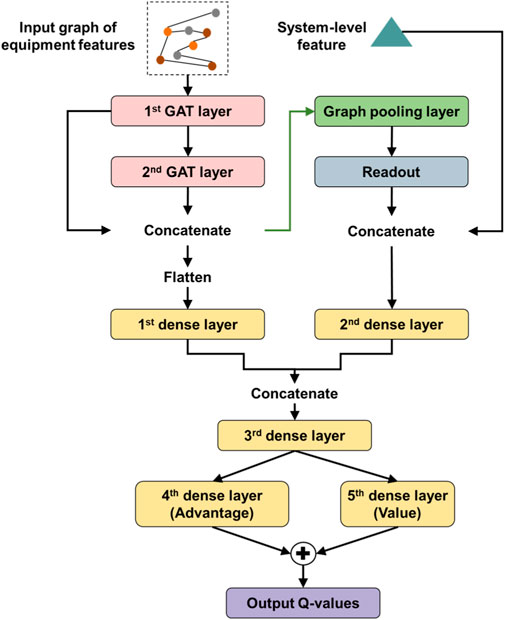
Finally, the self-learning graph-level representation and the prior-designed global-level feature are concatenated as the global representation. The global representation is then combined with the concrete representation via trainable weights and the multi-level differential integration of environment features is realized. The overall architecture of the adopted neural network is illustrated in Figure 2.

FIGURE 2

FIGURE 2. The proposed network architecture.

3.2 Deep Q-learning from demonstrations focusing on key corrective control trajectories

In many decision-making problems, the typical reinforcement learning method usually converges into a good policy from scratch after massive interactions with the environment. However, the diverse scenarios, few feasible solutions, and the complex electrical relation between power flow and node injection or topology in the active power corrective control problem make it challenging for DRL agents to learn an effective strategy by pure interaction, even with the help of simulation software. Additional work should be done to further promote the agent’s performance.

In power system corrective control, there always exists expert data like dispatcher operation records or model-based control strategies. This kind of data contains prior knowledge and usually performs well in alleviating overloads. Thus, in this paper, the deep Q-learning from demonstrations method is introduced to make full use of the expert knowledge. The domain knowledge is first utilized to pre-train the agent and then guide the agent during the rest of the training process, to improve the effectiveness of the learned corrective control policy.

In general, the DQfD method realizes merging prior knowledge into standard deep Q-learning by constructing a comprehensive loss function with four losses considered (Hester et al., 2018):

$L\left(\theta \right)=L_{DQ}\left(\theta \right)+{\alpha }_{\mathit{1}}{L}_n\left(\theta \right)+{\alpha }_{\mathit{2}}{L}_E\left(\theta \right)+{\alpha }_{\mathit{3}}{L}_{L\mathit{2}}\left(\theta \right)(16)$

where $\theta$ denote the Q-network parameters. $L_{DQ}\left(\theta \right),L_n\left(\theta \right),L_E\left(\theta \right),L_{L\mathit{2}}\left(\theta \right)$ denote the 1-step deep Q-learning loss, the n-step deep Q-learning loss, the expert loss, and the L2 regularization loss, respectively. $\alpha$ parameters represent the weights between different losses.

Among the losses, the deep Q-learning losses ensure the agent improves itself from temporal-difference (TD) learning, the expert loss is designed to guide the agent to follow the action strategy of the demonstrator, while the L2 regularization loss promotes the generalization ability of the agent by restricting the network parameters.

Specifically, considering the credit assignment problem, the n-step deep Q-learning loss is introduced to help better evaluate the actions’ long-term benefits and promote the entire training process. The n-step loss is computed based on the n-step return:

$L_n\left(\theta \right)={\mathbb{E}}_{\left(s,a,R^n\right)\sim U\left(\mathcal{D}\right)}\left[{\left(R^n-Q\left(s,a;\theta \right)\right)}^{\mathit{2}}\right](17)$

$R_t^n=r_t+\gamma r_{t+\mathit{1}}+\cdots +{\gamma }^n\underset{a^{\prime }\in \mathcal{A}}{\mathit{max}}Q\left(s_{t+n},a^{\prime }\right)(18)$

where $a$ is the agent action, $\mathcal{D}$ symbolizes the replay buffer, and $R^n$ denotes the n-step return.

As the most important part of all four losses, the expert loss is established under the assumption that the expert’s action prevails over other available actions in each scenario selected from demonstration data, as shown in Eq. 19. In the corresponding scenario, a large margin supervised loss is introduced to measure the equality between the greedy action and expert’s action (Piot et al., 2014). The supervised loss is 0 while the greedy action is the same as the expert’s action, and the supervised loss is a positive constant otherwise. Under this setting, the Q-values of other actions are at least a margin lower than the Q-value of the expert’s action, allowing the agent to imitate the expert while satisfying the Bellman equation and evaluating the unseen actions reasonably.

$L_E\left(\theta \right)=\underset{a\in \mathcal{A}}{\max }\left[Q\left(s,a\right)+l\left(a_E,a\right)\right]-Q\left(s,a_E\right)(19)$

where $l\left(a_E,a\right)$ represents the large margin supervised loss, $a_E$ denotes the expert’s action.

Based on the comprehensive loss function, the DQfD method merges the domain knowledge in the pre-training stage and formal training stage. During the pre-training phase, the DRL agent performs batch training by sampling from the collected demonstration data. Then, the pre-trained agent starts interacting with the environment and storing the self-generated data into the replay buffer $\mathcal{D}$. The self-generated data is updated continuously, while the demonstration data keeps unchanged to provide persistent guidance. And the proportion of demonstration data in experience replay is controlled to maintain the self-improving ability of the agent. Notably, when the sampled transition comes from the self-generated data, the expert loss doesn’t work and equals 0.

In the DRL-based active power corrective control architecture, the conducted action, e.g., switching the bus-bar or modifying the generator’s output, can alleviate the current heavy loads or overloads, as well as change the future operation point of the power grid. Thus, the long-term effect of the action must be precisely evaluated. The n-step return can help reduce the estimation bias to some extent, but in our problem, the proper selection of “n” can be challenging since the power system is highly complex. Meanwhile, despite the strong uncertainties of system disturbances, the power system can maintain stable operation at most times without additional actions. Thus, the proportion of preventive or corrective actions can be relatively low in the replay buffer, which may lead to the lack of sampling and training of these important control actions, even with tricks like the prioritized replay. The above two issues can hamper the training performance of the agent.

To further enable the DRL-based method in active power corrective control problems, based on our previous work (Xu et al., 2022), a double-prioritized DQfD(λ) training mechanism is introduced and developed in this paper. The critical corrective control trajectories are particularly analyzed with the ratio of the demonstration data and self-generated data carefully controlled.

Along with the experience replay, the λ-return is first introduced to estimate the long-term benefit of agent actions instead of the n-step return. The λ-return is defined as the exponential average of every n-step return (Watkins, 1989) as in Eq. 20, so the accurate evaluation of the actions can be realized without the selection of “n”.

$R_t^{\lambda }=\left(\mathit{1}-\lambda \right){\displaystyle \sum }_{n=\mathit{1}}^{T-t-\mathit{1}}{\lambda }^{n-\mathit{1}}{R}_t^n+{\lambda }^{T-t-\mathit{1}}{R}_t^{T-t}(20)$

where $\lambda \in \left[\mathit{0,1}\right]$ controls the decay rate of future returns.

In this way, the deep Q-learning losses can be replaced by the λ-discounted deep Q-learning loss as the λ-return considers every n-step return, $n=\mathit{1,2},\cdots ,T-t$. The comprehensive loss function can be expressed as in Eq. 21.

$\{\begin{array}{c}L\left(\theta \right)=L_{\lambda }\left(\theta \right)+{\alpha }_{\mathit{2}}{L}_E\left(\theta \right)+{\alpha }_{\mathit{3}}{L}_{L\mathit{2}}\left(\theta \right)\\ L_{\lambda }\left(\theta \right)={\mathbb{E}}_{\left(s,a,R^{\lambda }\right)\sim U\left(\mathcal{D}\right)}\left[{\left(R^{\lambda }-Q\left(s,a;\theta \right)\right)}^2\right]\end{array}(21)$

Practically, the λ-return can be computed recursively based on the trajectory of transitions as in (Daley and Amato, 2019), as illustrated in Eq. 22. The λ-returns of transitions from trajectories are stored into the replay buffer $\mathcal{D}$ and serve as the target network. The batch training based on experience replay can then be realized according to the new comprehensive loss function.

$R_t^{\lambda }=R_t^{\mathit{1}}+\gamma \lambda \left[R_{t+\mathit{1}}^{\lambda }-\underset{a^{\prime }\in \mathcal{A}}{\max }Q\left(s_{t+\mathit{1}},a^{\prime }\right)\right](22)$

As the calculation of the λ-return can be resource-consuming, when integrating the λ-return with the experience replay, a dynamic small cache $\mathcal{H}$ is constructed by sampling short trajectories of transitions from the repay buffer $\mathcal{D}$, to refresh and store the corresponding λ-returns. Specifically, during the entire training process, periodically, $C/B$ blocks, i.e., short trajectories containing neighboring transitions, are sampled to form the small cache $\mathcal{H}$. Different from the random sampling policy in (Daley and Amato, 2019), a demonstration-ratio-constraint attention-prioritized cache construction method is developed to improve the number of effective control transitions in the cache, with the ratio of the expert experience and the interaction experience restricted.

In the DQfD method, the repay buffer $\mathcal{D}$ is composed of two parts: the demonstration buffer ${\mathcal{D}}_{demo}$ and the interaction buffer ${\mathcal{D}}_{self}$ . To restrict the ratio of the expert experience within a certain range from the cache construction stage, the number of sampled blocks from the demonstration buffer ${\mathcal{D}}_{demo}$ is defined as:

$N_{demo}=\frac{C}{B}{\epsilon }_d(23)$

where ${\epsilon }_d$ denotes the expected demonstration ratio in the batch training.

Therefore, $N_{demo}$ and $N_{self}=\left(C/B\right)\bullet \left(\mathit{1}-{\epsilon }_d\right)$ blocks are sampled from the demonstration buffer ${\mathcal{D}}_{demo}$ and the interaction buffer ${\mathcal{D}}_{self}$, respectively. For the demonstration buffer ${\mathcal{D}}_{demo}$ with size $U_{demo}$, the number of candidate blocks is $U_{demo}-B+\mathit{1}$. We define the attention degree of each block as the diversity of the effective control actions within it, as illustrated in Eq. 24.

${\phi }_i=\frac{\Vert set\left({\mathit{a}}_i\right)\Vert -\mathit{1}}{B}(24)$

where ${\mathit{a}}_i$ represents the agent’s action trajectory in the ith block, where the “do nothing” action is included. $set\left(\cdot \right)$ denotes the function that selects non-repeatable elements to form a set. $\Vert \cdot \Vert$ calculates the number of elements. Thus, the blocks containing more kinds of effective control actions will have higher attention degrees.

Then, the $N_{demo}$ blocks are sampled from the demonstration buffer ${\mathcal{D}}_{demo}$ according to their attention degrees, the sampling probability of the ith block is illustrated as:

$P\left(i\right)=\frac{{\phi }_i}{{\displaystyle \sum }_{k=\mathit{1}}^{U_{demo}-B+\mathit{1}}{\phi }_k}(25)$

The methodology of sampling blocks from the interaction buffer ${\mathcal{D}}_{self}$ is the same as the demonstration method. Based on the proposed attention-prioritized blocks sampling strategy, we can promote a better evaluation of the action set as the established cache always contains various effective control experience, while the expert-imitation ability and the self-learning ability is controlled from the source.

Based on the cache, the computation of the λ-return is performed in each block. A directly prioritized replay policy is adopted to improve the transition sampling and batch training process. The transitions are sampled from the cache with the TD error-based probabilities:

$p\left(e_j\right)=\{\begin{array}{c}\frac{\left(\mathit{1}+\mu \right)}{C},\mathrm{i}\mathrm{f}\left|{\delta }_j\right|>{\delta }_{median}\\ \frac{\mathit{1}}{C},\mathrm{i}\mathrm{f}\left|{\delta }_j\right|={\delta }_{median}\\ \frac{\left(\mathit{1}-\mu \right)}{C},\mathrm{i}\mathrm{f}\left|{\delta }_j\right|<{\delta }_{median}\end{array}(26)$

where $e_j$ and ${\delta }_j$ denote the jth transition and its TD error, respectively. $\mu \in \left[\mathit{0,1}\right]$ controls the prioritized degree of sampling. ${\delta }_{median}$ represents the median TD error value of the cache.

Based on the double-prioritized DQfD(λ) training mechanism, the important corrective control experience can be emphasized during the entire training process.

Meanwhile, considering the massive restrictions presented in the dynamic operation, during the training and deployment process, a masked action regulation method is developed to prevent the DRL agent from taking actions violating the constraints. The greedy action can be selected as in Eq. 27:

$a_{greedy}=\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}{\mathbf{a}}_{mask}Q\left(s_t,\forall a\right)(27)$

where ${\mathbf{a}}_{mask}$ is a 0–1 action mask vector with the size of action space, while the ith action violates the constraints according to the simple prior knowledge based on the observation, the action is masked with ${\mathbf{a}}_{mask}$ set to 0, otherwise set to 1.

4 Case study

4.1 Experiment setup

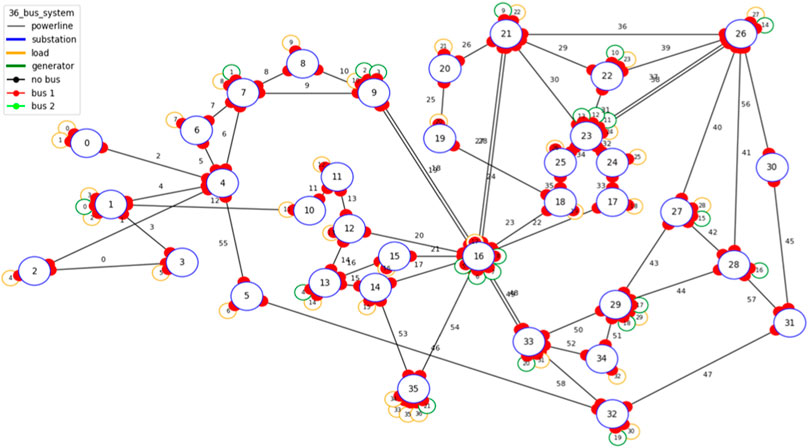
Same as our previous work (Xu et al., 2021), a modified 36-bus system originated from the IEEE 118-bus system is selected to verify the proposed method. The power grid consists of 59 transmission lines, 22 generators, and 37 loads, all the elements are connected to the bus-bars of the 36 substations, as illustrated in Figure 3. Among the generators, there are four wind farms and eight photovoltaic power plants, which will cause power fluctuations due to the uncertainties of their outputs. Besides, there can be at most two random “N-1” events occurring in the system within 1 day to reflect the strong system disturbance in future power networks.

FIGURE 3

FIGURE 3. The modified 36-bus system.

The corresponding strategies are deployed on the open-source platform Grid2Op (RTE-France, 2021) to perform active power corrective control every 5 min a day. The topological actions are considered in our action set with the number of simultaneous actions restricted to 1, avoiding too many changes to the network topology. Considering the reality of power grids, the cooldown time of each topological action is set to 15 min 245 effective topological control actions and 1 “do nothing” action compose the action set by pre-selection with the help of simulation (L2RPN, 2020).

In the following experiments, all the DRL-based agents are trained on a Linux server with 4 11 GB GPUs.

4.2 Performance of the proposed method

In this section, the performance of the proposed prior knowledge-embedded reinforcement learning method is evaluated by various operation scenarios. A dueling DQN structure as shown in Figure 2 is utilized to represent our agent, i.e., the PKE-RL agent. The details of the agent are illustrated in Table 1. 12,288-timestep active power corrective control trajectories are selected from the expert policy’s demonstrations (L2RPN, 2020) to serve as prior knowledge. The lambda value $\lambda$, replay buffer size U, cache size C, block size B, expected demonstration ratio ${\epsilon }_d$, and refresh frequency are set to 0.5, 32,768, 8,192, 128, 0.2, and 2048, respectively.

TABLE 1

TABLE 1. The details of the pke-rl agent.

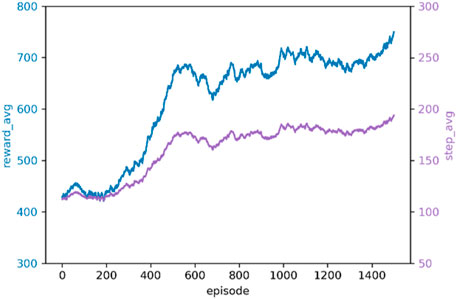
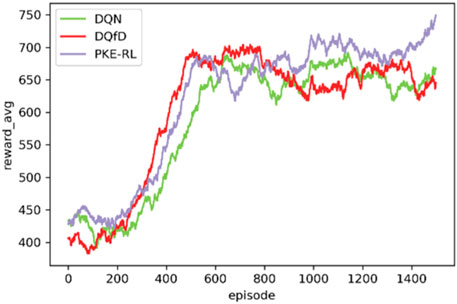
The PKE-RL agent is pre-trained with expert knowledge for 500 steps and then trained in the modified 36-bus system for 1,500 episodes. The averaged cumulative rewards curve and the averaged operation steps curve are shown in Figure 4.

FIGURE 4

FIGURE 4. The training performance of the PKE-RL agent.

As shown in Figure 4, despite the complexity of the scenarios, our agent keeps swiftly improving itself during the first 500 episodes and maintains a slow uptrend till the end of the training process, indicating the good learning ability of the proposed method.

To further evaluate the effectiveness of the proposed PKE-RL method, 100 random unseen scenarios containing renewable energy fluctuation and system disturbance are generated to serve as the test set. The aforementioned expert policy is adopted as the baseline method, where a simulation-based action enumeration strategy and a predefined empirical action selection strategy are combined to provide a thorough corrective control strategy. The trained PKE-RL model is deployed in a simulation-assisted manner: the top-3 actions with the largest Q-values are verified by the simulation software, and the action with the best estimated overload alleviating effect is chosen to execute. The related metrics of the two methods deployed on the test set are illustrated in Table 2.

TABLE 2

TABLE 2. performance comparison between the pke-rl method and expert policy.

According to Table 2, we can observe that the expert policy prevails over the proposed PKE-RL method in the operation-related metrics. As the expert policy is the combination of an empirical strategy and a simulation-based strategy, the projection from the power state to the control action can be complex for the proposed method to handle in a relatively short time. Besides, with only 12 trajectories sampled from the expert policy, the proposed method can achieve around 70% of the performance of the complicated demonstration policy, with only 18.5% of the time consumption to make corrective control decisions. More representative demonstration data may help the proposed method perform better. Specifically, the expert policy often demands over 200 DC power flow based-simulations to generate the decision, which will be more time-consuming when adopting accurate AC power flow or more actions are taken into consideration. The results indicate that the proposed method has the potential to effectively perform real-time active power corrective control in highly dynamic power systems with strong complexity.

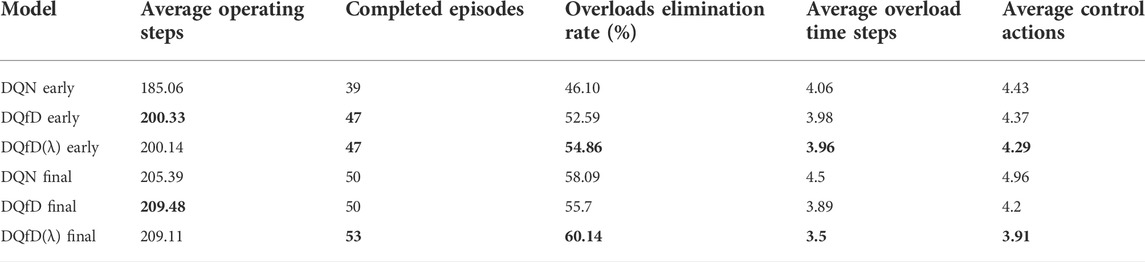
Two evaluation scenarios are selected to investigate the corrective control process of two methods in detail, namely Scenario I and Scenario II. The “N-1” contingencies, the max line load ratio in the grid, and the agents’ control actions in Scenario I are illustrated in Figure 5.

FIGURE 5

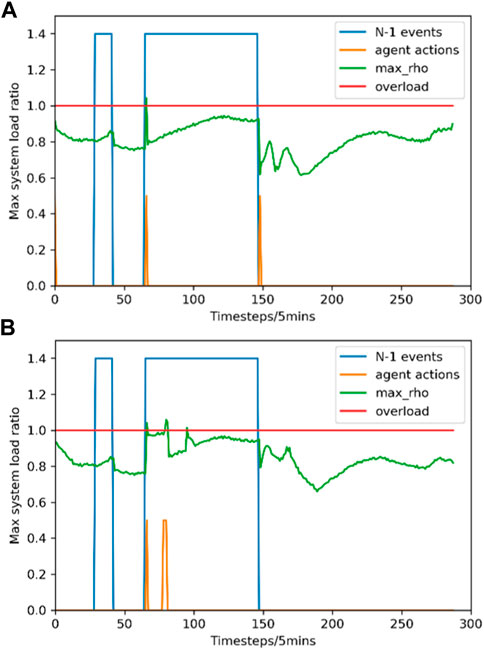
FIGURE 5. System operation status comparison between two methods in Scenario I. (A) Expert policy; (B) PKE-RL method.

In Scenario I, both two methods maintain the daylong operation with 2 “N-1” events strike. One overload and three overloads occur during the control of the expert policy and the PKE-RL method, respectively. Particularly, it can be seen from Figure 5 that an overload occurs after the second “N-1” event strike at time step 66, both two methods perform the corresponding corrective control action immediately, and the overload is eliminated in both scenarios. Notably, the expert policy yields the decision based on 209 simulations, while the PKE-RL method only needs a nearly computation-free deep network inference and three simulations. The above results indicate that the PKE-RL method can learn an efficient corrective control strategy with fair performance in maintaining the power girds stable operation.

The system operation status in Scenario II is illustrated in Figure 6.

FIGURE 6

FIGURE 6. System operation status comparison between two methods in Scenario II. (A) Expert policy; (B) PKE-RL method.

In Figure 6, it is clear that the proposed method realizes a successful daylong control with 2 “N-1” events attacks, while the expert policy fails to survive the first “N-1” event. It can be seen from Figure 6 that a severe overload occurs after the first “N-1” event strikes at time step 154, the expert policy cannot produce an effective strategy based on the initial preventive action, while the PKE-RL method performs the corresponding corrective control actions, alleviating the load ratio effectively to prevent the system collapse. Although two normal overloads occur in the following time steps due to power fluctuation, both overloads are eliminated swiftly under the proposed method. The conclusion may be drawn that the PKE-RL method has the capability of converging into a corrective control strategy exceeding the expert policy by combining the imitation ability and the self-learning ability.

4.3 Efficacy of the proposed double-prioritized DQfD (λ) training mechanism

As merging the demonstration data into deep Q-learning plays a critical role in prior knowledge enhancement, the DQN-based model, the standard DQfD-based model, and the double-prioritized DQfD(λ)-based model are evaluated to demonstrate the proposed method. The three models share the same parameters apart from training hyperparameters, i.e., the weights between different losses. The DQfD(λ)-based model originates from Section 4.2, the standard DQfD-based model is pre-trained with the same demonstration data for 500 steps and is also trained for 1,500 episodes with the DQN-based model. The averaged cumulative rewards curves of the above three models are shown in Figure 7.

FIGURE 7

FIGURE 7. The training performance of the DRL agents.

As illustrated in Figure 7, the performance of demonstration data enhanced models prevails over the DQN-based model at the initial learning phase at both speed and range. Besides, the demonstration data enhanced models show better operation promoting ability most time during the training. The results indicate that the introduction of expert knowledge can accelerate the learning process and improve the capability of the DRL agent in complex corrective control problems. Furthermore, the performance of the standard DQfD-based model suffers fluctuations after the middle of training, while the DQfD(λ)-based model keeps improving persistently. The conclusion can be drawn that the proposed double-prioritized DQfD(λ) training mechanism can better guide the agent to learn from the demonstration and interaction.

To further evaluate the effectiveness of the proposed training mechanism, The 100 random unseen scenarios mentioned in Section 4.2 are also utilized to demonstrate the feasibility of the proposed training mechanism. All the models are deployed in the same simulation-assisted manner as in Section 4.2. The models of the early training process, i.e., after 250 episodes of training, are also evaluated with the well-trained models. The related metrics of the three methods deployed on the test set are summarized in Table 3.

TABLE 3

TABLE 3. performance comparison between the DRL models.

According to Table 3, one can observe that the DQfD class models exhibit fair performance after the short-term training, indicating the merging of expert data can assist the DRL agent in efficiently gaining adequate corrective control knowledge without too much exploration within complex power systems. Meanwhile, the DQfD class models can still make progress and prevail over the DQN-based model at the end of the training, showing the ability of the DQfD class method to guide the agent to optimize its policy persistently. Specifically, the DQfD(λ)-based model performs satisfying from the start to the end, the related agent can alleviate the overloads with fewer control actions and maintain the long-term operation of the grids. Thus, we can infer that the proposed double-prioritized DQfD(λ) training mechanism can improve the DRL agent’s training efficiency and effectiveness in active power corrective control.

Similar to Section 4.2, two scenarios are selected to inspect the effectiveness of three well-trained DRL models in detail. Firstly, scenario II is selected again to evaluate the performance of the DQN-based model and the DQfD-based model in handling the severe post-contingency overload, the results are illustrated in Figure 8.

FIGURE 8

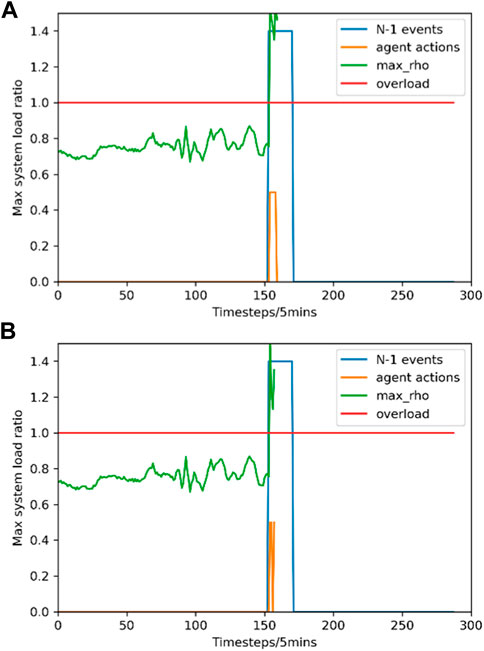
FIGURE 8. System operation status comparison between two basic DRL models in Scenario II. (A) DQN-based model; (B) DQfD-based model.

According to Figure 8, although the two models manage to alleviate the load ratio to some extent, specifically the DQfD-based model conducts more powerful corrective actions and realizes a larger reduction in the load ratio, they all fail to survive the first “N-1” event. The results demonstrate the feasibility of the proposed training mechanism.

A new scenario, namely scenario III, is chosen to evaluate the performance of the three models in handling the simpler situation. The system operation status in Scenario III is illustrated in Figure 9.

FIGURE 9

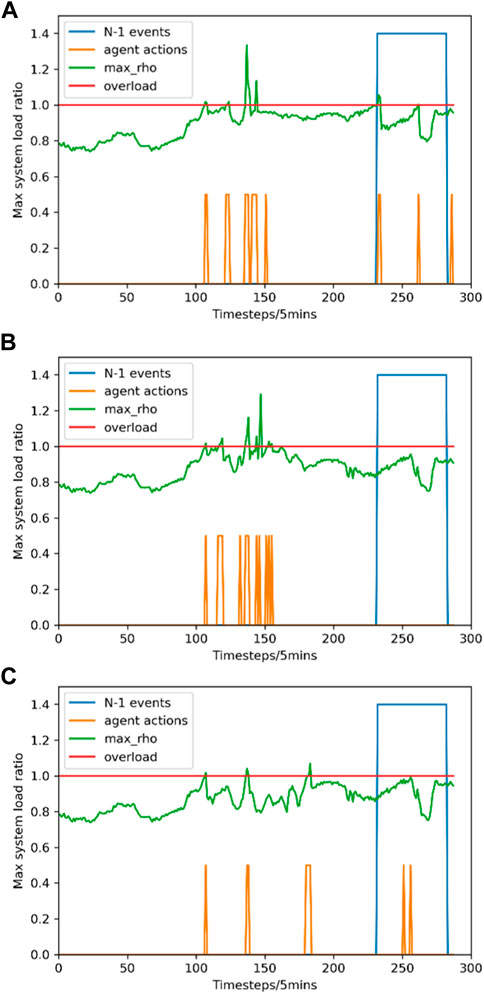
FIGURE 9. System operation status comparison between three DRL models in Scenario III. (A) DQN-based model; (B) DQfD-based model; (C) DQfD(λ)-based model.

In Scenario III, all three models maintain the daylong operation with 1 “N-1” event strikes. However, there are six overloads, six overloads, and three overloads that occur during the control of the DQN-based model, the DQfD-based model, and the DQfD(λ)-based model, respectively. Besides, we can easily find that multiple severe overloads happen between time step 100 to time step 200 under the two basic DRL models’ control, while the overload situation is much better under the control of the enhanced DRL model. Meanwhile, to alleviate the overloads, 17 and 14 corrective control actions are conducted by the DQN-based model and the DQfD-based model, respectively. The DQfD(λ)-based model only conducts five actions to deal with overloads. The results further demonstrate the effectiveness of the proposed double-prioritized DQfD(λ) training mechanism, where the trained model can promote the long-term stable operation of power grids by learning a simple but powerful corrective control strategy.

4.4 Performance comparison of different expected demonstration ratios

The expected demonstration ratio controls the agent’s imitation preference to the expert policy by altering the number of demonstration data in the cache. Thus, to evaluate the impact of this hyperparameter, three models with the expected demonstration ratios set to 0.1, 0.2, and 0.3 are trained by the proposed PKE-RL method with other parameters same as those in IV.2. The averaged cumulative rewards curves of the above three models are shown in Figure 10.

FIGURE 10

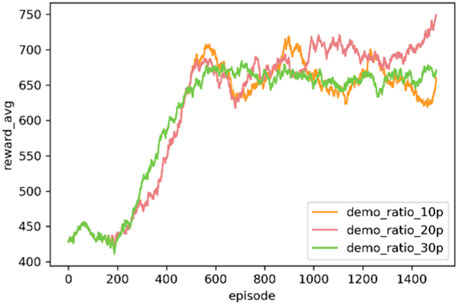
FIGURE 10. The training performance of the PKE-RL agents under different expected demonstration ratios.

As illustrated in Figure 10, in this problem, the agent with the highest expected demonstration ratio (simplified as “demo-ratio”) improves itself faster than other agents but maintains a stable but relatively poor performance for the rest of the training process, indicating that strong expert policy intervention can limit the further improvement of the agent. In contrast, the agent with the lowest demo-ratio learns a better policy first but suffers from frequent large fluctuations like the DQN agent in Figure 7, showing the unstableness brought by the weighted self-exploration process. Finally, the agent with the middle demo-ratio performs best during the entire training process. Based on the above results, the assumption can be made that a best demo-ratio point may exist to balance the imitation process and the self-exploration process.

5 Conclusion

In this paper, a prior knowledge-embedded reinforcement learning method is proposed to provide a solution to solve the complex active power corrective control problem with effectiveness and efficiency. Specifically, the differential integration method of the real-time power grid state based on graph convolution and graph pooling, as well as the double-prioritized DQfD(λ) training mechanism, are proposed to enhance the perception and the training efficiency of the DRL agent in complex power grids. Results show that the proposed method can learn from the complicated expert policy with fair performance without excessive demonstration data and deployed in a real-time manner. Besides, embedding the prior knowledge can promote a good initial control ability of the agent and alleviate the overall overloads with fewer actions than conventional DRL methods.

As we mainly verify the basic feasibility of the proposed method, the effectiveness of our method should be further improved. In our future works, the accurate selection of representative demonstration data, the delicate fusion of various expert policies, and the efficient utilization of the imperfect demonstration data are going to be studied to make our method applicable for the real-world active power corrective control problem.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: https://competitions.codalab.org/competitions/33121#learn_the_details-instructions.

Author contributions

PX implemented numerical simulation and wrote the manuscript. JZ proposed the idea and revised the manuscript. JL revised the manuscript. HZ helped conduct experiments. TG and SC assisted in data collection.

Funding

The work is supported by the National Key R&D Program of China under Grant 2018AAA0101504 and the Science and technology project of SGCC (State Grid Corporation of China): fundamental theory of human in-the-loop hybrid augmented intelligence for power grid dispatch and control. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.

Conflict of interest

Author JL was employed by NARI Group Corporation.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Cangea, C., Veličković, P., Jovanović, N., Kipf, T., and Liò, P. (2018). Towards sparse hierarchical graph classifiers. arXiv preprint Available at: https://arXiv/org/abs/1811.01287 (Accessed February 22, 2022).

Google Scholar

Cao, J., Du, W., and Wang, H. F. (2015). An improved corrective security constrained OPF for meshed AC/DC grids with multi-terminal VSC-HVDC. IEEE Trans. Power Syst. 31 (1), 485–495. doi:10.1109/tpwrs.2015.2396523

CrossRef Full Text | Google Scholar

Chen, S., Duan, J., Bai, Y., Zhang, J., Shi, D., and Sun, Y. (2021). Active power correction strategies based on deep reinforcement learning—part II: A distributed solution for adaptability. CSEE J. Power Energy Syst.8, 2096–0042.doi:10.17775/CSEEJPES.2020.07070

CrossRef Full Text | Google Scholar

Daley, B., and Amato, C. (2019). Reconciling λ-returns with experience replay. Adv. Neural Inf. Process. Syst. 32.

Google Scholar

Ding, L., Hu, P., Liu, Z. W., and Wen, G. (2020). Transmission lines overload alleviation: Distributed online optimization approach. IEEE Trans. Ind. Inf. 17 (5), 3197–3208. doi:10.1109/tii.2020.3009749

CrossRef Full Text | Google Scholar

Gao, Y., Xu, H., Lin, J., Yu, F., Levine, S., and Darrell, T. (2018). Reinforcement learning from imperfect demonstrations. arXiv preprint Available at: http://arXiv/org/abs/1802.05313 (Accessed March 5, 2022).

Google Scholar

Hester, T., Vecerik, M., Pietquin, O., Lanctot, M., Schaul, T., Piot, B., et al. (2018). Deep Q-learning from demonstrations.” in Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, February 2–7, 2018. Columbia Canada: PKP Publishing Services Network. 32, doi:10.1609/aaai.v32i1.11757

CrossRef Full Text | Google Scholar

Karbalaei, F., Shahbazi, H., and Mahdavi, M. (2018). A new method for solving preventive security-constrained optimal power flow based on linear network compression. Int. J. Electr. Power & Energy Syst. 96, 23–29. doi:10.1016/j.ijepes.2017.09.023

CrossRef Full Text | Google Scholar

L2RPN (2020). HoracioMartinez. Available at: https://github.com/horacioMartinez/L2RPN (Accessed April 8, 2022).

Google Scholar

Lee, J., Lee, I., and Kang, J. (2019). “Self-attention graph pooling,” in Proceeding International conference on machine learning, Vancouver, Canada, December 8–14, 2019. (PMLR), 3734–3743.

Google Scholar

Lenoir, L., Kamwa, I., and Dessaint, L. A. (2009). Overload alleviation with preventive-corrective static security using fuzzy logic. IEEE Trans. Power Syst. 24 (1), 134–145. doi:10.1109/tpwrs.2008.2008678

CrossRef Full Text | Google Scholar

Li, X., Wang, X., Zheng, X., Dai, Y., Yu, Z., Zhang, J. J., et al. (2022). Supervised assisted deep reinforcement learning for emergency voltage control of power systems. Neurocomputing 475, 69–79. doi:10.1016/j.neucom.2021.12.043

CrossRef Full Text | Google Scholar

Li, X., Wang, X., Zheng, X., Jin, J., Huang, Y., Zhang, J. J., et al. (2022). Sadrl: Merging human experience with machine intelligence via supervised assisted deep reinforcement learning. Neurocomputing 467, 300–309. doi:10.1016/j.neucom.2021.09.064

CrossRef Full Text | Google Scholar

Martin, J. A., and Hiskens, I. A. (2016). Corrective model-predictive control in large electric power systems. IEEE Trans. Power Syst. 32 (2), 1651–1662. doi:10.1109/tpwrs.2016.2598548

CrossRef Full Text | Google Scholar

Nacional de Colombia, Universidad. (2020). L2RPN-NEURIPS-2020. Available at: https://github.com/unaioperator/l2rpn-neurips-2020 (Accessed April 15, 2022).

Google Scholar

Piot, B., Geist, M., and Pietquin, O. (2014). “Boosted bellman residual minimization handling expert demonstrations,” in Proceeding Joint European Conference on machine learning and knowledge discovery in databases (Berlin, Heidelberg: Springer Nancy, France), September 15–19, 2014 8725 549.

CrossRef Full Text | Google Scholar

Rte-France, . (2021). Grid2Op. Available at: https://github.com/rte-france/Grid2Op (Accessed March 23, 2022).

Google Scholar

Talukdar, B. K., Sinha, A. K., Mukhopadhyay, S., and Bose, A. (2005). A computationally simple method for cost-efficient generation rescheduling and load shedding for congestion management. Int. J. Electr. Power & Energy Syst. 27 (5-6), 379–388. doi:10.1016/j.ijepes.2005.02.003

CrossRef Full Text | Google Scholar

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., and Polosukhin, I. (2017). Attention is all you need. Adv. neural Inf. Process. Syst. 30.

PubMed Abstract | Google Scholar

Veličković, P., Cucurull, G., Casanova, A., Romero, A., Lio, P., and Bengio, Y. (2017). Graph attention networks. arXiv preprint Available at: http://arXiv/org/abs.1710.10903 (Accessed March 17, 2022).

Google Scholar

Waseem, M., and Manshadi, S. D. (2021). Decomposing convexified security‐constrained AC optimal power flow problem with automatic generation control reformulation. Int. Trans. Electr. Energy Syst. 31 (9), e13027. doi:10.1002/2050-7038.13027

CrossRef Full Text | Google Scholar

Xu, P., Duan, J., Zhang, J., Pei, Y., Shi, D., and Sun, Y. (2021). Active power correction strategies based on deep reinforcement learning-part I: A simulation-driven solution for robustness. CSEE J. Power Energy Syst.8.1122–1133. 10.17775/CSEEJPES.2020.07090.

Google Scholar

Xu, P., Pei, Y., Zheng, X., and Zhang, J. (2020). “A simulation-constraint graph reinforcement learning method for line flow control,” in Proceeding 2020 IEEE 4th Conference on Energy Internet and Energy System Integration (EI2), Wuhan, China, October 30–Novermber 1, 2020, (Wuhan China: IEEE), 319–324. doi:10.1109/EI250167.2020.9347305

CrossRef Full Text | Google Scholar

Xu, P., Zhang, J., Gao, T., Chen, S., Wang, X., Jiang, H., et al. (2022). Real-time fast charging station recommendation for electric vehicles in coupled power-transportation networks: A graph reinforcement learning method. Int. J. Electr. Power. Energy Syst. 141, 108030. doi:10.1016/j.ijepes.2022.108030

CrossRef Full Text | Google Scholar

Xu, Y., Dong, Z. Y., Zhang, R., Wong, K. P., and Lai, M. (2013). Solving preventive-corrective SCOPF by a hybrid computational strategy. IEEE Trans. Power Syst. 29 (3), 1345–1355. doi:10.1109/tpwrs.2013.2293150

CrossRef Full Text | Google Scholar

Yan, M., Shahidehpour, M., Paaso, A., Zhang, L., Alabdulwahab, A., and Abusorrah, A. (2020). A convex three-stage SCOPF approach to power system flexibility with unified power flow controllers. IEEE Trans. Power Syst. 36 (3), 1947–1960. doi:10.1109/tpwrs.2020.3036653

CrossRef Full Text | Google Scholar

Yan, W., Cheng, L., Yan, S., Gao, W., and Gao, D. W. (2019). Enabling and evaluation of inertial control for PMSG-WTG using synchronverter with multiple virtual rotating masses in microgrid. IEEE Trans. Sustain. Energy 11 (2), 1078–1088. doi:10.1109/tste.2019.2918744

CrossRef Full Text | Google Scholar

Yan, W., Shah, S., Gevorgian, V., and Gao, D. W. (2021). “Sequence impedance modeling of grid-forming inverters,” in Proceeding2021 IEEE Power & Energy Society General Meeting (PESGM), Washington DC USA: IEEE, 1–5. doi:10.1109/PESGM46819.2021.9638001

CrossRef Full Text | Google Scholar

Yan, W., Wang, X., Gao, W., and Gevorgian, V. (2020). Electro-mechanical modeling of wind turbine and energy storage systems with enhanced inertial response. J. Mod. Power Syst. Clean Energy 8 (5), 820–830. doi:10.35833/mpce.2020.000272

CrossRef Full Text | Google Scholar

Watkins, C. J. C. H. (1989). Learning from delayed rewards. Surrey United Kingdom: Royal Holloway University of London

Google Scholar

Nomenclature

$\Delta {\mathbf{P}}_{\mathbf{G}},\Delta {\mathbf{P}}_{\mathbf{L}}$ Amount of generator redispatch and load shedding

$\Delta \mathbf{{\rm N}}$ Adjustment of the topology

$P_{ij},{\overline{P}}_{ij}$ Current power and capacity of the transmission line $l_{ij}$.

$X_{line}$, $X_{bus}$, $N_{\text{limit}}$ Number of line switching actions, bus-bar switching actions, and the limited topological actions, respectively

${\mathbf{P}}_{\mathbf{G}\max }$ , ${\mathbf{P}}_{\mathbf{G}\min }$ Upper and lower bounds of the generator outputs

${\mathbf{R}}_{\mathbf{u}\mathbf{p}}$ , ${\mathbf{R}}_{\mathbf{d}\mathbf{o}\mathbf{w}\mathbf{n}}$ Bidirectional ramping rates of the generators

T Control duration

$f_{net}\left(t\right)$ Network loss cost

$E_{loss}\left(t\right)$ Energy loss at time t when a blackout strikes

$p\left(t\right)$ Marginal price of the generators’ outputs

$\mathbf{P}$ Active power status of the power equipment

$\mathbf{\rho }$ Load ratio of each transmission line

$N_L$ Number of lines

$\alpha$ , $\beta$ Penalty factors of overload and heavy load

$P_{OR}$ , $P_{EX}$ Active power flow at the origin and the extremity of the transmission line, respectively.

$P_L$ Active consumption value of the load

$P_G$ Active power output of the generator

K Number of independent attention mechanisms

${\mathcal{N}}_i$ Neighboring node set of the ith node

${\alpha }_{ij}^k$ Normalized attention coefficients computed by the kth attention mechanism

${\mathbf{W}}^k$ kth weight matrix

${\mathbf{g}}_i$ Features of the ith important node

$N_C$ Number of the important nodes

$L_{DQ}\left(\theta \right),L_n\left(\theta \right),L_E\left(\theta \right),L_{L\mathit{2}}\left(\theta \right)$ 1-step deep Q-learning loss, n-step deep Q-learning loss, expert loss, and L2 regularization loss

$R^n$ n-step return

${\epsilon }_d$ Expected demonstration ratio in the batch training.