Entropy generation investigation of MHD Ag– and Au–H2O nanofluid above an exponential porous stretchable surface with thermal radiation and stagnation point flow

The current study presents an entropy generation investigation of magnetohydrodynamic Ag- and Au-H₂O nanofluid flows induced by an exponential stretchable sheet implanted in porous media accompanying suction/injection and heat radiation impact. Moreover, the stagnation point flow and silver and gold nanoparticles are considered. The consequences of ohmic heating and thermal radiation are also included as part of the heat transport examination. A physical process is transformed into a set of mathematical expressions using mathematical concepts, which can then be further simplified by using the necessary variables. Considering numerous physiological factors of interest, exact solutions for velocity and temperature profiles are calculated. Graphs and numerical tables are utilized to examine how different physical entities affect the distribution of velocity, temperature, and entropy. It is noted that enhancing the values of Ω reduces entropy inception. It is observed that the entropy inception field gains due to an increment in Ec_rt.

1 Introduction

Entropy is defined as a gauge of disorder inside a system and its surroundings or a measure of progress toward thermodynamic equilibrium under the scope of thermodynamics. Working with a thermodynamics process, an entropy generation investigation is essential since entropy calculates the effectiveness of every engineered thermofluid mechanism. The second law of thermodynamics determines the randomnessof any system. According to current research, the second law of thermodynamics is a significant tool for calculating the entropy of any system. Entropy inception has considerable fascinating application in the engineering and chemical industry such as extrusion procedures, lubrication phenomena, and schemes of geothermal energy, thermal mechanisms, heat management, and power production (Abbasi et al., 2021). Bejan (1979) was the first to introduce the concept of entropy production inside the flowing fluid and heat exchange mechanism. Later on, many researchers discussed entropy generation inside fluid and heat transport frameworks. Abbasi et al. (2021) studied the significant entropy inception with ohmic heating and thermal radiation effects of a viscoelastic nanofluid on a lubricated disk. Entropy production inside the MHD flow between porous media was discussed by Rashidi and Freidoonimehr (2014). Hayat et al. (2021) described the entropy in Newtonian nanofluid flow provoked by a curved stretchable sheet. Entropy inception within a Casson nanoliquid by a stretched surface soaked in porous media considering many impacts was investigated by Mahato et al. (2022). Wang et al. (2022) studied the Darcy–Forchheimer nanofluid for irreversibility inception. The entropy production in the Darcy–Forchheimer fluid in the presence of ohmic heat was scrutinized by Khan et al. (2022). Tayebi et al. (2021) examined the entropy and thermo-economics inside a convective nanofluid with the MHD effect. Afridi et al. (2018) analyzed the consequences of frictional and ohmic heating to find the entropy inception inside the used problem. Sithole et al. (2018) investigated the irreversibility of MHD nanofluid flow provoked by a stretchable surface for viscous dissipation influence. The impact of entropy inception inside the nanofluid with several effects is addressed in Noghrehabadi et al. (2013); Bhatti et al. (2017); and Abd El-Aziz and Afify (2019).

Despite the fact that a variety of approaches are used to promote heat transport, low thermal quality is a significant barrier in development of energy-efficient heat transfer fluids, which are in high need for a variety of industrial applications. The thermal capabilities of energy-carrying liquids are accountable for boosting the exchange of heat in a system. As a result, insufficient thermal conductivity is a disadvantage of conventional fluids, such as glycol, oil, water, and ethylene, in promoting the properties and efficiency of various engineered electronic devices. Integrating a fraction of nanometal particles within ordinary fluids is a novel way to improve the thermal conductivity of traditional liquids, which are known as nanofluids. The first time a nanofluid was used by adding nano-sized metallic particles into a conventional fluid was in 1995 by Choi (1995). Such kinds of nanofluids significantly enhance heat transport properties. After that, many scientists investigated the heat exchange rate of a nanofluid with several impacts. Prasannakumara (2021) analyzed the MHD Maxwell nanofluid provoked by a stretched surface by applying a numerical method. The influence of thermal radiation on the Casson nanofluid by shrinking/stretching walls was observed by Mahabaleshwara et al. (2022). The consequence of dissipation and radiation entities on an MHD bioconvective nanoliquid due to a stretching sheet was discussed by Neethu et al. (2022). B Awati et al. (2021) used the Haar wavelet method to study nanofluid flow with a nonlinear stretchable surface along with mass and energy transport. The impact of nanofluid flow provoked by a stretching sheet along with hydromagnetics is scrutinized by Manzoor et al. (2022). The impact of emerging entities on a nanofluid is presented in Oztop and Abu-Nada (2008); Khan and Pop (2010); Hamad (2011); Yacob et al. (2011); Noghrehabadi et al. (2012); Rohni et al. (2012).

Motivated by the aforementioned studies and interesting applications, entropy inception is calculated inside the magnetohydrodynamic nanofluid flow by incorporating Ag and Au nanoparticles on an exponentially stretchable surface with stagnation point flow, porous wall, and ohmic heating. Furthermore, the Bejan number and energy transport investigation are carried out along with thermal heating. The closed form solutions are acquired by utilizing hypergeometric functions to visualize the impact of numerous emerging parameters on the velocity field, temperature field, local skin friction, Nusselt number, and the chaos due to different effects in the used problem. Additionally, numerical tables and graphs are displayed.

2 Problem statement

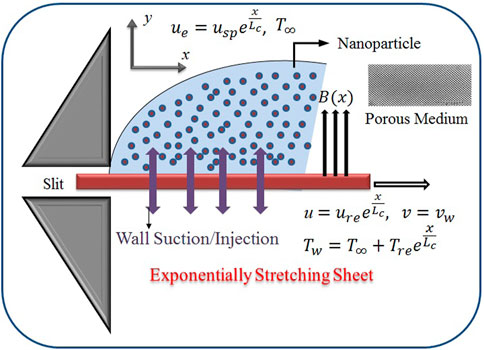
A two-dimensional, laminar, incompressible, steady flow of an Ag/Au-water MHD nanofluid provoked by an exponentially stretchable surface immersed in porous media with different body forces has been carried out. The impact of ohmic heating and thermal radiation is also considered part of the heat transfer study. The extending sheet is placed along the x-axis in the flow path, whereas the y-axis is assumed normal to the sheet. Figure 1 shows that the fluid is in the y ≥ 0 space. Considering a velocity of $u=u_{re}{e}^{x/L_c}$, the surface is pulled throughout the x dimension. In addition, the magnetic field (B₀) is introduced toward the flowing fluid in a normal direction. The basic equations that regulate the used fluid flow are as shown as follows (Rashidi and Freidoonimehr, 2014):

$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,(1)$

$\begin{array}{ll}\hfill & u\frac{\partial u}{\partial x}+v\frac{\partial v}{\partial y}=\frac{{\mu }_{sf}}{{\rho }_{sf}}\frac{{\partial }^{2}u}{\partial y^2}+u_{sp}\frac{\partial u_{sp}}{\partial x}-\frac{{\sigma }_{sf}B{\left(x\right)}^2}{{\rho }_{sf}}\left(u-u_{sp}\right)\hfill \\ \hfill & -\frac{{\mu }_{sf}}{{\rho }_{sf}k}\left(u-u_{sp}\right),\hfill \end{array}(2)$

in which B(x) = magnetic entity; u, v denote the velocity portions in the x and y directions, respectively, ρ_sf = density; μ_sf is the dynamic viscosity; the thermal diffusivity is expressed by α_sf; the specific heat capacitance is $={\left(\rho c_p\right)}_{sf}$; and ν_sf is the kinematic viscosity of the nanofluid. The thermal conductivity can be expressed as follows (Rashid et al., 2017):

$\left.\begin{array}{cc}\hfill & {\left(\rho c_p\right)}_{sf}=+\varphi {\left(\rho c_p\right)}_{sf}+\left({\left(\rho c_p\right)}_{hf}.1-{\left(\rho c_p\right)}_{hf}\varphi \right),\hfill \\ \hfill & {\alpha }_{sf}=\frac{k_{sf}}{{\left(\rho c_p\right)}_{sf}},{\mu }_{sf}=\frac{{\mu }_{hf}}{{\left(1-\varphi \right)}^{2.5}},\hfill \\ \hfill & {\rho }_{sf}=\varphi \left({\rho }_{sf}\right)+\left(1{\rho }_{hf}-{\rho }_{hf}\varphi \right),{\nu }_{sf}=\frac{{\mu }_{sf}}{{\rho }_{sf}},\hfill \\ \hfill & \frac{{\sigma }_{sf}}{{\sigma }_{hf}}=\frac{\left(3\frac{{\sigma }_{sf}}{{\sigma }_{hf}}\varphi -3\varphi \right)}{\left(\varphi -\frac{{\sigma }_{sf}}{{\sigma }_{hf}}\varphi \right)+\left(\frac{{\sigma }_{sf}}{{\sigma }_{hf}}+2\right)}+1,\hfill \\ \hfill & k_{sf}=\frac{\left(k_{hf}{k}_{sf}+2k_{hf}^2\right)-2\left(k_{hf}^2\varphi -k_{sf}{k}_{hf}\varphi \right)}{\left(k_{sf}+2k_{hf}\right)+\left(k_f\varphi -k_{sf}\varphi \right)},\hfill \end{array}\right\}.(3)$

In Eq. 5, k_sf=thermal conductivity; σ_sf =electrical conductivity; ${\left(\rho c_p\right)}_{hf}$ and ρ_hf are the effective heat capacity and density, respectively; and ϕ is the nanoparticle volume ratio of the nanofluid. k_hf =thermal conductivity and σ_hf =electrical conductivity of the host fluid. The appropriate boundary criteria of the aforementioned model are as follows (Bilal et al., 2017):

$\left.\begin{array}{cc}\hfill & u=u_{re}{e}^{x/L_c},v=v_{\mathit{wmt}}\text{at}y=0,\hfill \\ \hfill & u\to u_{sp}=u_{re}{e}^{x/L_c}\text{as}y\to \infty .\hfill \end{array}\right\}.(4)$

FIGURE 1

FIGURE 1. Pictorial view of the model.

The accompanying similarity variables have been established to non-dimensionalize the basic equations and boundary conditions (Bilal et al., 2017):

$\left.\begin{array}{cc}\hfill & \eta =y{\left(\frac{u_{rf}}{2{\nu }_{hf}{L}_c}\right)}^{1/2}{e}^{x/2L_c},\hfill \\ \hfill & v=-{\left(\frac{u_{rf}{\nu }_{hf}}{2L_c}\right)}^{1/2}{e}^{x/2L_c}\left(f+\eta f^{\prime }\right),\hfill \\ \hfill & u=u_{re}{e}^{x/L_c}{f}^{\prime }.\hfill \end{array}\right\}.(5)$

Expression Eq. 5 reduces Eq. 2 into a dimensionless form and is given as

$\begin{array}{ccc}\hfill & \hfill & f\prime \prime \prime +{\chi }_1{\chi }_{2}ff\prime \prime +2{\chi }_1{\chi }_2{A}_{vr}^2-2{\chi }_1{\chi }_2{f}^{\prime 2}-{\chi }_1{M}_{\mathit{egn}}{f}^{\prime }+\hfill \\ \hfill & \hfill & \left(K_{pr}{A}_{vr}-K_{pr}{f}^{\prime }\right)=0,\hfill \end{array}(6)$

and the boundary conditions are

$\left.\begin{array}{cc}\hfill & f\left(\eta \right)=S,f^{\prime }\left(\eta \right)=1,\text{at}\eta =0,\hfill \\ \hfill & f^{\prime }\left(\eta \right)\to \frac{u_{sp}}{u_{re}}=A_{vr}\text{as}\eta \to \infty .\hfill \end{array}\right\}.(7)$

In Eqs. 6, 7,

$\left.\begin{array}{cc}\hfill & {\chi }_2=\left(1-\varphi +\varphi \frac{{\rho }_{sf}}{{\rho }_{hf}}\right),S=-{\left(\frac{2L_c}{u_{re}{\nu }_{hf}}\right)}^{1/2}{e}^{-x/2L}{v}_w,\hfill \\ \hfill & M_{\mathit{egn}}=\frac{2u_{rf}\sigma B_0^2}{\rho },\hfill \\ \hfill & {\chi }_1={\left(1-\varphi \right)}^{2.5},K_{pr}=\frac{u_{re}{k}_0}{L_c{\nu }_{hf}},u_{sp}\hfill \\ \hfill & \text{the\hspace{0.17em}stagnation}-\text{point\hspace{0.17em}flow\hspace{0.17em}velocity},\hfill \\ \hfill & u_{re}\text{the\hspace{0.17em}reference\hspace{0.17em}velocity},\hfill \end{array}\right\}(8)$

where K_pr is the permeability parameter and M_egn = the Hartmann number. The closed form solution of such a kind of equation was introduced by Chakrabarti and Gupta, (1979):

$f\left(\eta \right)={\lambda }_1+{\lambda }_2{e}^{-\mathrm{\Psi }\eta }.(9)$

By solving Eqs. 7, 8,

$f\left(\eta \right)=\left(\frac{1-e^{-\mathrm{\Psi }\eta }}{\mathrm{\Psi }}\right)+S.(10)$

To obtain Ψ, λ₁, and λ₁, substitute Eq. 9 in Eq. 6:

$\mathrm{\Psi }=\frac{1}{2}{\chi }_1{\chi }_{2}S+\frac{1}{2}\sqrt{{\chi }_1^2{\chi }_2^2{S}^2-8A_{vr}^2{\chi }_1{\chi }_2-4A_{vr}{\chi }_1{M}_{\mathit{egn+\xi }}},(11)$

${\lambda }_1=\frac{1}{\frac{1}{2}{\chi }_1{\chi }_{2}S+\frac{1}{2}\sqrt{{\chi }_1^2{\chi }_2^2{S}^2-8A_{vr}^2{\chi }_1{\chi }_2-4A_{vr}{\chi }_1{M}_{\mathit{egn+\xi }}}}+S,(12)$

${\lambda }_2=-\frac{1}{\frac{1}{2}{\chi }_1{\chi }_{2}S+\frac{1}{2}\sqrt{{\chi }_1^2{\chi }_2^2{S}^2-8A_{vr}^2{\chi }_1{\chi }_2-4A_{vr}{\chi }_1{M}_{\mathit{egn+\xi }}}},(13)$

$\xi =-4A_{vr}4K_{pr}+8{\chi }_1{\chi }_2+4{\chi }_1{M}_{\mathit{egn}}+4K_{pr},(14)$

where Ψ, λ₁, and λ₁ are constants with Ψ > 0. After substituting Eqs. 11–13 in Eq. 9, the solution of the velocity filed is found as

$\left.\begin{array}{cc}f\left(\eta \right)=\hfill & \left(\frac{1}{\frac{1}{2}{\chi }_1{\chi }_{2}S+\frac{1}{2}\sqrt{{\chi }_1^2{\chi }_2^2{S}^2-8A_{vr}^2{\chi }_1{\chi }_2-4A_{vr}{\chi }_1{M}_{\mathit{egn+\xi }}}}\right)\hfill \\ \hfill & \left(1-e^{\frac{1}{2}{\chi }_1{\chi }_{2}S+\frac{1}{2}\sqrt{{\chi }_1^2{\chi }_2^2{S}^2-8A_{vr}^2{\chi }_1{\chi }_2-4A_{vr}{\chi }_1{M}_{\mathit{egn+\xi }}}\eta }\right)+S,\hfill \end{array}\right\}.(15)$

The skin friction at the sheet is calculated as follows:

$C_f=\frac{{\tau }_w}{\rho u_w^2}=\frac{f\prime \prime \left(0\right)}{R{e}_x^{1/2}{\chi }_1},R{e}_x^{-1/2}{\chi }_1{C}_f=f\prime \prime \left(0\right).(16)$

Here, the Reynolds number is shown by $R{e}_x=\frac{x{u}_w}{\nu }$, and the stress over the wall $={\tau }_w={\mu }_{n}f{\left(\frac{\partial u}{\partial y}\right)}_{y=0}$.

3 Heat transfer analysis

Heat transport analysis is carried out in this portion. Additionally, ohmic heating and thermal radiation are considered, which are presented by the following governing equation:

$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}={\alpha }_{sf}\frac{{\partial }^{2}T}{\partial y^2}+\frac{{\sigma }_{sf}B{\left(x\right)}^2}{{\left(\rho C_p\right)}_{sf}}{u}^2-\frac{1}{{\left(\rho C_p\right)}_{sf}}\frac{\partial q_{\mathit{rad}}}{\partial y},(17)$

where

$q_{\mathit{rad}}=-\frac{{\sigma }^{\ast }}{3k^{\ast }}\frac{\partial T^4}{\partial y}.(18)$

Here, σ^∗ is the Stefan–Boltzmann constant, k^∗ expresses the mass absorption coefficient, and the specific heat $={\left(C_p\right)}_{sf}$. Expression Eq. 16 takes the following form after substituting Eq. 17 in it (Rashid et al., 2017):

$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}={\alpha }_{nf}\frac{{\partial }^{2}T}{\partial y^2}+\frac{1}{3{\left(\rho Cp\right)}_{nf}}\frac{16{\sigma }^{\ast }{T}_{\infty }^3}{k^{\ast }}\frac{{\partial }^{2}T}{\partial y^2}+\frac{{\sigma }_{nf}B{\left(x\right)}^2}{{\left(\rho C_p\right)}_{nf}}{u}^2.(19)$

The suitable boundary conditions are

$\left.\begin{array}{cc}\hfill & T=T_w=T_{\infty }+T_{re}{e}^{x/L_c}\text{at}y=0,\hfill \\ \hfill & T\to T_{\infty }\text{as}y\to \infty ,\hfill \end{array}\right\}(20)$

where T_w is the temperature of the sheet, the characteristic length = L_c, T_re is the reference temperature, and T_∞ is the free stream temperature. The temperature field similarity variable is specified as follows (Rashid et al., 2017):

$\theta \left(\eta \right)=\frac{T-T_{\infty }}{T_w-T_{\infty }}.(21)$

The energy equation takes the following dimensionless form by utilizing Eqs. 5, 20:

$\kappa \theta \prime \prime -2Pr{f}^{\prime }\theta +Prf{\theta }^{\prime }+\frac{Pr{M}_{\mathit{egn}}}{{\chi }_4}E{c}_{rt}{f\prime \prime }^2=0,(22)$

where

$\begin{array}{ll}\hfill & \kappa =\left(\frac{{\chi }_3}{{\chi }_4}\right)\left(1+\frac{4}{3N_{tr}{\chi }_3}\right),E{c}_{rt}=\frac{u^2}{\left(T_w-T_{\infty }\right)Cp},\mathrm{Pr}=\frac{{\nu }_{hf}}{{\alpha }_{hf}},\hfill \\ \hfill & N_{tr}=\frac{K^{\ast }{K}_{hf}}{4{\sigma }^{\ast }{T}_{\infty }^3},\hfill \\ \hfill & {\chi }_3=\frac{\left(k_{sf}+2k_{hf}\right)-\left(k_{hf}2\varphi -k_{sf}2\varphi \right)}{\left(k_{sf}+2k_{hf}\right)+\left(k_{hf}2\varphi -k_{sf}2\varphi \right)},\hfill \\ \hfill & {\chi }_4=\left(\varphi \frac{{\left(\rho Cp\right)}_{sf}}{{\left(\rho Cp\right)}_{hf}}-\varphi +1\right).\hfill \end{array}(23)$

Here, Pr is the Prandtl number, N_tr is the radiation parameter, and Ec_rt is the Eckert number. The boundary conditions are

$\left.\begin{array}{cc}\hfill & \theta \left(\eta \right)=1\text{at}\eta =0,\hfill \\ \hfill & \theta \left(\eta \right)\to 0\text{as}\eta \to \infty .\hfill \end{array}\right\}.(24)$

Now, using Eq. 9 in Eq. 21,

$\begin{array}{ll}\hfill & \kappa \theta \prime \prime -2Pr{e}^{-\mathrm{\Psi }\eta }\theta +\mathrm{Pr}\left(S+\frac{1}{\mathrm{\Psi }}\left(\frac{1-e^{-\mathrm{\Psi }\eta }}{\mathrm{\Psi }}\right)\right){\theta }^{\prime }+\frac{Pr{M}_{\mathit{egn}}}{{\chi }_4}\hfill \\ \hfill & E{c}_{rt}{\left(e^{-\mathrm{\Psi }\eta }\right)}^2=0.\hfill \end{array}(25)$

introduces the following new variable to convert Eq. 24 into Kummer’s ordinary differential equation:

$\beta =-\frac{\mathrm{Pr}{e}^{-\mathrm{\Psi }\eta }}{\kappa {\mathrm{\Psi }}^2}.(26)$

Applying the new variable, Eq. 24 becomes as expressed below:

$\beta \frac{{\partial }^2\theta }{\partial {\beta }^2}+\left(Q-\beta \right)\frac{\partial \theta }{\partial \beta }+2\theta =-\frac{Pr{M}_{\mathit{egn}}}{{\chi }_4}E{c}_{rt}{\left(e^{-\mathrm{\Psi }\eta }\right)}^2,(27)$

where Q = (1 − H), and $H=\frac{\mathrm{Pr}}{\kappa \mathrm{\Psi }}\left(\frac{1}{\mathrm{\Psi }}+S\right)$.

The boundary conditions are

$\theta \left(\beta \right)=1,\theta \left(0\right)=0.(28)$

The closed form solution of Eq. 26 in the form of Kummer’s function (Abramowitz and Stegun, 1972) is

$\left.\begin{array}{cc}\theta \left(\beta \right)=\hfill & \left(\frac{M\left(-2+\frac{\mathrm{Pr}}{\kappa \mathrm{\Psi }}\left(S+\frac{1}{\mathrm{\Psi }}\right),1+\frac{\mathrm{Pr}}{\kappa \mathrm{\Psi }}\left(S+\frac{1}{\mathrm{\Psi }}\right),\beta \right){\beta }^{\frac{\mathrm{Pr}}{\kappa \mathrm{\Psi }}\left(S+\frac{1}{\mathrm{\Psi }}\right)}}{M\left(-2+\frac{\mathrm{Pr}}{\kappa \mathrm{\Psi }}\left(S+\frac{1}{\mathrm{\Psi }}\right),1+\frac{\mathrm{Pr}}{\kappa \mathrm{\Psi }}\left(S+\frac{1}{\mathrm{\Psi }}\right),-\frac{\mathrm{Pr}}{\kappa {\mathrm{\Psi }}^2}\right)2{\left(-\frac{\mathrm{Pr}}{\kappa {\mathrm{\Psi }}^2}\right)}^{\frac{\mathrm{Pr}}{\kappa \mathrm{\Psi }}\left(S+\frac{1}{\mathrm{\Psi }}\right)}}\right)\hfill \\ \hfill & \times \left(\frac{1}{\left(-2+\frac{\mathrm{Pr}}{\kappa \mathrm{\Psi }}\left(S+\frac{1}{\mathrm{\Psi }}\right)\right)\kappa {\mathrm{\Psi }}^2{\chi }_4}\right)\hfill \\ \hfill & +\left(\frac{\mathrm{Pr}}{\kappa \mathrm{\Psi }}{\left(S+\frac{1}{\mathrm{\Psi }}\right)}^2+\left(-\beta -3\right)\frac{\mathrm{Pr}}{\kappa \mathrm{\Psi }}\left(S+\frac{1}{\mathrm{\Psi }}\right)+{\beta }^2-2\right)\hfill \\ \hfill & \times \left(-M_{\mathit{egn}}E{c}_{rt}\kappa {\mathrm{\Psi }}^2\frac{2\xi -1+\frac{\mathrm{Pr}}{\kappa \mathrm{\Psi }}\left(S+\frac{1}{\mathrm{\Psi }}\right)}{2{\chi }_{4}Pr}+\frac{M_{\mathit{egn}}E{c}_{rt}\kappa {\mathrm{\Psi }}^2}{2{\chi }_{4}Pr\left(-2+\frac{\mathrm{Pr}}{\kappa \mathrm{\Psi }}\left(S+\frac{1}{\mathrm{\Psi }}\right)\right)}\right),\hfill \end{array}\right\},(29)$

where M is the confluent hypergeometric function (1st kind). The following is the solution to the energy equation:

$\left.\begin{array}{cc}\theta \left(\eta \right)=\hfill & \left(\frac{e^{-\mathrm{\Psi }\frac{\mathrm{Pr}}{\kappa \mathrm{\Psi }}\left(S+\frac{1}{\mathrm{\Psi }}\right)P\eta }M\left(-2+\frac{\mathrm{Pr}}{\kappa \mathrm{\Psi }}\left(S+\frac{1}{\mathrm{\Psi }}\right),1+\frac{\mathrm{Pr}}{\kappa \mathrm{\Psi }}\left(S+\frac{1}{\mathrm{\Psi }}\right),-\frac{\mathrm{Pr}}{\kappa {\mathrm{\Psi }}^2}{e}^{-\mathrm{\Psi }\eta }\right)}{2M\left(-2+\frac{\mathrm{Pr}}{\kappa \mathrm{\Psi }}\left(S+\frac{1}{\mathrm{\Psi }}\right),1+\frac{\mathrm{Pr}}{\kappa \mathrm{\Psi }}\left(S+\frac{1}{\mathrm{\Psi }}\right),-\frac{\mathrm{Pr}}{\kappa {\mathrm{\Psi }}^2}\right)}\right)\hfill \\ \hfill & \times \left(\frac{1}{\left(\kappa {\mathrm{\Psi }}^2{\chi }_4\right)\left(-2+\frac{\mathrm{Pr}}{\kappa \mathrm{\Psi }}\left(S+\frac{1}{\mathrm{\Psi }}\right)\right)}\right)\hfill \\ \hfill & +\left(\frac{\mathrm{Pr}}{\kappa \mathrm{\Psi }}{\left(S+\frac{1}{\mathrm{\Psi }}\right)}^2+\left(-\frac{\mathrm{Pr}}{\kappa {\mathrm{\Psi }}^2}{e}^{-\mathrm{\Psi }\eta }-3\right)\frac{\mathrm{Pr}}{\kappa \mathrm{\Psi }}\left(S+\frac{1}{\mathrm{\Psi }}\right)+{\left(\frac{\mathrm{Pr}}{\kappa {\mathrm{\Psi }}^2}{e}^{-\mathrm{\Psi }\eta }\right)}^2-4\frac{\mathrm{Pr}}{\kappa {\mathrm{\Psi }}^2}{e}^{-\mathrm{\Psi }\eta }+2\right)\hfill \\ \hfill & \times \left(\frac{M_{\mathit{egn}}E{c}_{rt}\kappa {\mathrm{\Psi }}^2}{2{\chi }_{4}Pr\left(-2+\frac{\mathrm{Pr}}{\kappa \mathrm{\Psi }}\left(S+\frac{1}{\mathrm{\Psi }}\right)\right)}-M_{\mathit{egn}}E{c}_{rt}\kappa {\mathrm{\Psi }}^2\frac{2\xi -1+\frac{\mathrm{Pr}}{\kappa \mathrm{\Psi }}\left(S+\frac{1}{\mathrm{\Psi }}\right)}{2{\chi }_{4}Pr}\right).\hfill \end{array}\right\}.(30)$

$\left.\begin{array}{cc}{\theta }_{\eta }\left(0\right)=\hfill & \frac{{\mathrm{Pr}}^2{\left(S+\frac{1}{{\mathrm{\Psi }}^2}\right)}^2{\lambda }_3\left(2{\chi }_{4}Pr\mathrm{\Psi }\left(S+\frac{1}{\mathrm{\Psi }}\right)-4{\chi }_4{\mathrm{\Psi }}^2\kappa -M_{\mathit{egn}}E{c}_{rt}\mathrm{Pr}\right)}{2{\kappa }^{2}a{\chi }_4{\mathrm{\Psi }}^2\left(-2+P\right)}\hfill \\ \hfill & +\left(\frac{\mathrm{Pr}\left(S+\frac{1}{\mathrm{\Psi }}\right)\left({\lambda }_4-{\lambda }_3\right)\left(2{\chi }_{4}Pr\mathrm{\Psi }\left(S+\frac{1}{\mathrm{\Psi }}\right)-4{\chi }_4{\mathrm{\Psi }}^2\kappa -M_{\mathit{egn}}E{c}_{rt}\mathrm{Pr}\right)}{{\kappa }^2{\lambda }_3{\chi }_4\mathrm{\Psi }}\right)\hfill \\ \hfill & -\left(\frac{1}{2a{\chi }_4\mathrm{\Psi }\kappa }\left(-\left({\lambda }_5-{\lambda }_4\right)\left(-1+\frac{\mathrm{Pr}S}{\kappa \mathrm{\Psi }}+\frac{\mathrm{Pr}}{\kappa {\mathrm{\Psi }}^2}\right)\mathrm{\Psi }+\left({\lambda }_4-{\lambda }_3\right)\right)\right)\left(-2\xi +\frac{\mathrm{Pr}S}{\kappa \mathrm{\Psi }}+\frac{\mathrm{Pr}}{\kappa {\mathrm{\Psi }}^2}\right)\mathrm{\Psi }\hfill \\ \hfill & \times \left(2{\chi }_{4}Pr\mathrm{\Psi }\left(S+\frac{1}{\mathrm{\Psi }}\right)-4{\chi }_4{\mathrm{\Psi }}^2\kappa -M_{\mathit{egn}}\mathrm{Pr}E{c}_{rt}\right)\hfill \\ \hfill & +\left(\frac{\left(\frac{-2Pr}{{\kappa }^2\mathrm{\Psi }}\left(S+\frac{1}{\mathrm{\Psi }}\right)+\frac{4Pr}{\kappa }\right)Ec{M}_{\mathit{egn}}{\mathrm{\Psi }}^2\kappa }{{\chi }_{4}Pr\left(-2+\frac{\mathrm{Pr}}{\kappa \mathrm{\Psi }}\left(S+\frac{1}{\mathrm{\Psi }}\right)\right)}+\frac{E{c}_{rt}{M}_{\mathit{egn}}{\mathrm{\Psi }}^2}{{\chi }_4}\right),\hfill \end{array}\right\},(31)$

where

$\begin{array}{ll}\hfill & {\lambda }_3=M\left(\frac{\mathrm{Pr}}{\kappa \mathrm{\Psi }}\left(S+\frac{1}{\mathrm{\Psi }}\right)-2,\frac{\mathrm{Pr}}{\kappa \mathrm{\Psi }}\left(S+\frac{1}{\mathrm{\Psi }}\right)+1,-\frac{\mathrm{Pr}}{{\mathrm{\Psi }}^2\kappa }\right),\hfill \\ \hfill & {\lambda }_4=M\left(\frac{\mathrm{Pr}}{\kappa \mathrm{\Psi }}\left(S+\frac{1}{\mathrm{\Psi }}\right)-1,\frac{\mathrm{Pr}}{\kappa \mathrm{\Psi }}\left(S+\frac{1}{\mathrm{\Psi }}\right)+1,-\frac{\mathrm{Pr}}{{\mathrm{\Psi }}^2\kappa }\right),\hfill \\ \hfill & {\lambda }_5=M\left(\frac{\mathrm{Pr}}{\kappa \mathrm{\Psi }}\left(S+\frac{1}{\mathrm{\Psi }}\right),\frac{\mathrm{Pr}}{\kappa \mathrm{\Psi }}\left(S+\frac{1}{\mathrm{\Psi }}\right)+1,-\frac{\mathrm{Pr}}{{\mathrm{\Psi }}^2\kappa }\right),\hfill \\ \hfill & \mathrm{\Psi }=\frac{1}{2}{\chi }_1{\chi }_{2}S+\frac{1}{2}\sqrt{{\chi }_1^2{\chi }_2^2{S}^2-8A_{vr}^2{\chi }_1{\chi }_2-4A_{vr}{\chi }_1{M}_{\mathit{egn+\xi }}}.\hfill \end{array}$

As a result, the non-dimensional wall temperature was generated by the aforementioned equation. The local Nusselt number is as follows:

$\begin{array}{ll}\hfill Nu=& \frac{-k_{sf}x{\left(\frac{\partial T}{\partial y}\right)}_{y=0}}{k_{hf}\left(\mathrm{\Delta }T\right)}=-\frac{k_{sf}}{k_{hf}}R{e}_x^{1/2}{\theta }^{\prime }\left(0\right)=\frac{k_{hf}}{k_{sf}}N{u}_{x}R{e}_x^{-1/2}\hfill \\ \hfill & =-{\theta }^{\prime }\left(0\right).\hfill \end{array}(32)$

4 Second law analysis

The interchange of momentum, temperature, and magnetic effects inside the fluid and at the surfaces generates a continual entropy accumulation, resulting in a non-equilibrium condition. The following formula can be used to compute the volumetric entropy inception factor (S_Gen):

$S_{\mathit{Gen}}=\frac{k_{sf}}{T_{\infty }^2}\left(1+\frac{16T^3{\sigma }^{\ast }}{3k^{\ast }}\right){\left(\frac{\partial T}{\partial y}\right)}^2+\frac{{\mu }_{sf}{u}^2}{T_{\infty }k}+\frac{{\sigma }^{\ast }{B}_0^2{u}^2}{T_{\infty }}.(33)$

The impact of three independent mechanisms generating entropy production is reflected in Eq. 33. The first term of Eq. 33 shows the entropy inception provoked by heat transport along with a thermal impact, which is expressed by (E_HT), the second term represents the entropy inception because of a magnetic impact (E_MGN), and the entropy inception due to porous (E_PM) is described by the third term. Entropy is a measure of disordered in a system and its surroundings. The amount of non-dimensional entropy production $E_G=\frac{S_{\mathit{Gen}}}{S_{\mathit{gen}}}$ is

$\begin{array}{ll}\hfill E_G=& {\chi }_{3}Re\left(1+N_{tr}\right){\theta }^{\prime }{\left(\eta \right)}^2+B{r}_{\mathit{kmn}}{K}_{pr}{f}^{\prime }{\left(\eta \right)}^2+B{r}_{\mathit{kmn}}\frac{M_{\mathit{egn}}}{\mathrm{\Omega }}\hfill \\ \hfill & f^{\prime }{\left(\eta \right)}^2,\hfill \end{array}(34)$

where

$\begin{array}{ll}\hfill S_{\mathit{gen}}=& \frac{k_{hf}}{T_{\infty }^2{\left(\frac{\mathrm{\Delta }T}{x}\right)}^2},B{r}_{\mathit{kmn}}=\frac{{\mu }_{sf}{u}_{re}{x}^2}{\mathrm{\Delta }T{k}_{sf}},\mathrm{\Omega }=\frac{T_{\infty }}{\mathrm{\Delta }T},\text{and}\hfill \\ \hfill & M_{\mathit{egn}}=\frac{\sigma B_0^{2}2u_{re}}{{\mu }_{hf}},\hfill \end{array}(35)$

where Ω is the ratio of free stream temperature to the change in temperature. Bejan (1979) proposed an additional parameter, the Bejan number (Be), to find out the irreversibility field. The Bejan number (Be) is the ratio of heat exchange irreversibility to the total amount of irreversibility inside the process, expressed as

$Be=\frac{E_{HT}}{E_{HT}+E_{\mathit{MGN}}+E_{PM}}.(36)$

5 Results and discussion

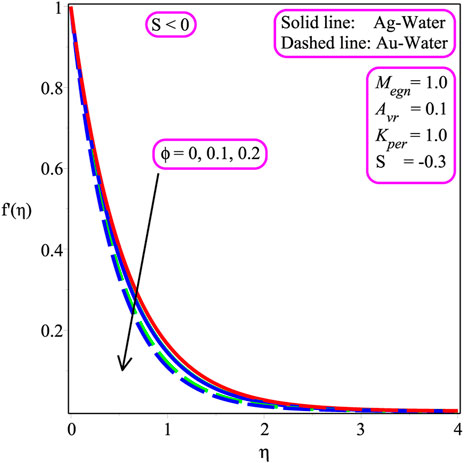
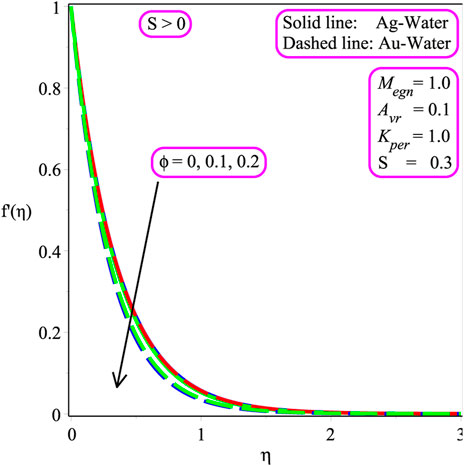
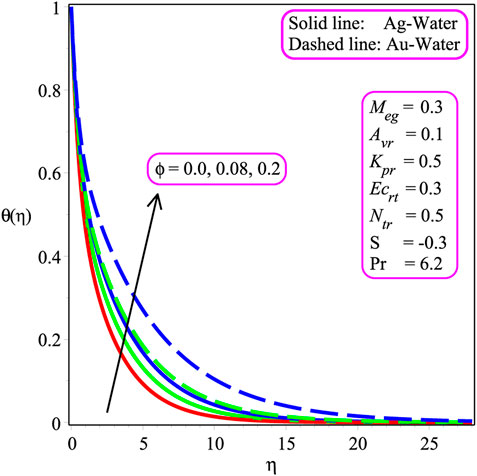
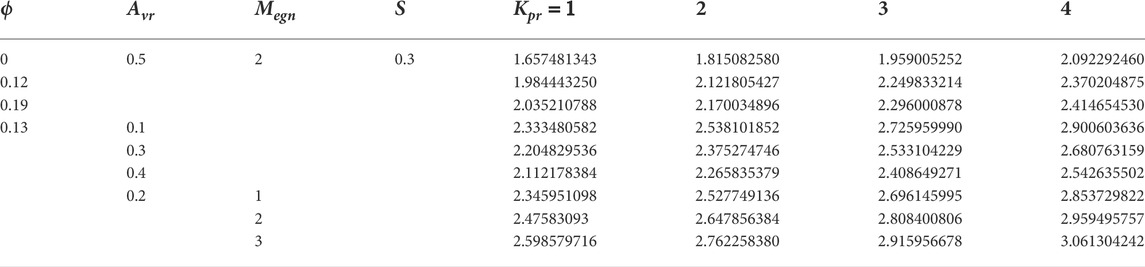
The influence of several emerging factors on the velocity, temperature, and entropy inception fields has been demonstrated in the current phase to examine the impact of these parameters. Furthermore, under the effect of suction/injection parameter (S), permeability parameter K_pr, and magnetic parameter M_egn, Ec_rt, ϕ, Br_kmn, Ω, and Rey, local skin friction, stream line, local Nusselt number, and Bejan (Be) number are presented. In this scenario, Figures 2–18 are plotted and Tables 1, 2, 3 are shown. Figures 2, 3 show the trend of the velocity field as the magnitude of ϕ is varied. It is to be noted that the velocity field is accelerated due to an increment in the magnitude of the nanoparticle volume friction in the case of Ag − and Au − water with S > 0 depicted in Figure 2. Physically, inter-molecular forces are increased in the presence of nanoparticles, which leads to a reduction in the velocity distribution. In the case of both Ag − and Au − water nanofluids with S < 0, the velocity distribution decreases due to an increase in ϕ as shown in Figure 3. The variation of nanoparticle friction on the temperature field is shown in Figure 4. An increment is observed in temperature distribution while gaining the magnitude of ϕ. Physically, the friction factor is enhanced with the existence of nanoparticles due to friction, and the overall internal temperature is accelerated in both Ag − and Au − water.

FIGURE 2

FIGURE 2. Outcome of ϕ (S < 0) on f^′(η).

FIGURE 3

FIGURE 3. Outcome of ϕ (S < 0) on f^′(η).

FIGURE 4

FIGURE 4. Outcome of ϕ on θ(η).

FIGURE 5

FIGURE 5. Outcome of Ec_rt on θ(η).

FIGURE 6

FIGURE 6. Outcome of M_egn on θ(η).

FIGURE 7

FIGURE 7. Outcome of M_egn on − f^′′(0).

FIGURE 8

FIGURE 8. Outcome of suction/injection on − f^′′(0).

FIGURE 9

FIGURE 9. Outcome of Ec_rt on − θ^′(0).

FIGURE 10

FIGURE 10. Outcome of K_pr on − θ^′(0).

FIGURE 11

FIGURE 11. Outcome of Br_kmn on E_G.

FIGURE 12

FIGURE 12. Outcome of Rey on E_G.

FIGURE 13

FIGURE 13. Outcome of Ω on E_G.

FIGURE 14

FIGURE 14. Outcome of M_egn on E_G.

FIGURE 15

FIGURE 15. Outcome of Ec_rt on Be.

FIGURE 16

FIGURE 16. Outcome of ϕ on Be.

FIGURE 17

FIGURE 17. Outcome of Ω on Be.

FIGURE 18

FIGURE 18. (A–C) Flow pattern of Ag − water for K_pr = 1, M_egn = 1, A_vr = 0.8, and S = 0.2.

TABLE 1

TABLE 1. Thermophysical characteristics of water, Ag, and Au (Mahalakshmi and Vennila, 2020).

TABLE 2

TABLE 2. Variation of ϕ, A_vr, M_egn, and M_egn on − f′′(0).

TABLE 3

TABLE 3. Numerical values of − θ′(0) for Ec_rt = 1, Pr  = 6.2, and N_tr = 1.5.

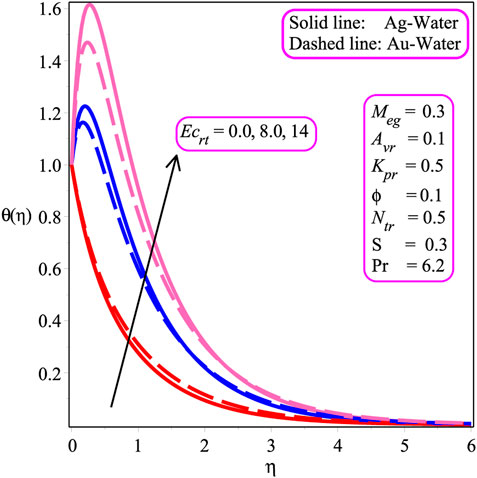
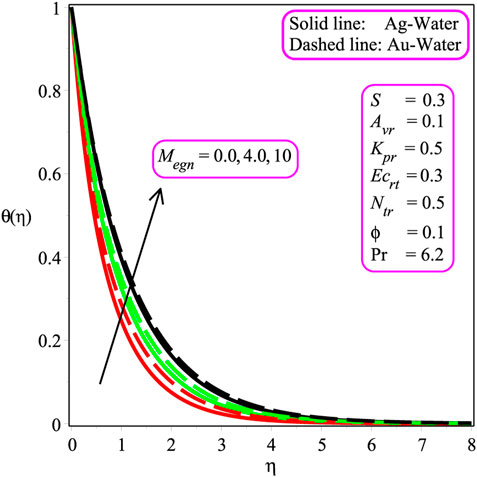
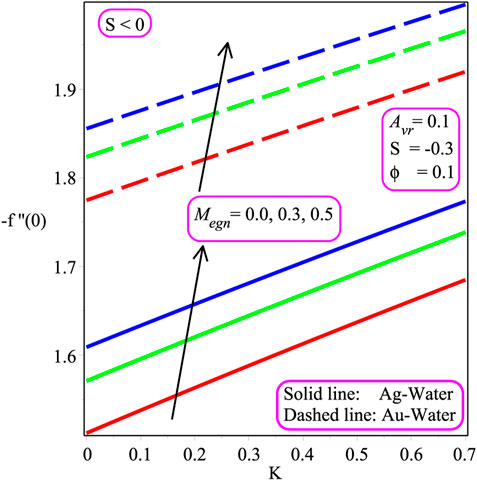
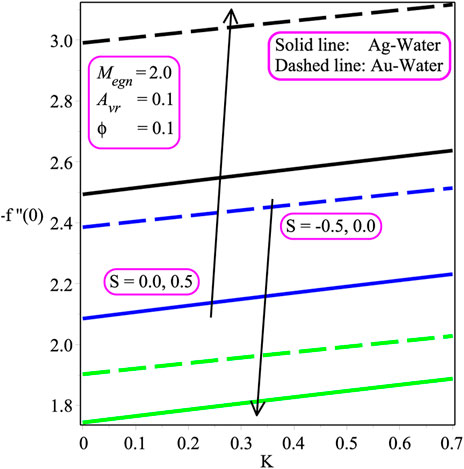
Figure 5 depicts the influence of Ec_rt on the temperature profile. As heat energy is produced in Ag − and Au − water nanofluids caused by friction heat, the temperature field is being augmented with an increasing value of Ec_rt. The impression of M_egn on the temperature field is shown in Figure 6. It is pointed out that the temperature distribution increases with a gain in M_egn. In fact, the Lorentz effect has a considerable influence on M_egn. A greater Lorentz force is associated with elevated M_egn, whereas a smaller Lorentz strength is linked with lower M_egn. The larger Lorentz force creates more energy in both Ag − and Au − water, resulting in an increase in temperature change. The consequences of M_egn on − f′′(0) are plotted in Figure 7. It is perceived that an augmentation in the magnetic entity escalates skin friction at the wall in both Ag − and Au − water. Moreover, Ag − water has a higher rate of skin friction than the Au − water nanofluid. Figure 8 shows the reaction of the wall mass transport entity on − f′′(0). The magnitude of − f′′(0) is stated to be reduced due to the decreasing amount of the wall mass transport entity (S) for both Ag − and Au − water. Additionally, Ag − water has a higher rate of skin friction than the Au − water nanofluid. The effects of Ec_rt and K_pr are shown in Figures 9, 10. The heat transport rate is seen to decrease with the magnitude of Ec_rt and K_pr for both Ag − and Au − water nanofluids. It is also noted that the heat exchange rate rapidly decreases in the occurrence of Au − water than in the Ag − water in Figures 9, 10. Physically, the magnitude of − θ′(0) decreases as the value of the permeability parameter decelerates. Physically, the existence of a porous structure restricts nanofluid flow, slowing fluid velocity and decreasing the heat transport rate at the wall.

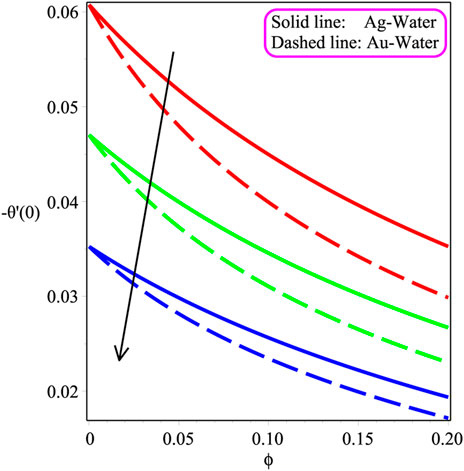
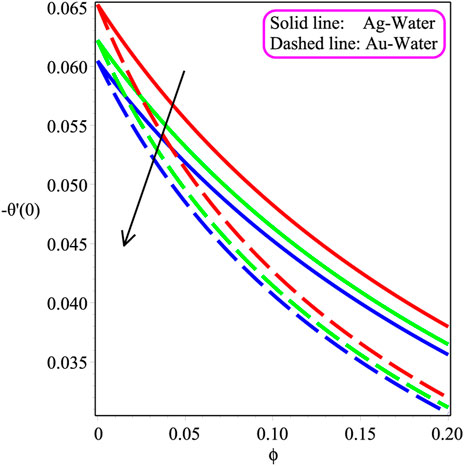
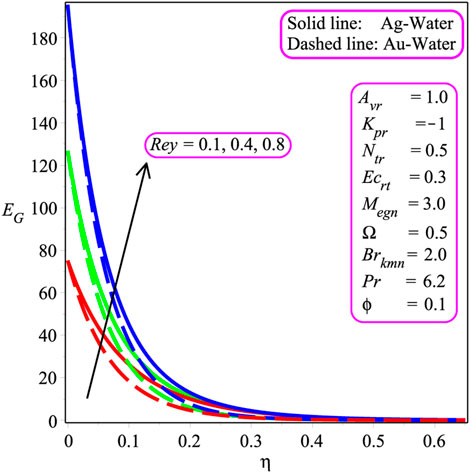
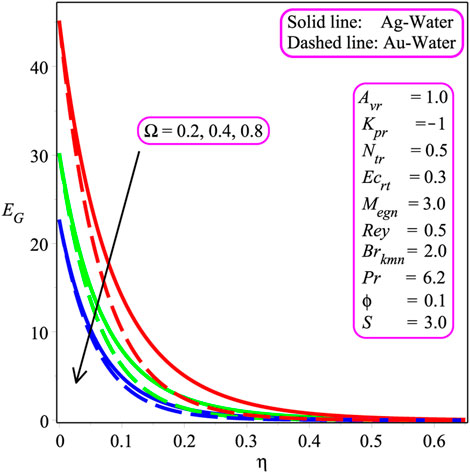
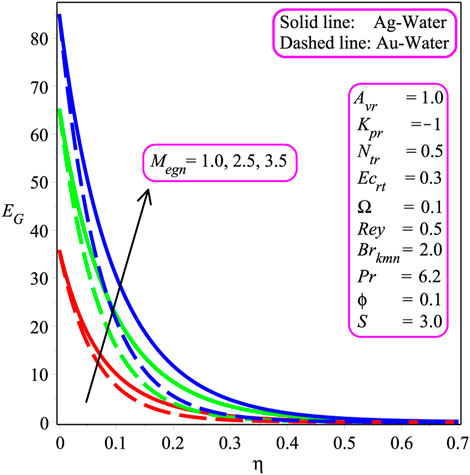
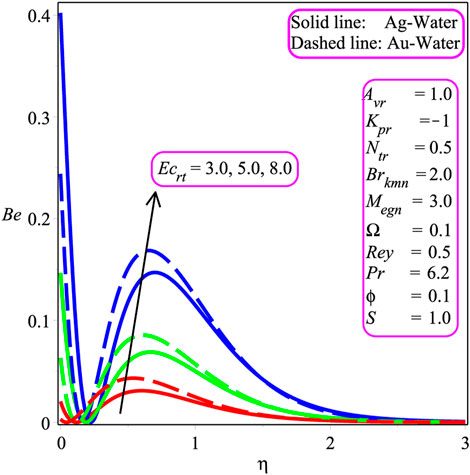
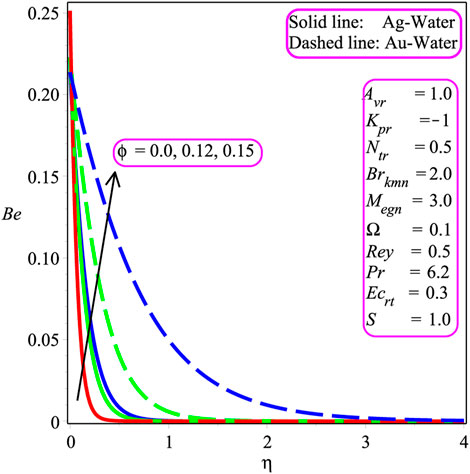
Figures 11, 17 plot the influence of different parameters on the entropy inception E_G and Bejan Be number to visualize the system’s chaos. Figure 11 portrays the result of the Br_kmn number. It is expressed that entropy inception is decreased with an increase in Br_kmn. Additionally, more chaos is reported in the case of silver–water in the system than the gold–water nanofluid. Similar trends are shown in Figures 12, 14 for Rey and M_egn, respectively The opposite behavior is observed in Figure 13 for Ω. In Figures 15, 17, the variation of Ec_rt, ϕ, and Ω is investigated. It is perceived that Be is increased while increasing the value of Ec_rt, ϕ, and Ω. Physically, the Bejan Be number is, indeed, a non-dimensional quantity that shows the proportion of overall entropy creation that is generated by thermal dissipation. As a result, the Bejan number is a description of the entropy created by heat transmission and resistance to flow rather than a heat transport parameter.

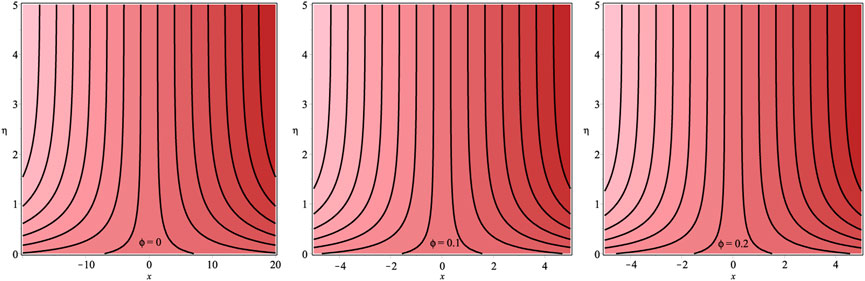
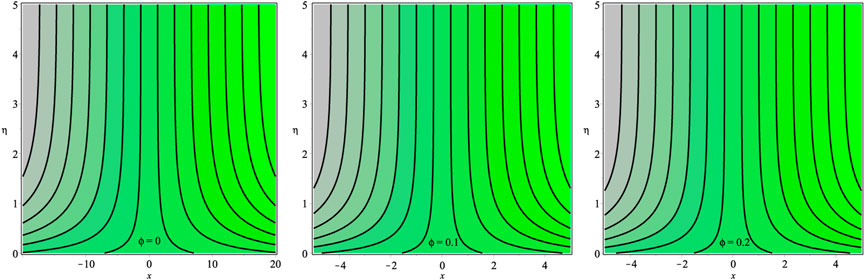
Table 1 lists the thermophysical characteristics of H₂O, Ag, and Au. Tables 2, 3 are constructed for numerical values of − f′′(0) and − θ′(0), respectively. Figures 18A–C, Figures 19A–C are plotted to provide insight into the flow pattern in the case of Ag − and Au − water (Figure 16).

FIGURE 19

FIGURE 19. (A–C) Flow pattern of Au − water for K_pr = 1, M_egn = 1, A_vr = 0.8, and S = 0.2.

6 Conclusion

The study presents an entropy inception investigation of magnetohydrodynamic Ag– and Au–H₂O nanofluid flows induced by an exponential stretching surface embedded in a porous medium with suction/injection and thermal conductivity. The investigation’s principal conclusions have been summarized as follows:

• In both Ag– and Au–H₂O, the solid volume percentage has an accelerating effect on the velocity profile with suction/injection parameters.

• In both Ag– and Au–H₂O, the Ec_rt and M_egn have an increasing impact on the temperature profile.

• It is perceived that an augmentation in the magnetic entity escalates skin friction at the wall in both Ag − and Au − water. Moreover, Ag − water has a higher rate of skin friction than the Au − water nanofluid.

• The heat transport rate is a decreasing function of Ec_rt and K_pr for both Ag − and Au − water nanofluids.

• It is also noted that the heat exchange rate rapidly decreases in the occurrence of Au − water than in Ag − water.

• The entropy inception is an increasing function of Br_kmn, Rey, and M_egn in both Ag − and Au − water.

• More chaos is observed in the case of Ag − water in the system than in the Au − water nanofluid.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

IR initiated the fluid model and methodology. TZ, IR, and MA solved the model using software. JA completed the write-up and assisted in fluid model development.

Funding

The work in this study has been supported by the Polish National Science Centre under the grant OPUS 14 No. 2017/27/B/ST8/01330.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abbasi, A., Farooq, W., Khan, M. I., Khan, S. U., Chu, Y. M., Hussain, Z., et al. (2021). Entropy generation applications in flow of viscoelastic nanofluid past a lubricated disk in presence of nonlinear thermal radiation and Joule heating. Commun. Theor. Phys. 73 (9), 095004.

CrossRef Full Text | Google Scholar

Abd El-Aziz, M., and Afify, A. A. (2019). MHD Casson fluid flow over a stretching sheet with entropy generation analysis and Hall influence. Entropy 21 (6), 592. doi:10.3390/e21060592

CrossRef Full Text | Google Scholar

Abramowitz, M., and Stegun, L. A. (1972). Handbook of Mathematical Functions 55. Washington, D. C.: National Bureau of Standards/Amer. Math. Sot. Providence.

Google Scholar

Afridi, M., Qasim, M., Khan, I., and Tlili, I. (2018). Entropy generation in MHD mixed convection stagnation-point flow in the presence of Joule and frictional heating. Case Stud. Therm. Eng. 12, 292–300. doi:10.1016/j.csite.2018.04.002

CrossRef Full Text | Google Scholar

B Awati, V., Kumar, M., and Wakif, A. (2021). Haar wavelet scrutinization of heat and mass transfer features during the convective boundary layer flow of a nanofluid moving over a nonlinearly stretching sheet. Partial Differ. Equations Appl. Math. 4, 100192. doi:10.1016/j.padiff.2021.100192

CrossRef Full Text | Google Scholar

Bejan, A. (1979). Study of entropy generation in fundamental convective heat transfer. J. Heat. Transf. 101 (4), 718–725. doi:10.1115/1.3451063

CrossRef Full Text | Google Scholar

Bhatti, M. M., Abbas, T., and Rashidi, M. M. (2017). Entropy generation as a practical tool of optimisation for non-Newtonian nanofluid flow through a permeable stretching surface using SLM. J. Comput. Des. Eng. 4 (11), 21–28. doi:10.1016/j.jcde.2016.08.004

CrossRef Full Text | Google Scholar

Bilal, S., Malik, M. Y., Awais, M., Rehman, K., Hussain, A., and Khan, I. (2017). Numerical investigation on 2D viscoelastic fluid due to exponentially stretching surface with magnetic effects: An application of non-fourier flux theory. Neural Comput. Applic 30 (9), 2749–2758.

PubMed Abstract | CrossRef Full Text | Google Scholar

Chakrabarti, A., and Gupta, A. S. (1979). Hydromagnetic flow and heat transfer over a stretching sheet. Quart. Appl. Math. 37, 73–78. doi:10.1090/qam/99636

CrossRef Full Text | Google Scholar

Choi, S. U. S. (1995). “Enhancing thermal conductivity of fluids with nanoparticles,” in International mechanical engineering congress and exposition (San Francisco, USA, 99–105. ASME, FED 231/MD, 66.

Google Scholar

Hamad, M. (2011). Analytical solution of natural convection flow of a nanofluid over a linearly stretching sheet in the presence of magnetic field. Int. Commun. Heat Mass Transf. 38 (4), 487–492. doi:10.1016/j.icheatmasstransfer.2010.12.042

CrossRef Full Text | Google Scholar

Hayat, T., Shinwari, W., Khan, S. A., and Alsaedi, A. (2021). Entropy optimized dissipative flow of Newtonian nanoliquid by a curved stretching surface. Case Stud. Therm. Eng. 27, 101263. doi:10.1016/j.csite.2021.101263

CrossRef Full Text | Google Scholar

Khan, S. A., Khan, M. I., Alsallami, S. A., Alhazmi, S. E., Alharbi, F. M., and El-Zahar, E. R. (2022). Irreversibility analysis in hydromagnetic flow of Newtonian fluid with joule heating: Darcy-forchheimer model. J. Pet. Sci. Eng. 212, 110206. doi:10.1016/j.petrol.2022.110206

CrossRef Full Text | Google Scholar

Khan, W., and Pop, I. (2010). Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat. Mass Transf. 53 (11-12), 2477–2483. doi:10.1016/j.ijheatmasstransfer.2010.01.032

CrossRef Full Text | Google Scholar

Mahabaleshwara, U. S., Aly, H. E., and Anushaa, T. (2022). MHD slip flow of a Casson hybrid nanofluid over a stretching/shrinking sheet with thermal radiation. Chin. J. Phys. doi:10.1016/j.cjph.2022

CrossRef Full Text | Google Scholar

Mahalakshmi, D., and Vennila, B. (2020). Boundary layer flow of sliver and gold nanofluids over a flat plate by adomain decomposition method. AIP Conf. Proc. 2277 (1), 170002. doi:10.1063/5.0025571

CrossRef Full Text | Google Scholar

Mahato, R., Das, M., Sen, S. S. S., and Shaw, S. (2022). Entropy generation on unsteady stagnation-point Casson nanofluid flow past a stretching sheet in a porous medium under the influence of an inclined magnetic field with homogeneous and heterogeneous reactions. Heat. Trans. 51, 5723–5747. doi:10.1002/htj.22567

CrossRef Full Text | Google Scholar

Manzoor, U., S Naqvi, S. M. R., Muhammad, T., Naeem, H., Waqas, H., and M Galal, A. (2022). Hydro-magnetic impact on the nanofluid flow over stretching/shrinking sheet using Keller-box method. Int. Commun. Heat Mass Transf. 135, 106114. doi:10.1016/j.icheatmasstransfer.2022.106114

CrossRef Full Text | Google Scholar

Neethu, T. S., Sabu, A. S., Mathew, A., Wakif, A., and Areekara, S. (2022). Multiple linear regression on bioconvective MHD hybrid nanofluid flow past an exponential stretching sheet with radiation and dissipation effects. Int. Commun. Heat Mass Transf. 135, 106115. doi:10.1016/j.icheatmasstransfer.2022.106115

CrossRef Full Text | Google Scholar

Noghrehabadi, A., Pourrajab, R., and Ghalambaz, M. (2012). Effect of partial slip boundary condition on the flow and heat transfer of nanofluids past stretching sheet prescribed constant wall temperature. Int. J. Therm. Sci. 54, 253–261. doi:10.1016/j.ijthermalsci.2011.11.017

CrossRef Full Text | Google Scholar

Noghrehabadi, A., Saffarian, M. R., Pourrajab, R., and Ghalambaz, M. (2013). Entropy analysis for nanofluid flow over a stretching sheet in the presence of heat generation/absorption and partial slip. J. Mech. Sci. Technol. 27 (3), 927–937. doi:10.1007/s12206-013-0104-0

CrossRef Full Text | Google Scholar

Oztop, H. F., and Abu-Nada, E. (2008). Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. Int. J. Heat. Fluid Flow. 29 (5), 1326–1336. doi:10.1016/j.ijheatfluidflow.2008.04.009

CrossRef Full Text | Google Scholar

Prasannakumara, B. C. (2021). Numerical simulation of heat transport in Maxwell nanofluid flow over a stretching sheet considering magnetic dipole effect. Partial Differ. Equations Appl. Math. 4, 100064. doi:10.1016/j.padiff.2021.100064

CrossRef Full Text | Google Scholar

Rashid, I., Haq, R. U., Khan, Z. H., and Al-Mdallal, Q. M. (2017). Flow of water based alumina and copper nanoparticles along a moving surface with variable temperature. J. Mol. Liq. 246, 354–362. doi:10.1016/j.molliq.2017.09.089

CrossRef Full Text | Google Scholar

Rashidi, M. M., and Freidoonimehr, N. (2014). Analysis of entropy generation in MHD stagnation-point flow in porous media with heat transfer. Int. J. Comput. Methods Eng. Sci. Mech. 15 (4), 345–355. doi:10.1080/15502287.2014.915248

CrossRef Full Text | Google Scholar

Rohni, A. M., Ahmad, S., and Pop, I. (2012). Flow and heat transfer over an unsteady shrinking sheet with suction in nanofluids. Int. J. Heat. Mass Transf. 55 (7-8), 1888–1895. doi:10.1016/j.ijheatmasstransfer.2011.11.042

CrossRef Full Text | Google Scholar

Sithole, H., Mondal, H., and Sibanda, P. (2018). Entropy generation in a second grade magnetohydrodynamic nanofluid flow over a convectively heated stretching sheet with nonlinear thermal radiation and viscous dissipation. Results Phys. 9, 1077–1085. doi:10.1016/j.rinp.2018.04.003

CrossRef Full Text | Google Scholar

Tayebi, T., Dogonchi, A. S., Karimi, N., Ge-JiLe, H., Chamkha, A. J., and Elmasry, Y. (2021). Thermo-economic and entropy generation analyses of magnetic natural convective flow in a nanofluid-filled annular enclosure fitted with fins. Sustain. Energy Technol. Assessments 46, 101274. doi:10.1016/j.seta.2021.101274

CrossRef Full Text | Google Scholar

Wang, F., Khan, S. A., Khan, M. I., El-Zahar, E. R., Yasir, M., Nofal, T. A., et al. (2022). Thermal conductivity performance in propylene glycol-based Darcy-Forchheimer nanofluid flow with entropy analysis. J. Pet. Sci. Eng. 215, 110612. doi:10.1016/j.petrol.2022.110612

CrossRef Full Text | Google Scholar

Yacob, N. A., Ishak, A., Pop, I., and Vajravelu, K. (2011). Boundary layer flow past a stretching/shrinking surface beneath an external uniform shear flow with a convective surface boundary condition in a nanofluid. Nanoscale Res. Lett. 6 (1), 314. doi:10.1186/1556-276x-6-314

PubMed Abstract | CrossRef Full Text | Google Scholar