Stability analysis of load frequency control for power systems with interval time-varying delays

This study investigates the stability problem of load frequency control (LFC) for power systems with interval time-varying delays. The two categories of time delays, the lower bound being zero and non-zero, are considered. The systems can be described as time delay systems of load disturbances. First, an augmented Lyapunov–Krasovskii functional (LKF) is constructed. Some delay-dependent nonintegral terms and single integral terms are additionally introduced to make full use of the information on the system state variables and the time-varying delays. Second, to overcome the problem of nonlinear inequalities caused by the augmented LKF, the nonlinear inequalities are converted into linear matrix inequalities (LMIs) by applying the new negative definite inequality equivalence transformation lemma, which can be solved easily by the MATLAB LMI toolbox. A new stability criterion is presented by applying the Lyapunov stability theory. The stability criterion is less conservative than some existing literature studies, which further improves the stability margin for the power systems based on LFC. Finally, some numerical examples are given to show the effectiveness of the proposed method and the superiority of the results.

1 Introduction

Load frequency control (LFC) has been used in power systems for many years, owing to its ability to be responsible for maintaining the grid frequency (an important indicator of grid quality) at an ideal level after disturbances (Kundur, 1994; Hassan, 2014; Aminov and Garievskii, 2019; Baykov et al., 2019; Ladygin et al., 2020; Shakibjoo et al., 2020; Giudice et al., 2021). For the traditional LFC schemes, dedicated independent communication networks are used to guarantee fast measurement and control signal transmission (Bhowmik et al., 2004; Khalil and Swee, 2018), and the transmission delays are very small and can usually be ignored. Nevertheless, with the continuous expansion of modern power systems and the increasingly decentralizedcontrol services, the LFC scheme requires a large amount of data and information to be exchanged over an open communication network. The use of open communication networks can introduce random delays and data packets into the LFC schemes (Martin et al., 1995), thus leading to instability of the LFC power system. Moreover, since the communication delays usually vary throughout the interval, the ideal value of the lower bound may not be equal to zero. Therefore, it is necessary to study the stability of LFC power systems with interval time-varying delays due to the existence of the non-zero lower bound for time-varying delays. Significantly, there is a lack of literature on the non-zero lower bound for the LFC power systems, which makes it crucial to address this gap.

For the LFC power systems based on open communication networks, time-varying delays are unavoidable in data transmission between the controller and the plant (Jiang et al., 2011; Xu et al., 2017; Shen et al., 2020; Feng et al., 2021). A number of scholars have studied the communication time delay from the control center to the governor (Ramakrishnan and Ray, 2015; Yang et al., 2017a; Chen et al., 2020; Manikandan and Kokil, 2020), where the LFC power systems based on open communication networks can be modeled as time delay systems. In addition, in order to ensure the operation stability and anti-interference ability of the LFC power systems, many control methods have been applied, such as the PI control design (Shangguan et al., 2021), the decentralized control strategy (Shangguan et al., 2021), the network predictive control method (Shangguan et al., 2022b), and the H_∞ control (Saravanakumar et al., 2018). In order to maintain stable system operations, it is extremely important to find the maximum allowable time delay of the LFC power systems (Shangguan et al., 2022a). Both frequency and time domain methods can be used to calculate the maximum allowable time delay. The accuracy of the maximum allowable delay can be calculated directly using the frequency domain method by obtaining the critical eigenvalue and eigenroot from the characteristic equation of the systems (Liu et al., 2008). It is impossible to extend the frequency domain method to the analysis and design of controllers for time delay systems. Instead, the time domain method can use the Lyapunov stability theory coupled with LMI to analyze system stability. Meanwhile, it is also the main way to deal with the maximum allowable delay (Yang et al., 2017b; Saravanakumar et al., 2018; Xiong et al., 2018). The stability criterion derived by this method is a sufficient condition and necessarily has certain conservatism. Recently, how to reduce the conservatism of the stability criterion has currently been the focus of a heated debate. One of the critical factors is to construct suitable Lyapunov–Krasovskii functionals (LKFs), such as LKFs with delayed decompositions (Duan et al., 2019; Hua et al., 2021), LKFs with multiple integral terms (Tian and Wang, 2020; Gholami, 2021), and LKFs with some augmented vectors (Zhang et al., 2017; Duan et al., 2020). Another critical factor is the technique for estimating the upper bounds on the derivatives of LKFs, such as free-weighted matrix zero equations (Wen et al., 2015), reciprocally convex matrix inequalities (Shi et al., 2022; Zhong et al., 2022), and integral inequalities including Jensen’s inequality (Ren and Tian, 2022) and the B-L inequality (Seuret and Gouaisbaut, 2015).

Recently, a new negative definite inequality equivalent transformation lemma for the linear time delay systems has been given in Oliveira and Souza (2020). The lemma can increase the degree of freedom of matrix inequalities and transform nonlinear inequalities into LMIs, which not only reduces the conservatism of the stability criterion but also reduces the complexity of solving them. Inspired by this, this study considers the stability problem of the LFC power systems with interval time-varying delays. The main contributions are as follows:

• When constructing the LKF, delay-dependent Lyapunov matrices are introduced into the nonintegral terms, which contain more coupling information between time-varying delay intervals and state variables than the LKFs constructed in some literature studies (Chen et al., 2020; Manikandan and Kokil, 2020; Shen et al., 2020). This can further reduce the conservatism of the stability criterion and improve the stability margin of the LFC power systems.

• In addition, four additional integral terms, ${\int }_{t-h_2}^{s}x(\theta )d\theta$, ${\int }_{h_d}^{t-h_1}x\left(\theta \right)d\theta$, ${\int }_{h_d}^{s}x(\theta )d\theta$, and ${\int }_{t-h_2}^{h_d}x(\theta )d\theta$, under two different subintervals [h₁, h_t] and [h_t, h₂] are augmented to the single integral terms φ₃(θ), φ₄(θ), and φ₅(θ), which are exactly some necessary terms of the integral inequality lemma so that the integral inequality lemma can be fully used to estimate the upper bound of the LKF derivatives. Thus, the augmented LKF can obtain a larger stability margin than those in some literature studies (Jiang et al., 2011; Ramakrishnan and Ray, 2015; Yang et al., 2017a).

• To further illustrate the advantages of the proposed method, the stability criterion of the non-zero lower bound of the time-varying delay is also applied to the case that the lower bound of the time-varying delay is zero. Finally, the numerical simulation analysis and discussion demonstrate the effectiveness of the proposed method.

This study is structured as follows. In Section 2, the system model, research content, some hypothetical constraints, and necessary lemmas are given. Some new delay-dependent stability criteria, including theorems and corollaries, are derived in Section 3. Some numerical simulation analyses and discussions are provided in Section 4. The conclusion is provided in Section 5.

Notation: The n-dimensional Euclidean space is represented by ${\mathbb{R}}^n$. All n × m real matrices make up the set ${\mathbb{R}}^{n\times m}$. The symmetric and symmetric positive definite matrices are denoted as ${\mathbb{S}}^n$ and ${\mathbb{S}}_{+}^n$, respectively. The diagonal n-order matrix with elements a₁, a₂, … , a_n is denoted by the notation $\text{diag}\left\{a_1,a_2,\dots ,a_n\right\}$. For $P\in {\mathbb{R}}^{n\times n}$, P^T stands for the transpose of the matrix P. P > 0 means that $P\in {\mathbb{S}}_{+}^n$. col{⋅} denotes a column vector Sym{Ξ} = Ξ + Ξ^T.

2 Problem formulation

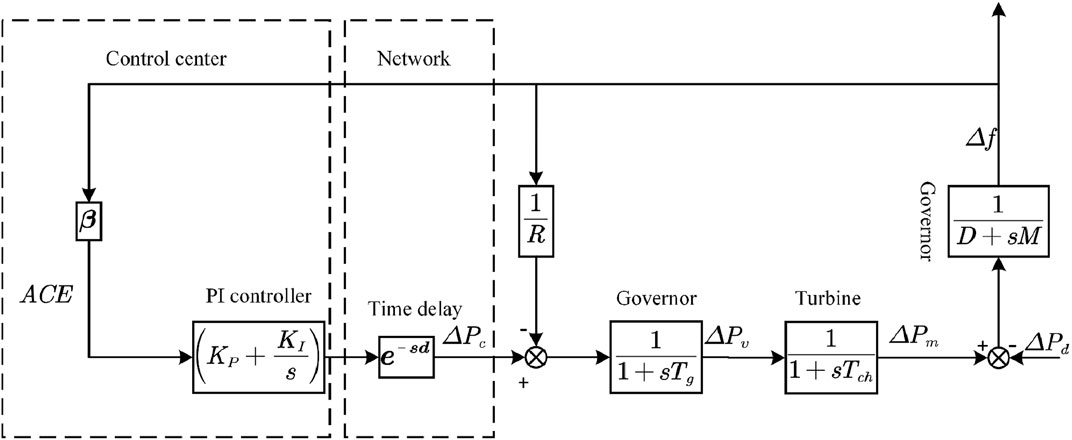
In this section, the PI controller-based time delay model for the one-area LFC power system is presented. The basic block diagram of the abovementioned power system is shown in Figure 1. From the figure, it is obvious that e^−sd is the time delay in communication from the control center to the governor. In addition to this, Δf is the deviation of frequency; ΔP_d is the deviation of the load; ΔP_v is the governor valve position; ΔP_m is the turbine output; T_g is the governor time constant; D is the damping coefficient of the generator; T_ch is the turbine time constant; ACE is the area control error; M is the moment of inertia; and R is the speed droop.

FIGURE 1

FIGURE 1. Basic diagram of the simplified one-area LFC power system.

According to the PI controller-based time delay block diagram and literature (Xu et al., 2017), the state space equations of the LFC power system are expressed as

$\left\{\begin{array}{cc}\hfill \dot{\stackrel{̃}{x}}\left(t\right)& =\tilde{A}\tilde{x}\left(t\right)+\tilde{B}u\left(t\right)+{\tilde{D}}_{w}w\left(t\right),\hfill \\ \hfill \tilde{y}\left(t\right)& =\tilde{C}\tilde{x}\left(t\right).\hfill \end{array}\right.(1)$

The system parameters are shown as follows:

$\begin{array}{ll}\hfill {\tilde{x}}^T\left(t\right)& =\left[\begin{array}{ccc}\hfill \mathit{\Delta }f\hfill & \hfill \mathit{\Delta }{P}_m\hfill & \hfill \mathit{\Delta }{P}_v\hfill \end{array}\right],\hfill \\ \hfill \tilde{y}\left(t\right)& =ACE,\hfill \\ \hfill \mathit{\Delta }{P}_c\left(t\right)& =u\left(t\right),\hfill \\ \hfill \mathit{\Delta }{P}_d\left(t\right)& =w\left(t\right),\hfill \end{array}$

$\begin{array}{ll}\hfill \tilde{A}& =\left[\begin{array}{ccc}\hfill -\frac{D}{M}\hfill & \hfill \frac{1}{M}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -\frac{1}{T_{ch}}\hfill & \hfill \frac{1}{T_{ch}}\hfill \\ \hfill -\frac{1}{R{T}_g}\hfill & \hfill 0\hfill & \hfill -\frac{1}{T_g}\hfill \end{array}\right],\hfill \\ \hfill \tilde{B}& =\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill \frac{1}{T_g}\hfill \end{array}\right],\hfill \\ \hfill {\tilde{D}}_w& =\left[\begin{array}{c}\hfill -\frac{1}{M}\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right],\hfill \\ \hfill \tilde{C}& ={\left[\begin{array}{c}\hfill \beta \hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right]}^T.\hfill \end{array}$

As can be seen in Figure 1, the one-area LFC power system does not have tie-line power exchange, so the ACE can be described as

$ACE=\beta \mathit{\Delta }f,(2)$

in which, the frequency bias factor β > 0.

The LFC is achieved by using the following PI controller with ACE as the input:

$u\left(t\right)=-K_{p}ACE-K_I\int ACE,(3)$

where K_P and K_I denote the controller gains.

In addition, it is also clear from Figure 1 that there is a communication delay between the governor and the control center. To ensure that $h\left(t\right)$ is differentiable and bounded, the non-negative constants h₁, h₂, and μ are given; the time-varying networked delay $h_t\triangleq h\left(t\right)$ satisfies the following condition:

$0⩽h_1<h_t<h_2,\left|{\dot{h}}_t\right|=\left|\dot{h}\left(t\right)\right|⩽\mu ,\forall t⩾0.$

Defining matrices $\kappa \triangleq \left[\begin{array}{c}\hfill K_P\hfill \\ \hfill K_I\hfill \end{array}\right],f\left(t\right)\triangleq \left[\begin{array}{c}\hfill ACE\hfill \\ \hfill \int ACE\hfill \end{array}\right].$ Then, the PI-type controller in one-area LFC power system (3) can be rewritten as

$u\left(t\right)=-\kappa f\left(t-h_t\right).(4)$

Redefining the state vector $\widehat{x}\left(t\right)\triangleq {\left[\begin{array}{cccc}\hfill \mathit{\Delta }f\hfill & \hfill \mathit{\Delta }{P}_m\hfill & \hfill \mathit{\Delta }{P}_v\hfill & \hfill \int ACE\hfill \end{array}\right]}^T$, the PI-type control problem is converted to a static output feedback control problem by adding (4) into (1). The closed-loop LFC power system takes the following forms:

$\left\{\begin{array}{cc}\hfill \dot{\widehat{x}}\left(t\right)& =\widehat{A}\widehat{x}\left(t\right)+{\widehat{A}}_d\widehat{x}\left(t-h_t\right)+{\widehat{D}}_{w}w\left(t\right),\hfill \\ \hfill \widehat{y}\left(t\right)& =\widehat{C}\widehat{x}\left(t\right),\hfill \\ \hfill \widehat{x}\left(t\right)& =\varphi \left(t\right),t\in \left[-h_2,0\right],\hfill \end{array}\right.(5)$

The system parameters are shown as follows:

$\begin{array}{ll}\hfill \widehat{A}& =\left[\begin{array}{cccc}\hfill -\frac{D}{M}\hfill & \hfill \frac{1}{M}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -\frac{1}{T_{ch}}\hfill & \hfill \frac{1}{T_{ch}}\hfill & \hfill 0\hfill \\ \hfill -\frac{1}{R{T}_g}\hfill & \hfill 0\hfill & \hfill -\frac{1}{T_g}\hfill & \hfill 0\hfill \\ \hfill \beta \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right],\hfill \\ \hfill {\widehat{D}}_w& =\left[\begin{array}{c}\hfill -\frac{1}{M}\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right],\hfill \\ \hfill {\widehat{A}}_d& =\left[\begin{array}{cccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -\frac{K_p\beta }{T_g}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -\frac{K_I}{T_g}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right],\hfill \\ \hfill \widehat{C}& ={\left[\begin{array}{cc}\hfill \beta \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \\ \hfill \hfill \end{array}\right]}^T.\hfill \end{array}$

Remark 1: for time-varying delay in power systems, unknown external load disturbances can be described as current and delay state vectors in the case of nonlinear disturbances (Ramakrishnan and Ray, 2015):

${\widehat{D}}_{w}w\left(t\right)=\eta \left(x\left(t\right),x\left(h_d\right)\right)(6)$

satisfying the constraint condition of the following inequality:

$‖\eta \left(\cdot \right)‖⩽\varpi ‖x\left(t\right)‖+\nu ‖x\left(h_d\right)‖(7)$

with the known non-negative scalars ϖ and ν. In a more general way, it is described as follows:

$\eta {\left(\cdot \right)}^T\eta \left(\cdot \right)⩽{\varpi }^2{x}^T\left(t\right)E^{T}Ex\left(t\right)+{\nu }^2{x}^T\left(h_d\right)N^{T}Nx\left(h_d\right),(8)$

where h_d = t − h_t, and E and N are known constant matrices with appropriate dimensions. To measure load disturbances in the power systems, non-negative scalars ϖ and ν along with matrices E and N can be used.

Lemma 1 (Seuret and Gouaisbaut, 2015). For any $Q\in {\mathbb{S}}_{+}^n$ and $g:\left[m,n\right]\to {\mathbb{R}}^n$, the following integral inequality holds

${\int }_m^n{\dot{g}}^T\left(\theta \right)Q\dot{g}\left(\theta \right)d\theta \ge \frac{1}{n-m}{\varrho }^T\bar{Q}\varrho ,$

where $\bar{Q}=\mathrm{diag}\left\{Q,3Q,5Q\right\}$, $\varrho =\mathrm{c}\mathrm{o}\mathrm{l}\left\{{\varrho }_1,{\varrho }_2,{\varrho }_3\right\}$ with ϱ₁ = g(n) − g(m),

$\begin{array}{ll}\hfill {\varrho }_2& =g\left(n\right)+g\left(m\right)-\frac{2}{n-m}{\int }_m^{n}g\left(\theta \right)d\theta ,\hfill \\ \hfill {\varrho }_3& ={\varrho }_1-\frac{6}{n-m}{\int }_m^{n}g\left(\theta \right)d\theta +\frac{12}{{\left(n-m\right)}^2}{\int }_m^n\left(n-\theta \right)g\left(\theta \right)d\theta .\hfill \end{array}$

Lemma 2 (Zhang et al., 2017). For the given scalar $\left(\left.\mathrm{0,1}\right]\right.$, ${\Lambda }_1,{\Lambda }_2\in {\mathbb{S}}_{+}^m$ and ${\vartheta }_1,{\vartheta }_2\in {\mathbb{R}}^m$. If there exist ${\varsigma }_1,{\varsigma }_2\in {\mathbb{S}}^m$ and ${{\rm Y}}_1,{{\rm Y}}_2\in {\mathbb{R}}^{m\times m}$, then

$\left[\begin{array}{cc}\hfill {\Lambda }_1-{\varsigma }_1\hfill & \hfill {{\rm Y}}_1\hfill \\ \hfill ✶\hfill & \hfill {\Lambda }_2\hfill \end{array}\right]\ge 0,\left[\begin{array}{cc}\hfill {\Lambda }_1\hfill & \hfill {{\rm Y}}_2\hfill \\ \hfill ✶\hfill & \hfill {\Lambda }_2-{\varsigma }_2\hfill \end{array}\right]\ge 0.$

The following inequality holds

$\begin{array}{ll}\hfill \frac{1}{\alpha }{\vartheta }_1^T{\Lambda }_1{\vartheta }_1+\frac{1}{1-\alpha }{\vartheta }_2^T{\Lambda }_2{\vartheta }_2& \ge 2{\vartheta }_1^T\left[\alpha {{\rm Y}}_1+\left(1-\alpha \right){{\rm Y}}_2\right]{\vartheta }_2\hfill \\ \hfill & +{\vartheta }_1^T\left[{\Lambda }_1+\left(1-\alpha \right){\varsigma }_1\right]{\vartheta }_1\hfill \\ \hfill & +{\vartheta }_2^T\left({\Lambda }_2+\alpha {\varsigma }_2\right){\vartheta }_2.\hfill \end{array}$

Lemma 3 (Oliveira and Souza, 2020). Let $P_2,P_1,P_0\in {\mathbb{S}}^p$ and $\zeta \in {\mathbb{R}}^p$. Then, the inequality

${\zeta }^T\left({h_t}^2{P}_2+h_t{P}_1+P_0\right)\zeta <0$

holds for all $h_t\in \left[h_1,h_2\right]$, if and only if there exist the matrix $M\in {\mathbb{S}}_{+}^p$ and skew-symmetric matrix $N\in {\mathbb{R}}^{k\times k}$; then

$\left[\begin{array}{cc}\hfill P_0\hfill & \hfill \frac{1}{2}{P}_1\hfill \\ \hfill ✶\hfill & \hfill P_2\hfill \end{array}\right]-{\left[\begin{array}{c}\hfill C\hfill \\ \hfill J\hfill \end{array}\right]}^T\left[\begin{array}{cc}\hfill -M\hfill & \hfill N\hfill \\ \hfill ✶\hfill & \hfill M\hfill \end{array}\right]\left[\begin{array}{c}\hfill C\hfill \\ \hfill J\hfill \end{array}\right]<0,$

where $C=\left[\begin{array}{cc}\hfill (h_{21}/2)I\hfill & \hfill 0\hfill \end{array}\right]$ and $J=\left[\begin{array}{cc}\hfill (h_{21}/2)I\hfill & \hfill -I\hfill \end{array}\right]$, and h₂₁ = h₂ − h₁.

3 Main results

In this section, for the one-area LFC power system with an interval time-varying delay, two cases of lower bounds h₁ > 0 and h₁ = 0 for h_t are discussed, respectively, and the stability criterion satisfying system (5) is derived.

The following notations are used in the derivation to make the representation of vectors and matrices simpler.

$\begin{array}{ll}\hfill h_{12}& =h_1+h_2,{\dot{h}}_{1t}=1-{\dot{h}}_t,\hfill \\ \hfill Z_{1t}& =\left(h_t-h_1\right)Z_{11}+Z_{12},Z_{2t}=\left(h_2-h_t\right)Z_{21}+Z_{22},\hfill \\ \hfill \zeta \left(t\right)& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{x\left(t\right),x\left(t-h_1\right),x\left(h_d\right),x\left(t-h_2\right),{\rho }_{1t},{\rho }_{2t},{\rho }_{3t},{\rho }_{4t},\right.\hfill \\ \hfill & {\rho }_{5t},{\rho }_{6t},\dot{x}\left(t-h_1\right),\dot{x}\left(h_d\right),\left.\dot{x}\left(t-h_2\right),w\left(t\right)\right\},\hfill \\ \hfill {\rho }_{1t}& ={\int }_{t-h_2}^{h_d}\frac{x\left(\theta \right)}{h_2-h_t}d\theta ,{\rho }_{2t}={\int }_{t-h_2}^{t-h_t}\frac{\left(t-h_t-\theta \right)x\left(\theta \right)}{{\left(h_2-h_t\right)}^2}d\theta ,\hfill \\ \hfill {\rho }_{3t}& ={\int }_{h_d}^{t-h_1}\frac{x\left(\theta \right)}{h_t-h_1}d\theta ,{\rho }_{4t}={\int }_{h_d}^{t-h_1}\frac{\left(t-h_1-\theta \right)x\left(\theta \right)}{{\left(h_t-h_1\right)}^2}d\theta ,\hfill \\ \hfill {\rho }_{5t}& ={\int }_{t-h_1}^t\frac{x\left(\theta \right)}{h_1}d\theta ,{\rho }_{6t}={\int }_{t-h_1}^t\frac{\left(t-\theta \right)x\left(\theta \right)}{h_1^2}d\theta ,\hfill \\ \hfill {\phi }_{0t}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{x\left(t\right),x\left(t-h_1\right),x\left(h_d\right),x\left(t-h_2\right)\right\},\hfill \\ \hfill {\phi }_{1t}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{x\left(t\right),x\left(t-h_1\right),x\left(h_d\right),{\int }_{h_d}^{t-h_1}x\left(\theta \right)d\theta \right\},\hfill \\ \hfill {\phi }_{2t}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{x\left(t\right),x\left(h_d\right),x\left(t-h_2\right),{\int }_{t-h_2}^{h_d}x\left(\theta \right)d\theta \right\},\hfill \\ \hfill {\phi }_3\left(\theta \right)& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{\dot{x}\left(\theta \right),x\left(\theta \right),{\phi }_{0t},{\int }_{\theta }^{t-h_1}x\left(\theta \right)d\theta ,{\int }_{h_d}^{\theta }x\left(\theta \right)d\theta ,\right.\hfill \\ \hfill & \left.{\int }_{t-h_2}^{h_d}x\left(\theta \right)d\theta \right\},\hfill \\ \hfill {\phi }_4\left(\theta \right)& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{\dot{x}\left(\theta \right),x\left(\theta \right),{\phi }_{0t},{\int }_{\theta }^{h_d}x\left(\theta \right)d\theta ,{\int }_{h_d}^{t-h_1}x\left(\theta \right)d\theta \right.,\hfill \\ \hfill & \left.{\int }_{t-h_2}^{\theta }x\left(\theta \right)d\theta \right\},\hfill \\ \hfill {\phi }_5\left(\theta \right)& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{\dot{x}\left(\theta \right),x\left(\theta \right),{\phi }_{0t},{\int }_{t-h_1}^{\theta }x\left(\theta \right)d\theta ,{\int }_{h_d}^{t-h_1}x\left(\theta \right)d\theta \right.,\hfill \\ \hfill & \left.{\int }_{t-h_2}^{h_d}x\left(\theta \right)d\theta \right\}.\hfill \end{array}$

3.1 Case 1: h₁ > 0

Theorem 1. System (5) is stable in the presence of scalars μ, h₁, and h₂ if there exist matrices $Z_{i1}\in {\mathbb{S}}^{4n},Z_{i2}\in {\mathbb{S}}_{+}^{4n},X_i\in {\mathbb{S}}^{3n},Y_i\in {\mathbb{R}}^{3n\times 3n},D_i\in {\mathbb{S}}_{+}^{\mathrm{14n}},Q_j\in {\mathbb{S}}_{+}^{9n},H_j\in {\mathbb{S}}_{+}^n,(i=\mathrm{1,2};j=\mathrm{1,2,3})$ and skew-symmetric matrices $G_i\in {\mathbb{R}}^{\mathrm{14}n\times \mathrm{14}n}$ for (i = 1, 2) such that the following matrix inequalities hold for 0 < h₁ < h_t⩽h₂ and ${\dot{h}}_t\stackrel{\mathrm{\Delta }}{=}{\mu }_i\in \{-\mu ,\mu \}$.

$h_{21}{Z}_{11}+Z_{12}>0,h_{21}{Z}_{21}+Z_{22}>0,(9)$

$\left[\begin{array}{cc}\hfill {\bar{H}}_1-X_1\hfill & \hfill Y_1\hfill \\ \hfill ✶\hfill & \hfill {\bar{H}}_2\hfill \end{array}\right]\ge 0,\left[\begin{array}{cc}\hfill {\bar{H}}_1\hfill & \hfill Y_2\hfill \\ \hfill ✶\hfill & \hfill {\bar{H}}_2-X_2\hfill \end{array}\right]\ge 0,(10)$

$\left[\begin{array}{cc}\hfill {\Omega }_0\left({\mu }_i\right)\hfill & \hfill \frac{1}{2}{\Omega }_1\left({\mu }_i\right)\hfill \\ \hfill ✶\hfill & \hfill {\Omega }_2\left({\mu }_i\right)\hfill \end{array}\right]-{\left[\begin{array}{c}\hfill C\hfill \\ \hfill J\hfill \end{array}\right]}^T\left[\begin{array}{cc}\hfill -D_i\hfill & \hfill G_i\hfill \\ \hfill ✶\hfill & \hfill D_i\hfill \end{array}\right]\left[\begin{array}{c}\hfill C\hfill \\ \hfill J\hfill \end{array}\right]<0,(11)$

where

$\begin{array}{ll}\hfill {\bar{H}}_j& =\mathrm{diag}\left\{H_j,3H_j,5H_j\right\},j=1,2,3,\hfill \\ \hfill C& =\left[\begin{array}{cc}\hfill \left(h_{21}/2\right)I\hfill & \hfill 0\hfill \end{array}\right],J=\left[\begin{array}{cc}\hfill \left(h_{21}/2\right)I\hfill & \hfill -I\hfill \end{array}\right],\hfill \\ \hfill {\Omega }_0\left({\dot{h}}_t\right)& =\mathrm{S}\mathrm{y}\mathrm{m}\left\{D_1^T\left(-h_1{Z}_{11}+Z_{12}\right)c_{11}+D_2^T\left(h_2{Z}_{21}+Z_{22}\right)c_{21}\right.\hfill \\ \hfill & \left.+D_3^T{Q}_1{c}_{70}+D_4^T{Q}_2{c}_{80}+D_5^T{Q}_3{d}_{20}\right\}+{\dot{h}}_t{c}_{11}^T{Z}_{11}{c}_{11}\hfill \\ \hfill & -{\dot{h}}_t{c}_{21}^T{Z}_{21}{c}_{21}+c_{31}^T{Q}_1{c}_{31}-{\dot{h}}_{1t}{c}_{41}^T{Q}_1{c}_{41}+{\dot{h}}_{1t}{c}_{51}^T{Q}_2{c}_{51}\hfill \\ \hfill & -c_{61}^T{Q}_2{c}_{61}+c_{91}^T{Q}_3{c}_{91}-d_{11}^T{Q}_3{d}_{11}+h_{21}{h}_2{\tau }_{11}^T{H}_1{\tau }_{11}\hfill \\ \hfill & -h_{21}{h}_1{\tau }_{13}^T{H}_2{\tau }_{13}+h_1^2{c}_0^T{H}_3{c}_0+\left(h_1/h_{21}\right){\mathrm{\Gamma }}_1^T{X}_1{\mathrm{\Gamma }}_1\hfill \\ \hfill & -{\mathrm{\Gamma }}_1^T{\bar{H}}_1{\mathrm{\Gamma }}_1-{\mathrm{\Gamma }}_2^T{\bar{H}}_2{\mathrm{\Gamma }}_2-{\mathrm{\Gamma }}_3^T{\bar{H}}_3{\mathrm{\Gamma }}_3-\left(h_2/h_{21}\right){\mathrm{\Gamma }}_2^T{X}_2{\mathrm{\Gamma }}_2\hfill \\ \hfill & +h_{21}{h}_{12}{\dot{h}}_{1t}{\tau }_{12}^T\left(H_2-H_1\right){\tau }_{12}\hfill \\ \hfill & -\mathrm{S}\mathrm{y}\mathrm{m}\left\{\left(h_2/h_{21}\right){\mathrm{\Gamma }}_1^T{Y}_1{\mathrm{\Gamma }}_2\right\}\hfill \\ \hfill & +\mathrm{S}\mathrm{y}\mathrm{m}\left\{\left(h_1/h_{21}\right){\mathrm{\Gamma }}_1^T{Y}_2{\mathrm{\Gamma }}_2\right\}+\lambda {\varpi }^2{\tau }_1^T{E}^{T}E{\tau }_1\hfill \\ \hfill & +\lambda {\nu }^2{\tau }_2^T{N}^{T}N{\tau }_2,\hfill \\ \hfill {\Omega }_1\left({\dot{h}}_t\right)& =\mathrm{S}\mathrm{y}\mathrm{m}\left\{D_1^T{Z}_{11}{c}_{11}-D_1^T\left(h_1{Z}_{11}+Z_{12}\right)c_{12}-D_2^T{Z}_{21}{c}_{21}\right.\hfill \\ \hfill & +D_2^T\left(h_2{Z}_{21}+Z_{22}\right)c_{22}+D_3^T{Q}_1{c}_{71}+D_4^T{Q}_2{c}_{81}\hfill \\ \hfill & +\dot{h}\left(t\right)c_{11}^T{Z}_{11}{c}_{12}-{\dot{h}}_t{c}_{21}^T{Z}_{21}{c}_{22}+c_{31}^T{Q}_1{c}_{32}-c_{61}^T{Q}_2{c}_{61}\hfill \\ \hfill & -{\dot{h}}_{1t}{c}_{41}^T{Q}_1{c}_{42}+{\dot{h}}_{1t}{c}_{51}^T{Q}_2{c}_{52}+c_{91}^T{Q}_3{c}_{92}+D_5^T{Q}_3{d}_{21}\hfill \\ \hfill & \left.-d_{11}^T{Q}_3{d}_{12}\right\}-h_{21}{\dot{h}}_{1t}{\tau }_{12}^T\left(H_2-H_1\right){\tau }_{12}-\left(1/h_{21}\right){\mathrm{\Gamma }}_1^T{X}_1{\mathrm{\Gamma }}_1\hfill \\ \hfill & +\left(1/h_{21}\right){\mathrm{\Gamma }}_2^T{X}_2{\mathrm{\Gamma }}_2+\mathrm{S}\mathrm{y}\mathrm{m}\left\{\left(1/h_{21}\right){\Gamma }_1^T\left(Y_1-Y_2\right){\Gamma }_2\right\},\hfill \\ \hfill {\Omega }_2\left({\dot{h}}_t\right)& =\mathrm{S}\mathrm{y}\mathrm{m}\left\{D_1^T{Z}_{11}{c}_{12}-D_2^T{Z}_{21}{c}_{22}+D_3^T{Q}_1{c}_{72}\right.\left.+D_4^T{Q}_2{c}_{82}\right\}\hfill \\ \hfill & +{\dot{h}}_t{c}_{12}^T{Z}_{11}{c}_{12}-{\dot{h}}_t{c}_{22}^T{Z}_{21}{c}_{22}+c_{32}^T{Q}_1{c}_{32}-c_{62}^T{Q}_2{c}_{62}\hfill \\ \hfill & -{\dot{h}}_{1t}{c}_{42}^T{Q}_1{c}_{42}+{\dot{h}}_{1t}{c}_{52}^T{Q}_2{c}_{52}+c_{92}^T{Q}_3{c}_{92}-d_{12}^T{Q}_3{d}_{12}\hfill \end{array}$

with

$\begin{array}{ll}\hfill {\tau }_i& =\left[\begin{array}{ccc}\hfill 0_{n\times \left(i-1\right)n}\hfill & \hfill I\hfill & \hfill 0_{n\times \left(14-i\right)n}\hfill \end{array}\right],i=\mathrm{1,2},\dots ,14,\hfill \\ \hfill \mathit{\Delta }& ={\tau }_0=\left[\begin{array}{cccccccccccccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right],\hfill \\ \hfill c_0& =\widehat{A}{\tau }_1+{\widehat{A}}_d{\tau }_3+{\widehat{D}}_w{\tau }_{14},\hfill \\ \hfill c_{11}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{{\tau }_1,{\tau }_2,{\tau }_3,-h_1{\tau }_7\right\},c_{12}=\mathrm{c}\mathrm{o}\mathrm{l}\left\{\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },-{\tau }_7\right\},\hfill \\ \hfill c_{21}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{{\tau }_1,{\tau }_3,{\tau }_4,h_5{\tau }_5\right\},c_{22}=\mathrm{c}\mathrm{o}\mathrm{l}\left\{\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },-{\tau }_5\right\},\hfill \\ \hfill c_{31}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{{\tau }_{11},{\tau }_2,{\tau }_1,{\tau }_2,{\tau }_3,{\tau }_4,\mathit{\Delta },-h_1{\tau }_7,h_2{\tau }_5\right\},\hfill \\ \hfill c_{32}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },{\tau }_7,-{\tau }_5\right\},\hfill \\ \hfill c_{41}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{{\tau }_{12},{\tau }_3,{\tau }_1,{\tau }_2,{\tau }_3,{\tau }_4,-h_1{\tau }_7,\mathit{\Delta },h_2{\tau }_5\right\},\hfill \\ \hfill c_{42}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },{\tau }_7,\mathit{\Delta },-{\tau }_5\right\},\hfill \\ \hfill c_{51}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{{\tau }_{12},{\tau }_3,{\tau }_1,{\tau }_2,{\tau }_3,{\tau }_4,\mathit{\Delta },-h_1{\tau }_7,h_2{\tau }_5\right\},\hfill \\ \hfill c_{52}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },{\tau }_7,-{\tau }_5\right\},\hfill \\ \hfill c_{61}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{{\tau }_{13},{\tau }_4,{\tau }_1,{\tau }_2,{\tau }_3,{\tau }_4,h_2{\tau }_5,-h_1{\tau }_7,\mathit{\Delta }\right\},\hfill \\ \hfill c_{62}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },-{\tau }_5,{\tau }_7,\mathit{\Delta }\right\},\hfill \\ \hfill c_{70}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{{\tau }_2-{\tau }_3,-h_1{\tau }_7,-h_1{\tau }_1,-h_1{\tau }_2,-h_1{\tau }_3,-h_1{\tau }_4,\right.\hfill \\ \hfill & \left.h_1^2\left({\tau }_7-{\tau }_8\right),h_1^2{\tau }_8,-h_1{h}_2{\tau }_5\right\},\hfill \end{array}$

$\begin{array}{ll}\hfill c_{71}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{\mathit{\Delta },{\tau }_7,{\tau }_1,{\tau }_2,{\tau }_3,{\tau }_4,2h_1\left({\tau }_8-{\tau }_7\right),-2h_1{\tau }_8,\left(h_1+h_2\right){\tau }_5\right\},\hfill \\ \hfill c_{72}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },{\tau }_7-{\tau }_8,{\tau }_8,-{\tau }_5\right\},\hfill \\ \hfill c_{80}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{{\tau }_3-{\tau }_4,h_2{\tau }_5,h_2{\tau }_1,h_2{\tau }_2,h_2{\tau }_3,h_2{\tau }_4,h_2^2\left({\tau }_5-{\tau }_6\right),\right.\hfill \\ \hfill & \left.-h_1{h}_2{\tau }_7,h_2^2{\tau }_6\right\},\hfill \\ \hfill c_{81}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{\mathit{\Delta },-{\tau }_5,-{\tau }_1,-{\tau }_2,-{\tau }_3,-{\tau }_4,2h_2\left({\tau }_6-{\tau }_5\right),\left(h_1+h_2\right){\tau }_7,\right.\hfill \\ \hfill & \left.-2h_2{\tau }_6\right\},\hfill \\ \hfill c_{82}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },{\tau }_5-{\tau }_6,-{\tau }_7,{\tau }_6\right\},\hfill \\ \hfill c_{91}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{c_0,{\tau }_1,{\tau }_1,{\tau }_2,{\tau }_3,{\tau }_4,h_1{\tau }_9,-h_1{\tau }_7,h_2{\tau }_5\right\},\hfill \\ \hfill c_{92}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },{\tau }_7,-{\tau }_5\right\},\hfill \\ \hfill d_{11}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{{\tau }_{11},{\tau }_2,{\tau }_1,{\tau }_2,{\tau }_3,{\tau }_4,\mathit{\Delta },-h_1{\tau }_7,h_2{\tau }_5\right\},\hfill \\ \hfill d_{12}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },{\tau }_7,-{\tau }_5\right\},\hfill \\ \hfill d_{20}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{{\tau }_1-{\tau }_2,h_1{\tau }_9,h_1{\tau }_1,h_1{\tau }_2,h_1{\tau }_3,h_1{\tau }_4,h_1^2{\tau }_{10},-h_1^2{\tau }_7,\right.\hfill \\ \hfill & \left.h_1{h}_2{\tau }_5\right\},\hfill \\ \hfill d_{21}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },\mathit{\Delta },h_1{\tau }_7,-h_1{\tau }_5\right\},\hfill \\ \hfill {\mathrm{\Gamma }}_1& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{{\tau }_3-{\tau }_4,{\tau }_3+{\tau }_4-2{\tau }_5,{\tau }_3-{\tau }_4-6{\tau }_5+12{\tau }_6\right\},\hfill \\ \hfill {\mathrm{\Gamma }}_2& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{{\tau }_2-{\tau }_3,{\tau }_2+{\tau }_3-2{\tau }_7,{\tau }_2-{\tau }_3-6{\tau }_7+12{\tau }_8\right\},\hfill \\ \hfill {\mathrm{\Gamma }}_3& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{{\tau }_1-{\tau }_2,{\tau }_1+{\tau }_2-2{\tau }_9,{\tau }_1-{\tau }_2-6{\tau }_9+12{\tau }_{10}\right\},\hfill \\ \hfill D_1& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{c_0,{\tau }_{11},{\dot{h}}_{1t}{\tau }_{12},{\tau }_2-{\dot{h}}_{1t}{\tau }_3\right\},\hfill \\ \hfill D_2& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{c_0,{\dot{h}}_{1t}{\tau }_{12},{\tau }_{13},{\dot{h}}_{1t}{\tau }_3-{\tau }_4\right\},\hfill \\ \hfill D_3& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{\mathit{\Delta },\mathit{\Delta },c_0,{\tau }_{11},{\dot{h}}_{1t}{\tau }_{12},{\tau }_{13},{\tau }_2,-{\dot{h}}_{1t}{\tau }_3,{\dot{h}}_{1t}{\tau }_3-{\tau }_4\right\},\hfill \\ \hfill D_4& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{\mathit{\Delta },\mathit{\Delta },c_0,{\tau }_{11},{\dot{h}}_{1t}{\tau }_{12},{\tau }_{13},{\dot{h}}_{1t}{\tau }_3,{\tau }_2-{\dot{h}}_{1t}{\tau }_3,-{\tau }_4\right\},\hfill \\ \hfill D_5& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{\mathit{\Delta },\mathit{\Delta },c_0,{\tau }_{11},{\dot{h}}_{1t}{\tau }_{12},{\tau }_{13},-{\tau }_2,{\tau }_2-{\dot{h}}_{1t}{\tau }_3,{\dot{h}}_{1t}{\tau }_3-{\tau }_4\right\}.\hfill \end{array}$

Proof: let us consider the LKF having integrable terms, where

$V=\sum _{u=1}^3{V}_u(12)$

with

$\begin{array}{ll}\hfill V_1& ={\phi }_{1t}^T{Z}_{1t}{\phi }_{1t}+{\phi }_{2t}^T{Z}_{2t}{\phi }_{2t},\hfill \\ \hfill V_2& ={\int }_{h_d}^{t-h_1}{\phi }_3^T\left(\theta \right)Q_1{\phi }_3\left(\theta \right)d\theta \hfill \\ \hfill & +{\int }_{t-h_2}^{h_d}{\phi }_4^T\left(\theta \right)Q_2{\phi }_4\left(\theta \right)d\theta \hfill \\ \hfill & +{\int }_{t-h_1}^t{\phi }_5^T\left(\theta \right)Q_3{\phi }_5\left(\theta \right)d\theta ,\hfill \\ \hfill V_3& =h_{21}{\int }_{h_d}^{t-h_1}\left(h_{12}-t+\theta \right){\dot{x}}^T\left(\theta \right)H_1\dot{x}\left(\theta \right)d\theta \hfill \\ \hfill & +h_{21}{\int }_{t-h_2}^{h_d}\left(h_{12}-t+\theta \right){\dot{x}}^T\left(\theta \right)H_2\dot{x}\left(\theta \right)d\theta \hfill \\ \hfill & +h_1{\int }_{t-h_1}^t\left(h_1-t+\theta \right){\dot{x}}^T\left(\theta \right)H_3\dot{x}\left(\theta \right)d\theta .\hfill \end{array}$

$Z_i\left(t\right),\left(i=\mathrm{1,2}\right)$ are affine functions in $h(t)\in \left[h_1,h_2\right]$. By applying Z_i2 > 0, h₂₁Z_i1 + Z_i2 > 0, we can ensure the LKF V(t) positive definite value. Now, differentiating V(t), it gives

${\dot{V}}_1={\phi }_{1t}^T{\dot{Z}}_{1t}{\phi }_{1t}+2{\dot{\phi }}_{1t}^T{Z}_{1t}{\phi }_{1t}+{\phi }_{2t}^T{\dot{Z}}_{2t}{\phi }_{2t}+2{\dot{\phi }}_{2t}^T{Z}_{2t}{\phi }_{2t},(13)$

$\begin{array}{ll}\hfill {\dot{V}}_2& ={\phi }_3^T\left(t-h_1\right)Q_1{\phi }_3\left(t-h_1\right)-{\dot{h}}_{1t}{\phi }_3^T\left(h_d\right)Q_1{\phi }_3\left(h_d\right)\hfill \\ \hfill & +2{\int }_{h_d}^{t-h_1}{\phi }_3^T\left(\theta \right)d\theta Q_1\frac{\partial }{\partial t}{\phi }_3\left(\theta \right)+{\dot{h}}_{1t}{\phi }_4^T\left(h_d\right)Q_2{\phi }_4\left(h_d\right)\hfill \\ \hfill & -{\phi }_4^T\left(t-h_2\right)Q_2{\phi }_4\left(t-h_2\right)+2{\int }_{t-h_2}^{h_d}{\phi }_4^T\left(\theta \right)d\theta Q_2\frac{\partial }{\partial t}{\phi }_4\left(\theta \right)\hfill \\ \hfill & +{\phi }_5^T\left(t\right)Q_3{\phi }_5\left(t\right)-{\phi }_5^T\left(t-h_1\right)Q_3{\phi }_5\left(t-h_1\right)\hfill \\ \hfill & +2{\int }_{t-h_1}^t{\phi }_5^T\left(\theta \right)d\theta Q_3\frac{\partial }{\partial t}{\phi }_5\left(\theta \right),\hfill \end{array}(14)$

$\begin{array}{ll}\hfill {\dot{V}}_3& =h_{21}{\dot{h}}_{1t}\left(h_{12}-h_t\right){\dot{x}}^T\left(h_d\right)\left(H_2-H_1\right)\dot{x}\left(h_d\right)\hfill \\ \hfill & +h_{21}{h}_2{\dot{x}}^T\left(t-h_1\right)H_1\dot{x}\left(t-h_1\right)\hfill \\ \hfill & -h_{21}{\int }_{h_d}^{t-h_1}{\dot{x}}^T\left(\theta \right)H_1\dot{x}\left(\theta \right)d\theta \hfill \\ \hfill & -h_{21}{h}_1{\dot{x}}^T\left(t-h_2\right)H_2\dot{x}\left(t-h_2\right)\hfill \\ \hfill & -h_{21}{\int }_{t-h_2}^{h_d}{\dot{x}}^T\left(\theta \right)H_2\dot{x}\left(\theta \right)d\theta \hfill \\ \hfill & +h_1^2{\dot{x}}^T\left(t\right)H_3\dot{x}\left(t\right)-h_1{\int }_{t-h_1}^t{\dot{x}}^T\left(\theta \right)H_3\dot{x}\left(\theta \right)d\theta ,\hfill \end{array}$

where

$\begin{array}{ll}\hfill {\dot{\phi }}_{1t}^T& ={\zeta }^T\left(t\right)D_1^T,{\dot{\phi }}_{2t}^T={\zeta }^T\left(t\right)D_2^T,\hfill \\ \hfill {\phi }_3\left(h_d\right)& =\left(h_t{c}_{42}+c_{41}\right)\zeta \left(t\right),\hfill \\ \hfill {\phi }_3\left(t-h_1\right)& =\left(h_t{c}_{32}+c_{31}\right)\zeta \left(t\right),\hfill \\ \hfill {\phi }_4\left(t-h_2\right)& =\left(h_t{c}_{62}+c_{61}\right)\zeta \left(t\right),\hfill \\ \hfill {\phi }_4\left(h_d\right)& =\left(h_t{c}_{52}+c_{51}\right)\zeta \left(t\right),\hfill \\ \hfill {\phi }_5\left(t-h_1\right)& =\left(h_t{d}_{12}+d_{11}\right)\zeta \left(t\right),\hfill \\ \hfill {\phi }_5\left(t\right)& =\left(h_t{c}_{92}+c_{91}\right)\zeta \left(t\right),\hfill \\ \hfill {\int }_{h_d}^{t-h_1}{\phi }_3^T\left(\theta \right)d\theta Q_1\frac{\partial }{\partial t}{\phi }_3\left(\theta \right)& ={\zeta }^T\left(t\right)\left(c_{70}^T+h_t{c}_{71}^T+h_t^2{c}_{72}^T\right)\hfill \\ \hfill & Q_1{D}_3\zeta \left(t\right),\hfill \\ \hfill {\int }_{t-h_2}^{h_d}{\phi }_4^T\left(\theta \right)d\theta Q_2\frac{\partial }{\partial t}{\phi }_4\left(\theta \right)& ={\zeta }^T\left(t\right)\left(c_{80}^T+h_t{c}_{81}^T+h_t^2{c}_{82}^T\right)\hfill \\ \hfill & Q_2{D}_4\zeta \left(t\right),\hfill \\ \hfill {\int }_{t-h_1}^t{\phi }_5^T\left(\theta \right)d\theta Q_3\frac{\partial }{\partial t}{\phi }_5\left(\theta \right)& ={\zeta }^T\left(t\right)\left(d_{20}^T+h_t{d}_{21}^T\right)Q_3{D}_5\zeta \left(t\right).\hfill \end{array}$

Let $\alpha =\left(h_2-h_t\right)/h_{21}$, α₁ = 1/α, and ${\alpha }_2=1/\left(1-\alpha \right)$. According to H₁ > 0, H₂ > 0 and H₃ > 0, the integral terms in V₃ can be obtained by Lemma 1 as the following integral inequalities:

$h_{21}{\int }_{t-h_2}^{h_d}{\dot{x}}^T\left(\theta \right)H_1\dot{x}\left(\theta \right)d\theta ⩾{\alpha }_1{\zeta }^T\left(t\right){\Gamma }_1^T{\bar{H}}_1{\Gamma }_1\zeta \left(t\right),(15)$

$h_{21}{\int }_{h_d}^{t-h_1}{\dot{x}}^T\left(\theta \right)H_2\dot{x}\left(\theta \right)d\theta ⩾{\alpha }_2{\zeta }^T\left(t\right){\Gamma }_2^T{\bar{H}}_2{\Gamma }_2\zeta \left(t\right),(16)$

$h_1{\int }_{t-h_1}^t{\dot{x}}^T\left(\theta \right)H_3\dot{x}\left(\theta \right)d\theta ⩾{\zeta }^T\left(t\right){\Gamma }_3^T{\bar{H}}_3{\Gamma }_3\zeta \left(t\right).(17)$

Inequalities (15) and (16) are transformed into the following inequality by Lemma 2:

$\begin{array}{ll}\hfill & -{\alpha }_1{\zeta }^T\left(t\right){\Gamma }_1^T{\bar{H}}_1{\Gamma }_1\zeta \left(t\right)-{\alpha }_2{\zeta }^T\left(t\right){\Gamma }_2^T{\bar{H}}_2{\Gamma }_2\zeta \left(t\right)\hfill \\ \hfill & ⩽-{\zeta }^T\left(t\right)\left\{2{\Gamma }_1^T\left[\left(1-\alpha \right)Y_2+\alpha Y_1\right]{\Gamma }_2\right.\hfill \\ \hfill & +{\Gamma }_1^T\left[\left(1-\alpha \right)X_1+{\bar{H}}_1\right]{\Gamma }_1\hfill \\ \hfill & +\left.{\Gamma }_2^T\left[{\bar{H}}_2+\alpha X_2\right]{\Gamma }_2\right\}\zeta \left(t\right).\hfill \end{array}(18)$

According to the nonlinear constraint (8), for any λ > 0, the inequality holds

$\lambda {\eta }^T\left(\cdot \right)\eta \left(\cdot \right)-\lambda {\varpi }^2{x}^T\left(t\right)E^{T}Ex\left(t\right)-\lambda {\nu }^2{x}^T\left(h_d\right)N^{T}Nx\left(h_d\right)⩽0.(19)$

Finally, from inequalities (13)–(19) in the derivation process, we can summarize and simplify into the following form.

$\dot{V}\left(t\right)\le {\zeta }^T\left(t\right)\left[h_t^2{\Omega }_2\left({\dot{h}}_t\right)+h_t{\Omega }_1\left({\dot{h}}_t\right)+{\Omega }_0\left({\dot{h}}_t\right)\right]\zeta \left(t\right),(20)$

where ${\Omega }_0({\dot{h}}_t)$, ${\Omega }_1({\dot{h}}_t)$, and ${\Omega }_2({\dot{h}}_t)$ given in theorem 1, respectively.

According to Lemma 3, if and only if there exist $D_i\in {\mathbb{S}}_{+}^{\mathrm{14}n}$ and skew-symmetric matrices $G_i\in {\mathbb{R}}^{\mathrm{14}n\times \mathrm{14}n}$, the nonlinear inequality (20) can be converted to the LMI (11) in theorem 1. Also, then $\dot{V}\left(t\right)<0$ holds. As a result, the Lyapunov stability theorem can guarantee that system (5) is stable. It is sufficient and complete and is thus proved.

Remark 2: Recently, an improved stability criterion has been proposed in 2020 (Oliveira and Souza, 2020), where the LKF was augmented by introducing augmented single integral terms and delay-dependent nonintegral terms. Inspired by this, four integral components are added and expanded to ${\phi }_3\left(\theta \right)$, ${\phi }_4\left(\theta \right)$, and ${\phi }_5\left(\theta \right)$ of V₂ when constructing the LKF. Compared with the literature Jiang et al. (2011), Ramakrishnan and Ray (2015), and Yang et al. (2017a), the LKF proposed in this study includes more coupling information between time delays and state variables, further reducing the conservatism of the stability criterion. In addition, the augmented LKF must be combined with some tight inequality techniques. The novel negative definite inequality equivalence transformation lemma (Lemma 3) proposed in Oliveira and Souza (2020) is used to convert inequality (20) into LMI (11). It can be easily solved with the MATLAB LMI toolbox.

Remark 3: In Jiang et al. (2011), Ramakrishnan and Ray (2015), Yang et al. (2017a), and Feng et al. (2021), when the lower bound of the time delay is zero, the stability of the LFC power system has been studied and some stability criteria have been obtained. However, in some cases, the time-varying delay always varies within a non-zero interval. Therefore, the stability criteria given in Jiang et al. (2011), Ramakrishnan and Ray (2015), Yang et al. (2017a), and Feng et al. (2021 are conservative because the importance of the non-zero lower bound on the time-varying delay is ignored. Based on this, theorem 1 provides a stability criterion in the case of h₁ > 0. Evidently, the stability criterion for h₁ = 0 is a special case of theorem 1, which can be given as a corollary in the next subsection.

3.2 Case 2: h₁ = 0

In this subsection, based on the analysis in remark 3, the following corollary 1 can be obtained based on theorem 1 for the case of h₁ = 0. The changes in notations during the derivation are as follows.

$\begin{array}{ll}\hfill \widehat{\zeta }\left(t\right)& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{x\left(t\right),x\left(h_d\right),x\left(t-h_2\right),{\rho }_{1t},{\rho }_{2t},{\rho }_{3t},{\rho }_{4t}\right.,\hfill \\ \hfill & w\left(t\right),\dot{x}\left(h_d\right),\left.\dot{x}\left(t-h_2\right)\right\},\hfill \\ \hfill {\widehat{\tau }}_i& =\left[\begin{array}{ccc}\hfill 0_{n\times \left(i-1\right)n}\hfill & \hfill I\hfill & \hfill 0_{n\times \left(10-i\right)n}\hfill \end{array}\right],i=\mathrm{1,2},\dots ,10.\hfill \end{array}$

Corollary 1. System (5) is stable in the presence of scalars μ and h₂, if there exist matrices $Z_{j1}\in {\mathbb{S}}^{3n},Z_{j2}\in {\mathbb{S}}_{+}^{3n},Q_j\in {\mathbb{S}}_{+}^{8n},X_j\in {\mathbb{S}}^{3n},Y_j\in {\mathbb{R}}^{3n\times 3n},H_j\in {\mathbb{S}}_{+}^n,D_j\in {\mathbb{S}}_{+}^{\mathrm{10}n}$ and skew-symmetric matrices $G_j\in {\mathbb{R}}^{\mathrm{10}n\times \mathrm{10}n}$, for j = 1, 2, such that the LMIs (9–10) and the following matrix inequalities hold for $h_t\in \left[0,h_2\right]$ and ${\dot{h}}_t\stackrel{\mathrm{\Delta }}{=}{\mu }_j\in \{-\mu ,\mu \}$

$\left[\begin{array}{cc}\hfill {\widehat{\Omega }}_0\left({\mu }_j\right)\hfill & \hfill \frac{1}{2}{\widehat{\Omega }}_1\left({\mu }_j\right)\hfill \\ \hfill ✶\hfill & \hfill {\widehat{\Omega }}_2\left({\mu }_j\right)\hfill \end{array}\right]-{\left[\begin{array}{c}\hfill C\hfill \\ \hfill J\hfill \end{array}\right]}^T\left[\begin{array}{cc}\hfill -D_j\hfill & \hfill G_j\hfill \\ \hfill ✶\hfill & \hfill D_j\hfill \end{array}\right]\left[\begin{array}{c}\hfill C\hfill \\ \hfill J\hfill \end{array}\right]<0,(21)$

where

$\begin{array}{ll}\hfill {\widehat{\Omega }}_0\left({\dot{h}}_t\right)& =\mathrm{S}\mathrm{y}\mathrm{m}\left\{{\widehat{D}}_1^T{Z}_{12}{\widehat{c}}_{11}+{\widehat{D}}_2^T\left(h_2{Z}_{21}+Z_{22}\right){\widehat{c}}_{21}\right.\hfill \\ \hfill & \left.+{\widehat{D}}_3^T{Q}_1{\widehat{c}}_{70}+{\widehat{D}}_4^T{Q}_2{\widehat{c}}_{80}\right\}\hfill \\ \hfill & +{\dot{h}}_t{\widehat{c}}_{11}^T{Z}_{11}{\widehat{c}}_{11}-{\dot{h}}_t{\widehat{c}}_{21}^T{Z}_{21}{\widehat{c}}_{21}+{\widehat{c}}_{31}^T{Q}_1{\widehat{c}}_{31}\hfill \\ \hfill & -{\dot{h}}_{1t}{\widehat{c}}_{41}^T{Q}_1{\widehat{c}}_{41}-{\widehat{c}}_{61}^T{Q}_2{\widehat{c}}_{61}\hfill \\ \hfill & +{\dot{h}}_{1t}{\widehat{c}}_{51}^T{Q}_2{\widehat{c}}_{51}+h_2^2{\widehat{c}}_0^T{H}_2{\widehat{c}}_0-{\widehat{\Gamma }}_2^T\left({\bar{H}}_2+X_2\right){\widehat{\Gamma }}_2\hfill \\ \hfill & -\mathrm{S}\mathrm{y}\mathrm{m}\left\{{\widehat{\Gamma }}_1^T{Y}_1{\widehat{\Gamma }}_1\right\}\hfill \\ \hfill & +h_2^2{\dot{h}}_{1t}{\widehat{\tau }}_9^T\left(H_1-H_2\right){\widehat{\tau }}_9-{\widehat{\Gamma }}_1^T{\bar{H}}_1{\widehat{\Gamma }}_1\hfill \\ \hfill & +\lambda {\epsilon }^2{\widehat{\tau }}_1^T{E}^{T}E{\widehat{\tau }}_1+\lambda {\theta }^2{\widehat{\tau }}_2^T{F}^{T}F{\widehat{\tau }}_2,\hfill \\ \hfill {\widehat{\Omega }}_1\left({\dot{h}}_t\right)& =\mathrm{S}\mathrm{y}\mathrm{m}\left\{{\widehat{D}}_1^T{Z}_{11}{\widehat{c}}_{11}+{\widehat{D}}_1^T{Z}_{12}{\widehat{c}}_{12}\right.\hfill \\ \hfill & +{\widehat{D}}_2^T\left(h_2{Z}_{21}+Z_{22}\right){\widehat{c}}_{22}-{\widehat{D}}_2^T{Z}_{21}{\widehat{c}}_{21}\hfill \\ \hfill & +{\widehat{D}}_3^T{Q}_1{\widehat{c}}_{71}+{\widehat{D}}_4^T{Q}_2{\widehat{c}}_{81}+{\dot{h}}_t{\widehat{c}}_{11}^T{Z}_{11}{\widehat{c}}_{12}\hfill \\ \hfill & -{\dot{h}}_t{\widehat{c}}_{21}^T{Z}_{21}{\widehat{c}}_{22}+{\widehat{c}}_{31}^T{Q}_1{\widehat{c}}_{32}\hfill \\ \hfill & -{\dot{h}}_{1t}{\widehat{c}}_{41}^T{Q}_1{\widehat{c}}_{42}+{\dot{h}}_{1t}{\widehat{c}}_{51}^T{Q}_2{\widehat{c}}_{52}\hfill \\ \hfill & -\left.{\widehat{c}}_{61}^T{Q}_2{\widehat{c}}_{62}\right\}-{\dot{h}}_{1t}{h}_2{\widehat{\tau }}_9^T\left(H_1-H_2\right){\widehat{\tau }}_9\hfill \\ \hfill & -\frac{1}{h_2}{\widehat{\Gamma }}_1^T{X}_1{\widehat{\Gamma }}_1+\frac{1}{h_2}{\widehat{\Gamma }}_2^T{X}_2{\widehat{\Gamma }}_2\hfill \\ \hfill & +\mathrm{S}\mathrm{y}\mathrm{m}\left\{\frac{1}{h_2}{\widehat{\Gamma }}_1^T\left(Y_1-Y_2\right){\widehat{\Gamma }}_2\right\},\hfill \\ \hfill {\widehat{\Omega }}_2\left({\dot{h}}_t\right)& =\mathrm{S}\mathrm{y}\mathrm{m}\left\{{\widehat{D}}_1^T{Z}_{11}{\widehat{c}}_{12}-{\widehat{D}}_2^T{Z}_{21}{\widehat{c}}_{22}+{\widehat{D}}_3^T{Q}_1{\widehat{c}}_{72}\right.\hfill \\ \hfill & \left.+{\widehat{D}}_4^T{Q}_2{\widehat{c}}_{82}\right\}\hfill \\ \hfill & +{\dot{h}}_t{\widehat{c}}_{12}^T{Z}_{11}{\widehat{c}}_{12}-{\dot{h}}_{1t}{\widehat{c}}_{42}^T{Q}_1{\widehat{c}}_{42}+{\widehat{c}}_{32}^T{Q}_1{\widehat{c}}_{32}\hfill \\ \hfill & -{\dot{h}}_t{\widehat{c}}_{22}^T{Z}_{21}{\widehat{c}}_{22}\hfill \\ \hfill & +{\dot{h}}_{1t}{\widehat{c}}_{52}^T{Q}_2{\widehat{c}}_{52}-{\widehat{c}}_{62}^T{Q}_2{\widehat{c}}_{62}\hfill \end{array}$

with

$\begin{array}{ll}\hfill \widehat{\mathit{\Delta }}& ={\widehat{\tau }}_0=\left[\begin{array}{cccccccccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right],\hfill \\ \hfill {\widehat{c}}_0& =\widehat{A}{\widehat{\tau }}_1+{\widehat{A}}_d{\widehat{\tau }}_2+{\widehat{D}}_w{\widehat{\tau }}_8,\hfill \\ \hfill {\widehat{c}}_{11}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{{\widehat{\tau }}_1,{\widehat{\tau }}_2,\widehat{\mathit{\Delta }}\right\},{\widehat{c}}_{12}=\mathrm{c}\mathrm{o}\mathrm{l}\left\{\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},{\widehat{\tau }}_6\right\},\hfill \\ \hfill {\widehat{c}}_{21}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{{\widehat{\tau }}_2,{\widehat{\tau }}_3,h_2{\widehat{\tau }}_4\right\},{\widehat{c}}_{22}=\mathrm{c}\mathrm{o}\mathrm{l}\left\{\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},-{\widehat{\tau }}_4\right\},\hfill \\ \hfill {\widehat{c}}_{31}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{{\widehat{c}}_0,{\widehat{\tau }}_1,{\widehat{\tau }}_1,{\widehat{\tau }}_2,{\widehat{\tau }}_3,\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},h_2{\widehat{\tau }}_4\right\},\hfill \\ \hfill {\widehat{c}}_{32}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},{\widehat{\tau }}_6,-{\widehat{\tau }}_4\right\},\hfill \end{array}$

$\begin{array}{ll}\hfill {\widehat{c}}_{41}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{{\widehat{\tau }}_9,{\widehat{\tau }}_2,{\widehat{\tau }}_1,{\widehat{\tau }}_2,{\widehat{\tau }}_3,\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},h_2{\widehat{\tau }}_4\right\},\hfill \\ \hfill {\widehat{c}}_{42}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},{\widehat{\tau }}_6,\widehat{\mathit{\Delta }},-{\widehat{\tau }}_4\right\},\hfill \\ \hfill {\widehat{c}}_{51}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{{\widehat{\tau }}_9,{\widehat{\tau }}_2,{\widehat{\tau }}_1,{\widehat{\tau }}_2,{\widehat{\tau }}_3,\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},h_2{\widehat{\tau }}_4\right\},\hfill \\ \hfill {\widehat{c}}_{52}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},{\widehat{\tau }}_6,-{\widehat{\tau }}_4\right\},\hfill \\ \hfill {\widehat{c}}_{61}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{{\widehat{\tau }}_{10},{\widehat{\tau }}_3,{\widehat{\tau }}_1,{\widehat{\tau }}_2,{\widehat{\tau }}_3,h_2{\widehat{\tau }}_4,\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }}\right\},\hfill \\ \hfill {\widehat{c}}_{62}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},-{\widehat{\tau }}_4,{\widehat{\tau }}_6,\widehat{\mathit{\Delta }}\right\},\hfill \\ \hfill {\widehat{c}}_{70}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{{\widehat{\tau }}_1-{\widehat{\tau }}_2,\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }}\right\},\hfill \\ \hfill {\widehat{c}}_{71}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{\widehat{\mathit{\Delta }},{\widehat{\tau }}_6,{\widehat{\tau }}_1,{\widehat{\tau }}_2,{\widehat{\tau }}_3,\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},h_2{\widehat{\tau }}_4\right\},\hfill \\ \hfill {\widehat{c}}_{72}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},{\widehat{\tau }}_6-{\widehat{\tau }}_7,{\widehat{\tau }}_7,-{\widehat{\tau }}_4\right\},\hfill \\ \hfill {\widehat{c}}_{80}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{{\widehat{\tau }}_2-{\widehat{\tau }}_3,h_2{\widehat{\tau }}_4,h_2{\widehat{\tau }}_1,h_2{\widehat{\tau }}_2,h_2{\widehat{\tau }}_3,h_2^2\left({\widehat{\tau }}_4-{\widehat{\tau }}_5\right),\widehat{\mathit{\Delta }},\right.\hfill \\ \hfill & \left.h_2^2{\widehat{\tau }}_5\right\},\hfill \\ \hfill {\widehat{c}}_{81}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{\widehat{\mathit{\Delta }},-{\widehat{\tau }}_4,-{\widehat{\tau }}_1,-{\widehat{\tau }}_2,-{\widehat{\tau }}_3,2h_2{\widehat{\tau }}_5-2h_2{\widehat{\tau }}_4,h_2{\widehat{\tau }}_6,\right.\hfill \\ \hfill & \left.-2h_2{\widehat{\tau }}_5\right\},\hfill \\ \hfill {\widehat{c}}_{82}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},{\widehat{\tau }}_4-{\widehat{\tau }}_5,-{\widehat{\tau }}_6,{\widehat{\tau }}_5\right\},\hfill \\ \hfill {\widehat{\Gamma }}_1& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{{\widehat{\tau }}_2-{\widehat{\tau }}_3,{\widehat{\tau }}_2+{\widehat{\tau }}_3-2{\widehat{\tau }}_4,{\widehat{\tau }}_2-{\widehat{\tau }}_3-6{\widehat{\tau }}_4+12{\widehat{\tau }}_5\right\},\hfill \\ \hfill {\widehat{\Gamma }}_2& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{{\widehat{\tau }}_1-{\widehat{\tau }}_2,{\widehat{\tau }}_1+{\widehat{\tau }}_2-2{\widehat{\tau }}_6,{\widehat{\tau }}_1-{\widehat{\tau }}_2-6{\widehat{\tau }}_6+12{\widehat{\tau }}_7\right\},\hfill \\ \hfill {\widehat{D}}_1& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{{\widehat{c}}_0,{\dot{h}}_{1t}{\widehat{\tau }}_9,{\widehat{\tau }}_1-{\dot{h}}_{1t}{\widehat{\tau }}_2\right\},\hfill \\ \hfill {\widehat{D}}_2& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{{\dot{h}}_{1t}{\widehat{\tau }}_9,{\widehat{\tau }}_{10},{\dot{h}}_{1t}{\widehat{\tau }}_2-{\widehat{\tau }}_3\right\},\hfill \\ \hfill {\widehat{D}}_3& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},{\widehat{c}}_0,{\dot{h}}_{1t}{\widehat{\tau }}_9,{\widehat{\tau }}_{10},{\widehat{\tau }}_1,-{\dot{h}}_{1t}{\widehat{\tau }}_2,{\dot{h}}_{1t}{\widehat{\tau }}_2-{\widehat{\tau }}_3\right\},\hfill \\ \hfill {\widehat{D}}_4& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{\widehat{\mathit{\Delta }},\widehat{\mathit{\Delta }},{\widehat{c}}_0,{\dot{h}}_{1t}{\widehat{\tau }}_9,{\widehat{\tau }}_{10},{\dot{h}}_{1t}{\widehat{\tau }}_2,{\widehat{\tau }}_1-{\dot{h}}_{1t}{\widehat{\tau }}_2,-{\widehat{\tau }}_3\right\}.\hfill \end{array}$

Proof: for h₁ = 0, the LKF (12) is reduced to the following forms:

$\begin{array}{ll}\hfill {\widehat{V}}_1& ={\widehat{\phi }}_{1t}^T{Z}_{1t}{\widehat{\phi }}_{1t}+{\widehat{\phi }}_{2t}^T{Z}_{2t}{\widehat{\phi }}_{2t},\hfill \\ \hfill {\widehat{V}}_2& ={\int }_{h_d}^t{\widehat{\phi }}_3^T\left(\theta \right)Q_1{\widehat{\phi }}_3\left(\theta \right)d\theta \hfill \\ \hfill & +{\int }_{t-h_2}^{h_d}{\widehat{\phi }}_4^T\left(\theta \right)Q_2{\widehat{\phi }}_4\left(\theta \right)d\theta ,\hfill \\ \hfill {\widehat{V}}_3& =h_2{\int }_{t-h_2}^{h_d}\left(h_2-t+\theta \right){\dot{x}}^T\left(\theta \right)H_1\dot{x}\left(\theta \right)d\theta \hfill \\ \hfill & +h_2{\int }_{h_d}^t\left(h_2-t+\theta \right){\dot{x}}^T\left(\theta \right)H_2\dot{x}\left(\theta \right)d\theta ,\hfill \end{array}$

where

$\begin{array}{ll}\hfill {\widehat{\phi }}_{0t}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{x\left(t\right),x\left(h_d\right),x\left(t-h_2\right)\right\},\hfill \\ \hfill {\widehat{\phi }}_{1t}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{x\left(t\right),x\left(h_d\right),{\int }_{h_d}^{t}x\left(\theta \right)d\theta \right\},\hfill \\ \hfill {\widehat{\phi }}_{2t}& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{x\left(h_d\right),x\left(t-h_2\right),{\int }_{t-h_2}^{h_d}x\left(\theta \right)d\theta \right\},\hfill \\ \hfill {\widehat{\phi }}_3\left(\theta \right)& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{\dot{x}\left(\theta \right),x\left(\theta \right),{\widehat{\phi }}_{0t},{\int }_{\theta }^{t}x\left(\theta \right)d\theta ,{\int }_{h_d}^{\theta }x\left(\theta \right)d\theta ,\right.\hfill \\ \hfill & \left.{\int }_{t-h_2}^{h_d}x\left(\theta \right)d\theta \right\},\hfill \\ \hfill {\widehat{\phi }}_4\left(\theta \right)& =\mathrm{c}\mathrm{o}\mathrm{l}\left\{\dot{x}\left(\theta \right),x\left(\theta \right),{\widehat{\phi }}_{0t},{\int }_{\theta }^{h_d}x\left(\theta \right)d\theta ,{\int }_{h_d}^{t}x\left(\theta \right)d\theta ,\right.\hfill \\ \hfill & \left.{\int }_{t-h_2}^{\theta }x\left(\theta \right)d\theta \right\}.\hfill \end{array}$

For simplicity, the rest of the proof is omitted as it is similar to the proof of theorem 1. It is sufficient and complete and is thus proved.

4 Case studies

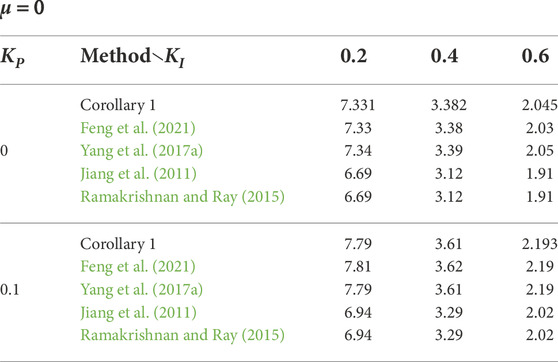
This section illustrates the effectiveness of the stability criterion for the one-area LFC system proposed in the study. By solving the LMIs in theorem 1 and corollary 1 via the MATLAB LMI toolbox application, the maximum admissible delay upper bound (MADUB) for various K_P and K_I can be obtained. In Table 1, the one-area LFC power system parameters are given as those in Jiang et al. (2011), Ramakrishnan and Ray (2015), Yang et al. (2017a), and Feng et al. (2021).

TABLE 1

TABLE 1. System parameters.

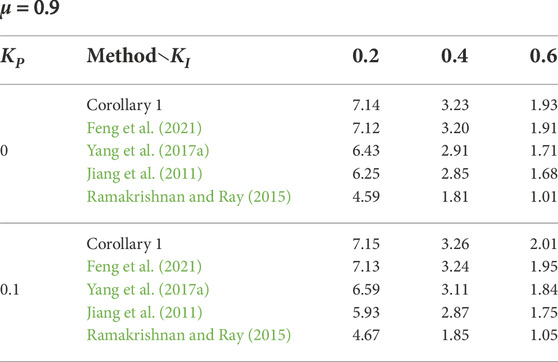
4.1 MADUBs for h₁ = 0

Based on the PI controller, the MADUBs to guarantee the stable operation of the one-area LFC power system can be calculated by solving the LMIs in corollary 1. For load disturbances, the parameters E = F = 0.1I₄, ɛ = 0, and θ = 0 are set. For the given various control gains of K_P and K_I, Table 2 lists MADUBs with μ = 0, and Table 3 lists MADUBs with μ = 0.9. From Tables 2, 3, for fixed K_I, MADUBs increase with the increase of K_P; for fixed K_P, MADUBs decrease with the increase of K_I. For μ = 0, the MADUBs are similar to those of Yang et al. (2017a) and Feng et al. (2021) but larger than those of Jiang et al. (2011) and Ramakrishnan and Ray (2015). However, for μ = 0.9, the MADUBs are larger than those of Jiang et al. (2011), Ramakrishnan and Ray (2015), Yang et al. (2017a), and Feng et al. (2021). In terms of reducing conservatism, our stability criterion is evident under time-varying delay. In addition, the stability criterion proposed in theorem 1 can also solve the case of h₁ > 0, which is ignored in the literature (Jiang et al., 2011; Ramakrishnan and Ray, 2015; Yang et al., 2017a; Feng et al., 2021).

TABLE 2

TABLE 2. MADUBs h₂ for fixed μ = 0 and various K_P and K_I.

TABLE 3

TABLE 3. MADUBs h₂ for fixed μ = 0.9 and various K_P and K_I.

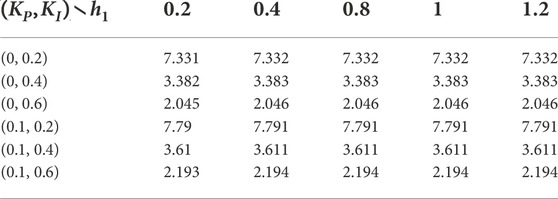
4.2 MADUBs for h₁ > 0

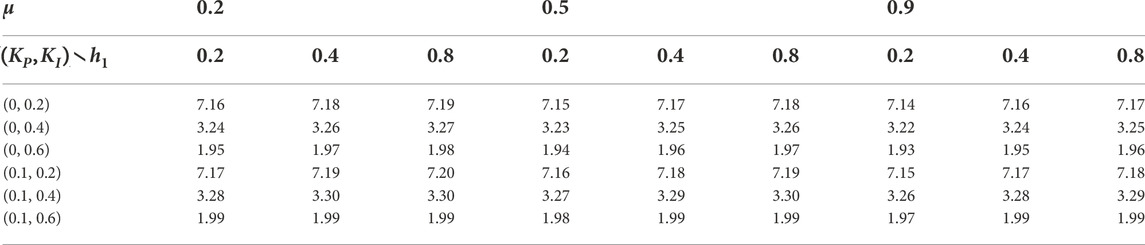
The MADUBs for fixed K_P and K_I and different μ are given in Tables 4, 5. Table 4 lists the MADUBs with μ = 0, h₁ = 0.2/0.4/0.8, and different controller gains. Table 5 lists the MADUBs with various μ, h₁ = 0.2/0.4/0.8, and different controller gains. From Tables 4, 5, the MADUBs increase with the increase of h₁. For fixed h₁, K_P, and K_I, the MADUBs decrease with the increase of μ. For fixed h₁, μ, and K_P, the MADUBs decrease with the increase of K_I. For fixed h₁, μ, and K_I, the MADUBs increase with the increase of K_P.

TABLE 4

TABLE 4. MADUBs h₂ for μ = 0 and various h₁ under theorem 1.

TABLE 5

TABLE 5. MADUBs h₂ for various μ > 0 and various h₁ under theorem 1.

4.3 Simulation

MATLAB simulations about the one-area LFC power system are run with a step load of 0.1pu at 1s. Some detailed simulation conditions are shown as follows. The responses of the power system with K_P = 0 and various K_I and μ can be seen in Figure 2. The responses of the power system with K_P = 0.1 and various K_I and μ can be seen in Figure 3. The LFC power system is stable, and it is clear that the LFC has succeeded in achieving its goals.

$\begin{array}{ll}\hfill \text{Figures}:2:& K_P=0\text{\hspace{0.17em}and\hspace{0.17em}}\text{various\hspace{0.17em}}\mu \text{\hspace{0.17em}and\hspace{0.17em}}{K}_I\hfill \\ \hfill & A.K_I=0.2,h_t=\frac{7.99}{2}+\frac{6.39}{2}\sin \left(\frac{0.4t}{6.39}\right)\hfill \\ \hfill & \text{with\hspace{0.17em}}0.8⩽h_t⩽7.19\text{\hspace{0.17em}and\hspace{0.17em}}\mu =0.2;\hfill \\ \hfill & B.K_I=0.4,h_t=2.03+1.23\sin \left(\frac{t}{1.23}\right)\hfill \\ \hfill & \text{with\hspace{0.17em}}0.8⩽h_t⩽3.26\text{\hspace{0.17em}and\hspace{0.17em}}\mu =0.5;\hfill \\ \hfill & C.K_I=0.6,h_t=\frac{2.35}{2}+\frac{1.55}{2}\sin \left(\frac{1.8t}{1.55}\right)\hfill \\ \hfill & \text{with\hspace{0.17em}}0.4⩽h_t⩽1.95\text{\hspace{0.17em}and\hspace{0.17em}}\mu =0.9.\hfill \end{array}$

$\begin{array}{ll}\hfill \text{Figures}:3:& K_P=0.1\text{\hspace{0.17em}and\hspace{0.17em}}\text{various\hspace{0.17em}}\mu \text{\hspace{0.17em}and\hspace{0.17em}}{K}_I\hfill \\ \hfill & A.K_I=0.2,h_t=4+3.2\sin \left(\frac{0.8t}{3.2}\right)\hfill \\ \hfill & \text{with\hspace{0.17em}}0.8⩽h_t⩽7.20\text{\hspace{0.17em}and\hspace{0.17em}}\mu =0.2;\hfill \\ \hfill & B.K_I=0.4,h_t=\frac{4.1}{2}+\frac{2.5}{2}\sin \left(\frac{t}{2.5}\right)\hfill \\ \hfill & \text{with\hspace{0.17em}}0.8⩽h_t⩽3.30\text{\hspace{0.17em}and\hspace{0.17em}}\mu =0.5;\hfill \\ \hfill & C.K_I=0.6,h_t=\frac{2.39}{2}+\frac{1.59}{2}\sin \left(\frac{1.8t}{1.59}\right)\hfill \\ \hfill & \text{with\hspace{0.17em}}0.4⩽h_t⩽1.99\text{\hspace{0.17em}and\hspace{0.17em}}\mu =0.9.\hfill \end{array}$

FIGURE 2

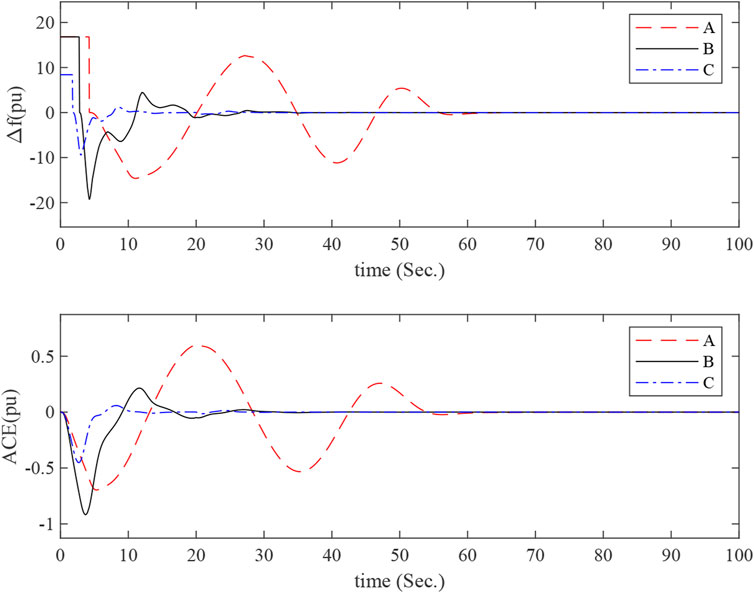
FIGURE 2. Frequency deviation and control error responses of the one-area LFC power system with K_P = 0 and different K_I.

FIGURE 3

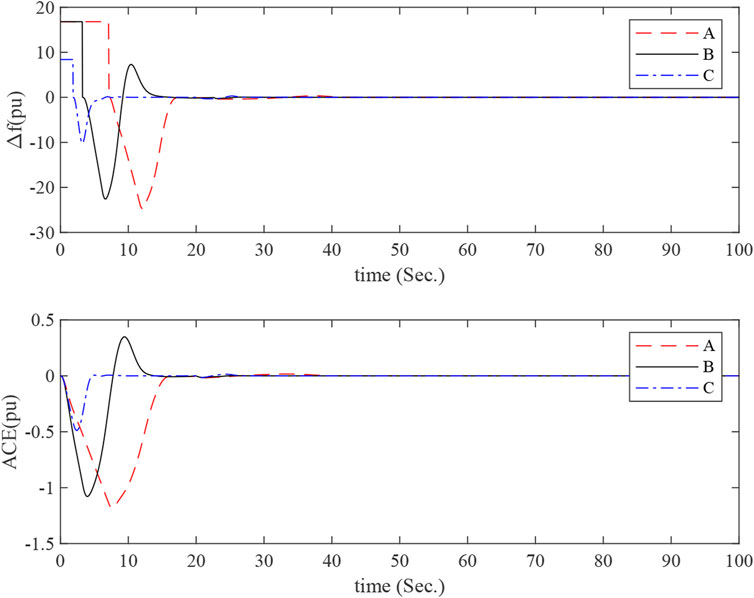
FIGURE 3. Frequency deviation and control error responses of the one-area LFC power system with K_P = 0.1 and different K_I.

The curves A, B, and C in Figures 2, 3 correspond to simulation conditions A, B, and C, respectively. The curves tend to be in a steady state as time increases. This proves that the maximum allowable delay range obtained from theorem 1 is within the actual range.

5 Conclusion

The stability analysis of the LFC power systems with interval time-varying delays is investigated in this study. The two cases of the time delay lower bound h₁ = 0 and h₁ > 0 are considered. An improved stability criterion is given based on the Lyapunov stability theory. First, for load disturbances, time delay linear systems are used to characterize one-area LFC power systems. Second, when constructing the augmented LKF, the state and time-varying delay information on the LFC power systems are fully utilized. The LKF contains the delay-dependent matrices and four single integral terms. Third, by applying the equivalence transformation lemma 3 for quadratic matrix functions, the stability criterion can be described as the LMI. At last, the efficiency of the method is demonstrated with a few examples. The stability criteria in this study reduce the conservatism, however increases the complexity of solving LMI. For the LFC power system, the results obtained in this study can be expanded to the multi-time delays and multi-areas. In Shi et al. (2022) and Zhong et al. (2022), the sampling period and decentralized LFC schemes are proposed, respectively, which can improve the method in this study. It may be our future topics.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Author contributions

YS has made the construction and derivation of the function and wrote the manuscript. XB and YS have analyzed the data and wrote part of the manuscript. WD has carried out the simulation. QL was responsible for the language expression of the manuscript. WD and QL supported the project both financially and technically.

Funding

This work was supported by the Natural Science Foundation of China under Grant 62003292 and the Funding for School-Level Research Project of Yancheng Institute of Technology under Grant xjr2019017.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aminov, R., and Garievskii, M. (2019). Effect of engagement in power and frequency control on the service life of Steam-Turbine power units. Power Technol. Eng. 53, 479–483. doi:10.1007/s10749-019-01102-z

CrossRef Full Text | Google Scholar

Baykov, D., Gulyaev, I., Inshakov, A., and Teplukhov, D. (2019). Simulation modeling of an induction motor drive controlled by an array frequency converter. Russ. Electr. Engin. 90, 485–490. doi:10.3103/S1068371219070034

CrossRef Full Text | Google Scholar

Bhowmik, S., Tomsovic, K., and Bose, A. (2004). Communication models for third party load frequency control. IEEE Trans. Power Syst. 19, 543–548. doi:10.1109/TPWRS.2003.818700

CrossRef Full Text | Google Scholar

Chen, B., Shangguan, X., Jin, L., and Li, D. (2020). An improved stability criterion for load frequency control of power systems with time-varying delays. Energies 13, 2101. doi:10.3390/en13082101

CrossRef Full Text | Google Scholar

Duan, W., Li, Y., and Chen, J. (2019). Further stability analysis for time-delayed neural networks based on an augmented Lyapunov functional. IEEE Access 7, 104655–104666. doi:10.1109/ACCESS.2019.2931714

CrossRef Full Text | Google Scholar

Duan, W., Li, Y., Sun, Y., Chen, J., and Yang, X. (2020). Enhanced master–slave synchronization criteria for chaotic Lur’e systems based on time-delayed feedback control. Math. Comput. Simul. 177, 276–294. doi:10.1016/j.matcom.2020.04.010

CrossRef Full Text | Google Scholar

Feng, W., Xie, Y., Luo, F., Zhang, X., and Duan, W. (2021). Enhanced stability criteria of network-based load frequency control of power systems with time-varying delays. Energies 14, 5820. doi:10.3390/en14185820

CrossRef Full Text | Google Scholar

Gholami, Y. (2021). Existence and global asymptotic stability criteria for nonlinear neutral-type neural networks involving multiple time delays using a quadratic-integral Lyapunov functional. Adv. Differ. Equ. 2021, 112–126. doi:10.1186/s13662-021-03274-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Giudice, D., Brambilla, A., Grillo, S., and Bizzarri, F. (2021). Effects of inertia, load damping and dead-bands on frequency histograms and frequency control of power systems. Int. J. Electr. Power & Energy Syst. 129, 106842. doi:10.1016/j.ijepes.2021.106842

CrossRef Full Text | Google Scholar

Hassan, B. (2014). Robust power system frequency control. Berlin, Germany: Springer.

Google Scholar

Hua, C., Qiu, Y., Wang, Y., and Guan, X. (2021). An augmented delays-dependent region partitioning approach for recurrent neural networks with multiple time-varying delays. Neurocomputing 423, 248–254. doi:10.1016/j.neucom.2020.10.047

CrossRef Full Text | Google Scholar

Jiang, L., Yao, W., Wu, Q., Wen, J., and Cheng, S. (2011). Delay-dependent stability for load frequency control with constant and time-varying delays. IEEE Trans. Power Syst. 27, 932–941. doi:10.1109/TPWRS.2011.2172821

CrossRef Full Text | Google Scholar

Khalil, A., and Swee, A. (2018). An accurate method for delay margin computation for power system stability. Energies 11, 3466. doi:10.3390/en11123466

CrossRef Full Text | Google Scholar

Kundur, P. (1994). Power system stability and control. New York, United States: McGraw-Hill.

Google Scholar

Ladygin, A., Bogachenko, D., and Kholin, V. (2020). Efficient control of induction motor current in a frequency-controlled electric drive. Russ. Electr. Engin. 91, 362–367. doi:10.3103/S106837122006005X

CrossRef Full Text | Google Scholar

Liu, Z., Zhu, C., and Jiang, Q. (2008). “Stability analysis of time delayed power system based on cluster treatment of characteristic roots method,” in 2008 IEEE Power and Energy Society General Meeting-Conversion and Delivery of Electrical Energy in the 21st Century (IEEE), Pittsburgh, PA, USA, 20-24 July 2008, 1–6.

Google Scholar

Manikandan, S., and Kokil, P. (2020). Stability analysis of load frequency control system with constant communication delays. IFAC-PapersOnLine 53, 338–343. doi:10.1016/j.ifacol.2020.06.057

CrossRef Full Text | Google Scholar

Martin, G., Begovic, M., and Taylor, D. (1995). Transient control of generator excitation in consideration of measurement and control delays. IEEE Trans. Power Deliv. 10, 135–141. doi:10.1109/61.368405

CrossRef Full Text | Google Scholar

Oliveira, F., and Souza, F. (2020). Further refinements in stability conditions for time-varying delay systems. Appl. Math. Comput. 369, 124866. doi:10.1016/j.amc.2019.124866

CrossRef Full Text | Google Scholar

Ramakrishnan, K., and Ray, G. (2015). Stability criteria for nonlinearly perturbed load frequency systems with time-delay. IEEE J. Emerg. Sel. Top. Circuits Syst. 5, 383–392. doi:10.1109/JETCAS.2015.2462031

CrossRef Full Text | Google Scholar

Ren, Z., and Tian, J. (2022). Improved stability criterion for distributed time-delay systems via a generalized delay partitioning approach. AIMS Math. 7, 13402–13409. doi:10.3934/math.2022740

CrossRef Full Text | Google Scholar

Saravanakumar, R., Ali, M., Huang, H., Cao, J., and Joo, Y. (2018). Robust H_∞ state-feedback control for nonlinear uncertain systems with mixed time-varying delays. Int. J. Control Autom. Syst. 16, 225–233. doi:10.1007/s12555-017-9263-6

CrossRef Full Text | Google Scholar

Seuret, A., and Gouaisbaut, F. (2015). Hierarchy of LMI conditions for the stability analysis of time-delay systems. Syst. Control Lett. 81, 1–7. doi:10.1016/j.sysconle.2015.03.007

CrossRef Full Text | Google Scholar

Shakibjoo, A., Mohammad, M., Moussavi, S., and Vandevelde, L. (2020). A novel technique for load frequency control of multi-area power systems. Energies 13, 2125. doi:10.3390/en13092125

CrossRef Full Text | Google Scholar

Shangguan, X., He, Y., Zhang, C., Jiang, L., and Wu, M. (2022a). Load frequency control of time-delayed power system based on event-triggered communication scheme. Appl. Energy 308, 118294. doi:10.1016/j.apenergy.2021.118294

CrossRef Full Text | Google Scholar

Shangguan, X., He, Y., Zhang, C., Jin, L., Jiang, L., Spencer, J. W., et al. (2021). Robust load frequency control for power system considering transmission delay and sampling period. IEEE Trans. Ind. Inf. 17, 5292–5303. doi:10.1109/TII.2020.3026336

CrossRef Full Text | Google Scholar

Shangguan, X., He, Y., Zhang, C., Yao, W., Zhao, Y., Jiang, L., et al. (2022b). Resilient load frequency control of power systems to compensate random time delays and time-delay attacks. IEEE Trans. Ind. Electron. 1, 1–13. doi:10.1109/TIE.2022.3186335

CrossRef Full Text | Google Scholar

Shen, C., Li, Y., Zhu, X., and Duan, W. (2020). Improved stability criteria for linear systems with two additive time-varying delays via a novel Lyapunov functional. J. Comput. Appl. Math. 363, 312–324. doi:10.1016/j.cam.2019.06.010

CrossRef Full Text | Google Scholar

Shi, K., Cai, X., She, K., Zhong, S., Soh, Y., and Kwon, O. (2022). Quantized memory proportional–integral control of active power sharing and frequency regulation in island microgrid under abnormal cyber attacks. Appl. Energy 322, 119540. doi:10.1016/j.apenergy.2022.119540

CrossRef Full Text | Google Scholar

Tian, Y., and Wang, Z. (2020). Stability analysis for delayed neural networks based on the augmented Lyapunov-Krasovskii functional with delay-product-type and multiple integral terms. Neurocomputing 410, 295–303. doi:10.1016/j.neucom.2020.05.045

CrossRef Full Text | Google Scholar

Wen, S., Yu, X., Zeng, Z., and Wang, J. (2015). Event-triggering load frequency control for multiarea power systems with communication delays. IEEE Trans. Ind. Electron. 63, 1308–1317. doi:10.1109/TIE.2015.2399394

CrossRef Full Text | Google Scholar

Xiong, L., Li, H., and Wang, J. (2018). LMI based robust load frequency control for time delayed power system via delay margin estimation. Int. J. Electr. Power & Energy Syst. 100, 91–103. doi:10.1016/j.ijepes.2018.02.027

CrossRef Full Text | Google Scholar

Xu, H., Zhang, C., Jiang, L., and Smith, J. (2017). Stability analysis of linear systems with two additive time-varying delays via delay-product-type Lyapunov functional. Appl. Math. Model. 45, 955–964. doi:10.1016/j.apm.2017.01.032

CrossRef Full Text | Google Scholar

Yang, F., He, J., and Wang, D. (2017a). New stability criteria of delayed load frequency control systems via infinite-series-based inequality. IEEE Trans. Ind. Inf. 14, 231–240. doi:10.1109/TII.2017.2751510

CrossRef Full Text | Google Scholar

Yang, F., He, J., and Wang, J. (2017b). Novel stability analysis of delayed LFC power systems by infinite-series-based integral inequality. New Jersey, United States: IEEE, 1384–1389.

Google Scholar

Zhang, X., Han, Q., Seuret, A., and Gouaisbaut, F. (2017). An improved reciprocally convex inequality and an augmented Lyapunov–Krasovskii functional for stability of linear systems with time-varying delay. Automatica 84, 221–226. doi:10.1016/j.automatica.2017.04.048

CrossRef Full Text | Google Scholar

Zhong, Q., Han, S., Shi, K., Zhong, S., and Kwon, O. M. (2022). Co-design of adaptive memory event-triggered mechanism and aperiodic intermittent controller for nonlinear networked control systems. IEEE Trans. Circuits Syst. II, 1. doi:10.1109/TCSII.2022.3188036

CrossRef Full Text | Google Scholar