Abstract
The integrated energy system with electric vehicles can realize multi-energy coordination and complementarity, and effectively promote the realization of low-carbon environmental protection goals. However, the temporary change of vehicle travel plan will have an adverse impact on the system. Therefore, a multi-layer coordinated optimization strategy of electric-thermal-hydrogen integrated energy system including vehicle to grid (V2G) load feedback correction is proposed. The strategy is based on the coordination of three-level optimization. The electric vehicle charging and discharging management layer comprehensively considers the variance of load curve and the dissatisfaction of vehicle owners, and the charging and discharging plan is obtained through multi-objective improved sparrow search algorithm, which is transferred to the model predictive control rolling optimization layer. In the rolling optimization process, according to the actual situation, selectively enter the V2G load feedback correction layer to update V2G load, so as to eliminate the impact of temporary changes in electric vehicle travel plans. Simulation results show that the total operating cost with feedback correction is 4.19% lower than that without feedback correction and tracking situation of tie-line planned value is improved, which verifies the proposed strategy.
1 Introduction
In order to solve global environmental problems, it is necessary to build a clean and low-carbon new energy system. The integrated energy system effectively improves the energy utilization efficiency and promotes the consumption of renewable energy through the multi energy coupling mechanism, thereby reducing carbon emissions (Ding et al., 2018; Yang et al., 2018; Cheng et al., 2019). The interaction between electric vehicle (EV) and integrated energy system can further tap flexible resources and promote the carbon reduction operation of the system (Zhou et al., 2021; Li et al., 2022). EVs can be connected to the power grid as mobile loads, and they have the characteristics of energy storage (Hu et al., 2015; Cheng et al., 2021). In order to take advantages of its characteristics, the vehicle to grid (V2G) mode has been proposed in recent years (Wang et al., 2015). Peak shaving and valley filling of load curve can be achieved by managing the charge and discharge of electric vehicles. However, the temporary change of EV travel plan will have an adverse impact on the economic and stable operation of the system.
In practice, EV travel plans are uncertain, and the photovoltaic power, wind power and predicted load power of electric-thermal-hydrogen integrated energy system (ETH-IES) also have randomness and volatility. Considering the characteristics that the prediction accuracy improves with the reduction of time scale, multi-time scale strategy is often used in energy management of integrated energy system (Yin et al., 2020; Tang et al., 2021; Wang et al., 2021). On the larger time range, the unit combination and the base value of operation plan is formulated based on the forecast data. On the smaller time range, the deviation left by the superior is corrected based on the real-time data. On this basis, according to the relationship between different nodes in the optimization process, the energy management is divided into static scheduling and dynamic scheduling. Static scheduling is the optimization of single section, and there will be a large power deviation in actual operation (Qi et al., 2022). Static optimization can be solved by nonlinear programming (Lv et al., 2016) and chance constrained programming (Li et al.,. 2019). Dynamic optimal scheduling considers the connections between different time nodes, and has better robustness (Huang et al., 2014). Generally, model predictive control (MPC) is used for dynamic optimal scheduling. Based on the idea of rolling optimization and feedback correction, it can well solve the optimal control problems with many uncertain factors (Xiao et al., 2016). In addition, unlike the day ahead optimal scheduling, MPC has higher accuracy, because it can continuously obtain real-time short-term power prediction information. The results of each rolling optimization correct the real-time state of the system, which can eliminate the influence of uncertainties on the optimal scheduling scheme to a greater extent (Zhang et al., 2017). At present, many researches apply rolling optimization to the scheduling of integrated energy system, but less to the joint optimal scheduling of system and electric vehicles.
In recent years, more and more studies on the optimal scheduling of integrated energy system with EVs have been published. Reference (Wang et al., 2016) establishes a multi-objective optimization model with optimal generation cost and environmental benefit of microgrid with EVs. Reference (Chen et al., 2020) proposes a fuzzy control algorithm to formulate EV charging plan. The proposed strategy has good real-time performance, but ignores the V2G machanism. Reference (Hou et al., 2019) optimizes the microgrid and EVs according to three levels, which can maximize the benefits. In (Jozi et al., 2022), EV charging and discharging plans are optimally scheduled to maximize parking profits and improve system reliability; Reference (Hu et al., 2019) proposes a real-time scheduling method to smooth photovoltaic power fluctuations through the flexibility of charging and discharging of clustered EVs; Reference (Zhao et al., 2016) motivates EV owners to participate in the dispatching of microgrid by adjusting the electricity price. The above references only formulate energy management strategies from the perspective of micro network operators, ignoring the interests of EV owners. Reference (Cheng et al., 2022) establishes a stochastic optimal scheduling model considering the forecast error of wind power output; Reference (Jia and Kang, 2022) quantifies the uncertainty of wind and photovoltaic output with the conditional value at risk of relative disturbance. Although the above literatures consider the uncertainty of distributed generators and load forecasting power, they ignore the uncertainty of EV travel plans. Reference (Wang et al., 2022) establishes a multi-stage optimal energy management system for participating in the deregulated electricity market. However, reference (Wang et al., 2022) does not consider electric vehicles. In (Alireza et al., 2021), a two-stage operation is presented according to day-ahead and 5 min real time energy markets. However, it uses non-layered architecture to optimize EV charging and discharging and does not consider EV owners’ feeling. Reference (Jia et al., 2022) proposes a hierarchical stochastic optimal scheduling model and it uses stochastic programming to deal with uncertainty. In real-time operation, when the number of unplanned EVs suddenly increases, the strategy cannot make corresponding corrections. Furthermore, reference (Jia et al., 2022) adopts static optimal strategy and there will be a large power deviation in actual operation.
For the adverse impact of temporary change in EV travel plan on system operation, this paper establishes a multi-layer coordinated optimization strategy of electric-thermal-hydrogen integrated energy system including the feedback correction of V2G load. On the basis of building the system model, EVs and ETH-IES are optimized hierarchically and solved by multi-objective improved sparrow search algorithm. Furthermore, in order to reduce the impact of temporary changes in EV travel plans, V2G load feedback correction layer is introduced. In the process of rolling optimization of the system, EV unplanned behaviors are identified and the charging and discharging plan is adjusted in time. Finally, taking an electric-thermal-hydrogen integrated energy industrial park as an example, the effectiveness of the proposed strategy is verified. The contributions of this paper are to:
1) Constructing multi-objective EV charging and discharging management model and two-stage MPC rolling optimization model to achieve accurate and economic formulation.
2) Presenting a multi-layer coordinated optimal scheduling model to improve the economy and stability of system operation, and improves the tracking situation of tie-line planned value.
3) Using the coupled Monte Carlo simulation and multi-objective improved sparrow search algorithm to solve the multi-scenario multi-objective optimal scheduling model.
4) Conducting simulation studies to verify the effectiveness of V2G load feedback correction layer and discussing the effect of the unplanned EVs’ proportion on scheduling results.
The rest of the study proceeds as follows: Section 2 introduces the architecture of ETH-IES; Section 3 presents multi-layer coordinated optimization framework based on feedback correction; Section 4 introduces the multi-layer coordinated optimization model in detail. In Section 5, the multi-objective improved sparrow search algorithm is proposed. Section 6 verifies the effectiveness of the V2G load feedback correction layer and discusses the effects of the unplanned EVs’ proportion on scheduling results. Finally, Section 7 draws the main conclusions.
2 Architecture of electric-thermal-hydrogen integrated energy system
As shown in Figure 1, the main equipment of ETH-IES includes hydrogen storage device, electrolyzer, proton exchange membrane fuel cell (PEMFC), thermal storage device, super capacitor, battery, wind turbine, photovoltaic, ground source heat pump, absorption machine and micro gas turbine. Among them, micro gas turbine and ground source heat pump unit belong to electrothermal coupling equipment, while electrolyzer and PEMFC belong to electric-thermal-hydrogen coupling equipment. Their introduction can not only realize multi-energy coordination and complementarity, but also improve the system operation flexibility and economy.
FIGURE 1

Electric-Thermal-Hydrogen integrated energy system architecture.
2.1 Conventional unit model
In the proposed electric-thermal-hydrogen integrated energy system architecture, the mathematical models of micro gas turbine, ground source heat pump and absorption refrigeration unit can be referred to reference (Li et al., 2021), and the models of wind turbine, photovoltaic and energy storage device can be found in reference (Jia et al., 2022). Due to limited space, this paper only introduces the models of electrolyzer, hydrogen storage device and proton exchange membrane fuel cell in detail.
2.2 Proton exchange membrane fuel cell model
The PEMFC output voltage is mainly influenced by the concentration polarization, the ohmic polarization and the active polarization, and it can be considered as the difference between the Nernst voltage and the loss voltage caused by them (Colleen, 2008). Activation loss can be expressed by Tafel formula:where,
The loss voltage caused by the active polarization could be calculated as:
The loss voltage caused by the ohmic polarization could be calculated as:
The loss voltage caused by the concentration polarization could be calculated as:
To calculate the Nernst voltage, some pressure values of oxygen, water and hydrogen are needed. Refer to (Colleen, 2008), it can be expressed as:
To sum up, the actual voltage can be expressed as:
2.3 Electrolyzer model
The electrolyzer consumes electric energy to produce heat and hydrogen energy. The relationship between electricity consumption and hydrogen production is approximately linear, which can be expressed as follows:
2.4 Hydrogen storage device model
The hydrogen stored in the hydrogen storage device at the current moment is related to the storage capacity, outgassing volume and storage volume at the previous moment. Therefore, the hydrogen stored in the device can be expressed as:
3 Multi-layer coordinated optimization framework for integrated energy system with electric vehicles based on feedback correction
As shown in Figure 2, the multi-layer coordinated optimization framework of ETH-IES proposed in this paper contains three layers altogether: EV charging and discharging management layer, MPC rolling optimization layer and V2G load feedback correction layer. First, the EV charging and discharging management layer simulates EV travel scenarios through Monte Carlo according to owners’ historical habit data, optimizes the charging and discharging of EVs in each scenario, and transmits the results to the MPC rolling optimization layer. Secondly, the MPC rolling optimization layer is divided into two stages. In the first stage, economic scheduling is carried out with 24 h as the time window and 1 h as the time step, and the results are passed into the second stage as the reference value. The second stage takes 1 h as the time window and 5 mins as the time step to coordinate the output of each distributed generator according to the received real-time prediction data, so that the tie-line power can track the superior planned value. Finally, during the operation of MPC rolling optimization layer, the number of EVs with temporary change in their travel plan is identified in real time. If the proportion is greater than the threshold, the V2G load feedback correction layer is carried out and the EV charging and discharging plan is re-established. The revised V2G equivalent load is fed back to the MPC rolling optimization layer and the operation continues from the breakpoint. The specific solution flow chart is shown in Figure 3.
FIGURE 2

ETH-IES multi-layer coordinated optimization framework.
FIGURE 3

ETH-IES multi-layer coordinated optimization flow chat.
4 Multi-layer coordinated optimization model of integrated energy system with electric vehicles
4.1 Electric vehicle charging and discharging management layer
By managing the charging and discharging of electric vehicles, peak shaving and valley filling of the load curve can be achieved. However, the large degradation of EVs battery will greatly increase the dissatisfaction of EV owners. Thus, the degradation cost should be considered in the proposed optimization model.
4.1.1 Electric vehicle degradation cost model
High degradation cost will greatly increase the EV owners dissatisfaction, which embodies in the reduction of cycle number and the actual full capacity (Smith et al., 2012). The times of frequent charging and discharging, charging and discharging rate and other factors will influence the EV degradation cost (Vetter et al., 2005).
After the calculation of discharge of depth (DOD), the degradation cost could be calculated as follows (Ju et al., 2018):
The cost of battery degradation within each time interval can only be determined after the end of a charging or discharging event. According to (Ju et al., 2018), the expression of the operating cost considering the degradation effect of the battery is shown in Eq. 12.
4.1.2 Electric vehicle charging and discharging optimization model
The dispersion of time and space and randomness of charging behavior of EVs may greatly increase the peak-to-valley effect of load curve, and the reduction of EV service life will greatly increase the dissatisfaction of owners. On the basis of this, this paper establishes a multi-objective optimization model aiming at minimizing the variance of the load curve and minimizing the degradation cost of EVs. Furthermore, the fuzzy membership function (
Xu et al., 2015) is used to select the compromise solution from Pareto front as the final solution
1) Objective function 1:
The first objective function is from the system operators’ point of view, which aims to decrease the variance of the load curve.
2) Objective function 2:
The second objective function is from the EV owners’ point of view. It is a linear function of degradation cost, with a range of 0–1.
3) Constraints:
The constraints mainly contain the charging and discharging power limitation and EVs’ SOC limitation.
4.2 Model predictive control rolling optimization layer
With the shortening of time step, the accuracy of prediction data is improved. By adjusting the output of distributed power supply, the scheduling economy can be improved and the tie-line power can better track the superior planned value. In addition, the battery is scheduled as a distributed generator, while supercapacitors can stabilize unbalanced power and respond quickly. Therefore, the rolling optimization can be divided into two stages. The short-term optimization stage can improve the operation economy of the system, and the ultra-short-term optimization stage can ensure the safe and stable operation of the system (Ju et al., 2018).
4.2.1 The first stage rolling optimization model
In the first stage, considering the maximum economic benefit, an economic optimization model is established. Since the capacity of the supercapacitor is relatively small compared with other units and its response speed is fast, it is only used to suppress the power prediction error in the second stage.
4.2.1.1 Objective function:
Equations 19–22 respectively represent the switching power cost with the main network, the maintenance cost of distributed power supply, the operation cost of micro gas turbine and the pollution gas treatment cost.
4.2.1.2 Constraints:
1) Constraints on electrothermal power balance:
2) Constraints on distributed generator output power:
3) Constraints on micro gas turbine ramp rate:
4) Constraints on tie-line power:
5) Mutual exclusion constraints of electricity purchase and sale signs:
6) Constraints on micro gas turbine start and stop time:
7) Battery operation constraints:
8) Thermal storage device constraints:
9) Operation constraints of electrolyzer:
10) Hydrogen storage device operation constraints:
4.2.2 The second stage rolling optimization model
The optimization goal of the second stage is to balance the influence of power prediction error on the basis of the output of each unit obtained in the first stage. The constraint conditions are the same as the first stage, and the objective function is as follows:where and are the cost weight coefficient of optimal scheduling in the second stage; is the operation and maintenance cost coefficient of supercapacitor; is the number of distributed power supply participating in adjustment in the second stage. Equations 42–44 respectively represent the adjustment cost of tie-line power, the adjustment cost of distributed generators, and the operation and maintenance cost of supercapacitor.
4.3 Vehicle to grid load feedback correction layer
When the proportion of EVs that temporarily change travel plan increases, the error of the V2G equivalent load corresponding to the original plan will also increase. If the rolling optimization continues according to the original data, it will deviate from the global optimal scheduling strategy, which will make the operation economy worse, and the scheduling power deviation caused by this is not conducive to the safe and stable operation of the system. Therefore, it is necessary to re-optimize its charging and discharging power based on the actual EV travel plan. The objective of this layer is to optimize the economy of EV charging and discharging and minimize the dissatisfaction of EV owners. The specific objective function is as follows:
1) Objective function 1:
2) Objective function 2:
5 Multi-objective improved sparrow search algorithm
In this paper, multi-objective improved sparrow search algorithm (MISSA) is used to solve the EV charging and discharging management layer and V2G load feedback correction layer, and CPLEX is used to solve the MPC rolling optimization layer. Based on SSA (Xue and Shen, 2020), ISSA introduces Levy flight strategy to make its step size obey heavy tail distribution and improve global optimization ability (Jia et al., 2022). Furthermore, in order to make it have multi-objective optimization ability, this paper introduces elite strategy, fast non-dominated sorting strategy, congestion and congestion comparison operator.
In order to solve the mixed integer non-linear programming problem in multiple random scenes, this paper combines the Monte Carlo simulation method with the MISSA to obtain the EV charging and discharging optimization strategy. The algorithm flow chart is shown in Figure 4.
FIGURE 4

Monte Carlo-MISSA algorithm flow chat.
6 Simulation results and discussion
6.1 Parameter setting
It is assumed that there are 60 EVs connected to the system and all EVs are divided into four categories. Category ① EVs always have no travel plans; Category ② EVs travel on a fixed schedule; Category ③ EVs require emergency charging and Category ④ EVs temporarily change travel plans. The basic information of the above four types EVs is simulated by Monte Carlo.
According to the parameters in Table 1, different kinds of EV loads are generated through Monte Carlo simulation. Other parameters of EV are shown in Table 2. The predicted real-time electricity price, wind power and photovoltaic power are referred in (Ju et al., 2018). The pollutant treatment cost and pollutant emission coefficient of micro gas turbine are referred in (Jia et al., 2022).
TABLE 1
| Random parameter | Average | Variance |
|---|---|---|
| SOC when category ② EVs leave | 0.2 | 0.1 |
| Initial SOC of category ③ EVs | 0.3 | 0.05 |
| Expected SOC of category ③ EVs | 0.8 | 0.05 |
| Departure time of category ② EVs | 7:00 | 30 mins |
| Return time of category ② EVs | 18:00 | 30 mins |
| Quantity of category ④ EVs | 4 | 9 |
Random parameters of various EV loads.
TABLE 2
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 30 | 0.2/0.9 | ||
| 15 000 | 7/−7 | ||
| 0.9 | 0.9 |
Other related parameters of EV.
MISSA parameters are set as follows: population size n = 100, maximum iterations . In gamma function of Levy flight strategy, . The number of Monte Carlo simulation scenes is 500.
6.2 Result analysis
6.2.1 Scheduling results of model predictive control rolling optimization layer
As shown in Figure 5A, from 4:00 to 7:00, the electric load is low and the electricity price is relatively cheap. The excess electric energy is stored in the battery, converted into hydrogen energy and stored in the hydrogen storage tank. From 10:00 to 11:00 and from 15:00 to 17:00, the electricity price is high, and the electric energy will be released on the basis of meeting the power demand, so as to sell electricity to the grid as much as possible to maximize economic benefits. The coordination of electric hydrogen thermal coupling equipment ensures the economy of system operation.
FIGURE 5
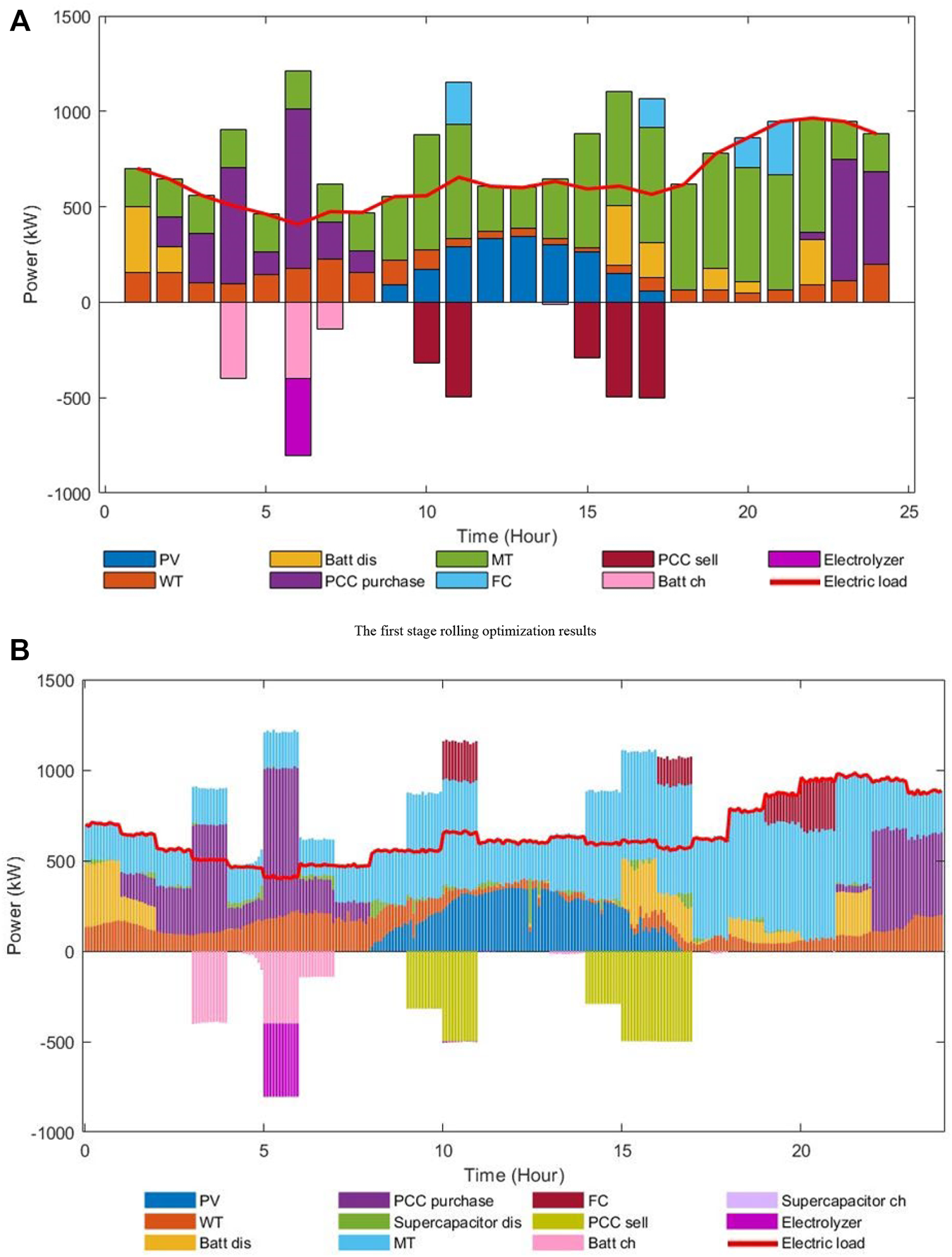
Winter electric optimization results of MPC rolling optimization layer. (A) The first stage rolling optimization results. (B) The second stage rolling optimization results.
As shown in Figure 5B, since the predicted power error is superimposed on the wind power photovoltaic output and load power, it is essential to coordinate each distributed generator to balance the resulting power deviation in real-time scheduling. It can be seen that supercapacitor and battery are preferred in the dispatching process. If the power deviation is still not met, the planned value of micro gas turbine and tie-line power will be changed.
As shown in Figure 6A, From 3:00 to 7:00, the electricity price is low, and the equivalent heat production cost is relatively low. The excess heat energy is stored in the heat storage device while meeting the heat load demand. From 10:00 to 17:00, the electricity price is relatively high, and the heat storage device outputs large power, reducing the output of electrothermal coupling equipment, so as to reduce the power purchase of the power grid and maintain the high economy of system operation. As shown in Figure 6B, the output of each unit in the heat network part is almost consistent with the first-stage dispatch plan value, and the predicted power error is mainly balanced by the thermal storage device.
FIGURE 6

Winter thermal optimization results of MPC rolling optimization layer. (A) The first stage rolling optimization results. (B) The second stage rolling optimization results.
As shown in Figures 7A,B, the thermal load characteristics in summer are quite different from those in winter. The electricity price is higher from 14:00 to 17:00. Thus, the heat storage device releases as much as possible, reducing the output of electrothermal coupling equipment, thereby reducing the power purchase. During the whole dispatching period, the thermal storage device stores heat in the low electricity price period, and releases heat in the high electricity price period, so as to reduce the system operation cost.
FIGURE 7

Summer thermal optimization results of MPC rolling optimization layer.
Compare and analyze three different strategies. Strategy 1 is to reduce the variance of load curve at all costs only from the operator’s own interests; strategy 2 only considers the wishes of EV owners and charges and discharges EVs disorderly; strategy 3 comprehensively considers the interests of both sides. As shown in Table 3, compared with strategy 1, the dissatisfaction of EV owners decreased by 0.7533, the scheduling cost of the proposed strategy increased by 10.61%, and the load variance increased by 23.48%; Compared with strategy 2, the scheduling cost decreased by 15.38%, the load variance decreased by 28.83%, and the dissatisfaction of EV owners increased by 0.1591. According to the fuzzy membership function, the proposed strategy has the highest comprehensive satisfaction, which indicates that it comprehensively considers the interests of both sides, and truly achieves a win-win situation.
TABLE 3
| Scheduling strategy | Scheduling cost(RMB) | Dissatisfaction of EV owners | Load variance() | Comprehensive satisfaction |
|---|---|---|---|---|
| 1 | 5,517.66 | 1 | 5,273 | 0.501 |
| 2 | 7,212.41 | 0.0876 | 9,149 | 0.412 |
| 3 | 6,103.24 | 0.2467 | 6,511 | 0.659 |
Index comparison under different strategies.
6.2.2 Verification of the vehicle to grid load feedback correction layer
Make 20% of category ① EVs temporarily change their plans and leave at 8:00. Compare with the circumstances without V2G load feedback correction layer. As shown in Figures 8, 9, the revised V2G equivalent load shifts the load from the period of higher electricity price to the lower period. The total operating cost with feedback correction is 5,858.2 RMB, which is 4.19% lower than that of 6,114.3 RMB without feedback correction.
FIGURE 8

Comparison of V2G equivalent load before and after running V2G load feedback correction layer.
FIGURE 9

Hourly cost change of MPC rolling optimization layer.
In order to further verify the effect of V2G load feedback correction layer on the tracking situation of tie-line planned value, 12 EVs are charged urgently during 10:00–2:00 and 18:00–19:00. It can be seen from Figures 10A,B that the strategy with feedback correction adjusts the tie-line planned value in the scheduling process, ensuring the economic and stable operation of the system after temporarily changes of EVs’ travel plan. Without feedback correction, the power relative tracking deviation of tie-line planned value is 8.82%, while the relative deviation with feedback correction is only 1.33%.
FIGURE 10

Tie-line power tracking situation. (A) Tie-line power tracking situation without feedback correction. (B) Tie-line power tracking situation after feedback correction.
6.2.3 The effect of the unplanned Electric vehicles’ proportion on scheduling results
As shown in Figure 11A, with the increase of the proportion of unplanned EVs, the deviation of original EV charging and discharging plan relative to the optimal plan in the actual situation is farther, and the economic benefit of the system operation after V2G load feedback correction is more obvious, so the relative cost change will greatly increase.
FIGURE 11

Influence of unplanned EV ratio on Scheduling Results. (A) Relationship between unplanned EV proportion and operating cost. (B) Relationship between unplanned EV proportion and relative deviation of tie-line power.
As shown in Figure 11B, the increase in the proportion of unplanned EVs will lead to the increase of source-load unbalanced power when operating according to the original plan. At this time, in the second stage of MPC rolling optimization layer, the output of other distributed generators is preferentially adjusted to balance the power deviation. However, when the unbalanced power is too high, the tie-line power has to be changed to maintain the source-load balance relationship. Therefore, with the increase of unplanned EVs’ proportion, the relative tracking deviation of tie-line planned value without feedback correction increases greatly, while the relative tracking deviation with feedback correction is basically unchanged.
7 Conclusion
Aiming at the adverse effects of the temporary change of EVs’ travel plan on the economic operation of the system and the tracking situation of tie-line planned value, this paper proposes a multi-layer coordinated optimization strategy of ETH-IES with EVs, which includes the feedback correction of V2G load. Taking an electric-thermal-hydrogen integrated energy industrial park as an example for research and analysis. The main conclusions are as follows:
1) The constructed multi-objective EV charging and discharging management model and two-stage MPC rolling optimization model can achieve accurate and win-win optimal scheduling.
2) Based on the two-layer optimization of EVs and ETH-IES, V2G load feedback correction is introduced. This can eliminate the adverse effect of EV unplanned behaviors, which improves the system economy and improves the tracking situation of tie-line planned value.
3) The coupled Monte Carlo simulation and multi-objective improved sparrow search algorithm can efficiently solve the proposed multi-objective optimal scheduling model with uncertain parameters.
4) The effectiveness of V2G load feedback correction is verified. In addition, as the proportion of unplanned EVs increases, the economic benefit is more obvious and the relative tracking deviation of tie-line planned value is basically unchanged.
Statements
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This work is supported by Shaanxi Key R&D Project (No. 2019ZDLGY18-06.) and State Grid Shaanxi Electric Power Company Sci&Tech Project (No. B626KY190001). The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.
Conflict of interest
The authors declare that this study received funding from State Grid Shaanxi Electric Power Company. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Nomenclature
charge transfer coefficient
protons exchanged per mole of reactant
Faraday constant
power consumption of electrolyzer at time t
power consumption coefficient of hydrogen production
hydrogen production of electrolyzer at time t
hydrogen stored at time t
hydrogen stored and released at time t-1
Avogadro constant
- K
Kelvin temperature
state of hydrogen charge of storage device at time t
volume of hydrogen storage tank
- a, b
proportional coefficients
rated pressure of hydrogen storage device
battery replacement cost
charge and discharge efficiency coefficient
actual full capacity of the battery
load power value
average load power
the variance of load curve
total number of EVs
minimum and maximum affordable EV degradation costs when signing the agreement
real-time electricity price
V2G equivalent load
dissatisfaction of EV owners participating in V2G mechanism
the EV’s charging and discharging signs
the EV’s charging and discharging power
fuel consumption factor
fuel cost factor of micro gas turbine
total number of Monte Carlo simulation scenarios
start-up cost of micro gas turbine
micro gas turbine’s start-stop state
unit pollution gas control cost
pollution gas emission
electrolyzer’s output power
power of the electrolyzer and its upper and lower limits
upper and lower limits of the climbing rate of the electrolyzer
rated capacity of thermal storage device
PEMFC’s output power
thermal storage device’s output power
maximum charging and discharging power of thermal storage device
thermal load power
maximum change range of battery SOC change after a scheduling cycle
status of purchasing and selling
MT’s maximum rising rate and falling rate
start-stop state of micro gas turbine at time t-k+1
minimum start time and stop time
battery charge and discharge status
allowable range of battery SOC in operation
battery’s maximum charging and discharging power
status of hydrogen storage equipment
maximum storage and discharge volume of hydrogen
rated capacity of hydrogen storage equipment
minimum and maximum capacity factor of thermal storage device
References
1
AlirezaA.DavoudS.MostafaS. (2021). Two-stage stochastic operation considering day-ahead and real-time scheduling of microgrids with high renewable energy sources and electric vehicles based on multi-layer energy management system. Electr. Power Syst. Res.201, 107527. 10.1016/j.epsr.2021.107527CrossRef Full Text | Google Scholar
2
ChenM.GaoJ.ChangG.BaiF. (2020). Research on orderly charging strategy of micro-grid electric vehicles in V2G model. Power Syst. Prot. Control48, 08.141–148. 10.19783/j.cnki.pspc.190697CrossRef Full Text | Google Scholar
3
ChengH.HuX.WangL.LiuY.YuQ. (2019). Review on research of regional integrated energy system planning. Automation Electr. Power Syst.43, 72–13. Google Scholar
4
ChengS.WangY.LiaoW.ZuoX.DaiJ. (2022). Bi-level multi-objective optimization of a new energy microgrid with electric vehicles. Power Syst. Prot. Control50, 1263–1271. 10.19783/j.cnki.pspc.211149CrossRef Full Text | Google Scholar
5
ChengS.WeiZ.ZhaoZ. (2021). Decentralized scheduling optimization for charging‐storage station considering multiple spatial‐temporal transfer factors of electric vehicles. Int. J. Energy Res.45 (5), 6800–6815. 10.1002/er.6272CrossRef Full Text | Google Scholar
6
ColleenS. (2008). PEM fuel cell modeling and simulation using matlab. Academic Press. 9780123742599. Page ix. 10.1016/B978-012374259-9.50001-XCrossRef Full Text | Google Scholar
7
DingT.MuC.BieZ.DuP.FanZ.ZouZ.et al (2018). Review of energy Internet and its operation. Proc. CSEE38 (15), 4318–4328. Google Scholar
8
HouH.XueM.ChenG.TangJ.XuT.LiuP. (2019). Multi-objective hierarchical economic dispatch for microgrid considering charging and discharging of electric vehicles. Automation Electr. Power Syst.43, 1755–1762. Google Scholar
9
HuJ.ZhouH. R.LiY. (2019). Real-time dispatching strategy for aggregated electric vehicles to smooth power fluctuation of photovoltaics. Power Syst. Technol.43 (7), 2552–2560. Google Scholar
10
HuZ.ZhanK.XuZ.XiangD.ZhangH. (2015). Analysis and outlook on the key problems of electric vehicle and power grid interaction. Electr. Power Constr.36, 76–13. Google Scholar
11
HuangW.HuangT.ZhouH.WangG.CuiY. (2014). Dynamic economical dispatch for microgrid based on improved differential evolution algorithm. Automation Electr. Power Syst.38 (9), 211–217. Google Scholar
12
JiaS.KangX.CuiJ.TianB.XiaoS. (2022). Hierarchical stochastic optimal scheduling of electric thermal hydrogen integrated energy system considering electric vehicles. Energies15, 5509. 10.3390/en15155509CrossRef Full Text | Google Scholar
13
JiaS.KangX. (2022). Multi-objective optimal scheduling of CHP microgrid considering conditional value-at-risk. Energies15, 3394. 10.3390/en15093394CrossRef Full Text | Google Scholar
14
JoziF.AbdaliA.MazlumiK.HosseiniS. H. (2022). Reliability improvement of the Smart distribution grid incorporating EVs and BESS via optimal charging and discharging process scheduling. Front. Energy Res.10, 920343. 10.3389/fenrg.2022.920343CrossRef Full Text | Google Scholar
15
JuC.WangP.GoelL.XuY. (2018). A two-layer energy management system for microgrids with hybrid energy storage considering degradation costs. IEEE Trans. Smart Grid9, 66047–66057. 10.1109/TSG.2017.2703126CrossRef Full Text | Google Scholar
16
LiJ.WuL.ZhangH.WangW.JiaR. (2021). Economic dispatch of CCHP microgrid based on sorting cross optimization algorithm. Power Syst. Prot. control49, 18137–18145. 10.19783/j.cnki.pspc.201556CrossRef Full Text | Google Scholar
17
LiK.ShaoC.WangY.YanS.ZhouQ.WangX.et al (2022). Urban integrated energy system planning considering electric-gas-traffic coupling. J. Electr. Eng. China, 1–10. Google Scholar
18
LiY.YangZ.LiG.ZhaoD.TianW. (2019). Optimal scheduling of an isolated microgrid with battery storage considering load and renewable generation uncertainties. IEEE Trans. Ind. Electron.66 (2), 1565–1575. 10.1109/TIE.2018.2840498CrossRef Full Text | Google Scholar
19
LvT.AiQ.ZhaoY. (2016). A bi-level multi-objective optimal operation of grid-connected microgrids. Electr. power Syst. Res.131, 60–70. 10.1016/j.epsr.2015.09.018CrossRef Full Text | Google Scholar
20
QiZ. Y.LiX. W.ZhangR. Y.WangQ.WangJ. W. (2022). Coordinated optimal scheduling of stand-alone micro-grid based on dynamic feedback correction. High. Volt. Eng.48 (03), 938–947. 10.13336/j.1003-6520.hve.20210263CrossRef Full Text | Google Scholar
21
SmithK.EarleywineM.WoodE.PesaranA. K. (2012). Battery wear from disparate duty-cycles: Opportunities for electric-drive vehicle battery health management. The 2012 American Control Conference. Google Scholar
22
TangX.HuY.GengQ.XuX. (2021). Multi-time-scale optimal scheduling of integrated energy system considering multi-energy flexibility. Automation Electr. Power Syst.45, 0481–0490. Google Scholar
23
VetterJ.NovákP.WagnerM. R.VeitC.MöllerK. C.BesenhardJ. O.et al (2005). Ageing mechanisms in lithium-ion batteries. J. Power Sources147 (1–2), 269–281. 10.1016/j.jpowsour.2005.01.006CrossRef Full Text | Google Scholar
24
WangJ.WangL.GuoY.SunY.GuanC. (2016). Microgrid economic dispatch method considering electric vehicles. Power Syst. Prot. Control44, 17111–17117. Google Scholar
25
WangL.ZhouJ.ZhuL.WangL.YinC.CongH. (2021). Multi-time-scale optimization scheduling of integrated energy system based on distributed model predictive control. Automation Electr. Power Syst.45, 1357–1365. Google Scholar
26
WangX.GuoQ.SunH.GeH.XinS.ZhangY.et al (2015). Distributed voltage stability assessment and control considering electric vehicle charging and discharging load. Power Syst. Prot. Control43, 1643–1648. Google Scholar
27
WangY.DongW.YangQ. (2022). Multi-stage optimal energy management of multi-energy microgrid in deregulated electricity markets. Appl. Energy301, 118528. 10.1016/j.apenergy.2022.118528CrossRef Full Text | Google Scholar
28
XiaoH.PeiW.KongL. (2016). Multi-time scale coordinated optimal dispatch of microgrid based on model predictive control. Automation Electr. Power Syst.40, 18.7–14+55. Google Scholar
29
XuY.ZhangR.DongZ.ZhangR.WongK. P. (2015). Optimal placement of static compensators for multi-objective voltage stability enhancement of power systems. IET Gener. Transm. &. Distrib.9 (15), 2144–2151. 10.1049/iet-gtd.2015.0070CrossRef Full Text | Google Scholar
30
XueJ.ShenB. (2020). A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng.8, 122–134. 10.1080/21642583.2019.1708830CrossRef Full Text | Google Scholar
31
YangJ.ZhangN.WangY.KangC. (2018). Multi-energy system towards renewable energy accommodation: Review and prospect. Automation Electr. Power Syst.42 (4), 11–24. Google Scholar
32
YinS.ZhangP.YangM.BaiH.YangQ. (2020). bMulti-time scale optimal scheduling of integrated energy system considering demand-side response. Proc. CSU-EPSA32, 1135–1142. 10.19635/j.cnki.csu-epsa.000435CrossRef Full Text | Google Scholar
33
ZhangY.ZhangT.MengF.WangY.LiuY. (2017). Model predictive control based distributed optimization and scheduling approach for the energy internet. Proc. CSEE37, 236829–236845+7074. Google Scholar
34
ZhaoX.WangS.WuX.LiuJ. (2016). Coordinated control strategy research of micro-grid including distributed generations and electric vehicles. Power Syst. Technol.40, 123732–123740. Google Scholar
35
ZhouJ.WuY.DongH.HeJ.XuC.GaoJ. (2021). Optimization planning of wind-photo-hydrogen integrated energy system considering random charging of electric vehicles. Power Syst. autom.45, 2430–2440. Google Scholar
Summary
Keywords
electric vehicle, V2G, electric-thermal-hydrogen integrated energy system, multilayer coordinated optimization, sparrow search algorithm
Citation
Jia S, Kang X, Cui J, Tian B, Zhang J and Xiao S (2022) Multi-layer coordinated optimization of integrated energy system with electric vehicles based on feedback correction. Front. Energy Res. 10:1008042. doi: 10.3389/fenrg.2022.1008042
Received
31 July 2022
Accepted
24 August 2022
Published
15 September 2022
Volume
10 - 2022
Edited by
Mohamed A. Mohamed, Minia University, Egypt
Reviewed by
Hong Tan, China Three Gorges University, China
Hassan Farh, Hong Kong Polytechnic University, Hong Kong SAR, China
Updates
Copyright
© 2022 Jia, Kang, Cui, Tian, Zhang and Xiao.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Shiduo Jia, jiashiduo@stu.xjtu.edu.cn; Xiaoning Kang, kangxn@mail.xjtu.edu.cn
This article was submitted to Smart Grids, a section of the journal Frontiers in Energy Research
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.