- 1School of Information and Control Engineering, Liaoning Petrochemical University, Fushun, Liaoning, China
- 2College of Economics and Management, Shenyang Agricultural University, Shenyang, Liaoning, China
In the construction of smart microgrids for petrochemical enterprises, the generating unit is an important part, and the rolling bearings are one of the key components of the generator. The condition of the rolling bearing directly affects the safe operation of the entire generating unit and an accurate fault diagnosis of the bearing not only can improve the stability of the smart microgrid, but also can reduce the risk of loss of the factory. This study proposes an improved fault diagnosis method based on variational modal decomposition (VMD) and a convolutional neural network (CNN). The VMD algorithm was used to remove random noise in the original signal and a CNN was used to extract useful data from the vibration signal processed by VMD. Since the modal number and penalty parameter of the VMD are difficult to choose and they have a profound impact on the decomposition results, differential evolution (DE) was used as the optimization method and envelope entropy was used as the fitness function to optimize the VMD parameters. Since it is difficult to ensure the best fit of the hyper-parameters of CNN, this study proposes a method for using the DE algorithm to obtain suitable hyper-parameters for the CNN, and then used the CNN to diagnose a fault. The test results using the vibration data of Case Western Reserve University show that the combination of VMD and CNN can improve the convergence speed more than 10% and the accuracy to over 99.6%.
1 Introduction
In recent years, with the continuous development of industry, more and more large petrochemical enterprises are opting for the construction of a smart microgrid. A smart microgrid owned by the company has a great advantage in guaranteeing production. As the foundation of a smart microgrid, the operation status of the alternator has an important impact on its safe and stable operation (Song et al., 2021). The rolling bearings are the main components of the alternator and have a higher risk of damage because of their continuous, long term, high-speed operation (Lei, 2015). Therefore, an effective fault diagnosis method is needed not only to maintain the bearings in a healthy condition, but also to probe the fault patterns (Hu et al., 2020). Research on fault monitoring and diagnosis of alternator problems has attracted widespread attention from the industry (Liu et al., 2022).
At present, the fault diagnosis methods for bearings are mainly divided into three steps, data processing, feature extraction, and fault identification. Vibration signals usually contain a large number of redundant features, which makes it difficult to extract and identify the fault features. In view of this situation, Liu et al. (2006) proposed empirical mode decomposition (EMD) and applied it to nonlinear and non-stationary signals; but the errors gradually accumulated during decomposition, resulting in modal aliasing and endpoint effects (Wu and Huang, 2009). Dragomiretskiy and Zosso (2014) proposed variational mode decomposition (VMD), which can decompose the signal into FM and AM signals, and solve the problem of modal aliasing and end point effects. However, its decomposition parameters need to be set according to the characteristics of the signal, and improper parameter selection will lead to over-decomposition or under-decomposition. Liu (2022) tested a genetic mutation particle-swarm optimization algorithm to optimize the parameters of VMD, and proposed sample entropy as the feature to apply to bearing fault diagnosis. VMD has the advantage of eliminating the noise of the non-stationary vibration signal of bearings by decomposing signals, but how to obtain the optimal parameters for VMD efficiently still needs more research. Since differential evolution (DE) has the advantage of few parameters and strong optimization ability, this study used DE to optimize the parameters of VMD.
Feature extraction and fault identification in fault diagnosis methods are mainly divided into two categories: Traditional fault classification methods and deep learning methods (Peng, 2022). Traditional fault classification methods include artificial neural network, k-means, and SVM (Zhou et al., 2020). Zhang et al. (2016) used a genetic algorithm and a fuzzy c-means clustering algorithm to optimize a BP network, providing a reference for real-time diagnosis. Wang and Du (2020) proposed an improved k-means method by using a new sparse representation of singular value decomposition. However, the performance of these methods mainly depends on the quality of feature extraction, and due to the complex environment in which the bearings operate, it is difficult to extract effective features from vibration signals (Huang et al., 2020). Nowadays people commonly use machine learning and deep learning to solve fault diagnosis problems. Guo et al. (2020) used machine learning (ML) technology and statistical features extracted from time domain vibration signals and spectral peaks to achieve automatic diagnosis of rolling bearings.
Recently, more and more researchers have been paying attention to deep learning algorithms as they help in the discovery of complex structures in big data. Li et al. (2018) proposed a fault diagnosis method combining short-time Fourier transform and a convolutional neural network (CNN). The time frequency domain information are considered at the same time and take the advantage of the self-adaptive extraction of fault features by a CNN, realizing end-to-end fault diagnosis. Pan et al. (2018) proposed a new structure by combining one-dimensional CNN and LSTM, in which the average accuracy rate in the testing dataset for bearing faults reached more than 99%.
Although deep learning algorithms have a great advantage in feature extraction, it is difficult to choose the most appropriate hyper-parameters (Hui, 2021). Hence, this study proposes improving the fault diagnosis method by taking advantage of DE and CNNs by combining DE and a one-dimensional CNN into one structure. By using this method, the limitations of traditional hyper-parameter selection can be eliminated since DE can be used and no traditional feature extraction is needed because the CNN can extract features from raw data.
This study includes the following contents: Section 1 briefly introduces the proposed method, which uses VMD, DE and a one dimensional CNN. Section 2 introduces the datasets for bearing fault diagnosis. Section 3 shows the effectiveness of the proposed method and a comparison with other models. Section 4 draws conclusion.
2 Methods
2.1 The novel fault diagnosis method
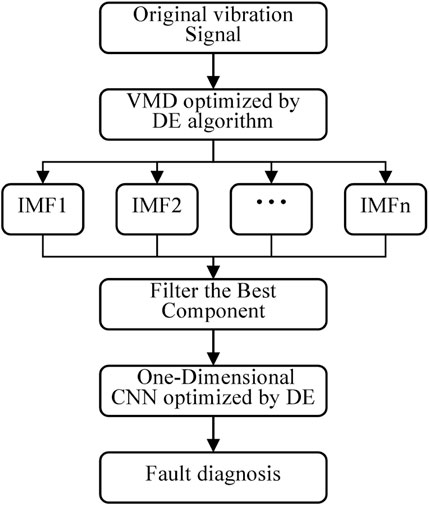
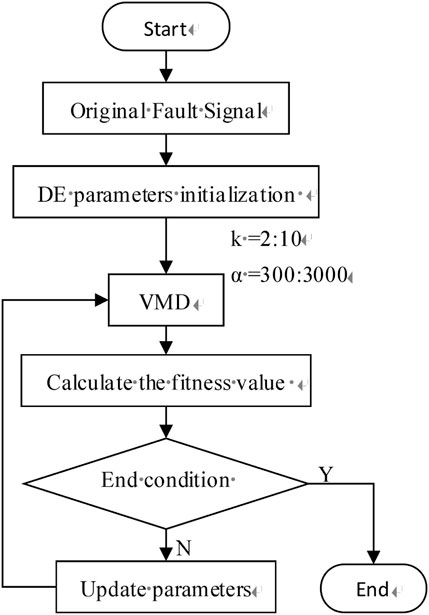
The structure of the proposed method is shown in Figure 1.
The specific steps of the fault diagnosis method of this study are described below:
Step 1. The original vibration signal datasets are divided into two parts: training datasets and testing datasets.
Step 2. The VMD optimized by DE is used to decompose both training datasets and testing datasets into IMFs.
To optimize the parameters, the concept of envelope entropy which was proposed by Tang and Wang (2015) was adopted as the evaluation standard of decomposition effect of the VMD method, and the envelope entropy Ep of time signal x(t) with length N is defined as:
where a(j) is the envelope signal after the Hilbert demodulation of x(j), and pj is the result of normalization of a(j).
Step 3. The training datasets and testing datasets are decomposed by VMD, which has been optimized by DE, and then the best components are selected by envelope entropy to constitute the new training datasets and testing datasets.
Step 4. DE is used to optimize the parameters of the CNN, and then the optimized one-dimensional CNN is trained using the new training datasets.
Step 5. The testing datasets are used to verify the effectiveness of the fault diagnosis model.
2.2 The VMD method
In the procedure of data processing, the VMD algorithm is used to decompose the original signal into intrinsic mode functions. The corresponding constrained model is described as follows:
where uk(t) is the modal component of the original signal, and wk is the center frequency of the components.
In order to find the optimal solution of the above problem, the secondary punishment factor α and the Lagrangian operator λ(t) were used.
The saddle point of the above augmented Lagrange function is obtained by using the alternating direction multiplier algorithm, which is the minimum of the constrained variational model of equation (4). As a result, the original signal is decomposed into k narrow-band IMF components.
The specific implementation process is as follows:
1) Initialize {
2) n = n+1, execute the whole cycle;
3) Execute the first inner loop and update uk according to
4) k = k + 1, repeat step (3) until k = K, and end the first cycle of the layer;
5) Execute the second inner loop and update wk according to
6) k = k + 1, repeat step (5) until k = K, and end the second cycle of the layer;
7) Update λ According to
8) Repeat steps (2) to (7) until the iteration stop condition
As described, there are four parameters of the VMD that have to be obtained before decomposition. The first one is the number of modal components K, and the second one is the quadratic penalty factor. These two parameters have a large impact on the decomposition results, and the last two parameters, namely noise tolerance and convergence error, have less influence on the decomposition results. The default value is usually used when the VMD is used, because the selection of the modal component K and the quadratic penalty factor seriously affect the VMD decomposition. If choose improperly, there will be over-decomposition or under-decomposition; the decomposition results will not meet the requirements.
2.3 The DE method
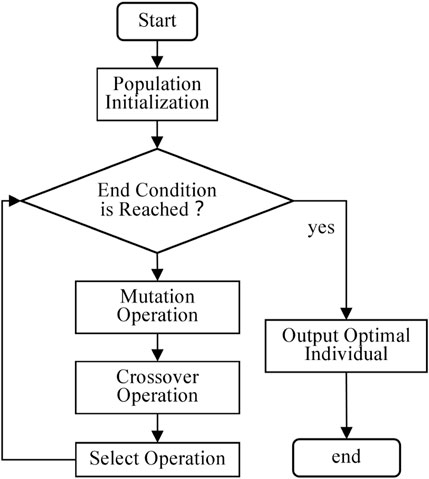
The DE algorithm is one of the intelligent optimization algorithms. It is a heuristic search algorithm based on population. Each individual in the population represents a solution vector and has many advantages in the settlement of large-scale optimization problems, such as a simple algorithm structure, ease of performance, high-level optimization, simple parameter setting, and excellent robustness. The DE algorithm has several steps which is shown in Figure 2.
Firstly, initialize population:
where
Secondly, the mutation operation is given by:
where Vi,g is one of the mutation individuals, Xr0,g, Xr1,g and Xr2,g are one of the generation, and they are different from each other and selected from the parent generation randomly. F is a scaling factor, which is a random number between 0 and 2.
Thirdly, the crossover operation is described by:
where Uj,i,g is the crossover vector and Cr is the crossover operator. The greater the Cr, the greater the likelihood of crossover. If rand(0,1)≤Cr or j = jrand, the crossover vector is the same as the mutation vector, and if rand(0,1)>Cr or j≠jrand, the crossover vector is the same as the original vector.
Fourthly, the select operation:
The DE algorithm uses an aggressive strategy to select individuals entering the next generation population:
where Xi,g+1 is the next generation, Ui,g is obtained by a crossover operation, Xi,g is the current generation, and f represents the fitness function.
When the final solution meets the conditions or the number of iterations reaches the maximum, it ends. Otherwise, repeat the above steps.
2.4 The one-dimensional convolutional neural network (CNN) method
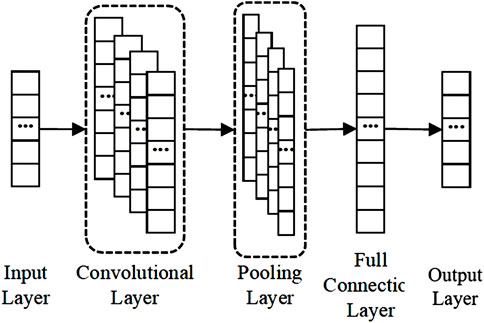
The CNN algorithm is one of the deep learning algorithms. It has several advantages such as reducing model complexity, avoiding complex feature extraction processes, and reducing the number of weights. The purpose of using the DE algorithm in this study is to set the hyper-parameters with the best fit for the CNN algorithm and achieve the goals of improving accuracy and convergence rate. In this study, a one-dimensional convolutional neural network was used to solve the bearing fault diagnosis as the vibration data is one dimension. The CNN was divided into three layers, the convolution layer, the pooling layer, and the full connection layer which is shown in Figure 3.
The convolution layer in this study was used to extract the features from the raw data. Multiple convolution kernels were used for the convolution operation with the input data, and the activation function was used to enhance linear separability and then obtain the characteristic matrix:
where yi,j,k presents the output of the convolutional layer, f presents the activation function, xi,k presents the input signal, * presents the convolution operation, wj,i presents weight, and bi presents bias.
The pooling layer in this study was used to compress the feature vectors. It can not only make the feature vectors smaller and network computing complexity simpler, but can also extract the main features. The pooling operation is divided into the maximum pooling and the average pooling; this study uses the average-pooling mode:
where l is the length of the pooling area.
The full connection layer in this study is used for mapping the learned feature representation to the sample tag space. In this study, the dropout layer is used before the full connection layer to ignore some neurons according to certain probability and then avoid over fitting during model training.
Although the CNN has a great advantage in feature extraction, it is hard to set the best hyper-parameters. The fitness hyper-parameters not only can increase the convergence speed, but can also improve the accuracy rate of the model.
3 Data
To verify the effectiveness of the proposed method, the training datasets and the testing datasets were obtained from the Case Western Reserve University; the test bench consisted of four parts: a 2 hp motor, a torque sensor, a power tester and an electronic controller.
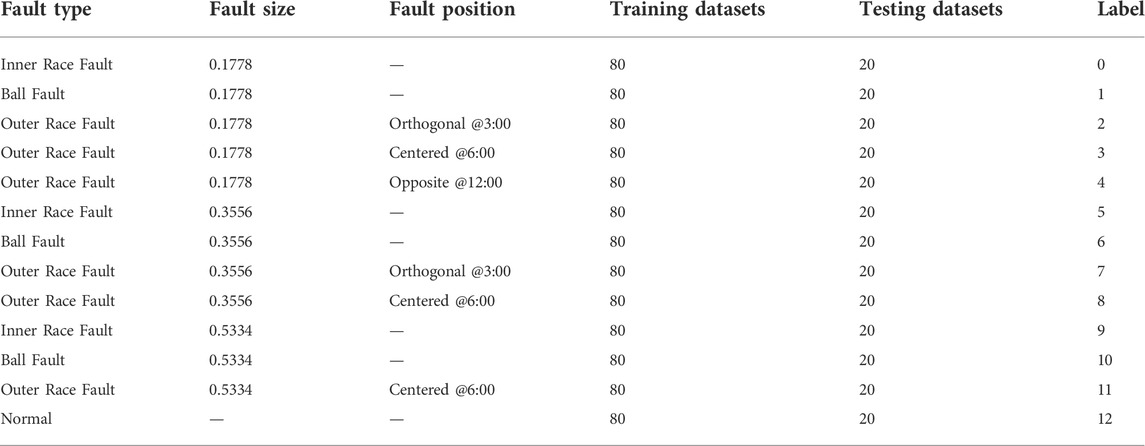
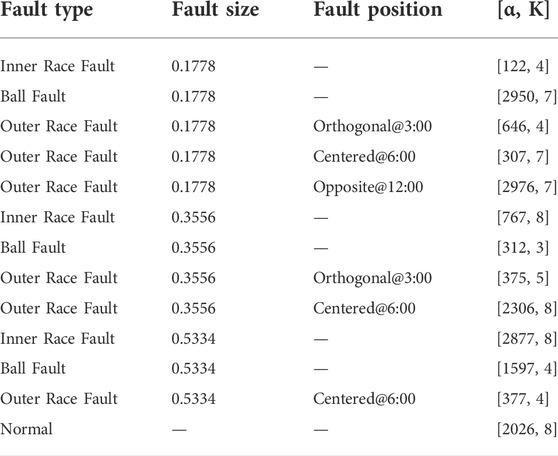
The datasets used in this study were obtained from the fan end. The model of the fan end bearing was skf6203, the type of the dataset was the fan end accelerometer data, the sampling frequency was 12 kHz, and the rotating speed of the shaft was 1797 r/min. In this study, there are 13 types used to test the proposed algorithm, including 12 fault types and one normal type. The 12 fault types include different fault sizes: 0.1778, 0.3556, 0.5334 mm, and different fault positions: orthogonal @3:00, centered @6:00 and opposite @12:00. Each dataset stands for a state of bearing health status and includes 100 samples, from which 80 samples were chosen randomly as the training datasets; the remaining 20 samples were applied to the test datasets, and the scale of each simple was 1,024 which is shown in Table 1.
4 Results
4.1 The VMD optimized by the DE algorithm
In order to select the one that contains the most features, the VMD method was used to decompose the vibration signals of bearings. To achieve the best decomposition effect, the modal number and the penalty parameter of the VMD needed to be optimized. In this study, the DE algorithm was used as the optimization algorithm of the VMD. The DE parameters were set as shown in Table 2. Gmax is the maximum evolution algebra, NP is the population size, D represents solution space size, which included the modal number and penalty parameter of the VMD, F is the mutation operator and Cr is the crossover operator. The algorithm flow is as Figure 4:
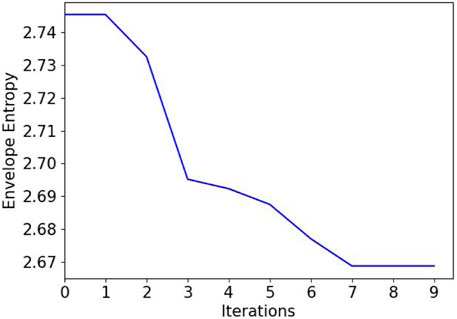
The envelope entropy was used as the fitness function of the DE algorithm. The smaller the envelope entropy value, the better the decomposition result. Figure 5 shows once the envelope entropy changes with the evolutionary algebra.
For vibration signals from the 13 states, the best parameter combinations [α, K] are shown in Table 3, which were searched by the DE algorithm.
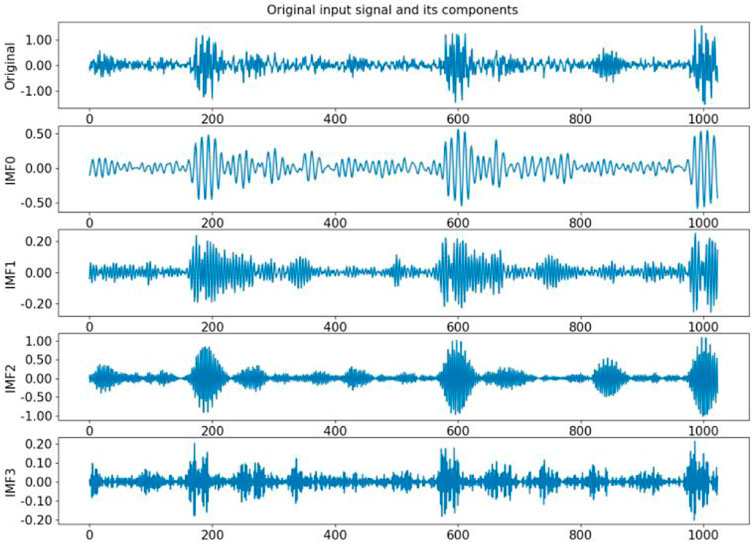
Because of limited space, this study introduces only the signal decomposition of the inner race fault. The fault size is 0.1778 mm and the best parameter combination optimized by the DE was [122, 4]. Figures 6, 7 shows the original signals and the IMFs decomposed by VND of the inner race fault.
The more noise the IMF component contains, the less obvious the periodic impact characteristics related to the faults, and the weaker the sparsity of the IMF component signal; and, as a result, the envelope entropy is large. On the contrary, the more fault characteristic information the IMF component contains, and the more regular shock pulses in the waveform, the stronger the sparse characteristics and as a result, the smaller the envelope entropy.
After calculating the envelope entropy value of each component, the IMF2 had the smallest value, and it was selected as the input signal of the CNN to train the model.
4.2 The CNN optimized by the DE algorithm
In order to select the most fitness hyper-parameters of the CNN, the DE algorithm was used as the optimized function, and the parameters of DE are shown in Table 4.
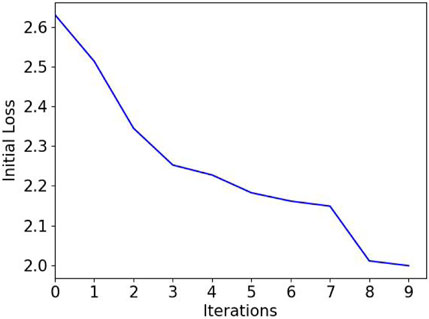
The D is 5, namely convolution kernel number, convolution kernel size, pooling size, dropout rate and batch size; the other parameters were the same as for the DE of the VMD. The individual solutions were generated randomly. The convolution kernel number was a random integer from 10 to 100, the convolution kernel size was a random integer from 10 to 100, the pooling size was a random integer from 10 to 100, the dropout rate ws random float from 0.1 to 0.5, the batch size was random integer from 10 to 100, and the fitness function in the DE was the initial loss of the CNN when the epoch is one. Figure 8 shows the loss changes with the evolutionary algebra.
After the DE, the hyper-parameters of the CNN were selected and shown in Table 5.
The IMFs decomposed by the VMD from vibration signals with 1,024 points were applied as the inputs of the CNN. The other parameters of the CNN were selected by experience. The stride of the pooling layer was 3, the epoch of the CNN was 40, the output channel was 13, the activation was relu, the classifier was softmax, and the optimizer was adam. In order to increase the convergent speed, this study used self-adaption learning to update the weight matrix in the back propagation network. The initial learning rate was 0.01, and it was reduce by half for every ten increases in epoch.
This proposed method was developed in Python and programmed with an open source tool (tensorflow).
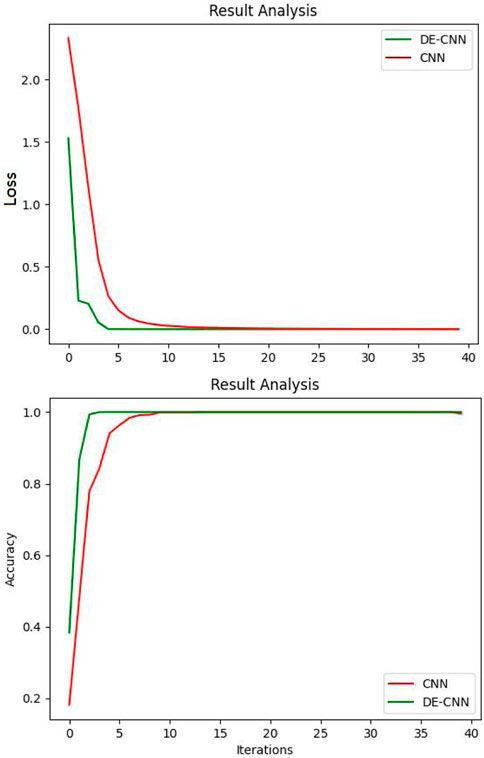
To verify the efficiency of the proposed model, this study made the comparison between the CNN and the DE-CNN, and the results show that the DE-CNN method had fewer iterative times and a faster convergent speed in the training datasets. At the same time, compared to the CNN model, the DE-CNN model had a higher accuracy rate in the training dataset which is shown in Figure 9.
The results of the comparison are shown as Table 6, together with comparisons of the other methods using the same testing.
5 Conclusion
A healthy running state is very important for the bearings in a generator unit in a smart microgrid. Thus, it is necessary to diagnose any faults immediately. In traditional methods for bearing fault diagnosis, the first step is feature extraction, and the result of extracting features largely determines the quality of the algorithm; but the noise of the original signal makes it harder to extract features. The deep learning algorithms have advantages in feature extraction, but overcoming the problem of noise increases the difficulty of feature extraction and choosing the most appropriate hyper-parameters of deep learning algorithms is still difficult. This study proposes a method combining DE and VMD to reduce the noise of the original signals, which not only uses a CNN to extract features from original data directly for fault diagnosis, but also can get the most fitness hyper-parameters of the CNN. The results showed that the average accuracy rate in the testing dataset was over 99.6%, and the convergence speed increased by more than 10%. However, the proposed methods have limitations. The process of determining fitness parameters of the VMD and the CNN using the DE requires a lot of calculation, and one must not be overly optimistic of the outcome. Future research will focus on the improvement of the DE algorithm and promote application of the proposed methods in other fields.
Data availability statement
Publicly available datasets were analyzed in this study. This data can be found here: https://github.com/yyxyz/CaseWesternReserveUniversityData.
Author contributions
YC: conceptualization, methodology, software, investigation, formal analysis, writing—original draft; XC: funding acquisition, validation, writing—original draft; QZ: data curation, visualization, investigation, writing—review and editing
Acknowledgments
The authors would like to thank the great support by the National Natural Science Foundation of China (Grant 71902121), Scientific Research Project of Educational Department of Liaoning Province (Grant L2020031), and Key Research and Development Project of Liaoning Province (Grant 2020JH2/10300040).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Dragomiretskiy, K., and Zosso, D. (2014). Variational mode decomposition. IEEE Trans. Signal Process. 62 (3), 531–544. doi:10.1109/tsp.2013.2288675
Guo, J. F., Liu, X. Y., Li, S. X., and Wang, Z. (2020). Bearing intelligent fault diagnosis based on wavelet transform and convolutional neural network. intelligent fault diagnosis based wavelet transform convolutional neural Netw. Shock Vib. 2020, 1–14. doi:10.1155/2020/6380486
Hu, Z. X., Wang, Yan, Ge, Ming Feng, and Liu, Jie (2020). Data-driven fault diagnosis method based on compressed sensing and improved multiscale network. IEEE Trans. Ind. Electron. 67 (4), 3216–3225. doi:10.1109/tie.2019.2912763
Huang, HaiRun, Li, Ke, Su, WenSheng, Bai, JianYi, Xue, ZhiGang, Zhou, Lang, et al. (2020). An improved empirical wavelet transform method for rolling bearing fault diagnosis. Sci. China Technol. Sci. 63 (11), 2231–2240. doi:10.1007/s11431-019-1522-1
Hui, Li (2021). CNN hyper-parameters optimization method based on the change ratio of relative probability[J]. J. Shanghai Univ. Technol. 43 (03), 219–226. doi:10.13255/j.cnki.jusst.20201023001
Lei, Y. G. (2015). A deep learning-based method for machinery health monitoring with big data. J. Mech. Eng. 51, 49–56. doi:10.3901/jme.2015.21.049
Li, Heng, Zhang, Qin, Qin, Xianrong, and Sun, Yuantao (2018). Fault diagnosis method for rolling bearings based on short-time Fourier transform and convolution neural network. J. Vib. Shock 37 (19), 124–131. doi:10.13465/j.cnki.jvs.2018.19.020
Liu, B., Riemenschneider, S., and Xu, Y. (2006). Gearbox fault diagnosis using empirical mode decomposition and Hilbert spectrum. Mech. Syst. Signal Process. 20 (3), 718–734. doi:10.1016/j.ymssp.2005.02.003
Liu, Jianchang (2022). Rolling bearing fault diagnosis based on parameter optimization VMD and sample entropy[J]. J. automation 48 (03), 808–819.
Liu, Shaowei, Jiang, Hongkai, Wu, Zhenghong, and Li, Xingqiu (2022). Data synthesis using deep feature Enhanc. generative adversarial Netw. Roll. Bear. imbalanced fault diagnosisMechanical Syst. Signal Process. 163, 108139. doi:10.1016/j.ymssp.2021.108139
Pan, H., He, X., Tang, S., and Meng, F. (2018). An improved bearing fault diagnosis method using one-dimensional CNN and LSTM. Strojniški vestnik - J. Mech. Eng. 64, 443–452. doi:10.5545/sv-jme.2018.5249
Peng, Chen (2022). Overview of rolling bearing fault diagnosis methods based on vibration signals. Bearing (06), 1–6.
Song, C., Sun, Y., Han, G., and Rodrigues Joel, J. P. C. (2021). Intrusion detection based on hybrid classifiers for smart grid. Comput. Electr. Eng. 93, 107212. doi:10.1016/j.compeleceng.2021.107212
Tang, Guiji, and Wang, Xiaolong (2015). Parameter optimized variational mode decomposition method with application to incipient fault diagnosis of rolling bearing. J. Xi'an Jiaot. Univ. 49 (05), 73–81. doi:10.7652/xjtuxb201505012
Wang, Hongchao, and Du, Wenliao (2020). A new K-means singular value decomposition method based on self-adaptive matching pursuit and its application in fault diagnosis of rolling bearing weak fault. Int. J. Distributed Sens. Netw. 16 (5), 155014772092078. doi:10.1177/1550147720920781
Wu, Z. H., and Huang, N. E. (2009). Ensemble empirical mode decomposition: A noise -assisted data analysis method. Adv. Adapt. Data Anal. 1 (1), 1–41. doi:10.1142/s1793536909000047
Zhang, Kefei, Yuan, Fang, Jiang, Guo, and Wang, Guoping (2016). A novel neural network approach to transformer fault diagnosis based on momentum-embedded BP neural network optimized by genetic algorithm and fuzzy c-means. Arab. J. Sci. Eng. 41, 3451–3461. doi:10.1007/s13369-015-2001-6
Keywords: smart microgrid, fault diagnosis, VMD, CNN, De
Citation: Cao Y, Cheng X and Zhang Q (2022) An improved method for fault diagnosis of rolling bearings of power generation equipment in a smart microgrid. Front. Energy Res. 10:1006215. doi: 10.3389/fenrg.2022.1006215
Received: 29 July 2022; Accepted: 31 August 2022;
Published: 26 September 2022.
Edited by:
Peng Zeng, Shenyang Institute of Automation (CAS), ChinaCopyright © 2022 Cao, Cheng and Zhang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xu Cheng, eHVjaGVuZ0BzeWF1LmVkdS5jbg==
 Yu Cao1
Yu Cao1 Xu Cheng
Xu Cheng