Newtonian heating effect in pulsating magnetohydrodynamic nanofluid flow through a constricted channel: A numerical study

This article investigates the pulsatile flow of viscous incompressible MHD nanofluid in a rectangular channel. At the upper and lower walls, the channel has symmetrical constrictions. The goal is to analyze the heat transfer features of the nanofluid flow under the effect of the magnetic field and thermal radiation. Five different nanofluids, formed with nanoparticles of copper $\left(Cu\right)$, magnetite $\left(F{e}_3{O}_4\right)$, silver $\left(Ag\right)$, titanium oxide $\left(Ti{O}_2\right)$, and single wall carbon nanotube $\left(SWCNT\right)$ in the base fluid of water, are considered in the study. The unsteady governing equations are transformed using the vorticity-stream function approach. The solution is obtained using the finite difference technique (FDM). The effect of various flow controlling parameters on velocity, temperature, Nusselt, and skin-friction profiles is inspected by using graphs. Across the channel, graphs of vorticity, streamlines, and temperature distribution are also displayed. The thickness of the thermal boundary layer upsurges with escalating values of the magnetic field, radiation parameters, and solid volume fraction, whereas it declines with escalating values of the Strouhal and Prandtl numbers. The profiles are usually found to have a more regular pattern upstream of the constriction than that downstream of the constriction. At the throat of the constriction, the carbon nanotube-based nanofluid attains higher temperatures than the other nanofluids downstream of the constriction. However, in the lee of the constriction, silver-based nanofluid attains higher temperatures than the other nanofluids downstream of the constriction. The behavior, in most cases, is opposite upstream of the constriction. The findings of the study can be utilized to cure stenosis in blood vessels, design biomechanical devices, and employ flow pulsation to control industrial operations.

1 Introduction

Conventional heat transfer liquid sources are incapable of satisfying current cooling requirements largely due to their poor convective heat transfer coefficients. Researchers have demonstrated that nanoparticles (NPs) usually made of metals or oxides enhance the coefficients of heat convection and conduction in fluids, allowing for higher heat transfer rates for the coolants. Thus, the heat transfer and thermal system effectiveness can be improved significantly by mixing NPs in pure fluid, forming nanofluid (NF). NFs have promising applications in many areas of industry and biomedicine due to their enhanced thermal conductivity. The characteristic of improved thermal conductivity might serve as a major factor for performance improvement. As NFs can enhance heat transfer, heat exchangers can be designed to be both energy efficient and small.

Wang and Mujumdar (2008) investigated the convective heat transfer of NF flow (NFF). Saidur et al. (2011a), Saidur et al. (2011b), Mahian et al. (2013), and Kasaeian et al. (2015) worked to enhance the thermophysical properties as well as heat transfer capacity of the fluids using NPs. The study of these flows through stretching surfaces got motivation from the perspective of its application, particularly in plastic film drawing. Hence, several researchers paid a lot of attention to this issue and studied the movement of boundary layers over different forms of stretching surfaces. Akbar et al. (2014) used a homogeneous model to study NFF at stagnation point above a stretching plate with slip boundary conditions. Analysis of pulsatile flow in a constricted channel under the impact of magnetic field was presented by Bandyopadhyay and Layek (2011) and Bandyopadhyay and Layek (2012). Nasir et al. (2019) explained the Darcy–Forchheimer 2D thin-film fluid of NF. Mustafa et al. (2011) considered the NFF at the stagnation point above a stretching sheet. Wong and Leon (2010) reported that the thermophysical properties of fluids are improved significantly, even at moderate NP concentrations. Haq et al. (2016) investigated the fully developed flow of water-functionalized magnetite NPs among two parallel disks by taking water as the base fluid. The peristaltic flow of incompressible viscous fluid having metallic NPs was examined by Akbar (2014) via an irregular duct. Aly (2020) explained a non-homogeneous two-phase model for ${Al}_2{O}_3$–water NF-filled annulus used for the simulation of an incompressible smoothed particle hydrodynamic system (ISPH) between a wavelength rectangle and the square cavity. Two-dimensional $F{e}_3{O}_4$–water NF under the combined impact of Lorentz and Kelvin forces was inspected by Sheikholeslami et al. (2017a). Said et al. (2015) analyzed the influence of short suspended SWCNT thermophysical properties in water and enhanced the thermal productivity of a flat plate solar collector. Sheikholeslami and Ganji (2013) explained the $Cu$-$H_{2}O$ NFF between parallel plates. Yang et al. (2020) explained air purification with total heat recovery using NFs for the first time, demonstrating the synergistic application of NFs for heat, mass transfer, photocatalysis, and sterilization.

In the magnetohydrodynamic (MHD) flow, the magnetic area induces an electric current in a moving conductive fluid. The induced current causes force on conductive fluid ions. Natural convection under the impact of the magnetic field remained a topic of great interest because of its comprehensive applications in the design of liquid-metal cooling systems, accelerators, and pumps, as well as MHD generators and flow meters (Cha et al., 2002). In a single constricted channel, Ali et al. (2020) investigated the steady and pulsatile modes of non-Newtonian MHD Casson fluid. Sheikholeslami (2017a) researched the hydrothermal study of MHD nanofluid in an open porous cavity by using the Lattice–Boltzmann method with the Brownian motion impact on NF properties. Shah et al. (2019) addressed the idea of the electrical MHD rotational flow of $\mathrm{S}\mathrm{W}\mathrm{C}\mathrm{N}\mathrm{T}\mathrm{s}$ and $\mathrm{M}\mathrm{W}\mathrm{C}\mathrm{N}\mathrm{T}\mathrm{s}$ for engine oils. Sheikholeslami et al. (2017b) researched the forced convection of MHD NFF. They considered the power of Brownian motion for modeling NF. Haq et al. (2017) supposed the heat transfer efficiency of engine oil between two dispersed cylinders with MHD effects in the presence of both $\mathrm{S}\mathrm{W}\mathrm{C}\mathrm{N}\mathrm{T}\mathrm{s}$ and $\mathrm{M}\mathrm{W}\mathrm{C}\mathrm{N}\mathrm{T}\mathrm{s}$, to monitor the spontaneous motion of the NPs. There are several studies, as well, regarding MHD NF flow problems past a plate/sheet under various physical conditions and objectives (Narayana and Venkateswarlu, 2016; Babu et al., 2018; Tarakaramu et al., 2019; Devaki et al., 2020; Tarakaramu et al., 2020; Venkateswarlu and Narayana, 2021; Alzahrani et al., 2022; Mahmood et al., 2022; Puneeth et al., 2022; Qi et al., 2022; Ramadan et al., 2022; Tlili and Alharbi, 2022; Tlili et al., 2022).

Kakarantzas et al. (2009) investigated the natural convection of MHD at the sinusoidal upper wall temperature in a vertical cylindrical cavity. Rashidi et al. (2016) examined the convective heat transfer of MHD NFF in a vertical channel with sinusoidal walls. Sheikholeslami (2017b) tested the Buongiorno model to investigate the melting heat transfer of NFF due to the magnetic field. The impacts of heat and mass transfer of NFF flow over a vertical infinite flat plate were investigated by Turkyilmazoglu and Pop (2013). They derived the exact analytical solutions for various water-based NFs containing $Cu$, $Ag$, $CuO$, $A{l}_2{O}_3$, and $Ti{O}_2$. Pakdaman et al. (2012) explored the thermophysical properties and overall efficiency of $MWCNT$ NFs flowing within vertical helically coiled tubes. In the occurrence of a non-uniform magnetic field, Sheikholeslami et al. (2015) explored the transport of forced convection heat within a lid-driven semi-annulus enclosure filled with $F{e}_3{O}_4$–water NF. Using a continuously stretching porous layer, Gopal et al. (2021) investigated the thermo-physical properties characteristics of complex order chemical processing and viscous dissipation on NF. Two space coordinates are used to model the porous medium, laminar, time-invariant, and MHD incompressible Newtonian NF. The role of heat source and Soret impacts on MHD convective Ferro-NF ($F{e}_3{O}_4$-water) flow across an inclined channel with a porous media were examined by Sabu et al. (2021). The heat transfer of NFF from an inclined channel in the occurrence of a magnetic field, heat flux, and mass diffusion was explored using the FDM by Kumar et al. (2021).

Krishna et al. (2021a) and Krishna et al., 2021b) investigated the radiative MHD flow of an incompressible viscous electrically conducting non-Newtonian Casson hybrid NF over vertical moving porous surface under the influence of slip velocity in a rotating frame. Kavya et al. (2022) explore the varying fluid momentum and thermal energy characteristics of the laminar, steady, incompressible, 2D, non-Newtonian pseudo-plastic Williamson hybrid NF over a stretching cylinder with MHD effects.

Shah et al. (2022) determined the heat transfer properties of a MHD Prandtl hybrid NF over a stretched surface in the presence of bioconvection and chemical reaction effects. Zhang et al. (2022) presented the solar source, although it can reduce energy consumption (EC) for buildings on cold days; in the summer, its presence on the envelopes intensifies EC. Gao et al. (2022) examined the hydrodynamic and thermal performances of liquid water in the attendance of two carbon structures by molecular dynamics simulation (MDS). Nayak et al. (2022) conducted a numerical treatment on flow and heat transfer of radiative hybrid NF past an isothermal stretched cylinder set in a porous medium.

The goal of the present work is to numerically investigate the heat transfer characteristics of pulsatile viscous MHD NFF in a constricted channel. The study is conducted for five different nano-impurities ($Cu$, $F{e}_3{O}_4$, $Ag$, $Ti{O}_2$, and $SWCNT$), which have been chosen for the preparation of NFs. The mathematical analysis is done using the transformation of the vorticity-stream function, and numerical computations are made using FDM. The impact of the flow controlling parameters $\left(M,St,\mathit{Pr},Rd\right)$ on the flow profiles of the five NFs, as well as on the skin-friction and Nusselt number profiles, are also observed. The objective is to examine the cumulative impact of the applied magnetic field and thermal radiation on the wall shear stress (WSS), velocity, and temperature profiles in 2D. The Newtonian pulsatile NF flows help in understanding the influence of various metallic NPs homogeneously suspended in the blood, which is driven by drug trafficking (pharmacology) applications.

The following is how the article’s next section is organized. Section 2 defines the mathematical model and transformation. The outcomes and relevant discussions are presented in Section 3. The final remarks are eventually presented in Section 4.

2 Mathematical model

We are working at an incompressible electrically conducting NF flowing via a rectangular channel that should be laminar at Reynolds number 700. The channel walls have a pair of symmetrical constrictions. The resulting electric field $\mathbf{J}$ is normal, and the direction of $\mathbf{B}$ is perpendicular to the plane of flow. We take a Cartesian coordinate system (x,y) in which the flow direction and the direction of $\mathbf{B}$ are, respectively, along the $\stackrel{\sim }{x}$-axis and $\stackrel{\sim }{y}$-axis. Because the magnetic Reynolds number $\left({Re}_m\right)$ for the flow is so small, the induced electric can be deemed insignificant. In the transformed coordinate system (to be discussed later on), as illustrated in Figure 1, the constrictions span from $x=-x_0$ to $x=x_0$, with the center at $x=0$

$\begin{array}{ccc}{y}_1\left(x\right)& =& \{\begin{array}{ll}\frac{h_1}{2}\left[1+\cos \left(\frac{\pi x}{x_0}\right)\right],& \left|x\right|\le x_0\\ 0,& \left|x\right|>x_0\end{array}\end{array}$

$\begin{array}{ccc}{y}_2\left(x\right)& =& \{\begin{array}{ll}1-\frac{h_2}{2}\left[1+\cos \left(\frac{\pi x}{x_0}\right)\right],& \left|x\right|\le x_0\\ 1,& \left|x\right|>x_0\end{array}\end{array}(1)$

where ${y=y}_1\left(x\right)$ and ${y=y}_2\left(x\right)$ symbolize the lower and upper walls, respectively, and $h_1$ and $h_2$ are the heights of the constrictions at the lower and upper walls, respectively (Bandyopadhyay and Layek, 2012; Ali et al., 2020).

FIGURE 1

FIGURE 1. The channel geometry with a constriction on each wall. The walls are defined by.

The flow phenomenon is represented by the unsteady incompressible viscous flow equations as follows.

The continuity equation:

$\frac{\partial \stackrel{\sim }{u}}{\partial \stackrel{\sim }{x}}+\frac{\partial \stackrel{\sim }{v}}{\partial \stackrel{\sim }{y}}=0.(2)$

The momentum equation:

$\frac{\partial \stackrel{\sim }{u}}{\partial \stackrel{\sim }{t}}+\stackrel{\sim }{u}\frac{\partial \stackrel{\sim }{u}}{\partial \stackrel{\sim }{x}}+\stackrel{\sim }{v}\frac{\partial \stackrel{\sim }{u}}{\partial \stackrel{\sim }{y}}=-\frac{1}{{\rho }_{nf}}\frac{\partial \stackrel{\sim }{p}}{\partial \stackrel{\sim }{x}}+\frac{{\mu }_{nf}}{{\rho }_{nf}}{\nabla }^{\mathrm{2}}\stackrel{\sim }{u}+\frac{1}{{\rho }_{nf}}{\left(\mathbf{J}\times \mathbf{B}\right)}_x,(3)$

$\frac{\partial \stackrel{\sim }{v}}{\partial \stackrel{\sim }{t}}+\stackrel{\sim }{u}\frac{\partial \stackrel{\sim }{v}}{\partial \stackrel{\sim }{x}}+\stackrel{\sim }{v}\frac{\partial \stackrel{\sim }{v}}{\partial \stackrel{\sim }{y}}=-\frac{1}{{\rho }_{nf}}\frac{\partial \stackrel{\sim }{p}}{\partial \stackrel{\sim }{y}}+\frac{{\mu }_{nf}}{{\rho }_{nf}}{\nabla }^{\mathrm{2}}\stackrel{\sim }{v}.(4)$

The energy equation:

$\frac{\partial \stackrel{\sim }{T}}{\partial \stackrel{\sim }{t}}+\stackrel{\sim }{u}\frac{\partial \stackrel{\sim }{T}}{\partial \stackrel{\sim }{x}}+\stackrel{\sim }{v}\frac{\partial \stackrel{\sim }{T}}{\partial \stackrel{\sim }{y}}=\frac{k_{nf}}{{\left(\rho C_p\right)}_{nf}}{\nabla }^2\stackrel{\sim }{T}-\frac{1}{{\left(\rho C_p\right)}_{nf}}\frac{\partial q}{\partial \stackrel{\sim }{y}},(5)$

where $q=-\left(\frac{4\sigma }{3k^{*}}4T_{\infty }^3\frac{\partial \stackrel{\sim }{T}}{\partial \stackrel{\sim }{y}}\right)$ is the radiative heat flux. We get by expanding ${\stackrel{\sim }{T}}^4$ about $T_{\infty }$ and omitting higher-order terms

$\begin{array}{ccc}{\stackrel{\sim }{T}}^{\mathrm{4}}& \cong & 4T_{\infty }^3\stackrel{\sim }{T}-3T_{\infty }^{\mathrm{4}}\end{array}$

Then, $q=-\left(\frac{4\sigma }{3k^{*}}4T_{\infty }^3\frac{\partial \stackrel{\sim }{T}}{\partial \stackrel{\sim }{y}}\right)$ and $\frac{\partial q}{\partial \stackrel{\sim }{y}}=-\left(\frac{16\sigma }{3k^{*}}{T}_{\infty }^3\frac{{\partial }^{\mathrm{2}}\stackrel{\sim }{T}}{\partial {\stackrel{\sim }{y}}^2}\right)$.

Eq. 5 becomes

$\frac{\partial \stackrel{\sim }{T}}{\partial \stackrel{\sim }{t}}+\stackrel{\sim }{u}\frac{\partial \stackrel{\sim }{T}}{\partial \stackrel{\sim }{x}}+\stackrel{\sim }{v}\frac{\partial \stackrel{\sim }{T}}{\partial \stackrel{\sim }{y}}=\frac{k_{nf}}{{\left(\rho C_p\right)}_{nf}}\left(\frac{{\partial }^{\mathrm{2}}\stackrel{\sim }{T}}{\partial {\stackrel{\sim }{x}}^{\mathrm{2}}}+\frac{{\partial }^{\mathrm{2}}\stackrel{\sim }{T}}{\partial {\stackrel{\sim }{y}}^{\mathrm{2}}}\right)+\frac{16\sigma T_{\infty }^3}{3k^{*}{\left(\rho C_p\right)}_{nf}}\frac{{\partial }^{\mathrm{2}}\stackrel{\sim }{T}}{\partial {\stackrel{\sim }{y}}^{\mathrm{2}}},(6)$

where $\stackrel{\sim }{u}$ (along $\stackrel{\sim }{x}$-axis) and $\stackrel{\sim }{v}$ (along $\stackrel{\sim }{y}$-axis) show the velocity components and the subscript “$nf$” represents the nanofluid, $\stackrel{\sim }{p}$ symbolizes the pressure, $\rho$ symbolizes the density, $U$ symbolizes the characteristic flow velocity, $\nu$ symbolizes the kinematic viscosity, and $\stackrel{\sim }{T}$ symbolizes the temperature. $k$ symbolizes the thermal conductivity, $C_p$ symbolizes the specific heat, $\mathbf{J}\equiv \left(J_x,J_y,J_z\right)$ symbolizes current density, $\mathbf{B}\equiv \left(0,B_0,0\right)$ symbolizes the magnetic field, $B_0$ symbolizes the strength of the uniform magnetic field, $\sigma$ symbolizes electric conductivity, and ${\mu }_m$ symbolizes the magnetic permeability of the medium. As the electric current direction is normal to the channel plane, therefore $\mathbf{E}\equiv \left(\mathrm{0,0},E_z\right)$. Ohm’s law gives

$J_x=0,J_y=0,J_z={\sigma }_f\left(E_z+\stackrel{\sim }{u}{B}_0\right).(7)$

Maxwell’s equation $\nabla \times \mathbf{E}=0$ $⟹E_z=C$ (constant) for the steady flow. For the present study, $E_z$ is assumed to be zero. Then, Eq. 7 gives $J_z=\sigma \stackrel{\sim }{u}{B}_0$. Therefore, $\mathbf{J}\times \mathbf{B}=-{\sigma }_f\stackrel{\sim }{u}{B}_0^2$. Hence, Eq. 3 becomes

$\frac{\partial \stackrel{\sim }{u}}{\partial \stackrel{\sim }{t}}+\stackrel{\sim }{u}\frac{\partial \stackrel{\sim }{u}}{\partial \stackrel{\sim }{x}}+\stackrel{\sim }{v}\frac{\partial \stackrel{\sim }{u}}{\partial \stackrel{\sim }{y}}=-\frac{1}{{\rho }_{nf}}\frac{\partial \stackrel{\sim }{p}}{\partial \stackrel{\sim }{x}}+\frac{{\mu }_{nf}}{{\rho }_{nf}}{\nabla }^{\mathrm{2}}\stackrel{\sim }{u}-\frac{1}{{\rho }_{nf}}{\sigma }_f\stackrel{\sim }{u}{B}_0^{\mathrm{2}}.(8)$

The dimensionless version of the governing model is created by considering the following quantities:

$\begin{array}{ccccccc}x=\frac{\stackrel{\sim }{x}}{L},& y=\frac{\stackrel{\sim }{y}}{L},& u=\frac{\stackrel{\sim }{u}}{U},& v=\frac{\stackrel{\sim }{v}}{U},& t=\frac{\stackrel{\sim }{t}}{T},& \theta =\frac{\stackrel{\sim }{T}-T_2}{T_1-T_2}& \\ p=\frac{\stackrel{\sim }{p}}{{\rho }_f{U}^2},& Re=\frac{{\rho }_{f}UL}{{\mu }_f},& St=\frac{L}{UT},& M=B_{0}L\sqrt{\frac{{\sigma }_f}{{\rho }_f{\nu }_f}},& \mathit{Pr}=\frac{{{\mu }_{f}C}_{p,f}}{k_f},& Rd=\frac{16\sigma T_{\infty }^3}{3k^{*}{k}_f}& \end{array}(9)$

Here, $L$ symbolizes the maximum width of the channel, $U$ symbolizes the characteristic flow velocity, $T$ symbolizes the period of the pulse, $Re$ symbolizes the Reynolds number, $St$ symbolizes the Strouhal number, $M$ symbolizes the Hartmann number, $\mathit{Pr}$ symbolizes the Prandtl number, and $Rd$ symbolizes the radiation parameter.

The effective dynamic viscosity ${\mu }_{nf}$, effective density ${\rho }_{nf}$, heat capacitance ${\left(\rho C_p\right)}_{nf}$, and effective thermal conductivity $k_{nf}$ of a NF are given as:

${\mu }_{nf}=\frac{{\mu }_f}{{\left(1-\varphi \right)}^{2.5}}$

${\rho }_{nf}=\left(1-\varphi \right){\rho }_f+\varphi {\rho }_s$

${\left(\rho C_p\right)}_{nf}=\left(1-\varphi \right){\left(\rho C_p\right)}_f+\varphi {\left(\rho C_p\right)}_s$

$\frac{k_{nf}}{k_f}=\frac{k_s+\mathrm{2}{k}_f-\mathrm{2}\varphi \left(k_f-k_s\right)}{k_s+\mathrm{2}{k}_f+\mathrm{2}\varphi \left(k_f-k_s\right)}(10)$

where$\varphi$ symbolizes the volume fraction of NF, and the subscripts $nf$ correspond to NF, $f$ corresponds to the pure fluid, and $s$ corresponds to the solid state. For the present work, the following five different NFs are considered:$Cu$-$H_{2}O$, $F{e}_3{O}_4$-$H_{2}O$, $Ag$-$H_{2}O$, $Ti{O}_2$-$H_{2}O$, and $SWCNT$-$H_{2}O$. The thermophysical properties of the five different NPs and water are shown in Table 1 (Sheikholeslami and Ganji, 2013; Sheikholeslami et al., 2017a). Using the quantities from Eqs 9, 10 in Eqs 2–4, 6 gives

$\frac{\partial u}{\partial x}+\frac{\partial u}{\partial y}=0(11)$

$St\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=-\frac{1}{{\varnothing }_1}\frac{\partial p}{\partial x}+\frac{1}{Re{\varnothing }_3}{\nabla }^{2}u-\frac{1}{{\varnothing }_1}\frac{M^2}{Re}u(12)$

$St\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}=-\frac{1}{{\varnothing }_1}\frac{\partial p}{\partial y}+\frac{1}{Re{\varnothing }_3}{\nabla }^{2}v(13)$

$St\frac{\partial \theta }{\partial t}+u\frac{\partial \theta }{\partial x}+v\frac{\partial \theta }{\partial y}=\frac{1}{PrRe}\frac{{\varnothing }_5}{{\varnothing }_4}\left(\frac{{\partial }^2\theta }{\partial x^2}+\left(1+\frac{Rd}{{\varnothing }_5}\right)\frac{{\partial }^2\theta }{\partial y^2}\right)(14)$

where ${\varnothing }_1=1-\varphi +\frac{{\rho }_s}{{\rho }_f}\varphi$, ${\varnothing }_2=\frac{1}{{\left(1-\varphi \right)}^{2.5}}$, ${\varnothing }_3={\left(1-\varphi \right)}^{2.5}\left(1-\varphi +\frac{{\rho }_s}{{\rho }_f}\varphi \right)$, ${\varnothing }_4=1-\varphi +\frac{{\left(\rho C_p\right)}_s}{{\left(\rho C_p\right)}_f}\varphi$, ${\varnothing }_5=\frac{k_{nf}}{k_f}$.

TABLE 1

TABLE 1. Thermophysical properties of different NPs and the base fluid.

2.1 Boundary conditions

For the steady case of the flow problem under consideration, the boundary conditions, obtained by solving the dimensionless form of Eq. 8 and performing some manipulations using Eq. 10, are given as follows:

$u\left(y\right)=\left[\frac{\cosh \left(\frac{M}{2}\right)\left[\cosh \left(\frac{M}{2\sqrt{{\varnothing }_2}}\right)-\cosh \left(\frac{M}{\sqrt{{\varnothing }_2}}\left(y-\frac{1}{2}\right)\right)\right]}{8{\sinh }^2\left(\frac{M}{4}\right)\cosh \left(\frac{M}{2\sqrt{{\varnothing }_2}}\right)}\right]v=0,M\ne 0.(15)$

When $M=0$, the $u$-velocity at the inlet takes the form:

$u\left(y\right)={y-y}^2,v=0.(16)$

The flow is classified as sinusoidal for the pulsatile flow:

$u\left(y,t\right)=u\left(y\right)\left[1+\sin \left(2\pi t\right)\right],v=0.(17)$

Furthermore, $u=0$ and $v=0$ (i.e., no-slip conditions) are assumed on the walls. For the outlet boundary, the fully developed flow conditions are incorporated. In the dimensionless form, the temperature condition at the lower wall, $\theta =1,$ and at the upper wall, $\theta =0$.

2.2 Vorticity-stream function formulation

$u=\frac{\partial \psi }{\partial y},v=-\frac{\partial \psi }{\partial x},\omega =\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}(18)$

We differentiate Eqs 12, 13 with respect to $y$ and $x$, respectively. Then, from their subtraction and using Eq. 18, we get transformed equations from the variables $\left(u,v\right)$ to vorticity-stream functions $\left(\psi ,\omega \right)$ as follows:

$St\frac{\partial }{\partial t}\left(\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\right)+u\frac{\partial }{\partial x}\left(\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\right)+v\frac{\partial }{\partial y}\left(\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\right)$

$\begin{array}{cc}=& \frac{1}{Re{\varnothing }_3}\left[\frac{{\partial }^2}{\partial x^2}\left(\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\right)+\frac{{\partial }^2}{\partial y^2}\left(\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\right)\right]+\frac{1}{{\varnothing }_1}\frac{M^2}{Re}\frac{\partial u}{\partial y}\end{array},$

$St\frac{\partial \omega }{\partial t}+\frac{\partial \psi }{\partial y}\frac{\partial \omega }{\partial x}-\frac{\partial \psi }{\partial x}\frac{\partial \omega }{\partial y}=\frac{1}{{\varnothing }_3}\frac{1}{Re}\left[\frac{{\partial }^2\omega }{\partial x^2}+\frac{{\partial }^2\omega }{\partial y^2}\right]+\frac{1}{{\varnothing }_1}\frac{M^2}{Re}\frac{{\partial }^2\psi }{\partial y^2}(19)$

And the stream function $\psi$ equation (Poisson equation) is given as

$\frac{{\partial }^2\psi }{\partial x^2}+\frac{{\partial }^2\psi }{\partial y^2}=-\omega .(20)$

2.3 Transformation of coordinates

For treating the channel walls as the straighten ones, the coordinates are transformed as

$\xi =x,\eta =\frac{y-y_1\left(x\right)}{y_2\left(x\right)-y_1\left(x\right)}(21)$

Thus, the lower wall symbolizes by $\eta =0$ and the upper wall symbolizes by $\eta =1$. In the updated coordinate system $\left(\xi ,\eta \right)$, Eqs 14, 19, 20 are

$St\frac{\partial \omega }{\partial t}+u\left(\frac{\partial \omega }{\partial \xi }-Q\frac{\partial \omega }{\partial \eta }\right)+vD\frac{\partial \omega }{\partial \eta }$

$\begin{array}{ccc}=& \frac{1}{{\varnothing }_3}\frac{1}{Re}\left[\frac{{\partial }^2\omega }{\partial {\xi }^2}-\left(P-2QR\right)\frac{\partial \omega }{\partial \eta }-2Q\frac{{\partial }^2\omega }{\partial \xi \partial \eta }+\left(Q^2+D^2\right)\frac{{\partial }^2\omega }{\partial {\eta }^2}\right]+\frac{1}{{\varnothing }_1}\frac{M^2}{Re}{D}^2\frac{{\partial }^2\psi }{\partial {\eta }^2},& \end{array}(22)$

$\frac{{\partial }^2\psi }{\partial {\xi }^2}-\left(P-2QR\right)\frac{\partial \psi }{\partial \eta }-2Q\frac{{\partial }^2\psi }{\partial \xi \partial \eta }+\left(Q^2+D^2\right)\frac{{\partial }^2\psi }{\partial {\eta }^2}=-\omega ,(23)$

$\begin{array}{c}St\frac{\partial \theta }{\partial t}+u\left(\frac{\partial \theta }{\partial \xi }-Q\frac{\partial \theta }{\partial \eta }\right)+vD\frac{\partial \theta }{\partial \eta }\end{array}$

$=\frac{1}{RePr}\frac{{\varnothing }_5}{{\varnothing }_4}\left[\frac{{\partial }^2\theta }{\partial {\xi }^2}-\left(P-2QR\right)\frac{\partial \theta }{\partial \eta }-2Q\frac{{\partial }^2\theta }{\partial \xi \partial \eta }+\left(Q^2+{\left(1+\frac{Rd}{{\varnothing }_5}\right)D}^2\right)\frac{{\partial }^2\theta }{\partial {\eta }^2}\right],(24)$

where

$\begin{array}{llll}P=P\left(\xi ,\eta \right)=\frac{\eta y_2^{″}\left(\xi \right)+\left(1-\eta \right)y_1^{″}\left(\xi \right)}{y_2\left(\xi \right)-y_1\left(\xi \right)},& Q=Q\left(\xi ,\eta \right)=\frac{\eta y_2^{\prime }\left(\xi \right)+\left(1-\eta \right)y_1^{\prime }\left(\xi \right)}{y_2\left(\xi \right)-y_1\left(\xi \right)},& & \\ R=R\left(\xi \right)=\frac{y_2^{\prime }\left(\xi \right)-y_1^{\prime }\left(\xi \right)}{y_2\left(\xi \right)-y_1\left(\xi \right)},& D=D\left(\xi \right)=\frac{1}{y_2\left(\xi \right)-y_1\left(\xi \right)}.& & \end{array}(25)$

The velocity components $u$ and $v$ in terms of $\left(\xi ,\eta \right)$ take the forms

$u=D\left(\xi \right)\frac{\partial \psi }{\partial \eta },v=Q\left(\xi ,\eta \right)\frac{\partial \psi }{\partial \eta }-\frac{\partial \psi }{\partial \xi }(26)$

Furthermore, the wall boundary conditions in $\left(\xi ,\eta \right)$ system for $\psi$ and $\omega$ are given by

$\begin{array}{cccc}\psi \left(\eta ,t\right)& =& \left[\frac{\sqrt{{\varnothing }_2}\cosh \left(\frac{M}{2}\right)\tanh \left(\frac{M}{2\sqrt{{\varnothing }_2}}\right)}{8M{\sinh }^2\left(\frac{M}{4}\right)}\right]\left[1+ϵ\sin \left(2\pi t\right)\right],& \mathrm{a}\mathrm{t}\eta =0\end{array},$

$\begin{array}{cccc}\psi \left(\eta ,t\right)& =& \frac{M\cosh \left(\frac{M}{2}\right)}{8\sqrt{{\varnothing }_2}{\sinh }^2\left(\frac{M}{4}\right)}\left[1-\frac{\sqrt{{\varnothing }_2}}{M}\tanh \left(\frac{M}{2\sqrt{{\varnothing }_2}}\right)\right]\left[1+ϵ\sin \left(2\pi t\right)\right],& \mathrm{a}\mathrm{t}\eta =1\end{array},$

where $ϵ$ symbolizes the pulsating amplitude. If $ϵ=0$, we get steady flow

$\begin{array}{ccc}\omega & =& -{\left[\left(Q^2+D^2\right)\frac{{\partial }^2\psi }{\partial {\eta }^2}\right]}_{\eta =\mathrm{0,1}}.\end{array}(27)$

The temperature’s converted boundary conditions are $\theta =1$, at $\eta =0$; $\theta =0$, at $\eta =1$.

The other concerning non-dimensional physical quantities comprise the skin-friction coefficient and Nusselt number, defined by

$\begin{array}{cc}{C}_f=\frac{{\tau }_w}{\rho u_w^2},& Nu=-\left(\frac{L}{k_f\left(T_1-T_2\right)}\right)\left(k_{nf}+\frac{16\sigma T_{\infty }^3}{3k^{*}}\right){\frac{\partial \stackrel{\sim }{T}}{\partial \stackrel{\sim }{y}}|}_{\stackrel{\sim }{y}=0}\end{array}$

where ${\tau }_w$ and $q_w$ are defined as

$\begin{array}{cc}{\tau }_w={\left[{\mu }_{nf}\frac{\partial \stackrel{\sim }{u}}{\partial \stackrel{\sim }{y}}\right]}_{\stackrel{\sim }{y}=0},& q_w={\left[\frac{\partial \stackrel{\sim }{T}}{\partial \stackrel{\sim }{y}}\right]}_{\stackrel{\sim }{y}=0}\end{array}$

By using dimensionless variables from Eq. 9 and the coordinate transformation from Eq. 21, we get

$C_f=\frac{1}{u_w^2}{\left[-\frac{1}{Re{\varnothing }_3}D\frac{\partial u}{\partial \eta }\right]}_{\eta =0},Nu={\left[-{\varnothing }_5\left(1+Rd\right)D\frac{\partial \theta }{\partial \eta }\right]}_{\eta =0}(28)$

where $Rd=\frac{16\sigma T_{\infty }^3}{3k^{*}{k}_{nf}}$ and ${\varnothing }_5=\frac{k_{nf}}{k_f}$.

3 Results and discussion

The problem Eqs 22–24 is computed using a numerical scheme based on FDM, subject to the relevant boundary conditions in Sections 2.1, 2.3. The numerical scheme adopts a standard approach, as used by Bandyopadhyay and Layek (2011), Bandyopadhyay and Layek (2012), and Ali et al. (2020). The computational domain is assumed as $\left\{\left(\xi ,\eta \right)|\xi \in \left[-x_1,x_1\right]\mathrm{a}\mathrm{n}\mathrm{d}\eta \in \left[\mathrm{0,1}\right]\right\}$. The resulting linear systems are solved using TDMA during each of the ADI process’s two half-steps. A Cartesian grid $\left({\xi }_i,{\eta }_j\right)$ of $400\times 50$ elements is formed for $-10\le \xi \le 10$ and $0\le \eta \le 1$, with $∆\xi =0.05$ and $∆\eta =0.02$. For time integration, a step size of $∆t=0.00005$ is considered. The constriction length is assumed as $2x_0=4.$ The constrictions on the lower and upper walls are assumed to have heights $h_1=h_2=0.35$; hence, at the constricted part of the channel, the minimum width is still 30% of the maximum channel width $L$. The computations for the current study are performed in a sequential fashion. The results can be found by parallel computing for time-efficient solutions (Ali and Syed, 2013).

The pulsatile motion is modeled by adding in the inflow boundary condition the sinusoidal time-dependent function $\sin \left(2\pi t\right)$. For comparison of the five NFs, the effects of the physical parameters such as $M$, $St$, $\mathit{Pr}$, and $Rd$ on the existence of the dimensionless streamwise velocity $\left(u\right)$ and temperature $\left(\theta \right)$ are analyzed. We perform simulations for a long enough time but display the results graphically only for $t=0.25$, the point at which the flow rate is at its maximum and taking the location $x=0$ (throat of the constriction) as well as $x=2$ (in the lee of the constriction) where the fluid has entered in the low-pressure zone from the high-pressure zone. For a pulse cycle, $0<t<0.25$ is the acceleration phase, and $0.25<t<0.75$ is the deceleration phase.

For validation, the present results for the pulsatile flow condition are compared with those obtained by Bandyopadhyay and Layek (2012) without the heat effect. Figure 2 shows a good agreement of the present results, specifically for the wall shear stress (WSS), with (Bandyopadhyay and Layek, 2012) for $M=5,\mathrm{a}\mathrm{n}\mathrm{d}10$ at $t=0.25$.

FIGURE 2

FIGURE 2. WSS distribution for the pulsatile flow, for $M=\mathit{5},\mathit{10},$ at $Re=\mathit{700}$, $h\mathit{1}=h\mathit{2}=\mathit{0.35}$, $St=\mathit{0.02}$, and $t=\mathit{0.25}$.

The effects of varying the volume fraction on the wall shear stresses (WSS) at the upper wall are computed for $\varphi =0,0.01,0.02,0.03$ with $M=5$, $St=0.02$, $\mathit{Pr}=1$, and $Rd=0.2$ of the five NFs. The results are shown in Figure 3 at $x=0$ and $t=0.25$. The WSS is maximum at $t=0.25$ as the flow rate is maximum. The WSS decreases for $SWCNT$-$H_{2}O$, $Ti{O}_2$-$H_{2}O$, and $F{e}_3{O}_4$-$H_{2}O$ on increasing $\varphi$, whereas the WSS slightly increases for $Cu$-$H_{2}O$ and $Ag$-$H_{2}O$ on increasing $\varphi$.

FIGURE 3

FIGURE 3. The WSS distribution for distinct values of $\varphi$ for the five NFs at $t=\mathit{0.25}$.

The velocity and temperature profiles for each of the five NFs for $M=0,5,10,15$ are shown in Figures 4, 5 and Figures 6, 7, respectively, by setting the other parameters as $St=0.02$, $\mathit{Pr}=1$, $Rd=0.2,$ and $\varphi =0.02$. The slope/gradient of the velocity profile rises with rising values of $M$, i.e., the viscous boundary layer declines with rising values of $M$. In Figure 4, $u$ profiles at $x=0$ and $t=0.25$ are shown. It has been noted that the peak value of $u$ rises with $M$ and exhibits a parabolic profile at $t=0.25$. The velocity reaches its maximum at the middle of the constriction. $SWCNT$-based NF attains the peak value of the velocity higher than that of the other NFs. In Figure 5, $u$ profiles at $x=2$ and $t=0.25$ are shown. The profiles are not parabolic as some backflow in the vicinity of the walls is observed. The backflow reduces with an increase in $M$. $Ag$-based NF attains the peak value of velocity higher than that of the other NFs. In Figures 6, 7, the temperature profiles $\theta$ for $t=0.25$ are shown at $x=0$ and $x=2$, respectively. It is seen that the thickness of the thermal boundary layer increases, resulting in the rise of the temperature as $M$ is increased. The temperature distribution across the channel at $t=0.25$ for distinct values of $M$ is shown in Figure 8.

FIGURE 4

FIGURE 4. The velocity profile $u$ versus $y$ at $x=\mathit{0}$ and $t=\mathit{0.25}$ for the five NFs for distinct values of $M$.

FIGURE 5

FIGURE 5. The velocity profile $u$ versus $y$ at $x=\mathit{2}$ and $t=\mathit{0.25}$ for the five NFs for distinct values of $M$.

FIGURE 6

FIGURE 6. The temperature profile $\theta$ versus $\eta$ at $x=\mathit{0}$ and $t=\mathit{0.25}$ for the five NFs for distinct values of $M$.

FIGURE 7

FIGURE 7. The temperature profile $\theta$ versus $\eta$ at $x=\mathit{2}$ and $t=\mathit{0.25}$ for the five NFs for distinct values of $M$.

FIGURE 8

FIGURE 8. The temperature distribution plots for distinct values of $M$ with $Re=\mathit{700}$, $St=\mathit{0.02}$, $\mathit{Pr}=\mathit{1}$, and $Rd=\mathit{0.2}$ for the NF $Cu$-$H_{\mathit{2}}O$.

The temperature profiles for each of the five NFs for $St=0.02,0.04,0.06,0.08$ are computed by setting the other parameters as $M=5$, $\mathit{Pr}=1$, $Rd=0.2,$ and $\varphi =0.02$. In Figures 9, 10, the temperature profiles $\theta$ for $t=0.25$ are shown at $x=0$ and $x=2$, respectively. It is seen that the thickness of the thermal boundary layer declines, resulting in a decline of the temperature profile as the $St$ rises.

FIGURE 9

FIGURE 9. The temperature profile $\theta$ versus $\eta$ at $x=\mathit{0}$ and $t=\mathit{0.25}$ for the five NFs for distinct values of $St$.

FIGURE 10

FIGURE 10. The temperature profile $\theta$ versus $\eta$ at $x=\mathit{2}$ and $t=\mathit{0.25}$ for the five NFs for distinct values of $St$.

The temperature profiles for each of the five NFs for $\mathit{Pr}=1,3,5,7$ are computed by setting the other parameters as $M=5$, $St=0.02$, $Rd=0.2,$ and $\varphi =0.02$. In Figures 11, 12, the temperature profiles $\theta$ for $t=0.25$ are shown at $x=0$ and $x=2$, respectively. It is seen that the thickness of the thermal boundary layer declines, resulting in a decline of the temperature profile as the $\mathit{Pr}$ increases. The temperature distribution across the channel at $t=0.25$ for distinct values of $\mathit{Pr}$ is shown in Figure 13.

FIGURE 11

FIGURE 11. The temperature profile $\theta$ versus $\eta$ at $x=\mathit{0}$ and $t=\mathit{0.25}$ for the five NFs for distinct values of $\mathit{Pr}$.

FIGURE 12

FIGURE 12. The temperature profile $\theta$ versus $\eta$ at $x=\mathit{2}$ and $t=\mathit{0.25}$ for the five NFs for distinct values of $M$.

FIGURE 13

FIGURE 13. The temperature distribution plots for distinct values of $\mathit{Pr}$ with $Re=\mathit{700}$, $M=\mathit{5}$, $St=\mathit{0.02}$, and $Rd=\mathit{0.2}$ for the NF $Cu$-$H_{\mathit{2}}O$.

The temperature profiles for each of the five NFs for $Rd=0.2,0.6,1,1.4$ are computed by setting the other parameters as $M=5$, $St=0.02$, $\mathit{Pr}=1=0.2,$ and $\varphi =0.02$. In Figures 14, 15, the temperature profiles $\theta$ for $t=0.25$ are shown at $x=0$ and $x=2$, respectively. It is seen that the thickness of the thermal boundary layer rises, resulting in the rise of the temperature as $Rd$ rises. The temperature distribution across the channel at $t=0.25$ for distinct values of $Rd$ is shown in Figure 16.

FIGURE 14

FIGURE 14. The temperature profile $\theta$ versus $\eta$ at $x=\mathit{0}$ and $t=\mathit{0.25}$ for the five NFs for distinct values of $Rd$.

FIGURE 15

FIGURE 15. The temperature profile $\theta$ versus $\eta$ at $x=\mathit{2}$ and $t=\mathit{0.25}$ for the five NFs for distinct values of $Rd$.

FIGURE 16

FIGURE 16. The temperature distribution plots for distinct values of $Rd$ with $Re=\mathit{700}$, $St=\mathit{0.02}$, and $\mathit{Pr}=\mathit{1}$ for the NF $Cu$-$H_{\mathit{2}}O$.

Nearly for all of the cases discussed above, for the variation of any of $M$, $St$, $\mathit{Pr}$, and $Rd$, a common behavior can be noticed. At the throat of the constriction, $SWCNT$-based NF attains higher temperatures than the other NFs downstream of the constriction. In the lee of the constriction, $Ag$-based NF attains higher temperatures than the other NFs downstream of the constriction. The behavior, in most cases, is opposite upstream of the constriction.

The velocity and temperature profiles for each of the five NFs for the four selected time levels: $t=0,0.25,0.5,0.75$, are shown in Figures 17, 18, respectively, by setting the parameters as $M=5$, $St=0.02$, $\mathit{Pr}=1$, $Rd=0.2,$ and $\varphi =0.02$. The selected time levels are related to the start of pulsatile motion, the maximum flow rate, the minimum flow rate, and the instant zero net flow, respectively. In Figure 17, it is observed that the streamwise velocity achieves its peak value when the flow rate is maximum during the pulse cycle. The profiles are parabolic at $t=0$. It is found that the $u$ profile is symmetric for all $t$. $Ag$-based NF attains the peak value of the velocity higher than that of the other NFs. In Figure 18, it is detected that during the acceleration ($0\le t\le 0.25$) and deceleration $(0.25\le t\le 0.75$) phases of the pulsation cycle, $Ag$- and $Cu$-based NFs attain higher temperature values than that of the other NFs downstream of the constriction. Whereas, for the same phases, $SWCNT$-based NF attains higher temperature values than that of the other NFs upstream of the constriction.

FIGURE 17

FIGURE 17. The velocity profile $u$ versus $y$ at $x=\mathit{2}$ for the five NFs at the four time levels.

FIGURE 18

FIGURE 18. The temperature profile $\theta$ versus $\eta$ at $x=\mathit{2}$ for the five NFs at the four time levels.

The effects of the variation of the solid volume fraction for $\varphi =0,0.01,0.02$ and $M=5,10$ on the temperature profiles are presented in Figure 19 for $Cu$-based NF. It is evident that the heat transfer rate is higher for the NF with a higher concentration of NPs. Moreover, the temperature gradients are higher near the lower wall of the channel.

FIGURE 19

FIGURE 19. The temperature profile $\theta$ versus $\eta$ for distinct values of $\varphi$ for $Cu$-$H_{\mathit{2}}O$.

The effects of $Re$, $\mathit{Pr}$, and $Rd$ on the Nusselt number, as well as skin-friction profiles, are shown in Figures 20, 21, respectively. It is observed that the Nusselt number rises for higher values of $Re$, $\mathit{Pr}$, and $Rd$. The Nusselt number grows as the flow becomes more turbulent due to the rising number of collisions among the fluid particles. Also, the skin friction coefficient as the values of $Re$ upsurges. However, it remains unchanged for $\mathit{Pr}$ and $Rd$.

FIGURE 20

FIGURE 20. Impact of (A) $Re$, (B) $\mathit{Pr}$, and (C) $Rd$ on $Nu$.

FIGURE 21

FIGURE 21. Impact of (A) $Re$, (B) $\mathit{Pr}$, and (C) $Rd$ on $Sk$.

The streamlines, vorticity, and temperature distribution plots at distinct instants of a pulse cycle with $Re=700$, $M=5$, $St=0.02$, $\mathit{Pr}=1$, and $Rd=0.2$ are shown in Figure 22 for $Cu$-based NF. In Figure 22, the formation of vertical eddies in the vicinity of the walls can be observed. Over time, the eddies grow for a specific value of $M$ and slowly occupy a greater part of the channel downstream. At $t=0.75$, the presence of the backflow is observed, and even before the constriction bump, the vertical eddies are formed. The formation of these vertical eddies and flow separation is essential. However, these can be handled by increasing the strength of the magnetic field.

FIGURE 22

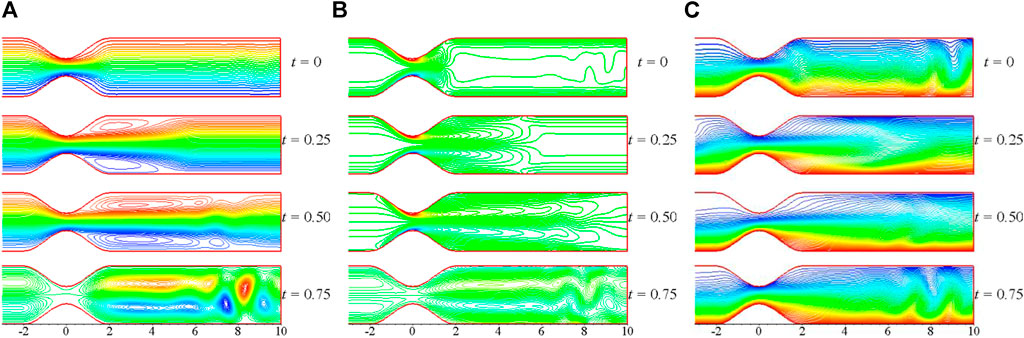
FIGURE 22. (A) Streamlines, (B) vorticity, and (C) temperature distribution plots at the four instants of a pulse cycle with $Re=\mathit{700}$, $M=\mathit{5}$, $St=\mathit{0.02}$, $\mathit{Pr}=\mathit{1}$, and $Rd=\mathit{0.2}$ for $Cu$-$H_{\mathit{2}}O$.

4 Concluding remarks

In this research, the numerical analysis of the pulsatile flow of five different NFs in a channel impacted by the magnetic field and thermal radiation through a rectangular channel having constricted walls is presented. The NPs include $Cu$, $F{e}_3{O}_4$, $Ag$, $Ti{O}_2$, and $SWCNT$ that are mixed in the base fluid, water $\left(H_{2}O\right)$, to form the five NFs. The impacts of each of $M$, $St$, $\mathit{Pr}$, and $Rd$ on the flow profiles are studied. In this analysis, the following major outcomes were observed:

• The streamwise velocity escalates as the values of $M$ upsurge. The slope/gradient of the velocity profile is higher for higher values of $M$, i.e., the viscous boundary layer declines with rising values of $M$. At the throat of the constriction, $SWCNT$-$H_{2}O$ attains the velocity’s peak value higher than that of the other NFs. However, in the lee of the constriction, $Ag$-$H_{2}O$ attains the velocity’s peak value higher than that of the other NFs.

• The thickness of the thermal boundary layer rises as any of $M$, $Rd$, and $\varphi$ is increased. This results in the rise of temperature.

• The thickness of the thermal boundary layer declines as any of $St$, and $\mathit{Pr}$ is increased. This results in a decline in the temperature profile.

• At the throat of the constriction, $SWCNT$-$H_{2}O$ attains higher temperatures than the other NFs downstream of the constriction.

• In the lee of the constriction, $Ag$-$H_{2}O$ attains higher temperatures than the other NFs downstream of the constriction. The behavior, in most cases, is opposite upstream of the constriction.

• The streamwise velocity attains its maximum at the middle of the constriction at $t=0.25$ during the pulse cycle. $Ag$-$H_{2}O$ attains the velocity’s peak value higher than that of the other NFs.

• During the acceleration and deceleration phases of the pulsation cycle, $Ag$- and $Cu$-based NFs attain higher temperature values than that of the other NFs downstream of the constriction. Whereas, for the same phases, $SWCNT$-based NF attains higher temperature values than that of the other NFs upstream of the constriction.

• The heat transfer rate is higher for the NF with a higher concentration of the NPs.

• The skin-friction coefficient escalates with escalating values of $Re$. However, no difference is found in the case of variation in $\mathrm{Pr}$ and $Rd$.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

AA: conceptualization; ZB: methodology; MA: validation; S.A.: Coding; ESM Tag El Din: Analysis; SM Hussain: Data Curation.

Funding

The authors are grateful to the Deanship of Scientific Research, Islamic University of Madinah, Ministry of Education, KSA, for supporting this research work through research project grant under Research Group Program/1/804.

Acknowledgments

The authors are thankful to the reviewer for the comments and suggestions. The authors highly appreciate the reviewer for the high standard review.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akbar, N. S., Khan, Z. H., and Nadeem, S. (2014). The combined effects of slip and convective boundary conditions on stagnation-point flow of CNT suspended nanofluid over a stretching sheet. J. Mol. Liq. 196, 21–25. doi:10.1016/j.molliq.2014.03.006

CrossRef Full Text | Google Scholar

Akbar, N. S. (2014). Metallic nanoparticles analysis for the peristaltic flow in an asymmetric channel with MHD. IEEE Trans. Nanotechnol. 13 (2), 357–361. doi:10.1109/tnano.2014.2304362

CrossRef Full Text | Google Scholar

Ali, A., Farooq, H., Abbas, Z., Bukhari, Z., and Fatima, A. (2020). Impact of Lorentz force on the pulsatile flow of a non-Newtonian Casson fluid in a Constricted channel using Darcy’s law: A numerical study. Sci. Rep. 10, 10629. doi:10.1038/s41598-020-67685-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Ali, A., and Syed, K. S. (2013). Adv. Comp. 91, 87–118.

Aly, A. M. (2020). ZAMM J. App. Math. Mech. 100 (9).

Alzahrani, J., Vaidya, H., Prasad, K. V., Rajashekhar, C., Mahendra, D. L., and Tlili, I. (2022). Micro-polar fluid flow over a unique form of vertical stretching sheet: Special emphasis to temperature-dependent properties. Case Stud. Therm. Eng. 34, 102037. doi:10.1016/j.csite.2022.102037

CrossRef Full Text | Google Scholar

Babu, H., Ajmath, K. A., Venkateswarlu, B., and Narayana, P. V. S. (2018). Thermal radiation and heat source effects on MHD non-Newtonian nanofluid flow over a stretching sheet. J. nanofluids 8, 1085–1092. doi:10.1166/jon.2019.1666

CrossRef Full Text | Google Scholar

Bandyopadhyay, S., and Layek, G. C. (2011). Numerical computation of pulsatile flow through a locally constricted channel. Commun. Nonlinear Sci. Numer. Simul. 16, 252–265. doi:10.1016/j.cnsns.2010.03.017

CrossRef Full Text | Google Scholar

Bandyopadhyay, S., and Layek, G. C. (2012). Study of magnetohydrodynamic pulsatile flow in a constricted channel. Commun. Nonlinear Sci. Numer. Simul. 17, 2434–2446. doi:10.1016/j.cnsns.2011.09.040

CrossRef Full Text | Google Scholar

Cha, J. E., Ahn, Y. C., and Kim, M. H. (2002). Flow measurement with an electromagnetic flowmeter in two-phase bubbly and slug flow regimes. Flow. Meas. Instrum. 12 (5-6), 329–339. doi:10.1016/s0955-5986(02)00007-9

CrossRef Full Text | Google Scholar

Devaki, P., Venkateswarlu, B., Srinivas, S., and Sreenadh, S. (2020). Nonlin. Eng. 9, 51–59.

Gao, J., Liu, J., Yue, H., Zhao, Y., Tlili, I., and Karimipour, A. (2022). Effects of various temperature and pressure initial conditions to predict the thermal conductivity and phase alteration duration of water based carbon hybrid nanofluids via MD approach. J. Mol. Liq. 351, 118654. doi:10.1016/j.molliq.2022.118654

CrossRef Full Text | Google Scholar

Gopal, D., Saleem, S., Jagadha, S., Ahmad, F., Almatroud, A. O., and Kishan, N. (2021). Numerical analysis of higher order chemical reaction on electrically MHD nanofluid under influence of viscous dissipation. Alexandria Eng. J. 60, 1861–1871. doi:10.1016/j.aej.2020.11.034

CrossRef Full Text | Google Scholar

Haq, R. U., Noor, N. F. M., and Khan, Z. H. (2016). Adv. Powder Technol. 27 (4), 1568–1575.

Haq, R. U., Shahzad, F., and Almdallal, Q. (2017). MHD pulsatile flow of engine oil based carbon nanotubes between two concentric cylinders. Results Phys. 7, 57–68. doi:10.1016/j.rinp.2016.11.057

CrossRef Full Text | Google Scholar

Kakarantzas, S. C., Sarris, I. E., Grecos, A. P., and Vlachos, N. S. (2009). Magnetohydrodynamic natural convection in a vertical cylindrical cavity with sinusoidal upper wall temperature. Int. J. Heat. Mass Transf. 52, 250–259. doi:10.1016/j.ijheatmasstransfer.2008.06.035

CrossRef Full Text | Google Scholar

Kasaeian, A., Eshghi, A. T., and Sameti, M. (2015). A review on the applications of nanofluids in solar energy systems. Renew. Sustain. Energy Rev. 43, 584–598. doi:10.1016/j.rser.2014.11.020

CrossRef Full Text | Google Scholar

Kavya, S., Nagendramma, V., Ahammad, N. A., Ahmad, S., Raju, C. S. K., and Shah, N. A. (2022). Magnetic-hybrid nanoparticles with stretching/shrinking cylinder in a suspension of MoS4 and copper nanoparticles. Int. Commun. Heat Mass Transf. 136, 106150. doi:10.1016/j.icheatmasstransfer.2022.106150

CrossRef Full Text | Google Scholar

Krishna, M. V., Ahammad, N. A., and Chamkha, A. J. (2021). Ain. Sh. Eng. J. 12 (3), 3043–3056.

Krishna, M. V., Ahammad, N. A., and Chamkha, A. J. (2021). Radiative MHD flow of Casson hybrid nanofluid over an infinite exponentially accelerated vertical porous surface. Case Stud. Therm. Eng. 27, 101229. doi:10.1016/j.csite.2021.101229

CrossRef Full Text | Google Scholar

Kumar, M. A., Reddy, Y. D., Rao, V. S., and Goud, B. S. (2021). Thermal radiation impact on MHD heat transfer natural convective nano fluid flow over an impulsively started vertical plate. Case Stud. Therm. Eng. 24, 100826. doi:10.1016/j.csite.2020.100826

CrossRef Full Text | Google Scholar

Mahian, O., Kianifar, A., Kalogirou, S. A., Pop, I., and Wongwises, S. (2013). A review of the applications of nanofluids in solar energy. Int. J. Heat. Mass Transf. 57, 582–594. doi:10.1016/j.ijheatmasstransfer.2012.10.037

CrossRef Full Text | Google Scholar

Mahmood, R. T., Asad, M. J., Hadri, S. H., El-Shorbagy, M. A., Mousa, A. A. A., et al. (2022). Hum. Ecol. risk assess.

Mustafa, M., Hayat, T., Pop, I., Asghar, S., and Obaidat, S. (2011). Stagnation-point flow of a nanofluid towards a stretching sheet. Int. J. Heat. Mass Transf. 54, 5588–5594. doi:10.1016/j.ijheatmasstransfer.2011.07.021

CrossRef Full Text | Google Scholar

Narayana, P. V. S., and Venkateswarlu, B. (2016). Front. Heat. Mass Trans. 7.

Nasir, S., Shah, Z., Islam, S., Bonyah, E., and Gul, T. (2019). Darcy Forchheimer nanofluid thin film flow of SWCNTs and heat transfer analysis over an unsteady stretching sheet. AIP Adv. 9, 015223–15310. doi:10.1063/1.5083972

CrossRef Full Text | Google Scholar

Nayak, M. K., Mabood, F., Dogonchi, A. S., Ramadan, K. M., Tlili, I., and Khan, W. A. (2022). Wave random complex.

Google Scholar

Pakdaman, M. F., Akhavan-Behabadi, M. A., and Razi, P. (2012). Exp. Therm. Fluid Sci. 40, 103–111.

Puneeth, V., Ali, F., Khan, M. R., Anwar, M. S., and Ahammad, N. A. (2022). Bio. Conv. Ref. 21.

Qi, X., Sidi, M. O., Tlili, I., Ibrahim, T. K., Elkotb, M. A., El-Shorbagy, M. A., et al. (2022). Optimization and sensitivity analysis of extended surfaces during melting and freezing of phase changing materials in cylindrical Lithium-ion battery cooling. J. Energy Storage 51, 104545. doi:10.1016/j.est.2022.104545

CrossRef Full Text | Google Scholar

Ramadan, K. M., Qisieh, O., and Tlili, I. (2022). Thermal creep effects on fluid flow and heat transfer in a microchannel gas cooling. Proc. Institution Mech. Eng. Part C J. Mech. Eng. Sci. 236, 5033–5047. doi:10.1177/09544062211057039

CrossRef Full Text | Google Scholar

Rashidi, M. M., Nasiri, M., Khezerloo, M., and Laraqi, N. (2016). Numerical investigation of magnetic field effect on mixed convection heat transfer of nanofluid in a channel with sinusoidal walls. J. Magn. Magn. Mat. 401, 159–168. doi:10.1016/j.jmmm.2015.10.034

CrossRef Full Text | Google Scholar

Sabu, A. S., Mathew, A., Neethu, T. S., and George, K. A. (2021). Statistical analysis of MHD convective ferro-nanofluid flow through an inclined channel with hall current, heat source and soret effect. Therm. Sci. Eng. Prog. 22, 100816. doi:10.1016/j.tsep.2020.100816

CrossRef Full Text | Google Scholar

Said, Z., Saidur, R., Sabiha, M. A., Rahim, N. A., and Anisur, M. R. (2015). Thermophysical properties of Single Wall Carbon Nanotubes and its effect on exergy efficiency of a flat plate solar collector. Sol. Energy 115, 757–769. doi:10.1016/j.solener.2015.02.037

CrossRef Full Text | Google Scholar

Saidur, R., Kazi, S. N., Husain, M. S., Rahman, M. M., and Mohammed, H. A. (2011). Renew. Sust. Energy Rev. 15, 310–323.

CrossRef Full Text

Saidur, R., Leong, K. Y., and Mohammed, H. A. (2011). A review on applications and challenges of nanofluids. Renew. Sustain. Energy Rev. 15 (3), 1646–1668. doi:10.1016/j.rser.2010.11.035

CrossRef Full Text | Google Scholar

Shah, S. A. A., Ahammad, N. A., Din, E. M. T. E., Gamaoun, F., Awan, A. U., and Ali, B., Nanomater. 12, 2174, (2022).

Shah, Z., Bonyah, E., Islam, S., and Gul, T. (2019). Impact of thermal radiation on electrical MHD rotating flow of Carbon nanotubes over a stretching sheet. AIP Adv. 9 (1), 015115–15213. doi:10.1063/1.5048078

CrossRef Full Text | Google Scholar

Sheikholeslami, M., and Ganji, D. D. (2013). Heat transfer of Cu-water nanofluid flow between parallel plates. Powder Technol. 235, 873–879. doi:10.1016/j.powtec.2012.11.030

CrossRef Full Text | Google Scholar

Sheikholeslami, M., Ganji, D. D., and Moradi, R. (2017). Forced convection in existence of Lorentz forces in a porous cavity with hot circular obstacle using nanofluid via Lattice Boltzmann method. J. Mol. Liq. 246, 103–111. doi:10.1016/j.molliq.2017.09.053

CrossRef Full Text | Google Scholar

Sheikholeslami, M., Hayat, T., and Alsaedi, A. (2017). Numerical study for external magnetic source influence on water based nanofluid convective heat transfer. Int. J. Heat. Mass Transf. 106, 745–755. doi:10.1016/j.ijheatmasstransfer.2016.09.077

CrossRef Full Text | Google Scholar

Sheikholeslami, M. (2017). Influence of magnetic field on nanofluid free convection in an open porous cavity by means of Lattice Boltzmann method. J. Mol. Liq. 234, 364–374. doi:10.1016/j.molliq.2017.03.104

CrossRef Full Text | Google Scholar

Sheikholeslami, M. (2017). Numerical simulation of magnetic nanofluid natural convection in porous media. Phys. Lett. A 381, 494–503. doi:10.1016/j.physleta.2016.11.042

CrossRef Full Text | Google Scholar

Sheikholeslami, M., Rashidi, M. M., and Ganji, D. D. (2015). Effect of non-uniform magnetic field on forced convection heat transfer ofFe3O4–water nanofluid. Comput. Methods Appl. Mech. Eng. 294, 299–312. doi:10.1016/j.cma.2015.06.010

CrossRef Full Text | Google Scholar

Tarakaramu, N., Narayana, P. V. S., and Venkateswarlu, B. (2019). App. Math. Sci. Comp. 87-97.

Tarakaramu, N., Narayana, P. V. S., and Venkateswarlu, B. (2020). Numerical simulation of variable thermal conductivity on 3D flow of nanofluid over a stretching sheet. Nonlinear Eng. 9, 233–243. doi:10.1515/nleng-2020-0011

CrossRef Full Text | Google Scholar

Tlili, I., and Alharbi, T. (2022). Investigation into the effect of changing the size of the air quality and stream to the trombe wall for two different arrangements of rectangular blocks of phase change material in this wall. J. Build. Eng. 52, 104328. doi:10.1016/j.jobe.2022.104328

CrossRef Full Text | Google Scholar

Tlili, I., Sajadi, S. M., Baleanu, D., and Ghaemi, F. (2022). Sustain. Energy Technol. Assess. 52, 102100.

CrossRef Full Text

Turkyilmazoglu, M., and Pop, I. (2013). Heat and mass transfer of unsteady natural convection flow of some nanofluids past a vertical infinite flat plate with radiation effect. Int. J. Heat. Mass Transf. 59, 167–171. doi:10.1016/j.ijheatmasstransfer.2012.12.009

CrossRef Full Text | Google Scholar

Venkateswarlu, B., and Narayana, P. V. S. (2021). Heat. Trans. 50, 432–449.

CrossRef Full Text

Wang, X. Q., and Mujumdar, A. (2008). A review on nanofluids - part II: Experiments and applications. Braz. J. Chem. Eng. 25 (4), 631–648. doi:10.1590/s0104-66322008000400002

CrossRef Full Text | Google Scholar

Wong, K. V., and Leon, O. D. (2010). Adv. Mech. Eng. 2, 1–11.

Yang, L., Huang, J. N., Ji, W., and Mao, M. (2020). Investigations of a new combined application of nanofluids in heat recovery and air purification. Powder Technol. 360, 956–966. doi:10.1016/j.powtec.2019.10.053

CrossRef Full Text | Google Scholar

Zhang, J., Sajadi, S. M., Tlili, I., and YangChen, I.Tlili and M. A. Fagiry, (2022). Effects of Al2O3 and TiO2 nanoparticles in order to reduce the energy demand in the conventional buildings by integrating the solar collectors and phase change materials. Sustain. Energy Technol. Assessments 52, 102114. doi:10.1016/j.seta.2022.102114

CrossRef Full Text | Google Scholar