Load shedding for frequency and voltage control in the multimachine system using a heuristic knowledge discovery method

The voltage profile of different buses and the rotor dynamics of generators are adversely affected by a generator outage. Generator outages can be minimized using a variety of strategies and algorithms. An AI-based knowledge discovery approach has been reported in this article. This article proposes a technique for identifying sensitive loads and the amount of active and reactive power curtailment for rotor speed regulation and voltage management at the terminals. The MATLAB^®/Simulink environment verifies and tests the method’s practicality on an IEEE-10-machine-39-bus system. Active power shedding is considered for rotor angle stability, while reactive power is also shedded for maintaining the terminal voltage at the loads. A sequential outage is considered to simulate a scenario where the two generators with the highest active and reactive power are taken out of service. The generator’s rotor speed, terminal voltage, and load are measured with and without load restriction. In all situations, the rotor and center of inertia speed are 1 p.u. The average steady-state load terminal voltage is 0.967 V. The average terminal voltage of all load buses improves from 0.933 to 0.972 and 0.936 to 0.971, case-wise. The reported results confirm and validate the effectiveness and applicability of the proposed technique.

1 Introduction

Industry and academic researchers have focused for decades on post-disaster power supply quality. A generator outage is an extreme contingency that might cause network instability. In a centralized context, the load is distributed when a generator leaves the network. The under-frequency condition arises when the active load on the power network hits its limit. Therefore, thermal and capacity ratings are violated in the reactive load escalation scenario. Active and passive shunt devices exchange active and reactive power to manage active and reactive imbalance through interaction with the existing power network. A power shortfall requires load shedding or curtailing to regulate the system’s voltage and frequency. Therefore, load shedding occurs during corrective and emergent power system control. It is recognized that load shedding is a challenging task to ensure power system security. In contrast, in the case of a decentralized environment, there is a tie-line power flow among different control areas.

Recently, researchers are working on load shedding and also on the priority of renewable energy integration in the smart grid. Domestic load shedding is performed in the literature to maintain the supply quality (Azasoo et al., 2020; Alrajhi, 2022), while various sensitivity parameters that combine the negative effects of frequency, voltage, and load shedding are studied through max–min optimization (Alshammari et al., 2018; Alsiraji and El-Shatshat, 2018; Cruz et al., 2020; Talaat et al., 2020; Gharebaghi et al., 2021; Hong and Hsiao, 2022). The authors (Alrajhi, 2018; Jiang et al., 2020) have linearized various components and the system dynamics for load shedding due to the nonlinearity of system voltage dynamics and frequency. An adaptive frequency control-based load frequency control has been described (Li et al., 2020). The authors (Lin, 2019) use an iterative technique to discover the load shedding. The authors (Alrajhi et al., 2018; Małkowski, 2020; Alrajhi Alsiraji and El-Shatshat, 2021) exhibit adaptive fuzzy load shedding for small power systems. The authors implemented (Nourollah et al., 2019; Nourollah and Gharehpetian, 2019; Potel et al., 2019; Masood et al., 2021) frequency-based multi-topological algorithms. Another study recommended hardening of the electrical system before a cyclone and softening it thereafter to prevent hurricane damage (Sang et al., 2020). Load shedding is implemented by monitoring the active and reactive power delivery and absorption of the synchronous condenser (Sauhats et al., 2021). The author deploys a principle component analysis based on online frequency-measured load shedding (Shi et al., 2019; Skrjanc et al., 2020). A universal load flow-based sensitivity analysis is performed for load shedding to prevent voltage collapse (Tian and Mou, 2019). A secure PV-region mathematical model is developed, and load shedding is conducted (Wang et al., 2020). The authors (Wang et al., 2021) show a dueling deep two-stage Q-learning-based load shedding. The authors (Zhou et al., 2019) provide two-stage load shedding to improve frequency management. LSTM neural network learning-based frequency prediction and load shedding are performed (Zhu and Luo, 2021). Authors (Santos et al., 2019; Deb et al., 2022) use the multi-agent intelligent load shedding method. Authors (Banijamali and Amraee, 2018; Alshammari et al., 2022) describe a method for tripping loads in the case of generator failure.

The state-of-the-art techniques reported in the literature are based on repeating algorithms that account mainly for the generation shortage (Lin, 2019; Jiang et al., 2020; Li et al., 2020; Małkowski, 2020; Masood et al., 2021). During a generation shortage, a load may need to be shedded, but owing to an emergent need, it cannot be scheduled to be disconnected. As a result, to the author’s best knowledge, no method or approach in state-of-the-art literature can satisfy this circumstance.

The main contribution of this work is that it describes and implements the heuristic knowledge-based method for load shedding. This study uses active and reactive load deduction in case of generator failure to maintain rotor speed and terminal voltage. The proposed method offers several load-shedding options with precise numerical proportionate rations. The proposed approach has been tested on the IEEE-10-machine-39-bus system.

2 Mathematical background and methodology development

The rotor speed dynamics of the generator in the multi-machine system follow the equation described as follows.

$\mathit{M}\frac{\mathit{d}\mathit{\omega }}{\mathit{d}\mathit{t}}={\mathit{p}}_{\mathit{m}\mathit{i}}-{\mathit{p}}_{\mathit{e}\mathit{i}}(1)$

$p_{ei}=E_{qi}^{,}\left[{\displaystyle \sum }_{j=1}^{j=n}{E}_{qj}^{,}\left(B_{ij}\sin {\delta }_{ij}+G_{ij}\cos {\delta }_{ij}\right)\right](2)$

Substituting Eq. 2 into Eq. 1 and dividing by M lead to obtaining Eq. 3 as follows, where $\left(\frac{{\mathit{H}}_{\mathit{i}}}{\mathit{\pi }\mathit{f}}\right)$ is used in place of M.

$\frac{d\omega }{dt}=\frac{\left(-E_{qi}^{,}\left[{\displaystyle \sum }_{j=1}^{j=n}{E}_{qj}^{,}\left(B_{ij}\sin {\delta }_{ij}+G_{ij}\cos {\delta }_{ij}\right)\right]+p_{me}\right)}{\frac{H_i}{\pi f}}(3)$

In this instance, B_ij and G_ij are the reduced Y bus matrix, and they can be calculated from the full order matrix of the Y as given in Eq. 4

$\{\begin{array}{c}{Y}^{BUS}=\begin{array}{c}G\\ R\end{array}\left[\stackrel{\begin{array}{cc}G& R\end{array}}{\overbrace{\begin{array}{cc}A& B\\ C& D\end{array}}}\right]\\ Y^{RED}=A-B^{-1}DC\end{array}(4)$

Where RED stands for the reduced order bus admittance matrix and the superscript BUS stands for the full order bus admittance matrix. From the Kron reduction formula, this relationship is straightforward to deduce. The admittance matrix elements relating to the generator bus and the remaining other buses, including the load bus, are denoted by the letters G and R, respectively. The sin (ij) and cos (ij) terms in Eq. 3 can be substituted by 0 and 1, respectively, since the impedance angle’s change window is very small. Therefore, Eq. 3 can be simplified and written as Eq. 5.

$\frac{d\omega }{dt}=\frac{\left(-E_{qi}^{,}\left[{\displaystyle \sum }_{j=1}^{j=n}{E}_{qj}^{,}{G}_{ij}\cos {\delta }_{ij}\right]+p_{me}\right)}{\frac{H_i}{\pi f}}(5)$

The entire system described by Eqs 6–8 is obtained by expanding Eq. 5 for an n-machine system shown as follows.

$\frac{d{\omega }_1}{dt}=\frac{\left(\left[-\left({E_{q1}^{,}}^2\right)G_{11}-E_{q1}^{,}{E}_{q2}^{,}{G}_{12}\cdots -E_{q1}^{,}{E}_{qn-1}^{,}{G}_{1n-1}-E_{q1}^{,}{E}_{qn}^{,}{G}_{in}\right]+p_{me}\right)}{\frac{H_1}{\pi f}}(6)$

$\{\begin{array}{c}{∆\alpha }_1\propto ∆G_{11}+∆G_{12}+∆G_{13}\dots \dots .+∆G_{1n}\\ {∆\alpha }_2\propto ∆G_{21}+∆G_{22}+∆G_{23}\dots \dots .+∆G_{2n}\\ ⋮\\ {∆\alpha }_n\propto ∆G_{n1}+∆G_{n2}+∆G_{n3}\dots \dots .+∆G_{nn}\end{array}(7)$

$\{\begin{array}{c}{G}_{ii}=\left\{Y_{i1}+Y_{i2}+Y_{i3}+Y_{i4}+\dots Y_{in}\right\}\\ G_{ij}=\left\{{-Y}_{ij}\right\}\end{array}(8)$

The value of ${\mathit{E}}_{\mathit{q}\mathbf{1}}^{,}{\dots \dots \mathit{E}}_{\mathit{q}\mathit{n}}^{,}$ varies near about 1p.u. and let $\frac{\mathit{d}{\mathit{\omega }}_{\mathbf{1}}}{\mathit{d}\mathit{t}}=\mathit{\alpha }$ where $\mathit{\alpha }$ is the angular acceleration

After removal of any load, ${\mathit{G}}_{\mathit{i}\mathit{n}}$ becomes ${\mathit{G}}_{\mathit{i}\mathit{n}}+\mathit{\Delta }{\mathit{G}}_{\mathit{i}\mathit{n}}$. Under balanced condition $\frac{\mathit{d}{\mathit{\omega }}_{\mathbf{1}}}{\mathit{d}\mathit{t}}=\mathit{\alpha }$ = 0. So considering these factors from Eq. 5, a new non-zero Δ $\mathit{\alpha }$ can be approximated as follows

$\begin{array}{ll}\hfill {∆\mathit{\alpha }}_{\mathbf{1}}& \begin{array}{c}\propto \\ \sim \end{array}∆{\mathit{G}}_{\mathbf{11}}+∆{\mathit{G}}_{\mathbf{12}}+∆{\mathit{G}}_{\mathbf{13}}\dots \dots .+∆{\mathit{G}}_{\mathbf{1}\mathit{n}}{∆\mathit{\alpha }}_{\mathbf{2}}\begin{array}{c}\propto \\ \sim \end{array}{\mathit{G}}_{\mathbf{21}}+∆{\mathit{G}}_{\mathbf{22}}+∆{\mathit{G}}_{\mathbf{23}}\dots \dots .+∆{\mathit{G}}_{\mathbf{2}\mathit{n}}{∆\mathit{\alpha }}_{\mathbf{3}}\hfill \\ \hfill & \begin{array}{c}\propto \\ \sim \end{array}∆{\mathit{G}}_{\mathbf{31}}+∆{\mathit{G}}_{\mathbf{32}}+∆{\mathit{G}}_{\mathbf{33}}\dots \dots .+∆{\mathit{G}}_{\mathbf{3}\mathit{n}}⋮{∆\mathit{\alpha }}_{\mathit{n}}\begin{array}{c}\propto \\ \sim \end{array}∆{\mathit{G}}_{\mathit{n}\mathbf{1}}+∆{\mathit{G}}_{\mathit{n}\mathbf{2}}+∆{\mathit{G}}_{\mathit{n}\mathbf{3}}\dots \dots .+∆{\mathit{G}}_{\mathit{n}\mathit{n}}\hfill \end{array}(9)$

Here, $\begin{array}{c}\propto \\ \sim \end{array}$ is the symbol of proportionality. Since

${\mathit{G}}_{\mathit{i}\mathit{i}}=\left\{{\mathit{Y}}_{\mathit{i}\mathbf{1}}+{\mathit{Y}}_{\mathit{i}\mathbf{2}}+{\mathit{Y}}_{\mathit{i}\mathbf{3}}+{\mathit{Y}}_{\mathit{i}\mathbf{4}}+\dots {\mathit{Y}}_{\mathit{i}\mathit{n}}\right\}\mathrm{a}\mathrm{n}\mathrm{d}{\mathit{G}}_{\mathit{i}\mathit{j}}=\left\{{-\mathit{Y}}_{\mathit{i}\mathit{j}}\right\}(10)$

So $\left|{∆\mathit{G}}_{\mathit{i}\mathit{i}}\right|”{\gg |∆\mathit{G}}_{\mathit{i}\mathit{j}}|$ So again

${∆\mathit{\alpha }}_{\mathit{i}}\begin{array}{c}\propto \\ \sim \end{array}{∆\mathit{G}}_{\mathit{i}\mathit{i}}(11)$

So the ${∆\mathit{\alpha }}_{\mathit{i}}$ reflection can be easily seen in ${\mathit{G}}_{\mathit{i}\mathit{i}}$

Now quadrature axis terminal voltage follows the dynamics of the equation as follows

$\dot{{\mathit{E}}_{\mathit{q}\mathit{i}}^{,}}=\raisebox{1ex}{$\left[-\left({\mathit{E}}_{\mathit{q}\mathit{i}}^{,}+\left({\mathit{x}}_{\mathit{d}\mathit{i}}-{\mathit{x}}_{\mathit{d}\mathit{i}}^{,}\right){\mathit{I}}_{\mathit{d}\mathit{i}}\right)+{\mathit{E}}_{\mathit{f}\mathit{i}}\right]$}\!\left/ \!\raisebox{-1ex}{${\mathit{T}}_{\mathit{d}\mathit{o}\mathit{i}}$}\right.(12)$

$\dot{E_{qi}^{,}}=\raisebox{1ex}{$\left[-\left(E_{qi}^{,}+\left(x_{di}-x_{di}^{,}\right){\displaystyle \sum }_{j=1}^{j=n}{E}_{qj}^{,}\left(G_{ij}\sin {\delta }_{ij}-B_{ij}\cos {\delta }_{ij}\right)\right)+E_{fi}\right]$}\!\left/ \!\raisebox{-1ex}{$T_{doi}$}\right.(13)$

Again angle ${\mathit{\delta }}_{\mathit{i}\mathit{j}}=\left[\mathbf{0}\mathbf{5}\right]$ so $\mathbf{sin}{\mathit{\delta }}_{\mathit{i}\mathit{j}}$ can be substituted by 0 and $\mathbf{cos}{\mathit{\delta }}_{\mathit{i}\mathit{j}}$ can be substituted by 1. After remodifying Eq. 13, we get Eq. 14

$\dot{E_{qi}^{,}}=\raisebox{1ex}{$\left[-\left(E_{qi}^{,}+\left(x_{di}-x_{di}^{,}\right){\displaystyle \sum }_{j=1}^{j=n}{E}_{qj}^{,}{B}_{ij}\right)+E_{fi}\right]$}\!\left/ \!\raisebox{-1ex}{$T_{doi}$}\right.(14)$

Again taking perturbation terms

$\dot{E_{qi}^{,}}+∆\dot{E_{qi}^{,}}=\raisebox{1ex}{$\left[-\left(E_{qi}^{,}+∆E_{qi}^{,}+\left(x_{di}-x_{di}^{,}\right){\displaystyle \sum }_{j=1}^{j=n}∆E_{qj}^{,}{B}_{ij}+\left(x_{di}-x_{di}^{,}\right){\displaystyle \sum }_{j=1}^{j=n}{E}_{qj}^{,}{∆B}_{ij}\right)+E_{fi}\right]$}\!\left/ \!\raisebox{-1ex}{$T_{doi}$}\right.(15)$

By substituting Eq. 12 from Eq. 13

$\dot{E_{qi}^{,}}+∆\dot{E_{qi}^{,}}=\raisebox{1ex}{$\left[-\left(E_{qi}^{,}+∆E_{qi}^{,}+\left(x_{di}-x_{di}^{,}\right){\displaystyle \sum }_{j=1}^{j=n}∆E_{qj}^{,}{B}_{ij}+\left(x_{di}-x_{di}^{,}\right){\displaystyle \sum }_{j=1}^{j=n}{E}_{qj}^{,}{∆B}_{ij}\right)+E_{fi}\right]$}\!\left/ \!\raisebox{-1ex}{$T_{doi}$}\right.(16)$

$∆\dot{{\mathit{E}}_{\mathit{q}\mathit{i}}^{,}}\begin{array}{c}\propto \\ \sim \end{array}\left({\mathit{x}}_{\mathit{d}\mathit{i}}-{\mathit{x}}_{\mathit{d}\mathit{i}}^{,}\right){\displaystyle \sum }_{\mathit{j}=\mathbf{1}}^{\mathit{j}=\mathit{n}}{\mathit{E}}_{\mathit{q}\mathit{j}}^{,}{∆\mathit{B}}_{\mathit{i}\mathit{j}}(17)$

$∆\dot{{\mathit{E}}_{\mathit{q}\mathbf{1}}^{,}\begin{array}{c}\propto \\ \sim \end{array}}\left({\mathit{x}}_{\mathit{d}\mathit{i}}-{\mathit{x}}_{\mathit{d}\mathit{i}}^{,}\right)\left[{∆\mathit{B}}_{\mathbf{11}}+{∆\mathit{B}}_{\mathbf{12}}+{∆\mathit{B}}_{\mathbf{13}}\dots \dots .+{∆\mathit{B}}_{\mathbf{1}\mathit{n}}\right](18)$

Again $∆{\mathrm{E}}_{\mathrm{q}\mathrm{i}}^{,}=0$ because $∆{\mathrm{E}}_{\mathrm{q}\mathrm{i}}^{,}$ is instantaneous change, and instantaneous change in voltage is always zero due to inductance of the circuit, and there is no control performance so $∆$ ${\mathrm{E}}_{\mathrm{f}\mathrm{i}}$ term does not appear. So putting $∆{\mathrm{E}}_{\mathrm{q}\mathrm{i}}^{,}$ term = 0. The final equation with proportional approximation can be obtained as follows and assuming that ${\mathrm{E}}_{\mathrm{q}\mathrm{j}}^{,}=1,⩝\mathrm{j}\in \mathbb{N}$[1…n]

$\Delta E_{q^{\mathrm{l}}\sim }^{;\alpha }\left(x_{di}-x_{di}\right){\sum }_{j=1}^{j=n}{E}_{qj}^{\prime }\Delta B_{ij}{E}_{q^{\mathrm{l}}\sim }^{,\alpha }\left(x_{di}-x_{di}^{\prime }\right)\left[\Delta B_{11}+\Delta B_{12}+\Delta B_{13}\dots \dots +\Delta B_{1n}\right](19)$

Since again ${∆\mathrm{B}}_{\mathrm{i}\mathrm{i}}=-\left[{∆\mathrm{B}}_{\mathrm{i}1}+{∆\mathrm{B}}_{\mathrm{i}2}+{∆\mathrm{B}}_{\mathrm{i}3}+\dots \dots \dots \dots {∆\mathrm{B}}_{\mathrm{i}\mathrm{n}}\right]$

So |${∆\mathrm{B}}_{\mathrm{i}\mathrm{i}}{\left|\gg ”{|∆\mathrm{B}}_{\mathrm{i}\mathrm{j}}\right|}^{″}$

Neglecting the ${∆\mathrm{B}}_{\mathrm{i}\mathrm{j}}$ due to very smaller in magnitude than ${∆\mathrm{B}}_{\mathrm{i}\mathrm{i}}$.So according to the aforesaid explanations and assumption

$\begin{array}{c}∆\dot{{\mathit{E}}_{\mathit{q}\mathbf{1}}^{,}}=\left({\mathit{x}}_{\mathit{d}\mathit{i}}-{\mathit{x}}_{\mathit{d}\mathit{i}}^{,}\right){∆\mathit{B}}_{\mathbf{11}}\\ ∆\dot{{\mathit{E}}_{\mathit{q}\mathbf{2}}^{,}}=\left({\mathit{x}}_{\mathit{d}\mathit{i}}-{\mathit{x}}_{\mathit{d}\mathit{i}}^{,}\right){∆\mathit{B}}_{\mathbf{22}}\\ \begin{array}{c}⋮\\ ∆\dot{{\mathit{E}}_{\mathit{q}\mathit{n}}^{,}}=\left({\mathit{x}}_{\mathit{d}\mathit{i}}-{\mathit{x}}_{\mathit{d}\mathit{i}}^{,}\right){∆\mathit{B}}_{\mathit{n}\mathit{n}}\end{array}\end{array}(20)$

3 Methodology

This article uses a rotor and voltage terminal paradigm to collect the information. The data are collected by rejecting the loads in a one-by-one fashion. The changes in load-rejection admittance matrices can be sampled. Later, loads for a particular generator are picked using inductive logic from rotor dynamics and machine voltage. The heuristic knowledge base has three levels, namely, 1) database creation/variable declaration, 2) finding the variable relationships by performing a preset database operation, and 3) systematically using the proposed knowledge-based technique.

3.1 Database creation using variables

Changes in conductance and susceptance cause variations in the rotor speed and the generator terminal voltage, as given in Eqs 6, 16. The load is eliminated in the simulation background, and the changes in conductance and susceptance are retained in a folder with the load as a heading. Repeat until all loads are coated. The subject variables considered are loads, and the object variables are generators.

3.1.1 Knowledge retrieval by identifying variable relationships through database operations

Load L_a is removed, and the diagonal elements G_ii and B_ii from Eqs 6, 16 are maintained in a separate block (2), as shown in Figure 1A. Higher values G_ii and B _ii are selected and maintained in the generator group G (i) block. Repeat until all significant active and reactive loads are removed. The mapping operation with the actual data set is presented in Figure 1A. The final generator load sensitivity (S₁) is represented in Table 1A. Tables 1A, B summarize generator load sensitivity for speed regulation and voltage regulation, respectively. The complete algorithm is shown in Figure 1B.

FIGURE 1

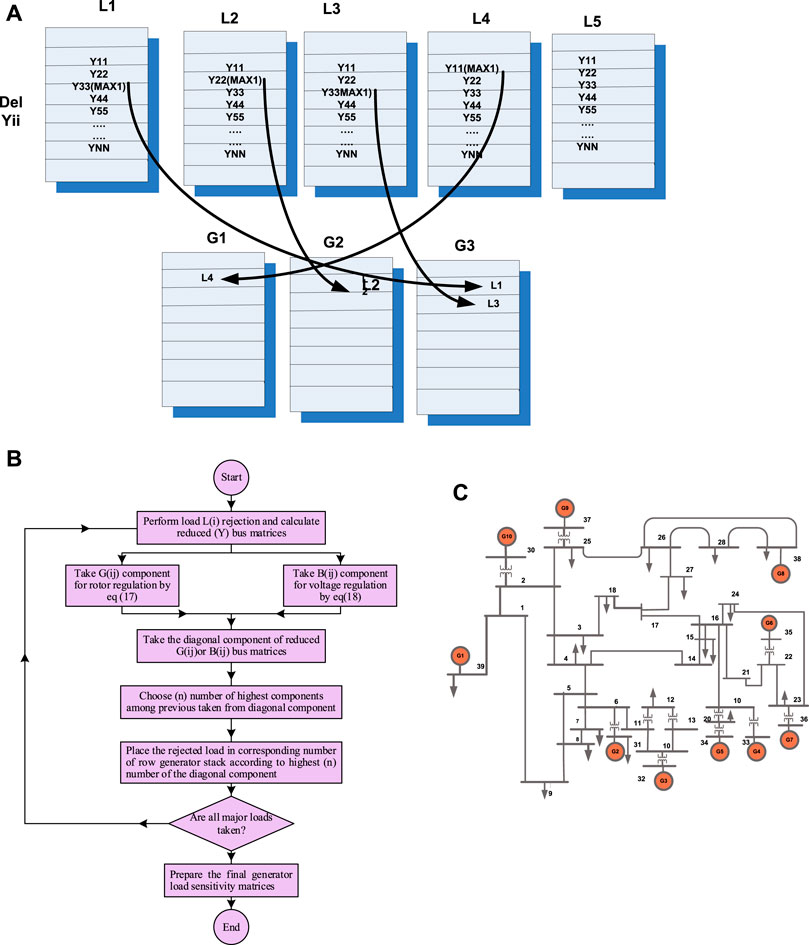
FIGURE 1. (A) Schematic diagram of mapping for knowledge discovery. (B) Flow chart of the complete proposed methodology. (C) IEEE 39-bus-10-machine system.

TABLE 1

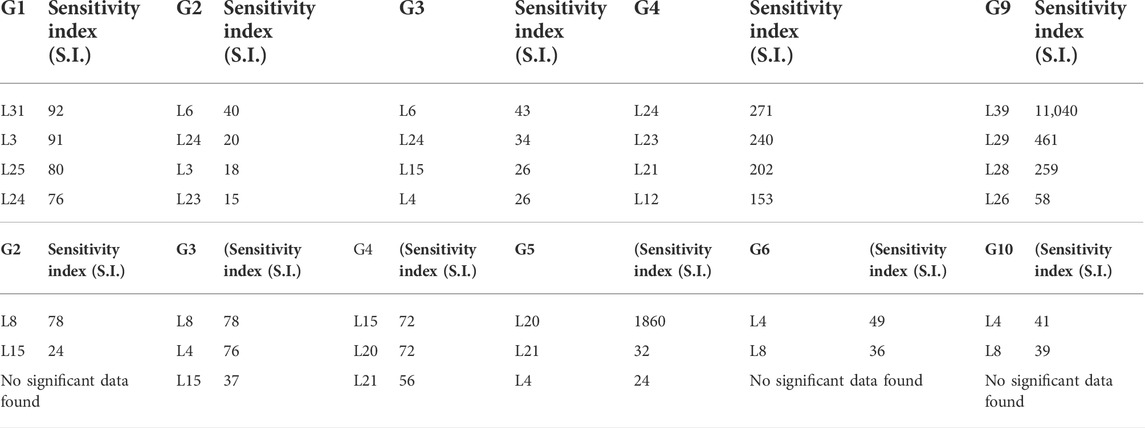
TABLE 1. (A) Load generator sensitivity indexes for rotor speed regulation. (B) Load generator sensitivity indexes for generator voltage regulation.

3.1.2 Deployment of proposed technique in load shedding

In the case of any particular generator outage of capacity P_GEN, it is found that three loads, L_a, L_b, and L_c have the highest sensitivity index with values w_La, w_Lb, and w_Lc. Then curtailment of power C_La, C_Lb, and C_Lc is defined as:

C_La = (P_GEN*w_La)/((w_La + w_Lb + w_Lc))

C_Lb = (P_GEN*w_Lb)/((w_La + w_Lb + w_Lc))

C_Lc = (P_GEN*w_Lc)/((w_La + w_Lb + w_Lc)).

If any of C_La, C_Lb, or C_Lc is greater than the installed capacity of a load L_a, L_b, and L_c, then that particular load is separated, and the remaining power is curtailed from other remaining loads.

The load generator sensitivity indexes, shown in Tables 1A, B, are prepared with four loads assigned with their priority in the target set for generators G₁, G₂, G₃, G₄, and G₅ for the concern of rotor stability. Table 1B is prepared for load terminal voltage according to Eq. 16. Each generator delivers active and reactive power to the network to meet the load demand.

4 Results and discussion

The proposed method is applied to a 10-machine-IEEE-39-bus system in the MATLAB^®/Simulink environment. It includes 10 different-sized generators G₁ ... G₁₀ and 19 loads L_a, L_b, and L_c. Here, a, b, and c are the bus numbers where the load is situated. The total capacity of the system is 61,408 MW, and the total load is 60,936 MW. The individual generator capacities of G₁ to G10 are [1,000,520.81, 650,632, 508,650, 560,540, 830,250] MW. All generators have voltage regulators, speed governors, and power system stabilizers. Any generator outage changes the generator’s rotor speed and terminal voltage.

4.1 Case of generator outage with only active power curtailment

In this section, only active power is deducted from the sensitive load to regulate the speed of the remaining generators and reactive power dispatch. Initially, generator G₃ of capacity 650 MW and G9 of capacity 830 MW are taken out one-by-one, further, generators G₂ and G₃ are taken out. The center of inertia is expressed as ${\omega }_{coi}=\frac{{\displaystyle \sum }_{i=1}^{i=n}{\omega }_i{H}_i}{{\displaystyle \sum }_{i=1}^{i=n}{H}_i}$. The center of interia speed reflects the total system speed. Tables 2A, B show the different load curtailments performed under the G₃ and G₉ outages. In tables, the first column summarizes the sensitivity index The different cases are shown in Figure 3.

TABLE 2

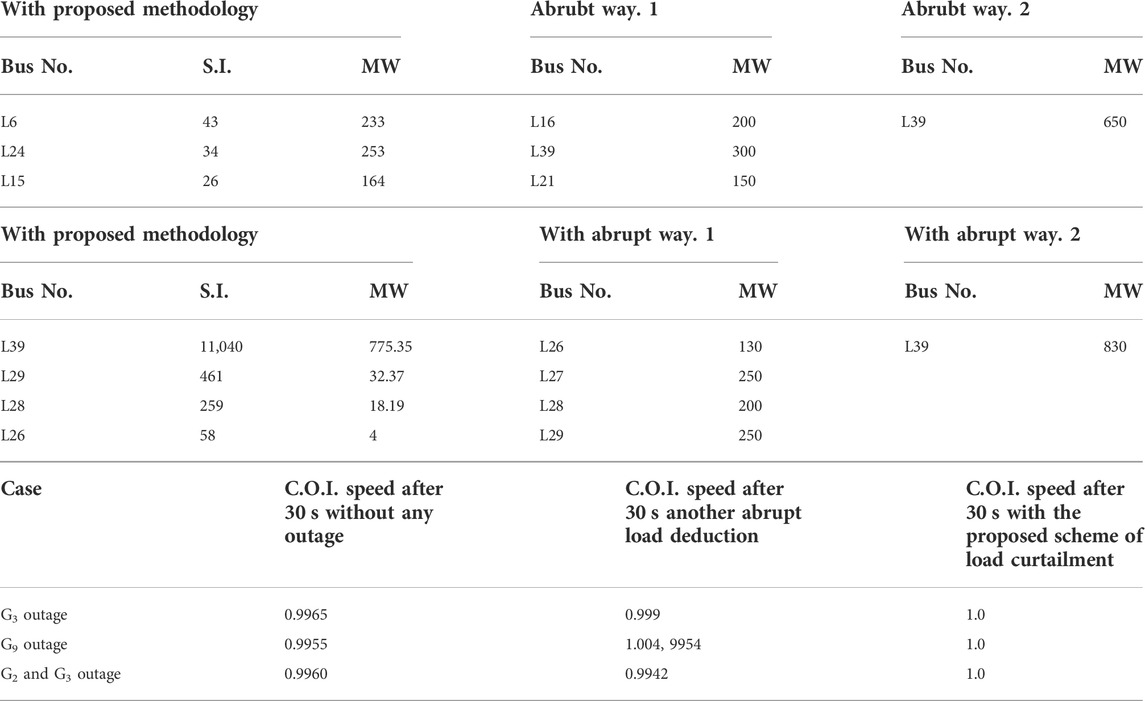
TABLE 2. (A) Active power deduction in case of G₃ outage. (B) Active power deduction in G₉ outage condition. (C) C.O.I steady-state value in different cases.

4.2 Both active and reactive power deduction

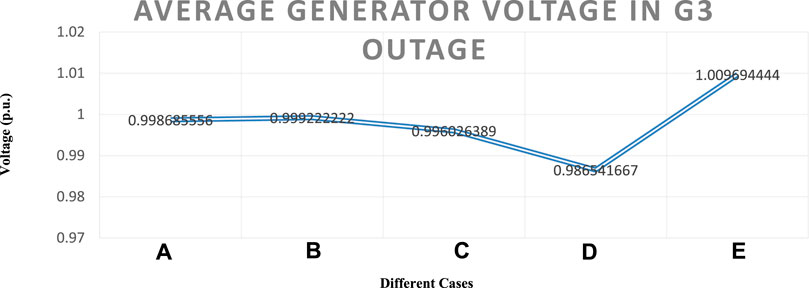
As discussed in sections #2 and #3 for the terminal voltage regulation scenario, generator G₃ in the first case and generator G₆ in the second case are subjected to the outage. As discussed in Section 3, for voltage profile maintenance, the reactive power should be shedded. In the generator G₃ outage case, power is deducted according to Table 3B, and in the case of G₆ outage, power deduction is carried out according to Table 3C. All the load voltages after power deduction are mentioned in Tables 3D, E and also bar charts in Figures 2A,B.

TABLE 3

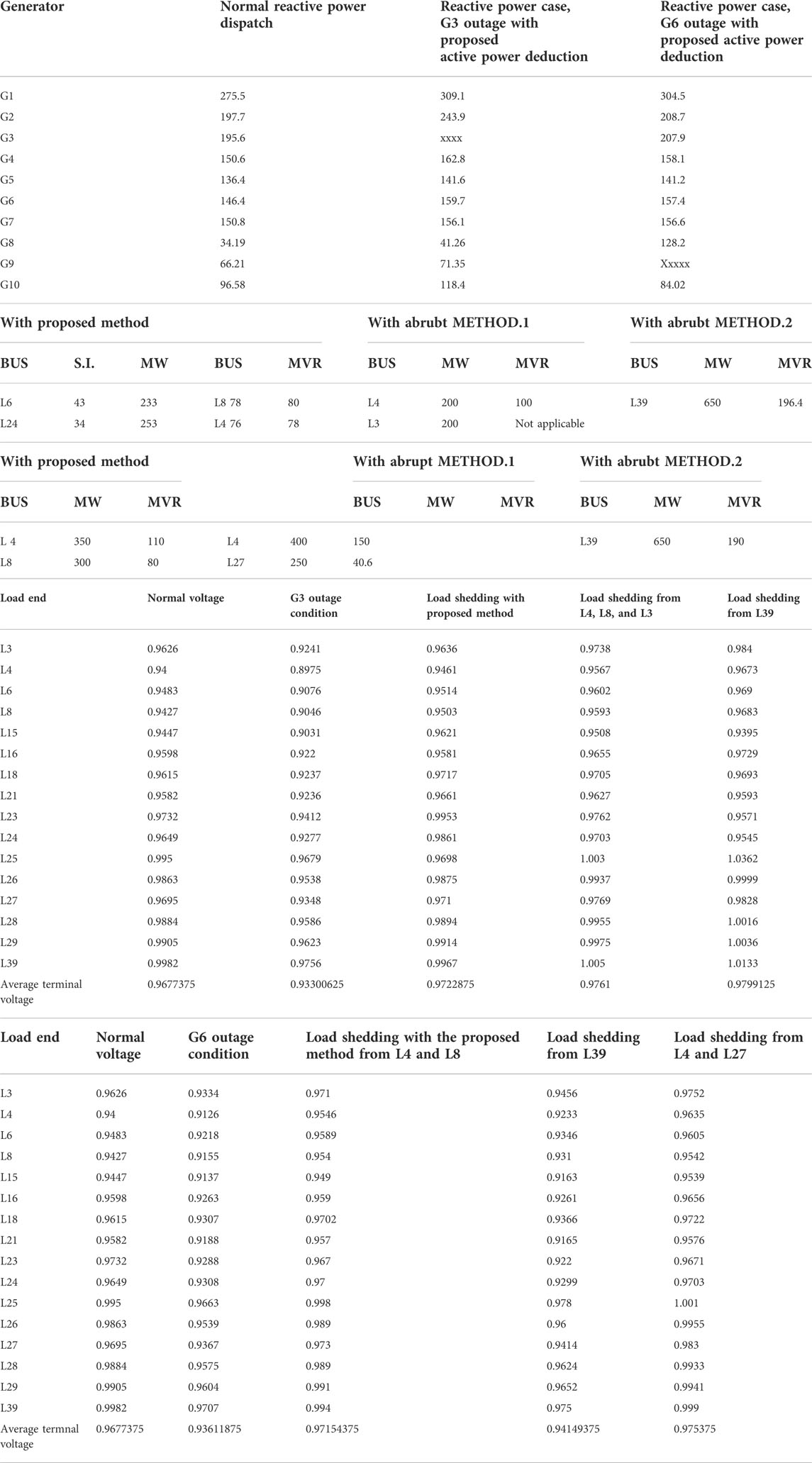
TABLE 3. (A) Reactive power delivery by generators in case of generator outage and with active power deduction. (B) Active and reactive power deduction in case of G₃ Outage. (C) Active and reactive power deduction in a different way in G6 outage. (D) Load voltage in G₃ outage condition with different load sheddings. (E) Load voltage in G₆ outage condition with different load sheddings.

FIGURE 2

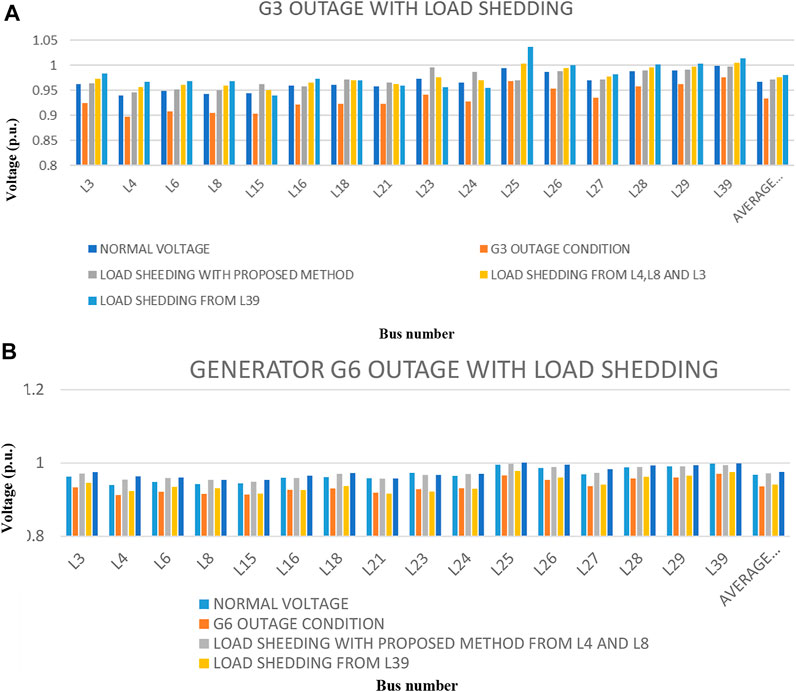
FIGURE 2. (A) Voltage profile of load terminal in case of generator G₃ outage with different manners of load shedding. (B) Voltage profile of load terminal in case of generator G₆ outage with different manners of load shedding.

5 Conclusion

In this article, a heuristic knowledge-based load shedding method is proposed. The load generator sensitivity matrices are assembled as the final process of knowledge discovery to provide the amount and location of power to be curtailed in case of a generator outage. The proposed methodology described in this article is applied to three generator outage cases, and the results are shown as a deviation of the center of inertia speed, as in Figure 3C. It is found that the proposed method of load shedding gives a C.O.I speed of 1 p.u while deducting only the active power, but the reactive power is more stressed on generators according to Table 3A. In contrast, if both active and reactive power is deducted using the proposed method, the load voltage is closer to normal than the other abrupt methods. Finally, the generator G₃ outage condition is examined in detail, as summarized in Table 4 and Figure 4. It is concluded that the proposed method is more cost-effective in reactive power management and voltage conditions.

FIGURE 3

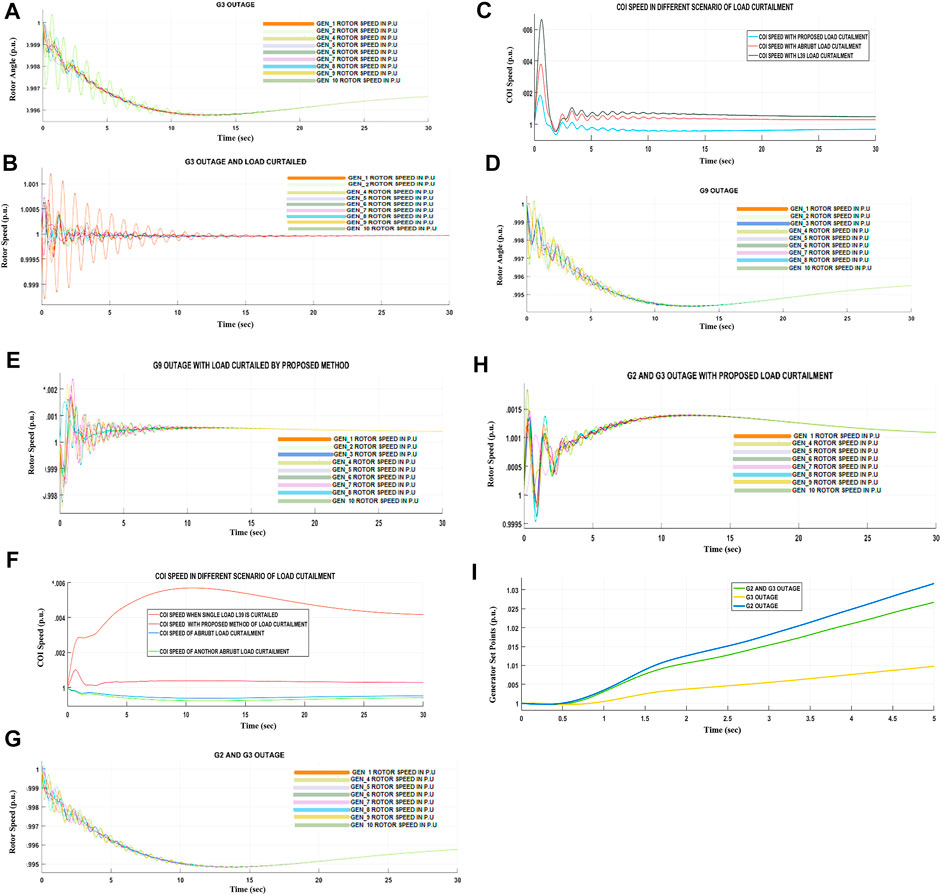
FIGURE 3. (A) Rotor speed of generator in case of G3 outage. (B) Rotor speed of generator in case of G₃ outage with proposed load shedding. (C) Center of inertia speed of generator in case of G₃ outage scenario in different combination load shedding. (D) Rotor speed of generator in case of G₉ outage. (E) Rotor speed of generator in case of G₉ outage with proposed load shedding. (F) Center of inertia speed of generator in G₉ outage scenario in different combinations of load shedding. (G) Rotor speed of generator in case of G₂ and G₃ outage. (H) Rotor speed of generator in case of G₂ and G₃ outage with proposed load shedding. (I) Generator set point variation of G₁ in simulation environment.

TABLE 4

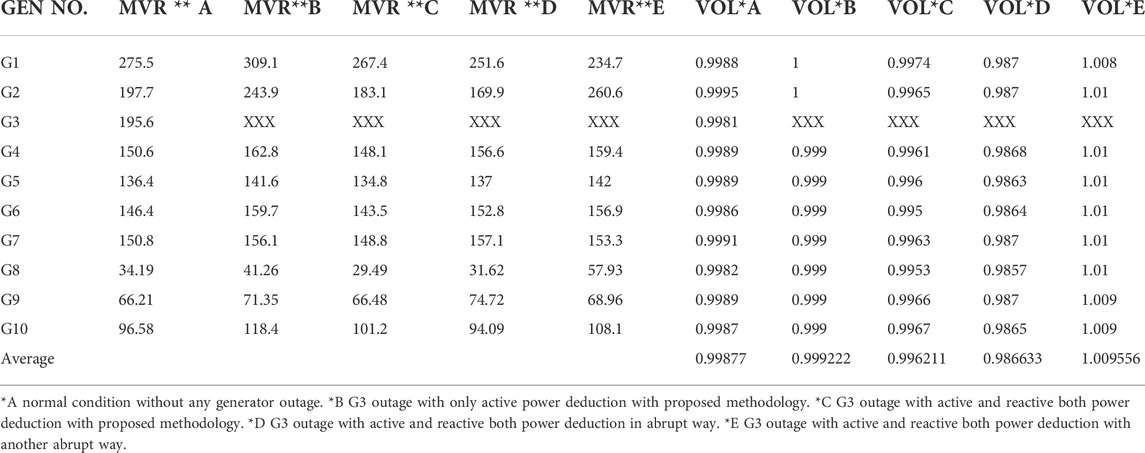
TABLE 4. Reactive power delivery and generator terminal voltage under all conditions of generator G₃ outage.

FIGURE 4

FIGURE 4. Average voltage of remaining generators in case of G₃ outage in all Cases.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. NRF-2022R1A2C2004874). This work was supported by the Korea Institute of Energy Technology Evaluation and Planning (KETEP) and the Ministry of Trade, Industry and Energy (MOTIE) of South Korea (No. 20214000000280).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alrajhi, A. H. (2018). A new virtual synchronous machine control structure for voltage source converter in high voltage direct current applications. umm al qura Univ. J. Eng. Archit. X 33, 1–6.

Google Scholar

Alrajhi Alsiraji, H., and El-Shatshat, R. (2021). Virtual synchronous machine/dual-droop controller for parallel interlinking converters in hybrid AC–DC microgrids. Arab. J. Sci. Eng. 46, 983–1000. doi:10.1007/s13369-020-04794-y

CrossRef Full Text | Google Scholar

Alrajhi, H. (2022). A generalized state space average model for parallel dc-to-dc converters. Comput. Syst. Sci. Eng. 41 (2), 717–734. doi:10.32604/csse.2022.021279

CrossRef Full Text | Google Scholar

Alshammari, K., Alrajhi, H., and El-Shatshat, R. (2022). Optimal power flow for hybrid AC/MTDC systems. Arab. J. Sci. Eng. 47, 2977–2986. doi:10.1007/s13369-021-05983-z

CrossRef Full Text | Google Scholar

Alshammari, K., Alsiraji, H. A., and Shatshat, R. E., (2018), "Optimal power flow in multi -terminal HVDC systems," 2018 IEEE Electrical Power and Energy Conference (EPEC), 10-11 October 2018, Toronto, ON, Canada, pp. 1–6. doi:10.1109/EPEC.2018.8598298

CrossRef Full Text | Google Scholar

Alsiraji, H. A., and El-Shatshat, R. (2018). “Serious operation issues and challenges related to multiple interlinking converters interfacing a hybrid AC/DC microgrid,” in 2018 IEEE Canadian Conference on Electrical & Computer Engineering (CCECE), Quebec, QC, Canada, 13-16 May 2018, 1–5. doi:10.1109/CCECE.2018.8447831

CrossRef Full Text | Google Scholar

Alsiraji, H. (2018). “Operational control and analysis of a hybrid AC/DC microgrid,”. Ph.DAdvisor (Hybrid, AC, and DC Microgrids: UWSpace). Available at: http://hdl.handle.net/10012/13053.

Google Scholar

Azasoo, J. Q., Kanakis, T, Al-Sherbaz, A, and Michael Opoku Agyeman, (2020). Heuristic optimization for microload shedding in generation constrained power systems. IEEE Access 8, 13294–13304. doi:10.1109/ACCESS.2020.2965819

CrossRef Full Text | Google Scholar

Banijamali, S. S., and Amraee, T (2018). Semi-adaptive setting of under frequency load shedding relays considering credible generation outage scenarios. IEEE Trans. Power Deliv. 34 (3), 1098–1108. doi:10.1109/tpwrd.2018.2884089

CrossRef Full Text | Google Scholar

Cruz, L M., Alvarez, D L., Al-Sumaiti, A S., and Rivera, S (2020). Load curtailment optimization using the PSO algorithm for enhancing the reliability of distribution networks. Energies 13, 3236–3312. doi:10.3390/en13123236

CrossRef Full Text | Google Scholar

Deb, S., Al Ammar, E. A., AlRaihi, H., Alsaidan, I., and Shariff, S. M. (2022). V2G pilot projects: Review and lessons learnt", developing charging infrastructure and technologies for electric vehicles. Pennsylvania, United States: IGI-Global, 252–267.

CrossRef Full Text | Google Scholar

Gharebaghi, S., Vennelaganti, S. G., Chaudhuri, N. R., Ting, H., Thomas, F., and La Porta, (2021). Inclusion of pre-existing undervoltage load shedding schemes in AC-QSS cascading failure models. IEEE Trans. Power Syst. 36 (6), 5645–5656. doi:10.1109/TPWRS.2021.3075210

CrossRef Full Text | Google Scholar

Hong, Y Y, and Hsiao, C Y (2022). Under-frequency load shedding in a standalone power system with wind-turbine generators using fuzzy PSO. IEEE Trans. Power Deliv. 37 (2), 1140–1150. doi:10.1109/TPWRD.2021.3077668

CrossRef Full Text | Google Scholar

Jiang, M, Guo, Q, Sun, H, and Ge, H (2020). Decoupled piecewise linear power flow and its application to under voltage load shedding. CSEE J. Power Energy Syst. 7 (5), 976–985. doi:10.17775/CSEEJPES.2019.02900

CrossRef Full Text | Google Scholar

Li, C, Wu, Y, Sun, Y, Zhang, H, Liu, Y, Liu, Y, et al. (2020). Continuous under-frequency load shedding scheme for power system Adaptive frequency control. IEEE Trans. Power Syst. 35 (2), 950–961. doi:10.1109/TPWRS.2019.2943150

CrossRef Full Text | Google Scholar

Lin, F. (2019). Worst-case load shedding in electric power networks. IEEE Trans. Control Netw. Syst. 6 (3), 1269–1277. doi:10.1109/TCNS.2019.2935559

CrossRef Full Text | Google Scholar

Małkowski, R. (2020). Małkowski, Nieznański_2020_Underfrequency load shedding an innovative algorithm based on fuzzy logic. Energies 13, 1456. doi:10.3390/en13061456

CrossRef Full Text | Google Scholar

Masood, N-A., Shazon, M. N. H., Rahman Deeba, S., and Modak, S. R. (2021). A frequency and voltage stability-based load shedding technique for low inertia power systems. IEEE Access 9, 78947–78961. doi:10.1109/ACCESS.2021.3084457

CrossRef Full Text | Google Scholar

Nourollah, S., Aminifar, F., and Gharehpetian, G. B. (2019). A hierarchical regionalization-based load shedding plan to recover frequency and voltage in microgrid. IEEE Trans. Smart Grid 10 (4), 3818–3827. doi:10.1109/TSG.2018.2837160

CrossRef Full Text | Google Scholar

Nourollah, S., and Gharehpetian, Gevork B. (2019). Coordinated load shedding strategy to restore voltage and frequency of microgrid to secure region. IEEE Trans. Smart Grid 10 (4), 4360–4368. doi:10.1109/TSG.2018.2857840

CrossRef Full Text | Google Scholar

Potel, Barnabé, Vincent, Debusschere, Cadoux, Florent, and Urban, Rudez (2019). A real-time adjustment of conventional under-frequency load shedding thresholds. IEEE Trans. Power Deliv. 34 (6), 2272–2274. doi:10.1109/TPWRD.2019.2900594

CrossRef Full Text | Google Scholar

Sang, Yuanrui, Xue, Jiayue, Sahraei-Ardakani, Mostafa, and Ou, Ge (2020). An integrated preventive operation framework for power systems during hurricanes. IEEE Syst. J. 14 (3), 3245–3255. doi:10.1109/JSYST.2019.2947672

CrossRef Full Text | Google Scholar

Santos, Athila Quaresma, Machado Monaro, Renato, Coury, Denis Vinicius, and Oleskovicz, Mario (2019). A new real-time multi-agent system for under frequency load shedding in a smart grid context. Electr. Power Syst. Res. 174, 105851. doi:10.1016/j.epsr.2019.04.029

CrossRef Full Text | Google Scholar

Sauhats, Antans, Utans, Andrejs, Silinevics, Jurijs, Junghans, Gatis, and Guzs, Dmitrijs (2021). Enhancing power system frequency with a novel load shedding method including monitoring of synchronous condensers' power injections. Energies 14, 1490–1495. doi:10.3390/en14051490

CrossRef Full Text | Google Scholar

Shi, Fang, Zhang, Hengxu, Cao, Yongji, Sun, Huadong, and Chai, Yun (2019). Enhancing event-driven load shedding by corrective switching with transient security and overload constraints. IEEE Access 7, 101355–101365. doi:10.1109/ACCESS.2019.2929304

CrossRef Full Text | Google Scholar

Skrjanc, T., Mihalic, R., and Rudez, U. (2020). Principal component analysis (PCA)-Supported underfrequency load shedding algorithm. Energies 13 (22), 5896. doi:10.3390/en13225896

CrossRef Full Text | Google Scholar

Talaat, M., Hatata, A. Y., Alsayyari, Abdulaziz S., and Alblawi, Adel (2020). A smart load management system based on the grasshopper optimization algorithm using the under-frequency load shedding approach. Energy 190, 116423. ISSN 0360-5442. doi:10.1016/j.energy.2019.116423

CrossRef Full Text | Google Scholar

Tian, A., and Mou, X. (2019). A network analysis-based distributed load shedding strategy for voltage collapse prevention. IEEE Access 7, 161375–161384. doi:10.1109/ACCESS.2019.2950628

CrossRef Full Text | Google Scholar

Wang, C., Mei, S., Dong, Q., Chen, R., and Zhu, B. (2020). Coordinated load shedding control scheme for recovering frequency in islanded microgrids. IEEE Access 8, 215388–215398. doi:10.1109/ACCESS.2020.3041273

CrossRef Full Text | Google Scholar

Wang, C., Yu, H., Chai, Lin, Liu, H., and Zhu, B. (2021). Emergency load shedding strategy for microgrids based on dueling Deep Q-learning. IEEE Access 9, 19707–19715. doi:10.1109/ACCESS.2021.3055401

CrossRef Full Text | Google Scholar

Zhou, Q., Li, Z., Wu, Q., and Shahidehpour, M. (2019). Two-stage load shedding for secondary control in hierarchical operation of islanded microgrids. IEEE Trans. Smart Grid 10 (3), 3103–3111. doi:10.1109/TSG.2018.2817738

CrossRef Full Text | Google Scholar

Zhu, L., and Luo, Y. (2021). Deep feedback learning based predictive control for power system undervoltage load shedding. IEEE Trans. Power Syst. 36, 4 3349–3361. doi:10.1109/TPWRS.2020.3048681

CrossRef Full Text | Google Scholar

Nomenclature

${\mathit{E}}_{\mathit{q}\mathit{i}}^{,}$ sub transient quadrature axis of the stator

${\mathit{E}}_{\mathit{f}\mathit{i}}$ rotor field voltage reference

${\mathit{G}}_{\mathit{i}\mathit{j}}$ conductance of reduced bus matrices between bus

${\mathit{B}}_{\mathit{i}\mathit{j}}$ susceptance of reduced bus matrices between bus

${\mathit{\delta }}_{\mathit{i}\mathit{j}}$ angle difference between buses

${\mathit{x}}_{\mathit{d}\mathit{i}}$ direct axis reactance of the generator

${\mathit{x}}_{\mathit{d}\mathit{i}}^{,}$ sub transient direct axis reactance of the generator

${\mathit{T}}_{\mathit{d}\mathit{o}\mathit{i}}$ the open axis time constant of the rotor field circuit

${\Delta \mathit{E}}_{\mathit{q}\mathit{i}}^{,}$ an instantaneous change in sub transient quadrature axis voltage of the stator

$\Delta {\mathit{E}}_{\mathit{f}\mathit{i}}$ an instantaneous change in the rotor field

$\Delta {\mathit{B}}_{\mathit{i}\mathit{j}}$ an instantaneous change in susceptance of reduced bus matrices between buses

$\Delta$${\mathit{G}}_{\mathit{i}\mathit{j}}$ an instantaneous change in conductance of reduced bus matrices between buses

$\mathit{G}\left(\mathit{i}\right)$ generator number

$\mathit{L}\left(\mathit{i}\right)$ load situated at bus i