Introduction
One of the main issues of the application of photovoltaic (PV) system in practice is the mismatch between PV modules caused by partial shading (PS) (Iqbal et al., 2021; Zhao et al., 2021). The consequence of this phenomenon is that the energy generated by PV array is not fully utilized, which damages PV modules, shortens the service lifetime, and leads to economic losses. To mitigate this impact, PV reconfiguration technologies are recommended to disperse shadows uniformly, which are divided into static array reconfiguration and dynamic array reconfiguration (Yang et al., 2021a). In contrast to static array reconfiguration method, dynamic reconfiguration brings targeted change to the electrical connection between the PV modules according to the present irradiation on the PV array, which is more flexible and efficient. The above-mentioned method is implemented through a set of electrical switches embedded between the PV modules (Faiza and Cherif, 2021). However, the practical application of a reconfiguration technique will face many challenges. First of all, the current research papers lack expatiation about hardware realization of the PV array reconfiguration method. Second, after realizing the above-mentioned hardware requirements, it is worth thinking how to balance the economic benefits brought by reconfiguration and the potential risks brought by equipment reliability. This paper gives a clarification of the above-mentioned issues and brings some views on different PV reconfiguration technologies.
Static Reconfiguration
Static reconfiguration approach changes the physical location of modules by some specific patterns to disperse the shading effect on the PV array, and there is no need for switches or other redesigned hardware. Hence, static reconfiguration is of lower complexity, easy to configure, and more manageable from the operation perspective. Providing an optimal scheme of module interconnections for PV array is the key in order to achieve the highest energy gain. The Sudoku reconfiguration approach designed for total cross-tied (TCT)-connected PV array rearranges the modules according to the Su Do Ku puzzle pattern (Rani et al., 2013). A particular work (Dhanalakshmi and Rajasekar, 2018a) proposed another puzzle-based reconfiguration scheme named the dominant square reconfiguration approach. Similarly, literature (Dhanalakshmi and Rajasekar, 2018b) introduced a competence square reconfiguration method to execute the physical relocation of PV modules. A more recent study proposed a method to increase output power by rearranging the PV modules based on the Magic Square puzzle (Reddy and Yammani, 2020). Researchers also developed a zigzag scheme for rearranging the modules (Vijayalekshmy et al., 2017). It is worth noting that the zigzag technique is available for a PV array with different numbers of rows and columns, which enhances the expansibility of the proposed method. The drawbacks of these methods are additional line losses due to the increased wire length and ineffective dispersion due to the redundant constraints of the reconfiguration scheme. Therefore, an optimal Sudoku arrangement is developed to solve these problems (Potnuru et al., 2015). Considering wiring complexity and line loss, the extra wire length required depends on the relative position of the module with respect to the modules above and below in the same column, which minimizes the wiring loss. In addition, to improve the engineering practicability, the authors proposed a strategy for the optimal Sudoku technique applied in large-scale PV stations, i.e., view a large-scale PV array as a system that consists of micro-arrays. The large-scale array and micro-arrays are all reconfigured by the optimal Sudoku method. However, all methods mentioned above can only be applied to a TCT-connected PV array. Complex wiring requirements also limit the application of static reconfiguration technology. Therefore, to implement static reconfiguration to large-scale PV power stations is a brand new and challenging task.
Dynamic Reconfiguration
Dynamic reconfiguration technologies use switching matrix to change the electrical interconnections of PV modules. The adaptive electrical array reconfiguration of PV modules is the earliest technology to use switching matrix in PV reconfiguration (Nguyen and Lehman, 2008). According to model-based control algorithm, the adaptive part and the fixed part of a PV array is connected by an alterable switching matrix (Karakose et al., 2016). The shadows are dispersed through connecting the less shaded rows of the adaptive part with the more shaded rows of the fixed part. Thus, row current can be equalized. This method is of low complexity, but the power loss mitigation is relatively small, and there is the need for a huge amount of switches, which leads to an increase in cost. The adaptive array reconfiguration approach divides the PV array into two sub-arrays. The adaptive sub-array is reconfigured by micro-control units to equalize the irradiance distribution (Liu et al., 2010). This method has a relatively high complexity and therefore is appropriate for a PV system in individual buildings or small geographic areas.
Meta-heuristic algorithm-based PV reconfiguration strategy is a very active area of research in recent years because of its flexibility, and there is no need of a precise system model (Yang et al., 2020a; Yang et al., 2020b; Dasu et al., 2021; Sakthivel and Sathya, 2021; Wang et al., 2021). So far, genetic algorithm (Deshkar et al., 2015), gravitational search algorithm (Hasanien et al., 2016), particle swarm algorithm (Babu et al., 2018), modified Harris hawks algorithm (Yousri et al., 2020a), marine predators algorithm (Yousri et al., 2020b), grey wolf optimization algorithm (Balraj and Stonier, 2020), butterfly optimization algorithm (Fathy, 2020), artificial ecosystem-based optimization (Yousri et al., 2020c), democratic political algorithm (Yang et al., 2021b), and other several meta-heuristic algorithms are applied in PV reconfiguration research. It should be noted that these strategies are all designed for TCT structure, the principle of which is changing the electrical interconnection of modules in the same column so as to equalize the row current. Some works (Deshkar et al., 2015; Babu et al., 2018; Balraj and Stonier, 2020; Fathy, 2020; Yousri et al., 2020a; Yousri et al., 2020b; Yousri et al., 2020c) used row current as one of the evaluation criteria of the reconfiguration scheme, which reflects the principle of reconfiguration intuitively. Hasanien et al. (2016) designed the irradiance level mismatch index to analyze the irradiance level mismatch on the row level, which provides a new research idea of reconfiguration. Specifically, one work (Babu et al., 2018) took total income per year into account, which is worth using as a reference. Other works (Balraj and Stonier, 2020; Fathy, 2020; Yousri et al., 2020a; Yousri et al., 2020b; Yousri et al., 2020c; Yang et al., 2021b) used fill factor as an evaluation criterion of the reconfiguration results. It is debatable because fill factor is usually used to evaluate the performance of PV cells (Min et al., 2020). To verify the performance of algorithms, there is a need to introduce some parameters, such as the execution time used (Hasanien et al., 2016; Babu et al., 2018; Yousri et al., 2020a; Yousri et al., 2020b; Yousri et al., 2020c; Yang et al., 2021b) and the standard deviation (Babu et al., 2018; Yang et al., 2021b). The details of the evaluation criteria used by prior research are shown in Table 1. The array sizes applied in literatures are different, mostly arrays with the same number of rows and columns, such as 9 × 9 and 16 × 16. Others are non-square arrays with varied sizes, such as 6 × 4 and 6 × 20. It should be appropriate for researchers to apply non-square arrays to expand the applicability of the method studied in PV reconfiguration.
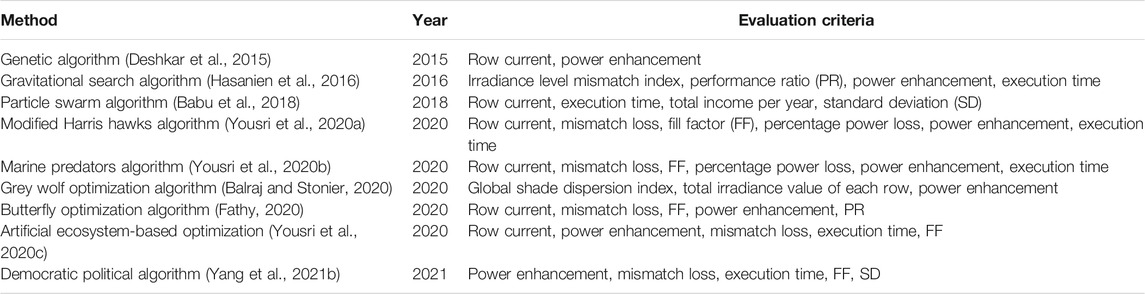
TABLE 1. Summary of the evaluation criteria used in prior research papers on photovoltaic reconfiguration studies.
The investigated cases in Deshkar et al. (2015) and Yousri et al. (2020a) applied four shading patterns, i.e., short and wide, long and wide, short and narrow, and long and narrow. One work (Hasanien et al., 2016) applied single-row PS, double-row PS, and quarter-array PS; these are three types of shadows. There are other shadow types like uneven row, uneven column, diagonal, outer, center, and random shadow (Yang et al., 2021b). Hence, it is necessary to develop a benchmark to support researchers in conducting a more reasonable study (Chen et al., 2018; Yang et al., 2019; Yao et al., 2019; Liu et al., 2020; Zhou et al., 2020; Huang et al., 2021; Xiong et al., 2021; Zhang K. et al., 2021). Moreover, simulations should be implemented in a standard test condition, which is 1,000 W/m2 and 25°C.
TCT topology is the mainly used topology in existing research about PV reconfiguration, and the rest used series–parallel (SP) topology as the hardware structure of the PV array. In practice, SP topology is the sole structure of PV power station (Shams et al., 2021). It is worth noting that TCT topology-based PV reconfiguration improves the energy efficiency and the reliability of the PV system, but due to the increased wiring loss, high system complexity as well as high operational and maintenance cost, the SP topology has a higher efficiency than TCT. Under this circumstance, it is more appropriate to shift the research emphasis from TCT to SP. Significantly, reconfiguration solutions in large-scale PV stations should be developed to fit the actual engineering needs.
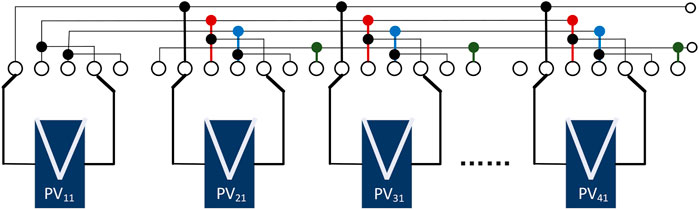
One of the most important parts to realize in reconfiguration technology is the hardware design of PV reconfiguration technology. It is worth learning from works (Yousri et al., 2020a; Yousri et al., 2020b) that proposed a switching matrix consisting of single-pole, multiple throw switches, which greatly reduced the number of switches compared to TCT (see Figure 1). The required number of switches of a 4 × 6 PV array in this method is 48, but for a TCT-interconnected array of the same size, the number of switches is 258, which is calculated by the following equation:
where P is the number of rows, and Q is the number of columns.
Zhang et al. (2021) designed a varying PS to simulate shadows of moving clouds in 10 min, which means that the switching matrix should be switched in minutes. This will bring dependability issues due to various conditions like switch fault or increased expenses. Thus, it is worth considering how to balance the benefits and potential risks of optimal array reconfiguration. Moreover, researchers should focus on experiments instead of simulations, which has a far-reaching significance for applying reconfiguration into practical engineering.
Finally, due to the inherent defect of randomness in meta-heuristic algorithms, the quality of an optimal solution varies with the number of iterations and the number of populations (Yang et al., 2015; Zhang et al., 2015; Zhang et al., 2016; Yang et al., 2020c). The weight parameters assigned to algorithms should also be carefully chosen. For a PV array of different sizes, algorithm parameters need to be set purposefully to weigh the computational burden of the algorithm and the solution quality. In addition, previous methods found it difficult to solve a large-scale PV system optimization because the computing time is increased with system scale, which becomes an urgent problem to be solved in the application of PV reconfiguration.
Discussion and Conclusion
PV reconfiguration technology is an effective strategy to extract the power of a PV system under partial shading condition, but it is still in its research and development phase. The efficiency and engineering practicability of this technique are major challenges, detailed as follows:
(a) Despite its cheap cost, static reconfiguration faces complex wiring difficulties and ineffective shadow dispersion. Setting reasonable constraints can avoid the invalid rearrangements of PV modules. Furthermore, the next step of researchers is to investigate some strategies to apply static reconfiguration into a large-scale PV station.
(b) The research keystone of dynamic reconfiguration is strategies for SP-connected PV array. Besides this, a benchmark of studied cases including PV array sizes and shading patterns can be formulated to verify the correctness of the studied results.
(c) Another important aspect of this technique is the hardware design of the dynamic reconfiguration. The switching frequency of the switching matrix is a critical research issue. Moreover, the material, price, and applicability of the switch used in the proposed technique should be considered carefully.
(d) To cover the shortcomings of prior studies of meta-heuristic algorithm-based reconfiguration approaches, there is an urgent need to develop an effective and efficient control algorithm to apply a reconfiguration technique to meet the needs of a practical engineering project.
Author Contributions
RS contributed to writing the original draft and editing. BY contributed to conceptualization. YH contributed to visualization and the discussion of the topic.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
References
Babu, T. S., Ram, J. P., Dragicevic, T., Miyatake, M., Blaabjerg, F., Rajasekar, N., et al. (2018). Particle Swarm Optimization Based Solar PV Array Reconfiguration of the Maximum Power Extraction under Partial Shading Conditions. IEEE Trans. Sust.x Energ. 9 (1), 74–85. doi:10.1109/tste.2017.2714905
Balraj, R., and Stonier, A. A. (2020). A Novel PV Array Interconnection Scheme to Extract Maximum Power Based on Global Shade Dispersion Using Grey Wolf Optimization Algorithm under Partial Shading Conditions. Circuit World 48, 28–38. doi:10.1108/CW-07-2020-0143
Chen, J., Yao, W., Zhang, C., Ren, Y., and Jiang, L. (2018). Design of Robust MPPT Controller for Grid-Connected PMSG-Based Wind Turbine via Perturbation Observation Based Nonlinear Adaptive Control. Renew. Energ. 101, 34–51. doi:10.1016/j.renene.2018.11.048
Dasu, B., Mangipudi, S., and Rayapudi, S. (2021). Small Signal Stability Enhancement of a Large Scale Power System Using a Bio-Inspired Whale Optimization Algorithm. Prot. Control. Mod. Power Syst. 6 (16), 1–17. doi:10.1186/s41601-021-00215-w
Deshkar, S. N., Dhale, S. B., Mukherjee, J. S., Babu, T. S., and Rajasekar, N. (2015). Solar PV Array Reconfiguration under Partial Shading Conditions for Maximum Power Extraction Using Genetic Algorithm. Renew. Sust. Energ. Rev. 43, 102–110. doi:10.1016/j.rser.2014.10.098
Dhanalakshmi, B., and Rajasekar, N. (2018a). Dominance Square Based Array Reconfiguration Scheme for Power Loss Reduction in Solar Photovoltaic (PV) Systems. Energ. Convers. Manag. 156, 84–102. doi:10.1016/j.enconman.2017.10.080
Dhanalakshmi, B., and Rajasekar, N. (2018b). A Novel Competence Square Based PV Array Reconfiguration Technique for Solar PV Maximum Power Extraction. Energ. Convers. Manag. 174, 897–912. doi:10.1016/j.enconman.2018.08.077
Faiza, B., and Cherif, L. (2021). PV Array Reconfiguration Techniques for Maximum Power Optimization under Partial Shading Conditions: A Review. Solar Energy 230, 558–582. doi:10.1016/j.solener.2021.09.089
Fathy, A. (2020). Butterfly Optimization Algorithm Based Methodology for Enhancing the Shaded Photovoltaic Array Extracted Power via Reconfiguration Process. Energ. Convers. Manag. 220, 113115. doi:10.1016/j.enconman.2020.113115
Hasanien, H. M., Al-Durra, A., and Muyeen, S. M. (2016). “Gravitational Search Algorithm-Based Photovoltaic Array Reconfiguration for Partial Shading Losses Reduction,” in IET International Conference on Renewable Power Generation, London, UK. September 21–23, 2016, 1–6. doi:10.1049/cp.2016.0577
Huang, S., Wu, Q., Liao, W., Wu, G., Li, X., and Wei, J. (2021). Adaptive Droop-Based Hierarchical Optimal Voltage Control Scheme for Vsc-Hvdc Connected Offshore Wind Farm. IEEE Trans. Ind. Inform. 17 (12), 8165–8176. doi:10.1109/tii.2021.3065375
Iqbal, B., Nasir, A., and Murtaza, A. F. (2021). Stochastic Maximum Power point Tracking of Photovoltaic Energy System under Partial Shading Conditions. Prot. Control. Mod. Power Syst. 6 (30), 1–13. doi:10.1186/s41601-021-00208-9
Karakose, M., Baygin, M., Murat, K., Baygin, N., and Akin, E. (2016). Fuzzy Based Reconfiguration Method Using Intelligent Partial Shadow Detection in PV Arrays. Int. J. Comput. Intell. Syst. 9 (2), 202–212. doi:10.1080/18756891.2016.1150004
Liu, J., Yao, W., Wen, J. Y., Fang, J. K., Jiang, L., He, H. B., et al. (2020). Impact of Power Grid Strength and PLL Parameters on Stability of Grid-Connected DFIG Wind Farm. IEEE Trans. Sust. Energ. 11 (1), 545–557. doi:10.1109/tste.2019.2897596
Liu, Y., Pang, Z., and Cheng, Z. (2010). “Research on an Adaptive Solar Photovoltaic Array Using Shading Degree Model-Based Reconfiguration Algorithm,” in Chinese Control and Decision Conference, Xuzhou, China. May 26–28, 2010, 2356–2360. doi:10.1109/ccdc.2010.5498823
Min, K. H., Kim, T., Kang, M. G., Song, H. E., Kang, Y., Lee, H. S., et al. (2020). An Analysis of Fill Factor Loss Depending on the Temperature for the Industrial Silicon Solar Cells. Energies 13 (11), 2931. doi:10.3390/en13112931
Nguyen, D., and Lehman, B. (2008). An Adaptive Solar Photovoltaic Array Using Model-Based Reconfiguration Algorithm. IEEE Trans. Ind. Elect. 55 (7), 2644–2654. doi:10.1109/tie.2008.924169
Potnuru, S. R., Pattabiraman, D., Ganesan, S. I., and Chilakapati, N. (2015). Positioning of PV Panels for Reduction in Line Losses and Mismatch Losses in PV Array. Renew. Energ. 78, 264–275. doi:10.1016/j.renene.2014.12.055
Rani, B. I., Ilango, G. S., and Nagamani, C. (2013). Enhanced Power Generation from PV Array under Partial Shading Conditions by Shade Dispersion Using Su Do Ku Configuration. IEEE Trans. Sust. Energ. 4 (3), 594–601. doi:10.1109/tste.2012.2230033
Reddy, S. S., and Yammani, C. (2020). A Novel Magic-Square Puzzle Based One-Time PV Reconfiguration Technique to Mitigate Mismatch Power Loss Under Various Partial Shading Conditions. Optik 222, 165289. doi:10.1016/j.ijleo.2020.165289
Sakthivel, V. P., and Sathya, P. D. (2021). Single and Multi-Area Multi-Fuel Economic Dispatch Using a Fuzzified Squirrel Search Algorithm. Prot. Control. Mod. Power Syst. 6 (11), 1–13. doi:10.1186/s41601-021-00188-w
Shams, I., Mekhilef, S., and Tey, K. S. (2021). Advancement of Voltage Equalizer Topologies for Serially Connected Solar Modules as Partial Shading Mitigation Technique: A Comprehensive Review. J. Clean. Prod. 285, 124824. doi:10.1016/j.jclepro.2020.124824
Vijayalekshmy, S., Bindu, G. R., and Iyer, S. R. (2017). “Performance Comparison of Zig-Zag and Su Do Ku Schemes in a Partially Shaded Photovoltaic Array under Static Shadow Conditions,” in Innovations in Power and Advanced Computing Technologies, Vellore, India, April 21–22, 2017, 1–6. doi:10.1109/ipact.2017.8245109
Wang, P., Song, J., Liang, F., Shi, F., Kong, X., Xie, G., et al. (2021). Equivalent Model of Multi-type Distributed Generators under Faults with Fast-Iterative Calculation Method Based on Improved PSO Algorithm. Prot. Control. Mod. Power Syst. 6 (29), 1–12. doi:10.1186/s41601-021-00207-w
Xiong, Y., Yao, W., Wen, J., Lin, S., Ai, X., Fang, J., et al. (2021). Two-Level Combined Control Scheme of VSC-MTDC Integrated Offshore Wind Farms for Onshore System Frequency Support. IEEE Trans. Power Syst. 36 (1), 781–792. doi:10.1109/tpwrs.2020.2998579
Yang, B., Jiang, L., Yao, W., and Wu, Q. H. (2015). Perturbation Estimation Based Coordinated Adaptive Passive Control for Multimachine Power Systems. Control. Eng. Pract. 44, 172–192. doi:10.1016/j.conengprac.2015.07.012
Yang, B., Zhu, T., Wang, J., Shu, H., Yu, T., Zhang, X., et al. (2020a). Comprehensive Overview of Maximum Power point Tracking Algorithms of PV Systems under Partial Shading Condition. J. Clean. Prod. 268, 121983. doi:10.1016/j.jclepro.2020.121983
Yang, B., Wang, J., Zhang, X., Yu, T., Yao, W., Shu, H., et al. (2020b). Comprehensive Overview of Meta-Heuristic Algorithm Applications on PV Cell Parameter Identification. Energ. Convers. Manag. 208, 112595. doi:10.1016/j.enconman.2020.112595
Yang, B., Wang, J. B., Zhang, X. S., Wang, J. T., Shu, H. C., Li, S. N., et al. (2020c). Applications of Battery/Supercapacitor Hybrid Energy Storage Systems for Electric Vehicles Using Perturbation Observer Based Robust Control. J. Power Sourc. 448, 227444. doi:10.1016/j.jpowsour.2019.227444
Yang, B., Ye, H., Wang, J. J. B., Li, J., Wu, S., Li, Y., et al. (2021a). PV Arrays Reconfiguration for Partial Shading Mitigation: Recent Advances, Challenges and Perspectives. Energ. Convers. Manag. 247, 114738. doi:10.1016/j.enconman.2021.114738
Yang, B., Shao, R. N., Zhang, M. T., Ye, H., Liu, B., Bao, T., et al. (2021b). Socio-Inspired Democratic Political Algorithm for Optimal PV Array Reconfiguration to Mitigate Partial Shading. Sustain. Energy Technol. Assess. 48, 101627. doi:10.1016/j.seta.2021.101627
Yang, B., Zhong, L., Zhang, X., Shu, H., Yu, T., Li, H., et al. (2019). Novel Bio-Inspired Memetic Salp Swarm Algorithm and Application to MPPT for PV Systems Considering Partial Shading Condition. J. Clean. Prod. 215, 1203–1222. doi:10.1016/j.jclepro.2019.01.150
Yao, Q., Liu, J., and Hu, Y. (2019). Optimized Active Power Dispatching Strategy Considering Fatigue Load of Wind Turbines during De-loading Operation. IEEE Access 7, 17439–17449. doi:10.1109/access.2019.2893957
Yousri, D., Allam, D., and Eteiba, M. B. (2020a). Optimal Photovoltaic Array Reconfiguration for Alleviating the Partial Shading Influence Based on a Modified harris Hawks Optimizer. Energ. Convers. Manag. 206, 112470. doi:10.1016/j.enconman.2020.112470
Yousri, D., Babu, T. S., Beshr, E., Eteiba, M. B., and Allam, D. (2020b). A Robust Strategy Based on marine Predators Algorithm for Large Scale Photovoltaic Array Reconfiguration to Mitigate the Partial Shading Effect on the Performance of PV System. IEEE Access 8, 112407–112426. doi:10.1109/access.2020.3000420
Yousri, D., Babu, T. S., Mirjalili, S., Rajasekar, N., and Elaziz, M. A., (2020c). A Novel Objective Function with Artificial Ecosystem-Based Optimization for Relieving the Mismatching Power Loss of Large-Scale Photovoltaic Array. Energ. Convers. Manag. 225, 113385. doi:10.1016/j.enconman.2020.113385
Zhang, K., Zhou, B., Or, S. W., Li, C., Chung, C. Y., and Voropai, N. I. (2021). Optimal Coordinated Control of Multi-Renewable-To-Hydrogen Production System for Hydrogen Fueling Stations. IEEE Trans. Ind. Appl. doi:10.1109/TIA.2021.3093841
Zhang, X., Li, C., Li, Z., Yin, X., Yang, B., Gan, L., et al. (2021). Optimal Mileage-Based PV Array Reconfiguration Using Swarm Reinforcement Learning. Energ. Convers. Manag. 232 (2), 113892. doi:10.1016/j.enconman.2021.113892
Zhang, X. S., Yu, T., Yang, B., and Li, L. (2016). Virtual Generation Tribe Based Robust Collaborative Consensus Algorithm for Dynamic Generation Command Dispatch Optimization of Smart Grid. Energy 101, 34–51. doi:10.1016/j.energy.2016.02.009
Zhang, X. S., Yu, T., Yang, B., Zheng, L. M., and Huang, L. N. (2015). Approximate Ideal Multi-Objective Solution Q(λ) Learning for Optimal Carbon-Energy Combined-Flow in Multi-Energy Power Systems. Energ. Convers. Manag. 106, 543–556. doi:10.1016/j.enconman.2015.09.049
Zhao, Y., An, A., Xu, Y., Wang, Q., and Wang, M. (2021). Model Predictive Control of Grid-Connected PV Power Generation System Considering Optimal MPPT Control of PV Modules. Prot. Control. Mod. Power Syst. 6 (32), 1–12. doi:10.1186/s41601-021-00210-1
Keywords: solar energy, photovoltaic array, partial shading, reconfiguration, optimization
Citation: Shao R, Yang B and Han Y (2022) Evaluations of Practical Engineering Application of Photovoltaic Reconfiguration Technology. Front. Energy Res. 9:831249. doi: 10.3389/fenrg.2021.831249
Received: 08 December 2021; Accepted: 22 December 2021;
Published: 26 January 2022.
Edited by:
Bin Zhou, Hunan University, ChinaReviewed by:
Yixuan Chen, The University of Hong Kong, Hong Kong SAR, ChinaXuehan Zhang, Korea University, South Korea
Copyright © 2022 Shao, Yang and Han. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yiming Han, MzczNDgyNzUzQHFxLmNvbQ==
 Ruining Shao
Ruining Shao Bo Yang
Bo Yang Yiming Han
Yiming Han