Surface Evolver Simulation of Droplet Wetting Morphologies on Fiber Without Gravity

Droplet wetting phenomenon is encountered in many engineering applications. Three wetting morphologies, namely, barrel, clamshell, and liquid bridge, are investigated by the finite element method, Surface Evolver (SE) simulations. The barrel shape shrinks gradually as contact angle increases. In the shrinkage process, the dimensionless wetting length reduces, and maximum diameter increases. As the increase of the contact angle, the gas–liquid contact line of clamshell droplets bends and contracts inward gradually. The geometry parameters are extracted from the results from simulations. In addition, the critical spacing of liquid bridge rupture is determined. The critical spacing increases rapidly with the expanding of liquid bridge volume. The liquid bridge volume has a significant effect on critical spacing.

Introduction

Understanding the behavior of fine droplets on fiber is important for many engineering applications such as condensation heat transfer (Deng et al., 2017; Preston et al., 2018; Adera et al., 2020), gas–liquid separation (Zhang et al., 2018; Abishek et al., 2019), dyeing of textiles (Wu et al., 2010), surface wetting (Wang et al., 2018), and water collection (Gao et al., 2021). The studies on fine droplet behaviors can provide useful information for those industry processes. Compared with the extensive understanding of droplets on a plane (Sheng et al., 2007), the behavior of droplets on a cylinder is obviously different. There are two essential shapes for droplet on fiber surface: axisymmetric barrel shape and non-axisymmetric clamshell shape (Rebouillat et al., 1999). The barrel shape tends to occur for large droplets or for small Young–Laplace Contact Angle (YLCA). The clamshell shape appears on the opposite sides.

To date, the adhesion morphologies of droplets on single fiber have been extensively investigated by mathematic model (Carroll, 1976; Lu et al., 2016), numerical simulation (Mchale et al., 2001; Chen et al., 2015; Deng et al., 2017; Chen and Deng, 2017), and experimental test (Gilet et al., 2010; Fang et al., 2015; Amrei et al., 2017). The adhesion morphologies of droplets-on-fiber depend on fiber diameter, wettability of fiber surface, volume of droplet, and surface tension of droplet. Based on the Young–Laplace equation, Carroll (1976) was the pioneer in suggesting the explicit mathematical expressions of the barrel shape. Subsequently, several studies conducted the measurement experiments to enhance the accuracy of the mathematic model (Wagner, 1990; Song et al., 1998). This model is inapplicable to the clamshell shape due to its non-axisymmetric conformation. The Young–Laplace equation is hardly solved for clamshell shape. A fast modeling of clamshell shape was developed based on a variable-radius cap approach (Lu et al., 2016). This model can rapidly describe the clamshell-shaped droplet on fiber when contact angle is greater than 20° and fiber radius is greater than droplet. In addition, many researchers (Mchale and Newton, 2002; Chou et al., 2011) studied the morphology transition between the barrel and clamshell shapes using a surface finite element numerical simulation (Surface Evolver [SE]) developed by Brakke (2000). Besides, Amrei et al. (2017) determined the effect of fiber surface roughness on the adhesion shape. Most of these studies, however, were emphasized on how to accurately extract the contact angle, the critical conditions of shape transition, and the variation of free energy. The geometry characteristic dimensions are significant factors for the next evolution of fine droplets on fiber and were neglected in previous papers.

Liquid bridge is another common conformation of droplets on multiple filaments. The formation, evolution, and rupture of liquid bridge also play a crucial role in those applications. For instance, the liquid bridges may evolve into liquid film. The formation of liquid film causes extra energy consumption and several problems in gas–liquid separation processes (Wilcox et al., 2012). Wu et al. (2010) studied the transition of liquid bridge on two parallel fibers and determined the characteristic curves of liquid bridge in droplet volume versus fiber spacing. Princen (1970) proposed the analytical description of liquid bridge shape on two parallel fibers. Moreover, several authors simulated the three-dimensional shape of liquid bridges and predicted the capillary forces using SE (Virozub et al., 2009; Bedarkar et al., 2010; Aziz and Tafreshi, 2019). However, these studies were focused on dependent factors of morphologies, energies, and forces of liquid bridge. It is very significant to study the rupture of liquid bridge for industry processes.

In this paper, the SE (Brakke, 2000) is utilized to simulate the equilibrium shape of two essential conformations. We extracted the geometry characteristic dimensions of shape from the simulation data by ImageJ software. The effect of contact angle on geometry characteristic dimensions is investigated. In addition, the critical factors of liquid bridge rupture are discussed.

Simulation Methods

The morphologies of fine droplets attached on fiber can be described by the public domain SE package that is widely used to simulate the gas–liquid interface stability (Chou et al., 2011; Liang et al., 2013; Aziz and Tafreshi, 2015). The surface energy minimization method is implemented in SE code. The total free energy (E) of droplet on fiber with volume V containing surface free energy and gravitation energy can be written as:

$E={\gamma }_{LG}{A}_{LG}+\left({\gamma }_{SL}-{\gamma }_{SG}\right)A_{SL}+{\displaystyle \int {\displaystyle \int {\displaystyle {\int }_V\left(\rho gh\right)}}}dV(1)$

where, ${\gamma }_{LG}$ is the surface tension of fine droplet. ${\gamma }_{SL}$ and ${\gamma }_{SG}$ are the interfacial tensions of solid–liquid and solid–gas, respectively. $A_{LG}$ and $A_{SL}$ represent the liquid–gas and solid–liquid interfacial areas, respectively. The third term depicts the gravitational energy. In our work, the diameter of fine droplets is less than the capillary length ${\text{l}}_C={\left({\gamma }_{LG}/\rho g\right)}^{1/2}$; thus, the gravitational effect is excluded for fine droplet, and the third term in equation is zero. In addition, for convenience, the dimensionless volume of fine droplet $V^{\ast }=V^{1/3}//d_{\mathrm{f}}$, the dimensionless fiber spacing $L^{\ast }=L/{\text{d}}_f$, and L is the real fiber spacing. According to the Young’s equation, $\cos \theta =\left({\gamma }_{SG}-{\gamma }_{SL}\right)/{\gamma }_{LG}$, Eq. 1 becomes

$E={\gamma }_{LG}\left(A_{LG}-\cos \theta A_{SL}\right)+{\displaystyle \int {\displaystyle \int {\displaystyle {\int }_V\left(\rho gh\right)}}}dV(2)$

For each case, we adopt the different initial rectangular cuboid shapes: I. wrapping around for barrel shape, II. sitting on for clamshell shape, and III. putting in the middle leads to liquid bridge shape, as shown in Figure 1. The SE model surface mesh uses a triangle unit and evolves iteratively from the initial shape until minimum E is obtained. The surface tension of liquid is 0.032 N/m. The calculation is done when the tolerance of surface energy is less than 10⁻⁸ units.

FIGURE 1

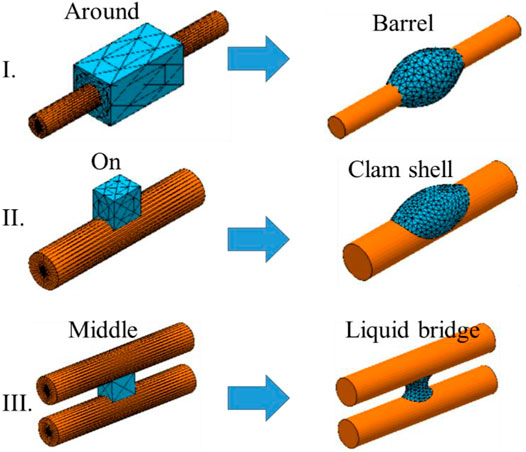
FIGURE 1. The initial shape of different conformations. I. Barrel shape, II. clam shell shape, III. liquid bridge shape.

Results and Discussions

Barrel

The gas–liquid free surface of barrel-shaped droplet under different contact angles was investigated, as shown in Figure 2A. For convenience, we define the dimensionless free surface of gas–liquid as $A_{LG}^{\ast }=A_{LG}^{1/2}/d_f$. In this case, the dimension volume of droplet V* is fixed at 5. The computational images of barrel shape are shown in Figure 2A. It can be seen that the contact lines at two ends move to each other and the barrel shape exhibits the shrinkage tendency with the increase of contact angle. In addition, the dimensionless free surface decreases from 14.63 to 13.87 as the contact angle changes from 5° to 65°. The decline trend becomes slow gradually after 40°.

FIGURE 2

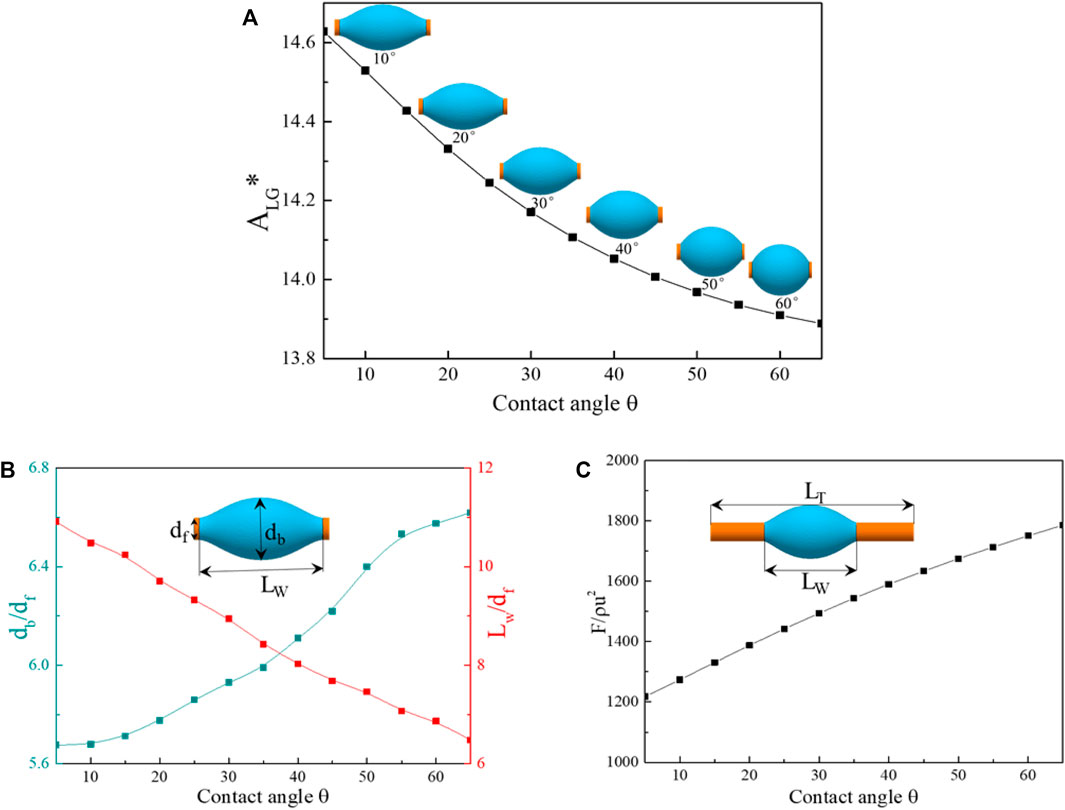
FIGURE 2. (A) Variation of dimensionless free surface with contact angle. (B) Change of dimensionless maximum diameter and wetting length with contact angle. (C) Influence of contact angle on dimensionless air resistance of barrel-shaped droplet.

There are two geometric parameters accounting for barrel shape, maximum diameter d_b and wetting length L_w. Similarly, the dimensionless parameters, $d_b\ast =d_b/d_f$ and $L_w\ast =L_w/d_f$, are illustrated in Figure 2B. In the shrinkage process of barrel-shaped droplet, the dimensionless wetting length L_w* reduces, and the dimensionless maximum diameter d_b* increases. The thicker the maximum diameter, the higher probability the liquid bridge formation is. The increment of d_b* at the range of 20°–55° is higher than that of other ranges. In addition, the wetting length decreases linearly over the contact angle increase. The value of L_w* decreases by more than 1.7 times as the contact angle increases from 5° to 65°.

The morphology of barrel-shaped droplets has an obvious deformation with the change of contact angle. The effect of the droplets shape variation corresponds to the changes of flow field around fiber and air resistance of fiber. Given the geometric parameters of barrel-shaped droplet, the drag force of fiber with barrel-shaped droplet can be described as (Dawar and Chase, 2010; Mead-Hunter et al., 2012).

$F=\frac{1}{2}\rho u^2{C}_D\left(\frac{\pi }{4}{d}_b^2-\left(L_T-L_W\right)d_f\right)(3)$

where, F is the drag force, ρ is the density of air, d_f is the fiber diameter, u is the air flow velocity, d_b is the maximum diameter of barrel-shaped droplet, L_W is the wetting length of barrel-shaped droplet, and L_T is a fixed length of fiber and equal to the L_W at contact angle 5°. C_D is the drag coefficient of air flow around droplet and given by (Dawar and Chase, 2010)

$C_D=\{\begin{array}{l}\frac{24}{{\mathrm{Re}}_a}\mathrm{for}{\mathrm{Re}}_a\le 1\\ \frac{24}{{\mathrm{Re}}_a}\left(1+0.14{\mathrm{Re}}_a^{0.7}\right)\mathrm{for}1\le {\mathrm{Re}}_a\le 1000\end{array}(4)$

for $1\le {\mathrm{Re}}_a\le 1000$. where Re_a is the Reynolds number.

Figure 2C depicts the correlation between the dimensionless air resistance ($F/\rho u^2$) and contact angle of fiber with fixed length. As the contact angle increases, the dimensionless air resistance increases linearly. The amplification of air resistance is about 47% as the contact angle increases from 5° to 65°. This result indicates that barrel-shaped droplet interference in flow field increases with contact angle increase.

Clamshell

Clamshell, an asymmetric morphology, is a common adhesion shape. In this case, dimensionless volume of droplet is fixed at 1. The influence of contact angle on A_LG* of clamshell shape is presented in Figure 3A. As the increase of the contact angle, the gas–liquid contact line of clamshell droplets bends and contracts inward gradually. The value of A_LG* decreases by 3.7% as the contact angle increases from 5° to 65°. The decline rate becomes slow after contact angle 45°.

FIGURE 3

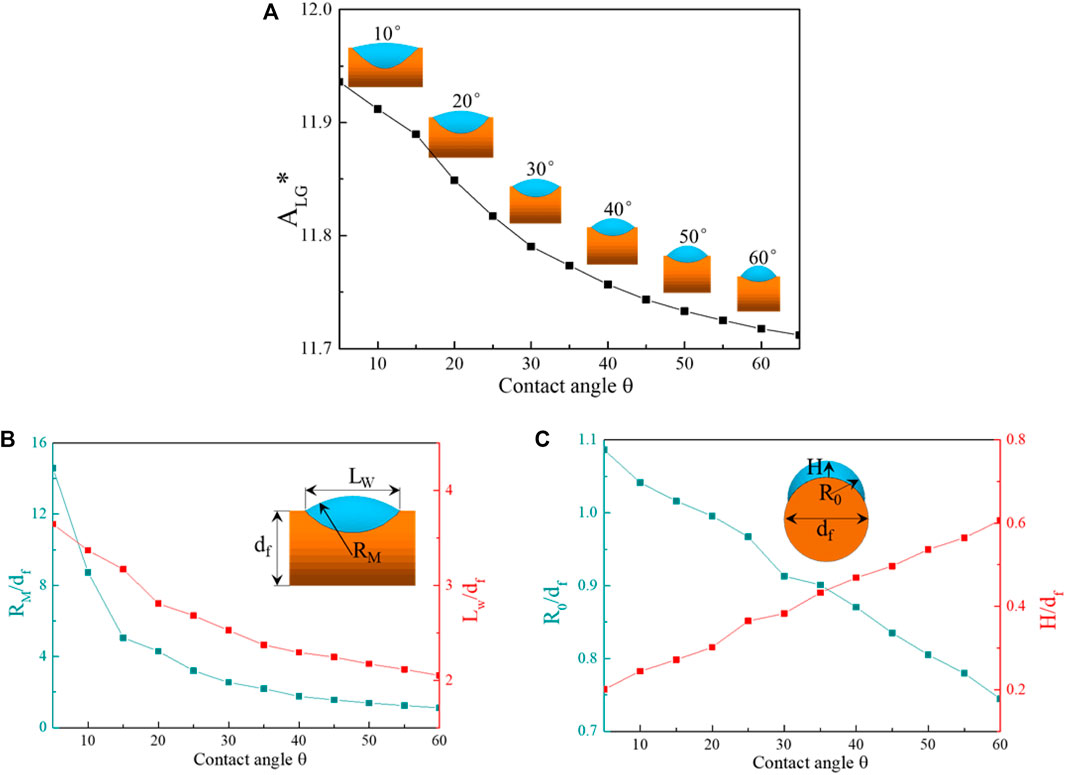
FIGURE 3. (A) Change of dimensionless free surface A_LG* with contact angle. Variation of dimensionless geometric parameters with contact angle: (B) R_M* ($R_M/d_f$) and L_W* ($L_W/d_f$), (C) R₀* ($R_0/d_f$) and H* ($H/d_f$).

In order to investigate the clamshell shape feature clearly, it is necessary to define several geometric parameters of clamshell, outer contour radius R_M and R₀, wetting length L_W, and droplet thickness H, illustrated by the inset in Figure 3. The wetting area (liquid–solid interface), free surface area (gas–liquid), and air resistance are closely linked with these parameters.

The variation of dimensionless geometric parameters of clamshell shape is obtained by ImageJ, as shown in Figures 3B,C. When the contact angle increases, R_M* declines exponentially, R₀* and L_W* decrease linearly, and H* increases linearly. As the contact angle is 5°, the thickness of clamshell droplet is almost negligible relative to the fiber diameter. Nevertheless, the H* increases to 0.6 at contact angle 65°. In addition, the larger the H*, the higher evolution probability of liquid bridge is. The adjacent droplet is coalesced easily along with the stretching of wetting length.

Liquid Bridge Rupture

Fiber spacing is an important factor affecting the formation and breakage of liquid bridge. When the distance between the fibers is too low, the barrel- or clamshell-shaped droplets connect with other droplets to merge then form liquid bridge. Figure 4A presents the computational images of liquid bridge in two parallel fibers with the change of fiber spacing. It can be seen that the middle throat of the liquid bridge gradually shrinks until separation with the increase of fiber spacing. Certainly, there is a critical fiber spacing for the rupture of liquid. The pre-existing liquid bridge will break when the fiber spacing reaches this critical value.

FIGURE 4

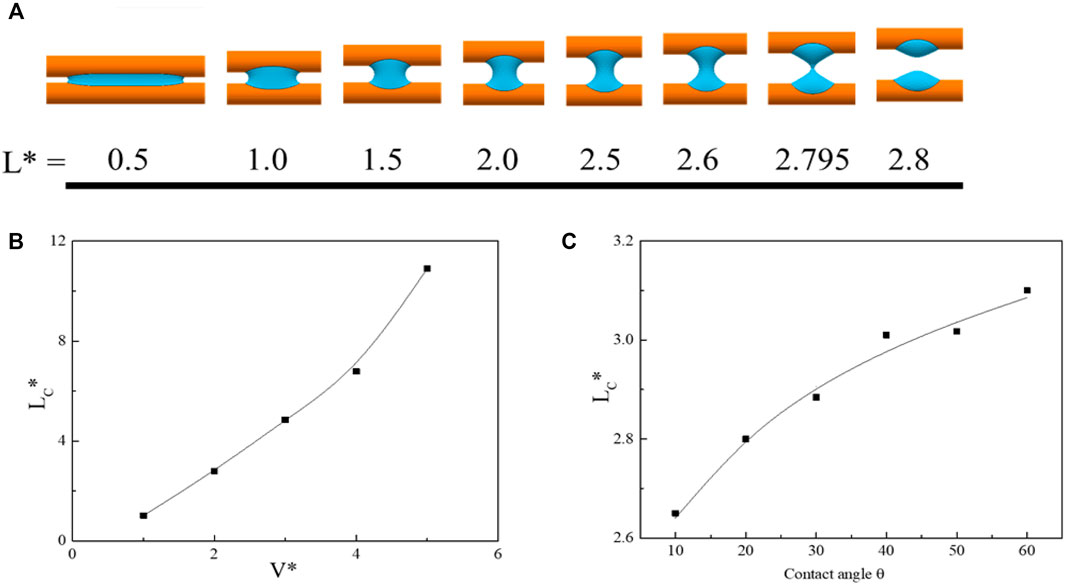
FIGURE 4. (A) Evolution of liquid bridge with fiber spacing from simulation in the parallel fibers. (B) Variation of the dimensionless critical spacing with the V*. (C) Variation of the dimensionless critical spacing with the contact angle.

The effect of V* and contact angle on critical spacing is determined by SE simulation. Figure 4B shows the influence of dimensionless volume of liquid bridge on critical spacing. As the increase of V*, the critical spacing also presents an increasing trend. When the V* of liquid bridge is 1, critical spacing is only 1.018. However, the critical spacing increases by more than 10 times as the V* increases to 5. The critical spacing associated with contact angle is analyzed, as shown in Figure 4C. As a result, the critical spacing increases with the increase of contact angle. When the contact angle is at 10°, the critical spacing is 2.65. When the contact angle increased to 60°, the critical spacing increases by 17%.

Based on the data presented in Figures 4B,C, the correlation between critical spacing L_C*, dimensionless volume V*, and contact angle θ can be obtained by fitting:

$L_C\ast =0.73{\theta }^{0.087}{\left(V\ast \right)}^{1.5623}(5)$

According to Eq. 5, as the θ and V* are given, we can adjust the fiber spacing for controlling the formation or rupture of liquid bridge. In addition, the conformation of liquid bridge can be manipulated by varying the volume of liquid bridge, the fiber surface wettability, and the fiber spacing.

Conclusion

In summary, we employed the SE to simulate the shape of droplets on fiber. The geometry parameters of shape are extracted based on the simulation data. The effect of contact angle on geometry characteristic dimensions is investigated. In addition, we define the critical spacing between two fibers for estimating the rupture of liquid bridge. Meanwhile, the effect of bridge volume and contact angle on critical spacing is discussed.

1) The barrel shape shrinks gradually as contact angle increases. The dimensionless maximum diameter d_b* increases with the increase of contact angle. The value of L_W* decreases by more than 1.7 times as the contact angle increases from 5° to 65°. The amplification of air resistance is about 47% as the contact angle increases from 5° to 65°.

2) When the contact angle increases, for clamshell shape, R_M* declines exponentially, R₀* and L_W* decrease linearly, and H* increases linearly.

3) The middle throat of the liquid bridge gradually shrinks until separation with the increase of fiber spacing. As the V* increases from 1 to 5, the critical spacing increases by more than 10 times. When the contact angle increased from 10° to 60°, the critical spacing increases by 17%. Finally, the fitting formula of the correlation between critical spacing L_C*, dimensionless volume V*, and contact angle θ is proposed based on simulation results.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Author Contributions

CX and ZL conducted the simulations and prepared the article. CX and LL contributed to the analysis of simulation data. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (Grant No. 52100131), the Natural Science Foundation of the Jiangsu Higher Education Institutions of China (Grant No. 20KJB470007), and the Natural Science Foundation of Jiangsu Province of China (Grant No. BK20210819).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abishek, S., Mead-Hunter, R., King, A. J. C., and Mullins, B. J. (2019). Capture and Re-entrainment of Microdroplets on Fibers. Phys. Rev. E 100, 042803. doi:10.1103/PhysRevE.100.042803

PubMed Abstract | CrossRef Full Text | Google Scholar

Adera, S., Alvarenga, J., Shneidman, A. V., Zhang, C. T., Davitt, A., and Aizenberg, J. (2020). Depletion of Lubricant from Nanostructured Oil-Infused Surfaces by Pendant Condensate Droplets. ACS Nano 14, 8024–8035. doi:10.1021/acsnano.9b10184

PubMed Abstract | CrossRef Full Text | Google Scholar

Amrei, M. M., Davoudi, M., Chase, G. G., and Tafreshi, H. V. (2017). Effects of Roughness on Droplet Apparent Contact Angles on a Fiber. Sep. Purif. Tech. 180, 107–113. doi:10.1016/j.seppur.2017.02.049

CrossRef Full Text | Google Scholar

Amrei, M. M., and Tafreshi, H. V. (2015). Effects of Pressure on Wetted Area of Submerged Superhydrophobic Granular Coatings. Part II: Poly-Dispersed Coatings. Colloids Surf. A: Physicochemical Eng. Aspects 481, 547–560. doi:10.1016/j.colsurfa.2015.05.030

CrossRef Full Text | Google Scholar

Aziz, H., and Tafreshi, H. V. (2019). Competing Forces on a Liquid Bridge between Parallel and Orthogonal Dissimilar Fibers. Soft Matter 15, 6967–6977. doi:10.1039/c9sm00489k

PubMed Abstract | CrossRef Full Text | Google Scholar

Bedarkar, A., Wu, X.-F., and Vaynberg, A. (2010). Wetting of Liquid Droplets on Two Parallel Filaments. Appl. Surf. Sci. 256, 7260–7264. doi:10.1016/j.apsusc.2010.05.061

CrossRef Full Text | Google Scholar

Brakke, K. A. (2000). Surface Evolver. Available at: www.susqu.edu/facstaff/b/vrajjer/evolver.

Google Scholar

Carroll, B. J. (1976). The Accurate Measurement of Contact Angle, Phase Contact Areas, Drop Volume, and Laplace Excess Pressure in Drop-On-Fiber Systems. J. Colloid Interf. Sci. 57 (3), 488–495. doi:10.1016/0021-9797(76)90227-7

CrossRef Full Text | Google Scholar

Chen, Y., and Deng, Z. (2017). Hydrodynamics of a Droplet Passing through a Microfluidic T-junction. J. Fluid Mech. 819, 401–434. doi:10.1017/jfm.2017.181

CrossRef Full Text | Google Scholar

Chen, Y., Wu, L., and Zhang, L. (2015). Dynamic Behaviors of Double Emulsion Formation in a Flow-Focusing Device. Int. J. Heat Mass Transfer 82, 42–50. doi:10.1016/j.ijheatmasstransfer.2014.11.027

CrossRef Full Text | Google Scholar

Chou, T.-H., Hong, S.-J., Liang, Y.-E., Tsao, H.-K., and Sheng, Y.-J. (2011). Equilibrium Phase Diagram of Drop-On-Fiber: Coexistent States and Gravity Effect. Langmuir 27, 3685–3692. doi:10.1021/la2000969

PubMed Abstract | CrossRef Full Text | Google Scholar

Dawar, S., and Chase, G. G. (2010). Correlations for Transverse Motion of Liquid Drops on Fibers. Sep. Purif. Tech. 72, 282–287. doi:10.1016/j.seppur.2010.02.018

CrossRef Full Text | Google Scholar

Deng, Z., Zhang, C., Shen, C., Cao, J., and Chen, Y. (2017). Self-propelled Dropwise Condensation on a Gradient Surface. Int. J. Heat Mass Transfer 114, 419–429. doi:10.1016/j.ijheatmasstransfer.2017.06.065

CrossRef Full Text | Google Scholar

Fang, J., Davoudi, M., and Chase, G. G. (2015). Drop Movement along a Fiber axis Due to Pressure Driven Air Flow in a Thin Slit. Sep. Purif. Tech. 140, 77–83. doi:10.1016/j.seppur.2014.11.015

CrossRef Full Text | Google Scholar

Gao, W., Lei, Z., Liu, X., and Chen, Y. (2021). Dynamic Liquid Gating Artificially Spinning System for Self-Evolving Topographies and Microstructures. Langmuir 37, 1438–1445. doi:10.1021/acs.langmuir.0c02910

PubMed Abstract | CrossRef Full Text | Google Scholar

Gilet, T., Terwagne, D., and Vandewalle, N. (2010). Droplets Sliding on Fibres. Eur. Phys. J. E 31, 253–262. doi:10.1140/epje/i2010-10563-9

CrossRef Full Text | Google Scholar

Liang, Y.-E., Chang, C.-C., Tsao, H.-K., and Sheng, Y.-J. (2013). An Equilibrium Phase Diagram of Drops at the Bottom of a Fiber Standing on Superhydrophobic Flat Surfaces. Soft Matter 9, 9867–9875. doi:10.1039/c3sm51453f

CrossRef Full Text | Google Scholar

Lu, Z., Ng, T. W., and Yu, Y. (2016). Fast Modeling of Clam-Shell Drop Morphologies on Cylindrical Surfaces. Int. J. Heat Mass Transfer 93, 1132–1136. doi:10.1016/j.ijheatmasstransfer.2015.10.064

CrossRef Full Text | Google Scholar

Mchale, G., Newton, M. I., and Carroll, B. J. (2001). The Shape and Stability of Small Liquid Drops on Fibers. Oil Gas Sci. Tech. - Rev. IFP 56, 47–54. doi:10.2516/ogst:2001006

CrossRef Full Text | Google Scholar

Mchale, G., and Newton, M. I. (2002). Global Geometry and the Equilibrium Shapes of Liquid Drops on Fibers. Colloids Surf. A: Physicochemical Eng. Aspects 206, 79–86. doi:10.1016/s0927-7757(02)00081-x

CrossRef Full Text | Google Scholar

Mead-Hunter, R., King, A. J. C., and Mullins, B. J. (2012). Plateau Rayleigh Instability Simulation. Langmuir 28, 6731–6735. doi:10.1021/la300622h

PubMed Abstract | CrossRef Full Text | Google Scholar

Preston, D. J., Lu, Z., Song, Y., Zhao, Y., Wilke, K. L., Antao, D. S., et al. (2018). Heat Transfer Enhancement during Water and Hydrocarbon Condensation on Lubricant Infused Surfaces. Sci. Rep. 8 (1), 540. doi:10.1038/s41598-017-18955-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Princen, H. M. (1970). Capillary Phenomena in Assemblies of Parallel Cylinders: III Liquid Columns Between Horizontal Parallel Cylinders. J. Colloid Interf. Sci. 34, 171–184. doi:10.1016/0021-9797(70)90167-0

CrossRef Full Text | Google Scholar

Rebouillat, S., Letellier, B., and Steffenino, B. (1999). Wettability of Single Fibres - beyond the Contact Angle Approach. Int. J. Adhes. Adhesives 19, 303–314. doi:10.1016/s0143-7496(99)00006-8

CrossRef Full Text | Google Scholar

Sheng, Y.-J., Jiang, S., and Tsao, H.-K. (2007). Effects of Geometrical Characteristics of Surface Roughness on Droplet Wetting. J. Chem. Phys. 127, 234704. doi:10.1063/1.2804425

CrossRef Full Text | Google Scholar

Song, B., Bismarck, A., Tahhan, R., and Springer, J. (1998). A Generalized Drop Length-Height Method for Determination of Contact Angle in Drop-On-Fiber Systems. J. Colloid Interf. Sci. 197 (1), 68–77. doi:10.1006/jcis.1997.5218

PubMed Abstract | CrossRef Full Text | Google Scholar

Virozub, A., Haimovich, N., and Brandon, S. (2009). Three-dimensional Simulations of Liquid Bridges between Two Cylinders: Forces, Energies, and Torques. Langmuir 25, 12837–12842. doi:10.1021/la902578j

PubMed Abstract | CrossRef Full Text | Google Scholar

Wagner, H. D. (1990). Spreading of Liquid Droplets on Cylindrical Surfaces: Accurate Determination of Contact Angle. J. Appl. Phys. 67, 1352–1355. doi:10.1063/1.345689

CrossRef Full Text | Google Scholar

Wang, J., Gao, W., Zhang, H., Zou, M., Chen, Y., and Zhao, Y. (2018). Programmable Wettability on Photocontrolled Graphene Film. Sci. Adv. 4, eaat7392. doi:10.1126/sciadv.aat7392

PubMed Abstract | CrossRef Full Text | Google Scholar

Wilcox, M., Kurz, R., and Brun, K. (2012). Technology Review of Modern Gas Turbine Inlet Filtration Systems. Int. J. Rotating Machinery 2012, 1–15. doi:10.1155/2012/128134

CrossRef Full Text | Google Scholar

Wu, X.-F., Bedarkar, A., and Vaynberg, K. A. (2010). Droplets Wetting on Filament Rails: Surface Energy and Morphology Transition. J. Colloid Interf. Sci. 341, 326–332. doi:10.1016/j.jcis.2009.09.019

CrossRef Full Text | Google Scholar

Zhang, R., Liu, B., Yang, A., Zhu, Y., Liu, C., Zhou, G., et al. (2018). In Situ investigation on the Nanoscale Capture and Evolution of Aerosols on Nanofibers. Nano Lett. 18, 1130–1138. doi:10.1021/acs.nanolett.7b04673

PubMed Abstract | CrossRef Full Text | Google Scholar