
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res. , 26 January 2022
Sec. Nuclear Energy
Volume 9 - 2021 | https://doi.org/10.3389/fenrg.2021.822780
This article is part of the Research Topic Reactor Physics: Methods and Applications View all 27 articles
A high-fidelity model for the first criticality of pebble-bed reactor HTR-PM is built using Monte Carlo (MC) code RMC and discrete element method (DEM) code LAMMPS. Randomly packed TRi-structural ISOtropic (TRISO) particles and fuel pebbles are modeled explicitly. A cone structure on the top of the pebble bed is also taken into account. Criticality calculation result agrees well with the experiment. Uncertainty analysis is carried out considering three inherent aspects: the randomness of MC code, the randomness of TRISO particle and pebble position, and the randomness of mixed pebbles. Results show that these factors have a significant impact on the uncertainty of effective multiplication factor (keff). And the most influential factor is expected to be the randomness of mixed pebbles. The influence of several configuration factors is studied as well. It is observed that the effects of cross-section library, the heterogeneity of TRISO particles, and the angle of pebble bed cone are nonnegligible contributors. However, the results between randomly and regularly placed TRISO particles are not noticeably different.
As the fourth-generation nuclear power plant, high-temperature gas-cooled reactors (HTGRs) have been gaining attention because of their safety features. Recently, the world's first 200 MWe pebble-bed modular high-temperature gas-cooled reactor demonstration plant (HTR-PM) (Zhang et al., 2006) built in Shandong, China, reached its first criticality. With the experiment data provided, it is a good opportunity to carry out high-fidelity modeling research. As a pebble-bed reactor like HTR-10, HTR-PM has the feature of double heterogeneity and randomness as well, but the reactor core is larger and has more pebbles. It would be more challenging to perform a high-precision modeling for HTR-PM.
There has been research on the simulation of pebble-bed reactors. For example, the high-fidelity model of HTR-10 was built using MCNP (Version 5) (X-5 Monte Carlo Team, 2003) with double heterogeneity taken into account (Abedi and Vosoughi, 2012). HTR-10 was also modeled using a regularly packed pebble bed (Abedi et al., 2011). The influence of the heterogeneity of the pebble bed was studied based on HTR-PROTEUS (Auwerda et al., 2010). HTR-10 was studied focusing on the effect of the randomness of TRi-structural ISOtropic (TRISO) particles (Çolak and Seker, 2005). The first solid-fueled thorium molten salt reactor (TMSR-SF1) was modeled explicitly, and the influence of randomness of TRISO particles was studied (Sun et al., 2018). The influence of a cross-section library was studied based on the explicit model of the pebble bed reactor of ASTRA facility (Rintala et al., 2015). Even so, comparing to these facilities, the scale of HTR-PM is significantly larger, resulting in higher complexity of the model.
There are also several research projects on HTR-PM. She et al. (2021) studied the high-fidelity model based on deterministic code PANGU; sensitivity analysis was carried out focusing on filling fraction and uranium loading (Hao et al., 2015); uncertainty analysis on thermal features was launched using CUSA and ATHENA codes (Hao et al., 2020). However, research on HTR-PM Monte Carlo (MC) high-fidelity model and uncertainty is relatively insufficient.
This study builds a high-fidelity model of the first criticality of HTR-PM, realizing the meticulous modeling of large-scale pebble-bed reactor. MC code RMC (Wang et al., 2015) and discrete element method (DEM) code LAMMPS (Plimpton, 1995) are used. The randomly packed pebbles and TRISO particles are modeled explicitly. Uncertainty analysis is carried out, and the uncertainty of mixed pebbles is proposed. The influence of cross-section library, heterogeneity of TRISO particles, and angle of pebble bed cone is also studied.
The paper is organized as follows. Section 2 shows the details of the model. Section 3 describes the uncertainty analysis of inherent factors. Section 4 presents the effects of several configuration aspects. And Section 5 summarizes this paper.
The reactor core vessel of HTR-PM is a large cylinder with a cone structure and discharge tube at the bottom. The core is filled with pebbles, including fuel pebble and graphite pebble. Within each fuel pebble, UO2 fuel is contained in separate TRISO particles instead of evenly distributed. These features make the double heterogeneity of the pebble-bed reactor. In the first criticality condition, the core is first filled with graphite pebbles, on the top of which a mixture of fuel pebbles and graphite pebbles is loaded with a ratio of 7:8.
In this study, a high-fidelity model of HTR-PM is built according to the information of “base condition” provided by She et al. (2021). In the base condition, the core is filled with air instead of helium. The temperature of the whole model is set at 293.6 K. The layout of the model is shown in Figure 1. The cone structure at the bottom is converted equivalently to cylinder as She et al. (2021) did. To model double heterogeneity explicitly, the positions of pebbles are firstly determined using DEM method with LAMMPS code. These positions are then used to construct the MC model with RMC code. And positions of TRISO particles are directly determined by RMC code, using RSA method (Liu et al., 2015). Though TRISO particles are randomly placed, fuel pebbles have identical inner TRISO particle distributions in order to save calculation time.
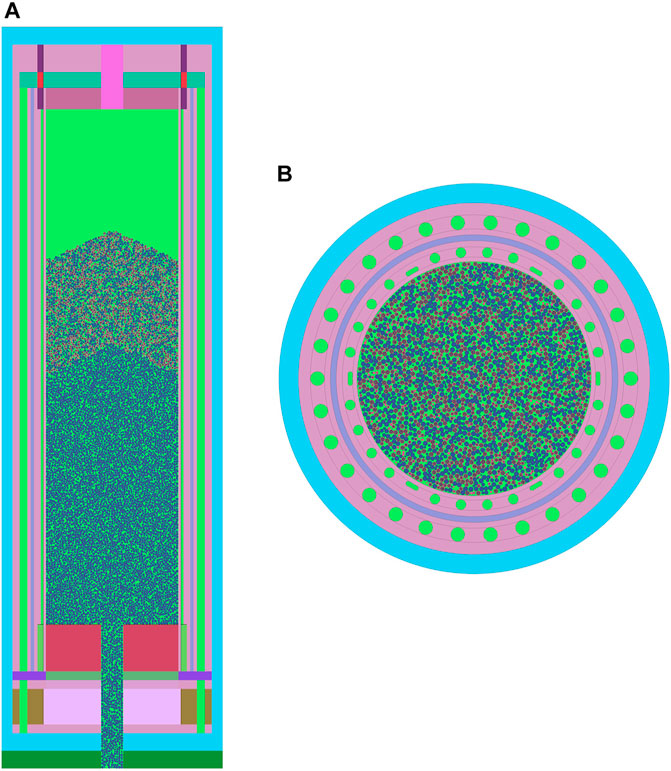
FIGURE 1. (A) The axial cross section at the center of the model and (B) radial cross section at the height of 1,026.17 cm from the bottom.
LAMMPS code can model the movement of pebbles according to Newton's laws. To generate the pebble bed, a process of packing pebbles is modeled. Pebbles are first randomly placed at the top of the reactor core vessel. They then drop freely under the influence of gravity and are accumulated at the bottom of the vessel. The simulation ends when enough pebbles are packed. Parameters used in this model, such as elastic constant and friction coefficient, are referenced from Rycroft et al. (2013). It should be noted that the time step is set to be 10 times larger than the reference, which is
Pebbles modeled by the LAMMPS code are described as elastic spheres. Thus, the packed pebbles can be slightly overlapped. However, when modeling the pebble bed geometry using the MC code RMC, any overlap is unacceptable. Therefore, the size of pebbles is set to be a little larger in the LAMMPS model to eliminate overlap. When packing pebbles with a diameter of 6 cm, a maximum overlap of 0.002 cm is observed, so the diameter of pebbles in the LAMMPS model is set to 6.002 cm. Using the position information derived by LAMMPS, the diameter of pebbles in RMC model is still set to 6 cm. Thus, no overlapping is observed in RMC model, and the influence on pebble packing fraction can be neglected.
In the first criticality experiment of HTR-PM, pebbles are loaded into the reactor vessel from a single tube. Obviously, a cone structure will form at the top of the pebble bed. As the mixed pebbles are loaded after graphite pebbles, there will be a cone structure at the top of the graphite pebble pile as well. Because of the similar mass and friction coefficient of fuel and graphite pebble, the cone angles of the graphite pebble pile and the mixed pebble pile are the same, as shown in Figure 1A. The keff of the reactor can be significantly affected by the cone angle (will be further discussed in Section 4), making it necessary to model the cone correctly. However, no experiment result of HTR-PM cone angle is currently available. Thus, this study refers to a previous experiment done by Yang et al. (2009). According to the photo taken from the pebble packing experiment (Figure 2), the cone angle is approximately 25°, which is chosen to be the cone angle value in this model. To generate the cone structure, using LAMMPS directly is highly time-consuming because more time steps must be calculated if the pebbles are inserted one by one. So this study uses the following method instead. First, a cylinder-shaped pebble bed with larger height but no cone is generated using LAMMPS. Then, pebbles are examined by a Python script according to the expected cone geometry. Pebbles in different regions are defined as graphite pebble or mixed pebble or deleted respectively. Thus, the cone structure shown in Figure 1A is achieved. This method is also applied to model different cone angles in Section 4.3.

FIGURE 2. Photo of the pebble packing experiment (Yang et al., 2009).
The equivalent height of the graphite pebble pile is 6.05 m, with a packing fraction of 61% (She et al., 2021). Note that there are also graphite pebbles in the discharge tube at the bottom of the core. The total number of graphite pebbles is estimated to be 234,957. According to the first criticality experiment in Shandong, China, the number of mixed pebbles is approximately 102,300 when reaching criticality.
Using the parameters mentioned above, keff obtained by RMC is 0.99968, which is very close to the experimental value of 1. The uncertainty of keff will be further discussed in Section 3.
The actual pebble-bed reactor can be uncertain in may parameters, such as the diameter of pebbles or mass of uranium in each pebble. Uncertainty of these parameters will result in the uncertainty of reactor physics or thermal property (Guo et al., 2021). However, for a computer simulation model, most of these parameters are completely certain, which means the uncertainty of the model results from only a few factors. As for the model used in this study, inherent uncertainty is only caused by the following three factors.
The first factor is the uncertainty of MC method. Because MC method is essentially statistical, results obtained by MC calculation always come with statistical uncertainties. It should be noted that the uncertainty of MC method is related to the number of neutrons simulated. In this study, all RMC calculations are carried out with 50 million neutron histories in total where 100 inactive generations, 900 active generations, and 50,000 particles per generation were used. This will result in a keff standard deviation of 10 pcm.
The second factor is the randomness of TRISO particles and pebble positions. Obviously, the calculation result will be uncertain because TRISO particles and pebbles are randomly packed.
The third factor is the randomness of the mixed pebbles. In order to discuss this factor, the method used in this study to model the mixed pebbles needs to be first explained.
HTR-PM first criticality core contains a mixture of fuel pebbles and graphite pebbles with a ratio of 7:8. To model this mixture, a randomly packed pebble pile with 102,300 pebbles is first generated using LAMMPS. In this step, there is no difference among pebbles. Then 47,740 of these pebbles are randomly chosen to be fuel pebble, and the remaining 54,560 pebbles will be graphite pebbles. The choosing process is done using random.sample function in Python 3.9.5.
Rigorously speaking, the mixture of fuel and graphite pebbles is not completely random. If the bed is packed with pebbles with different densities, the proportion of light pebbles would be larger near the wall, and heavy pebbles would be more concentrated near the center (Wu et al., 2019). However, considering that the difference between fuel and graphite pebble density is relatively small (about 3%), this phenomenon is neglected in this study.
It is observed that even the positions of 102,300 pebbles are fixed; the keff calculation result can be different if the 47,740 fuel pebbles are chosen differently. As shown in Figure 3, the positions of each pebble in these two pebble piles are completely the same. The only difference is which pebble is fuel and which pebble is graphite. In this study, this feature is called the randomness of mixed pebbles.
Quantitative study of uncertainty is carried out using statistical sampling method (Helton et al., 2006). When investigating the influence of some factors, 100 examples are calculated considering these factors. And the standard deviation of keff is derived from the result.
First, the uncertainty under the influence of all the three factors is studied. One hundred examples with random TRISO particle and pebble positions, and randomly chosen fuel pebbles, are calculated. A histogram of results is shown in Figure 4. The mean value of keff is 0.99972, and the standard deviation is 53 pcm. This indicates that when modeling HTR-PM, the inherent uncertainty is not only caused by MC calculation. Thus, it is unnecessary to excessively reduce the uncertainty of MC calculation by increasing the neutron history.
Next, the influence of each factor is studied respectively. However, it should be stressed that some factors cannot be separated, including: 1) MC method is applied in every example, making it difficult to separate its effect, and 2) when positions of pebbles change, it is meaningless to make the mixed pebble stay the same. Thus, the effect of random pebble position cannot be separated from the effect of mixed pebbles.
Considering the facts mentioned above, the following studies are carried out: 1) uncertainty under the influence of MC method and mixed pebbles and 2) uncertainty under the influence of MC method and TRISO particle positions.
In order to study the influence of MC method and mixed pebbles, 100 examples are calculated with fixed TRISO particle and pebble positions and randomly chosen fuel pebbles. A histogram of results is shown in Figure 5. The mean value of keff is 1.00006, and the standard deviation is 46 pcm. The mean value of keff here (1.00006) is different from that in Figure 4 (0.99972). The reason is that although the fixed TRISO particle and pebble positions chosen in this calculation are from 1 of the 100 examples in Figure 4, it is not the one whose result is closest to the mean value of Figure 4.
To study the influence of MC method and TRISO particle positions, 100 examples are calculated with fixed pebble positions and mixed pebbles and random TRISO particle positions. Results show that the standard deviation of keff is 10 pcm. Note that the standard deviation under only the influence of MC method is 10 pcm. It can be inferred from this result that the influence of randomness of TRISO particle positions can be neglected. The same conclusion was obtained by Çolak and Seker when studying HTR-10 (Çolak and Seker, 2005).
Results shown in this section suggest that the randomness of mixed pebbles is the main factor causing the uncertainty of the HTR-PM high-fidelity model.
Section 4 shows the influence of several configuration factors on the keff value. To compare these results, it is necessary to determine their standard deviations. These results may be influenced by different factors mentioned in Section 3.1, which means different standard deviations should be applied. This will be further discussed in Section 4.
This section shows the influence of several configuration factors on the high-fidelity model, including the cross-section library, the heterogeneity of TRISO particles, and the angle of the cone formed by pebble packing.
The high-fidelity model described in Section 2 is calculated based on ENDF/B-VIII.0 library. Its keff result is 0.99968. When using ENDF/B-VII.1 library, the keff is 0.99797, with a difference of approximately 200 pcm, which is significantly larger than the standard deviation of 10 pcm from the MC calculation. The positions of TRISO particles and pebbles, as well as the mixed pebbles, are set to be the same between these two examples, which indicates that this error is caused by the difference of nuclear data libraries.
The source of this difference is speculated to be the difference of graphite cross sections between the two libraries, especially the difference of thermal neutron scattering cross sections of “Reactor Graphite” (Brown et al., 2018). Since carbon-based graphite is the moderator in HTR-PM, the change of graphite cross sections is supposed to have an appreciable impact on the simulation.
Within the fuel pebble, UO2 fuel is contained in separately distributed TRISO particles, forming the heterogeneity of TRISO particles. To study its effect, three examples are considered using randomly placed TRISO particles, regularly placed TRISO particles, and homogeneous material, respectively, as shown in Figure 6. Material compositions in the fuel pebbles are kept the same between the three examples. The keff of the reactor and kinf of a single fuel pebble are calculated. The results are shown in Table 1.

FIGURE 6. (A) randomly placed TRISO particles; (B) regularly placed TRISO particles; and (C) homogeneous material.
The difference of keff of the reactor using different fuel enrichment is also calculated. The results are shown in Table 2. Note that the enrichment of the high-fidelity model is 4.2%.
It is worth mentioning that the regularly placed TRISO particle model is not directly generated using the lattice geometry (Liu et al., 2015) of RMC code. Instead, the positions of TRISO particles are determined using a Python script. The script first generates a large lattice of particles, with the lattice pitch determined based on the packing fraction. Then particles located beyond the fuel pebble region are deleted. Using this method, regularly placed TRISO particles without overlapping with the fuel pebble boundary are generated, as shown in Figure 6B. The packing fraction of regularly and randomly placed TRISO particles used in this study are very close, with 11,665 and 11,666 particles in each pebble, respectively.
Pebble positions and mixed pebbles are set to be the same between these three examples; thus, the uncertainty is only influenced by MC method and TRISO particle positions. According to Section 3.2, the standard deviation of multiplication factor from MC calculation is 10 pcm. The results suggest that the difference between randomly and regularly placed TRISO particles are insignificant, but the result using homogeneous material is unacceptable.
To study the effect of the pebble bed cone angle, six models with different cone angles (as shown in Figure 7) are constructed and calculated. The consistent 234,957 graphite pebbles and 102,300 mixed pebbles are used in each model. The results are shown in Table 3.
Obviously, pebble positions and mixed pebbles cannot stay the same when the cone angle changes. Thus, the uncertainty of this result is influenced by all the three factors mentioned in Section 3.1, making the standard deviation 53 pcm.
The results show that the cone angle can significantly influence keff. With a larger cone angle, the keff is smaller. This is because a larger cone angle results in more neutron leakage. It should also be noticed that at the angle of 25°, a change of 5° in the cone angle can lead to a difference of 200 pcm in keff, indicating that it is necessary to use the correct angle when modeling HTR-PM.
A high-fidelity model for the first criticality of pebble-bed reactor HTR-PM is built using MC code RMC and DEM code LAMMPS. The uncertainty of the model is studied based on three inherent factors: randomness of MC method, randomness of TRISO particle and pebble positions, and randomness of mixed pebbles. Results suggest that the main factor causing uncertainty of the model is the randomness of mixed pebbles, and the influence of TRISO particle positions can be neglected.
The effects of cross-section library, heterogeneity of TRISO particles, and angle of cone formed by pebble packing are also studied. Results show that these factors can significantly influence the keff result. keff using ENDF/B-VIII.0 is about 200 pcm larger than that of ENDF/B-VII.1. The results of randomly or regularly placed TRISO particles are not remarkably different, but it is not favorable to simply homogenize the material in MC simulation. The influence of pebble bed cone angle is relatively large. With larger cone angle, the keff is smaller. A difference of 200 pcm can result from a change of 5° in the cone angle at 25°.
Due to the limitation of calculation time, the cone structure of the pebble bed is not generated directly by LAMMPS code, which can be improved in further studies. It is also suggested in future work to carry out MC depletion calculation of HTR-PM considering pebble flow.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
RL: methodology, numerical simulation, and writing—original draft preparation. ZL: computing resources, simulation result evaluation, and writing—reviewing and editing. ZF: code development and simulation result evaluation. JL: conceptualization, supervision, writing—reviewing and editing, and funding acquisition. LZ: supervision and resources.
The research was supported by the faculty startup funds of Tsinghua University.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
We gratefully acknowledge the reactor physics team of the Institute of Nuclear and New Energy Technology, Tsinghua University, for providing recommendations in constructing the model. We acknowledge RMC development team from the Department of Engineering Physics, Tsinghua University, for providing the RMC code used in this work.
Abedi, A., Vosoughi, N., and Ghofrani, M. B. (2011). “An Exact MCNP Modeling of Pebble Bed Reactors,” in 2011 International Nuclear Atlantic Conference, Belo Horizonte, MG, Brazil, October 24–28, 2011.
Abedi, A., and Vosoughi, N. (2012). Neutronic Simulation of a Pebble Bed Reactor Considering its Double Heterogeneous Nature. Nucl. Eng. Des. 253, 277–284. doi:10.1016/j.nucengdes.2012.08.030
Auwerda, G. J., Kloosterman, J. L., Lathouwers, D., and van der Hagen, T. H. J. J. (2010). Effects of Random Pebble Distribution on the Multiplication Factor in HTR Pebble Bed Reactors. Ann. Nucl. Energ. 37, 1056–1066. doi:10.1016/j.anucene.2010.04.008
Brown, D. A., Chadwick, M. B., Capote, R., Kahler, A. C., Trkov, A., Herman, M. W., et al. (2018). ENDF/B-VIII.0: The 8 Th Major Release of the Nuclear Reaction Data Library with CIELO-Project Cross Sections, New Standards and Thermal Scattering Data. Nucl. Data Sheets 148, 1–142. doi:10.1016/j.nds.2018.02.001
Chen, H., Fu, L., Jiong, G., and Lidong, W. (2015). Uncertainty and Sensitivity Analysis of Filling Fraction of Pebble Bed in Pebble Bed HTR. Nucl. Eng. Des. 292, 123–132. doi:10.1016/j.nucengdes.2015.05.032
Çolak, Ü., and Seker, V. (2005). Monte Carlo Criticality Calculations for a Pebble Bed Reactor with MCNP. Nucl. Sci. Eng. 149 (2), 131–137. doi:10.13182/NSE04-17
Guo, J., Wang, Y., Zhang, H., Cui, M., and Li, F. (2021). Challenges and Progress of Uncertainty Analysis for the Pebble-Bed High-Temperature Gas-Cooled Reactor. Prog. Nucl. Energ. 138, 103827. doi:10.1016/j.pnucene.2021.103827
Hao, C., Li, P., She, D., Zhou, X., and Yang, R. (2020). Sensitivity and Uncertainty Analysis of the Maximum Fuel Temperature under Accident Condition of HTR-PM. Sci. Technol. Nucl. Installations 2020, 1–21. doi:10.1155/2020/9235783
Helton, J. C., Johnson, J. D., Sallaberry, C. J., and Storlie, C. B. (2006). Survey of Sampling-Based Methods for Uncertainty and Sensitivity Analysis. Reliability Eng. Syst. Saf. 91, 1175–1209. doi:10.1016/j.ress.2005.11.017
Liu, S., She, D., Liang, J.-G., and Wang, K. (2015). Development of Random Geometry Capability in RMC Code for Stochastic Media Analysis. Ann. Nucl. Energ. 85, 903–908. doi:10.1016/j.anucene.2015.07.008
Plimpton, S. (1995). Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 117, 1–19. doi:10.1006/jcph.1995.1039
Rintala, V., Suikkanen, H., Leppänen, J., and Kyrki-Rajamäki, R. (2015). Modeling of Realistic Pebble Bed Reactor Geometries Using the Serpent Monte Carlo Code. Ann. Nucl. Energ. 77, 223–230. doi:10.1016/j.anucene.2014.11.018
Rycroft, C. H., Dehbi, A., Lind, T., and Güntay, S. (2013). Granular Flow in Pebble-Bed Nuclear Reactors: Scaling, Dust Generation, and Stress. Nucl. Eng. Des. 265, 69–84. doi:10.1016/j.nucengdes.2013.07.010
She, D., Xia, B., Guo, J., Wei, C.-L., Zhang, J., Li, F., et al. (2021). Prediction Calculations for the First Criticality of the HTR-PM Using the PANGU Code. Nucl. Sci. Tech. 32, 90. doi:10.1007/s41365-021-00936-5
Sun, K., Wilson, J., Hauptman, S., Ji, R., Dave, A. J., Zou, Y., et al. (2018). Neutronics Modeling and Analysis of the TMSR-SF1 Fuel Lattice and Full Core with Explicit Fuel Particle Distribution and Random Pebble Loadings. Prog. Nucl. Energ. 109, 171–179. doi:10.1016/j.pnucene.2018.08.005
Wang, K., Li, Z., She, D., Liang, J. G., Xu, Q., Qiu, Y., et al. (2015). RMC - A Monte Carlo Code for Reactor Core Analysis. Ann. Nucl. Energ. 82, 121–129. doi:10.1016/j.anucene.2014.08.048
Wu, M., Gui, N., Wu, H., Yang, X., Tu, J., and Jiang, S. (2019). Numerical Study of Mixing Pebble Flow with Different Density in Circulating Packed Bed. Ann. Nucl. Energ. 130, 483–492. doi:10.1016/j.anucene.2019.03.020
X-5 Monte Carlo Team (2003). MCNP-A General Monte Carlo N-Particle Transport Code, Version 5, Vol. I & II: User's Guide. Los Alamos National Laboratory. LA-13709-M.
Yang, X., Hu, W., and Jiang, S. (2009). Experimental Investigation on Feasibility of Two-Region-Designed Pebble-Bed High-Temperature Gas-Cooled Reactor. J. Nucl. Sci. Technol. 46, 374–381. doi:10.3327/jnst.46.37410.1080/18811248.2007.9711543
Keywords: HTR-PM, Monte Carlo, discrete element method, high-fidelity, uncertainty, double heterogeneity
Citation: Li R, Liu Z, Feng Z, Liang J and Zhang L (2022) High-Fidelity MC-DEM Modeling and Uncertainty Analysis of HTR-PM First Criticality. Front. Energy Res. 9:822780. doi: 10.3389/fenrg.2021.822780
Received: 26 November 2021; Accepted: 20 December 2021;
Published: 26 January 2022.
Edited by:
Tengfei Zhang, Shanghai Jiao Tong University, ChinaReviewed by:
Jiankai Yu, Massachusetts Institute of Technology, United StatesCopyright © 2022 Li, Liu, Feng, Liang and Zhang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jingang Liang, amluZ2FuZ0B0c2luZ2h1YS5lZHUuY24=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.