Molecular Dynamics Investigation on Thermal Conductivity and Photon Behaviors of Graphene With Sierpinski Carpet Fractal Defects

The thermal conductivity (TC) of graphene with Sierpinski carpet fractal (SCF) and regular carpet (RC) defects is numerically studied by the non-equilibrium molecular dynamics (NEMD) method. The influences of porosity, fractal levels, and types of defects on the TC of graphene are clarified, and the underlying mechanisms of phonon behaviors are uncovered. The numerical results indicate that the defects in graphene induce the atoms that have the heat transfer blockage effect, and thus, the TC of defective graphene decreases with increasing porosity. With the increase in fractal levels, more atoms have the heat transfer blockage effect, which induces the TC of graphene with SCF defects to sharply decrease. Moreover, compared with the graphene with RC defects, more atoms participate in the heat transfer blockage under the graphene with SCF defects, which leads to the lower TC of graphene with SCF defects.

Introduction

Owing to the quantum effect at the nanoscale, graphene has high carrier mobility, excellent thermal conductivity (TC), and ultra-high strength, which has a potentially huge application value in semiconductors (Novoselov et al., 2004; Balandin et al., 2008; Ghosh et al., 2008; Lee et al., 2008; Wei et al., 2011; Aldrigo et al., 2013; Wang et al., 2018; Han et al., 2019b). The TC of graphene is a key parameter for thermal management in nanoelectronic devices (Balandin et al., 2008; Ghosh et al., 2008; Anno et al., 2017), which has attracted increasing interest in both academia and industry. Therefore, it is of great significance to study the tuning of the thermal property of graphene to meet the thermal management we need.

The TC of graphene can be changed by constructing the structures of graphene (Yarifard et al., 2017); introducing defects into graphene is an available method to adjust the graphene structure (Hao et al., 2011). As a good way to study the thermal mechanisms of graphene and the impacts of influence factors (Chen et al., 2015; Chen and Deng, 2017), the effects of defects on the TC of one-dimensional material were numerically investigated by molecular dynamics (MD) simulation (Cui et al., 2016; Bazrafshan and Rajabpour, 2017; Hu et al., 2017; Han et al., 2019a; Han et al., 2019b). The numerical results indicate that increasing the ratio of defects can decrease the TC of defective graphene (Han et al., 2019a). The silicon nanowires with surface defects have higher TC and average phonon participation than the silicon nanowires with inner defects (Li et al., 2021). Considering the structure of self-similarity in nature, nanofabrication technologies are adopted to construct self-similar structures (Zhang et al., 2014; Deng et al., 2017; Zhang et al., 2020). As one of the self-similar set, the Sierpinski carpet fractal (SCF) structure is introduced to construct the defective graphene (Kang et al., 2018; Han et al., 2019a; Han et al., 2020). The SCF defects in graphene can significantly increase the boundary scattering of phonon and thus significantly reduce the TC (Zhang et al., 2014; Wei et al., 2015; Shao et al., 2018). When the fractal level increases from 0 to 3, the TC of the SCF graphene monolayer decreases from 164.4 to 19.6 W/mK (Kang et al., 2018).

In summary, many investigations have been conducted to study the regular and vacancy defects of graphene. However, the phonon behaviors in defective graphene, including the phonon density of states and the participation ratio were not well analyzed in previous studies, which was not sufficient to clarify the mechanisms underlying the thermal transport of defective graphene. In this article, to study the controlled method of the TC of graphene, the effect of fractal structure on the TC of graphene is clarified. Additionally, the phonon behaviors, including the phonon participation ratio and phonon density of states are analyzed to reveal the mechanisms underlying the phonon transport of the graphene with SCF and regular carpet (RC) defects.

Mathematical Model

Removing or replacing some carbon atoms on a graphene monolayer is a common method to construct defective graphene. As shown in Figures 1A,B, the SCF graphene (fractal level, k = 0, 1, 2, 3) and the RC graphene with a size of 27 nm × 27 nm are constructed in the simulation.

FIGURE 1

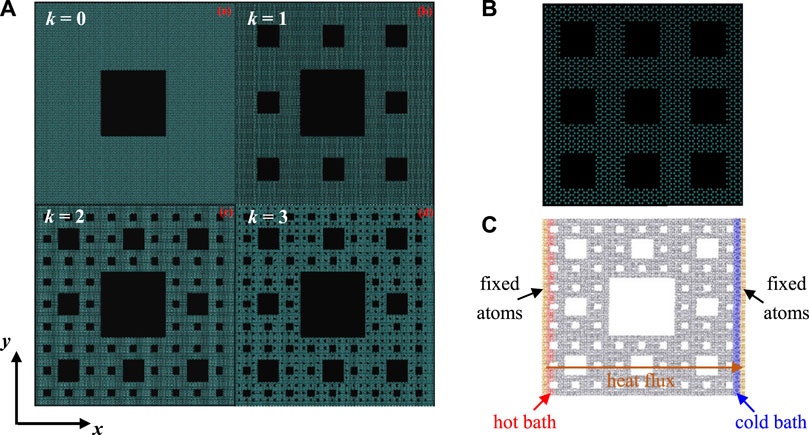
FIGURE 1. Schematic of heat transfer in defective graphene: (A) SCF defects; (B) RC defects; and (C) thermal boundary condition.

To investigate the influence of defect structure on the TC of graphene, the porosity (p) of the graphene with SCF and RC defects under the same porosity is defined as

$p=\frac{S_{\text{defect}}}{S_{\text{total}}},(1)$

where S_defect is the area of defects and S_total is the total volume of graphene monolayer. The corresponding porosities under different fractal levels are 8.42, 15.9, 22.69, and 27.04%, respectively.

The non-equilibrium molecular dynamics (NEMD) method is adopted to investigate the TC of graphene monolayer with SCF and RC defects. As shown in Figure 1C, the heat flux is imposed in the direction from the hot bath to the cold bath. Each layer of graphene monolayer has a thickness of 2 nm with 1,000 atoms, which can guarantee the reliability of the numerical results.

The initial temperature of the system is 500 K, and the time step is 0.5 fs The simulations first are performed in NVT for 1×10⁶ steps and then in NVE for 4×10⁸ steps. The increasing energy in the hot bath and decreasing energy in the cold bath are set as 2.5 to establish the temperature gradient. Therefore, the TC of graphene is calculated as

$\kappa =\frac{Q}{S\nabla T},(2)$

where Q is the increasing heat flux from heat bath or decreasing heat flux from the cold bath, ∇T is the temperature gradient, and S is the cross-sectional area.

Results and Discussions

Thermal Conductivity of Defective Graphene

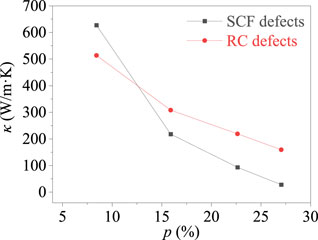
The TC of material in the macroscale is a physical parameter that has no change with the material structure. However, the TC of graphene is relevant to the structure of the atomic system as a low-dimensional material. Therefore, the TC of graphene with SCF and RC defects under different porosity calculated by Eq. 1 is plotted in Figure 2. The TC of graphene with SCF defects has a sharp decrease with increasing porosity. When the porosity increases from 8 to 27%, the TC of graphene with SCF defects decreases from 627.4 W/mK to 93.65 W/mK, and the TC of graphene with RC defects decreases from 513.8 W/mK to 159.4W/mK. This result indicates that the decreasing effect of porosity on the TC of graphene with SCF defects is stronger than that of graphene with RC defects.

FIGURE 2

FIGURE 2. TC of two defective graphene.

PDOS of Defective Graphene

The physical mechanisms of heat transfer in defective graphene can be expounded by the phonon behaviors, which are analyzed by the phonon density of states (PDOS). The concentration of phonons in the low-frequency region demonstrates that graphene has a high thermal resistance. In order to explain the influence of the SCF and RC defects on the TC of graphene, PDOS of two defective graphene is analyzed, which can be calculated by taking the Fourier transform of the velocity autocorrelation function (Mortazavi et al., 2016)

$g\left(\omega \right)=\underset{\Delta \omega \to 0}{\lim }\left(\frac{\Delta n}{\Delta \omega }\right),(3)$

where Δn is the modulus of the lattice vibration in the interval Δω, which can be calculated as

$\Delta n=\frac{V_c}{{\left(2\pi \right)}^3}{\displaystyle \int \mathrm{d}s\mathrm{d}q},(4)$

where dq is the vertical distance between the two equal frequency planes and ds is the area element.

The total modulus and total degrees of freedom are equal, and a simple crystal has N atoms

$\underset{0}{\overset{{\omega }_m}{{\displaystyle \int }}}g\left(\omega \right)d\omega =3N,(5)$

where ω_m is the maximum frequency. Combing the above equations, the PDOS can be obtained by

$g\left(\omega \right)={\displaystyle \sum }_{\alpha =1}^{3p}\frac{V_c}{{\left(2\pi \right)}^3}\underset{s_{\alpha }}{{\displaystyle \int }}\frac{\mathrm{d}s}{\left|{\nabla }_{\mathrm{q}}{\omega }_{\alpha }\left(q\right)\right|}.(6)$

Figure 3A shows the PDOS of graphene with SCF defects (k = 2, 3, 4), and Figure 3B shows the comparison between the PDOS of graphene with SCF and RC defects (RC defects and SCF defects with k = 4 have the same porosity). As shown in Figure 3A, the corresponding frequency peaks of PDOS concentrate in the low-frequency region with increasing k. The frequency peaks of PDOS for SCF graphene with k = 2, 3, and 4 are respectively about 30, 26.7, and 20 HTz. The concentration of frequency peaks in the low-frequency region demonstrates that the influence of boundary scattering of phonons on the heat transfer is enlarged during the heat transfer, which leads to the decrease in TC. Furthermore, as shown in Figure 3B, the concentration of frequency peaks in the low-frequency region for graphene with SCF defect is more obvious than that for graphene with RC defects. This result indicates that the heat transfer blockage effect of SCF defects is stronger than that of RC defects. It explains why the TC of graphene with SCF defects is lower than that with RC defects under the same porosity.

FIGURE 3

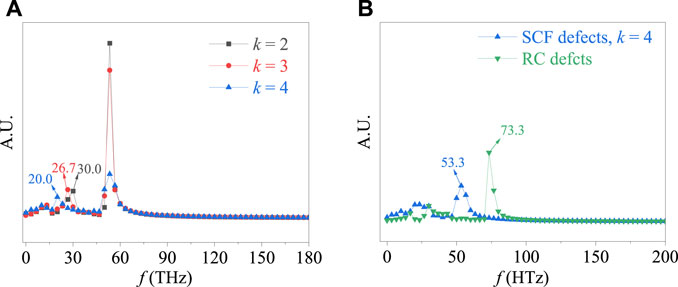
FIGURE 3. PDOS of graphene with two defective defects: (A) effect of the fractal level and (B) Comparison between SCF and RC defects.

Phonon Participation Ratio

In order to get a better insight into the suppression of TC, the phono participation ratio (P) is used to reveal the influence of defects on TC. The value of P represents the number of atoms participating in the motion. If only one atom among N atoms in the system participates in the heat transfer, p = 1/N. If all the atoms participate in the heat transfer, p = 1. P can be calculated as (Yang et al., 2013; Shao et al., 2018; Han et al., 2019b):

$P=N{{\displaystyle \sum _{i=1}^N\left({\displaystyle \sum _{\alpha =1}^3{u}_{i\alpha ,\lambda }^{\ast }{u}_{i\alpha ,\lambda }}\right)}}^2,(7)$

where N is the total number of atoms and u_iα,k is the eigenvector component of mode λ in the α direction of the ith atom.

Figure 4A illustrates the P of graphene with SCF defects (k = 2, 3, 4), and Figure 4B illustrates the comparison between the P of graphene with SCF and RC defects (graphene with RC defects and SCF defects k = 4 have the same porosity). As shown in Figure 4A, P has more peaks with decreasing k, which indicates the number of atoms that have the heat transfer blockage effect increases and these atoms have no participation in the heat transfer. Additionally, Figure 4B shows that more atoms that have the heat transfer blockage effect occur in the graphene with SCF defects than that in the graphene with RC defects. Therefore, the heat transfer blockage effect of the graphene with SCF defects on TC is stronger than that of the graphene with RC defects.

FIGURE 4

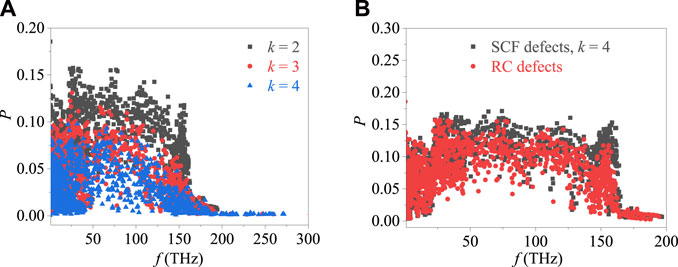
FIGURE 4. Phonon participation rate of graphene with SCF and RC defects: (A) effect of fractal level and (B) comparison between SCF and RC defects.

Conclusion

In this study, the heat transfer of graphene with SCF and RC defects is numerically investigated by the NEMD method. The phonon behaviors are analyzed to reveal the underlying mechanisms of the heat transfer of graphene with different defects. The main conclusions are as follows:

1) The defects of graphene induce the atoms that have the heat transfer blockage effect, which leads to the decrease in TC. Additionally, the TC of defective graphene decreases with increasing porosity.

2) As the increase of fractal levels, the frequency peaks concentrate in the low-frequency region, and the number of atoms that have the heat transfer blockage effect significantly increases, which leads to the TC of graphene with SCF defects sharply decreasing with increasing fractal levels.

3) Under the same porosity, the TC and frequency peaks of graphene with SCF defects are lower than that of graphene with RC defects; this is attributed to the fact that more atoms have the heat transfer blockage effect under the graphene with SCF defects.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

XW conducted the simulations and prepared the article. YW and XS contributed to analysis of simulation data. WY contributed to design of structure, discussions of the results, and article preparation. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (Grant No. 52006187), the Natural Science Foundation of the Jiangsu Higher Education Institutions of China (20KJB470006), and Jiangsu Provincial Double-Innovation Doctor Program (JSSCBS20211059).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aldrigo, M., Dragoman, M., Costanzo, A., and Dragoman, D. (2013). Graphene as a High Impedance Surface for Ultra-wideband Electromagnetic Waves. J. Appl. Phys. 114 (18), 184308. doi:10.1063/1.4830018

CrossRef Full Text | Google Scholar

Anno, Y., Imakita, Y., Takei, K., Akita, S., and Arie, T. (2017). Enhancement of Graphene Thermoelectric Performance through Defect Engineering. 2D Mater. 4 (2), 025019. doi:10.1088/2053-1583/aa57fc

CrossRef Full Text | Google Scholar

Balandin, A. A., Ghosh, S., Bao, W., Calizo, I., Teweldebrhan, D., Miao, F., et al. (2008). Superior thermal Conductivity of Single-Layer Graphene. Nano Lett. 8 (3), 902–907. doi:10.1021/nl0731872

PubMed Abstract | CrossRef Full Text | Google Scholar

Bazrafshan, S., and Rajabpour, A. (2017). Thermal Transport Engineering in Amorphous Graphene: Non-equilibrium Molecular Dynamics Study. Int. J. Heat Mass Transfer 112, 379–386. doi:10.1016/j.ijheatmasstransfer.2017.04.127

CrossRef Full Text | Google Scholar

Chen, Y., and Deng, Z. (2017). Hydrodynamics of a Droplet Passing through a Microfluidic T-junction. J. Fluid Mech. 819, 401–434. doi:10.1017/jfm.2017.181

CrossRef Full Text | Google Scholar

Chen, Y., Wu, L., and Zhang, L. (2015). Dynamic Behaviors of Double Emulsion Formation in a Flow-Focusing Device. Int. J. Heat Mass Transfer 82, 42–50. doi:10.1016/j.ijheatmasstransfer.2014.11.027

CrossRef Full Text | Google Scholar

Cui, L., Du, X., Wei, G., and Feng, Y. (2016). Thermal Conductivity of Graphene Wrinkles: A Molecular Dynamics Simulation. J. Phys. Chem. C 120 (41), 23807–23812. doi:10.1021/acs.jpcc.6b07162

CrossRef Full Text | Google Scholar

Deng, Z., Liu, X., Zhang, C., Huang, Y., and Chen, Y. (2017). Melting Behaviors of PCM in Porous Metal Foam Characterized by Fractal Geometry. Int. J. Heat Mass Transfer 113, 1031–1042. doi:10.1016/j.ijheatmasstransfer.2017.05.126

CrossRef Full Text | Google Scholar

Ghosh, S., Calizo, I., Teweldebrhan, D., Pokatilov, E. P., Nika, D. L., Balandin, A. A., et al. (2008). Extremely High thermal Conductivity of Graphene: Prospects for thermal Management Applications in Nanoelectronic Circuits. Appl. Phys. Lett. 92 (15), 151911. doi:10.1063/1.2907977

CrossRef Full Text | Google Scholar

Han, D., Ding, W., Wang, X., and Cheng, L. (2019a). Tunable thermal Transport in a WS2 Monolayer with Isotopic Doping and Fractal Structure. Nanoscale 11 (42), 19763–19771. doi:10.1039/c9nr02835h

PubMed Abstract | CrossRef Full Text | Google Scholar

Han, D., Fan, H., Wang, X., and Cheng, L. (2020). Atomistic Simulations of Phonon Behaviors in Isotopically Doped Graphene with Sierpinski Carpet Fractal Structure. Mater. Res. Express 7 (3), 035020. doi:10.1088/2053-1591/ab7e4b

CrossRef Full Text | Google Scholar

Han, D., Wang, X., Ding, W., Chen, Y., Zhang, J., Xin, G., et al. (2019b). Phonon thermal Conduction in a Graphene-C3N Heterobilayer Using Molecular Dynamics Simulations. Nanotechnology 30 (7), 075403. doi:10.1088/1361-6528/aaf481

PubMed Abstract | CrossRef Full Text | Google Scholar

Hao, F., Fang, D., and Xu, Z. (2011). Mechanical and thermal Transport Properties of Graphene with Defects. Appl. Phys. Lett. 99 (4), 041901. doi:10.1063/1.3615290

CrossRef Full Text | Google Scholar

Hu, S., Chen, J., Yang, N., and Li, B. (2017). Thermal Transport in Graphene with Defect and Doping: Phonon Modes Analysis. Carbon 116, 139–144. doi:10.1016/j.carbon.2017.01.089

CrossRef Full Text | Google Scholar

Kang, Y., Duan, F., Shangguan, S., Zhang, Y., Zhou, T., and Si, B. (2018). Thermal Transport of Graphene Sheets with Fractal Defects. Molecules 23 (12), 3294. doi:10.3390/molecules23123294

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, C., Wei, X., Kysar, J. W., and Hone, J. (2008). Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene. Science 321 (5887), 385–388. doi:10.1126/science.1157996

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, H., Rui, Q., Wang, X., and Yu, W. (2021). Molecular Dynamics Simulations on Influence of Defect on Thermal Conductivity of Silicon Nanowires. Front. Energ. Res. 9, 664891. doi:10.3389/fenrg.2021.664891

CrossRef Full Text | Google Scholar

Mortazavi, B., Fan, Z., Pereira, L. F. C., Harju, A., and Rabczuk, T. (2016). Amorphized Graphene: A Stiff Material with Low thermal Conductivity. Carbon 103, 318–326. doi:10.1016/j.carbon.2016.03.007

CrossRef Full Text | Google Scholar

Novoselov, K. S., Geim, A. K., Morozov, S. V., Jiang, D., Zhang, Y., Dubonos, S. V., et al. (2004). Electric Field Effect in Atomically Thin Carbon Films. Science 306 (5696), 666–669. doi:10.1126/science.1102896

PubMed Abstract | CrossRef Full Text | Google Scholar

Shao, C., Rong, Q., Li, N., and Bao, H. (2018). Understanding the Mechanism of Diffuse Phonon Scattering at Disordered Surfaces by Atomistic Wave-Packet Investigation. Phys. Rev. B 98 (15), 155418. doi:10.1103/PhysRevB.98.155418

CrossRef Full Text | Google Scholar

Wang, J., Gao, W., Zhang, H., Zou, M., Chen, Y., and Zhao, Y. (2018). Programmable Wettability on Photocontrolled Graphene Film. Sci. Adv. 4 (9), eaat7392. doi:10.1126/sciadv.aat7392

PubMed Abstract | CrossRef Full Text | Google Scholar

Wei, N., Xu, L., Wang, H.-Q., and Zheng, J.-C. (2011). Strain Engineering of thermal Conductivity in Graphene Sheets and Nanoribbons: a Demonstration of Magic Flexibility. Nanotechnology 22 (10), 105705. doi:10.1088/0957-4484/22/10/105705

PubMed Abstract | CrossRef Full Text | Google Scholar

Wei, Z., Yang, J., Bi, K., and Chen, Y. (2015). Phonon Transport Properties in Pillared Silicon Film. J. Appl. Phys. 118 (15), 155103. doi:10.1063/1.4933284

CrossRef Full Text | Google Scholar

Yang, L., Yang, N., and Li, B. (2013). Reduction of Thermal Conductivity by Nanoscale 3D Phononic Crystal. Sci. Rep. 3, 1143. doi:10.1038/srep01143

PubMed Abstract | CrossRef Full Text | Google Scholar

Yarifard, M., Davoodi, J., and Rafii-Tabar, H. (2017). Computation of the thermal Resistance in Graphene Sheets with a Rectangular Hole. Comput. Mater. Sci. 126, 29–34. doi:10.1016/j.commatsci.2016.09.009

CrossRef Full Text | Google Scholar

Zhang, C.-B., Cheng, Q.-K., and Chen, Y.-P. (2014). Molecular Dynamics Simulation on thermal Conductivity of Nanocomposites Embedded with Fractal Structure. Acta Phys. Sin. 63 (23), 236601. doi:10.7498/aps.63.236601

CrossRef Full Text | Google Scholar

Zhang, C., Li, J., and Chen, Y. (2020). Improving the Energy Discharging Performance of a Latent Heat Storage (LHS) Unit Using Fractal-Tree-Shaped Fins. Appl. Energ. 259, 114102. doi:10.1016/j.apenergy.2019.114102

CrossRef Full Text | Google Scholar