Research on Dynamic Response of Slopes With Weak Interlayers Under Mining Blasting Vibration

As blasting technology starts to be used in a wide range of areas, blast loading has led to an increasing number of geological disasters such as slope deformation, collapses, and soil slippage. Slopes with weak interlayers are more likely to be deformed and damaged under the influence of blast loading. It is of great importance to study the evolution for the deformation of slopes with weak interlayers during blasting excavation. This study constructed a slope model with a weak interlayer to investigate the influence of different factors of blasting, including explosive charge, blast radius, blast origin, and multi-hole blasting, on the internal dynamic response. The deformation mechanism of slopes with weak interlayers under the influence of blast loading was analyzed. Test results show that each layer of the model had a different displacement response (uncoordinated dynamic response) to blasting with various factors. Explosive energy and the pattern of dynamic response of each layer varied depending on different settings of blasting factors such as explosive charge, blast radius, blast origin, and detonation initiation method. When the explosive energy produced under the influence of various factors was small, the change in the uncoordinated dynamic response between layers was significant, and the change gradually became less significant as the explosive energy increased. Therefore, this study has proposed the concept of critical explosive energy, and it is speculated that when the explosive energy produced with various factors is less than critical explosive energy, the dynamic response is mainly affected by the internal structure of the slope (property difference induced geologic layers). In other words, the uncoordinated motion of material’s particles in each layer is caused by different limitations and the degree of movement of the particles, which leads to the uncoordinated dynamic response and uncoordinated deformation of each layer. If the explosive energy is greater than the critical value, the dynamic response of each layer is mainly affected by the explosive energy. The differences in the internal structure of the slope are negligible, and the incoordination of dynamic responses between layers gradually weakens and tends to synchronize.

Highlights

1) Blasting engineering often induces instability of surrounding slopes, especially slopes with weak interlayers.

2) Under the action of blasting vibration, the layers of slopes with weak interlayers presented uncoordinated dynamic response.

3) Uncoordinated dynamic response leads to uncoordinated deformation.

4) When the blasting energy is larger than the critical blasting energy, the uncoordinated dynamic response tends to be synchronized.

Introduction

In recent decades, as infrastructure and mine excavations continue to develop rapidly, blasting technology has been used in different types of large-scale engineering projects and mining engineering. While blasting technology brings great benefits to project construction, it also gives rise to an increasing number of issues in slope stability. Up to 25 landslides were induced by blasting in the Daye iron mine in Hubei province, China (Liu, 2009). Many landslides were caused by blasting excavation in a limestone mining area in Mount Emei in Sichuan province (Bai et al., 1995). At Pasir mine in Kalimantan, several slope failure accidents were caused by blasting in layered deposits with a high dip angle, resulting in considerable production interruption and economic losses (Deb et al., 2011). Some other slope failure accidents caused by blasting in different open-pit mines in China can also be found in the literature reports (Li et al., 2001; Luo et al., 2015; Song et al., 2017; Deng et al., 2018; He et al., 2021). Blasting-generated seismic waves were the main cause of disturbance to the overlaying open-pit slopes in triggering instability of slopes (Dvořák, 1977; Singh and Singh, 1995; Jiang et al., 2018; Adushkin, 2019; Hempen, 2019). Investigations into the effect of mine blast vibrations on the surrounding slopes are the key point to assess the effect of blasting on the stability of the nearby slopes. One of the most important studies is to obtain the propagation and attenuation of the blast vibration data in the rock slope by in situ monitoring of ground vibration (Ozcelik, 1998; Kesimal et al., 2008; Lu et al., 2015; Fan and Ge, 2020; Lu et al., 2020). Wang et al. (2007) studied the dynamic responses of continuous rock masses under blast loading and found blast tensile damage induced by wave propagation. It has been promoted that the level of rock fragmentation by blasting was largely affected by the distribution of structural planes (Ozcelik, 1998). Blasting acceleration was the main cause of plane shear failure inside the slope (Kesimal et al., 2008; Wang et al., 2019). Chang et al. (2007) conducted the study of numerical modeling of blast wave propagation through rock mass and effects of water and joints. With the development of computer technology, codes, such as DDA, FLAC3D, ANSYS/LS-DYNA, and GEO-SLOPE et al. are frequently adopted to study the influence of blast on rock slopes.

Excepting blasting, although many factors such as rainfall, geological conditions, and groundwater induce the loss of the slope stabilities, control over blasting in quarry should be more important since the geology of a pit cannot be changed. The adverse effects of blasting operations can be controlled by conducting optimization of the blast design. Blasting pattern, such as hole depth and diameter, explosive charge, bench geometry, blast timing, and position, is the key parameter within the control of the blasting risk. Besides the different blasting patterns having different influence on the dynamic response of slopes with weak interlayers, more complicated methods may be used for blasting, such as multi-hole blasting and blasting from different angles. Peak particle velocity, acceleration, and displacement are considered to be the reliable vibration monitoring parameters (Hakan et al., 2009; Li et al., 2021a; Li et al., 2021b).

The previous studies are mainly based on numerical or physical simulations of the patterns of dynamic responses of relatively homogeneous rock slopes under the influence of blasting. Some scholars point out that the vibration intensity caused by blasting is closely related to the lithology and structural characteristics of rock mass (Görgülü et al., 2013; González-Nicieza et al., 2014; Benchelha et al., 2017; Mohamad et al., 2018). Therefore, compared with normal rock slopes, the dynamic response of slopes with weak interlayers under blast loading is different from that of normal rock slopes because of their special geological structures. Under the influence of blasting vibration, slopes with weak interlayers are more prone to deformation and failure, and they can eventually cause geological disasters such as landslides. However, there are few research studies on the dynamic response of weak intercalated slopes under different blasting patterns.

The purpose of this study is to better study the patterns of dynamic response of slopes with weak interlayers in an actual blasting process and provide a reference for engineering practice. A typical blasting cracked slope in the Lingshi County of Shanxi province of China was chosen as the case, and physical model simulations of blast loading were constructed. Based on the proto-model, we investigated the dynamic response patterns of acceleration and strain of each layer of slope with a weak interlayer under the influence of blasting factors such as explosive charge, blast radius, blast directions, and multi-hole blasting. In addition, the study has analyzed the deformation mechanism of the slope with a weak interlayer under the effect of blasting, which provides a theoretical basis for studying the deformation and failure of slopes under blast loading.

Plans of Blasting Physical Simulation Tests

Model Design

The study area is located in Lingshi County, Shanxi Province, China. The area has rich mines in resources and has a long history of mining, especially in recent years where coal mining has become the main local industry. The unstable slope was selected as the research object, which is located in Beizhuang village, Lingshi County. The elevation of the rear edge of the slope is about 1,005 m, and the elevation of the leading edge is about 900 m. There is a slightly thick Quaternary mid-late Pleistocene loess on the top of the slope, bedrock exposed in the middle and upper slope, and an overburden composed of residual and slope sediments in the middle and lower part of the slope. The slope is composed of a soft- and hard-interbedded structure of sandstone and mudstone. Three groups of joints are developed: the first group is a rock layer (Sun et al., 2008; Wang, 2017), whose occurrence is 330–350° ∠ 5–10° (dip direction ∠ dip angle); the second group is a steeply inclined fissure J1, which is 330–340° ∠ 80–85°; and the third group is a steeply inclined fissure J2, whose occurrence is 50–55° ∠ 75–80°. There are 20 mining points within 1 km of the slope. The slope showed no signs of deformation before 2013. The closest to the slope is the ZL coalmine. In 2014, the coalmine was mined, and cracks appeared on the rear edge of the slope in June 2015. In 2016, the number of cracks increased to 12, and rift troughs appeared on the left and right sides of the slope. In 2017, 5 local rock avalanches occurred. By 2019, 18 cracks have been developed; the longest crack is about 35 m, and the widest crack is about 1 m. According to Google Earth images and a detailed visit to the study area, it was found that there was no deformation before mining in 2014. Therefore, we think that the effect of blasting vibration during the mining in the mining area may be the main reason for the deformation and damage of the slope.

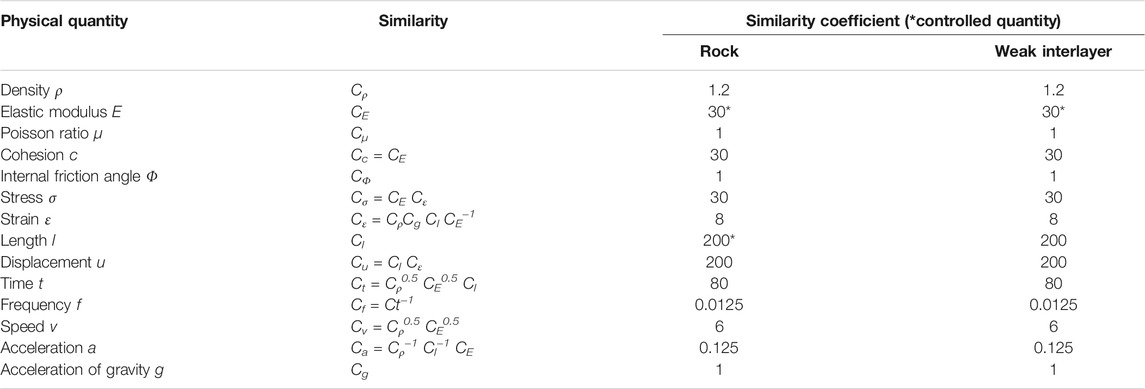
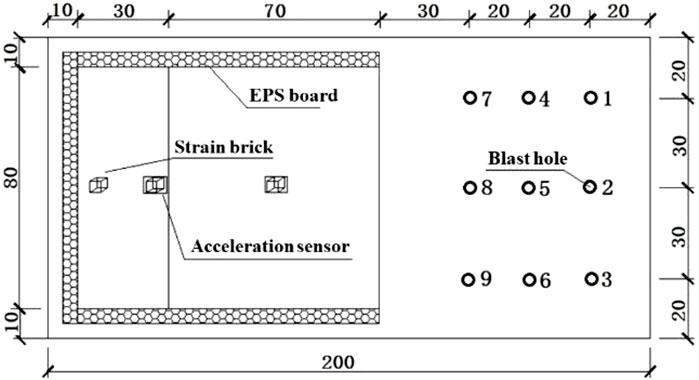
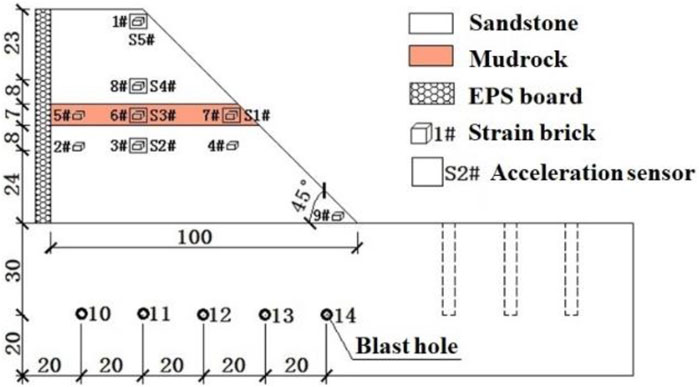
The similarity between the test model and the prototype (Table 1), and physical and mechanical parameters (Table 2) were established based on the second theorem of similarity. The hard rock was semiarid by materials composed of quartz sand and barite powder. Gypsum and glycerin were used as the cementing agent for hard rock. Regarding soft rock similar materials, quartz sand and clay were used as aggregates for the simulation of soft rock. Gypsum and paraffin were chosen to cement other materials. Specific ratios and properties are listed in Table 3. The test model was designed as shown in Figures 1, 2. It can be seen that the model consists of two parts. The bottom part was the base of the mode, which was made of cement mortar, and the upper part made of our similar materials for the soft layer and hard layer was the studied slope.

TABLE 1

TABLE 1. Similarity system for blasting physical model test.

TABLE 2

TABLE 2. Physical and mechanical parameters of blasting physical model and photo model.

TABLE 3

TABLE 3. Proportion of similar materials and related properties.

FIGURE 1

FIGURE 1. Plan figure of the test model.

FIGURE 2

FIGURE 2. Sectional view of the test model.

Blasting Equipment

The physical model test adopted the method of “explosive blasting energy approximation”, and the test approximately meets the explosion dynamic criterion. Due to the lack of site blasting data, the explosive selected in this test is emulsion explosive to provide a certain equivalent blasting load for a similar model. This study aims to study the dynamic response of the slope model under different weights of explosive conditions. In addition, a plastic detonator with high safety performance is selected, as shown in Figure 3. The parameters of emulsion explosives are as follows: densityρ_c = 1.32 g/cm³, detonation velocity D_v = 3,350 m/s, heat of explosion Q_v = 4200 k J/kg, and intensity △h = 11.5 mm. The specific amount of explosive charge is listed in Table 4. The method of decoupling charging was used for our tests. The upper part of the blast hole was filled with bentonite, and the soil bags were prepared and covered the hole. After that, the plastic detonator was detonated by using the high voltage spark.

FIGURE 3

FIGURE 3. Materials for blasting physical simulation test.

TABLE 4

TABLE 4. Design of blasting plans.

Design of Testing

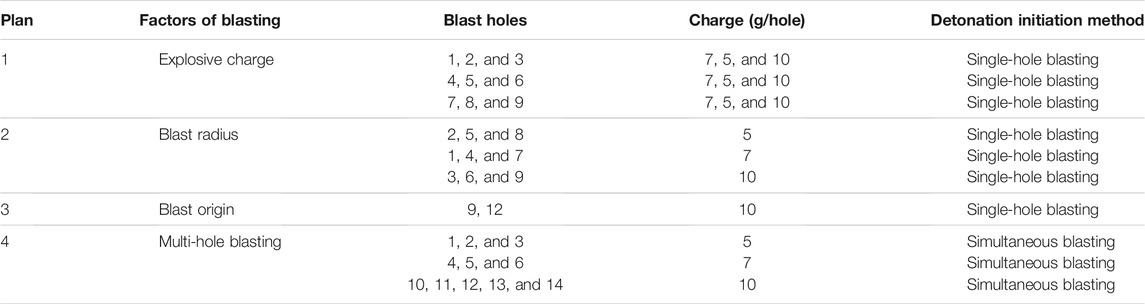
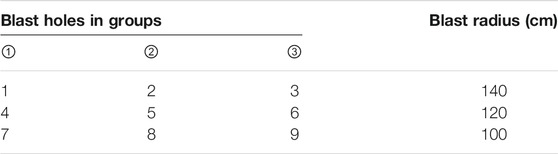
The factors of explosive charge, blasting radios, blasting directions, and multi-hole blasting were considered in our tests. The factor value shown in Tables 4, 5 was set according to the “approximate blasting energy of explosives” (Yuan, 2016). The value of 5, 7, and 10 g were used for the explosive charge factor. There were 14 blasting holes used in our tests; 1–9 blasting holes were used for the cases of explosive charge and blasting radius. The cases for blasting directions were involved with the 9 and 12 blasting holes. There were three cases involving 1–3, 4–6, and 10–14 blasting holes, respectively, for studying the effect of multi-hole blasting. These values were also used for the multi-hole blasting cases (Table 4). The blast radius of 100, 120, and 140 mm was used in our tests (Table 5).

TABLE 5

TABLE 5. Blast radius for each group of blast holes.

Results

Analysis of Acceleration Response Characteristics

The time-series data of accelerations in the horizontal (X) and vertical (Z) directions measured in the upper hard layer, soft layer, and lower hard layer are shown in Supplementary Figure S1. The acceleration time-history curves showed an asymmetrical spindle shape. The blasting vibration was characterized by an instantaneous feature. The duration of acceleration violent fluctuations was very short. The main blasting vibration was concentrated in a limited period of time in all our cases of test, such as the duration of 0.013–0.03 s, in Supplementary Figure S1A. The curve of the main blasting vibration is enlarged and shown in Supplementary Figure S1B.

1) Analysis of acceleration characteristics of each layer with different explosive charges

This section analyzes the data obtained from the blasting holes 1, 2, and 3 in the first plan (Table 4). Supplementary Figures 2–4 show the horizontal (X) acceleration characteristic curves of the upper and lower hard and soft layers with explosive charges of 5, 7, and 10 g, respectively.

It can be seen from the figures that when the amount of explosive charge was small (5 g), the difference in acceleration response of different layers was large. The acceleration response of the lower hard layer was the largest, that of the soft layer was second and the upper hard layer, the third. The peak acceleration of the three layers from the largest to the smallest was lower hard layer > soft layer > upper hard layer. The peak and minimum values of the accelerations for each layer were different, and there was a clear displacement. With the increase of the explosive charge (such as 7 and 10 g), the acceleration difference between each layer gradually decreased, and at the same time, the displacement in peaks and valleys of each layer gradually disappeared and tended to synchronize. It can be seen that when the amount of the explosive charge was small, the explosive energy was small and the acceleration response between each layer was mainly affected by the material medium, which shows an uncoordinated dynamic variation, i.e., the lower hard layer > soft layer > upper hard layer. As the amount of explosive charge increased, it resulted in the increase of the explosive energy. The acceleration response due to the influence of the material medium in each layer decreased gradually, while the influence of the explosive energy on the acceleration response increases. It can be predicted that there might be a critical value of blasting energy. When the explosive charge reaches a certain critical value and the explosive energy reaches the critical explosive energy, the acceleration response will be mainly affected by the explosive energy. The uncoordinated dynamic response of different layers will also be disappeared and tend to change synchronously. The horizontal (X) acceleration characteristic curves between layers show similar response characteristics in the cases of blast holes 4, 5, 6, 7, 8, and 9.

Based on the analysis of the vertical (Z) acceleration characteristic curves (Supplementary Figures S5–S7), it can be seen that the response characteristics are slightly different from that of the horizontal (X) acceleration curves. Overall, the acceleration response characteristics in the vertical (Z) direction of each layer are as follows: lower hard layer > soft layer > upper hard layer. At the same time, the peaks and valleys in the acceleration trace for each layer still have displacement. However, the acceleration response of the soft layer in the vertical direction was more violent than that of the horizontal. The amplitude of the acceleration in the soft layer was even close to or exceeded that in the lower hard layer at a certain time. The displacement in the peaks and valleys of the acceleration trace of the soft layer and the lower hard layer at the same time was relatively small, but at the same time, the values at the peaks and valleys of acceleration were much larger than that of the upper hard layer. However, with the increase in the amount of the explosive charge, the displacement in the peaks and valleys for each layer gradually became more and more synchronized.

According to the horizontal (X) acceleration response characteristics of each layer, it can be seen that when the explosive charge was small, the movement of the medium particles of each layer was slightly limited in the horizontal direction, and the nature of the restricted motion of the medium particles of each layer was basically the same. Therefore, the acceleration response characteristics (lower hard layer > soft layer > upper hard layer) were more prominent, and the anomalies were not prominent. However, by analyzing the acceleration response characteristics in the vertical (Z) direction, it can be speculated that when the amount of the explosive charge was small, there were obvious differences in the limitation of the movement of the medium particles in different layers in the vertical direction.

Given different material properties in each layer, the particle density is different. The movement space of the media particles in each layer is then different. In addition, during blasting vibration, the density of the material medium increases with the depth. Considering all the above, the motion of the medium particles in the lower hard layer is more restricted in the vertical direction than in the soft layer. Therefore, the acceleration of the soft layer in the vertical direction responded more violently, and its variation even approached or exceeded that of the lower hard layer at a certain time. Theoretically, the motion limit of the medium particles in the upper hard layer is smaller than that of the lower hard layer, and its vertical acceleration response should be greater than that of the lower hard layer. However, in reality, the reflection or superposition cancellation occurred when the blasting wave reached the soft layer in the process of bottom-up propagation, leading to the weakest vertical acceleration response in the upper hard layer. It should be mentioned that when the amount of the explosive charge is sufficient and can generate energy more than the critical explosive energy, regardless of the horizontal or vertical acceleration of layers, the variation in the response will tend to synchronize. In other words, the uncoordinated dynamic variation of the dynamic response of different layers will be gradually weakened. In this regard, the dynamic response is mainly affected by the blasting energy and is little affected by the material medium.

2) Analysis of acceleration characteristics of each layer with different blast radii

Based on the analysis of the test data of the second group of blast holes (2, 5, and 8), the trend curve of the peak acceleration of each layer with the distance to the center of the blast was obtained, as shown in Supplementary Figures S8, S9. The influence of blast radius on the acceleration response characteristics of each layer can be summarized as follows:

① The acceleration response of each layer tended to decay with the increase in the blast radius. Specifically, at the same measurement point, the farther the distance to the explosion source, the smaller the acceleration. The peak acceleration value appeared to decline as the blast radius increased.

② Different levels of acceleration have different attenuation trends. The attenuation trend of the acceleration of the lower hard layer was the most significant, and the attenuation of the acceleration response of the soft layer and the upper hard layer was relatively slow.

③ Horizontal and vertical acceleration attenuation rates were different. The horizontal acceleration decay rate in the lower hard layer was less than the vertical acceleration decay rate; the horizontal acceleration decay rates in the soft layer and the upper hard layer were slightly greater than the vertical acceleration decay rates;

④ It can be predicted that when the blast radius is small and reaches a certain limit value and the explosive energy reaches the critical explosive energy, the acceleration response attenuation rate of each layer will tend to be consistent. Data analysis results of the first and third groups of blast hole tests were similar.

3) Analysis of acceleration characteristics of layers in different blast directions

Based on the analysis of the test data of hole 12 at the bottom of the slope model and hole 9 at the leading edge of the slope, their characteristic acceleration curves are shown in Supplementary Figures S10–15. Specifically, Supplementary Figures S10–12 are the horizontal acceleration characteristic curves in the lower hard layer, soft layer, and upper hard layer, respectively. Supplementary Figures S13–15 are the vertical acceleration characteristic curves. Overall, the acceleration response of each layer is different in different blast directions. Specifically:

① The acceleration response of each layer during blasting at the bottom was stronger than that of the leading edge. As shown in Supplementary Figures S10–12, during blasting at the bottom of the slope, the maximum values of the peak horizontal acceleration in the lower hard layer, soft layer, and upper hard layer could reach 48.75332, 50, and 39.851071, respectively. During blasting at the leading edge of the slope, the maximum values of the peak horizontal acceleration in the above layers were 30.822168, 29.33868, and 17.92352, respectively. This pattern was more significant in the vertical acceleration response (Supplementary Figures S13–15).

② The vertical acceleration response of the same layer was more sensitive to blast directions than the horizontal acceleration. As shown in Table 6, when the location of the explosion source was different, the mean differences of the peak horizontal acceleration of the lower hard layer, soft layer, and upper hard layer were 18.3376, 21.8050, and 18.1285, respectively. The mean differences of the peak vertical acceleration of the above layers were 27.1788, 28.0374, and 30.9529, respectively. It is clear that when the blast directions were different, the vertical acceleration response of each layer was stronger.

③ Regarding the soft layer and the upper hard layer, the use of bottom blasting had a stronger effect on the acceleration than the leading edge blasting, mainly due to the different propagation methods of the blast wave.

(4) Analysis of acceleration characteristics of each layer during multi-hole blasting

TABLE 6

TABLE 6. Mean differences of the peak horizontal and vertical acceleration of each layer in different blast directions.

Supplementary Figures S16, 17 show the time-history curves of horizontal and vertical acceleration of each layer when holes 1, 2, and 3 were simultaneously detonated. Unlike single-hole blasting, the acceleration response of each layer during multi-hole blasting exhibits two instantaneous violent fluctuations, which have been amplified separately in characteristic acceleration curves I and II (Supplementary Figures S18–21), respectively.

Based on the analysis of characteristic acceleration curves Ⅰ and Ⅱ, it can be known that the acceleration response characteristics of each layer during multi-hole blasting were still lower hard layer > soft layer > upper hard layer. At the same time, the peaks and valleys in the acceleration trace for each layer were different, and a clear displacement was observed. This result indicates that the acceleration response of each layer is in an uncoordinated dynamic change, indicating that there is an uncoordinated deformation characteristic between each layer. This pattern is more prominent in the vertical acceleration characteristic curve, but it gradually weakens in the horizontal acceleration characteristic curve. It is mainly related to the difference in the restricted nature of the movement of the medium particles in different directions in each layer and the reflection or superimposed cancellation of the blast wave from the bottom to the top. The principle is the same as explained before.

It is worth noting that even if the explosive charge, blast radius, and blast origin were the same, the explosive energy produced by multi-hole blasting was much larger than that produced by single-hole blasting. Therefore, during multi-hole blasting, the uncoordinated dynamics of the acceleration response between layers in the slope with weak interlayers is relatively weak.

Analysis of Strain Response Characteristics

In order to obtain effective strain wave waveforms and strain wave parameters (i.e., strain wave peak value and time) of each layer in the model, the data collection frequency was adjusted appropriately, and the clutter was filtered out to process the recorded signal in order to obtain strain time-history curves that can truly reflect the deformation characteristics of each layer in the model (Supplementary Figures S22, S23). A strain time-history curve is roughly divided into three parts: front, middle, and tail. The strain fluctuations in the front part were small, indicating that there was no major deformation in each layer. The severe strain fluctuations in the middle part indicate that the media in each layer were subjected to tensile or stamping under the action of stress waves, and tensile or compressive strains began to occur inside with large strain fluctuations. The strain fluctuation of the tail part was relatively stable, indicating that a certain degree of plastic creep appeared in each layer as the stress wave gradually disappeared. The middle and tail parts of the strain time-history curves were selected for analyzing the strain response characteristics of layers. The middle and tail parts of the strain time-history curves are referred to as the strain characteristic curve Ⅰ and the strain characteristic curve Ⅱ (Supplementary Figures S24–S27).

1) Analysis of strain response characteristics of each layer with different explosive charges

Supplementary Figures S22–S27 are the strain time-history curves and corresponding strain characteristic curves of each layer during the single-hole blasting of holes 2 and 3 when the charges were 5 and 10 g, respectively.

Compared with the strain characteristic curve I, it can be seen that when the explosive charge was small (e.g., 5 g), the fluctuation of the strain response of each layer was violent and complex, and the duration was longer (about 0.2 s); the strain fluctuation of the soft layer was much greater than that of the upper and lower hard layers. The strain fluctuations of the upper and lower hard layers were basically synchronized. When the explosive charge was large (e.g., 10 g), the strain response fluctuations of each layer were gentle and simple, and the duration was short (only 0.007 s); the strain fluctuation of the soft layer was greater than that of the upper and lower hard layers. Similarly, the strain fluctuations of the upper and lower hard layers were basically synchronized. The above results suggest that when the explosive charge is small, the stress provided by the generated explosive energy is close to the yield strength of the soft layer and is far less than that of the upper and lower hard layers, resulting in severe yield deformation of the soft layer and further causing complex strain fluctuations in the upper and lower hard layers. When the explosive charge is large, the generated explosive energy can overcome the yield strength of each layer of the material medium, causing direct plastic deformation of each layer and regular strain fluctuations as the blasting vibration continues.

Based on the analysis of the strain characteristic curve II, it can be known that a certain plastic creep has occurred in each layer after blasting, and the creep continued to occur as the stress wave gradually disappeared. The difference between the two curves is that when the amount of the explosive charge was small, the plastic creep of the soft layer was the largest, followed by the lower hard layer and the upper hard layer, both of which were tensile strains. When the explosive charge was large, the plastic creep of the lower hard layer was the largest, followed by the upper hard layer and the soft layer, both of which were tensile strains, and the plastic creep of each layer presented a similar pattern of fluctuations. Following the same logic as before, when the amount of explosive charge is small, the soft layer has severe yield deformation, resulting in tensile fracture of the internal structure, and then large creep fluctuations occur. In addition, due to the severe yield deformation of the soft layer, small tensile deformation occurs inside the upper and lower hard layers, which leads to smaller creep fluctuations in the later period. When the explosive charge is large, each layer has direct plastic deformation. The upper and lower layers have brittle fractures, given the features of the material, while the soft layer has elastoplastic damage. Although the three layers have shown similar patterns of fluctuations, the strain values differed greatly in the tail section of the fluctuation, and the plastic deformation of the soft layer recovered to a certain extent. Therefore, the strain value of the soft layer was smaller than that of the upper hard layer and then the lower hard layer.

It should be noted that uncoordinated deformation characteristics of layers were observed regardless of the amount of explosive charge. In addition, the strain time-history curve and the strain characteristic curve obtained after the blasting of hole 1 with 7 g charge was similar to the curves obtained after the blasting of hole 3 with 10 g charge.

The vertical and radial strains of different layers have shown similar characteristics, but there were slight differences. This is mainly related to the limited nature of the movement of the medium particles, so it will not be further explained here.

2) Analysis of strain response characteristics of each layer with different blast radii

Supplementary Figures S28. S29 are the trend lines of the variation of the peak horizontal strain of each layer with the distance to the center of the blast during the single-hole blasting of holes 1, 4, and 7 (with 7 g charge) and holes 3, 6, and 9 (with 10 g charge). It can be seen from the figures that ①The strain response of each layer decreased with the increase of the blast radius; ②The peak strain of different layers shows a different degree of attenuation trend with the increase of the blast radius; the soft layer has the largest attenuation rate, followed by the lower hard layer and the upper hard layer; ③ It can be predicted that as the blast radius increases indefinitely, the peak strain attenuation rates of layers will tend to be consistent.

The pattern of variation of the peak vertical strain with the distance to the center of the blast is similar to that of the horizontal strain.

3) Analysis of the strain response characteristics of each layer in different blast directions

Based on the analysis of data about blasting holes 9 and 12 (with 10 g charge), the horizontal and vertical strain time-history curves of each layer during blasting from different origins are shown in Supplementary Figures S30. It is evident that the patterns of the strain response of each layer are different in different blast directions. Overall, the strain response of each layer was faster during blasting at the bottom of the slope model, and each layer had a certain plastic creep. The radial residual creep strain was larger than the vertical residual creep strain. However, during the blasting of the leading edge of the slope, the strain response of each layer was relatively slow, and the strong response occurred between 2 and 3 s without a large residual creep strain.

In the comparison of radial and vertical strains, the reason why the radial residual creep strain was greater than the vertical residual creep strain is mainly related to the limited nature of the motion of medium particles. The principle is the same as before, so it will not be analyzed again here.

It is worth noting that blast holes 9 and 12 have a small distance to the center of the blast and large charges, so the blasting of these holes can generate large blast energy. Therefore, the trend of the strain response of each layer was close to the same (Supplementary Figures S31, S32), but uncoordinated deformation could still be observed, which is consistent with the previous analysis. When the explosive energy reaches the limiting value, the dynamic response of each layer is mainly affected by the explosive energy, and the material medium has little effect on the response.

4) Analysis of response characteristics of each layer strain during multi-hole blasting

As analyzed before, the acceleration response of each layer during multi-hole blasting fluctuated violently twice. Correspondingly, each layer also had two violent strain responses during multi-hole blasting. Figures 4, 5 are the radials and vertical strain time-history curves of each layer when the blast holes 1, 2, and 3 were simultaneously detonated (with 5 g charge). In a similar way as before, the two strain fluctuations in the acceleration time-history curve for multi-hole blasting were amplified and presented in strain characteristic curves I and II (Figures 6–9).

FIGURE 4

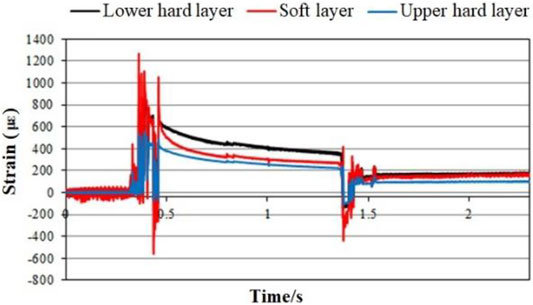
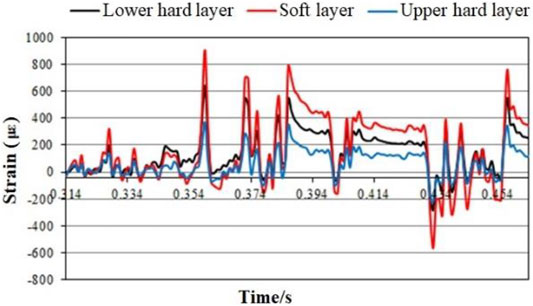
FIGURE 4. Time-history curve of the radial strain of each layer during simultaneous blasting of Nos 1, 2, and 3.

FIGURE 5

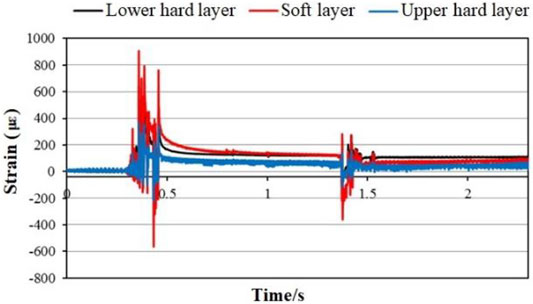
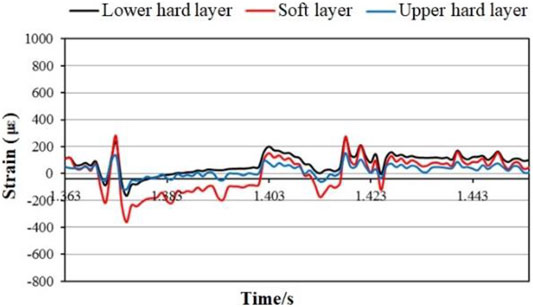
FIGURE 5. Time-history curve of the vertical strain of each layer during simultaneous blasting of Nos 1, 2, and 3.

FIGURE 6

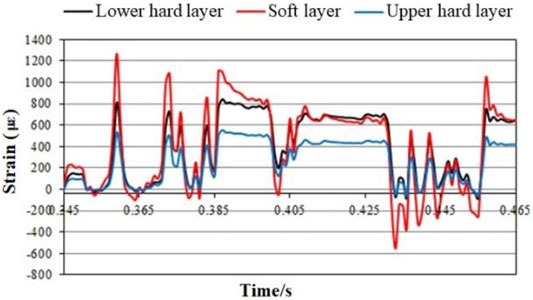
FIGURE 6. Radial strain characteristic curve Ⅰ of each layer during simultaneous blasting of Nos 1, 2, and 3.

FIGURE 7

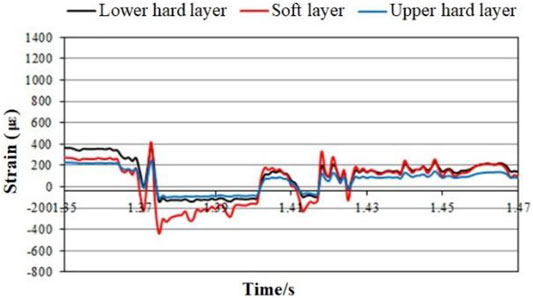
FIGURE 7. Radial strain characteristic curve Ⅱ of each layer during simultaneous blasting of Nos 1, 2, and 3.

FIGURE 8

FIGURE 8. Vertical strain characteristic curve Ⅰ during simultaneous blasting of Nos 1, 2, and 3.

FIGURE 9

FIGURE 9. Vertical strain characteristic curve Ⅱ during simultaneous blasting of Nos 1, 2, and 3.

It can be seen from the figure: ① During multi-hole blasting, the strain response of each layer showed two violent fluctuations, of which the first fluctuation was greater than the second fluctuation; ② The overall strain response characteristics appear to follow the pattern of soft layer > lower hard layer > upper hard layer; ③ The patterns of strain response of different layers were approximately synchronous, but uncoordinated deformation still occurred, which was more obvious in the vertical strain characteristic curve. It can be seen that when the explosive charge, blast radius, and blast direction were the same, the explosive energy produced by multi-hole blasting was greater than that of single-hole blasting; each layer was more affected by the explosive energy, and the material medium has little effect on the response.

Analysis of the Uncoordinated Deformation Mechanism

Based on the above test results, it can be known that under the influence of blasting, there is certain incoordination in the dynamic response of each layer of the slope with weak interlayers. Specifically ① The incoordination of the particle movement of the material in each layer is reflected by the uncoordinated dynamics of the acceleration response of the layers; ② Due to the uncoordinated movements of particles, it will inevitably lead to the uncoordinated deformation inside the medium, which can be seen from the uncoordinated pattern of strain characteristics of different layers.

According to the test results, with large explosive charge, small blast radius, bottom blasting, and multi-hole blasting, the dynamic responses of different layers appeared to be synchronized, and the incoordination gradually weakened. From another perspective, this result suggests that when the explosive energy is small (less than the critical explosive energy), the dynamic response of each layer of the slope is mainly affected by the internal structure of each layer under the effect of blasting. In reality, the surrounding slopes are often within the influence range of small explosive energy. Therefore, the deformation of the slope is mainly affected by the internal structure of each layer, which requires special attention.

Uncoordinated Particle Motion

Based on the analysis of the acceleration response characteristics, it can be known that there is an uncoordinated dynamic variation in the acceleration responses of different layers, and such variation is more significant between the horizontal and vertical directions. This may be related to the uncoordinated movement of medium particles in each layer during the blasting process.

In the blasting test, the acceleration sensor can be seen as a particle, and the vibration of the stress wave can be regarded as the movement of the particle. In each layer in a slope with a weak interlayer, the particle motion is not only affected by the stress wave but also by the size of the space it is located.

① Due to the different dielectric materials of the upper and lower hard layers and the soft layer, the density of the media in each layer and the movement space of the media particles are different. In addition, the stress wave is reflected, superimposed, and destructed during the propagation process from bottom to top, so the movement of the medium particles in each layer is different, presenting uncoordinated dynamic movements;

② As blasting vibration progresses, the density of the slope media particles increases with depth, which results in the vertical motion of the media particles in each layer being more restricted than the horizontal direction. Therefore, the vertical (Z) acceleration characteristic curve is slightly different from the horizontal (X) acceleration characteristic curve, but both of them have shown uncoordinated dynamic responses.

Uncoordinated Deformation

Considering the uncoordinated movements of medium particles in each layer and different yield strengths and ultimate strengths of the material, it will inevitably lead to uncoordinated deformation of the layers, which is mainly reflected by the difference in the plastic creep of the layers. When the explosive energy is small, the difference is particularly significant, indicating that the slope deformation is mainly affected by the internal structure of each layer. For example, when the explosive charge was small (5 g), the radial strain characteristic curve I of each layer under blasting of hole 2 shows that the strain fluctuation of the soft layer was much larger than that of the upper and lower hard layers, while the strain fluctuations of the upper and lower hard layers basically synchronized. This result suggests that when the explosive charge is small, the stress provided by the generated explosive energy is close to the yield strength of the soft layer and is far less than the yield strength of the upper and lower hard layers, resulting in severe yield deformation of the soft layer and further causing complex strain fluctuations in the upper and lower hard layers.

Since blasting vibration and seismic vibration have certain similarities to the deformation and destruction of engineering buildings, it can be inferred that during seismic vibration, there may be uncoordinated deformation characteristics of the layers of slopes with weak interlayers. This inference can be supported by a previous study (Cui et al., 2019; Cui 2017; Cui, et al., 2021).

Summary

Based on blasting physical simulations, this study has investigated the influence of explosive charge, blast radius, blast directions, and multi-hole blasting on the dynamic response of a slope with a weak interlayer. The conclusions are as follows:

1) With a certain amount of the explosive charge, the acceleration response of each layer of the model showed a sharp fluctuation during single-hole blasting, and the overall performance of the three layers is as follows: lower hard layer > soft layer > upper hard layer. The peak and valley values of the acceleration curves of different layers appeared to be displaced, indicating that the dynamic responses of different layers were inconsistent, and their performance was slightly different in the vertical and horizontal directions. In addition, the smaller the explosive charge (such as 5 g), the more obvious the displacement of the peak and valley values of the acceleration curve and the more significant the uncoordinated dynamic responses. As the explosive charge increased (i.e., 7g, 10 g), the displacement of peak and valley values of the acceleration curve gradually decreased, and the incoordination of the dynamic responses of different layers gradually weakened and tended to synchronize. During multi-hole blasting, similar characteristics were observed as the above, but the acceleration response showed two sharp fluctuations, and the uncoordinated dynamic response gradually weakened.

2) The acceleration response of each layer decayed with the increase of the blast radius, and the acceleration response decay rate was different for different layers in different directions. As the blast radius further increased, the acceleration response decay rate of each layer gradually synchronized.

3) The acceleration response of each layer was different in different blast directions, and the acceleration response of each layer was more violent during bottom blasting than leading-edge blasting.

4) Under the effect of blasting, the strain waveform of each layer changed in three phases: front, middle, and tail. The strain curve of the middle phase fluctuated violently. The strain fluctuation of the tail phase was relatively stable but showed a certain degree of plastic creep. The uncoordinated deformation of each layer was obvious in the middle and tail phases. The uncoordinated deformation trend of different layers changed in varying degrees depending on the variation of blasting factors such as explosive charge, blast radius, blast direction, and blasting method.

5) The uncoordinated dynamic response of each layer has caused uncoordinated deformation. The uncoordinated dynamic change in the response was particularly significant when the explosive energy was less than the critical explosive energy, indicating that the change was mainly affected by the internal structure of the slope, i.e., the uncoordinated movement of medium particles. Furthermore, it is closely related to the strength of the material, propagation path of the blast wave, refraction, and the degree of superposition cancellation. When the explosive energy is large and exceeds the critical explosive energy, it can be speculated that the uncoordinated dynamic response of different layers would gradually weaken and tend to synchronize.

The physical model applied in this study is generalized from the geological prototype based on the similarity principle. Although our results were based on the scale test, the dynamic responses and basic laws of the slope model under blasting loading were effective. The blasting vibration in the mining area is very complex. It is difficult to fully meet the similarity. The obtaining of on-site blasting data is also difficult. In this study, the engineering analogy method was used to select blasting parameters. We argue that the test results can show the influence of the blasting dynamic load on the slope.

However, in actual working conditions, the surrounding slopes are mostly within the influence range of the smaller explosive energy. Our explosions are very close to the measurement points. It would be better to vary the physical model with blasts at distances farther away from those carried out. The deformation of the slope far away from the blasting position is mostly affected by the internal structure of the slopes. It is advised to pay special attention to this kind of situation and deploy appropriate measures to monitor any deformation. The critical explosive energy needs to be further studied, and it should be noted that the critical explosive energy varies with different lithology. Research is still required on how to establish the relationship between critical explosive energy and factors of blasting, such as the explosive charge and blast radius. In addition, the laws of motion for particles of different materials under blasting vibration still need to be explored to confirm the speculations in this study. It should be noted that more examples are needed to verify these results. Its validity for real cases should be supported by more research.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

XZ designed the conceptualization, methodology, data curation, and the original draft preparation. QY performed data curation and formal analysis. XP was responsible for supervision and project administration. RD was responsible for resources, supervision, and reviewing and editing of the manuscript.

Funding

This project was partially supported by the National Key R&D Program of China (No. 2017YFC1501002), the National Science Foundation of China (No. 41907254 and 41931296), the Postdoctoral Foundation of China (No. 2020M683272).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors particularly appreciate the valuable comments made by the editors and reviewers to make a substantial improvement to this manuscript.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2021.812492/full#supplementary-material

References

Adushkin, V. V. (2019). Hill Slope Falls and Long-Runout Rockslides under Large-Scale Underground Blasting. J. Min. Sci. 55, 893–904. doi:10.1134/s1062739119066271

CrossRef Full Text | Google Scholar

Bai, Z., Huang, S., and Lu, M. (1995). Effects of Blasting on Stability of Slope Rock Mass. Subgrade Eng., 19–23. (in Chinese).

Google Scholar

Benchelha, T., Remmal, T., El Hamdouni, R., Ejjaouani, H., Mansouri, H., El Kamel, F., et al. (2017). Combined Effects of Blasting and Geological Structure on Rock Mass Stability-A Case Study from the Marrakech-Agadir Highway, Morocco. Bull. Eng. Geol. Environ. 76, 815–828. doi:10.1007/s10064-016-0867-5

CrossRef Full Text | Google Scholar

Chang, J. X., Song, Z., Tian, L., Liu, H., Wang, L., and Wu, X. (2007). Numerical Analysis of Effect of Water on Explosive Wave Propagation in Tunnels and Surrounding Rock. J. Univ. China Min. Tech. 17 (3), 368–371. doi:10.1016/S1006-1266(07)60107-2

CrossRef Full Text | Google Scholar

Cui, S., Pei, X., Jiang, Y., Wang, G., Fan, X., Yang, Q., et al. (2021). Liquefaction Within a Bedding Fault: Understanding the Initiation and Movement of the Daguangbao Landslide Triggered by the 2008 Wenchuan Earthquake (Ms = 8.0). Eng. Geol. 295, 106455.

CrossRef Full Text | Google Scholar

Cui, S., Pei, X., and Huang, R. (2019). Initiation Mechanism of Daguangbao Landslide: Uncoordinated Deformation of Sliding Zone and Dynamic Damage to Rock Mass during strong Earthquakes. Chin. J. Rock Mech. Eng. 38 (2), 237–253. (in Chinese). doi:10.13722/j.cnki.jrme.2018.1041

CrossRef Full Text | Google Scholar

Cui, S. (2017). Seismic Responses of Wake Interlayer and Initiation Mechanisms of Large Landslide during Strong Earthquake. Ph.D. thesis. Chengdu (China): Chengdu University of Technology. (in Chinese).

Google Scholar

Deb, D., Kaushik, K. N. R., Choi, B. H., Ryu, C. H., Jung, Y. B., and Sunwoo, C. (2011). Stability Assessment of a Pit Slope under Blast Loading: A Case Study of Pasir Coal Mine. Geotech. Geol. Eng. 29, 419–429. doi:10.1007/s10706-010-9387-4

CrossRef Full Text | Google Scholar

Deng, E., Yang, W., Lei, M., Yin, R., and Zhang, P. (2018). Instability Mode Analysis of Surrounding Rocks in Tunnel Blasting Construction with Thin Bedrock Roofs. Geotech. Geol. Eng. 36, 2565–2576. doi:10.1007/s10706-018-0483-1

CrossRef Full Text | Google Scholar

Dvořák, A. (1977). Landslides Caused by Blasting. Bull. Int. Assoc. Eng. Geology 16, 166–168.

Google Scholar

Fan, C., and Ge, J. (2020). Dynamic Calculation Method of Vibration Response of Building Blasting Based on Differential Equation. Environ. Technol. Innovation 20, 101178. doi:10.1016/j.eti.2020.101178

CrossRef Full Text | Google Scholar

Görgülü, K., Arpaz, E., Demirci, A., Koçaslan, A., Dilmaç, M. K., and Yüksek, A. G. (2013). Investigation of Blast-Induced Ground Vibrations in the Tülü boron Open Pit Mine. Bull. Eng. Geol. Environ. 72, 555–564. doi:10.1007/s10064-013-0521-4

CrossRef Full Text | Google Scholar

González-Nicieza, C., Álvarez-Fernandez, M. I., Alvarez-Vigil, A. E., Arias-Prieto, D., López-Gayarre, F., and Ramos-Lopez, F. L. (2014). Influence of Depth and Geological Structure on the Transmission of Blast Vibrations. Bull. Eng. Geol. Environ. 73, 1211–1223. doi:10.1007/s10064-014-0595-7

CrossRef Full Text | Google Scholar

Hakan, Ak., Melih, I., Mahmut, Y., and Adnan, K. (2009). Evaluation of Ground Vibration Effect of Blasting Operations in a Magnesite Mine. Soil Dyn. Earthquake Eng. 29 (4), 669–676. doi:10.1016/j.soildyn.2008.07.003

CrossRef Full Text | Google Scholar

He, L., Zhong, D., Liu, Y., and Song, K. (2021). Prediction of Bench Blasting Vibration on Slope and Safety Threshold of Blasting Vibration Velocity to Undercrossing Tunnel. Shock and Vibration 2021, 1–14. doi:10.1155/2021/9939361

CrossRef Full Text | Google Scholar

Hempen, G. L. (2019). “Reducing Impacts Potentially Triggered by Blasting,” in IAEG/AEG Annual Meeting Proceedings, San Francisco, California, September 17–23, 2018. Editors A. Shakoor, and K. Cato. 2018–Volume 6. doi:10.1007/978-3-319-93142-5_17

CrossRef Full Text | Google Scholar

Jiang, N., Zhou, C., Lu, S., and Zhang, Z. (2018). Effect of Underground Mine Blast Vibrations on Overlaying Open Pit Slopes: A Case Study for Daye Iron Mine in China. Geotech. Geol. Eng. 36, 1475–1489. (in Chinese). doi:10.1007/s10706-017-0402-x

CrossRef Full Text | Google Scholar

Kesimal, A., Ercikdi, B., and Cihangir, F. (2008). Environmental Impacts of Blast-Induced Acceleration on Slope Instability at a limestone Quarry. Environ. Geol. 54, 381–389. doi:10.1007/s00254-007-0825-4

CrossRef Full Text | Google Scholar

Li, J., Zhang, L., and Yan, R. (2001). Mechanism of Rock Slope Unstability and Critical Vibration Velocity under Action of Blasting Seism Wave. Mining Metall. 10 (1), 11–15. (in Chinese).

Google Scholar

Li, H., Deng, J., Feng, P., Pu, C., Arachchige, D. D. K., and Cheng, Q. (2021a). Short-Term Nacelle Orientation Forecasting Using Bilinear Transformation and ICEEMDAN Framework. Front. Energ. Res. 9, 780928. doi:10.3389/fenrg.2021.780928

CrossRef Full Text | Google Scholar

Li, H., Deng, J., Yuan, S., Feng, P., and Arachchige, D. D. K. (2021b). Monitoring and Identifying Wind Turbine Generator Bearing Faults Using Deep Belief Network and EWMA Control Charts. Front. Energ. Res. 9, 799039. doi:10.3389/fenrg.2021.799039

CrossRef Full Text | Google Scholar

Liu, Y. (2009). Study on the Failure Mechanism and Safety of Layered Rock Slopessubjected to Dynamic Loads. Ph.D. Dissertation. Chinese Academy of Science.

Google Scholar

Lu, S., Zhou, C., Jiang, N., and Xu, X. (2015). Effect of Excavation Blasting in an Under-cross Tunnel on Airport Runway. Geotech. Geol. Eng. 33, 973–981. doi:10.1007/s10706-015-9879-3

CrossRef Full Text | Google Scholar

Lu, S., Zhou, C., Zhang, Z., Ji, L., and Jiang, N. (2020). PPV Criterion of a Rock Slope Imbedded with a Fault Subjected to Blasting P-Waves. Shock and Vibration 2020, 1–7. doi:10.1155/2020/8865981

CrossRef Full Text | Google Scholar

Luo, Z., Qin, Y., Xie, C., and Wang, W. (2015). Instability Process of the Cut Slopes under Complex Mining Environment. Chin. J. Geol. Hazard Control. 26 (03), 81–85. (in Chinese).

Google Scholar

Mohamad, E. T., Yi, C. S., Murlidhar, B. R., and Saad, R. (2018). Effect of Geological Structure on Flyrock Prediction in Construction Blasting. Geotech. Geol. Eng. 36, 2217–2235. doi:10.1007/s10706-018-0457-3

CrossRef Full Text | Google Scholar

Ozcelik, Y. (1998). Effect of Discontinuities on Fragment Size Distribution in Open–Pit Blasting-A Case Study. Trans. Inst. Mining Metall. 107 (A), 146–151.

Google Scholar

Singh, V. K., and Singh, D. P. (1995). Controlled Blasting in an Open-Pit Mine for Improved Slope Stability. Geotech. Geol. Eng. 13, 51–57. doi:10.1007/bf00600523

CrossRef Full Text | Google Scholar

Song, J., Hao, S., Yue, L., and Li, H. (2017). Analysis of the Dumping Deformation Mechanism of Jiangjunyayan Painting Area Caused by Mining and Control Measures. Chin. J. Geol. Hazard Control. 28 (04), 40–46. (in Chinese). doi:10.16031/j.cnki.issn.1003-8035.2017.04.07

CrossRef Full Text | Google Scholar

Sun, J., Li, Z., Liu, G., Chen, M., and Jiang, Q. (2018). Dynamic Stress and Vibration Characteristics of Geomaterials in Slopes Induced by Blasting Vibration. J. Vibration Shock 37 (10), 141–148. doi:10.13465/j.cnki.jvs.2018.10.021

CrossRef Full Text | Google Scholar

Wang, Z.-L., Li, Y.-C., and Shen, R. F. (2007). Numerical Simulation of Tensile Damage and Blast Crater in Brittle Rock Due to Underground Explosion. Int. J. Rock Mech. Mining Sci. 44 (5), 730–738. doi:10.1016/j.ijrmms.2006.11.004

CrossRef Full Text | Google Scholar

Wang, W., Yuan, Q., Jiang, H., and Chen, P. S. (2019). Influence and Safety Control of Blasting Vibration on Existing Lining for Closely Tunnel Expansion. IOP Conf. Ser. Earth Environ. Sci. 351, 012043. doi:10.1088/1755-1315/351/1/012043

CrossRef Full Text | Google Scholar

Wang, J. (2017). Spread Regularity of Blasting Vibration on the Slope and the Influence on Slope Stability. Mianyang (China): Southwest University of Science and Technology. (in Chinese).

Google Scholar

Yuan, P. (2016). Model-based Testing Research on Deep Rock Mass Rupture under Blast Loading. Hefei (China): Anhui University of Science and Technology. (in Chinese).

Google Scholar