Configuration of an Energy Storage System Considering the Frequency Response and the Dynamic Frequency Dispersion

The high proportion of renewable energy sources (RESs) in the system reduces the frequency support capacity and aggravates the generation of unbalanced power, while the dynamic frequency dispersion makes it difficult for a centralized energy storage system (ESS) to take into account the frequency requirements of different regions. In this context, the research takes the region with high penetration of RESs and frequent power fluctuations as the grid node of the ESS. By configuring the parameters of the ESS under the control strategy of virtual synchronous generators, the inertia and the primary frequency reserve of the system are supplemented, and the regulation characteristics of the ESS are depicted. Taking the steady-state recovery time and the amplitude coefficient as the evaluation indexes, the effects of the virtual inertia constant, the virtual damping coefficient, and the virtual frequency regulation coefficient on the behavior of the ESS are deeply analyzed. Finally, the quantitative configuration of the ESS is realized by considering the frequency response and the dynamic frequency dispersion.

1 Introduction

The substitution of RESs for fossil fuels is an effective way to achieve carbon neutrality. However, the frequency regulation characteristics of the power electronic converter–based RESs differ from those of the traditional synchronous units (Zhang and Sun, 2020; Zhang et al., 2020). Therefore, a high proportion of RES penetration will reduce the stability of the system operation to a certain extent (Nasirov and Agostini, 2021).

After generating the unbalanced power, the system establishes a new stable state through the inertia response (IR), the primary frequency regulation (PFR), the secondary frequency regulation (SFR), and the tertiary frequency regulation (TFR) (Rodrigues et al., 2020). Most of the fluctuations caused by the load and RESs are frequent, and their predictability is weak. This should be adjusted by the IR and the PFR automatically (Yi et al., 2020). During the adjustment process, the rate of change of frequency (ROCOF) and the steady-state frequency deviation (SSFD) are the main indices to evaluate the frequency stability of the system (Homan et al., 2021).

To improve the frequency supportability of the system, RESs usually simulate the inertia response and the frequency regulation process of the synchronous generators by optimizing the control strategy (Vidyanandan and Senroy, 2013; Gholamrezaie et al., 2018; Peng et al., 2019; Tang et al., 2019). But this method needs the active power reserve of the RESs, which makes it difficult to operate at the maximum power, resulting in low power conversion efficiency. Therefore, to absorb the redundant power, a combined strategy for the frequency regulation control of wind and its storage has been adopted that considers the wind speed fluctuation range (Zhang et al., 2017). The technology of demand side management (DSM) based on various energy storage devices was proposed in the studies by Douglass et al., 2013; Qi et al., 2021; and Sm et al., 2021. However, the location of the energy storage equipment at the RESs and the users is scattered, which makes it difficult to regulate centrally. This also reduces the reliability and flexibility of the regulation process.

The development of large-scale energy storage technology results in the wide use of the ESS for the frequency support of the grid (Miguel et al., 2014; Yue and Wang, 2015; Knap et al., 2016; Liu et al., 2018; Zhao et al., 2019; Sockeel et al., 2020; Zhang et al., 2020; Liu et al., 2021; Pinthurat and Hredzak, 2021; Wei et al., 2021). By simulating the external characteristics of the synchronous units in the control strategy, the response speed of the ESS can be consistent with the frequency regulation process of the system (Miguel et al., 2014; Liu et al., 2018; Zhang et al., 2020; Pinthurat and Hredzak, 2021; Wei et al., 2021). In the study by Miguel et al., (2014), an adaptive control strategy for adjusting the ESS output with the state of charge and the frequency deviation was proposed, which took into account both the frequency regulation effect and the charge retention rate of the ESS. In the study by Zhang et al., (2020), the integral control based on the frequency deviation was introduced into the ESS controller, where the system frequency was adjusted without an error through the coordination of the end frequency converter. In the study by Liu et al., (2018), a virtual synchronous generator control strategy based on the third-order model of the synchronous generators was proposed by simulating the process of automatic excitation voltage regulation, which further enhanced the support capacity of the ESS. However, these research studies mainly focused on the design of the VSG control strategies so that the influence of the ESS capacity and the parameter configuration on the frequency supportability was less concerned.

As an important study part of the VSG, the energy storage unit realizes the reasonable configuration of the capacity and the parameters, which can greatly reduce the cost of the configuration and promote the popularization of the ESS technology. To make the ESS provide better frequency supportability for a high RES penetration system, the current research mainly focused on the following two aspects:

In order to optimize the investment and the economic benefit of the ESS, improving the multi-objective optimization model and algorithm to realize the rational allocation of the multi-energy systems has become one of the hotspots of current research. The reference (Li et al., 2020) established a dual-mode energy management model and proposed a distributed dynamic event-triggered Newton–Raphson algorithm to realize the optimal allocation of power, heat, and gas energy prices in multi-energy systems. The reference (Li et al., 2021) further optimized the algorithm on this basis. By analyzing the impact of the persistent DoS attacks on the system, the stability and the economy of the multi-energy system are improved. Aiming at the combined economic environmental dispatch, a distributed consensus-based algorithm combined with dynamic weights was proposed in the reference (Liu et al., 2021) to realize the reasonable allocation of the ESS. In the above research, the ESS configuration was studied through algorithms, which cannot analyze in detail the participation of the ESS in the frequency adjustment.

To analyze the frequency supportability of the ESS, the configuration parameters of the ESS are usually taken as variables to evaluate their contribution to the frequency response (Yue and Wang, 2015; Knap et al., 2016; Zhao et al., 2019; Sockeel et al., 2020; Liu et al., 2021). The relationship curves of the virtual inertia provided by the ESS along with its size and control parameters were described in the studies by Yue and Wang, 2015; Zhao et al., 2019; and Sockeel et al., 2020. Based on the target values of the inertia constant and the droop coefficient, the capacity of the ESS in different frequency support stages was estimated (Knap et al., 2016). To optimize the configuration result of the ESS, the coordination relationship between the ESS capacity and its control parameters was established (Liu et al., 2021). However, the ESS configuration process mainly considers the magnitude of the unbalanced power in recent research; it lacks a discussion on the spatial position of the power fluctuation, and the study on the differences between the effects of different control parameters was superficial, which partly reduces the accuracy of the ESS configuration results.

Therefore, based on the generation position of the unbalanced power, this research investigates the influence of the dispersion of the dynamic frequency in the system on the behaviors of the ESS under the VSG control strategy, compares the active output curves of the ESS and the synchronous generator through theoretical analysis and simulations, and analyzes the frequency regulation characteristics of the ESS. Finally, the regions with high RES permeability and frequent power fluctuations are selected as the grid connection node of the ESS to ensure the optimal regulation performance. On this basis, the steady-state recovery time and the amplitude coefficient are defined as evaluation indexes. Based on these indexes, the effects of the virtual inertia constant, the virtual damping coefficient, and the virtual frequency regulation coefficient on the dynamic behavior and the support capacity of the ESS are analyzed, and their optimal configuration is realized, to realize the quantitative configuration of the ESS that meets the frequency response and the dynamic frequency dispersion of the system.

2 Characteristics of the Frequency Response

2.1 Frequency Response Requirements

The difference in the increment between the load and the power output in the system is defined as an unbalanced power ΔP_sys. If only the supporting effect of the synchronous unit is considered before the governor is started, the expression of the initial ROCOF concerning the ΔP_sys can be expressed as follows:

$\frac{2{\mathit{H}}_{\mathit{sys}}}{{\mathit{f}}_0}\frac{\mathit{df}}{\mathit{dt}}=-\frac{\Delta {\mathit{P}}_{\mathit{sys}}}{{\mathit{S}}_{\mathit{sys}}},(1)$

where H_sys and S_sys are the equivalent inertia constant and the installed capacity of the system, respectively. H_sys describes the value of the mechanical inertia, which can be obtained by the following equation:

${\mathit{H}}_{\mathit{sys}}{\mathit{S}}_{\mathit{sys}}={\sum }_{i=1}^n{\mathit{H}}_{\mathit{i}}{\mathit{S}}_{\mathit{i}},(2)$

where H_i and S_i are the inertia constant and rated capacity of each synchronization unit in the system.

After the governor is put into operation, the system enters the stage of the PFR. If no further regulation process is considered, the relationship between the SSFD and the ΔP_sys can be expressed as follows:

$\Delta \mathit{f}=-\frac{\Delta {\mathit{P}}_{\mathit{sys}}}{{\mathit{K}}_{\mathit{sys}}},(3)$

where K_sys is the frequency regulation coefficient of the system, which can be obtained as follows:

${\mathit{K}}_{\mathit{sys}}={\sum }_{i=1}^n\frac{1}{{\mathit{f}}_0}\frac{{\mathit{S}}_{\mathit{i}}}{{\mathit{\sigma }}_{\mathit{i}}},(4)$

where σ_i is the adjustment coefficient of each synchronization unit.

Therefore, when the maximum unbalanced power ΔP_sysm and the frequency response requirements of the system are known, the relationship between the inertia constant, the frequency regulation coefficient, and the capacity of the frequency support unit that the system needs to supplement can be established using the relevant equations.

2.2 Dynamic Frequency Dispersion

The frequency of each region is synchronous when the system is in a steady state. However, the fluctuation in the output of the RESs and the load switching causes the system to go through the process of balancing the supply and the demand balance for a long time, which leads to the continuous redistribution of the unbalanced power among the units. Due to the different electrical distances between the power fluctuation point and each bus, the uneven geographical distribution of the generators and the loads, different inertia and damping among the synchronous units, and the frequency of each node in the power grid cannot be adjusted synchronously in a short time scale, and the transient process is complex. The frequency response presents a spatial-temporal distribution, i.e., the dynamic frequency dispersion (Li et al., 2019).

As a result, the response mode of the synchronous unit after the unbalanced power is generated and can be expressed as a three-stage principle (Sonny, 2007). When the power fluctuates, the impact power is distributed according to the electrical distance, and the unit which is closer to the disturbance location bears the most power; in the inertia support stage, the transient process is described by the rotor motion equation, and the unit with a larger inertia constant and damping coefficient has a higher proportion of the support power. When the system is stabilized after the primary frequency regulation, each regulation unit allocates the unbalanced power according to the frequency regulation coefficient. Affected by this, it is difficult to accurately configure the virtual inertia according to the requirements of the specified region only by the theoretical derivation.

3 Control Strategy of the ESS

Without considering the limitations of the ESS source characteristics, the energy throughput of the ESS is mainly decided by the control strategy of its grid-connected inverter. The virtual synchronous generator (VSG) control is usually adopted to make the ESS have the same frequency regulation characteristics as the synchronous units and to improve the power angle stability.

Most of the research studies found that the difference between the droop control and the VSG control is mainly reflected in the introduction of the virtual angular velocity and the use of the phase-locked loop. Some studies also regard droop control as a typical VSG control. Although the related control is different in structure, it has its applicable scenarios and advantages.

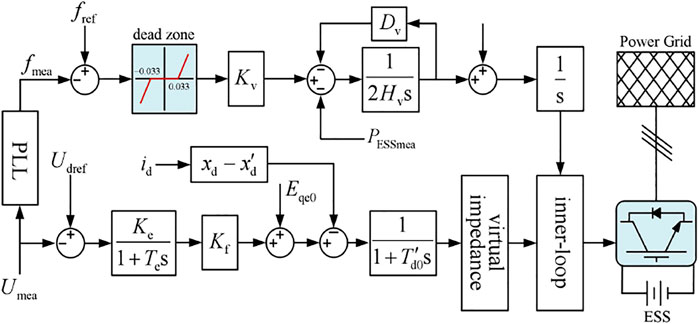
To simulate the external characteristics of synchronous generators preferably and supplement the inertia, the damping, and the capacity of the PFR distinctively, the ESS in this study adopts the control strategy shown in Figure 1. By simulating the IR and the PFR processes of the synchronous units, the time scale of the ESS speed regulation system can be consistent with the adaptive process of the system, which ensures the smooth power angle switching of the converter.

FIGURE 1

FIGURE 1. Control block diagram of the ESS.

Among these, the second-order rotor motion equation of the synchronous generator is as follows:

$\{\begin{array}{c}2{\mathit{H}}_{\mathit{v}}\frac{\mathit{d\omega }}{\mathit{dt}}={\mathit{P}}_{\mathit{t}}-{\mathit{P}}_{\mathit{e}}-{\mathit{D}}_{\mathit{v}}\Delta \omega \\ \frac{\mathit{d\delta }}{\mathit{dt}}={\mathit{\omega }}_0\Delta \omega \end{array},(5)$

where H_v is the virtual inertia constant, D_v is the virtual damping coefficient, ω is the virtual angular velocity, Δω is the virtual angular velocity deviation, δ is the virtual power angle, and P_t and P_e are the mechanical power and the electromagnetic power of the generator, corresponding to the reference power and the output power of the ESS, respectively.

On this basis, by simulating the power-frequency process of the synchronous units, the ESS realizes the automatic allocation of the unbalanced power with the synchronous units in the PFR:

${\mathit{P}}_{\mathit{ref}}={\mathit{K}}_{\mathit{v}}\mathit{ }\left({\mathit{f}}_{\mathit{ref}}-{\mathit{f}}_{\mathit{mea}}\right),(6)$

where K_v is the virtual frequency regulation coefficient, f_ref is the reference frequency, f_mea is the measured frequency, and P_ref is the reference value of the steady-state ESS output power.

Meanwhile, based on the traditional second-order control model of the VSG, the first-order transient voltage equation of the synchronous generator is simulated, and the transient voltage regulation process is introduced to improve the transient voltage regulation process of the ESS converter. The third-order model of the VSG is established, and the equation is as follows:

${\mathit{T}}_{\mathit{d}0}^{\mathit{\prime }}\frac{\mathit{d}{\mathit{E}}_{\mathit{q}}^{\mathit{\prime }}}{\mathit{dt}}={\mathit{E}}_{\mathit{qe}}-{\mathit{E}}_{\mathit{q}}^{\mathit{\prime }}-{\mathit{i}}_{\mathit{d}}\left({\mathit{x}}_{\mathit{d}}-{\mathit{x}}_{\mathit{d}}^{\mathit{\prime }}\right),(7)$

where E_q’ is the transient electromotive force, E_qe is the forced no-load electromotive force, i_d is the direct axis current component, x_d is the direct axis synchronous reactance, and x’_d is the direct axis transient reactance. T_d0’ is the time constant of excitation windings of the synchronous generator.

On this basis, to maintain the terminal voltage stability of the ESS grid-connected inverter, the automatic regulating excitation system is introduced into the control, which is equivalent to the first-order inertia link, where the starting signal is the voltage deviation.

$\left({\mathit{U}}_{\mathit{mea}}-{\mathit{U}}_{\mathit{ref}}\right)\times \frac{{\mathit{K}}_{\mathit{e}}}{1+\mathrm{s}{T}_e}=\frac{1}{{\mathit{K}}_{\mathit{f}}}\Delta {\mathit{E}}_{\mathit{qe}},(8)$

where U_mea is the measured value of the inverter outlet voltage, U_ref is the reference value of the inverter outlet voltage, ΔE_qe is the forced no-load electromotive force deviation, K_e is the equivalent magnification, T_e is the time constant, and K_f is the excitation proportional coefficient.

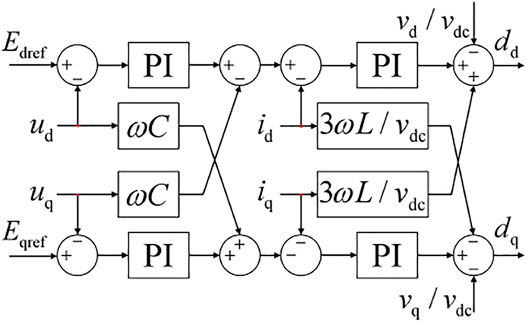
The VSG control strategy shown in Figure 1 can be obtained by combining formulas (Eqs 5–8), in which the inner-loop control is realized by using the voltage and current double-loop control, as shown in Figure 2 (Liu and Yang, 2021), that is, the droop control of the ESS grid-connected inverter is realized through the power outer loop and the voltage and current inner loop, and finally, the modulation signal is the output through SVPWM.

FIGURE 2

FIGURE 2. Voltage and current double loop control.

From the above derivation process, it can be seen that H_v determines the duration of the power output and the inertia support capacity of the ESS in the phase of IR, D_v determines the oscillations in the ESS frequency regulation output during the transient phase, which significantly affects the steady-state recovery time of the system, and K_v determines the frequency regulation depth of the ESS to meet the PFR demand of the grid.

In addition, the voltage regulation process of the ESS is also designed in the control strategy, which is thoroughly described in (Liu et al., 2018). Since the configuration of the ESS is mainly applied to the active power/frequency support requirements of the system, the change in the node voltage and the reactive power output of the ESS will not be discussed in depth.

4 Configuration of the ESS

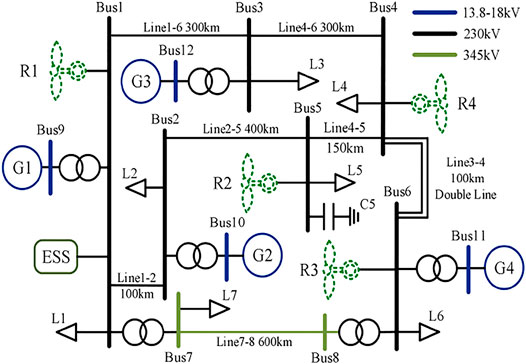
To validate the proposed work, the 12-bus power system shown in Figure 3 is built in the PowerFactory/DIgSILENT, where the system is divided into 7 regions according to the bus and the load location. Among them, the total installed capacity of the system is 2248MVA (1124MVA for RESs R1–R4 and 1124MVA for traditional power plants G1–G4), the total active load L1–L7 is 1450MW, the maximum output power of the ESS is 70MW, and the inertia constant and the adjustment coefficient of the synchronous units are 5s and 0.04, respectively. Under the time scales and the assumptions discussed in the study, the RES units operate at the maximum power, ignoring the frequency support capacity.

FIGURE 3

FIGURE 3. 12 bus power system.

Without considering the fault, the unbalanced power in the 12-bus system is mainly caused by the switching of the generator, the uncertainty of the RES output, and the fluctuation in the load. Compared to the pure power fluctuation, the switching of synchronous units will change the inertia and the PFR capacity of the system itself; as a result, the influence on the frequency response should be more obvious. However, the time scale of the traditional unit switching is beyond the discussion scope of the IR and the PFR, and so, in this study, the load power increment of 145 MW is taken as the reference maximum power increment ΔP_sysm to configure the control parameters of the ESS.

4.1 The Influence of the Dynamic Frequency Dispersion

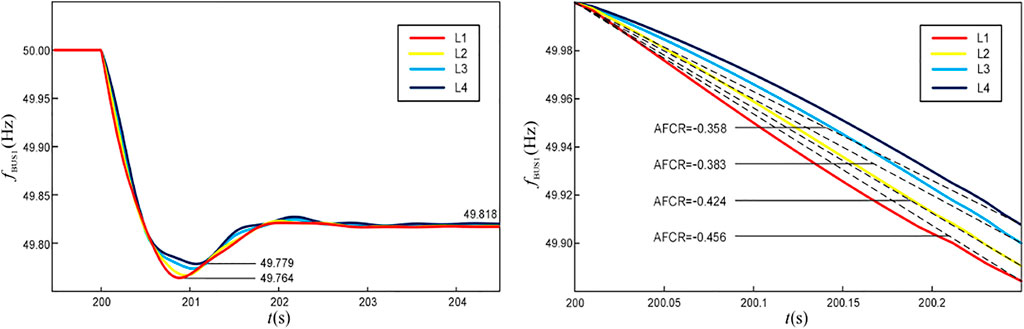
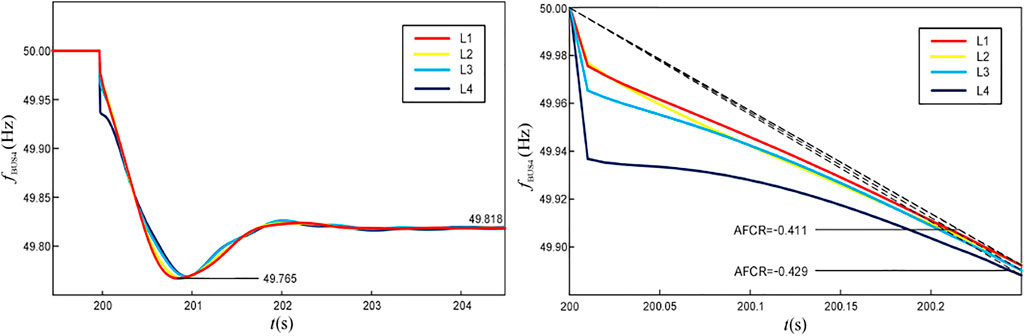
To analyze the influence of the dynamic frequency dispersion on the frequency response at different regions in the system, bus 1 and bus 4 are taken as the measuring points in this case, and the same active power increment of 145 MW is set for L1–L4 in 200s, respectively. The waveforms of the frequency response are obtained and are shown in Figures 4, 5.

FIGURE 4

FIGURE 4. Frequency response of the system at Bus 1.

FIGURE 5

FIGURE 5. Frequency response of the system at Bus 4.

As shown in Figure 4, when the same power increment is generated in different regions of the system, the SSFD after the PFR will not be affected, but the transient process differs. Specifically, the closer the frequency measurement point is to the power fluctuation point, the faster is the change rate of the frequency measurement value. This is also reflected in Figure 5.

On this basis, comparing Figures 4, 5, it can be seen that in the initial stages of power fluctuation, the frequency measurement data at bus 1 are smoother than that at bus 4. The main reason is that bus 1 is directly connected to the synchronous power plant G1, which has a strong inertia support capacity, while the RES plant R4 at bus 4 operates at a constant power, and so, initially it is unable to supplement the active power shortage.

In general, the measurement window (frequency sampling period) of the ROCOF is between 40 ms and 2s (Ten and Crossley, 2008). The smaller the measurement window, the more accurate is the measurement result for the ROCOF. However, the influence of the high-frequency signal is pronounced. Conversely, the larger the measurement window, the smoother is the ROCOF measurement result, but it is more difficult to accurately describe the trend of the ROCOF. Therefore, to avoid the error caused by the ROCOF measurement process and considering the actual engineering requirements, the average frequency change rate (AFCR) within 0–0.25 s after the unbalanced power is generated is defined as the initial ROCOF, and the corresponding inertia of the system is defined as the equivalent inertia constant H_ess according to (1). This processing method can reduce the influence of high-frequency signals on the measurement results of the PLL, and it converts the effect of the damping and the electrical distance into relative inertia, which lays the foundation for the quantitative configuration of the virtual inertia below.

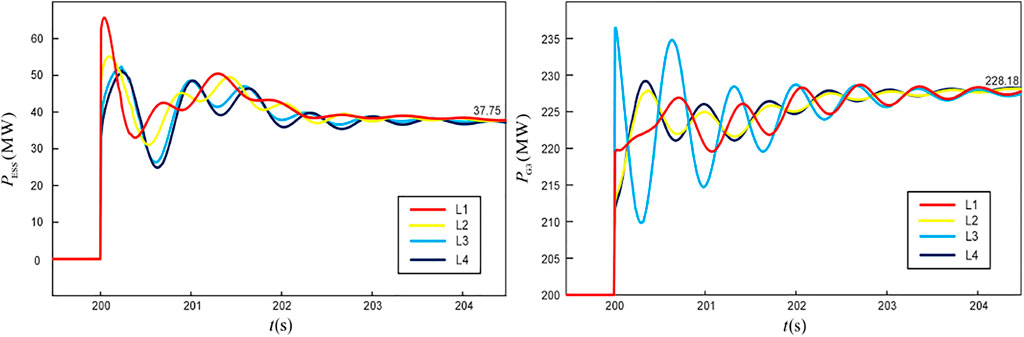
The active power output curves of the ESS and the G3 are shown in Figure 6. It can be seen that the ESS under the control strategy of the VSG has similar frequency regulation characteristics as the synchronous unit. That is, the ESS or the synchronous unit close to the power fluctuation point provides more power support in the event of the unbalanced power generation, which eventually reaches the steady state through the IR and the PFR according to the three-stage principle mentioned above.

FIGURE 6

FIGURE 6. Output of the ESS and the synchronous unit under ΔP_L1–ΔP_L4.

In summary, due to the dispersion of the dynamic frequency, the position of the power fluctuation will significantly impact the output power of frequency support units and the frequency response in different regions, within a short time period. Therefore, to ensure the frequency response requirements of different time scales and different regions, the ESS should select the region with the most serious power fluctuation to configure its parameters without considering the capacity limitation. Considering the distribution of the generators and the load in the system, the following example takes the frequency response requirements of region 1 under the maximum power increment to configure the related parameters of the ESS.

4.2 Configuration of the Damping

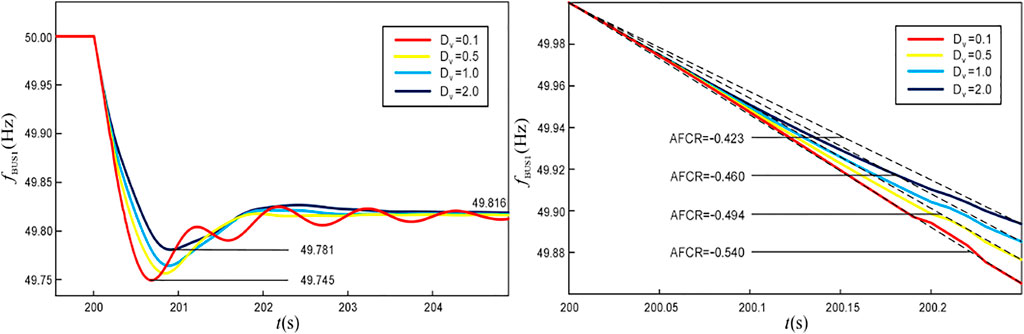
The virtual damping coefficient D_v mainly affects the oscillation mode of the frequency and the unit output, which determine the steady-state recovery time of the system after the disturbance, so it needs to be prioritized. In case 2, bus 1 is taken as the frequency measurement point, and the active power increment of 145 MW is set for L1 at 200s. The system frequency response and the ESS output waveforms under different D_v are obtained as shown in Figures 7, 8.

FIGURE 7

FIGURE 7. Frequency response of the system for different D_v.

FIGURE 8

FIGURE 8. Output of the ESS under different D_v.

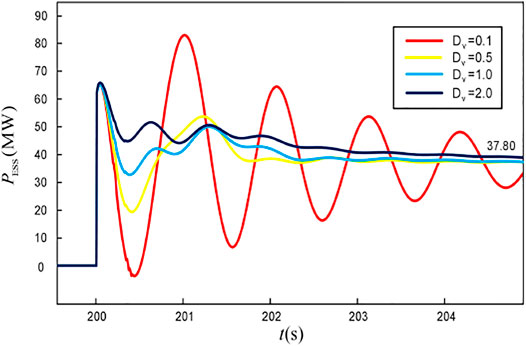
It can be seen from the figure that the improvement of the virtual damping coefficient can effectively suppress the frequency oscillation and smoothen the transient output of the ESS. Under the control strategy of the grid-connected inverter, the value of D_v will not affect the steady-state output power of the ESS, so it will not change the PFR result of the system. Moreover, both the rotor motion equation in Eq. 5 and the simulation results in Figure 7 show that the existence of the damping can reduce the ROCOF of the system, and its effect increases with the increase of Δf before the governor acts.

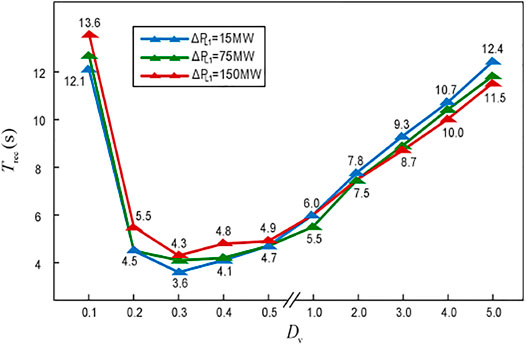
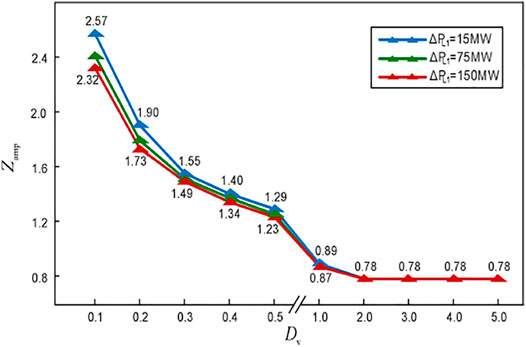
Furthermore, to quantitatively analyze the influence of the virtual damping coefficient on the system frequency recovery process, the time interval from the power fluctuation to system frequency fluctuation less than 1% is defined as the steady-state recovery time T_rec, and the ratio of the difference between the maximum and minimum output power of the ESS and its steady-state output power is defined as the amplitude coefficient Z_amp. The changing trends of the T_rec and the Z_amp under different power fluctuations and different virtual damping coefficients are shown in Figures 9, 10, respectively, and the simulation waveforms are shown in Supplementary Appendix Figure SA1.

FIGURE 9

FIGURE 9. Variation in T_rec with respect to D_v.

FIGURE 10

FIGURE 10. Variation in Z_amp with respect to D_v.

As shown in Figure 9, the variation in T_rec with respect to D_v is the same under different power increments. The specific performance is as follows: when D_v is very small, T_rec is large and the system frequency’s steady-state recovery process takes a long time; with the increase in D_v, T_rec decreases, and it again increases when D_v reaches a certain value. It can be seen that the unreasonable damping value will have adverse effects on the steady-state recovery of the system.

The amplitude coefficient Z_amp in Figure 10 describes the oscillation characteristics of the ESS output power. Thus, it is clear that a large value of Z_amp will not only aggravate the output fluctuation of the ESS but also increases the power capacity requirement. Therefore, considering the indices, T_rec and the Z_amp, the D_v is set as 1.0 in the example.

4.3 Configuration of the Inertia

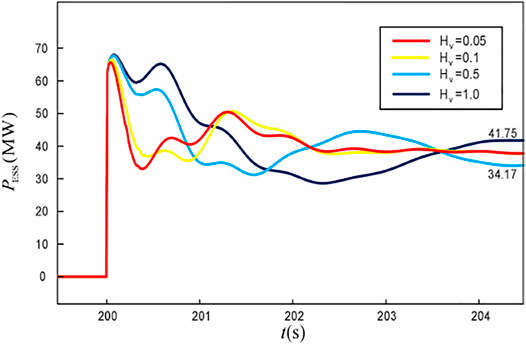
The inertia is the ability of the system to block the sudden change in the frequency, which mainly affects the ROCOF and the smoothness of the unit output. In case 3, bus 1 is still taken as the frequency measurement point, and the active power increment of 145 MW is set for L1 at 200s. The frequency response and the ESS output waveforms for the different virtual inertia constants H_v are obtained, as shown in Figures 11, 12.

FIGURE 11

FIGURE 11. Frequency response of the system for different H_v.

FIGURE 12

FIGURE 12. Output of the ESS for different H_v.

As seen from Figure 11, the increase in the virtual inertia constant can reduce the ROCOF within a certain range. Compared to Figures 7, 11, it can be seen that H_v improves the ROCOF in a short time scale after the unbalanced power generation. This improvement is more profound than that achieved using D_v.

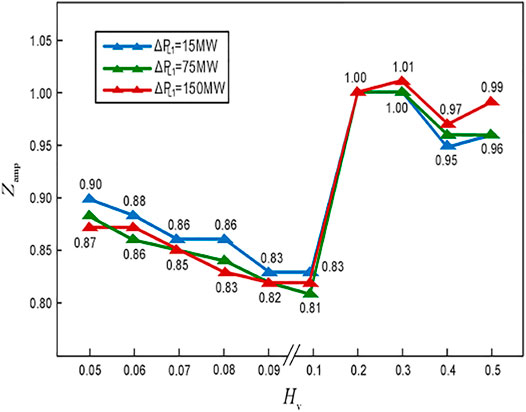
To further compare the effect of H_v and D_v on the ESS dynamic behavior and frequency recovery process, the variations in T_rec and Z_amp for different power fluctuations and different virtual inertia constants are shown in Figures 13, 14, respectively, while the corresponding simulations are shown in Supplementary Appendix Figure SA2.

FIGURE 13

FIGURE 13. Variations in T_rec with respect to H_v.

FIGURE 14

FIGURE 14. Variations in Z_amp with respect to H_v.

It can be seen that the variations in T_rec with respect to H_v are similar for different power increments, i.e., the steady-state recovery time of the frequency increases with the increase in H_v. In addition, although Z_amp has no fixed trend with respect to H_v, it does not change on a large scale, so the value of H_v will not significantly affect the upper and lower limits of the ESS output power.

In conclusion, both the enhancement of H_v and D_v can reduce the ROCOF after the power fluctuation, but the regulation characteristics are different. Among them, D_v can suppress the frequency oscillation and smoothen the ESS output, but when the configuration value is unreasonable, the steady-state recovery time of the system will be prolonged. Compared to the D_v, H_v can restrain the ROCOF faster, but it cannot eliminate the oscillation and even prolong the oscillation time of the frequency. In addition, an increase in H_v produces adverse effects on the recovery process. Therefore, for the control of the ESS grid-connected inverter, H_v and D_v need to be configured coordinately according to the requirements of the ROCOF, to reduce the change of the frequency, suppress the oscillation, and promote the steady-state recovery at the same time.

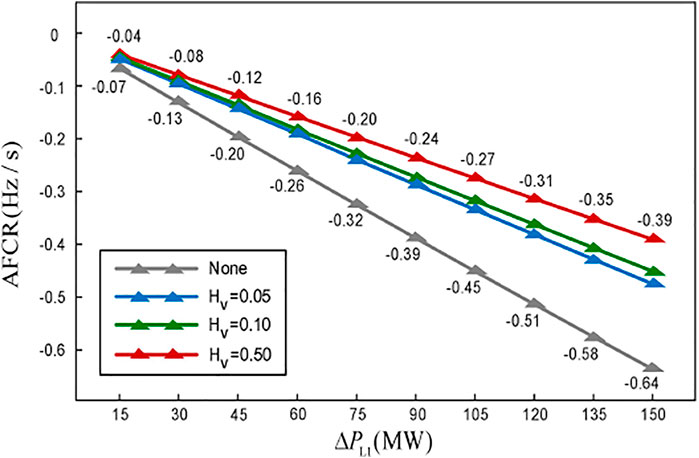
Figure 15 shows the relationship of the initial ROCOF with respect to the ΔP_L1 measured at region 1 under different values of H_v. It can be seen that the input of the ESS can effectively reduce the ROCOF, and the initial ROCOF is approximately linear with ΔP_L1. So, the equivalent inertia constant H_ess contributed by the ESS is invariant, i.e., according to the requirements of the ROCOF, the quantitative configuration of the H_v can be realized in a controlled way.

FIGURE 15

FIGURE 15. Variation in the AFCR with respect to H_v.

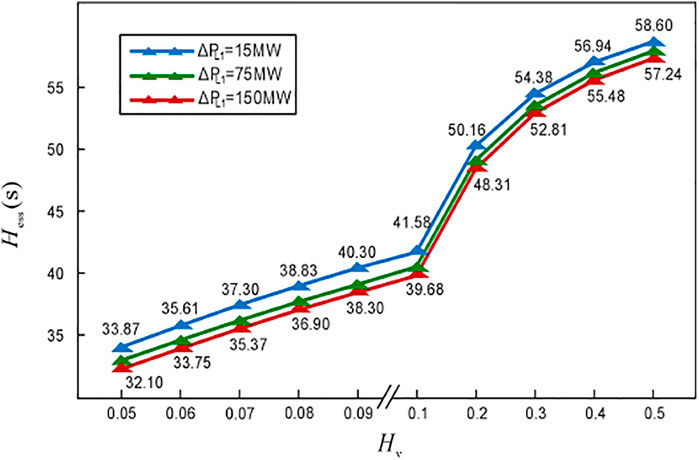
On this basis, the relationship of H_ess with respect to H_v for different power increments is depicted in Figure 16, where H_ess is obtained by the Eqs 1, 2 and the simulation results of the initial ROCOF.

FIGURE 16

FIGURE 16. Variations in the H_ess with respect to ΔP_L1.

It can be seen that although H_ess is approximately proportional to the value of H_v in a certain range, H_ess is not always proportional to the H_v even under the premise of the sufficient ESS capacity so that the inertia support work of the system cannot be fully allocated according to the inertia constant. It can be understood as the influence of the first stage of the three-stage principle, that is, the influence of the electrical distance on the IR in the transient process.

In addition, the value of H_ess changes slightly with respect to ΔP_L1, as shown in Figure 16. This is because the relative inertia defined in the study is equivalent to regulating the effect of damping, and the effect of the damping depends on the size of the frequency deviation and the power increment before the PFR. As a result, there is a certain coupling relationship between the H_ess and the ΔP_L1, that is, the equivalent inertia constant decreases with the increase in the ΔP_L1.

4.4 Configuration of the Frequency Regulation Coefficient

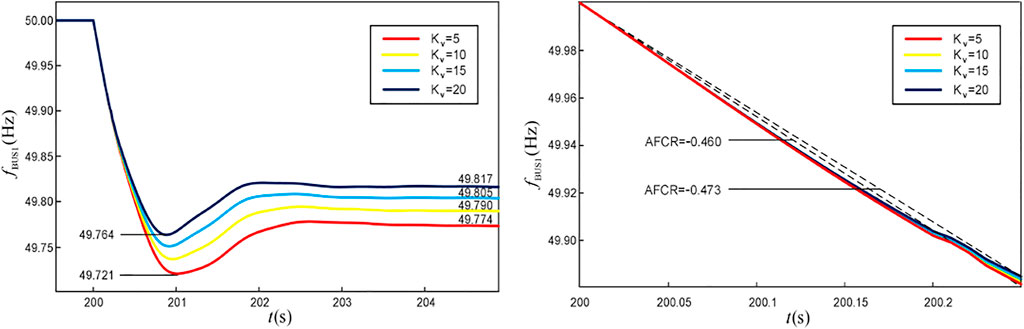
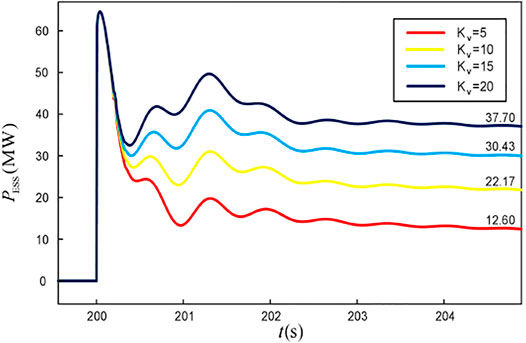
The simulation results from case 1 to case 3 show that the position of the power fluctuation and the values of H_v and D_v will not have a significant impact on the steady-state output of the ESS and the PFR results of the system. Therefore, the virtual frequency regulation coefficient K_v of the ESS can be configured separately according to the SSFD requirements, and it does not have to be limited by the factors such as geographical locations. To further discuss the influence of K_v on the frequency regulation characteristics of the ESS, bus 1 is taken as the frequency measurement point in case 4, and the active power increment of 145 MW is set for L1 at 200s. The frequency response and the ESS output waveforms for different virtual frequency regulation coefficients are shown in Figures 17, 18.

FIGURE 17

FIGURE 17. Frequency response of the system for different K_v.

FIGURE 18

FIGURE 18. Output of the ESS for different K_v.

The value of K_v will not affect the initial ROCOF and the active power of the ESS in a short time scale, i.e., the configuration results of the H_v and the D_v need not be further adjusted according to the K_v. In addition, under the premise of sufficient ESS capacity, the simulation results in Figures 17, 18 show that the equivalent frequency regulation coefficient K_ess provided by the ESS during the PFR is proportional to the magnitude of K_v, and it can also be proved in the study by Liu et al. (2021).

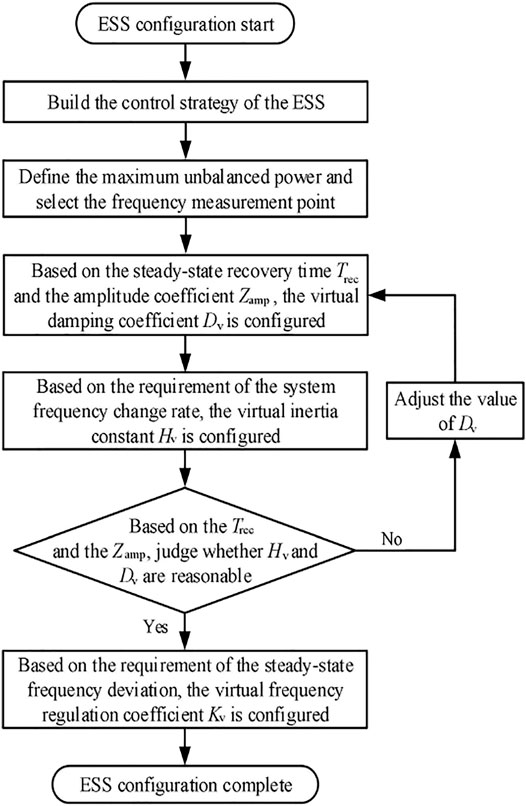
Finally, the flow chart of the ESS configuration method considering the frequency response and dynamic frequency dispersion is shown in Figure 19.

FIGURE 19

FIGURE 19. Flow chart of the ESS configuration method.

5 Conclusion and Prospect

To supplement the missing inertia and the PFR capacity of the high RES penetration system, the study takes the initial ROCOF and the SSFD after the unbalanced power generation as restrictions and proposes an ESS configuration method under the VSG control strategy on the basis of considering the dynamic dispersion; the conclusions are as follows:

1) The ESS with the VSG control strategy has similar frequency support and regulation characteristics as synchronous units, and the transient process will be greatly affected by the dynamic frequency dispersion.

2) The improvement in the virtual inertia constant and the virtual damping coefficient in the ESS can effectively reduce the change rate of the frequency, but the regulation characteristics are different; so, they need to be coordinated according to the ROCOF requirements of the system.

3) When the inertia of the system is sufficient or the ROCOF requirement is low, the ESS can choose the region far away from the power fluctuation to reduce its assembly capacity; when the inertial demand of the system is high, the ESS configuration in the region with the most severe power fluctuation can better take into account the frequency response requirements of the whole system, but the demand of the ESS capacity also increases.

To sum up, the configuration method of the ESS and the regulation characteristics of its related parameters are compared and analyzed deeply by defining the relative inertia, the steady-state recovery time, and the amplitude coefficient. However, the characteristics of RES units and ESS are not considered in this study. Therefore, the next work will be carried out on the basis of considering the type of ESS and the control of RES units.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

HL proposed the methodology. YL and CZ designed the model and the computational framework and analyzed the data. YL and CZ wrote the original draft which was reviewed and edited by LS and XW. All authors agree to be accountable for the content of the work.

Funding

This research was financially supported by the National Key Research and Development Program of China (2017YFB0902000).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2021.807763/full#supplementary-material

References

Douglass, P. J., Garcia-Valle, R., Nyeng, P., Ostergaard, J., and Togeby, M. (2013). Smart Demand for Frequency Regulation: Experimental Results. IEEE Trans. Smart Grid. 4 (3), 1713–1720. doi:10.1109/tsg.2013.2259510

CrossRef Full Text | Google Scholar

Gholamrezaie, V., Dozein, M. G., Monsef, H., and Wu, B. (2018). An Optimal Frequency Control Method through a Dynamic Load Frequency Control (LFC) Model Incorporating Wind Farm. IEEE Syst. J. 12 (1), 392–401. doi:10.1109/jsyst.2016.2563979

CrossRef Full Text | Google Scholar

Homan, S., Dowell, N. M., and Brown, S. (2021). Grid Frequency Volatility in Future Low Inertia Scenarios: Challenges and Mitigation Options. Appl. Energ. 290, 116723. doi:10.1016/j.apenergy.2021.116723

CrossRef Full Text | Google Scholar

Knap, V., Chaudhary, S. K., Stroe, D.-I., Swierczynski, M., Craciun, B.-I., and Teodorescu, R. (2016). Sizing of an Energy Storage System for Grid Inertial Response and Primary Frequency reserve. IEEE Trans. Power Syst. 31 (5), 3447–3456. doi:10.1109/tpwrs.2015.2503565

CrossRef Full Text | Google Scholar

Li, X., Lu, L., Cheng, L., Wang, J., Lu, Z., and Li, W. (2019). Virtual Synchronous Power Decoupling Control Strategy Based on Adaptive Virtual Impedance Improved Reactive Power Loop. Power grid Technol. 43 (10), 3752–3760. (in China). doi:10.13335/j.1000-3673.pst.2019.0012

CrossRef Full Text | Google Scholar

Li, Y., Gao, D. W., Gao, W., Zhang, H., and Zhou, J. (2020). Double-Mode Energy Management for Multi-Energy System via Distributed Dynamic Event-Triggered Newton-Raphson Algorithm. IEEE Trans. Smart Grid. 11 (6), 1. doi:10.1109/tsg.2020.3005179

CrossRef Full Text | Google Scholar

Li, Y., Wang, J., Wang, R., Gao, D. W., Sun, Q., and Zhang, H. (2021). A Switched Newton-Raphson-Based Distributed Energy Management Algorithm for Multienergy System Under Persistent DoS Attacks. IEEE Trans. Automat. Sci. Eng., 1–13. doi:10.1109/TASE.2021.3104393

CrossRef Full Text | Google Scholar

Liu, C., Sun, T., and Cai, G. (2018). Active Support Control and Primary Frequency Modulation Contribution Analysis of Battery Energy Storage Power Station Based on Synchronous Machine Third Order Model. Chin. J. Electr. Eng. 40 (15), 4854–4866. (in China). doi:10.13334/j.0258-8013.pcsee.191277

CrossRef Full Text | Google Scholar

Liu, H., Zhang, C., Peng, X., and Zhang, S. (2021). Configuration of an Energy Storage System for Primary Frequency Reserve and Inertia Response of the Power Grid. IEEE Access. 9, 41965–41975. doi:10.1109/access.2021.3065728

CrossRef Full Text | Google Scholar

Liu, L.-N., and Yang, G.-H. (2021). Distributed Optimal Economic Environmental Dispatch for Microgrids Over Time-Varying Directed Communication Graph. IEEE Trans. Netw. Sci. Eng. 8 (2), 1913–1924. doi:10.1109/TNSE.2021.3076526

CrossRef Full Text | Google Scholar

Miguel, A., Torres, L., Luiz, A. C., Lopes, L. A., Moran, T., Jose, R., et al. (2014). Self-Tuning Virtual Synchronous Machine: a Control Strategy for Energy Storage Systems to Support Dynamic Frequency Control. IEEE Trans. Energ. Convers. 29 (4), 833–840. doi:10.1109/tec.2014.2362577

CrossRef Full Text | Google Scholar

Nasirov, S., and Agostini, C. A. (2021). The Role of Frequency Regulation Remuneration Schemes in an Energy Matrix with High Penetration of Renewable Energy. Renew. Energ. 171 (2), 1097–1114. doi:10.1016/J.RENENE.2021.02.167

CrossRef Full Text | Google Scholar

Peng, X., Yao, W., Yan, C., Wen, J., and Cheng, S. (2019). Two-stage Variable Proportion Coefficient Based Frequency Support of Grid-Connected DFIG-WTs. IEEE Trans. Power Syst. 35 (2), 962–974.

Google Scholar

Pinthurat, W., and Hredzak, B. (2021). Fully Decentralized Control Strategy for Heterogeneous Energy Storage Systems Distributed in Islanded DC Datacentre Microgrid. Energy 231 (11), 120914. doi:10.1016/j.energy.2021.120914

CrossRef Full Text | Google Scholar

Qi, H., Yue, H., Zhang, J., and Lo, K. L. (2021). Optimisation of a Smart Energy Hub with Integration of Combined Heat and Power, Demand Side Response and Energy Storage. Energy 234, 121268. doi:10.1016/j.energy.2021.121268

CrossRef Full Text | Google Scholar

Rodrigues, Y. R., Monteiro, M., Abdelaziz, M., Wang, L., and Ribeiro, P. F. (2020). Improving the Autonomy of Islanded Microgrids Through Frequency Regulation. Int. J. Electr. Power Energ. Syst. 115, 105499. doi:10.1016/j.ijepes.2019.105499

CrossRef Full Text | Google Scholar

Sm, A., Acba, B., Sk, C., Wnb, A., and Db, A. (2021). Strategic Design Optimisation of Multi-Energy-Storage-Technology Micro-Grids Considering a Two-Stage Game-Theoretic Market for Demand Response Aggregation. Appl. Energ. 287, 116563. doi:10.1016/J.apenergy.2021.116563

CrossRef Full Text | Google Scholar

Sockeel, N., Gafford, J., Papari, B., and Mazzola, M. (2020). Virtual Inertia Emulator-Based Model Predictive Control for Grid Frequency Regulation Considering High Penetration of Inverter-Based Energy Storage System. IEEE Trans. Sustain. Energ. 11 (4), 2932–2939. doi:10.1109/tste.2020.2982348

CrossRef Full Text | Google Scholar

Sonny, B. (2007). Power System Stability and Control. Oxford: Taylor & Francis.

Google Scholar

Tang, X., Yin, M., Shen, C., Xu, Y., Dong, Z. Y., and Zou, Y. (2019). Active Power Control of Wind Turbine Generators via Coordinated Rotor Speed and Pitch Angle Regulation. IEEE Trans. Sustain. Energ. 10 (2), 822–832. doi:10.1109/tste.2018.2848923

CrossRef Full Text | Google Scholar

Ten, C. F., and Crossley, P. A. (2008). “Evaluation of Rocof Relay Performances on Networks with Distributed Generation,” in let International Conference on Developments in Power System Protection (Glasgow: DPSP), 523–528. doi:10.1049/cp:20080092

CrossRef Full Text | Google Scholar

Vidyanandan, K. V., and Senroy, N. (2013). Primary Frequency Regulation by Deloaded Wind Turbines Using Variable Droop. IEEE Trans. Power Syst. 28 (2), 837–846. doi:10.1109/tpwrs.2012.2208233

CrossRef Full Text | Google Scholar

Wei, X., Wang, H., Lu, L., Han, X., and Ouyang, M. (2021). An Adaptive Virtual Inertia Control Strategy for Distributed Battery Energy Storage System in Microgrids. Energy. 233, 121155. doi:10.1016/j.energy.2021.121155

CrossRef Full Text | Google Scholar

Yi, C. A., Aa, B., Sa, C., Lei, D. D., and Vt, A. (2020). Smart Frequency Control in Low Inertia Energy Systems Based on Frequen Response Techniques: A Review. Appl. Energ. 279, 115798. doi:10.1016/j.apenergy.2020.115798

CrossRef Full Text | Google Scholar

Yue, M., and Wang, X. (2015). Grid Inertial Response-Based Probabilistic Determination of Energy Storage System Capacity under High Solar Penetration. IEEE Trans. Sustain. Energ. 6 (3), 1039–1049. doi:10.1109/tste.2014.2328298

CrossRef Full Text | Google Scholar

Zhang, F., Hu, Z., Xie, X., Zhang, J., and Song, Y. (2017). Assessment of the Effectiveness of Energy Storage Resources in the Frequency Regulation of a Single-Area Power System. IEEE Trans. Power Syst. 32 (5), 3373–3380. doi:10.1109/tpwrs.2017.2649579

CrossRef Full Text | Google Scholar

Zhang, M., and Sun, L. (2020). PLL and Additional Frequency Control Constituting an Adaptive Synchronization Mechanism for VSCs. IEEE Trans. Power Syst. 35 (6), 4920–4923. doi:10.1109/tpwrs.2020.3020725

CrossRef Full Text | Google Scholar

Zhang, Q., Li, Y., Ding, Z., Xie, W., and Li, C. (2020). Self-Adaptive Secondary Frequency Regulation Strategy of Micro-Grid with Multiple Virtual Synchronous Generators. IEEE Trans. Ind. Applicat. 56 (5), 6007–6018. doi:10.1109/tia.2020.2975144

CrossRef Full Text | Google Scholar

Zhao, H., Hong, M., Lin, W., and Loparo, K. A. (2019). Voltage and Frequency Regulation of Microgrid with Battery Energy Storage Systems. IEEE Trans. Smart Grid. 10 (1), 414–424. doi:10.1109/tsg.2017.2741668

CrossRef Full Text | Google Scholar