Generalized Empirical Interpolation Method With H1 Regularization: Application to Nuclear Reactor Physics

The generalized empirical interpolation method (GEIM) can be used to estimate the physical field by combining observation data acquired from the physical system itself and a reduced model of the underlying physical system. In presence of observation noise, the estimation error of the GEIM is blurred even diverged. We propose to address this issue by imposing a smooth constraint, namely, to constrain the H¹ semi-norm of the reconstructed field of the reduced model. The efficiency of the approach, which we will call the H¹ regularization GEIM (R-GEIM), is illustrated by numerical experiments of a typical IAEA benchmark problem in nuclear reactor physics. A theoretical analysis of the proposed R-GEIM will be presented in future works.

1 Introduction and Preliminaries

In nuclear reactor simulations, data assimilation (DA) with reduced basis (RB) enables the reconstruction of the physical field, e.g., for constructing a fast/thermal flux and power field within a nuclear core in an optimal way based on neutronic transport/diffusion model and observations (Gong et al., 2016; Argaud et al., 2017a; Gong et al., 2017; Argaud et al., 2018; Gong, 2018). In practice, the existing methods are based on a reduced basis, however, this approach is not robust with respect to observation noise and there are some additional constraints or regularization on the low-dimensional subspaces, i.e., the related coefficients, have been proposed as possible remedies in several recent works (Argaud et al., 2017b; Gong et al., 2020; Gong et al., 2021). The idea of introducing box constraints was originally introduced in Argaud et al. (2017a) to stabilize the generalized empirical interpolation method in the presence of noise (Maday and Mula, 2013). The same idea has been applied to the POD basis and the background space (Gong et al., 2019) of the so-called parametrized-background data-weak (PBDW) data assimilation (Maday et al., 2015a). Recently, the regularization of the GEIM/POD coefficients has been studied in Gong et al. (2021). The corresponding theoretical analysis can be found in Gong (2018), Herzet et al. (2018), and Gong et al. (2019). This article introduces H¹ regularization schemes for the approximation, and numerical experiments in nuclear reactor physics indicate its potential to address this obstruction.

Our goal is to approximate the physical state u from a given compact set $\mathcal{M}\subset \mathcal{X}$ (manifold), which represents the possible state of a physical system taking place in Ω. Where $\mathcal{X}$ is a Banach space over a domain $\mathrm{\Omega }\subset {\mathbb{R}}^d(d\ge 1)$ being equipped with the norm $\Vert .{\Vert }_{\mathcal{X}}$. In the framework of data assimilation with reduced basis, any $u\in \mathcal{M}$ can be estimated by combining two parts. The first term is a certain amount (m) of observation of u acquired directly from sensors of the underline physical system, which can be represented by a combination of linear functionals of ${\mathcal{X}}^{\prime }$ (the dual space of $\mathcal{X}$) evaluated on u. The second term is the use of a family of (reduced) subspaces ${\mathcal{Z}}_n$ of finite dimension n which is assumed to approximate well with the manifold $\mathcal{M}$ in a given accuracy.

The algorithms used to build the reduced subspace ${\{{\mathcal{Z}}_n\}}_n$ and find appropriate linear functionals have already been reported in the community of reduced modeling [see Maday and Mula, 2013; Maday et al., 2015b; Maday et al., 2015c; Maday et al., 2016]. Note that even if this is not necessary in the previous statements, the construction of the reduced spaces ${\mathcal{Z}}_n$ could be recursive, i.e., we have ${\mathcal{Z}}_{n-1}\subset {\mathcal{Z}}_n$. The field $u\in \mathcal{M}$ can be approximated by interpolation (Argaud et al., 2018) or data assimilation (Gong, 2018; Gong et al., 2019).

For reading convenience, let us first introduce some notations used throughout this article. We first introduces the standard L²(Ω) or $\mathcal{H}$ Hilbert space over the special domain $\mathrm{\Omega }\subset {\mathbb{R}}^d$ equipped with an inner product ${(w,v)}_{L^2(\mathrm{\Omega })}\equiv {\int }_{\mathrm{\Omega }}wvdx$ and the induced norm $\Vert w{\Vert }_{L^2(\mathrm{\Omega })}=\sqrt{{(w,w)}_{L^2(\mathrm{\Omega })}}$. The semi-norm H¹ is defined by $|w{|}_{H^1(\mathrm{\Omega })}=\sqrt{{(\nabla w,\nabla w)}_{H^1(\mathrm{\Omega })}}$, where the inner product is ${(w,v)}_{H^1(\mathrm{\Omega })}\equiv {\int }_{\mathrm{\Omega }}\nabla w\nabla vdx$. For a given Hilbert space $\mathcal{U}$ and the related dual space ${\mathcal{U}}^{\prime }$, the Riesz operator $R_{\mathcal{U}}:{\mathcal{U}}^{\prime }\to \mathcal{U}$ satisfies: for any given $\ell \in {\mathcal{U}}^{\prime }$, we have $(R_{\mathcal{U}}\ell ,v)=\ell (v),\forall v\in \mathcal{U}$.

Let us denote by u (r; μ) the solution of a parameter-dependent partial differential equation (PDE) set on Ω and on a closed parametric domain $\mathcal{D}\subset {\mathbb{R}}^p$. For any given $\mu \in \mathcal{D}$, the physical field u (r; μ) belongs to $\mathcal{U}\subset L^2(\mathrm{\Omega })\text{or}{H}^1(\mathrm{\Omega })$, a functional space derived from the PDE. We call the set $\mathcal{M}\equiv \{u(\mathit{r};\mu );\mu \in \mathcal{D}\}$ of all parameter-dependent solution manifold. Let ${\mathcal{L}}_M:\mathcal{U}\to {\mathbb{R}}^M$ be the vector-valued observation functional ${\mathcal{L}}_M(u)={({\ell }_1(u),\dots ,{\ell }_M(u))}^T$ of $u\in \mathcal{U}$.

2 Field Reconstruction With Regularization

Our goal in this work is to infer any state $u\in \mathcal{U}$ over a spacial domain $\mathrm{\Omega }\in {\mathbb{R}}^d$ given only some corresponding noisy observations $\mathit{y}={(y_1^{obs},\dots ,y_M^{obs})}^T$. This empirical learning problem from a limited data set is always underdetermined. In general, with observation noise, a regularization term R (u) is added to the loss function, and then a general convex model fitting problem can be written in the form:

$\underset{u\in \mathcal{U}}{minimize}J(u)≔V(\mathcal{L}(u),\mathit{y})+\lambda R(u),$(2.1)

where $V:{\mathbb{R}}^M\to \mathbb{R}$ is a convex loss function that describes the cost of predicting u when the observation is y. λ is a parameter which presents the importance of the regularization term. R (u) is usually a convex regularization function to impose a penalty on the complexity of u through some prior knowledge.

2.1 H¹ Regularization

The goal of regularization is to prevent overfitting or to denoise in mathematics and particularly in the fields of inverse problems (Ivanov, 1976; Andreui et al., 1977; Balas, 1995; Arnold, 1998; Vladimir, 2012; Benning and Burger, 2018), by introducing additional information in order to solve ill-posed problems. From a Bayesian (James Press, 1989) point of view, regularization techniques correspond to introduce some prior distributions on model parameters. The general choice of R (u) is a norm-like form $\Vert u{\Vert }_{\chi }^2$, where χ represents different kinds of norm depending on the underlying application. The simplest choice of R (u) is L² norm, say, $\Vert u{\Vert }_{L^2(\mathrm{\Omega })}^2$, which has been well studied in the literature, either from a theoretical or algorithmic point of view. The regularization is also called Tikhonov regularization (Andreui et al., 1977), which is essentially a trade-off between fitting the data and reducing the norm of the solution. For some real-world problems, there has been much interest in alternative regularization terms. For example, total variation (TV) regularization, $R(u)=\Vert \nabla u{\Vert }_{L^1(\mathrm{\Omega })}$, is popular in image reconstruction or other domains (Rudin et al., 1992; Rudin et al., 1992; Chan et al., 1997; Chan and Tai, 2003; Wachsmuth and Wachsmuth, 2011; De los Reyes and Schönlieb, 2012). By using a L¹ norm, sharp edges would be allowed as the penalty is finite, and it also allows discontinuous controls which can be important in certain applications.

If one would like to impose a smooth control, the H¹ semi-norm can be used:

$R(u)=\Vert \nabla u{\Vert }_{L^2(\mathrm{\Omega })}.$(2.2)

Examples can be found in the context of parameter estimation problems (Keung and Zou, 1998; Cai et al., 2008; Wilson et al., 2009; Barker et al., 2016), image-deblurring (Chan et al., 1997; Li et al., 2010; Cimrák and Melicher, 2012), image reconstruction (Ng et al., 2000), and flow control (Heinkenschloss, 1998; Collis et al., 2001). The work in Van Den Doel et al. (2012) shows that the proposed H¹ semi-norm regularization performs better than L¹ regularization cousin, total variation, for problems with very noisy data due to the smooth nature of controlled variables. The authors in Srikant did a comparison of H¹ and TV regularization methods and also studied the shortcomings and limitations of some of the implementations schemes, such as a Gaussian filter. H¹ regularization would perform well over uniform regions in the domain but would perform poorly over edges. Furthermore, to solve the PDE-constrained optimization problem as reported in Haber and Hanson (2007), the authors suggested a synthetic regularization functional of the form:

$R(u)=\Vert u{\Vert }_{L^2(\mathrm{\Omega })}^2+\gamma \Vert \nabla u{\Vert }_{L^2(\mathrm{\Omega })},$(2.3)

where the parameter γ can be adapted. Note that this synthetic regularization is now commonly used to solve the ill-posed inverse problems.

2.2 Generalized Empirical Interpolation Method

Recall that our goal is to estimate the state $u^{true}[\mu ]\in \mathcal{U}$ of a physical system for a given parameter $\mu \in \mathcal{D}$, by using a parameterized best-knowledge model and M (potentially noisy) observations.

The first step is to choose a sequence of n-dimensional subspaces ${\{{\mathcal{Z}}_n\}}_n$ such that the best approximation of any given u^true [μ] in the space ${\mathcal{Z}}_n$ converges to zero when n goes to infinity, i.e.,

$\underset{n\to \infty }{\lim }\underset{w\in {\mathcal{Z}}_n}{\inf }\Vert u^{true}[\mu ]-w\Vert \le {ϵ}_{\mathcal{Z}}\forall \mu \in \mathcal{D}$(2.4)

for an acceptable tolerance ${ϵ}_{\mathcal{Z}}$. We further assume that the selected subspaces satisfy

${\mathcal{Z}}_1\subset \cdots \subset {\mathcal{Z}}_{N_{\mathit{max}}}\subset \cdots \subset \mathcal{U}.$(2.5)

In other words, we choose the subspaces such that the most dominant physical system is well represented for a relatively small n. In particular, these subspaces may be constructed through the application of model reduction methods to a parameterized PDE.

The second step is to model the data acquisition procedure. Given a system in of a parameter $\mu \in \mathcal{D}$, we assume the observations are of the form

$\forall m=1,\dots ,M,y_m^{obs}[\mu ]={\ell }_m(u^{true}[\mu ])+e_m,$(2.6)

where $y_m^{obs}[\mu ]$ is the value of the mth observation, ℓ_m is the linear functional associated with the mth sensor, and e_m is the observation noise associated with the mth sensor. The detailed form of the functional ℓ_m depends on the specific sensor used to acquire data. For example, if the sensor measures a local value of the state, then we may model the observation value as Gaussian convolution

${\ell }_m(v)\equiv {\int }_{\mathrm{\Omega }}\left({(2\pi r_m^2)}^{-d/2}\text{exp}\left(-\frac{\Vert x-x_m^c{\Vert }_{{\ell }^2({\mathbb{R}}^d)}^2}{2r_m^2}\right)\right)v(x)dx,$(2.7)

where ${(2\pi r_m^2)}^{-d/2}\text{exp}\left(-\frac{\Vert x-x_m^c{\Vert }_{{\ell }^2({\mathbb{R}}^d)}^2}{2r_m^2}\right)$ is a Gaussian distributed function to present the response of the sensor for a given physical field v, and $x_m^c\in {\mathbb{R}}^d$ is the center of the sensor in the special domain Ω, and $r_m\in {\mathbb{R}}_{>0}$ is the physical width of the sensor. In particular, the localized sensor is of interest in this work.

We assume that e_m is independent and identically distributed (IID), and with a density of p_m on $\mathbb{R}$. In practice, the mean and covariance of the observation data acquired are more readily quantifiable than the distribution p_m. Thus, we assume the mean and the covariance of the distribution exist and make the following assumptions on the noise term: (i) zero mean: E [e_m] = 0, m = 1, … , M; (ii) variance: $E[e_m^2]={\sigma }_m^2,m=1,\dots ,M$; (iii) and uncorrelated: E [e_me_n] = 0, m ≠ n.

By running the greedy algorithm of the so-called generalized empirical interpolation method [GEIM (Maday and Mula, 2013)], a set of basis ${\{q_n\}}_n$ is generated and spanned the reduced space ${\mathcal{Z}}_n=\text{span}\{q_1,\dots ,q_n\}$. Then, the generalized interpolation process is well defined as follows:

${\mathcal{I}}_N[u]=\sum _{j=1}^N{\alpha }_j{q}_j\text{subject\hspace{0.17em}to:\hspace{0.17em}}\forall i=1,\dots ,M,{\ell }_i({\mathcal{I}}_N[u])={\ell }_i(u).$(2.8)

With noisy observations, GEIM is, however, not robust with respect to observation noise (Argaud et al., 2017b), and in that work, a so-called constrained stabilized GEIM (CS-GEIM) by using a constrained least squares approximation was proposed to address this obstruction, where numerical experiments indicate its potential.

3 H¹ Regularization Formulation of GEIM

Now, we state the H¹ regularization scheme for GEIM (R-GEIM). Given a reduced space ${\mathcal{Z}}_N=\text{span}\{q_1,\dots ,q_N\}\subset \mathcal{U}$ of dimension N spanned by N basis ${\{q_i\}}_{i=1}^N$ and M measurement functionals ${\mathcal{L}}_M≔{({\ell }_1,\dots ,{\ell }_M)}^T$ and the corresponding noisy measurements $\mathit{y}={(y_1^{obs},\dots ,y_M^{obs})}^T$, M ≥ N, then the reconstruction problem from measurements is: find $u\in {\mathcal{Z}}_N$ such that:

$u=\underset{u\in {\mathcal{Z}}_N}{argmin}V(\mathcal{L}(u),\mathit{y})+\xi \Vert \nabla u{\Vert }_{L^2(\mathrm{\Omega })}^2,$(3.1)

where $V:{\mathbb{R}}^M\to \mathbb{R}$ is loss function that evaluates the cost of estimating u giving the observation y which depends on the underlying application. The symbol “$\underset{\cdot }{argmin}$” is argument of the minimum, thus $\underset{u\in {\mathcal{Z}}_N}{argmin}f(u)$ is the value of u for which f(u) attains its minimum. The parameter ξ is a trade-off factor between the regularization term and the loss function term. Furthermore, if we have no information about the noise distribution, three proposed typical forms of V could be $\Vert \mathcal{L}(u)-\mathit{y}{\Vert }_l^2,$, where l = ∞, 1, 2. For the above R-GEIM, we have the following remarks:

• The basis and measurements of the chosen scheme could be based on GEIM, POD, or any other approach.

• Later, we will show that l = 2 corresponds to the least squares method, and l = 1 corresponds to the least absolute deviations (LAD) (Bloomfield and Steiger, 1980). Compared to the traditional least squares method, the LAD is much robust and finds its applications in many areas.

• By using the H¹ regularization for the reduced basis field reconstruction, the first assumption is that the field u is in H¹ space; for the most regular physical problem, this condition is satisfied automatically, and the H¹ regularization term is a kind of smooth control for the underlying field reconstruction problem.

If we have no prior information about noise, a commonly used way to formulize Eq. 3.1 is taking 2 norm for the loss function term, we have the following results:

R-GEIM: Given a reduced space ${\mathcal{Z}}_N=\text{span}\{q_1,\dots ,q_N\}\subset \mathcal{U}$ of dimension N spanned by N basis ${\{q_i\}}_{i=1}^N$ and M(≥ N) measurement functionals ${\mathcal{L}}_M≔{({\ell }_1,\dots ,{\ell }_M)}^T$ and the corresponding noisy measurements $\mathit{y}={(y_1^{obs},\dots ,y_M^{obs})}^T$, then the reconstruction problem from measurements is: find $u\in {\mathcal{Z}}_N$ such that:

$u=\underset{u\in {\mathcal{Z}}_N}{argmin}\frac{1}{M}\Vert \mathcal{L}(u)-\mathit{y}{\Vert }_2^2+\xi \Vert \nabla u{\Vert }_{L^2(\mathrm{\Omega })}^2.$(3.2)

Let $\mathbb{M}$ be an M × N full-column rank matrix with elements ${\mathbb{M}}_{i,j}={\ell }_i(q_j),i=1,\dots ,M,j=1,\dots ,N$ and $\mathbb{N}$ be an N × N matrix with elements ${\mathbb{N}}_{i,j}=(\nabla q_i,\nabla q_j),i,j=1,\dots ,N$, then the algebraic form of Eq. 3.2 is: find $\mathit{\alpha }={({\alpha }_1,\dots ,{\alpha }_N)}^T\in {\mathbb{R}}^N$ or $v={\sum }_{j=1}^N{\alpha }_j{q}_j\in {\mathcal{Z}}_N$ such that:

${\mathit{\alpha }}^{\ast }=\text{arg\hspace{0.17em}}\underset{\mathit{\alpha }\in {\mathbb{R}}^N}{\min }{(\mathbb{M}\mathit{\alpha }-\mathit{y})}^T(\mathbb{M}\mathit{\alpha }-\mathit{y})+M\xi {\mathit{\alpha }}^T\mathbb{N}\mathit{\alpha },$(3.3)

the solution is

${\mathit{\alpha }}^{\ast }={({\mathbb{M}}^T\mathbb{M}+M\xi \mathbb{N})}^{-1}{\mathbb{M}}^T\mathit{y}.$(3.4)

Proof Let $J(\mathit{\alpha },\mathit{y})={(\mathbb{M}\mathit{\alpha }-\mathit{y})}^T(\mathbb{M}\mathit{\alpha }-\mathit{y})+M\xi {\mathit{\alpha }}^T\mathbb{N}\mathit{\alpha }$, then we have:

$\nabla J(\mathit{\alpha },\mathit{y})=2{\mathbb{M}}^T\mathbb{M}\mathit{\alpha }+2M\xi \mathbb{N}\mathit{\alpha }-2{\mathbb{M}}^T\mathit{y},$

the solution to minimize J (α,y) is the α∗ that satisfies ∇J (α∗,y) = 0. Because, $\mathbb{M}$ is an M × N full-column rank matrix, so that ${\mathbb{M}}^T\mathbb{M}$ is a symmetric positive definite (SPD) matrix.From the definition of $\mathbb{N}$, it is a symmetric positive semi-definite matrix, so ${\mathbb{M}}^T\mathbb{M}+M\xi \mathbb{N}$ is an N × N invertible matrix, which completes the proof.Let $\mathbb{D}$ be the M × M covariance matrix of the measurement with elements ${\mathbb{D}}_{i,j}=E[e_i{e}_j],i,j=1,\dots ,M$. If e_m is uncorrelated, ${\mathbb{D}}_{i,j}=0$ for i ≠ j, then $\mathbb{D}$ is a diagonal matrix with ${\mathbb{D}}_{i,i}={\sigma }_i^2$ and the variance of the ith measurement, Eq. 3.3 can be improved by

${\mathit{\alpha }}^{\ast }=\underset{\mathit{\alpha }\in {\mathbb{R}}^N}{argmin}{(\mathbb{M}\mathit{\alpha }-\mathit{y})}^T{\mathbb{D}}^{-1}(\mathbb{M}\mathit{\alpha }-\mathit{y})+M\xi {\mathit{\alpha }}^T\mathbb{N}\mathit{\alpha },$(3.5)

and the solution is

${\mathit{\alpha }}^{\ast }={({\mathbb{M}}^T{\mathbb{D}}^{-1}\mathbb{M}+M\xi \mathbb{N})}^{-1}{\mathbb{M}}^T{\mathbb{D}}^{-1}\mathit{y}.$(3.6)

Later, we will show this is also the algebraic formulation for Gaussian noise with covariance $\mathbb{D}$. If we can make use of the prior information of noise, we have the following remark:

Remark Let r(u) be the bias of the reduced model from the truth $\mathcal{L}(u)-\mathit{y}=\mathit{e}+r(u)$. By using maximum likelihood (ML) estimation for the following common noise densities, we have:

• Uniform noise, when the noise term e_m is uniformly independent and identically distributed on ( − e₀, e₀), then the reconstruction problem is: find $u\in {\mathcal{Z}}_N$ such that:

$u=\underset{u\in {\mathcal{Z}}_N}{argmin}\Vert \nabla u{\Vert }_{L^2(\mathrm{\Omega })}^2,\text{subject\hspace{0.17em}to\hspace{0.17em}}\Vert \mathcal{L}(u)-\mathit{y}{\Vert }_{\infty }\le e_0+\Vert r(u){\Vert }_{\infty }.$(3.7)

If the noise bounds are different for different measurements, the constraint in Eq. 3.7 becomes $|{\ell }_m(u)-y_m^{obs}|\le e_m+|r_m(u)|,m=1,\dots ,M$.

• Gaussian noise, when the noise e_m is Gaussian with the zero mean and covariance matrix $\mathbb{D}$, then the reconstruction problem is: find $u\in {\mathcal{Z}}_N$ such that

$u=\underset{u\in {\mathcal{Z}}_N}{argmin}{(\mathcal{L}(u)-\mathit{y})}^T{\mathbb{D}}^{-1}(\mathcal{L}(u)-\mathit{y})+M\xi \Vert \nabla u{\Vert }_{L^2(\mathrm{\Omega })}^2.$(3.8)

• Laplacian noise, when the noise e_m is Laplacian independent, identically distributed with density $p(e)=\frac{1}{2e_0}{e}^{-|e|/e_0}$, then the reconstruction problem is: find $u\in {\mathcal{Z}}_N$ such that

$u=\underset{u\in {\mathcal{Z}}_N}{argmin}\Vert \mathcal{L}(u)-\mathit{y}{\Vert }_1^2+\xi \Vert \nabla u{\Vert }_{L^2(\mathrm{\Omega })}^2.$(3.9)

We refer readers to Boyd and Vandenberghe (2004) for further theoretical analysis on this remark. Through this remark, the physical means of the term $\Vert \mathcal{L}(u)-\mathit{y}{\Vert }_l^2$ in Eq. 3.1 for different l is easier to understand. The ∞, 1, and 2 norms interpret the maximum likelihood estimation with a noise density, that is, uniform, Laplacian, and Gaussian, respectively. Considering for the most engineering problems, the noise density is Gaussian and also bounded, and thus we only present numerical results of uniform noise and Gaussian noise in this work.Another remark is that, in this work, numerical results are illustrated based on GEIM, more precisely. The reduced basis in Eq. 3.2 is derived with GEIM, but this regularization is fit for the POD basis or the basis selected from the greedy reduced basis method (Grepl et al., 2007) without any modification.

4 Numerical Results and Analysis

In this section, we illustrate the performance of R-GEIM on a typical benchmark problem in nuclear reactor physics. The test example is adapted based on the classical 2D IAEA benchmark problem (Benchmark Problem Book, 1977; Gong et al., 2017); the geometry of the 2D core is shown in Figure 1. This problem represents the mid-plane z = 190 cm of the 3D IAEA benchmark problem, that is used by references (Theler et al., 2011). The reactor spacial domain is Ω = region (1, 2, 3, 4). The core and control regions are Ω_core = region (1, 2, 3) and Ω_control = region (3), respectively. We consider the value of ${\mathrm{\Sigma }}_{a,2}{|}_{{\mathrm{\Omega }}_1}$, ${\mathrm{\Sigma }}_{a,2}{|}_{{\mathrm{\Omega }}_2}$, and ${\mathrm{\Sigma }}_{a,2}{|}_{{\mathrm{\Omega }}_3}$ in the core region Ω_1,2,3 as a parameter (so p = 3 and $\mu =[{\mathrm{\Sigma }}_{a,2}{|}_{{\mathrm{\Omega }}_1},{\mathrm{\Sigma }}_{a,2}{|}_{{\mathrm{\Omega }}_2},{\mathrm{\Sigma }}_{a,2}{|}_{{\mathrm{\Omega }}_3}]$). We assume that ${\mathrm{\Sigma }}_{a,2}{|}_{{\mathrm{\Omega }}_i}\in [0.080,0.150]$ for i = 1, 2, 3. The rest of the coefficients of the diffusion model are fixed to the values indicated in Table 1 of Gong et al. (2017).

FIGURE 1

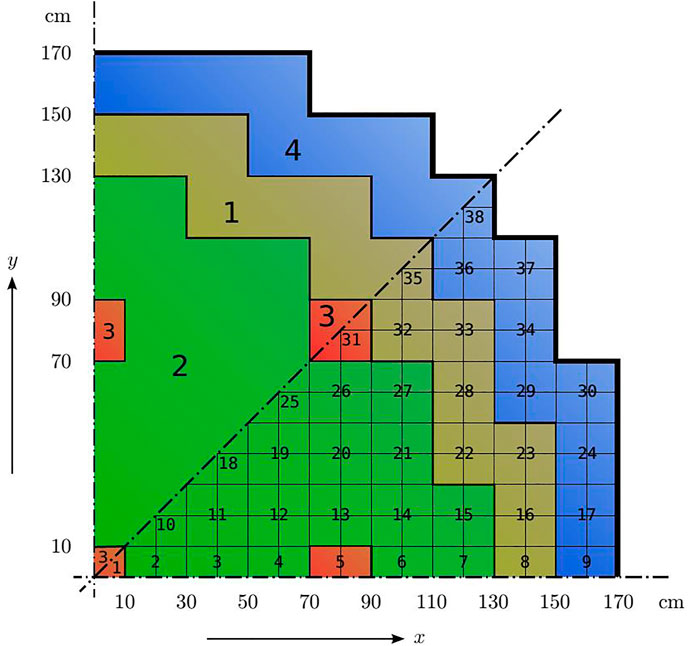
FIGURE 1. Geometry of a 2D IAEA benchmark. Upper octant: region assignments; lower octant: fuel assembly identification [from reference (Benchmark Problem Book, 1977; Theler et al., 2011)].

TABLE 1

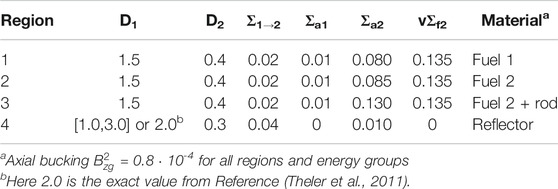
TABLE 1. Coefficient value: diffusion coefficients D_i (in cm) and macroscopic cross sections (in cm^-1).

The neutronic field (fast and thermal flux, power distribution) is derived by solving two group diffusion equations. The numerical algorithm is implemented by employing the free finite elements solver FreeFem++ (Hecht, 2012). The norm $\Vert \cdot {\Vert }_{L^2(\mathrm{\Omega })}$ is induced by the inner product ${(w,v)}_{L^2(\mathrm{\Omega })}={\int }_{\mathrm{\Omega }}wvdx$, and the semi-norm $\Vert \cdot {\Vert }_{H^1(\mathrm{\Omega })}$ is induced by the inner product ${(w,v)}_{H^1(\mathrm{\Omega })}={\int }_{\mathrm{\Omega }}\nabla w\nabla vdx$. The measurement we employed here is same as Eq. 2.7 with r_m = 1 cm and set ${\{w_i\}}_{i=1}^N$ being the corresponding Riesz representation with H¹ inner product. Finally, we set the finite element size to d = 0.1 cm, which is enough for our analysis. We refer to Argaud et al. (2017b) for detailed implementation of this problem with FreeFem++.

The regularization factor ξ is essential for R-GEIM. It can significantly affect the reconstruction error of R-GEIM, and if they are incorrectly specified then the field reconstructed with R-GEIM is suboptimal. We show the variation of the errors in L^∞, H¹, and L² norms for R-GEIM with respect to different regularization factors ξ in Figure 2. The dimension of reduced basis is fixed to n = 80, the number of measurements is set to m = 2n, and the observation noise is uniformly distributed, with a noise level σ = 10⁻², 10⁻³. It can be observed that the optimal ξ is different for different error metrics. For the errors evaluated in L² norm, the optimal ξ_op ∼ 0.1, and for L^∞ norm or H¹ norm, the optimal ξ_op ∼ 1. In the left of this work, we fix ξ to be the optimal value and evaluate the errors in L² norm and H¹ norm, which reflect the average error of the reconstructed field itself and its gradient.

FIGURE 2

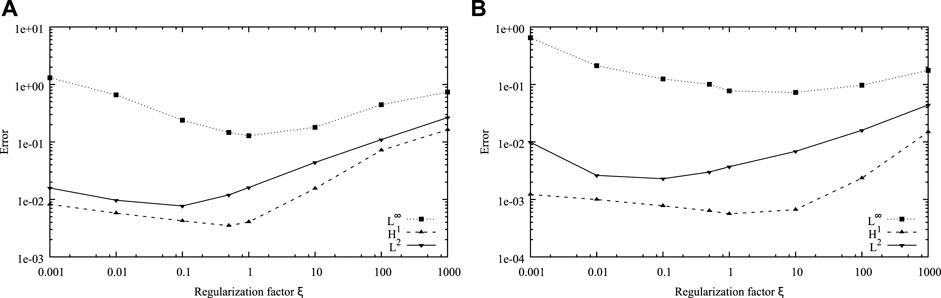
FIGURE 2. Variation of the errors in L^∞, H¹, and L² norms for R-GEIM with respect to the different regularization factor ξ. The reduced dimension is n = 80, number of measurement is m = 2n, and the observation noise is uniformly distributed with noise levels 10⁻² (A) and 10⁻³ (B).

This section illustrates the behavior of GEIM, CS-GEIM, and R-GEIM, in case of noisy observations. We first show the variation of the errors in L² norm and H¹ norm for GEIM, CS-GEIM, and R-GEIM with respect to different reduced dimensions n in Figure 3. The observation noise is assumed to be uniformly distributed, with a noise level σ = 10⁻². The number of measurements is m = 2n. Figure 4 illustrates the case for the noise level σ = 10⁻³. The cases with Gaussian-distributed observation noise are shown in Figure 5 for the noise level σ = 10⁻² and in Figure 6 for the noise level 10⁻³.

FIGURE 3

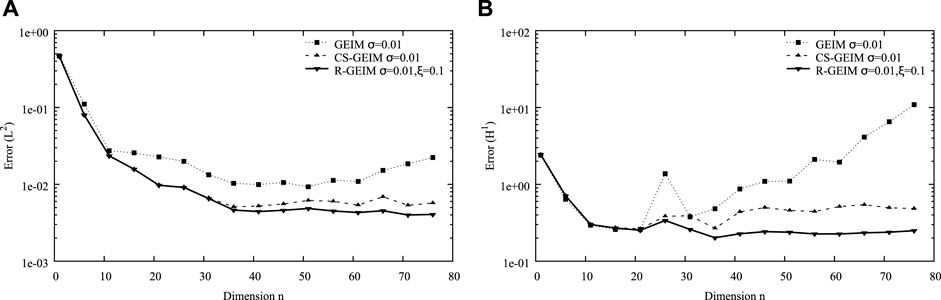
FIGURE 3. The variation of the errors in L² norm (A) H¹ norm (B) for GEIM, CS-GEIM, and R-GEIM with respect to different reduced dimension n. The number of measurement is m = 2n, and the observation noise is uniformly distributed with a noise level σ = 10⁻².

FIGURE 4

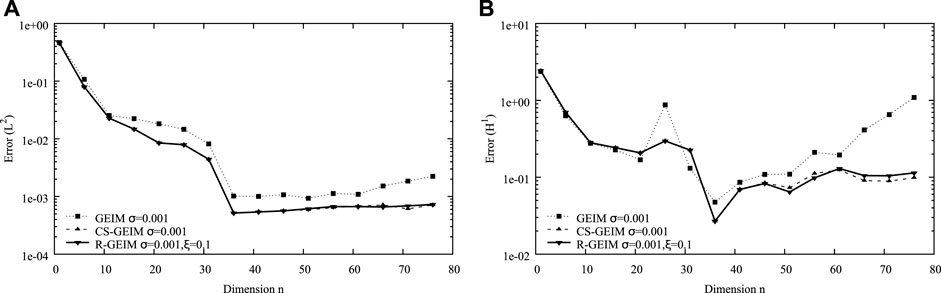
FIGURE 4. Variation of the errors in L² norm (A) and H¹ norm (B) for GEIM, CS-GEIM, and R-GEIM with respect to different reduced dimension n. The number of measurement is m = 2n, and the observation noise is uniformly distributed with a noise level σ = 10⁻³.

FIGURE 5

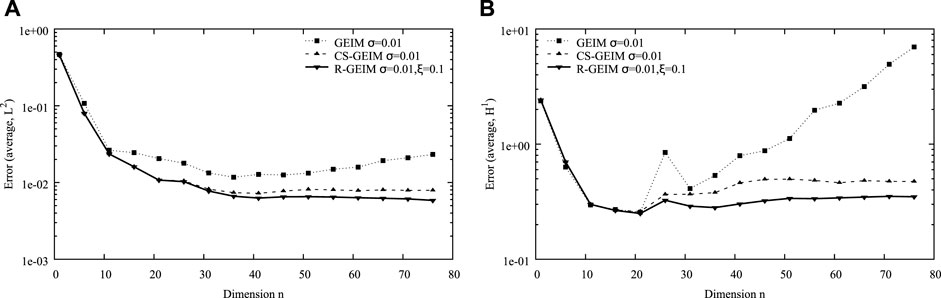
FIGURE 5. Variation of the errors in L² norm (A) and H¹ norm (B) for GEIM, CS-GEIM, and R-GEIM with respect to different reduced dimension n. The number of measurement is m = 2n, and the observation noise is Gaussian distributed with a noise level σ = 10⁻².

FIGURE 6

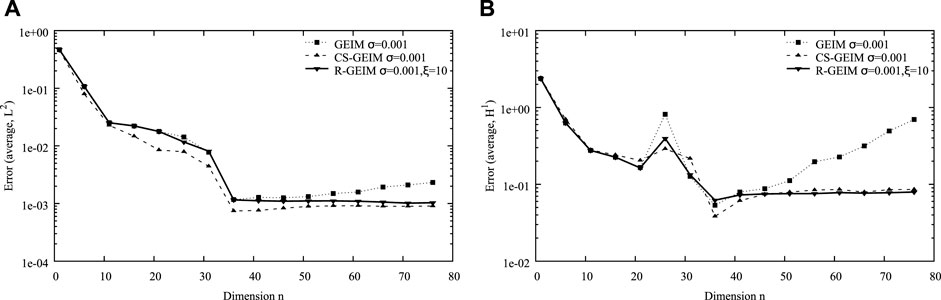
FIGURE 6. Variation of the errors in L² norm (A) and H¹ norm (B) for GEIM, CS-GEIM, and R-GEIM with respect to different reduced dimension n. The number of measurement is m = 2n, and the observation noise is Gaussian distributed with a noise level σ = 10⁻³.

From these figures, we can conclude that R-GEIM shows a better stability performance in the case of noisy measurement. The accuracy can be as good as CS-GEIM, but the R-GEIM algorithm is much simpler, with relatively low computational cost; the main cost for the online stage is to solve the matrix system Eq. 3.4. But for CS-GEIM, the relative complex constrained quadratic programming problem has to be solved.

5 Conclusion and Future Works

The traditional generalized empirical interpolation method is well studied for data assimilation in many domains. However, this reduced modeling-based data assimilation method is not robust with respect to observation noise. We propose addressing this issue by imposing a smooth constraint, namely, an H¹ semi-norm of the reconstructed field to involve some prior knowledge of the noise. The efficiency of the approach, which we call R-GEIM, is illustrated by an IAEA benchmark numerical experiment, dealing with the reconstruction of the neutronic field derived from neutron diffusion equations in nuclear reactor physics. With H¹ regularization, the behavior of the reconstruction is improved in the case of noisy observation. Further works are ongoing: i) mathematical analysis of the stable and accurate behavior of this regularization approach and ii) the regularization trade-off factor will be studied to give an outline on how to choose these factors for generic problems.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

HG contributed to conceptualization, methodology, software, data curation, and writing—original draft and editing. ZC contributed to conceptualization. QL contributed to conceptualization, supervision, and review.

Funding

This work is supported by the National Natural Science Foundation of China (Grant No. 11905216 and Grant No. 12175220).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors are grateful to three reviewers for the useful remarks on the manuscript.

References

Andreui, N. T., Vasiliui, I. A., and Fritz, J. (1977). Solutions of Ill-Posed Problems, Volume 14. Washington, DC: Winston.

Google Scholar

Argaud, J.-P., Bouriquet, B., Gong, H., Maday, Y., and Mula, O. (2017). “Stabilization of (G) EIM in Presence of Measurement Noise: Application to Nuclear Reactor Physics,” in Spectral and High Order Methods for Partial Differential Equations ICOSAHOM 2016 (Berlin, Germany: Springer), 133–145.

CrossRef Full Text | Google Scholar

Argaud, J.-P., Bouriquet, B., de Caso, F., Gong, H., Maday, Y., and Mula, O. (2018). Sensor Placement in Nuclear Reactors Based on the Generalized Empirical Interpolation Method. J. Comput. Phys. 363, 354–370. doi:10.1016/j.jcp.2018.02.050

CrossRef Full Text | Google Scholar

Argaud, J. P., Bouriquet, B., Gong, H., Maday, Y., and Mula, O. (2017). Stabilization of (G)EIM in Presence of Measurement Noise: Application to Nuclear Reactor Physics. Cham: Springer International Publishing, 133–145. doi:10.1007/978-3-319-65870-4_8

CrossRef Full Text | Google Scholar

Arnold, N. (1998). Solving Ill-Conditioned and Singular Linear Systems: A Tutorial on Regularization. SIAM Rev. 40 (3), 636–666.

Google Scholar

Balas, K. N. (1995). Sparse Approximate Solutions to Linear Systems. SIAM J. Comput. 24 (2), 227–234.

Google Scholar

Barker, A. T., Rees, T., and Stoll, M. (2016). A Fast Solver for anH1Regularized PDE-Constrained Optimization Problem. Commun. Comput. Phys. 19 (1), 143–167. doi:10.4208/cicp.190914.080415a

CrossRef Full Text | Google Scholar

Benchmark Problem Book (1977). Computational Benchmark Problem Comitee for the Mathematics and Computation Division of the American Nuclear Society. Argonne Code Center: Benchmark Problem Book.

Google Scholar

Benning, M., and Burger, M. (2018). Modern Regularization Methods for Inverse Problems. Acta Numerica 27, 1–111. doi:10.1017/s0962492918000016

CrossRef Full Text | Google Scholar

Bloomfield, P., and Steiger, W. (1980). Least Absolute Deviations Curve-Fitting. SIAM J. Sci. Stat. Comput. 1 (2), 290–301. doi:10.1137/0901019

CrossRef Full Text | Google Scholar

Boyd, S., and Vandenberghe, L. (2004). Convex Optimization. Cambridge: Cambridge University Press.

Google Scholar

Cai, X-C., Liu, S., and Zou, J. (2008). An Overlapping Domain Decomposition Method for Parameter Identification Problems. Domain Decomposition Methods Sci. Eng. XVII 2008, 451–458.

CrossRef Full Text | Google Scholar

Chan, R. H., Chan, T. F., and Wan, W. L. (1997). Multigrid for Differential-Convolution Problems Arising from Image Processing. Proc. Workshop Scientific Comput. 1997, 58–72.

Google Scholar

Chan, T. F., and Tai, X.-C. (2003). Identification of Discontinuous Coefficients in Elliptic Problems Using Total Variation Regularization. SIAM J. Sci. Comput. 25 (3), 881–904. doi:10.1137/s1064827599326020

CrossRef Full Text | Google Scholar

Cimrák, I., and Melicher, V. (2012). Mixed Tikhonov Regularization in Banach Spaces Based on Domain Decomposition. Appl. Maths. Comput. 218 (23), 11583–11596.

Google Scholar

Collis, S. S., Ghayour, K., Heinkenschloss, M., Ulbrich, M., and Ulbrich, S. (2001). Numerical Solution of Optimal Control Problems Governed by the Compressible Navier-Stokes Equations. Int. Ser. Numer. Math. 139, 43–55. doi:10.1007/978-3-0348-8148-7_4

CrossRef Full Text | Google Scholar

De los Reyes, J-C., and Schönlieb, C-B. (2012). Image Denoising: Learning Noise Distribution via Pde-Constrained Optimization. arXiv preprint arXiv:1207.3425.

Google Scholar

Gong, H., Argaud, J.-P., Bouriquet, B., and Maday., Y. (2016). “The Empirical Interpolation Method Applied to the Neutron Diffusion Equations with Parameter Dependence,” in Proceedings of PHYSOR.

Google Scholar

Gong, H., Argaud, J. P., Bouriquet, B., Maday, Y., and Mula, O. (2017). “Monitoring Flux and Power in Nuclear Reactors with Data Assimilation and Reduced Models,” in International Conference on Mathematics and Computational Methods Applied to Nuclear Science and Engineering (M&C 2017), Jeju, Korea.

Google Scholar

Gong, H. (2018). “Data Assimilation with Reduced Basis and Noisy Measurement: Applications to Nuclear Reactor Cores,” (Paris, France: Sorbonne University). PhD thesis.

Google Scholar

Gong, H., Maday, Y., Mula, O., and Tommaso, T. (2019). Pbdw Method for State Estimation: Error Analysis for Noisy Data and Nonlinear Formulation. arXiv preprint arXiv:1906.00810.

Google Scholar

Gong, H., Chen, Z., Maday, Y., and Li, Q. (2021). Optimal and Fast Field Reconstruction with Reduced Basis and Limited Observations: Application to Reactor Core Online Monitoring. Nucl. Eng. Des. 377, 111113. doi:10.1016/j.nucengdes.2021.111113

CrossRef Full Text | Google Scholar

Gong, H., Yu, Y., and Li, Q. (2020). Reactor Power Distribution Detection and Estimation via a Stabilized Gappy Proper Orthogonal Decomposition Method. Nucl. Eng. Des. 370, 110833. doi:10.1016/j.nucengdes.2020.110833

CrossRef Full Text | Google Scholar

Grepl, M. A., Maday, Y., Nguyen, N. C., and Patera, A. T. (2007). Efficient Reduced-Basis Treatment of Nonaffine and Nonlinear Partial Differential Equations. Esaim: M2an 41 (3), 575–605. doi:10.1051/m2an:2007031

CrossRef Full Text | Google Scholar

Haber, E., and Hanson, L. (2007). Model Problems in PDE-Constrained Optimization. Report. Atlanta, GA, USA: Emory University.

Google Scholar

Hecht, F. (2012). New Development in FreeFem++. J. Numer. Math. 20 (3-4), 251–265. doi:10.1515/jnum-2012-0013

CrossRef Full Text | Google Scholar

Heinkenschloss, M. (1998). “Formulation and Analysis of a Sequential Quadratic Programming Method for the Optimal Dirichlet Boundary Control of Navier-Stokes Flow,” in Optimal Control, Theory, Algorithms, and Applications (Alphen aan den Rijn, Netherlands: Kluwer Academic Publishers BV). doi:10.1007/978-1-4757-6095-8_9

CrossRef Full Text | Google Scholar

Herzet, C., Diallo, M., and Héas, P. (2018). An Instance Optimality Property for Approximation Problems with Multiple Approximation Subspaces. hal-01913339.

Google Scholar

Ivanov, A. A. (1976). The Theory of Approximate Methods and Their Applications to the Numerical Solution of Singular Integral Equations, Volume 2. Berlin, Germany: Springer Science & Business Media.

Google Scholar

James Press, S. (1989). Bayesian Statistics: Principles, Models, and Applications, Volume 210. Hoboken, NJ, USA: John Wiley & Sons.

Google Scholar

Keung, Y. L., and Zou, J. (1998). Numerical Identifications of Parameters in Parabolic Systems. Inverse Probl. 14 (1), 83–100. doi:10.1088/0266-5611/14/1/009

CrossRef Full Text | Google Scholar

Li, F., Shen, C., and Li, C. (2010). Multiphase Soft Segmentation with Total Variation and H 1 Regularization. J. Math. Imaging Vis. 37 (2), 98–111. doi:10.1007/s10851-010-0195-5

CrossRef Full Text | Google Scholar

Maday, Y., and Mula, O. (2013). “A Generalized Empirical Interpolation Method: Application of Reduced Basis Techniques to Data Assimilation,” in Analysis and Numerics of Partial Differential Equations (Berlin, Germany: Springer), 221–235. doi:10.1007/978-88-470-2592-9_13

CrossRef Full Text | Google Scholar

Maday, Y., Mula, O., and Turinici, G. (2016). Convergence Analysis of the Generalized Empirical Interpolation Method. SIAM J. Numer. Anal. 54 (3), 1713–1731. doi:10.1137/140978843

CrossRef Full Text | Google Scholar

Maday, Y., Patera, A. T., Penn, J. D., and Yano, M. (2015). A Parameterized-Background Data-Weak Approach to Variational Data Assimilation: Formulation, Analysis, and Application to Acoustics. Int. J. Numer. Meth. Engng 102 (5), 933–965. doi:10.1002/nme.4747

CrossRef Full Text | Google Scholar

Maday, Y., T, A., Penn, J. D., and Yano, M. (2015). PBDW State Estimation: Noisy Observations; Configuration-Adaptive Background Spaces; Physical Interpretations. Esaim: Proc. 50, 144–168. doi:10.1051/proc/201550008

CrossRef Full Text | Google Scholar

Maday, Y., T, A., Penn, J. D., and Yano, M. (2015). Pbdw State Estimation: Noisy Observations; Configuration-Adaptive Background Spaces; Physical Interpretations. Esaim: Proc. 50, 144–168. doi:10.1051/proc/201550008

CrossRef Full Text | Google Scholar

Ng, M. K., Chan, R. H., Chan, T. F., and Yip, A. M. (2000). Cosine Transform Preconditioners for High Resolution Image Reconstruction. Linear Algebra its Appl. 316 (1-3), 89–104. doi:10.1016/s0024-3795(99)00274-8

CrossRef Full Text | Google Scholar

Rudin, L. I., Stanley, O., and Fatemi, E. (1992). Nonlinear Total Variation Based Noise Removal Algorithms. Physica D: Nonlinear Phenomena 60 (1-4), 259–268. doi:10.1016/0167-2789(92)90242-f

CrossRef Full Text | Google Scholar

Srikant, K. I. (0000). Comparison of H1 and Tv De-noising Schemes and Their Implementation.

Google Scholar

Theler, G., Bonetto, F. J., and Clausse, A. (2011). Solution of the 2D IAEA PWR Benchmark with the Neutronic Code Milonga. Actas de la Reunión Anual de la Asociación Argentina de Tecnología Nucl. XXXVIII.

Google Scholar

Van Den Doel, K., Ascher, U., and Haber, E. (2012). The Lost Honour of L2-Based Regularization. Large Scale Inverse Problems, Radon Ser. Comput. Appl. Math. 13, 181–203.

Google Scholar

Vladimir, A. M. (2012). Methods for Solving Incorrectly Posed Problems. Berlin, Germany: Springer Science & Business Media.

Google Scholar

Wachsmuth, D., and Wachsmuth, G. (2011). “Necessary Conditions for Convergence Rates of Regularizations of Optimal Control Problems,” in System Modelling and Optimization (Berlin, Germany: Springer), 145–154.

Google Scholar

Wilson, J., Neal, P., and Guevara Vasquez, F. (2009). “Regularization Methods for Radio Tomographic Imaging,” in 2009 Virginia Tech Symposium on Wireless Personal Communications.

Google Scholar