Operation State Evaluation Method of Smart Distribution Network Based on Free Probability Theory

In view of the current situation that the new generation of smart grids with “double high” characteristics is in urgent need of effective state evaluation methods due to the characteristics of strong volatility and diverse demands, a method of operation state evaluation of smart distribution networks based on free probability theory is proposed, which is combined with high-order moment indexes to describe the operation trajectory of distribution networks from a data-driven perspective. First, the state assessment problem of smart distribution networks is modeled as a binary hypothesis testing problem, and the asymptotic free equation is established based on free probability theory to provide a framework for state assessment of distribution networks. Then, a high-order moment evaluation index is proposed, combined with the sliding time window processing, and the high-order moment sequence was obtained based on the high-dimensional data of the distribution network, which is used to describe the state evolution of the distribution network. Finally, this method is applied to a certain 110-kV distribution network. The analysis of an example shows that the proposed evaluation framework and indicators can effectively reflect the data changes in the distribution network and support the state assessment and evolution analysis of the distribution network.

Introduction

As China proposes “to achieve carbon peak before 2030 and achieve carbon neutrality before 2060,” improving overall energy utilization efficiency and focusing on developing renewable energy has become an inevitable choice. The power system is closely related to the production, transportation, and consumption of renewable energy, which also plays a key role in promoting energy transformation (Zhou et al., 2018). Moreover, the new generation smart grid has the characteristics of “double high”: the high proportion of renewable energy and the high proportion of power electronic equipment. Distributed power supply, charging pile/station, and controllable load, along with other devices, are developing rapidly, and their large-scale access to the distribution network has brought strong uncertainties to the distribution network due to their characteristics of strong intermittent and diverse demands, making the operation mode of the distribution network increasingly complex and changeable.

As a pivotal link of energy, an intelligent distribution network is the key to the smooth operation of “the production-supply-marketing” of electric energy. The ultimate goal of the intelligent distribution network is to build and form a panoramic real-time system covering the distribution network. The basis of supporting the panoramic real-time system of the distribution network is the collection, transmission, and storage of panoramic real-time data of the distribution network and the effective technology for rapid analysis of massive multi-source data (Liu, 2010; Yang et al., 2019; Shen and Raksincharoensak, 2021a; Yang et al., 2021a; Shen and Raksincharoensak, 2021b; Yang et al., 2021b; Zhang et al., 2021). The application of cloud computing, big data, Internet of Things, 5G information communication technology, and artificial intelligence in the power system provides a data basis for the realization of real-time state estimation and situation awareness of the smart distribution network (Yang et al., 2018; Shen et al., 2020a; Ma et al., 2020; Wang et al., 2020). However, the existing distribution network state estimation and situation awareness methods find it difficult to meet the requirements in many aspects of calculation accuracy, calculation speed, and visualization. Thus, it has become a hot topic for experts, scholars, and engineers at home and abroad to construct an effective state estimation and situation awareness system for the intelligent distribution network to support comprehensive, accurate, and real-time control of the operation situation of the distribution network.

In the field of power system state assessment, apart from the specific model method, classical research methods also include the analytic hierarchy process (AHP), the fuzzy comprehensive evaluation method, and principal component analysis (PCA). The literature (Cao et al., 2007) has proposed a comprehensive evaluation method for a new rural low-voltage distribution network based on the AHP and realized practical application. However, this method mainly solved the problems of distribution network construction planning and transformation in the near future and could not evaluate the real-time status. The literature (Sun et al., 2017) combined PCA and system clustering analysis to establish a comprehensive evaluation system of county power grids, which could evaluate the power grid from five aspects of security, economy, reliability, adaptability, and quality, but also could not evaluate the real-time state.

In recent years, data-driven state assessment has also been applied in the power field. The literature (Xu et al., 2016) proposed a correlation analysis method based on random matrix theory (RMT). Combining real-time separation window technology with RMT, the mean spectrum radius (MSR) index was used to evaluate the correlation of distribution network data. In the literature (Xu et al., 2018), the evaluation indexes of the hit ratio and the false alarm rate were proposed, and the vulnerability of the distribution network was evaluated based on RMT. The literature (He et al., 2017a) used the basic breakthrough of high-dimensional statistics in recent years to put forward the research framework of space-time big data of the distribution network based on the random matrix. For power system fault identification, the literature (Xu et al., 2019) proposed a feature self-learning method based on deep learning for high-dimensional space-time fault samples, which had fast calculation speed and strong robustness. However, the method itself had high requirements on source data but low comprehensibility. The literature (Wei et al., 2016) proposed a high-dimensional power data fusion method based on correlation mining in order to solve the key problem of online stability analysis of large power grids. This method mainly solved the problem of data fusion and did not directly evaluate the status of the large power grid.

The key of power system state evaluation based on high-dimensional big data should be the construction of an evaluation framework and an evaluation index system and identification of a power grid or equipment evolution situation. In this study, the free probability theory (FPT) is introduced into the electric power field for the first time in China, providing a complete and clear evaluation framework for the operation status of the smart distribution network, combining with sliding time window processing to solve the high-dimensional source data to obtain the time series of the index. In this study, the high-order moment index is also proposed to analyze the distribution network from the perspective of the state assessment and evolution trend and is applied to the state assessment of the 110-kV distribution network to verify the effectiveness of the proposed method.

Free Probability Theory and Big Data Processing Methods

Introduction to Free Probability Theory

A random matrix is a matrix whose elements are random variables. Through the high-dimensional statistical analysis, important information can be extracted from massive disordered data in a random matrix.

Free probability theory can provide an effective analysis framework for the asymptotic spectrum distribution of high-dimensional random matrices. In the 1980s, Voiculescu proposed FPT to deal with abstract “non-commutative space,” and the random matrix is a special case of “non-commutative space” (Dan, 1986; Voiculescu, 1987). The purpose of FPT is to introduce a concept similar to “independence” in classical probability theory, namely, “freedom,” and make it applicable to non-commutative random variables such as random matrices and extend it to the case of large dimensions, namely, “asymptotic freedom.”

Different from traditional mathematical theory, FPT defines some new operators, including additive-free convolution ⊞ and its inverse operation additive-free deconvolution $\mathrm{\boxminus }$, multiplicative-free convolution ⊠ and its inverse operation multiplicative-free deconvolution $\mathrm{⊡}$, similar to the addition, subtraction, multiplication, and division operations in classical mathematics. Based on the asymptotic spectrum theory of RMT, combining the concept of asymptotic freedom with the above new operators, some difficult problems in classical mathematics can be solved. In traditional mathematics, if and only if two matrices are commutative, the eigenvalues of their sum matrix or product matrix can be obtained from their respective eigenvalues. In FPT, if two random matrices are asymptotically free and their respective asymptotic spectral distributions are known, the asymptotic spectral distributions of their sum matrix or product matrix can be obtained and vice versa. It is worth mentioning that in FPT, the semicircular law is similar to the classical Gaussian distribution, that is, the normalization of the free random matrix (given spectral distribution) and the spectral distribution of matrix converge to the semicircular law; the Marchenk–Pastur law (M-P law) is similar to the classical Poisson distribution, that is, the normalization of those single-rank free random matrices and the spectral distribution of matrices converge to the M–P law (Tulino and Verdu, 2004).

FPT has become a powerful tool to describe the characteristics of wireless communication systems. Spectrum sensing algorithms based on FPT have fast convergence, which are also suitable for the limited number of samples, and have high sensing performance in the case of low signal-to-noise ratio (Tulino and Verdu, 2004). Domestic and foreign scholars have made great academic achievements in this field. This study is the first attempt to apply the FPT to the electric power field, which selects the operation of the smart distribution network as the application scenario and evaluates the operation status of the distribution network based on FPT, providing real-time and efficient support for intelligent operation and maintenance.

Free Probability Theory

Definition 1 (Dan, 1986) The empirical spectrum distribution of an $N\times N$ random matrix $B_N$ is defined as follows:

${\mu }_{B_N}\left(x\right)=\frac{1}{N}{\displaystyle \sum _{i=1}^{N}I\left({\lambda }_i\left(B_N\right)\le x\right)},(1)$

where ${\lambda }_i\left(B_N\right),i=\mathrm{1,2},\dots ,N$ are the eigenvalues of $B_N$, $I(·)$ is the indicator function.In RMT, the asymptotic spectral distribution (ASD) is the empirical spectral distribution of $B_N$ when $N\to \infty$, which is represented by the symbol ${\mu }_B$, and can be expressed uniquely by the following moment:

$m_k=\underset{N\to \infty }{\lim }\frac{1}{N}E\left\{\mathit{tr}\left(B_N^k\right)\right\}={\displaystyle \int x^{k}d{\mu }_B\left(x\right)},(2)$

where $\mathrm{tr}(·)$ represents the rank of the matrix and k represents the order of moments. In mathematics and statistics, moments can represent the distribution and morphological characteristics of variables. The specific moment algorithm of the method proposed in this study will be introduced in detail in Calculation of High-Order Moment Index section.As mentioned above, Voiculescu proposed FPT in order to introduce the concept of “freedom” and summarize the law applicable to non-commutative variables such as random matrices, which is similar to the law in classical probability theory.Random matrices are just one kind of non-commutative variable, and non-commutative variables are all elements of “non-commutative probability space.” The concept of a non-commutative probability space is as follows.

Definition 2 (Couillet and Debbah, 2011) Let B be a non-commutative algebraic system with unit element I; if $\varphi$ is a linear function on B and meet $\varphi \left(I\right)=1$, then the order pair $\left(B,\varphi \right)$ is called a non-commutative probability space.For random matrices, the identity element I is the identity matrix $I_N$, and $\varphi$ is defined as follows:

$\varphi \left(C\right)=\frac{1}{N}{\displaystyle \sum _{i=1}^{N}E\left\{C_{\mathit{i}\mathit{i}}\right\}=}\frac{1}{N}E\left\{\mathit{tr}\left(C\right)\right\},(3)$

where $C\in B$, $C_{ii}$ represents the ith row and the ith column element of C. It can be seen from Eq. 3 that $\varphi$ is the function of solving the moment. This kind of non-commutative probability space meets trace lemma, that is, ϕ(ab) = ϕ(ba).

Definition 3 (Couillet and Debbah, 2011) Let $\left(B,\varphi \right)$ be a non-commutative probability space, and for all n-dimensional sequences $\left(b_1{b}_2\dots b_n\right)$, if $\varphi \left(b_1{b}_2\dots b_n\right)=0$ satisfies the following conditions:

1) $b_j\in B_{i_j}$, where $i_j\le K$

2) i₁≠i₂,i₂≠i₃, … ,i_n-1≠i_n

3) for all $j\in \left\{1,\dots n\right\}$, ϕ(b_j) = 0

Then, a family of the subalgebra systems of B $\left\{B_1,\dots ,B_K\right\}$ is free.Obviously, if $\left\{\left\{b_1\right\},\dots ,\left\{b_n\right\}\right\}$ is free (each subalgebra system consists of only one of their elements), then random variables $\left\{b_1,\dots ,b_n\right\}$ are free.Furthermore, let us extend the concept of “freedom” to “asymptotic freedom.”

Definition 4 (Couillet and Debbah, 2011) If the following two conditions are met

1) for all k∈{1,…,K}, X_N,K has an asymptotic spectral distribution;

2) for all {i₁,…i_n} $\subset$ {1,…,K}, i₁≠i₂,i₂≠i₃, … ,i_n-1≠i_n and family of unary polynomials {P₁,…,P_n},

$\underset{N\to \infty }{\lim }\varphi \left\{P_j\left(X_{N,i_j}\right)\right\}=0,j\in \left\{1,\mathrm{...},n\right\}(4)$

and

$\underset{N\to \infty }{\lim }\varphi \left\{{\displaystyle \prod _{j=1}^n{P}_j\left(X_{N,i_j}\right)}\right\}=0.(5)$

Then the $N\times N$ random matrix family $\left\{X_{N,1},\dots ,X_{N,K}\right\}$ of non-commutative probability spaces $\left(B_N,\varphi \right)$ is asymptotically free.Based on the above definition of asymptotic freedom, combined with new operators such as additive-free convolution, the following illustration is made. If two random matrices A_N∈ $\mathrm{ℂ}$ ^{N × N} and B_N∈ $\mathrm{ℂ}$ ^{N × N} are asymptotically free, with their asymptotic spectral distributions denoted as μ_A and μ_B, respectively, and A_N + B_N is known to have asymptotic spectral distribution μ_A+B, then

${\mu }_{A+B}={\mu }_A\mathrm{⊞}{\mu }_B,(6)$

where $\mathrm{⊞}$ is called additive-free convolution, namely, μ_A+B is the additive-free convolution of μ_A and μ_B.Furthermore, $\mathrm{\boxminus }$ is defined as additive-free deconvolution, that is, if ${\mu }_{\mathrm{C}}={\mu }_A\mathrm{⊞}{\mu }_B$, then ${\mu }_A={\mu }_C\mathrm{\boxminus }{\mu }_B$, and ${\mu }_B={\mu }_C\mathrm{\boxminus }{\mu }_A$. So additive-free convolution and additive-free deconvolution are inverse operations of each other.Similarly, if A_NB_N has an asymptotic spectral distribution μ_AB, then

${\mu }_{\mathrm{AB}}={\mu }_A\mathrm{⊠}{\mu }_B,(7)$

where $\mathrm{⊠}$ is called multiplicative-free convolution, namely, μ_AB is the multiplicative-free convolution of μ_A and μ_B.Furthermore, $\mathrm{⊡}$ is defined as additive-free deconvolution, that is, if ${\mu }_C={\mu }_A\mathrm{⊠}{\mu }_B$, then ${\mu }_A={\mu }_C\mathrm{⊡}{\mu }_B$, and ${\mu }_B={\mu }_C\mathrm{⊡}{\mu }_A$. So multiplicative-free convolution and multiplicative-free deconvolution are inverse operations of each other. Both additive- and multiplicative-free convolution are commutative, namely, ${\mu }_A\mathrm{⊞}{\mu }_B={\mu }_B\mathrm{⊞}{\mu }_A$, ${\mu }_A\mathrm{⊠}{\mu }_B={\mu }_B\mathrm{⊠}{\mu }_A$. In this way, non-commutative variables (such as random matrices) can be exchanged in the operation.

Distribution Network State Estimation Method Based on FPT

Data Pre-Processing

Supervisory Control and Data Acquisition (SCADA) is widely applied in the power system and collects the branch power, branch current amplitude, and node voltage amplitude in the system with high maturity, mainly through the remote terminal unit (RTU) and the feeder terminal unit (FTU) (Yang et al., 2020a; Shen et al., 2020b; Zhu et al., 2020; Li et al., 2021a; Shen et al., 2021a; Shen et al., 2021b; Qi et al., 2021; Xiang et al., 2021). The data collected by SCADA has the characteristics of mass and high dimension, so a high-dimension random matrix can be constructed according to the collected data. Combined with the sliding time window processing, the data characteristics of the distribution network can be analyzed based on FPT, and the distribution network state before and after can be compared in time to further realize the evolution of the distribution network operation state.

Assume that i nodes in the distribution network are equipped with measuring devices, and the sampling interval is 0.01 s. At the sampling time t_n, i nodes each generate a state data (which can be voltage, current, and power angle), and the state data of all nodes at this time constitute a column vector x (t_n), as shown in the following formula:

$x\left(t_n\right)={\left[x_{1t_n},x_{2t_n},\mathrm{...},x_{i{t}_n}\right]}^T.(8)$

When there are a total of j sampling moments, the j column vectors are arranged to form a high-dimensional random matrix X_i×j, as shown below:

$X_{i\times j}=\left[\begin{array}{cccc}{x}_{11}& x_{12}& \mathrm{...}& x_{1j}\\ x_{21}& x_{22}& \mathrm{...}& x_{2j}\\ ⋮& \mathrm{...}& \mathrm{...}& \mathrm{...}\\ x_{i1}& x_{i2}& \mathrm{...}& x_{ij}\end{array}\right],(9)$

In the above formula, each row of X_i×j is the state data of the same node at different times, and each column is the state data of different nodes at the same time.

The normalization process is carried out according to Eq. 10 below, and the normalized matrix $\tilde{X}$ with mean value E = 0 and variance σ² = 1 is obtained as follows:

${\tilde{X}}_l=\left(X_l-E\left(X_l\right)\right)/{\sigma }^2\left(X_l\right),l=\mathrm{1,2},\mathrm{...},i,(10)$

where X_l is the lth row of X.

In statistical analysis of high-dimensional data, when the amount of data is large enough, the data as a whole will show certain random statistical characteristics after corresponding processing, such as the single ring theorem and the M–P law (Ling et al., 2018; Jain et al., 2019; Deepa et al., 2020; Xiong et al., 2020; Yang et al., 2020b; Li et al., 2021b; Li et al., 2021c; Yang et al., 2021c; Li et al., 2021d; Ye et al., 2021; Dong and Li, 2021; Liu et al., 2021; Mousavizadeh et al., 2021; Ouyang and Xu, 2021; Zhu et al., 2021). In the statistical analysis of high-dimensional power data, the corresponding linear eigenvalue statistics (LES) are constructed, such as MSR, high-order moment, etc., which can effectively represent the state of the distribution network. When there are only random fluctuations and measurement errors in the measured data, the data present a random statistical characteristic as a whole. If abnormal events occur in the power system, the original stable operation state of the system will be broken, and the measured data will change accordingly.

State Assessment Model Construction

The problem of distribution network operation state assessment is understood as a binary hypothesis testing problem, as follows:

$y\left(n\right)=\{\begin{array}{cc}v\left(n\right),& H_0\\ x\left(n\right)+v\left(n\right),& H_1\end{array},(11)$

where $y\left(n\right)$ represents the received sampled signal, $x\left(n\right)$ represents the event signal component, and $v\left(n\right)$ represents the noise component.

The above binary hypothesis testing problem is further explained. $H_0$ means that no abnormal events occur, and the received sampled signal only has randomly distributed noise components. $H_1$ indicates that abnormal events occur, event signals exist in the sampled signals, and the original stable operation state of the system is broken.

In this study, the basic idea of the distribution network state estimation method based on FPT is to estimate the asymptotic spectrum distribution of the event signal component $x\left(n\right)$ by establishing and solving the asymptotic free equation and then calculate the high-order moment index $m_i$ (i = 1, 2, … , n) of the event signal component $x\left(n\right)$. Thus, the high-order moment is the detection statistic of the algorithm.

Assuming that N received sampled signals y (1), y (2), …, y(N) are used for distribution network state estimation and each sampled signal is composed of M signal components, the sample covariance matrix of received sampled signals is as follows:

${\widehat{\sum }}_y=\frac{1}{N}{\displaystyle \sum _{n=1}^{N}y\left(n\right)y{\left(n\right)}^H}.(12)$

The sample covariance matrix of signal component $x\left(n\right)$ is as follows:

${\displaystyle \sum _x^{\wedge }=\frac{1}{N}{\displaystyle \sum _{n=1}^{N}x\left(n\right)x{\left(n\right)}^H}}.(13)$

In FPT, for the signal–noise model, the asymptotic spectral distributions of the above two sample covariance matrices ${\widehat{\Sigma }}_y$ and ${\widehat{\Sigma }}_x$ satisfy the following asymptotic free equation (Ryan and Debbah, 2007):

${\mu }_{{\widehat{\sum }}_y}\mathrm{⊡}{\mu }_c=\left({\mu }_{{\widehat{\sum }}_x}\mathrm{⊡}{\mu }_c\right)\mathrm{⊞}{\mu }_{{\sigma }^{2}I},(14)$

where $c=M/N$, and μ_σ²_I represents a probability distribution that has value only at point σ².

After rigorous mathematical derivation, the spectral distribution between the sample covariance matrix and the statistical covariance matrix of the event signal components can be obtained to satisfy the following relation:

${\mu }_{{\widehat{\sum }}_x}={\mu }_{{\sum }_x}\mathrm{⊠}{\mu }_{\frac{M}{N}}.(15)$

Substituted into Eq. 10, the asymptotic free equation becomes the following:

${\mu }_{{\widehat{\sum }}_y}\mathrm{⊡}{\mu }_c=\left({\mu }_{{\sum }_x}\mathrm{⊠}{\mu }_{\frac{M}{N}}\mathrm{⊡}{\mu }_c\right)\mathrm{⊞}{\mu }_{{\sigma }^{2}I}.(16)$

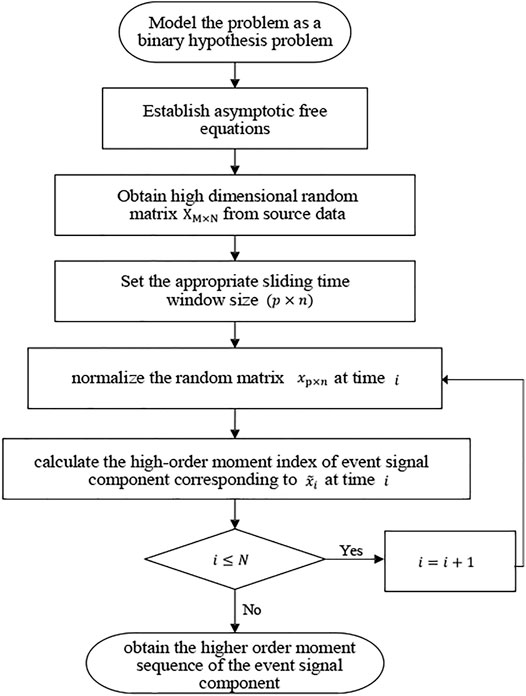
The asymptotic spectrum distribution of event signal component $x\left(n\right)$ can be obtained by solving the asymptotic free equation as follows:

${\mu }_{{\widehat{\sum }}_x}=\left[\left({\mu }_{{\widehat{\sum }}_y}\mathrm{⊡}{\mu }_{\frac{M}{N}}\right)\mathrm{\boxminus }{\mu }_{{\sigma }^{2}I}\right]\mathrm{⊠}{\mu }_c\mathrm{⊡}{\mu }_{\frac{M}{N}}.(17)$

Based on the established asymptotic free equation and the sliding time window method, the high-order moment index of the continuous time window matrix is obtained to observe the state of the distribution network.

The state assessment process of the distribution network is shown in Figure 1 below.

FIGURE 1

FIGURE 1. Distribution network status evaluation process based on FPT.

Calculation of High-Order Moment Index

From the above analysis, it can be seen that the calculation process of solving the high-order moment index is based on the asymptotic free equation, which involves new operators defined by FPT, namely, additive-free convolution and its inverse operation and multiplicative-free convolution and its inverse operation. It is a relatively simple calculation method to calculate additive-free convolution through the moment-cumulant formula (Ryan and Debbah, 2007).

1) Additive-free convolution

The moment-cumulant formula describes the relationship between the moments of a certain measure and the related R transformation. The R transformation of a probability distribution μ is defined as follows:

$R_{\mu }={\displaystyle \sum _n{\alpha }_n^{\mu }}{z}^n,(18)$

where ${\alpha }_n^{\mu }$ is the nth order cumulant of μ. Based on R transformation, additive-free convolution can be realized, as shown in the following formula:

$R_{{\mu }_A\mathrm{⊞}{\mu }_B}=R_{{\mu }_A}\left(z\right)+R_{{\mu }_B}\left(z\right),(19)$

which is equivalent to that the cumulative measure has additivity under additive-free convolution. That is,

${\alpha }_n^{{\mu }_A\mathrm{⊞}{\mu }_B}={\alpha }_n^{{\mu }_A}+{\alpha }_n^{{\mu }_A}.(20)$

The moment-cumulant of the distribution μ is given as follows:

$m_k^{\mu }={\displaystyle \sum _{n\le k}{\alpha }_n^{\mu }}\mathit{coe}{\mathrm{f}}_{k-n}({\left(1+m_1^{\mu }z+m_2^{\mu }{z}^2+\mathrm{...}\right)}^n),(21)$

where $coe{f}_n(·)$ is the coefficient of $z^n$.

The bidirectional conversion between the cumulant sequence and the moment sequence can be completed by using the above formula, that is, the first n-order cumulants can be obtained from the first n-order moments and vice versa.

This article gives a brief description of the use of the moment-cumulant formula in free convolution calculation, and the specific process is described as follows:

1) Taking the sequence of moments as input, vector f=(1,m₁,…,m_n) with length n+1 is formed, where m₁ is the first-order moment, and m_n is the nth-order moment. Then n vectors are obtained by convolution calculation according to the following formula:

$F_1=f,F_2=f\ast f,\mathrm{...},F_n={\ast }_{n}f,$

where * stands for the convolution operation, and *n stands for n-fold classical convolution with itself. With the accumulation of the convolution operation, the length of vector F increases gradually. Since only the first n+1 elements of M₁,…,M_n are used in subsequent operations, the length of vector F is uniformly trimmed to n+1 after the convolution operation in order to simplify calculation and reduce the storage space of the operation.

2) Calculate each cumulant iteratively. After the cumulants α₁, …, α_n-1 are obtained by solving the moment-cumulant formula shown in Eq. 21 for n-1 times, α_n can be obtained by solving the equation for the nth time. It should be added that the relation between each F vector in Step 1) and Eq. 21 can be expressed by the following:

$\mathit{coe}{\mathrm{f}}_{n-k}({\left(1+{\mu }_{1}z+{\mu }_2{z}^2+\mathrm{...}\right)}^k)=F_k\left(n-k\right).(22)$

This equation can also be understood as writing the coefficients in the moment-cumulant formula as k-fold convolution. Based on this formula, it can be known that the kth cumulant is equivalent to the following expression:

${\alpha }_k=\frac{M_1\left(n+1\right)-{\displaystyle {\sum }_{1\le r\le k-1}{\alpha }_r}{M}_r\left(k-r\right)}{M_k\left(0\right)}.(23)$

Thus, the additive-free convolution and additive-free deconvolution can be easily calculated by means of the moment-cumulant formula.

2) Multiplicative-free convolution

Computation involving multiplicative-free convolution and its inverse operation requires the transformation of boxed convolution, denoted as ⧆. Boxed convolution can be understood as a convolution operation acting on a power series polynomial, which involves the concept of non-cross partition not being repeated. Among the various forms of power series, the commonly used power series is Zeta-series, defined as $Zeta\left(z\right)={\displaystyle \sum }_i{z}^i$. The sequence of moments under the deterministic measure is defined as $M\left(\mu \right)\left(z\right)={\displaystyle \sum }_{k=1}^{\infty }{m}_k{z}^k$. The literature has proven that the above R transformation is equivalent to the following equation:

$M\left(\mu \right)=R\left(\mu \right)⧆Zeta.(24)$

It can be proven that the boxed convolution acting on the power series polynomial is the combination of multiplicative-free convolution on each measure, where the boxed convolution of power series $c^{n-1}Zeta$ represents the convolution of measure ${\mu }_c$, as shown in the following formula:

$M_{\mu \mathrm{⊠}{\mu }_c}=M_{\mu }⧆\left(c^{n-1}Zeta\right)(25)$

also written as follows:

$c{M}_{\mu \mathrm{⊠}{\mu }_c}=\left(c{M}_{\mu }\right)⧆Zeta.(26)$

It can be found that, in fact, the above equation is the moment-cumulant formula, which is equivalent to Eq. 21. Thus, in the calculation process, the cumulant is replaced by the coefficient of $c{M}_{\mu }$, and the moment is replaced by $c{M}_{\mu \times {\mu }_c}$. It is concluded that the calculation process of additive-free convolution is also applicable to multiplicative-free convolution operation.

Case Studies

Data Sources

Based on Matlab, this study uses the voltage data of 40 buses under the maximum operation mode of the 110-kV distribution network in a certain province in the summer of 2020 to conduct simulation verification. The total duration of voltage data is 5s, the number of each sampled signal components is $M=40$, and the sampling interval is $\Delta t=0.01s$, so the high-dimensional random matrix $X_{40\times 500}$ of source data can be obtained. The specific case description is shown in Table 1. In the following two cases, the high-order moments of the event signal component are obtained based on FPT, and the operation status of the distribution network is analyzed and compared with the classical PCA method (Rong et al., 2019) and the MSR indicator (Zheng et al., 2020) in the commonly used random matrix theory to further verify the effectiveness of the indicators proposed in this study.

TABLE 1

TABLE 1. Case scenario description.

Analysis of Cases

In this study, the high-dimensional random matrix of source data is $X_{40\times 500}$, that is, M = 40 and N = 500, and the sliding time window size is set as $40\times 60$, that is, $p=40,n=60$, so $c=p/n\in \left(\mathrm{0,1}\right)$. The index selected in the method based on FPT is the third-order moment $m_3$ of the event signal component $x\left(n\right)$. The classical PCA assessment indexes for abnormal state detection are $T^2$ statistics and SPE statistics. The control limit of $T^2$ statistics is $T_{\alpha }$, and $T^2<T_{\alpha }$ should be satisfied if the system runs normally; otherwise, it can be considered abnormal. The control limit of SPE statistics is $Q_{\alpha }$. If the system is running properly, it should meet the $\text{SPE}<Q_{\alpha }$ requirement; otherwise, it can be considered abnormal. In the evaluation of the MSR index based on RMT, and the calculated inner ring radius is 0.52. If MSR falls below the threshold of the inner ring radius, it indicates the occurrence of abnormal events. As the width of the sliding time window is 60, all moments and MSR indicators in the following figures are 0 before the 60th sampling moment, as hereby stated.

In addition, in the power system, the voltage of each user must be kept at the rated value or within the allowable range of voltage offset. Currently, the percentage of voltage offset at the power supply end of 35 kV and above is defined as ±5% in China.

1) Case 1

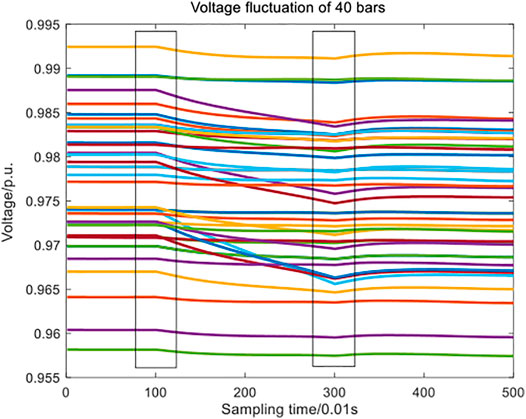
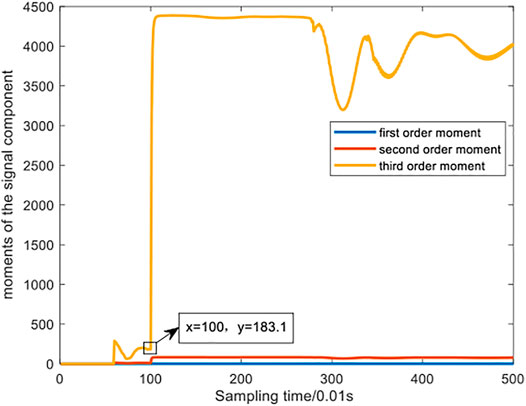
By observing the voltage fluctuation of the 40 buses in Figure 2 below, it can be seen intuitively that the voltage unit values of the 40 buses are initially distributed between (0.955,0.995), which are in a normal level, and obvious drops occur at about the 100th sampling time point, that is, the bus voltage drops at about 1s. Subsequently, the buses’ voltage stops falling around the 300th sampling time point, that is, the bus voltage gradually stabilized after 3s and successfully reached a new stable state.

FIGURE 2

FIGURE 2. Original voltage data of 40 buses in case 1.

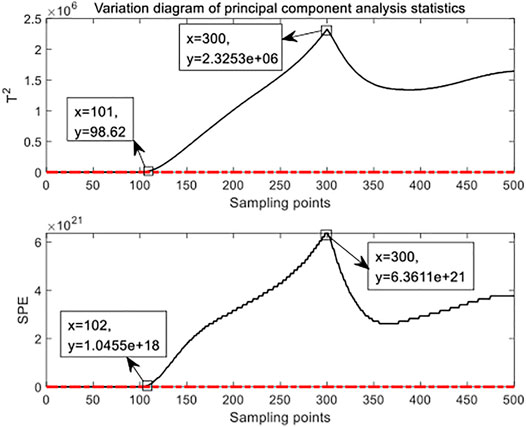
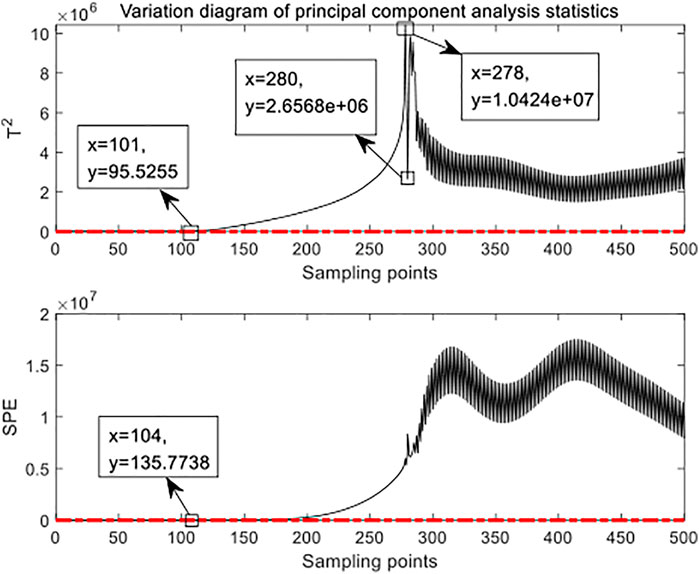
In Figure 3, the red dotted lines are control limits $T_{\alpha }$ and $Q_{\alpha }$, which is the same in Figure 7. Observing various indicators in the figures of case 1 (i.e. Figures 3, 4, Figure 5), the $T^2$ index in the PCA method changes dramatically at the 101th sampling point and exceeds $T_{\alpha }$, indicating abnormal status. It climbs to the 300th sampling point and then begins to fall but fails to return to the control limit level, indicating that the power grid tried to re-establish a new balance after the third second, but it does not return to the normal state (not in line with the actual situation). Here, the SPE indicator is similar to the $T^2$ indicator. The MSR index begins to fall significantly at the 100th sampling point and falls below the inner ring radius at the 150th sampling point, indicating that the power grid is in an abnormal state (also not in line with the actual situation) and then gradually recovers to above the inner ring radius at the 200th sampling point. In the moment index of each order, obviously, the first-order moment and the second-order moment are not sensitive to voltage changes, while the third-order moment is more sensitive to power grid fluctuations. Therefore, the third-order moment is selected as the final index in case 1, and the case of case 2 is the same as that of case 1. The third-order moment $m_3$ changes around the value of 1.5 under normal circumstances and changes dramatically at the 100th sampling point, almost climbing in a straight line. The value of $m_3$ reaches at 1900, which means that the event signal shows up during 1–1.5 s; so $H_1$ is true. After the 150th sampling point, $m_3$ begins to decline and shows a downward trend, indicating that the power grid tried to establish a new equilibrium state in this period. Then $m_3$ fluctuates at the 300th sampling point and recovers to the normal level after the 400th sampling point, representing that the power grid successfully establishes a new stable state, which means that $H_0$ is true. Based on the above analysis, in this case, the third-order moment index $m_3$ can reflect the original data more truly.

2) Case 2

FIGURE 3

FIGURE 3. ${\mathit{T}}^2$ and SPE indices of case 1.

FIGURE 4

FIGURE 4. MSR index of case 1.

FIGURE 5

FIGURE 5. Moments of the signal component in case 1.

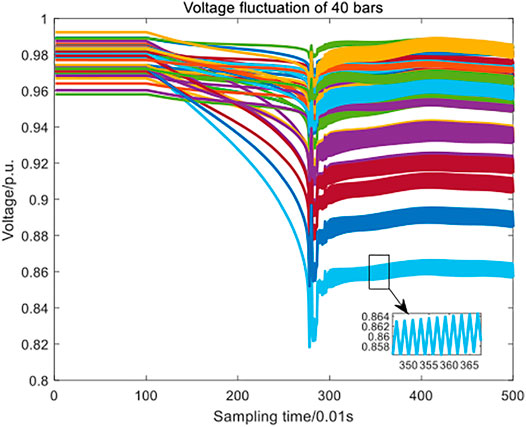
By observing the voltage fluctuation of the 40 buses in Figure 6, it can be seen intuitively that the voltage unit values of the 40 buses are initially distributed between (0.95,1), which are in a normal level. After the 100th sampling point, as the impact load continues to increase, the voltage level drops sharply, and the minimum voltage unit value is as low as 0.82, which is at the abnormal operation level. After the 300th sampling point, the load level remains 3 times that of the original load, and the power grid tries to re-establish a stable state. It can be speculated that due to the limited capacity of the system, the new equilibrium state is not reached, and the voltage level is in continuous oscillation during 3–5 s.

FIGURE 6

FIGURE 6. Original voltage data of 40 buses in case 2.

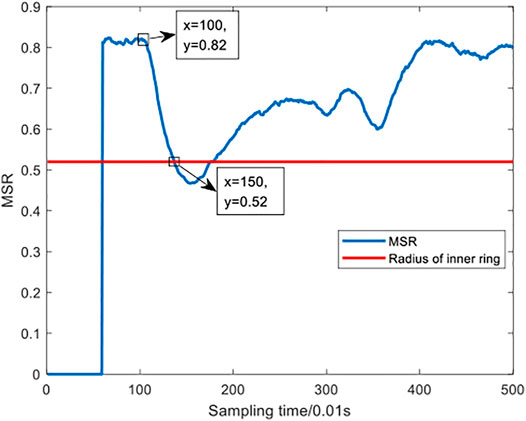
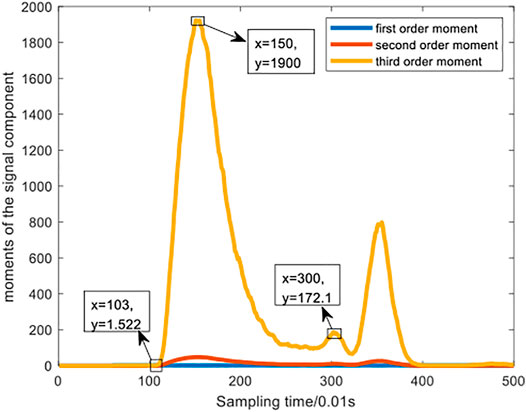
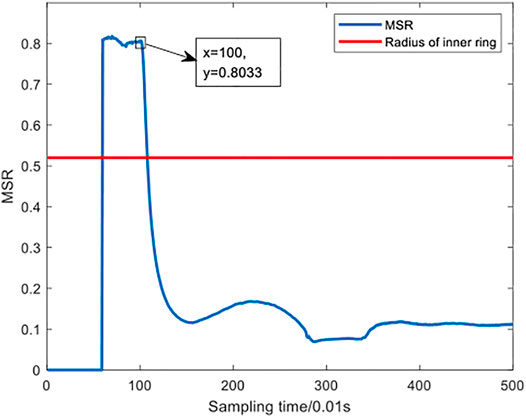
By observing various indicators in the figures of case 2 (i.e. Figures 7, 8, 9), the ${\mathit{T}}^2$ index in PCA begins to climb gradually at the 101th sampling point, exceeding $T_{\alpha }$ and indicating abnormal status. The violent fluctuation occurs at the 280th sampling point, showing that the power grid is in an extremely unstable state. Then the ${\mathit{T}}^2$ index begins to fall and enters an oscillation state without returning to the control limit level, representing that the power grid tried to re-establish a new balance at about 3 s but failed to restore the normal state. Here, the trend of the SPE index and ${\mathit{T}}^2$ index is slightly different after the 280th sampling point, but generally consistent, indicating that the power grid fails to return to the normal level and is in oscillation. The MSR index begins to decline at the 100th sampling point and then falls below the inner ring radius and remains below the threshold of the inner ring radius, failing to return to normal. The third-order moment $m_3$ changes dramatically at the 100th sampling point and remains at a high level, which means $H_0$ is true, and fluctuates near the 300th sampling point and then remains at a high level at about 4,000, indicating that the power grid tried to establish a new equilibrium in this period but failed, that is, $H_1$ is true.

FIGURE 7

FIGURE 7. ${\mathit{T}}^2$ and SPE indices of case 2.

FIGURE 8

FIGURE 8. MSR index of case 2.

FIGURE 9

FIGURE 9. Moments of the signal component in case 2.

Through the analysis of the above two cases, it can be found that the performance of the third-order moment index is better than that of the $T^2$ index, SPE index, and MSR index in the small disturbance monitoring of the power grid. When detecting abnormal events, all four indexes can reflect the operation state of the power grid effectively.

Conclusion

This study proposes a state evaluation method based on FPT, aiming to evaluate the operation of the distribution network according to high-order moment indexes. Through simulation cases, the following conclusions are obtained:

1) Based on the high-dimensional measurement data of the distribution network, the relevant asymptotic free equation is established, and the high-order moment index is proposed to evaluate the distribution network state, which verifies the feasibility of the proposed evaluation framework based on FPT, applied to the distribution network state analysis.

2) The free probability theory itself tends to be abstract. When calculating the high-order moment index, the moment-cumulant formula can effectively simplify the calculation process of the high-order moment. In addition, the evaluation index is the high-order moment. Theoretically, the index system can be extended to N-order moments, and the selection of specific indicators should be determined based on the actual application scenarios.

3) The proposed high-order moment index is compared with the classical $T^2$ index, SPE index, and the commonly used MSR index. The simulation results show that the above indexes can accurately detect the occurrence of abnormal events in the distribution network, and the high-order moment index performs better than other indexes mentioned in this article when only a small disturbance occurs in the distribution network.

In this study, the free probability theory is applied to the electric power field for the first time, and the proposed evaluation framework can be extended to high-dimensional electric power data processing, such as power dispatching, operation and maintenance control, new energy consumption, reliability evaluation, and other scenarios to provide decision support. Based on the above analysis, the follow-up work of this study will focus on three aspects: the application of multiple power scenarios, internal performance comparison of high-order moment indicators, and further expansion as well as optimization of the evaluation index system (Xue and Lai, 2016, He et al., 2016, Liu et al., 2016, Wang et al., 2019, Chen et al., 2017, He et al., 2017b, Zhang et al., 2018, Xue, 2015).

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

JZ selected and studied the sources, designed the structure of the manuscript, and wrote the first draft of the manuscript. BW and HW contributed with supervision over the study of the literature and the writing of the manuscript. All authors contributed to manuscript revision and read and approved the submitted version.

Funding

This research is supported by a project from the National Natural Science Foundation of China (51907096).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Cao, Y., Meng, H., Zhao, L., Wang, T., and Chen, S. (2007). Comprehensive Evaluation Method of New Rural Low-Voltage Distribution Network Based on ANALYTIC Hierarchy Process. Power Grid Tech. (08), 68–72. doi:10.3389/fenrg.2021.800906

CrossRef Full Text | Google Scholar

Chen, P., Tao, S., and Xiao, X. (2017). Network Model for Correlation Analysis of Short-Term Electricity Consumption Behavior. Automation Electric Power Syst. 41 (03), 61–69. doi:10.7500/AEPS20160127014

CrossRef Full Text | Google Scholar

Couillet, R., and Debbah, M. (2011). Random Matrix Methods for Wireless Communications. London: Cambridge University Press.

Google Scholar

Dan, V. (1986). Addition of Certain Non-commuting Random Variables. J. Funct. Anal. 66 (3), 323–346. doi:10.1016/0022-1236(86)90062-5

CrossRef Full Text | Google Scholar

Deepa, S. K., Savier, J. S., and Biju, S. S. (2020). Micro-synchrophasor Based Special protection Scheme for Distribution System Automation in a Smart City. Prot. Control. Mod. Power Syst. 5 (1), 97–110. doi:10.1186/s41601-020-0153-1

CrossRef Full Text | Google Scholar

Dong, W., and Li, S. (2021). Reliability Sensitivity of Wind Power System Considering Correlation of Forecast Errors Based on Multivariate NSTPNT Method. Prot. Control. Mod. Power Syst. 6 (1), 136–146. doi:10.1186/s41601-021-00192-0

CrossRef Full Text | Google Scholar

He, X., Ai, Q., Qiu, C., Zang, J., and Xu, X. (2017). Application of Stochastic Matrix Theory in Power System Cognition. Power grid Technol. 41 (04), 1165–1173. doi:10.13335/j.1000-3673.pst.2016.1956

CrossRef Full Text | Google Scholar

He, X., Qiu, C., Ai, Q., Chu, L., and Ling, Z. (2017). Research on Spatial and Temporal Big Data of Distribution Network Based on Random Matrix Theory. Power supply and consumption 34 (06), 14–19+7. doi:10.19421/j.cnki.1006-6357.2017.06.003

CrossRef Full Text | Google Scholar

He, X., Qiu, R. C., Ai, Q., Chu, L., Xu, X., and Ling, Z. (2016). Designing for Situation Awareness of Future Power Grids: An Indicator System Based on Linear Eigenvalue Statistics of Large Random Matrices. IEEE Access 4, 3557–3568. doi:10.1109/access.2016.2581838

CrossRef Full Text | Google Scholar

Jain, T., Ghosh, D., and Mohanta, D. K. (2019). Augmentation of Situational Awareness by Fault Passage Indicators in Distribution Network Incorporating Network Reconfiguration. Prot. Control. Mod. Power Syst. 4 (4), 323–336. doi:10.1186/s41601-019-0140-6

CrossRef Full Text | Google Scholar

Li, H., Deng, J., Feng, P., Pu, C., Arachchige, D. D., and Cheng, Q. (2021). Short-term Nacelle Orientation Forecasting Using Bilinear Transformation and ICEEMDAN Framework. Front. Energ. Res. 9, 697. doi:10.3389/fenrg.2021.780928

CrossRef Full Text | Google Scholar

Li, H., Deng, J., Yuan, S., Feng, P., and Arachchige, D. D. Monitoring and Identifying Wind Turbine Generator Bearing Faults Using Deep Belief Network and EWMA Control Charts. Front. Energ. Res. 9, 770. doi:10.3389/fenrg.2021.799039

CrossRef Full Text | Google Scholar

Li, Z., Jiang, W., Abu-Siada, A., Li, Z., Xu, Y., and Liu, S. (2021). Research on a Composite Voltage and Current Measurement Device for HVDC Networks. IEEE Trans. Ind. Electron. 68 (9), 8930–8941. doi:10.1109/tie.2020.3013772

CrossRef Full Text | Google Scholar

Li, Z., Wan, J., Wang, P., Weng, H., and Li, Z. (2021). A Novel Fault Section Locating Method Based on Distance Matching Degree in Distribution Network. Prot. Control. Mod. Power Syst. 6 (2), 253–263. doi:10.1186/s41601-021-00194-y

CrossRef Full Text | Google Scholar

Ling, Z., Qiu, R., and He, X. (2018). A New Approach of Exploiting Self-Adjoint Matrix Polynomials of Large Random Matrices for Anomaly Detection and Fault Location. arXiv:1802.03503v1.

Google Scholar

Liu, W., Zhang, D., and Wang, X. (2016). Power System Transient Stability Analysis Based on Random Matrix Theory. Proc. CSEE 36 (18), 4854–4864. doi:10.13334/j.0258-8013.pcsee.160779

CrossRef Full Text | Google Scholar

Liu, Y., Chen, S., Cong, Z., Jiang, Q., Yan, Y., and Jiang, X. (2021). Key Technology and Application Prospect of Digital Twin in Power Equipment Industry. High Voltage Tech. 47 (05), 1539–1554. doi:10.13336/j.1003-6520.hve.20210194

CrossRef Full Text | Google Scholar

Liu, Z. (2010). Modern Signal Processing. Beijing: China Electric Power Press.

Google Scholar

Ma, F., Wang, B., and Dong, X. (2020). Power Vision Edge Intelligence: Power Depth Vision Acceleration Technology Driven by Edge Computing. Power Syst. Tech. 44 (06), 2020–2029. doi:10.13335/j.1000-3673.pst.2019.2382

CrossRef Full Text | Google Scholar

Mousavizadeh, S., Alahyari, A., Ghodsinya, S. R. M., and Haghifam, M. (2021). Incorporating Microgrids Coupling with Utilization of Flexible Switching to Enhance Self-Healing Ability of Electric Distribution Systems. Prot. Control. Mod. Power Syst. 6 (3), 300–310. doi:10.1186/s41601-021-00197-9

CrossRef Full Text | Google Scholar

Ouyang, S., and Xu, W. (2021). Power Grid Fault Identification and Cause Identification Method Considering External Environmental Information. High Voltage Tech. 47 (03), 1075–1082. doi:10.13336/j.1003-6520.hve.20200106

CrossRef Full Text | Google Scholar

Qi, B., Zhang, P., Zhang, S., Zhao, L., Wang, H., Huang, M., et al. (2021). Application Status and Development Prospect of Digital Twin Technology in State Evaluation of Power Transmission and Transformation Equipment. High Voltage Tech. 47 (05), 1522–1538. doi:10.13336/j.1003-6520.hve.20210093

CrossRef Full Text | Google Scholar

Rong, Z., Qi, B., Zhang, P., Li, C., Yang, Y., Gu, C., et al. (2019). Fast Identification of Abnormal State of Oil Chromatography Online Monitoring Device Based on Nuclear Principal Component Analysis. High voltage Technol. 45 (10), 3308–3316. doi:10.13336/j.1003-6520.hve.20190624006

CrossRef Full Text | Google Scholar

Ryan, Ø., and Debbah, M. (2007). “Free Deconvolution for Signal Processing Applications[C],” in Proceeding of the Information Theory, 2007. ISIT 2007. IEEE International Symposium on, Nice, France, June 2007 (IEEE), 1846–1850.

Google Scholar

Shen, X., Ouyang, T., Khajorntraidet, C., Li, Y., Li, S., and Zhuang, J. (2021). “Mixture Density Networks-Based Knock Simulator,” in Proceeding of the IEEE/ASME Trans. Mechatron., February 2021 (IEEE), 1. doi:10.1109/TMECH.2021.3059775

CrossRef Full Text | Google Scholar

Shen, X., Ouyang, T., Yang, N., and Zhuang, J. (2021). “Sample-based Neural Approximation Approach for Probabilistic Constrained Programs,” in Proceeding of the IEEE Trans. Neural Netw. Learning Syst., August 2021 (IEEE), 1–8. doi:10.1109/TNNLS.2021.3102323

CrossRef Full Text | Google Scholar

Shen, X., and Raksincharoensak, P. (2021). “Pedestrian-aware Statistical Risk Assessment,” in Proceeding of the IEEE Transactions on Intelligent Transportation Systems, June 2021 (IEEE), 1–9. doi:10.1109/TITS.2021.3074522

CrossRef Full Text | Google Scholar

Shen, X., and Raksincharoensak, P. (2021). Statistical Models of Near-Accident Event and Pedestrian Behavior at Non-signalized Intersections. J. Appl. Stat., 1–21. doi:10.1080/02664763.2021.1962263

CrossRef Full Text | Google Scholar

Shen, X., Zhang, X., Ouyang, T., Li, Y., and Raksincharoensak, P. (2020). Cooperative Comfortable-Driving at Signalized Intersections for Connected and Automated Vehicles. IEEE Robot. Autom. Lett. 5 (4), 6247–6254. doi:10.1109/LRA.2020.3014010

CrossRef Full Text | Google Scholar

Shen, X., Zhang, Y., Sata, K., and Shen, T. (2020). Gaussian Mixture Model Clustering-Based Knock Threshold Learning in Automotive Engines. Ieee/asme Trans. Mechatron. 25 (6), 2981–2991. doi:10.1109/TMECH.2020.3000732

CrossRef Full Text | Google Scholar

Sun, Y., Li, Q., Ding, Y., Quan, S., Guan, Z., Yang, D., et al. (2017). Power System protection and Control, 45, 30–36.

Google Scholar

Tulino, A. M., and Verdu, S. (2004). Random Matrix Theory and Wireless Communications. Hanover, USA: Now Publishers Inc.

Google Scholar

Voiculescu, D. (1987). Multiplication of Certain Non-commuting Random Variables. J. Oper. Theor. 18 (2), 223–235. doi:10.1016/0022-1236(86)90062-5

CrossRef Full Text | Google Scholar

Wang, B., Ma, F., Ge, L., Ma, H., Wang, H., and Mohamed, M. A. (2020). Icing-EdgeNet: A Pruning Lightweight Edge Intelligent Method of Discriminative Driving Channel for Ice Thickness of Transmission Lines. IEEE Trans. Instrum. Meas. 70, 1–12. Art no. 2501412. doi:10.1109/TIM.2020.3018831

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, B., Wang, J., Liu, D., and Chen, S. (2019). Research on Evaluating Vulnerability of Power Network Based on High-Dimensional Random Matrix Theory. Proc. CSE 39 (06), 1682–1691+1864. doi:10.13334/j.0258-8013.pcsee.180284

CrossRef Full Text | Google Scholar

Wei, D., Wang, B., Liu, D., Chen, D., Tang, F., and Guo, K. (2016). WAMS/SCADA Data Fusion Method Based on Time-Series Data Correlation Mining. High voltage Technol. 42 (01), 315–320.

Google Scholar

Xiang, C., Zeng, X., Yan, P., Zhao, J., and Jia, B. (2021). Typical Application and Prospect of Digital Twin Technology in Power Grid Operation. High Voltage Tech. 47 (05), 1564–1575.

Google Scholar

Xiong, S., Liu, Y., Fang, J., Cong, Z., Yan, Y., and Jiang, X. (2020). Detection Method of Incipient Faults of Power Distribution Lines. High voltage technolo-gy 46 (11), 3970–3976.

Google Scholar

Xu, S., Qiu, C., Zhang, D., He, X., Chu, L., and Yang, H. (2019). Identification of Transmission Line Fault Type Based on Deep Learning. Proc. CSEE 39 (01), 65–74+321.

Google Scholar

Xu, X., He, X., and Ai, Q. (2016). A Correlation Analysis Method Foroperation Status of Distribution Network Based on Random Matrixtheory. Power Syst. Tech. 40 (3), 5414–5420. doi:10.13335/j.1000-3673.pst.2016.03.018

CrossRef Full Text | Google Scholar

Xu, Z., Han, Y., He, X., Zhuo, Y., and Shi, X. (2018). Design of Distribution Network Array Vulnerability Evaluation System Based on Random Matrix Theory. Electr. Appliances Energ. Efficiency Manag. Tech. 2018 (09), 54–59. doi:10.16628/j.cnki.2095-8188.2018.09.011

CrossRef Full Text | Google Scholar

Xue, H. (2015). Research on Spectrum Sensing Technology Based on Free Probability Theory. Nanjing: Nanjing University of Posts and Telecommunications.

Google Scholar

Xue, Y., and Lai, Y. (2016). The Integration of Big Energy Thinking and Big Data Thinking (I) Big Data and Power Big Data. Automation electric Power Syst. 40 (01), 1–8. doi:10.7500/AEPS20151208005

CrossRef Full Text | Google Scholar

Yang, F., Wei, M., and Ling, Z. (2020). Brown Measure Based Spectral Distribution Analysis for Spatial-Temporal Localization of Cascading Events in Power Grids. IEEE Trans. Smart Grid 12 (99), 1805–1820. doi:10.1109/tsg.2020.3037542

CrossRef Full Text | Google Scholar

Yang, N., Huang, Y., and Hou, D. (2019). Adaptive Nonparametric Kernel Density Estimation Approach for Joint Probability Density Function Modeling of Multiple Wind Farms. Energies 2019, 12. doi:10.3390/en12071356

CrossRef Full Text | Google Scholar

Yang, N., Liu, S., Deng, Y., and Xing, C. (2020). An Improved Robust SCUC Approach Considering Multiple Uncertainty and Correlation. IEEJ Trans. Elec Electron. Eng. 16, 21–34. doi:10.1002/tee.23265

CrossRef Full Text | Google Scholar

Yang, N., Qin, T., Wu, L., Huang, Y., Huang, Y., Xing, C., et al. (2021). A Multi-Agent Game Based Joint Planning Approach for Electricity-Gas Integrated Energy Systems Considering Wind Power Uncertainty. Electric Power Syst. Res. 2021, 107673. ISSN 0378-7796. doi:10.1016/j.epsr.2021.107673

CrossRef Full Text | Google Scholar

Yang, N., Yang, C., Wu, L., Shen, X., Jia, J., Li, Z., et al. (2021). “Intelligent Data-Driven Decision-Making Method for Dynamic Multi-Sequence: An E-Seq2Seq Based SCUC Expert System,” in Proceeding of the IEEE Transactions on Industrial Informatics, August 2021 (IEEE), 1. doi:10.1109/TII.2021.3107406

CrossRef Full Text | Google Scholar

Yang, N., Yang, C., Xing, C., Ye, D., Jia, J., Chen, D., et al. (2021). Deep Learning-Based SCUC Decision-Making: An Intelligent Data-Driven Approach with Self-Learning Capabilities. IET Gener. Transm. Distrib., 1–12. doi:10.1049/gtd2.12315

CrossRef Full Text | Google Scholar

Yang, N., Ye, D., Zhou, Z., Cui, J., Chen, D., and Wang, X. (2018). Research on Modelling and Solution of Stochastic SCUC under AC Power Flow Constraints. IET Generation, Transm. Distribution 12 (15), 3618–3625. doi:10.1049/iet-gtd.2017.1845

CrossRef Full Text | Google Scholar

Ye, J., Zhao, D., and Zhang, L. (2021). Research on Combined Electricity and Heating System Scheduling Method Considering Multi-Source Ring Heating Network. Front. Energ. Res. 9. doi:10.3389/fenrg.2021.800906

CrossRef Full Text | Google Scholar

Zhang, L., Xie, Y., and Ye, J. (2021). Intelligent Frequency Control Strategy Based on Reinforcement Learning of Multi-Objective Collaborative Reward Function. Front. Energ. Res. 9. doi:10.3389/fenrg.2021.760525

CrossRef Full Text | Google Scholar

Zhang, L., Zhang, Z., and Gu, J. (2018). State Analysis and Disturbance Positioning Method of Power Grid Based on Random Matrix Theory. Automation Electric Power Syst. 42 (12), 93–99+126. doi:10.7500/AEPS20171106006

CrossRef Full Text | Google Scholar

Zheng, K., Geng, Z., Wang, H., Ma, F., and Zhang, G. (2020). Detection and Location Method of Single-phase Grounding Fault in Distribution Network Based on Synchronous Measurement Data. Power Grid Clean. Energy 36 (09), 50–56. doi:10.3969/j.issn.1674-3814.2020.09.008

CrossRef Full Text | Google Scholar

Zhou, X., Chen, S., and Lu, Z. (2018). Technology Features of the New Generation Power System in China. Proc. CSEE 38 (07), 1893–1904+2205. doi:10.13334/j.0258-8013.pcsee.180067

CrossRef Full Text | Google Scholar

Zhu, B., Ding, F., and Vilathgamuwa, D. M. (2020). Coat Circuits for DC-DC Converters to Improve Voltage Conversion Ratio. IEEE Trans. Power Electron. 35 (4), 3679–3687. doi:10.1109/tpel.2019.2934726

CrossRef Full Text | Google Scholar

Zhu, M., Xu, C., Dong, S., Tang, K., and Gu, C. (2021). An Integrated Multi-Energy Flow Calculation Method for Electricity-Gas-thermal Integrated Energy Systems. Prot. Control. Mod. Power Syst. 6 (1), 65–76. doi:10.1186/s41601-021-00182-2

CrossRef Full Text | Google Scholar