A Novel Technique Based on Peafowl Optimization Algorithm for Maximum Power Point Tracking of PV Systems Under Partial Shading Condition

One of the most critical tasks during the application of photovoltaic (PV) systems is to harvest the optimal output power at various environmental scenarios, which is called maximum power point tracking (MPPT). Though plenty of advanced techniques are developed to achieve this purpose, most of them have corresponding prominent disadvantages, such as inefficient tracking ability, high computation burden, and complex convergence mechanism. Therefore, this work aims to propose a novel and powerful bio-inspired meta-heuristic optimization algorithm called peafowl optimization algorithm (POA), which is inspired by the group food searching behaviors of peafowl swarm. It can effectively achieve a suitable balance between local exploitation and global exploration thanks to its efficient exploratory and exploitative searching operators. Thus, a satisfactory MPPT performance for PV systems under partial shading condition (PSC) can be obtained based on POA. Moreover, two case studies, e.g., start-up test and step change in solar irradiation with constant temperature, are adopted to fairly and comprehensively validate the superiority and effectiveness of POA in contrast with particle swarm optimization (PSO) and teaching-learning-based optimization (TLBO), respectively.

Introduction

With the deepening of research in the field of sustainable energy, various alternative renewable energies, such as wind energy, hydro energy, geothermal energy, tidal energy, biological energy, solar energy, and so on, are receiving widespread attention and exploitation. According to the report 2016–2020 Global Market Outlook for Solar Power, solar energy has been regarded as the most valuable renewable energy power generation resource (Yang et al., 2017), which acts as a powerful tool to deal with global warming issues. According to International Energy Agency (IEA) forecast, global photovoltaic (PV) cumulative installation is expected to reach 1721GW by 2030, which will further increase to 4670GW by 2050, which indicates great and promising development potential. Therefore, it is of great significance to investigate PV power generation and develop PV industry to alleviate the global energy crisis and restrain severe atmosphere problems, which can also promote energy reform and improve the ecological environment (Yang et al., 2020).

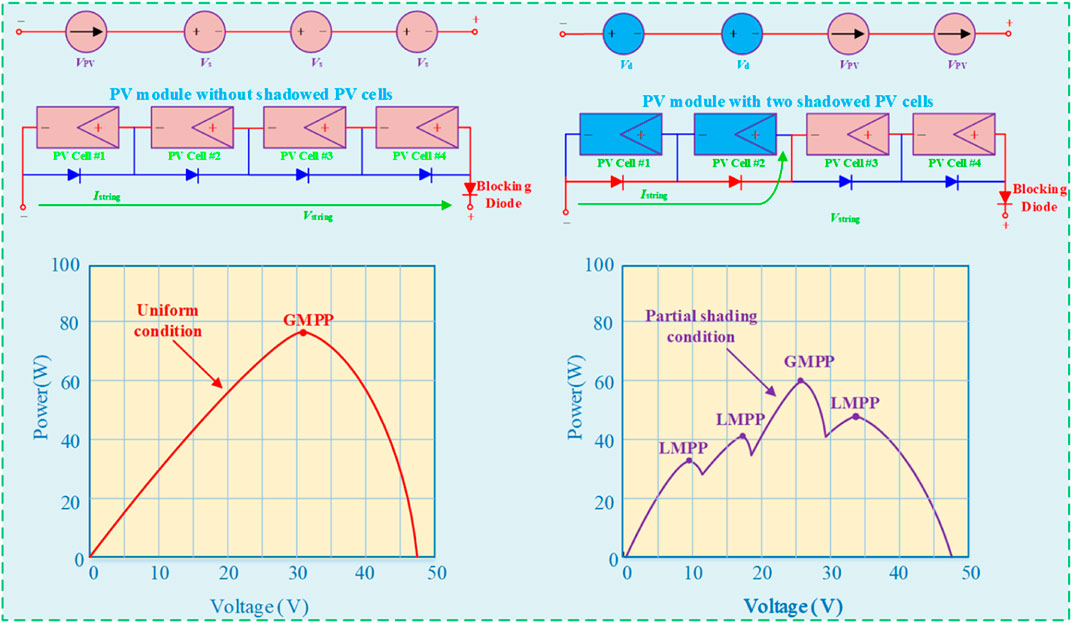
As the increase of installation scale of PV equipment in built-up urban areas, partial shading conditions (PSC) has become an inevitable problem for PV systems (Belhaouas et al., 2021). Specifically, PV modules and PV array are composed of several paralleled connected PV cells and modules, while the Sun illumination on PV module or PV array is uneven during PV power generation due to the PSC effect, which might result in the change of PV cells output characteristics. Therefore, PSC effect tends to seriously reduce the conversion efficiency of PV cells, which will then exert a negative impact on the normal operation of PV power generation system. Thus, the regulation and optimization of PV systems under PSC is a crucial task that directly influence the power generation efficiency of PV power generation system, which has been a hot research topic in the field of PV power generation technology in recent years. In general, the main purpose of maximum power point tracking (MPPT) that aims at solving the problem caused by PSC of PV systems is to obtain the optimal output power at various scenarios (Mao et al., 2020).

Basically, MPPT algorithms can be divided into serval main groups, e.g., conventional techniques, control methods based on modern control theory, and meta-heuristic techniques. In detail, conventional MPPT techniques mainly include constant voltage tracking (CVT), open-circuit voltage tracking (OVT), short-circuit current tracking (SCT), parasitic capacitance (PC), etc. CVT is a simplified MPPT method, which is actually a voltage stabilizing control strategy but not a real MPPT technique in essence. For regions suffering large daily temperature difference or large daily radiation difference, CVT cannot completely track maximum power point (MPP) under all environmental environments (Ishaque and Salam, 2013). Besides, OVT (Ahmad et al., 2019) is similar to fixed-voltage tracking method in principle, but the main difference is that the fixed-voltage tracking method tracks the constant electric voltage, while this method tracks the changing voltage. The tracking control mechanism of SCY (Kandemir et al., 2017) is very similar to OVT, but the difference is that this method tracks the variation of current. Moreover, PC is a tracking method that is quite similar to IC, while parasitic connection capacitance values in the circuit are taken into account in PC. The generation of parasitic junction capacitance is mainly due to the charging and discharging of P-N junction in PV cells and the inductance between PV cells (Belhachat and Larbes, 2018). Common MPPT methods based on modern control theory include fuzzy logic control (FLC), which is also known as fuzzy control. It is a widely used artificial intelligence (AI) algorithm, which owns significant merits of fast tracking rate, high dynamic, and steady-state performance. Nevertheless, the definition of fuzzy sets, the determination of the shape of membership functions, and the formulation of rule tables are significant design steps that need abundant experience of designers or engineers (Alajmi et al., 2010). In addition, the main principle of classic slide mode control (SMC) is to use switch devices to modulate step size to achieve MPPT control, which can considerably boost the tracking speed of MPPT, but it is worth noting that the acceleration of tracking speed will inevitably affect the stability of PV array output (Chiu et al., 2012).

Meta-heuristic algorithm is one desirable tool when solving complex optimization problems at present, which has been successfully applied in the MPPT of PV systems, for instance, particle swarm optimization (PSO), differential evolution (DE), teaching-learning-based optimization (TLBO), and so forth. For example, based on the unique characteristics of multi-peak power-voltage (P-V) curve, PSO proposed in literature (Ishaque and Salam, 2012) disperses the initial positions of particles at possible peak point voltages, which ensures this method will not fall into local optimal solutions. Besides, in literature (Fathy, 2015), authors apply artificial bee colony (ABC) algorithm for MPPT of PV systems under PSC, which shows higher tacking speed and stronger tracking stability compared against that of PSO. Moreover, a standard DE is adopted in literature (Ramli et al., 2015) to track the global MPP under PSC. Although desirable tracking performance is achieved, it also has some certain limitations, such as large computation burden. Besides, artificial colony optimization (ACO) is also a population based random optimization calculation method, which has been utilized in solving this problem. Compared with PSO, ACO only needs to store location information, and its main advantage is better real-time optimization performance. In literature (Jiang et al., 2013), ACO is used to optimize the traditional tracking controller to improve the tracking performance of the controller and enhance its robustness against PSC. Furthermore, literature (Chao and Wu, 2016) designs an enhanced teaching-learning-based optimization (E-TLBO) technique, which aims to combine self-adaptive tracking mechanism with self-study principle for MPPT of PV systems under PSC. Nevertheless, these meta-heuristic techniques all have considerable deficiencies for MPPT of PV systems, namely, large power fluctuation, complex converge mechanism, and high computation burden, which can still be further improved. Hence, this paper designs a novel MPPT technique called peafowl optimization algorithm (POA) (Naseer et al., 2018), which aims to obtain a high-quality MPPT performance for PV system under PSC; its major contribution can be summarized as follows:

1) Effective and efficient exploratory and exploitative searching operators are devised to achieve an appropriate trade-off between global exploration and local exploitation. Peacocks conduct a unique rotation dancing mechanism that contains two different rotation modes, namely, in situ rotating and circling around the food source to achieve powerful exploration;

2) Adaptive searching and approaching mechanism are adopted by peahens and peafowl throughout the iterations to dynamically adjust their searching behaviors, upon which an appropriate balance between local exploitation and global exploration can be realized;

3) Courtship behaviors and foraging behaviors are comprehensively considered in POA, and no extra parameters need to be tuned in POA.

PV Systems Modelling Under PSC

PV Cell Modelling

Basically, PV cells are connected to in both series and parallel to form PV modules, which aims to produce desirable output power (Yang et al., 2017). The generated photocurrent $I_{\text{ph}}$ can be computed by

$I_{\text{ph}}=\left(I_{\text{SCR}}+k_i\left(T_{\text{c}}-T_{\text{r}}\right)\right)\frac{G}{1000}(1)$

where the detailed meaning of each parameter and variable can be referred to literature (Yang et al., 2017).

Besides, the P-N junction in PV cell can be considered a diode, and the total current flowing through the diode $I_{\text{D}}$ can be calculated as

$I_{\text{D}}=I_{\text{S}}\left(\text{exp}\left[\frac{q\left(V+I{R}_{\text{s}}\right)}{Ak{T}_{\text{c}}}\right]-1\right)(2)$

where the detailed meaning of each parameters and variables can be referred to literature (Yang et al., 2017).

Moreover, PV cell’s reverse saturation current $I_{\text{S}}$ can be computed as follows

$I_{\text{s}}=I_{\text{or}}{\left[\frac{T_{\text{c}}}{T_{\text{r}}}\right]}^3\text{exp}\left[\frac{q{E}_{\text{g}}}{Ak}\left(\frac{1}{T_{\text{r}}}-\frac{1}{T_{\text{c}}}\right)\right] (3)$

where $I_{\text{or}}=19.9693\times {10}^{-6}\text{A}$.

The shunt leakage current $I_{\text{sh}}$ can be expressed by

$I_{\text{sh}}=\frac{V+I_{\text{out}}{R}_{\text{s}}}{R_{\text{P}}}(4)$

where $R_{\text{P}}$ means cell’s parallel resistance; $I_{\text{out}}$ denotes the entire PV output current.

The P-V relationship of a single PV cell is able to be defined as

$I_{\text{out}}=I_{\text{ph}}-I_{\text{D}}-I_{\text{sh}}(5)$

PSC Effect

The output characteristic of a single PV cell is usually highly nonlinear, and the output characteristics of PV modules based on series and parallel connection tend to become more complex. When PSC occurs in series and parallel connected PV cells, the power output of the entire module will be greatly affected. When PV modules are affected by PSC, not only the output power of PV modules is significantly reduced, PV cells also consume power in the form of heat. Under serious cases, PV modules will even be burned out and the hot spot effect will be formed, which can damage cell materials and permanently damage the cell package (Yang et al., 2020). Aiming at solving this problem, bypass diode is connected in parallel to prevent PV cells or components from thermal damage under PSC (Belhaouas et al., 2021). Traditional methods own simple implementation structure but cannot fundamentally solve this problem. Moreover, as shown in Figure 1, P-V characteristic of a PV array appears several local maximum power points (LMPPs) and only one global MPP (GMPP) under PSC; thus, it is an extremely thorny but critical task to distinguish GMPP and LMPPs.

FIGURE 1

FIGURE 1. P-V characteristic of PV systems under PSC.

Peafowl Optimization Algorithm

Basic Concept

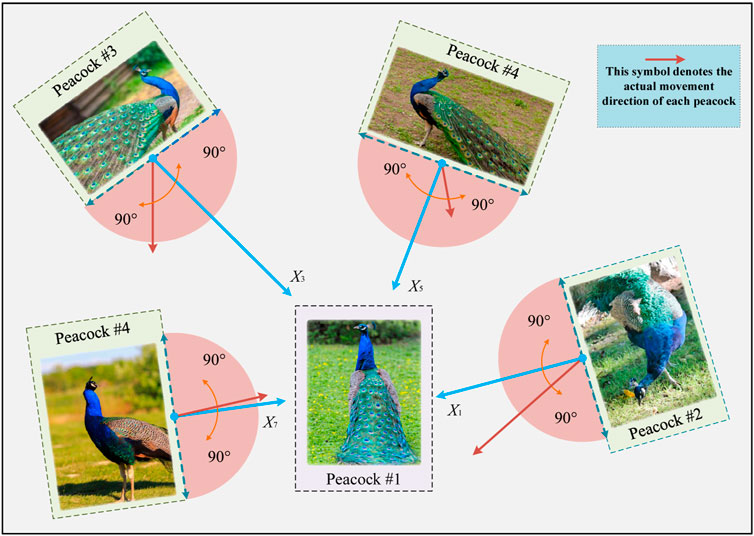
Peafowl behaviors can be roughly divided into breeding behavior, food searching behavior, community behavior, and spatial behavior. The algorithm is based on food searching behaviors of green peafowl, upon which a common and general mathematical model is established. Note that once peacock finds a food source, they not only open their feathers, but further undertake dancing behaviors to extend the domain region to attract females, as shown in Figure 2. The dancing modes are composed of in situ spinning, and walking around and circling (Naseer et al., 2018).

FIGURE 2

FIGURE 2. Courtship behaviors of peacocks: (A) tail spreading and displaying; (B) rotating; (C) flapping feathers.

Mathematical Model and Algorithm

Role Assignment

To establish an efficient mathematical model for various individual behaviors of peafowls swarm, e.g., courtship, foraging, and chasing, a peafowl population is divided into three roles: adult peacocks, adult peahens, and peafowl cubs. In practical optimization problems, all individuals are ranked based on their fitness value, among which the first five solutions are regarded as adult peacocks named Peacock #1, Peacock #2, Peacock #3, Peacock #4, and 20 Peacock #5, respectively. Besides, the remaining first 30% of individuals are defined as adult peahens and others as peafowl cubs. Besides, such artificial peafowl swarm is different from actual natural population that the roles of each individual could be changed as iterations, which means that individuals roles need to be reassigned based on their fitness value after each iteration to ensure enforceability of POA.

Peacocks Courtship Behaviors

After a food source is found by peacocks, they will undertake rotation behavior around the food source to display and show off to attract the attention of peahens, so as to increase the probability of mating. Specific estrus courtship behaviors are composed of three main phases, namely, tail spreading and displaying, rotating, flapping feathers. Note that rotation behaviors of male peacocks after tail spreading contain two forms, i.e., in situ rotating and circling around the food source, while the selection of two rotation mechanisms completely depends on their fitness value. Specifically, the better fitness value they possess, the greater probability they will circle around the food source but with smaller circle radius; meanwhile, peacocks with poor fitness value are more likely to rotate in situ with larger circle radius, while such mathematical model is able to be established as

$X_{\text{Pc}1}=X_{\text{Pc}1}\left(t\right)+1·R_{\text{S}}·\frac{X_{\text{r}1}}{\Vert X_{\text{r}1}\Vert }(6)$

$X_{\text{Pc}2}=\{\begin{array}{l}{X}_{\text{Pc}2}\left(t\right)+1.5·R_{\text{S}}·\frac{X_{\text{r}2}}{\Vert X_{\text{r}2}\Vert } , r_1<0.9\hfill \\ X_{\text{Pc}2}\left(t\right) , \text{otherwise}\hfill \end{array}(7)$

$X_{\text{Pc}3}=\{\begin{array}{l}{X}_{\text{Pc}3}\left(t\right)+2·R_{\text{S}}·\frac{X_{\text{r}3}}{\Vert X_{\text{r}3}\Vert } , r_2<0.8\hfill \\ X_{\text{Pc}3}\left(t\right) , \text{otherwise}\hfill \end{array}(8)$

$X_{\text{Pc}4}=\{\begin{array}{l}{X}_{\text{Pc}4}\left(t\right)+3·R_{\text{S}}·\frac{X_{\text{r}4}}{\Vert X_{\text{r}4}\Vert } , r_3<0.6\hfill \\ X_{\text{Pc}4}\left(t\right) , \text{ otherwise}\hfill \end{array}(9)$

$X_{\text{Pc}5}=\{\begin{array}{l}{X}_{\text{Pc}5}\left(t\right)+5·R_{\text{S}}·\frac{X_{\text{r}5}}{\Vert X_{\text{r}5}\Vert } , r_4<0.3\hfill \\ X_{\text{Pc}5}\left(t\right) , \text{ otherwise}\hfill \end{array}(10)$

$X_{\text{r}}=2·\text{rand}\left(1, Dim\right)-1(11)$

where $X_{\text{Pc}i}$ denotes the position vector of the $i$th male peacock, $i=1, 2, \cdots , 5$; $R_S$ denotes the rotation radius when circling around; $X_{\text{r}}$ denotes a stochastic vector; $X_{\text{r}}$ stands for the modules of$X_{\text{r}}$; $r_1$, $r_2$, $r_3$, $r_4$ means four stochastic numbers which are uniformly distributed in (0, 1); $Dim$ denotes the number of variables.

Moreover, rotation radius $R_{\text{S}}$ is designed to change dynamically with iterations, which can be described by

$R_{\text{S}}\left(t\right)=R_{\text{S}0}-\left(R_{\text{S}0}-0\right)·{\left(\frac{t}{t_{\text{max}}}\right)}^{0.01}(12)$

where $t$ and $t_{\text{max}}$ stand for the current number and maximum number of iterations; $R_{\text{S}0}$ denotes the initial rotation radius vector which can be judged by the search range of the optimized problem, as follows

$R_{\text{S}0}=C_{\text{v}}·\left(X_{\text{U}}-X_{\text{L}}\right)(13)$

where $X_{\text{U}}$ and $X_{\text{L}}$ denote the upper and lower bounds of the searching space; $C_{\text{v}}$ can be defined as the visibility factor of peacocks dancing in circles, which value is set as 0.2.

Peahens Adaptive Approaching Behaviors

Peahens are liable to adopt an adaptive searching and approaching mechanism during the entire searching process to dynamically regulate their behaviors in different stages. When peahens see a peacock courtship dance, they tend to firstly approach the male peacock and then observe around, and the probability that a peahen is attracted is proportional to the fitness value of peacocks. The following mathematical model is used to describe such behaviors of peahens.

$X_{\text{Ph}}=\{\begin{array}{r}\hfill \begin{array}{c}{X}_{\text{Ph}}\left(t\right)+3·\theta ·\left(X_{\text{Pc}1}-X_{\text{Ph}}\left(t\right)\right) , 0.6\le r_5\le 1 \\ X_{\text{Ph}}\left(t\right)+3·\theta ·\left(X_{\text{Pc}2}-X_{\text{Ph}}\left(t\right)\right) , 0.4\le r_5<0.6\end{array}\\ \hfill X_{\text{Ph}}\left(t\right)+3·\theta ·\left(X_{\text{Pc}3}-X_{\text{Ph}}\left(t\right)\right) , 0.2\le r_5<0.4\\ \hfill \begin{array}{c}{X}_{\text{Ph}}\left(t\right)+3·\theta ·\left(X_{\text{Pc}4}-X_{\text{Ph}}\left(t\right)\right) , 0.1\le r_5<0.2\\ X_{\text{Ph}}\left(t\right)+3·\theta ·\left(X_{\text{Pc}5}-X_{\text{Ph}}\left(t\right)\right) , 0\le r_5<0.1 \end{array}\end{array}(14)$

$\theta ={\theta }_0+\left({\theta }_1-{\theta }_0\right)·\frac{t}{t_{\text{max}}}(15)$

where $r_5$ stands for a stochastic number uniformly distributed in the interval (0,1); $X_{\text{Ph}}$ represents the position vector of peahens, while ${\theta }_0$ and ${\theta }_1$ are within (0,1).

As can be clearly seen from Eq. 14 and Eq. 15, when $\theta <1/3$ (early stage of iteration), the peahens mainly move towards the selected peacock. When $\theta >1/3$ (middle and late stage of iteration), the peahens runs to a symmetrical position relative to the selected peacock, which simulates the observed behaviors of peahens that denote the global exploration during the searching process.

Peafowl Cubs Adaptive Searching Behaviors

In addition to approaching peacocks with better food (high fitness value), peafowl will also run randomly in search of a higher-quality food. For each young peacocks, one of the five peacocks will be randomly selected as the targeted object, and the stochastic running behavior can be described by Levy flight, as follows

$Levy=0.01·\frac{{\mathit{r}}_6·\sigma }{{\left|{\mathit{r}}_7\right|}^{\frac{1}{\gamma }}}(16)$

$\sigma ={\left(\frac{\Gamma \left(1+\gamma \right)·\text{sin}\left(\frac{\gamma ·\pi }{2}\right)}{\Gamma \left(\frac{1+\gamma }{2}\right)·\gamma ·2^{\left(\frac{\gamma -1}{2}\right)}}\right)}^{\frac{1}{\gamma }}(17)$

$\Gamma \left(x\right)=\left(x-1\right)!(18)$

where $r_6$ and $r_7$ mean two different $Dim$ dimensional stochastic vectors that are uniformly distributed within (−1, 1) and (0, 1); $\gamma$ is a constant which is equal to 1.5.

Therefore, the specific behaviors of each peafowl cub can be described by

$X_{\text{SPc}}=\{\begin{array}{c}\begin{array}{c}{X}_{\text{Pc}1}\left(t\right) , 0.8<r_8\le 1 \\ X_{\text{Pc}2}\left(t\right) , 0.6<r_8\le 0.8\end{array}\\ X_{\text{Pc}3}\left(t\right) , 0.4<r_8\le 0.6\\ \begin{array}{c}{X}_{\text{Pc}4}\left(t\right) , 0.2<r_8\le 0.4\\ X_{\text{Pc}5}\left(t\right) , 0\le r_8\le 0.2 \end{array}\end{array}(19)$

$X_{\text{PcC}}=X_{\text{PcC}}\left(t\right)+\alpha ·Levy·\left(X_{\text{Pc}1}\left(t\right)-X_{\text{PcC}}\left(t\right)\right)+\delta ·\left(X_{\text{SPc}}-X_{\text{PcC}}\left(t\right)\right)(20)$

where $r_8$ denotes a stochastic number uniformly distributed on (0, 1); $X_{\text{SPc}}$ and $X_{\text{PcC}}$ mean the position vectors of selected peacock and peacock cub, respectively; $\alpha$ and $\delta$ denote two coefficient factors that vary dynamically with the number of iterations, which can be described by

$\alpha =0.9-\left(0.9-0.4\right)·{\left(\frac{t}{t_{\text{max}}}\right)}^2(21)$

$\delta =0.1+(1-0.1)·{\left(\frac{t}{t_{\text{max}}}\right)}^{0.5}(22)$

Equations 20–22 show that $\alpha$ is larger than $\delta$ at the beginning of iteration, and the peafowl cubs mainly conduct stochastic search. At the end of the iteration, the ratio of $\delta$ to $\alpha$ is larger, and the peafowl cubs converge to the five optimal solutions (peacocks).

Interaction Behaviors Among Peacocks

Since Peacock #1 has the best food source, the other four peacocks will be induced to gradually move towards it. However, instead of moving straight to Peacock #1, the remaining four males tend to move toward Peacock #1 in a random direction within 90 of the line between Peacock #1 and the other one, as shown in Figure 3.

FIGURE 3

FIGURE 3. Interaction mechanism among different peacocks.

So far, the relationship among different peacocks can be established as follows:

$\{\begin{array}{l}{X}_1=X_{\text{Pc}1}-X_{\text{Pc}2}\hfill \\ X_2=X_{\text{r}6}-\frac{\left(X_{\text{r}6}\ast X_1\right)}{\left(X_1\ast X_1\right)}·X_1\hfill \\ X_{\text{Pc}2}=X_{\text{Pc}2}\left(t\right)+\theta ·X_1+r_9·\frac{X_2}{\Vert X_2\Vert }\hfill \end{array}(23)$

$\{\begin{array}{l}{X}_3=X_{\text{Pc}1}-X_{\text{Pc}3}\hfill \\ X_4=X_{\text{r}7}-\frac{\left(X_{\text{r}7}\ast X_3\right)}{\left(X_3\ast X_3\right)}·X_3\hfill \\ X_{\text{Pc}3}=X_{\text{Pc}3}\left(t\right)+\theta ·X_3+r_{10}·\frac{X_4}{\Vert X_4\Vert }\hfill \end{array}(24)$

$\{\begin{array}{l}{X}_5=X_{\text{Pc}1}-X_{\text{Pc}4}\hfill \\ X_6=X_{\text{r}8}-\frac{\left(X_{\text{r}8}\ast X_5\right)}{\left(X_5\ast X_5\right)}·X_5\hfill \\ X_{\text{Pc}4}=X_{\text{Pc}4}\left(t\right)+\theta ·X_5+r_{11}·\frac{X_6}{\Vert X_6\Vert }\hfill \end{array}(25)$

$\{\begin{array}{l}{X}_7=X_{\text{Pc}1}-X_{\text{Pc}5}\hfill \\ X_8=X_{\text{r}9}-\frac{\left(X_{\text{r}9}\ast X_7\right)}{\left(X_7\ast X_7\right)}·X_7\hfill \\ X_{\text{Pc}5}=X_{\text{Pc}5}\left(t\right)+\theta ·X_7+r_{12}·\frac{X_8}{\Vert X_8\Vert }\hfill \end{array}(26)$

where $X_{\text{r}6}$, $X_{\text{r}7}$, $X_{\text{r}8}$, and $X_{\text{r}9}$ mean four different stochastic vectors; $r_9$, $r_{10}$, $r_{11}$, and $r_{12}$ represent stochastic numbers uniformly distributed within (0,1) and $\left(x\ast y\right)$ is defined as the inner product of vectors $x$ and $y$.

POA Based MPPT Design of PV Systems

Application of POA for MPPT

PV system often combines a boost converter to offer energy for multitudinous loads. For the population of peacocks, duty cycle $D$ $\left(0\le D\le 1\right)$ can correspond to the location of each peafowl during iterations. To ensure PV system always operate at GMPP, it is imperative to regulate the output voltage $V_{\text{L}i}$ to approach the optimal operation point. During each control period, the fitness value is able to be regarded as the product of the real-time acquisition voltage and current outputs, as follows:

$Fit\left({\mathit{x}}_i\right)=V_{\text{L}}\left({\mathit{x}}_i\right)·I\left({\mathit{x}}_i\right)(27)$

where $V_{\text{L}}\left({\mathit{x}}_i\right)$ and $I\left({\mathit{x}}_i\right)$ stand for the steady voltage and current outputs.

Thus, the fitness function of POA is able to be written as follows:

$P\left(D_i^k\right)>P\left(D_i^{k-1}\right)(28)$

where $P$ denotes the output power; $i$ means the number of current peafowl; and $k$ denotes the number of iterations.

Execution Flowchart

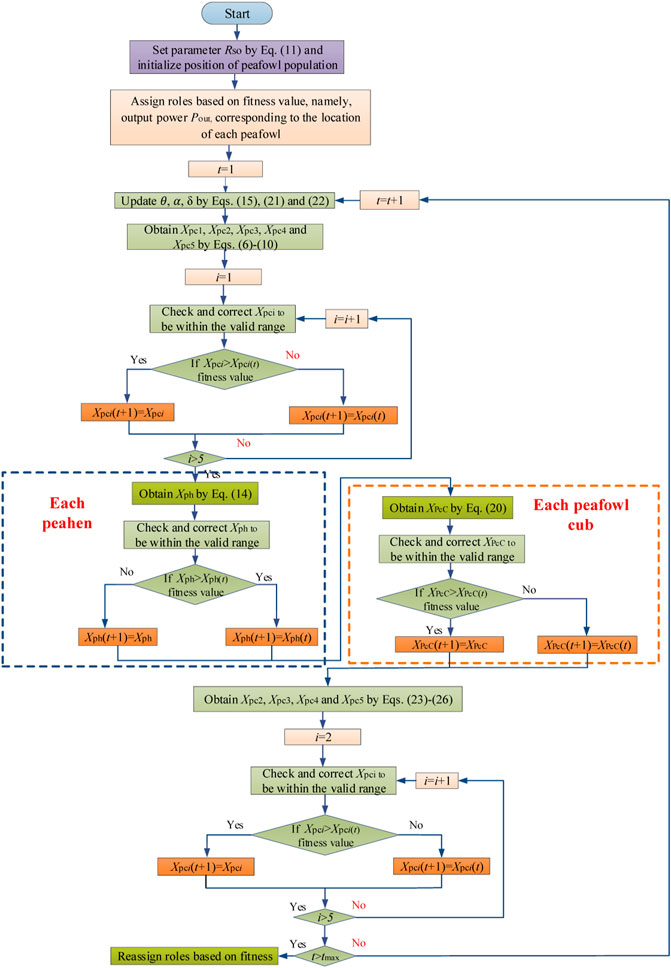
In conclusion, the whole execution flowchart of POA based MPPT of PV systems under PSC is demonstrated in Figure 4, where t_max stands for the maximum iteration number.

FIGURE 4

FIGURE 4. Entire execution flowchart of FOA for MPPT of PV systems under PSC.

Case Studies

Two cases, namely, 1) start-up test and 2) step change in solar irradiation with constant temperature, are undertaken to validate the MPPT performance of POA under PSC, which is compared with PSO (Fathy, 2015) and TLBO (Rezk and Fathy, 2017; Zhang et al., 2021), respectively. Besides, for a fair comparison, the parameter settings of all the approaches are set to be identical, as illustrated in Table 1. The simulation is conducted on Matlab/Simulink 2019a via a personal computer with an Intel^R CoreTMi7 CPU at 2.2 GHz and 32 GB of RAM. Moreover, the solver is ode 45 (Dormand-Prince) with an auto variable-step size.

TABLE 1

TABLE 1. Parameters of three methods.

Start-Up Test

The first test aims to investigate the MPPT performance at start-up (from zero point) under PSC, in which the solar irradiation of four PV arrays is stated to be 1000, 200, and 300 W/m², respectively. Particularly, the MPPT performance of different techniques can be demonstrated in Figure 5. One can observe that PSO and TLBO easily converge to a LMPP because of their high dependence on the initial solution under PSC. On the contrary, POA is able to ensure the entire PV system obtain much higher active power due to its adaptive global searching ability. Besides, the output energy results generated by three techniques are illustrated in Table 2. The output energy obtained by POA is the highest among these three techniques, while its power fluctuation is also the smallest along with the fastest converge ability. This effectively proves that POA can not only converge to a high-quality optimum for MPPT, but also assure the convergence stability by a unique rotation dancing mechanism of peacocks, which can be known as in situ rotating and circling around the food source to realize powerful exploration. Note that effective and efficient exploratory and exploitative searching operators are devised in POA, which aims to offer an adequate trade-off between global exploration and local exploitation.

FIGURE 5

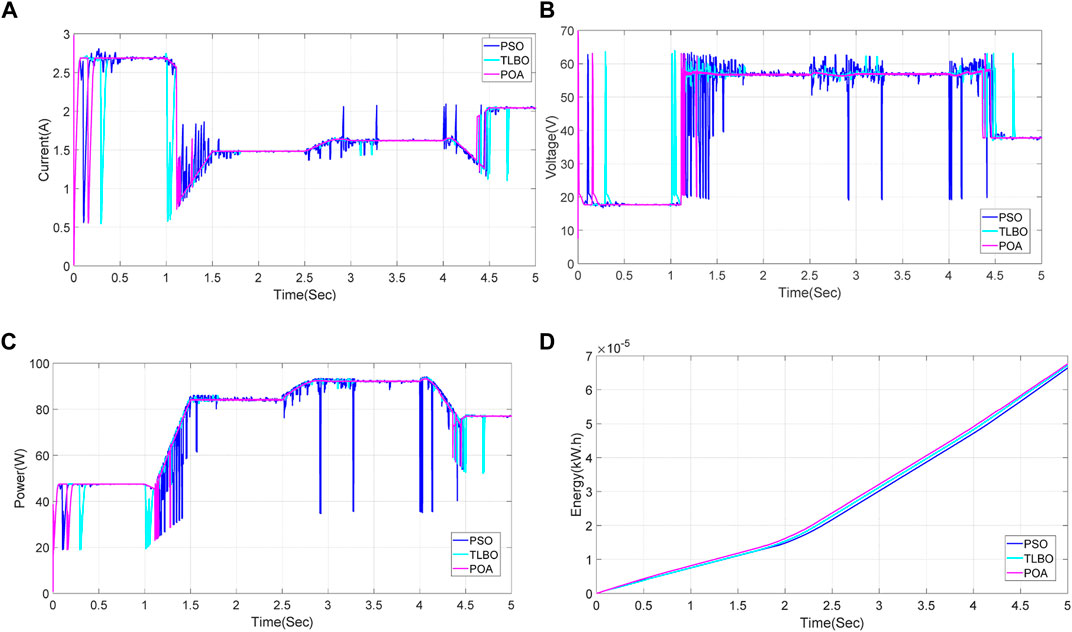
FIGURE 5. PV system responses of three techniques generated on the start-up test. (A) Current, (B) Voltage, (C) Power, and (D) Energy.

TABLE 2

TABLE 2. Output energy results obtained by three techniques under two scenarios (unit: Ws).

Step Change in Solar Irradiation With Constant Temperature

For the purpose of alleviating the effect when a cloud rapidly passes over a PV array while validating the MPPT performance, a series of solar irradiation steps are employed on the PV array. Note that the temperature keeps at 25°C during the entire test. Particularly, the optimization results of different techniques for MPPT under step change in solar irradiations can be demonstrated in Figure 6. Also, the output energy generated by three techniques are given in Table 2. Moreover, the other two meta-heuristic algorithms, namely, PAO and PSO, both outperform TLBO as they can produce higher energy under such solar conditions. Besides, the energy generated by POA is the highest among the three methods, which output energy is 2.98% higher than that of TLBO. Obviously, POA can easily generate the smallest oscillations in the output current, voltage, and power compared with PSO and TLBO when the solar irradiance rapidly varies. One can easily observe that POA can achieve a high-quality MPPT performance under step change in solar irradiations along with the fastest convergence ability, while the other two meta-heuristic techniques are prone to a low-quality LMPP. The adaptive searching and approaching mechanism adopted by peahens and peafowl throughout the iterations can dynamically adjust their searching behaviors, upon which a proper balance between local exploitation and global exploration can be realized.

FIGURE 6

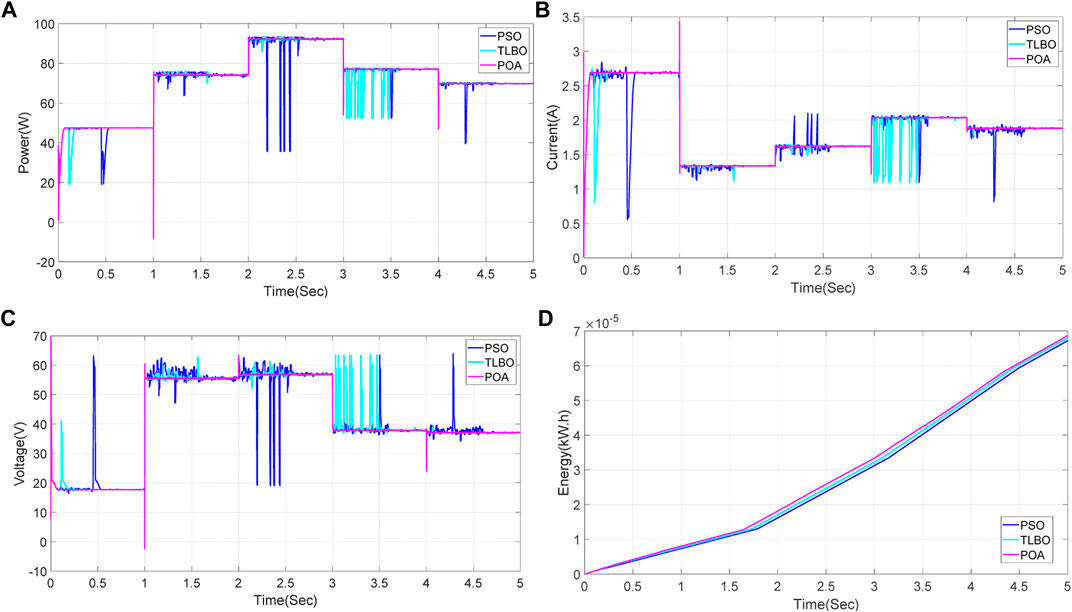
FIGURE 6. PV system responses of three techniques obtained on the step change in solar irradiation with constant temperature. (A) Current, (B) Voltage, (C) Power, and (D) Energy.

Conclusion

A novel technique based on POA for MPPT of PV systems under PSC, which benefits/novelties are outlined as follows:

1) The design of POA includes effective and efficient exploratory and exploitative searching operators to provide an proper trade-off between global exploration and local exploitation to avoid local optimums, e.g., unique rotation dancing operations of peacocks, adaptive searching behaviors of peahens and peafowl cubs in different searching stages, along with interactions among different peacocks.

2) An adaptive searching and approaching mechanism is adopted by peahens and peafowl throughout the iterations to dynamically adjust their searching behaviors, upon which local optimal solutions can be effectively avoided.

3) Two case studies are undertaken to validate the effectiveness and benefits of POA in comparison with other techniques, which indicates that POA can always guarantee PV systems to obtain the maximum output energy along with the highest convergence rate and the smallest oscillations under various operation scenarios.

Future studies will focus on the further improvement of the structure of the proposed POA, which aims to reduce parameters tuning burden to enhance its implementation feasibility. Also, on-line and real-time MPPT is a promising working direction.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary material. Further inquiries can be directed to the corresponding author.

Author Contributions

DL: Conceptualization and writing—reviewing and editing. JL: Writing—original draft preparation and investigation. NW: Writing—reviewing and editing and supervision.

Conflict of Interest

DL was employed by the company Yunnan Baichuan Power Technology Co., Ltd. JL was employed by the company CISDI Electric Technology Co., Ltd. NW was employed by the company Guian New District Electricity Distribution Co., Ltd.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahmad, R., Murtaza, A. F., and Sher, H. A. (2019). Power Tracking Techniques for Efficient Operation of Photovoltaic Array in Solar Applications - A Review. Renew. Sustain. Energ. Rev. 101, 82–102. doi:10.1016/j.rser.2018.10.015

CrossRef Full Text | Google Scholar

Alajmi, B. N., Ahmed, K. H., Finney, S. J., and Williams, B. W. (2010). Fuzzy-logic-control Approach of a Modified hill-climbing Method for Maximum Power point in Microgrid Standalone Photovoltaic System. IEEE Trans. Power Electron. 26 (4), 1022–1030. doi:10.1109/TPEL.2010.2090903

CrossRef Full Text | Google Scholar

Belhachat, F., and Larbes, C. (2018). A Review of Global Maximum Power point Tracking Techniques of Photovoltaic System under Partial Shading Conditions. Renew. Sustain. Energ. Rev. 92, 513–553. doi:10.1016/j.rser.2018.04.094

CrossRef Full Text | Google Scholar

Belhaouas, N., Mehareb, F., Assem, H., Kouadri-Boudjelthia, E., Bensalem, S., Hadjrioua, F., et al. (2021). A New Approach of PV System Structure to Enhance Performance of PV Generator under Partial Shading Effect. J. Clean. Prod. 317, 128349. doi:10.1016/j.jclepro.2021.128349

CrossRef Full Text | Google Scholar

Chao, K.-H., and Wu, M.-C. (2016). Global Maximum Power point Tracking (MPPT) of a Photovoltaic Module Array Constructed through Improved Teaching-Learning-Based Optimization. Energies 9 (12), 986–1005. doi:10.3390/en9120986

CrossRef Full Text | Google Scholar

Chiu, C.-S., Ouyang, Y.-L., and Ku, C.-Y. (2012). Terminal Sliding Mode Control for Maximum Power point Tracking of Photovoltaic Power Generation Systems. Solar Energy 86 (10), 2986–2995. doi:10.1016/j.solener.2012.07.008

CrossRef Full Text | Google Scholar

Fathy, A. (2015). Reliable and Efficient Approach for Mitigating the Shading Effect on Photovoltaic Module Based on Modified Artificial Bee Colony Algorithm. Renew. Energ. 81, 78–88. doi:10.1016/j.renene.2015.03.017

CrossRef Full Text | Google Scholar

Ishaque, K., and Salam, Z. (2012). A Deterministic Particle Swarm Optimization Maximum Power point Tracker for Photovoltaic System under Partial Shading Condition. IEEE Trans. Ind. Electron. 60 (8), 3195–3206. doi:10.1109/tie.2012.2200223

CrossRef Full Text | Google Scholar

Ishaque, K., and Salam, Z. (2013). A Review of Maximum Power point Tracking Techniques of PV System for Uniform Insolation and Partial Shading Condition. Renew. Sustain. Energ. Rev. 19, 475–488. doi:10.1016/j.rser.2012.11.032

CrossRef Full Text | Google Scholar

Jiang, L. L., Maskell, D. L., and Patra, J. C. (2013). A Novel Ant colony Optimization-Based Maximum Power point Tracking for Photovoltaic Systems under Partially Shaded Conditions. Energy and Buildings 58, 227–236. doi:10.1016/j.enbuild.2012.12.001

CrossRef Full Text | Google Scholar

Kandemir, E., Cetin, N. S., and Borekci, S. (2017). A Comprehensive Overview of Maximum Power Extraction Methods for PV Systems. Renew. Sustain. Energ. Rev. 78, 93–112. doi:10.1016/j.rser.2017.04.090

CrossRef Full Text | Google Scholar

Mao, M., Zhang, L., Huang, H., Chong, B., and Zhou, L. (2020). Maximum Power Exploitation for Grid-Connected PV System under Fast-Varying Solar Irradiation Levels with Modified Salp Swarm Algorithm. J. Clean. Prod. 268, 122158. doi:10.1016/j.jclepro.2020.122158

CrossRef Full Text | Google Scholar

Naseer, J., Anjum, K. M., Munir, M. A., Nazir, M. A., Yousaf, M. Z., Naseer, O., et al. (2018). A Study on Indian Peafowl (Pavo cristatus) Emphasising Breeding Season and Feeding Behaviour in Captivity. Indian J. Anim. Res. 52 (11), 1664–1666. doi:10.18805/ijar.b-800

CrossRef Full Text | Google Scholar

Ramli, M. A. M., Ishaque, K., Jawaid, F., Al-Turki, Y. A., and Salam, Z. (2015). A Modified Differential Evolution Based Maximum Power point Tracker for Photovoltaic System under Partial Shading Condition. Energy and Buildings 103, 175–184. doi:10.1016/j.enbuild.2015.06.058

CrossRef Full Text | Google Scholar

Rezk, H., and Fathy, A. (2017). Simulation of Global MPPT Based on Teaching-Learning-Based Optimization Technique for Partially Shaded PV System. Electr. Eng. 99 (3), 847–859. doi:10.1007/s00202-016-0449-3

CrossRef Full Text | Google Scholar

Yang, B., Zhang, X., Yu, T., Shu, H., and Fang, Z. (2017). Grouped Grey Wolf Optimizer for Maximum Power point Tracking of Doubly-Fed Induction Generator Based Wind Turbine. Energ. Convers. Manage. 133, 427–443. doi:10.1016/j.enconman.2016.10.062

CrossRef Full Text | Google Scholar

Yang, B., Zhu, T., Wang, J., Shu, H., Yu, T., Zhang, X., et al. (2020). Comprehensive Overview of Maximum Power point Tracking Algorithms of PV Systems under Partial Shading Condition. J. Clean. Prod. 268, 121983. doi:10.1016/j.jclepro.2020.121983

CrossRef Full Text | Google Scholar

Zhang, K., Zhou, B., Or, S. W., Li, C., Chung, C. Y., and Voropai, N. I. (2021). “Optimal Coordinated Control of Multi-Renewable-To-Hydrogen Production System for Hydrogen Fueling Stations,” in IEEE Trans. Ind. Applicat. (IEEE), 1. doi:10.1109/TIA.2021.3093841

CrossRef Full Text | Google Scholar