Research on Combined Electricity and Heating System Scheduling Method Considering Multi-Source Ring Heating Network

Heating network constraint is one of the important factors that affect the scale of electro-thermal coupling scheduling. This paper first establishes an electrothermal coupling scheduling model considering the multi-source ring heating network pipe structure and then proposes a method of simplifying a multi-source cyclic heating network topology approximation. Second, the electrothermal coupling scheduling system is coordinated and solved. Finally, Through the simulation example results, the annular heating network topological approximate equivalent can simplify the model complexity of the original heating network while also retaining the thermal dynamic characteristics of the initial multi-source ring heating network. This study will greatly improve the efficiency of solving the electrothermal coupling system.

Introduction

The Combined Electricity and Heating System can realize the cascade utilization of different energy efficiency, which is an important way for the low-carbon economic operation of the power generation link. Considering the heat storage characteristics of the District Heating Network (DHN) can bring coordination and flexibility to the entire coupled electricity–heat energy system. In recent years, many scholars have studied the heat storage characteristics of heat network pipes (Li et al., 2021; Tang et al., 2021). The node method is effective to describe the temperature dynamic model of DHN (Li et al., 2017; Zheng et al., 2018; Wang et al., 2019; Yu et al., 2019; Shen et al., 2020; Shen et al., 2021; Shen and Raksincharoensak, 2021). The above study only considers the supply pipe network as a tree heating network structure which is harmful to the solution of the electrothermal coupling scheduling model. However, it does not match the structure of the multi-heat source combined with the multi-heat source, which will directly affect the applicability of the model.

Further, compared with the conventional tree heating network structure, the different heat sources of the multi-source cyclic heating network structure can be spared to each other, and the mutual coordination provides heat (Tian et al., 2017; Yang et al., 2019a; Shi et al., 2020; Yang, 2020). The heating network structure has been applied in some cities in the Nordics and China (Wu et al., 2019). Therefore, it is possible to further improve the flexibility between the electrothermal coupling system in the electrothermal coupling schedule. The scale and laying area of the actual heating pipe network are very huge, and it has brought difficulties to the solution of the model. In recent years, scholars have conducted research on reducing the complexity of scheduling models (Jiang et al., 2019; Lu et al., 2019). Document (Larsen et al., 2002) is subtracted into a conventional tree heating network, but the actual multi-heat source combined heating network is more complex. The traditional simplification method cannot be applied to the actual operation of the current large-scale multi-heat source ring network.

In response to the questions raised above, this paper proposes a combined heat and power scheduling method based on ring heating network topological approximate equivalent. For the complex topology of the ring heating network, topology equivalent transformation and pipeline node aggregation are carried out on ring heating pipeline under the condition of ensuring accuracy, and the electric-thermal joint scheduling model is solved. There are many ways to solve the model (Yang et al., 2019b; Yang et al., 2021a; Yang et al., 2021b; Zhang et al., 2021). Finally, the effectiveness and accuracy of the method mentioned in this study is verified by example analysis.

Topological Equivalent Method of Loop Removal for Multi-Heat Source Ring Heat Grid

Topological Approximate Equivalent Method

In the actual multi-heat source heating ring network, due to the joint heating of multiple heat sources, the heat flow direction flowing through the same ring can be divided into the same direction and different direction, as shown in Figure 1A. On the basis of retaining most dynamic characteristics of the original pipe, this section will be used to topologically approximate the annular pipe network of the condition that satisfies the same flow direction and polymerizes the topology of the relatively simple tree network then use the node method to model the temperature dynamic model of DHN after the simplification. For heating networks and their models, the physical parameters of the pipe and the state variables of heat transfer process are very important. Its physical parameters are heating network topologies and pipeline parameters such as pipe mass flow $m$, pipe cross-sectional area S, pipe length L, pipe heat transfer coefficient $u$, etc. The state variable parameters are each load node temperature $T_i$, each node temperature $T_x$ passed during water flow transfer, and the heat source to the time delay $\tau$ of each load node.

FIGURE 1

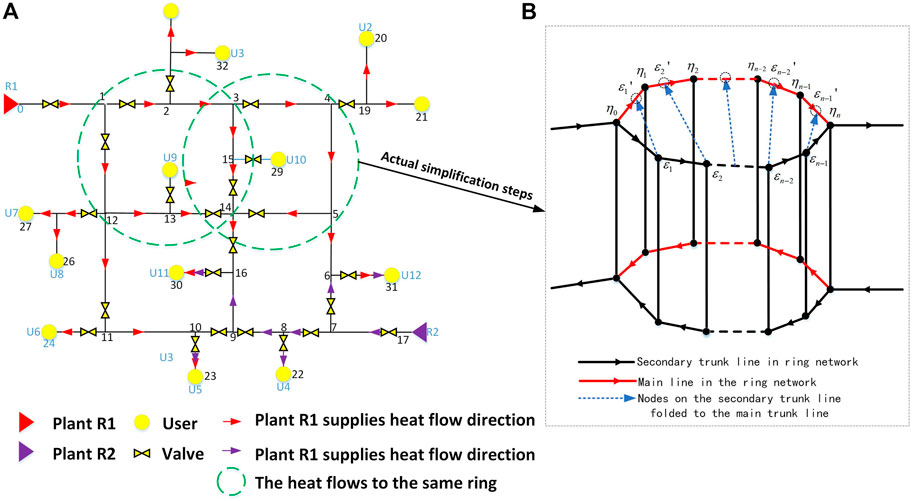
FIGURE 1. (A) Two-heat source heating pipe network diagram under actual conditions. (B) Simplification process of general ring heating pipe network.

For the ring-shaped heating pipe network with the same heat flow (marked in green in Figure 1A), it can be equivalently simplified into a polymerization pipe. In order to ensure that the dynamic characteristics of heat transfer after the topological transformation of the heating network are equivalent, the heating network state variable needs to meet the following thermal equivalent conditions:

Assumption Condition 1: The total volume of water in the pipeline before and after the simplification of the model structure remains unchanged.

${\displaystyle {\sum }_{x\in V^{+}}{V}_x^{\prime }}={\displaystyle \sum _{x\in V^{+}}{V}_x}(1)$

In Formula (1), $x$ represents any pipe, and $V_x$ represents the water volume of the conduit $x$. $V^{+}$ represents a collection of all pipes in the heating network, the tag ′ represents the corresponding parameters after the heating network topology is equivalent.

Assumption Condition 2: The mass flow of each sub-branch flow into and out of each node remains unchanged.

$m_x^{\prime }=m_x(2)$

In Formula (2), $m_x$ represents the mass flow of water in the pipe.

Assumption Condition 3: The temperature of the node before and after polymerization does not change.

$T_x^{\prime }=T_x(3)$

In Formula (3), $T_x$ represents the temperature of any node before and after polymerization.

When the above three thermal equivalent conditions are met, the operating time of heating water in the pipe can be expressed as

$\text{τ}=\frac{V\cdot \rho }{m}(4)$

On the basis of preserving the thermal dynamic characteristics of the original pipe, the process of loop removal is essentially a topological approximate equivalent method which changes the original pipeline parameters to a tree-shaped heating pipe network, as shown in Figure 1B. Before the ring network is removed, this paper takes the starting point of the ring network shunting as the initial point and defines the ring heating network after shunting as the main line and secondary line. According to Formula (4), the heat flow is obtained by the starting point to flow through the time required for each node, and the time delay flowing through the respective nodes on the main/secondary line is ${\eta }_n$/${\epsilon }_n$, where $n$ represents the time set that flows through the main/secondary trunk nodes. The resulting time is arranged in size to obtain the time set sequence $\text{φ}$. $\text{φ}$ is a time series consisting of $\epsilon$ and $\eta$. The nodes that have not alternated in the collection φ are considered a redundant node, such as ${\epsilon }_{i-1},{\epsilon }_i$ in ${\epsilon }_{n-3},{\eta }_{i-2},{\epsilon }_{i-1},{\epsilon }_i,{\eta }_{i+1},{\epsilon }_{i+2}$, where $i$ represents any node on the pipe. The redundant node is removed by conventional tree heating network simplification (Wu et al., 2019). After the redundant node is removed, the new $\text{φ}$ is obtained as an alternating time sequence that occurs by $\epsilon$ and $\eta$.

$\text{φ}:\left\{{\tau }_{\eta 0},{\tau }_{\epsilon 1},{\tau }_{\eta 1},{\tau }_{\epsilon 2},{\tau }_{\eta 2},\cdots ,{\tau }_{\eta \epsilon -1},{\tau }_{\eta n-1},{\tau }_{\eta n}\right\}(5)$

The secondary trunk is aggregated to the main line. The mass flow of each pipeline after polymerization is

$m_{{\epsilon }_i}^{\prime }=m_{{\epsilon }_i}+m_{{\eta }_i}(6)$

$m_{{\eta }_i}^{\prime }=m_{{\epsilon }_{i+1}}+m_{{\eta }_i}(7)$

In the above Formulas (6) and (7), $m_{{\eta }_i}$ and $m_{{\epsilon }_i}$ represent the mass flow of the main trunk and the secondary trunk polymerization.

The weighting average of the mass flow of each conduit on the secondary trunk and the weight of the mass flow corresponding to the main line can delay the flow of water flow through the new polymerization node time delay as follows:

${\tau }_{{\epsilon }_i}^{\prime }=\frac{m_{{\eta }_i}}{m_{{\eta }_i}+m_{{\epsilon }_i}}{\displaystyle {\sum }_{\theta =1}^i{\tau }_{{\eta }_{\theta }}}+\frac{m_{{\epsilon }_i}}{m_{{\eta }_i}+m_{{\epsilon }_i}}{\displaystyle {\sum }_{\theta =1}^i{\tau }_{{\epsilon }_{\theta }}}(8)$

${\tau }_{{\eta }_i}^{\prime }=\frac{m_{{\eta }_i}}{m_{{\eta }_i}+m_{{\epsilon }_{i+1}}}{\displaystyle {\sum }_{\theta =1}^i{\tau }_{{\eta }_{\theta }}}+\frac{m_{{\epsilon }_i}}{m_{{\eta }_i}+m_{{\epsilon }_{i+1}}}{\displaystyle {\sum }_{\theta =1}^i{\tau }_{{\epsilon }_{\theta }}}(9)$

The equivalent water volume of each pipeline is obtained by Formulas (4), (8), and (9).

$V_{{\epsilon }_i}^{\prime }=\frac{1}{\rho }\left(m_{{\epsilon }_i}+m_{{\eta }_i}\right)\left(\frac{m_{{\eta }_i}}{m_{{\eta }_i}+m_{{\epsilon }_i}}{\displaystyle {\sum }_{\theta =1}^i{\tau }_{{\eta }_{\theta }}}+\frac{m_{{\epsilon }_i}}{m_{{\eta }_i}+m_{{\epsilon }_i}}{\displaystyle {\sum }_{\theta =1}^i{\tau }_{{\eta }_{\theta }}}\right)(10)$

$V_{{\eta }_i}^{\prime }=\frac{1}{\rho }\left(m_{{\epsilon }_{i+1}}+m_{{\eta }_i}\right)\left(\frac{m_{{\eta }_i}}{m_{{\eta }_i}+m_{{\epsilon }_{i+1}}}{\displaystyle {\sum }_{\theta =1}^i{\tau }_{{\eta }_{\theta }}}+\frac{m_{{\epsilon }_i}}{m_{{\eta }_i}+m_{{\epsilon }_{i+1}}}{\displaystyle {\sum }_{\theta =1}^i{\tau }_{{\epsilon }_{\theta }}}\right)(11)$

The current flow rate of the original carrier in the main trunk line is the initial flow rate. By changing the volume of the pipeline before and after polymerization, the flow rate of the heating carrier in the pipeline polymerization is kept constant, then the tube length is determined based on the piping of the heat flow through the polymerization in the conduit and the ratio of the predecessor travel time during the pipeline. The equivalent length L of each pipe obtained by Formula (8) can be obtained.

$L_{{\epsilon }_i}^{\prime }=\left({\displaystyle {\sum }_{\theta =1}^i{\tau }_{\epsilon \theta }}/{\displaystyle {\sum }_{\theta =1}^i{\tau }_{\eta \theta }}\right)L_{{\eta }_i}(12)$

$L_{{\eta }_i}^{\prime }=L_{{\eta }_i}-L_{{\epsilon }_i}^{\prime }(13)$

where ${\displaystyle \sum _{\theta =1}{\tau }_{{\epsilon }_{\theta }}}$, ${\displaystyle \sum _{\theta =1}{\tau }_{{\eta }_{\theta }}}$ respectively represent the sum of the time it takes for the heat flow of all nodes in the secondary trunk line and the main trunk line to flow through the pipe 1 to pipe $i$.

Bring Eqs (10)–(13) to volume formula equivalent cross-sectional area:

$S_{{\epsilon }_i}^{\prime }=\frac{\left(m_{{\epsilon }_i}+m_{{\eta }_i}\right){\displaystyle {\sum }_{\theta =1}^i{\tau }_{{\eta }_{\theta }}}}{\rho L_{{\eta }_i}{\displaystyle {\sum }_{\theta =1}^i{\tau }_{{\eta }_{\theta }}}}\left(\frac{m_{{\eta }_i}}{m_{{\eta }_i}+m_{{\epsilon }_i}}{\displaystyle {\sum }_{\theta =1}^i{\tau }_{{\eta }_{\theta }}}+\frac{m_{{\epsilon }_i}}{m_{{\eta }_i}+m_{{\epsilon }_{i+1}}}{\displaystyle {\sum }_{\theta =1}^i{\tau }_{{\epsilon }_{\theta }}}\right)(14)$

$S_{{\eta }_i}^{\prime }=\frac{\left(m_{{\epsilon }_{i+1}}+m_{{\eta }_i}\right)}{\rho \left(L_{{\eta }_i-}{L}_{{\epsilon }_i}^{\prime }\right)}\left(\frac{m_{{\eta }_i}}{m_{{\eta }_i}+m_{{\epsilon }_{i+1}}}{\displaystyle {\sum }_{\theta =1}^i{\tau }_{{\eta }_{\theta }}}+\frac{m_{{\epsilon }_i}}{m_{{\eta }_i}+m_{{\epsilon }_{i+1}}}{\displaystyle {\sum }_{\theta =1}^i{\tau }_{{\epsilon }_{\theta }}}\right)(15)$

Thus, the equivalent model heat transfer coefficient $u$ should be adjusted as follows:

${\mu }_{{\epsilon }_i}^{\prime }=\frac{c\cdot m_i^{\prime }}{\pi \cdot d_i^{\prime }\cdot L_i^{\prime 2}}\cdot ln\frac{T_{i,in}-T^U}{T_{i,out}^{\prime }-T^U}(16)$

${\mu }_{{\eta }_i}^{\prime }=\frac{c\cdot m_i^{\prime }}{\pi \cdot d_i^{\prime }\cdot L_i^{\prime 2}}\cdot ln\frac{T_{i,in}-T^U}{T_{i,out}^{\prime }-T^U}(17)$

As can be seen from Formula (3), the temperature of the node before and after the polymerization does not change. $T_{i,\text{out}}\text{′}$ is the temperature of the terminal outlet after the tube $i$ polymerization; $T_{i,i\text{n}}$ is the temperature of the exit before the piping $i$ is polymerized, where $c$ is a specific heat capacity of the heating flow, $d_i^{\prime }$ is a polymerized pipeline radius, and $T^{\text{U}}$ is a natural ambient temperature.

After the above simplification, in the case of retaining most of the thermal dynamic characteristics, the multi-source annular DHN model completes the ring removal processing, which reduces the complexity of the original pipeline.

Multi-Source Ring Network Regional Heating System Model

1) CHP unit heating output

$h_{i,t}=c\cdot m_j^{HS}\cdot \left(T_{n,t}^s-T_{n,t}^r\right),\forall i\in I^{CHP}, j\in I^{HS}, n=N_j^{HS}, t\in T(18)$

${\underset{¯}{T}}_n^s\le T_{n,t}^s\le {\overline{T}}_n^s(19)$

where $m_j^{HS}$ is the mass flow of the heating first station $j$; $h_{i,t}$ is the output of heat unit. $N_j^{HS}$ is a node connected to the heating head $j$. ${\underset{¯}{T}}_n^s, {\overline{T}}_n^s$ is the upper and lower range limit for supplying pipe node temperatures. $I^{CHP}$, $I^{HS}$, and $N_j^{HS}$ are connected to the CHP unit, and the tube collection of the heating first station and the collection of nodes belong to the heating.

2) Temperature station model:

In order to realize the exchange of heat load in the heating system, the heat transfer station model is constructed.

$c^w\cdot m_l^{HES}\cdot \left(T_{n,t}^s-{\tau }_{n,t}^r\right)=H_{l,t}^{HES}, \forall l\in I^{HES}, n=N_l^{HES}, t\in T_d(20)$

${\underset{¯}{T}}_n^r\le {\tau }_{n,t}^r\le {\overline{T}}_n^r(21)$

where $m_l^{HES}$ is the mass flow of the heat exchange station (HES) $l$, $m_{l,t}^{HES}$ is the heat load ${\underset{¯}{T}}_{n }^r$ of the switch $l$ at the period $t$, and ${\overline{T}}_n^r$ is the upper and lower range limit of the returns of the pipe node temperature.

3) Temperature mixing: Mass flowing into the same node is mixed, and the temperature of the mixed mass as a result of energy conservation is as follows:

${\displaystyle {\sum }_{b\in V^{-}}\left(T_{b,t}^{s,out}{m}_b^s\right)}=T_{i,t}^S{\displaystyle {\sum }_{b\in {\text{Ω}}_{V^{-}}}{m}_b^s, t\in T_d}(22)$

${\displaystyle {\sum }_{b\in V^{+}}\left(T_{b,t}^{r,out}{m}_b^r\right)}=T_{i,t}^r{\displaystyle {\sum }_{b\in {\text{Ω}}_{V^{+}}}{m}_b^r, t\in T_d}(23)$

where $V^{-}$ indicates a set of pipelines at the end of the node V, and $V^{+}$ means a set of pipes that start with node V.

4) Temperature network pipeline dynamic model based on node method

It can be seen from Formula (2) that the mass flow does not change, and the amount of water flowing and flowing out does not change. The historical inlet temperature is used to estimate the outlet temperature without heat loss as follows:

$T_{b,t}^{\prime x,out}=\left(1-k_b\right)T_{b,t-{\gamma }_b-1}^{x,in}+k_b{T}_{b,t-{\gamma }_b}^{x,in}, \forall b\in I^{pipe}, x\in \left\{s,r\right\}, t\in T_d(24)$

$T_{b,t}^{x,out}=T_t^{am}+J_{b,t}\left(T_{b,t}^{\prime x,out}-T_{G,t}\right),\forall b\in I^{pipe}, x\in \left\{s,r\right\}, t\in T_d(25)$

$\{\begin{array}{c}{\gamma }_b={\text{min}}_{n\in N}\left\{n:s.t. n{\mu }_b\text{Δ}t\ge \rho A_b{L}_b\right\}\\ R_b={\gamma }_b{\mu }_b\Delta t\\ k_b=\left(R_b-\rho A_b{L}_b\right)/{\mu }_b\Delta t\\ J_b=exp\left[-\frac{h_b\text{Δ}t}{c^w{\rho }^w{A}_b}\left({\gamma }_b+\frac{1}{2}-k_b\right)\right]\end{array}(26)$

Among them, $T{\prime }_{b,t}^x$ represents the mass flow temperature of the pipe b at the t hour. The superscript out and in respectively indicate the inflow end and outflow end of the pipe. $I^{pipe}$ indicates a collection of heating networks. $T_d$ represents the time collection of the scheduling cycle. $T_{b,t}^x$ represents the mass flow temperature flowing out of the t hour after the heat loss. $T_{G,t}$ represents the ambient temperature of the T moment. $c^w$ indicates a specific heat capacity of water in the water flow in the pipeline.

Modeling and Solution of Electrothermal Coupling System

Objective Function

$\text{min}\left(C^{NC}+C^W+C^{CHP}\right)(27)$

$C^{\text{NC}}$ denotes the operation cost of non-CHP thermal units, $C^{\text{W}}$ denotes the penalty cost of wind power spillage, and $C^{\text{CHP}}$ denotes the operation cost of CHP units. $I$ represents a collection of units.

1) The operation cost of a non-CHP thermal unit is defined as a quadratic function of the generation dispatch

$C^{NC}={\displaystyle {\sum }_{t=1}^T{\displaystyle {\sum }_{i\in I^{NC}}\left(a_i{P}_{i,t}^2+b_i{P}_{i,\text{t}}+c_i\right)}}(28)$

$a_i$, $b_i$, and $c_i$ are the cost factors of the conventional unit; $T$ is the scheduling period; $I^{NC}\text{ is a collection of conventional units}$; $P_{i,\text{t}}$ is the electric power output of the unit i at time t.

2) Wind abandonment cost of wind farm

$C^W={\displaystyle {\sum }_{t=1}^T{\displaystyle {\sum }_{i\in I^W}{\sigma }_{i\cdot }\left({\overline{P}}_{i,t}^w-p_{i,t}\right)}}(29)$

${\sigma }_i$ is the penalty factor for abandonment of wind farm i; ${\overline{P}}_{i,t}^w$ is forecasted output for wind farm i at time period t; $I^W$ is the set for wind farms.

3) Operation cost of CHP unit

$C^{CHP}={\displaystyle {\sum }_{t=1}^T{\displaystyle {\sum }_{i\in I^{CHP}}\left({\gamma }_1{P}_{i,t}^2+{\gamma }_2{P}_{i,\text{t}}+{\gamma }_3{h}_{i,j}^2+{\gamma }_4{h}_{i,t}+{\gamma }_5{P}_{i,\text{t}}{h}_{i,t}+{\gamma }_6\right)}}(30)$

${\gamma }_1,{\gamma }_2,{\gamma }_{3,}{\gamma }_4,{\gamma }_5,{\gamma }_6$ is the cost coefficient of i CHP unit. $i^{CHP}$ is the set for CHP; $h_{i,t}$ is the thermal power output of unit $i$ at time t.

Constraint Condition

1) Power balance constraints:

${\displaystyle {\sum }_{i\in I^{NC}}{P}_{i,t}}+{\displaystyle {\sum }_{i\in I^{CHP}}{P}_{i,t}}+{\displaystyle {\sum }_{i\in I^W}{P}_{i,t}^W}=L_t(31)$

$L_t$ is the electric load at time t.

2) Generation output constraints for non-CHP units:

$P¯i\le P_{i,t}\le {\overline{P}}_i, \forall i\in I^{NC}(32)$

$P¯i$ and ${\overline{P}}_i$ represent the minimum and maximum output power of unit i.

3) Spinning reserve constraint for non-CHP units:

$0\le r{u}_{i,t}\le RAM{P}_i^{up}(33)$

$0\le r{d}_{i,t}\le RAM{P}_i^{down}, r{d}_{i,t}\le p_{i,t}-P¯i(34)$

$r{u}_{i,t}$ and $r{d}_{i,t}$ are reserved for the up/down rotation of the unit at time; $RAM{P}_i^{up}$ is upward ramping capability of generation unit $i$. $RAM{P}_i^{down}$ Downward ramping capability of generation unit $i$.

4) Operation constraints of wind power plant:

$0\le p_{i,t}^w\le {\overline{p}}_{i,t}^w(35)$

$p_{i,t}^w$ is wind farm output; ${\overline{p}}_{i,t}^w$ is predicted available wind energy of wind farm $i$ at period $t$.

5) Ramping constraints:

$-RAM{P}_i^{down}\le P_{i,t}-P_{i,t-1}\le RAM{P}_i^{up}, \forall i\in I^{NC}\cup I^{CHP}, t\in T(36)$

6) Feasible region constraint of CHP unit:

$P_{i,t}\ge r_i{h}_{i,t},i\in I^{CHP}(37)$

$F_{i,\text{min}}\le {\rho }_i^p{P}_{i,t}+{\rho }_i^q{h}_{i,t}\le F_{i,\text{max}}(38)$

$0\le h_{i,t}\le h_{i,\text{max}}(39)$

$r_i$ is CHP unit electrothermal coupling coefficient, $F_{i,\text{min}}$/$F_{i,\text{max}}$ is minimum/maximum fuel consumption, ${\rho }_i^p$ is fuel consumption rate of electricity output, ${\rho }_i^q$ is fuel consumption rate of heat output, and $h_{i,\text{max}}$ is the maximum heat output of the CHP unit.

7) CHP unit constraints: Defined in Eqs (18) and (19)

8) HES constraints: Defined in Eqs (20) and (21)

9) Temperature mixing constraints: Defined in Eqs (22) and (23)

10) Temperature dynamics constraints: Defined in Eqs (24) and (26)

Simulation Results

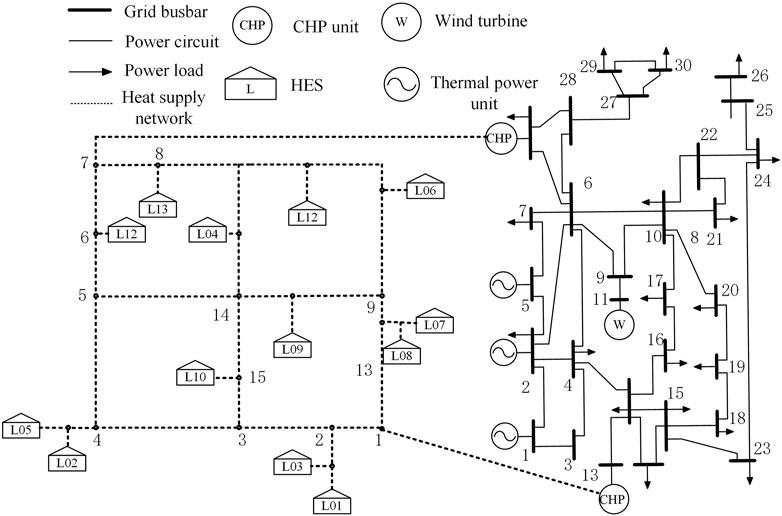
The structure of this calculation example adopts the combined heat and power system shown in Figure 2. The power supply type and unit parameters of the system are shown in Supplementary Appendix Tables A1–A3. The calculation example is day-ahead scheduling, and its scheduling period is 24 h which takes 1 h as the scheduling unit. The time resolution of the heat network model is 5 min. The electrical load of the system, the total heat load of the district heating system, and the predicted maximum output of wind power are shown in Supplementary Appendix Tables B1–B3, and the heating network pipeline parameters are shown in Supplementary Appendix Table 1.

FIGURE 2

FIGURE 2. Example model of combined electric heating system.

Precision Analysis of the Ring Network After Loop Removal

To verify the accuracy of the proposed strategy, four different control modes are compared in the paper:

Model 1: The initial model of the original 35-pipe multi-source ring heating network.

Model 2: After the first loop removal, model 1 is equivalent to an approximate equivalent model of 32 heating network pipes.

Model 3: After the second loop removal, model 2 is equivalent to the approximate equivalent model of 29 heating network pipes.

Model 4: Model 3 is further resolved into a topological equivalent heating network model of 12 heating pipes.

The pipe simplification results of the model are shown in Table 1, model 2, and model 3; the loop removal operation is carried out for the multi-source annular heating network model 1. After the loop removal, the total length of model 1 is reduced to a certain extent, and the loop structure is removed, which greatly reduces the complexity of the entire network. On the basis of model 3, model 4 further simplifies the model after loop removal and equivalence (using reference 14, traditional tree-shaped heating pipe simplification method), reducing the total number of pipes to 34.29% of the original network. The error of the time delay may be due to the loop structure of the heating pipeline; at least one node will have two different time delays when the loop is removed. This article only uses the weighted average of its time delay to calculate, which will cause a certain error. After the above steps, the topological de-ring of the multi-source ring heating network is approximately equivalent while ensuring that the total heat loss remains unchanged.

TABLE 1

TABLE 1. The pipeline simplification result of the model.

In addition to the above, we also need to consider the accuracy of different models after simplification. The initial water supply temperature is set in this paper. the return temperature and pipeline supply temperature curves of model 1 were compared with those of models 2, 3, and 4, respectively. The temperature of each model before and after simplification is compared and analyzed to verify whether the temperature is roughly the same before and after simplification.

For model 2 and model 3, the initial supply temperature and return temperature of the initial node and end point of loop removal were selected to compare with the temperature of the node before loop removal. It can be seen from Figure 3(A1, A2) that the supply temperature curve remains basically unchanged before and after the pipeline is simplified, and the return temperature is the same in Figure 3(A3, A4). The blue line in Figure 3(A3, A4) shows no significant change in temperature; because there is a time delay in the heat transfer process of the heating pipeline, the load node that is close to the heat source first feeds back the change of temperature, but the mass flow of a single load is limited, so the previous change is not obvious.

FIGURE 3

FIGURE 3. (A) Temperature comparison curve after ring. (B) Each unit output dispatch plan.

After removing the loop first and simplifying it later, the loop heating network of multi-heat source combined heating is gradually simplified, which reduces the complexity of the current multi-source loop heating pipeline model. Using the equivalent simplification method of multi-source heating network to get rid of loops, model 4 is obtained, and model 1 is equivalently simplified to 12 pipes. Compared with the initial loop heating network of 35 pipes, the heating network is simplified by 65.717%, and the heating network pipe constraints are reduced by 65.717% in the scheduling model, which greatly reduces the complexity of the model′s topology and the difficulty of solution. Figure 3(5) shows the accuracy comparison of the final pipeline simplification.

Analysis of the Result of Combined Electric and Heating Dispatching for Loop Heating Network

In order to verify the accuracy and validity of the combined electric heating dispatching results based on the approximate equivalent model of heat network after loop removal, in this section, the electrothermal scheduling results of model 1 and model 4 are compared. Figures 3(B1, B2) show the optimal electric output of units of the two models, where Figures 3(B1, B2) are the thermal output of CHP unit; Figure 3B shows the unit power output scheduling plan, where Figure 3(B3) is the output of wind farm. Figures 3(B4, B5, B6) are the output of three thermal power units, respectively, and Figures 3(B7, B8) are the thermal output of CHP units. It can be seen that the electrical and thermal outputs of the two models are basically the same, except that there is a large error between the thermal and electrical outputs of CHP unit 1 at the initial stage (1, 2 h).

The experimental results show that the scheduling costs of model 1 and model 4 are respectively 1,193,400 yuan and 1,190,300 yuan, indicating that the simplification of the model does not affect the scheduling costs. Moreover, the computation time of simplified model 4 is reduced by 60.11% compared with the scheduling time of model 1.

Conclusion

This paper proposes a method of simplifying a multi-source cyclic heating network topology approximation. The simulation results show that the multi-heat source ring heating network was first removed and then simplified. On the premise of ensuring accuracy, the topology complexity of the ring heating pipeline model was reduced by 65.717%, the complexity of calculation was reduced, and the solving time in the scheduling process was further reduced.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

JY put forward the main research points. JY and DZ completed the manuscript writing and revision. LZ completed the simulation research. ZL collected the relevant background information. TZ revised the grammar and expression.

Funding

This manuscript was supported in part by the National Natural Science Foundation of China 52007103.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2021.800906/full#supplementary-material

References

Jiang, Y., Wan, C., Audun, B., and Song, Y. (2019). “Combined Heat and Power Dispatch Using Simplified District Heat Flow Model[C],” in 2019 IEEE Power & Energy Society General Meeting (PESGM) (Atlanta, GA, USA: IEEE). doi:10.1109/PESGM40551.2019.8973926

CrossRef Full Text | Google Scholar

Larsen, H. V., Pálsson, H., Bøhm, B., and Ravn, H. F. (2002). Aggregated Dynamic Simulation Model of District Heating Networks. Energ. Convers. Manag. 43, 995–1019. doi:10.1016/s0196-8904(01)00093-0

CrossRef Full Text | Google Scholar

Li, H., Zhang, X., and Zhou, H. (2021). Day-Ahead Economic Dispatch of Integrated Energy System Considering the Uncertainty of Source and Load [J]. Sci. Tech. Eng. 21 (18), 7.

Google Scholar

Li, Z., Wu, W., Shahidehpour, M., Wang, J., and Zhang, B. (2017). “Combined Heat and Power Dispatch Considering Pipeline Energy Storage of District Heating Network[C],” in 2017 IEEE Power & Energy Society General Meeting (PESGM) (IEEE). doi:10.1109/TSTE.2015.2467383

CrossRef Full Text | Google Scholar

Lu, S., Gu, W., Yu, W., and Zhou, S. (2019). High Resolution Modeling and Decentralized Dispatch of Heat and Electricity Integrated Energy System[J]. IEEE Trans. Sust. Energ. 99, 1451–1463. doi:10.1109/TSTE.2019.2927637

CrossRef Full Text | Google Scholar

Shen, X., Ouyang, T., Khajorntraidet, C., Li, Y., Li, S., and Zhuang, J. (2021). Mixture Density Networks-Based Knock Simulator. Ieee/asme Trans. Mechatron. 2021, 1. doi:10.1109/TMECH.2021.3059775

CrossRef Full Text | Google Scholar

Shen, X., and Raksincharoensak, P. (2021). Pedestrian-aware Statistical Risk Assessment. IEEE Trans. Intell. Transport. Syst. 2021, 1–9. doi:10.1109/TITS.2021.3074522

CrossRef Full Text | Google Scholar

Shen, X., Zhang, Y., Sata, K., and Shen, T. (2020). Gaussian Mixture Model Clustering-Based Knock Threshold Learning in Automotive Engines. Ieee/asme Trans. Mechatron. 25 (6), 2981–2991. doi:10.1109/TMECH.2020.3000732

CrossRef Full Text | Google Scholar

Shi, G., Yang, L., and Zhang, H. (2020). Multi-heat Source Dispatching Optimization Model for central Heating System[J]. Therm. Power Generation 049 (003), 68–75. doi:10.19666/j.rlfd.201909203

CrossRef Full Text | Google Scholar

Tang, M., Luo, Y., and Hu, B. (2021). Summary of Electric and Heating Joint Dispatching Model [J]. Power Syst. Prot. Control 48 (23), 15.

Google Scholar

Tian, Y., Song, J., and Li, S. (2017). Development Status and Trend of Multi-Heat Source Looped Pipe Network Operation Technology[J]. SHANXI Architecture 8, 142–143. doi:10.13719/j.cnki.cn14-1279/tu.2017.22.079

CrossRef Full Text | Google Scholar

Wang, D., Zhi, Y.-q., Jia, H.-j., Hou, K., Zhang, S.-x., Du, W., et al. (2019). Optimal Scheduling Strategy of District Integrated Heat and Power System with Wind Power and Multiple Energy Stations Considering thermal Inertia of Buildings under Different Heating Regulation Modes. Appl. Energ. 240 (240), 341–358. doi:10.1016/j.apenergy.2019.01.199

CrossRef Full Text | Google Scholar

Wu, C., Huang, S., Peng, X., and Liu, F. (2019). Optimal Design of Multi-Heat Source central Heating System [J]. Reg. governance 253 (27), 145–149. doi:10.1177/1687814018789504

CrossRef Full Text | Google Scholar

Yang, L. (2020). Optimal Analysis of Multi-Heat Source Dispatching in central Heating System[J]. Process and Equipment 07, 245–248. doi:10.3969/j.issn.1673-0038.2020.21.179

CrossRef Full Text | Google Scholar

Yang, N., Huang, Y., Hou, D., Liu, S., Ye, D., Dong, B., et al. (2019). Adaptive Nonparametric Kernel Density Estimation Approach for Joint Probability Density Function Modeling of Multiple Wind Farms. Energies 12, 1356. doi:10.3390/en12071356

CrossRef Full Text | Google Scholar

Yang, N., Liu, S., Deng, Y., and Xing, C. (2021). An Improved Robust SCUC Approach Considering Multiple Uncertainty and Correlation. IEEJ Trans. Elec Electron. Eng. 16, 21–34. doi:10.1002/tee.23265

CrossRef Full Text | Google Scholar

Yang, N., Yang, C., Xing, C., Ye, D., Jia, J., Chen, D., et al. (2021). Deep Learning-Based SCUC Decision-Making: An Intelligent Data-Driven Approach with Self-Learning Capabilities. IET Gener. Transm. Distrib. 2021, 1–12. doi:10.1049/gtd2.12315

CrossRef Full Text | Google Scholar

Yang, Z., Chang, W., and Xia, M. (2019). Research on Optimal Scheduling of Multi-Heat Source Combined Heating System[J]. Energy and Energy Saving 12, 56–58. doi:10.16643/j.cnki.14-1360/td.2019.12.024

CrossRef Full Text | Google Scholar

Yu, Y., Chen, H., Chen, J., Chen, C., and Wu, J. (2019). Optimal Operation of the Combined Heat and Power System Equipped with Power-To-Heat Devices for the Improvement of Wind Energy Utilization. Energy Sci Eng 7, 1605–1620. doi:10.1002/ese3.375

CrossRef Full Text | Google Scholar

Zhang, L., Xie, Y., Ye, J., Xue, T., Cheng, J., Li, Z., et al. (2021). Intelligent Frequency Control Strategy Based on Reinforcement Learning of Multi-Objective Collaborative Reward Function. Front. Energ. Res. 9, 1. doi:10.3389/fenrg.2021.760525

CrossRef Full Text | Google Scholar

Zheng, J., Zhou, Z., Zhao, J., and Wang, J. (2018). Integrated Heat and Power Dispatch Truly Utilizing thermal Inertia of District Heating Network for Wind Power Integration. Appl. Energ. 211, 865–874. doi:10.1016/j.apenergy.2017.11.080

CrossRef Full Text | Google Scholar