A Control Parameters Design Method With Multi-Constrains for an LCL-Filtered Grid-Connected Inverter in a Weak Grid

Under weak grid conditions, the variation of the grid impedance will affect the steady-state and dynamic performance of the LCL-filtered grid-connected inverter and even make the inverter unstable. To ensure the system stability and further improve the dynamic performance in a weak grid, a control parameter design method with multi-constrains considering the system bandwidth for the current controller and active damping is proposed in this paper. First, based on the current controller and active damping with only grid current feedback, the effects of control parameters and grid impedance on the LCL resonant suppression and the performance of the inverter are analyzed. Moreover, the parameter constraints of the controllers are derived considering the grid impedance, including stability, resonance suppression, and margin constraints. Furthermore, as the system bandwidth affects the dynamic performance of the inverter, combined with the obtained multi-constraints, the optimal control parameters are determined by achieving the maximum bandwidth of the system against the impedance variation. Compared with other two methods, when the proposed method is applied, the system can operate with a better dynamic and steady-state performance. Finally, experiments are performed on a 2 kW three-phase grid-connected inverter in the weak grid, which verify the effectiveness of the parameter design method proposed in this paper.

1 Introduction

Currently, distributed power generation systems based on renewable energy have been widely used in power grids (Zhang et al., 2021; Li et al., 2021), and the three-phase grid-connected inverter with an LCL or L filter, as an important interface between the distributed generation system and the grid, plays an important role in it (Busada et al., 2005; Wu and Lehn, 2006; Malinowski and Bernet, 2008; Xin et al., 2017; Xing et al., 2018).

Although the LCL filter has better performance and switching harmonic attenuation ability than the L filter (Lindgren and Svensson, 1998; Hava et al., 1995), the inherent resonance problem of the LCL filter is harmful to the quality of grid current and even affects the stability of the system (Parker and McGrath, 2012). Compared with passive damping solutions proposed in Liserre et al. (2005), Dannehl et al. (2011) that cause non-negligible power loss, the active damping (AD) method is more flexible and efficient. In the literature (Jiao and Lee, 2015), an RLC damping circuit for the LCL filter is investigated to solve the resonant frequency peak of an LCL grid-connected inverter, which is equivalent to an AD control method essentially. The literature (Pena-Alzola et al., 2014) proposes an AD method by adding a notch filter to the forward channel for canceling the LCL filter resonant peak, but its robustness should be improved, and the parameter adjustment is relatively complex. The literature (Dannehl et al., 2010; Chenlei Bao et al., 2014; Wang et al., 2015) proposes AD algorithms with three different kinds of feedback signals, which are the filter capacitor current, the filter capacitor voltage, and the grid-side current. In order to decrease power losses caused by multiple sensors and reduce the system cost, the grid-current-feedback AD method is adopted in Xu et al. (2013a), Zhou et al. (2018). Meanwhile, a proportional resonant (PR) controller is preferred to provide suitable power quality to the grid for the inverter, which can significantly increase the gain at the intended frequency, track of the sinusoidal waveform with zero steady-state error, and have better disturbance rejection capability (Holmes et al., 2017; Zmood and Holmes, 2003). According to the method in Liu et al. (2020), a parameter range can be obtained for the PR controller and AD loop, which could ensure the grid current quality and system stability under ideal grid conditions.

However, due to the direct interconnection with power grids, system control performance and stability may be affected by weak grid conditions, for example, gird impedance variation (Sun, 2011). It is known that grid impedance can lead to sustained harmonic resonance or other instability problems, which destabilizes the grid-connected inverter (Liserre et al., 2006). Furthermore, the wide-range variation of the grid impedance may affect the resonant suppression for the LCL filter in a weak grid (Liu et al., 2020; Xu et al., 2013b). Therefore, it is necessary to design the control parameters reasonably considering grid impedance in the weak grid.

The existing approaches have been proposed to maintain the grid-connected inverter work normally and stably under weak grid conditions. The literature (Sun, 2011) proposed a method to determine inverter-grid system stability using the inverter output impedance and the grid impedance. It is shown that a grid-connected inverter system will remain stable if the ratio between the grid impedance and the inverter output impedance satisfies the Nyquist stability criterion. Then, based on the impedance-based stability criterion for grid-connected inverters, the literature (Cespedes and Sun, 2014a; Yang et al., 2014; Xu et al., 2018; Zhu et al., 2020) proposed different methods to ensure the stable operation of the grid-connected inverter system in the weak grid. However, this analysis method based on the impedance-based stability criterion needs to design the parameters in advance for the stable operation of the grid-connected inverter system, without considering the grid impedance. Moreover, this method is normally used to analyze the stability of the grid-connected inverter in the weak grid, in which the analysis of the dynamic performance is not considered. In addition, other scholars proposed a control strategy by the grid impedance detection technique to eliminate the impact of the grid impedance on the grid-connected inverter system (Liserre et al., 2007; Cespedes and Sun, 2014b). Although the automatic adaptive control technology based on the grid impedance online measurement can improve the adaptability of the grid-connected inverter system to the weak grid effectively, and the harmonics injected during impedance detection will deteriorate the quality of grid currents. Besides, the control performance of the inverter system depends on the rapidity and accuracy of the grid impedance online measurement, and the dynamic performance of system is still not well addressed.

Above all, under the weak grid, the multi-constrains including stability constraints, resonance suppression constraints, and margin constraints have not been considered to design the current controller and active damping loop comprehensively in these solutions, which determine stability, grid-current quality, and dynamic and steady-state performance of the inverter. Furthermore, considering the variation of grid impedance, the impact of grid impedance on the bandwidth of the inverter system should also be concerned, which also affects the dynamic performance of the system.

In this paper, aiming at improving the dynamic and stability performance of the three-phase LCL-filtered grid-connected inverter with a good quality of the grid current in the weak grid, a parameter design method for the current controller and active damping with grid-side current feedback is proposed in this paper. In Section 2, the mathematical model of the three-phase LCL-filtered grid-connected inverter in the weak grid is established. The influence of the PR controller and the active damping circuit on the resonance peak suppression of the LCL filter and the stability of the inverter under weak grid conditions are analyzed. In Section 3, the parameter constraints of the current controller and active damping loop are analyzed in the weak grid, including stability, resonance suppression, and margin constraints. In Section 4, based on the derived multi-constraints, a parameter design method for the active damping and current controller is proposed, which can achieve the maximum bandwidth of the inverter considering the impedance variation so that the system can operate with a good dynamic and steady-state performance. The experimental results in Section 5 verify the effectiveness of the parameter design method proposed in this paper.

2 Modeling and Control of the LCL-Filtered Grid-Connected Inverter in the Weak Grid

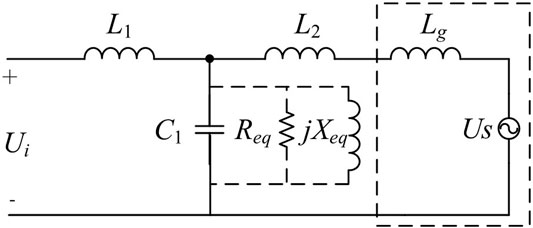
Figure 1 shows the main circuit of the three-phase LCL-filtered grid-connected inverter under the weak grid. L_1x (x = a,b,c) are LCL filter inverter-side three-phase inductors, whose value is L₁. C_x (x = a,b,c) are LCL filter three-phase capacitors, whose value is C₁. L_2x (x = a,b,c) are LCL filter grid-side three-phase inductors, whose value is L₂. The weak grid consists of ideal voltage sources e_x (x = a,b,c) and inductive grid impedances L_gx (x = a,b,c), and the value of grid impedance is L_g. u_ix (x = a,b,c) are inverter three-phase output voltages, i_1x (x = a,b,c) are three-phase inverter-side currents of the LCL filter, and i_2x (x = a,b,c) are three-phase grid-side currents of the filter. V_dc is the dc-bus voltage.

FIGURE 1

FIGURE 1. Main circuit diagram of the three-phase LCL-filtered grid-connected inverter.

In the two-phase static coordinate system (αβ), the closed-loop control block diagram of the three-phase LCL-filtered grid-connected inverter is shown in Figure 2, where K_pwm = V_dc/2 is the gain of the PWM inverter. G_c(s) is the proportional resonance controller expressed as

$G_c\left(s\right)=K_p+K_r\frac{2{\omega }_{i}s}{s^2+2{\omega }_{i}s+{\omega }_o^2}(1)$

where K_p and K_r are the proportional gain and the resonant gain of the PR controller, ω_i is the cut-off angular frequency of the PR controller, and ω_o is the grid fundamental angular frequency (Chenlei Bao et al., 2014).

FIGURE 2

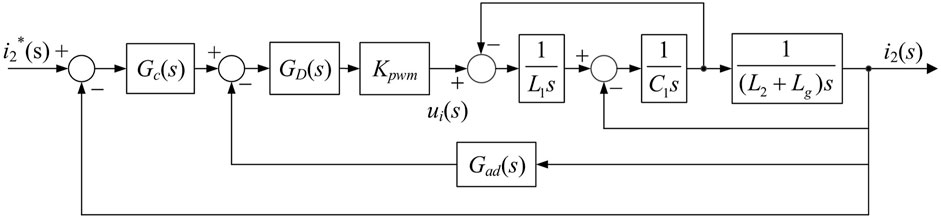
FIGURE 2. Closed loop control block diagram of the grid-connected inverter in the αβ coordinate system.

G_ad(s) is the transfer function of the AD loop. Considering the complexity of the AD loop which affects the characteristic of three-phase LCL-filtered grid-connected inverter in the low-frequency range, G_ad(s) is implemented by a second-order differential term in the s-domain (Liu et al., 2020). G_ad(s) can be expressed as

$G_{ad}\left(s\right)=k_{ad}\cdot s^2(2)$

where k_ad is the AD coefficient.

G_D(s) is the transfer function of the total delay due to digital control, consisting of the computation delay, the zero-order holder, and the sampling switch. Considering that the computation delay may reduce the control loop bandwidth and make the system unstable, a previously reported time-delay compensator (Lu et al., 2018), as a first-order digital filter with a phase-lead characteristic, is directly adopted to mitigate time delay here. G_D(s) is expressed as

$G_D\left(s\right)=\frac{1}{T_s}\cdot \frac{1-e^{-s{T}_s}}{s}\approx \frac{1}{1+0.5s{T}_s}(3)$

where T_s is the sampling period.

The transfer function from u_i(s) to i₂(s) for the LCL filter can be derived as

$G_1\left(s\right)=\frac{i_2\left(s\right)}{u_i\left(s\right)}=\frac{1}{C_1{L}_1\left(L_2+L_g\right)s\left(s^2+{\omega }_{res}^2\right)}(4)$

${\omega }_{res}=\sqrt{\frac{L_1+L_2+L_g}{C_1{L}_1\left(L_2+L_g\right)}}(5)$

where ω_res is defined the resonant frequency when grid impedance L_g is considered.

Generally, the resonant gain K_r of the PR controller can be neglected at the cutoff frequency ω_c and the frequencies higher than ω_c (Chenlei Bao et al., 2014; Geng et al., 2018). Hence, in the process of analyzing system stability, the current controller G_c(s) can be approximated as K_p. From (1–4), the open-loop transfer function of the system can be derived as

$G_{op}\left(s\right)=\frac{G_c\left(s\right)G_1\left(s\right)K_{\text{PWM}}}{1+0.5s{T}_s+G_1\left(s\right)K_{\text{PWM}}{k}_{ad}{s}^2}(6)$

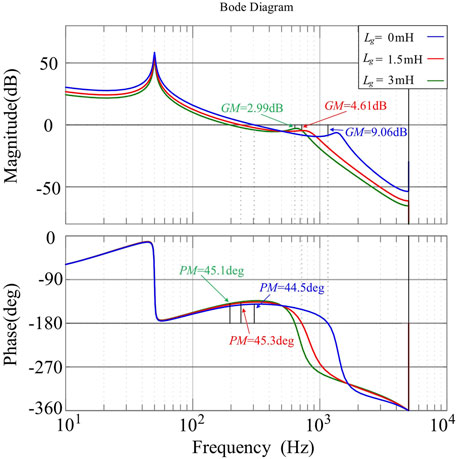
In order to analyze the influence of the PR controller and the active damping loop on the resonance peak suppression of the LCL filter and the stability of the inverter under weak grid conditions, Figure 3 shows the Bode diagram of the open-loop transfer function of the system. LCL filter parameters are shown in Table 1, where f_s is the sampling frequency.

FIGURE 3

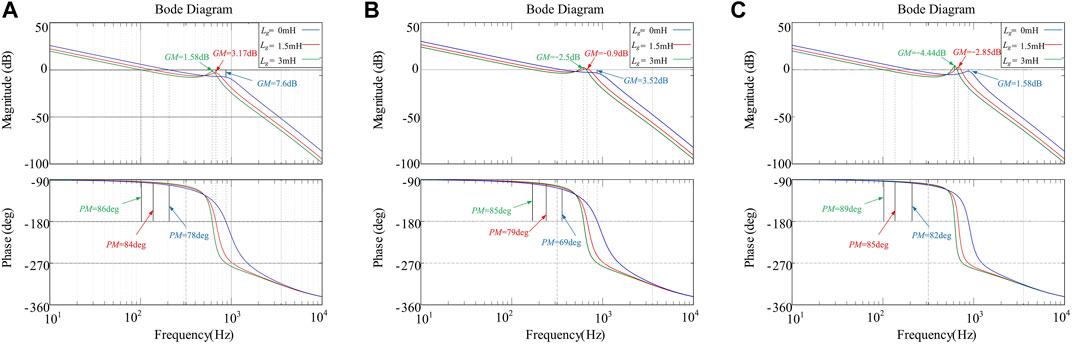
FIGURE 3. Bode diagram of the system open-loop transfer function. (A)K_p = 0.025, k_ad = 2 × 10^–9. (B) K_p = 0.04, k_ad = 2 × 10^–9. (C) K_p = 0.025, k_ad = 1 × 10^–9.

TABLE 1

TABLE 1. Parameters of the LCL filter.

From Figure 3A, it can be seen that when K_p = 0.025 and k_ad = 2 × 10^–9, the system can maintain stable under different L_g conditions. Supposing that K_p is modified to 0.04, as shown in Figure 3B, when L_g increases, the gain margin (GM) of the system changes from positive to negative, and the grid-connected inverter becomes unstable. Otherwise, supposing that k_ad is modified to 1 × 10^–9, as shown in Figure 3C, when L_g increases, the GM of the system also changes from positive to negative, which means that the grid-connected inverter becomes unstable. Besides, when L_g varies, the resonant frequency of the system will shift, which affects the ability of the LCL resonant suppression. Another problem worthy of attention is that the bandwidth of the open-loop transfer function decreases with the increase of L_g. Taking L_g = 3 mH as an example, the bandwidth of the system is close to fundamental frequency, which may not maintain the inverter a good dynamic performance (Dorf and Bishop, 2011).

Above all, both the control parameters and L_g affect the ability of the LCL resonant suppression and the performance of the LCL grid-connected inverter. Therefore, in order to ensure the stable operation of the system and improve the dynamic performance under the weak grid, a multi-constrain parameter design method for the active damping loop and current controller considering system bandwidth is proposed in Sections 3, 4.

3 Constraints of Active Damping and the Current Controller for the LCL-Filtered Grid-Connected Inverter

3.1 Stability, Resonance Suppression, and Gain Margin Constraints with the Variation of Grid Impedance

In order to ensure the effective operation of the LCL grid-connected inverter and make it have better stability and dynamic response performance, the parameters of the current controller and active damping loop for the grid-connected inverter need to meet certain constraints.

Based on (6), by the Routh-Hurwitz criterion, the constrain to ensure the system stability is

$0<K_{\text{p}}<K_{\text{p}1}\left(k_{ad},L_g\right)(7)$

where

$K_{\text{p}1}\left(k_{ad},L_g\right)=\frac{k_{ad}\left(L_1+L_2+L_g\right)}{C_1{L}_1\left(L_2+L_g\right)}(8)$

Due to the existence of the delay G_D(s), the resonant frequency ω_res of the LCL filter will shift after adding the active damping control loop, note that as ω_res'. Figure 4 can be obtained by equivalent transformation of Figure 2. With this representation, it immediately informs that a virtual impedance Z_eq in parallel with filter capacitor C₁ is introduced by the AD control loop. Z_eq can be expressed as

$Z_{\mathrm{eq}}\left(s\right)=\frac{L_1\left(L_2+L_g\right)\left(1+0.5s{T}_s\right)}{K_{\mathrm{PWM}}{k}_{ad}}(9)$

FIGURE 4

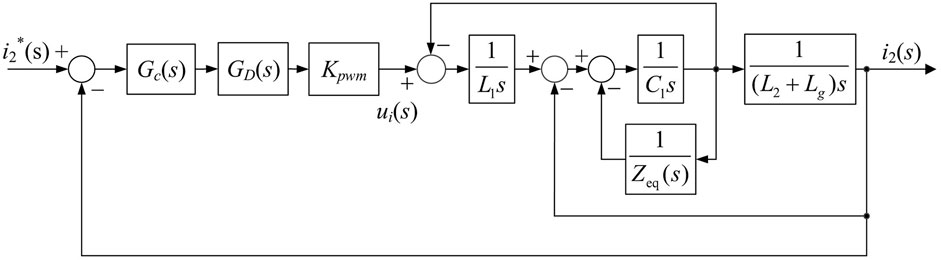
FIGURE 4. Equivalent closed loop control block diagram of the grid-connected inverter in the αβ coordinate system.

Figure 5 shows the equivalent physical circuit of the LCL filter, where Z_eq = R_eq//X_eq. Substitute s = jω into (9), the expressions of R_eq and X_eq are given in (10)

$\begin{array}{l}{R}_{\mathrm{eq}}=\frac{L_1\left(L_2+L_g\right)\left(1+0.25{\omega }^2{T}_s^2\right)}{K_{\mathrm{PWM}}{k}_{ad}}\\ X_{\mathrm{eq}}=\frac{L_1\left(L_2+L_g\right)\left(1+0.25{\omega }^2{T}_s^2\right)}{0.5\omega T_s{K}_{\mathrm{PWM}}{k}_{ad}}\end{array}(10)$

FIGURE 5

FIGURE 5. Equivalent virtual impedance of active damping.

From Figure 5, the expression of ω_res′ of the system after adding active damping is

${\omega }_{res}\prime =\sqrt{\frac{2k_{ad}{K}_{\mathrm{PWM}}{T}_s-4C_1{L}_1\left(L_2+L_g\right)+\left(L_1+L_2+L_g\right)T_s^2+\sqrt{A}}{2T_s^2{C}_1{L}_1\left(L_2+L_g\right)}}(11)$

where

$\begin{array}{l}A=16C_1{L}_1\left(L_2+L_g\right)\left(L_1+L_2+L_g\right)T_s^2\\ +{\left(4C_1{L}_1\left(L_2+L_g\right)-2k_{ad}{K}_{\mathrm{PWM}}{T}_s-\left(L_1+L_2+L_g\right)T_s^2\right)}^2\end{array}(12)$

Generally, the gain of G_op (s = jω) should be less than 0dB at ω_res′, which maintains the suppression ability for the resonant peak. Through making 20lg|G_op (s = jω_res′)|≤0, K_p can be derived as

$K_{\text{p}}<K_{\text{p}2}\left(k_{ad},L_g\right)(13)$

where

$\begin{array}{l}{K}_{p2}\left(k_{ad},L_g\right)=\frac{\sqrt{x^2+y^2}}{K_{\mathrm{PWM}}}\\ x=0.5C_1{L}_1\left(L_2+L_g\right)T_s{\omega }_{res}^{\prime 4}-\left(0.5\left(L_1+L_2+L_g\right)T_s+k_{ad}{K}_{\mathrm{PWM}}\right){\omega }_{res}^{\prime 2}\\ y=\left(L_1+L_2+L_g\right){\omega }_{res}^{\prime }-C_1{L}_1\left(L_2+L_g\right){\omega }_{res}^{\prime 3}\end{array}(14)$

Considering the phase of G_op (s = jω) is −180° at crossing frequency ω_h, G_op (s = jω) is absolutely real at ω_h. Making Im (G_op (s = jω)) = 0, the expression of ω_h can be obtained as

${\omega }_h=\sqrt{\frac{L_1+L_2+L_g}{C_1{L}_1\left(L_2+L_g\right)}}(15)$

The grid-connected inverter system needs to have a certain gain margin (GM) to ensure sufficient stability. We assume that the ideal gain margin is GM₀ at ω_h, which is generally 3dB (Guan et al., 2019). In order to ensure GM ≥ GM₀, the gain margin constraint of K_p is

$K_{\text{p}}\le K_{\text{p}3}\left(k_{ad},L_g\right)(16)$

where

$K_{\text{p}3}\left(k_{ad},L_g\right)=\frac{k_{ad}\left(L_1+L_2+L_g\right)}{C_1{L}_1\left(L_2+L_g\right)}\cdot {10}^{-\frac{{\text{GM}}_0}{20}}(17)$

In Etxegarai et al. (2012), the maximum value of the grid impedance L_g is expressed as

$L_{g\_\max }=\frac{U_s}{{\omega }_o{I}_N\cdot \mathrm{SCR}}(18)$

where U_s is the root mean square of grid-connected voltage and I_N is the root mean square of grid-connected current.

When the grid inductance L_g is in the range [0, L_{g_max}], in order to ensure that K_p simultaneously satisfies the three constraints in (7, 13, 16), K_p needs to be less than or equal to the minimum among them as

$K_p\le \min \left\{K_{\mathrm{p}\mathrm{1}}\left(k_{ad},L_g\right),K_{\mathrm{p}2}\left(k_{ad},L_g\right),K_{\mathrm{p}3}\left(k_{ad},L_g\right)|0\le L_g\le L_{g\_\max }\right\}(19)$

which is

$K_p\le K_{\mathrm{p}3}\left(k_{ad},L_{g\_\max }\right)(20)$

3.2 Phase Margin Constraint With the Variation of Grid Impedance

In addition, the system also needs to meet the phase margin (PM) requirement for good stability and dynamic performance, and the expression of PM is

$\begin{array}{l}\mathrm{PM}=180°+\angle {\mathit{G}}_{\mathit{o}\mathit{p}}\left(s=j{\omega }_{\mathit{c}}\right)\\ =180°+\arctan \frac{{\omega }_c^2-{\omega }_{res}^2}{0.5{\mathit{T}}_{\mathit{s}}{\mathit{\omega }}_{\mathit{c}}^3-0.5{\mathit{T}}_{\mathit{s}}{\omega }_{\mathit{c}}{\omega }_{\mathit{r}\mathit{e}\mathit{s}}^2-\frac{{\mathit{k}}_{\mathit{a}\mathit{d}}{\mathit{K}}_{\mathit{PWM}}{\mathit{\omega }}_{\mathit{c}}}{{\mathit{C}}_1{\mathit{L}}_1\left({\mathit{L}}_2+{\mathit{L}}_{\mathit{g}}\right)}}\end{array}(21)$

Then, the AD coefficient k_ad can be expressed as

$k_{ad}=\frac{0.5C_1{L}_1\left(L_2+L_g\right)T_s{\omega }_c^2-0.5\left(L_1+L_2+L_g\right)T_s}{K_{\text{PWM}}}+\frac{{\omega }_{res}^2-{\omega }_c^2}{K_{\mathrm{PWM}}{\omega }_c\tan \left(\mathrm{PM}\right)}(22)$

Furthermore, the partial differential of k_ad with respect to PM is

$\frac{\partial k_{ad}}{\partial \mathrm{PM}}=\frac{{\omega }_{res}^2-{\omega }_c^2}{K_{\mathrm{PWM}}{\omega }_c}\left(-\frac{1}{{\sin }^2\mathrm{PM}}\right)(23)$

In order to make the system parameter design reasonable, the cut-off frequency ω_c should be smaller than ω_res. From (23), the active damping parameter k_ad and the phase margin PM are in a monotonically decreasing relationship.

We assuming that the ideal phase margin is PM₀, which is generally 45°. In order to ensure PM ≥ PM₀, combining (22) with (23), k_ad needs to meet

$k_{ad}\le k_{ad}\prime \left(L_g,{\omega }_c\right)(24)$

where

$\begin{array}{l}{k}_{ad}\prime \left(L_g,{\omega }_c\right)=\frac{0.5C_1{L}_1\left(L_2+L_g\right)T_s{\omega }_c^2-0.5\left(L_1+L_2+L_g\right)T_s}{K_{\mathrm{PWM}}}\\ +\frac{{\omega }_{rec}^2-{\omega }_c^2}{K_{\mathrm{PWM}}{\omega }_c\tan \left({\mathrm{PM}}_0\right)}\end{array}(25)$

The partial derivative of k_ad′ (L_g, ω_c) with respect to L_g in (25) can be obtained

$\{\begin{array}{l}\frac{\partial k_{ad}\prime \left(L_g,{\omega }_c\right)}{\partial L_g}\ge 0,{\omega }_{\mathrm{o}}<{\omega }_c\le \frac{1}{\sqrt{C_1{L}_1}}\\ \frac{\partial k_{ad}\prime \left(L_g,{\omega }_c\right)}{\partial L_g}<0,\frac{1}{\sqrt{C_1{L}_1}}<{\omega }_c<{\omega }_{res}\prime \end{array}(26)$

According to (26), when $1\text{/}\sqrt{C_1{L}_1}$ <ω_c<ω_res′, k_ad′ (L_g, ω_c) decreases monotonously with respect to L_g; when ω_o<ω_c≤ $1\text{/}\sqrt{C_1{L}_1}$, k_ad′ (L_g, ω_c) increases monotonously with respect to L_g. To make the phase margin of the system meet the requirements when L_g is in the range [0, L_{g_max}], k_ad needs to meet the following requirements:

$\{\begin{array}{l}{k}_{ad}\le k_{ad}\prime \left(0,{\omega }_c\right),{\omega }_{\mathrm{o}}<{\omega }_c\le \frac{1}{\sqrt{C_1{L}_1}}\\ k_{ad}\le k_{ad}\prime \left(L_{g\_\max },{\omega }_c\right),\frac{1}{\sqrt{C_1{L}_1}}<{\omega }_c<{\omega }_{res}\prime \end{array}(27)$

Above all, the stability, resonance suppression, gain margin, and phase margin constraints with the variation of grid impedance are derived, ensuring that the system has a good performance while suppressing LCL resonance. Besides, under the weak grid, according to 7, 13, 16, and 25, the range of K_p is affected by k_ad and L_g, and the range of k_ad is affected by ω_c and L_g. Considering the grid impedance L_g, the control parameters K_p and k_ad can be determined according to the requirements of the system for ω_c which determines the bandwidth of the system.

4 Parameter Design for Active Damping and the Current Controller of the LCL-Filtered Grid-Connected Inverter

In order to maintain the grid-connected inverter, a good dynamic performance with the stability, resonance suppression, and gain margin and phase margin constraints in the weak grid, the bandwidth (ω_c) of the system should be set to the maximal value considering the variation of the grid impedance.

According to the two cases in (27), K_p of the current controller and k_ad of the active damping loop are analyzed and solved at different ωc ranges.

4.1 Case I: $1\text{/}\sqrt{C_1{L}_1}$ <ω_c<ω_res′

From (27), in this case, if the phase margin of the system meets the requirements when L_g is in the range [0, L_{g_max}], k_ad needs to meet

$k_{ad}\le k_{ad11}\left({\omega }_c\right)(28)$

where

$k_{ad11}\left({\omega }_c\right)=k_{ad}\prime \left(L_{g\_\max },{\omega }_c\right)(29)$

At ω_c, the gain of the system open-loop transfer function equals to 1. By making |G_op (s = jω_c)| = 1, K_p can be expressed as

$K_p\left(k_{ad},L_g,{\omega }_c\right)=\frac{\sqrt{m^2+n^2}}{K_{\mathrm{PWM}}}(30)$

where

$\begin{array}{l}m=0.5C_1{L}_1\left(L_2+L_g\right)T_s{\omega }_c^4-\left(0.5\left(L_1+L_2+L_g\right)T_s+k_{ad}{K}_{\text{PWM}}\right){\omega }_c^2\\ n=\left(L_1+L_2+L_g\right){\omega }_c-C_1{L}_1\left(L_2+L_g\right){\omega }_c^3\end{array}(31)$

and then when L_g = L_{g_max}, K_p = K_p(k_ad, L_{g_max}, ω_c), K_p should also meet the constraint in (20) as

$\{\begin{array}{l}{K}_{\mathrm{p}}=K_{\mathrm{p}}\left(k_{ad},L_{g\_\max },{\omega }_c\right)\\ K_{\mathrm{p}}\le K_{\mathrm{p}3}\left(k_{ad},L_{g\_\max }\right)\end{array}(32)$

By solving (32), k_ad also needs to meet

$k_{ad}\ge k_{ad12}\left({\omega }_c\right){\omega }_c<\sqrt[4]{{10}^{-0.1\mathrm{GM}}}{\omega }_{res}\prime (33)$

where

$\begin{array}{l}{k}_{ad12}\left({\omega }_c\right)=0.5C_1{L}_1{\left(L_2+L_{g\_\max }\right)}^2\left(C_1{L}_1{L}_2{\omega }_c^2-L_1-L_2-L_{g\_\max }\right)\\ ·\frac{\left(C_1{L}_1\left(L_2+L_{g\_\max }\right){\omega }_c^3+\sqrt{B}\right){\omega }_c}{\left(C_1^2{L}_1^2{\left(L_2+L_{g\_\max }\right)}^2{\omega }_c^4-{10}^{-0.1GM}{\left(L_1+L_2+L_{g\_\max }\right)}^2\right)K_{\mathrm{P}\mathrm{W}\mathrm{M}}}\\ B=-4C_1^2{L}_1^2{\left(L_2+L_{g\_\max }\right)}^2{\omega }_c^4+{10}^{-0.1GM}{\left(L_1+L_2+L_{g\_\max }\right)}^2{T}_s^2{\omega }_c^2\\ +4\cdot {10}^{-0.1GM}{\left(L_1+L_2+L_{g\_\max }\right)}^2\end{array}(34)$

Substituting system parameters into (28, 33), when $1\text{/}\sqrt{C_1{L}_1}$ <ω_c<ω_res′, we get

$k_{ad12}\left({\omega }_c\right)>k_{ad11}\left({\omega }_c\right)(35)$

Therefore, in this case, the active damping parameter k_ad that satisfies all constraints cannot be obtained.

4.2 Case II: ω_o<ω_c< $1/\sqrt{C_1{L}_1}$

Similar to the analysis in case I, if the phase margin of the system meets the requirements when L_g is in the range [0, L_{g_max}], k_ad needs to meet

$k_{ad}\le k_{ad21}\left({\omega }_c\right)(36)$

where

$k_{ad21}\left({\omega }_c\right)=k_{ad}\prime \left(0,{\omega }_c\right)(37)$

and then when L_g = 0, K_p = K_p(k_ad, 0, ω_c), K_p should also meet the constraint in (20) as

$\{\begin{array}{l}{K}_{\mathrm{p}}=K_{\mathrm{p}}\left(k_{ad},0,{\omega }_c\right)\\ K_{\mathrm{p}}\le K_{\mathrm{p}3}\left(k_{ad},L_{g\_\max }\right)\end{array}(38)$

By solving (38), k_ad also needs to meet

$k_{ad}\ge k_{ad22}\left({\omega }_c\right)(39)$

where

$\begin{array}{c}{k}_{ad22}\left({\omega }_c\right)=0.5C_1{L}_1{\left(L_2+L_{g\_\max }\right)}^2\left(C_1{L}_1{L}_2{\omega }_c^2-L_1-L_2\right)\\ ·\frac{\left(C_1{L}_1\left(L_2+L_{g\_\max }\right){\omega }_c^3+\sqrt{B}\right){\omega }_c}{\left(C_1^2{L}_1^2{\left(L_2+L_{g\_\max }\right)}^2{\omega }_c^4-{10}^{-0.1GM}{\left(L_1+L_2+L_{g\_\max }\right)}^2\right)K_{\mathrm{PWM}}}\end{array}(40)$

Combining (37) with (40), the partial derivative of k_ad21 (ω_c) and k_ad22 (ω_c) with respect to L_g in (25) can be obtained

$\{\begin{array}{l}\frac{\partial k_{ad21}\left({\omega }_c\right)}{\partial {\omega }_c}<0\\ \frac{\partial k_{ad22}\left({\omega }_c\right)}{\partial {\omega }_c}>0\end{array}(41)$

It can be seen from (41) that k_ad21 (ω_c) decreases monotonously with respect to ω_c, and k_ad22 (ω_c) increases monotonously with respect to ω_c. By solving k_ad21 (ω_c) = k_ad22 (ω_c), the expressions of optimal active damping parameter k_{ad_opt} and optimal proportional gain K_{p_opt} can be derived as

$\{\begin{array}{l}{k}_{ad\_\mathrm{opt}}=\frac{0.5C_1{L}_1{L}_2{T}_s{\omega }_{c\_\max }^2-0.5\left(L_1+L_2\right)T_s}{K_{\mathrm{PWM}}}\\ +\frac{L_1+L_2-C_1{L}_1{L}_2{\omega }_{c\_\max }^2}{K_{\mathrm{PWM}}{\omega }_{c\_\max }\tan \left(PM\right)}\\ K_{\mathrm{p}\_\mathrm{o}\mathrm{p}\mathrm{t}}=\frac{k_{ad\_\mathrm{opt}}\left(L_1+L_2+L_{g\_\max }\right)}{C_1{L}_1\left(L_2+L_{g\_\max }\right)}\cdot {10}^{-\frac{GM}{20}}\end{array}(42)$

According to (18, 42) and system parameters in Table 2, the values of k_{ad_opt} and K_{p_opt} are respectively

$\{\begin{array}{l}{k}_{ad\_\text{opt}}=5\times {10}^{-9}\\ K_{\text{p\_opt}}=0.05\end{array}(43)$

TABLE 2

TABLE 2. Parameters of the LCL grid-connected inverter.

Therefore, to maintain the system a good dynamic performance in the weak grid, considering the maximal bandwidth of the system in the weak grid, the optimal K_p and k_ad are derived from the stability, resonance suppression, and gain margin and phase margin constraints.

In order to realize digital control, it is necessary to discretize each part of the grid-connected inverter control system. Applying the ZOH z-transformation, the transfer function of the LCL filter in (4) can be given by

$G_1\left(z\right)=\frac{{\omega }_{res}{T}_s\left(z^2-2z\cos {\omega }_{res}{T}_s+1\right)-{\left(z-1\right)}^2\sin {\omega }_{res}{T}_s}{{\omega }_{res}\left(L_1+L_2+L_g\right)\left(z-1\right)\left(z^2-2z\cos {\omega }_{res}{T}_s+1\right)}(44)$

By the Tustin method with pre-warping, the transfer function of the PR controller in (1) can be transformed to G_c(z), which can be derived as

$G_c\left(z\right)=K_p+K_r\frac{{\omega }_i\sin \left({\omega }_o{T}_s\right)\left(z^2-1\right)}{{\omega }_o\left(z^2-2z\cos {\omega }_o{T}_s+1\right)+{\omega }_i\sin \left({\omega }_o{T}_s\right)\left(z^2-1\right)}(45)$

G_ad(z) is the transfer function of the AD loop in the z-domain, by applying the backward-difference transformation to (2), G_ad(z) can be described as

$G_{ad}\left(z\right)=\frac{k_{ad}{\left(z-1\right)}^2}{T_s^2{z}^2}(46)$

The expression of the open-loop transfer function of the LCL grid-connected inverter after discretization is

$G_{\mathrm{op}}\left(z\right)=G_c\left(z\right)\cdot \frac{K_{\mathrm{pwm}}{G}_1\left(z\right)}{1+K_{\mathrm{pwm}}{G}_1\left(z\right)G_{ad}\left(z\right)}(47)$

Based on (43) and system parameters in Table 2, Figure 6 shows the Bode plot for G_op(z) with L_g variation. It can be seen that the system can remain stable and have a sufficient margin and the bandwidth of the system is relatively large. When L_g = 0 mH, L_g = 1.5 mH, and L_g = 3 mH, the bandwidths of the system are 320, 250, and 205 Hz, respectively.

FIGURE 6

FIGURE 6. Bode plot for G_op(z).

Compared with Figure 3, when the optimal parameters K_p and k_ad in (43) are applied considering the variation of L_g, not only can the constraint conditions in Section 3 be met to ensure the stable operation of the inverter but also a large bandwidth can be obtained to improve the dynamic performance.

5 Experimental Results

To verify the effectiveness of the parameter design method proposed in this paper under the weak grid, an experimental prototype of the three-phase LCL-filtered grid-connected inverter is built. The parameters of the experimental prototype are listed in Table 2. In the experimental platform, as shown in Figure 7A, a digital control system consists of a TMS320F28335 DSP and a EPM1270T CPLD. The DSP is applied for the implementation of the control algorithm mainly, which also completes the sampling of grid phase voltages and grid phase currents. Besides, the CPLD is used to arrange digital signals and realize protections for power switches. The photograph of the experimental platform is shown in Figure 7B, where the oscilloscope and power analyzer are Tektronix MDO3000 and HIOKI PW6001, respectively. By applying the proposed method and the methods in Jiao and Lee (2015) and Liu et al. (2020), comparisons of the experimental results are shown in Figures 8–13.

FIGURE 7

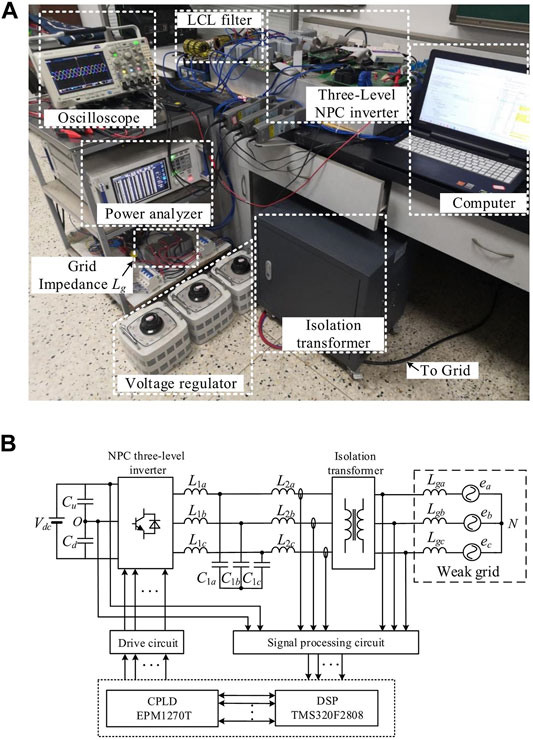
FIGURE 7. Schematic diagram and experimental photograph of the system. (A) Schematic diagram of the system. (B) Experimental photograph of the system.

FIGURE 8

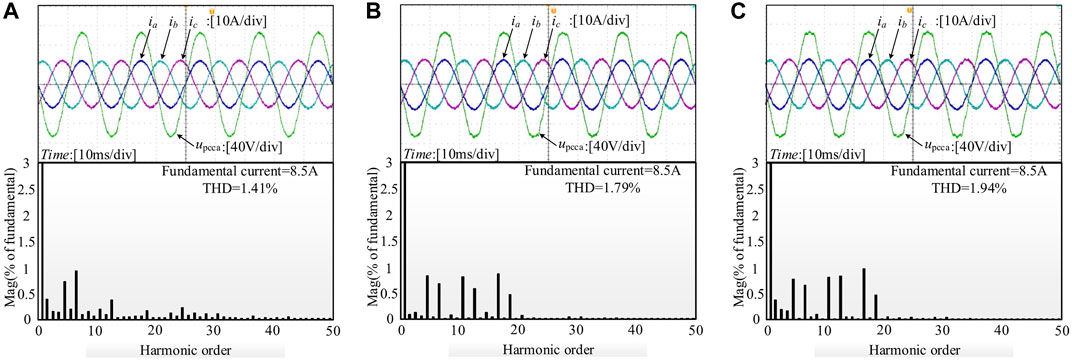
FIGURE 8. Steady-state experimental waveforms of the inverter at L_g = 0 mH: (A) with the proposed method in this paper, (B) with the method in Liu et al. (2020), and (C) with the method in Jiao and Lee (2015).

FIGURE 9

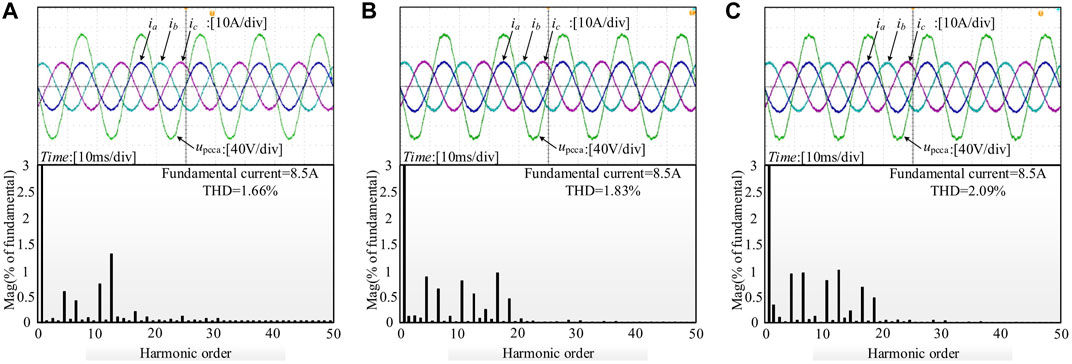
FIGURE 9. Steady-state experimental waveforms of the inverter at L_g = 1.5 mH: (A) with the proposed method in this paper, (B) with the method in Liu et al. (2020), and (C) with the method in Jiao and Lee (2015).

FIGURE 10

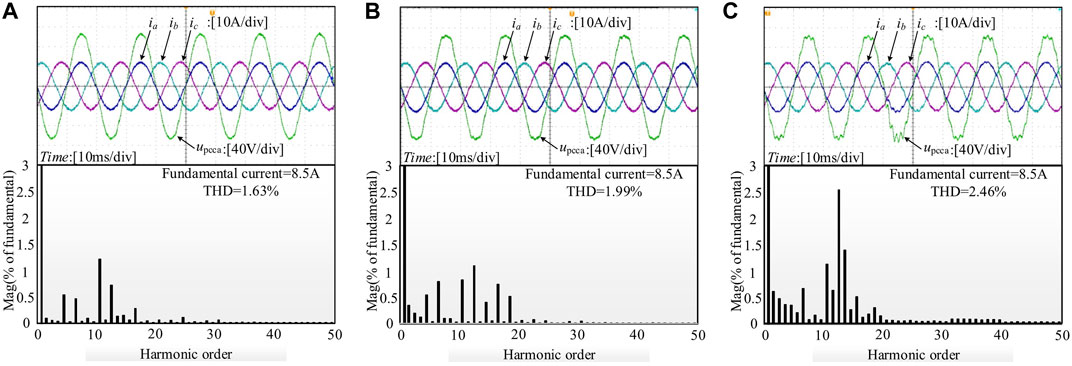
FIGURE 10. Steady-state experimental waveforms of the inverter at L_g = 3 mH: (A) with the proposed method in this paper, (B) with the method in Liu et al. (2020), and (C) with the method in Jiao and Lee (2015).

FIGURE 11

FIGURE 11. Dynamic experimental results of the inverter at L_g = 0 mH: (A)) with the proposed method in this paper, (B) with the method in Liu et al. (2020), and (C) with the method in Jiao and Lee (2015).

FIGURE 12

FIGURE 12. Dynamic experimental results of the inverter at L_g = 1.5 mH: (A) with the proposed method in this paper, (B) with the method in Liu et al. (2020), and (C) with the method in Jiao and Lee (2015).

FIGURE 13

FIGURE 13. Dynamic experimental results of the inverter at L_g = 3 mH: (A) with the proposed method in this paper, (B) with the method in Ref. Liu et al. (2020), and (C) with the method in Jiao and Lee (2015).

Figures 8–10 (L_g = 0 mH, L_g = 1.5 mH, and L_g = 3 mH, respectively) show the steady-state experimental waveforms of the inverter against different grid impedances with the three methods, in which i_a, i_b, and i_c are the three-phase grid currents and v_pcca is the PCC voltage of phase A. It can be seen that when the grid impedance varies, the proposed method can achieve a better quality of grid currents for the inverter, and the THD of grid currents are 1.41, 1.66, and 1.63%, respectively, which satisfy the harmonic distortion standard (IEEE Recommended Practice and Requirements for Harmonic Control in Electric Power Systems, 2014) (IEEE Std. 519-2014) for the grid currents of the inverter. In addition, the THD result with the proposed method is lower than that with other two methods in Jiao and Lee (2015) and Liu et al. (2020) obviously.

Moreover, according to the THD results of the grid current, compared with other two methods in Ref Jiao and Lee (2015) and Liu et al. (2020), when the proposed method is applied, the resonance peak (at 850 Hz in Figure 8, 750 Hz in Figure 9, and 650 Hz in Figure 10) around the LCL resonant frequency is suppressed more effectively under different grid impedance conditions, especially when L_g is 3 mH in Figure 10.

Furthermore, to demonstrate the advantage of the proposed method against different grid impedances, Figures 11–13 show the dynamic experimental waveforms of the inverter with the three methods when the current reference steps from half to full loads. In Figures 11A, 12A, 13A, supposing that L_g varies from 0 to 3 mH (0, 1.5, and 3 mH), the adjustment time Δt is 20, 23, and 31 ms, respectively, with the proposed method in this paper. The adjustment time with the other two methods in Jiao and Lee (2015) and Liu et al. (2020) is listed in Table 3, which shows the comparisons of the dynamic adjustment time with the three methods above. It can be seen that although the grid-connected inverter system can operate stably with the above three methods, the proposed method in this paper has a shorter adjustment time that is less than a fundamental frequency period against different grid impedances among the three methods.

TABLE 3

TABLE 3. Comparison of dynamic performances with the three methods.

Above all, according to comparisons of experimental results with the three methods against different grid impedances, the proposed method can obtain the optimal proportional gain K_p of the PR controller and the AD coefficient k_ad of the AD loop for the LCL-filtered grid-connected inverter system, which maintains that the inverter system achieves better grid current quality, and the resonance peak of the LCL filter is suppressed more effectively under weak grid conditions. Besides, the experimental results show that the dynamic adjustment time of the proposed method is shortened obviously, which illustrates a better dynamic performance of the grid-connected inverter system.

6 Conclusion

In order to improve the stability and dynamic performance of the three-phase LCL-filtered grid-connected inverter under the weak grid, based on the PR controller and active damping with only grid current feedback, a control parameter design method with multi-constrains considering system bandwidth for the inverter is proposed in this paper. According to the stability constraint, resonance suppression constraint, and margin constraint, the maximal bandwidth of the system with variation of L_g is considered, which can ensure a better dynamic performance of the grid-connected inverter under the weak grid. Besides, the proposed method realizes resonance suppression more effectively and maintains a better performance for the inverter, compared with other two methods. With the parameters obtained from the proposed method, the experimental results show the better dynamic performance of the LCL filter in the weak grid with different grid impedances as well as the better steady-state performance and more effective resonance suppression.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

Theoretical promotion and manuscript edition, FW and JL; theoretical analysis and experiment, ZS and WX; simulation and analysis, ZL. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This study was supported by the Natural Science Foundation of the Jiangsu Higher Education Institutions of China (Grant: 20KJB470029).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.

References

Busada, C. A., Jorge, S. G., and Solsona, J. A. (2005). Resonant Current Controller with Enhanced Transient Response for Grid-Tied Inverters. IEEE Trans. Ind. Appl. 65 (4), 1281–1291.

Google Scholar

Cespedes, M., and Sun, J. (2014). Adaptive Control of Grid-Connected Inverters Based on Online Grid Impedance Measurements. IEEE Trans. Sustain. Energ. 5 (2), 516–523. doi:10.1109/tste.2013.2295201

CrossRef Full Text | Google Scholar

Cespedes, M., and Sun, J. (2014). Impedance Modeling and Analysis of Grid-Connected Voltage-Source Converters. IEEE Trans. Power Electron. 29 (3), 1254–1261.

CrossRef Full Text | Google Scholar

Chenlei Bao, C., Xuehua Wang, X., Donghua Pan, X., and Kailei, W. (2014). Step-by-Step Controller Design for LCL-type Grid-Connected Inverter with Capacitor-Current-Feedback Active-Damping. IEEE Trans. Power Electron. 29 (3), 1239–1253. doi:10.1109/tpel.2013.2262378

CrossRef Full Text | Google Scholar

Dannehl, J., Fuchs, F. W., Hansen, S., and Thøgersen, P. B. (2010). Investigation of Active Damping Approaches for PI-Based Current Control of Grid-Connected Pulse Width Modulation Converters with LCL Filters. IEEE Trans. Ind. Applicat. 46 (4), 1509–1517. doi:10.1109/tia.2010.2049974

CrossRef Full Text | Google Scholar

Dannehl, J., Liserre, M., and Fuchs, F. W. (2011). Filter-Based Active Damping of Voltage Source Converters with $LCL$ Filter. IEEE Trans. Ind. Electron. 58 (8), 3623–3633. doi:10.1109/tie.2010.2081952

CrossRef Full Text | Google Scholar

Dorf, R. C., and Bishop, R. H. (2011). Modern Control Systems. 12th ed. Upper Saddle River, NJ: Prentice-Hall.

Google Scholar

Etxegarai, A., Eguia, P., Torres, E., and Fernandez, E. (2012). Impact of Wind Power in Isolated Power Systems. In 2012 16th IEEE Mediterranean Electrotechnical Conference. Tunisia: Yasmine Hammamet, 63–66.

CrossRef Full Text | Google Scholar

Geng, Y., Yun, Y., Chen, R., Wang, K., Bai, H., and Wu, X. (2018). Parameters Design and Optimization for LC-type Off-Grid Inverters with Inductor-Current Feedback Active Damping. IEEE Trans. Power Electron. 33 (1), 703–715. doi:10.1109/tpel.2017.2664812

CrossRef Full Text | Google Scholar

Guan, Y., Wang, Y., Xie, Y., Liang, Y., Lin, A., and Wang, X. (2019). The Dual-Current Control Strategy of Grid-Connected Inverter with LCL Filter. IEEE Trans. Power Electron. 34 (6), 5940–5952. doi:10.1109/tpel.2018.2869625

CrossRef Full Text | Google Scholar

Hava, A. M., Lipo, T. A., and Erdman, W. L. (1995). Utility Interface Issues for Line Connected PWM Voltage Source Converters: a Comparative Study. In Proc.10th IEEE Appl. Power Electron. Conf. Expo. USA: TX, 125–132.

Google Scholar

Holmes, D. G., Lipo, T. A., McGrath, B., and Kong, W. Y. (2017). Optimized Design of Stationary Frame Three Phase Ac Current Regulator. IEEE Trans. Power Electron. 24 (11), 3216–3228.

Google Scholar

Ieee Recommended Practice and Requirements for Harmonic Control in Electric Power Systems (2014). IEEE Std 519-2014. (Revision of IEEE Std 519-1992), 3 Park Avenue. New York, USA.

Google Scholar

Jiao, Y., and Lee, F. C. (2015). LCL Filter Design and Inductor Current Ripple Analysis for a Three-Level NPC Grid Interface Converter. IEEE Trans. Power Electron. 30 (9), 4659–4668. doi:10.1109/tpel.2014.2361907

CrossRef Full Text | Google Scholar

Li, Y., Gao, W., Yan, W., Huang, S., Wang, R., Gevorgian, V., et al. (2021). Data-driven Optimal Control Strategy for Virtual Synchronous Generator via Deep Reinforcement Learning Approach. J. Mod. Power Syst. Clean. Energ. 9 (4), 919–929. doi:10.35833/mpce.2020.000267

CrossRef Full Text | Google Scholar

Lindgren, M., and Svensson, J. (1998). Control of a Voltage-Source Converter Connected to the Grid through an LCL-Filter-Application to Active Filtering. in Proc. PESC. Fukuoka, Japan, 229–235.

Google Scholar

Liserre, M., Blaabjerg, F., and Hansen, S. (2005). Design and Control of an LCL-Filter-Based Three-phase Active Rectifier. IEEE Trans. Ind. Applicat. 41 (5), 1281–1291. doi:10.1109/tia.2005.853373

CrossRef Full Text | Google Scholar

Liserre, M., Blaabjerg, F., and Teodorescu, R. (2007). Grid Impedance Estimation via Excitation of $LCL$-Filter Resonance. IEEE Trans. Ind. Applicat. 43 (5), 1401–1407. doi:10.1109/tia.2007.904439

CrossRef Full Text | Google Scholar

Liserre, M., Teodorescu, R., and Blaabjerg, F. (2006). Stability of Photovoltaic and Wind Turbine Grid-Connected Inverters for a Large Set of Grid Impedance Values. IEEE Trans. Power Electron. 21 (1), 263–272. doi:10.1109/tpel.2005.861185

CrossRef Full Text | Google Scholar

Liu, T., Liu, J., Liu, Z., and Liu, Z. (2020). A Study of Virtual Resistor-Based Active Damping Alternatives for LCL Resonance in Grid-Connected Voltage Source Inverters. IEEE Trans. Power Electron. 35 (1), 247–262. doi:10.1109/tpel.2019.2911163

CrossRef Full Text | Google Scholar

Lu, M., Wang, X., Loh, P. C., Blaabjerg, F., and Dragicevic, T. (2018). Graphical Evaluation of Time-Delay Compensation Techniques for Digitally Controlled Converters. IEEE Trans. Power Electron. 33 (3), 2601–2614. doi:10.1109/tpel.2017.2691062

CrossRef Full Text | Google Scholar

Malinowski, M., and Bernet, S. (2008). A Simple Voltage Sensorless Active Damping Scheme for Three-phase PWM Converters with an $LCL$ Filter. IEEE Trans. Ind. Electron. 55 (4), 1876–1880. doi:10.1109/tie.2008.917066

CrossRef Full Text | Google Scholar

Parker, S. G., and McGrath, B. P. (2012). Regions of Active Damping Control for LCL Filters. In Proc. IEEE Energy Convers. Congr. Expo. Raleigh, USA, 53–60. doi:10.1109/ecce.2012.6342412

CrossRef Full Text | Google Scholar

Pena-Alzola, R., Liserre, M., Blaabjerg, F., Ordonez, M., and Kerekes, T. (2014). A Self-Commissioning Notch Filter for Active Damping in a Three-phase LCL -Filter-Based Grid-Tie Converter. IEEE Trans. Power Electron. 29 (12), 6754–6761. doi:10.1109/tpel.2014.2304468

CrossRef Full Text | Google Scholar

Sun, J. (2011). Impedance-Based Stability Criterion for Grid-Connected Inverters. IEEE Trans. Power Electron. 26 (11), 3075–3078. doi:10.1109/tpel.2011.2136439

CrossRef Full Text | Google Scholar

Wang, X., Blaabjerg, F., and Loh, P. C. (2015). Grid-current-feedback Active Damping for LCL Resonance in Grid-Connected Voltage Source Converters. IEEE Trans. Power Electron. 31 (1), 213–223.

Google Scholar

Wu, E., and Lehn, P. W. (2006). Digital Current Control of a Voltage Source Converter with Active Damping of LCL Resonance. IEEE Trans. Power Electron. 21 (5), 1364–1373. doi:10.1109/tpel.2006.880271

CrossRef Full Text | Google Scholar

Xin, Z., Wang, X., Loh, P. C., and Blaabjerg, F. (2017). Grid-Current-Feedback Control for LCL-Filtered Grid Converters with Enhanced Stability. IEEE Trans. Power Electron. 32 (4), 3216–3228. doi:10.1109/tpel.2016.2580543

CrossRef Full Text | Google Scholar

Xing, X., Zhang, C., Chen, A., Geng, H., and Qin, C. (2018). Deadbeat Control Strategy for Circulating Current Suppression in Multiparalleled Three-Level Inverters. IEEE Trans. Ind. Electron. 65 (8), 6239–6249. doi:10.1109/tie.2017.2786234

CrossRef Full Text | Google Scholar

Xu, J., Xie, S., and Tang, T. (2013). Active Damping-Based Control for Grid-Connected LCL -filtered Inverter with Injected Grid Current Feedback Only. IEEE Trans. Ind. Electron. 61 (9), 4746–4758.

Google Scholar

Xu, J., Xie, S., and Tang, T. (2013). Evaluations of Current Control in Weak Grid Case for Grid‐connected LCL‐filtered Inverter. IET Power Elect. 6 (2), 227–234. doi:10.1049/iet-pel.2012.0192

CrossRef Full Text | Google Scholar

Xu, J., Xie, S., Zhang, B., and Qian, Q. (2018). Robust Grid Current Control with Impedance-phase Shaping for LCL-Filtered Inverters in Weak and Distorted Grid. IEEE Trans. Power Electron. 33 (12), 10240–10250. doi:10.1109/tpel.2018.2808604

CrossRef Full Text | Google Scholar

Yang, D., Ruan, X., and Wu, H. (2014). Impedance Shaping of the Grid-Connected Inverter with LCL Filter to Improve its Adaptability to the Weak Grid Condition. IEEE Trans. Power Electron. 29 (11), 5795–5805. doi:10.1109/tpel.2014.2300235

CrossRef Full Text | Google Scholar

Zhang, N., Sun, Q., Wang, J., and Yang, L. (2021). Distributed Adaptive Dual Control via Consensus Algorithm in the Energy Internet. IEEE Trans. Ind. Inf. 17 (7), 4848–4860. doi:10.1109/tii.2020.3031437

CrossRef Full Text | Google Scholar

Zhou, L., Zhou, J. M. X., Lv, Y. Z., He, Z., Wu, W., Yang, L., et al. (2018). Inverter-Current-Feedback Resonance-Suppression Method for LCL-type DG System to Reduce Resonance-Frequency Offset and Grid-Inductance Effect. IEEE Trans. Ind. Electron. 65 (9), 7036–7048. doi:10.1109/tie.2018.2795556

CrossRef Full Text | Google Scholar

Zhu, K., Sun, P., Zhou, L., Du, X., and Luo, Q. (2020). Frequency-Division Virtual Impedance Shaping Control Method for Grid-Connected Inverters in a Weak and Distorted Grid. IEEE Trans. Power Electron. 35 (8), 8116–8129. doi:10.1109/tpel.2019.2963345

CrossRef Full Text | Google Scholar

Zmood, D., and Holmes, D. (2003). Stationary Frame Current Regulation of PWM Inverters with Zero Steady-State Error. IEEE Trans. Power Electron. 18 (3), 3216–3228. doi:10.1109/tpel.2003.810852

CrossRef Full Text | Google Scholar

Nomenclature

AD active damping

C₁ capacitor in the LCL filter

f_s sampling frequency

G₁ transfer function from u_i(s) to i₂(s) for the LCL filter

G_ad transfer function of the AD loop

G_c proportional resonance controller

G_cl closed-loop transfer function of the system

G_D total time delay model

GM gain margin

GM₀ ideal gain margin

G_op open-loop transfer function of the system

i₁ Inverter-side currents in the LCL filter

i₂ grid-side currents in the LCL filter

i_a, i_b, i_c three-phase grid currents

I_N root mean square of grid current

k_ad aD coefficient

k_{ad_opt} optimal AD parameter

K_pwm gain of the PWM inverter

K_p proportional gain of the PR controller

K_{p_opt} optimal proportional gain of the PR controller

K_r resonant gain of the PR controller

L₁ inverter-side inductor in the LCL filter

L₂ grid-side inductor in the LCL filter

L_g grid impedance

L_{g_max} maximum grid impedance

PCC point of common coupling

PM phase margin

PM₀ ideal phase margin

R_eq virtual resistance in parallel with filter capacitor C₁

SCR short-circuit ratio

T_s sampling period

u_i inverter output voltage

U_s root mean square of grid voltage

V_dc DC-bus voltage

v_pcca PCC voltage of phase A

X_eq virtual reactance in parallel with filter capacitor C₁

Z_eq virtual impedance in parallel with filter capacitor C₁

Δt adjustment time

ω_c cutoff angular frequency of the system

ω_{c_max} maximum cutoff frequency of system

ω_h crossing frequency

ω_i cutoff angular frequency of the PR controller

ω_o grid fundamental angular frequency

ω_res resonant frequency of the LCL filter

ω_res′ actual resonant frequency considering the AD loop