Modeling the Heat-Hydrogen Balance Characteristic of Hydrogen Energy Storage and Cooperative Dispatch of Wind-Hydrogen Hybrid System

The heat and hydrogen balance of the hydrogen energy storage system’s intermittent operation becomes a key factor affecting the performance of the wind-hydrogen hybrid system (W-HHS). This work designed a hydrogen energy storage system (HESS), including waste heat utilization. Then, a dual state of charge (SOC) model is established, in which hydrogen and heat storage is considered. Furthermore, based on the distributionally robust method, an optimal dispatch method of W-HHS is proposed to reduce the operation cost of conventional units in the grid and increase the revenue of the W-HHS. The previously proposed dual SOC model of heat-hydrogen balance is regarded as a constraint in this cooperative dispatch. The effectiveness and efficiency of the dual SOC model were verified on the IEEE 30-bus system with an actual wind plant data set. The results show that the hydrogen-heat dual SOC model can fully reflect the influence of heat and hydrogen balance on the operation of the W-HHS. The cooperative dispatch method improves the reliability of the W-HHS operation under the premise of ensuring the heat-hydrogen balance. When the constraints of hydrogen balance SOC and heat balance SOC are met simultaneously, the available power of the wind plant is 6–8% lower than the ideal situation. Parameter analysis indicates that reducing the heat dissipation coefficient can reduce the influence of the SOC constraint of heat balance on the dispatch strategy and increase the power output of the wind plant. When the heat dissipation coefficient is less than 1/1,200, the heat balance SOC constraint fails.

Introduction

With the change of energy structure, a new power system with a high proportion of renewable energy will become the mainstream for the development of energy system transformation in the future (Zhang and Chen, 2020). Wind and solar have become the primary power sources (Jiayu et al., 2021). However, the wide application of renewable energy raises many problems. The ensuing stability and security issues have become a critical bottleneck restricting the development of a high-proportion renewable power grid (Impram et al., 2020).

Wind power is one of the primary forms of renewable energy, and its participation in the power system dispatch has received extensive attention. Some researchers use stochastic optimization (Zhu et al., 2020), robust optimization (Yu et al., 2020), distributionally robust optimization (Guo et al., 2020), and other optimization methods to try to describe the existing uncertainties in the cooperative dispatch integrated with wind power. Among them, the distributionally robust method is a data-driven optimization method, which constructs the ambiguity set of uncertain parameter probability by using the information implicit in the actual data. Significantly, the distributionally robust method based on waister distribution has been developed rapidly. Ref. (Guo et al., 2020) compared and analyzed the adaptability of distributionally robust optimization methods based on Wasserstein divergence distribution. (Esfahani and Kuhn, 2018) demonstrated this method’s performance guarantee and ease of treatment in detail. At the same time, it should also be pointed out that according to lemma 8 (HOTA et al., 2019), the premise of transforming the distributionally robust model of uncertainty into a set of CVar constraints is that the optimization problem studied is convex, which limits the application of this method to a certain extent. In (Yang et al., 2020), a distributionally robust chance constraint (DRCC) model is proposed for the optimal power gas flow (OPGF) problem with uncertain wind power. The DRCC-OPGF model is reformulated as a treatable mixed-integer convex programming problem.

Besides, some works focus on the different forms of hybrid systems with a wind plant. Different types of energy storage were considered to suppress the wind fluctuation, such as batteries (Xu et al., 2020), compressed air energy storage (Alirahmi et al., 2021), hot dry rock geothermal energy (Si et al., 2021), and hydrogen energy storage system (HESS) (Xiao et al., 2020), etc. constitute the optimal dispatch of the hybrid system. The cooperative dispatch strategy of these different hybrid systems was also well studied.

At present, the hybrid system formed by wind plants and energy storage has become an important form to realize the stable operation with a high proportion of wind power. On this basis, the research about reducing the operating costs of conventional units, increasing the power output of wind plants, and raising the operating efficiency of energy storage systems has become more and more popular. HESS has the advantages of fast response speed, large energy storage capacity, and cross-season energy storage. Also, it can adapt to the operating environment of cold climates and significant temperature differences between day and night (Petkov and Gabrielli, 2020). The application of HESS on the wind-storage hybrid system has attracted scholars’ attention in recent years (Li et al., 2020).

In the existing works, some aim to suppress the uncertainty of wind power and improve the system economy. Ref. (Zhang and Wan, 2014) established a hydrogen energy storage model to reduce power curtailment and gave a scheme for wind/hydrogen production through water electrolysis. Ref. (Qiu et al., 2020) proposed a two-stage robust optimization method with stability constraints considering the HESS’s safety and small disturbance stability and dynamic response characteristics. The power output range of the HESS was then determined. Ref. (Xu et al., 2020) further proposed a distributionally robust chance-constrained (DRCC) dispatch method for W-HHS in the day-ahead power market and transformed it into a standard second-order cone programming problem for a solution.

Other scholars regard the electrolyzer as an adjustable load and research from the perspective of demand response. Ref. (Mirzaei et al., 2018) proposed a safety constrained unit commitment model with high-proportion wind power in coordination with demand response. The HESS was used in this work to reduce energy consumption and improve system reliability. Ref. (Mansour-Saatloo et al., 2020) used the HESS in the energy hub to construct a robust dispatch method, which considered the demand response of the HESS and the characteristics of cogeneration.

The existing research shows that in the operation of the HESS, cogeneration can happen both in the hydrogen production and fuel cell generation stages. Its thermal characteristics have an important influence on the reliable and efficient operation of the HESS. On this basis, some work studied the future development of hybrid systems with ultra-high penetration of renewable energy. A thermoelectric hydrogen model with startup/shutdown constraints and a new seasonal hydrogen energy storage model was proposed (Wen et al., 2020). Ref. (Pan et al., 2020) studied the influence of heat load increase on the operation cost of the hybrid system and proposed a day-ahead dispatch scheme for the power system with high-proportion wind power and HESS. Ref. (Wei et al., 2021) further established a heat-hydrogen efficiency model for the intermittent operation of the electrolyzer by describing the heat exchange process in detail. Ref. (Kovač et al., 2021) carried out research on the thermal management of distributed photovoltaic-hydrogenation stations, put forward the optimized thermal management strategy, and improved the energy utilization efficiency. In order to ensure the energy efficiency of the renewable hydrogen energy system, the thermal management of the metal hydride tank is studied (Endo et al., 2021). Research shows that heat management can improve energy efficiency by 50%.

It can be seen that in the grid-connected operation of the hybrid system with renewable energy, the HESS can use the electrolyzer to transform the excess wind power into hydrogen to provide a down-reserves. At the same time. The fuel cell equipped in the HESS can consume hydrogen to generate power to provide an up-reserves for the hybrid system. The electrolyzer and the fuel cell work alternately and intermittently to suppress the power fluctuation. Notice that the electrolyzer and fuel cell’s operation efficiency and response speed are closely related to their operating temperature. Therefore, the ability of HESS to respond to wind power fluctuations quickly, long-term, and efficiently is restricted by the following two factors. First, the balance between hydrogen production in the electrolyzer and the hydrogen consumption of the fuel cell should always be satisfied. Second, the balance between heat production under operation conditions and heat consumption under reserve mode should be held as well. Thus, the operation of W-HHS should meet both heat and hydrogen production-consumption balance simultaneously when it is connected to the grid.

Existing works have neglected the heat balance between electrolyzers and fuel cells in the reserve mode and the inherent relationship between hydrogen and heat balance. While maintaining heat balance and hydrogen balance is the key to ensuring the economic operation of the hybrid power equipped with HESS. Therefore, based on the operating characteristics of the HESS, this paper first designs a brand new structure of the HESS, including the waste heat utilization system, and gives the heat-hydrogen state of charge (SOC) models. Furthermore, the distributionally robust optimization approach is used to model the uncertainty of wind plant power output. Then, an optimal dispatch method for the W-HHS considering the heat and hydrogen balance is proposed. The models and method are verified with the IEEE 30-bus system. The actual data set of a wind plant in Qinghai Province is used in this simulation. Finally, the key parameters are analyzed, and their impacts on system performance are well studied.

The rest of this article is organized as follows. Mathematical Model of HESS With Waste Heat Utilization System elaborates the overall design scheme and mathematical model of the HESS with waste heat utilization system. Mathematical Models of the Wind Plant introduces the mathematical models of wind plants. The cooperative dispatch method of W-HHS considering dual SOC constraints is proposed in Cooperative Dispatch Method of W-HHS Considering Dual SOC Constraints. Case Study verifies the effectiveness of the proposed method through a case consisting of actual data, followed by the disscusions in Discussions.

Mathematical Model of HESS With Waste Heat Utilization System

Structure of HESS With Waste Heat Utilization System

The structure of a HESS with the waste heat utilization system is shown in Figure 1. The whole system consists of an electrolyzer, fuel cell, hydrogen storage system, and waste heat utilization system. This HESS adopts the alkaline electrolyzer as the water electrolysis device due to its mature technology and fast response speed. The electrolyzer is used to absorb the excess wind power to produce hydrogen. As for the fuel cell, the proton-exchange membrane fuel cell (PEMFC) is chosen to consume hydrogen and generate electricity considering the requirement of the operating temperature match.

FIGURE 1

FIGURE 1. Diagram of the wind-hydrogen hybrid system.

The hydrogen storage system includes a hydrogen tank, an air/oxygen system, and a water supply cycle. The waste heat utilization system consists of a thermal tank, a heat storage exchanger, and a heat cycle system. The heat cycle system builds a heating/cooling cycle between the electrolyzer, PEMFC, water supply tank, and heat storage tank to stabilize the system temperature. The mathematical models of the various components of the HESS are given in the following sections.

Model of HESS With Waste Heat Utilization System

Model of Alkaline Electrolyzer and PEMFC

The alkaline electrolyzer has the advantages of short response time and mature technology. It is very suitable to be used in a HESS with wind plants. Its simplified model (Clua et al., 2018; Xiong et al., 2021) can be expressed as:

$\{\begin{array}{l}{P}_{ele}^t={\dot{n}}_{H2}^t{H}_{HV}+Q_{ele}^t\\ {\eta }_{ele}=\frac{{\dot{n}}_{H2}^t{H}_{HV}}{P_{ele}^t}\end{array},(1)$

where $P_{ele}^t$ and $Q_{ele}^t$, respectively, represent the electricity consumed and the heat produced by the electrolyzer at time $t$. ${\dot{n}}_{H2}^t$ represents the rate of hydrogen production, and $H_{HV}$ represents the higher heating value of hydrogen. ${\eta }_{ele}$ represents the efficiency of the electrolyzer.

The operating temperature of the PEMFC should match that of the alkaline electrolyzer to facilitate the recovery and utilization of the waste heat of the HESS. Its model can be expressed as:

$\{\begin{array}{l}{\dot{m}}_{H2}^t{H}_{HV}=P_{fuel}^t+Q_{fuel}^t\\ {\eta }_{fuel}=\frac{P_{fuel}^t}{{\dot{m}}_{H2}^t{H}_{HV}}\end{array},(2)$

where $P_{fuel}^t$ and $Q_{fuel}^t$ represent the electricity and heat produced by the fuel cell at time $t$, respectively. ${\dot{m}}_{H2}^t$ represents the hydrogen consumption rate of PEMFC. ${\eta }_{fuel}$ represents the efficiency of PEMFC.

Dual SOC Model for Hydrogen and Heat Balance

The HESS stores the hydrogen produced by the electrolyzer in the hydrogen tank and supplies the hydrogen and oxygen to the PEMFC when electricity is needed. At the same time, water is supplied to the electrolyzer, and the electricity generation products of the PEMFC are collected through the water supply cycle. Taking the total energy stored in the hydrogen tank as the parameter to describe the hydrogen energy storage state, we establish SOC model of the hydrogen balance as:

$SO{C}_{H2}^t=SO{C}_{H2}^{t-1}+\frac{1}{S_{H2}^{\text{max}}}\left({\eta }_{ele}{P}_{ele}^t-P_{fuel}^t/{\eta }_{fuel}\right)\Delta \tau ,(3)$

where $SO{C}_{H2}^t$ represents the SOC of hydrogen energy stored in the tank at time $t$. $S_{H2}^{\max }$ represents the maximum capacity of the hydrogen tank, and $\Delta \tau$ represents the time interval.

The waste heat utilization system provides thermal energy for each link and collects waste heat. On the one hand, the waste heat is used to preheat the water entering the electrolyzer, and on the other hand, it is used to maintain the rated temperature of the PEMFC in reserve mode. Also, when the PEMFC is in operation mode, the waste heat needs to provide heat to the electrolyzer and recover the heat generated from the PEMFC. After meeting the heat balance requirements of the electrolyzer and PEMFC, the waste heat utilization system can also use the remaining thermal energy to provide heat for extra heat loads in the hybrid system. The SOC model of heat balance is:

$SO{C}_{th}^t=SO{C}_{th}^{t-1}+\frac{1}{S_{th}^{\max }}\left[{\eta }_{ex}\left(Q_{ele}^t+Q_{fuel}^t-Q_{sys}^t\right)-Q_{load}^t\right]\Delta \tau ,(4)$

where $SO{C}_{th}^t$ represents the SOC of thermal energy stored in the thermal tank at time $t$. $S_{th}^{\text{max}}$ represents the maximum thermal energy storage capacity of the thermal tank. $Q_{ele}^t$ and $Q_{fuel}^t$ represent the heat generated by the electrolyzer and the PEMFC, respectively. $Q_{sys}^t$ and $Q_{load}^t$ represent the heat consumed by the HESS and the heat provided for the extra heat loads, respectively. ${\eta }_{ex}$ represents the efficiency of the heat exchanger.

In Eq. 4, $Q_{sys}^t$ is composed of three losses: the heat dissipation of the electrolyzer, the heat dissipation of the fuel cell, and the preheating of the water supply cycle. Thus, $Q_{sys}^t$ can be expressed as:

$Q_{sys}^t=\left(T_{ele}^t-T_{atm}^t\right){\lambda }_{ele}{P}_{ele}+\left(T_{ele}^t-T_{atm}^t\right){\lambda }_{fuel}{P}_{fuel}+{\dot{n}}_w^t{c}_p\left(T_{ele}^t-T_w^t\right),(5)$

where $T_{ele}^t$ and $T_{fuel}^t$ represent the operating temperature of the electrolyzer and PEMFC. $T_{atm}^t$ represent the ambient temperature. $P_{ele}$ and $P_{fuel}$ are the installed capacity of electrolyzer and PEMFC. ${\dot{n}}_w^t$, $c_p$, and $T_w^t$ represent the molar mass flow rate, specific heat capacity and temperature of the water entering the electrolyzer. ${\lambda }_{ele}$ and ${\lambda }_{fuel}$ represent the heat dissipation coefficient of the unit capacity electrolyzer and PEMFC (Hwang, 2005), which are defined as the heat dissipation area per unit capacity $A_{ele}/A_{fuel}$ to unit area thermal resistance $R_{ele}/R_{fuel}$. ${\lambda }_{ele}$ and ${\lambda }_{fuel}$ can be expressed as:

${\lambda }_{ele}=\frac{A_{ele}}{R_{ele}};{\lambda }_{fuel}=\frac{A_{fuel}}{R_{fuel}}.(6)$

Mathematical Models of the Wind Plant

Models of Wind Plant Output Power

The power output of a wind plant can be modeled with wind speed and installed power (Guo et al., 2020). By further equating the wind speed change as a power output impact factor ${\lambda }_W^t$, a simplified model of the wind plant output can be expressed as

${\tilde{P}}_W^t={\mathit{\lambda }}_{\mathit{W}}^{\mathit{t}}{P}_W·(7)$

where $P_W$ represents the installed power of the wind plant. ${\tilde{P}}_W^t$ represents the actual power output of the wind plant.

While, in an actual situation, the system operator usually uses the predicted wind plant output to determine the dispatch decisions and the dispatchable power. The predicted power output and dispatchable power can be expressed as:

${\widehat{P}}_W^t={\widehat{\mathit{\lambda }}}_W^t{P}_W,(8)$

$P_W^t=\delta {\widehat{P}}_W^t,(9)$

where ${\widehat{\lambda }}_W^t$ represents the predicted power output impact factor. ${\widehat{P}}_W^t$ and $P_W^t$ represent the predicted output and dispatchable power of the wind plant. ${\widehat{\lambda }}_W^t$ reflects the availability of power grid dispatch with wind power forecasting. $P_W^t$ represents the dispatchable power, forming the dispatching curve of the wind plant, which is the grid-connected power guaranteed by the wind plant. $\delta$ means availability factor of wind plant. Based on this, we can further define the dispatch tracking deviation index of the wind plant (Guo et al., 2020), which is:

${\Delta }_W=\left({\displaystyle \sum _{t=1}^T{\tilde{P}}_W^t}-{\displaystyle \sum _{t=1}^T{P}_W^t}\right)/{\displaystyle \sum _{t=1}^T{\tilde{P}}_W^t},(10)$

where ${\Delta }_W$ represents the total power deviation in the whole period of dispatch.

A Distributionally Robust Model of Wind Plant Output Uncertainty

Distributionally robust optimization is a data-driven analysis approach and has been widely studied and applied. This method does not require an accurate probability distribution to characterize the uncertainties. Its conservativeness lies between robust optimization and stochastic optimization. Therefore, the distributionally robust optimization approach is applied in this work. In this method, we adopt the Wasserstein divergence (Guo et al., 2020) as the ambiguous set to measure the uncertainties of wind power output. Hence, we have:

$M^{\epsilon }=\left\{P\in M\left(\Xi \right):d_W\left(P,\widehat{P}\right)\le \epsilon \right\},(11)$

where $P$ represents the probability distribution of the actual power output of the wind plant. $\widehat{P}$ represents the empirical distribution of the power output. $M\left(\Xi \right)$ represents the set formed by all possible distributions satisfying Wasserstein divergence $d_w$, where $\epsilon$ is the radius of the ambiguous set. The calculation method of the parameters mentioned above can be found in (Esfahani and Kuhn, 2018).

Cooperative Dispatch Method of W-HHS Considering Dual SOC Constraints

The optimal dispatch of the W-HHS should reduce the operation costs of conventional units in the grid as much as possible and then increase the grid-connected power generated by wind plants to make full use of clean energy and reduce carbon emissions. Hence, we try to optimize the dispatch strategy of the HESS to ensure that the power output of the W-HHS can track the dispatchable power accurately, thereby reducing the impact of wind power fluctuation on the power grid.

Objective Function

In the cooperative dispatch, historical wind power data is commonly used to predict the wind plant output. The model that we establish combines the dispatchable power of wind plants with the availability coefficients to optimize the output of conventional units and increase the grid-connected output of wind plants. The operation cost of conventional units and carbon emissions can also be reduced. Therefore, the goal of the W-HHS’s optimal dispatch is:

$\begin{array}{l}F=\underset{{\tilde{P}}_W^t}{\max }\underset{P_{gen}^{t,i},\delta }{\text{min}}{\displaystyle \sum _{t=1}^T{\displaystyle \sum _{i=1}^N\left[a_i{\left(P_{gen}^{t,i}\right)}^2+b_i{P}_{gen}^{t,i}+c_i\right]}}-c_e\delta {\widehat{P}}_W^{t,i}+c_p{\Delta }_W\\ P\left({\tilde{P}}_W^t\right)\in M\left(\Xi \right),t\in T,i\in N\end{array},(12)$

where $P\left({\tilde{P}}_W^t\right)$ represents the probability distribution of the actual wind plant output. $c_e$ represents the on-grid power tariff. $c_p$ represents the penalty coefficient. $P_{gen}^{t,i}$ represents the power output of the units. $a_i$, $b_i$, and $c_i$ represent the operation cost coefficients of the conventional unit. $i$ represents the bus index. $N$ represents the set of all buses.

Constrains

Dual SOC Constrains

In order to ensure that the HESS can dispatch the electrolyzer and PEMFC to provide reserves for the hybrid system, the optimal dispatch strategy must meet the balance of the hydrogen production (generated by electrolyzer) and the hydrogen consumption (consumed by the PEMFC). Also, the strategy should hold the heat balance between heat production and consumption.

The hydrogen balance requires that the system does not need to supplement hydrogen from outside during the operation, and the hydrogen in the storage tank will never be lower than the lower bound of the rated value after operating for a period $T$. Thus, we have the hydrogen balance SOC constraint is:

$\{\begin{array}{l}SO{C}_{H2}^t\ge 0\\ SO{C}_{H2}^{ini}\le SO{C}_{H2}^{T+1}\end{array},(13)$

where $SO{C}_{H2}^{ini}$ is the initial value of the hydrogen tank.

Similarly, the heat balance requires that the waste heat utilization system supports the W-HHS to operate continuously and efficiently within the specified operation period without the input of external thermal energy. Its SOC constraint can be expressed as:

$\{\begin{array}{l}SO{C}_{th}^t\ge 0\\ SO{C}_{th}^{ini}\le SO{C}_{th}^{T+1}\end{array},(14)$

where $SO{C}_{th}^{ini}$ is the initial value of the thermal tank.

Besides of heat SOC constraint, heat balance also includes heat power balance constraint in operation.

$Q_{ele}^t+Q_{fuel}^t=Q_{sys}^t+\left(Q_{load}^t+Q_{storage}^t\right)/{\eta }_{ex}(15)$

where $Q_{storage}^t$ represents the heat stored in the thermal tank.

Constraints for Grid

The constraints of power grid dispatch include power flow constraints, line capacity constraints, and power balance constraints. In this section, the linear AC power flow model is adopted. Then, we have the power flow constraints as follows:

$\{\begin{array}{l}{P}_l^t=g_l\frac{V_i^t-V_j^t}{2}-b_l\left({\theta }_i^t-{\theta }_j^t\right)+P_{Ll}^t\\ Q_l^t=-b_l\frac{V_i^t-V_j^t}{2}-g_l\left({\theta }_i^t-{\theta }_j^t\right)+Q_{Ll}^t\end{array},(16)$

where $P_l^t$ and $Q_l^t$ represent the active and reactive power flow on line $l$ at time $t$. $V_i^t$ and ${\theta }_i^t$ represent the voltage magnitude and phase angle of bus $i$. $P_{Ll}^t$ and $Q_{Ll}^t$ represent the active and reactive power flow errors on line $l$ (Guo et al., 2020).

The constraint of line capacity is:

${\left(P_l^t\right)}^2+{\left(Q_l^t\right)}^2\le {\left(S_l^t\right)}^2,(17)$

where $S_l^t$ represents the capacity of line $l$. Eq. 17 can be linearized by the outer approximation approach as

$\{\begin{array}{l}-S_l^t\le P_l^t\le S_l^t\\ -S_l^t\le Q_l^t\le S_l^t\\ -\sqrt{2}{S}_l^t\le P_l^t+Q_l^t\le \sqrt{2}{S}_l^t\\ -\sqrt{2}{S}_l^t\le P_l^t-Q_l^t\le \sqrt{2}{S}_l^t\end{array},(18)$

The power balance constraint is

$\{\begin{array}{l}{P}_i^t={\displaystyle \sum _l{P}_l^t+V_i^t}{\displaystyle \sum _{j=1}^N{G}_{ij}=P_W^{t,i}+P_{gen}^{t,i}-P_{ld}^{t,i}}\\ Q_i^t={\displaystyle \sum _l{Q}_l^t-V_i^t}{\displaystyle \sum _{j=1}^N{B}_{ij}=Q_{gen}^{t,i}-Q_{ld}^{t,i}}\end{array},(19)$

where $P_i^t$ and $Q_i^t$ represent the active and reactive power injected into bus $i$, that is, the power generated by the generator connected to the bus minus the active/reactive load $P_{ld}^{t,i}$/$Q_{ld}^{t,i}$ on the same bus. $G_{ij}$ and $B_{ij}$ are the real and imaginary parts of elements in the network admittance matrix.

Model Solution

The problem established in Eqs. 12–19 is a max-min optimization problem. The actual power output of the wind plant is modeled by the uncertain ambiguous set given in Eq. 11, which cannot be solved directly. To this end, we adopt the method proposed in (Guo et al., 2020) to transform the set into a set of linear chance constraints, which are:

$\{\begin{array}{l}\epsilon \left(1-{\Delta }_W\right)+\frac{1}{K}{\displaystyle \sum _{k=1}^K{s}_i^k-{\gamma }_i\alpha \le 0}\\ s_i^k\ge \left(1-{\Delta }_W\right){\displaystyle \sum _{t=1}^T{\tilde{P}}_{Wi}^{k,t}-{\displaystyle \sum _{t=1}^T{P}_W^{k,t,i}}+{\gamma }_i}\\ s_i^k\ge 0\end{array},(20)$

where $K$ is the number of data samples. $\alpha$ is the confidence level. ${\tilde{P}}_{Wi}^{k,t}$ and $P_{Wi}^{k,t}$ are the actual wind plant output and dispatchable grid-connected power represented by samples. $s_i^t$ and ${\gamma }_i$ are corresponding dual variables.

At this time, since we use samples to describe the uncertainties of the wind plants outputs, the power balance constraint of each line in Eq. 19 can be rewritten as:

$\{\begin{array}{l}{P}_i^{k,t}={\displaystyle \sum _l{P}_l^{k,t}+V_i^{k,t}}{\displaystyle \sum _{j=1}^N{G}_{ij}=P_W^{k,t,i}+P_{gen}^{t,i}+P_{fuel}^{k,t,i}-P_{ele}^{k,t,i}-P_{load}^{t,i}}\\ Q_i^{k,t}={\displaystyle \sum _l{Q}_l^{k,t}-V_i^{k,t}}{\displaystyle \sum _{j=1}^N{B}_{ij}=Q_{gen}^{t,i}-Q_{load}^{t,i}}\end{array},(21)$

The lower and upper bounds of each variable restricted by the limitations of technology and environment are all considered in modeling, which is not listed due to the space limitation. Besides, we notice that product terms of two decision variables exist in Eq. 5, making the model nonlinear. This term can be piecewise linearized by the Boolean expansion method (Pereira et al., 2005).

So far, the W-HHS proposed cooperative dispatch method is transformed into a mixed-integer linear program, which can be solved with matlab 2016b and Cplex12.6.

Case Study

System Parameters

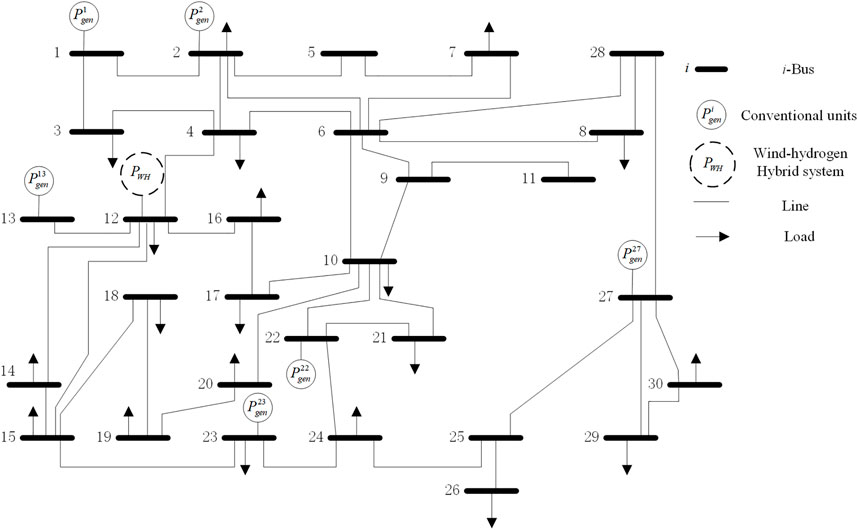
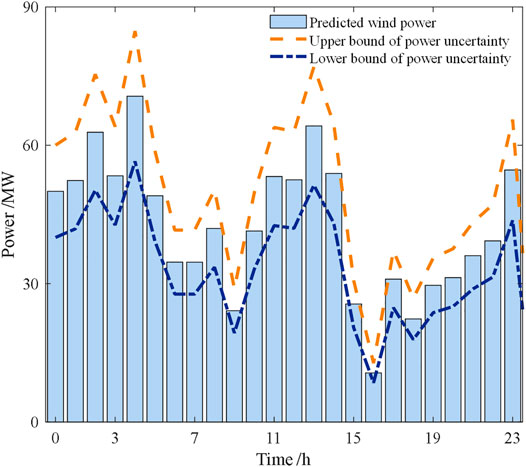
In this section, we test our models and method on the IEEE 30-bus testbed. The actual historical data obtained from the Qinghai Province’s 90 MW wind plant is used as samples. The parameters of the system are shown in Table 1. The W-HHS is integrated on bus #12, which is also given in Figure 2. The capacity of HESS is selected according to the local energy storage configuration policy, equal to 10% of the wind plant capacity. The specific historical data is selected as the predicted value of the wind plant output. 20% prediction error is set according to the current wind power prediction level.

TABLE 1

TABLE 1. System parameters.

FIGURE 2

FIGURE 2. Diagram of the IEEE 30 power system.

The Latin hypercube method generates 100 samples (Shu et al., 2014) to construct the proposed distributionally robust optimization model. The upper and lower bounds of predicted output, available power, and uncertainties of wind plants are shown in Figure 3.

FIGURE 3

FIGURE 3. Power chart of the wind plant.

Cooperative Dispatch Results of W-HHS

To analyze the influence of heat balance and hydrogen balance on the dispatch strategy of HPS, we study four different scenarios, which are listed as follows. The results are shown in Table 2.

TABLE 2

TABLE 2. Cooperative dispatch results.

Case 1: Heat and hydrogen balance constraints are not considered;

Case 2: Only heat balance constraints are considered;

Case 3: Only hydrogen balance constraints are considered;

Case 4: Both hydrogen and heat balance constraints are considered.

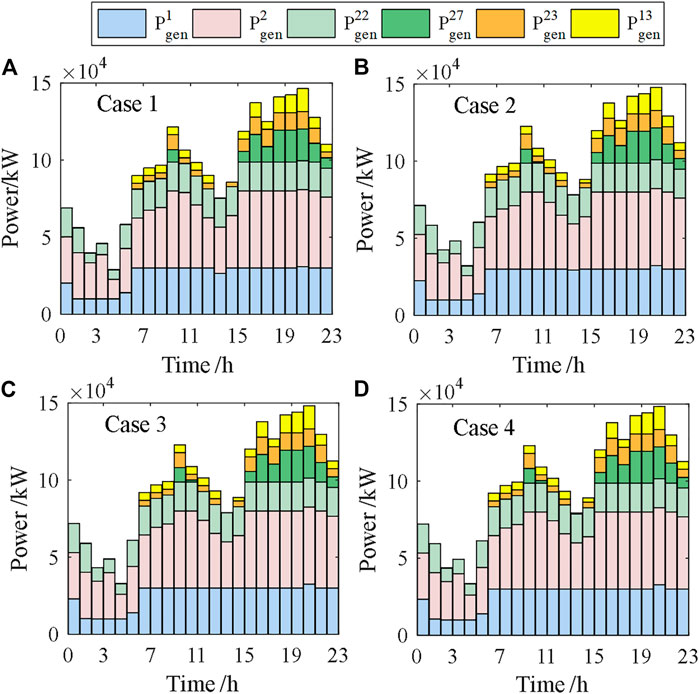
It can be seen from Table 2 that where the hydrogen and heat balance constraints are ignored (Case 1), the dispatchable power of the wind plant is equal to the predicted value, and the operation cost of conventional units is the lowest. However, 25.04 kg extra hydrogen is needed to support the 24-h operation of the hybrid system. As constraints are added into the model, the availability coefficient of the wind plant decreases to meet hydrogen and heat balance requirements, and the cost of conventional units increases. Compared with Case 1, the wind plant availability coefficient in Case 4 has dropped by 6.33%, and the cost of conventional units has increased by 3.4%. The results of conventional unit dispatch in the four scenarios are shown in Figure 4.

FIGURE 4

FIGURE 4. Dispatch results of conventional units.

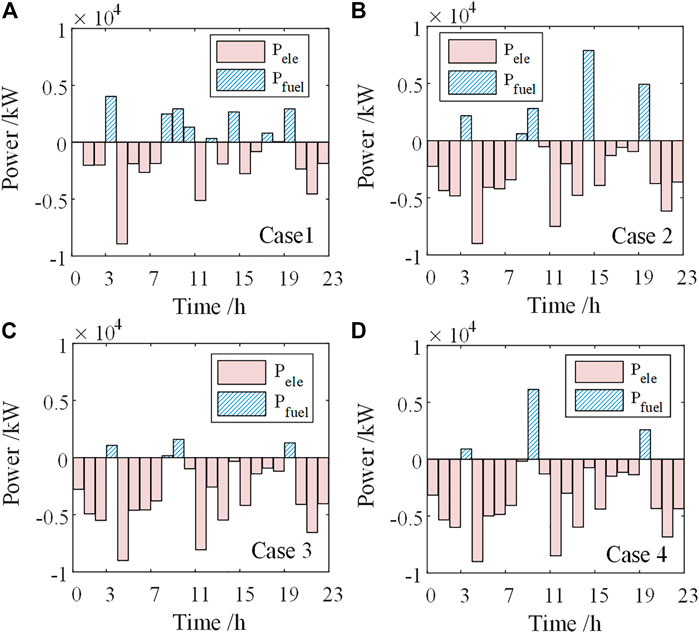
According to the results in Case 2 and 3, we can figure out that the dispatch strategy that only satisfies the hydrogen balance or the heat balance requires the extra hydrogen or thermal supplement. It can be seen that when the system has sufficient day-ahead initial hydrogen storage or thermal storage, the corresponding dispatch strategy can also be adapted to increase the grid-connected power output of wind plants. When the initial hydrogen energy storage and the thermal storage are insufficient, the wind plant availability coefficient can only be reduced, and the dispatch strategy in Case 4 is adopted to maintain this efficient and economical operation of the HESS. Figure 5 shows the operation of the HESS in the four Cases.

FIGURE 5

FIGURE 5. Operation of hydrogen energy storage system.

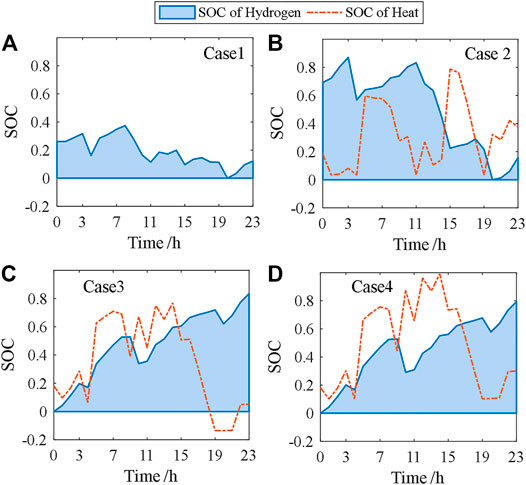
It can be seen from Figure 5 that the PEMFC in Case 2 consumes extra hydrogen to provide an up-reserve for the hybrid system, improving the availability coefficient of wind power and meeting the heat balance constraints. In Case 3, the availability coefficient of the wind plant decreases. We can see that the probability of wind power curtailment increases while the probability of load curtailment decreases. The W-HHS calls the electrolyzer to increase hydrogen production, and the PEMFC is controlled to consume less hydrogen, thereby satisfying the hydrogen balance constraint. The SOC changes of hydrogen balance and heat balance are shown in Figure 6.

FIGURE 6

FIGURE 6. SOC change of hydrogen energy storage system.

Figure 6 shows that only the dispatch strategy adopted in Case 4 can simultaneously satisfy the heat and hydrogen balance constraints. In this case, the hydrogen tank will have the remaining hydrogen. The remaining hydrogen can be used in the subsequent optimal dispatch to increase the grid-connected output of the wind plant, reflecting the character of hydrogen energy storage’s cross-cycle energy storage. When the heat balance SOC shown in Figure 6 is less than 0, it indicates that the hydrogen energy storage system must rely on additional supplementary heat energy to maintain the regular operation. This working condition means that the hydrogen energy storage system’s thermal energy generated and stored is not enough to maintain the heat balance of intermittent work. In practice, the system’s hydrogen production and power generation efficiency will decline to generate sufficient thermal energy.

Compared with Case 3, the optimal strategy in Case 4 further reduces the wind plant’s available power and grid-connected power to satisfy the heat balance. It can be seen that the heat balance constraint reduces the profits of the hybrid system. Thus, the factors that affect the heat balance constraint should be further analyzed to reduce the impact of heat balance on the operation of HESS.

Analysis of Impact Factors on Heat Balance

From the results in Figures 5, 6, we can easily find out that when the W-HHS is in operation, the electrolyzer and PEMFC run intermittently. The electrolyzer cannot run at full power, and the PEMFC is always in reserve mode for a long time in an operation cycle. According to the heat balance model given in Eq. 5, 15, whether the heat produced can meet the heat lost by the system mainly depends on the heat dissipation coefficient of the electrolyzer and PEMFC. Therefore, the influence of the heat dissipation coefficient on the heat balance SOC constraint should be analyzed. Thus, we take the heat dissipation coefficient in a range of [1/900, 1/1,500] to study the performance of the waste heat utilization system. The results are shown in Table 3.

TABLE 3

TABLE 3. Influence of heat dissipation coefficient.

Table 3 shows that as the heat dissipation coefficient decreases, the operation is less influenced by the heat balance constraints. The high availability coefficient of the wind plant results in a decreased operation probability of the electrolyzer and an increased working time of the PEMFC. Hydrogen storage drops accordingly. Also, due to the decrease of heat dissipation, the thermal energy stored in the thermal tank gradually increases.

When the heat dissipation coefficient is less than 1/1,200, Case 4 is equivalent to Case 3. The hybrid system is no longer affected by heat balance constraints. Thus, we can conclude that improving the heat insulation performance and reducing the heat dissipation power will help raise the system’s operating efficiency. Meanwhile, the available grid-connected power of the wind plant increased, and the profit of the W-HHS improved.

Discussion

According to the W-HHS energy storage system’s electricity, hydrogen, and heat characteristics, this work designs a HESS with a waste heat utilization system. Then, the hydrogen and heat dual SOC constraints are established to describe the operation of the electrolyzer and PEMFC in the HESS. On this basis, a cooperative dispatch method for the W-HHS is proposed, aiming to reduce the operation cost of conventional units in the grid and increase wind plants’ profit. The distributionally robust optimization approach models the uncertainties in the system. Then, the formulated model is transformed into a set of chance constraints and can be solved with an offline solver. Finally, we test our model with the IEEE 30-bus system, and actual wind power data from a Qinghai province wind plant is used.

The results show that without considering the hydrogen balance, the system has a significant wind power availability factor, which can improve the grid-connected power of the wind plant, but in practice, it needs to consume additional hydrogen to ensure fuel cell power generation. It can be seen that considering the hydrogen balance and heat balance will reduce the grid connection availability factor of the wind plant to generate enough hydrogen and thermal energy. In the operation of W-HHS, the available power of the wind plant is 6–8% lower than the ideal situation to meet the SOC constraints of hydrogen and heat balance. The heat dissipation coefficient of HESS has a significant influence on the SOC constraint of heat balance. When the heat dissipation coefficient is small enough, the SOC constraint of heat balance becomes invalid, and the SOC constraints of hydrogen balance only restrict the system operation strategy.

In addition, it should also be seen that after 24 h of continuous operation of the case4 in this paper, both hydrogen storage tank and heat storage tank have residual energy. This shows that in multi-day dispatching scene when there is hydrogen and heat energy in the hydrogen storage tank and heat storage tank, the system dispatching can also adopt an optimistic availability factor to use the remaining hydrogen and heat energy to improve the grid-connected power of wind plant and reduce the generation cost of conventional units. This problem needs further research in the future.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

YS: conceptualization, writing-original draft preparation, software. LC: funding acquisition, validation. LM: funding acquisition, conceptualization, methodology, and editing. HM: validation. MG: project administration. SM: supervision. All authors have read and agreed to the published version of the article.

Funding

This research was funded in part by the Joint Fund Project of National Natural Science Foundation of China (U1766203), in part by Key R and D and Transformation Plan of Qinghai Province (2021-GX-109), and in part by the Basic Research Project of Qinghai Province (2021-ZJ-948).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to thank Prof. Feng Liu and Wei Wei for very helpful discussions on the cooperative game, Dr. Xiaodai Xue and Xuelin Zhang for discussions on the HDR geothermal generator model, Dr. Zhongjie Guo and Jiayu Bai for suggestions on practical issues.

References

Alirahmi, S. M., Razmi, A. R., and Arabkoohsar, A. (2021). Comprehensive Assessment and Multi-Objective Optimization of a green Concept Based on a Combination of Hydrogen and Compressed Air Energy Storage (CAES) Systems. Renew. Sust. Energ. Rev. 142, 110850. doi:10.1016/j.rser.2021.110850

CrossRef Full Text | Google Scholar

Endo, N., Goshome, K., Tetsuhiko, M., Segawa, Y., Shimoda, E., and Nozu, T. (2021). Thermal Management and Power Saving Operations for Improved Energy Efficiency within a Renewable Hydrogen Energy System Utilizing Metal Hydride Hydrogen Storage. Int. J. Hydrogen Energ. 46 (1), 262–271. doi:10.1016/j.ijhydene.2020.10.002

CrossRef Full Text | Google Scholar

Esfahani, P. M., and Kuhn, D. (2018). Data-driven Distributionally Robust Optimization Using the Wasserstein Metric: Performance Guarantees and Tractable Reformulations. Math. Programming 171 (1), 115–166. doi:10.1007/s10107-017-1172-1

CrossRef Full Text | Google Scholar

García Clúa, J. G., Mantz, R. J., and De Battista, H. (2018). Optimal Sizing of a Grid-Assisted Wind-Hydrogen System. Energ. Convers. Manag. 166, 402–408. doi:10.1016/j.enconman.2018.04.047

CrossRef Full Text | Google Scholar

Guo, Z., Wei, W., Chen, L., Xie, R., and Mei, S. (2020). Sizing Energy Storage to Reduce Renewable Power Curtailment Considering Network Power Flows: a Distributionally Robust Optimisation Approach. IET Renew. Power Generation 14 (16), 3273–3280. doi:10.1049/iet-rpg.2020.0354

CrossRef Full Text | Google Scholar

Hota, A. R., Cherukuri, A., and Lygeros, J. (2019). Data-driven Chance Constrained Optimization under Wasserstein Ambiguity Sets. Am. Control. Conf. (Acc). doi:10.23919/ACC.2019.8814677

CrossRef Full Text | Google Scholar

Hwang, J. J. (2006). Thermal-electrochemical Modeling of a Proton Exchange Membrane Fuel Cell. J. Electrochem. Soc. 153 (2), A216. doi:10.1149/1.2137652

CrossRef Full Text | Google Scholar

Impram, S., Varbak Nese, S., and Oral, B. (2020). Challenges of Renewable Energy Penetration on Power System Flexibility: A Survey. Energ. Strategy Rev. 31, 100539. doi:10.1016/j.esr.2020.100539

CrossRef Full Text | Google Scholar

Jiayu, B., Xingang, W., Chaoshan, X., Zhiyong, Y., Shoutao, T., and He, C. (2021). “Development Status and Measures to Promote the Development of Renewable Energy in China,” in 2021 3rd Asia Energy and Electrical Engineering Symposium (Chengdu, China: AEEES), 1102–1107. doi:10.1109/AEEES51875.2021.9403132

CrossRef Full Text | Google Scholar

Kovač, A., Marciuš, D., and Paranos, M. (2020). Thermal Management of Hydrogen Refuelling Station Housing on an Annual Level. Int. J. Hydrogen Energ. 46 (57), 29400–29410. doi:10.1016/j.ijhydene.2020.11.013

CrossRef Full Text | Google Scholar

Li, Z., Zhang, W., Zhang, R., and Sun, H. (2020). Development of Renewable Energy Multi-Energy Complementary Hydrogen Energy System (A Case Study in China): A Review. Energy Exploration & Exploitation 38 (6), 2099–2127. doi:10.1177/0144598720953512

CrossRef Full Text | Google Scholar

Mansour-Saatloo, A., Agabalaye-Rahvar, M., Mirzaei, M. A., Mohammadi-Ivatloo, B., Abapour, M., and Zare, K. (2020). Robust Scheduling of Hydrogen Based Smart Micro Energy Hub with Integrated Demand Response. J. Clean. Prod. 267, 122041. doi:10.1016/j.jclepro.2020.122041

CrossRef Full Text | Google Scholar

Mirzaei, M. A., Yazdankhah, A. S., and Mohammadi-Ivatloo, B. (2018).Integration of Demand Response and Hydrogen Storage System in Security Constrained Unit Commitment with High Penetration of Wind Energy. In Electrical Engineering (ICEE), Iranian Conference on. IEEE, 1203–1208. doi:10.1109/ICEE.2018.8472631

CrossRef Full Text | Google Scholar

Pan, G., Gu, W., Lu, Y., Qiu, H., Lu, S., and Yao, S. (2020). Optimal Planning for Electricity-Hydrogen Integrated Energy System Considering Power to Hydrogen and Heat and Seasonal Storage. IEEE Trans. Sustain. Energ. 11 (4), 2662–2676. doi:10.1109/tste.2020.2970078

CrossRef Full Text | Google Scholar

Pereira, M. V., Granville, S., Fampa, M. H. C., Dix, R., and Barroso, L. A. (2005). Strategic Bidding under Uncertainty: a Binary Expansion Approach. IEEE Trans. Power Syst. 20 (1), 180–188. doi:10.1109/tpwrs.2004.840397

CrossRef Full Text | Google Scholar

Petkov, I., and Gabrielli, P. (2020). Power-to-hydrogen as Seasonal Energy Storage: an Uncertainty Analysis for Optimal Design of Low-Carbon Multi-Energy Systems. Appl. Energ. 274, 115197. doi:10.1016/j.apenergy.2020.115197

CrossRef Full Text | Google Scholar

Qiu, Y., Yang, H., Xu, Y., Chen, W., and Wang, P. (2020). Stability-constrained Two-Stage Robust Optimization for Integrated Hydrogen Hybrid Energy System. Csee Jpes 7 (1), 162–171. doi:10.17775/CSEEJPES.2020.00810

CrossRef Full Text | Google Scholar

Shu, Z., Jirutitijaroen, P., Leite da Silva, A. M., and Singh, C. (2014). Accelerated State Evaluation and Latin Hypercube Sequential Sampling for Composite System Reliability Assessment. IEEE Trans. Power Syst. 29 (4), 1692–1700. doi:10.1109/TPWRS.2013.2295113

CrossRef Full Text | Google Scholar

Si, Y., Chen, L., Zhang, X., Chen, X., Zheng, T., and Mei, S. (2021). Game Approach to HDR-TS-PV Hybrid Power System Dispatching. Appl. Sci. 11 (3), 914. doi:10.3390/app11030914

CrossRef Full Text | Google Scholar

Wei, F., Sui, Q., Li, X., Lin, X., and Li, Z. (2021). Optimal Dispatching of Power Grid Integrating Wind-Hydrogen Systems. Int. J. Electr. Power Energ. Syst. 125, 106489. doi:10.1016/j.ijepes.2020.106489

CrossRef Full Text | Google Scholar

Wen, T., Zhang, Z., Lin, X., Li, Z., Chen, C., and Wang, Z. (2020). Research on Modeling and the Operation Strategy of a Hydrogen-Battery Hybrid Energy Storage System for Flexible Wind Farm Grid-Connection. IEEE Access 8, 79347–79356. doi:10.1109/ACCESS.2020.2990581

CrossRef Full Text | Google Scholar

Xiao, P., Hu, W., Xu, X., Liu, W., Huang, Q., and Chen, Z. (2020). Optimal Operation of a Wind-Electrolytic Hydrogen Storage System in the Electricity/hydrogen Markets. Int. J. Hydrogen Energ. 45 (46), 24412–24423. doi:10.1016/j.ijhydene.2020.06.302

CrossRef Full Text | Google Scholar

Xiong, Y., Si, Y., Zheng, T., Chen, L., and Mei, S. (2021). Optimal Configuration of Hydrogen Storage in Industrial Park Integrated Energy System Based on Stackelberg Game. Trans. China Electrotechnical Soc. 36 (3), 507–516. doi:10.19595/j.cnki.1000-6753.tces.200576

CrossRef Full Text | Google Scholar

Xu, X., Hu, W., Cao, D., Huang, Q., Liu, Z., Liu, W., et al. (2020). Scheduling of Wind-Battery Hybrid System in the Electricity Market Using Distributionally Robust Optimization. Renew. Energ. 156, 47–56. doi:10.1016/j.renene.2020.04.057

CrossRef Full Text | Google Scholar

Yang, L., Xu, Y., Gu, W., and Sun, H. (2020). Distributionally Robust Chance-Constrained Optimal Power-Gas Flow under Bidirectional Interactions Considering Uncertain Wind Power. IEEE Trans. Smart Grid 12 (2), 1. doi:10.1109/TSG.2020.3029027

CrossRef Full Text | Google Scholar

Yu, D., Zhang, T., He, G., Nojavan, S., Jermsittiparsert, K., and Ghadimi, N. (2020). Energy Management of Wind-PV-Storage-Grid Based Large Electricity Consumer Using Robust Optimization Technique. J. Energ. Storage 27, 101054. doi:10.1016/j.est.2019.101054

CrossRef Full Text | Google Scholar

Zhang, G., and Wan, X. (2014). A Wind-Hydrogen Energy Storage System Model for Massive Wind Energy Curtailment. Int. J. Hydrogen Energ. 39 (3), 1243–1252. doi:10.1016/j.ijhydene.2013.11.003

CrossRef Full Text | Google Scholar

Zhang, Q., and Chen, W. (2020). Modeling China's Interprovincial Electricity Transmission under Low Carbon Transition. Appl. Energ. 279, 115571. doi:10.1016/j.apenergy.2020.115571

CrossRef Full Text | Google Scholar

Zhu, F., Zhong, P.-a., Xu, B., Liu, W., Wang, W., Sun, Y., et al. (2020). Short-term Stochastic Optimization of a Hydro-Wind-Photovoltaic Hybrid System under Multiple Uncertainties. Energ. Convers. Manag. 214, 112902. doi:10.1016/j.enconman.2020.112902

CrossRef Full Text | Google Scholar

Nomenclature

DRCC Distributionally robust chance-constrained

HESS Hydrogen energy storage system

PEMFC Proton-exchange membrane fuel cell

SOC State of charge

W-HHS Wind-hydrogen hybrid system

Variables

$A_{ele}$ electrolyzer heat dissipation area per unit capacity

$A_{fuel}$ PEMFC heat dissipation area per unit capacity

$a_i$,$b_i$,$c_i$ operation cost coefficients of the conventional unit $i$

$B_{ij}$ imaginary parts of elements in network admittance matrix

$c_e$ on-grid power tariff

$c_p$ penalty coefficient

$d_w$ Wasserstein divergence

$G_{ij}$ real parts of elements in network admittance matrix

$H_{HV}$ higher heating value of hydrogen

$K$ number of data samples

${\dot{m}}_{H2}^t$ hydrogen consumption rate of PEMFC

$M\left(\Xi \right)$ set formed by all possible distributions

${\dot{n}}_{H2}^t$ rate of hydrogen production at time $t$

$P$ probability distribution of the actual wind plant output

$\widehat{P}$ empirical distribution of the wind plant output

$P_{ele}^t$ electricity consumed by the electrolyzer at time $t$

$P_{fuel}^t$ electricity consumed by the fuel cell at time $t$

$P_{gen}^{t,i}$ power output of the units $i$ at time $t$

$P_i^t$ active power injected into bus $i$

$P_l^t$ active power flow on line $l$ at time $t$

$P_{Ll}^t$ active power flow errors on line $l$

$P_{ld}^{t,i}$ active load into bus $i$

$P_W$ installed power of the wind plant

$P_W^t$ dispatchable power of the wind plant at time $t$

${\widehat{P}}_W^t$ predicted output power of the wind plant at time $t$

${\tilde{P}}_W^t$ actual power output of the wind plant at time $t$

$P\left({\tilde{P}}_W^t\right)$ probability distribution of the actual wind plant output

$Q_{ele}^t$ heat produced by the electrolyzer at time $t$

$Q_{fuel}^t$ heat produced by the fuel cell at time $t$

$Q_i^t$ reactive power injected into bus $i$

$Q_l^t$ reactive power flow on line $l$ at time $t$

$Q_{Ll}^t$ reactive power flow errors on line $l$

$Q_{ld}^{t,i}$ reactive load into bus $i$

$Q_{load}^t$ heat provided for extra heat loads

$Q_{sys}^t$ heat consumed by the HESS

$R_{ele}$ unit area thermal resistance of electrolyzer

$R_{fuel}$ unit area thermal resistance of PEMFC

$S_{H2}^{\max }$ maximum capacity of the hydrogen tank

$S_l^t$ capacity of line $l$

$S_{th}^{\text{max}}$ maximum capacity of the thermal tank

$SO{C}_{H2}^t$ SOC of hydrogen energy stored in the tank at time $t$

$SO{C}_{th}^t$ SOC of thermal energy stored in the tank at time $t$

$T_{atm}^t$ ambient temperature

$T_{ele}^t$ operating temperature of the electrolyzer

$T_{fuel}^t$ operating temperature of the PEMFC

$T_w^t$ temperature of the water entering the electrolyzer

$V_i^t$ voltage magnitude of bus $i$.

$\alpha$ confidence level

${\eta }_{ele}$ efficiency of the electrolyzer

${\eta }_{ex}$ efficiency of the heat exchanger

${\eta }_{fuel}$ efficiency of PEMFC

${\theta }_i^t$ Phase angle of bus $i$

${\lambda }_{ele}$ heat dissipation coefficient of unit capacity electrolyzer

${\lambda }_{fuel}$ heat dissipation coefficient of unit capacity PEMFC

${\lambda }_W^t$ power output impact factor of wind plant

${\widehat{\lambda }}_W^t$ predicted power output impact factor of wind plant

${\gamma }_i$,$s_i^t$ dual variables

$\delta$ availability factor of wind plant

$\epsilon$ radius of the ambiguous set

${\Delta }_W$ total power deviation in the whole period of dispatch

$\Delta \tau$ time interval