Equivalent Firm Capacity Assessment of HDR-PV Hybrid Power System: A Distributionally Robust Approach

Aiming at the reliable grid connection of photovoltaic (PV) systems in frigid plateau regions, this work first designs a flexible hot dry rock (HDR) hybrid power system (HPS), making full use of the potential of HDR for energy storage and power generation. Based on the operation of HPS, a comprehensive energy system credible capacity assessment method considering the overall economy of the system and the reliability of the grid is established. In this method, the power allowable fluctuation rate of the grid as the equivalent firm capacity (EFC) constraint is considered. Then, the constraint is converted into a set of linear chance conditions through the distributionally robust method so that the capacity assessment of the HDR-PV HPS can be converted into a mixed-integer linear optimization problem for a solution. The proposed assessment method is verified by real HDR-PV HPS in the Gonghe Basin of Qinghai Province. The results show that the flexible HDR plant increases the credible capacity of the HPS by 113.38%. The profit of the flexible HDR plant was increased by 3.02% at the same time. The parameter analysis shows that the HDR-PV HPS obtains the most profit when the allowable fluctuation rate is 7%, but 10% can fully utilize the geothermal. The assessment method can effectively assess the credible capacity of the system under the premise of ensuring the overall economy of the HPS, thereby guiding power grid dispatching.

Introduction

As the concept of clean energy has reached a consensus worldwide, clean energy, such as photovoltaics (PV), has developed rapidly (Singh, 2013). The proportion of PV installed capacity in the power system is increasing year by year. At the same time, the proportion of conventional thermal power stations is decreasing year by year due to the requirements of environmental protection and carbon emission reduction. It can be seen that integrating PV plants into the grid reliably has become an urgent problem to be solved.

The assessment of the credible capacity of grid-connected PV plants has attracted widespread attention worldwide (Islam et al., 2014). Some researchers have studied the optimal grid-connected capacity of different scales and multiple types of energy resources from the perspective of passive consumption by the grid (Injeti and Kumar, 2003) and modeled the uncertainties of renewable sources by robust optimization, stochastic optimization, and distributionally robust optimization (Guo et al., 2020). Ref (Yuan et al., 2012) studied the optimal capacity assessment of grid-connected PV plants by using the bus voltage threshold of the low-voltage side of the distribution transformer. Ref (Wang et al., 2019) put forward a method for calculating the credible capacity of PV plants in rural power systems considering the risk of overload. The distributionally robust method can balance conservatism and computational efficiency, which has attracted extensive attention in recent years. A method to transform the ambiguous set composed of Wasserstein divergence into chance constraints was addressed (Esfahani and Kuhn, 2018). Ref (Hota et al., 2019) further proved the performance of the distributionally robust method based on Wasserstein divergence.

Other researchers use existing PV plants and energy storage systems (ESSs) to form a hybrid power system (HPS) to improve the power quality with PV integration. From the perspective of power scheduling, different indicators, such as effective load-carrying capability (ELCC), equivalent firm capacity (EFC), loss of probability (LOP), are proposed to represent the credible capacity of the HPS in the sense of dispatchable grid. By optimizing the dispatch of ESSs, the HPS as a whole is equivalent to a dispatchable power source so that the overall power generation can meet the power fluctuation requirements (Zhang L. et al., 2014; Dent et al., 2014; Sulaeman et al., 2016). Further, the reliability of HPS is improved, and the cost is reduced at the same time (Esmaili and Nasiri, 2009; Tapetado and Usaola, 2019). Ref (Song et al., 2012) improved the dispatchable power through the coordinated operation of the PV plant and the electrochemical energy storage device, thereby increasing the credible capacity of the HPS. Ref (He et al., 2013) proposed a Markov-decision-process-based control strategy to evaluate the credible capacity of PV plants in an HPS. The results showed that ESSs could improve the PV system’s reliability in weak solar irradiance and a high proportion of renewable energy. It can be seen that ESS plays a vital role in the stable operation of the power grid. Ref (Zhang et al., 2017) further used the EFC theory to optimize the configuration of a distributed HPS equipping with wind, solar, and storage, reducing the system investment cost. A method using EFC to estimate the equivalent energy storage capacity of grid-connected parking lots is proposed for the capacity assessment of electric vehicle urban virtual energy storage systems (Zeng et al., 2020). Moreover, EFC can also be used as the contribution index of electric field capacity to power supply security, and a market capacity value method for large-scale investment dispatching is proposed (Peter and Wagner, 2021).

For the grid, the grid dispatcher will make a dispatching plan according to the generation capacity of the connected plants to ensure a safe, stable, and economical operation. However, due to the uncertainty of the output power of renewable plants in HPS, the grid will not optimize the dispatching according to HPS’s installed capacity. The grid must assess credible capacity to plan the dispatching curves. For HPS, accurate assessment of credible capacity is helpful to track the dispatching curves in actual operation, reduce the impact on the power grid, increase the grid-connected power and reduce the penalty. To sum up, the credible capacity assessment of HPS can provide an essential reference for the actual system operation. It can effectively reduce the cost of grid dispatching and improve system performance. Nowadays, the existing research mainly focuses on the HPS with electrochemical ESS and PV plants. When electrochemical ESSs are applied in plateau and frigid environments, they will face the problem of low cycle life and high self-consumption. These disadvantages limit the use of electrochemical ESSs on a large scale. Hence, insufficient energy storage makes some high-altitude areas equipped with high-proportion renewable sources lack dispatchable power sources. In this dilemma, new techniques are urgently needed to solve the reliable connection of large-scale PV plants in these frigid plateau regions.

The geothermal energy of hot dry rock (HDR) has the advantages of stable power generation, simple operation and maintenance, and complete cleanliness (Yan et al., 2019). It can replace electrochemical energy storage to build an HPS in frigid plateau regions. It has excellent potential for increasing the dispatchable capacity of the grid and improving reliability. Nevertheless, because of the geographical location restriction of resources, the long dynamic response time (Brown, 2009), and the high investment cost (Zhang Y.-J. et al., 2014), the existing HDR system can only be used as a base power source without participating in auxiliary services of the grid. Many studies have been proposed to improve the thermal process of the HDR geothermal power system and promote the comprehensive utilization of HDR geothermal energy. Ref (Zare, 2016) proposed an HDR-HPS that can realize a supply of cold, heat, and electricity to utilize the heating and cooling potential of HDR geothermal energy comprehensively. In order to improve the flexibility of the HDR system, Ref (Si et al., 2020). proposed a multi-energy HPS for HDR, wind, solar, and other renewable sources that were considered to meet the needs of cooling, heating, and electrical loads of independent microgrids. Further, a hybrid power system composed of an HDR plant heat storage plant was proposed and addressed the cooperative game dispatching model (Si et al., 2021).

The existing research has not paid attention to the influence of HDR geothermal energy on the credible capacity of the HPS. The HDR power system has its unique characteristics, and the operation mode of the HPS integrated with HDR is different from other systems. In the research on HDR power systems, the operation strategy of HDR is rarely considered to stabilize the fluctuation of the integrated PV plant, increase the credible capacity, and improve the system’s reliability. To solve these problems, we first introduce the thermal storage generation cycle (TSGC) to improve the operational flexibility of the HDR power system. Then, the potential of HDR geothermal energy is explored, and a flexibly dispatchable HDR-PV HPS is designed. Moreover, the operation of this complex system is carefully studied.

Furthermore, combined with the EFC theory, taking power fluctuation requirements of the HPS’s output as the EFC constraint, a credible capacity assessment method of the HDR-PV HPS considering the overall economy is established. The uncertainty of EFC constraints is modeled, and the corresponding solution method is given. The proposed model and method are verified with the actual weather and HDR resource data composition in the Gonghe Basin of Qinghai Province. The simulation results indicate the effectiveness and the efficiency of the proposed method.

The rest of this article is organized as follows. HDR–PV Hybrid Power System Architecture elaborates the overall design scheme of the flexible HDR system and the HDR-PV hybrid power system structure. Mathematical Models of the HDR-PV HPS introduces the mathematical models of the HDR-PV hybrid power system. The credible capacity assessment method for HDR-PV hybrid power system is proposed in Credible Capacity Assessment Method Bbased on Distributionally Robust. Case Study verifies the effectiveness of the proposed method through a case consisting of actual data of the Gonghe Basin, followed by the discussions in Discussion.

HDR–PV Hybrid Power System Architecture

Flexible HDR System

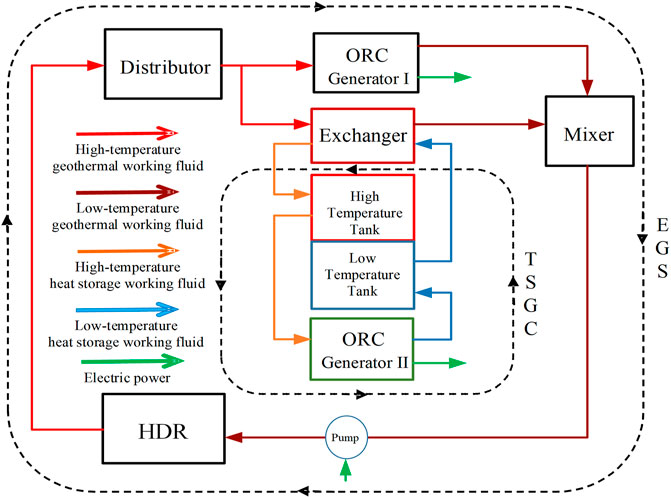
The conventional HDR power system is not flexible enough to provide sufficient reserve for the HPS. Therefore, based on the conventional enhanced geothermal system (EGS), we design an HDR power system with flexible operation capabilities, a flexible HDR system. The composition of the flexible HDR system is shown in Figure 1.

FIGURE 1

FIGURE 1. Composition diagram of flexible HDR system.

The system consists of EGS and TSGC. In the system, EGS is composed of an HDR geothermal mining cycle (GMC) and organic Rankine cycle (ORC) power generation system. Geothermal working fluid distributor, ORC generator I, geothermal working fluid mixer, and reinjection pump are included, realizing geothermal energy for extraction, distribution, conversion, and reinjection. Brine often acts as a geothermal working fluid, forming the outer circle in Figure 1.

The TSGC consists of a heat exchange/storage system and an ORC power generation system, as shown in the inner circle of Figure 1. A heat storage/exchanger, a thermal storage tank, and an ORC generator II are included in the TSGC. The heat transfer oil (HTO) is always used as the heat storage medium to realize the time-sharing storage and utilization of continuous geothermal energy.

The performance of the ORC generator both in EGS and TSGC directly affects the operating characteristics of a flexible HDR plant. According to our previous work (Zhang et al., 2020), the subcritical ORC structure with dry steam can better adapt to the geothermal utilization scenario in the temperature zone of 180–200°C. Therefore, the results in (Zhang et al., 2020) are used in this paper, and butane is used as the organic working fluid for both ORC generator I and ORC generator II.

Structure of HDR-PV HPS

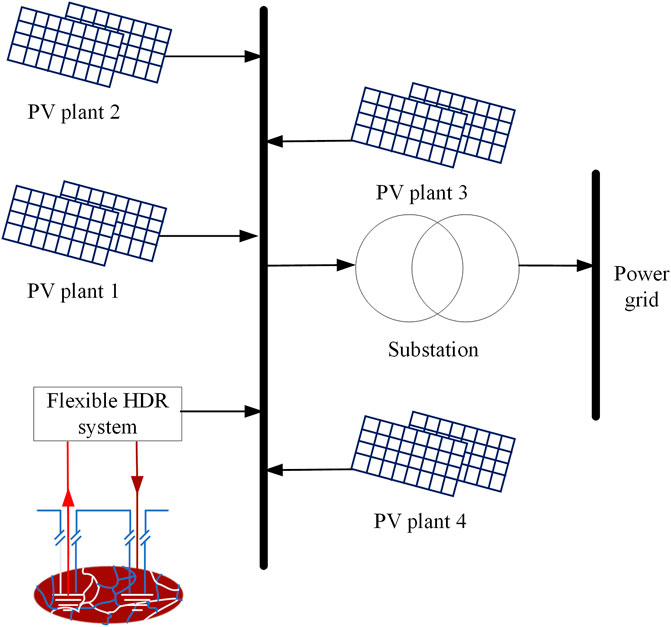
The HDR-PV HPS is formed with multiple PV plants and an HDR power system that serves as a storage to balance the energy exchange and eliminate the volatilities. The basic structure of HDR-PV HPS is shown in Figure 2.

FIGURE 2

FIGURE 2. Structure of HDR-PV HPS.

In actual cases, due to the limitation of HDR resources and GMC capacity, the ability of the HDR power system to provide reserve is restricted. Also, the weather forecast accuracy cannot be guaranteed due to the uncertainties induced by different weather factors (Nespoli et al., 2019). Therefore, the credible capacity of HDR-PV HPS will also be affected by weather factors, and there is uncertainty in the assessment process of the credible capacity.

The HDR-PV HPS designed in this work uses an HDR power system as the ESS to provide energy reserves to the PV generation, increasing the overall credible capacity and improving system reliability while meeting economic efficiency. The key to realizing this target is establishing an operating model that considers the day-ahead forecast of PV generation and the HDR power system. Then, we can evaluate the maximum credible capacity of the system with EFC constraints. The assessment results lay the foundation for subsequently coordinated scheduling. Thus, the following work will focus on the operation and the credible capacity assessment of the HDR-PV HPS.

Mathematical Models of the HDR-PV HPS

Models of Flexible HDR System

As shown in Figure 1, the flexible HDR system consists of EGS and TSGC. EGS can be modeled through the GMC and the ORC power generation (Yao et al., 2018). The geothermal working fluid distributor realizes the flexible brine distribution between the ORC generator I and the heat exchanger. The ESG model can be expressed as follows:

$m_{\alpha }^t+m_{\beta }^t=m_r^t,(1)$

where $m_r^t$ represents the mass flow rate of brine in the GMC; $m_{\alpha }^t$ and $m_{\beta }^t$ represent the brine mass flow rate for ORC generator I power generation and for heat exchange in the heat storage/exchanger, respectively.

The output $P_I^t$of ORC generator I can be modeled as

$P_I^t={\eta }_P{m}_{\alpha }^t{c}_{pr}(T_r-T_{\alpha }),(2)$

where ${\eta }_P$ represents the power generation efficiency of the ORC generator; $c_{pr}$ represents the specific heat capacity of the brine; $T_r$ represents the initial temperature of the brine in the production well; $T_{\alpha }$ represents the residual heat temperature of the brine after passing through the power generation system. $T_r$ and $T_{\alpha }$ can be considered as a fixed value during regular operation (Kaplanis and Kaplani, 2007).

The geothermal working fluid mixer model is as follows:

$m_{\alpha }^t{T}_{\alpha }+m_{\beta }^t{T}_{\beta }=m_t^t{T}_W^t,(3)$

where $T_{\beta }$ represents the residual heat temperature of the brine after exchanging heat through the heat storage/exchange system; $T_W^t$ represents the reinjection temperature of the heat extraction cycle. Due to the long response time of the HDR GMC, $m_r^t$ and $T_r$ can be regarded as constants.

In TSGC, the heat storage/exchange system transfers the heat from the brine to the HTO through the heat storage/exchanger and stores the energy in the high-temperature tank. When power generation is needed, the system inputs high-temperature HTO into the ORC generator II to generate electricity, and the cooled-down HTO after power generation flows back to the low-temperature tank.

The heat storage/exchanger model in the system can be expressed as

$Q_{\beta }^t=m_{\beta }^t{c}_{pr}\left(T_r-T_{\beta }\right),(\mathrm{4a})$

$Q_c^t=m_c^t{c}_{po}\left(T_c-T_l\right),(\mathrm{4b})$

$Q_c^t={\eta }_{ex}{Q}_{\beta }^t,(\mathrm{4c})$

where $Q_{\beta }^t$ is the thermal power input from the geothermal working fluid distributor; $Q_c^t$ is the heat charge power from the heat exchanger; ${\eta }_{ex}$ is the efficiency of the heat exchanger; $m_c^t$ is the mass flow of the HTO during heat storage; $T_c$ is the temperature of the HTO after heat exchange; $T_l$ is the initial temperature of the HTO; $c_{po}$ is the specific heat capacity of the HTO.

TSGC uses ORC generator II to output electricity, and its model is

$P_{II}^t={\eta }_P{Q}_{dc}^t,(5)$

where $P_{II}^t$ is the electric power output of the ORC generator II; $Q_{dc}^t$ is the thermal power consumed by the ORC generator II when generating electricity, that is, the heat discharge power of the high-temperature tank.

The process of heat storage and heat power output of high-temperature tanks can be expressed as follows:

$S_h^{t\mathrm{+}1}={\eta }_h{S}_h^t\mathrm{+(}{Q}_c^t\mathrm{-}{Q}_{dc}^t\mathrm{/}{\eta }_{dc}\mathrm{)}\Delta \tau ,(\mathrm{6a})$

$Q_{dc}^t=m_{dc}^t{c}_{po}\left(T_c-T_l\right),(\mathrm{6b})$

where $S_h^t$ is the heat charged at the time $t$; ${\eta }_h$ is the insulation coefficient; ${\eta }_{dc}$ is the heat discharge efficiency; $m_{dc}^t$ is the mass flow of the HTO when the high-temperature tank generates heat; and $\Delta \tau$ is the time interval of heat storage/heat release process.

In the heat charging and discharging process, the HTO is continuously exchanged between the high-temperature and the low-temperature tanks. Its quality state models are

$M_h^{t+1}=M_h^t+m_c^t\Delta \tau -m_{dc}^t\Delta \tau ,(\mathrm{7a})$

$M_l^{t+1}=M_l^t-m_c^t\Delta \tau +m_{dc}^t\Delta \tau ,(\mathrm{7b})$

where $M_h^t$ and $M_l^t$ denote the mass of HTO in the high-temperature tank and the low-temperature tank, respectively.

Considering that energy storage in TSGC can smooth power fluctuation, the HDR power system can set the operation interval in advance according to the power output prediction of the PV plant and provide reserves. The models for the reserve are

$R^t=R_I^t\mathrm{+}{R}_{II}^t,(\mathrm{8a})$

$R_I^t=u_I^{+}(P_I^{\max }-P_I^t)+u_I^{-}(P_I^t-P_I^{\min }),(\mathrm{8b})$

$R_{II}^t=u_{II}^{+}(P_{II}^{\max }-P_{II}^t)+u_{II}^{-}(P_{II}^t-P_{II}^{\min }),(\mathrm{8c})$

$u_I^{+}+u_I^{-}\le 1,u_{II}^{+}+u_{II}^{-}\le 1,(\mathrm{8d})$

where $R^t$represents the total reserve; $R_I^t$ and $R_{II}^t$ represent the reserve provided by ORC generators I and II respectively; $P_{I/II}^{\max }$ and $P_{I/II}^{\text{min}}$ are the power output’s upper and lower bounds of ORC generators respectively; $u_{I/II}^{+/-}$ is a binary variable to ensure that the positive and negative reserves are not called at the same time.

Models of PV Plant

According to (Duan et al., 2018), the power output of a PV plant considering solar irradiance can be modeled as

$P_{PV}^t={\lambda }^t{P}_{PV},(\mathrm{9a})$

${\widehat{\xi }}_{PV}^t={\lambda }_{\xi }^t{P}_{PV},(\mathrm{9b})$

where ${\lambda }^t$ is the PV power output coefficient according to the predicted value of solar irradiance; ${\lambda }_{\xi }^t$ is the actual PV power output coefficient; $P_{PV}$ is the credible capacity of the PV plant in the HPS; $P_{PV}^t$ is the predicted value of the power output of the PV plant related to the trusted capacity $P_{PV}$ of the PV plant and the predicted value of solar irradiance ${\lambda }^t$; ${\widehat{\xi }}_{PV}^t$ is the actual power output corresponding to the credible capacity of the PV plant.

Credible Capacity Assessment Method Based on Distributionally Robust

The Formulation of the Assessment Method

The purpose of the credible capacity assessment of HDR-PV HPS is to determine the maximum credible capacity that meets the power grid’s requirements for power volatilities. Sufficient credible capacity can enable the HPS to provide reserves by dispatching the HDR power system to deal with the uncertainty of the PV plant, thereby indirectly ensuring the reliable operation of the power grid. It can be seen that the credible capacity assessment of the HPS can be modeled as an optimization problem, including dispatchable power sources. This problem aims to maximize the system’s generation profit and give full play to the regulating role of the HDR power system. The assessment model can be formed as:

$\begin{array}{l}\text{max}f\left(x\right)={\displaystyle \sum _{t=1}^T{V}_{HDR}^t+V_{PV}^t}\\ s.t.\{\begin{array}{l}{g}_r^t(x,R^t)\le 0\\ \forall R^t:\\ g_g^t(x,R^t,{\widehat{\xi }}_{PV}^t)\le 0\\ \forall {\widehat{\xi }}_{PV}^t:\\ P\left({\widehat{\xi }}_{PV}^t\right)\in M\left(\Xi \right)\\ t\in T\end{array}\end{array},(10)$

where $x$ represents the decision variable, including the credible capacity $P_{PV}$ of the PV plant, the brine mass flow $m_{\alpha }^t$ of the ORC generator I, the HTO mass flow $m_c^t$ of the heat storage/exchanger, and the HTO mass flow $m_{dc}^t$ of ORC generator II; $V_{HDR}^t$ represents the profit of the flexible HDR system; $V_{PV}^t$ represents the profit of the PV plant; $g_r^t(x,R_t)\le 0$ represents the operating constraint of the HDR power system; $g_g^t(x,R^t,{\widehat{\xi }}_{PV}^t)\le 0$ represents the EFC constraint satisfying requirements of power fluctuation; $P\left({\widehat{\xi }}_{PV}^t\right)$ represents the probability distribution of the PV power uncertainty, and $M\left(\Xi \right)$ represents the ambiguous set of the probability of the photovoltaic power output.

$V_{HDR}^t=c_e^t(P_I^t+P_{II}^t)-c_Q{Q}_{cur}^t,(11)$

where $c_e^t$ represents the time-of-use electricity price, $c_Q$ represents the penalty coefficient for abandonment of heat, and $Q_{cur}^t$ represents the abandonment power that cannot be stored after heat exchange when taking the minimum reinjection temperature as a reference.

The profit of the PV plant can be modeled as

$V_{PV}^t=c_e^t(P_{PV}^t-P_{PVcur}^t)-p{c}_e^t{P}_{PVal}^t,(12)$

where $P_{PVcur}^t$ and $P_{PVal}^t$ represent the PV and load curtailment of the PV plant’s credible capacity; $p$ is the penalty coefficient of load curtailment. For $P_{PVcur}^t$ and $P_{PVal}^t$, they can be expressed as

$P_{PVcur}^t=\max \text{{}{\widehat{\xi }}_{PV}^{k,t}-P_{PV}^t,\mathrm{0\}},(13)$

$P_{PVal}^t=\max \{P_{PV}^t-{\widehat{\xi }}_{PV}^t,0\},(14)$

Distributionally Robust EFC Constrains

The HDR-PV HPS provides a reserve for the PV plant through the HDR power system. The whole HPS is equivalent to a dispatchable power source to meet the requirements of power fluctuation. Taking the predicted power output of the PV plant as the dispatchable power curve, we have the EFC constraint as follows:

$(1-\sigma )P_{PV}^t\le {\widehat{\xi }}_{PV}^t+R^t\le (1+\sigma )P_{PV}^t,(15)$

where represents the power fluctuation rate allowed by the grid. Eq. 15 restricts the range of the sum of the PV plant’s actual power output and the reserve provided by the HDR power system at any time. In such a case, the PV plant is equivalent to a dispatchable power source, thereby obtaining the credible capacity as

$P_{sys}=P_I+P_{II}+P_{PV},(16)$

where $P_{sys}$ represents the credible capacity of the HPS; $P_I$ and $P_{II}$ represent the capacity of ORC power generation system I and II, respectively.

Due to the PV plant’s power uncertainty, we adopt the distributionally robust method to model these uncertainties (Duan et al., 2018). The distributionally robust method uses the data-driven method to construct the uncertain probability distribution based on stochastic optimization. The method can ensure the robustness of the system under the worst probability distribution strategy within the confidence interval. It can be seen that the conservatism of the worst operation scenario described by the distributionally robust method is between robust optimization and stochastic optimization, which makes the system capacity assessment not only achieve the robustness within the full confidence interval but also reduce the system redundancy capacity to deal with extreme scenarios. The ambiguous set using Wasserstein divergence is used to measure the uncertainty measure and is given as follows:

$M^{\epsilon }=\{P\in M\left(\Xi \right):d_W(P,\widehat{P})\le \epsilon \},(17)$

where $P$represents the probability distribution of the actual power output of the PV plant; $\widehat{P}$ represents the empirical distribution of the power output; $M\left(\Xi \right)$represents the space consisting of all probability distributions with the Wasserstein divergence; $\epsilon$is the radius of the ambiguous set, which can be referred to as (Esfahani and Kuhn, 2018); and $d_w$represents Wasserstein divergence (Hota et al., 2019).

Then, we reformulate Eq. 15 and consider the probability distribution of the power output in the worst case. The distribution should satisfy:

$\underset{P\in M^{\epsilon }}{\text{inf}}P\text{{}|{\widehat{\xi }}_{PV}^t+{\mathit{R}}^{\mathit{t}}-{\mathit{P}}_{\mathit{P}V}^t|\le \sigma P_{PV}^t\text{}}\ge 1-\alpha ,(18)$

where $\alpha$ represents the confidence level, that is, the minimum probability that the derivation between ${\widehat{\xi }}_{PV}^t+R^t$ (satisfying $M\left(\Xi \right)$) and $P_{PV}^t$ does not exceed $\sigma$ is greater than $1-\alpha$.

Reformulate Eq. 18, and we have:

$\underset{P\in M^{\epsilon }}{\text{sup}}\text{Pr}\text{{}|{\widehat{\xi }}_{PV}^t+R^t-P_{PV}^t|-\sigma P_{PV}^t\ge 0\text{}}\le \alpha .(19)$

According to (Rockafellar and Uryasev, 2000). Eq. 19 can be equivalent to the following risk condition constraint

$\underset{P\in M_i^{\epsilon }}{\text{sup}}CVa{R}_{1-\alpha }^P\left(L({\widehat{\xi }}_{PV}^t,R^t)\right)\le 0,(\mathrm{20a})$

$L({\widehat{\xi }}_{PV}^t,R^t)=\text{|}{\widehat{\xi }}_{PV}^t+R^t-P_{PV}^t\text{|}-\sigma P_{PV}^t,(\mathrm{20b})$

In this work, we use the method proposed in (Fiaschi et al., 2017) to transform Eq. 19 into a set of linear constraints, which is listed as follows:

$\epsilon H_L+\frac{1}{K}{\displaystyle \sum _{k=1}^K{s}^{k,t}}-{\gamma }^t\alpha \le 0,(\mathrm{21a})$

$s^{k,t}\ge {\xi }_{PV}^{k,t}+R^{k,t}-(1+\sigma )P_{PV}^t+{\gamma }^t,(\mathrm{21b})$

$s^{k,t}\ge -{\xi }_{PV}^{k,t}-R^{k.t}+(1-\sigma )P_{PV}^t+{\gamma }^t,(\mathrm{21c})$

$s^{k,s}\ge 0,\forall k\in K,t\in T,(\mathrm{21d})$

where ${\xi }_{PV}^{k,t}$ represents the kth sample of PV power output ${\widehat{\xi }}_{PV}^t$, i.e., ${\xi }_{PV}^{k,t}={\lambda }_{\xi }^{k,t}{P}_{PV}$; K represents the number of samples, and $T$ represents the whole scheduling period. Eq. 21 requires $L({\widehat{\xi }}_{PV}^t,R^t)$ to satisfy Lipschitz continuity while $H_L$ represents the measure of Lipschitz continuity.

According to the actual operating conditions of the PV station, when the power output equals 0, the dispatched reserves should be equal to the dispatch value. Thus, there is $R^t=P_{PV}^t$ when ${\widehat{\xi }}_{PV}^t=0$. Then we have:

$L(\text{0},R^t)=-\sigma P_{PV}^t,(22)$

$L({\widehat{\xi }}_{PV}^t,R^t)-L(\text{0},R^t)=\text{|}{\widehat{\xi }}_{PV}^t+R^t-P_{PV}^t\text{|},(23)$

Since the actual power output of the PV plant is not less than the lower bound of the predicted value, ${\widehat{\xi }}_{PV}^t\ge (1-\varphi )P_{PV}^t$ satisfies $\varphi$ represents the prediction error. Combining Eqs 18d–d21d, we can obtain

$\text{||}L({\widehat{\xi }}_{PV}^t,R^t)-L(\text{0},R^t)\text{||}\le \frac{\sigma }{1-\varphi }{\widehat{\xi }}_{PV}^t.(24)$

Eq. 24 is used to prove that $L({\widehat{\xi }}_{PV}^t,R^t)$ satisfies Lipschitz continuity. To prove that, we can take $H_L=\sigma /(1-\varphi )$. On this basis, Eqs 21a–d gives the EFC constraint for the PV plant with dispatchable reserves.

Operation Constraints

Considering the current technical conditions of HDR resources, the stable operation of the flexible HDR system should also meet the following upper and lower bounds:

$P_r^{\min }\le P_{I/II}^t\le P_r^{\max },(\mathrm{25a})$

$0\le m_c^t\le m_c^{\max },(\mathrm{25b})$

$0\le m_{\mathit{dc}}^t\le m_{dc}^{\max },(\mathrm{25c})$

$S_h^{\min }\le S_h^t\le S_h^{\max },(\mathrm{25d})$

where Eq. 25a is the capacity constraints of ORC generators I and II restricted by the GMC. Eqs 25b, 25c are the constraints on the mass flow of HTO in the process of heat exchange. Eq. 25d is the constraint of heat storage. To satisfy the minimum power operation requirements of ORC generator II, the heat storage capacity of the high-temperature tank should be greater than $S_h^{\min }$.

The operation of HDR power system should also meet the following reliability and system safe operation constraints

$m_{\alpha }^{\min }\le m_{\alpha }^t\le m_r^t,(\mathrm{26a})$

$T_W^{\min }\le T_W^t,(\mathrm{26b})$

$M_l^t+M_h^t=M_{\mathrm{all}},(\mathrm{26c})$

$-\left(1-u^t\right)\mathrm{M}\le R_I^t\le u^t\mathrm{M},(\mathrm{26d})$

$-\left(1-u^t\right)\mathrm{M}\le R_{II}^t\le u^t\mathrm{M},(26e)$

where Eq. 26a indicates that the brine used for ORC generator I is not less than the minimum value that guarantees the reliability of plant power. Eq. 26b restricts the reinjection temperature to ensure the stability of the underground thermal reservoir. Eq. 26c is the mass balance constraint of the thermal storage tank to ensure the safe operation of the high/low-temperature thermal storage tanks. Eqs 26d,26e are the constraints to ensure that the reserve dispatch of the two ORC power generation systems will not interfere with each other. $\text{M}$is a sufficiently large positive number.

In addition, the product of variables $m_{\beta }^t$ and $T_{\beta }$ exists in Eqs 3, 4, making the entire model non-linear. To simplify the model, the curtailed heat power $Q_{cur}^t$ is used to represent this product term. At this time, the nonlinear model is transformed into a linear form. Eqs 3, 4a can be rewritten as

$m_{\alpha }^t{T}_{\alpha }+{\mathit{Q}}_{cur}^t\text{/}{c}_{pr}=m_r^t{T}_W,(27)$

${\mathit{Q}}_{\beta }^t=m_{\beta }^t{c}_{pr}(T_r-T_W^{\min })+{\mathit{Q}}_{cur}^t,(\mathrm{28a})$

$0\le Q_{cur}^t.(\mathrm{28b})$

HDR-PV HPS’s credible capacity assessment problem is transformed into a mixed-integer optimization problem (MILP) through the above reformulation, which can be directly solved with Matlab 2016b and CPLEX12.8.

Case Study

System Parameters

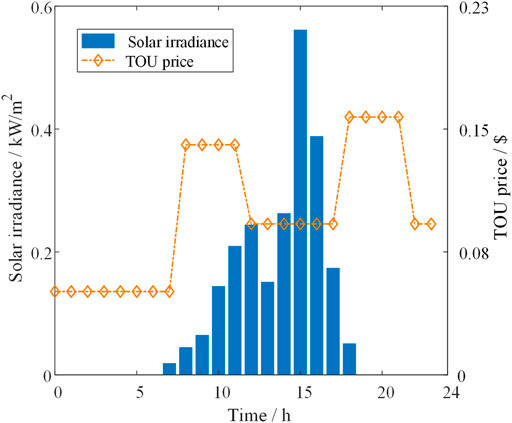
The studied case is constructed based on the actual data of HDR and PV resources in the Gonghe Basin of Qinghai Province. The time-of-use (TOU) electricity price is adopted. Both solar irradiance data and time-of-use electricity prices are taken from local historical data, as shown in Figure 3.

FIGURE 3

FIGURE 3. Curve of solar irradiance and time-of-use power price.

In this case, the capacity of the PV plant is selected according to the local typical power station of 300 MWp. The operating parameters of the flexible HDR system are selected based on the local resources (Si et al., 2020). The capacity of the generator is selected based on the GMC parameters and the current status of geothermal development technology. The detailed parameters of the system are shown in Table 1.

TABLE 1

TABLE 1. The rated parameters of the HDR-PV hybrid power system.

Simulation Results

We set up the following three cases to compare and analyze the capacity assessment results.

Case 1: Only the EGS with the HDR power system provides reserves for the PV plant; the TSGC is not used; Case 2: Based on the settings of scenario 1, the TSGC of the HDR power system is further configured to recover waste heat energy for power generation, but the TSGC provides no reserve; Case 3: Based on the settings of scenario 2, both EGS and TSGC provide reserves.

First, we set the allowable power fluctuation as 0% for the following analysis. The parameters of solar irradiance and TOU electricity price are the same in all scenarios.

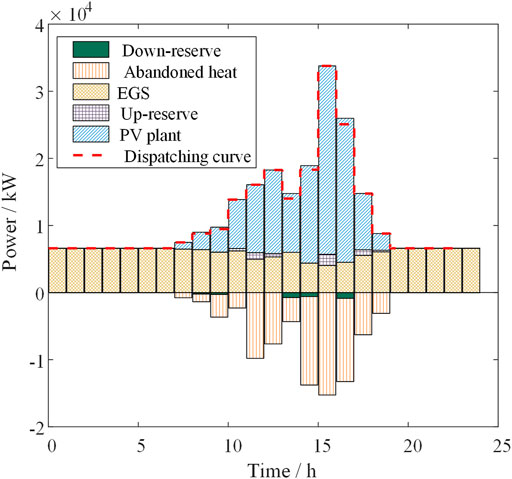
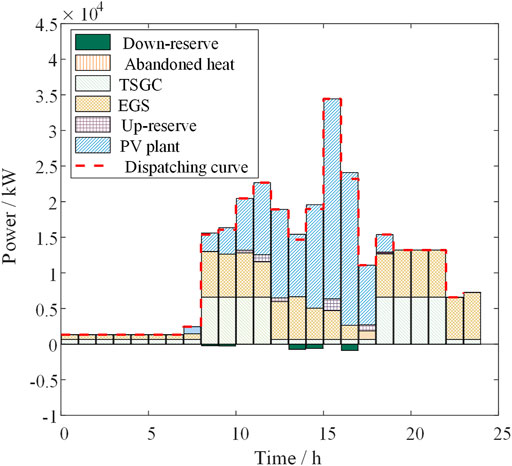
The results in Table 2 show that, with a 0% allowable power fluctuation, only using EGS to provide the reserve for the PV plant will generate a large amount of waste heat. The comparisons show that the HPS equipped with EGS realizes the dispatch ability of the PV plant by curtailing heat. To better illustrate the results, we give the power output of each part in Case 1 in Figure 4.

TABLE 2

TABLE 2. Assessment results of each case.

FIGURE 4

FIGURE 4. System operation in case 1.

Due to the high investment cost of EGS (Zhang L. et al., 2014), the operation mode in case 1 is challenging to meet the financial requirements in practice. TSGC can store the curtailed heat well and then convert it back into electricity, improving the overall economic benefits and maintaining the credible capacity of the PV plant.

Figure 5 shows the power output of each part in case 2. The results show that TSGC plays a vital role in waste heat recovery. When the time-of-use electricity price is applied, the TSGC can store geothermal energy during the low electricity price from 00:00 to 7:00 and generate electricity during the high electricity price, thereby achieving peak shaving. This has increased the profit of the flexible HDR system by 36.78%.

FIGURE 5

FIGURE 5. System operation in case 2.

In case 3, when TSGC also participates in providing reserves, the credible capacity of the HPS is nearly doubled. Although the overall profit of the flexible HDR system decreased by 2.97%, the overall profit of the HPS increased due to the increased credible capacity. At the same time, it is also noticed that the thermal energy stored by TSGC was not fully utilized. After 24 h of operation, the remaining thermal energy in the thermal storage tank is 45.64 MWh, increasing 192.75% compared to case 2. In this case, geothermal energy is not fully utilized, so it is necessary to analyze the key parameters further. The operation curve of the HDR power system in the HPS is shown in Figure 6.

FIGURE 6

FIGURE 6. Operation curves of HDR power system in case 3.

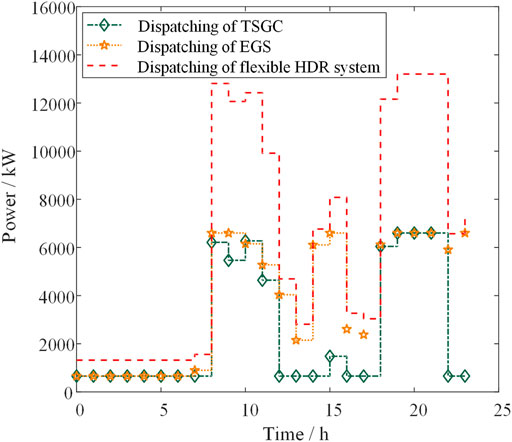
Figure 6 that, first of all, the flexible HDR system adopts the minimum power generation strategy during the low electricity price period (0:00–7:00) and in the high electricity price period (8:00–12:00, 18:00–22:00) adopt maximum power generation strategy to maximize profit. Secondly, during the PV plant power generation period (8:00–19:00), the output power of the HDR power system will be adjusted with the fluctuation of the actual PV power output according to EFC constraints. Especially during the period from 10:00 to 18:00, thanks to dispatchable reserves provided by the HDR power system, the PV plant’s power output can meet the grid’s dispatching requirements, thereby improving the reliability of HPS. Figure 7 exhibits the reserve dispatch under a specific actual operation condition. It can be seen from the results that EGS mainly provides negative reserve, while TSGC mainly provides positive reserve. This is to minimize heat exchange and storage losses and maximize profit. Finally, the thermal energy stored in the high-temperature thermal storage tank will be converted into electrical energy by the ORC generator II during the high electricity price period from 20:00 to 22:00.

FIGURE 7

FIGURE 7. Dispatching of reserve in case 3.

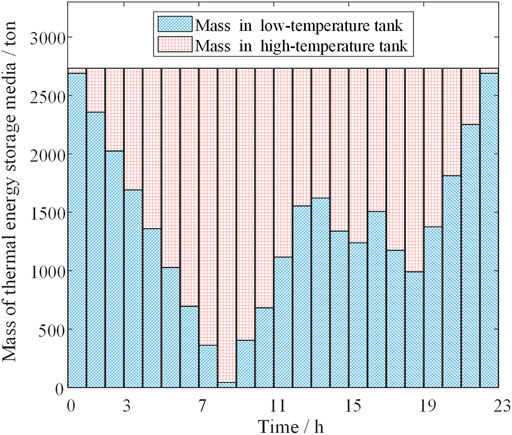
In the thermal storage tank, the mass of the HTO also changes with the power output fluctuation. Figure 8 shows the mass change of the HTO between the high-temperature and the low-temperature tank in case 3. In the figure, the mass of the HTO in the high-temperature tank increases from 0: 00 to 7: 00, indicating that the geothermal energy is heated by the heat storage/exchanger and stored in the high-temperature tank. During the high electricity price period from 8:00 to 12:00, TSGC converts heat into electricity, and the mass of HTO in the high-temperature tank decreases. During the power generation period of the PV plant from 10:00 to 18:00, the HDR power system dispatches reserves to ensure that the system’s output can meet the requirements of grid operation. In the same period, the mass of the HTO in the heat storage system fluctuates accordingly. After the PV plant power generation cycle ends, the heat stored in the storage will be converted into electricity during the high electricity price period from 20:00 to 22:00 to increase economic benefits.

FIGURE 8

FIGURE 8. Mass change of heat transfer oil in case 3.

Impact of Allowable Fluctuation rate on the Credible Capacity of the HPS.

With the parameter setting of case 3, we further study the influence of the allowable fluctuation rate of grid power on the credible capacity of the HPS. Take the allowable fluctuation rate as 3, 5, 7, and 10% for simulation, respectively. The comparison results are shown in Table 3.

TABLE 3

TABLE 3. Impact of allowable fluctuation rate on the credible capacity of HPS.

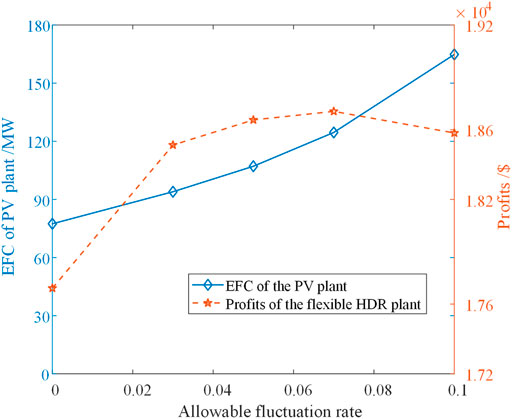
The results in Table 3 indicate that, as the grid’s ability to withstand power fluctuation increases, the credible capacity of the HPS increases accordingly. Compared with the case with a 0% allowable fluctuation rate, the credible capacity of the PV plant is increased by 113% when the allowable fluctuation rate is equal to 10%. To increase the credible capacity of the HPS, the profit of the flexible HDR system increased by 5.03%. This is because the geothermal energy stored in the thermal storage tank is fully utilized, which is reduced from 45.64 MWh to 0 MWh.Since the total geothermal energy obtained by the HDR geothermal extraction cycle remains stable quickly, the mass of the total HTO required from 3 to 10% is not much different. The relationship between the profit of the HDR power system, the PV plant’s credible capacity, and the power fluctuation is shown in Figure 9.

FIGURE 9

FIGURE 9. Relationship of PV’s credible capacity, HDR’s profit, and allowable fluctuation rate.

As we can see, the PV plant’s credible capacity increases monotonically with the increase in power fluctuation rate, and the profit of the flexible HDR system has a local maximum when the fluctuation rate is 7%. However, we obtain the minor remaining thermal energy of the thermal storage tank in Table 3, which shows that the geothermal energy is fully utilized with a 10% allowable fluctuation rate.

Influence of Uncertainty Modeling Method on Capacity Assessment

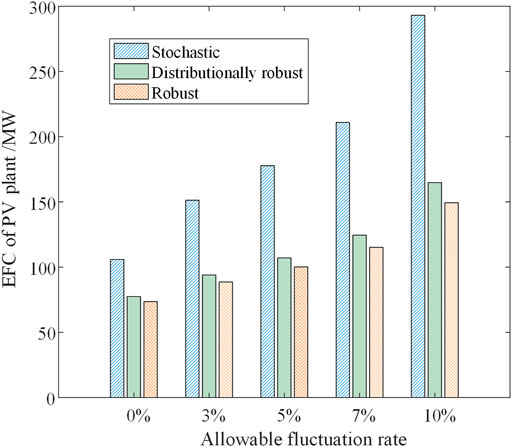
The distributionally robust method based on Wasserstein divergence is an optimization method driven by actual historical data. It can make full use of the implicit information of PV generation data and obtain a moderately conservative EFC assessment. Taking allowable fluctuation rate as 0%, 3 ,5, 7, and 10%, the credible capacity of the hybrid system is assessed by robust optimization, stochastic optimization to compare with the distributionally robust method, respectively. The EFC assessments of the PV plant are shown in Figure 10.

FIGURE 10

FIGURE 10. Credible capacity assessment of PV plant based on different optimization methods.

It can be seen from Figure 10 that the credible capacity of PV plant obtained by stochastic optimization is the largest, followed by distributionally robust method, and the result obtained by robust optimization is the smallest. This further shows that the results obtained by stochastic optimization are too optimistic; The results obtained by the robust optimization are too conservative. In order to deal with the worst scenarios, its credible capacity is only 69.48–50.96% of the former compared with the stochastic optimization, and its conservatism becomes more and more evident with the increase of allowable fluctuation; The EFC assessment using the distributionally robust method proposed in this paper is between the results of stochastic optimization and robust optimization, which can ensure the robustness of the system in the sense of confidence.

Discussion

To solve the problem of grid connection of large-scale PV plants in extreme-cold and high-altitude areas, we design a flexible HDR system consisting of an enhanced geothermal system and a thermal storage generation cycle. Then, a model of HDR-PV HPS is constructed with the HDR power system and PV plant. On this basis, a credible capacity assessment method of the proposed HPS with EFC constraint is proposed. This method can be transformed into a scheduling optimization problem of HPS to maximize profit. The EFC constraints are reformulated as a set of value-at-risk constraints by applying the distributionally robust method.

At last, the credible capacity assessment method is represented as a MILP with risk constraints for the solution. To verify the effectiveness of our work, we take the actual system in the Gonghe Basin of Qinghai Province as an example. The results show that the credible capacity assessment method can effectively assess the maximum credible capacity of the proposed HDR-PV HPS. Also, the HDR power system can enhance the reliability of connection between PV station and grid while increasing the overall profit of the HPS.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

YS: conceptualization, writing-original draft preparation, software. LC: funding acquisition, validation. LM: funding acquisition, conceptualization, methodology, and editing. HM: validation. XC: project administration. SM: supervision. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded in part by the Joint Fund Project of National Natural Science Foundation of China (U1766203), in part by Key R and D and Transformation Plan of Qinghai Province (2021-GX-109), and in part by the Basic Research Project of Qinghai Province (2021-ZJ-948).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to thank Prof. Feng Liu and Wei for very helpful discussions on the cooperative game, Dr. Xiaodai Xue and Xuelin Zhang for discussions on the HDR geothermal generator model, Dr. Zhongjie Guo and Jiayu Bai for suggestions on practical issues.

Abbreviations

EFC, Equivalent firm capacity; EGS, Enhanced geothermal system; ELCC, Effective load-carrying capability; ESS, Energy storage system; GMC, Geothermal mining cycle; HDR, Hot dry rock; HPS, Hybrid power system; HTO, Heat transfer oil; LOP, Loss of probability; MILP, Mixed-integer optimization problem; ORC, Organic Rankine cycle; PV, Photovoltaic; TOU, Time of use; TSGC, Thermal storage generation cycle.

References

Brown, D. W. (2009). “February). Hot Dry Rock Geothermal Energy: Essential Lessons from Fenton Hill,” in Thirty-Fourth Workshop on Geothermal Reservoir Engineering (Stanford: Stanford University), 9–11. Available at: https://pangea.stanford.edu/ERE/pdf/IGAstandard/SGW/2009/brown.pdf.

Google Scholar

Dent, C. J., Hernandez-Ortiz, A., Blake, S. R., Miller, D., and Roberts, D. (2015). Defining and Evaluating the Capacity Value of Distributed Generation. IEEE Trans. Power Syst. 30 (5), 2329–2337. doi:10.1109/TPWRS.2014.2363142

CrossRef Full Text | Google Scholar

Duan, C., Fang, W., Jiang, L., Yao, L., and Liu, J. (2018). Distributionally Robust Chance-Constrained Approximate AC-OPF with Wasserstein Metric. IEEE Trans. Power Syst. 33 (5), 4924–4936. doi:10.1109/TPWRS.2018.2807623

CrossRef Full Text | Google Scholar

Esmaili, A., and Nasiri, A. (2009). “A Case Study on Improving ELCC by Utilization of Energy Storage with Solar PV,” in 2009 35th Annual Conference of IEEE Industrial Electronics (IEEE), 3957–3962. doi:10.1109/IECON.2009.5415336

CrossRef Full Text | Google Scholar

Fallah, M., Mahmoudi, S. M. S., Yari, M., and Akbarpour Ghiasi, R. (2016). Advanced Exergy Analysis of the Kalina Cycle Applied for Low Temperature Enhanced Geothermal System. Energ. Convers. Manag. 108, 190–201. doi:10.1016/j.enconman.2015.11.017

CrossRef Full Text | Google Scholar

Fiaschi, D., Manfrida, G., Rogai, E., and Talluri, L. (2017). Exergoeconomic Analysis and Comparison between ORC and Kalina Cycles to Exploit Low and Medium-High Temperature Heat from Two Different Geothermal Sites. Energ. Convers. Management 154, 503–516. doi:10.1016/j.enconman.2017.11.034

CrossRef Full Text | Google Scholar

Guo, Z., Wei, W., Chen, L., Xie, R., and Mei, S. (2020). Sizing Energy Storage to Reduce Renewable Power Curtailment Considering Network Power Flows: a Distributionally Robust Optimisation Approach. IET Renew. Power Generation 14 (16), 3273–3280. doi:10.1049/iet-rpg.2020.0354

CrossRef Full Text | Google Scholar

He, J., Deng, C., Xu, Q., Liu, C., and Pan, H. (2013). Optimal Configuration of Distributed Generation System Containing Wind PV Battery Power Sources Based on Equivalent Credible Capacity Theory. Power Syst. Technology 37 (12), 3317–3324.

Google Scholar

Hota, A. R., Cherukuri, A., and Lygeros, J. (2019). “Data-Driven Chance Constrained Optimization under Wasserstein Ambiguity Sets,” in In 2019 American Control Conference (ACC) (IEEE), 1501–1506. doi:10.23919/ACC.2019.8814677

CrossRef Full Text | Google Scholar

Injeti, S. K., and Prema Kumar, N. (2013). A Novel Approach to Identify Optimal Access point and Capacity of Multiple DGs in a Small, Medium and Large Scale Radial Distribution Systems. Int. J. Electr. Power Energ. Syst. 45 (1), 142–151. doi:10.1016/j.ijepes.2012.08.043

CrossRef Full Text | Google Scholar

Islam, M. R., Guo, Y., and Zhu, J. (2014). A Multilevel Medium-Voltage Inverter for Step-Up-Transformer-Less Grid Connection of Photovoltaic Power Plants. IEEE J. Photovoltaics 4 (3), 881–889. doi:10.1109/JPHOTOV.2014.2310295

CrossRef Full Text | Google Scholar

Kaplanis, S., and Kaplani, E. (2007). A Model to Predict Expected Mean and Stochastic Hourly Global Solar Radiation I(h;nj) Values. Renew. Energ. 32 (8), 1414–1425. doi:10.1016/j.renene.2006.06.014

CrossRef Full Text | Google Scholar

Mohajerin Esfahani, P., and Kuhn, D. (2018). Data-driven Distributionally Robust Optimization Using the Wasserstein Metric: Performance Guarantees and Tractable Reformulations. Math. Program 171 (1), 115–166. doi:10.1007/s10107-017-1172-1

CrossRef Full Text | Google Scholar

Nespoli, A., Ogliari, E., Leva, S., Massi Pavan, A., Mellit, A., Lughi, V., et al. (2019). Day-ahead Photovoltaic Forecasting: A Comparison of the Most Effective Techniques. Energies 12 (9), 1621. doi:10.3390/en12091621

CrossRef Full Text | Google Scholar

Peter, J., and Wagner, J. (2021). Optimal Allocation of Variable Renewable Energy Considering Contributions to Security of Supply. Ej 42 (1). doi:10.5547/01956574.42.1.jpet

CrossRef Full Text | Google Scholar

Rockafellar, R. T., and Uryasev, S. (2000). Optimization of Conditional Value-At-Risk. Jor 2, 21–41. doi:10.21314/jor.2000.038

CrossRef Full Text | Google Scholar

Si, Y., Chen, L., Zhang, X., Chen, X., Zheng, T., and Mei, S. (2021). Game Approach to HDR-TS-PV Hybrid Power System Dispatching. Appl. Sci. 11 (3), 914. doi:10.3390/app11030914

CrossRef Full Text | Google Scholar

Si, Y., Chen, L., Zhang, X., and Mei, S. (2020). Capacity Optimization of Micro Energy Network with Hot Dry Rock Enhanced Geothermal System. Power Syst. Technol. 44, 1603–1611.

Google Scholar

Singh, G. K. (2013). Solar Power Generation by PV (Photovoltaic) Technology: A Review. Energy 53, 1–13. doi:10.1016/j.energy.2013.02.057

CrossRef Full Text | Google Scholar

Song, J., Krishnamurthy, V., Kwasinski, A., and Sharma, R. (2012). Development of a Markov-Chain-Based Energy Storage Model for Power Supply Availability Assessment of Photovoltaic Generation Plants. IEEE Trans. Sustainable Energ. 4 (2), 491–500. doi:10.1109/TSTE.2012.2207135

CrossRef Full Text | Google Scholar

Sulaeman, S., Benidris, M., Tian, Y., and Mitra, J. (2016). Modeling and Evaluating the Capacity Credit of PV Solar Systems Using an Analytical Method,” in 2016 IEEE/PES Transmission and Distribution Conference and Exposition (T&D) (IEEE), 1–5. doi:10.1109/TDC.2016.7519949

CrossRef Full Text | Google Scholar

Tapetado, P., and Usaola, J. (2019). Capacity Credits of Wind and Solar Generation: The Spanish Case. Renew. Energ. 143, 164–175. doi:10.1016/j.renene.2019.04.139

CrossRef Full Text | Google Scholar

Wang, Y., Cheng, J., Fan, F., Chen, Z., Xiao, Z., and Deng, K. (2019). “Maximum PV Access Capacity Planning Method for Rural Power Grid Considering Overload Risk,” in In 2019 IEEE 3rd Conference on Energy Internet and Energy System Integration (EI2) (IEEE), 387–391. doi:10.1109/EI247390.2019.9062179

CrossRef Full Text | Google Scholar

Yan, X., Liu, Y., Wang, G., and Lu, Y. (2019). Optimal Injection Rate of Water in the Guide Basin Hot Dry Rock Mining Project. Energy Exploration & Exploitation 37 (2), 721–735. doi:10.1177/0144598718800729

CrossRef Full Text | Google Scholar

Yao, J., Zhang, X., Sun, Z., Huang, Z., Liu, J., Li, Y., et al. (2018). Numerical Simulation of the Heat Extraction in 3D-EGS with thermal-hydraulic-mechanical Coupling Method Based on Discrete Fractures Model. Geothermics 74, 19–34. doi:10.1016/j.geothermics.2017.12.005

CrossRef Full Text | Google Scholar

Yuan, Y., Liu, T. Q., and Cheng, D. W. (2012). Research on Maximum Access Capacity of Grid-Connected Photovoltaic Power. Kezaisheng Nengyuan(Renewable Energ. Resources) 30 (6), 9–14. doi:10.13941/j.cnki.21-1469/tk.2012.06.023

CrossRef Full Text | Google Scholar

Zare, V. (2016). A Comparative Thermodynamic Analysis of Two Tri-generation Systems Utilizing Low-Grade Geothermal Energy. Energ. Convers. Manag. 118, 264–274. doi:10.1016/j.enconman.2016.04.011

CrossRef Full Text | Google Scholar

Zeng, B., Sun, B., Wei, X., Gong, D., Zhao, D., and Singh, C. (2020). Capacity Value Estimation of Plug-In Electric Vehicle Parking-Lots in Urban Power Systems: A Physical-Social Coupling Perspective. Appl. Energ. 265, 114809. doi:10.1016/j.apenergy.2020.114809

CrossRef Full Text | Google Scholar

Zhang, L., Wu, Y., Lou, S., Yang, Y., and Wang, Y. (2014a). “Photovoltaic Generation Capacity Credit Evaluation Method Considering its Daily Output Characteristics,” in 2014 International Conference on Power System Technology (IEEE), 2763–2768. doi:10.1109/POWERCON.2014.6993726

CrossRef Full Text | Google Scholar

Zhang, X., Zhang, T., Xue, X., Si, Y., Zhang, X., and Mei, S. (2020). A Comparative Thermodynamic Analysis of Kalina and Organic Rankine Cycles for Hot Dry Rock: a prospect Study in the Gonghe Basin. Front. Energ. 14 (4), 889–900. doi:10.1007/s11708-020-0704-1

CrossRef Full Text | Google Scholar

Zhang, Y.-J., Li, Z.-W., Guo, L.-L., Gao, P., Jin, X.-P., and Xu, T.-F. (2014b). Electricity Generation from Enhanced Geothermal Systems by Oilfield Produced Water Circulating through Reservoir Stimulated by Staged Fracturing Technology for Horizontal wells: A Case Study in Xujiaweizi Area in Daqing Oilfield, China. Energy 78, 788–805. doi:10.1016/j.energy.2014.10.073

CrossRef Full Text | Google Scholar

Zhang, Z., Chen, Y., Huang, S., and Zhang, X. (2017). IEEE, 1–5. doi:10.1109/PESGM.2017.8274181Credible Capacity Evaluation of a PV Plant with Energy Storages Governed by MDP Control StrategyIn 2017 IEEE Power & Energy Society General Meeting.

CrossRef Full Text | Google Scholar